Abstract
The mountain cryosphere is crucial for socio-economic processes, especially during the dry seasons. However, anthropogenic climate change has had a detrimental impact on the cryosphere due to its sensitivity. Over the past two decades, there has been a decline in precipitation and a temperature rise, leading to a substantial reduction in the timing and extent of snow cover. This increase in temperature also elevates the snow line elevation (SLE), further diminishing the volume of available freshwater in the snow-driven basins of the Andes. In this study, we use 22 years (2000–2021) of 8-day snow product (MOD10A2) from the Moderate Resolution Imaging Spectroradiometer (MODIS) to analyze the annual and seasonal variability of snow cover area, SLE, and snow persistence (SP, an indicator of the duration of snow) in the Yeso River basin in Central Chile and the correlation of SP and SLE with hydrometeorological variables and climatic indices. We introduce a new approach called the Maximum Dissimilarity Method to obtain the SLE even on cloudy days. The results are as follows: (1) Snow cover area reductions of 34.0 km2 at low elevations in spring and 86.5 km2 at mid elevations in summer were found when comparing the period 2016–2021 to 2000–2004; (2) SP trends at the annual scale revealed a significant decrease in 89% of its area and an average of 3.6 fewer days of snow cover per year; (3) an upward and significant trend of 21 m‧year−1 in the annual SLE was found; and (4) annual SP and SLE were highly correlated with annual hydrometeorological variables, and spring and summer snow variables were significantly correlated with dry streamflow. This methodology can potentially serve as a valuable tool for detecting trends in snow-covered surfaces, and thereby associate these changes with climate change or other anthropogenic effects in future research.
Keywords:
snow basin; snow persistence; snow line detection; climatic trend; climate change; MODIS; Andes 1. Introduction
Snow and glaciers are fundamental to life on Earth and human sustenance. As freshwater reservoirs, they support the planetary ecosystems and influence our daily lives, even for human settlements that live far away from snow-covered areas, allowing the development of socio-economic activities, such as hydroelectric power, tourism, water consumption, and agriculture [1,2,3]. Snowpack is the primary water resource in snow-driven basins through stream discharge [4,5]. However, the snowpack is highly sensitive to climate changes and is mainly controlled by two essential and covarying influences on snow: temperature and precipitation [6,7]. In general, increasing temperature produces a rise in the SLE, which causes a decrease in the fraction of solid precipitation and snow cover [8,9]. Likewise, as pointed out in the last IPCC report, rising temperatures of 1.1 °C have been identified since 1960 due to the increases in greenhouse gases in the atmosphere [10]. Positive temperature trends in alpine regions throughout the world have been reported by different authors [7,11,12], which enhance snowmelt and the elevation of the snow line and, consequently, impact the hydrological cycle during the dry season and affect water availability [13,14,15].
Significant efforts have been made to analyze trends in snow cover, particularly in mountain regions, to understand the impacts of climate change [2,5,16,17], and their impacts on the spatiotemporal variations of snow cover in watersheds worldwide [18,19]. Remote sensing has become a valuable tool for analyzing snow variables because direct measurements at high elevations are limited by challenging weather conditions and the vast coverage areas [20,21]. Using snow products derived from MODIS, global studies have detected decreasing trends of SP over an area of 2.7 Mkm2 (which stands for “million square kilometers”) worldwide from 2000 to 2016, mainly in Asia, Europe, North America, and South America, with reductions of up to 16 fewer days of snow [22,23]. Asia, especially in the Tibetan Plateau, accounts for half of these negative trends. In the Tianshan Mountains (1.4 Mkm2), a region of the Tibetan Plateau, a decreasing trend of SP in 41% of the area above 3000 masl was reported between 2000 and 2015 [19]. Similarly, negative SP trends have been observed in western North America (covering 2.3 Mkm2), with 7% of its area exhibiting a significant positive trend of early snowmelt at mid-elevation (1000–2500 masl), leading to a reduction of 7 snow days [24].
Another approach to analyzing the snow cover trends is through SLE, which has been examined in the literature using various methods [25,26,27]. Notably, a positive trend in SLE was observed in some regions. For instance, Nepal (0.15 Mkm2) exhibited a positive trend of 33, 33, and 67 m‧year−1 in Western, Central, and Eastern parts of the country, respectively, between 2003 and 2018 [28]. In the Karakoram Region (7050 km2), remote sensing identified a significant upward trend of 13 m‧year−1 between 2003 and 2018 [29].
In the case of the Chilean Andes, researchers have analyzed different snow variables to detect the changes in the cryosphere. For instance, a significant decrease in snow duration of 2–5 days was observed between 29 and 36°S in the Andes Mountains [11]. Further south, the snow cover area of the Mocho-Choshuenco (250 km2; 40°S) experienced a notable permanent snow (SP > 95%) reduction of approximately 42.4 km2 in winter between 2015 and 2019 and between 1984 and 1990 [30]. The Aysen River catchment (11,540 km2; 45–46°S) in the Chilean Patagonia exhibited a decreasing trend with an annual reduction of 20 km2‧year−1 in its snow cover area for the period 2000–2016 [31]. In addition, other investigations have focused on SLE changes, revealing increasing trends of 10–30 m‧year−1 in the range of 2000–4000 masl between 30 and 36°S on the east and west sides of the Andes [12]. These global findings highlight significant snow reduction trends over the past century, reducing freshwater supply for local communities.
Worldwide, several authors have studied snow cover trends and explored statistical relationships between hydrometeorological variables and climate signals (teleconnections), which have proven valuable for hydrologic forecasting [12,23,32,33]. For example, El Niño-Southern Oscillation (ENSO), a prominent climate pattern, strongly influences precipitation worldwide, leading to increased snowfall at high altitudes and/or latitudes. Furthermore, various studies have reported a significant strong correlation between snow variables and ENSO’s climate signals [34,35,36,37]. In addition, Southern Annual Mode (SAM) [38], another influential climate driver affecting global moisture patterns, exhibits a dominant spatial correlation with snow persistence (with pixels over SP > 30%) in 45% of the territory of South America, and as a second dominant presence in 31%, 27%, and 25% of the territory of Asia, Africa, and Europe, respectively [23]. In the case of mainland Chile (18–57°S), snow variables are mainly influenced by large-scale modes of variability such as ENSO and SAM. It is well-documented that, during the El Niño phase, a humid regime occurs in the Central Chile region (between 29 and 42°S), resulting in increased snow accumulation in snow-dominated basins [4,35,39]. In addition, a strong correlation has been observed between SP and ENSO’s climate index from May to July (MJJ) between 24 and 31°S [12]. A robust correlation was identified between the 3-month average December to February (DJF) of SAM and precipitation weather stations from South Chile between 38 and 48°S [40]. Moreover, Saavedra et al. [12] reported that the 3-month average (DJF) of SAM is primarily correlated with SP for the mid-latitudes between 31 and 36°S.
Other studies have focused on establishing correlations of climate indices with streamflow or using them for streamflow forecasting in snow-driven basins. For example, in China [41] and the USA [42], the 3-month averages of climate indices and snow variables were used to predict runoff in the study area, demonstrating a strong predictive skill in high-flow events. Similarly, Maurer et al. [43] found that snow measurements and climate teleconnections are vital components for improving the forecasting of surface runoff across North America. Likewise, the relationship between streamflow signatures and SP has been investigated in the same region, revealing a significant positive association between SP and low flow, irrespective of the basin’s seasonality [44]. Nevertheless, there is a lack of studies examining the link between SP and streamflow in Chile. Understanding these correlations could allow water managers and stakeholders to make informed decisions during periods of water scarcity by using forecasting models in the snow-dominated basins.
Assessing the spatiotemporal trends in snow cover along the Chilean Andes is crucial for the effective management of water resources [12,45]. Previous studies have examined these trends at a regional scale, providing extensive spatial coverage but without sufficient detail to inform decision-making processes [12,30,31], as most of the relevant Andean basins, in terms of their drinking water supply and hydropower generation, are smaller than 500 km2 [33,46]. Motivated by this, this study aims to characterize the spatiotemporal changes in snow variables in the El Yeso River basin, which provides fresh water to seven million people in Santiago (Chile’s capital), representing approximately 40% of the country’s total population [47]. The snow variables considered are the snow cover area, SLE, and SP, which are obtained using snow products derived from MODIS. In addition, this study examines the correlation (teleconnection) between the snow variables and hydrometeorological variables (climatic indices). The research aims to address the following research questions: What has been the extent of the reduction in the snow cover area and SP over the years and seasons? What are the spatiotemporal trends observed in snow variables during the first 22 years of the 21st century (2000–2021)? What correlation (teleconnection) can be identified between snow variables and hydrometeorological variables (climatic indices) to facilitate streamflow forecasting?
2. Materials and Methods
2.1. Study Area
The study area corresponds to the Yeso River basin (YRB), located in the semi-arid Andes of central Chile (33.6°S, 70.0°W). The basin covers an area of 627 km2, with an elevation range of 1240–6030 masl. The YRB exhibits steep slopes and contains two lagoons (5.8 km2) and the Yeso reservoir (8.7 km2). The drainage area upstream of the Yeso Reservoir corresponds to the Yeso Reservoir basin (YReB), which has an area of 354 km2 and an elevation range of 2510–6030 masl. In addition, the YRB has covered glaciers (CG), uncovered glaciers (UG), and rock glaciers (RG) (Figure 1), with three major glaciers: the Yeso (2.9 km2, UG), Bello (4.6 km2, UG), and Piramide (4.7 km2, CG) glaciers, which contribute between 3 and 32% of the basin’s streamflow during the dry season [11].
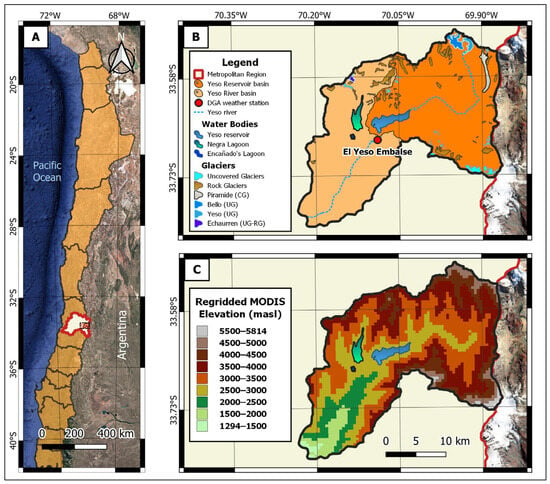
Figure 1.
Map of the Yeso River basin. (A) Location of the Yeso River basin (YRB) in Chile and South America. (B) Boundaries of the YRB and Yeso Reservoir (YReB) basins, including a meteorological station (“El Yeso Embalse”), two lagoons, Yeso reservoir, and glaciers which are defined as covered glaciers, uncovered glaciers, and rock glaciers in IPG 2014. (C) Regridded MODIS Elevations of the YRB.
The climate in the basin corresponds to a mild Mediterranean climate, with a snow-glacier regime [48]. This region experiences a hot and dry summer season, while winter (May to September) is cold and rainy, primarily influenced by cold fronts [49]. Peak flows occur in December and January as a result of the snow melting during the summer (Figure A7, Appendix A). On average, the snow line elevation of the study zone (33.6°S) is above 2400 masl [12]. Regarding weather characteristics, the average annual temperature (2000–2022) at “El Yeso Embalse” (Figure 1B, 2475 masl) is 8.8 °C for the Chilean hydrological year (CHY, April of the current year to March of the following year), with a minimum (maximum) average monthly temperature in winter (summer) of −2 °C (17 °C) and the mean annual precipitation corresponds to 567 mm (Figure A8, Appendix A). However, previous studies have registered a significant positive trend of temperatures of 0.25 °C‧decade−1 at “El Yeso Embalse” [50] and a decrease in rainfall between 25 and 45% in Central Chile (30–38°S) since 2010, a period known as the “Mega Drought” (MD) [51]. Both phenomena have implications for snow accumulation and melting in this basin, resulting in a negative balance in the water supply [52].
During winter, the snow in the study area occurs above 1786 masl. Thus, the SLE trend analysis is conducted using data from the YRB with a minimum elevation of 1286 masl, which is lower than the average SLE. This approach allows us to evaluate temporal variability while considering the influence of spatial factors in calculating SLE. The trend and correlation (teleconnection) analysis of snow persistence (SP) with hydrometeorological variables (climatic indices) is performed in the YReB. This decision is based on the proximity of meteorological and streamflow stations to this sub-basin. Additionally, water bodies in the basin are excluded from the snow analysis because the snow product cannot detect the presence of snow in these zones.
2.2. Data Sets
2.2.1. Remote Sensing Products
The snow cover analysis was conducted using the MODIS/Terra Snow Cover 8-day L3 Global 500 m Grid Version 61 image dataset (MOD10A2) [53] for 22 years (2000–2021). This product provides an 8-day Maximum Snow Cover Extent with 500 m grid spatial resolution. In each image, pixels contain numerical values to define the presence of different elements, such as snow or clouds. The dataset was analyzed considering the Chilean hydrological year (from April of the present year until March of the next year). Each year has 46 time-steps, resulting in 1012 images for the entire study period (2000–2021). For more details, see Table A1 (Appendix A).
We acknowledge that the coarse resolution of the MODIS product (500 m) can introduce uncertainties due to the mixed pixel effects caused by the topography. Despite this limitation, we conducted a comparative analysis, involving six MODIS scenes (MOD10A2) alongside six Landsat-8 scenes from Collection 2 Level 2 data. The six scenes correspond to three distinct seasons (winter, spring, and summer) from a wet (2015) and a dry (2020) year. This variety of scenes allowed for comparing data obtained from both satellites and assessing any discrepancies. To estimate the snow cover using Landsat data, we employed a threshold of NDSI > 0.4 to distinguish between snow and non-snow pixels [54]. The selection of Landsat scenes was based on cloudless images via visual inspection.
We computed the ‘agreement’ between MODIS and Landsat pixels for each scene. This ‘agreement’ represents the percentage of Landsat pixels that match the corresponding MODIS pixel. An ‘agreement’ of 100% indicates that all pixels are correctly classified as snow-covered or snow-free (True Positives/Negatives). Conversely, if the ‘agreement’ implies that all pixels are classified oppositely, this represents False Negatives/Positives. For values falling between these extremes, we consider values over 50% as indicating a correct classification (True Positives/Negatives) and values below 50% as incorrect (False Negatives/Positives). To summarize the results, the confusion matrix (Table A2, Appendix A) shows the values assigned to the four possible cases of pixel classification.
In the final step, we completed the ‘confusion matrix’ by counting the number of pixels corresponding to each case and computing the agreement for the six scenes considered. Our results (Table A3, Appendix A) indicate a strong agreement between both satellite data sources during winter, with an agreement of 80–90%. For the other seasons, the rate of false positives increases as we approach summer (more pixels classified as having snow in MODIS but not in Landsat); however, the agreement remains high (above 60%). These results suggest that, although the snow line elevation in summer could be underestimated compared to the Landsat data, the percentage of discrepancy is not high, which validates the use of MODIS in this work. Figure A1, Figure A2, Figure A3, Figure A4, Figure A5 and Figure A6 (Appendix A) offer a detailed comparison between the two satellite datasets.
2.2.2. Digital Elevation Model
To analyze the effect of elevation on snow patterns, we used the digital elevation model (DEM) developed by the Shuttle Radar Topography Mission (SRTM), which has a spatial resolution of 30 m [55]. This DEM was regridded to a 500 m grid using a bilinear method to maintain consistency with the resolution of the MODIS products.
2.2.3. Hydrometeorological Data
In the study area, there is one meteorological ground station (“El Yeso Embalse”—Figure 1B) located at 2475 masl, which is managed by the Chilean Water Directorate (Dirección General de Aguas, DGA). The station provides daily records of the maximum and minimum temperature and precipitation (https://snia.mop.gob.cl/BNAConsultas/reportes (accessed on 12 June 2022)). The streamflow released by the Yeso Reservoir basin is estimated indirectly using a mass balance, with information provided by Aguas Andinas (AA, a water supply and sanitation company located in the Metropolitan Region). More detailed information about the hydrometeorological variables can be found in Table 1.

Table 1.
Detailed information of hydrometeorological variables and climatic indices.
2.2.4. Climatic Indices
We retrieved 3-month running mean values from spring (of the previous year) to winter (of the present year) of monthly ENSO-related time series (Multivariate ENSO Index, MEI; Southern Oscillation Index, SOI) from the National Ocean and Atmospheric Administration (NOAA, https://psl.noaa.gov/data/climateindices/list/ (accessed on 31 July 2022)). We also obtained the SAM index, also known as the Annular Antarctic Oscillation (AAO), from the British Antarctic Survey (BAS, https://legacy.bas.ac.uk/met/gjma/sam.html (accessed on 31 July 2022)). These large-scale climate indices were considered because of their strong teleconnections with snow variables at high elevations reported in previous studies in the Andes [4,12,35,39,56]. More detailed information about the climatic indices can be found in Table 1.
2.3. Methods
2.3.1. Snow Persistence
The snow persistence (SP) was obtained using the method of Richer et al. [18] which estimates the snow duration percentage in a pixel, given that a specific level of cloudiness is not exceeded. To identify pixels with cloudiness, we computed the cloud confidence index (CCI) following Moore et al. [57]. The SP and CCI for each pixel are defined as follows:
where S, C, and N represent the number of time steps with snow, cloud, and the total time steps in a year or season for each pixel in the MOD10A2 product. Annual and seasonal SP was recomputed for pixels with CCI > 30% [57,58]. The pixels that meet the previous condition were filled using the annual (seasonal) linear regression between precipitation and SP fitted for time steps from the entire period (22 Chilean hydrological years) where SP was below CCI < 30%.
We considered the classifications of SP proposed by Moore et al. [57] and Chavez et al. [30], which describe the snow persistence zones (SPZ) as Ephemeral Snow (ES; SP [0–25%]), Intermittent Snow (IS; SP [25–50%]), Temporal Snow (TS; SP [50–75%]), High Persistent Snow (HPS; SP [75–95%]), and Permanent Snow (PS; SP > 95%).
2.3.2. Snow Line Elevation
Several methods have been used to estimate the elevation of the SLE in a snow drive basin, and most of them rely on the visible snow information from satellite images [25,27,29]. However, the main limiting factor for their application is cloud coverage, which is particularly large in mountain regions [26,27,59]. To overcome this problem, we propose a new methodology for SLE detection, called the “Maximum Dissimilarity Method” (MDM), that can estimate SLE even if there is a high percentage of clouds in the scene of analysis. The method is based on the detection of boundary pixels between snow-covered and uncovered regions inside the basin to estimate the elevation of that belt. For this, snow products from MOD10A2 are converted to binary images to facilitate the detection of boundary pixels, i.e., values of 1 and 0 are assigned to pixels with Snow (S) and No Snow (NS), respectively (Figure 2A,B). Then, the method considers the standard deviation (SD) of nine contiguous pixels as the metric to detect a boundary pixel (Figure 2C). Thus, the central pixel of the nine-pixel array configuration corresponds to a boundary pixel if the SD of the array is higher than a predefined threshold. We set an SD value of 0.47 as the threshold based on the SD values obtained for different S and NS pixel combinations for a nine-pixel array configuration (Figure 2D).
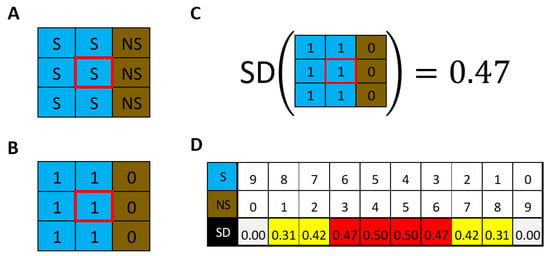
Figure 2.
Snow pixels and boundary pixels classification (A) Distribution example of nine pixels with S (cyan) and NS (brown). The red box corresponds to the central pixel. (B) The same as before, but with binaries values (S = 1, NS = 0). (C) Standard deviation (SD) of 9 pixels example. The SD value is assigned to the central pixel. (D) The table displays how variations in the number of pixels of S and NS (first and second row) correspond to changes in SD (third row). The SD threshold considered for boundary pixels is 0.47 (red, 6S-3NS, and 5S-4NS configurations or vice versa). The other configurations represent the near boundary pixels (0 < SD < 0.47; yellow) and full similarity (grey, SD = 0).
This process is repeated for all pixels in the basin, obtaining SD and classifying them as boundary pixels (BP), near boundary pixels (NBP), full similarity (FS), or cloud (Figure 3A). The elevation of the boundary pixels is extracted from the regridded DEM considering the abovementioned conditions. We defined the representative SLE of the basin based on statistical metrics of the SLE distribution of the boundary pixels, such as the mean, median, and maximum of the kernel density estimation (maxdk, Figure 3C). To identify which statistical metric best represents the SLE obtained using MDM, we compare these metrics with the SLE obtained using the Regional Snowline Elevation Estimation Method (RSLEEM) [27]. The RSLEEM consists of obtaining the SLE that minimizes the function , which represents the sum of the percentage of NS pixels above the SLE and the percentage of S pixels below the SLE.
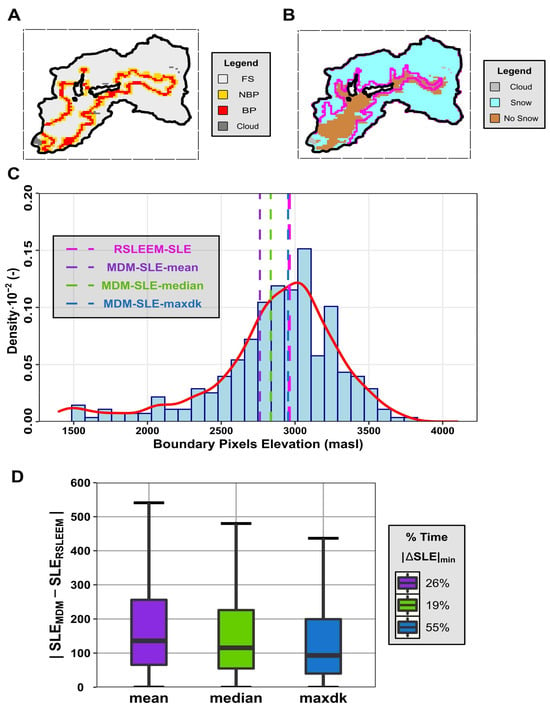
Figure 3.
SLE detection example for a MODIS time-step (Time step 7—2009) and selection of best statistical measure for MDM-SLE. (A) SD classification example for a time-step of YRB, (B) SLE delineation (solid magenta line) using the RSLEEM for the same time-step. (C) Histogram of elevation from boundary pixels and statistical metrics (mean, median, and maxdk). (D) Boxplots of the absolute difference between the two methods obtained per each statistical measure for available time steps. The legend displays the percentage of the time that the absolute difference between the methods using the statistical metric is the minimum. The lower (upper) hinges from boxplots correspond to the first (third) quartiles, while the center value corresponds to the median. The upper (lower) whisker extends from the hinge to the largest (smallest) value no further than 1.5‧IQR (inter-quartile range).
We computed this function for all the elevation values of the regridded DEM and selected the elevation that minimizes the function. This elevation corresponds to the SLE (Figure 3B). The SLE obtained using RSLEEM (RSLEEM-SLE) is compared with the SLE obtained using MDM (MDM-SLE) for each statistical measure (Figure 3C). This procedure was repeated for each time step from the 22-year series (1012 MODIS images), where 114 time steps showed an entirely snowed basin, 4 were no available images, and 83 were checked visually. Then, to test which statistical measure from MDM is the most appropriate compared with results from RSLEEM, the difference in absolute value between both methods is quantified for suitable time steps (a total of 894 scenes). Lastly, the validation process illustrated that the maxdk, median, and mean were more appropriate 55%, 19%, and 26% of the time, respectively (Figure 3D). Moreover, maxdk presented a closer range to zero than the other two, with a median error value of 103 m. Therefore, to characterize the SLE in the YRB, we used the MDM with the maxdk as the statistical measure for the entire study period. It is important to note that the four non-available images were completed with information from the concurrent precipitation (same time-step). We only checked seven scenes because of irregular patches of snow.
2.3.3. Snow Variables Trend and Their Correlations
We used the Mann–Kendall Trend Test (MKTT) [60,61] to detect temporal trends of the variables analyzed. The MKTT has been used widely to identify trends in hydrometeorological series and their significance worldwide [62,63,64]. Once the MKTT was applied, the results were summarized in 5 cases: negative and significant trend (TD (−), p < 0.05), negative and non-significant trend (TD (−), p > 0.05), no trend (TD (↔), p > 0.05), positive and non-significant trend (TD (+), p > 0.05), and positive and significant trend (TD (+), p < 0.05). Additionally, we computed the Thiel–Sen slope estimator (TSEE) [65] to obtain the magnitude of the trends in SP and SLE.
We considered Spearman’s rank correlation coefficient (SRCC) [66] with a 95% confidence level to detect the correlation (teleconnections) of SP with the hydrometeorological variables (climatic indices) at annual and seasonal scales.
3. Results and Discussion
3.1. Spatiotemporal Variation in the Snow Cover and Persistence
3.1.1. Elevation Bands Definition
As expected, Figure 4 shows the SP increases with the elevation, meaning the snow lasts longer due to the temperature reduction with the altitude. The zones IS, TS, and HPS, which together represent 82.6% of the basin area (280.8 km2), present a linear behavior (R2 = 0.59), revealing that snow persists, on average, between 91 and 346 days‧year−1, with a positive trend of 4.1%‧10−2‧m−1. This trend implies that snow lasts an additional 15 days per each increase of 100 m in elevation. Also, almost half of the basin (43.8%) corresponds to TS (3000–4000 m), suggesting that most snow lasts between 183 and 274 days‧year−1. Only 18.4% of the basin area (59.1 km2) presents an annual > 95% (PS), which is the zone where the snow lasts more than 11 months. The snow cover exhibits a = 100% above 4000 masl, which is associated to the presence of glaciers. We noted that two pixels at the same elevation may have different values due to factors related to the topography and snow transport processes, such as the orientation of slopes, slope gradient, and wind transport [67]. Lastly, we defined elevation bands in the basin that correspond to elevation levels associated with SP = 25%, 65%, and 95% based on the linear regression (Figure 4A). Then, we categorized these bands as low elevation (L; [2510 masl–3410 masl]), medium elevation (M; [3410 masl–4140 masl]), and high elevation band (H; [4140 masl–6000 masl]), to study spatiotemporal changes in snow cover area. The lowest elevation for the L band is defined according to the lowest elevation of the YReB.
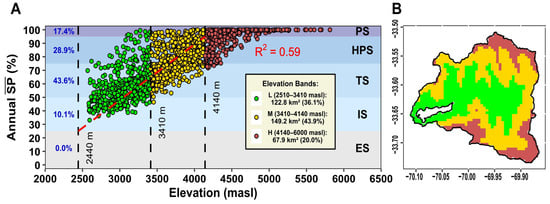
Figure 4.
Elevation bands categorization. (A) Scatter plot of annual versus elevation per pixel. The five colored boxes indicate the SPZ. The red dashed line corresponds to a linear regression of all the pixels with annual < 95%. The black dashed lines show the elevation levels corresponding to 25%, 65%, and 95% of SP based on a linear regression. (B) Band elevation of YReB, where green, gold, and firebrick represent L, M, and H, respectively.
3.1.2. Spatiotemporal Variation in Snow
Together with the analysis based on elevation bands, we divide the study period into 4 subperiods: first-half pre-MD (2000–2004), second-half pre-MD (2005–2009), first-half MD (2010–2015), and second-half MD (2016–2021). Figure 5 shows the snow-covered area and SP classification for each subperiod and the three elevation bands (L, M, and H). The next annual and seasonal scale findings are based on comparing the persistence changes and snow cover area between the fourth and first subperiods. At the annual scale (Figure 5A), the L band shows the most abrupt change in IS, increasing from 13.8 km2 to 61.0 km2, indicating that half of the area has a duration of 137 days‧year−1 of snow. The M band exhibits the highest increase in TS, having 26.4 km2 to 105.7 km2, meaning that more than 70% of the band presents 228 days‧year−1 of snow. The H band is most affected at PS, decreasing from 54.7 km2 to 34.2 km2, with most of the reduction occurring in the last two periods strongly related to the MD.
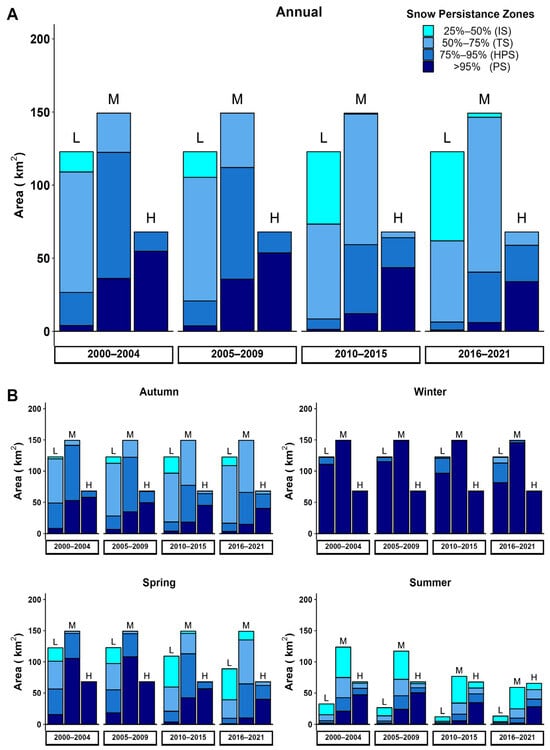
Figure 5.
Evolution of snow area and persistence. Annual (A) and seasonal (B) change in mean area and SP in the Yeso Reservoir basin for four subperiods between 2000 and 2022. Bars indicate the mean area of each elevation band (L, M, and H). Colors in the bars indicate the mean area corresponding to each SPZ. The ES range was not included.
At the seasonal scale (Figure 5B), the cold season presents minor changes in SP and a non-substantial reduction in snow cover area. For example, only the L band in winter decreases 29.4 km2 in PS, which is compensated by an increase of 20.3 km2 in HPS and 8.7 km2 in TS. Each elevation band and SP change in autumn is similar to the annual scale. However, the most affected zones are the L band, which reduces 26.6 km2 in HPS, and the M band, which depletes 37.0 km2 in HPS and 38.3 km2 in PS. As expected, the dry season is the most affected in all elevation bands, with a major depletion of snow cover area and SP. For the snow cover area, the total depletion in spring at L and M bands corresponds to 34.0 km2 (10% of basin area), where the L band is the most affected with a reduction of 33.7 km2 (122.6 to 88.9 km2). Moreover, an abrupt decrease in snow cover area is observed at all band elevations in summer (L: 19.5 km2, M: 64.7 km2, and H: 2.4 km2), with a total reduction of 86.5 km2 (25.4% of area basin). This result emphasizes that the M band is the most affected in terms of snow cover area reduction (123.7 to 59.0 km2). In the case of SP, spring exhibits a reduction in PS at all elevation bands (L: 14.7 km2, M: 95.4 km2, and H: 28.1 km2). Also, there is a diminishing 32.0 km2 in HPS and 15.1 km2 in TS at the L band, highlighting that the M band is the most affected altitude in persistence (95.4 km2). Finally, in summer, as in spring, PS is reduced at all elevation bands (L: 1.9 km2, M: 18.6 km2, and H: 19.0 km2). Also, at the M band a diminishing of 14.7 km2 in IS, 17.3 km2 in TS, and 14.1 km2 in HPS is observed, highlighting that the last band (like spring and autumn) is the most affected altitude in persistence (64.7 km2). Detailed information between subperiods can be found in Table A4 (Appendix A).
3.2. Snow Persistence Trends
3.2.1. Temporal Variation in SP at Basin Scale
During the study period, the average SP in the Yeso Reservoir basin shows a significant decreasing trend at the seasonal and annual time scales at basin scale (Figure 6). At the annual scale, SP values decrease from 80.7% to 56.7% with a negative TSSE of 0.80%‧year−1, which implies 2.9 fewer days of snow each year (FDOS). At the seasonal scale, SP values are similar to the annual scale for autumn, with a decreasing TSSE of 0.62%‧year−1 (0.6 FDOS). The winter season shows a stable behavior in SP with values between 94.6 and 99.9% and a minor decreasing trend of 0.08%‧year−1 (0.1 FDOS). Spring and summer are the most affected seasons, with negative trends of 1.41%‧year−1 and 1.33%‧year−1 (1.4 and 1.2 FDOS), and SP values varying between 44.0 and 95.9% and between 19.6 and 64.2%, respectively. As expected, winter presents the greatest snow persistence, with an = 98.7%, whereas the summer presents the lowest SP values, with = 40.7%. While the autumn and spring show similar values ( = 78.3% and 77.8%), the spring tends to present larger persistence than autumn for some years. In addition, before 2010 (before the MD), spring showed more persistence than autumn for most years because of the wet period (high precipitation in the cold season, Figure A8, Appendix A), which results in large amounts of snow accumulating at the beginning of spring. There are only two years, 2004 and 2007, where spring presents lower persistence than autumn, which is explained by the fact that these are the driest years of the period. After 2010 (the beginning of MD), autumn SP is persistently greater than that of spring, as this is a period marked by a dry season with severe precipitation deficits in the cold season, which causes a reduction in the amount of snow available for melting in spring. However, the behavior was different in 2011, 2015, and 2018, which could be explained by lower precipitation in autumn (below 150 mm) than in winter (Figure A8, Appendix A), except for 2019 and 2021, the driest years. For example, in 2015, a year influenced by El Niño conditions [68], there was no precipitation in autumn, and snowfall was concentrated in winter and spring. These findings lead to the conclusion that the amount and frequency of precipitation in the cold season controls the available snow for the dry season and, therefore, the available freshwater derived from the snow melting.
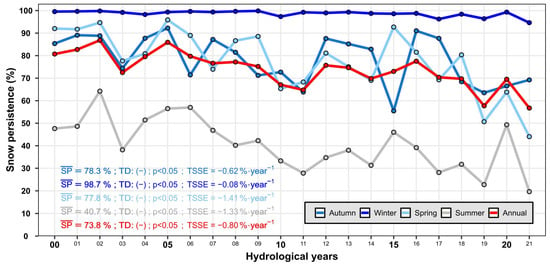
Figure 6.
Average annual and seasonal SP time series in the YReB from 2000 to 2021 at basin scale.
3.2.2. Spatial Distribution and Variation
Figure 7A–E shows the annual and seasonal averages of the spatial distribution of SP in the YReB for the entire study period (2000–2021), along with a histogram representing the area for each SPZ. At the annual scale (Figure 7A), the basin presents a spatial average of = 73.8%, where 5.4% (18.4 km2) of the basin area corresponds to uncovered glaciers (UG, 4000–6000 masl); these do not show temporal changes during the study period, maintaining = 100%. If we compare our results to IPG 2014 [69], there was an initial UG area of 24.3 km2 (date of satellite acquisition: 31 March 2000), which implies a retreat of 5.9 km2 in the last 22 years. Seasonally, the spatial distribution of SP for autumn (Figure 7B) is similar to that of the annual scale, with 39.9% of the area corresponding to TS (2500–4000 masl) and a spatial average of 78.3%. In winter (Figure 7C), as expected, the spatial average of SP is close to 100% ( = 98.6%), with 73.7% of the basin corresponding to PS ( = 100%, >3000 masl) and remaining invariant for the entire period. During spring and summer (Figure 7D,E), the basin average of SP reduces to 77.8% and 40.7%, respectively. In spring, 37% of the basin area is classified as HPS in the elevation range of 3500–4000 masl, while 43.8% is classified as ES between 2500 and 3500 masl for summer. These results reveal the interannual variations of the snow cover in the basin, showing that most snow is concentrated in winter because of the high precipitation and low temperatures in the cold season (Figure A7, Appendix A). The melting of the ES, IS, and TS at medium and low elevations begins in spring, followed by the thawing of HPS, PS, and glaciers, because of the increase in temperatures during summer. Finally, in autumn, snowfall begins, temperature decreases, and SP increases again, repeating the cycle again.
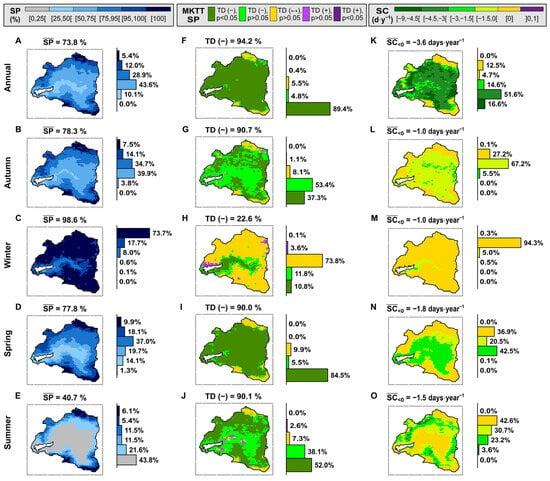
Figure 7.
Snow persistence trends in the Yeso Reservoir basin for the entire study period. (A–E) Mean annual SP () for 22 hydrological years (2000–2021). Annually in the first row and each season from the second to fifth rows. (F–J) MKTT SP per year and season for the entire study period. (K–O) SP but as a change in the number of days per year (season) and per pixel (SC, snow change). The value above each graph represents the mean SP for 22 hydrological years at basin scale (first column), the percentage of the area with a negative trend (p < 0.05 and p > 0.05) in SP (second column), and the mean of negative snow change values in the basin (third column). To the right of each graph, there is a histogram that summarizes the percentage of the basin area used by each variable (, MKTT SP, and SC). The close brackets ([]) denote that endpoints are included in the set, while open brackets (] [) indicate the exclusion of them.
To assess the temporal trend of SP, we compute the significance and magnitude of its trend using MKTT (Figure 7F–J) and TSSE (Figure 7K–O), where the latter is expressed as the reduction in days of snow per year (days‧year−1, abbrev. as d‧y−1). At the annual scale, 89.4% of the basin shows a significant negative temporal trend (Figure 7F), corresponding to the region below 4500 masl. In addition, there is an average of 3.6 fewer days of snow cover per year in the basin (Figure 7K), which can be expressed as 79 FDOS for the 22 years. This highlights that 51.6% and 16.6% of the basin area present a trend of [−4.5, −3] and [−9, −4.5] days‧year−1 with snow. Regarding the cold seasons, autumn shows a significant decreasing trend in 37.3% of the area (Figure 7G) associated with an elevation range of 3500–4500 masl, with a snow reduction of 1 day per year (Figure 7L), where 67.2% of the area presented a trend [−1.5, 0] days‧year−1. For winter, only 10.8% of the area has a significant negative trend (Figure 7H, the region under 3000 masl) with an average of 1.0 fewer snow days per year (Figure 7M, only 5.5% of the basin area). Notably, 73.8% of the basin shows no temporal trend because most of the basin is entirely snowed over during this season. In the case of the dry seasons, spring and summer present significant negative trends in 84.5% and 52.0% of the area (Figure 7I,J), respectively. In the case of spring, the significant trends are distributed over almost all the region under 4500 masl, while, in summer, they are mainly located between 3500 and 4500 masl. Both have an average reduction of 1.8 and 1.5 days of snow cover per year (Figure 7N,O), which indicates 40 and 33 FDOS for the study period.
Previous findings in the Andes reported 23–63 FDOS (31–40°S) between 2000 and 2016 [70]. Likewise, Notarnicola [71] observed 4–38 FDOS (29–42°S) at the elevation range between 2500 and 4000 m, and Saavedra et al. [12] reported that snow tends to persist 2–5 fewer days of snow‧year−1 at annual scale (34–85 FDOS, 8–36°S). In this study, we observed 79 FDOS, which is consistent with the range presented by Saavedra et al. [12] but higher than other investigations. This could be related to the persistence of the MD (from 2010 to the present), with significant negative (positive) trends of precipitation (temperature), which have increased a dry regime in the zone [15,40,51]. A limitation of this analysis corresponds to the coarse spatial resolution of MODIS (500 m) and a temporal resolution of 8 days that can limit the detection of snow and, consequently, increase its uncertainty. However, this spatial and temporal resolution is enough to detect seasonal patterns [18,58].
3.2.3. Change in SP between Pre and Megadrought Periods
To assess the change in SP (as shown in Figure A9, Appendix A) between the pre-Chilean MD periods (2000–2009) and the Chilean MD period (2010–2021), and to determine which elevation range has experienced the greatest impact, Figure 8 displays the annual and seasonal difference in SP () per pixel. At the annual scale (Figure 8A), there is a reduction in of a 9.2%, meaning there were less than 35 FDOS on average in the basin. Moreover, 69.2% of the basin area below 4000 masl presents a reduction in the interval [−16%, −8%] (29–58 FDOS). Similar behavior is observed in autumn (Figure 8B) when there is a reduction in of 7.7% (7 FDOS), and only 47.8% of the basin (between 3000 and 4000 masl) presents reduction in the interval [−16%, −8%] (7–14 FDOS). In winter (Figure 8C), 73.7% of the basin shows no reduction in SP over 3000 masl, with a reduction of 1.1% (1 FDOS). Dry seasons (spring and summer, Figure 8D,E) are the most affected, with a reduction of 13.6% and 13.7% (12–13 FDOS). Spring presents a reduction of 47.3% (41.3% plus 6.0%) in the interval [−32%, −16%] (15–29 FDOS) below 4000 masl. Meanwhile, in summer, there is a reduction of 35.7% in the interval [−56%, −16%] (15–51 FDOS) between 3500 and 4500 masl.
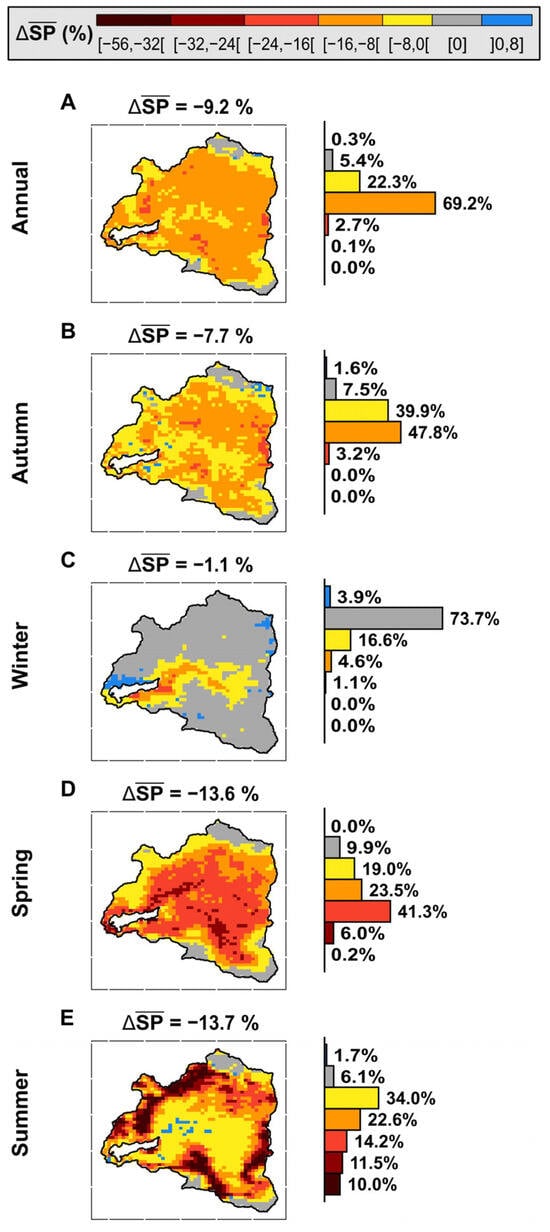
Figure 8.
SP difference between the period pre-megadrought (2000–2009) and during the Mega Drought (2010–2021) in the YReB. Annually (A) in the first row and for each season from the second to fifth rows (B–E). The value above each graph represents the mean difference in SP between periods of the basin. To the right of each graph, there is a histogram that summarizes the percentage of the basin area used for ranges of . The close brackets ([]) denote that endpoints are included in the set, while open brackets (] [) indicate the exclusion of them.
3.3. Snow Line Elevation Trend
3.3.1. Temporal Variation in SLE
Figure 9A shows that at an annual timescale, the SLE had a significant positive trend of 21 m‧year−1, increasing from 2508 to 3085 masl (2000–2021), which indicates an average area depletion of 151 km2 (from 536 to 385 km2). On a seasonal scale, winter SLE has an average value of 1768 masl, covering 100% of the YReB and 97.5% of the YRB. Until 2009, only 1 year (2003) presents an increase in their SLE over their average value, which could be explained because this was the year with the lowest winter and spring precipitation of the period (Figure A8, Appendix A) before the Chilean MD. However, since 2010, the beginning of MD, there has been a constant increase in annual SLE with values over 2700 masl (18% area without snow). The general trend in winter is significantly positive at 21 m‧year−1, where SLE varies from 1550 to 2190 masl (2000–2021), equivalent to a diminishing of 37 km2 of snow cover area in the YRB. The main reason why the winter SLE increases is because of the abrupt decrease in winter precipitation. In the autumn season, is 2550 masl, with a non-significant positive trend of 19 m‧year−1 for the study period. This non-significance is attributed to the abrupt intra-annual variability of SLE, which could be explained by the early or late arrival of the rainy season during this period. It stands out that autumn SLE was over the average in 2010–2011, 2015, and 2018–2021; meanwhile, SLE was under the average in 2012–2014 and 2016–2017. This behavior is also related to precipitation. While the first group presented precipitation under 150 mm in autumn, the second group presented values approximately over this threshold.
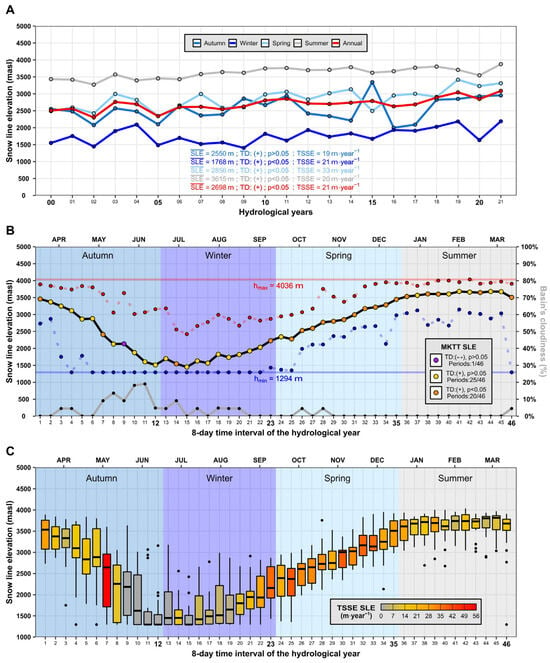
Figure 9.
Snow line elevation evolution. (A) Seasonal and annual mean SLE time series, including the MKTT, TSSE, and mean. (B) Interannual variation in the 8-day historical mean SLE time series (solid black line). The color dot on the black line corresponds to MKTT. The dashed red (blue) line specifies the maximum (minimum) SLE per time scene. The solid red (blue) line corresponds to the maximum (minimum) value for the entire period (22 years). The grey line corresponds to the average basin’s cloudiness per time scene. (C) SLE Boxplots per time step. The color inside represents TSSE, and the black dots are outliers. The lower and upper hinges correspond to the first and third quartiles, while the center value corresponds to the median. The upper (lower) whisker extends from the hinge to the largest (smallest) value no further than 1.5 IQR (inter-quartile range).
While most observed trends are statistically significant, we emphasized that these results should be interpreted cautiously due to the limited length of the SLE time series (22 hydrological years).
Spring shows a of 2856 masl with a significant positive trend of 33 m‧year−1. After 2010, spring SLE has an increasing trend (except for 2015), with the last three years being the critical ones (behavior almost similar to the summer season). There is an increase of 822 m if we compare the first and last year (from 2491 to 3313). This SLE increase implies a diminishing snow cover area from 539 km2 to 307 km2 (a depletion of 231 km2, 57% of the initial area remains in the YRB). It is important to note that the spring SLE of 2009 and 2015 show values under autumn SLE when the general trend was the contrary. This could be explained because there were late rains (mostly in winter) in both years, and temperatures were the highest and lowest (both near 10 °C) in the study period for autumn and spring, respectively (Figure A8, Appendix A). In summer, as expected, SLE is highly related to the presence of two major and highest UG corresponding to Yeso and Bello glaciers (Figure 1), which, according to IPG 2014, have a minimum elevation of 3827 and 3987 masl, respectively. The summer has a significant positive trend of 20 m‧year−1, which is a response to the ablation of permanent snow, such as glaciers mentioned before, and that snow lasts more than one year. This result denotes a glacial retreat in the 22 years of the study from the minimum elevation values detected from both glaciers in IPG 2014 because of the long period of a dry regime (MD) detected by the “El Yeso Embalse” weather station.
Other studies worldwide have reported an increase in SLE of 33–67 m‧year−1 between 2003 and 2018 (initial SLE of 4250 masl and area of 0.15 Mkm2) in Nepal [28], which is higher than those findings in this study. Nevertheless, in Karakoram Region (7050 km2), a significant upward trend of 13 m‧year−1 between 2003 and 2018 was reported [29], a minor magnitude in comparison to the findings of this study. Moreover, these results are consistent with those found in the Andes (8–36°S) by Saavedra et al. [12], who found a significant increase in the elevation of the snow line at 10–30 m‧year−1 at an annual scale.
3.3.2. Interannual Variation in SLE
Figure 9B shows the interannual variation in SLE, displaying the minimum, average, and maximum values of SLE for 46 8-day time intervals (MODIS temporal resolution). In total, 45/46 of the time intervals presented a positive trend (98% of the time), but this trend is significant for only 20/46 of these intervals (44% of the time). During the CHY, there is a high altitude range of SLE in the cold season, with minimum values close to 1294 masl (elevation under YRB, where the basin is entirely snowed) and the maximum varying between 2500 and 4000 masl because of late rains in the season. It is noted that autumn has a constant decrease in SLE from 3500 to 1500 masl from the 1st to 14th time-lapse (April to July); meanwhile, in winter, SLE begins slightly to increase from the 15th to 23rd time-lapse. This can be explained because snowfall concentrates in the cold season (mainly April to September), which also correlates with the higher cloudiness in the basin during these months. Furthermore, although winter and autumn SLE exhibit a positive trend for the study period (Figure 9A), most time-lapses present non-significant values (18/23 time-lapses). However, autumn shows a trend range of TSSE between 0 and 56 m‧year−1 (14 m‧year−1 on average), implying a high intra-seasonal variability (Figure 9C). Winter presents a trend range of TSSE between 0 and 37 m‧year−1 (12 m‧year−1 on average), with the highest values at the end of the season, which is related to the rise in temperature and the beginning of the spring season.
The worrying situation occurs in spring, where the change in SLE presented a significant positive trend in most time-lapses (11/12) with a TSSE range of 24 and 40 m‧year−1 (with 32 m‧year−1 on average). Although it is not feasible to infer the magnitude of the cumulative snow depth on a temporal and spatial scale, previous results reveal that SLE from the cold season showed mostly non-significant trends, which could imply that the snow depth from autumn and winter is changing. The season when melting occurs (August to January), and the impact observed in the snow cover and SLE is related to the rapid melting of the low amount of accumulated snow in the cold season. Lastly, summer shows SLE values ranging between 3000 and 4000 masl (around 3500 masl on average), except for outliers related to summer rain because of atmospheric rivers [72]. This season is mainly controlled by the melting of the remaining accumulated snow and glaciers, displaying a TSSE range between 7 and 28 m‧year−1 (16 m‧year−1 on average), and more than half presented a non-significant positive trend value (6/11 time-lapses).
3.4. Correlation of Snow Variables with Hydrometeorological Variables and Large-Scale Climate Indices
3.4.1. Annual Correlation with SP
Figure 10 displays the correlation between the mean annual SP at each grid point and annual hydrometeorological variables and climatic indices. As mentioned before, 5.4% of the YReB presented UG (annual = 100%). Therefore, the next results concentrate on the annual < 100% range. Both precipitation and streamflow (Figure 10A,B) show a significant positive SRCC, ranging from moderate to strong (P: [0.65,0.97]; Q: [0.50, 0.85]) for 84.7% and 85.9% of the YReB, respectively. For the annual mean temperature (Figure 10C), there is a significant negative but moderate SRCC (T: [−0.65, −0.45]) for 67.2% of the basin area. Furthermore, we assess the correlation for only grid points where < 95% (82.6%, no permanent snow zone) and > 95% (17.4% − 5.4% = 12.0%, permanent snow zone, which excludes UG). If we consider no permanent snow zone, 99.9% and 99.0% of grid points have significant positive SRCC with P and Q, respectively. Meanwhile, T presents a significant negative SRCC for 86.7% of the grid points. For the permanent snow zone, SRCC tends to decrease (increase) as SP increases for precipitation and streamflow (temperature). However, only 72.0%, 69.3%, and 27.5% of these grid points show a significant SRCC for P, Q, and T, respectively. These results reveal that the area with no permanent snow (SP < 95%), mainly located in L and M regions (<4140 masl), is highly correlated with short-term (current hydrological year) hydrometeorological variables. In comparison, the region located at a high altitude and related to permanent snow (>4140 masl and SP > 95%) does not correlate with those variables. This absence of correlation could be explained by high elevation, orientation, slope gradient, and/or proximity to glaciers, which produces lower temperatures, reduces snowpack ablation, and increases their SP.
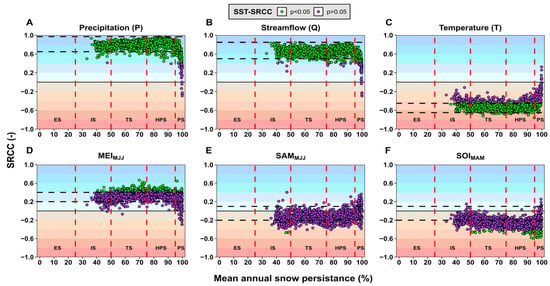
Figure 10.
Correlation between mean annual SP at each grid point and annual hydrometeorological variables (large-scale climate indices). The first row displays SRCC between annual SP and hydrometeorological variables: (A) annual cumulative precipitation, (B) annual average streamflow, and (C) annual average temperature. The second row denotes SRCC between large-scale climatic indices: mean (D) MEI in MJJ (May to July), (E) SAM in MJJ, and (F) SOI in MAM (March to May). The fill color points in the graphs show the statistical significance test for SRCC (SST-SRCC), where green points denote significant SRCC at a 95% confidence level and purple the opposite.
In the case of large-scale climate indices (Figure 10D–F), for MEI and SAM, the best correlations are obtained for MJJ, while for the SOI, the best correlation is seen for MAM. Regarding the correlation significance, all the indices present a non-significant correlation for most of the basin area (83.6%, 94.4%, and 90.9% of the area for MEI, SAM, and SOI). Nevertheless, MEI presents a positive but weak correlation; SOI and SAM show a negative and weak correlation. This finding does not match the high correlation between those climatic indices and hydrometeorological variables (e.g., precipitation and snow height) documented by some previous studies in central Chile, but is supported by the weakening of the ENSO teleconnection at the end of the 20th century reported in other studies [73,74,75]. Some of the causes that are associated with the weakening of the Walker circulation and an increase in greenhouse gases changing the gradient in sea surface temperatures [73,74,76,77]. More detailed information about the correlation assessment is displayed in Table A5 (Appendix A).
3.4.2. Seasonal Correlation with SP
As shown in Figure 5 and Figure 7, the highest negative SP trends occur in the dry seasons. Thus, for the seasonal correlation, we focus on spring and summer and the same hydrometeorological variables considered at the annual scale. Figure 11 displays the SRCC between the gridded seasonal mean (summer and spring) SP and hydrometeorological variables from the same or another season with the highest correlation. For spring SP, as expected, total winter precipitation (Figure 11A) presents a significant positive correlation for 83.2% of the basin area, with a strong to moderate SRCC ([0.60, 0.85]) in 53.2% of the area. This reduction in SRCC between annual and seasonal scales is because autumn precipitation is as important as winter precipitation for SP in the dry season (Figure A8, Appendix A). In the case of the mean spring temperature (Figure 11B), 76.4% of the basin area shows a significant negative SRCC, ranging from strong to moderate ([−0.7, −0.45]) for 73.1% of the basin. In addition, the mean spring (summer) streamflow (Figure 11C,D) shows a significant positive correlation for 83.2% (86.7%) of the basin area, with a moderate to strong SRCC (spring: [0.60, 0.80], summer: [0.70, 0.97]) for 53.0% (67.9%) of the basin area. Note that the high correlation between the spring SP and summer mean streamflow offers prospects for implementing seasonal flow forecasting models, which could be helpful for water managers and stakeholders during water scarcity periods. For SP > 85% (almost permanent snow), as in Figure 10, there is a reduction in SRCC (absolute value).
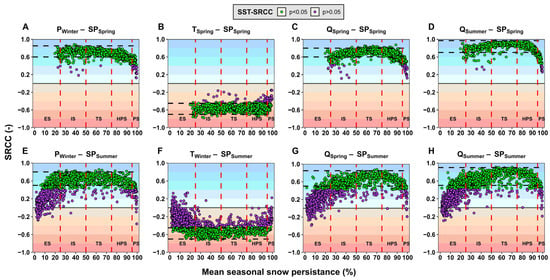
Figure 11.
Correlation between seasonal mean SP at each grid point and seasonal mean hydrometeorological variables. The first row corresponds to the SRCC of spring SP with (A) winter precipitation, (B) spring temperature, (C) spring streamflow, and (D) summer streamflow. The second row denotes the SRCC of summer SP with (E) winter precipitation, (F) winter temperature, (G) spring streamflow, and (H) summer streamflow. Green points denote significant SRCC at a 95% confidence level.
The summer mean SP shows the same SRCC sign reported in spring for hydrometeorological variables considered but with a reduction in the SRCC magnitude. The winter precipitation (Figure 11E) has a significant positive correlation in 52.5% of the basin area, while the winter mean temperature (Figure 11F) shows a significant negative correlation in 42.0% of the basin area. Moreover, 43.4% and 36.7% of the basin area present moderate to strong correlation (P: [0.5, 0.8]; T: [−0.7, −0.45]). For spring and summer mean streamflow (Figure 11G,H), there is a significant positive correlation at 46.6% and 54.8% of the basin area, respectively. The decrease in significant correlation is because of low elevation grid points (ES), which are related to snow that melts mainly in spring.
3.4.3. Annual Correlation with Snow Variables at Basin Spatial Scale
SRCC is calculated for all variables that presented a high correlation (Figure 10 and Figure 11) but aggregated in a basin spatial scale (Table 2). It is observed that the annual SP (first row) presents a significant and higher correlation than the annual SLE with all the hydrometeorological variables. For the dry season (second and third row), meteorological variables (precipitation and temperature) correlate better with SP than SLE. Likewise, spring SP presents a better correlation with dry streamflow than spring SLE. Nevertheless, the summer SLE correlates better with dry streamflow than the summer SP. These findings are highly correlated with significant negative trends of streamflow in spring and summer (Figure A7 and Figure A8, Appendix A), revealing that the dry season is mainly influenced by the precipitation from the cold season (autumn and winter) and temperatures from the winter and spring. This result implies that the snow would increase its persistence during the dry season if there is an increase in precipitation during the cold season and reduction in temperatures in winter and spring.

Table 2.
Correlation between snow variables (SP and SLE aggregated at a basin-scale) and hydrometeorological variables. SRCC values between snow variables and hydrometeorological variables such as Precipitation (P), Temperature (T), and Streamflow (Q) at different temporal scales. The first and third columns indicate the temporal scale of the corresponding variables.
Our results imply a significant negative trend of SP, a significant positive trend of SLE, and uncovered glacier retreat, which produced a reduction in the available streamflow and acceleration of the runoff peak. To support these ideas, we plotted the mean monthly streamflow pre-megadrought and during the MD (Figure A10, see Appendix A), where we see there was an approximate streamflow reduction of 50% between the periods. While we observe that peak flow tends to take place in January (Figure A10A,B), there are only two CHY (2000, 2001) in the first period (pre-MD) where the peak flow occurs in December (Figure A10A). This contrasts with the four episodes (2011, 2013, 2017, and 2020) observed during the MD (Figure A10B).
Lastly, we detected a statistically significant reduction in streamflow during spring and summer (Figure A8, see Appendix A), demonstrating adverse impacts on the availability of water resources. The latter is reaffirmed by the correlation analysis between snow variables (SP and SLE) and hydrometeorological variables (Table 2), where we identified a robust correlation between snow variables and dry season streamflow, suggesting that the decrease in streamflow can be detected through either of these snow variables. All these findings suggest a reduction in freshwater supply in the dry season, when most of the population employs the water resource for socio-economic activities, such as agriculture, industry, energy, and water consumption [1,2,4,7]. This shortage may produce conflicts between stakeholders, considering the increased freshwater demands in Santiago, the capital city of Chile [48,78].
4. Conclusions
This study examines the snow product MOD10A2 for 22 hydrological years from 2000 to 2021 to detect spatiotemporal variation in snow cover in the Yeso River Basin (YRB, 1240–6030 masl) and its sub-basin, the Yeso Reservoir Basin (YReB, 2510–6030 masl), located in the Chilean Andes (33.6°S, 70.0°W), near to Yeso Reservoir, which supplies freshwater to six million habitants in Santiago (capital city). We analyzed the spatiotemporal change in the snow cover area, SP (in YReB), and SLE (in YRB) trends and the correlation of snow variables with hydrometeorological variables and large-scale climatic indices. To obtain the snow line elevation (SLE), we introduced a new methodology called the Maximum Dissimilarity Method (MDM). The main goals of this research are to assess the spatiotemporal changes in the snow cover area and SP in the YReB, the trends of snow variables (SP and SLE), and their correlation with hydrometeorological variables and large-scale climatic indices.
We conclude that SP, an indicator of the duration of snow, has experienced a severe reduction in the YReB for all elevations bands (except winter over 3000 masl), but only the dry season decreased its snow cover area, with losses concentrated at low elevations and medium elevations for spring (34.0 km2) and summer (86.5 km2), respectively. In the case of snow cover trends, annual and seasonal average SP (SLE) presented a negative (positive) and significant trend, with the dry season being the most affected. Regarding SP’s spatial distribution and variation at annual and seasonal scales, more than 90% of the YReB area (except winter) presented a decreasing trend under 4500 masl. In addition, at the annual scale, SLE showed an upward significant trend of 21 m‧year−1, increasing from 2508 to 3085 m in the study period.
The correlation analysis between snow variables (SP and SLE) and hydrometeorological variables showed significant correlations at annual and seasonal scales. The large-scale climate indices showed low and non-significant correlation with SP, as the trends found for spring and summer snow variables (SP and SLE) are tightly linked to streamflow in the dry season.
All these previous results provide encouraging perspectives for using snow variables in flow forecasting models during the dry season, which could be helpful for water managers and stakeholders during dry periods. The potential effectiveness of this approach could be expanded to cover the entire Andes, contingent upon the availability of adequate satellite data throughout the study area. This would allow for the examination of trends in snow-derived variables, such as the snow-covered area, which may suggest changes in streamflow magnitude or timing in unmonitored regions. The continuous monitoring of the spatial patterns of snow cover trends using satellite data, as presented in this work, will help identify the effects of climate change in snow-driven basins, which supply freshwater for socio-economic activities in the dry season.
Author Contributions
Conceptualization, F.A., D.M., L.C., Á.O., R.P.F. and T.R.B.-O.; methodology, F.A., D.M., L.C., Á.O. and R.O.; software, F.A.; validation, F.A.; formal analysis, F.A.; investigation, F.A. and D.M.; resources, L.C, F.A. and D.M.; writing—original draft preparation, F.A.; writing—review and editing, L.C., Á.O., R.P.F. and T.R.B.-O.; visualization, F.A.; supervision, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research and Development Agency of Chile (ANID), namely, ANID-FONDECYT 1231494, ANID FONDECYT Iniciación 11220482, ANID-FONDECYT 3230555, and the ANID Scholarship Program/MAGISTER NACIONAL 2022-22220854 (to the first author, F.A.) projects.
Data Availability Statement
Data provided on request.
Acknowledgments
We would like to thank the MODIS-NASA, DGA, NOAA, BAS, and AA scientific teams and their associated personnel for the production of the data in this research effort.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Shows the total periods per year. Period 1 represents the days between 1st January and 8th January and so on. Furthermore, it shows the season, the time step for the Chilean hydrological year used, and the approximate initial and final date of the period.
Table A1.
Shows the total periods per year. Period 1 represents the days between 1st January and 8th January and so on. Furthermore, it shows the season, the time step for the Chilean hydrological year used, and the approximate initial and final date of the period.
| Period | Days of the Year | Season | Time Step | Initial Date | Final Date |
|---|---|---|---|---|---|
| 1 | 1–8 | Summer | 36 | 01-January | 08-January |
| 2 | 9–16 | 37 | 09-January | 16-January | |
| 3 | 17–24 | 38 | 17-January | 24-January | |
| 4 | 25–32 | 39 | 25-January | 01-February | |
| 5 | 33–40 | 40 | 02-February | 09-February | |
| 6 | 41–48 | 41 | 10-February | 17-February | |
| 7 | 49–56 | 42 | 18-February | 25-February | |
| 8 | 57–64 | 43 | 26-February | 05-March | |
| 9 | 65–72 | 44 | 06-March | 13-March | |
| 10 | 73–80 | 45 | 14-March | 21-March | |
| 11 | 81–88 | 46 | 22-March | 29-March | |
| 12 | 89–96 | Autumn | 1 | 30-March | 06-April |
| 13 | 97–104 | 2 | 07-April | 14-April | |
| 14 | 105–112 | 3 | 15-April | 22-April | |
| 15 | 113–120 | 4 | 23-April | 30-April | |
| 16 | 121–128 | 5 | 01-May | 08-May | |
| 17 | 129–136 | 6 | 09-May | 16-May | |
| 18 | 137–144 | 7 | 17-May | 24-May | |
| 19 | 145–152 | 8 | 25-May | 01-June | |
| 20 | 153–160 | 9 | 02-June | 09-June | |
| 21 | 161–168 | 10 | 10-June | 17-June | |
| 22 | 169–176 | 11 | 18-June | 25-June | |
| 23 | 177–184 | 12 | 26-June | 03-July | |
| 24 | 185–192 | Winter | 13 | 04-July | 11-July |
| 25 | 193–200 | 14 | 12-July | 19-July | |
| 26 | 201–208 | 15 | 20-July | 27-July | |
| 27 | 209–216 | 16 | 28-July | 04-August | |
| 28 | 217–224 | 17 | 05-August | 12-August | |
| 29 | 225–232 | 18 | 13-August | 20-August | |
| 30 | 233–240 | 19 | 21-August | 28-August | |
| 31 | 241–248 | 20 | 29-August | 05-September | |
| 32 | 249–256 | 21 | 06-September | 13-September | |
| 33 | 257–264 | 22 | 14-September | 21-September | |
| 34 | 265–272 | 23 | 22-September | 29-September | |
| 35 | 273–280 | Spring | 24 | 30-September | 07-October |
| 36 | 281–288 | 25 | 08-October | 15-October | |
| 37 | 289–296 | 26 | 16-October | 23-October | |
| 38 | 297–304 | 27 | 24-October | 31-October | |
| 39 | 305–312 | 28 | 01-November | 08-November | |
| 40 | 313–320 | 29 | 09-November | 16-November | |
| 41 | 321–328 | 30 | 17-November | 24-November | |
| 42 | 329–336 | 31 | 25-November | 02-December | |
| 43 | 337–344 | 32 | 03-December | 10-December | |
| 44 | 345–352 | 33 | 11-December | 18-December | |
| 45 | 353–360 | 34 | 19-December | 26-December | |
| 46 | 361–368 * | 35 | 27-December | 03-January |
* Includes 2 or 3 days from the next year.

Table A2.
Confusion matrix values.
Table A2.
Confusion matrix values.
| Confusion Matrix | Landsat | ||
|---|---|---|---|
| Snow (1) | No Snow (0) | ||
| MODIS | Snow (1) | 11 | 10 |
| No Snow (0) | 01 | 00 | |

Table A3.
Confusion matrix results for six Landsat and MODIS scenes.
Table A3.
Confusion matrix results for six Landsat and MODIS scenes.
| CHY | Season | Figure | Date MODIS | Date Landsat-8 | Confusion Matrix Values | True +/− | False +/− | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 10 | 01 | 00 | |||||||
| 2015 | Winter | Figure A1 | 23 July 2015 | 23 July 2015 | 2560 | 267 | 0 | 9 | 90.6% | 9.4% |
| Spring | Figure A2 | 12 December 2015 | 28 November 2015 | 1569 | 375 | 16 | 888 | 86.3% | 13.7% | |
| Summer | Figure A3 | 14 March 2016 | 19 March 2016 | 46 | 637 | 0 | 2168 | 77.7% | 22.3% | |
| 2020 | Winter | Figure A4 | 28 July 2020 | 29 July 2020 | 2596 | 243 | 0 | 9 | 91.5% | 8.5% |
| Spring | Figure A5 | 8 October 2020 | 8 October 2020 | 1336 | 1079 | 0 | 436 | 62.2% | 37.8% | |
| Summer | Figure A6 | 19 February 2021 | 22 February 2021 | 189 | 892 | 0 | 1769 | 68.7% | 31.3% | |

Table A4.
Results of annual and seasonal spatiotemporal variation in snow cover area and snow persistence in YReB per SP’s classification and elevation band.
Table A4.
Results of annual and seasonal spatiotemporal variation in snow cover area and snow persistence in YReB per SP’s classification and elevation band.
| Period | Elevation Band | Low (L): 2510–3410 masl | Low (L): 3410–4140 masl | Low (L): 4140–6000 masl | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SP (%) | 25–50 | 50–75 | 75–95 | >95 | 25–50 | 50–75 | 75–95 | >95 | 25–50 | 50–75 | 75–95 | >95 | |
| Range | IT | TS | HPS | PS | IT | TS | HPS | PS | IT | TS | HPS | PS | |
| Annual | 2000–2004 | 13.8 | 82.4 | 22.7 | 3.9 | 0.0 | 26.8 | 86.3 | 36.1 | 0.0 | 0.0 | 13.2 | 54.7 |
| 2005–2009 | 17.5 | 84.6 | 17.1 | 3.7 | 0.0 | 37.2 | 76.3 | 35.7 | 0.0 | 0.0 | 14.3 | 53.6 | |
| 2010–2015 | 49.5 | 64.9 | 7.1 | 1.3 | 0.6 | 89.3 | 47.1 | 12.1 | 0.0 | 3.9 | 20.5 | 43.5 | |
| 2016–2021 | 61.0 | 55.6 | 5.4 | 0.9 | 2.8 | 106.0 | 34.4 | 6.1 | 0.0 | 9.1 | 24.9 | 34.0 | |
| Autumn | 2000–2004 | 3.2 | 70.9 | 40.4 | 8.2 | 0.0 | 8.0 | 88.4 | 52.8 | 0.0 | 0.0 | 10.2 | 57.7 |
| 2005–2009 | 10.4 | 84.6 | 21.2 | 6.7 | 0.0 | 27.0 | 87.6 | 34.6 | 0.0 | 0.6 | 17.9 | 49.3 | |
| 2010–2015 | 26.2 | 78.1 | 14.5 | 4.1 | 0.0 | 72.0 | 59.0 | 18.2 | 0.0 | 4.1 | 18.8 | 45.0 | |
| 2016–2021 | 13.8 | 92.1 | 13.2 | 3.5 | 0.0 | 83.5 | 50.8 | 14.9 | 0.0 | 4.8 | 23.1 | 40.0 | |
| Winter | 2000–2004 | 0.2 | 0.6 | 11.0 | 110.9 | 0.0 | 0.0 | 0.0 | 149.2 | 0.0 | 0.0 | 0.0 | 67.9 |
| 2005–2009 | 0.2 | 0.9 | 6.7 | 115.0 | 0.0 | 0.0 | 0.2 | 149.0 | 0.0 | 0.0 | 0.0 | 67.9 | |
| 2010–2015 | 0.2 | 1.9 | 24.2 | 96.4 | 0.0 | 0.0 | 0.2 | 149.0 | 0.0 | 0.0 | 0.0 | 67.9 | |
| 2016–2021 | 0.9 | 9.1 | 31.4 | 81.5 | 0.0 | 0.2 | 3.7 | 145.3 | 0.0 | 0.0 | 0.0 | 67.9 | |
| Spring | 2000–2004 | 21.6 | 44.5 | 40.7 | 15.8 | 0.2 | 3.5 | 40.0 | 105.5 | 0.0 | 0.0 | 0.0 | 67.9 |
| 2005–2009 | 25.5 | 42.2 | 36.8 | 18.4 | 0.2 | 3.9 | 37.0 | 108.1 | 0.0 | 0.0 | 0.0 | 67.9 | |
| 2010–2015 | 49.5 | 38.7 | 17.3 | 3.7 | 3.7 | 32.7 | 70.5 | 42.4 | 0.0 | 0.2 | 11.0 | 56.7 | |
| 2016–2021 | 49.7 | 29.4 | 8.7 | 1.1 | 13.8 | 70.5 | 54.5 | 10.2 | 0.0 | 5.8 | 22.3 | 39.8 | |
| Summer | 2000–2004 | 17.3 | 9.5 | 3.7 | 2.2 | 48.9 | 32.2 | 21.6 | 21.0 | 2.4 | 8.0 | 10.4 | 47.1 |
| 2005–2009 | 13.0 | 8.2 | 3.2 | 2.2 | 45.2 | 26.4 | 21.6 | 24.0 | 2.8 | 6.7 | 8.0 | 50.4 | |
| 2010–2015 | 7.1 | 2.2 | 2.2 | 0.6 | 42.8 | 17.7 | 10.4 | 5.8 | 9.7 | 9.3 | 14.1 | 34.6 | |
| 2016–2021 | 8.9 | 1.7 | 2.4 | 0.2 | 34.4 | 14.7 | 7.6 | 2.4 | 10.2 | 15.1 | 12.1 | 28.1 | |

Table A5.
Percentage of basin area with significant (p < 0.05) and non-significant (p > 0.05) SRCC in Yeso Reservoir basin per SPZ. The row total describes the total percentage area per SPZ.
Table A5.
Percentage of basin area with significant (p < 0.05) and non-significant (p > 0.05) SRCC in Yeso Reservoir basin per SPZ. The row total describes the total percentage area per SPZ.
| SP Time Scale | Variable Time Scale | SP (%) | 0–25% | 25–50% | 50–75% | 75–95% | >95% | 100% | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPZ | ES | IT | TS | HPS | PS | - | |||||||
| Variable | p > 0.05 | p < 0.05 | p > 0.05 | p < 0.05 | p > 0.05 | p < 0.05 | p > 0.05 | p < 0.05 | p > 0.05 | p < 0.05 | - | ||
| Annual | Annual | P | 0.0% | 0.0% | 0.1% | 9.9% | 0.0% | 43.8% | 0.0% | 28.8% | 3.4% | 8.7% | 5.4% |
| Annual | T | 0.0% | 0.0% | 0.2% | 9.8% | 0.0% | 43.8% | 0.6% | 28.1% | 3.7% | 8.3% | 5.4% | |
| Annual | Q | 0.0% | 0.0% | 3.4% | 6.6% | 3.8% | 40.1% | 3.8% | 25.0% | 8.7% | 3.3% | 5.4% | |
| MJM | MEI | 0.0% | 0.0% | 9.7% | 0.4% | 37.8% | 5.7% | 24.5% | 4.4% | 11.6% | 0.4% | 5.4% | |
| MJM | SOI | 0.0% | 0.0% | 9.9% | 0.2% | 43.6% | 0.0% | 28.9% | 0.0% | 12.0% | 0.0% | 5.4% | |
| MAM | AAO | 0.0% | 0.0% | 10.1% | 0.0% | 42.9% | 0.6% | 27.7% | 1.2% | 10.2% | 1.8% | 5.4% | |
| Total | 0.0% | 10.1% | 43.6% | 28.9% | 12.0% | 5.4% | |||||||
| Spring | Winter | P | 0.1% | 1.2% | 0.4% | 13.7% | 0.1% | 19.6% | 0.1% | 36.9% | 6.3% | 11.8% | 9.9% |
| Spring | T | 0.0% | 1.3% | 0.4% | 13.6% | 0.6% | 19.0% | 1.6% | 35.4% | 11.0% | 7.1% | 9.9% | |
| Spring | Q | 0.1% | 1.1% | 0.8% | 13.3% | 0.0% | 19.7% | 0.1% | 36.9% | 5.9% | 12.2% | 9.9% | |
| Summer | Q | 0.0% | 1.3% | 0.2% | 13.9% | 0.0% | 19.7% | 0.0% | 37.0% | 3.2% | 14.9% | 9.9% | |
| Total | 1.3% | 14.1% | 19.7% | 37.0% | 18.1% | 9.9% | |||||||
| Summer | Winter | P | 33.0% | 11.1% | 1.9% | 19.5% | 0.8% | 10.7% | 1.7% | 9.8% | 4.0% | 1.4% | 6.1% |
| Winter | T | 35.7% | 8.3% | 4.1% | 17.3% | 2.6% | 8.9% | 4.8% | 6.7% | 4.7% | 0.7% | 6.1% | |
| Spring | Q | 37.7% | 6.4% | 5.0% | 16.5% | 1.0% | 10.5% | 0.8% | 10.7% | 2.8% | 2.6% | 6.1% | |
| Summer | Q | 32.7% | 11.3% | 2.4% | 19.1% | 0.7% | 10.8% | 0.6% | 10.9% | 2.7% | 2.7% | 6.1% | |
| Total | 44.0% | 21.4% | 11.5% | 11.5% | 5.4% | 6.1% | |||||||
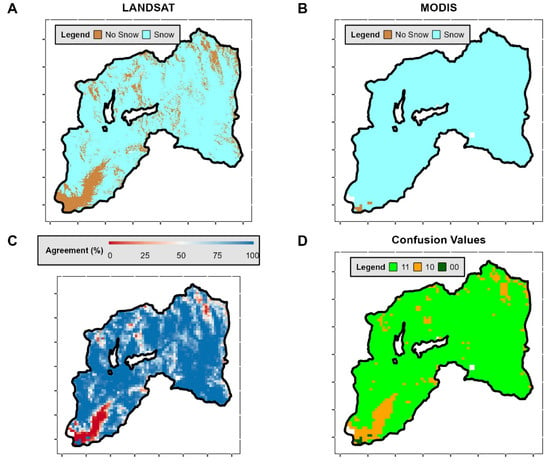
Figure A1.
Pixel comparison between Landsat and MODIS products for Winter—2015. (A) Landsat scene (30 m of spatial resolution). (B) MODIS scene (500 m of spatial resolution). (C) Percentage of Agreement in detecting snow-covered and snow-free pixels for both satellites. This “Agreement” essentially signifies the accuracy of how many percentage of Landsat image pixels within a MODIS pixel are correctly represented. A 100% agreement indicates a precise classification of all pixels as either snow-covered or snow-free for both satellites, while 0% reflects the opposite. (D) Confusion Values Classification, where we defined whether a pixel presents an “Agreement” of 100%, indicates that all Landsat pixels within a MODIS pixel are correctly classified as snow-covered or snow-free. These cases indicate True Positives (Negatives), defined as “11” (“00”) (see Table A2). Conversely, if the “Agreement” implies that all pixels are classified oppositely, this represents False Negatives (Positives), defined as “01” (“10”) (see Table A2). For values falling between these extremes (some of them are snow-free and others snow-covered), we consider values over 50% as indicative of a correct classification (True Positives/Negatives) and values below 50% as incorrect (False Negatives/Positives).
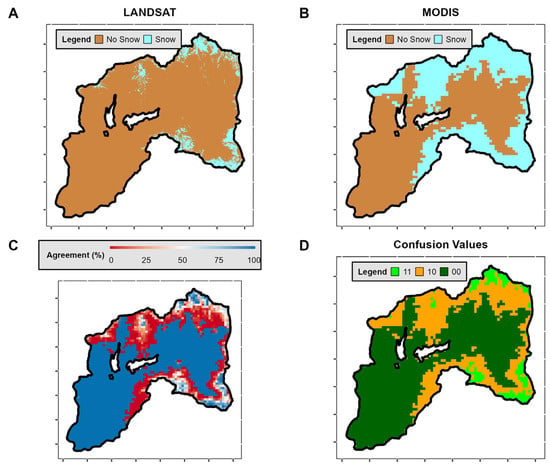
Figure A2.
As in Figure A1 but for Spring—2015. (A) Landsat scene (30 m of spatial resolution). (B) MODIS scene (500 m of spatial resolution). (C) Percentage of Agreement in detecting snow-covered and snow-free pixels for both satellites. (D) Confusion Values Classification, where we defined whether a pixel presents an “Agreement” of 100%, indicates that all Landsat pixels within a MODIS pixel are correctly classified as snow-covered or snow-free.
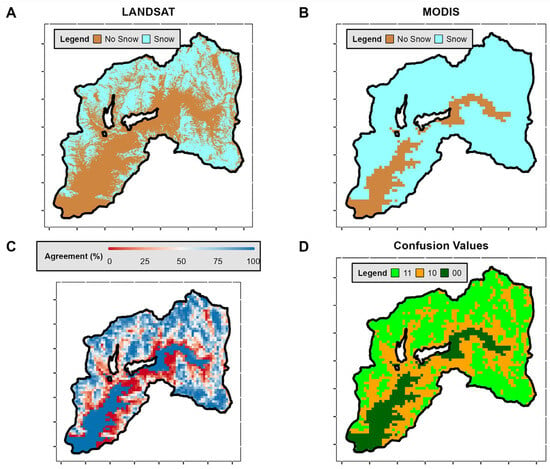
Figure A3.
As in Figure A1 but for Summer—2015. (A) Landsat scene (30 m of spatial resolution). (B) MODIS scene (500 m of spatial resolution). (C) Percentage of Agreement in detecting snow-covered and snow-free pixels for both satellites. (D) Confusion Values Classification, where we defined whether a pixel presents an “Agreement” of 100%, indicates that all Landsat pixels within a MODIS pixel are correctly classified as snow-covered or snow-free.
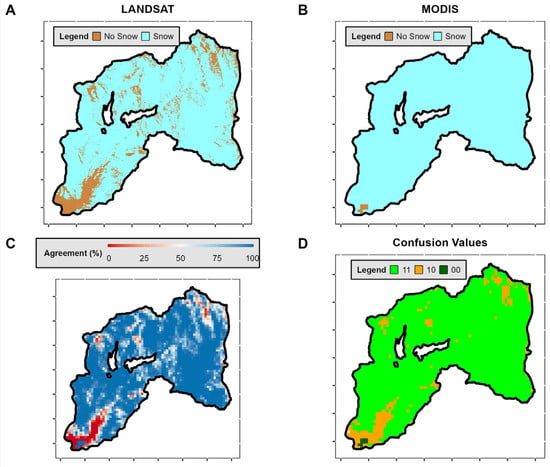
Figure A4.
As in Figure A1 but for Winter—2020. (A) Landsat scene (30 m of spatial resolution). (B) MODIS scene (500 m of spatial resolution). (C) Percentage of Agreement in detecting snow-covered and snow-free pixels for both satellites. (D) Confusion Values Classification, where we defined whether a pixel presents an “Agreement” of 100%, indicates that all Landsat pixels within a MODIS pixel are correctly classified as snow-covered or snow-free.
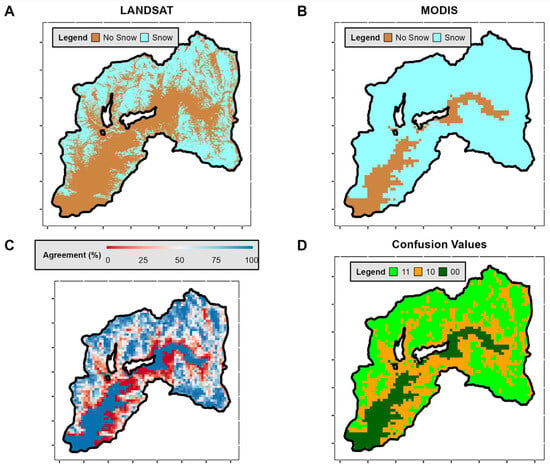
Figure A5.
As in Figure A1 but for Spring—2020. (A) Landsat scene (30 m of spatial resolution). (B) MODIS scene (500 m of spatial resolution). (C) Percentage of Agreement in detecting snow-covered and snow-free pixels for both satellites. (D) Confusion Values Classification, where we defined whether a pixel presents an “Agreement” of 100%, indicates that all Landsat pixels within a MODIS pixel are correctly classified as snow-covered or snow-free.
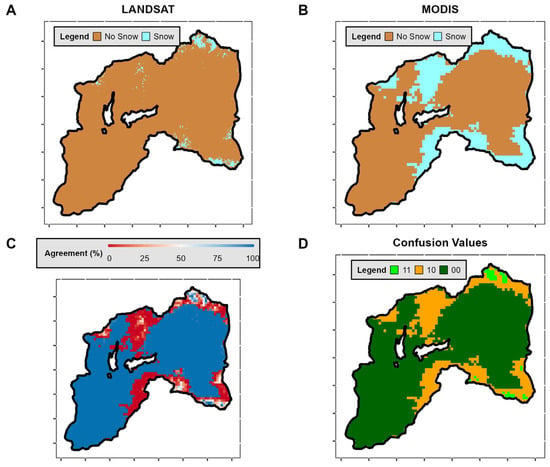
Figure A6.
As in Figure A1 but for Summer—2020. (A) Landsat scene (30 m of spatial resolution). (B) MODIS scene (500 m of spatial resolution). (C) Percentage of Agreement in detecting snow-covered and snow-free pixels for both satellites. (D) Confusion Values Classification, where we defined whether a pixel presents an “Agreement” of 100%, indicates that all Landsat pixels within a MODIS pixel are correctly classified as snow-covered or snow-free.
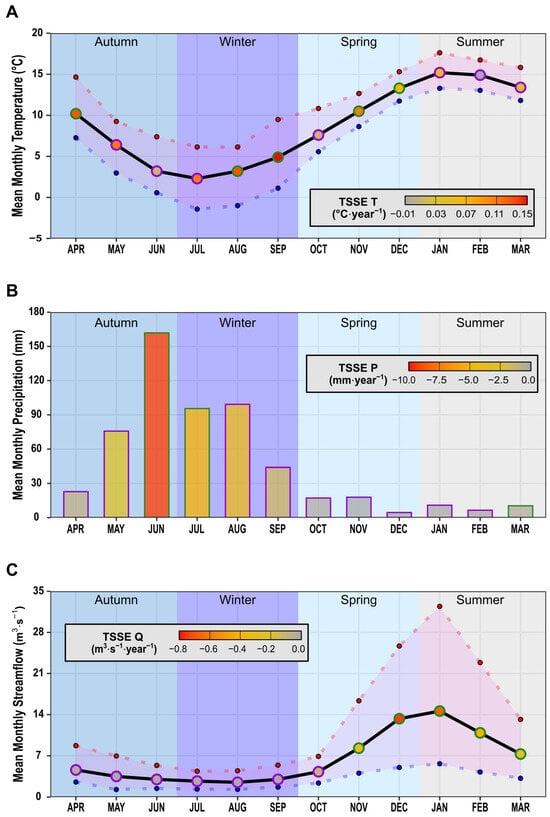
Figure A7.
Interannual hydrometeorological variables trends for the entire study period. The height of bars (B) and solid black lines (A,C) represent the average monthly values for (A) precipitation, (B) temperature, and (C) streamflow. The legend presents the magnitude of TSSE per each bar and dot. The green (purple) color around the bar or dot represents if the series is statistically significant (non-significant) with p < 0.05 (p > 0.05). The red (blue) dots and dashed lines represent the series’ maximum (minimum) value.
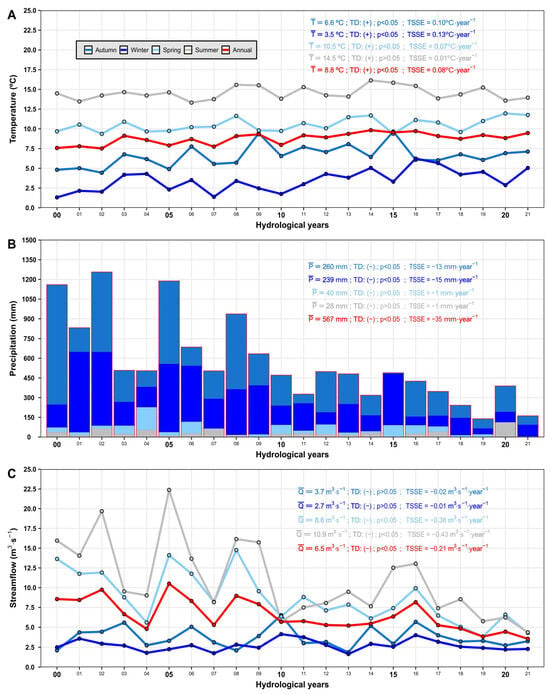
Figure A8.
(A) Annual and seasonal average temperature series. (B) Seasonal cumulative precipitation series. The annual cumulative precipitation corresponds to the total height of the bar per year, which is represented by a thin red line around the bars. (C) Annual and seasonal average streamflow series. All of them present their average at annual and seasonal scales, MKTT and TSSE.
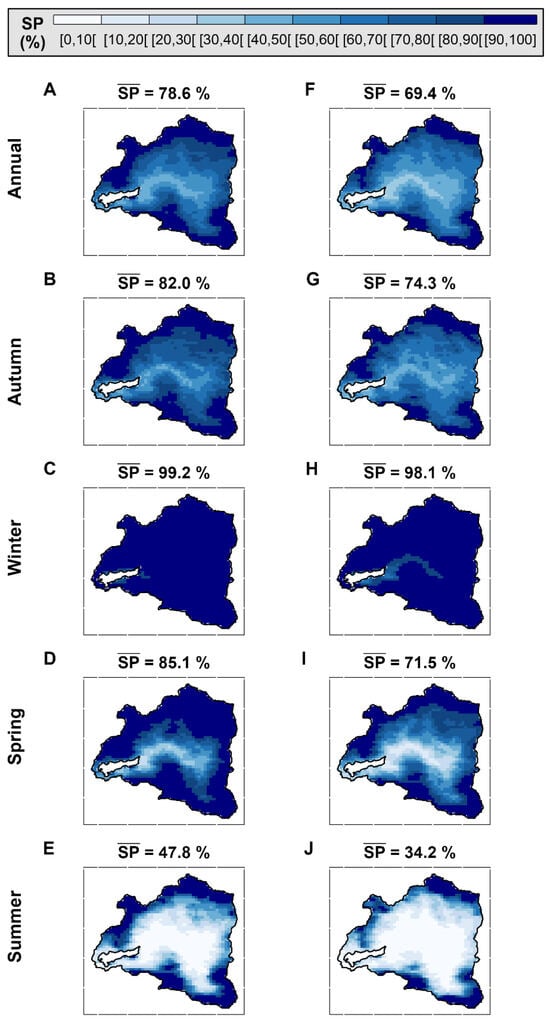
Figure A9.
First column (A–E) shows the for 10 hydrological years (2000–2009, period before “Mega Drought”); meanwhile, the second column (F–J) displays the for 12 hydrological years (2010–2021, period during “Mega Drought”). Annually in the first row and for each season from the second to fifth rows. The value above each graph represents the mean SP between periods of the basin (first and second columns). The close brackets ([]) denote that endpoints are included in the set, while open brackets (] [) indicate the exclusion of them.
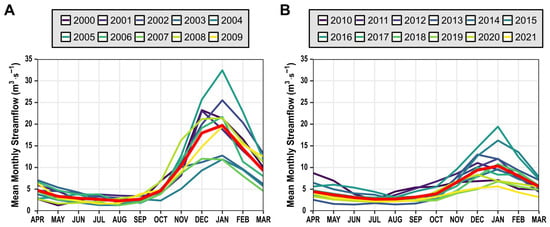
Figure A10.
Mean monthly streamflow in pre-megadrought ((A), 2000–2009) and during Mega Drought ((B), 2010–2021) per each Chilean Hydrological Year in the YReB.
References
- Beniston, M. Impacts of climatic change on water and associated economic activities in the Swiss Alps. J. Hydrol. 2012, 412–413, 291–296. [Google Scholar] [CrossRef]
- Meza, F.J.; Wilks, D.S.; Gurovich, L.; Bambach, N. Impacts of Climate Change on Irrigated Agriculture in the Maipo Basin, Chile: Reliability of Water Rights and Changes in the Demand for Irrigation. J. Water Resour. Plan. Manag. 2012, 138, 421–430. [Google Scholar] [CrossRef]
- Su, B.; Xiao, C.; Chen, D.; Qin, D.; Ding, Y. Cryosphere services and human well-being. Sustainability 2019, 11, 4365. [Google Scholar] [CrossRef]
- Masiokas, M.; Villalba, R.; Luckman, B.H.; Le Quesne, C.; Aravena, J.C. Snowpack variations in the central Andes of Argentina and Chile, 1951–2005: Large-scale atmospheric influences and implications for water resources in the region. J. Clim. 2006, 19, 6334–6352. [Google Scholar] [CrossRef]
- Meza, F.J.; Vicuña, S.; Jelinek, M.; Bustos, E.; Bonelli, S. Assessing water demands and coverage sensitivity to climate change in the urban and rural sectors in central Chile. J. Water Clim. Chang. 2014, 5, 192–203. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: The role of internal variability. Clim. Dyn. 2012, 38, 527–546. [Google Scholar] [CrossRef]
- Barrett, B.S.; Garreaud, R.D.; Falvey, M. Effect of the Andes Cordillera on precipitation from a midlatitude cold front. Mon. Weather Rev. 2009, 137, 3092–3109. [Google Scholar] [CrossRef]
- Klos, P.Z.; Link, T.E.; Abatzoglou, J.T. Extent of the rain-snow transition zone in the western U.S. under historic and projected climate. Geophys. Res. Lett. 2014, 41, 4560–4568. [Google Scholar] [CrossRef]
- Mardones, P.; Garreaud, R.D. Future changes in the free tropospheric freezing level and rain–snow limit: The case of central Chile. Atmosphere 2020, 11, 1259. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. IPCC: Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Burger, F.; Brock, B.; Montecinos, A. Seasonal and elevational contrasts in temperature trends in Central Chile between 1979 and 2015. Glob. Planet. Chang. 2018, 162, 136–147. [Google Scholar] [CrossRef]
- Saavedra, F.A.; Kampf, S.K.; Fassnacht, S.R.; Sibold, J.S. Changes in Andes snow cover from MODIS data, 2000–2016. Cryosphere 2018, 12, 1027–1046. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Huss, M.; Bookhagen, B.; Huggel, C.; Jacobsen, D.; Bradley, R.; Clague, J.; Vuille, M.; Buytaert, W.; Cayan, D.; Greenwood, G.; et al. Towards mountains without permanent snow and ice: Mountains without permanent snow and ice. Earth’s Future 2017, 5, 418–435. [Google Scholar] [CrossRef]
- Masiokas, M.; Rabatel, A.; Rivera, A.; Ruiz, L.; Pitte, P.; Ceballos, J.L.; Barcaza, G.; Soruco, A.; Bown, F.; Berthier, E.; et al. A Review of the Current State and Recent Changes of the Andean Cryosphere. Front. Earth Sci. 2020, 8, 99. [Google Scholar] [CrossRef]
- Demaria, E.M.C.; Maurer, E.P.; Thrasher, B.; Vicuña, S.; Meza, F.J. Climate change impacts on an alpine watershed in Chile: Do new model projections change the story? J. Hydrol. 2013, 502, 128–138. [Google Scholar] [CrossRef]
- Migliavacca, F.; Confortola, G.; Soncini, A.; Senese, A.; Diolaiuti, G.A.; Smiraglia, C.; Barcaza, G.; Bocchiola, D. Hydrology and potential climate changes in the Rio Maipo (Chile). Geogr. Fis. E Din. Quat. 2015, 38, 155–168. [Google Scholar] [CrossRef]
- Richer, E.E.; Kampf, S.K.; Fassnacht, S.R.; Moore, C.C. Spatiotemporal index for analyzing controls on snow climatology: Application in the Colorado Front Range. Phys. Geogr. 2013, 34, 85–107. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, X.; Wang, J.; Wang, X.; Li, H.; Jiang, Z. Spatiotemporal variation of snow cover in Tianshan Mountains, Central Asia, based on cloud-free MODIS fractional snow cover product, 2001–2015. Remote Sens. 2017, 9, 1045. [Google Scholar] [CrossRef]
- Dozier, J. Spectral signature of alpine snow cover from the landsat thematic mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Notarnicola, C. Overall negative trends for snow cover extent and duration in global mountain regions over 1982–2020. Sci. Rep. 2022, 12, 13731. [Google Scholar] [CrossRef] [PubMed]
- Hammond, J.C.; Saavedra, F.A.; Kampf, S.K. Global snow zone maps and trends in snow persistence 2001–2016. Int. J. Climatol. 2018, 38, 4369–4383. [Google Scholar] [CrossRef]
- O’Leary, D.S.; Hall, D.K.; DiGirolamo, N.E.; Riggs, G.A. Regional trends in snowmelt timing for the western United States throughout the MODIS era. Phys. Geogr. 2022, 43, 285–307. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, J.; Li, H.; Liang, J.; Li, C.; Wang, X. Extraction and assessment of snowline altitude over the Tibetan plateau using MODIS fractional snow cover data (2001 to 2013). J. Appl. Remote Sens. 2014, 8, 084689. [Google Scholar] [CrossRef]
- Racoviteanu, A.E.; Rittger, K.; Armstrong, R. An Automated Approach for Estimating Snowline Altitudes in the Karakoram and Eastern Himalaya From Remote Sensing. Front. Earth Sci. 2019, 7, 220. [Google Scholar] [CrossRef]
- Krajčí, P.; Holko, L.; Perdigão, R.A.P.; Parajka, J. Estimation of regional snowline elevation (RSLE) from MODIS images for seasonally snow covered mountain basins. J. Hydrol. 2014, 519, 1769–1778. [Google Scholar] [CrossRef]
- Khadka, N.; Khadka, N.; Ghimire, S.K.; Chen, X.; Thakuri, S.; Hamal, K.; Shrestha, D.; Sharma, S. Dynamics of Maximum Snow Cover Area and Snow Line Altitude Across Nepal (2003–2018) Using Improved MODIS Data. J. Inst. Sci. Technol. 2020, 25, 17–24. [Google Scholar] [CrossRef]
- Thapa, A.; Muhammad, S. Contemporary snow changes in the karakoram region attributed to improved modis data between 2003 and 2018. Water 2020, 12, 2681. [Google Scholar] [CrossRef]
- Chávez, R.O.; Briceño, V.F.; Lastra, J.A.; Harris-Pascal, D.; Estay, S.A. Snow Cover and Snow Persistence Changes in the Mocho-Choshuenco Volcano (Southern Chile) Derived From 35 Years of Landsat Satellite Images. Front. Ecol. Evol. 2021, 9, 643850. [Google Scholar] [CrossRef]
- Pérez, T.; Mattar, C.; Fuster, R. Decrease in snow cover over the Aysén river catchment in Patagonia, Chile. Water 2018, 10, 619. [Google Scholar] [CrossRef]
- Bevington, A.R.; Gleason, H.E.; Foord, V.N.; Floyd, W.C.; Griesbauer, H.P. Regional influence of ocean-atmosphere teleconnections on the timing and duration of MODIS-derived snow cover in British Columbia, Canada. Cryosphere 2019, 13, 2693–2712. [Google Scholar] [CrossRef]
- Zalazar, L.; Ferri, L.; Castro, M.; Gargantini, H.; Gimenez, M.; Pitte, P.; Ruiz, L.; Masiokas, M.; Costa, G.; Villalba, R. Spatial distribution and characteristics of Andean ice masses in Argentina: Results from the first National Glacier Inventory. J. Glaciol. 2020, 66, 938–949. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Angel, J.R. Relationship of ENSO to snowfall and related cyclone activity in the contiguous United States. J. Geophys. Res. Atmos. 1999, 104, 19425–19434. [Google Scholar] [CrossRef]
- Escobar, F.; Aceituno, P. Influencia del fenómeno ENSO sobre la precipitación nival en el sector andino de Chile Central durante el invierno. Bull. L’inst. Fr. D’études Andin. 1998, 27, 753–759. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, R.; Yang, S.; Lu, M. An Interdecadal Change in the Influence of ENSO on the Spring Tibetan Plateau Snow-Cover Variability in the Early 2000s. J. Clim. 2022, 35, 725–743. [Google Scholar] [CrossRef]
- Shaman, J.; Tziperman, E. The effect of ENSO on Tibetan Plateau snow depth: A stationary wave teleconnection mechanism and implications for the south Asian monsoons. J. Clim. 2005, 18, 2067–2079. [Google Scholar] [CrossRef]
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Montecinos, A.; Aceituno, P. Seasonality of the ENSO-related rainfall variability in central Chile and associated circulation anomalies. J. Clim. 2003, 16, 281–296. [Google Scholar] [CrossRef]
- Masiokas, M.; Christie, D.A.; Le Quesne, C.; Pitte, P.; Ruiz, L.; Villalba, R.; Luckman, B.H.; Berthier, E.; Nussbaumer, S.U.; González-Reyes, Á.; et al. Reconstructing the annual mass balance of the Echaurren Norte glacier (Central Andes, 33.5°S) using local and regional hydroclimatic data. Cryosphere 2016, 10, 927–940. [Google Scholar] [CrossRef]
- Boisier, J.P.; Alvarez-Garreton, C.; Cordero, R.R.; Damiani, A.; Gallardo, L.; Garreaud, R.D.; Lambert, F.; Ramallo, C.; Rojas, M.; Rondanelli, R. Anthropogenic drying in central-southern Chile evidenced by long-term observations and climate model simulations. Elementa 2018, 6, 74. [Google Scholar] [CrossRef]
- Xu, K.; Brown, C.; Kwon, H.H.; Lall, U.; Zhang, J.; Hayashi, S.; Chen, Z. Climate teleconnections to Yangtze river seasonal streamflow at the Three Gorges Dam, China. Int. J. Climatol. 2007, 27, 771–780. [Google Scholar] [CrossRef]
- Ossandón, Á.; Brunner, M.I.; Rajagopalan, B.; Kleiber, W. A space-time Bayesian hierarchical modeling framework for projection of seasonal maximum streamflow. Hydrol. Earth Syst. Sci. 2022, 26, 149–166. [Google Scholar] [CrossRef]
- Maurer, E.P.; Lettenmaier, D.P.; Mantua, N.J. Variability and potential sources of predictability of North American runoff. Water Resour. Res. 2004, 40, W09306. [Google Scholar] [CrossRef]
- Le, E.; Ameli, A.A.; Janssen, J.; Hammond, J. Snow Persistence Explains Stream High Flow and Low Flow Signatures with Differing Relationships by Aridity and Climatic Seasonality. Hydrol. Earth Syst. Sci. 2022, 1–22. [Google Scholar]
- Stehr, A.; Aguayo, M. Snow cover dynamics in Andean watersheds of Chile (32.0–39.5°S) during the years 2000–2016. Hydrol. Earth Syst. Sci. 2017, 21, 5111–5126. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Pablo Boisier, J.; Garreaud, R.; Seibert, J.; Vis, M. Progressive water deficits during multiyear droughts in basins with long hydrological memory in Chile. Hydrol. Earth Syst. Sci. 2021, 25, 429–446. [Google Scholar] [CrossRef]
- Montaner-Fernández, D.; Morales-Salinas, L.; Rodriguez, J.S.; Cárdenas-Jirón, L.; Huete, A.; Fuentes-Jaque, G.; Pérez-Martínez, W.; Cabezas, J. Spatio-temporal variation of the urban heat island in Santiago, Chile during summers 2005–2017. Remote Sens. 2020, 12, 3345. [Google Scholar] [CrossRef]
- Uribe, F. Comparación De La Cobertura Nival E Hidrogramas Simulados a Distintas Escalas Temporales En La Cuenca Alta Del Río Maipo, Por Distintas Conceptualizaciones Del Proceso Nival; Universidad de Chile: Santiago, Chile, 2015; p. 78. [Google Scholar]
- Falvey, M.; Garreaud, R. Wintertime precipitation episodes in Central Chile: Associated meteorological conditions and orographic influences. J. Hydrometeorol. 2007, 8, 171–193. [Google Scholar] [CrossRef]
- Falvey, M.; Garreaud, R. Regional cooling in a warming world: Recent temperature trends in the southeast Pacific and along the west coast of subtropical South America (1979–2006). J. Geophys. Res. Atmos. 2009, 114, 1–16. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Boisier, J.P.; Rondanelli, R.; Montecinos, A.; Sepúlveda, H.H.; Veloso-Aguila, D. The Central Chile Mega Drought (2010–2018): A climate dynamics perspective. Int. J. Climatol. 2020, 40, 421–439. [Google Scholar] [CrossRef]
- Boisier, J.P.; Rondanelli, R.; Garreaud, R.D.; Muñoz, F. Anthropogenic and natural contributions to the Southeast Pacific precipitation decline and recent megadrought in central Chile. Geophys. Res. Lett. 2016, 43, 413–421. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Terra Snow Cover 8-Day L3 Global 500m Grid, Version 61 (MOD10A2); NASA National Snow and Ice Data Center: Boulder, CO, USA, 2021. [CrossRef]
- Dadashi, S.; Matkan, A.; Ziaiian, P.; Ashorlo, D. Evaluation of Pixelbase and Subpixel Methods for Snow Cover Studying in Regional Scale. In Proceedings of the 65th Eastern Snow Conference, Fairlee, VT, USA, 28–30 May 2008. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Aceituno, P. El Niño, the Southern Oscillation, and ENSO: Confusing Names for a Complex Ocean–Atmosphere Interaction. Bull. Am. Meteorol. Soc. 1992, 73, 483–485. [Google Scholar] [CrossRef][Green Version]
- Moore, C.; Kampf, S.; Stone, B.; Richer, E. A GIS-based method for defining snow zones: Application to the western United States. Geocarto Int. 2015, 30, 62–81. [Google Scholar] [CrossRef]
- Saavedra, F.A.; Kampf, S.K.; Fassnacht, S.R.; Sibold, J.S. A snow climatology of the Andes Mountains from MODIS snow cover data. Int. J. Climatol. 2017, 37, 1526–1539. [Google Scholar] [CrossRef]
- Lei, L.; Zeng, Z.; Zhang, B. Method for detecting snow lines from MODIS data and assessment of changes in the nianqingtanglha mountains of the Tibet Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 769–776. [Google Scholar] [CrossRef]
- Kendall, M. Charles Griffin; Holden Day: San Francisco, CA, USA, 1975. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Atta-ur-Rahman; Dawood, M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Clim. Dyn. 2017, 48, 783–797. [Google Scholar] [CrossRef]
- Ke, C.Q.; Yu, T.; Yu, K.; Tang, G.D.; King, L. Snowfall trends and variability in Qinghai, China. Theor. Appl. Climatol. 2009, 98, 251–258. [Google Scholar] [CrossRef]
- Ali, R.O.; Abubaker, S.R. Trend analysis using mann-kendall, sen’s slope estimator test and innovative trend analysis method in Yangtze river basin, China: Review. Int. J. Eng. Technol. 2019, 8, 110–119. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Glasser, G.J.; Winter, R.F. Critical Values of the Coefficient of Rank Correlation for Testing the Hypothesis of Independence. Biometrika 1961, 48, 444. [Google Scholar] [CrossRef]
- Saydi, M.; Ding, J. li Impacts of topographic factors on regional snow cover characteristics. Water Sci. Eng. 2020, 13, 171–180. [Google Scholar] [CrossRef]
- Garreaud, R.; Alvarez-Garreton, C.; Barichivich, J.; Pablo Boisier, J.; Christie, D.; Galleguillos, M.; LeQuesne, C.; McPhee, J.; Zambrano-Bigiarini, M. The 2010–2015 megadrought in central Chile: Impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef]
- DGA. Estrategia Nacional de Glaciares Fundamentos; Ministerio de Obras Públicas, Dirección General de Aguas: Santiago, Chile, 2009.
- Malmros, J.K.; Mernild, S.H.; Wilson, R.; Tagesson, T.; Fensholt, R. Snow cover and snow albedo changes in the central Andes of Chile and Argentina from daily MODIS observations (2000–2016). Remote Sens. Environ. 2018, 209, 240–252. [Google Scholar] [CrossRef]
- Notarnicola, C. Hotspots of snow cover changes in global mountain regions over 2000–2018. Remote Sens. Environ. 2020, 243, 111781. [Google Scholar] [CrossRef]
- Saavedra, F.; Cortés, G.; Viale, M.; Margulis, S.; McPhee, J. Atmospheric Rivers Contribution to the Snow Accumulation Over the Southern Andes (26.5–37.5°S). Front. Earth Sci. 2020, 8, 261. [Google Scholar] [CrossRef]
- Garreaud, R. Tres niños sorprendentes. Bol. Téc. Inst. Geofís. del Perú 2018, 5. [Google Scholar]
- Hrudya, P.H.; Varikoden, H.; Vishnu, R. A review on the Indian summer monsoon rainfall, variability and its association with ENSO and IOD. Meteorol. Atmos. Phys. 2021, 133, 1–14. [Google Scholar] [CrossRef]
- Kumar, K.K.; Rajagopalan, B.; Cane, M.A. On the weakening relationship between the indian monsoon and ENSO. Science 1999, 284, 2156–2159. [Google Scholar] [CrossRef]
- Yeh, S.W.; Cai, W.; Min, S.K.; McPhaden, M.J.; Dommenget, D.; Dewitte, B.; Collins, M.; Ashok, K.; An, S., II; Yim, B.Y.; et al. ENSO Atmospheric Teleconnections and Their Response to Greenhouse Gas Forcing. Rev. Geophys. 2018, 56, 185–206. [Google Scholar] [CrossRef]
- Reboita, M.S.; Ambrizzi, T.; Crespo, N.M.; Dutra, L.M.M.; Ferreira, G.W.d.S.; Rehbein, A.; Drumond, A.; da Rocha, R.P.; de Souza, C.A. Impacts of teleconnection patterns on South America climate. Ann. N. Y. Acad. Sci. 2021, 1504, 116–153. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).