A Cloud Water Path-Based Model for Cloudy-Sky Downward Longwave Radiation Estimation from FY-4A Data
Abstract
:1. Introduction
2. Data
2.1. FY-4A Products
2.2. ERA5 Reanalysis
2.3. Field Measurements
3. Methods
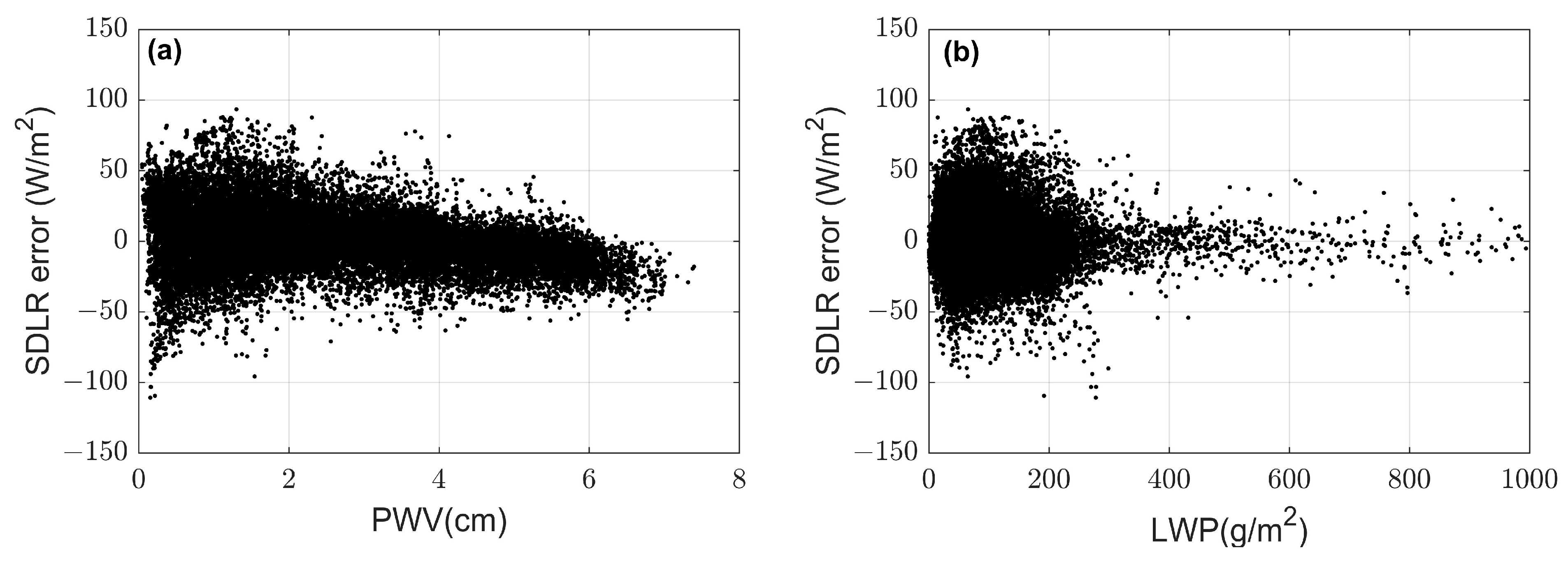
3.1. Problem Analysis of Zhou2007 Model
3.2. Constructing a CWP-Based Model Considering Cloud Phase and LWP Range
3.2.1. Model Principal
3.2.2. Model Coefficient Derivation
3.3. Calibrated-Zhou Model
4. Results
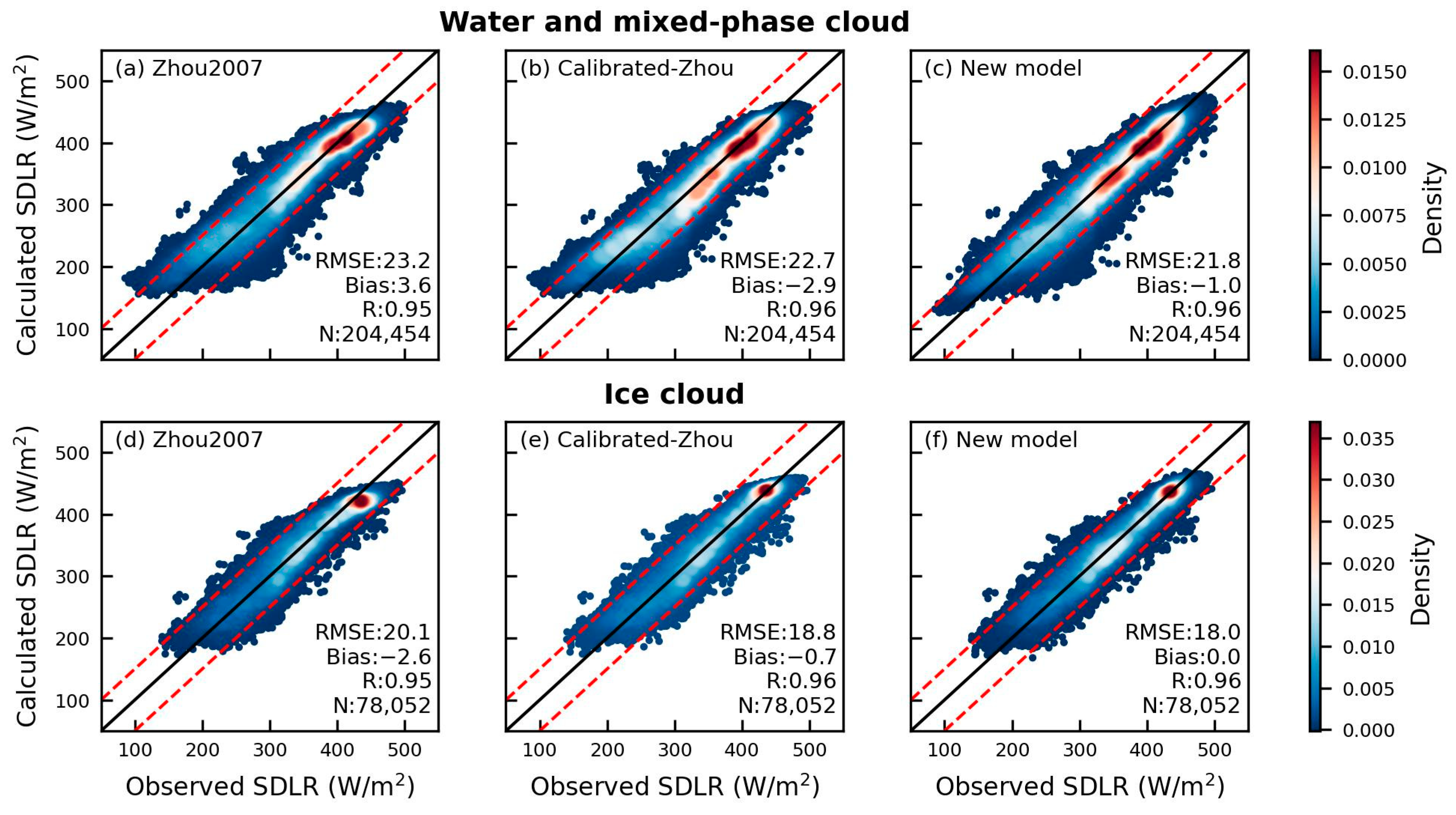
4.1. SDLR Retrievals of Training Dataset
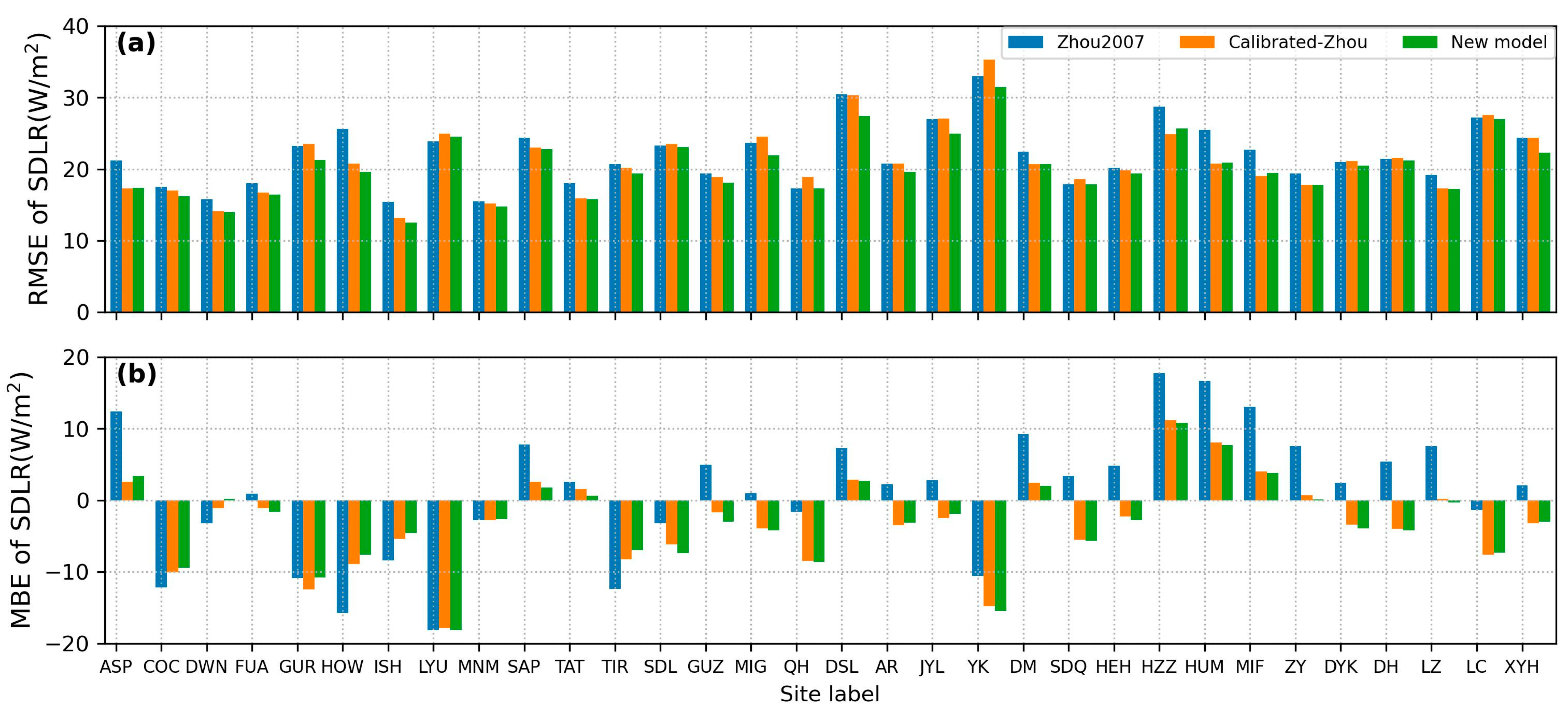
4.2. SDLR Retrievals of Testing Dataset
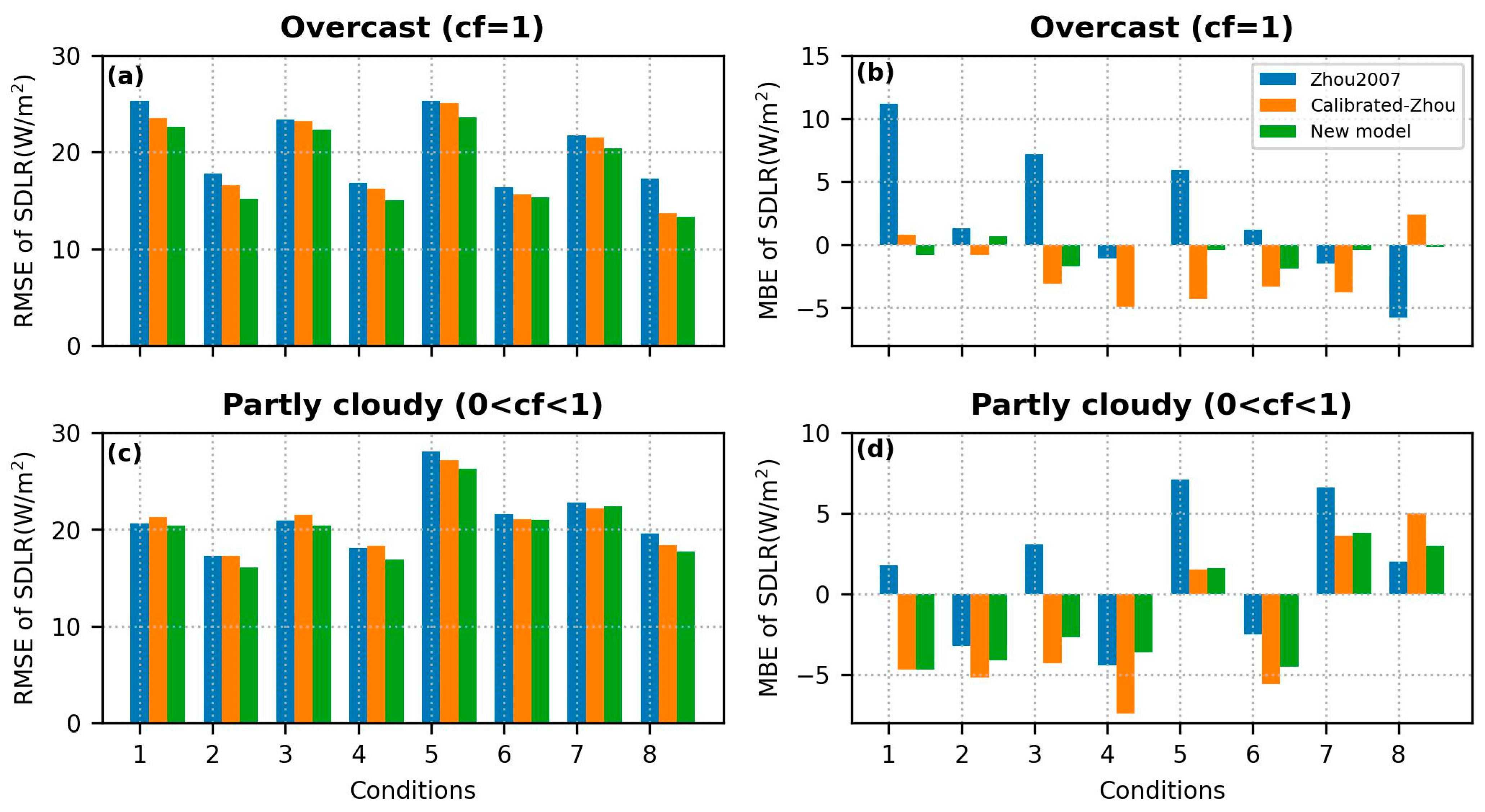
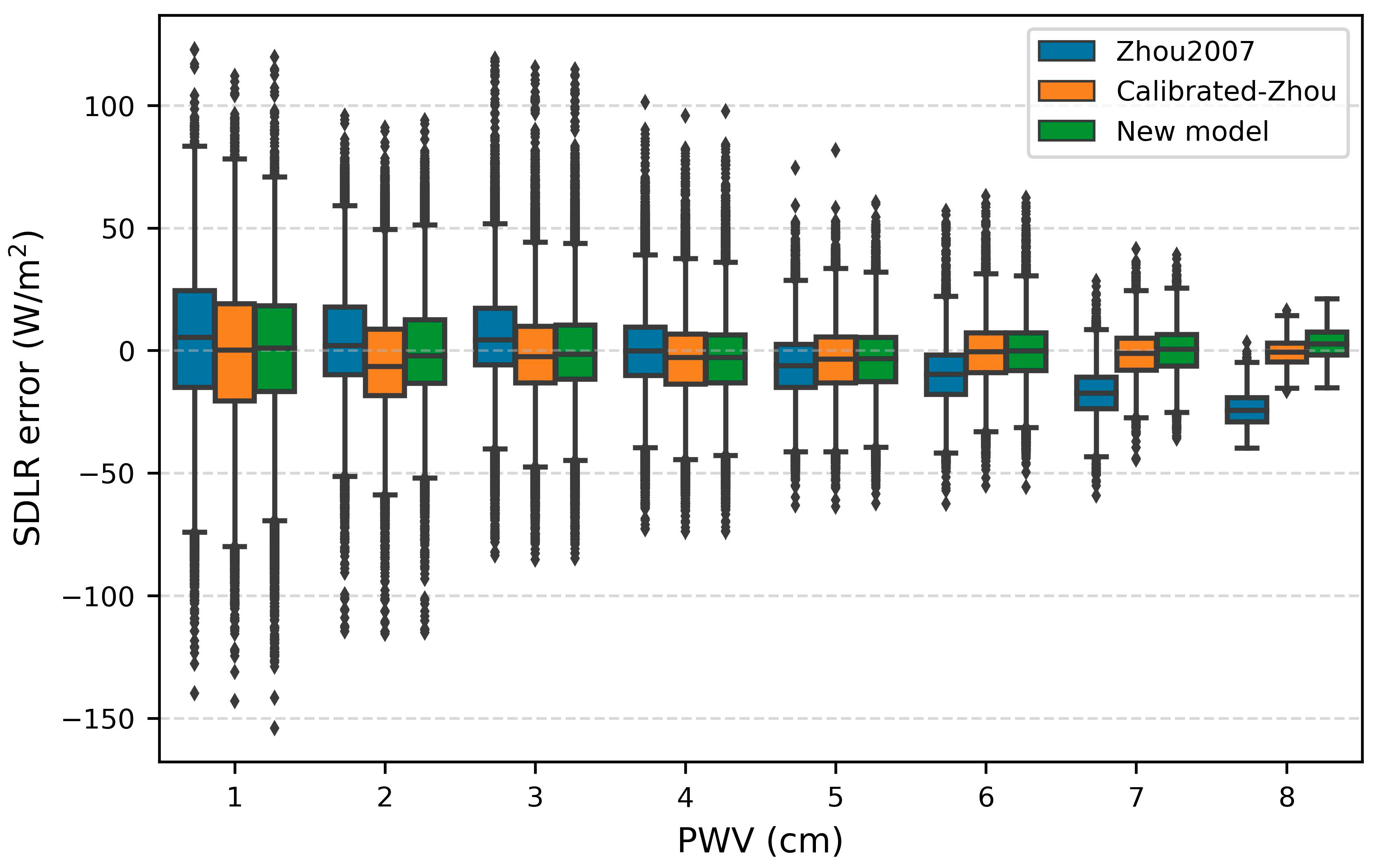
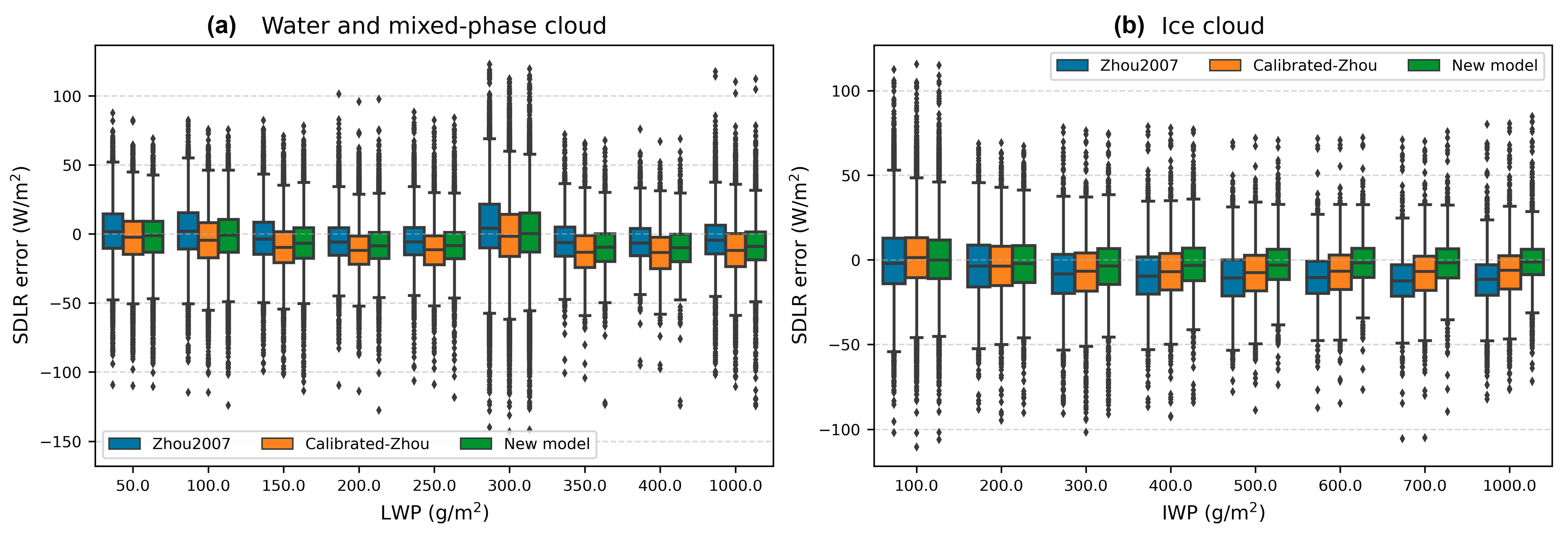
4.3. SDLR Results of Different Atmospheric and Cloud Conditions
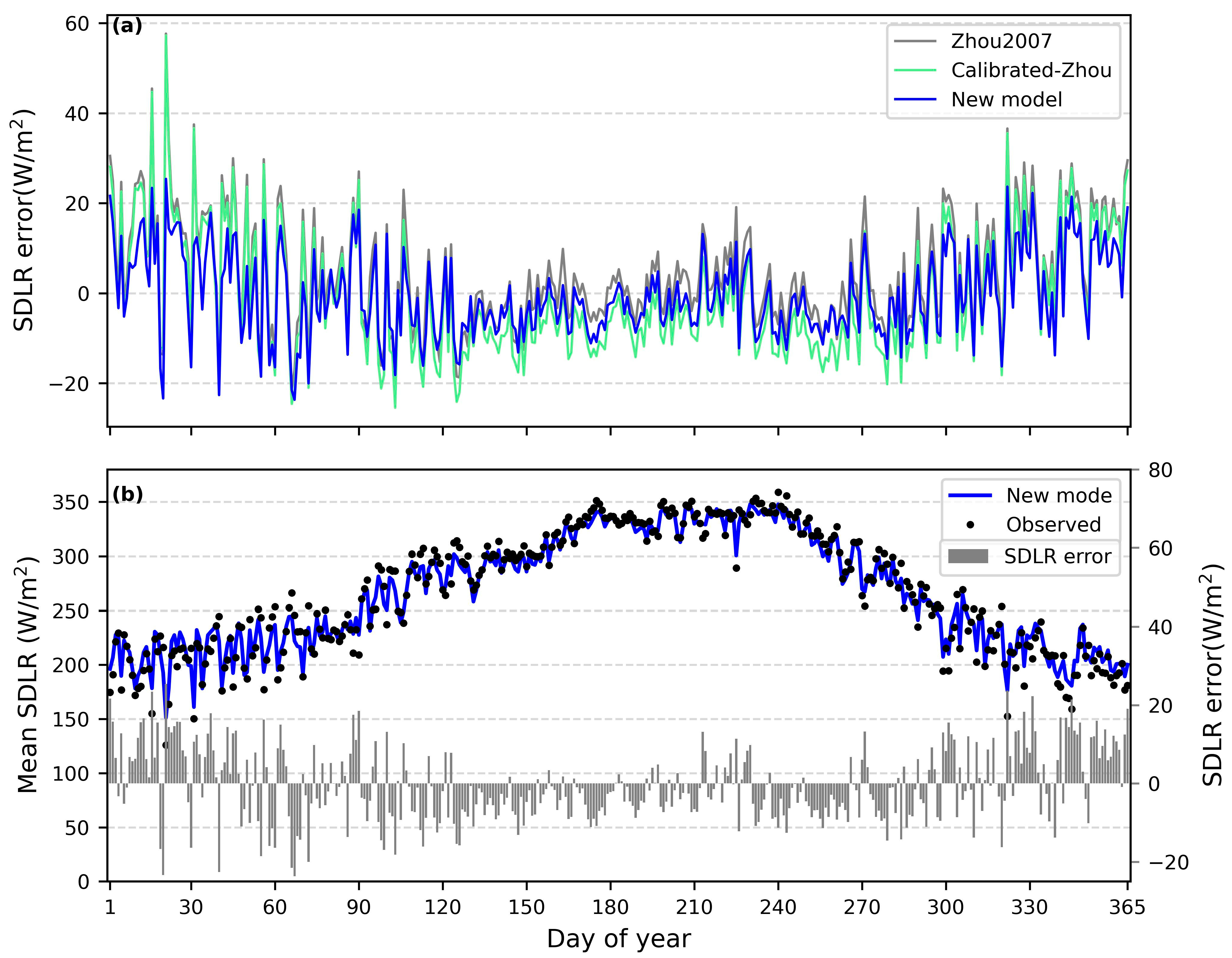
4.4. Seasonal Changes of Cloudy Skies SDLR
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Label | Full Name | Latitude (Deg) | Longitude (Deg) | Elevation (m) | Land Cover | Temporal Resolution (min) |
|---|---|---|---|---|---|---|
| ASP a | Alice Springs | −23.798 | 133.888 | 547 | Grassland | 1 |
| COC a | Cocos Island | −12.193 | 96.835 | 6 | Grassland | 1 |
| DWN a | Darwin Met Office | −12.424 | 130.8925 | 32 | Grassland | 1 |
| FUA a | Fukuoka | 33.5817 | 130.375 | 3 | Asphalt | 1 |
| GUR a | Gurgaon | 28.4249 | 77.156 | 259 | Shrub | 1 |
| HOW a | wrah | 22.5535 | 88.3064 | 51 | Shrub | 1 |
| ISH a | Ishigakijima | 24.3367 | 124.1633 | 6 | Asphalt | 1 |
| LYU a | Lanyu Island | 22.037 | 121.5583 | 324 | Mixed forest | 1 |
| MNM a | Minamitorishima | 24.2883 | 153.9833 | 7 | Grassland | 1 |
| SAP a | Sapporo | 43.06 | 141.3283 | 17 | Asphalt | 1 |
| TAT a | Tateno | 36.05 | 140.1333 | 25 | Grassland | 1 |
| TIR a | Tiruvallur | 13.0923 | 79.9738 | 36 | Rock | 1 |
| SDL b | Sidalong | 38.428 | 99.926 | 3146 | Forest | 10 |
| GUZ b | Guazhou | 41.405 | 95.673 | 2014 | Desert | 10 |
| MIG b | Mixed grassland super station | 37.7032 | 98.5949 | 3718 | Mixed grass | 30 |
| QH b | Qinghai Lake | 36.5909 | 100.4999 | 3209 | Water | 10 |
| DSL b | DaShaLong | 38.8399 | 98.9406 | 3739 | Wet meadow | 10 |
| AR b | Arou | 38.0473 | 100.4643 | 3033 | Grassland | 10 |
| JYL b | JingYangLing | 37.8384 | 101.116 | 3750 | Grassland | 10 |
| YK b | YaKou | 38.0142 | 100.2421 | 4148 | Grassland | 10 |
| DM b | DaMan | 38.8555 | 100.3722 | 1556 | Cropland | 10 |
| SDQ b | SiDaoQiao | 42.0012 | 101.1374 | 873 | Shrub | 10 |
| HEH b | HeiHe | 38.827 | 100.4756 | 1560 | Grassland | 10 |
| HZZ b | HuaZhaiZi | 38.7659 | 100.3201 | 1731 | Desert | 10 |
| HUM b | HuangMo | 42.1135 | 100.9872 | 1054 | Desert | 10 |
| MIF b | Mixed forest | 41.9903 | 101.1335 | 874 | Mixed shrub | 10 |
| ZY b | ZhangYe Wetland | 38.9751 | 100.4464 | 1460 | Wetland | 10 |
| DYK b | DaYeKou | 38.556 | 100.286 | 2703 | Grassland | 10 |
| DH b | Dunhuang WestLake | 40.348 | 93.709 | 993 | Wetland | 10 |
| LZ b | LinZe | 39.238 | 100.062 | 1402 | Cropland | 10 |
| LC b | LianCheng | 36.692 | 102.737 | 2903 | Forest | 10 |
| XYH b | XiYingHe | 37.561 | 101.855 | 3616 | Grassland | 10 |
References
- Kratz, D.P.; Gupta, S.K.; Wilber, A.C.; Sothcott, V.E. Validation of the CERES Edition 2B Surface-Only Flux Algorithms. J. Appl. Meteorol. Climatol. 2010, 49, 164–180. [Google Scholar] [CrossRef]
- Zeng, Q.; Cheng, J.; Dong, L. Assessment of the Long-Term High-Spatial-Resolution Global LAnd Surface Satellite (GLASS) Surface Longwave Radiation Product Using Ground Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2032–2055. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Yu, Y.; Husi, L.; Ling, C. Cloudy-sky land surface longwave downward radiation (LWDR) estimation by integrating MODIS and AIRS/AMSU measurements. Remote Sens. Environ. 2018, 205, 100–111. [Google Scholar] [CrossRef]
- Jiang, Y.; Tang, B.-H.; Zhang, H. Estimation of downwelling surface longwave radiation for cloudy skies by considering the radiation effect from the entire cloud layers. Remote Sens. Environ. 2023, 298, 113829. [Google Scholar] [CrossRef]
- Crawford, T.M.; Duchon, C.E. An Improved Parameterization for Estimating Effective Atmospheric Emissivity for Use in Calculating Daytime Downwelling Longwave Radiation. Appl. Meteorol. Climatol. 1999, 38, 474–480. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Li, M.Y.; Jiang, Y.J.; Coimbra, C.F.M. On the determination of atmospheric longwave irradiance under all-sky conditions. Sol. Energy 2017, 144, 40–48. [Google Scholar] [CrossRef]
- Schmetz, P.; Schmetz, J.; Raschke, E. Estimation of daytime downward longwave radiation at the surface from satellite and grid point data. Theor. Appl. Climatol. 1986, 37, 136–149. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Cess, R.D. Algorithm development strategies for retrieving the downwelling longwave flux at the Earth’s surface. J. Geophys. Res. Atmos. 2001, 106, 12477–12488. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Kratz, D.P.; Wilber, A.C.; Gupta, S.K.; Cess, R.D. An improved algorithm for retrieving surface downwelling longwave radiation from satellite measurements. J. Geophys. Res. Atmos. 2007, 112, D15102. [Google Scholar] [CrossRef]
- Forman, B.A.; Margulis, S.A. High-resolution satellite-based cloud-coupled estimates of total downwelling surface radiation for hydrologic modelling applications. Hydrol. Earth Syst. Sci. 2009, 13, 969–986. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J. A framework for estimating cloudy sky surface downward longwave radiation from the derived active and passive cloud property parameters. Remote Sens. Environ. 2020, 248, 111972. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, X.; Wei, Y.; Zhang, W.; Hou, N.; Xu, J.; Jia, K.; Yao, Y.; Xie, X.; Jiang, B.; et al. Estimating Surface Downward Longwave Radiation Using Machine Learning Methods. Atmosphere 2020, 11, 1147. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Ma, Y.; Letu, H.; Li, X. All-sky longwave downward radiation from satellite measurements: General parameterizations based on LST, column water vapor and cloud top temperature. ISPRS J. Photogramm. Remote Sens. 2020, 161, 52–60. [Google Scholar] [CrossRef]
- Wang, T.; Wang, G.; Shi, C.; Du, Y.; Letu, H.; Zhang, W.; Xue, H. Improved Algorithm to Derive All-Sky Longwave Downward Radiation From Space: Application to Fengyun-4A Measurements. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4103213. [Google Scholar]
- Zhu, F.; Li, X.; Qin, J.; Yang, K.; Cuo, L.; Tang, W.; Shen, C. Integration of Multisource Data to Estimate Downward Longwave Radiation Based on Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4103015. [Google Scholar] [CrossRef]
- Lopes, F.M.; Dutra, E.; Trigo, I.F. Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation. Remote Sens. 2022, 14, 1704. [Google Scholar] [CrossRef]
- Shao, J.; Letu, H.; Ri, X.; Tana, G.; Wang, T.; Shang, H. Estimation of Surface Downward Longwave Radiation and Cloud Base Height Based on Infrared Multichannel Data of Himawari-8. Atmosphere 2023, 14, 493. [Google Scholar] [CrossRef]
- Xu, J.; Liang, S.; Ma, H.; He, T.; Zhang, Y.; Zhang, G. A daily 5-km all-sky sea-surface longwave radiation product based on statistically modified deep neural network and spatiotemporal analysis for 1981–2018. Remote Sens. Environ. 2023, 290, 113550. [Google Scholar] [CrossRef]
- Trigo, I.F.; Barroso, C.; Viterbo, P.; Freitas, S.C.; Monteiro, I.T. Estimation of Downward Long-wave Radiation at the Surface Combining Remotely Sensed Data and NWP Data. J. Geophys. Res. Atmos. 2010, 115, D24118. [Google Scholar] [CrossRef]
- Viúdez-Mora, A.; Costa-Surós, M.; Calbó, J.; González, J.A. Modeling atmospheric longwave radiation at the surface during overcast skies: The role of cloud base height. J. Geophys. Res. Atmos. 2015, 120, 199–214. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, F.; Guo, Y. A Comparative Study of Bulk Parameterization Schemes for Estimating Cloudy-Sky Surface Downward Longwave Radiation. Remote Sens. 2019, 11, 528. [Google Scholar] [CrossRef]
- Gubler, S.; Gruber, S.; Purves, R.S. Uncertainties of parameterized surface downward clear-sky shortwave and all-sky longwave radiation. Atmos. Chem. Phys. 2012, 12, 5077–5098. [Google Scholar] [CrossRef]
- Niemelä, S.; Räisänen, P.; Savijärvi, H. Comparison of surface radiative flux parameterizations: Part I: Longwave radiation. Atmos. Res. 2001, 58, 1–18. [Google Scholar] [CrossRef]
- Gupta, S.K.; Darnell, W.L.; Wilber, A.C. A parameterization for longwave surface radiation from satellite data-recent improvement. J. Appl. Meteorol. 1992, 31, 1361–1367. [Google Scholar] [CrossRef]
- Diak, G.R.; Bland, W.L.; Mecikalski, J.R.; Anderson, M.C. Satellite-based estimates of longwave radiation for agricultural applications. Agric. For. Meteorol. 2000, 103, 349–355. [Google Scholar] [CrossRef]
- Yu, S.; Xin, X.; Liu, Q.; Zhang, H.; Li, L. Comparison of Cloudy-Sky Downward Longwave Radiation Algorithms Using Synthetic Data, Ground-Based Data, and Satellite Data. J. Geophys. Res. Atmos. 2018, 123, 5397–5415. [Google Scholar] [CrossRef]
- Yu, S.; Li, L.; Cao, B.; Zhang, H.; Zhu, L.; Xin, X.; Liu, Q. Surface downward longwave radiation estimation from new generation geostationary satellite data. Atmos. Res. 2022, 276, 106255. [Google Scholar] [CrossRef]
- Wang, T.; Luo, J.; Liang, J.; Wang, B.; Tian, W.; Chen, X. Comparisons of AGRI/FY-4A Cloud Fraction and Cloud Top Pressure with MODIS/Terra Measurements over East Asia. J. Meteorol. Res. 2019, 33, 705–719. [Google Scholar] [CrossRef]
- Li, M.; Luo, Y.; Min, M. Characteristics of Pre-summer Daytime Cloud Regimes over Coastal South China from the Himawari-8 Satellite. Adv. Atmos. Sci. 2022, 39, 2008–2023. [Google Scholar] [CrossRef]
- Min, M.; Wu, C.; Li, C.; Liu, H.; Xu, N.; Wu, X.; Chen, L.; Wang, F.; Sun, F.; Qin, D.; et al. Developing the science product algorithm testbed for Chinese next-generation geostationary meteorological satellites: Fengyun-4 series. J. Meteorol. Res. 2017, 31, 708–719. [Google Scholar] [CrossRef]
- Minnis, P.; Heck, P.W. GOES-R Advanced Baseline Imager (ABI) Algorithm Theoretical Basis Document for Nighttime Cloud Optical Depth, Cloud Particle Size, Cloud Ice Water Path, and Cloud Liquid Water Path. NOAA/NESDIS Center for Satellite Applications and Research; 2012. Available online: https://www.star.nesdis.noaa.gov/goesr/documents/ATBDs/Baseline/ATBD_GOES-R_Cloud_NCOMP_v3.0_Jul2012.pdf (accessed on 26 January 2022).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Pressure Levels from 1979 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels (accessed on 20 April 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels (accessed on 20 April 2021).
- Lee, H.T.; Laszlo, I.; Gruber, A. ABI Earth Radiation Budget-Downward Longwave Radiation: Surface (DLR). NOAA Nesdis Center for Satellite Applications and Research, Algorithm Theoretical Basis Document. 2010. Available online: https://www.goes-r.gov/products/ATBDs/option2/RadBud_DLR_v2.0_no_color.pdf (accessed on 26 January 2022).
- Yu, S.; Xin, X.; Liu, Q.; Zhang, H.; Li, L. An Improved Parameterization for Retrieving Clear-Sky Downward Longwave Radiation from Satellite Thermal Infrared Data. Remote Sens. 2019, 11, 425. [Google Scholar] [CrossRef]
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; König-Langlo, G.; McArthur, B.; Müller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New Precision Radiometry for Climate Research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Liu, S.; Li, H.; Xu, Z.; Tan, J.; Zhang, Y.; Ren, Z.; Xiao, L.; Deng, J.; et al. Integrated hydrometeorological, snow and frozen-ground observations in the alpine region of the Heihe River Basin, China. Earth Syst. Sci. Data 2019, 11, 1483–1499. [Google Scholar] [CrossRef]
- Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q.; Ma, M.G.; Liu, Q.H.; Jin, R.; Guo, J.W.; Wang, L.X.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 180072. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, R. Cold and Arid Research Network of Lanzhou University (An Observation System of Meteorological Elements Gradient of Sidalong Station, 2019). National Tibetan Plateau/Third Pole Environment Data Center. 2020. Available online: https://data.tpdc.ac.cn/en/data/b2034867-68c4-4cf4-8b3a-c345e5b26759/ (accessed on 26 January 2022).
- Li, X. Qilian Mountains Integrated Observatory Network: Dataset of Qinghai Lake Integrated Observatory Network (An Observation System of Meteorological Elements Gradient of Yulei Station on Qinghai Lake, 2019). 2020. National Tibetan Plateau/Third Pole Environment Data Center. Available online: https://data.tpdc.ac.cn/en/data/08a95cc1-19ba-41b5-9b9d-353f4f6b9d1e/ (accessed on 26 January 2022).
- Li, X.Y.; Yang, X.F.; Ma, Y.J.; Hu, G.R.; Hu, X.; Wu, X.C.; Wang, P.; Huang, Y.M.; Cui, B.L.; Wei, J.Q. Qinghai Lake Basin Critical Zone Observatory on the Qinghai-Tibet Plateau. Vadose Zone J. 2018, 17, 180069. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Li, B.Y.; Liu, L.S.; Zheng, D. Redetermine the region and boundaries of Tibetan Plateau. Geogr. Res. 2021, 40, 1543–1553. [Google Scholar]
- Wang, K.; Dickinson, R.E. Global atmospheric downward longwave radiation at the surface from ground-based observations, satellite retrievals, and reanalyses. Rev. Geophys. 2013, 51, 150–185. [Google Scholar] [CrossRef]
- Long, C.N.; Dutton, E.G. BSRN Global Network Recommended QC Tests, V2.0. Available online: https://bsrn.awi.de/fileadmin/user_upload/bsrn.awi.de/Publications/BSRN_recommended_QC_tests_V2.pdf (accessed on 9 August 2023).





| Sources | Products | Parameters | Resolution | Function |
|---|---|---|---|---|
| FY-4A | L1 GEO | Latitude, longitude | 4 km | Geolocation |
| CLM | Cloud mask | 4 km | Cloud detection | |
| CFR | Cloud fraction | 4 km | SDLR estimation | |
| CLP | Cloud phase | 4 km | ||
| CPD and CPN | Cloud liquid water path (LWP) and ice water path (IWP) | 4 km | ||
| ERA5 reanalysis | ERA5 hourly data on pressure and single levels | 2 m air temperature (Ta), PWV | 0.25° hourly | SDLR estimation |
| USGS | GMTED2010 | Surface elevation (DEM) | 0.05° | Atmospheric profile interpolation |
| Cloud Conditions | LWP Range (g/m2) | PWV (cm) | a0 | a1 | a2 | a3 | a4 |
|---|---|---|---|---|---|---|---|
| Water and mixed phase cloud | (0, 50] | (0, 2] | 32.9619 | 0.5469 | 70.3615 | 28.5630 | −2.2896 |
| (2, 8) | −237.0998 | 0.7254 | 334.4421 | −78.9135 | 6.4414 | ||
| (50, 100] | (0, 2] | −10.6017 | 0.5154 | 27.8440 | 73.3841 | 12.9042 | |
| (2, 8) | 9.6408 | 0.5733 | 15.1083 | 57.3603 | 8.3065 | ||
| (100, 4000) | (0, 2] | 20.7546 | 0.3292 | 245.0102 | −46.1900 | — | |
| (2, 8) | 123.5700 | 0.4503 | −27.6544 | 75.0153 | — | ||
| Ice cloud | 0 | (0, 2] | 14.9959 | 0.3667 | 184.0043 | −28.0156 | 6.2955 |
| (2, 8) | 87.8222 | 0.4838 | −21.7233 | 71.6096 | 3.4303 |
| Cloud Conditions | LWP Range (g/m2) | PWV (cm) | N | Zhou2007 | Calibrated-Zhou | New Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MBE | R | RMSE | MBE | R | RMSE | MBE | R | ||||
| Water and mixed- phase cloud | (0, 50] | (0, 2] | 808 | 26.2 | 10.7 | 0.83 | 24.2 | −0.5 | 0.82 | 23.8 | −1.7 | 0.83 |
| (2, 8) | 1517 | 18.2 | −0.4 | 0.88 | 17.4 | −1.9 | 0.85 | 15.0 | 0.0 | 0.88 | ||
| All | 2325 | 21.3 | 3.4 | 0.94 | 20.0 | −1.4 | 0.94 | 18.6 | −0.6 | 0.95 | ||
| (50, 100] | (0, 2] | 2414 | 23.3 | 8.3 | 0.91 | 22.4 | −1.9 | 0.91 | 21.7 | −0.6 | 0.91 | |
| (2, 8) | 2105 | 17.9 | −1.5 | 0.88 | 16.9 | −4.9 | 0.88 | 15.2 | 0.0 | 0.89 | ||
| ALL | 4519 | 20.9 | 3.7 | 0.96 | 20.0 | −3.3 | 0.96 | 19.0 | −0.3 | 0.96 | ||
| (100, 4000) | (0, 2] | 21,241 | 25.0 | 6.3 | 0.88 | 24.3 | −4.1 | 0.88 | 23.3 | −0.1 | 0.89 | |
| (2, 8) | 20,995 | 16.9 | 3.2 | 0.86 | 15.2 | −1.1 | 0.88 | 15.0 | 0.0 | 0.88 | ||
| ALL | 42,236 | 21.4 | 4.7 | 0.95 | 20.3 | −2.6 | 0.95 | 19.6 | 0.0 | 0.95 | ||
| Ice cloud | 0 | (0, 2] | 12,281 | 21.7 | −2.0 | 0.88 | 21.4 | −4.4 | 0.88 | 20.3 | −0.4 | 0.89 |
| (2, 8) | 12,695 | 17.1 | −5.9 | 0.90 | 13.7 | 2.3 | 0.92 | 13.1 | 0.0 | 0.92 | ||
| ALL | 24,976 | 19.5 | −4.0 | 0.95 | 17.9 | −1.0 | 0.96 | 17.0 | −0.2 | 0.96 | ||
| Cloud Conditions | LWP Range (g/m2) | PWV (cm) | N | Zhou2007 | Calibrated-Zhou | New Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MBE | R | RMSE | MBE | R | RMSE | MBE | R | ||||
| Water and mixed- phase cloud | (0, 50] | (0, 2] | 5948 | 22.4 | 5.2 | 0.91 | 22.1 | −2.7 | 0.91 | 21.2 | −3.3 | 0.91 |
| (2, 8) | 5735 | 17.5 | −1.4 | 0.86 | 17.0 | −3.4 | 0.86 | 15.8 | −2.2 | 0.88 | ||
| All | 11,683 | 20.1 | 1.9 | 0.95 | 19.8 | −3.1 | 0.95 | 18.7 | −2.7 | 0.96 | ||
| (50, 100] | (0, 2] | 10,319 | 22.4 | 5.5 | 0.91 | 22.5 | −3.6 | 0.91 | 21.6 | −2.1 | 0.91 | |
| (2, 8) | 7133 | 17.4 | −2.5 | 0.86 | 17.2 | −6.0 | 0.87 | 15.8 | −1.6 | 0.87 | ||
| ALL | 17,452 | 20.5 | 2.2 | 0.96 | 20.5 | −4.6 | 0.96 | 19.4 | −1.9 | 0.96 | ||
| (100, 4000) | (0, 2] | 106,999 | 26.5 | 6.4 | 0.90 | 26.0 | −1.9 | 0.90 | 24.8 | 0.4 | 0.90 | |
| (2, 8) | 68,320 | 18.3 | 0.0 | 0.82 | 17.6 | −4.1 | 0.84 | 17.3 | −2.7 | 0.84 | ||
| ALL | 175,319 | 23.7 | 3.9 | 0.95 | 23.1 | −2.8 | 0.95 | 22.2 | −0.8 | 0.96 | ||
| Ice cloud | 0 | (0, 2] | 45,033 | 21.8 | −0.7 | 0.89 | 21.5 | −3.1 | 0.89 | 20.6 | 0.0 | 0.90 |
| (2, 8) | 33,019 | 17.4 | −5.3 | 0.89 | 14.1 | 2.6 | 0.91 | 13.6 | 0.0 | 0.91 | ||
| ALL | 78,052 | 20.1 | −2.6 | 0.95 | 18.8 | −0.7 | 0.96 | 18.0 | 0.0 | 0.96 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Xin, X.; Zhang, H.; Li, L.; Zhu, L.; Liu, Q. A Cloud Water Path-Based Model for Cloudy-Sky Downward Longwave Radiation Estimation from FY-4A Data. Remote Sens. 2023, 15, 5531. https://doi.org/10.3390/rs15235531
Yu S, Xin X, Zhang H, Li L, Zhu L, Liu Q. A Cloud Water Path-Based Model for Cloudy-Sky Downward Longwave Radiation Estimation from FY-4A Data. Remote Sensing. 2023; 15(23):5531. https://doi.org/10.3390/rs15235531
Chicago/Turabian StyleYu, Shanshan, Xiaozhou Xin, Hailong Zhang, Li Li, Lin Zhu, and Qinhuo Liu. 2023. "A Cloud Water Path-Based Model for Cloudy-Sky Downward Longwave Radiation Estimation from FY-4A Data" Remote Sensing 15, no. 23: 5531. https://doi.org/10.3390/rs15235531
APA StyleYu, S., Xin, X., Zhang, H., Li, L., Zhu, L., & Liu, Q. (2023). A Cloud Water Path-Based Model for Cloudy-Sky Downward Longwave Radiation Estimation from FY-4A Data. Remote Sensing, 15(23), 5531. https://doi.org/10.3390/rs15235531






