A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy
Abstract
:1. Introduction
2. Shortwave Camera Suite
- 1.
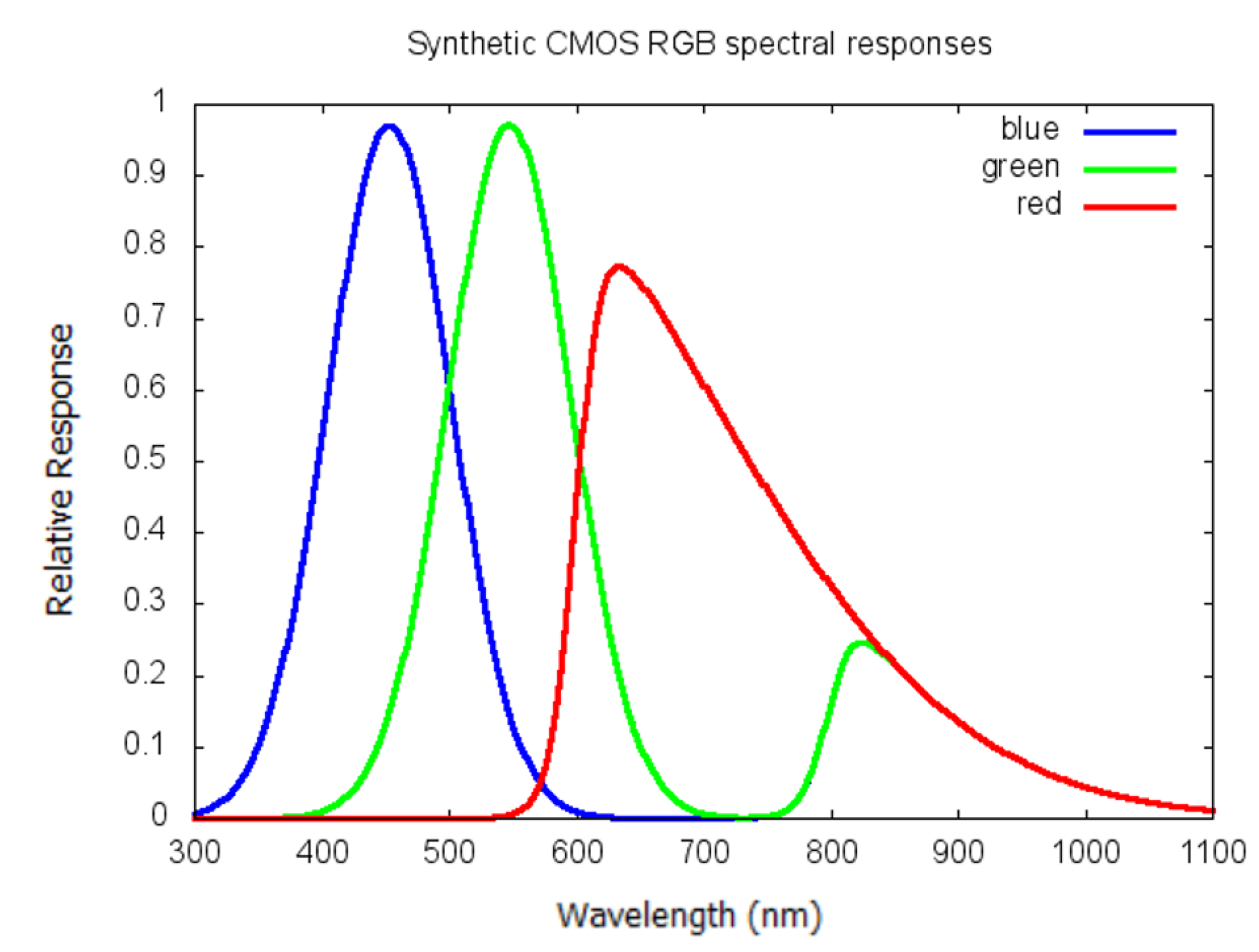
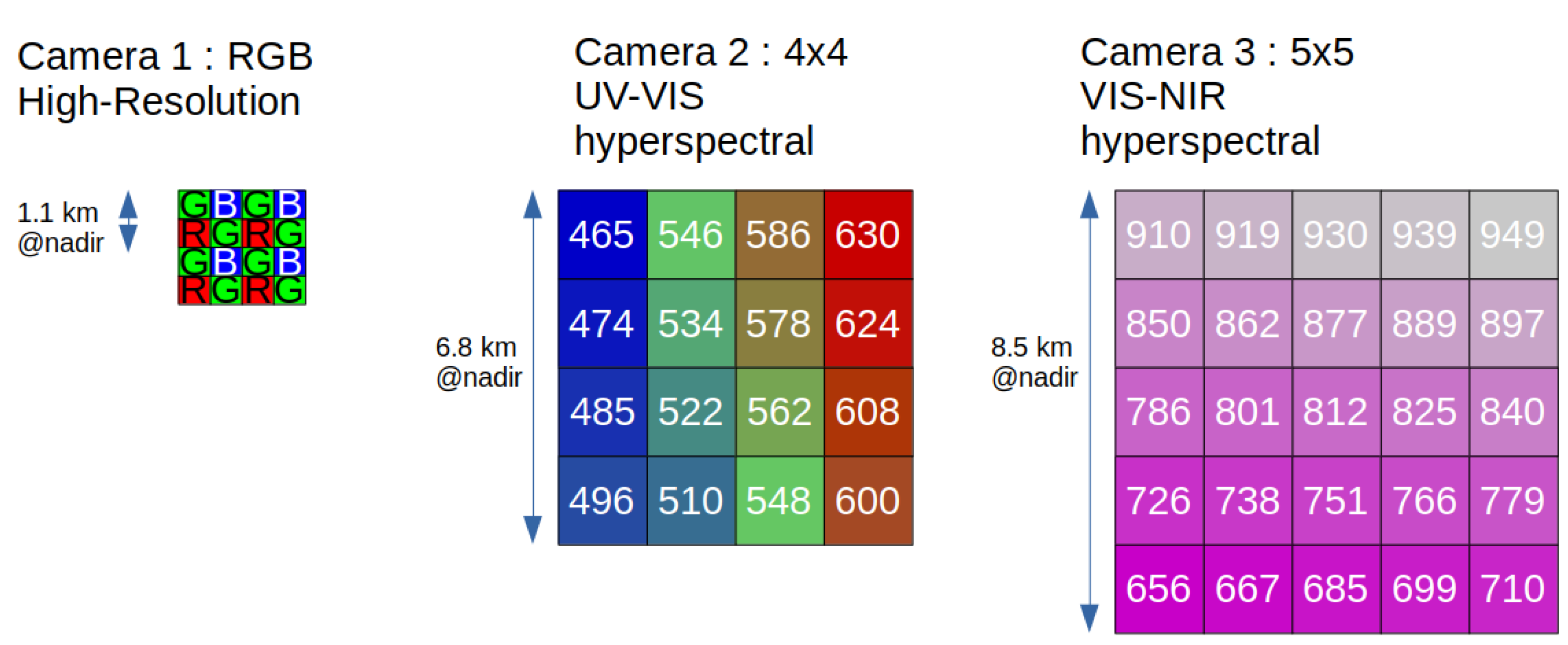
- ECO SW Camera 1 will be the RGB high-resolution SW camera, formed of a CMOS sensor, with spectral response between 400 and 1000 nm, with standard ‘RGGB’ Bayer pattern. The active area of the CMOS sensor will be 3000 × 3000 pixels, yielding a nadir resolution for a single pixel of 0.57 km and a nadir resolution for the 2 × 2 RGGB pixels of 1.1 km. The pixel pattern of SW Camera 1 is illustrated in the left part of Figure 6.
- 2.
- 3.
3. Optical Design High-Resolution SW Camera
3.1. The Design Parameters
3.2. Optical Performance
3.2.1. RMS Error
3.2.2. Seidel Aberrations
3.2.3. Point Spread Function (PSF)
3.3. Simulated Performance for Earth Observation
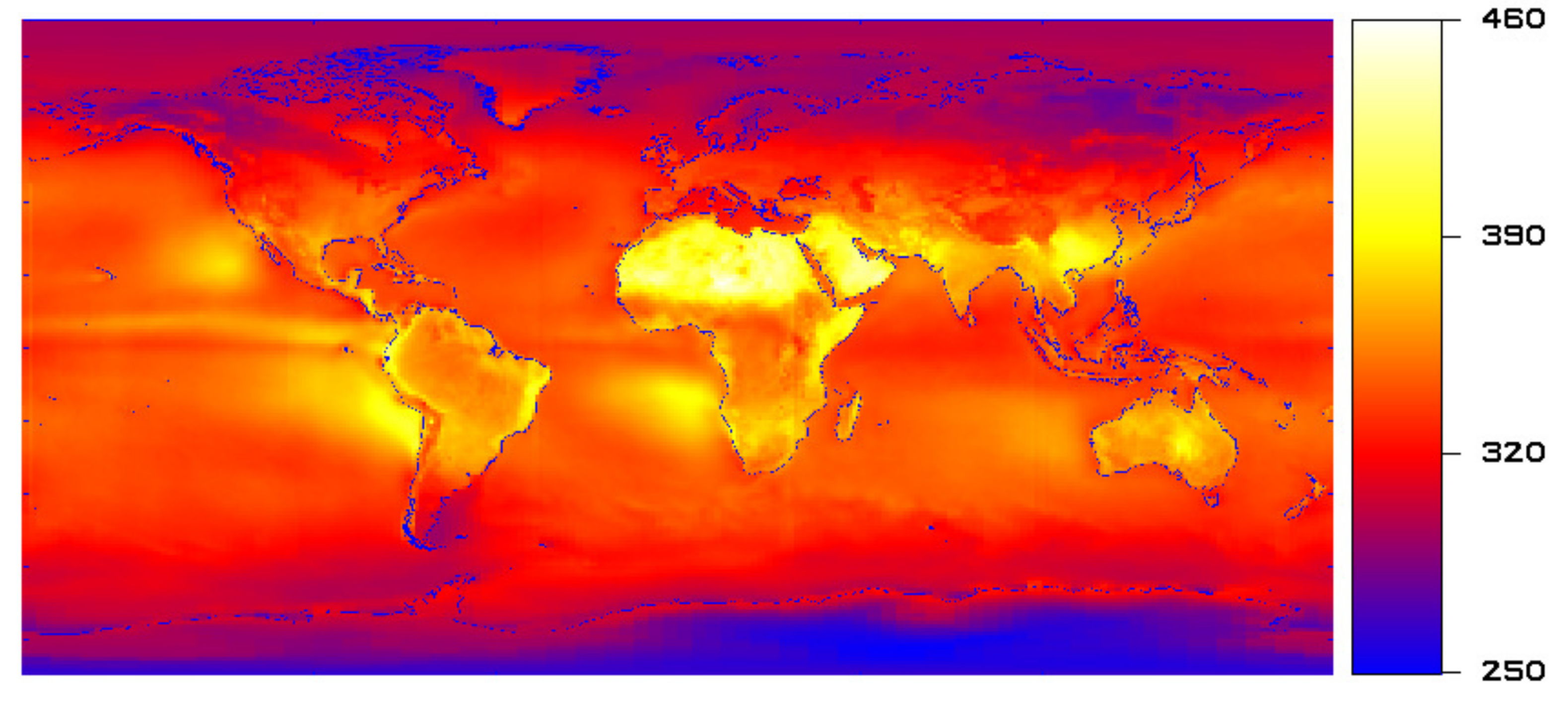
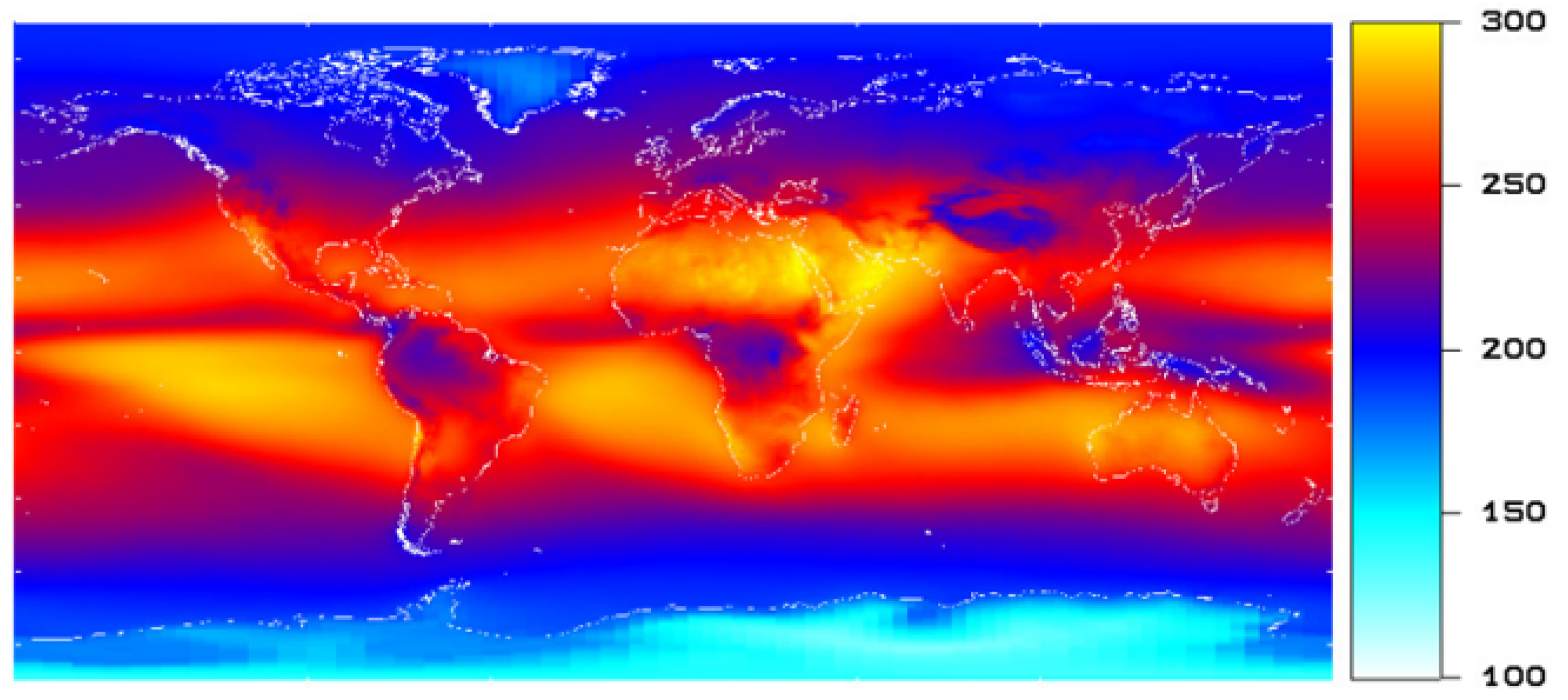
3.3.1. SNR High-Resolution 4K-RGB Camera
3.3.2. SNR Multispectral Cameras
4. Longwave Camera Suite
4.1. Multispectral Thermal Cameras
4.2. Noise-Equivalent Differential Temperature (NEDT)
4.3. Longwave Spectral Regression
- 1.
- Conversion of the narrowband irradiance to a narrowband brightness temperature .
- 2.
- Conversion of the narrowband brightness temperature to a broadband brightness temperature .
- 3.
- Conversion of the broadband brightness temperature to the OLR.
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EEI | Earth Energy Imbalance |
| FWHM | Full Width at Half Maximum |
| OLR | Outgoing Longwave Radiation |
| RSR | Reflected Solar Radiation |
| WFOV | wide field of view |
| VIS | Visible |
| VIS-NIR | Visible and Near-infrared |
| CMOS | complementary metal oxide semiconductor |
| FOV | field of view |
| RMS | root mean square |
| PSF | Point Spread Function |
| SNR | Signal-to-Noise Ratio |
| LSB | least significant bit |
| NEDT | Noise-Equivalent Differential Temperature |
References
- Dewitte, S.; Clerbaux, N. Measurement of the Earth radiation budget at the top of the atmosphere—A review. Remote Sens. 2017, 9, 1143. [Google Scholar] [CrossRef]
- Trenberth, K.; Fasullo, J.; Von Schuckmann, K.; Cheng, L. Insights into Earth’s energy imbalance from multiple sources. J. Clim. 2016, 29, 7495–7505. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Cheng, L.; Palmer, M.; Hansen, J.; Tassone, C.; Aich, V.; Adusumilli, S.; Beltrami, H.; Boyer, T.; Cuesta-Valero, F.; et al. Heat stored in the Earth system: Where does the energy go? Earth Syst. Sci. Data 2020, 12, 2013–2041. [Google Scholar] [CrossRef]
- Hansen, J.; Nazarenko, L.; Ruedy, R.; Sato, M.; Willis, J.; Del Genio, A.; Koch, D.; Lacis, A.; Lo, K.; Menon, S.; et al. Earth’s energy imbalance: Confirmation and implications. Science 2005, 308, 1431–1435. [Google Scholar] [CrossRef] [PubMed]
- Von Schuckmann, K.; Palmer, M.; Trenberth, K.; Cazenave, A.; Chambers, D.; Champollion, N.; Hansen, J.; Josey, S.; Loeb, N.; Mathieu, P.; et al. An imperative to monitor Earth’s energy imbalance. Nat. Clim. Chang. 2016, 6, 138–144. [Google Scholar] [CrossRef]
- Schifano, L.; Smeesters, L.; Geernaert, T.; Berghmans, F.; Dewitte, S. Design and analysis of a next-generation wide field-of-view earth radiation budget radiometer. Remote Sens. 2020, 12, 425. [Google Scholar] [CrossRef]
- Rutan, D.; Smith, G.; Wong, T. Diurnal Variations of Albedo Retrieved from Earth Radiation Budget Experiment Measurements. J. Appl. Meteorol. Climatol. 2014, 53, 2747–2760. [Google Scholar] [CrossRef]
- Smith, G.; Rutan, D. The Diurnal Cycle of Outgoing Longwave Radiation from Earth Radiation Budget Experiment Measurements. J. Atmos. Sci. 2003, 60, 1529–1542. [Google Scholar] [CrossRef]
- Gristey, J.J.; Chiu, J.C.; Gurney, R.J.; Morcrette, C.J.; Hill, P.G.; Russell, J.E.; Brindley, H.E. Insights into the diurnal cycle of global Earth outgoing radiation using a numerical weather prediction model. Atmos. Chem. Phys. 2018, 18, 5129–5145. [Google Scholar] [CrossRef]
- Doelling, D.; Keyes, D.; Nordeen, M.; Morstad, D.; Nguyen, C.; Wielicki, B.; Young, D.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Loeb, N.; Doelling, D.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.; Liang, L.; Mitrescu, C.; Rose, F.; Kato, S. Clouds and the earth’s radiant energy system (CERES) energy balanced and filled (EBAF) top-of-atmosphere (TOA) edition-4.0 data product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.; Rose, F.; Thorsen, T.; Rutan, D.; Ham, S.H.; Doelling, D. Earth Radiation Budget Climate Record Composed of Multiple Satellite Observations; GFZ German Research Centre for Geosciences: Berlin, Germany, 2023; p. IUGG23-4506. [Google Scholar]
- Harries, J.E.; Russell, J.E.; Hanafin, J.A.; Brindley, H.; Futyan, J.; Rufus, J.; Kellock, S.; Matthews, G.; Wrigley, R.; Last, A.; et al. The Geostationary Earth Radiation Budget Project. Bull. Am. Meteorol. Soc. 2005, 86, 945–960. [Google Scholar] [CrossRef]
- Hocking, T.; Mauritsen, T.; Megner, L. Sampling strategies for Earth Energy Imbalance measurements using a satellite radiometer. In Proceedings of the Earth Energy Imbalance Assessment Workshop, Frascati, Italy, 15–17 May 2023. [Google Scholar]
- Li, Z.; Leighton, H.G. Narrowband to Broadband Conversion with Spatially Autocorrelated Reflectance Measurements. J. Appl. Meteorol. Climatol. 1992, 31, 421–432. [Google Scholar] [CrossRef]
- Lee, H.T.; Gruber, A.; Ellingson, R.; Laszlo, I. Development of the HIRS Outgoing Longwave Radiation Climate Dataset. J. Atmos. Ocean. Technol. 2007, 24, 2029–2047. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S. Estimating high-resolution top of atmosphere albedo from Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2016, 178, 93–103. [Google Scholar] [CrossRef]
- Urbain, M.; Clerbaux, N.; Ipe, A.; Tornow, F.; Hollmann, R.; Baudrez, E.; Velazquez Blazquez, A.; Moreels, J. The CM SAF TOA Radiation Data Record Using MVIRI and SEVIRI. Remote Sens. 2017, 9, 466. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.; Harrison, E.; Lee, R.B., III; Smith, L.G.; Cooper, J. Clouds and the Earth’s Radiant Energy System (CERES): An Earth Observing System Experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Dewitte, S.; Gonzalez, L.; Clerbaux, N.; Ipe, A.; Bertrand, C.; De Paepe, B. The Geostationary Earth Radiation Budget Edition 1 data processing algorithms. Adv. Space Res. 2008, 41, 1906–1913. [Google Scholar] [CrossRef]
- Loeb, N.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B. Angular Distribution Models for Top-of-Atmosphere Radiative Flux Estimation from the Clouds and the Earth’s Radiant Energy System Instrument on the Tropical Rainfall Measuring Mission Satellite. Part I: Methodology. J. Appl. Meteorol. Climatol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Dewitte, S.; Cornelis, J.P.; Müller, R.; Munteanu, A. Artificial Intelligence Revolutionises Weather Forecast, Climate Monitoring and Decadal Prediction. Remote Sens. 2021, 13, 3209. [Google Scholar] [CrossRef]
- Schifano, L.; Smeesters, L.; Berghmans, F.; Dewitte, S. Optical system design of a wide field-of-view camera for the characterization of earth’s reflected solar radiation. Remote Sens. 2020, 12, 2556. [Google Scholar] [CrossRef]
- Schifano, L.; Smeesters, L.; Berghmans, F.; Dewitte, S. Wide-field-of-view longwave camera for the characterization of the earth’s outgoing longwave radiation. Sensors 2020, 21, 4444. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Doelling, D.; Morstad, D.; Angal, A.; Bhatt, R. Characterization of Terra and Aqua MODIS VIS, NIR, and SWIR spectral bands’ calibration stability. IEEE Trans. Geosci. Remote Sens. 2012, 51, 4330–4338. [Google Scholar] [CrossRef]
- Decoster, I.; Clerbaux, N.; Baudrez, E.; Dewitte, S.; Ipe, A.; Nevens, S.; Blazquez, A.; Cornelis, J. Spectral aging model applied to meteosat first generation visible band. Remote Sens. 2014, 6, 2534–2571. [Google Scholar] [CrossRef]
- Sterckx, S.; Adriaensen, S.; Dierckx, W.; Bouvet, M. In-orbit radiometric calibration and stability monitoring of the PROBA-V instrument. Remote Sens. 2016, 8, 546. [Google Scholar] [CrossRef]
- Geelen, B.; Blanch, C.; Gonzalez, P.; Tack, N.; Lambrechts, A. A tiny VIS-NIR snapshot multispectral camera. In Proceedings of the Advanced Fabrication Technologies for Micro/Nano Optics and Photonics VIII, San Francisco, CA, USA, 8–11 February 2015; Volume 9374, pp. 194–201. [Google Scholar]
- Weidmann, D.; Antonini, K.; Pino, D.; Brodersen, B.; Patel, G.; Hegglin, M.; Sioris, C.; Bell, W.; Miyazaki, K.; Alminde, L.; et al. Cubesats for monitoring atmospheric processes (CubeMAP): A constellation mission to study the middle atmosphere. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIV, Online, 21–25 September 2020; Volume 11530, pp. 141–159. [Google Scholar]
- Michel, P.; Küppers, M.; Bagatin, A.; Carry, B.; Charnoz, S.; De Leon, J.; Fitzsimmons, A.; Gordo, P.; Green, S.; Hérique, A.; et al. The ESA Hera mission: Detailed characterization of the DART impact outcome and of the binary asteroid (65803) Didymos. Planet. Sci. J. 2022, 3, 160. [Google Scholar] [CrossRef]
- Adibekyan, A.; Kononogova, E.; Monte, C.; Hollandt, J. High-accuracy emissivity data on the coatings Nextel 811-21, Herberts 1534, Aeroglaze Z306 and Acktar Fractal Black. Int. J. Thermophys. 2017, 38, 1–14. [Google Scholar] [CrossRef]
- Okada, T.; Tanaka, S.; Sakatani, N.; Shimaki, Y.; Arai, T.; Senshu, H.; Demura, H.; Sekiguchi, T.; Kouyama, T.; Kanamaru, M.; et al. Calibration of the Thermal Infrared Imager TIRI onboard Hera. In Proceedings of the European Planetary Science Congress, Granada, Spain, 18–23 September 2022; p. EPSC2022-1191. [Google Scholar]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to Meteosat second generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Ouaknine, J.; Viard, T.; Napierala, B.; Foerster, U.; Fray, S.; Hallibert, P.; Durand, Y.; Imperiali, S.; Pelouas, P.; Rodolfo, J.; et al. The FCI on board MTG: Optical design and performances. In Proceedings of the International Conference on Space Optics, Okinawa, Japan, 14–16 November 2017; Volume 10563, pp. 617–625. [Google Scholar]
- Tissot, J.; Tinnes, S.; Durand, A.; Minassian, C.; Robert, P.; Vilain, M. High-performance uncooled amorphous silicon VGA and XGA IRFPA with 17 µm pixel-pitch. In Proceedings of the Electro-optical and infrared systems: Technology and applications VII, Toulouse, France, 21–23 September 2010; Volume 7834, pp. 147–154. [Google Scholar]
- Arad, B.; Timofte, R.; Yahel, R.; Morag, N.; Bernat, A.; Wu, Y.; Wu, X.; Fan, Z.; Xia, C.; Zhang, F.; et al. NTIRE 2022 spectral demosaicing challenge and data set. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 882–896. [Google Scholar]
- Zeng, H.; Feng, K.; Huang, S.; Cao, J.; Chen, Y.; Zhang, H.; Luong, H.; Philips, W. MSFA-Frequency-Aware Transformer for Hyperspectral Images Demosaicing. arXiv 2023, arXiv:2303.13404. [Google Scholar] [CrossRef]


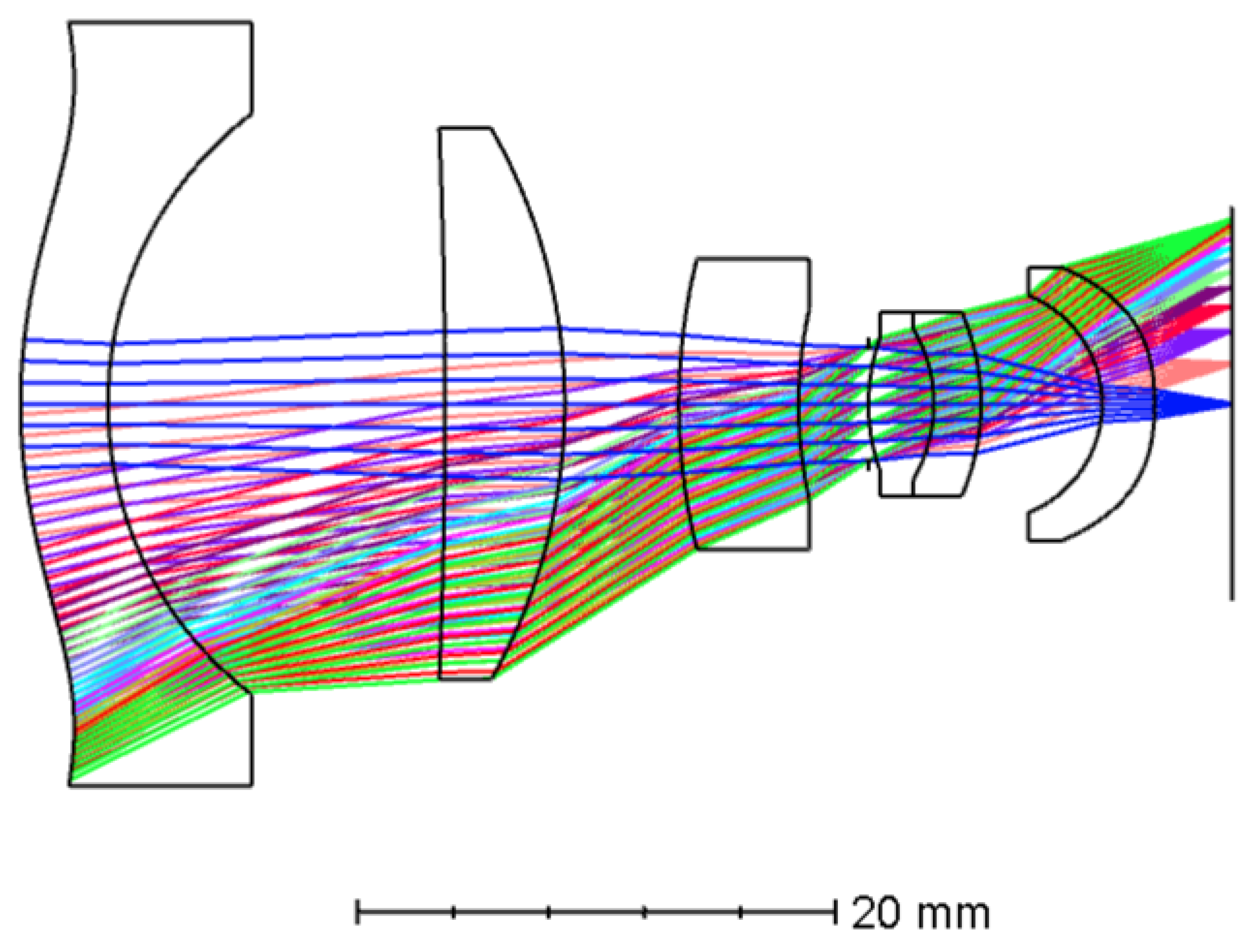

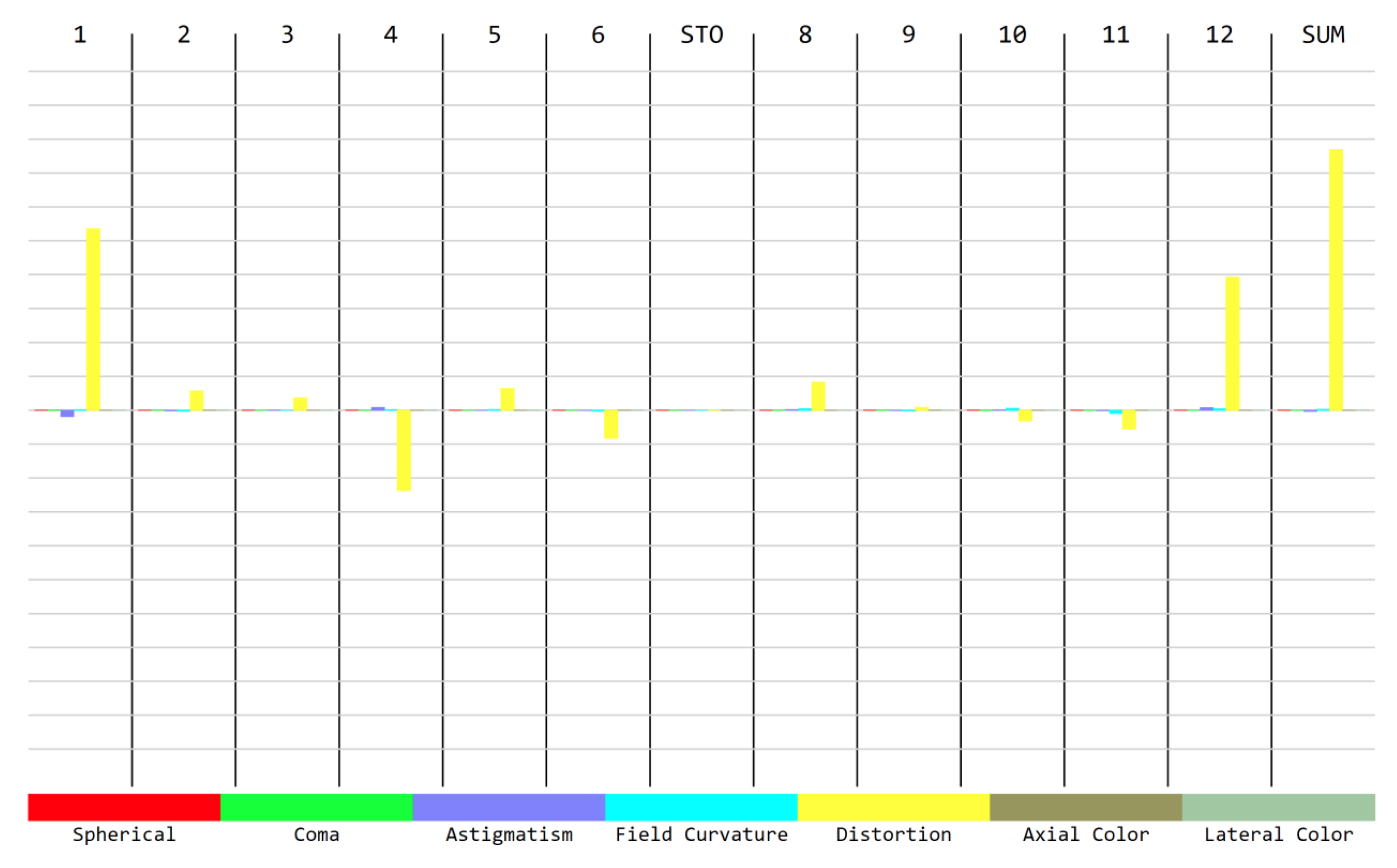
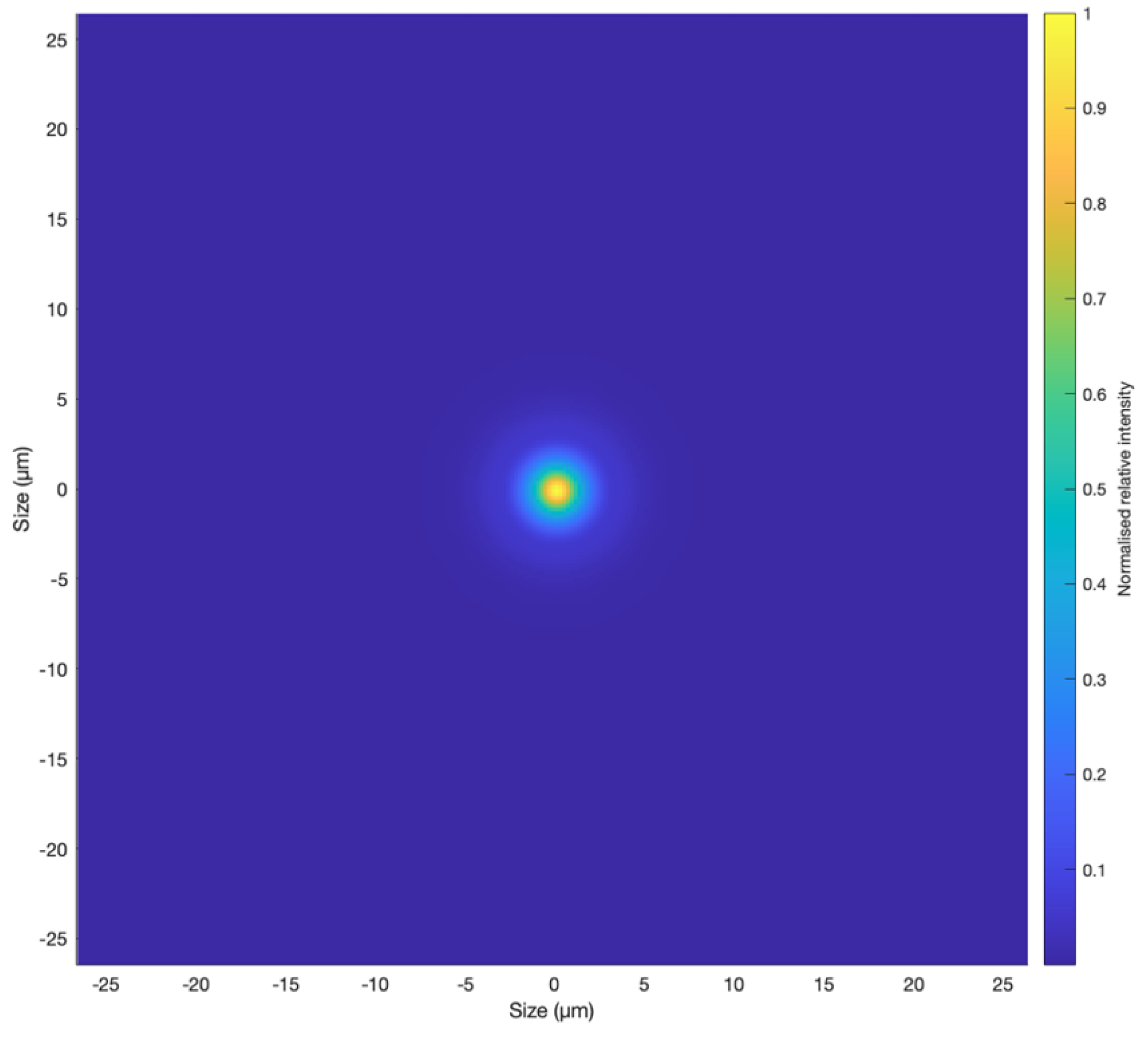

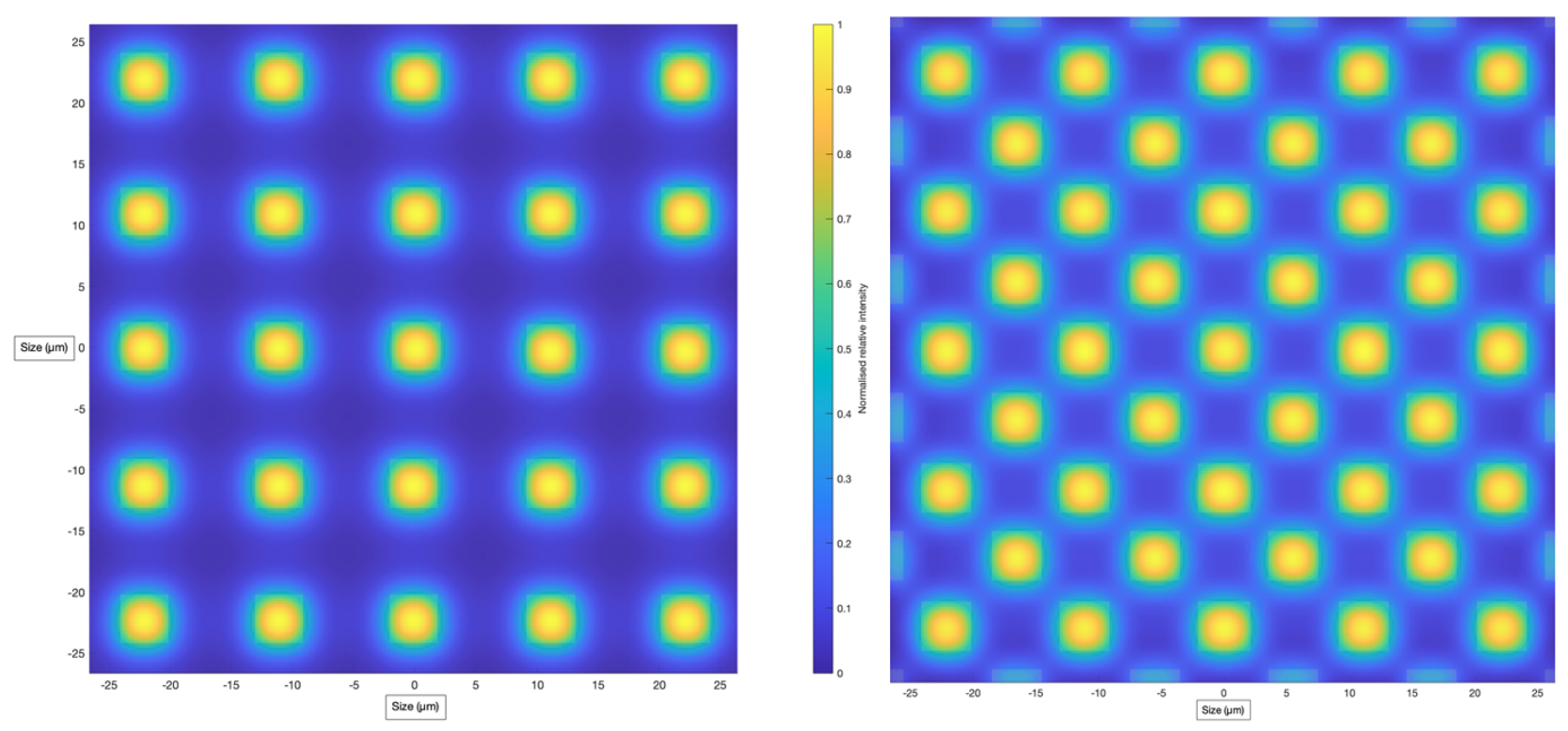
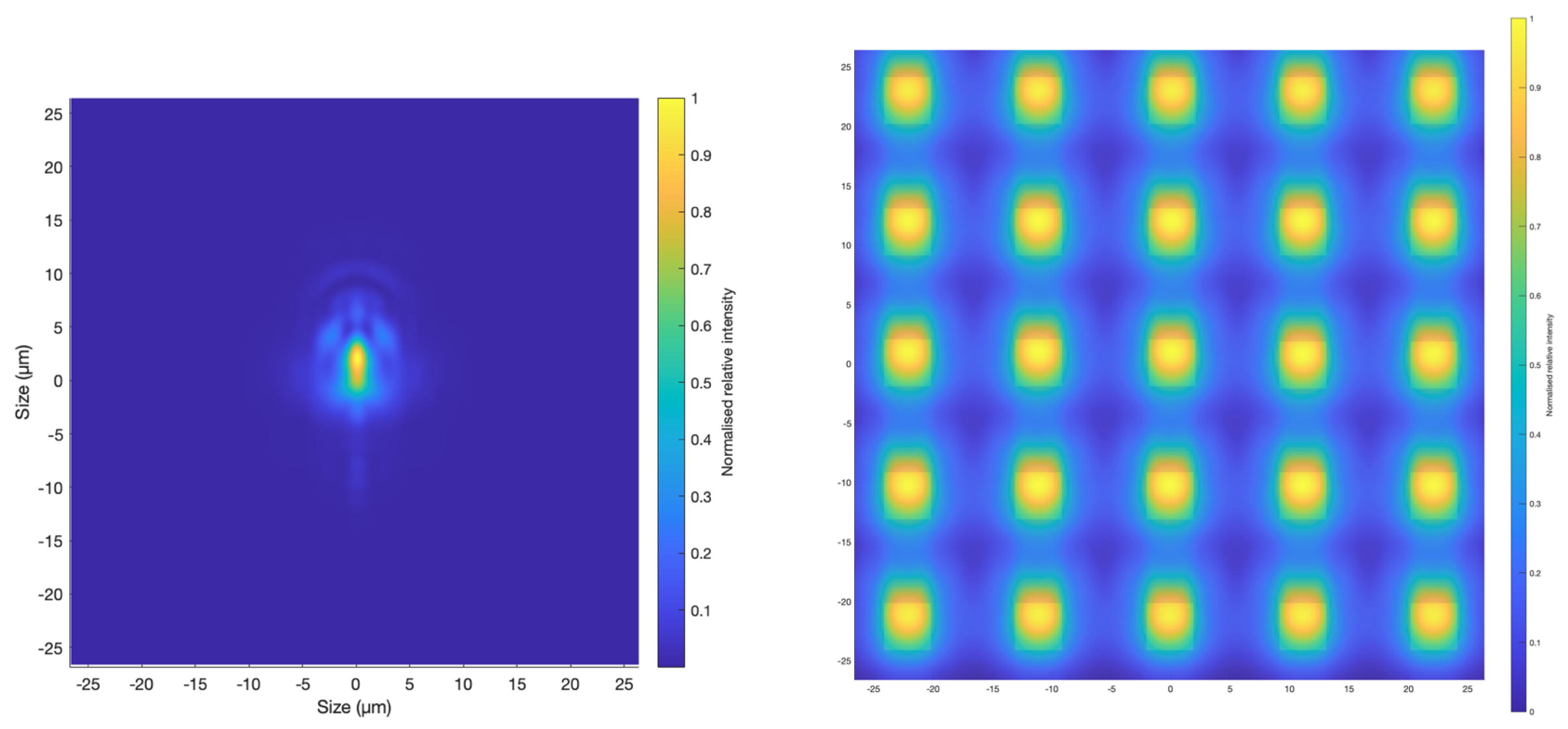
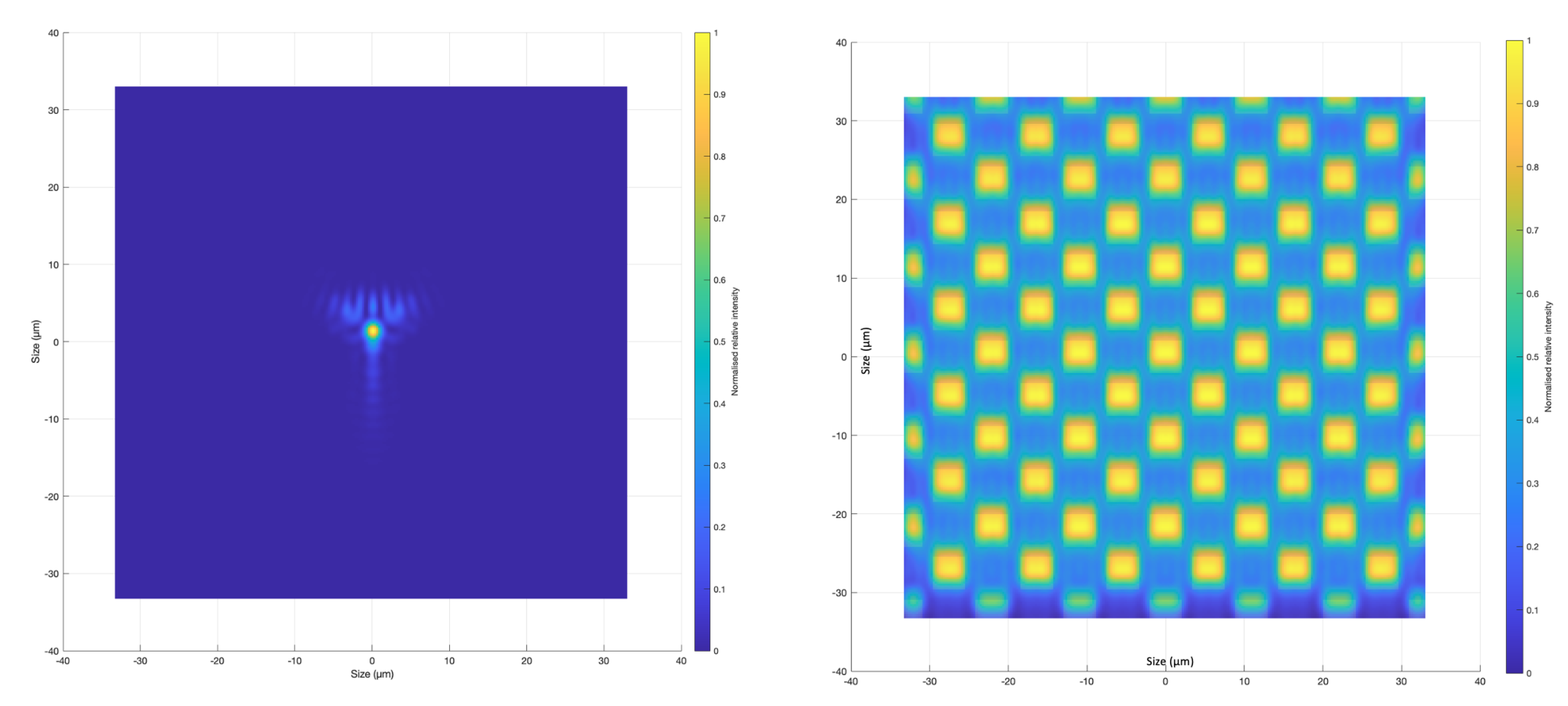
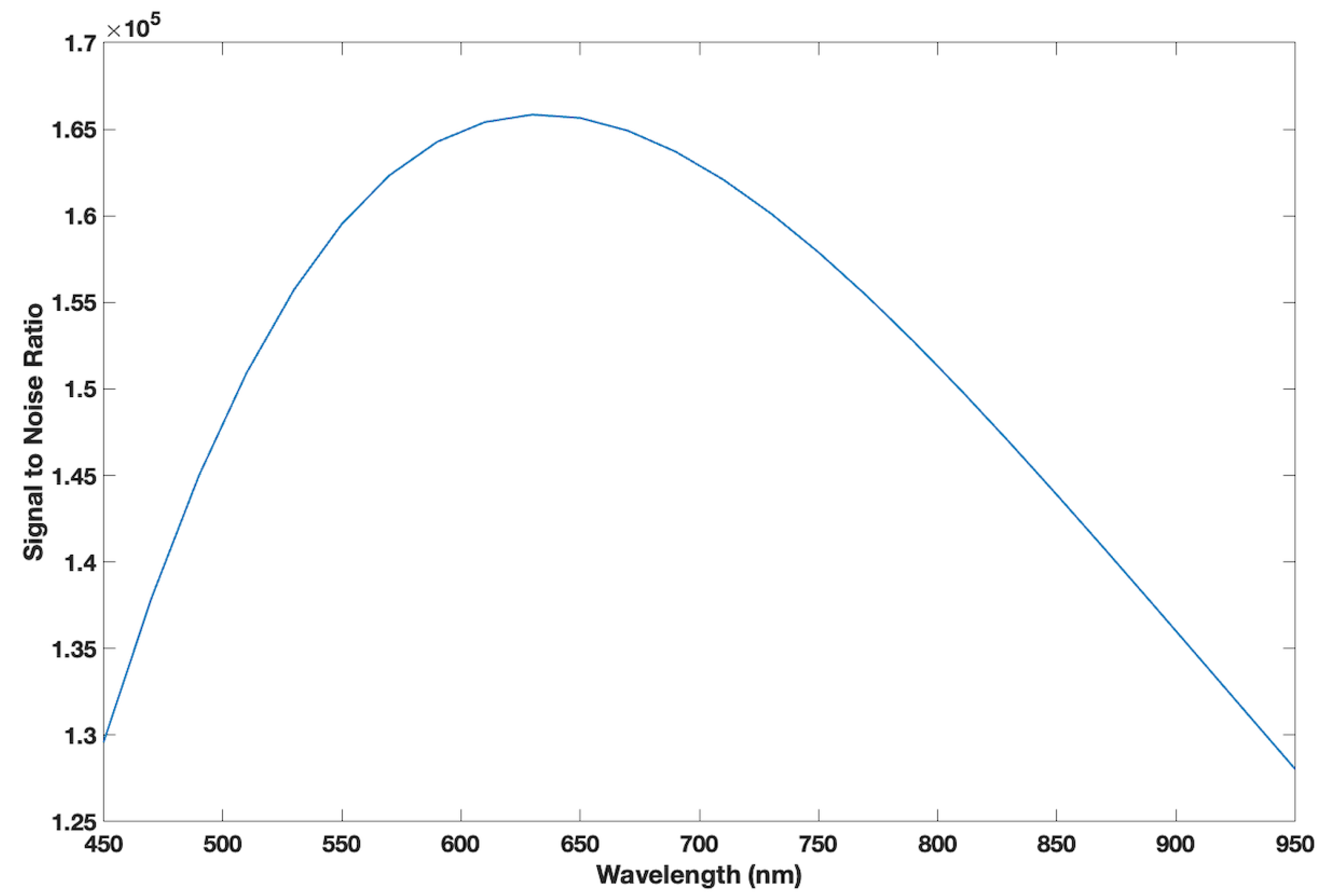
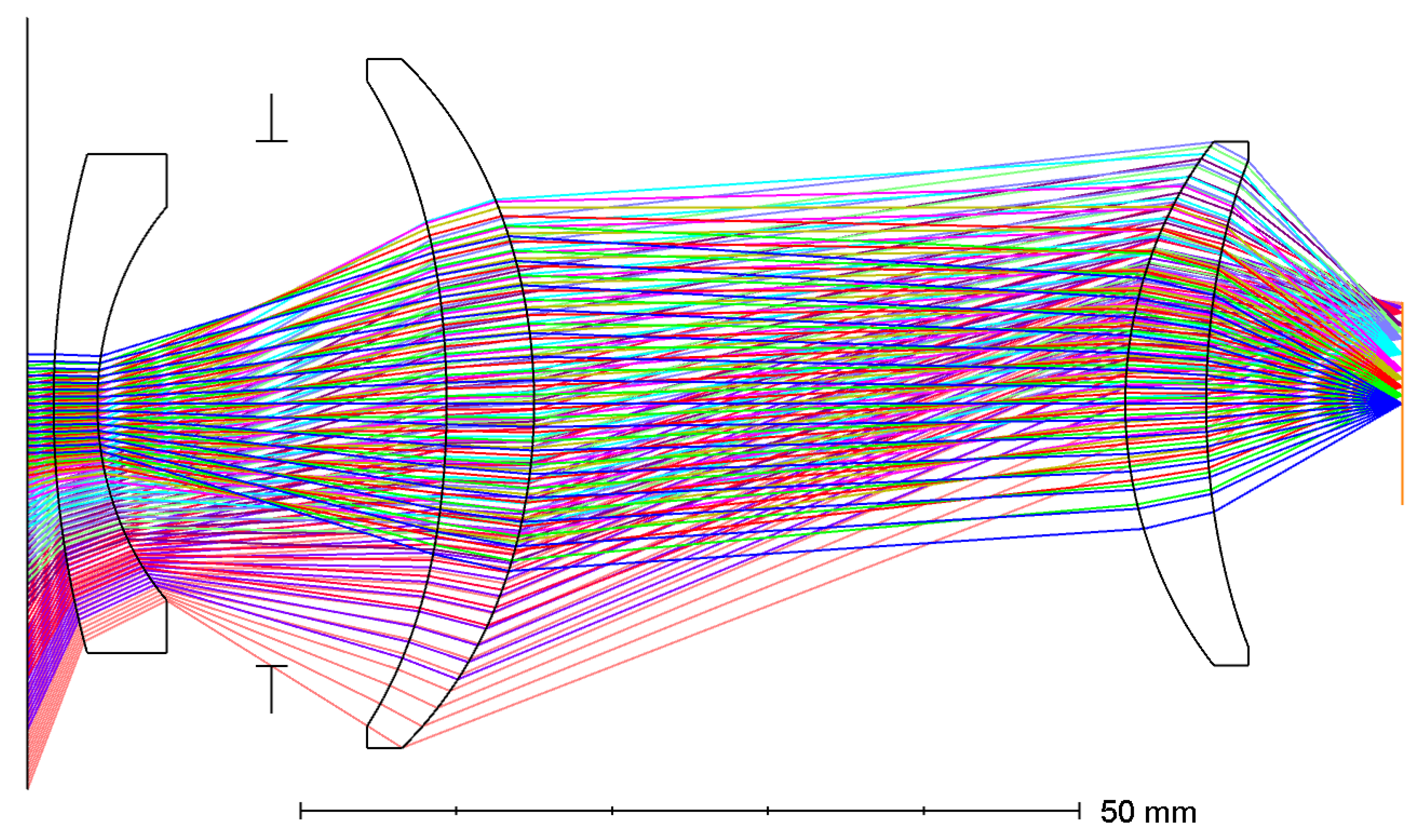

| Lens Order (Singlet/Doublet) | Front Surface Type | Rear Surface Type | Material | Thickness (mm) | Diameter (mm) |
|---|---|---|---|---|---|
| First lens (s: singlet) | Aspherical | Spherical | LAK14 | 3.7 | 32 |
| Second lens (s) | Spherical | Spherical | LAK14 | 5 | 23 |
| Third lens (s) | Spherical | Spherical | SF6 | 5 | 12 |
| Fourth lens (d: doublet) | Spherical | Spherical | N-FK51A | 2.7 | 7.6 |
| Fifth lens (d) | Spherical | Aspherical | N-SF6 | 2 | 7.6 |
| Sixth lens (s) | Spherical | Aspherical | LAK14 | 2.2 | 11.4 |
| Band | Limits |
|---|---|
| LW-1 | 8–9 μm |
| LW-2 | 9–10 μm |
| LW-3 | 10–11 μm |
| LW-4 | 11–12 μm |
| LW-5 | 12–13 μm |
| LW-6 | 13–14 μm |
| Band 1 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | |
|---|---|---|---|---|---|---|
| Fraction of black body radiation | 0.1087 | 0.1155 | 0.1083 | 0.0908 | 0.0643 | 0.0362 |
| NEDT per band (mK) | 51.55 | 50.03 | 51.66 | 56.40 | 67.02 | 89.3785 |
| Scene | OLR (W/m2) | OLR Error (%) |
|---|---|---|
| US standard—clear sky | 257.59 | 0.21 |
| Tropical—clear sky | 284.46 | |
| Midlatitude summer—clear sky | 277.87 | |
| Midlatitude winter—clear sky | 227.95 | |
| Subarctic summer—clear sky | 260.81 | |
| Subarctic winter—clear sky | 197.04 | |
| US standard—water cloud | 214.31 | 0.61 |
| US standard—thin ice cloud | 184.32 | 0.04 |
| US standard—thick ice cloud | 124.75 | |
| Midlatitude winter—water cloud | 200.64 | |
| Midlatitude winter—thin ice cloud | 171.44 | |
| Midlatitude winter—thick ice cloud | 125.25 | 0.23 |
| Subarctic summer—water cloud | 227.57 | |
| Subarctic summer—thin ice cloud | 196.57 | |
| Subarctic summer—thick ice cloud | 142.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dewitte, S.; Abdul Nazar, A.A.; Zhang, Y.; Smeesters, L. A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy. Remote Sens. 2023, 15, 5487. https://doi.org/10.3390/rs15235487
Dewitte S, Abdul Nazar AA, Zhang Y, Smeesters L. A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy. Remote Sensing. 2023; 15(23):5487. https://doi.org/10.3390/rs15235487
Chicago/Turabian StyleDewitte, Steven, Al Ameen Abdul Nazar, Yuan Zhang, and Lien Smeesters. 2023. "A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy" Remote Sensing 15, no. 23: 5487. https://doi.org/10.3390/rs15235487
APA StyleDewitte, S., Abdul Nazar, A. A., Zhang, Y., & Smeesters, L. (2023). A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy. Remote Sensing, 15(23), 5487. https://doi.org/10.3390/rs15235487






