Abstract
As the degradation factors of remote sensing images become increasingly complex, it becomes challenging to infer the high-frequency details of remote sensing images compared to ordinary digital photographs. For super-resolution (SR) tasks, existing deep learning-based single remote sensing image SR methods tend to rely on texture information, leading to various limitations. To fill this gap, we propose a remote sensing image SR algorithm based on a multi-scale texture transfer network (MTTN). The proposed MTTN enhances the texture feature information of reconstructed images by adaptively transferring texture information according to the texture similarity of the reference image. The proposed method adopts a multi-scale texture-matching strategy, which promotes the transmission of multi-scale texture information of remote sensing images and obtains finer-texture information from more relevant semantic modules. Experimental results show that the proposed method outperforms state-of-the-art SR techniques on the Kaggle open-source remote sensing dataset from both quantitative and qualitative perspectives.
1. Introduction
Remote sensing is an important ground observation technology that has developed rapidly in recent years. Given its unique advantages of extensive coverage, regular temporal regularity, and high accessibility, it has been widely used in disaster detection and early alerting [1], resource exploration [2], and land cover classification [3,4,5,6]. There are broad application prospects in environmental testing and other fields [7,8,9,10,11,12]. Due to space imaging equipment and communication bandwidth limitations, the resolution of images captured from satellite sensors is limited. In addition, the image quality is subject to various factors, including atmospheric turbulence, imaging process noise, and motion blur, leading to further reduced resolution and quality. Super-resolution (SR) algorithms can enhance acquired remote sensing images, thus, bypassing hardware limitations.
In the past few decades, SR technology has been widely applied to enhance the quality and resolution of remote sensing images. Existing remote sensing SR methods can be categorized into two main types: methods based on traditional algorithms [13] and methods based on deep learning [14,15]. The traditional learning-based super-resolution methods can learn prior knowledge from a data sample library by constructing learning models, thereby establishing a mapping relationship between low-resolution (LR) and high-resolution (HR) images. This process generates high-frequency details and texture information lost during the downscaling. Zheng et al. [16] first applied sparse representation theory to the field of remote sensing image SR, establishing overcomplete coupled high–low resolution dictionaries and solving sparse coefficients using an orthogonal matching pursuit strategy. Hou et al. [17] introduced a global joint dictionary model and non-local self-similarity for global and local constraints, establishing the intrinsic connections between image blocks and global information. Zhang et al. [18] proposed a sparse residual dictionary learning method, directly reconstructing residual images with a residual dictionary to alleviate the ringing effects of unstructured pixel-domain high-low resolution dictionaries. Wu et al. [19] proposed a SR framework based on a multi-feature dictionary, constructing multiple LR dictionaries for representation and overlay in the HR space.
With the widespread use of convolutional neural networks (CNN) in SR tasks, the deep learning-based remote sensing SR method has become the mainstream research direction of image SR methods. Deep learning-based methods usually learn complex mapping functions between LR and HR patches through CNN. Considering its outstanding learning ability, Shi et al. [20] built a sub-pixel CNN that builds a mapping mechanism from LR to HR. Kim et al. [21] proposed a novel network method with deep residual learning to ease the training process. Lai et al. [22] designed a pyramid network that fuses multi-scale residuals in the feature domain. Luo et al. [23] achieved excellent results by replacing zero paddings with self-similarity to prevent useless information. Wang et al. [24] proposed an SR method that preserves the temporal correlation between frames. Ledig et al. [25] introduced perceptual loss and proposed an SR method for generative adversarial networks (GAN) to obtain images with more realistic textures. The generation network guides image reconstruction with a perceptual loss so that the reconstruction result is close to the original HR image. The discriminant network compares the reconstructed image to the original HR image, and the reconstructed image is output if it can pass the discriminant network.
Current SR methods primarily target natural images, but they fall short when applied to the diverse shooting angles and multi-scale characteristics present in large-scale remote sensing data. Existing methods lack consideration for these factors, making it crucial to develop an SR method specifically tailored for accurately reconstructing remote sensing images with intricate textures. Drawing inspiration from the effectiveness of multi-angle priors in enriching prior information [26], this paper introduces reference images (Ref) to enhance the prior information of training samples. The algorithm is adapted for the reconstruction of remote sensing images by aligning feature texture information. The proposed network initially matches local texture information between the Ref image and the LR image, then conveys the identified texture features to the reconstruction network via the depth residual module. The final output is high-quality remote sensing images with detailed texture information. Extensive experimental results demonstrate the algorithm’s superiority over other state-of-the-art methods, both quantitatively and qualitatively.
We summarize the major contributions of this work as follows:
(1) We propose a novel remote sensing image RefSR method based on a multi-scale texture transfer network (MTTN), which can effectively address the issue of insufficient texture detail information in the reconstruction process of the single remote sensing image SR method.
(2) We propose a novel multi-scale texture transfer method. The proposed method uses residual blocks with different convolution kernel sizes to extract texture information of different scales from LR and Ref remote sensing images and take advantage of the texture details provided by Ref images to facilitate the reconstruction of LR images.
(3) We conduct extensive experiments on the challenging Kaggle open dataset, and the experimental results demonstrate the effectiveness and adaptability of our suggested MTTN method. In addition, the results also point to its great potential in subsequent remote sensing image classification tasks.
The remainder of this article is structured as follows. Section 2 presents related work, including existing SISR of remote sensing images and reference-based SR methods. Section 3 describes the principal method of this model in detail. Section 4 introduces the experimental results. Section 5 concludes this study and Section 6 discusses future work.
2. Related Work
Over the past decades, deep learning-based SR methods have demonstrated excellent reconstruction performance in evaluation indicators or visual quality compared to traditional methods. This section introduces the single image super-resolution (SISR) and reference-based super-resolution (RefSR) of remote sensing images.
2.1. SISR of Remote Sensing Images
The SISR method for remote sensing images has recently drawn increasing attention due to the unique value of high-quality remote sensing images in application scenarios. In addition to relying on advanced hardware, the SR method offers an efficient way to enhance the quality of remote sensing images. Recently, with the rapid popularity of convolutional neural networks in acquiring high-quality images, many researchers have proposed a large number of deep learning-based SISR methods for remote sensing images. Lei et al. [27] designed a CNN-based network framework to learn the local details and global prior information of remote sensing images. Xu et al. [28] proposed a deep memory connection network that reconstructs high-quality remote sensing images through local and global memory connections, so the reconstruction performance of remote sensing images is effectively improved. Lu et al. [29] employed a novel multi-scale residual neural network method. This method extracts image blocks of different sizes as multi-scale information and then fuses multi-scale high-frequency information to reconstruct images. Jiang et al. [30] designed an edge enhancement-based SR network to enhance the features of remote sensing images using edge detail information extracted by the network. Dong et al. [31] designed a multi-sensory attention method to obtain multi-level information of remote sensing features through the proposed feature extraction module. Haut et al. [32] designed a network to extract more related features through combining residual units and skipping connections. Qin et al. [33] designed a deep gradient-aware network with image-specific enhancement to preserve more gradient details in reconstructed images. Zhang et al. [34] proposed a novel attention module to capture finer remote sensing image texture information through this module. Lei et al. [35] created a new remote sensing image SR framework by introducing a transformer to extract multi-level features and better fuse the features of different dimensions. Liu et al. [36] designed a graph neural network (GNN) based SISR method, which can better consider the ill-conditioned phenomena in remote sensing images.
Despite the great progress in aforementioned SISR methods, most of these methods rely on paired images and local information. However, when confronted with certain specific and complex textures, they fail to capture sufficient prior information. Therefore, the SISR methods that handle remote sensing imagery have been criticized for their limitations in handling multi-source data.
2.2. Reference-Based Super-Resolution
In contrast to the SISR method, the RefSR method achieves the SR reconstruction process by introducing other related images. For the Ref image to effectively aid the SR reconstruction process, texture information similar to the LR image is typically required. Consequently, the Ref image is usually selected from related video frames [37,38] or photos taken from various angles [39]. Recently, SR methods based on Ref images have made great progress in general image methods. Zheng et al. [40] used cross-scale warping to create an end-to-end fully convolutional deep neural network. This network improves the accuracy of reconstructed images by performing end-to-end spatial alignment at the pixel level. Zhang et al. [41] employed a novel RefSR model that restores the target image through texture migration of the Ref image. Xie et al. [42] designed a matching and exchange module for the RefSR task to extract similar texture and high-frequency features from the Ref image by appropriately assigning the gradient to the previous feature encoding module. Yang et al. [43] designed a novel texture transformer model that transmits HR texture from the Ref image through a texture converter and attention module. Huang et al. [44] proposed a novel RefSR framework, which includes a texture extraction module and a texture transfer module to more fully transfer textures in an adaptive manner. Dong et al. [45] employed a GAN-based RefSR network, mainly using the relevant attention module that improves the network’s reconstruction ability through gradient-assisted alignment. Cai et al. [46] designed a texture transformer for remote sensing image SR algorithm, which reduces the SR model’s dependence on Ref images through U-Transformer.
The above-mentioned RefSR method introduces a new perspective for addressing remote sensing SR tasks. While the RefSR method offers more possibilities for remote sensing image super-resolution compared to SISR methods, existing RefSR methods often overlook the spatial diversity features of remote sensing images. These features contain valuable information that can significantly benefit remote sensing SR tasks. To address this gap, we have developed an innovative multi-scale texture transfer model to enhance the performance and robustness of RefSR. By extracting texture information from reference remote sensing images, this model further aids in extracting multi-scale information from the original low-resolution images, thereby reconstructing more refined remote sensing images.
3. Method
The main idea of the proposed method is to reconstruct SR images from LR remote sensing images and similar Ref images , and then synthesize a reasonable texture subject to , while maintaining consistency with the content. The proposed model’s overall network structure is shown in Figure 1. The multi-scale texture transfer method takes into account the semantic and textural similarity of and images and can better suppress irrelevant textures while transferring related remote sensing image texture features.
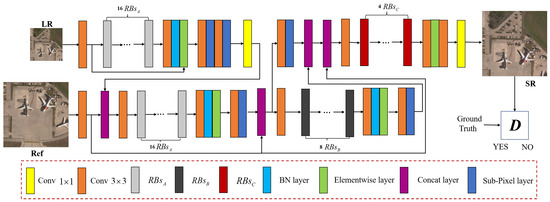
Figure 1.
Framework of the proposed multi-scale texture transfer network (MTTN). The specific structure of , , and are shown in Figure 2.
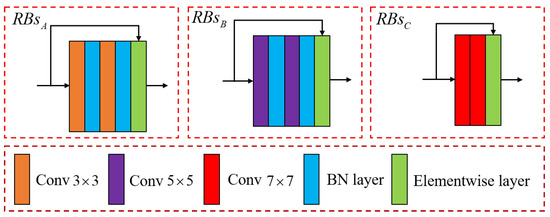
Figure 2.
Illustration of the residual blocks (RBs) in the proposed MTTN model. The , , and represent RBs with different convolution kernel sizes.
3.1. Feature Swapping
The first step in our MTTN is to swap remote sensing image features. The design algorithm searches the entire remote sensing reference image for locally similar multi-scale textures, and these extracted multi-scale textures can be used to exchange the texture features of with enhanced remote sensing SR image reconstruction. The multi-scale texture is then transferred directly to the final output via feature search in HR space coordinates. Specifically, we first extract the corresponding feature map on the , and then sample the extracted feature map twice to obtain an enlarged LR image with the same resolution as the . We also apply the same upscaling factor for before performing bicubic interpolation sampling to obtain a Ref image block matching the up-sampled . As the LR and Ref images’ data sources may differ, we compute texture similarity in the high-resolution feature space to emphasize structure and texture information, and we apply the inner product method to compute feature similarity between image pairs:
where denotes the i-th patch obtained from the high-resolution space, denotes feature normalization. The Ref feature block performs the best matching for the reference image features through a normalization function. Then we calculate the similarity between image pairs via convolution operations on the LR patch. The kernel operation expression of the Ref patch follows:
where represents the Ref patch’s similarity graph. represents the texture similarity between LR and Ref. We represent LR texture patches based on similarity scores by creating swapped feature maps. The image patches in the feature map are represented as:
where corresponds to the patch center and the patch index. Note that while is used for matching (Equation (2)), the original Ref is used for exchange (Equation (3)) to retain the high-frequency feature information. The final generated swap feature map is then fed to the subsequent multi-scale texture transfer by calculating the average between the swap feature maps.
3.2. Multi-Scale Texture Transfer
Our multi-scale texture transfer method merges the transferred texture data into the generation network of various feature layers corresponding to various scales after the layer-by-layer transfer of the feature maps extracted from the feature extraction network and high-resolution reference images. The above-described procedure builds the exchanging feature map for multi-scale layer l, where the texture encoder corresponds to the scale being used.
To build the fundamental generative network, we use residual blocks (RBs) with various convolution kernel sizes. The output of layer l can be recursively expressed as:
where represents the RBs, ∇ represents the channel cascade, and represents the use of sub-pixel convolution layer for magnification. The remote sensing reconstruction image is generated once the L layer has reached the desired HR resolution:
Unlike the traditional SISR method that only considers the texture difference between and , the proposed MTTN network considers the texture variation between and . In other words, the texture of must be similar to the swap feature map . Therefore, we define the texture loss as:
where calculates the gamma matrices, and is the normalized exponent of the l layer. represents the weight map of the input LR remote sensing image patch. The difference between this weight map and is the fact that texture owns a lower weight, leading to lower texture loss. Thus, the texture transferred from to can be enforced adaptively based on the image quality of Ref image, resulting in more robust texture features.
3.3. Loss Function
To improve the visual quality of remote sensing reconstructed images, we design four loss functions. In addition to introducing texture loss , our algorithm also introduces reconstruction loss , perceptual loss , and adversarial loss . The is a commonly used loss function in SR, and the and the are the losses introduced by the generation confrontation network in order to reconstruct a more realistic image. We describe these loss functions below.
3.3.1. Reconstruction Loss
The is typically defined by the mean square error. The function aims to achieve a higher peak signal-to-noise ratio (PSNR), and the L1-norm is adopted:
3.3.2. Perceptual Loss
Many SR networks have introduced perceptual loss to achieve more realistic visual quality. Therefore, our network also uses the perceptual loss function ():
where V and C denote the volume and channel of the feature map, respectively. indicates the i-th channel of the output feature map, and represents the Frobenius norm.
3.3.3. Adversarial Loss
The function can improve the sharpness of SR reconstructed images. Our network uses the improved function in WGAN [26]:
where D is a relativistic average discriminator [47].
4. Experiements
This section mainly introduces the experiments of the proposed MTTN network, including the dataset in Section 4.1, the evaluation indicators in Section 4.2, the implementation details of the experiments in Section 4.3, the quantitative and qualitative analyses with different methods in Section 4.4, and the ablation studies in Section 4.5.
4.1. Dataset
In this study, we use the Kaggle open-source remote sensing competition dataset (https://www.kaggle.com/c/draper-satellite-image-chronology/data). For the RefSR-based remote sensing image problem, the texture similarity between input remote sensing image pairs poses a significant impact on the SR results. In general, for training and evaluating RefSR algorithms, Ref images with various similarities to LR images are preferred. However, the Kaggle open-source dataset contains a wide variety of numbers and subject matter, including 324 different scenarios. Therefore, we constructed a dataset of reference images with various similarities based on the Kaggle dataset. We use the SIFT [48] feature-matching method to collect image pairs with different similarities. This feature-matching method collects Ref remote sensing images that are consistent with local texture-matching targets. We also segment these images with a size of , leading to a total of 1200 remote sensing images, of which 600 are used as input images, and the other 600 are used as reference images for training. Note that the Ref image fed to the algorithm is the same scene as the input image but with different angles. Figure 3 presents some selected samples of our dataset.

Figure 3.
Selected samples of RefSR remote sensing datasets. (High-resolution image (left) and Reference image (right)).
4.2. Evaluation Indicators
In this experiment, we use five popular objective evaluation metrics, including peak signal-to-noise ratio (PSNR), structural similarity (SSIM) [49], feature similarity (FSIM) [50], visual information fidelity (VIF) [51], and relative dimensionless global error in synthesis (ERGAS) [52].
Peak Signal-to-Noise Ratio (PSNR), with decibel (dB) as unit, evaluates the similarity between two images from the pixel similarity level. It is one of the most commonly used objective measures to evaluate image quality:
where is the mean square error between the original image X and the reconstructed image Y, N is the number of bits of image pixels (most general optical images have 8 bits). The image’s width and height are denoted by W and H, respectively. The PSNR ranges from , where a higher value indicates more similarity between the images.
Structural Similarity (SSIM) is an objective evaluation index designed based on the human visual system. By decomposing the image, it comprehensively evaluates the degree of similarity between two images based on image brightness, contrast, and structure. For images and , SSIM can be calculated as:
where and are the mean and luminance components between image pairs, respectively, and and are the variance and contrast components of the two images, respectively. is the covariance of images and , used for structural contrast components. , , and are the balance parameters. The value range of SSIM is [0, 1]. The larger the value, the greater the degree of image similarity.
Feature Similarity Index Mersure (FSIM) uses low-level image features to replace image statistical features in SSIM and evaluates the feature similarity between two images from three feature levels of image phase consistency and gradient magnitude. For images and , FSIM can be are calculated as follows:
where represents the pixel domain of the whole image, and represent the phase consistency and fusion similarity of the two images, respectively. The value range of FSIM is [0, 1]. The higher the value, the more similar the images are.
Visual Information Fidelity (VIF) is based on statistical models of natural scenes, image distortions, and the human visual system. For images and , VIF can be calculated as:
where and represent the information extracted from specific subbands of the input image. N is the number of sub-bands in the wavelet domain, C is the set of random vector fields, E is the random coefficient vector of the wavelet sub-band of the original image, F is the random coefficient vector of the wavelet sub-band of the distorted image, and S is an independent scalar factor.
The Erreur Relative Globale Adimensionnelle de Synthèse (ERGAS) provides a global fusion evaluation. The smaller the value (the closer to zero), the better the performance. ERGAS is defined as:
where h and l represent the spatial resolution of the panchromatic image and the multispectral image, respectively, P represents the number of bands of the fusion map, is the i-band of the mean Ref multispectral image, and is the Ref image and the fusion map MSE.
4.3. Experimental Details
In this study, we adopt VGG19 [53] as the pre-training model of the network and design an end-to-end remote sensing SR network. We first downsample the original remote sensing images to LR images of pixels, and then perform data augmentation by random horizontal flipping and 90-degree rotation during training, and adopt a learning rate decay strategy during training. The batch size of the network is set to 9, and the learning rate is initially set to with the reduction rate of each epoch of 0.9. We use the ADAM optimizer [54] for network optimization, and the momentum parameter is set to and .
For training and testing, we use a server with NVIDIA 1080Ti GPU and Intel I7-8700 CPU. Our MTTN network is implemented based on the TensorFlow framework under Ubuntu 16.04, CUDA 8.0 and CUDNN 5.1 systems. In our experiments, it takes about 20 h to train our model with a 1080Ti GPU under the above settings for 50 epochs.
4.4. Quantitative and Qualitative Comparison with Different Methods
To demonstrate the superiority of MTTN, we compare it to recent SISR and RefSR remote sensing imagery algorithms. The SR methods to be compared include Bicubic, SRCNN [55], VDSR [21], SRResnet [25], SRFBN [56], SRRFN [57], SEAN [58], HAN [59], MHAN [34], SRNTT [41], DLGNN [36], and HSENet [60]. Among them, DLGNN [36] and HSENet [60] are the latest remote sensing SR algorithms that demonstrate great reconstruction results. The competing algorithm also includes a RefSR method, i.e., SRNTT [41], a classic RefSR method.
All of the competing methods were trained and tested on the Kaggle public dataset that was recreated in this study to ensure a fair comparison. Table 1 displays the objective evaluation indicators for all the algorithms, and the best outcomes are highlighted in red. It can be seen from Table 1 that the proposed MTTN shows great performance on the five objective evaluation indicators, i.e., PSNR, SSIM, FSIM, VIF, and ERGAS.

Table 1.
Comparison of average PSNR, SSIM, FSIM, VIF, and ERGAS results obtained from the Kaggle Open Source dataset. ↑ means that the larger the value, the better the reconstruction effect. ↓ means that the smaller the value, the better the reconstruction effect.
The above results prove that certain SR models designed for natural images are not suitable for remote sensing images. The multi-scale texture transfer network we designed is more effective in learning the texture and structure of remote sensing images, as it uses texture information from Ref remote sensing images to assist in reconstructing texture detail information in LR images.
Figure 4 and Figure 5 presents a visual comparison of the experimental results and further the advantage of the proposed MTTN network. We selected typical scenes, including playgrounds, parking lots, ports, airports, buildings and roads, to evaluate the superiority of the MTTN network. From the zoomed-in details in Figure 4 and Figure 5, we notice the CNN-based approach can reconstruct some texture details. However, as some models are directly transferred to remote sensing SR tasks, the reconstructed remote sensing images contain notable blurred contours. The GAN-based method presents better visual effects, but the generated artifacts deteriorate the reconstructed remote sensing image. In comparison, our proposed MTTN algorithm produces sharper edges and finer details than other competing algorithms. We also observe that the proposed MTTN further enhances the visual performance of the reconstructed image by combining the multi-scale residual information of Ref images.

Figure 4.
Subjective comparison of our method with other algorithms on the Kaggle open dataset (playgrounds, parking lots and ports). From left to right, top to bottom, they are the result of Bicubic, SRCNN [55], VDSR [21], SRResnet [25], SRFBN [56], SRRFN [57], SEAN [58]), HAN [59], MHAN [34], SRNTT [41], DLGNN [36], and HSEnet [60], proposed methods and HR. Best view via zoomed-in view.

Figure 5.
Subjective comparison of our method with other algorithms on the Kaggle open dataset (airports, buildings and roads). From left to right, top to bottom, they are the result of Bicubic, SRCNN [55], VDSR [21], SRResnet [25], SRFBN [56], SRRFN [57], SEAN [58]), HAN [59], MHAN [34], SRNTT [41], DLGNN [36], and HSEnet [60], proposed methods and HR. Best view via zoomed-in view.
4.5. Ablation Studies
4.5.1. Effectiveness of Reference Image
To verify the effectiveness of Ref images on MTTN networks, we set up ablation experiments with different configurations. Table 2 lists the experimental results of various ablation experiments. The SISR model performs worse than the original network by 0.17 dB in terms of PSNR. However, our model still achieves comparable performance to some SISR algorithms without introducing Ref into remote sensing images. The MSE comparison chart in Figure 6 shows that after adding Ref remote sensing images, the reconstructed remote sensing images present richer texture details, indicating that SR performance can be enhanced when incorporating Ref images.

Table 2.
Comparative results of different modes of ablation experiments on the Kaggle Open Source dataset with a scale factor of 4.
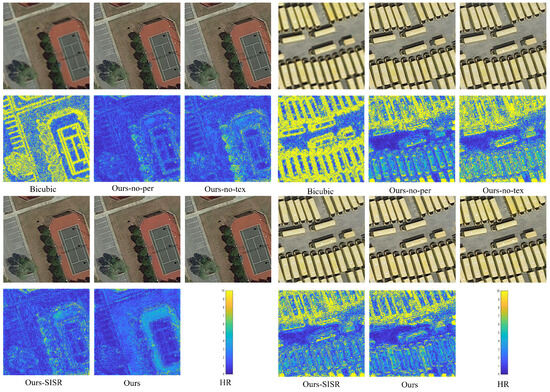
Figure 6.
The MSE maps display the disparities between reconstructions and ground truths in various ablation experiments. The color of the MSE map corresponds to the magnitude of the error, which varies as the images’ dissimilarity increases or decreases.
4.5.2. Effectiveness of Loss Function
Our proposed MTTN model uses a novel texture loss, making it distinct from most SR methods. Different from other texture transfer methods, the MTTN network transfers the most relevant texture of the reference image to the target image. Specifically, the local matching method maintains the texture consistency of remote sensing images; the adaptive neural migration improves texture transfer; and the spatial regularization achieves better global spatial consistency. The test results for texture loss are shown in Table 2. The PSNRs of MTTN with and without texture loss tested on the Kaggle dataset are 30.48 dB and 30.10 dB, respectively. It proves that the texture information from Ref cannot be effectively transferred to the target image without texture loss.
We also incorporate perceptual loss into this network to enhance the visual appeal of reconstructed remote sensing images. To verify the effectiveness of this loss, we conducted relevant ablation experiments. The experimental results are shown in Table 2. Regarding the test PSNR results on the Kaggle dataset, the PSNR values after introducing perceptual loss are significantly higher than the test results without perceptual loss. From Figure 6, we notice that the two loss functions in our proposed MTTN effectively reduce the disparity between SR images and the corresponding ground-truth images.
4.5.3. Effectiveness of Residual Blocks
In this study, we extract multi-scale texture information from remote sensing images using different numbers of residual blocks (RBs). Similar to other works [61,62], in order to make full use of the multi-scale texture information of remote sensing images, our different residual blocks adopt a combination of different convolution kernel sizes, and the specific structure is shown in Figure 2. According to the experience sharing of other work [41], we set the number of RBs at different scales to different numbers ( convolution uses 16 , convolution uses 8 and convolution uses 4 ), which proves that the MTTN network can ensure that the parameter quantity of the network does not increase additionally, and at the same time, it also guarantees a good reconstruction ability of the network. To verify the effects of different numbers of design methods of on the performance of MTTN, we designed a set of ablation experiments. As shown in Figure 7, the reconstruction performance of our network decreases as the number of residual blocks increases. Therefore, considering the network’s parameters and the reconstruction performance of remote sensing images, the MTTN network adopts the above settings to obtain better reconstruction performance when transmitting texture information.
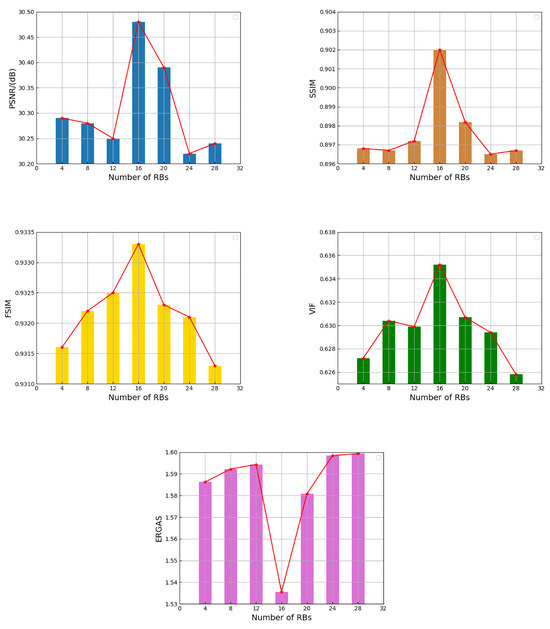
Figure 7.
Performance comparison of MTTN with the number of .
4.5.4. Effectiveness of Remote Sensing Scene Classification
The SR algorithm for remote sensing images is considered a pre-processing step for some downstream tasks, e.g., change detection and semantic segmentation. To further support the efficacy of the suggested MTTN, we evaluate the reconstruction outcomes of various networks using an unsupervised semantic segmentation algorithm (ISODATA). We set the number of categories to five and the maximum number of iterations to five [63]. It is particularly challenging for ISODATA to obtain precise classification results because the results of the comparison experiments show significant spectral distortions and fuzzy patterns. The comparison of the experimental results of the classification algorithm is shown in Figure 8. In particular, we notice the misclassification of ships and the lack of texture information from the results of DLGNN and HSEnet, while SRNTT fails to recover detailed ship edge information. The results demonstrate that the reconstructed images by the MTTN network contain fine details, evidenced by the ISODATA classification results.

Figure 8.
The classification outcomes achieved by various algorithms using the ISODATA classification method.
5. Conclusions
In this study, we propose MTTN, a novel RefSR method for remote sensing images with multi-scale residual transfer. Specifically, the proposed MTTN extends the prior information of training samples by introducing additional texture information from reference images. In addition, the use of multi-scale methods to transfer texture information also enriches the prior information required by the network at different stages. The MTTN network introduces multi-scale residual blocks to enhance the image edge and texture information. We perform a comprehensive evaluation of the experimental results in the Kaggle remote sensing competition dataset. Extensive experimental results demonstrate that MTTN can enhance the texture details and visual effects of reconstructed images. Quantitatively, the MTTN network outperforms other competing algorithms in all selected objective evaluation metrics. The self-reference ablation experiments demonstrate that MTTN achieves outstanding reconstructed results with and without reference images.
6. Discussion
This paper has conducted relevant research on remote sensing super-resolution algorithms based on reference images, laying a certain foundation for future related work. However, in the practical acquisition scenarios of remote sensing images, the process of obtaining low-resolution remote sensing images is complex, and there are factors such as noise, downsampling, and blur, making existing methods unsuitable for direct application in the super-resolution reconstruction of remote sensing images in real-world scenarios. Therefore, future research directions may consider investigating remote sensing image super-resolution reconstruction in complex real-world scenarios, aiming to enhance the model’s generalization capability and applicability.
Author Contributions
Conceptualization, Y.W., Z.S. and T.L.; methodology, Y.W., T.L. and J.W.; software, Y.W. and Z.S.; validation, Y.W., J.W. and X.C.; formal analysis, Y.W., H.H. and X.Z.; investigation, Y.W., J.W. and X.C.; resources, Y.W., Z.S. and T.L.; writing—original draft preparation, Y.W. and J.W.; writing—review and editing, Y.W. and X.H.; visualization, H.H. and X.Z.; supervision, Z.S. and T.L.; project administration, T.L.; funding acquisition, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This article is supported in part by the National Natural Science Foundation of China (42090012), Guangxi Science and Technology Plan Project (Guike 2021AB30019), Hubei Province Key R&D Project (2022BAA048), Sichuan Province Key R&D Project (2022YFN0031, 2023YFN0022, 2023YFS0381), Zhuhai Industry-University-Research Cooperation Project (ZH22017001210098PWC), Shanxi Provincial Science and Technology Major Special Project (202201150401020), Guangxi Key Laboratory of Spatial Information and Surveying and Mapping Fund Project (21-238-21-01), Opening Fund of Hubei Key Laboratory of Intelligent Robot under Grant (HBIR202103), and Supported by Hubei Provincial Natural Science Foundation of China (2023AFB158).
Data Availability Statement
The data that support the fndings of this study are available from the corresponding author, upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bredemeyer, S.; Ulmer, F.G.; Hansteen, T.H.; Walter, T.R. Radar path delay effects in volcanic gas plumes: The case of Láscar Volcano, Northern Chile. Remote Sens. 2018, 10, 1514. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral unmixing with robust collaborative sparse regression. Remote Sens. 2016, 8, 588. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- He, N.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Remote sensing scene classification using multilayer stacked covariance pooling. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6899–6910. [Google Scholar] [CrossRef]
- Fang, L.; Liu, G.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Hyperspectral image classification with squeeze multibias network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1291–1301. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Wang, L.; Zhang, C. Land cover classification from remote sensing images based on multi-scale fully convolutional network. Geo-Spat. Inf. Sci. 2022, 25, 278–294. [Google Scholar] [CrossRef]
- Zhang, S.; Shao, Z.; Huang, X.; Bai, L.; Wang, J. An internal-external optimized convolutional neural network for arbitrary orientated object detection from optical remote sensing images. Geo-Spat. Inf. Sci. 2021, 24, 654–665. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, W.; Li, D. Spatio-temporal-spectral observation model for urban remote sensing. Geo-Spat. Inf. Sci. 2021, 24, 372–386. [Google Scholar] [CrossRef]
- Liu, J.; Xiang, J.; Jin, Y.; Liu, R.; Yan, J.; Wang, L. Boost Precision Agriculture with Unmanned Aerial Vehicle Remote Sensing and Edge Intelligence: A Survey. Remote Sens. 2021, 13, 4387. [Google Scholar] [CrossRef]
- Ren, J.; Wang, R.; Liu, G.; Wang, Y.; Wu, W. An SVM-Based Nested Sliding Window Approach for Spectral–Spatial Classification of Hyperspectral Images. Remote Sens. 2021, 13, 114. [Google Scholar] [CrossRef]
- Bai, T.; Wang, L.; Yin, D.; Sun, K.; Chen, Y.; Li, W.; Li, D. Deep learning for change detection in remote sensing: A review. Geo-Spat. Inf. Sci. 2022, 26, 262–288. [Google Scholar] [CrossRef]
- Yu, X.; Pan, J.; Wang, M.; Xu, J. A curvature-driven cloud removal method for remote sensing images. Geo-Spat. Inf. Sci. 2023, 1–22. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Gao, X.; Tao, D.; Ning, B. A multi-frame image super-resolution method. Signal Process. 2010, 90, 405–414. [Google Scholar] [CrossRef]
- Wang, J.; Shao, Z.; Huang, X.; Lu, T.; Zhang, R.; Ma, J. Enhanced image prior for unsupervised remoting sensing super-resolution. Neural Netw. 2021, 143, 400–412. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, Z.; Lu, T.; Liu, L.; Huang, X.; Wang, J.; Jiang, K.; Zeng, K. A lightweight distillation CNN-transformer architecture for remote sensing image super-resolution. Int. J. Digit. Earth 2023, 16, 3560–3579. [Google Scholar] [CrossRef]
- Zhihui, Z.; Bo, W.; Kang, S. Single remote sensing image super-resolution and denoising via sparse representation. In Proceedings of the 2011 International Workshop on Multi-Platform/Multi-Sensor Remote Sensing and Mapping, Xiamen, China, 10–12 January 2011; pp. 1–5. [Google Scholar]
- Hou, B.; Zhou, K.; Jiao, L. Adaptive super-resolution for remote sensing images based on sparse representation with global joint dictionary model. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2312–2327. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, W.; Dai, Y.; Yang, X.; Yan, B.; Lu, W. Remote sensing images super-resolution based on sparse dictionaries and residual dictionaries. In Proceedings of the 2013 IEEE 11th International Conference on Dependable, Autonomic and Secure Computing, Chengdu, China, 21–22 December 2013; pp. 318–323. [Google Scholar]
- Wu, W.; Yang, X.; Liu, K.; Liu, Y.; Yan, B. A new framework for remote sensing image super-resolution: Sparse representation-based method by processing dictionaries with multi-type features. J. Syst. Archit. 2016, 64, 63–75. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 624–632. [Google Scholar]
- Luo, Y.; Zhou, L.; Wang, S.; Wang, Z. Video satellite imagery super resolution via convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2398–2402. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, P.; Jiang, K.; Jiang, J.; Han, Z.; Lu, T.; Ma, J. Multi-memory convolutional neural network for video super-resolution. IEEE Trans. Image Process. 2018, 28, 2530–2544. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5767–5777. [Google Scholar]
- Lei, S.; Shi, Z.; Zou, Z. Super-resolution for remote sensing images via local–global combined network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Xu, W.; Guangluan, X.; Wang, Y.; Sun, X.; Lin, D.; Yirong, W. High quality remote sensing image super-resolution using deep memory connected network. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8889–8892. [Google Scholar]
- Lu, T.; Wang, J.; Zhang, Y.; Wang, Z.; Jiang, J. Satellite image super-resolution via multi-scale residual deep neural network. Remote Sens. 2019, 11, 1588. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-enhanced GAN for remote sensing image superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Dong, X.; Xi, Z.; Sun, X.; Gao, L. Transferred multi-perception attention networks for remote sensing image super-resolution. Remote Sens. 2019, 11, 2857. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J. Remote sensing single-image superresolution based on a deep compendium model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1432–1436. [Google Scholar] [CrossRef]
- Qin, M.; Mavromatis, S.; Hu, L.; Zhang, F.; Liu, R.; Sequeira, J.; Du, Z. Remote sensing single-image resolution improvement using a deep gradient-aware network with image-specific enhancement. Remote Sens. 2020, 12, 758. [Google Scholar] [CrossRef]
- Zhang, D.; Shao, J.; Li, X.; Shen, H.T. Remote sensing image super-resolution via mixed high-order attention network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5183–5196. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Mo, W. Transformer-Based Multistage Enhancement for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5615611. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, R.; Wang, L.; Han, W.; Zeng, T. Dual Learning-Based Graph Neural Network for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5628614. [Google Scholar] [CrossRef]
- Liu, C.; Sun, D. A bayesian approach to adaptive video super resolution. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 209–216. [Google Scholar]
- Caballero, J.; Ledig, C.; Aitken, A.; Acosta, A.; Totz, J.; Wang, Z.; Shi, W. Real-time video super-resolution with spatio-temporal networks and motion compensation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4778–4787. [Google Scholar]
- Wang, Y.; Lu, T.; Xu, R.; Zhang, Y. Face Super-Resolution by Learning Multi-view Texture Compensation. In MultiMedia Modeling, Proceedings of the 26th International Conference, MMM 2020, Daejeon, Republic of Korea, 5–8 January 2020, Proceedings, Part II 26; Springer: Berlin/Heidelberg, Germany, 2020; pp. 350–360. [Google Scholar]
- Zheng, H.; Ji, M.; Wang, H.; Liu, Y.; Fang, L. Crossnet: An end-to-end reference-based super resolution network using cross-scale warping. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 88–104. [Google Scholar]
- Zhang, Z.; Wang, Z.; Lin, Z.; Qi, H. Image super-resolution by neural texture transfer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7982–7991. [Google Scholar]
- Xie, Y.; Xiao, J.; Sun, M.; Yao, C.; Huang, K. Feature representation matters: End-to-end learning for reference-based image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 230–245. [Google Scholar]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning Texture Transformer Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5791–5800. [Google Scholar]
- Huang, Y.; Zhang, X.; Fu, Y.; Chen, S.; Zhang, Y.; Wang, Y.F.; He, D. Task Decoupled Framework for Reference-Based Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5931–5940. [Google Scholar]
- Dong, R.; Zhang, L.; Fu, H. RRSGAN: Reference-based super-resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Cai, D.; Zhang, P. T3SR: Texture Transfer Transformer for Remote Sensing Image Superresolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7346–7358. [Google Scholar] [CrossRef]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard GAN. arXiv 2018, arXiv:1807.00734. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef]
- Ranchin, T.; Wald, L. Fusion of high spatial and spectral resolution images: The ARSIS concept and its implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556 2014. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Computer Vision—ECCV 2014, Proceedings of the 13th European Conference, Zurich, Switzerland, 6–12 September 2014, Proceedings, Part IV 13; Springer: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3867–3876. [Google Scholar]
- Li, J.; Yuan, Y.; Mei, K.; Fang, F. Lightweight and Accurate Recursive Fractal Network for Image Super-Resolution. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3814–3823. [Google Scholar]
- Fang, F.; Li, J.; Zeng, T. Soft-Edge Assisted Network for Single Image Super-Resolution. IEEE Trans. Image Process. 2020, 29, 4656–4668. [Google Scholar] [CrossRef]
- Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single image super-resolution via a holistic attention network. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 191–207. [Google Scholar]
- Lei, S.; Shi, Z. Hybrid-scale self-similarity exploitation for remote sensing image super-resolution. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5401410. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, Z.; Lu, T.; Wu, C.; Wang, J. Remote sensing image super-resolution via multiscale enhancement network. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5000905. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, T.; Wu, Z.; Wu, Y.; Zhang, Y. Face super-resolution via hierarchical multi-scale residual fusion network. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2021, 104, 1365–1369. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 667–682. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).