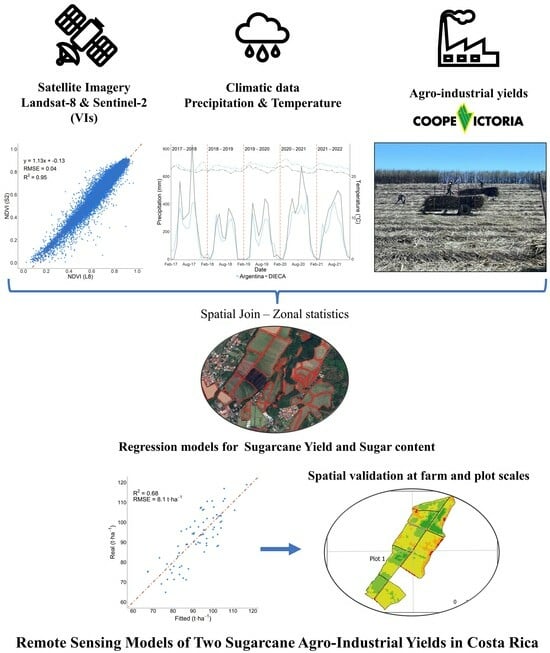
Modelling Two Sugarcane Agro-Industrial Yields Using Sentinel/Landsat Time-Series Data and Their Spatial Validation at Different Scales in Costa Rica
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
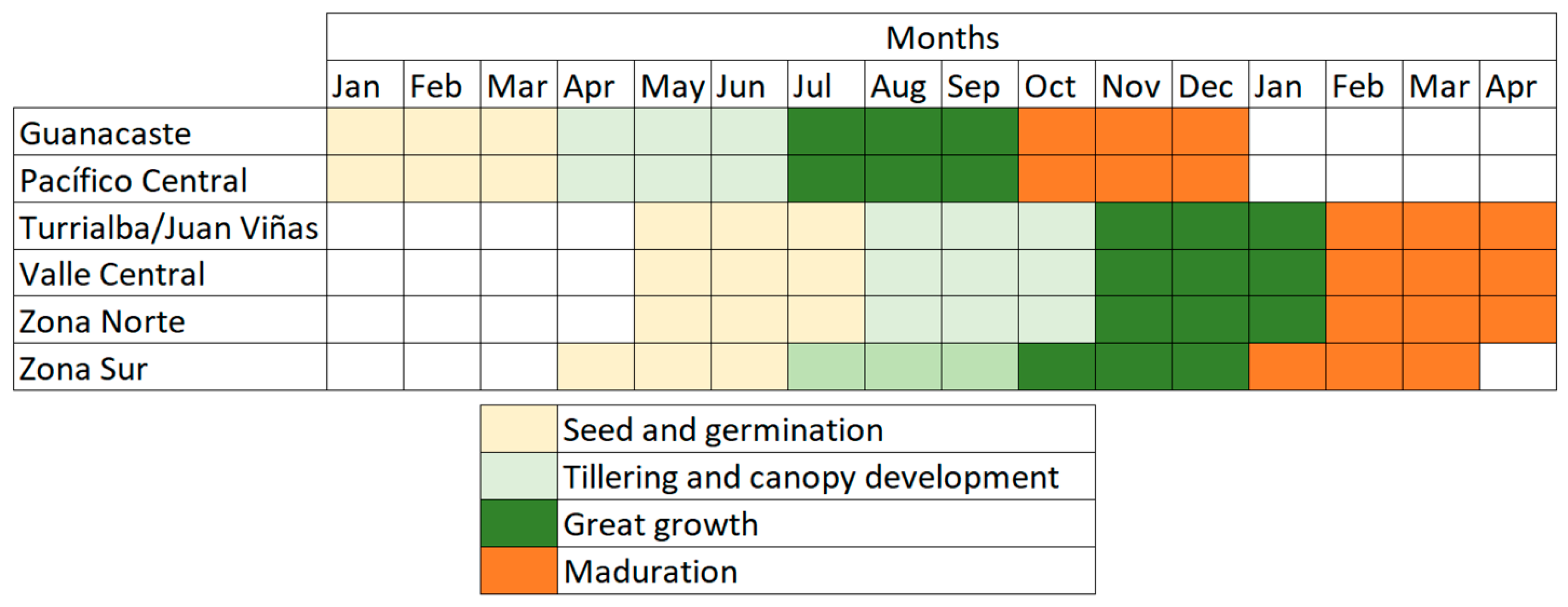
2.2. Sugarcane Crop Cycle in Costa Rica
2.3. Available Data
2.3.1. Yield and Climatic Data
2.3.2. Satellite Images and Vegetation Indexes
2.4. Multivariate Statistical Analysis and Spatio-Temporal Validation
3. Results
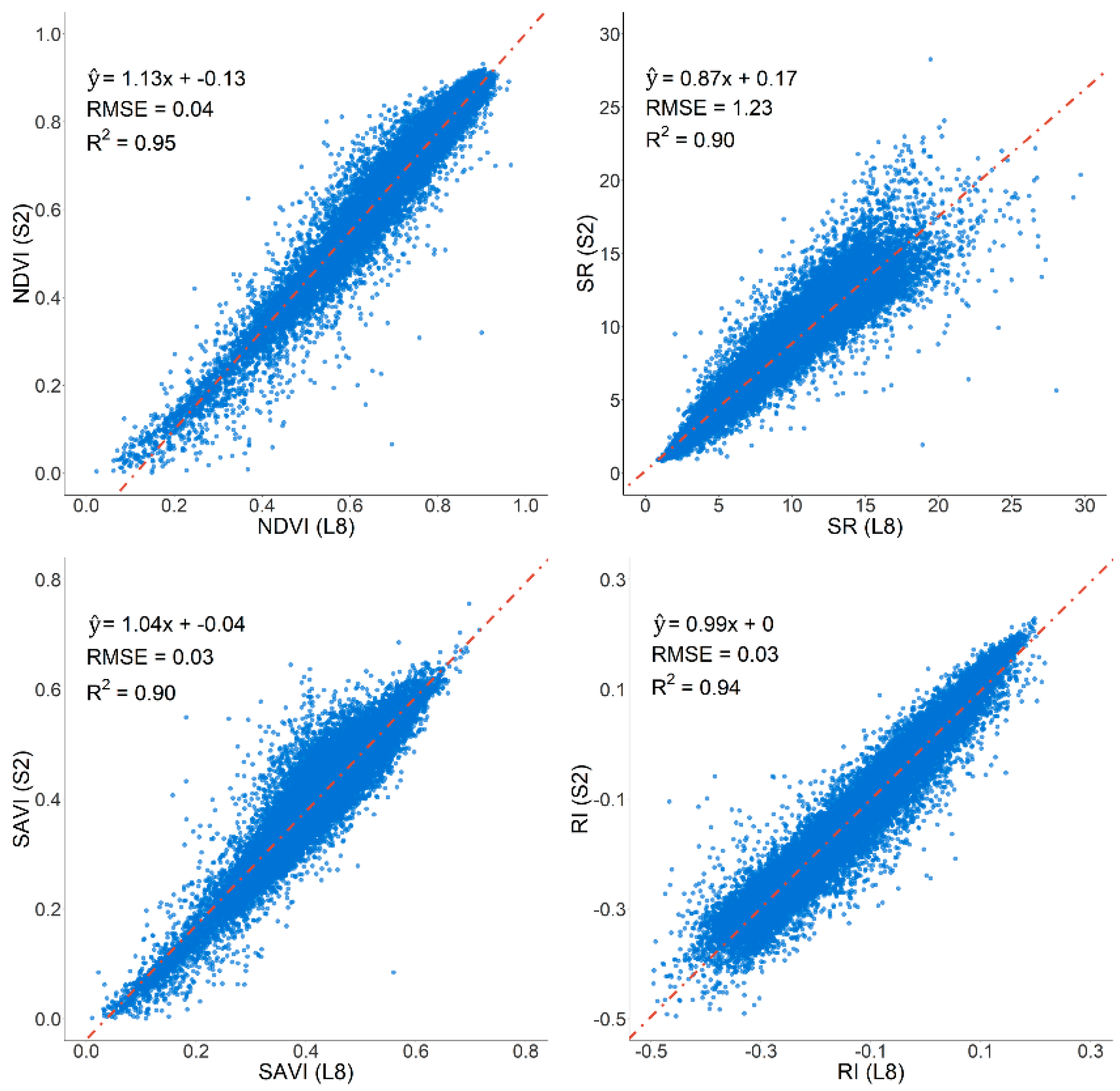
3.1. Harmonization of Vegetation Indexes and Temporal Phenological Signatures
3.2. Sugarcane Yield Models
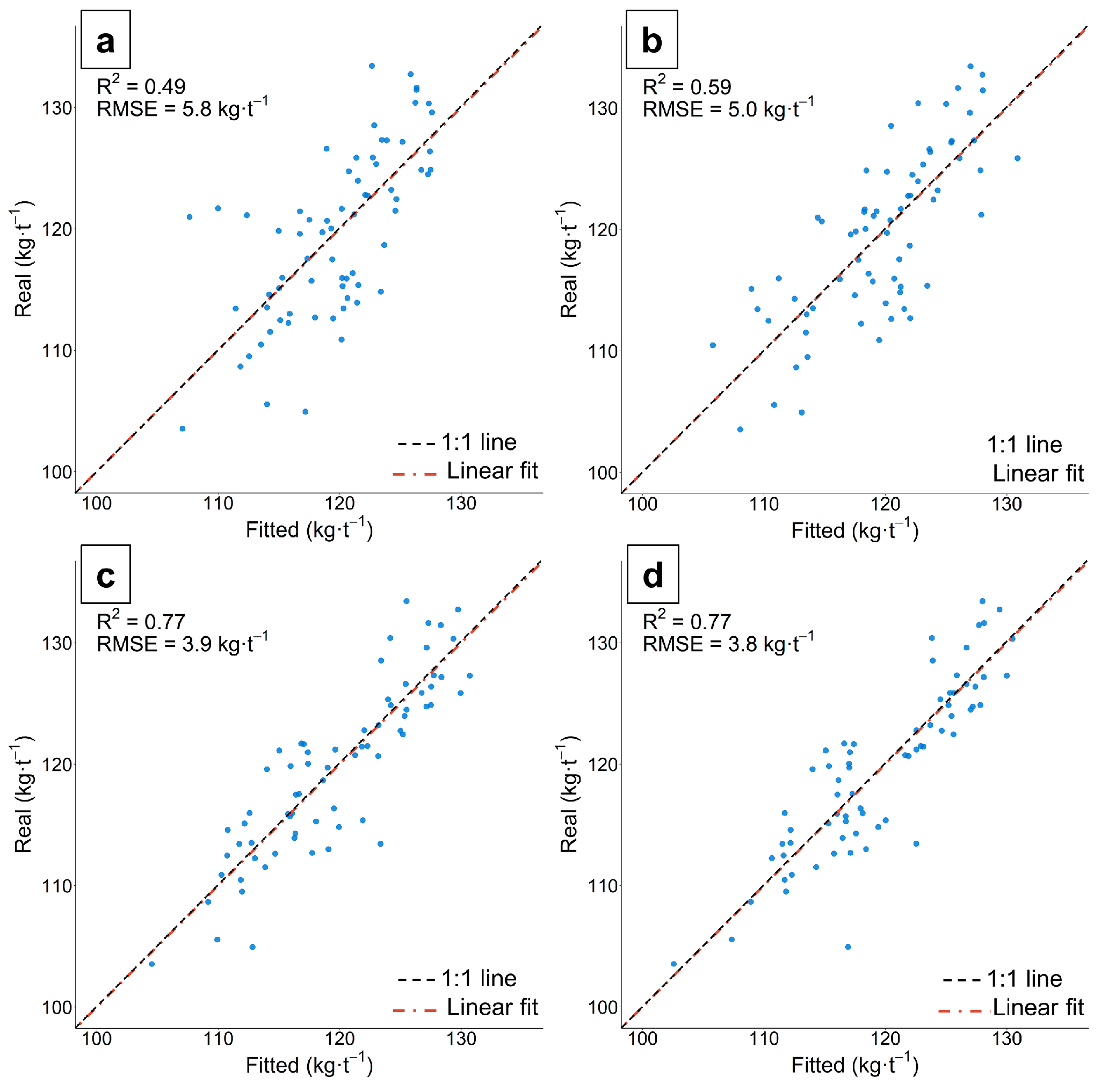
3.2.1. Modelling Sugarcane Yield at the Farm Scale
3.2.2. Spatial Validation of Sugarcane Yield at Farm and Plot Scales
3.3. Sugar Content Models
3.3.1. Modelling Sugar Content at Farm Scale
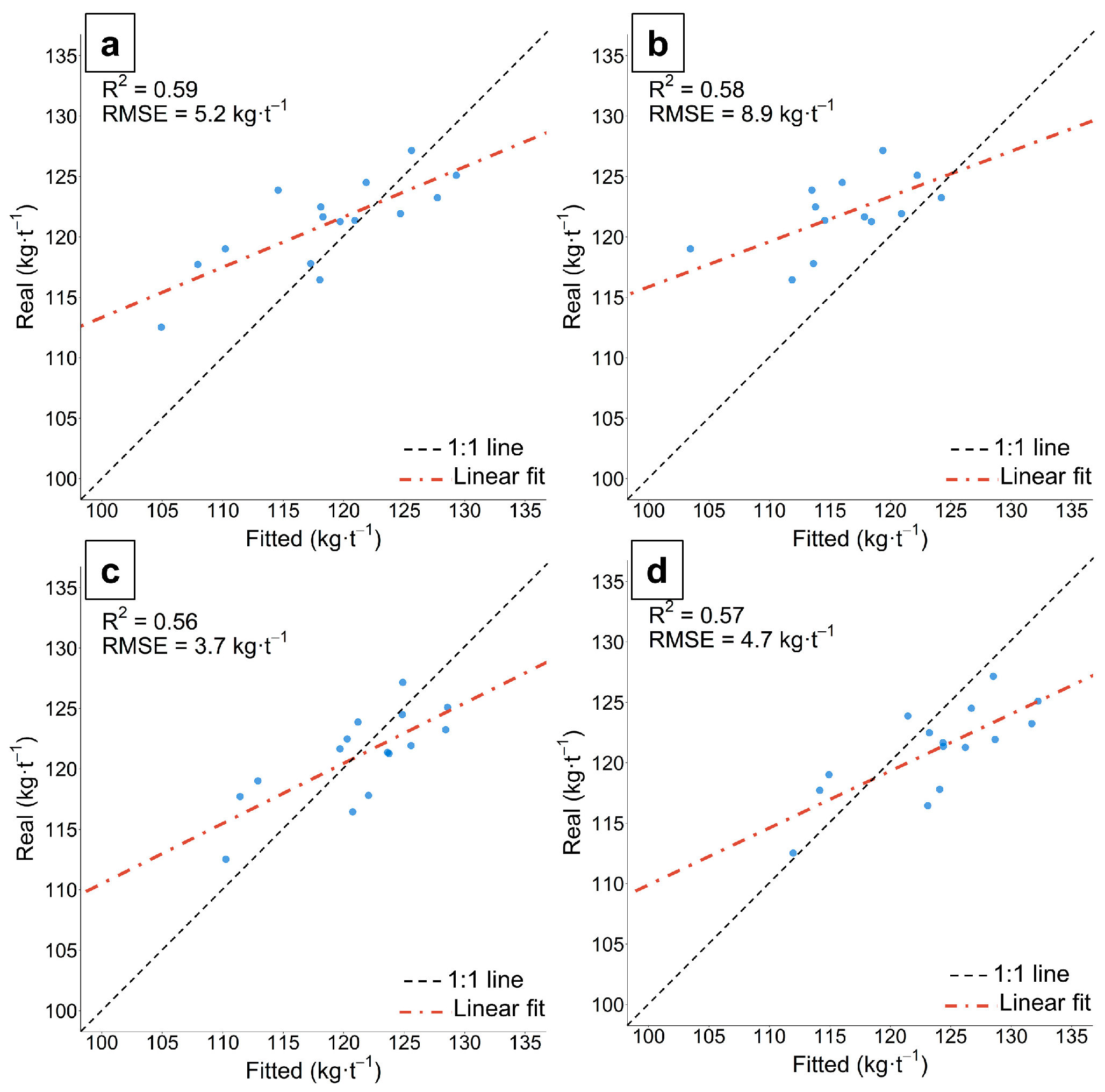
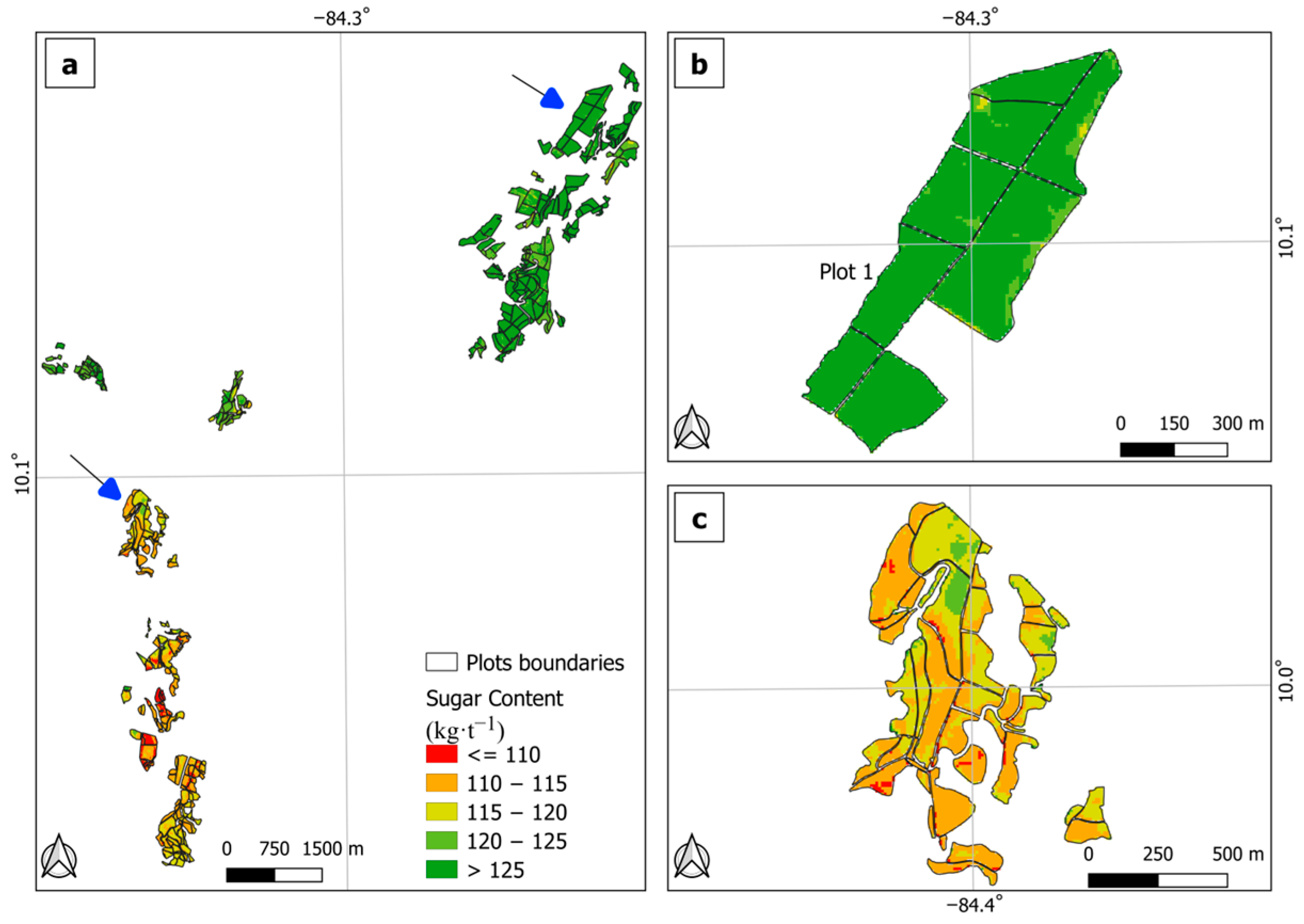
3.3.2. Spatial Validation of Sugar Content at Farm and Plot Scales
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Angulo, Á.; Rodríguez, M.; Chaves, M. Guía Técnica Cultivo Caña De Azúcar Región: Guanacaste. Available online: https://servicios.laica.co.cr/laica-cv-biblioteca/index.php/Library/download/jieyzwRDmVvUeWJGLRfYLzXbibjfLZNW (accessed on 18 April 2023).
- INEC (Instituto Nacional de Estadística y Censos). Encuesta Nacional Agropecuaria 2021 Resultados Generales de La Actividad Agrícola y Forestal. Available online: https://inec.cr/estadisticas-fuentes/encuestas/encuesta-nacional-agropecuaria?page=3 (accessed on 18 April 2023).
- Chaves, M.; Bermúdez, L. Agroindustria Azucarera Costarricense: Un Modelo Organizacional y Productivo Efectivo Con 75 Años de Vigencia. Available online: https://servicios.laica.co.cr/laica-cv-biblioteca/index.php/Library/download/DSCmSdyqoIJhQAUmeqVMAwOPjrySXJdh (accessed on 1 September 2021).
- Som-Ard, J.; Atzberger, C.; Izquierdo-Verdiguier, E.; Vuolo, F.; Immitzer, M. Remote Sensing Applications in Sugarcane Cultivation: A Review. Remote Sens. 2021, 13, 4040. [Google Scholar] [CrossRef]
- Allison, J.C.S.; Pammenter, N.W.; Haslam, R.J. Why Does Sugarcane (Saccharum Sp. Hybrid) Grow Slowly? S. Afr. J. Bot. 2007, 73, 546–551. [Google Scholar] [CrossRef]
- Cock, J.H. Sugarcane Growth and Development. Int. Sugar J. 2003, 105, 540–552. [Google Scholar]
- Inman-Bamber, N.G. Temperature and Seasonal Effects on Canopy Development and Light Interception of Sugarcane. Field Crop. Res. 1994, 36, 41–51. [Google Scholar] [CrossRef]
- Saez, J.V. Dinámica de Acumulación de Sacarosa en Tallos de Caña de Azúcar (Saccharum spp.) Modulada por Cambios en la Relación Fuente-Destino. Ph.D. Thesis, Facultad de Ciencias Agropecuarias, Universidad Nacional de Cordoba, 2017. Available online: http://hdl.handle.net/11086/6836 (accessed on 3 December 2020).
- Molijn, R.A.; Iannini, L.; Rocha, J.V.; Hanssen, R.F. Sugarcane Productivity Mapping through C-Band and L-Band SAR and Optical Satellite Imagery. Remote Sens. 2019, 11, 1109. [Google Scholar] [CrossRef]
- Pinter, P.J.; Hatfield, J.L.; Schepers, J.S.; Barnes, E.M.; Moran, M.S.; Daughtry, C.S.; Upchurch, D.R. Remote Sensing for Site-Specific Crop Management. Photogramm. Eng. Remote Sens. 2003, 69, 647–664. [Google Scholar] [CrossRef]
- Liaghat, S.; Balasundram, S.K. A Review: The Role of Remote Sensing in Precision Agriculture. Am. J. Agric. Biol. Sci. 2010, 5, 50–55. [Google Scholar] [CrossRef]
- Segarra, J.; Buchaillot, M.L.; Araus, J.L.; Kefauver, S.C. Remote Sensing for Precision Agriculture: Sentinel-2 Improved Features and Applications. Agronomy 2020, 10, 641. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Ahmed, F.B. The Application of Remote Sensing Techniques to Sugarcane (Saccharum spp. Hybrid) Production: A Review of the Literature. Int. J. Remote Sens. 2008, 29, 3753–3767. [Google Scholar] [CrossRef]
- Rudorff, B.F.T.; Batista, G.T. Yield Estimation of Sugarcane Based on Agrometeorological-Spectral Models. Remote Sens. Environ. 1990, 33, 183–192. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A Review of Vegetation Indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Rao, P.V.K.; Rao, V.V.; Venkataratnam, L. Remote Sensing: A Technology for Assessment of Sugarcane Crop Acreage and Yield. Sugar Technol. 2002, 4, 97–101. [Google Scholar] [CrossRef]
- Almeida, T.I.R.; De Souza Filho, C.R.; Rossetto, R. ASTER and Landsat ETM+ Images Applied to Sugarcane Yield Forecast. Int. J. Remote Sens. 2006, 27, 4057–4069. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Rocha, J.V.; Lamparelli, R.A.C. Sugarcane Yield Estimates Using Time Series Analysis of Spot Vegetation Images. Sci. Agric. 2011, 68, 139–146. [Google Scholar] [CrossRef]
- Mutanga, S.; van Schoor, C.; Olorunju, P.L.; Gonah, T.; Ramoelo, A. Determining the Best Optimum Time for Predicting Sugarcane Yield Using Hyper-Temporal Satellite Imagery. Adv. Remote Sens. 2013, 2, 269–275. [Google Scholar] [CrossRef]
- Mulianga, B.; Bégué, A.; Simoes, M.; Todoroff, P. Forecasting Regional Sugarcane Yield Based on Time Integral and Spatial Aggregation of MODIS NDVI. Remote Sens. 2013, 5, 2184–2199. [Google Scholar] [CrossRef]
- Dubey, S.K.; Gavli, A.S.; Yadav, S.K.; Sehgal, S.; Ray, S.S. Remote Sensing-Based Yield Forecasting for Sugarcane (Saccharum officinarum L.) Crop in India. J. Indian Soc. Remote Sens. 2018, 46, 1823–1833. [Google Scholar] [CrossRef]
- Morel, J.; Todoroff, P.; Bégué, A.; Bury, A.; Martiné, J.F.; Petit, M. Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island. Remote Sens. 2014, 6, 6620–6635. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A. Integrating Landsat-8 and Sentinel-2 Time Series Data for Yield Prediction of Sugarcane Crops at the Block Level. Remote Sens. 2020, 12, 1313. [Google Scholar] [CrossRef]
- Abebe, G.; Tadesse, T.; Gessesse, B. Combined Use of Landsat 8 and Sentinel 2A Imagery for Improved Sugarcane Yield Estimation in Wonji-Shoa, Ethiopia. J. Indian Soc. Remote Sens. 2022, 50, 143–157. [Google Scholar] [CrossRef]
- dos Santos Luciano, A.C.; Picoli, M.C.A.; Duft, D.G.; Rocha, J.V.; Leal, M.R.L.V.; le Maire, G. Empirical Model for Forecasting Sugarcane Yield on a Local Scale in Brazil Using Landsat Imagery and Random Forest Algorithm. Comput. Electron. Agric. 2021, 184, 106063. [Google Scholar] [CrossRef]
- Som-ard, J.; Hossain, M.D.; Ninsawat, S.; Veerachitt, V. Pre-Harvest Sugarcane Yield Estimation Using UAV-Based RGB Images and Ground Observation. Sugar Technol. 2018, 20, 645–657. [Google Scholar] [CrossRef]
- Sumesh, K.C.; Ninsawat, S.; Som-ard, J. Integration of RGB-Based Vegetation Index, Crop Surface Model and Object-Based Image Analysis Approach for Sugarcane Yield Estimation Using Unmanned Aerial Vehicle. Comput. Electron. Agric. 2021, 180, 105903. [Google Scholar] [CrossRef]
- Alemán-Montes, B.; Henríquez-Henríquez, C.; Ramírez-Rodríguez, T.; Largaespada-Zelaya, K. Estimación de Rendimiento En El Cultivo de Caña de Azúcar (Saccharum officinarum) a Partir de Fotogrametría Con Vehículos Aéreos No Tripulados (VANT). Agron. Costarric. 2021, 45, 67–80. [Google Scholar] [CrossRef]
- Akbarian, S.; Xu, C.; Wang, W.; Ginns, S.; Lim, S. Sugarcane Yields Prediction at the Row Level Using a Novel Cross-Validation Approach to Multi-Year Multispectral Images. Comput. Electron. Agric. 2022, 198, 107024. [Google Scholar] [CrossRef]
- Barbosa Júnior, M.R.; Moreira, B.R.d.A.; de Brito Filho, A.L.; Tedesco, D.; Shiratsuchi, L.S.; da Silva, R.P. UAVs to Monitor and Manage Sugarcane: Integrative Review. Agronomy 2022, 12, 661. [Google Scholar] [CrossRef]
- Hidalgo, N. Análisis del Rendimiento del Cultivo de Caña de Azúcar Mediante Índices de Vegetación y Monitores de Rendimiento Durante el Periodo de Zafra 2021–2022 en la Empresa Central Azucarera Tempisque S.A. (CATSA) Guanacaste, Costa Rica. Licenciature’s Thesis, Escuela de Ingeniería Agrícola, Instituto Tecnológico de Costa Rica, 2022. Available online: https://repositoriotec.tec.ac.cr/handle/2238/13994 (accessed on 25 April 2023).
- Jeffries, G.R.; Griffin, T.S.; Fleisher, D.H.; Naumova, E.N.; Koch, M.; Wardlow, B.D. Mapping Sub-Field Maize Yields in Nebraska, USA by Combining Remote Sensing Imagery, Crop Simulation Models, and Machine Learning. Precis. Agric. 2020, 21, 678–694. [Google Scholar] [CrossRef]
- Dimov, D.; Uhl, J.H.; Löw, F.; Seboka, G.N. Sugarcane Yield Estimation through Remote Sensing Time Series and Phenology Metrics. Smart Agric. Technol. 2022, 2, 100046. [Google Scholar] [CrossRef]
- Canata, T.F.; Wei, M.C.F.; Maldaner, L.F.; Molin, J.P. Sugarcane Yield Mapping Using High-Resolution Imagery Data and Machine Learning Technique. Remote Sens. 2021, 13, 232. [Google Scholar] [CrossRef]
- Bégué, A.; Lebourgeois, V.; Bappel, E.; Todoroff, P.; Pellegrino, A.; Baillarin, F.; Siegmund, B. Spatio-Temporal Variability of Sugarcane Fields and Recommendations for Yield Forecast Using NDVI. Int. J. Remote Sens. 2010, 31, 5391–5407. [Google Scholar] [CrossRef]
- Shendryk, Y.; Davy, R.; Thorburn, P. Integrating Satellite Imagery and Environmental Data to Predict Field-Level Cane and Sugar Yields in Australia Using Machine Learning. Field Crop. Res. 2021, 260, 107984. [Google Scholar] [CrossRef]
- LAICA Ley Orgánica de La Agricultura e Industria de La Caña de Azúcar N° 7818 Del 22 de Setiembre de 1998. Available online: http://www.pgrweb.go.cr/scij/Busqueda/Normativa/Normas/nrm_texto_completo.aspx?param2=NRTC&nValor1=1&nValor2=44897&strTipM=TC (accessed on 8 May 2023).
- Montenegro Ballestero, J.; Chaves Solera, M. Análisis de Ciclo de Vida Para La Producción Primaria de Caña de Azúcar En Seis Regiones de Costa Rica. Rev. Ciencias Ambient. 2022, 56, 96–119. [Google Scholar] [CrossRef]
- Chaves, M.; Chavarría, E. Estimación Del Área Sembrada Con Caña de Azúcar En Costa Rica Según Región Productora. Periodo 1985–2020 (36 Zafras). Available online: https://laica.cr/wp-content/uploads/2022/05/revista-entre-caneros-no22.pdf (accessed on 8 May 2023).
- Mata, R.; Rosales, A.; Sandoval, D.; Vindas, E.; Alemán, B. Subórdenes de Suelos de Costa Rica [Mapa Digital]. Escala 1:200000. Available online: http://www.cia.ucr.ac.cr/es/mapa-de-suelos-de-costa-rica (accessed on 30 September 2022).
- Alfaro, E.J. Caracterización del “Veranillo” en dos Cuencas de la Vertiente Del Pacífico de Costa Rica, América Central. Rev. Biol. Trop. 2014, 62, 1–15. [Google Scholar] [CrossRef]
- Vignola, R.; Poveda, K.; Watler, W.; Vargas, A.; Berrocal, Á. Cultivo de Caña de Azúcar En Costa Rica. Available online: https://www.mag.go.cr/bibliotecavirtual/F01-8327.pdf (accessed on 8 May 2023).
- Chaves, M. Suelos, Nutrición y Fertilización de la Caña de Azúcar en Costa Rica. Available online: https://servicios.laica.co.cr/laica-cv-biblioteca/index.php/Library/download/xznuAsbXHGPzjuDRWFDDwEOtAUrWraua (accessed on 8 May 2023).
- Ramburan, S.; Wettergreen, T.; Berry, S.D.; Shongwe, B. Effects of Variety, Environment and Management on Sugarcane Ratoon Yield Decline. Int. Sugar J. 2012, 85, 180–192. [Google Scholar]
- Dlamini, N.E.; Zhou, M. Soils and Seasons Effect on Sugarcane Ratoon Yield. Field Crop. Res. 2022, 284, 108588. [Google Scholar] [CrossRef]
- Panigrahy, S.; Sharma, S.A. Mapping of Crop Rotation Using Multidate Indian Remote Sensing Satellite Digital Data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 85–91. [Google Scholar] [CrossRef]
- Zhao, Y.; Della Justina, D.; Kazama, Y.; Rocha, J.V.; Graziano, P.S.; Lamparelli, R.A.C. Dynamics Modeling for Sugar Cane Sucrose Estimation Using Time Series Satellite Imagery. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII; Neale, C.M.U., Maltese, A., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9998, p. 99980J. [Google Scholar]
- Chaves, M.; Picoli, M.; Sanches, I. Recent Applications of Landsat 8/OLI and Sentinel-2/MSI for Land Use and Land Cover Mapping: A Systematic Review. Remote Sens. 2020, 12, 3062. [Google Scholar] [CrossRef]
- USGS (United States Geological Survey). Landsat 8-9 Collection 2 (C2) Level 2 Science Product (L2SP) Guide. Available online: https://www.usgs.gov/media/files/landsat-8-9-collection-2-level-2-science-product-guide (accessed on 28 September 2022).
- Mueller-Wilm, U.; Devignot, O.; Pessiot, L. Sen2Cor Configuration and User Manual. Available online: http://step.esa.int/thirdparties/sen2cor/2.3.0/[L2A-SUM] S2-PDGS-MPC-L2A-SUM [2.3.0].pdf (accessed on 30 June 2023).
- Jiménez-Jiménez, S.I.; Marcial-Pablo, M.d.J.; Ojeda-Bustamante, W.; Sifuentes-Ibarra, E.; Inzunza-Ibarra, M.A.; Sánchez-Cohen, I. VICAL: Global Calculator to Estimate Vegetation Indices for Agricultural Areas with Landsat and Sentinel-2 Data. Agronomy 2022, 12, 1518. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing Vegetation from Soil Background Information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS- MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite (ERTS) Symposium, Washington, DC, USA, 10–14 December 1973; Volume 351, pp. 309–317. [Google Scholar]
- Escadafal, R.; Huete, A. Étude Des Propriétés Spectrales Des Sols Arides Appliquée à Lamélioration Des Indices de Vegetation Obtenus Par Télédection. CR Académie Sci. Paris 1991, 312, 1385–1391. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of Shortgrass Prairie, Pawnee National Grasslands, Colorado. In Proceedings of the 8th International Symposium on Remote Sensing of the Environment, Ann Arbor, MI, USA, 2–6 October 1972. [Google Scholar]
- Huete, A. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Simões, M.d.S.; Rocha, J.V.; Lamparelli, R.A.C. Variáveis Espectrais e Indicadores de Desenvolvimento e Produtividade da Cana-de-Açúcar. Sci. Agric. 2005, 62, 199–207. [Google Scholar] [CrossRef]
- Li, J.; Lu, X.; Cheng, K.; Liu, W. Package ‘StepReg’. Available online: https://cran.r-project.org/web/packages/StepReg/index.html (accessed on 15 October 2020).
- Max, A.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Ziem, A.; Scrucca, L.; et al. Package ‘Caret’ R. Available online: https://cran.r-project.org/web/packages/caret/index.html (accessed on 17 October 2020).
- Alemán-Montes, B.; Serra, P.; Zabala, A. Modelos Para La Estimación Del Rendimiento de La Caña de Azúcar En Costa Rica Con Datos de Campo e Índices de Vegetación. Rev. Teledetección 2023, 2023, 1–13. [Google Scholar] [CrossRef]
- Meroni, M.; Waldner, F.; Seguini, L.; Kerdiles, H.; Rembold, F. Yield Forecasting with Machine Learning and Small Data: What Gains for Grains? Agric. For. Meteorol. 2021, 308–309, 108555. [Google Scholar] [CrossRef]









| Month | Harvest Cycles | ||||
|---|---|---|---|---|---|
| 2017–2018 | 2018–2019 | 2019–2020 | 2020–2021 | 2021–2022 | |
| May | L8-2017-05-18 | S2-2018-05-11 | S2-2019-05-16 | L8-2020-05-26 | S2-2021-05-15 |
| June | L8-017-06-19 | L8-2018-06-22 | S2-2019-06-30 | ND | S2-2021-06-19 |
| July | S2-2017-07-15 | L8-2018-07-24 | L8-2019-07-27 | ND | L8-2021-07-16 |
| August | L8-2017-08-22 | L8-2018-08-25 | S2-2019-08-24 | S2-2020-08-28 | L8-2021-08-17 |
| September | L8-2017-09-07 | S2-2018-09-13 | S2-2019-09-08 | L8-2020-09-15 | S2-2021-10-02 * |
| October | L8-2017-11-10 * | S2-2018-11-07 * | L8-2019-10-31 | S2-2020-10-22 | ND |
| November | S2-2017-11-17 | L8-2018-11-13 | S2-2019-11-22 | S2-2020-11-26 | S2-2021-11-26 |
| December | S2-2017-12-22 | S2-2018-12-27 | S2-2019-12-27 | S2-2020-12-21 | S2-2021-12-31 |
| January | S2-2018-01-26 | S2-2019-01-31 | S2-2020-01-31 | S2-2021-01-30 | S2-2022-01-20 |
| Vegetation Index | Equation | Source |
|---|---|---|
| DVI | [52] | |
| EVI | [53] | |
| GNDVI | [54] | |
| NDVI | [55] | |
| RI | [56] | |
| RVI | [57] | |
| SAVI | [58] | |
| SR * | [59] |
| Month | May | June | July | August | September | October | November | December | January | |
|---|---|---|---|---|---|---|---|---|---|---|
| DVI | R2 | * | * | * | * | 0.48 | 0.50 | * | * | 0.61 |
| RMSE | 10.2 | 10.1 | 9.1 | |||||||
| EVI | R2 | * | * | * | 0.48 | 0.49 | * | * | * | * |
| RMSE | 10.7 | 10.1 | ||||||||
| GNDVI | R2 | * | * | * | * | * | * | * | 0.56 | 0.56 |
| RMSE | 9.2 | 9.2 | ||||||||
| NDVI | R2 | * | * | * | * | * | 0.53 | 0.56 | 0.60 | 0.63 |
| RMSE | 10.2 | 9.5 | 9.0 | 8.9 | ||||||
| RI | R2 | * | * | * | 0.48 | 0.55 | 0.61 | 0.64 | 0.64 | 0.66 |
| RMSE | 10.8 | 9.4 | 9.1 | 8.7 | 8.7 | 8.5 | ||||
| RVI | R2 | * | * | * | * | 0.47 | 0.53 | 0.55 | 0.60 | 0.60 |
| RMSE | 10.2 | 10.3 | 9.6 | 9.0 | 9.0 | |||||
| SAVI | R2 | * | * | * | * | * | * | * | * | * |
| RMSE | ||||||||||
| SR | R2 | * | * | * | 0.47 | 0.53 | 0.56 | 0.57 | 0.65 | 0.68 |
| RMSE | 10.8 | 9.9 | 9.6 | 9.2 | 8.4 | 8.1 |
| Month | May | June | July | August | September | October | November | December | January | |
|---|---|---|---|---|---|---|---|---|---|---|
| DVI | R2 | 0.29 | * | * | * | 0.28 | 0.37 | 0.37 | * | * |
| RMSE | 6.7 | 6.3 | 5.8 | 6.0 | ||||||
| EVI | R2 | 0.29 | * | * | * | 0.39 | 0.39 | 0.38 | 0.48 | 0.49 |
| RMSE | 6.7 | 5.9 | 5.8 | 6.0 | 5.7 | 5.8 | ||||
| GNDVI | R2 | 0.26 | * | * | * | 0.33 | * | * | * | * |
| RMSE | 6.9 | 6.1 | ||||||||
| NDVI | R2 | 0.28 | * | * | * | 0.34 | 0.39 | * | * | * |
| RMSE | 6.8 | 6.1 | 5.7 | |||||||
| RI | R2 | 0.29 | * | * | * | 0.30 | 0.35 | 0.34 | 0.40 | 0.40 |
| RMSE | 6.7 | 6.2 | 5.9 | 6.1 | 6.0 | 6.0 | ||||
| RVI | R2 | 0.29 | * | * | 0.27 | 0.34 | 0.39 | 0.46 | 0.46 | 0.46 |
| RMSE | 6.8 | 6.7 | 6.1 | 5.8 | 5.6 | 5.6 | 5.6 | |||
| SAVI | R2 | 0.29 | * | * | * | 0.28 | 0.38 | * | * | * |
| RMSE | 6.7 | 6.3 | 5.8 | |||||||
| SR | R2 | 0.28 | * | * | * | 0.31 | 0.40 | 0.48 | 0.48 | 0.48 |
| RMSE | 6.8 | 6.2 | 5.8 | 5.6 | 5.6 | 5.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemán-Montes, B.; Zabala, A.; Henríquez, C.; Serra, P. Modelling Two Sugarcane Agro-Industrial Yields Using Sentinel/Landsat Time-Series Data and Their Spatial Validation at Different Scales in Costa Rica. Remote Sens. 2023, 15, 5476. https://doi.org/10.3390/rs15235476
Alemán-Montes B, Zabala A, Henríquez C, Serra P. Modelling Two Sugarcane Agro-Industrial Yields Using Sentinel/Landsat Time-Series Data and Their Spatial Validation at Different Scales in Costa Rica. Remote Sensing. 2023; 15(23):5476. https://doi.org/10.3390/rs15235476
Chicago/Turabian StyleAlemán-Montes, Bryan, Alaitz Zabala, Carlos Henríquez, and Pere Serra. 2023. "Modelling Two Sugarcane Agro-Industrial Yields Using Sentinel/Landsat Time-Series Data and Their Spatial Validation at Different Scales in Costa Rica" Remote Sensing 15, no. 23: 5476. https://doi.org/10.3390/rs15235476
APA StyleAlemán-Montes, B., Zabala, A., Henríquez, C., & Serra, P. (2023). Modelling Two Sugarcane Agro-Industrial Yields Using Sentinel/Landsat Time-Series Data and Their Spatial Validation at Different Scales in Costa Rica. Remote Sensing, 15(23), 5476. https://doi.org/10.3390/rs15235476