Sentinel-1 Imagery Used for Estimation of Soil Organic Carbon by Dual-Polarization SAR Vegetation Indices
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Field Data Collection
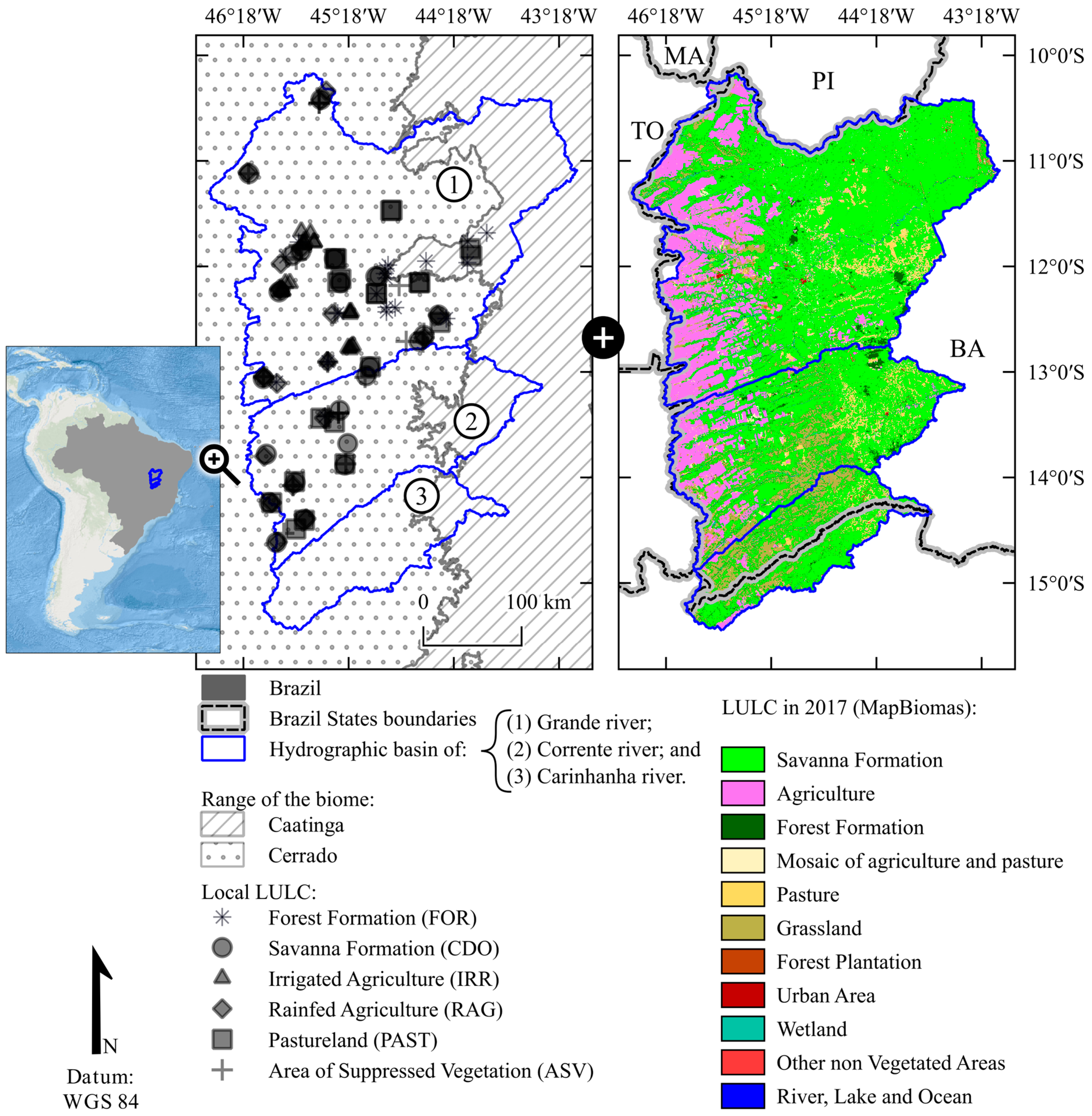
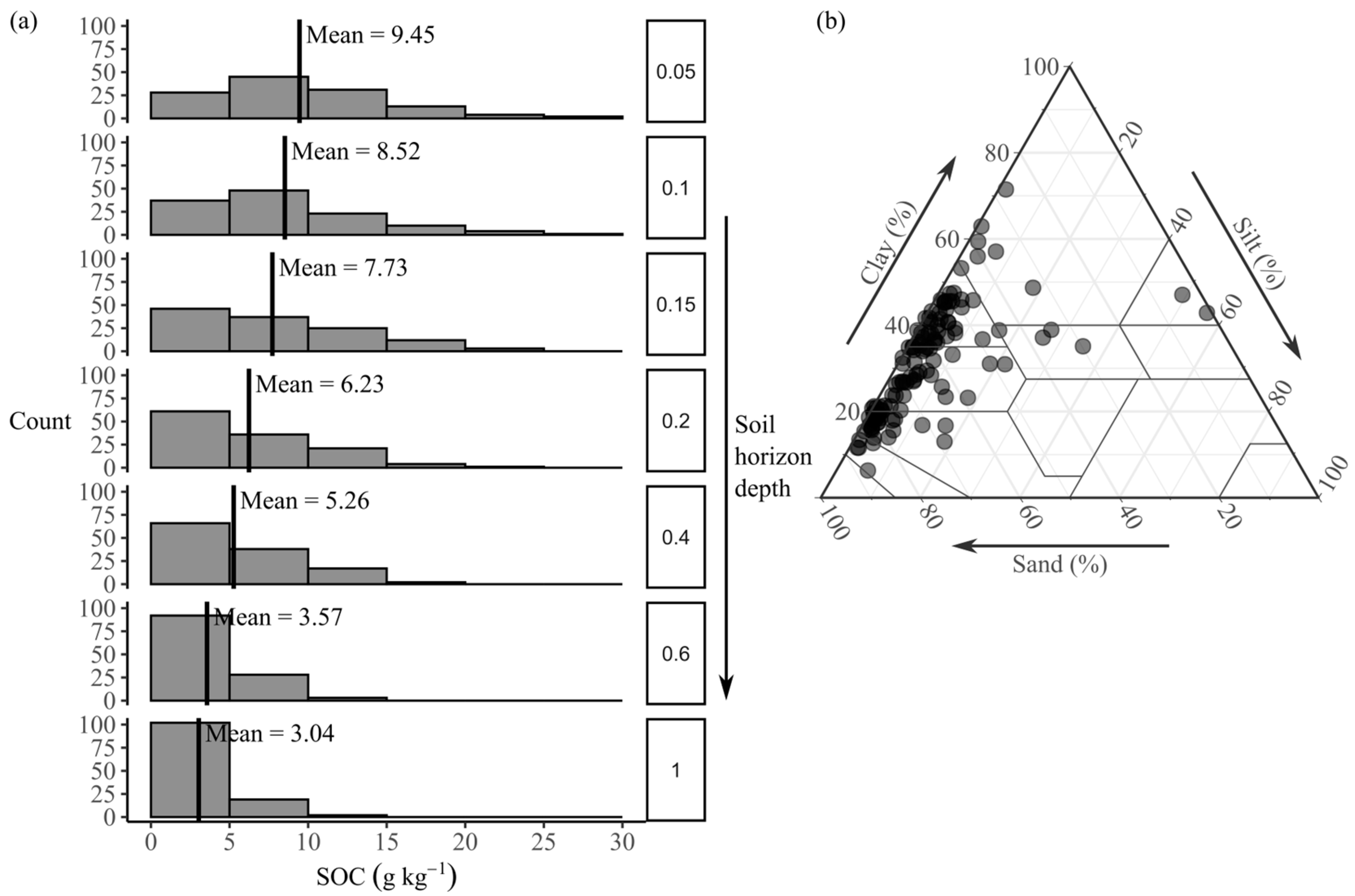
2.2. Remote Sensing Data Acquisition and Processing
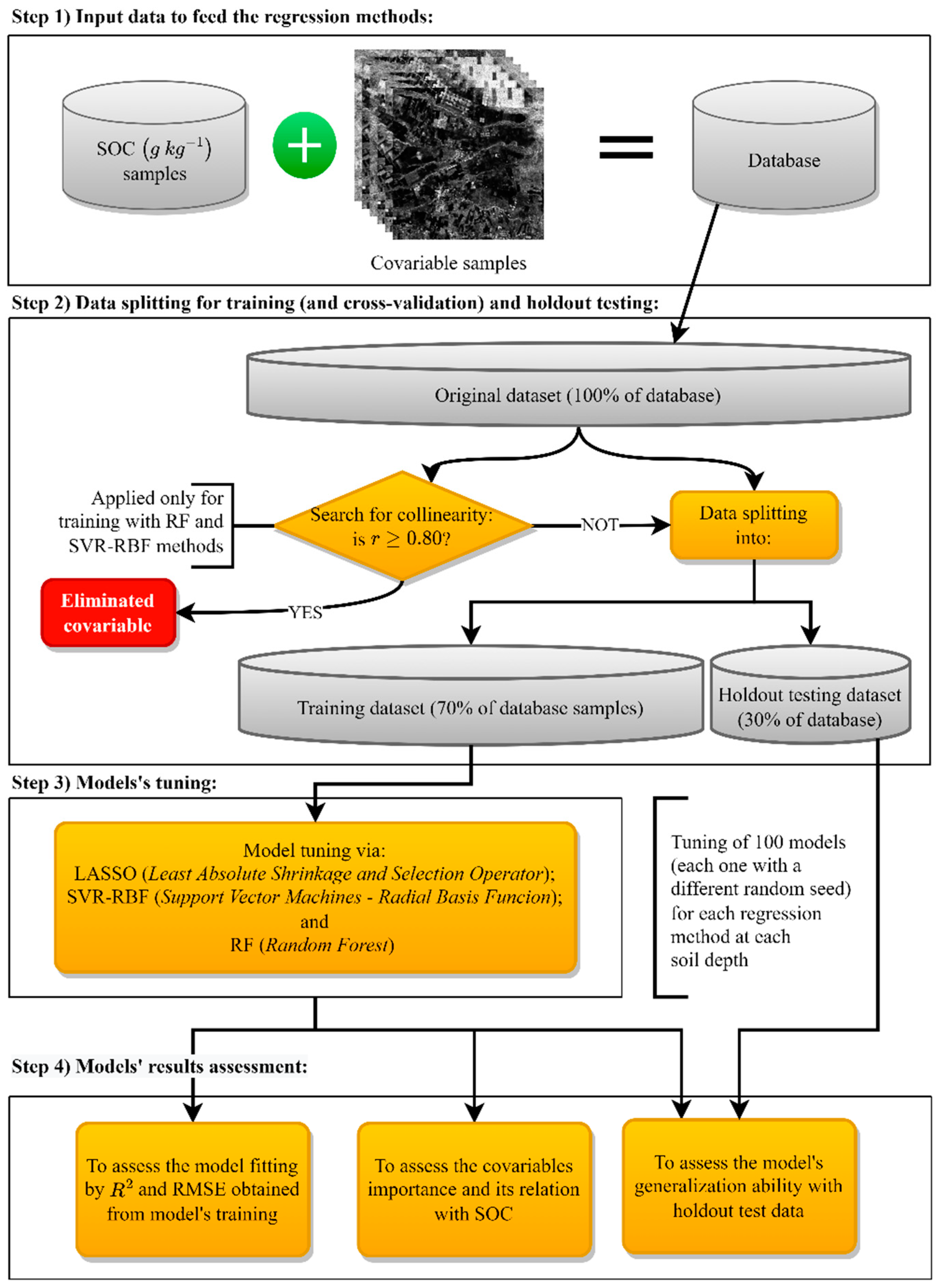
2.3. Modeling Soil Organic Carbon by Machine Learning Methods
2.4. Results Assessment
3. Results
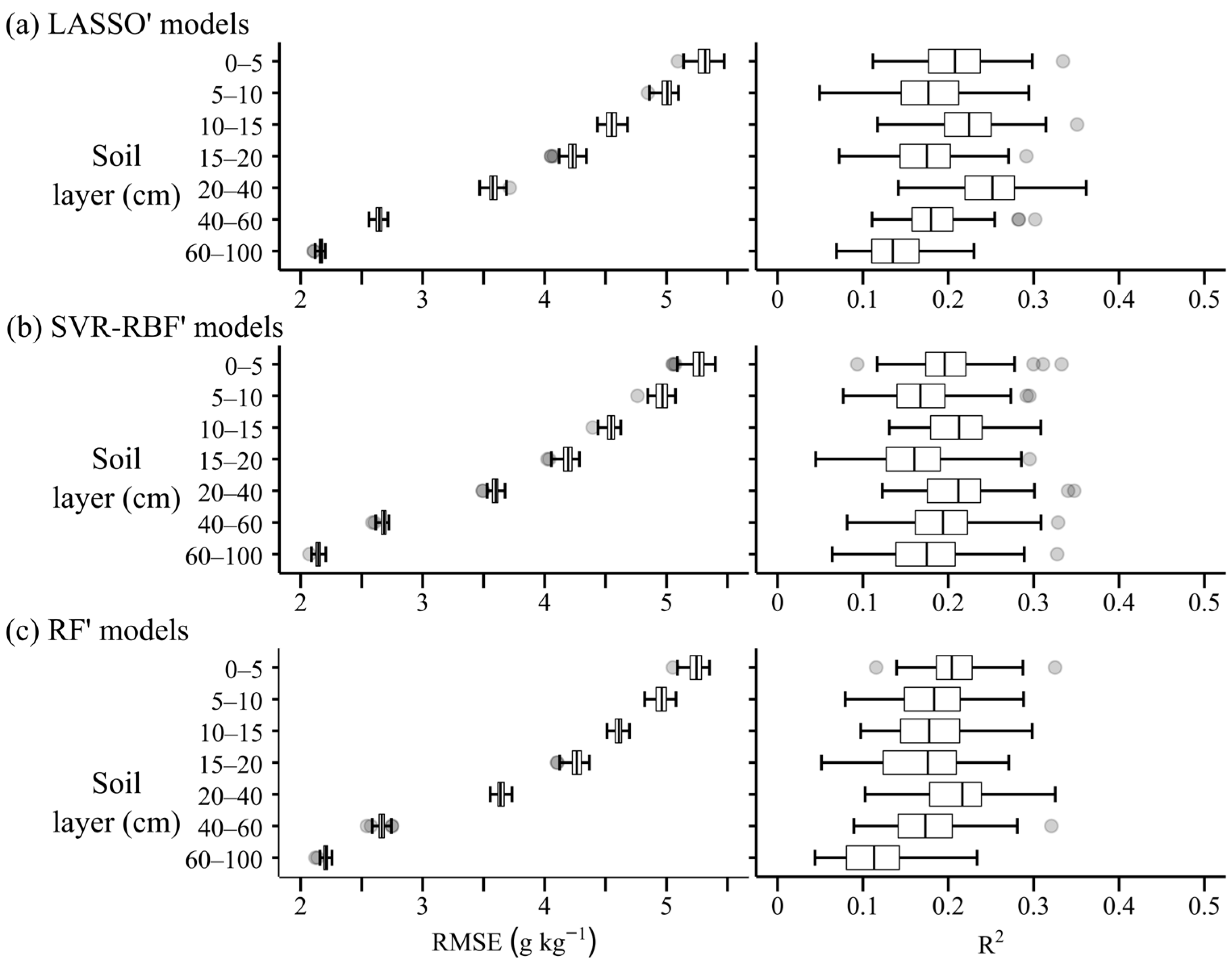
3.1. Accuracy of Soil Organic Carbon Prediction
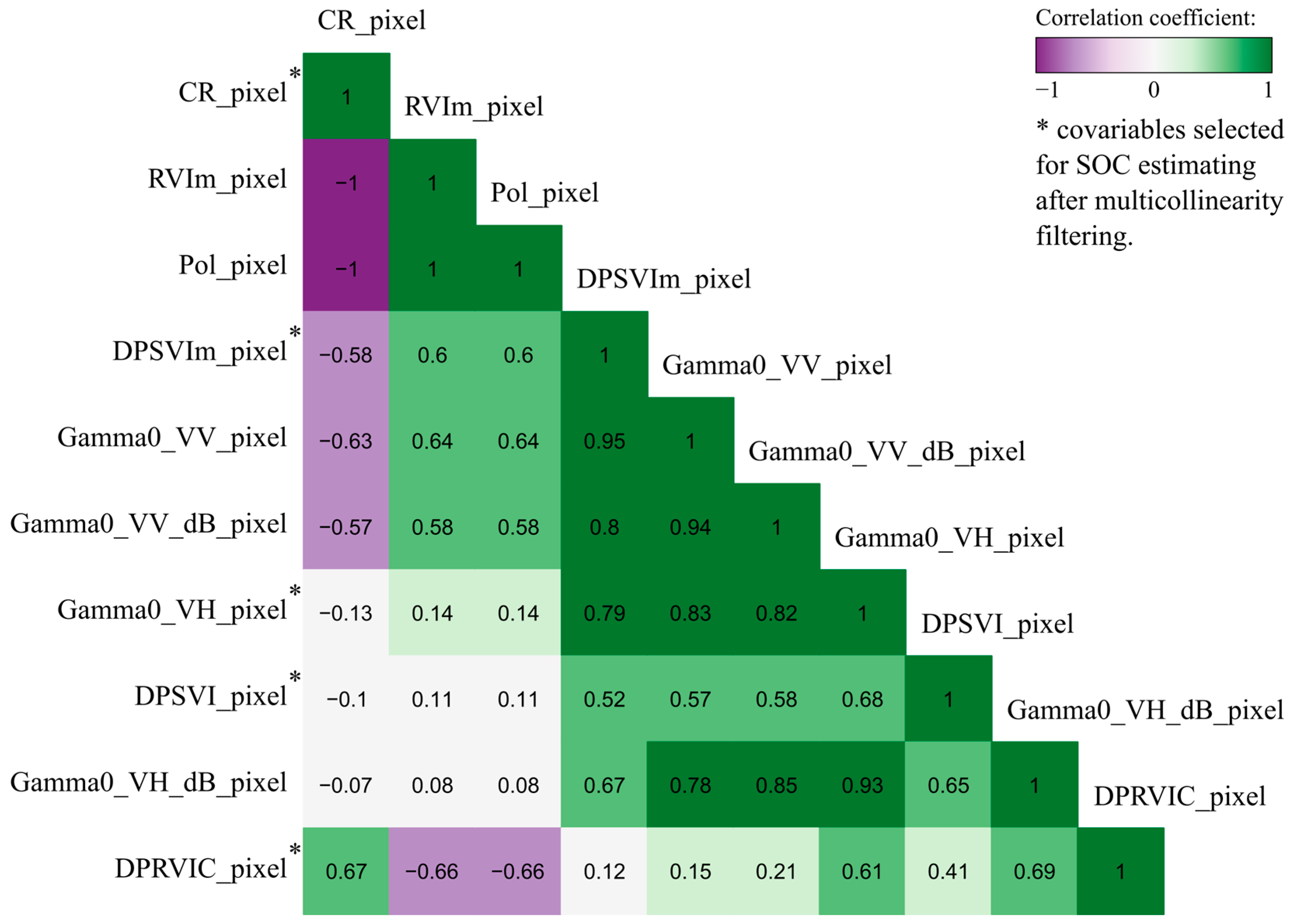
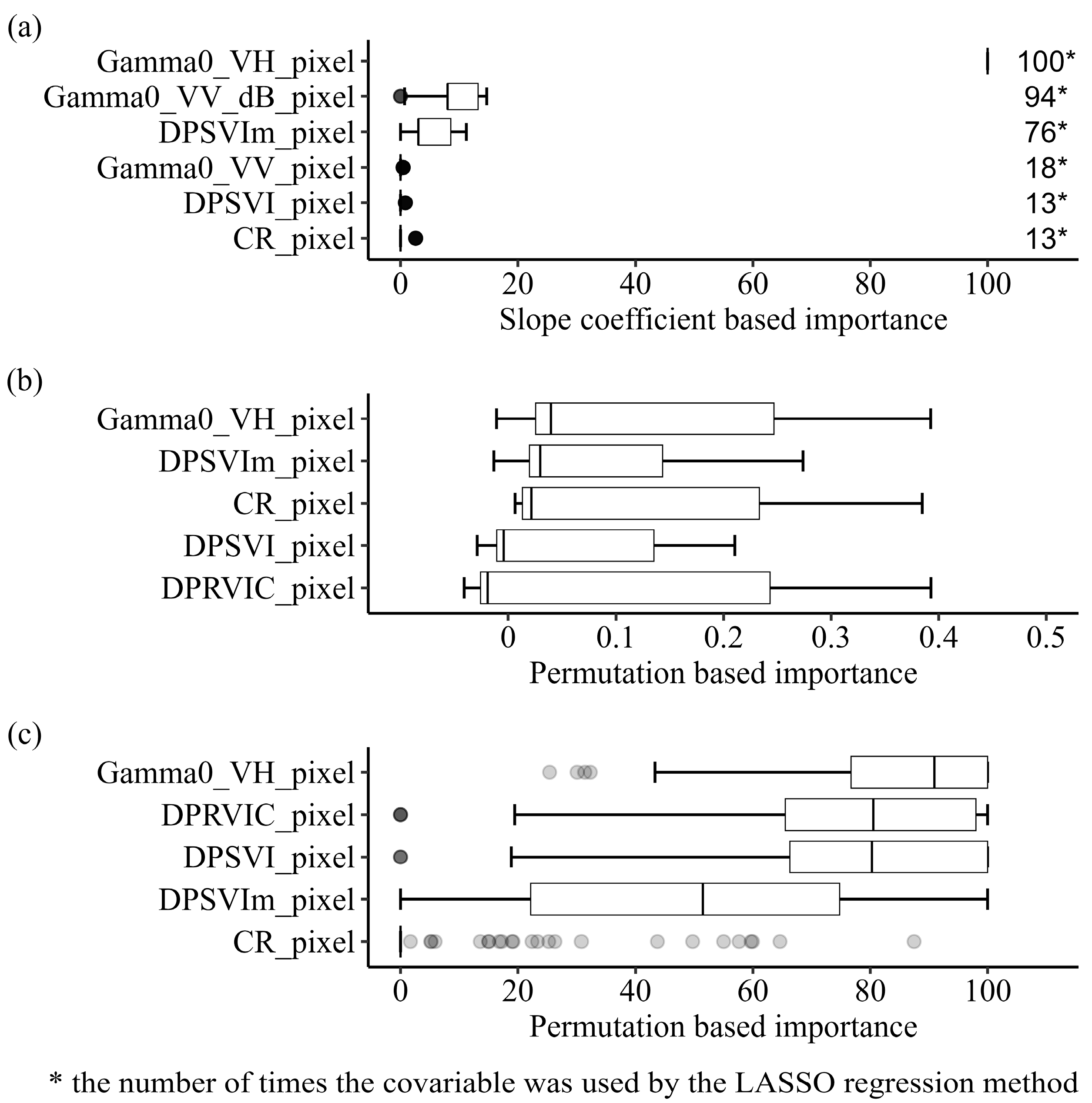
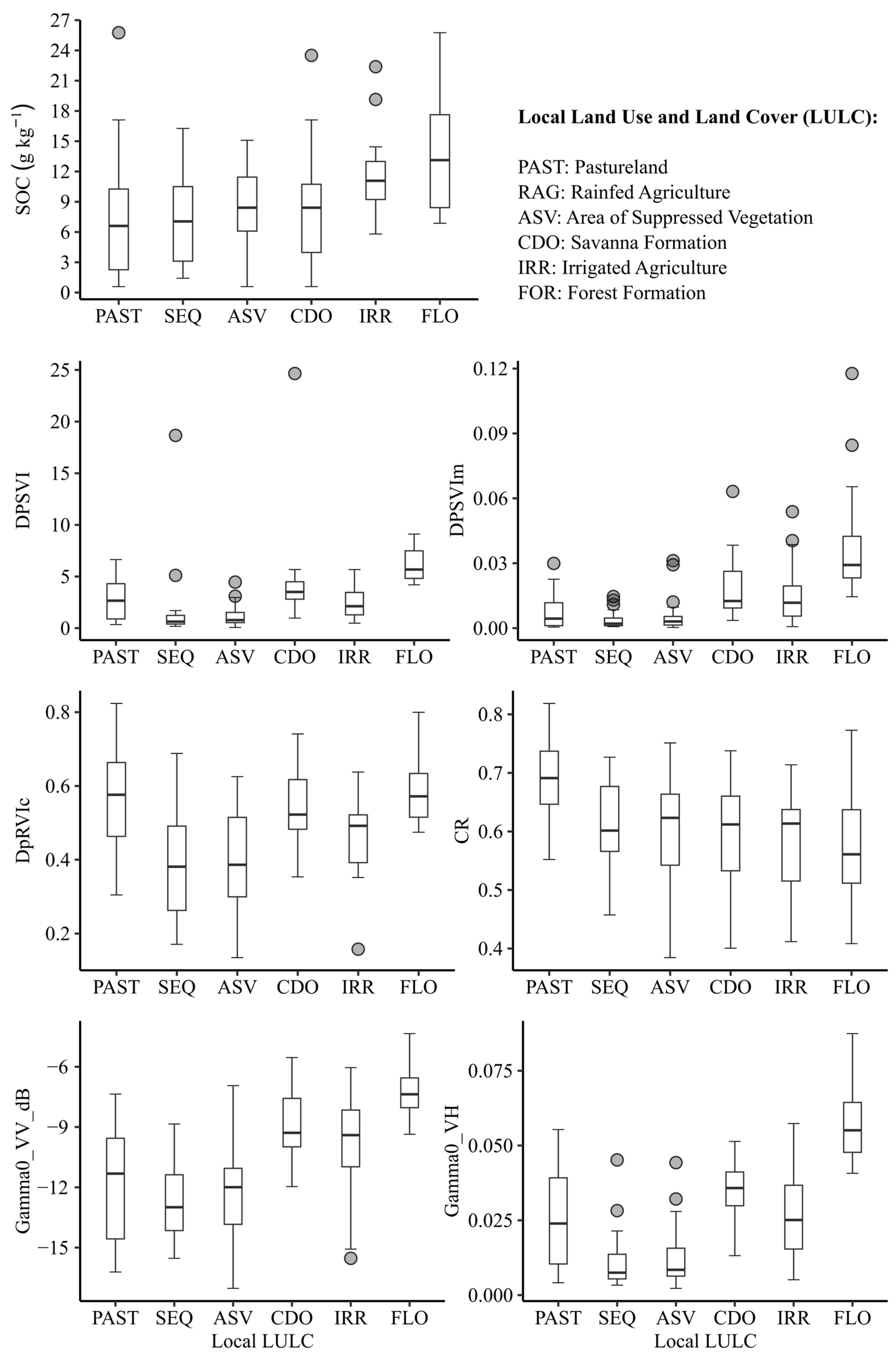
3.2. Covariables’ Importance and Their Relationship to Soil Organic Carbon
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lombardo, L.; Saia, S.; Schillaci, C.; Mai, P.M.; Huser, R. Modeling Soil Organic Carbon with Quantile Regression: Dissecting Predictors’ Effects on Carbon Stocks. Geoderma 2018, 318, 148–159. [Google Scholar] [CrossRef]
- Yost, J.L.; Hartemink, A.E. Soil Organic Carbon in Sandy Soils: A Review. In Advances in Agronomy; Academic Press Inc.: London, UK, 2019; Volume 158, pp. 217–310. ISBN 978-0-12-817412-8. [Google Scholar]
- FAO; ITPS. Global Soil Organic Carbon Map (GSOCmap) Version 1.5; FAO: Rome, Italy, 2020; ISBN 978-92-5-132144-7. [Google Scholar]
- Kunkel, V.R.; Wells, T.; Hancock, G.R. Modelling Soil Organic Carbon Using Vegetation Indices across Large Catchments in Eastern Australia. Sci. Total Environ. 2022, 817, 152690. [Google Scholar] [CrossRef] [PubMed]
- Padarian, J.; Minasny, B.; McBratney, A.; Smith, P. Soil Carbon Sequestration Potential in Global Croplands. PeerJ 2022, 10, e13740. [Google Scholar] [CrossRef]
- Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing Soil Information for the Globe with Quantified Spatial Uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.; Shi, T.; Chen, Y.; Jiang, Q.; Linderman, M. Prediction of Soil Organic Carbon Stock by Laboratory Spectral Data and Airborne Hyperspectral Images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital Mapping of Soil Carbon Fractions with Machine Learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Odebiri, O.; Mutanga, O.; Odindi, J.; Peerbhay, K.; Dovey, S. Predicting Soil Organic Carbon Stocks under Commercial Forest Plantations in KwaZulu-Natal Province, South Africa Using Remotely Sensed Data. GIScience Remote Sens. 2020, 57, 450–463. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Hole, F.D. Effects of Animals on Soil. Geoderma 1981, 25, 75–112. [Google Scholar] [CrossRef]
- Saatchi, S. SAR Methods for Mapping and Monitoring Forest Biomass. In The Synthetic Aperture Radar (SAR) Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; Flores-Anderson, A.I., Herndon, K.E., Thapa, R.B., Cherrington, E., Eds.; NASA: Huntsville, AL, USA, 2019. [Google Scholar]
- Woodhouse, I.H. Introduction to Microwave Remote Sensing; CRC Press: Boca Raton, FL, USA, 2006; ISBN 0-415-27123-1. [Google Scholar]
- Paradella, W.R.; Mura, J.C.; Gama, F.F. Monitoramento DInSAR Para Mineração e Geotecnia; Oficina de Textos: São Paulo, Brazil, 2021; ISBN 978-65-86235-19-7. [Google Scholar]
- Bartsch, A.; Widhalm, B.; Kuhry, P.; Hugelius, G.; Palmtag, J.; Siewert, M.B. Can C-Band Synthetic Aperture Radar Be Used to Estimate Soil Organic Carbon Storage in Tundra? Biogeosciences 2016, 13, 5453–5470. [Google Scholar] [CrossRef]
- Ceddia, M.B.; Gomes, A.S.; Vasques, G.M.; Pinheiro, É.F.M. Soil Carbon Stock and Particle Size Fractions in the Central Amazon Predicted from Remotely Sensed Relief, Multispectral and Radar Data. Remote Sens. 2017, 9, 124. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Minaei, F.; Talebi-khiyavi, H.; Xu, T.; Homaee, M. Synergetic Use of Multi-Temporal Sentinel-1, Sentinel-2, NDVI, and Topographic Factors for Estimating Soil Organic Carbon. Catena 2022, 212, 106077. [Google Scholar] [CrossRef]
- Sothe, C.; Gonsamo, A.; Arabian, J.; Snider, J. Large Scale Mapping of Soil Organic Carbon Concentration with 3D Machine Learning and Satellite Observations. Geoderma 2022, 405, 115402. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Liu, M.; Haase, D.; Lausch, A. Mapping Soil Organic Carbon Content Using Multi-Source Remote Sensing Variables in the Heihe River Basin in China. Ecol. Indic. 2020, 114, 106288. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Pan, J.; Haase, D.; Lausch, A. High-Resolution Digital Mapping of Soil Organic Carbon and Soil Total Nitrogen Using DEM Derivatives, Sentinel-1 and Sentinel-2 Data Based on Machine Learning Algorithms. Sci. Total Environ. 2020, 729, 138244. [Google Scholar] [CrossRef]
- Kim, Y.; van Zyl, J. On the Relationship between Polarimetric Parameters. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120), Honolulu, HI, USA, 24–28 July 2000; IEEE: New York, NY, USA, 2000; Volume 3, pp. 1298–1300. [Google Scholar]
- Chang, J.G.; Shoshany, M.; Oh, Y. Polarimetric Radar Vegetation Index for Biomass Estimation in Desert Fringe Ecosystems. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7102–7108. [Google Scholar] [CrossRef]
- Periasamy, S. Significance of Dual Polarimetric Synthetic Aperture Radar in Biomass Retrieval: An Attempt on Sentinel-1. Remote Sens. Environ. 2018, 217, 537–549. [Google Scholar] [CrossRef]
- dos Santos, E.P.; da Silva, D.D.; do Amaral, C.H. Vegetation Cover Monitoring in Tropical Regions Using SAR-C Dual-Polarization Index: Seasonal and Spatial Influences. Int. J. Remote Sens. 2021, 42, 7581–7609. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual Polarimetric Radar Vegetation Index for Crop Growth Monitoring Using Sentinel-1 SAR Data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Pousa, R.; Costa, M.H.; Pimenta, F.M.; Fontes, V.C.; Castro, M. Climate Change and Intense Irrigation Growth in Western Bahia, Brazil: The Urgent Need for Hydroclimatic Monitoring. Water 2019, 11, 933. [Google Scholar] [CrossRef]
- Dionizio, E.A.; Pimenta, F.M.; Lima, L.B.; Costa, M.H. Carbon Stocks and Dynamics of Different Land Uses on the Cerrado Agricultural Frontier. PLoS ONE 2020, 15, e0241637. [Google Scholar] [CrossRef] [PubMed]
- SGB. GeoSGB; Serviço Geológico do Brasil: Brasília, Brazil, 2022.
- dos Santos, H.G.; Jacomine, P.K.T.; dos Anjos, L.H.C.; de Oliveira, V.Á.; Lumbreras, J.F.; Coelho, M.R.; de Almeida, J.A.; de Araújo-Filho, J.C.; Cunha, T.J.F. Brazilian Soil Classification System, 5th ed.; Embrapa: Brasília, Brazil, 2018; ISBN 978-85-7035-800-4. [Google Scholar]
- Dionizio, E.A.; Costa, M.H. Influence of Land Use and Land Cover on Hydraulic and Physical Soil Properties at the Cerrado Agricultural Frontier. Agriculture 2019, 9, 24. [Google Scholar] [CrossRef]
- Souza, C.M.; Shimbo, J.Z.; Rosa, M.R.; Parente, L.L.; Alencar, A.A.; Rudorff, B.F.T.; Hasenack, H.; Matsumoto, M.; Ferreira, L.G.; Souza-Filho, P.W.M.; et al. Reconstructing Three Decades of Land Use and Land Cover Changes in Brazilian Biomes with Landsat Archive and Earth Engine. Remote Sens. 2020, 12, 2735. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An Examination of the Degtjareff Method for Determining Soil Organic Matter, and a Proposed Modification of the Chromic Acid Titration Method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- ESA. Sentinel-1: ESA’s Radar Observatory Mission for GMES Operational Services; Fletcher, K., Ed.; European Space Agency: Paris, France, 2012. [Google Scholar]
- ESA. Sentinel-1 SAR Technical Guide. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-1-sar (accessed on 18 November 2022).
- ASF Copernicus Sentinel Data 2017, 2018, and 2019. Retrieved from ASF DAAC, Processed by ESA. Available online: https://asf.alaska.edu/ (accessed on 17 November 2022).
- Small, D. Flattening Gamma: Radiometric Terrain Correction for SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Filipponi, F. Supplementary Materials: Sentinel-1 GRD Preprocessing Workflow. Proceedings 2019, 18, 11. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Balik Sanli, F.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef]
- Hird, J.; DeLancey, E.; McDermid, G.; Kariyeva, J. Google Earth Engine, Open-Access Satellite Data, and Machine Learning in Support of Large-Area Probabilistic Wetland Mapping. Remote Sens. 2017, 9, 1315. [Google Scholar] [CrossRef]
- Frison, P.-L.; Fruneau, B.; Kmiha, S.; Soudani, K.; Dufrêne, E.; Toan, T.L.; Koleck, T.; Villard, L.; Mougin, E.; Rudant, J.-P. Potential of Sentinel-1 Data for Monitoring Temperate Mixed Forest Phenology. Remote Sens. 2018, 10, 2049. [Google Scholar] [CrossRef]
- Bhogapurapu, N.; Dey, S.; Mandal, D.; Bhattacharya, A.; Karthikeyan, L.; McNairn, H.; Rao, Y.S. Soil Moisture Retrieval over Croplands Using Dual-Pol L-Band GRD SAR Data. Remote Sens. Environ. 2022, 271, 112900. [Google Scholar] [CrossRef]
- Filgueiras, R.; Mantovani, E.C.; Althoff, D.; Fernandes Filho, E.I.; Cunha, F.F. da Crop NDVI Monitoring Based on Sentinel 1. Remote Sens. 2019, 11, 1441. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2023. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mishra, U.; Yeo, K.; Adhikari, K.; Riley, W.J.; Hoffman, F.M.; Hudson, C.; Gautam, S. Empirical Relationships between Environmental Factors and Soil Organic Carbon Produce Comparable Prediction Accuracy to Machine Learning. Soil Sci. Soc. Am. J. 2022, 86, 1611–1624. [Google Scholar] [CrossRef]
- Xiao, Y.; Xue, J.; Zhang, X.; Wang, N.; Hong, Y.; Jiang, Y.; Zhou, Y.; Teng, H.; Hu, B.; Lugato, E.; et al. Improving Pedotransfer Functions for Predicting Soil Mineral Associated Organic Carbon by Ensemble Machine Learning. Geoderma 2022, 428, 116208. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer Texts in Statistics; Springer: New York, NY, USA, 2013; Volume 103, ISBN 978-1-4614-7137-0. [Google Scholar]
- Boehmke, B.; Greenwell, B. Hands-On Machine Learning with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; ISBN 978-0-367-81637-7. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6848-6. [Google Scholar]
- Moura-Bueno, J.M.; Dalmolin, R.S.D.; ten Caten, A.; Dotto, A.C.; Demattê, J.A.M. Stratification of a Local VIS-NIR-SWIR Spectral Library by Homogeneity Criteria Yields More Accurate Soil Organic Carbon Predictions. Geoderma 2019, 337, 565–581. [Google Scholar] [CrossRef]
- Brus, D.J.; Kempen, B.; Heuvelink, G.B.M. Sampling for Validation of Digital Soil Maps. Eur. J. Soil Sci. 2011, 62, 394–407. [Google Scholar] [CrossRef]
- Gomes, L.C.; Faria, R.M.; de Souza, E.; Veloso, G.V.; Schaefer, C.E.G.R.; Filho, E.I.F. Modelling and Mapping Soil Organic Carbon Stocks in Brazil. Geoderma 2019, 340, 337–350. [Google Scholar] [CrossRef]
- McKight, P.E.; Najab, J. Kruskal-Wallis Test. In The Corsini Encyclopedia of Psychology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; p. 1. ISBN 978-0-470-47921-6. [Google Scholar]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; Macdonald, L.M.; McLaughlin, M.J. The Performance of Visible, Near-, and Mid-Infrared Reflectance Spectroscopy for Prediction of Soil Physical, Chemical, and Biological Properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- dos Santos, U.J.; de Demattê, J.A.M.; Menezes, R.S.C.; Dotto, A.C.; Guimarães, C.C.B.; Alves, B.J.R.; Primo, D.C.; Sampaio, E.V.d.S.B. Predicting Carbon and Nitrogen by Visible Near-Infrared (Vis-NIR) and Mid-Infrared (MIR) Spectroscopy in Soils of Northeast Brazil. Geoderma Reg. 2020, 23, e00333. [Google Scholar] [CrossRef]
- Moura-Bueno, J.M.; Dalmolin, R.S.D.; Horst-Heinen, T.Z.; ten Caten, A.; Vasques, G.M.; Dotto, A.C.; Grunwald, S. When Does Stratification of a Subtropical Soil Spectral Library Improve Predictions of Soil Organic Carbon Content? Sci. Total Environ. 2020, 737, 139895. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N.; et al. Soil Organic Carbon Storage as a Key Function of Soils—A Review of Drivers and Indicators at Various Scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Guo, L.B.; Gifford, R.M. Soil Carbon Stocks and Land Use Change: A Meta Analysis. Glob. Change Biol. 2002, 8, 345–360. [Google Scholar] [CrossRef]
- Woodhouse, I.H.; Mitchard, E.T.A.; Brolly, M.; Maniatis, D.; Ryan, C.M. Radar Backscatter Is Not a “direct Measure” of Forest Biomass. Nat. Clim. Change 2012, 2, 556–557. [Google Scholar] [CrossRef]
- Bispo, P.d.C.; Rodríguez-Veiga, P.; Zimbres, B.; do Couto de Miranda, S.; Henrique Giusti Cezare, C.; Fleming, S.; Baldacchino, F.; Louis, V.; Rains, D.; Garcia, M.; et al. Woody Aboveground Biomass Mapping of the Brazilian Savanna with a Multi-Sensor and Machine Learning Approach. Remote Sens. 2020, 12, 2685. [Google Scholar] [CrossRef]
- Joshi, N.; Mitchard, E.T.A.; Brolly, M.; Schumacher, J.; Fernández-Landa, A.; Johannsen, V.K.; Marchamalo, M.; Fensholt, R. Understanding “saturation” of Radar Signals over Forests. Sci. Rep. 2017, 7, 3505. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.M.A.; Avitabile, V.; Araza, A.; de Bruin, S.; Herold, M.; Quegan, S.; Rodríguez-Veiga, P.; et al. The Global Forest Above-Ground Biomass Pool for 2010 Estimated from High-Resolution Satellite Observations. Earth Syst. Sci. Data 2021, 13, 3927–3950. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; Lewis, S.L.; Feldpausch, T.R.; Woodhouse, I.H.; Sonké, B.; Rowland, C.; Meir, P. Measuring Biomass Changes Due to Woody Encroachment and Deforestation/Degradation in a Forest–Savanna Boundary Region of Central Africa Using Multi-Temporal L-Band Radar Backscatter. Remote Sens. Environ. 2011, 115, 2861–2873. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration Analysis of SAR Signals in the C and L Bands for Wheat, Maize, and Grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical Vegetation Indices for Monitoring Terrestrial Ecosystems Globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Ferreira, A.C.S.; Pinheiro, É.F.M.; Costa, E.M.; Ceddia, M.B. Predicting Soil Carbon Stock in Remote Areas of the Central Amazon Region Using Machine Learning Techniques. Geoderma Reg. 2023, 32, e00614. [Google Scholar] [CrossRef]
- dos Santos, E.P.; da Silva, D.D.; do Amaral, C.H.; Fernandes-Filho, E.I.; Dias, R.L.S. A Machine Learning Approach to Reconstruct Cloudy Affected Vegetation Indices Imagery via Data Fusion from Sentinel-1 and Landsat 8. Comput. Electron. Agric. 2022, 194, 106753. [Google Scholar] [CrossRef]
- Flores-Anderson, A.I.; Herndon, K.E.; Thapa, R.B.; Cherrington, E. (Eds.) The Synthetic Aperture Radar (SAR) Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; NASA: Huntsville, AL, USA, 2019.
- NASA JPL NASADEM Merged DEM Global 1 Arc Second V001 [Data Set]. NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/nasadem_hgtv001/ (accessed on 10 September 2022).
- Embrapa Mapa de Solos Do Brasil; Empresa Brasileira de Pesquisa Agropecuária: Brasília, Brazil, 2011.
| Acquisition Date | Product Unique Identifier | Relative Orbit Number |
|---|---|---|
| 6 July 2017 | B8D5 | 126 |
| 6 July 2017 | 0966 | |
| 1 November 2017 | 82D6 | |
| 1 November 2017 | D608 | |
| 1 November 2017 | 1ADD | |
| 1 November 2017 | 3E97 | |
| 8 November 2017 | 3366 | 24 |
| Vegetation Index | Equation | Theoretical Bounds | Source |
|---|---|---|---|
| DPSVI | [23] | ||
| DPSVIm | [24] | ||
| CR | [41] | ||
| Pol | [40] | ||
| RVIm | Unreported | [39] | |
| DpRVIc | [42] |
| Regression Method | Soil Layer | Md (MBE) | Md (RMSE) | Md (MAE) | Md (R2) | Md (CCC) | Md (d) |
|---|---|---|---|---|---|---|---|
| LASSO | 0–5 cm | 0.869 | 4.864 | 3.914 | 0.243 | 0.231 | 0.442 |
| 5–10 cm | −1.248 | 5.135 | 3.869 | 0.167 | 0.127 | 0.345 | |
| 10–15 cm | −0.824 | 5.557 | 4.532 | 0.027 | 0.079 | 0.297 | |
| 15–20 cm | −0.727 | 4.099 | 3.489 | 0.059 | 0.083 | 0.291 | |
| 20–40 cm | 0.670 | 3.912 | 3.278 | 0.007 | 0.050 | 0.314 | |
| 40–60 cm | −0.005 | 2.414 | 1.956 | 0.001 | 0.017 | 0.318 | |
| 60–100 cm | 0.093 | 2.322 | 2.015 | 0.000 | −0.004 | 0.167 | |
| SVR-RBF | 0–5 cm | 0.899 | 4.959 | 3.942 | 0.238 | 0.196 | 0.400 |
| 5–10 cm | −0.989 | 4.953 | 3.686 | 0.172 | 0.212 | 0.452 | |
| 10–15 cm | −1.123 | 5.556 | 4.582 | 0.039 | 0.086 | 0.325 | |
| 15–20 cm | −0.812 | 4.213 | 3.513 | 0.015 | 0.053 | 0.362 | |
| 20–40 cm | 0.824 | 3.876 | 3.307 | 0.002 | 0.021 | 0.265 | |
| 40–60 cm | −0.035 | 2.306 | 1.928 | 0.040 | 0.042 | 0.193 | |
| 60–100 cm | 0.285 | 2.436 | 2.151 | 0.011 | −0.043 | 0.135 | |
| RF | 0–5 cm | 0.777 | 4.955 | 3.898 | 0.208 | 0.184 | 0.360 |
| 5–10 cm | −1.196 | 5.082 | 3.829 | 0.180 | 0.151 | 0.372 | |
| 10–15 cm | −1.084 | 5.670 | 4.724 | 0.003 | 0.016 | 0.236 | |
| 15–20 cm | −0.666 | 4.187 | 3.567 | 0.015 | 0.046 | 0.294 | |
| 20–40 cm | 0.740 | 3.811 | 3.219 | 0.010 | 0.037 | 0.272 | |
| 40–60 cm | −0.064 | 2.304 | 1.899 | 0.034 | 0.067 | 0.287 | |
| 60–100 cm | 0.110 | 2.297 | 2.014 | 0.003 | 0.007 | 0.129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, E.P.d.; Moreira, M.C.; Fernandes-Filho, E.I.; Demattê, J.A.M.; Dionizio, E.A.; Silva, D.D.d.; Cruz, R.R.P.; Moura-Bueno, J.M.; Santos, U.J.d.; Costa, M.H. Sentinel-1 Imagery Used for Estimation of Soil Organic Carbon by Dual-Polarization SAR Vegetation Indices. Remote Sens. 2023, 15, 5464. https://doi.org/10.3390/rs15235464
Santos EPd, Moreira MC, Fernandes-Filho EI, Demattê JAM, Dionizio EA, Silva DDd, Cruz RRP, Moura-Bueno JM, Santos UJd, Costa MH. Sentinel-1 Imagery Used for Estimation of Soil Organic Carbon by Dual-Polarization SAR Vegetation Indices. Remote Sensing. 2023; 15(23):5464. https://doi.org/10.3390/rs15235464
Chicago/Turabian StyleSantos, Erli Pinto dos, Michel Castro Moreira, Elpídio Inácio Fernandes-Filho, José Alexandre M. Demattê, Emily Ane Dionizio, Demetrius David da Silva, Renata Ranielly Pedroza Cruz, Jean Michel Moura-Bueno, Uemeson José dos Santos, and Marcos Heil Costa. 2023. "Sentinel-1 Imagery Used for Estimation of Soil Organic Carbon by Dual-Polarization SAR Vegetation Indices" Remote Sensing 15, no. 23: 5464. https://doi.org/10.3390/rs15235464
APA StyleSantos, E. P. d., Moreira, M. C., Fernandes-Filho, E. I., Demattê, J. A. M., Dionizio, E. A., Silva, D. D. d., Cruz, R. R. P., Moura-Bueno, J. M., Santos, U. J. d., & Costa, M. H. (2023). Sentinel-1 Imagery Used for Estimation of Soil Organic Carbon by Dual-Polarization SAR Vegetation Indices. Remote Sensing, 15(23), 5464. https://doi.org/10.3390/rs15235464









