Spatial Reconstruction of Quantitative Precipitation Estimates Derived from Fengyun-2G Geostationary Satellite in Northeast China
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Ground Reference
2.3. Fengyun-Based Quantitative Precipitation Estimates
2.4. PERSIANN-CCS
2.5. Fengyun-Based Land Surface Characteristics
2.6. Topographic Characteristic
3. Methods
3.1. Geographically Weighted Regression
3.2. Random Forest
3.3. Geographical Differential Analysis
3.4. Inverse Distance Weighting
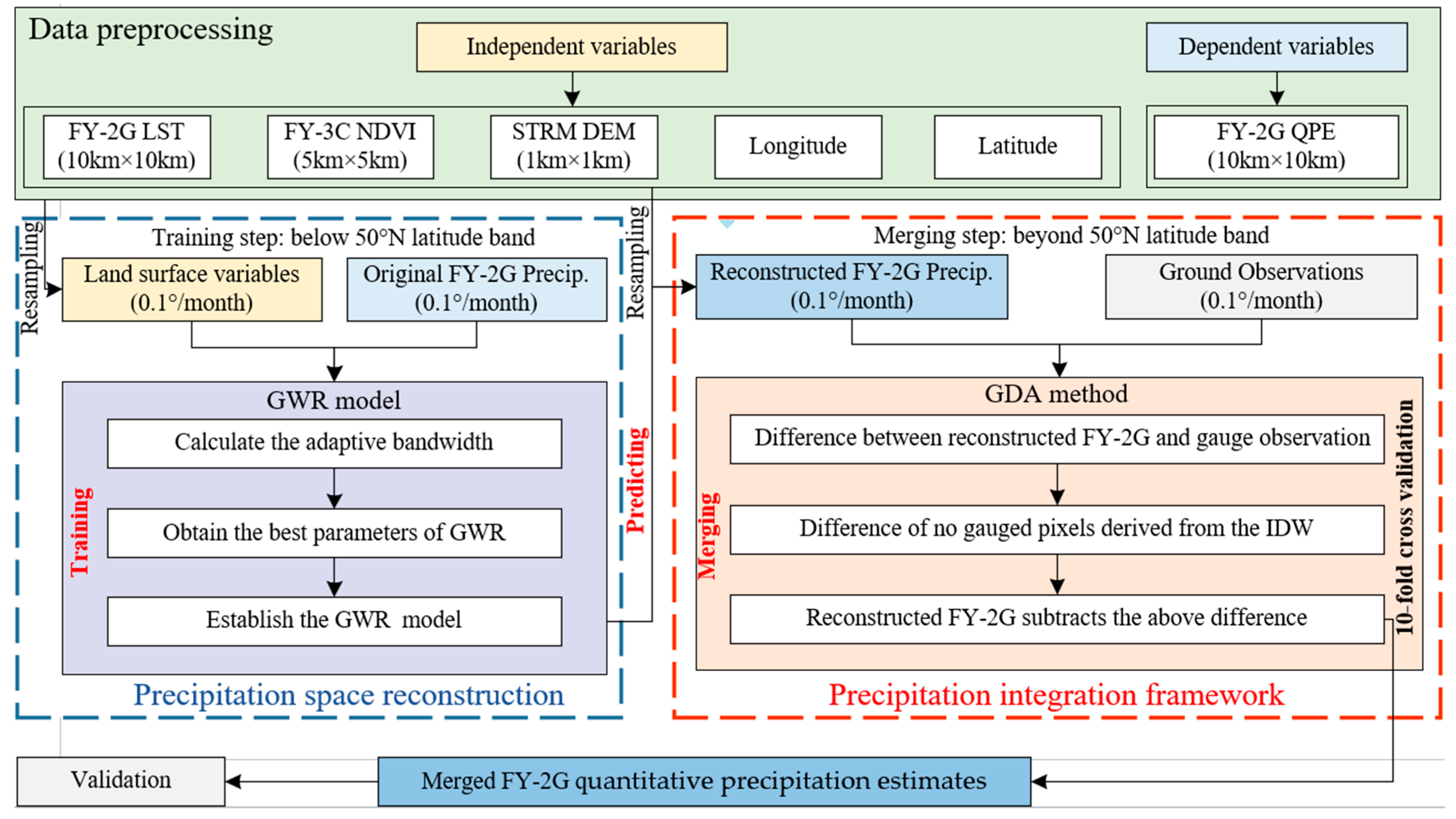
3.5. Proposed Precipitation Space Reconstruction Model
- (1)
- Data resampling. Given that the spatial resolution of FY-2G QPE is 0.1° × 0.1°, to fully utilize the relationship between the LSC variables and FY-2G QPE, it is necessary to spatially match the 5 km spatial resolution of FY-3C NDVI with FY-2G QPE. In this study, the method of cumulative averaging is used to spatially resample the FY-3C NDVI. As for DEM, this study employs the nearest-neighbor interpolation method to resample DEM data to the spatial resolution of 0.1° × 0.1°.
- (2)
- Model training. The calculation of bandwidth and kernel function is a crucial step in training the GWR model. In this study, the GWR algorithm was implemented using the “GWmodel” package in the R programming language. The “GWmodel” package offers two primary parameters for the GWR model, i.e., bw (bandwidth) and gweight (kernel function). To determine the optimal bandwidth value, an adaptive approach was employed. The optimization process was guided by the AIC value, where the goal was to minimize the AIC. In this study, a widely used Gaussian kernel function was selected for modeling purposes. Once the optimal bandwidth was determined, the GWR model for FY-2G QPE within the training area was established.
- (3)
- Precipitation reconstruction. By inputting the LSC factors from the prediction area into the final GWR model established within the training area, the reconstructed FY-2G QPE for the target area can be computed. Specifically, the NDVI, LST, DEM, and location information (longitude and latitude) are used as explanatory variables in the reconstruction model.
- (4)
- Merging correction. The GDA method is used for the fusion correction of the reconstructed results. Firstly, the reconstructed FY-2G QPE is subtracted from the ground observation to obtain the rainfall error at the station locations. The IDW interpolation method is used to estimate the rainfall error at locations outside the stations. Then, these two sets of error values are combined to obtain the complete rainfall error values within the prediction area. Finally, the reconstructed FY-2G QPE is corrected by subtracting the corresponding rainfall error values. It is worth noting that in the actual calculations, this study uses a 10-fold CV approach to compute the rainfall errors, to ensure that the validation data are mutually independent. The IDW algorithm in this study is implemented based on the “gstat” algorithm package in the R language. Similarly, the GDA method is also implemented and compiled in R language.
- (1)
- Data preparation. Gather the rainfall differences between the ground observation points, the reconstructed precipitation data, and the geographical coordinates at the gauged grid cell, including longitude and latitude.
- (2)
- Grid generation. Determine the spatial area that needs interpolation and create a regular grid covering the entire region. These grid cells will serve as the basis for the interpolated continuous surface.
- (3)
- Distance calculation. Calculate the distances between grid cells without stations and observation stations.
- (4)
- Weight allocation. Assign weights to each ungauged grid cell based on their distances and weight parameters. Closer gauged grid cells typically have higher weights, while more distant gauged grid cells have lower weights.
- (5)
- Interpolation calculation. Calculate the estimated rainfall differences for ungauged locations based on the rainfall differences at gauged grid cells and their respective weights.
- (6)
- Create a continuous Surface. Using the interpolation calculations, generate an estimate for each ungauged grid cell, thereby creating a continuous surface of rainfall differences.
3.6. Evaluation Method
3.7. Rainfall Anomaly Index
4. Results
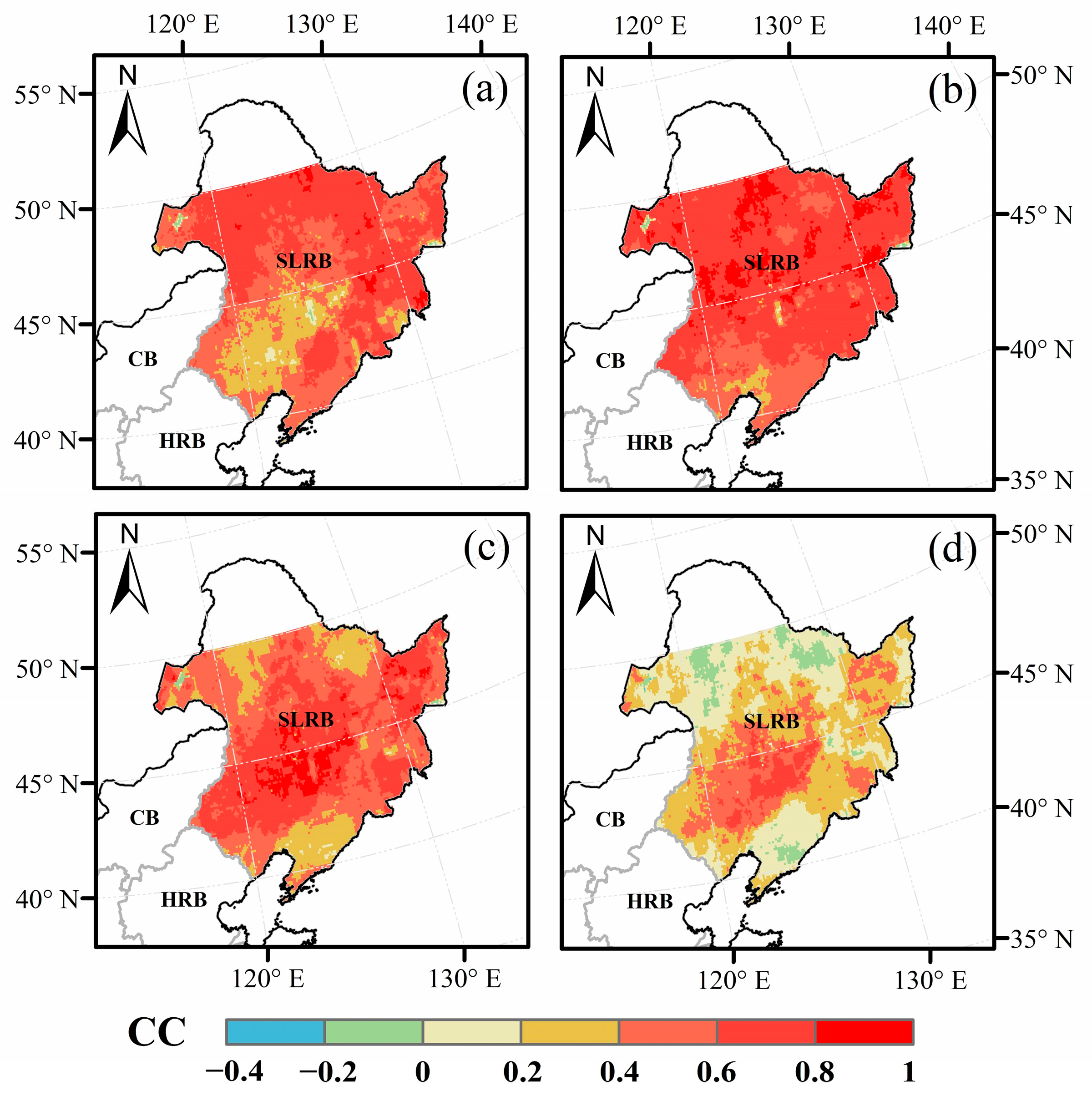
4.1. Determine the Lagging Time of NDVI Response to Precipitation
4.2. Performance of Fitting Precipitation
4.3. Overall Performance of Reconstructed Precipitation
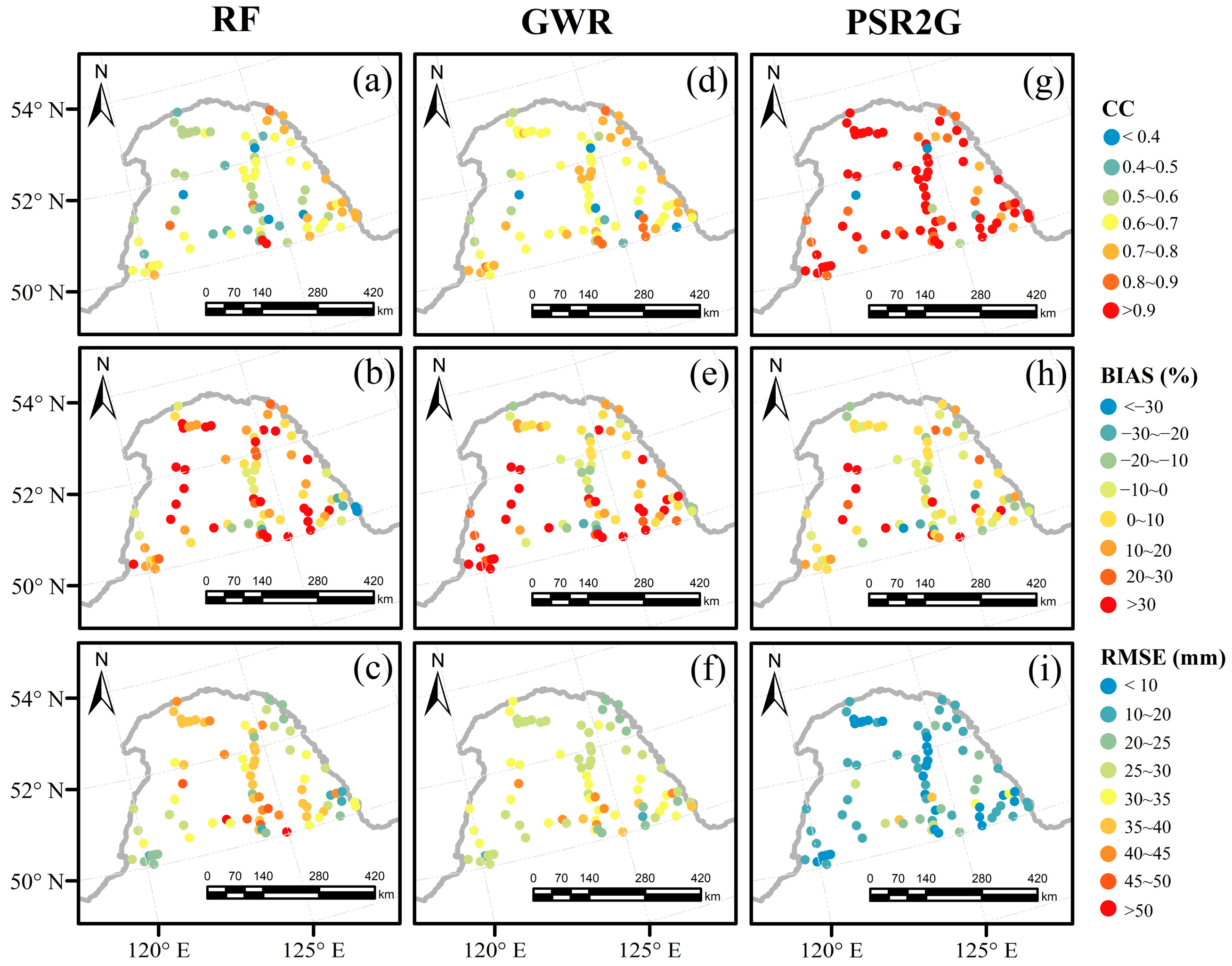
4.4. Spatial Performance of Reconstructed Precipitation
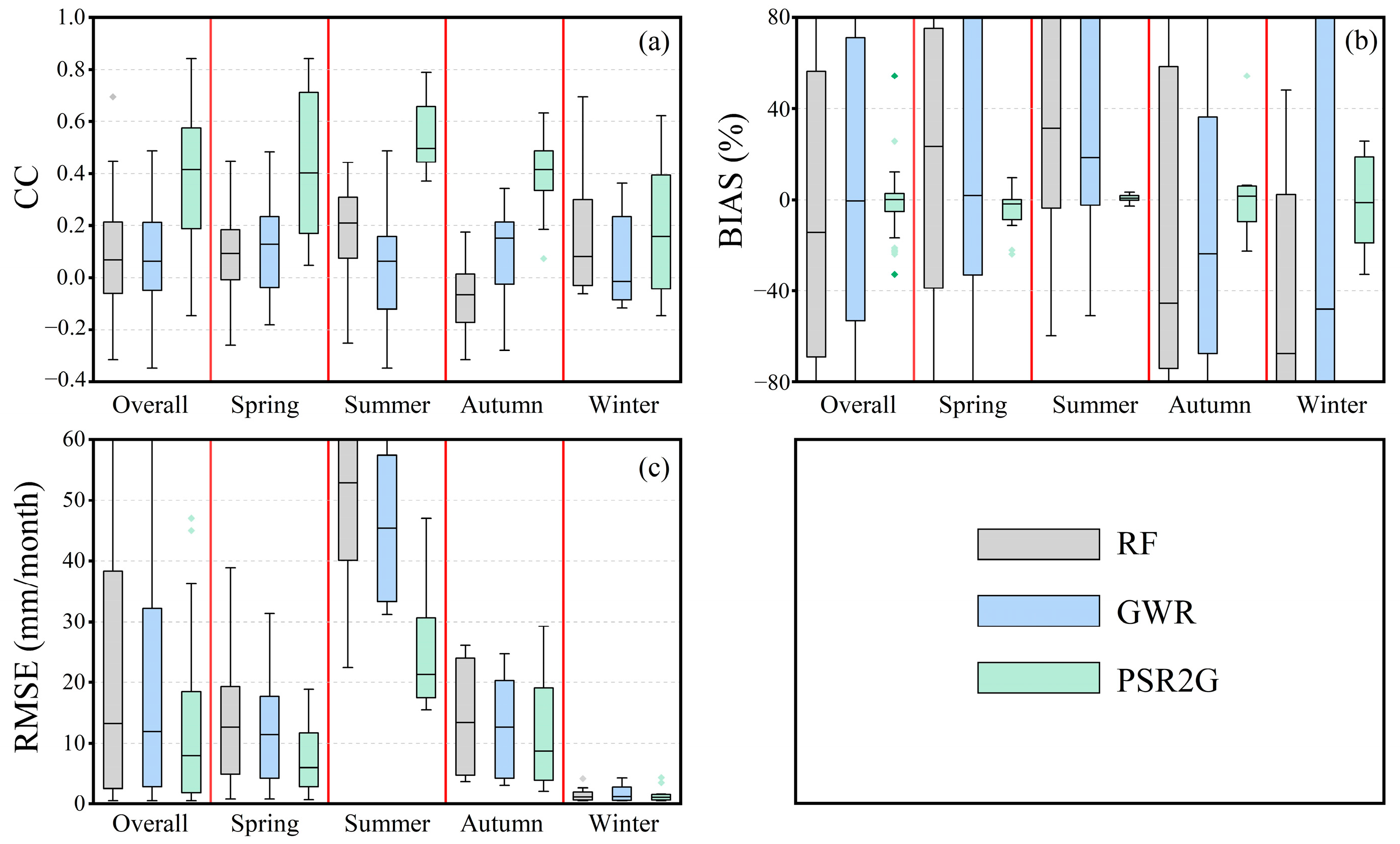
4.5. Temporal Performance of Reconstructed Precipitation
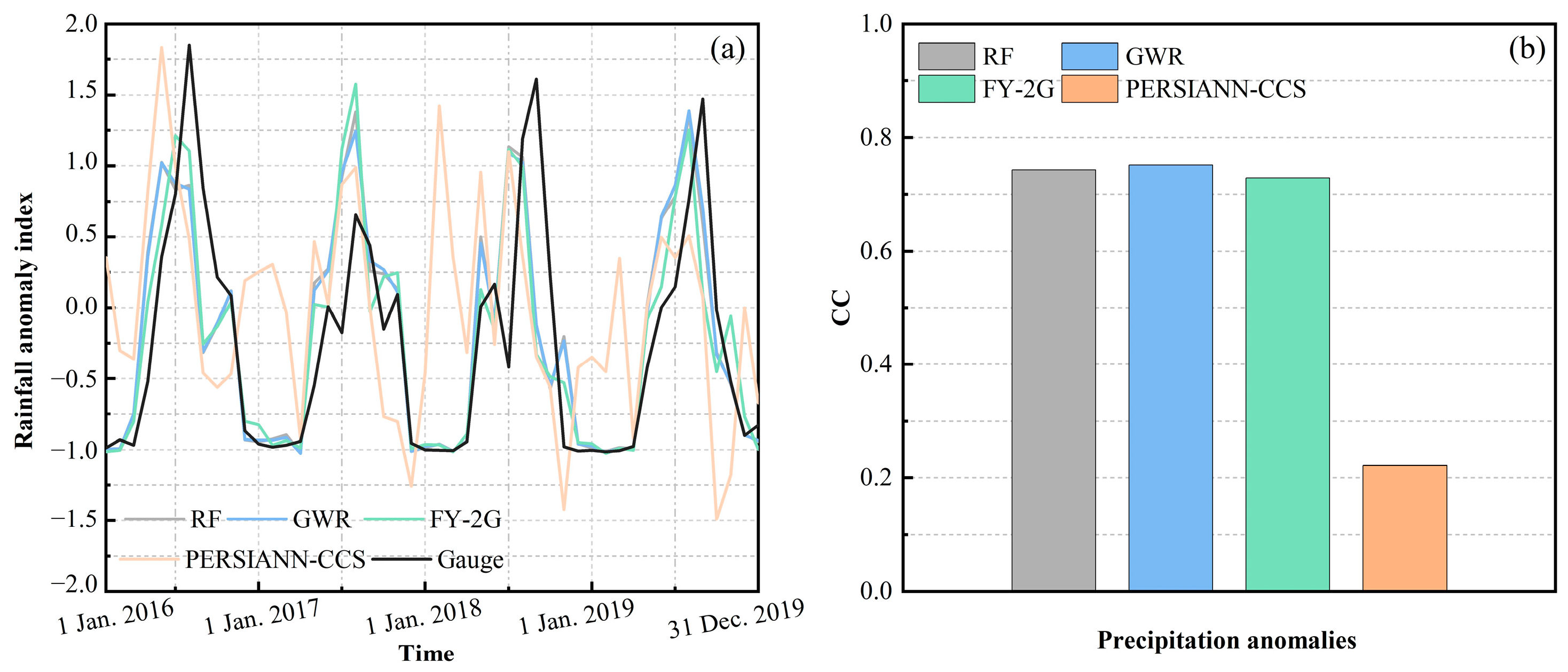
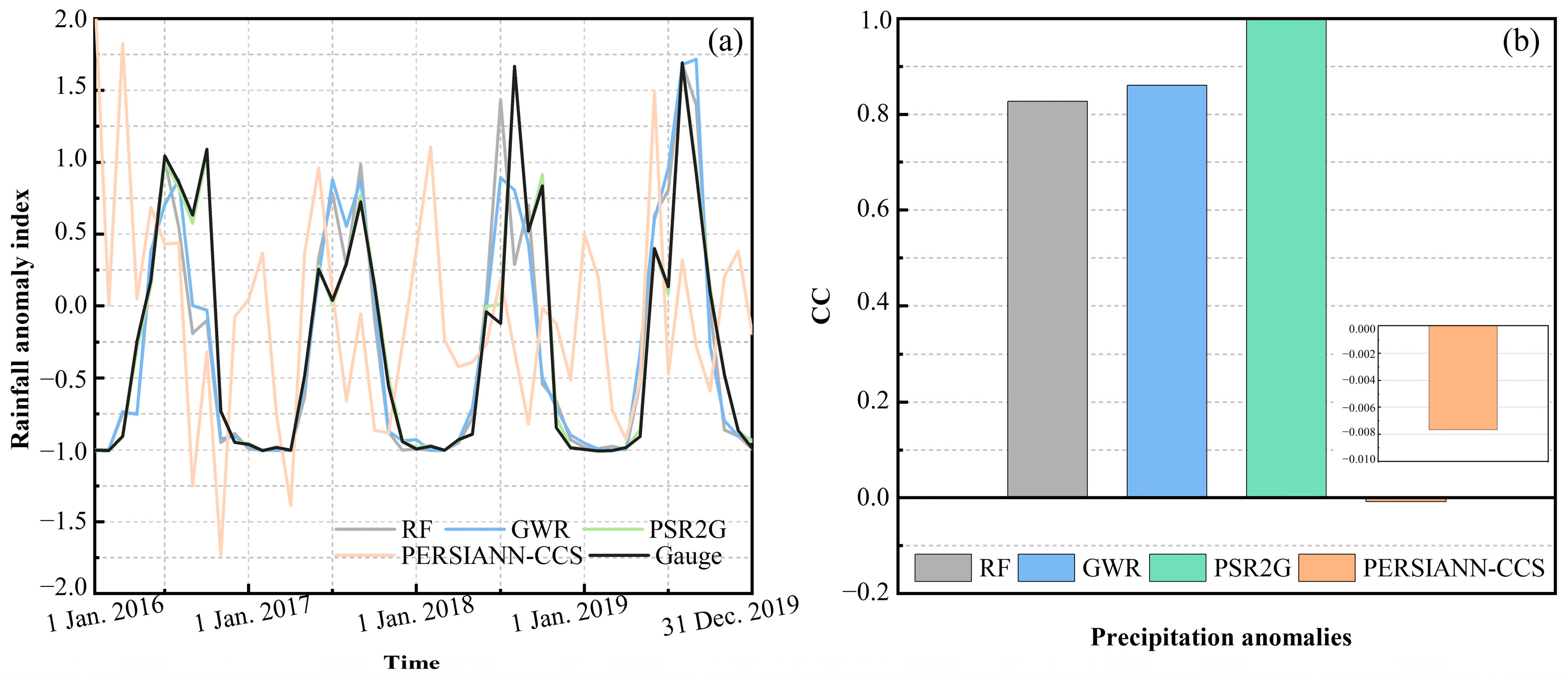
4.6. Temporal Analysis of Precipitation Anomalies
5. Discussion
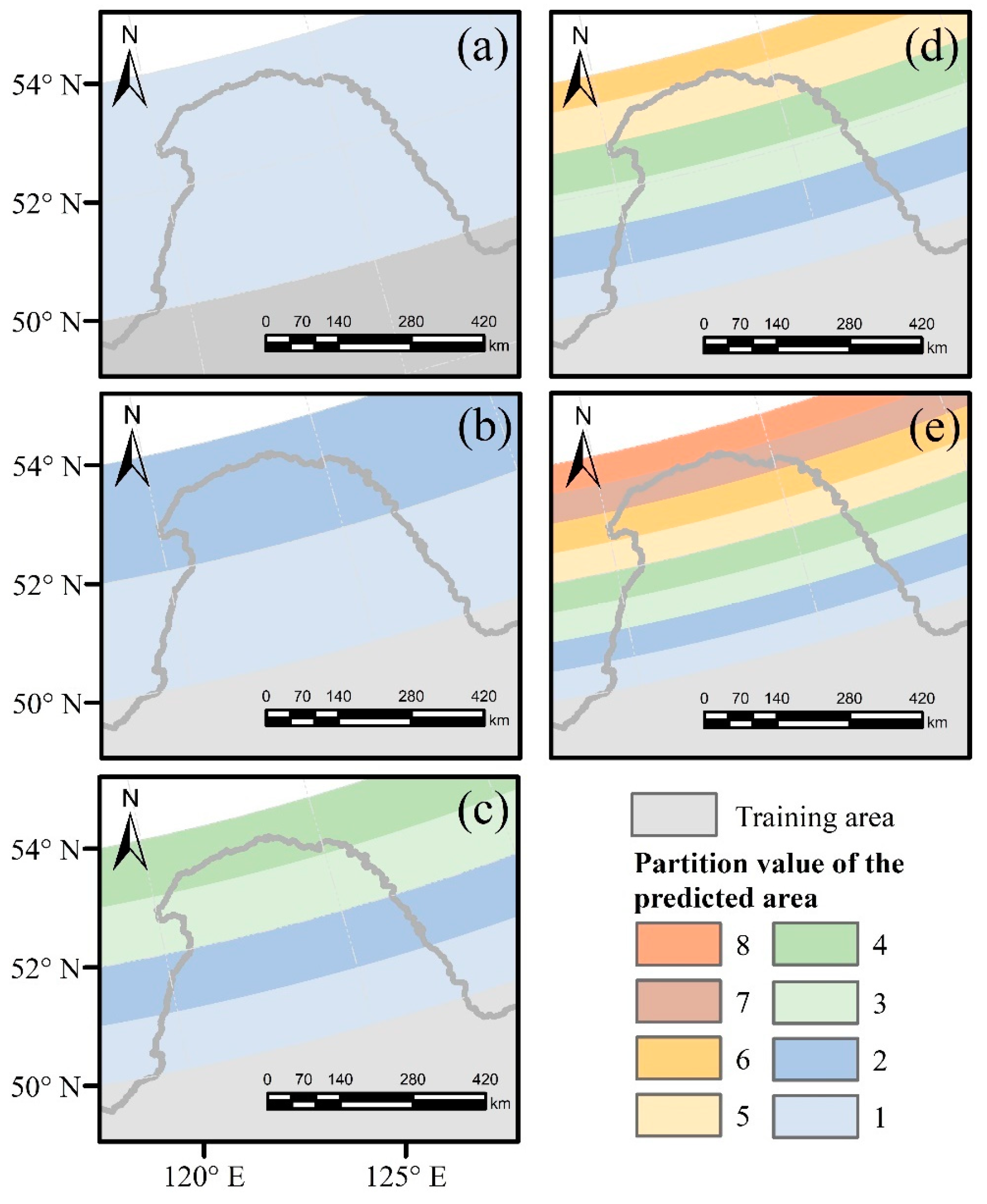
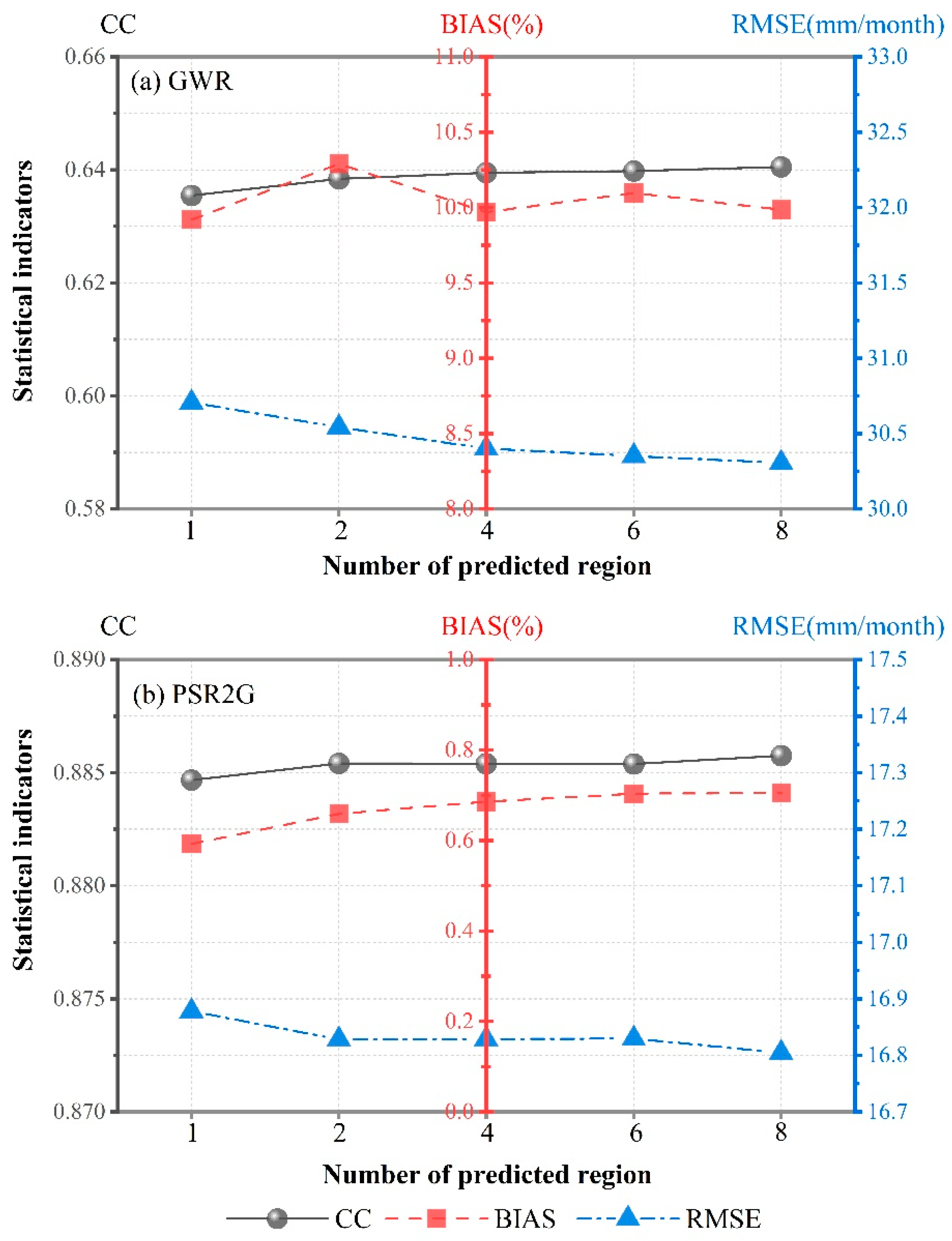
5.1. Sensitivity Analysis of the Proposed Algorithm to the Size of the Prediction Area
5.2. Strengths of the Proposed Method
5.3. Sources of Uncertainty and Future Research
6. Conclusions
- The relationship between monthly FY-2G QPE and FY-3C NDVI highlights significant lagging times in the response of NDVI to precipitation. The results showed that the highest correlation between FY-2G QPE and FY-3C NDVI in the Songliao River Basin was achieved when the lagging time was one month, and FY-2G QPE and FY-3C NDVI had no correlation in most areas of the Songliao River Basin when the lagging time was three months. Therefore, we determined that the NDVI response time to precipitation for the reconstruction model is one month.
- From the assessment results for fitted QPEs, the CC values of the fitted FY-2G QPEs derived by GWR and RF were significantly improved compared to the original FY-2G QPE in the study area with a latitude below 50°N, and the BIAS and RMSE values were also significantly reduced, with GWR outperforming RF. As For the reconstructed results, it is noted that the accuracy of the GWR model, which considers spatial non-stationarity, is still better than that of RF. This further demonstrates that the GWR method could more accurately describe the relationship between land surface environmental variables and precipitation than RF in Northeast China.
- Statistical evaluation revealed that the PSR2G QPE has the highest accuracy in estimating precipitation in regions where FY-2G satellite coverage is lost among the three reconstructed products, followed by GWR and RF. The performance of reconstruction precipitation after the merging correction is significantly superior to the only reconstructed precipitation product. This also indicates that GDA algorithms successfully reduced the rainfall errors of the GWR QPE by introducing ground observations, which further improves the consistency of the reconstructed QPE with ground observation.
- Comparison of GWR QPE based on the slide prediction in different subregions with gauged data showed that the GWR QPE has a higher performance as the distances between the prediction area and the training area were closer. The increase in sample numbers in the training area may also be responsible for the GWR QPE has better performance than other subregions when the number of slide predictions is maximum. Although the accuracy of GWR QPE exists instability, PSR2G presents similar behaviors, in which such results from short-distance prediction have the highest accuracy while long-distance prediction has the worst accuracy. This means that the accuracy of PSR2G QPE still depends on the performance of the original data even if PSR2G significantly improves the performance of GWR.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hou, A.; Kakar, R.; Neeck, S.; Azarbarzin, A.; Kummerow, C.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Yong, B.; Gourley, J.J.; Qi, W.; Lu, D.; Liu, J.; Ren, L.; Hong, Y.; Zhang, J. Recent global performance of the Climate Hazards group Infrared Precipitation (CHIRP) with Stations (CHIRPS). J. Hydrol. 2020, 591, 125284. [Google Scholar] [CrossRef]
- Zhou, Z.; Yong, B.; Liu, J.; Liao, A.; Wang, N.; Zhu, Z.; Lu, D.; Li, W.; Zhang, J. Preliminary evaluation of the hobo data logging rain gauge at the Chuzhou hydrological experiment station, China. Adv. Meteorol. 2019, 2019, 5947976. [Google Scholar] [CrossRef]
- Wen, X.; Ma, X.; Zhang, C.; Zheng, S. Comparative study of piezoelectric precipitation sensor and tipping bucket precipitation sensor. Autom. Appl. 2021, 11, 38–40+45. (In Chinese) [Google Scholar] [CrossRef]
- Fiser, O.; Wilfert, O. Novel processing of Tipping-bucket rain gauge records. Atmos. Res. 2009, 92, 283–288. [Google Scholar] [CrossRef]
- Santana, M.A.; Guimarães, P.L.; Lanza, L.G.; Vuerich, E. Metrological analysis of a gravimetric calibration system for tipping-bucket rain gauges. Meteorol. Appl. 2015, 22, 879–885. [Google Scholar] [CrossRef]
- Leeper, R.D.; Kochendorfer, J. Evaporation from weighing precipitation gauges: Impacts on automated gauge measurements and quality assurance methods. Atmos. Meas. Tech. 2015, 8, 2291–2300. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; De Bievre, B.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Bournas, A.; Baltas, E. Determination of the ZR Relationship through spatial analysis of X-band weather radar and rain gauge data. Hydrology 2022, 9, 137. [Google Scholar] [CrossRef]
- Dinku, T.; Anagnostou, E.N.; Borga, M. Improving Radar-Based Estimation of Rainfall over Complex Terrain. J. Appl. Meteorol. 2002, 41, 1163–1178. [Google Scholar] [CrossRef]
- Sharif, H.O.; Ogden, F.L.; Krajewski, W.F.; Xue, M. Numerical simulations of radar rainfall error propagation. Water Resour. Res. 2002, 38, 1140. [Google Scholar] [CrossRef]
- Kidd, C. Satellite rainfall climatology: A review. Int. J. Climatol. 2001, 21, 1041–1066. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P. GPM Integrated Multi-Satellite Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document (ATBD) Version 4.4. PPS, NASA/GSFC, 30 pp. 2014. Available online: http://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.4.pdf (accessed on 1 December 2019).
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2014, 5, 487–503. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1852. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Tang, G.; Ji, Q.; Min, X.; Wan, W.; Shi, Z. Quantitative Evaluations and Error Source Analysis of Fengyun-2-Based and GPM-Based Precipitation Products over Mainland China in Summer, 2018. Remote Sens. 2019, 11, 2992. [Google Scholar] [CrossRef]
- Lu, H.; Ding, L.; Ma, Z.; Li, H.; Lu, T.; Su, M.; Xu, J. Spatiotemporal Assessments on the Satellite-Based Precipitation Products from Fengyun and GPM Over the Yunnan-Kweichow Plateau, China. Earth Space Sci. 2020, 7, e2019EA000857. [Google Scholar] [CrossRef]
- Wu, H.; Yong, B.; Shen, Z.; Qi, W. Comprehensive error analysis of satellite precipitation estimates based on Fengyun-2 and GPM over Chinese mainland. Atmos. Res. 2021, 263, 105805. [Google Scholar] [CrossRef]
- Sun, Z.; Long, D.; Hong, Z.; Hamouda, M.A.; Mohamed, M.M.; Wang, J. How China’s Fengyun Satellite Precipitation Product Compares with Other Mainstream Satellite Precipitation Products. J. Hydrometeorol. 2022, 23, 785–806. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Relationships between precipitation and surface temperature. Geophys. Res. Lett. 2005, 32, L14703. [Google Scholar] [CrossRef]
- Spracklen, D.V.; Arnold, S.R.; Taylor, C.M. Observations of increased tropical rainfall preceded by air passage over forests. Nature 2012, 489, 282–285. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling–calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, P.; Jiang, H.; Zhao, X. Reconstructing Satellite-Based Monthly Precipitation over Northeast China Using Machine Learning Algorithms. Remote Sens. 2017, 9, 781. [Google Scholar] [CrossRef]
- Schultz, P.A.; Halpert, M.S. Global analysis of the relationships among a vegetation index, precipitation and land surface temperature. Remote Sens. 1995, 16, 2755–2777. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Fang, J.; Du, J.; Xu, W.; Shi, P.; Li, M.; Ming, X. Spatial downscaling of TRMM precipitation data based on the orographical effect and meteorological conditions in a mountainous area. Adv. Water Resour. 2013, 61, 42–50. [Google Scholar] [CrossRef]
- Eltahir, E.A.B. A Soil Moisture-Rainfall Feedback Mechanism: 1. Theory and observations. Water Resour. Res. 1998, 34, 765–776. [Google Scholar] [CrossRef]
- Brunsell, N. Characterization of land-surface precipitation feedback regimes with remote sensing. Remote Sens. Environ. 2006, 100, 200–211. [Google Scholar] [CrossRef]
- Lu, X.; Tang, G.; Wang, X.; Liu, Y.; Jia, L.; Xie, G.; Li, S.; Zhang, Y. Correcting GPM IMERG precipitation data over the Tianshan Mountains in China. J. Hydrol. 2019, 575, 1239–1252. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Ji, X.; Luo, X.; Li, X. Fine-resolution precipitation mapping in a mountainous watershed: Geostatistical downscaling of TRMM products based on environmental variables. Remote Sens. 2018, 10, 119. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A comparison of different regression algorithms for downscaling monthly satellite-based precipitation over North China. Remote Sens. 2016, 8, 835. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, S.; Duan, Z.; Qin, Z. An improved spatial downscaling procedure for TRMM 3B43 precipitation product using geographically weighted regression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4592–4604. [Google Scholar] [CrossRef]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR downscaling method to reconstruct high-resolution precipitation dataset based on GSMaP-Gauge data: A case study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI–rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Ma, Z.; Xu, J.; Zhu, S.; Yang, J.; Tang, G.; Yang, Y.; Shi, Z.; Hong, Y. AIMERG: A new Asian precipitation dataset (0.1°/half-hourly, 2000–2015) by calibrating the GPM-era IMERG at a daily scale using APHRODITE. Earth Syst. Sci. Data 2020, 12, 1525–1544. [Google Scholar] [CrossRef]
- Quiroz, R.; Yarlequé, C.; Posadas, A.; Mares, V.; Immerzeel, W.W. Improving daily rainfall estimation from NDVI using a wavelet transform. Environ. Model. Softw. 2011, 26, 201–209. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Davenport, M.L.; Malo, A.R. A comparison of the vegetation response to rainfall in the Sahel and East Africa, using normalized difference vegetation index from NOAA AVHRR. Clim. Chang. 1990, 17, 209–241. [Google Scholar] [CrossRef]
- Shen, Z.; Yong, B. Downscaling the GPM-based satellite precipitation retrievals using gradient boosting decision tree approach over Mainland China. J. Hydrol. 2021, 602, 126803. [Google Scholar] [CrossRef]
- Hu, C.; Xia, J.; She, D.; Xu, C.; Zhang, L.; Song, Z.; Zhao, L. A modified regional L-moment method for regional extreme precipitation frequency analysis in the Songliao River Basin of China. Atmos. Res. 2019, 230, 104629. [Google Scholar] [CrossRef]
- Qi, J.; Song, J.; Liu, H. Characteristics of temperature and precipitation in Northeast China from 1951 to 2000. J. Meteorol. Environ. 2006, 22, 1–5. (In Chinese) [Google Scholar]
- Xu, J.; Zhang, W.; Yang, J.; Zhao, L. Practical Manual of Fengyun-2 Satellite Business Products and Satellite Data Format; China Meteorological Press: Beijing, China, 2008; pp. 11–16. (In Chinese) [Google Scholar]
- Tang, F.; Zou, X.; Yang, H.; Weng, F. Estimation and Correction of Geolocation Errors in FengYun-3C Microwave Radiation Imager Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 407–420. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, F.; Niu, Z.; Li, B.; Yu, B.; Jia, H.; Zhang, M. An active fire detection algorithm based on multi-temporal FengYun-3C VIRR data. Remote Sens. Environ. 2018, 211, 376–387. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, J.; Li, S.; Li, S. Spatial pattern of non-stationarity and scale-dependent relationships between NDVI and climatic factors—A case study in Qinghai-Tibet Plateau, China. Ecol. Indic. 2012, 20, 170–176. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-Euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical identification model. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Shen, Z.; Wu, H. A comparative analysis of merging strategies for satellite precipitation estimates and ground observations over Chinese mainland. J. Atmos. Sol. Terr. Phys. 2023, 246, 106072. [Google Scholar] [CrossRef]
- Watson, D.F.; Philip, G.M. A refinement of inverse distance weighted interpolation. Geo-processing 1985, 2, 315–327. [Google Scholar]
- Yong, B.; Ren, L.; Hong, Y.; Gourley, J.; Tian, Y.; Huffman, G.; Chen, X.; Wang, W.; Wen, Y. First evaluation of the climatological calibration algorithm in the real-time TMPA precipitation estimates over two basins at high and low latitudes. Water Resour. Res. 2013, 49, 2461–2472. [Google Scholar] [CrossRef]
- Raziei, T. Revisiting the Rainfall Anomaly Index to serve as a Simplified Standardized Precipitation Index. J. Hydrol. 2021, 602, 126761. [Google Scholar] [CrossRef]
- Aryal, A.; Maharjan, M.; Talchabhadel, R.; Thapa, B.R. Characterizing Meteorological Droughts in Nepal: A Comparative Analysis of Standardized Precipitation Index and Rainfall Anomaly Index. Earth 2022, 3, 409–432. [Google Scholar] [CrossRef]
- Guan, H.; Wilson, J.L.; Xie, H. A cluster-optimizing regression-based approach for precipitation spatial downscaling in mountainous terrain. J. Hydrol. 2009, 375, 578–588. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Li, H.; Hong, Y.; Xie, P.; Gao, J.; Niu, Z.; Kirstetter, P.; Yong, B. Variational merged of hourly gauge-satellite precipitation in China: Preliminary results. J. Geophys. Res. Atmos. 2015, 120, 9897–9915. [Google Scholar] [CrossRef]
- Tang, G.; Long, D.; Behrangi, A.; Wang, C.; Hong, Y. Exploring deep neural networks to retrieve rain and snow in high latitudes using multisensor and reanalysis data. Water Resour. Res. 2018, 54, 8253–8278. [Google Scholar] [CrossRef]

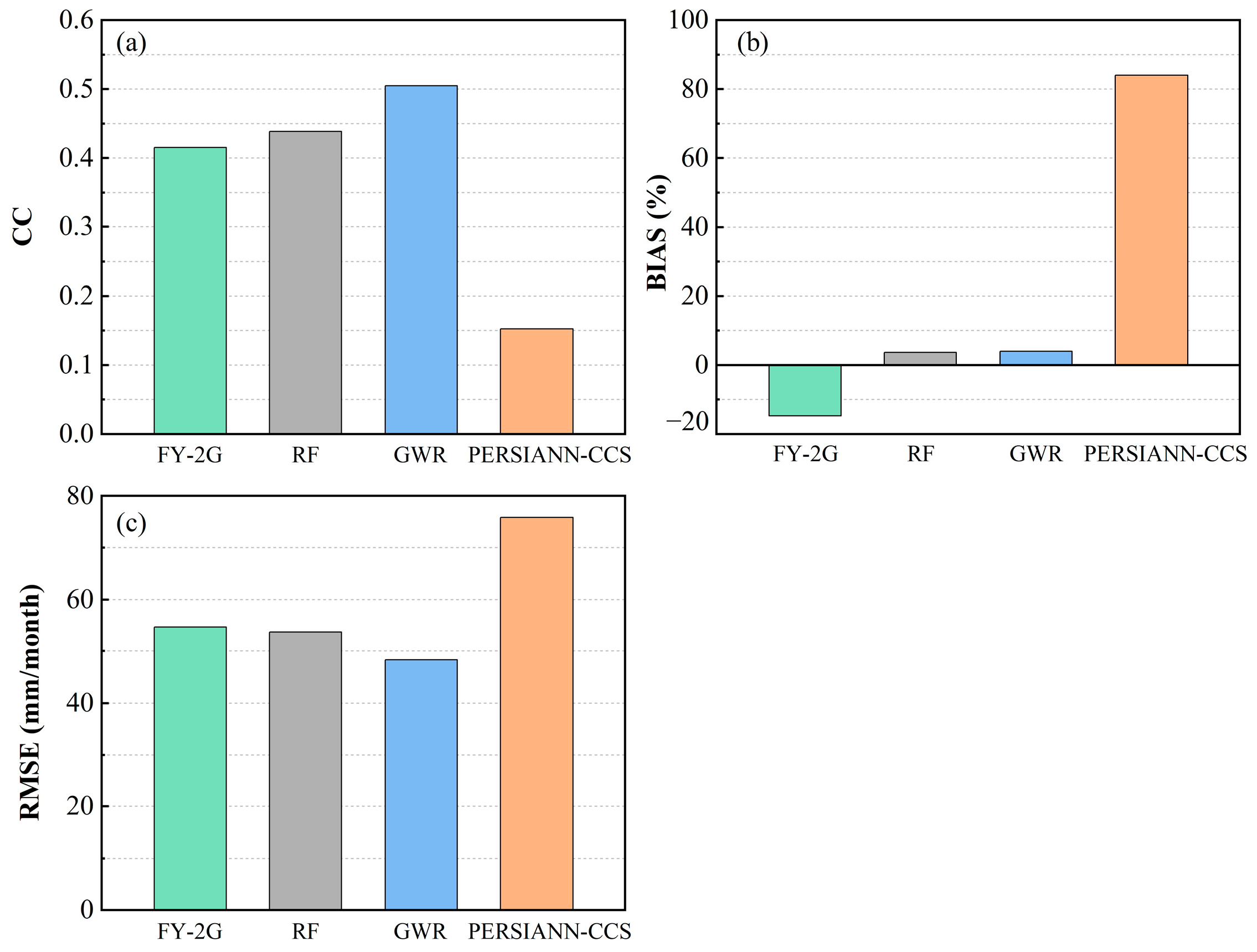
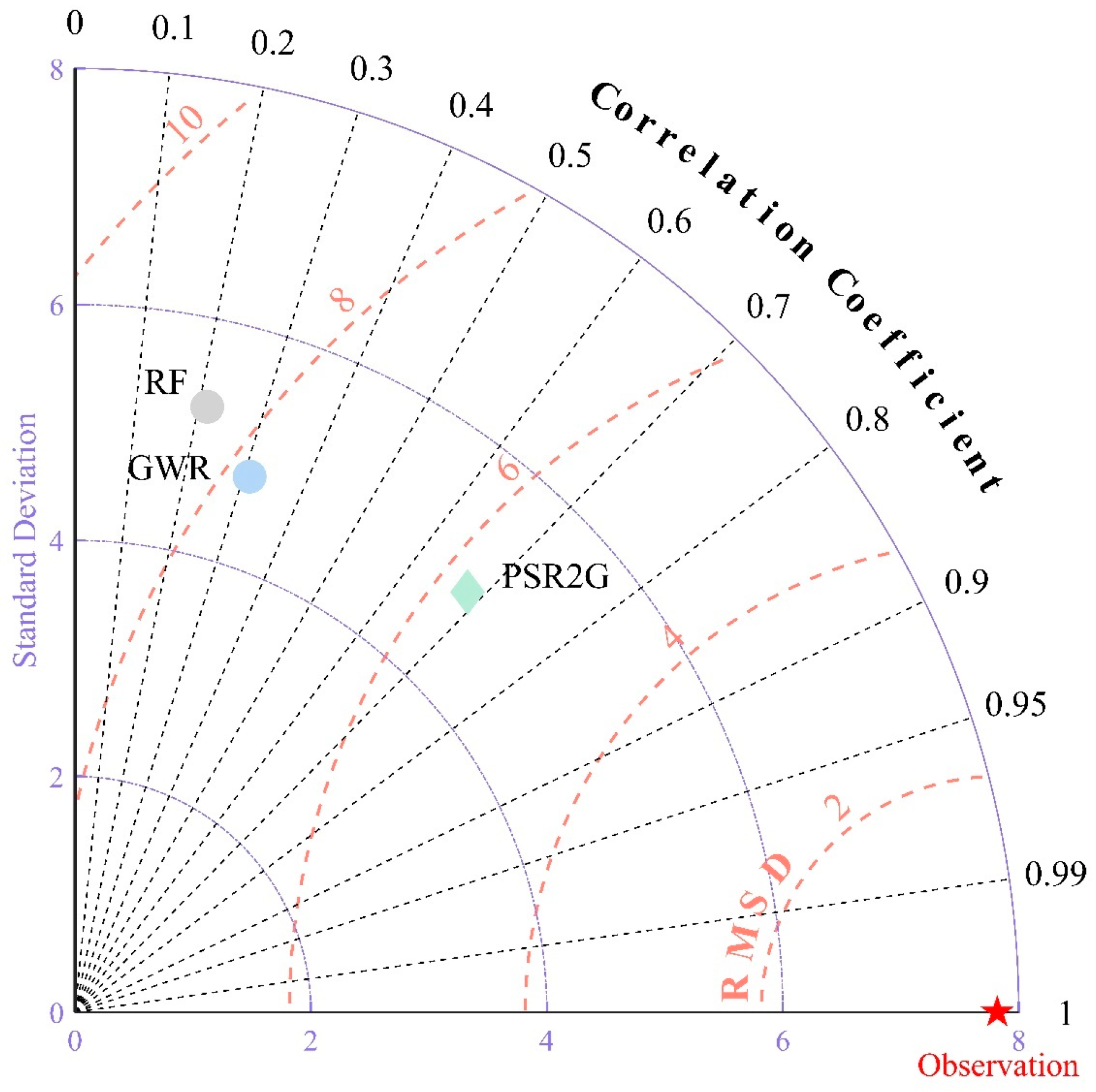
| Statistical Metric | FY-2G | PERSIANN-CCS | RF | GWR | PSR2G |
|---|---|---|---|---|---|
| CC | 0.42 | 0.04 | 0.57 | 0.64 | 0.89 |
| BIAS (%) | −14.62 | 166.27 | 12.78 | 9.99 | 0.71 |
| RMSE (mm/month) | 54.71 | 75.09 | 35.29 | 30.31 | 16.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Yong, B.; Shen, Z. Spatial Reconstruction of Quantitative Precipitation Estimates Derived from Fengyun-2G Geostationary Satellite in Northeast China. Remote Sens. 2023, 15, 5251. https://doi.org/10.3390/rs15215251
Wu H, Yong B, Shen Z. Spatial Reconstruction of Quantitative Precipitation Estimates Derived from Fengyun-2G Geostationary Satellite in Northeast China. Remote Sensing. 2023; 15(21):5251. https://doi.org/10.3390/rs15215251
Chicago/Turabian StyleWu, Hao, Bin Yong, and Zhehui Shen. 2023. "Spatial Reconstruction of Quantitative Precipitation Estimates Derived from Fengyun-2G Geostationary Satellite in Northeast China" Remote Sensing 15, no. 21: 5251. https://doi.org/10.3390/rs15215251
APA StyleWu, H., Yong, B., & Shen, Z. (2023). Spatial Reconstruction of Quantitative Precipitation Estimates Derived from Fengyun-2G Geostationary Satellite in Northeast China. Remote Sensing, 15(21), 5251. https://doi.org/10.3390/rs15215251





