Improving 3D Digital Soil Mapping Based on Spatialized Lab Soil Spectral Information
Abstract
:1. Introduction
2. Materials and Methods
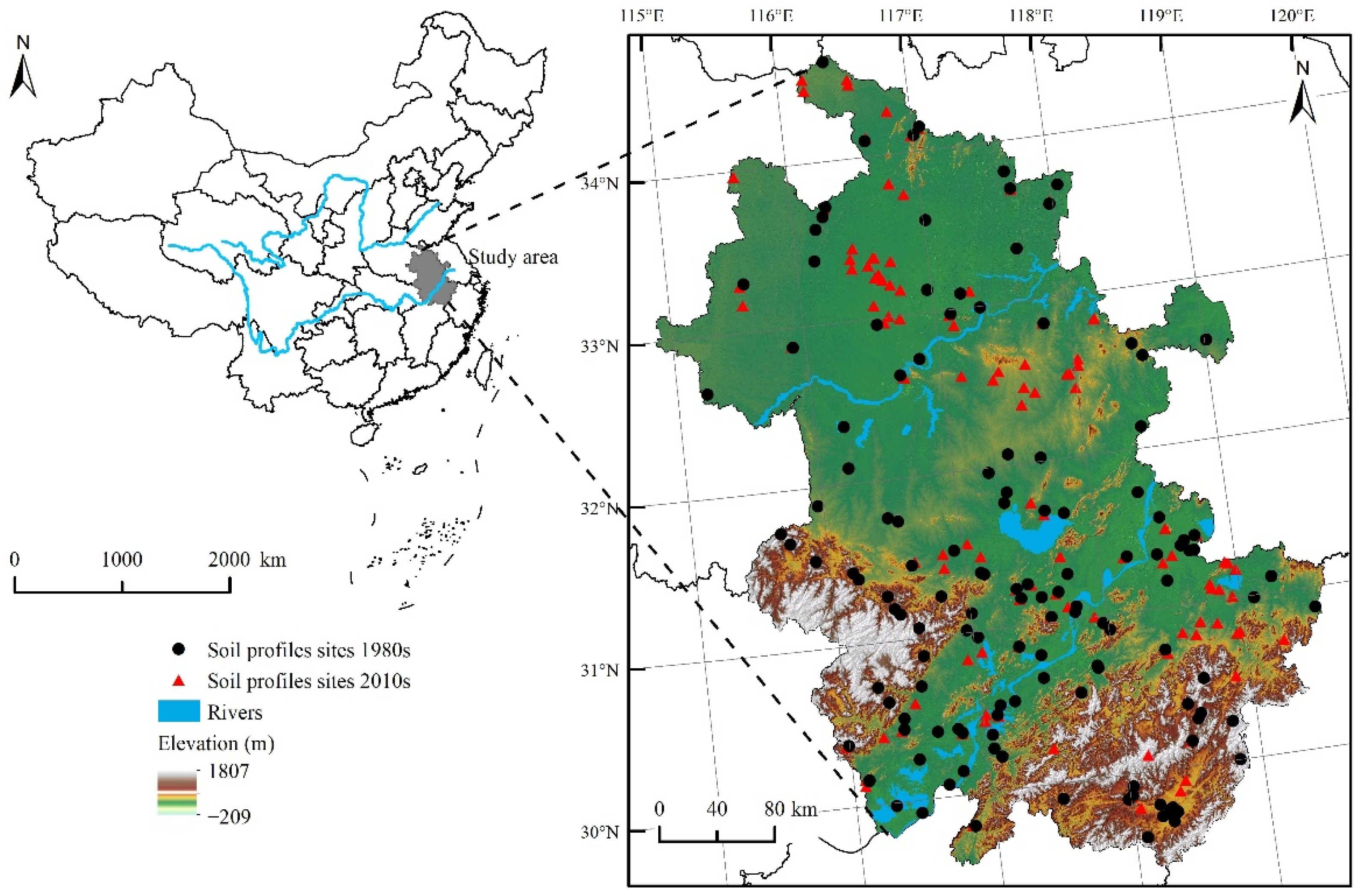
2.1. Study Area
2.2. Soil Attributes Data
2.3. Laboratory Soil Spectral Data
2.4. Environmental Covariates
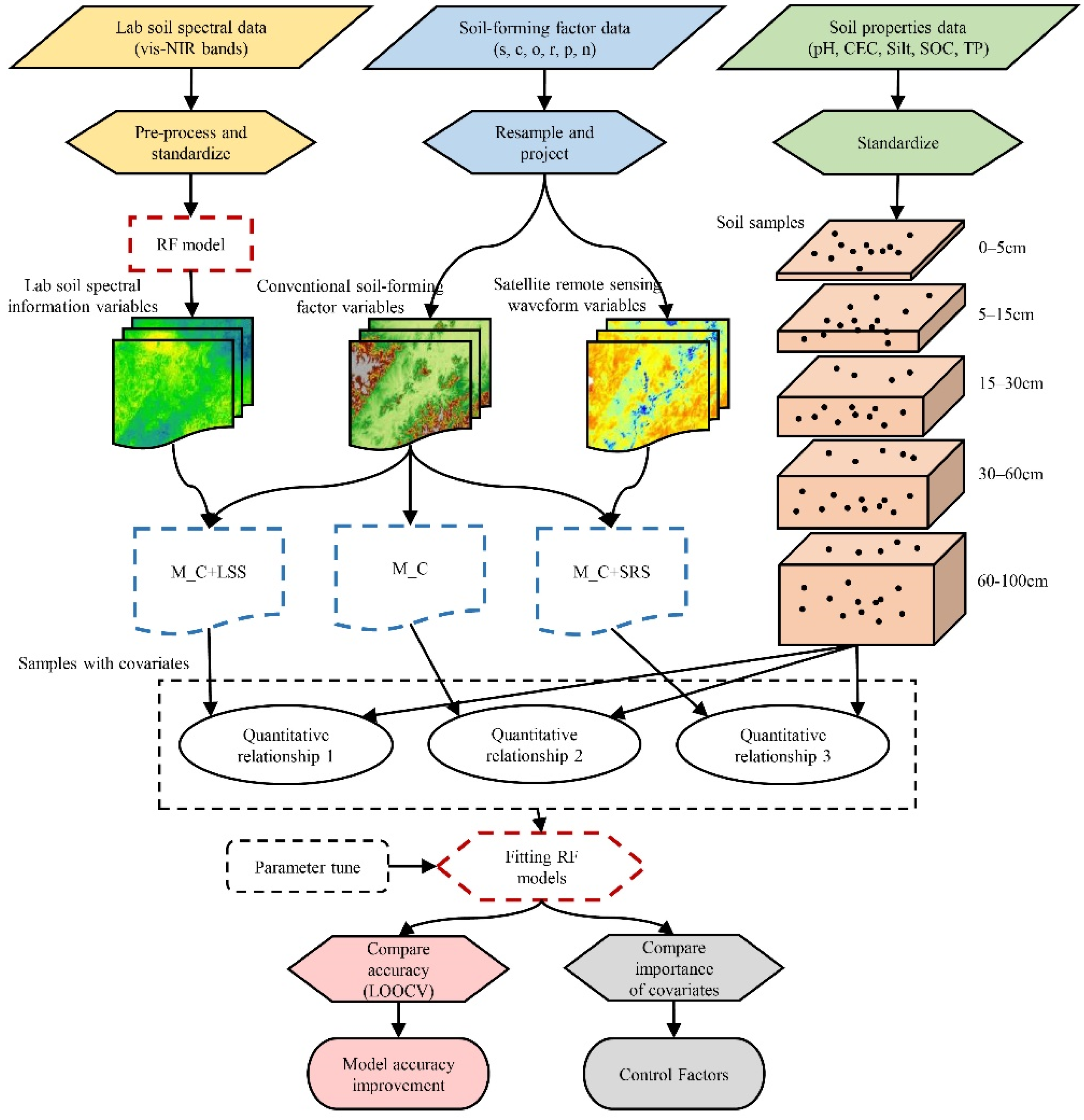
2.5. Methods
2.5.1. Spatialization of Laboratory Soil Spectra
2.5.2. Constructing Sets of Environmental Covariates
2.5.3. Assessing Accuracy Improvements in 3D Soil Attribute Predictions
3. Results
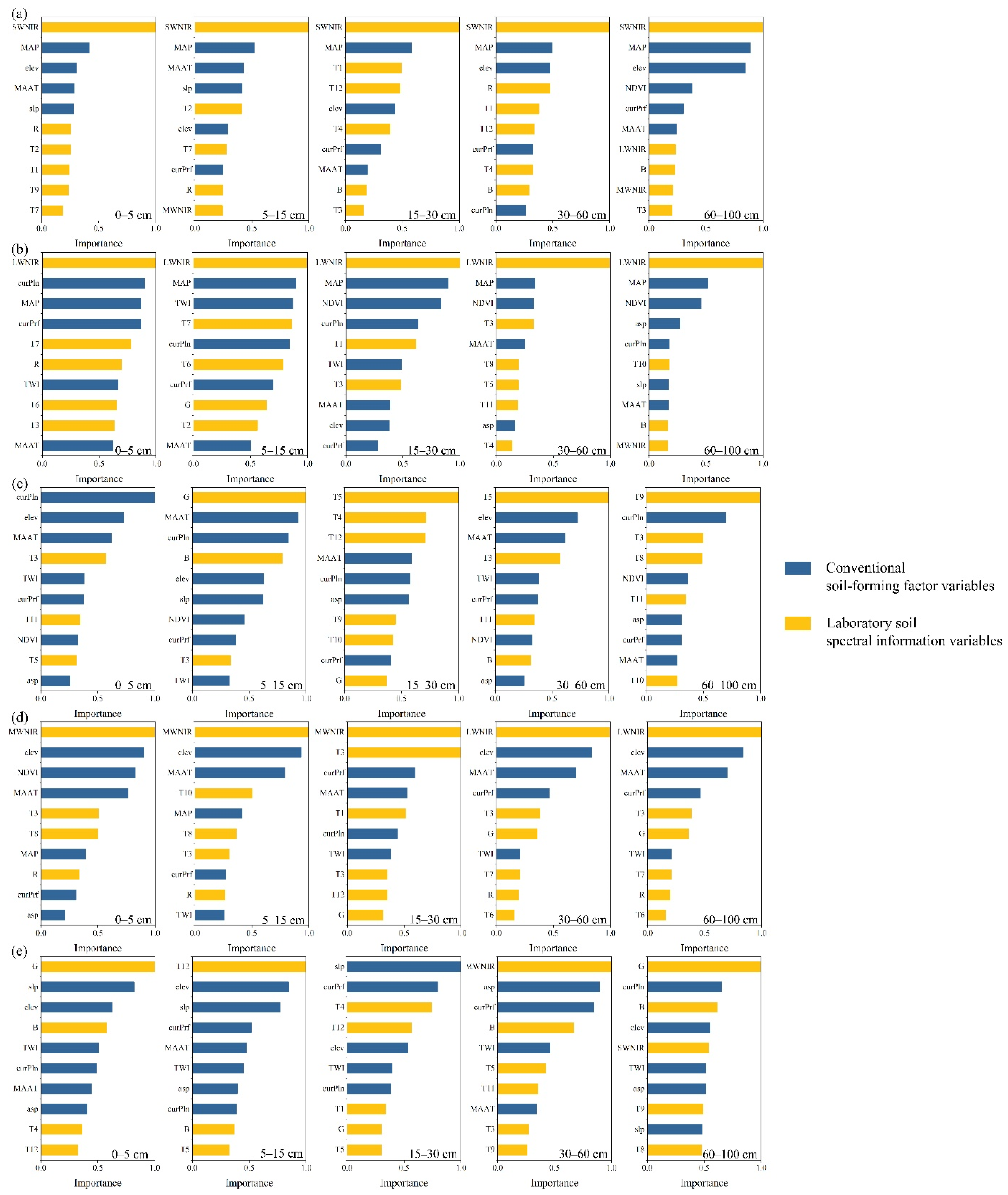
3.1. Covariates of Laboratory Soil Spectra
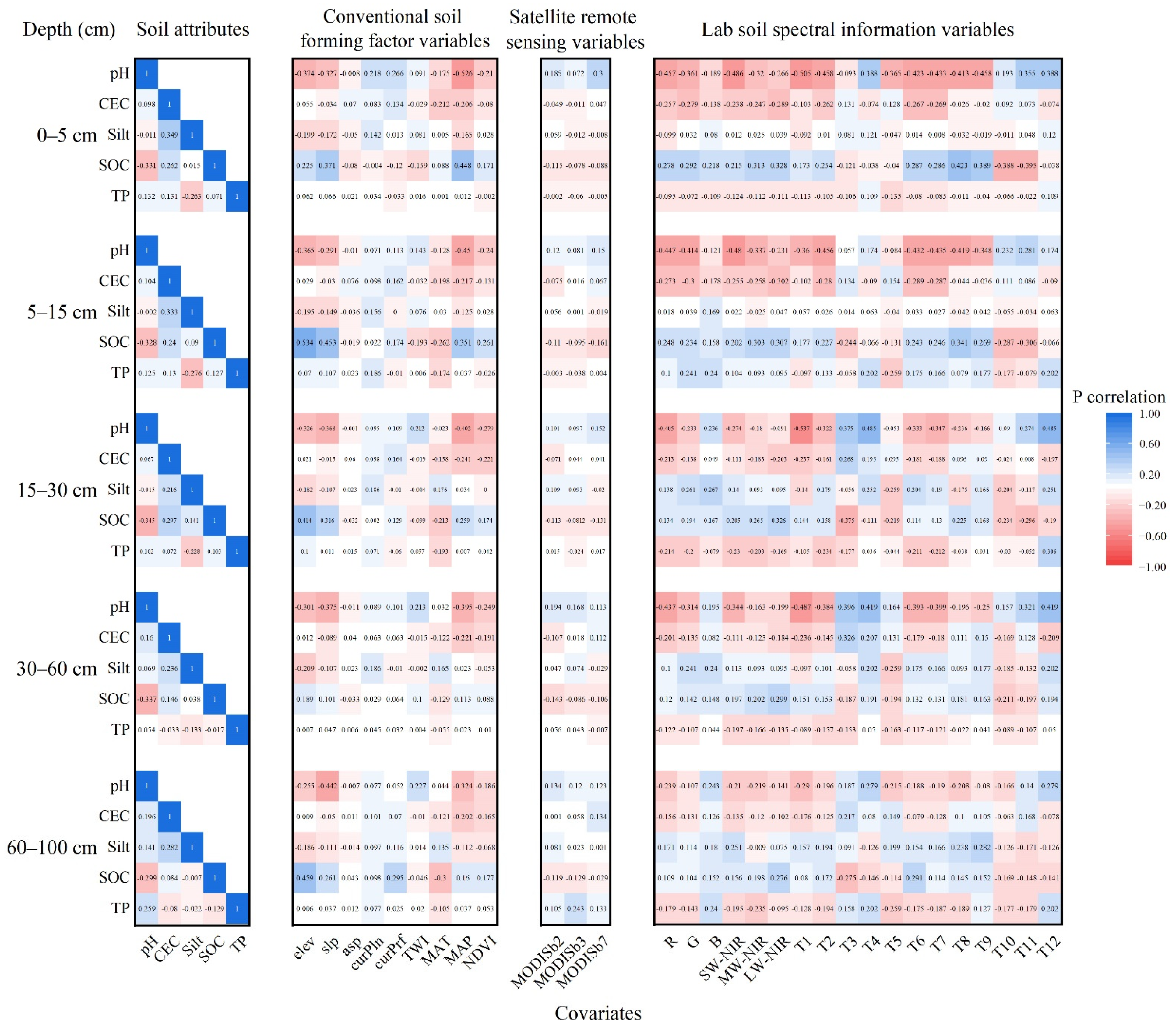
3.2. Correlations between Soil Attributes and Spatialized Laboratory Soil Spectral Information with Covariates
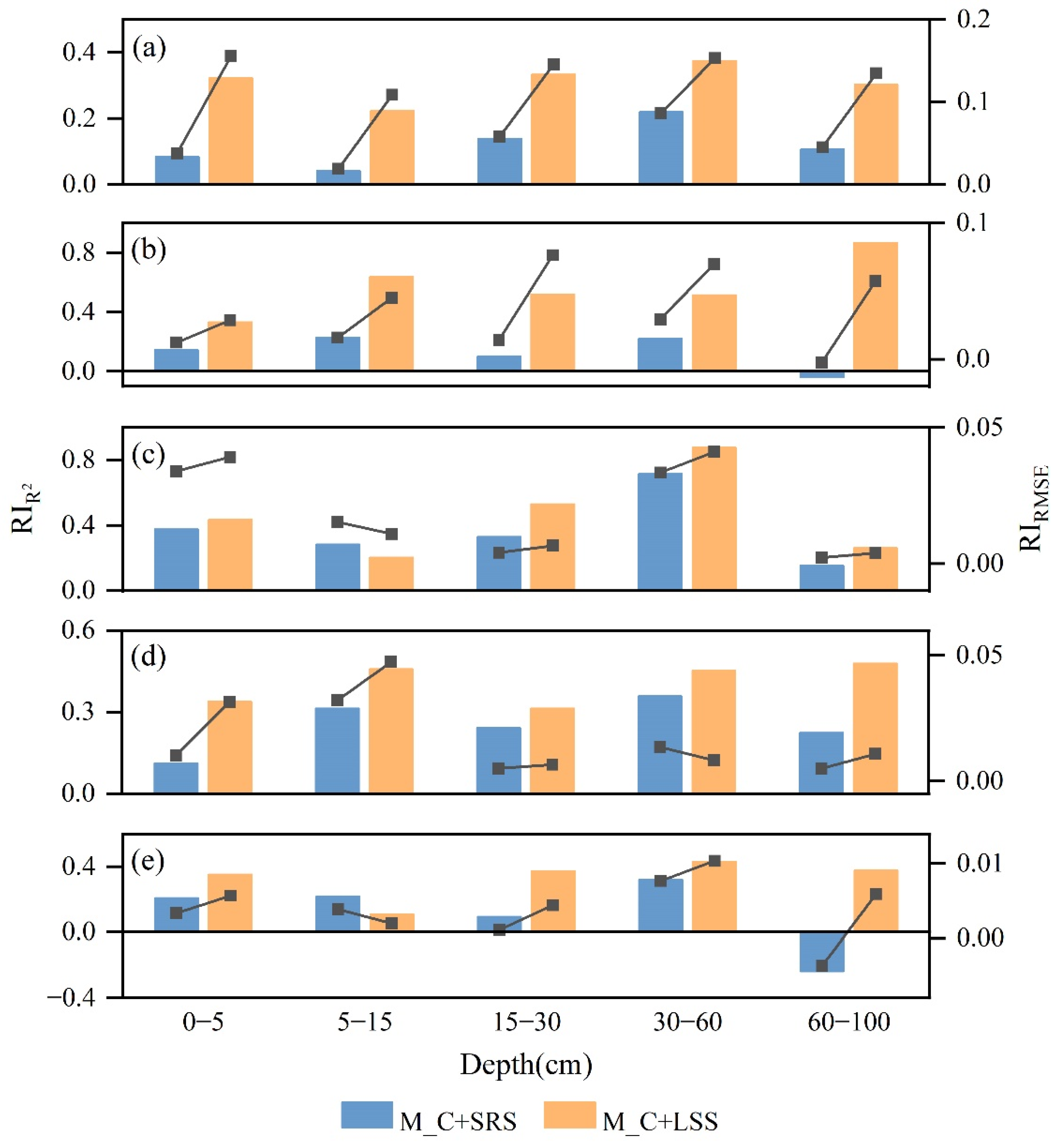
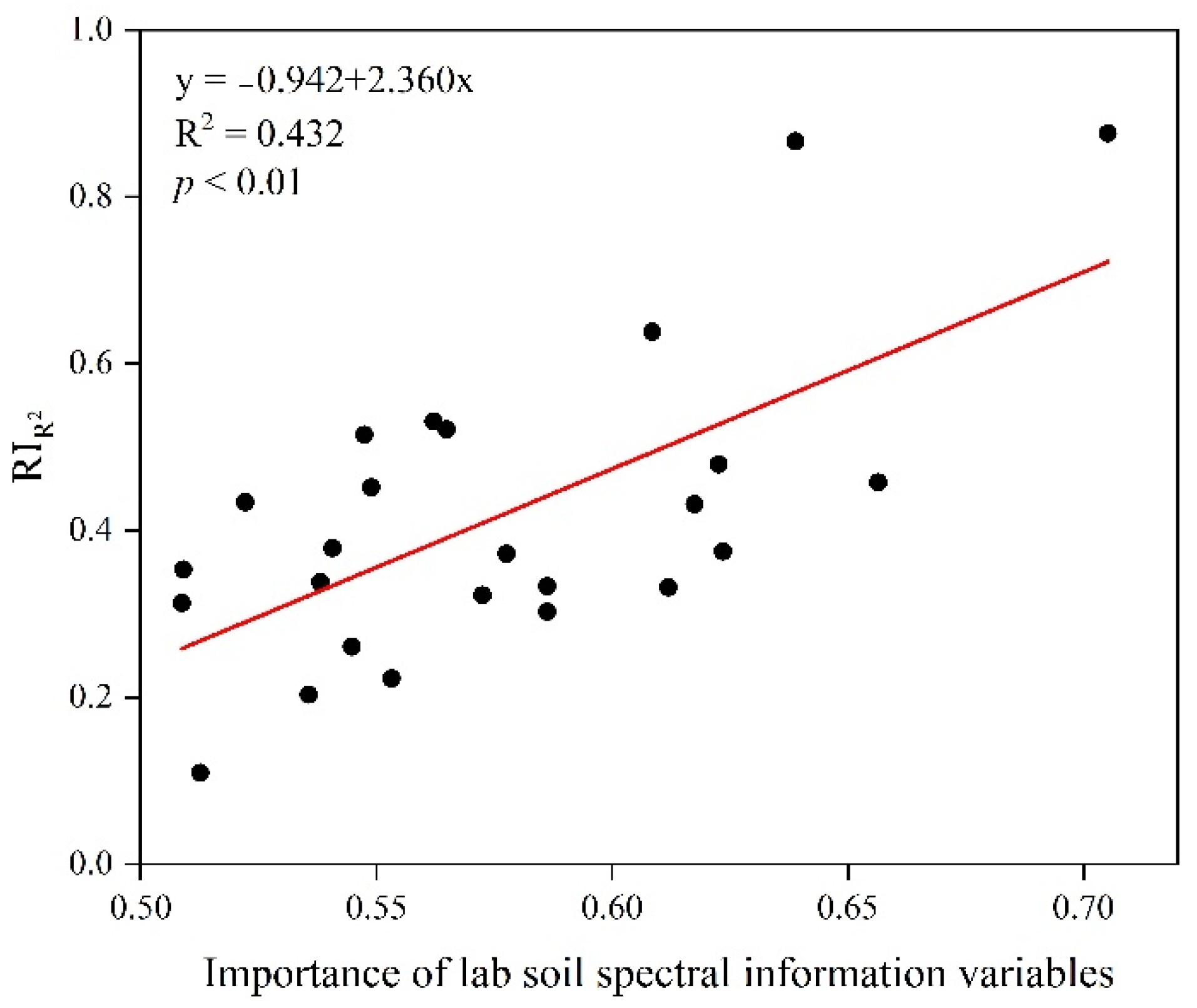
3.3. Performance Improvement of 3D Soil Attribute Mapping
4. Discussion
4.1. Predictability of Laboratory Soil Spectral Information
4.2. Advantages of Laboratory Soil Spectral Information as Covariates
4.3. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McBratney, A.B.; Santos, M.L.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Liu, F.; Geng, X.Y.; Zhu, A.X.; Fraser, W.; Waddel, A. Soil texture mapping over low relief areas using land surface feedback dynamic patterns extracted from MODIS. Geoderma 2012, 171–172, 44–52. [Google Scholar] [CrossRef]
- Liu, F.; Rossiter, D.G.; Zhang, G.L.; Li, D.C. A soil colour map of China. Geoderma 2020, 379, 114556. [Google Scholar] [CrossRef]
- Chen, S.C.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Mechanistic soil-landscape modelling as an approach to developing pedogenetic classifications. Geoderma 2006, 113, 138–149. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B.; Mendonça-Santas, M.L.; Odeh, I.O.A.; Guyan, B. Prediction and digital mapping of soil carbon storage in the Lower Namoi Valley. Aust. J. Soil Res. 2006, 44, 233–244. [Google Scholar] [CrossRef]
- Malone, B.P.; McBratney, A.B.; Minasny, B.; Laslett, G.M. Mapping continuous depth functions of soil carbon storage and available water capacity. Geoderma 2009, 154, 138–152. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.L.; Sun, Y.J.; Zhao, Y.G.; Li, D.C. Mapping the Three-Dimensional Distribution of Soil Organic Matter across a Subtropical Hilly Landscape. Soil Sci. Soc. Am. J. 2013, 77, 1241–1253. [Google Scholar] [CrossRef]
- Heung, B.; Bulmer, C.E.; Schmidt, M.G. Predictive soil parent material mapping at a regional-scale: A Random Forest approach. Geoderma 2014, 214–215, 141–154. [Google Scholar] [CrossRef]
- Loiseau, T.; Richer-de-Forges, A.C.; Martelet, G.; Bialkowski, A.; Nehlig, P.; Arrouays, D. Could airborne gamma-spectrometric data replace lithological maps as co-variates for digital soil mapping of topsoil particle-size distribution? A case study in Western France. Geoderma Reg. 2020, 22, e00295. [Google Scholar] [CrossRef]
- Taylor, M.J.; Smettem, K.; Pracilio, G.; Verboom, W. Relationships Between Soil Properties and High-Resolution Radiometrics, Central Eastern Wheatbelt, Western Australia. Explor. Geophys. 2002, 33, 95–102. [Google Scholar] [CrossRef]
- Priori, S.; Bianconi, N.; Costantini, E.A.C. Can γ-radiometrics predict soil textural data and stoniness in different parent materials? A comparison of two machine-learning methods. Geoderma 2014, 226–227, 354–364. [Google Scholar] [CrossRef]
- Romero, D.J.; Ben-Dor, E.; Demattê, J.A.M.; e Souza, A.B.; Vicente, L.E.; Tavares, T.R.; Martello, M.; Strabeli, T.F.; da Silva Barros, P.P.; Fiorio, P.R.; et al. Internal soil standard method for the Brazilian soil spectral library: Performance and proximate analysis. Geoderma 2017, 312, 95–103. [Google Scholar] [CrossRef]
- Møller, A.B.; Koganti, T.; Beucher, A.; Iversen, B.V.; Greve, M.H. Downscaling digital soil maps using electromagnetic induction and aerial imagery. Geoderma 2021, 385, 114852. [Google Scholar] [CrossRef]
- Viscarra Rossel, R. The Soil Spectroscopy Group and the development of a global soil spectral library. NIR News 2009, 20, 14–15. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Jrons, J.R.; Epema, G.F. Soil reflectance. In Remote Sensing for the Earth Science; Rencz, A.N., Ed.; John Wiley & Sons: New York, NY, USA, 1999; pp. 111–1888. [Google Scholar]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, min infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Cambule, A.H.; Rossiter, D.G.; Stoorvogel, J.J.; Smaling, E.M.A. Building a near infrared spectral library for soil organic carbon estimation in the Limpopo National Park, Mozambique. Geoderma 2012, 183–184, 41–48. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Office of Soil Survey in Anhui Province. In Soil Series of Anhui Province; Science Press: Beijing, China, 1996. (In Chinese)
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014 International soil classification system for naming soils and creating legends for soil maps. In World Soil Resources Reports, No. 106; FAO: Rome, Italy, 2014. [Google Scholar]
- Ponce-Hernandez, R.; Marriott, F.H.C.; Beckett, P.H.T. An improved method for reconstructing a soil profile from analysis of a small number of samples. Eur. J. Soil Sci. 1986, 37, 455–467. [Google Scholar] [CrossRef]
- Bishop, T.F.A.; McBratney, A.B.; Laslett, G.M. Modelling soil attribute depth functions with equal-area quadratic smoothing splines. Geoderma 1999, 91, 27–45. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, Q.L.; Peng, J.; Ji, W.J.; Liu, H.J.; Li, X. Development of a national VNIR soil-spectral library for soil classification and prediction of organic matter concentrations. Sci. China Earth Sci. 2014, 44, 978–988. [Google Scholar] [CrossRef]
- Arrouays, D.; Grundy, M.G.; Hartemink, A.E.; Hempel, J.W.; Heuvelink, G.B.M.; Hong, S.Y.; Lagacherie, P.; Lelyk, G.; McBratney, A.B.; McKenzie, N.J.; et al. GlobalSoilMap: Toward a Fine-Resolution Global Grid of Soil Properties. Adv. Agron. 2014, 125, 93–134. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2010, 25, 1965–1978. [Google Scholar] [CrossRef]
- Peng, S.Z.; Ding, Y.X.; Liu, W.Z.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards Jr, T.C. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239–240, 68–83. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L.; et al. Mapping Soil Properties of Africa at 250 m Resolution: Random Forests Significantly Improve Current Predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef] [PubMed]
- Nussbaum, M.; Spiess, K.; Baltensweiler, A.; Grob, U.; Keller, A.; Greiner, L.; Schaepman, M.E.; Papritz, A. Evaluation of digital soil mapping approaches with large sets of environment covariates. Soil 2018, 4, 1–22. [Google Scholar] [CrossRef]
- Wang, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recogn. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Lin, L.I. A Concordance Correlation-Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: http://www.R-project.org (accessed on 11 October 2021).
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. Available online: https://CRAN.R-project.org/doc/Rnews (accessed on 11 October 2021).
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Bivand, R.; Keitt, T.; Rowlingson, B. rgdal: Bindings for the “Geospatial” Data Abstraction Library; R Package Version 1.6-6; R Foundation: Vienna, Austria, 2023; Available online: https://CRAN.R-project.org/package=rgdal (accessed on 11 October 2021).
- Hijmans, R.J. raster: Geographic Data Analysis and Modeling; R Package Version 3.6-20; R Foundation: Vienna, Austria, 2023; Available online: https://CRAN.R-project.org/package=raster (accessed on 11 October 2021).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Liu, F.; Zhang, G.L.; Song, X.D.; Li, D.C.; Zhao, Y.G.; Yang, J.L.; Wu, H.Y.; Yang, F. High-resolution and three-dimensional mapping of soil texture of China. Geoderma 2019, 361, 114061. [Google Scholar] [CrossRef]
- Shepherd, K.D.; Walsh, M.G. Development of reflectance spectral libraries for characterization of soil properties. Soil Sci. Soc. Am. J. 2002, 66, 988–998. [Google Scholar] [CrossRef]
- Cozzolino, D.; Morón, A. The potential of near-infrared reflectance spectroscopy to analyse soil chemical and physical characteristics. J. Agric. Sci. 2003, 140, 65–71. [Google Scholar] [CrossRef]
- Chang, C.W.; Laird, D.A. Near-infrared reflectance spectroscopic analysis of soil C and N. Soil Sci. 2002, 167, 110–116. [Google Scholar] [CrossRef]
- Daniel, K.W.; Tripathi, N.K.; Honda, K. Artificial neural network analysis of laboratory and in situ spectra for the estimation of macronutrients in soils of Lop Buri (Thailand). Aust. J. Soil Sci. Res. 2003, 41, 47–59. [Google Scholar] [CrossRef]
- Clark, R.N. Spectroscopy of Rocks and Minerals, and Principles of Spectroscopy. In Remote Sensing for the Earth Science: Manual of Remote Sensing; Rencz, A.N., Ed.; John Wiley & Sons: New York, NY, USA, 1999; pp. 3–52. [Google Scholar]
- Van Breemen, N.; Driscoll, C.T.; Mulder, J. Acidic deposition and internal proton sources in acidification of soils and waters. Nature 1984, 307, 599–604. [Google Scholar] [CrossRef]
- Poppiel, R.R.; Lacerda, M.P.C.; Safanelli, J.L.; Rizzo, R.; Oliveira, M.P., Jr.; Novais, J.J.; Demattê, J.A.M. Mapping at 30 m resolution of soil attributes at multiple depths in midwest Brazil. Remote Sens. 2019, 11, 2905. [Google Scholar] [CrossRef]
- Pirie, A.; Singh, B.; Islan, K. Ultra-violet, visible, near-infrared, and min-infrared diffuse reflectance spectroscopic techniques to predict several soil properties. Aust. J. Soil Res. 2005, 43, 713–721. [Google Scholar] [CrossRef]
- Whiting, M.L.; Li, L.; Ustin, S.L. Predicting water content using Gaussian model on soil spectra. Remote Sens. Environ. 2004, 89, 535–552. [Google Scholar] [CrossRef]
- Vasques, G.M.; Grunwald, S.; Sickman, J.O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B.; Bellon-Maurel, V.; Roger, J.M.; Gobrecht, A.; Ferrand, L.; Joalland, S. Removing the effect of soil moisture from NIR diffuse reflectance spectra for the prediction of soil organic carbon. Geoderma 2011, 167–168, 118–124. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and Near Infrared Spectroscopy in Soil Science. Adv. Agron. 2010, 107, 163–215. [Google Scholar] [CrossRef]
- Kuang, B.; Mahmood, H.S.; Quraishi, M.Z.; Hoogmoed, W.B.; Mouazen, A.M.; van Henten, E.J. Sensing soil properties in the laboratory, in situ, and on-Line: A review. Adv. Agron. 2012, 114, 155–223. [Google Scholar] [CrossRef]
- Song, Y.X.; Li, F.L.; Yang, Z.F.; Ayoko, G.A.; Frost, R.L.; Ji, J.F. Diffuse reflectance spectroscopy for monitoring potentially toxic elements in the agricultural soils of Changjiang River Delta, China. Appl. Clay Sci. 2012, 64, 75–83. [Google Scholar] [CrossRef]
- Boettinger, J.L.; Ramsey, R.D.; Bodily, R.D.; Cole, N.J.; Kienast-Brown, S.; Nield, S.J.; Saunders, A.M.; Stum, A.K. Landsat Spectral Data for Digital Soil Mapping. In Digital Soil Mapping with Limited Data; Hartemink, A.E., McBratney, A.B., Mendonça-Santos, M.D., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 193–202. [Google Scholar] [CrossRef]


| Soil Attributes | Depth (cm) | Mean (%) | SD (%) | CV | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| pH | 0–5 | 6.385 | 1.282 | 0.201 | 0.437 | −0.908 |
| 5–15 | 6.484 | 1.221 | 0.188 | 0.404 | −0.918 | |
| 15–30 | 6.757 | 1.150 | 0.170 | 0.045 | −0.993 | |
| 30–60 | 6.923 | 1.136 | 0.164 | −0.247 | −0.924 | |
| 60–100 | 7.034 | 1.115 | 0.158 | −0.413 | −0.689 | |
| CEC | 0–5 | 15.506 | 7.147 | 0.461 | 0.680 | −0.304 |
| 5–15 | 15.140 | 6.909 | 0.456 | 0.661 | −0.381 | |
| 15–30 | 14.654 | 7.087 | 0.484 | 0.560 | −0.524 | |
| 30–60 | 15.297 | 7.506 | 0.493 | 0.603 | −0.706 | |
| 60–100 | 15.025 | 7.203 | 0.479 | 0.555 | −0.431 | |
| Silt | 0–5 | 34.122 | 12.252 | 0.359 | 0.284 | −0.203 |
| 5–15 | 34.115 | 11.326 | 0.332 | 0.164 | −0.299 | |
| 15–30 | 33.860 | 11.032 | 0.326 | 0.034 | −0.093 | |
| 30–60 | 33.494 | 12.209 | 0.365 | 0.403 | 1.441 | |
| 60–100 | 33.048 | 12.220 | 0.370 | 0.007 | 1.572 | |
| SOC | 0–5 | 15.894 | 13.718 | 0.863 | 3.174 | 12.864 |
| 5–15 | 14.407 | 11.473 | 0.796 | 2.821 | 11.265 | |
| 15–30 | 10.658 | 8.996 | 0.844 | 2.616 | 9.790 | |
| 30–60 | 7.528 | 10.499 | 1.395 | 5.666 | 43.163 | |
| 60–100 | 5.499 | 7.005 | 1.274 | 5.276 | 37.203 | |
| TP | 0–5 | 0.557 | 0.319 | 0.573 | 2.020 | 5.743 |
| 5–15 | 0.549 | 0.291 | 0.530 | 1.677 | 3.696 | |
| 15–30 | 0.529 | 0.303 | 0.573 | 2.588 | 13.015 | |
| 30–60 | 0.474 | 0.258 | 0.544 | 1.959 | 7.086 | |
| 60–100 | 0.449 | 0.264 | 0.589 | 2.240 | 9.941 |
| Category | Covariate | Description | Resolution |
|---|---|---|---|
| Parent material | pmcls | Type of parent materials | 90 m |
| Terrain | elev | Elevation (m) | 90 m |
| anHis | Mountain shadow | 90 m | |
| slp | Slope (%) | 90 m | |
| asp | Aspect (°) | 90 m | |
| curPln | Plan curvature | 90 m | |
| curPrf | Profile curvature | 90 m | |
| TWI | Topographic wetness index | 90 m | |
| TPI | Topographic position index | 90 m | |
| MrVBF | Multiscale Valley flatness index | 90 m | |
| MrRTF | Multiscale ridge flatness index | 90 m | |
| Climate | MAT | Mean annual temperature (°C) | 1000 m |
| rangDiurnal | Mean diurnal range (°C) | 1000 m | |
| rangAnnual | Mean annual range (°C) | 1000 m | |
| isother | Isothermality (°C) | 1000 m | |
| tempSeason | Air temperature seasonality (°C) | 1000 m | |
| tempMaxWarm | Maximum air temperature of warmest month (°C) | 1000 m | |
| tempMinCold | Minimum air temperature of coldest month (°C) | 1000 m | |
| tempWettest | Air temperature of wettest season (°C) | 1000 m | |
| tempDriest | Air temperature of driest season (°C) | 1000 m | |
| tempMeanWarm | Mean air temperature of warmest month (°C) | 1000 m | |
| tempMeanCold | Mean air temperature of coldest month (°C) | 1000 m | |
| MAP | Mean annual precipitation (mm yr−1) | 1000 m | |
| precSeason | Precipitation seasonality (mm yr−1) | 1000 m | |
| precWettest | Precipitation of wettest month (mm mh−1) | 1000 m | |
| precDriest | Precipitation of driest month (mm mh−1) | 1000 m | |
| precWarm | Precipitation of warmest month (mm mh−1) | 1000 m | |
| precCold | Precipitation of coldest month (mm mh−1) | 1000 m | |
| solarRed | Mean annual solar radiation (J m−2 yr−1) | 500 m | |
| windSpeed | Wind speed (m s−1) | 1000 m | |
| vaporPress | Water vapor pressor (kpa) | 1000 m | |
| evaTra | Terrestrial evaporation | 500 m | |
| LST | Land surface temperature (°C) | 500 m | |
| Biological | NDVI | Mean NDVI | 250 m |
| EVI | Mean EVI | 250 m | |
| Satellite remote sensing | MODISb1 | Reflectance of the red band (620–672 nm) | 500 m |
| MODISb2 | Reflectance of near-infrared short wave (841–890 nm) | 500 m | |
| MODISb3 | Reflectance of the blue band (459–479 nm) | 500 m | |
| MODISb4 | Reflectance of the green band (545–565 nm) | 500 m | |
| MODISb5 | Reflectance of near-infrared medium wave (1230–1250 nm) | 500 m | |
| MODISb6 | Reflectance of near-infrared medium wave (1628–1652 nm) | 500 m | |
| MODISb7 | Reflectance of near-infrared long wave (2105–2155 nm) | 500 m |
| Soil Spectral Correlation Factors | Computed Expression |
|---|---|
| T1 | |
| T2 | |
| T3 | |
| T4 | |
| T5 | |
| T6 | |
| T7 | |
| T8 | |
| T9 | |
| T10 | |
| T11 | |
| T12 |
| Laboratory Soil Spectral Bands | Depth (cm) | ME | RMSE | R2 | CCC |
|---|---|---|---|---|---|
| R | 0–5 | −0.129 | 2.982 | 0.209 | 0.436 |
| 5–15 | −0.098 | 2.890 | 0.239 | 0.499 | |
| 15–30 | 0.341 | 2.962 | 0.279 | 0.477 | |
| 30–60 | −0.022 | 2.807 | 0.385 | 0.597 | |
| 60–100 | −0.480 | 2.819 | 0.518 | 0.687 | |
| G | 0–5 | −0.261 | 2.748 | 0.142 | 0.398 |
| 5–15 | −0.338 | 2.702 | 0.176 | 0.401 | |
| 15–30 | 0.251 | 2.422 | 0.224 | 0.449 | |
| 30–60 | 0.334 | 2.564 | 0.286 | 0.587 | |
| 60–100 | −0.203 | 2.434 | 0.426 | 0.584 | |
| B | 0–5 | −0.017 | 1.864 | 0.331 | 0.520 |
| 5–15 | −0.026 | 1.747 | 0.380 | 0.550 | |
| 15–30 | 0.064 | 1.794 | 0.349 | 0.498 | |
| 30–60 | −0.038 | 1.680 | 0.332 | 0.510 | |
| 60–100 | 0.063 | 1.608 | 0.400 | 0.598 | |
| SW-NIR | 0–5 | −0.182 | 2.700 | 0.404 | 0.586 |
| 5–15 | −0.184 | 2.538 | 0.431 | 0.625 | |
| 15–30 | −0.106 | 2.153 | 0.515 | 0.515 | |
| 30–60 | 0.100 | 2.423 | 0.515 | 0.682 | |
| 60–100 | 0.055 | 3.358 | 0.433 | 0.611 | |
| MW-NIR | 0–5 | −0.182 | 3.482 | 0.279 | 0.405 |
| 5–15 | −0.846 | 2.946 | 0.429 | 0.633 | |
| 15–30 | −0.093 | 4.139 | 0.499 | 0.669 | |
| 30–60 | −0.311 | 4.829 | 0.406 | 0.587 | |
| 60–100 | −0.208 | 5.104 | 0.371 | 0.559 | |
| LW-NIR | 0–5 | −0.359 | 1.113 | 0.459 | 0.614 |
| 5–15 | −0.424 | 4.162 | 0.394 | 0.543 | |
| 15–30 | −0.205 | 4.174 | 0.410 | 0.573 | |
| 30–60 | −0.347 | 4.481 | 0.395 | 0.564 | |
| 60–100 | −0.354 | 4.769 | 0.308 | 0.493 |
| Soil Attributes | Depth (cm) | Satellite Remote Sensing | Lab Soil Spectral Information | p Value |
|---|---|---|---|---|
| pH | 0–5 | 0.186 ± 0.114 b | 0.364 ± 0.113 a | 0.021 |
| 5–15 | 0.117 ± 0.035 b | 0.305 ± 0.139 a | 0.034 | |
| 15–30 | 0.117 ± 0.031 a | 0.285 ± 0.141 a | 0.058 | |
| 30–60 | 0.158 ± 0.041 b | 0.313 ± 0.111 a | 0.030 | |
| 60–100 | 0.126 ± 0.007 b | 0.199 ± 0.058 a | 0.045 | |
| CEC | 0–5 | 0.036 ± 0.021 b | 0.165 ± 0.096 a | 0.035 |
| 5–15 | 0.053 ± 0.032 b | 0.182 ± 0.097 a | 0.038 | |
| 15–30 | 0.052 ± 0.017 b | 0.145 ± 0.074 a | 0.044 | |
| 30–60 | 0.079 ± 0.053 b | 0.167 ± 0.057 a | 0.022 | |
| 60–100 | 0.067 ± 0.071 b | 0.124 ± 0.039 a | 0.049 | |
| Silt | 0–5 | 0.026 ± 0.028 a | 0.049 ± 0.039 a | 0.343 |
| 5–15 | 0.025 ± 0.028 a | 0.045 ± 0.034 a | 0.352 | |
| 15–30 | 0.074 ± 0.047 b | 0.177 ± 0.065 a | 0.017 | |
| 30–60 | 0.050 ± 0.023 b | 0.152 ± 0.061 a | 0.012 | |
| 60–100 | 0.035 ± 0.041 b | 0.157 ± 0.065 a | 0.006 | |
| SOC | 0–5 | 0.094 ± 0.019 b | 0.249 ± 0.124 a | 0.049 |
| 5–15 | 0.122 ± 0.035 b | 0.225 ± 0.079 a | 0.042 | |
| 15–30 | 0.108 ± 0.025 b | 0.203 ± 0.074 a | 0.045 | |
| 30–60 | 0.112 ± 0.030 b | 0.177 ± 0.045 a | 0.017 | |
| 60–100 | 0.092 ± 0.055 b | 0.163 ± 0.061 a | 0.043 | |
| TP | 0–5 | 0.022 ± 0.033 b | 0.089 ± 0.035 a | 0.006 |
| 5–15 | 0.015 ± 0.020 b | 0.149 ± 0.063 a | 0.002 | |
| 15–30 | 0.019 ± 0.005 b | 0.143 ± 0.090 a | 0.030 | |
| 30–60 | 0.035 ± 0.025 b | 0.107 ± 0.050 a | 0.028 | |
| 60–100 | 0.127 ± 0.020 b | 0.187 ± 0.044 a | 0.029 |
| Soil Attributes | Depth (cm) | Average of Accuracy Improvement | |
|---|---|---|---|
| M_C+SRS | M_C+LSS | ||
| pH | 0–60 | 0.208 | 0.334 |
| 60–100 | 0.106 | 0.303 | |
| CEC | 0–60 | 0.189 | 0.505 |
| 60–100 | −0.038 | 0.867 | |
| Silt | 0–60 | 0.523 | 0.633 |
| 60–100 | 0.154 | 0.260 | |
| SOC | 0–60 | 0.290 | 0.411 |
| 60–100 | 0.223 | 0.479 | |
| TP | 0–60 | 0.247 | 0.355 |
| 60–100 | −0.239 | 0.379 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Liu, F.; Wang, D.; Wu, H.; Zhang, G. Improving 3D Digital Soil Mapping Based on Spatialized Lab Soil Spectral Information. Remote Sens. 2023, 15, 5228. https://doi.org/10.3390/rs15215228
Sun Z, Liu F, Wang D, Wu H, Zhang G. Improving 3D Digital Soil Mapping Based on Spatialized Lab Soil Spectral Information. Remote Sensing. 2023; 15(21):5228. https://doi.org/10.3390/rs15215228
Chicago/Turabian StyleSun, Zheng, Feng Liu, Decai Wang, Huayong Wu, and Ganlin Zhang. 2023. "Improving 3D Digital Soil Mapping Based on Spatialized Lab Soil Spectral Information" Remote Sensing 15, no. 21: 5228. https://doi.org/10.3390/rs15215228
APA StyleSun, Z., Liu, F., Wang, D., Wu, H., & Zhang, G. (2023). Improving 3D Digital Soil Mapping Based on Spatialized Lab Soil Spectral Information. Remote Sensing, 15(21), 5228. https://doi.org/10.3390/rs15215228







