Abstract
This study examines the effectiveness of various deep learning algorithms in nowcasting using weather radar data from South Korea. Herein, the algorithms examined include RainNet, ConvLSTM2D U-Net, a U-Net-based recursive model, and a generative adversarial network. Moreover, this study used S-band radar data from the Ministry of Environment to assess the predictive performance of these models. Results show the efficacy of these algorithms in short-term rainfall prediction. Specifically, for a threshold of 0.1 mm/h, the recursive RainNet model achieved a critical success index (CSI) of 0.826, an F1 score of 0.781, and a mean absolute error (MAE) of 0.378. However, for a higher threshold of 5 mm/h, the model achieved an average CSI of 0.498, an F1 score of 0.577, and a MAE of 0.307. Furthermore, some models exhibited spatial smoothing issues with increasing rainfall-prediction times. The findings of this research hold promise for applications of societal importance, especially for preventing disasters due to extreme weather events.
1. Introduction
The frequency of sudden and localized heavy rainfall events is increasing due to climate change [1]. Radar-based nowcasting, which has higher accuracy than numerical forecasting models at short forecasts of less than 3 h, is valuable for obtaining early flood warnings. Generally, very short-term rainfall-prediction information is calculated through extrapolation and advection–based prediction techniques using radar. The Korea Meteorological Administration currently employs the McGill Algorithm for Precipitation Nowcasting by Lagrangian Extrapolation. However, because the agency has secured access to long-term radar observation data and established sufficient computing resources, rainfall prediction based on artificial intelligence deep learning (e.g., recurrent neural network, convolutional neural network (CNN), and convolutional long short-term memory (ConvLSTM)) using radar data has recently been expanding. Studies using ConvLSTM have been conducted in South Korea [2,3,4,5,6,7,8]. As mentioned in previous studies, CNN deep neural network-based nowcasting models tend to outperform extrapolation-based forecasts. However, as the forecast lead time increases, spatial smoothing becomes substantial, making it difficult to predict distinct, high-intensity precipitation features and distorting the small-scale weather phenomena that are important for improving forecast accuracy [3,6,8]. Additionally, existing methods based on deterministic forecasts of rainfall movement and locations over the entire precipitation field are limited in availability due to the difficulty of making consistent forecasts that consider spatio-temporal complexity. Therefore, probabilistic forecasts are known to have higher economic and decision-making value than deterministic forecasts [9,10,11]. Ravuri et al. (2021) developed a deep generative model of radar (DGMR) based on generative adversarial networks (GANs) for probabilistic radar for very-short-term rainfall prediction. DGMR can also be described as a statistical model that learns the probability distribution of data, and it can easily generate samples from the learned distribution. Moreover, training DGMR using UK Met Office radar data and performing forecasts with a lead time of 5–90 min improved accuracy was compared to PySTEPS, an existing rainfall prediction model, and U-Net, a CNN-based deep learning model.
In this study, we employed four deep learning models, each with a unique approach to rainfall prediction: RainNet, which specializes in precipitation prediction; ConvLSTM2D U-Net, which incorporates convolutional layers into traditional LSTM networks; a U-Net-based recursive model, which utilizes recursive prediction strategies; and a generative adversarial network, which is designed to generate realistic rainfall patterns. These models were individually applied and evaluated using Korean radar rainfall data by the Ministry of Environment for very-short-term forecasts of up to one hour. To ensure a balanced comparison, all four models were trained and assessed using the same dataset. Each deep learning model was applied to Korean radar rainfall data to evaluate its performance in very-short-term rainfall prediction (up to one hour in advance).
2. Materials and Methods
This study uses four kinds of deep learning-based nowcasting models. Table 1 provides a summary and comparison of the different network architectures. The details of each model are explained in each section.

Table 1.
Summary of deep learning–based nowcasting models.
2.1. RainNet
In this study, RainNet, a prediction model using a convolutional deep neural network with an existing U-Net structure, was used as the basic model [8]. RainNet has been used in Korea with radar data from the Korea Meteorological Administration, and its predictive applicability has been evaluated [6]. The neural network structure used in RainNet is based on U-Net and SegNet, which have encoder–decoder structures with skip connections between branches [13,14]. RainNet employs an encoder–decoder architecture in which the encoder progressively reduces the spatial resolution by utilizing pooling, then adds a convolutional layer. The decoder uses the upsampling method to gradually upscale the patterns in the trained image to a higher spatial resolution, and this image is followed by a convolutional layer. To ensure semantic connectivity between features across layers, it includes a skip connection from the encoder to the decoder, which is proposed to avoid the problem of gradient vanishing [15]. The model uses convolutional filters with sizes of up to 512 channels, along with kernel sizes of 1 × 1 and 3 × 3, and rectified linear unit activation functions for the convolutional layer, following the existing domestic RainNet studies [6,16].
As input, the RainNet model takes four sets of radar-generated gridded rainfall data (Observation at times T − 3, T − 2, T − 1, T), observed up to 30 min in the past at 10-min intervals at prediction time T. It performs a prediction (Predict T + 1) for the next 10 min and learns to minimize the error by comparing it with the observed radar-generated gridded rainfall data (Observation T + 1). Therefore, the pretrained model is optimized for a 10-min forecast.
To train RainNet, mean absolute error (MAE) was used as the loss function. Nadam (Nesterov-accelerated Adaptive Moment Estimation) was used to update the parameters, and the learning rates of the Nadam optimizer, beta_1, and beta_2 were set to 0.0001, 0.9, and 0.999, respectively. The training of the RainNet model was initially configured with 200 epochs and batch size 32, and the loss function was minimized at 26 epochs using early stopping. The RainNet in this study used the Keras framework, and training was performed on Dual GPU (NVIDIA RTX A6000).
2.2. ConvLSTM2D U-Net
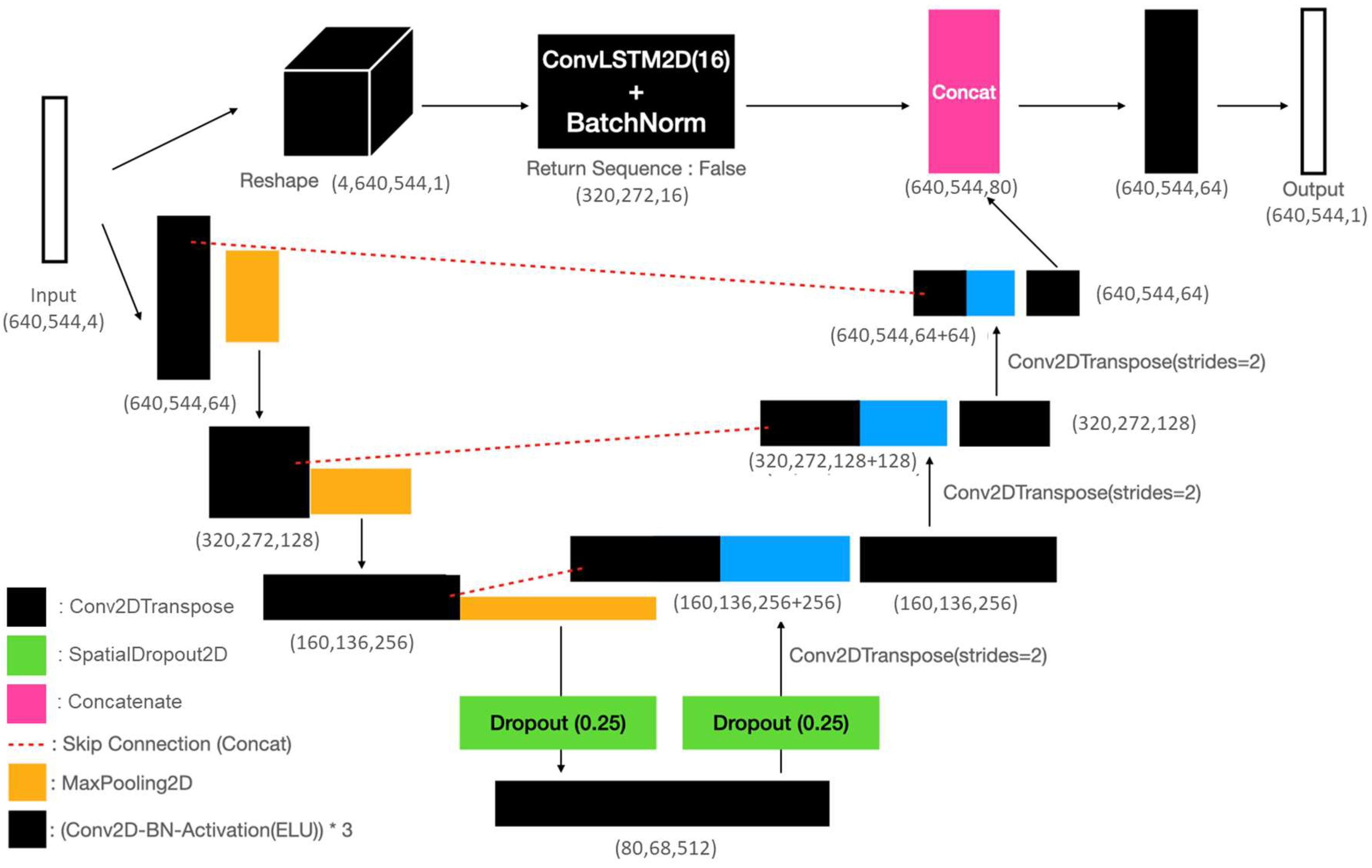
The ConvLSTM2D U-Net model integrates the U-Net architecture with the ConvLSTM2D structure to predict rainfall by considering the temporal continuity of radar image data [7]. In this context, the U-Net comprises contracting pathways for capturing global image features and expanding pathways for precise localization, thereby forming a symmetrical U-shaped network. The ConvLSTM2D structure is characterized by its ability to capture spatiotemporal correlations and includes convolutional layers in input-to-state and state-to-state transitions. The model’s architecture is depicted in Figure 1. The rationale for incorporating ConvLSTM2D into the U-Net structure lies in the similarity between the computation of filters in the convolution and dense layers, which may obscure the temporal order of the time series. Furthermore, in a change from the original RainNet, we opted to use Conv2DTranspose instead of an upsampling layer. Conv2Dtranspose performs a convolutional operation with a trained filter to enhance resolution, as opposed to traditional upsampling layers, which interpolate lower-resolution data. Additionally, we employed SpatialDropout2D at dropout locations during the training of RainNet. SpatialDropout2D is capable of excluding entire two-dimensional feature maps, aiding in the prevention of overfitting. The activation function used during training was the exponential linear unit. Notably, a linear bottleneck structure was implemented for filters 256 and 512 to reduce the number of parameters. This bottleneck structure reduces dimensionality using a 1 × 1 convolution, increases dimensionality using a 3 × 3 convolution, and deepens dimensionality once more with a final 1 × 1 convolution layer. This design effectively reduces computational complexity. The ConvLSTM2D U-Net takes four radar-generated gridded rainfall data as input, observed up to 30 min in the past at 10-min intervals. It performs a prediction (Predict T + 1) for the next 10 min.
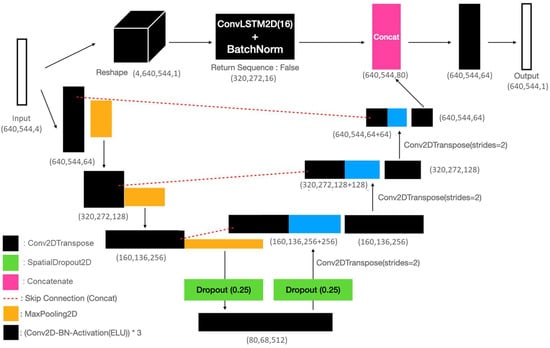
Figure 1.
ConvLSTM2D U-Net architecture [7].
In the optimization of ConvLSTM2D U-Net, the MAE served as the loss function. Parameter updates were conducted via the Adam optimizer, utilizing a learning rate of 1 × 10−4; the remaining parameters adhered to default settings, as suggested by Kingma and Ba (2015) [17]. The training of the ConvLSTM2D U-Net model was initially configured with 1000 epochs and a batch size of 2, using early stopping to obtain the best model at the 20th epoch.
2.3. Generative Adversarial Network
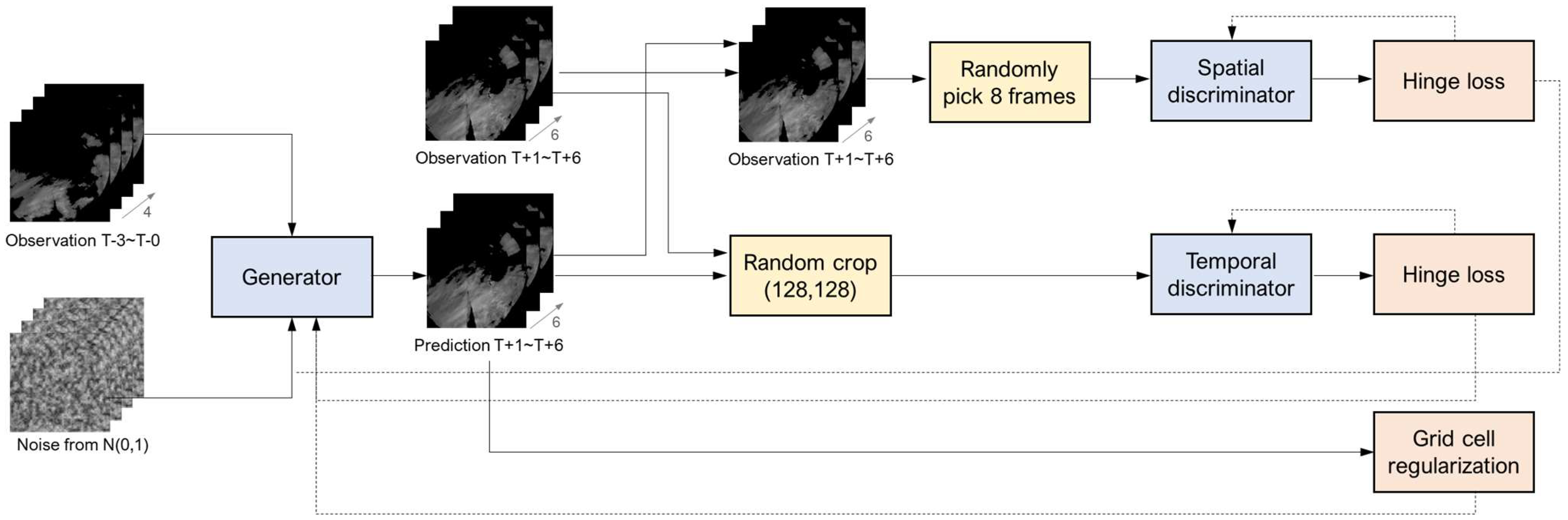
Additionally, this study employed a nowcasting technique utilizing a GAN. A GAN comprises two neural networks, a generator and a discriminator, which engage in adversarial competition to learn. GANs enable the learning of data probability distributions and facilitate the generation of samples from the learned distribution. Particularly, in this study, the Deep Generative Model for Rainfall (DGMR) is based on a conditional adversarial generative neural network, known as a conditional GAN (cGAN). A cGAN conditions the generator and discriminator with additional information during training, allowing the introduction of specific conditions to generate the desired data artificially. In the case of DGMR, it conditions the observed rainfall information at the time of prediction, thereby generating random noise resembling the predicted rainfall field [10]. As shown in Figure 2, DGMR comprises a generator, two discriminators, and their respective blocks, and the learning process of the model can be described as follows.
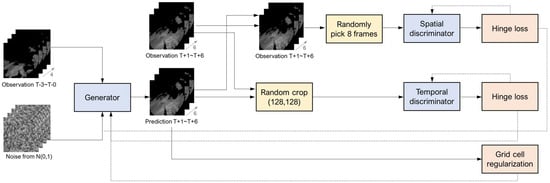
Figure 2.
Modified DGMR overview [10].
First, radar rainfall fields from the past 40 min at 10-min intervals serve as context vectors in the generator, which is trained with two loss functions and one weight regularization. The generator takes a context vector and produces an image. Eight frames are randomly selected from this image and used to calculate a loss value when compared to real data. The generator’s role includes transforming the input randomized noise vector into information intended to match patterns in actual images. To achieve the goal of generating images indistinguishable from real radar images, it undergoes adversarial training with a discriminator, which is responsible for evaluating the realism of the generated images. The spatial discriminator, structured as a CNN, focuses on distinguishing between observed and generated radar rainfall fields, thereby ensuring spatial consistency and reducing ambiguous predictions. Meanwhile, with randomized inputs of generated images, the temporal discriminator distinguishes observed from generated radar sequences to ensure temporal consistency and reduce erratic predictions stemming from overfitting or instability.
Additionally, grid-cell regularization was applied to the observed and model-generated mean values to enhance accuracy. This regularization introduces a term penalizing differences between the two, facilitating accurate predictions based on location. Moreover, the generative neural network model is inherently probabilistic and capable of simulating multiple data generations using conditional probability distributions of input radar information. The resulting approach resembles an ensemble technique. Furthermore, DGMR has the advantage of learning from observational data and representing uncertainty across various spatiotemporal scales. However, its performance deteriorates rapidly for convective cell forecasts or forecasts extending beyond 90 min, primarily due to the challenges associated with predicting physical properties related to rainfall development and dissipation [10,18].
DGMR was trained with up to 5 × 105 generator steps, as suggested by Ravuri et al. (2021). Two discriminator steps were performed for each generator step. The learning rate of the generator is 5 × 10−5, and the learning rate of the discriminator is 2 × 10−4. The Adam optimizer was used, and β1 and β2 were set to 0.0 and 0.999, respectively. Moreover, the scaling parameter for grid-cell normalization was set to λ = 20. DGMR used the PyTorch framework (https://pytorch.org, accessed on 30 October 2023). DGMR stopped learning at epoch 130 because the model was optimized. Specifically, in the case of GAN, it is difficult to determine whether it is optimized simply based on loss; hence, we checked the rainfall-prediction image generated by the learned model and whether mode collapse occurred to assess optimization. Furthermore, the GAN model was trained for a 60-min lead time to maintain consistency with the other algorithms.
2.4. Recursive RainNet
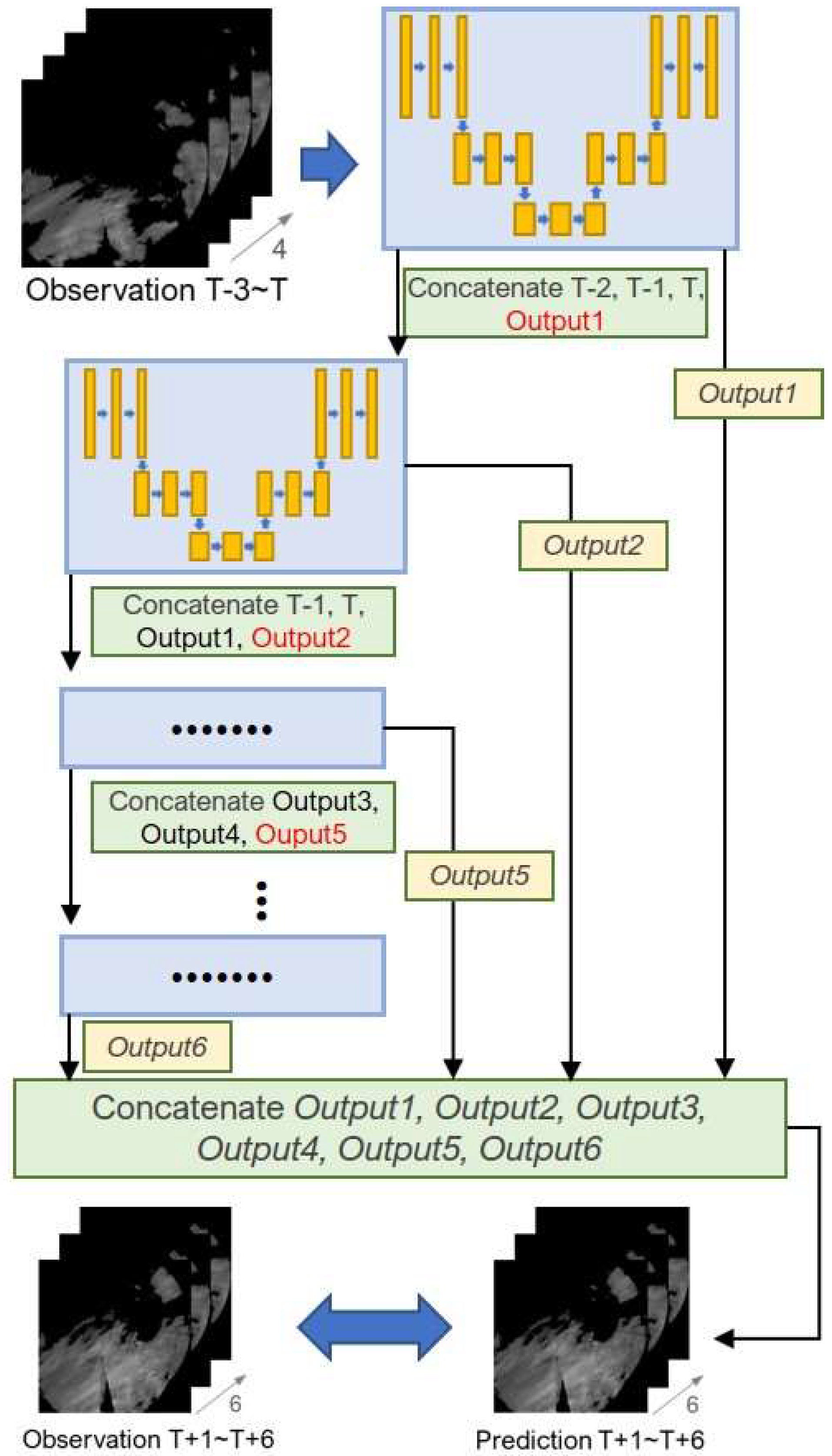
Recursive RainNet (RainNet-REC) employs a model that is pretrained using the existing 10-min forecast to mitigate error accumulation and the smoothing effects that typically occur during iterative forecasting. This approach uses the U-Net network to implement a recursive prediction strategy (Figure 3) [12]. The forecasting process is as follows. Initially, four radar-generated gridded rainfall datasets recorded at 10-min intervals (Observation T − 3, T − 2, T − 1, and T) and observed up to 30 min in the past serve as inputs at the simulation time (T). These inputs are processed through the established RainNet model structure to generate a 10-min forecast of radar rainfall data (Output1). Subsequently, the forecast time advances by another 10 min and Output1 is concatenated with observed rainfall data (Observation T − 2, T − 1, T) to create input data for the subsequent forecast. This iterative process continues until rainfall forecasts for the next 10–60 min are obtained. To refine the model, each hourly prediction result (Output1, Output2, ..., Output6) is compared with the observed radar-generated gridded rainfall (Observation T + 1–T + 6) to calculate errors. Training is then conducted to minimize these errors. Consequently, the pretrained model is optimized for 10-min and 60-min forecasts. For recursive RainNet model training, MAE was used as the loss function and the learning rate of the Nadam optimizer, beta_1, and beta_2 were set to 0.0001, 0.9, and 0.999, respectively. Training was performed for 200 epochs and batch size of 8, and the loss function value was minimized at 133 epochs. While RainNet and RainNet-REC fundamentally share identical network architectures, their differences in performance and number of parameters can be attributed to variations in training objectives, prediction strategies, and architectural configurations. Specifically, RainNet is optimized for a short 10-min forecast. In contrast, RainNet-REC essentially stacks 6 RainNet models and optimizes the parameters for each of these 6 models individually, which explains the greater number of total parameters. Each of these stacked models in RainNet-REC employs a more complex recurrent prediction approach spanning up to 60 min. The temporal dependency of the model during training is a crucial factor affecting prediction accuracy. Furthermore, divergent weight configurations between the two models suggest that RainNet-REC may have navigated a more favorable optimization landscape during training. RainNet, trained on a narrower dataset for 10-min predictions, overfits to its training data, thereby compromising its ability to generalize effectively.
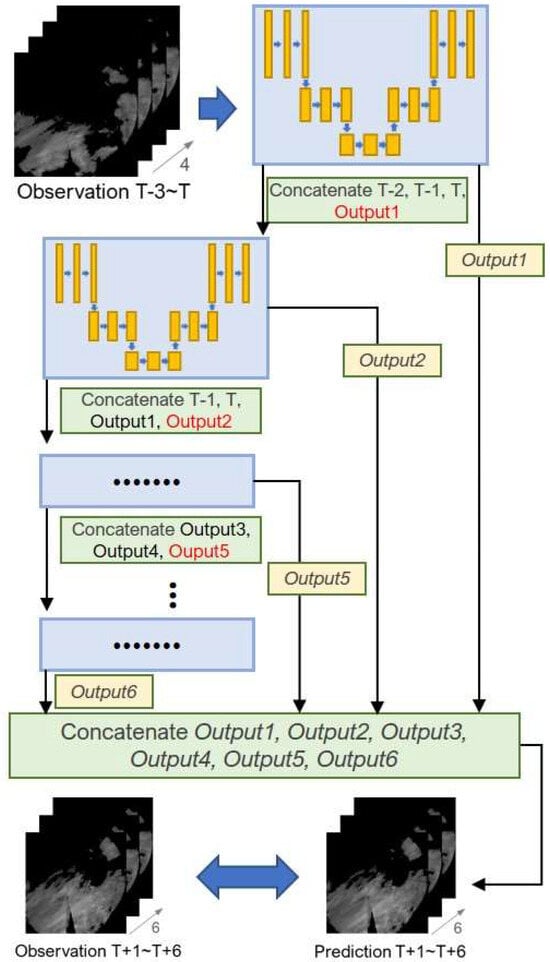
Figure 3.
Recursive RainNet architecture [12].
3. Applications
3.1. Data
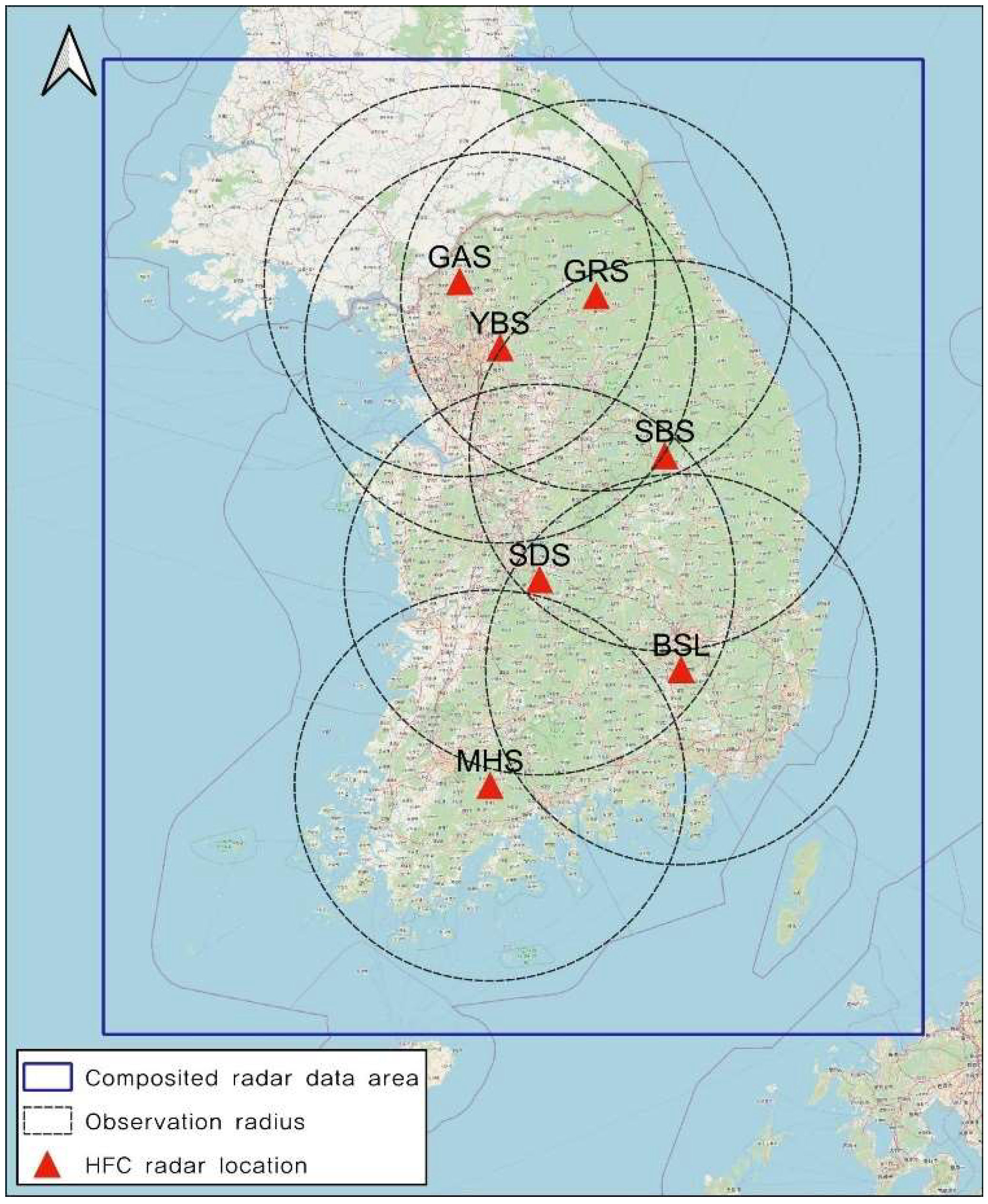
This study focused on developing and evaluating a deep learning-based rainfall prediction model using two-dimensional gridded rainfall data obtained from the S-band rain radar network operated by the Ministry of Environment (Figure 4). The Ministry of Environment oversees the operation of several radar installations, including the Biseulsan Mountain (BSL), Sobaeksan Mountain (SBS), Mohusan Mountain (MHS), Seodaesan Mountain (SDS), Garisan Mountain (GRS), Yebongsan Mountain (YBS), and Gamaksan Mountain (GAS) radar systems. These radar systems play a crucial role in monitoring near-surface rainfall within a 125-km observation radius and are instrumental in flood forecasting. For this study, nationally synthesized gridded radar rainfall data (quantitative precipitation estimates) were utilized, combining data from six radar sources and excluding the Gamaksan radar system, which commenced operations in June 2022. The grid coverage area is represented by the blue square in Figure 4. The dataset spans 274 days, focusing on heavy rainfall events occurring between 2018 and 2021. To enhance the accuracy of rainfall predictions, a conditional merging technique that considers altitude effects was applied to generate quantitative precipitation estimates (QPEs) [19]. This process involved incorporating data from 604 ground rain gauge stations. The QPE dataset generated has a grid size of 525 × 625 and offers a spatiotemporal resolution of 1 km every 10 min. Rainfall data are in mm/h. From the training data, 17,200 samples were allocated for training the model, while an additional 2149 samples were designated for validation. The remaining 2147 samples were excluded from the evaluation phase. The radar data were stored using a multidimensional array library (NumPy) data structure.
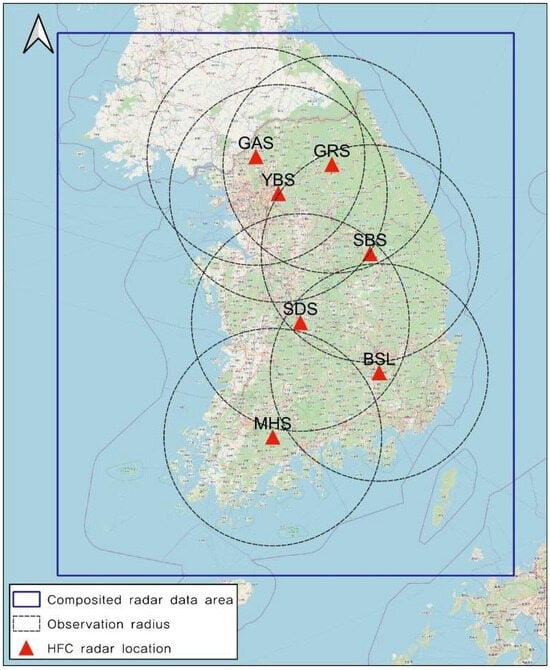
Figure 4.
S-band Rain radar network of Ministry of Environment, Korea.
3.2. Forecasted Rainfall Using Pretrained Models
The deep learning models used in this study to generate rainfall forecasts were initially pretrained using the QPE data, as described in Section 3.1.
To assess and present the accuracy of rainfall predictions, five heavy-rain events from the dataset that were excluded from model training and testing were selected, as depicted in Table 2. These selected rainfall events exhibited diverse characteristics, including heavy rainfall associated with cyclones, rain fronts, and typhoons in 2021. The very-short-term forecasting models investigated in this study are of significant relevance to flood prediction. To assess their performance, we strategically chose five cases that encapsulate a diverse spectrum of meteorological conditions. Notably, our selection was guided by the objective to cover both typical and extreme rainfall scenarios known to trigger flooding events in South Korea.

Table 2.
Characteristics of the evaluated events.
Using the deep learning models trained on the selected rain events, rainfall predictions were generated at 10-min intervals, covering a period from 10 min before the onset of rainfall to 180 min into the event. Notably, the existing RainNet and ConvLSTM2D U-Net models were originally designed for 10-min forecasts, resulting in the production of six forecast data points through a recursive inference process. Conversely, RainNet-REC employs a model structure in which DGMR takes four forecast data points from the previous 30 min as input and generates 18 rainfall predictions without relying on a recursive inference process.
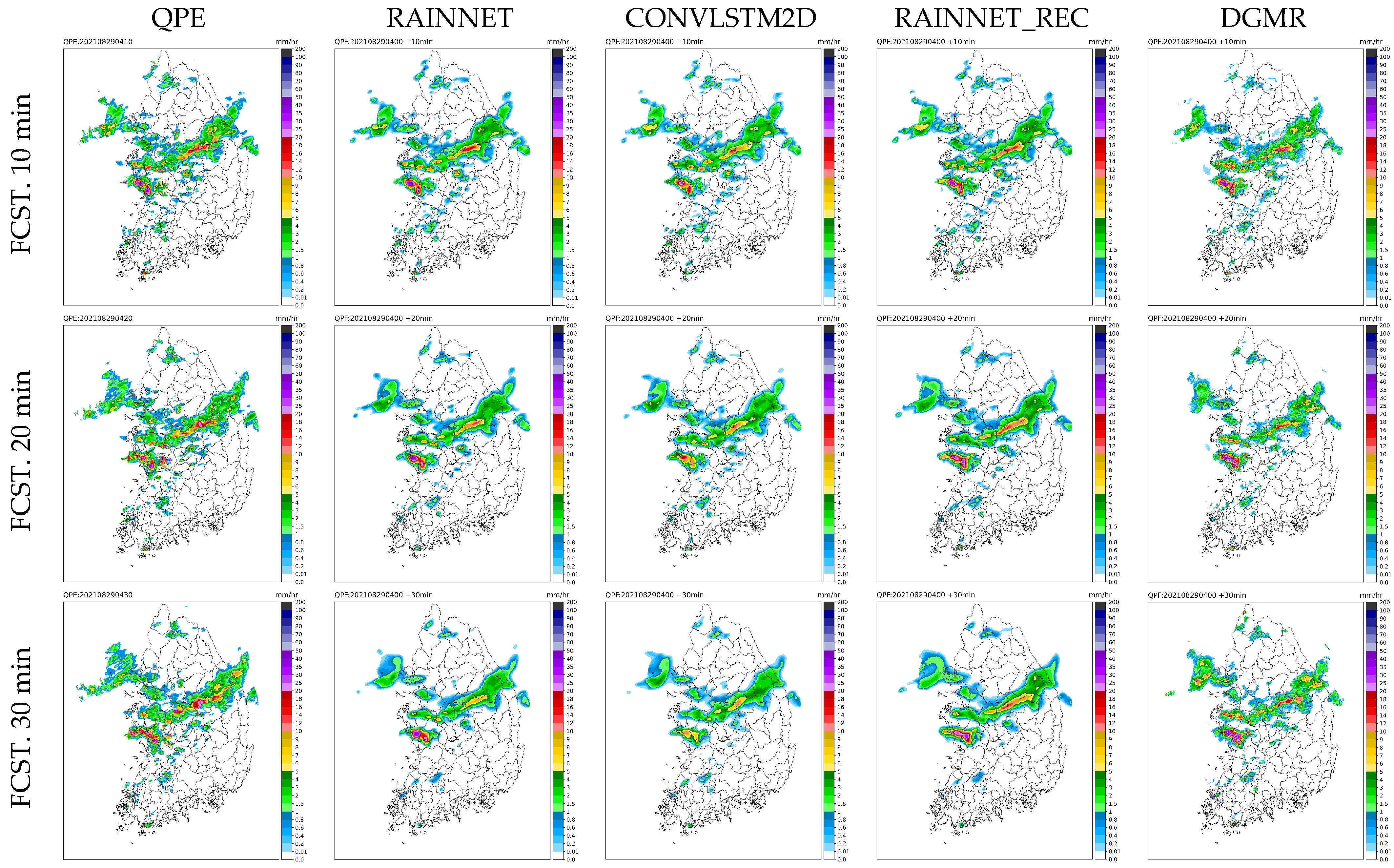
A schematic analysis was conducted for three selected heavy-rain events (Event 2, Event 4, and Event 5). Figure 5 represents the results observed at 10:10 on 21 August 2021. This particular instance of heavy rainfall was triggered by rain clouds originating from a robust low-pressure system, which resulted in widespread rainfall across the country, with the most intense rainfall concentrated in the central region of South Korea. The temporal evolution of observed rainfall patterns reveals that the area with heavy rainfall, primarily centered on the central region, continued to experience sustained precipitation. Initial results from rainfall estimation indicate the spatial distribution from QPE, and the four forecasting techniques showed minimal divergence during the first 10 min of the forecast. However, as the forecasting period grew longer, it became apparent that RainNet predictions tended to exhibit spatial smoothing. This smoothing effect implies that RainNet struggled to accurately forecast the persistence of heavy rainfall in the central region. However, while it did show some geographical differences, RainNet-REC yielded an accurate representation of areas with intense rainfall, successfully predicting sustained heavy rainfall. ConvLSTM2D U-Net forecasts indicated continued heavy rainfall in the central part of the country while showing reduced rainfall in other areas. DGMR predictions suggested an escalation in rainfall intensity as the rainfall area expanded.
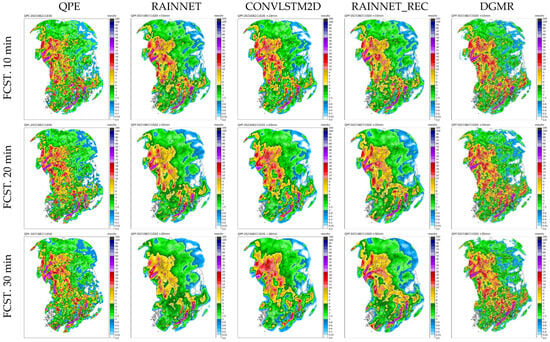
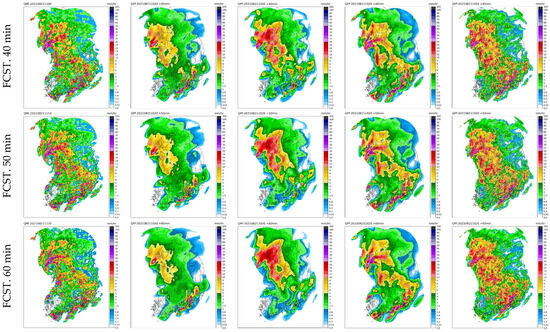
Figure 5.
Forecasted radar rainfall distributions for lead times from 10 to 60 min (predicted at 10:20 on 21 August 2021).
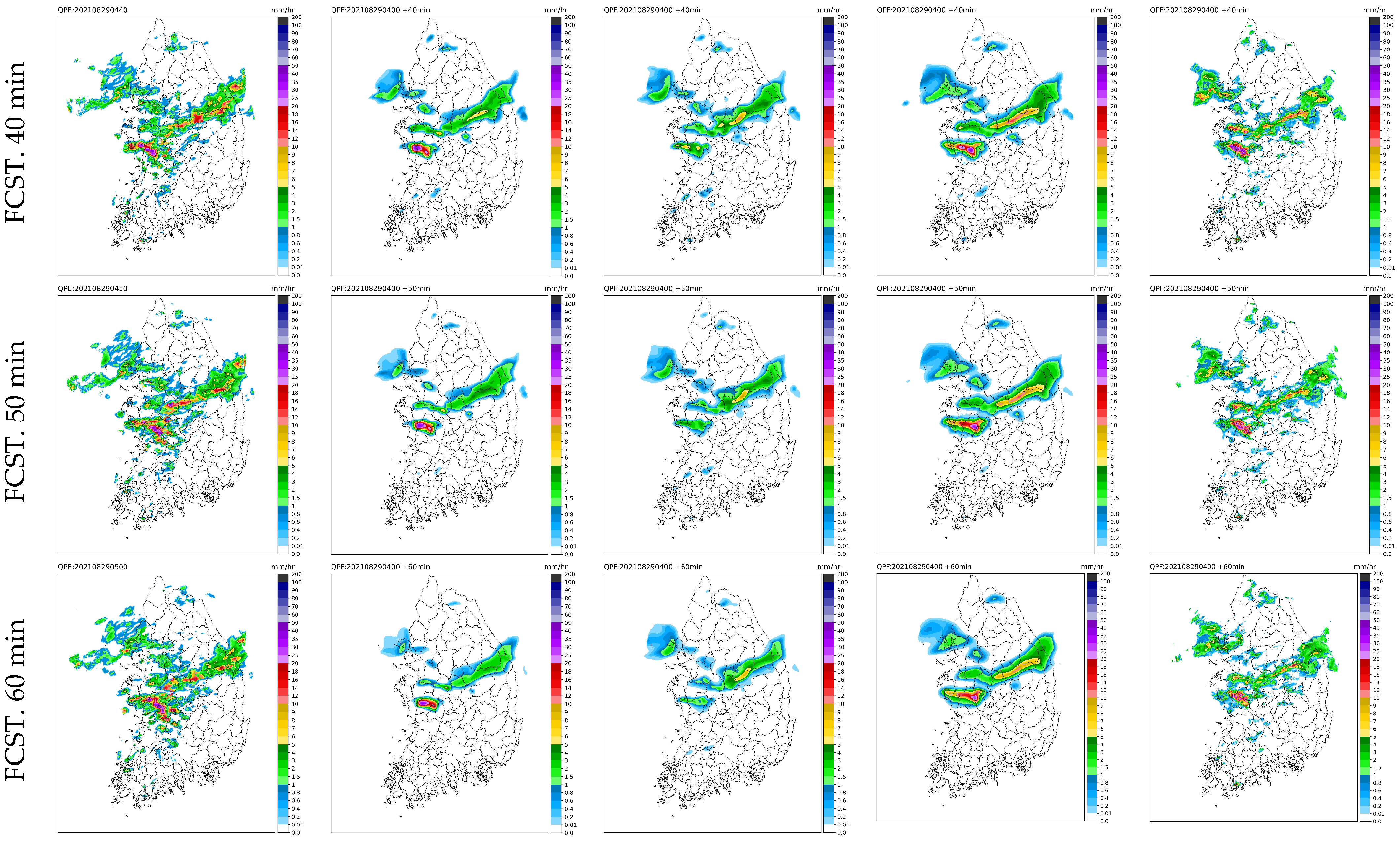
Figure 6 illustrates the results obtained at 03:20 on 29 August 2021, which corresponds to an instance of heavy rainfall influenced by a stagnant front. The spatial distribution of observed rainfall revealed that precipitation intensified over time, resulting in a wider coverage of rainfall events. During the first 60 min of rainfall prediction, DGMR yielded predictions with characteristics closely resembling those of the observed rainfall, including similar rainfall intensity. In contrast, ConvLSTM2D U-Net predicted that the rain front would remain stationary and that the rainfall would weaken in intensity, while RainNet predictions indicated a decrease in rainfall intensity and a reduction in rainfall coverage. Meanwhile, RainNet-REC forecasted a trend toward stronger rainfall intensities, with a persisting broad rain front.
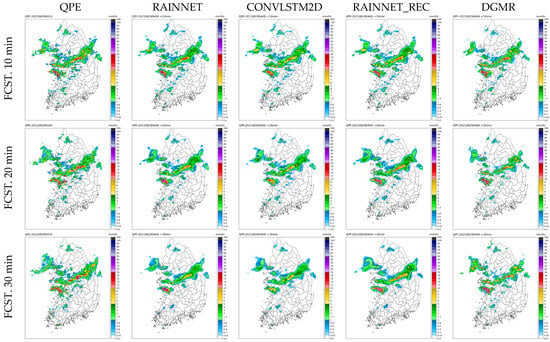
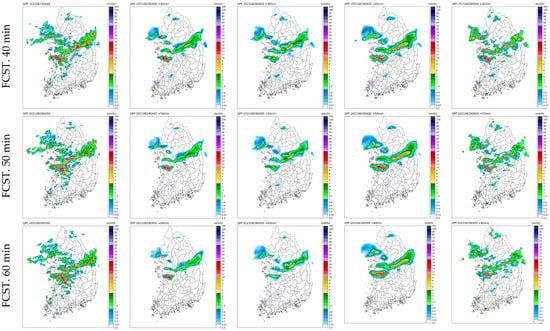
Figure 6.
Forecasted radar rainfall distributions for lead times from 10 to 60 min (predicted at 04:00 on 29 August 2021).
Figure 7 displays the outcomes observed at 16:40 on 31 August 2021, exemplifying a scenario characterized by the arrival of a robust rain cloud from the west, which leads to intense rainfall in the central part of the country. Over time, the rainfall intensity gradually diminished and rainfall shifted toward the east. However, three hours later, a resurgence of heavy rainfall occurred in the West Sea region. During this period, RainNet predicted no change in rainfall intensity, while ConvLSTM2D U-Net predicted a reduction in the overall rainfall area and the DGMR’s rainfall forecast suggested that precipitation would continue to increase.
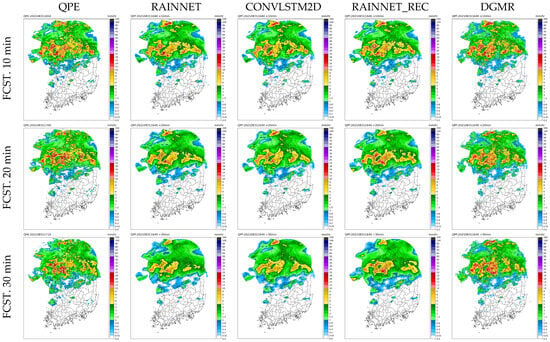
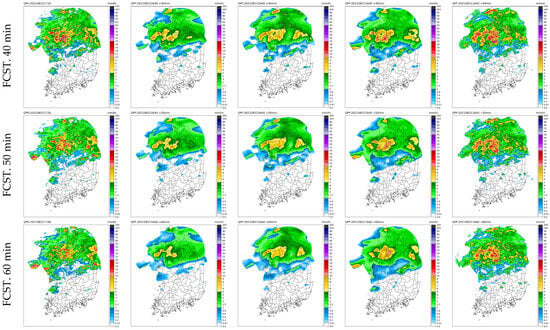
Figure 7.
Forecasted radar rainfall distributions for lead times from 10 to 60 min (predicted at 16:40 on 31 August 2021).
Overall, the schematic analysis of predicted rainfall distributions reaffirms certain characteristics of the models. RainNet, as noted in previous studies (refer to references), exhibits a notable smoothing tendency and struggles to predict high-intensity and distinct precipitation features. In contrast, ConvLSTM2D U-Net tends to yield a smaller overall rainfall area in its predictions. The predictions of DGMR generally align well with the observed rainfall distribution, but in instances of widespread heavy rainfall, DGMR tends to predict ongoing increases in rainfall. This behavior stems from the nature of GAN models, which are trained to generate outputs resembling the probability distribution of the input data. Consequently, if the trends in input data show a continuous increase, the model will predict a similar trend. RainNet-REC stands out in predicting the intensification of rainfall more effectively than other techniques, owing to its ability to mitigate smoothing through its recursive approach. In this study, the Structural Similarity Index (SSIM) is calculated and presented in the Results section to quantify the smoothing effect of each deep learning model of QPF (Quantitative Precipitation Forecasts).
4. Results
In this section, we conduct an evaluation of the predicted rainfall using four metrics, namely critical success index (CSI), MAE, F1 score, and SSIM. The CSI is calculated by counting the number of grid points where predictions and observations closely match for rainfall exceeding a specified threshold, as defined in Equation (1). This count is then divided by the total number of cases involving precipitation events. To calculate the CSI, we employ a rain contingency table, which serves as a matrix indicating the presence or absence of predicted and observed rainfall.
The MAE quantifies the disparity between predicted and observed rainfall, as depicted in Equation (2). Finally, the F1 score is employed. This metric combines precision and recall by computing their harmonic mean. Maximizing the F1 score implies optimizing precision and recall simultaneously.
SSIM is a perception-based metric that considers luminance, contrast, and structure to compare two images, making it ideal for evaluating the quality of our precipitation forecast maps.
True Positive (TP) is the number of samples correctly predicted as “positive.” False Positive is the number of samples wrongly predicted as “positive.” True Negative is the number of samples correctly predicted as negative. Furthermore, nowi and obsi are the predicted and observed rainfall intensities (mm/h) at location i, and n is the number of radar grids. The threshold rainfall intensity was 0.1 mm/h for overall rainfall and 5 mm/h to evaluate the difference from deep learning models for predicting heavy rainfall. Here, and are the two images (QPE and QPF) being compared and and are the averages of images and respectively. Additionally, and are the variances of and and is the covariance of and Additionally, C1, and C2 are two variables to stabilize the division with a weak denominator [20].
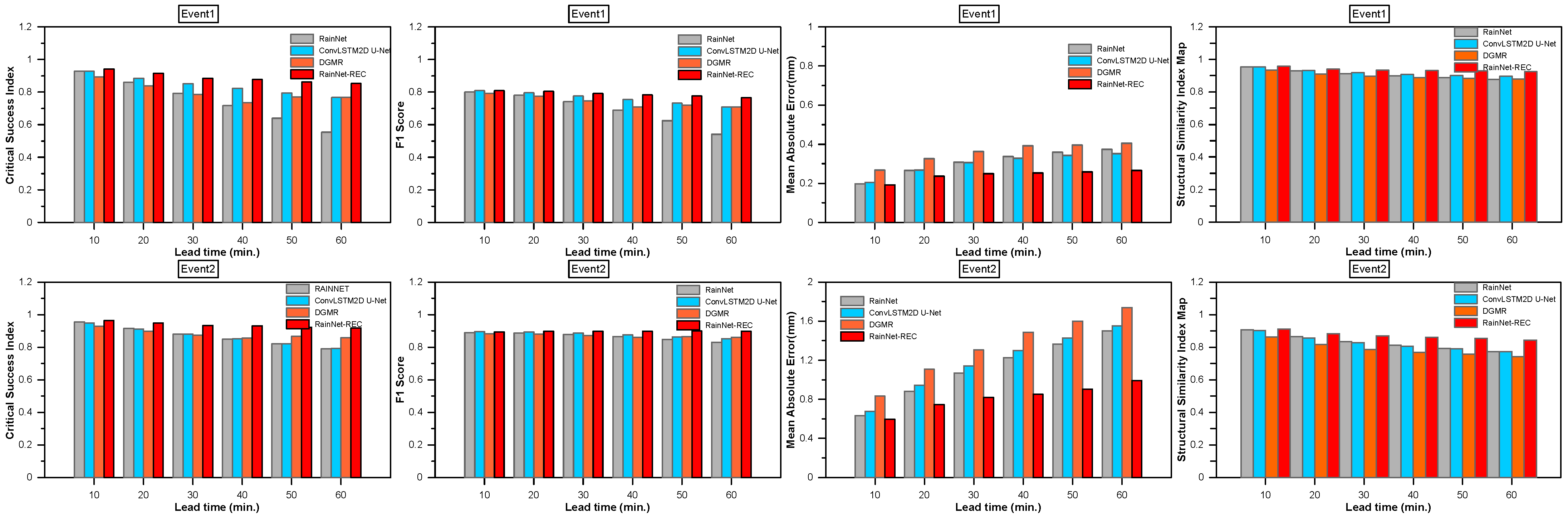
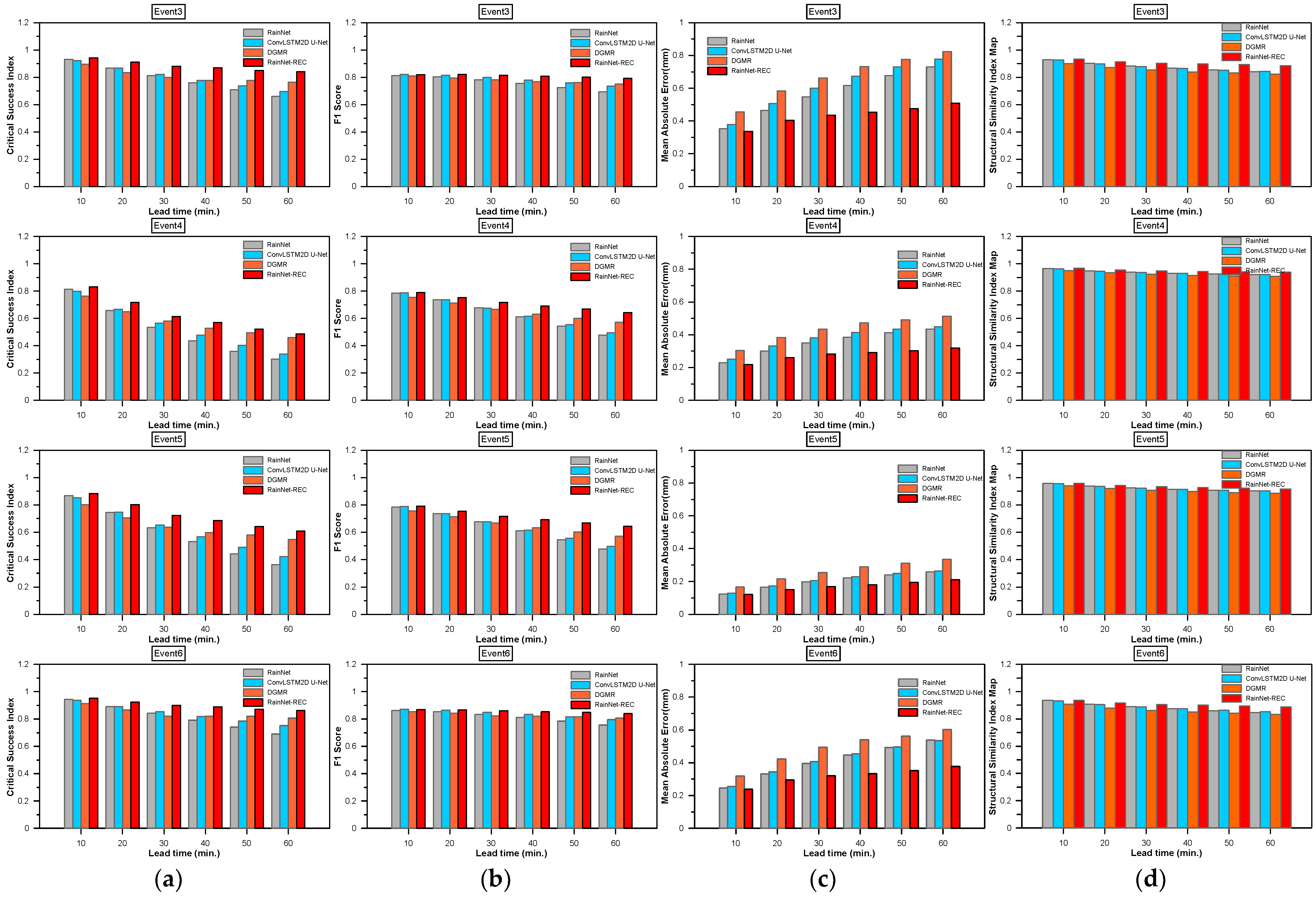
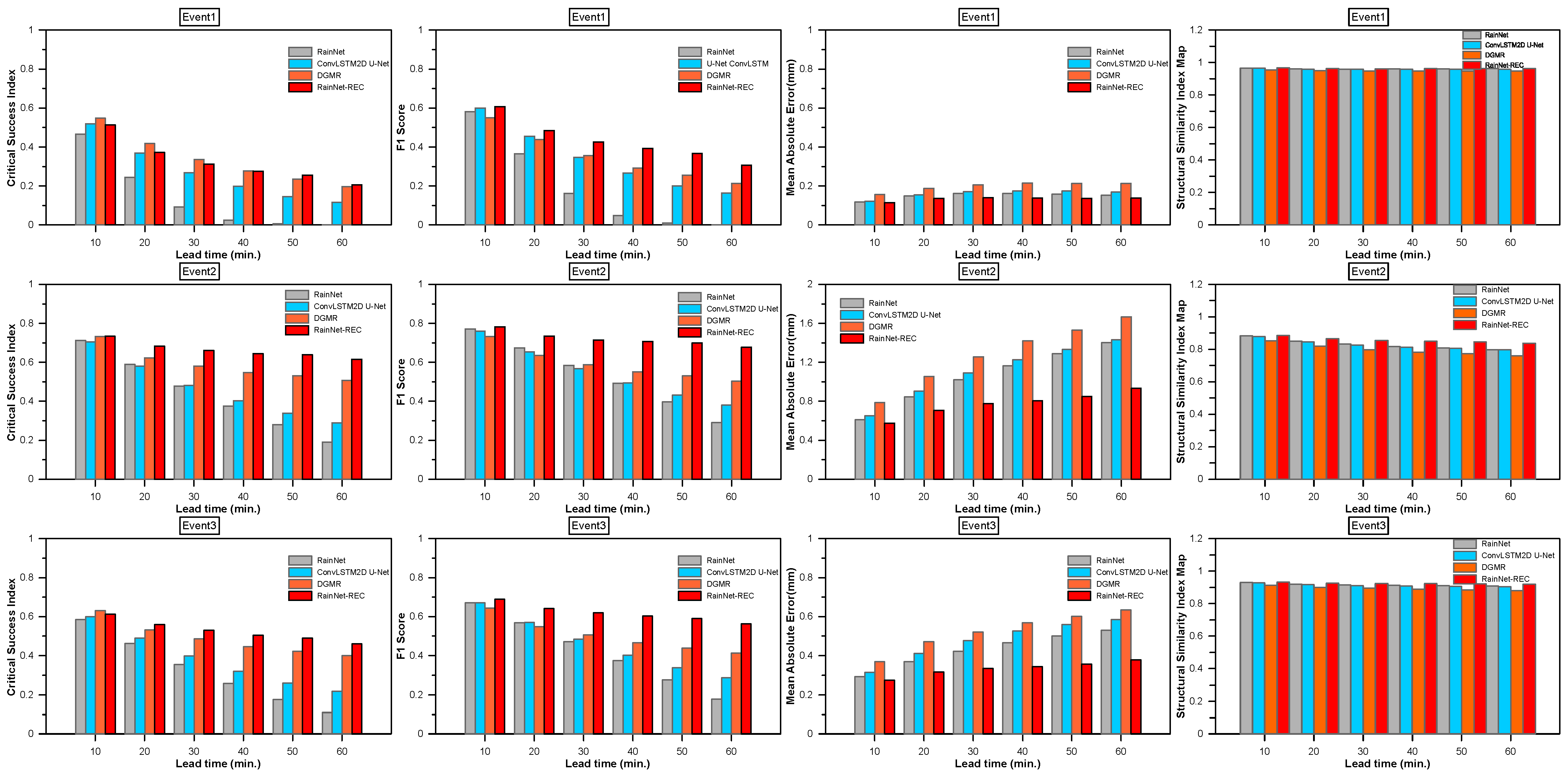
Figure 8 displays the CSI, F1 score, and MAE of each method’s rainfall-forecast output based on radar-observed rainfall for each heavy-rainfall case, categorized by forecast lead time and with a threshold rainfall of 0.1 mm/h. As the lead time increases, variations in performance among the different rainfall prediction methods become more apparent. In terms of CSI, RainNet-REC consistently demonstrated superior performance across all heavy-rainfall cases. DGMR also exhibited higher accuracy compared to RainNet and ConvLSTM2D U-Net. F1 scores exhibited minimal variation among the prediction techniques. Notably, DGMR yielded a considerably greater MAE compared to the other predictors. SSIM did not show a noticeable difference for each model, but RainNet-REC showed the highest value. Figure 9 presents the rainfall-prediction results for each method using a threshold rainfall of 5 mm/h. The deviations from the 0.1 mm/h threshold are evident, particularly highlighting the strong prediction performance of RainNet-REC and DGMR in terms of CSI and F1 score, as they effectively forecasted regions of heavy rainfall. However, DGMR’s MAE was higher than that of other models due to its tendency to predict continuous increases in rainfall events. In the evaluation relative to the threshold value of 5 mm/h, there was no significant difference in SSIM by technique. Although DGMR’s rainfall forecasts offer visually convincing renderings, the SSIM of DGMR scores lower than compared to those of the other deep learning approaches. This outcome is posited to stem from DGMR’s unique method of generating forecasts, which relies on a probability distribution resembling that of the input data. While this approach minimizes smoothing effects, it results in a forecasted rainfall distribution that deviates to some extent from the observed patterns.
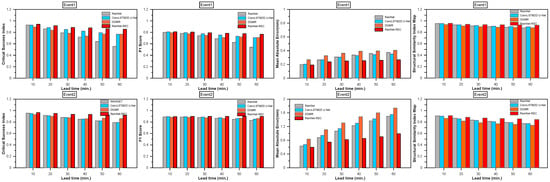
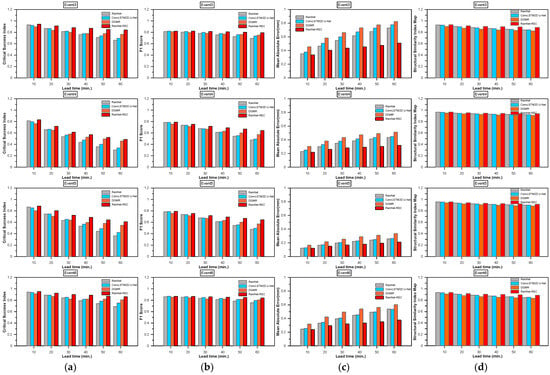
Figure 8.
Forecasted radar rainfall accuracy of lead time for rain events threshold 0.1 mm/h. (a) Critical success index. (b) F1 score. (c) MAE. (d) SSIM.
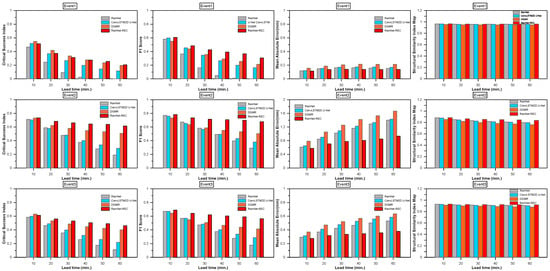
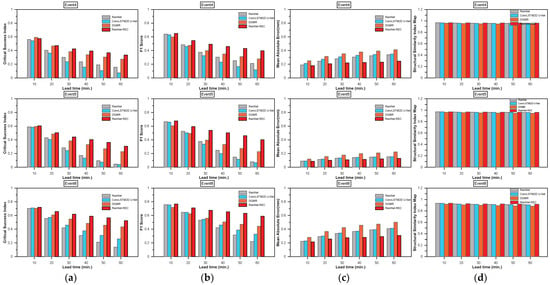
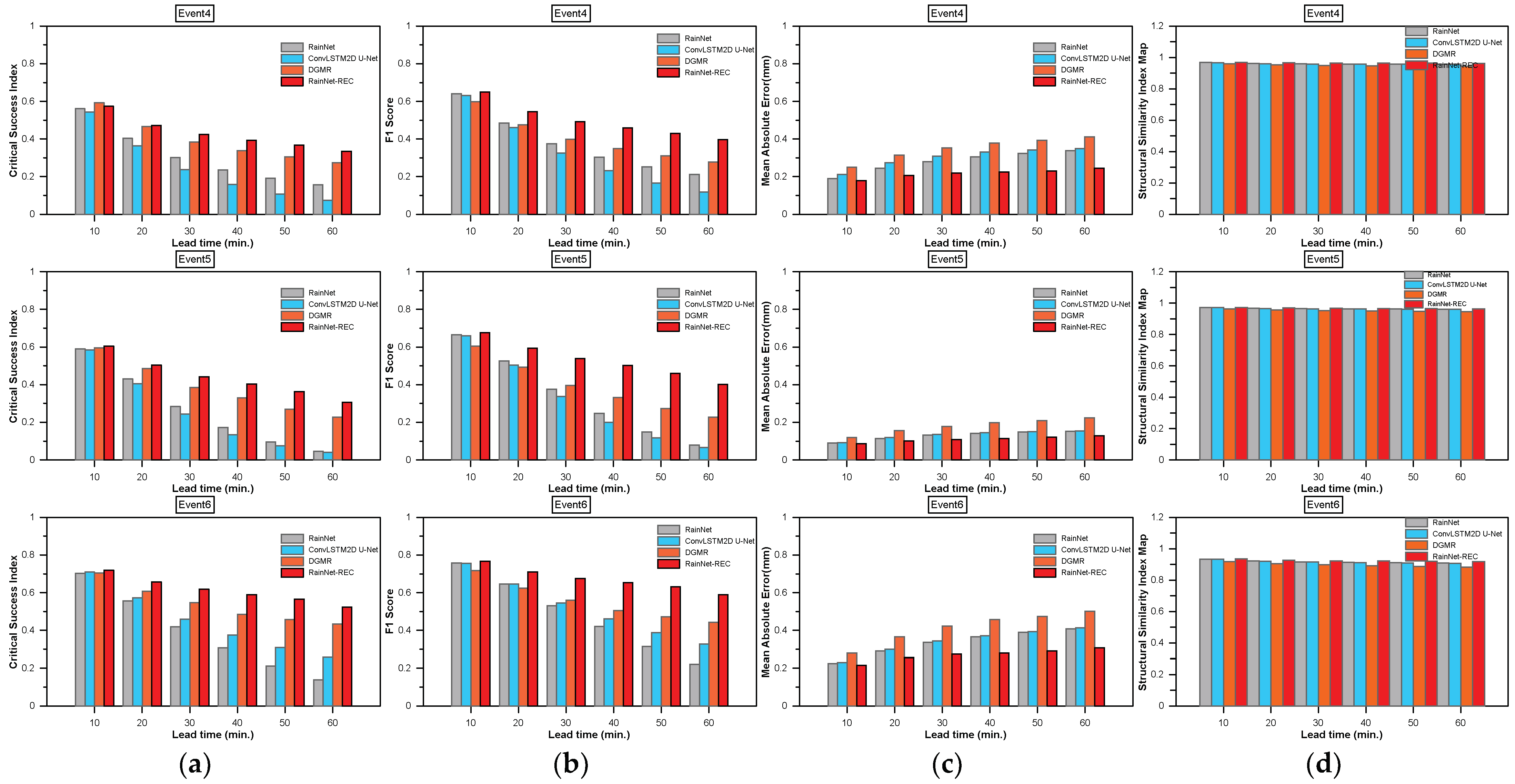
Figure 9.
Forecasted radar rainfall accuracy of lead time for rain events at a threshold of 5 mm/h. (a) Critical success index. (b) F1 score. (c) MAE. (d) SSIM.
Table 3 and Table 4 present average evaluation results for the prediction accuracy of heavy-rainfall cases with critical rainfall thresholds of 0.1 mm/h and 5 mm/h, respectively.

Table 3.
Evaluation of forecasted radar rainfall for rain events (threshold 0.1 mm/h).

Table 4.
Evaluation of forecasted radar rainfall for rain events (threshold 5 mm/h).
For the 0.1 mm/h threshold, RainNet’s performance metrics, such as CSI, fluctuated between a maximum of 0.907 at the 10-min lead time and a minimum of 0.560 at the one-hour forecast. RainNet-REC consistently showed superior results, with the highest CSI being 0.920 and the lowest being 0.762 across the specified lead times. As shown in Table 3, RainNet-REC consistently achieves the highest SSIM values across all lead times, with values ranging from 10 to 60 min. This result indicates that RainNet-REC is does well at preserving structural details in the forecasted rainfall patterns, thereby confirming its effectiveness in mitigating the smoothing effect, as mentioned earlier.
In evaluation at the 5 mm/h threshold, RainNet’s CSI varied from a peak of 0.603 at the 10-min lead time to a low of 0.107 at the 60-min mark. Thus, RainNet-REC demonstrated exceptional performance, with a highest CSI of 0.626 and a lowest CSI of 0.408 across the timespans.
The results from four models, namely RainNet, ConvLSTM2D U-Net, DGMR, and RainNet-REC, were analyzed for success in forecasting radar rainfall at lead times ranging from 10 to 60 min. In the short-term forecasting window of 10–30 min, RainNet-REC emerged as the top performer, excelling in CSI and F1 score, while DGMR lagged, as it had the highest MAE, indicating lower accuracy in predicting rainfall amounts. As we extended our analysis to medium-term lead times (between 40 and 60 min), RainNet-REC continued to dominate, although its performance slightly deteriorated with increasing lead time—a trend observed across all models. DGMR consistently exhibited the least precision, as evidenced by its consistently high MAE values. In summary, RainNet-REC consistently outperformed all other models across all evaluated metrics and timeframes, closely followed by ConvLSTM2D U-Net, which could be considered a viable alternative. RainNet performed well at shorter lead times but faced challenges at longer intervals. Additionally, DGMR consistently underperformed across all metrics and lead times, making it the less-recommended option. Therefore, for those seeking a model with superior accuracy and precision across various forecasting times, RainNet-REC is the most advisable choice.
5. Conclusions
This study utilized Korean radar rainfall data and applied various deep learning algorithms for very short-term rainfall predictions, up to 1 h in advance. The algorithms included CNN-based U-Net, ConvLSTM for considering temporal continuity, a recursive model based on U-Net with a recursive strategy, and a GAN-based model. The input radar rainfall was estimated using a conditional merging technique. The study evaluated the prediction performance of each technique for different rainfall events, presenting results based on metrics such as CSI, F1 score, MAE, and SSIM. Two rainfall-intensity thresholds, 0.1 mm/h and 5 mm/h, were used during the evaluation of various models for forecasting radar rainfall across different lead times.
For lower-intensity rainfall (0.1 mm/h), RainNet’s CSI scores varied widely, ranging from 0.907 to 0.560 depending on the forecast lead time. In contrast, RainNet-REC consistently outperformed other models, with CSI scores ranging from 0.762 to 0.920. RainNet-REC also excelled in preserving structural details in rainfall patterns, as indicated by its consistently high SSIM values. Although its performance declined slightly with increasing forecast times, it remained superior to other models such as RainNet, ConvLSTM2D U-Net, and DGMR.
For higher-intensity rainfall (5 mm/h), RainNet-REC outperformed other models like RainNet, ConvLSTM2D U-Net, and DGMR across various lead times. It performed exceptionally well in short-term predictions (10–30 min) and remained robust even in the medium term (40–60 min), though with a slight decline in performance. In these cases, DGMR yielded high CSI values, thereby demonstrating improved rainfall field-prediction capabilities compared to its own lower-intensity performance. Conversely, RainNet-REC continued to demonstrate high forecast accuracy, as evidenced by its low MAE values.
Overall, this study offers valuable insights into the effectiveness of deep learning algorithms for very-short-term weather forecasting using Korean radar data. Specifically, the recursive RainNet-REC model achieved high scores in predicting short-term rainfall up to 1 h in advance, highlighting its potential utility in disaster management.
Author Contributions
Conceptualization, S.-S.Y. and H.S.; methodology, S.-S.Y. and H.S.; software, S.-S.Y.; formal analysis, S.-S.Y. and K.-B.C.; investigation, S.-S.Y. and H.S.; resources, S.-S.Y. and J.-Y.H.; data curation, J.-Y.H.; writing—original draft preparation, S.-S.Y.; writing—review and editing, S.-S.Y., H.S. and K.-B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by KOREA HYDRO & NUCLEAR POWER CO., LTD, grant number H21S031000.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, M.O.; Lee, J.W.; Cho, K.H.; Kim, S.H. Korean Climate Change Assessment Report 2020—The Physical Science Basis 40; Korea Meteorological Administration: Seoul, Republic of Korea, 2021. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceeding of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Tran, Q.K.; Song, S.K. Computer vision in precipitation nowcasting: Applying image quality assessment metrics for training deep neural networks. Atmosphere 2019, 10, 244. [Google Scholar] [CrossRef]
- Yoon, S.S.; Park, H.S.; Shin, H.J. Very short-term rainfall prediction based on radar image learning using deep neural network. J. Korea Water Resour. Assoc. 2020, 53, 1159–1172. [Google Scholar]
- Shin, H.J.; Yoon, S.S.; Choi, J.M. Radar rainfall prediction based on deep learning considering temporal consistency. J. Korea Water Resour. Assoc. 2021, 54, 301–309. [Google Scholar]
- Ayzel, G.; Scheffer, T.; Heistermann, M. RainNet v1.0: A convolutional neural network for radar-based precipitation nowcasting. Geosci. Model Dev. 2020, 13, 2631–2644. [Google Scholar] [CrossRef]
- Palmer, T.N.; Räisänen, J. Quantifying the risk of extreme seasonal precipitation events in a changing climate. Nature 2002, 415, 512–514. [Google Scholar] [CrossRef] [PubMed]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Richardson, D.S. Skill and relative economic value of the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 2000, 126, 649–667. [Google Scholar] [CrossRef]
- Yoon, S.S. Recursive model based on U-net for very short range forecast. J. Digit. Contents Soc. 2022, 23, 2481–2488. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. Available online: https://link.springer.com/chapter/10.1007/978-3-319-24574-4_28 (accessed on 30 October 2023).
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training very deep networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2377–2385. Available online: https://proceedings.neurips.cc/paper/2015/file/215a71a12769b056c3c32e7299f1c5ed-Paper.pdf (accessed on 30 October 2023).
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th international conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. Available online: https://dl.acm.org/doi/10.5555/3104322.3104425#d3521064e1 (accessed on 30 October 2023).
- Kingma, D.P.; Ba, J. A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zhang, Y.; Long, M.; Chen, K.; Xing, L.; Jin, R.; Jordan, M.I.; Wang, J. Skillful nowcasting of extreme precipitation with NowcastNet. Nature 2023, 619, 526–532. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Bae, D. Optimal rainfall estimation by considering elevation in the Han River basin, South Korea. J. Appl. Meteorol. Climatol. 2013, 52, 802–818. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).