Abstract
To analyze the difference in the microphysical development characteristics of orographic rainfall, several Parsivel disdrometers were installed along the windward and leeward slope of a mountain. There were differences in the raindrop size distribution according to the difference in height and distance from the center of the mountain. In low-altitude coastal areas and adjacent areas, the number concentration of raindrops smaller than 1 mm was relatively lower than in mountainous areas, and the rain rate increased with the growth in the size of the raindrops. On the other hand, a higher rain rate was observed as the number concentration of raindrops smaller than 1 mm increased in the hillside area. The increase in the number concentration of small raindrops was evident at the LCL (lifting condensation level) altitude. The main factors affecting the increase in the rain rate on the windward and leeward slopes were the concentration of raindrops and the growth of raindrops, which showed regional differences. As a result of a PCA (principal component analysis), it was found that raindrop development by vapor deposition and weak convection were the main rainfall development characteristics on the windward and leeward slopes, respectively. The difference in regional precipitation development characteristics in mountainous areas affects the parameters of the rainfall estimation relational expression. This means that the rainfall relation calculated through the disdrometer observation data observed in a specific mountainous area can cause spatial and quantitative errors.
1. Introduction
Understanding the hydrometeor particle size characteristics of orographic rainfall is a fundamental part of calculating rainfall estimation relations applied to remote sensing observation data [1] and improving the microphysical schemes of numerical models [2,3,4]. In addition, the precipitation particle distribution is a physical parameter that represents the result of the physical phenomena of the interaction between precipitation particles [5,6]. Therefore, understanding the hydrometeor particle size distribution characteristics related to precipitation development in various environments is closely related to improving the retrieval accuracy of microphysical parameters for precipitation [7]. The variability in the drop size distribution, which is a result of the microphysical processes of rainfall, is an indicator of environmental characteristics such as cloud-scale processes, vertical motion of air, and the liquid water production of the cloud [8]. The strong upward flow in the cloud contributes to the growth of hail and graupel by accretion by supplying the supercooled water droplets to the mixed layer of the hydrometeors above the melting layer altitude. Sufficiently-grown particles fall into the lower layer and gradually grow further through coalescence with slight precipitation in the vicinity [9]. Raindrops falling from a layer below 0 °C may be removed by size sorting and evaporation [10]. The concentration of raindrops observed on the ground may decrease significantly due to attachment to other large particles [11,12]. As such, analysis of the precipitation particle size distribution is an efficient and essential research component for remote sensing and cloud physics.
Many previous studies have been conducted on drop size distribution characteristics worldwide. Rosenfeld and Ulbrich [13] explained the general contents of the distribution of raindrops according to the microphysical characteristics of precipitation. They discussed the characteristics of the development of warm raindrops in topographical rainfall. They noted that large amounts of water vapor entering mountain slopes trigger the growth of small raindrops so that precipitation systems passing over mountainous terrain are characterized by large concentrations of small particles. Bringi et al. [14] classified stratiform and convective precipitation types using ground disdrometer observation data collected from all over the world, including the United States and Australia, and compared and analyzed the rainfall characteristics of each region in terms of type of rainfall. According to previous studies, areas with marine climatic characteristics have a small diameter of precipitation particles and large water concentrations, and regions with continental climatic characteristics are compared with maritime climatic characteristics [15,16,17]. The research results revealed that differences in the climatic and geographic characteristics of regions where the precipitation system was developed also affected precipitation development.
East Asian regions, including Korea [18,19], Taiwan [20,21,22,23], Japan [24,25], and China [26,27,28], are affected by heavy precipitation during the summer rainy season every year. Many studies on the mechanisms of precipitation development and the estimation of rainfall revealing the number concentration of precipitation using in situ disdrometer data have been conducted. The study of raindrop size distribution mainly focuses on precipitation case analyses [29,30,31], geographic characteristics [32,33], climatic characteristics [34], seasonal variation [35,36], rainfall type [37,38], and day/night daily variation [39,40]. Many previous studies have focused on differences in precipitation system development due to atmospheric conditions. Studies on local precipitation development and precipitation distribution characteristics due to orographic effects are insufficient due to the difficulty of installing observation instruments and a lack of long-term observation data. Some previous studies [41,42,43,44,45] on orographic rainfall have been conducted, but they focus on case analyses.
Kim et al. [41] studied the microphysical characteristics of the convective precipitation system passing over Mt. Halla on South Korea’s Jeju Island, south of the Korean peninsula using ground Parsivel disdrometer and Doppler radar observation data. While the convective precipitation system passed over the coastal area, rainfall development occurred at a lower altitude of about 1 km due to orographically-enhanced lifting. The LWC (liquid water content) calculated by using a Parsivel disdrometer increased with the reflectivity at 1 km caused by an upward wind. When the precipitation system crosses a mountain slope at an altitude higher than the LCL (lifted condensation level), the supply of lower layer water vapor continuously inflowing from the ocean helps the development of small raindrops on the mountain slope. The rainfall distribution in the lower layer was also affected by increasing the number of drops. Feng and Wang [42] found that microphysical interactions such as the collision and coalescence processes of small hydrometeors inside convective precipitation cells in an MCS (mesoscale convective system) are activated by orographically-enhanced lifting while the MCS passes over mountainous terrain, and it was found that the hydrometeors developed in the convective precipitation cell were supplied to the stratiform precipitation following the convective precipitation cell, thereby affecting the development of the stratiform rainfall.
As shown in the previous study results, regional differences in the distribution of precipitation particles occur due to the growth of local precipitation passing over mountains. The local quantitative number concentration characteristics also affect the parameter values of the quantitative precipitation estimation equation based on the observation data. Therefore, in this study, the results of the analysis of raindrop size distribution characteristics for the orographic rainfall are described using disdrometer data collected during the long summer rainy season in mountainous areas.
2. Observational Data and Methodology
2.1. Disdrometer Observation on the Mountain
To analyze the microphysical development characteristics of orographic rainfall in the summers of 2012–2014 (Table 1), 10 Parsivel disdrometers were installed along the slopes of Mt. Halla that collected observational data (Figure 1). For the analysis of regional rainfall characteristics while orographic rainfall passed over the mountainous terrain, a number of observation sites were set at different elevations of the upwind/downwind side of the mountain slope (Table 2).

Table 1.
Observation period of orographic rainfall during the summer rainy season.
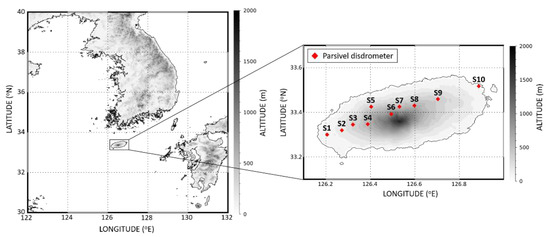
Figure 1.
The observation site map. The red colored diamonds indicate Parsivel sites. The gray contour shows the topography (contour interval: 200 m).

Table 2.
Information on the location and altitude of the Parsivel observation sites on the slope of Mt. Halla on Jeju Island.
2.2. Number Concentration and DSD Parameters
Through Parsivel disdrometer observation, it is possible to obtain the number concentration information on the fall velocity of each diameter channel of raindrops. In this study, the observation time resolution was set to 1 min due to the rapid development of orographic rainfall characteristics over a short time. The DSD (drop size distribution) parameters, such as Dm (mass-weighted mean diameter), Nw (normalized intercept parameter), μ (shape parameter), and Λ (slope parameter) that were used for the microphysical analysis of rainfall were calculated based on the observed diameter, fall velocity, and number concentration values.
After preprocessing [46,47] the observation data by removing information on non-weather data such as insects and leaves to increase the reliability of the rainfall data, the DSD parameters were calculated. The first and second diameter channels of the Parsivel disdrometer were not considered in the calculation because of the low signal-to-noise channels [48,49,50]. In addition, rainfall data on time with a rain rate greater than 0.1 mm h−1 were used. The maximum observed diameter of raindrops was set to 8 mm in an attempt to prevent the collection of erroneous observational data such as raindrops that collided with and hit an observation device while falling. When considering the terminal velocity [46,51], which is the ideal fall velocity that raindrops can have while falling, error values that may have been caused by non-weather data and wind were removed. In this study, the constant (C) in Equation (2) was set to 0.6, as suggested by Freidrich et al. [47].
where D is the diameter of the raindrop, Vmeasured is the fall velocity for each diameter channel, and Videal is the reference terminal velocity proposed by [46,51].
After data preprocessing, we calculated the DSD parameters involved in the gamma distribution equation (Equation (3)) proposed by Ulbrich [52].
The gamma distribution equation is the crucial function for the microphysical schemes in the numerical model. It is an advanced equation of the exponential distribution (Equation (4)) proposed by Marshall [53].
In Equation (3), N(D) (mm−1 m−3) indicates the number concentration value per unit volume for each particle channel set, N0 (mm−1−μ m−3) is an intercept parameter representing the number concentration value when the raindrop diameter has a value of 0, and Λ (mm−1) and μ (dimensional parameter) represent the slope and shape parameter of the gamma distribution, respectively. The gamma distribution has the advantage of being able to estimate rainfall using only three moments and reflects the characteristics of an exponential distribution [54,55,56]. In addition, since simulation is possible through dual-polarization parameters [52,57], it has the advantage of being able to analyze the developmental structure of the precipitation system through the simulation results. For these reasons, a number of microphysical studies using gamma distribution parameters have been performed [52,58].
Equation (5) represents a function calculating the moment value for the nth order. Dn and dD indicate the order of diameter and the interval for each diameter channel, respectively.
NT (Total number concentration, m−3) represents the number of raindrops per unit volume. η was used to calculate μ and Λ (Equation (6)). In this study, the 2nd, 4th, and 6th moments (M2, M4, and M6, respectively) were used [54].
The formulas for μ and Λ are shown in Equations (7) and (8), respectively.
Dm (mm) is the mass-weighted mean diameter, which indicates the average mass of raindrops contained in the unit volume.
The normalized intercept parameter Nw (mm−1 m−3) and LWC (g m−3), which represents the water content of the liquid contained in the unit volume, are defined in Equations (10) and (11), where ρw is the density value of liquid water (1 g cm−3) and Nw is the value of the scaling parameter in the distribution of the number concentration by the diameter of raindrops normalized for LWC and Dm [59].
2.3. Dual-Polarization Radar Parameters with T-Matrix
To calculate the rate of change of ZDR (differential reflectivity) according to the increase in ZH (radar reflectivity) at each Parsivel disdrometer observation site, the dual-polarimetric parameters were retrieved using the number concentration data at each site. It is possible to calculate the dual-polarization parameters, such as ZH, ZDR, KDP (specific differential phase), and ρHV (correlation coefficient), by applying the data of the raindrop distribution with 1 min time resolution to the T-matrix scattering simulation derived by Waterman [60]. In this study, the T-matrix scattering simulation program written by Leinonen [61] was used to estimate the dual-polarization parameters, such as ZH (mm6m−3), ZDR (dB), and KDP (degree km−1). The oblateness relation (Equations (12)–(14)) of raindrops proposed by Thurai et al. [62] was used. The set temperature variable was assumed to be 2 °C, and the result was calculated. It was applied by taking a Gaussian distribution with an average canting angle of 0° for raindrops and a canting angle width of 20°.
In Equations (12)–(14), a and b indicate the lengths of the horizontal and vertical axes of the raindrops and Deq is the diameter of the raindrops.
3. Results
3.1. Raindrop Size Distribution
Since the number concentration (hereafter N(D)) varies depending on the rainfall intensity, the rain rate is divided into six categories (R1: 0.1 mm h−1 ≤ R < 1.0 mm h−1; R2: 1.0 mm h−1 ≤ R < 5.0 mm h−1; R3: 5.0 mm h−1 ≤ R < 10.0 mm h−1; R4: 10.0 mm h−1 ≤ R < 20.0 mm h−1; R5: 20.0 mm h−1 ≤ R < 30.0 mm h−1; R6: 30.0 mm h−1 ≤ R) for the analysis of the microphysical characteristics of each rainfall intensity.
The average N(D) versus diameter at each site is displayed in Figure 2. At all observation sites, an increase in the N(D) due to an increase in rainfall intensity was noticeable. According to the rainfall intensity, there were differences in the N(D) of raindrop diameters between the observation sites. In the rain rate category with less than 10 mm h−1, the N(D) of raindrops of 1 mm or more did not show a difference. However, a difference in the N(D) for small drops of 1 mm or less was seen. On the other hand, in the rain rate of 10 mm h−1 or more, the difference in some sites for raindrops larger than 3 mm was relatively larger than that of the rain rate below 10 mm h−1.
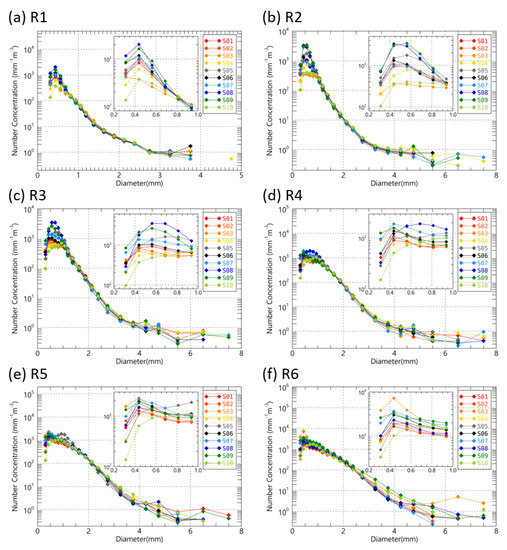
Figure 2.
The average N(D) versus diameter of raindrops for rain rate categories at the 10 Parsivel sites during the entire analysis period. The inner subfigures show the average N(D) versus diameter from 0.2 mm to 1.0 mm.
In the rain rate categories of less than 10 mm h−1, the N(D) values for small drops less than 1 mm at sites S8 and S9 on the leeward slope were higher than those of other sites. In particular, the N(D) above 2000 mm−1 m−3 was shown to be in the R3 rain rate category (Figure 2a–c). On the other hand, at sites S1 and S10, located in the coastal areas, the number of small drops had a lower value than the other sites, and S10 on the leeward side had the lowest N(D) in the entire rain rate categories. With a rain rate of more than 10 mm h−1, the N(D) of small drops was relatively small, but the N(D) of large drops larger than 3 mm was similar and higher than the mountain slope sites (Figure 2d–f). The N(D) for small drops was different according to the sites higher and lower than LCL (average LCL was 312 m during the observation period in this study). In particular, the N(D) at sites S3 and S9 higher than LCL altitude showed higher N(D) for raindrops smaller than 1 mm.
At the observation sites on the slope of the windward side (S3, S4, S6), as the rain rate increased, the N(D) of middle-sized raindrops smaller than 3 mm increased. In particular, the S3 site recorded higher N(D) values than other sites for a rain rate intensity higher than 20 mm h−1. In the mountain slope area, the N(D) of drops smaller than 1 mm was higher than other sites regardless of the difference in rain rate. However, there was a difference in the N(D) between the windward and leeward locations. On the windward side, when the rain rate intensity was weaker than 10 mm h−1, the N(D) of small drops was lower than 1000 mm−1 m−3. However, as the rain rate intensity increased over 20 mm h−1, the N(D) of small and large drops increased gradually. On the leeward side, the increase in N(D) was similar to that of the windward side, but the N(D) value of small drops was higher.
The N(D) distribution results in Figure 2 are affected by the LWC difference correlating with rainfall. For comparison considering only the characteristics of the drop size distribution, the normalized DSDs were compared and analyzed at the sites (Figure 3). At the S4, S7, and S9 sites, located on the hillside, the concentration of small drops in the rain rate less than 20 mm h−1 was high compared to the other sites. At sites S4 and S9, the N(D)s of small drops and large drops were relatively high (Figure 3e,f). In the coastal area (S1 and S10), it can be seen that the normalized concentration increased rapidly in the section where the normalized diameter (D/Dm) is 1.5 or more (Figure 3a–e). S6, which had the highest altitude among the observation sites, had a lower concentration value compared to S3 site in rain rate more than 10 mm h−1. When S6 site had the same rain rate as other sites, the raindrop diameter section with the highest N(D) among other sites was not seen. This does not mean that the rain rate increases due to the development of raindrops of a specific diameter, but the rain rate increase through overall generation and growth in all drop diameters.
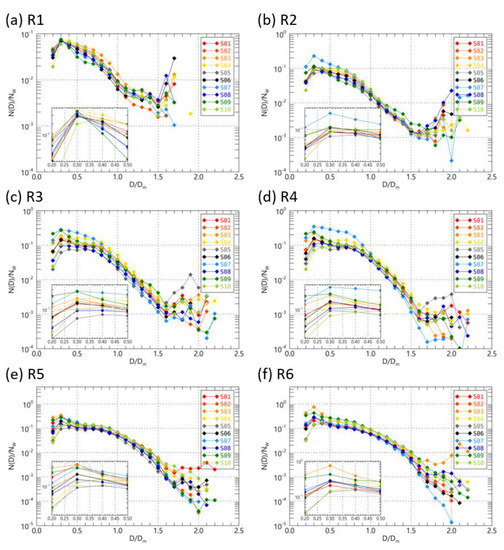
Figure 3.
The normalized N(D) versus normalized diameter of raindrops for rain rate categories at the 10 Parsivel sites during the entire analysis period. The inner subfigures show the average normalized N(D) versus normalized diameter from 0.0 mm to 0.5 mm.
Because the microphysical development process (e.g., collision, coalescence, breakup) of raindrops is a result of the difference in falling speed between rainfall particles, we tried to estimate the cause of rainfall particle development through the ratio of the fall velocity and terminal velocity for each diameter of the rainfall particle. When the fall velocity is smaller than the terminal velocity, the ratio of velocities has a value less than 1, which means that the fall velocity is lowered by the influence of upward wind flow in the atmosphere. Figure 4 shows the ratio of the rainfall particle fall velocity to terminal velocity for each particle diameter channel at each site. The red color in the picture means that it has a lower fall velocity and implies that the floating time of airborne particles may be longer. Overall, the tendency of the fall velocity according to the intensity of the rain rate was similar, and there was a difference in the fall velocity for each raindrop diameter at different observation sites.
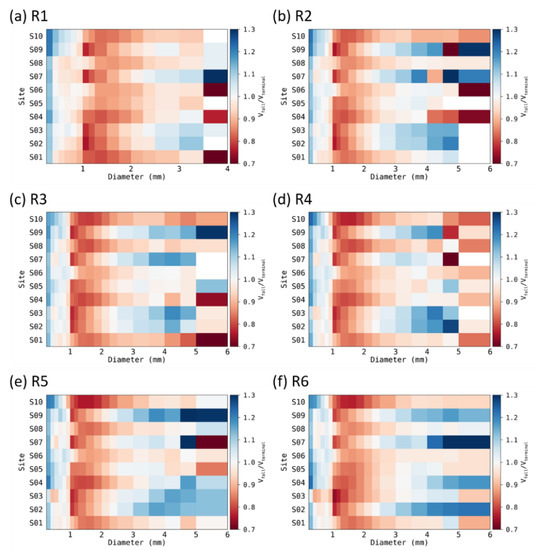
Figure 4.
The ratio of fall velocity to terminal velocity of raindrops for rain rate categories at the 10 Parsivel sites.
In areas S2, S7, and S9, the ratio of the velocity of raindrops of 1–2 mm was less than 1. On the other hand, the velocity ratio for raindrops larger than 3 mm had a value greater than 1. The fall velocity of 1–2 mm had low value compared to the other sites. These results mean that a large number of small raindrops (Figure 2) have a long time aloft at the low-elevation locations, while a large number of large raindrops (>3 mm diameter) have a short time aloft (high fall speeds) at the low-elevation locations. Thus, the possibility of collision may be higher at low-elevation sites than that at high-elevation sites. At S4, S6, and S8 (high-elevation sites), the fall velocity of raindrops less than 3.5 mm diameter was lower than that of their terminal velocity. This was caused by lower layer ascending flow, which developed over the mountainous terrain, that opposed the fall of the drops.
Unlike the mountain slopes, where the ratio of fall velocity to terminal velocity of raindrops larger than about 2 mm was larger than 1, the velocity ratio of 0.5–4 mm diameter was less than 1 on coastal areas such as S1 and S10. In coastal areas, the ratio of fall velocity did not exceed 1 for larger diameters of about 3 mm. In addition, coastal areas had higher standard deviation values of the fall velocity than other sites (Figure 5). The large standard deviation of the fall velocity of raindrops means that raindrops can become larger by increasing their collision rate of raindrops in the atmosphere [63]. The standard deviation value of the fall velocity was higher at the slope sites (S3 and S4 in Figure 5) than at the coastal sites. At the S3 site, high standard deviation more than 0.5 m s−1 was shown for diameters larger than 1 mm. In particular, the standard deviation was higher than 0.8 m s−1 for diameters of 2–3 mm. At the S3 site, when the rain rate intensity was less than 30 mm h−1, we observed a low standard deviation of fall velocities (i.e., <0.4 m s−1) for 3 mm drops, and as the rain rate intensity increased to more than 30 mm h−1, the standard deviation increased to more than 1 m s−1. With an increase in the standard deviation, the N(D) also increased. At the S9 site, on a leeward slope, the standard deviation of the fall velocity for very small raindrops (i.e., <0.5 mm) was high where the rain rate intensity was >20 mm h−1. Overall, the standard deviation values of the windward slope sites were higher than those of the leeward side sites. Higher standard deviations (i.e., 0.5 m s−1) at the windward slope sites (S3 and S4) than other sites were clearly shown as the rain rate increased to 30 mm h−1.
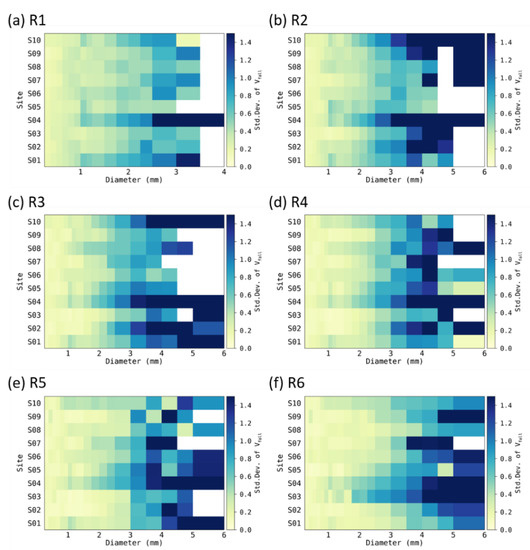
Figure 5.
The standard deviation of the fall velocity of raindrops for rain rate categories at the 10 Parsivel sites.
To see how a difference in the development of the microphysical properties of raindrops depending on the mountainous area and altitude contributes to the change in precipitation, the NT (total number concentration) by raindrop diameters and the contribution rate to the rain rate were calculated.
In category R1, where the rain rate is less than 1 mm h−1, smaller drops less than 1 mm accounted for more than 90% of NT (Figure 6a) at all observation sites. When the rain rate was higher than 1 mm h−1, the proportion of raindrops larger than 1 mm gradually increased to more than 10% of the total NT. When the rain rate was higher than 10 mm h−1, the proportion of raindrops larger than 2 mm had a maximum value close to about 5% (Figure 6d). Overall, the NT proportion of raindrops smaller than 2 mm had a high value of about 90% or more. With a weak rain rate of less than 10 mm h−1, the proportion of raindrops smaller than 1 mm at the leeward slope sites (S8 and S9) had a greater effect on the rain rate compared to the windward slope sites (Figure 6b,c). Moreover, the proportion of raindrops larger than 1 mm was lower than 20%. However, in the coastal area of the leeward side, the proportion of small drops smaller than 1 mm was the lowest among all sites, while the proportion of raindrops of 1 to 3 mm was the highest (Figure 6a–e). At the observation sites on the windward slope-sides, except for S3, the proportion of small drops decreased as the rain rate increased, and the proportion of large drops gradually increased. At the S3 site, the proportion of small drops smaller than 1 mm increased as the rain rate increased (Figure 6f).
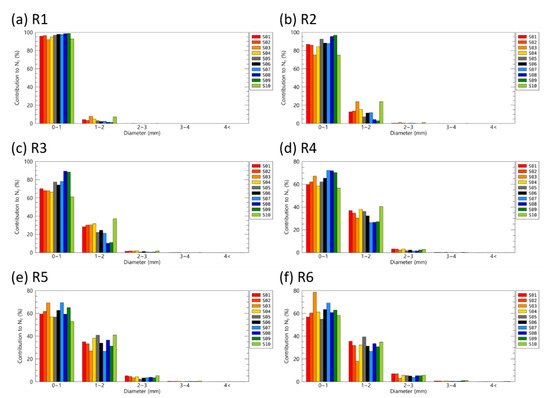
Figure 6.
The contribution rate of the N(D) of each diameter category to NT.
When the rain rate was less than 5 mm h−1, raindrops larger than 1 mm at S3 had a high contribution to the rain rate compared to other sites (Figure 7a,b). In contrast to the S3 site, the S8 and S9 sites had less than 30% of raindrops larger than 1 mm, so the raindrops constituting the rain rate were mainly composed of very small drops of less than 1 mm (Figure 7a). In the coastal areas, the raindrops mainly contributing to the rain rate increase were 2–3 mm, but in the mountain slopes, the contribution rate of middle side raindrops of 1–3 mm was higher (Figure 7e,f). Depending on the mountainous area, there is a difference in the diameter of raindrops that affects precipitation. Due to the difference in particle diameter and N(D) distribution, differences in rainfall estimation relations with reflectivity parameters may occur between sites.
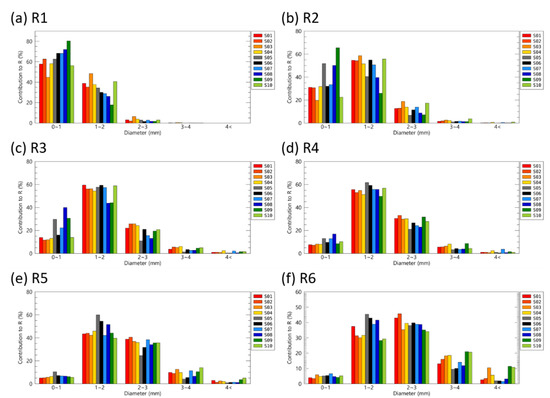
Figure 7.
The contribution rate of the N(D) of each diameter category to the rain rate.
3.2. DSD Parameter Characteristics
The difference in N(D) distribution by raindrop diameter generates a difference in the DSD parameters, such as Dm (mass-weighted mean diameter), Nw (normalized intercept parameter), μ (shape parameter of DSD model), and Λ (slope parameter of DSD model), and transforms the DSD model equation. Therefore, the accuracy of the rainfall distribution simulation when using the DSD model is crucial because it affects the microphysical development process of precipitation implemented in the numerical model, the rain rate, and the LWC estimation through remote sensing data, including weather, radar, and satellite observations.
Figure 8 shows the average Nw versus Dm distribution for the rain rate intensity interval at each site. Overall, the windward sites had a larger Dm distribution and a smaller Nw distribution than the leeward sites. Dm tended to increase at all sites as the rain rate increased, whereas Nw changed inconsistently at different rain rates. In the coastal area (S1 and S10) and the mountain slopes (S2, S3, S4) on the windward side, Nw increased with Dm. In the leeward side area (S8 and S9), Nw increased from 5 to 10 mm h−1; however, Nw decreased despite an increase in the rain rate. On the mountain slopes, Dm was relatively small (maximum value was less than 2 mm), and Nw was large compared to other sites (minimum value was more than 3.8 mm−1 m−3). Mt. Halla had higher Nw values with increasing altitude.
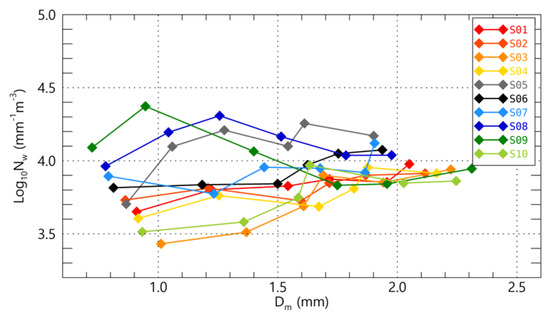
Figure 8.
The average Nw versus Dm for the rain rate categories at the 10 Parsivel sites. The different colors indicate each Parsivel site and each symbol from left to right on the same color line represents rain rate categories.
Figure 9 shows the area included in 20–30% of the normalized frequency distribution for the Dm versus Nw distribution. In the section where the rainfall intensity is less than 1 mm h−1, the Dm value is about 0.2 to 0.5 mm smaller than the fitting line of stratiform precipitation proposed by Bringi et al. [14]. The distribution result overlapped with the fitting line at 1–10 mm h−1. In Figure 9a, only sites S7 and S8 had higher log10Nw values of more than 3.8 mm−1 m−3, while the other sites mainly showed values of less than 3.9 mm−1 m−3. At 1–10 mm h−1, there was a clear difference in the location of the distribution centers between sites S5, S7, and S9 and the other sites. The fluctuation width, the range from minimum to maximum of the gaussian two-dimensional fitting circle, of log10Nw was also larger at sites S2–S4, which were on the slope of the windward side, compared to the S5, S7, and S9 sites (Figure 9b,c). Rainfall stronger than 10 mm h−1 that affected Jeju Island was mainly included in the classification of marine type convective precipitation systems mentioned by Bringi et al. [14]. However, S9 had a relatively large (small) Dm (log10Nw) value at more than 30 mm h−1 and is included in the continental convective precipitation system classification area (Figure 9f).
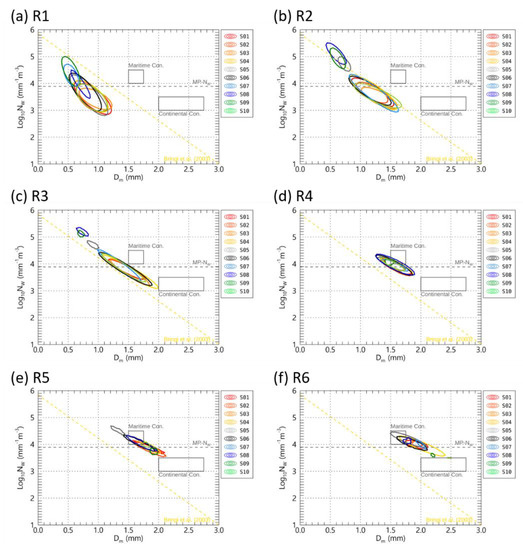
Figure 9.
The Gaussian two-dimensional fitting circle with (a,b) 30% or (c–f) 20% of the normalized frequency of Nw versus Dm distribution for rain rate categories. The yellow dashed lines indicate the stratiform precipitation fitting line by Bringi et al. [14].
Figure 10 and Figure 11 show the cumulative distribution for rain rate categories of Λ and μ, which are gamma DSD model parameters. Overall, as the rain rate increased, the Λ value decreased. Sites S8 S9, where the proportion of small raindrops with weak rainfall intensity (10 mm h−1) was high, showed a relatively gentle increase to about 80 mm−1, unlike other sites where the CDF change was abrupt when Λ was less than 20 mm−1. These relative differences in distribution showed similar characteristics up to the rain rate range of less than 20 mm h−1 (Figure 10a–d). S6, which was highest among observation sites, had a higher Λ value than other sites except for S5 in the rain rate range higher than 20 mm h−1. This means that the shape of the N(D) distribution at S6 is characteristic of the N(D) decreasing as the raindrop diameter increases. The qualitative distribution trends for each site of Λ and μ appear similar. It should be noted that when the rainfall intensity at the mountain slope of the windward (S2–S4) and leeward (S7–S9) sides was greater than 10 mm h−1, the frequency of the negative μ was about 10% with a high value of up to 50% (Figure 11f). These results show many negative μ values due to the very high proportion of the small drops on the slope of the mountain.
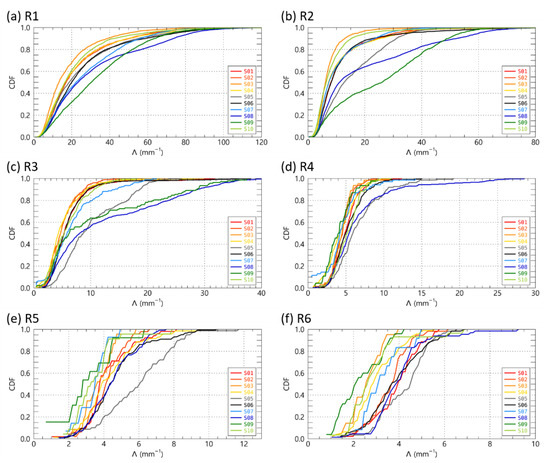
Figure 10.
The cumulative distribution function of Λ (mm−1) for rain rate categories at the 10 Parsivel sites.
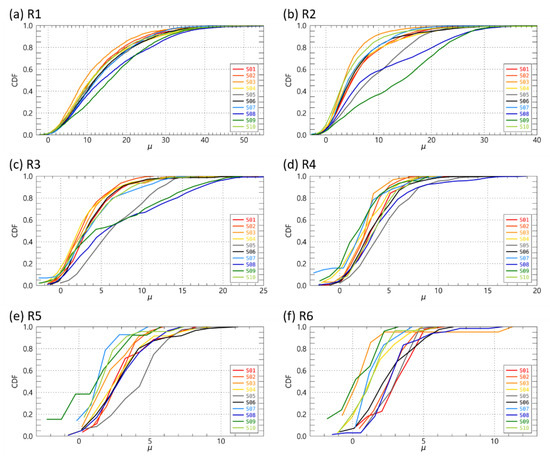
Figure 11.
The cumulative distribution function of μ for rain rate categories at the 10 Parsivel sites.
3.3. Representative Raindrop Size Distribution
Figure 12 shows the normalized frequency density of the joint distribution of PC1 (first principal component) and PC2 (second principal component), considering the DSD parameters at each Parsivel observation site. The six DSD parameters considered in the PCA (principal component analysis) were NT, Nw, rain rate, reflectivity, Dm, and LWC.
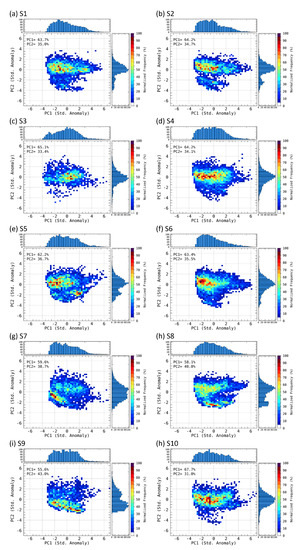
Figure 12.
The normalized frequency density of the joint distribution of PC1 and PC2 for S1–S10 sites.
To normalize the differences in scale and value of each parameter, all parameters were converted to log scale and then normalized through their respective means and standard deviations. A PCA with six parameters creates a set of vectors called EOFs (empirical orthogonal functions). The generated vectors enable a dimensional reduction that can best represent the characteristics of all parameters. Among the set of vectors, the vector with the largest variance for all variables is called EOF1, and the vector with the second-largest variance is called EOF2. Each variable value is rearranged to EOF1 (EOF2), which indicates the direction in which the variance of the data distribution found through PCA is the largest, and is called PC1 (PC2).
At all sites, dimensional reduction through PC1 and PC2 represented more than 98% of the characteristics for the existing parameter values (Table 3; Figure 12 and Figure 13). We extracted PC1 and PC2 values corresponding to the grid with the largest value of the normalized frequency density of the joint distribution. N(D) and log10Nw versus Dm corresponding to the PC1 and PC2 values are shown in Figure 14.

Table 3.
Percent variance explained by the first two EOFs at each site.
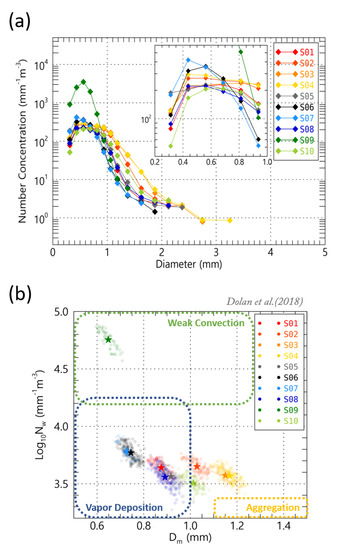
Figure 13.
(a) The average N(D) versus diameter and (b) log10Nw versus Dm distribution for the maximum normalized frequency in Figure 12 and Figure 13. The dot colored boxes are shown in the different microphysical development process areas with log10Nw versus Dm suggested by Dolan et al. [9]. The colored stars mean the average value of log10Nw and Dm at each site.
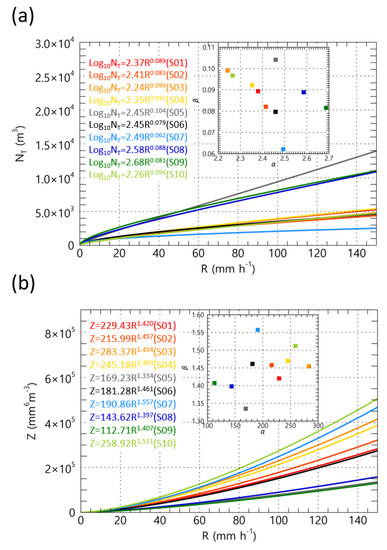
Figure 14.
The fitting lines for (a) NT versus rain rate, and (b) reflectivity versus rain rate. The inside graphs show the parameters of the relationships. The colored solid lines indicate each Parsivel site.
At the S9 site, the N(D) was higher than 3000 mm−1 m−3 for a diameter less than 1 mm, and there was difference of more than 2500 mm−1 m−3 from other sites. Among the observation sites, S6 and S7, close to the center of the mountain, had a N(D) higher than 300 mm−1 m−3 of very small rainfall particles (≤0.7 mm), which were much higher than those of other sites. In S4, located on the mountain slope of the windward side, and the coastal area (S1, S10), the concentration value for medium-sized drops of 1–2 mm was higher than that of the other sites. In particular, the S4 site had a higher value than 30 mm−1 m−3 (Figure 13a). The difference in the number of small and medium drops at each observation site changed the log10Nw versus Dm distribution position.
The colored boxes in Figure 13b are the classification result of the microphysical development process proposed by Dolan et al. [9] using the disdrometer and dual-polarization radar data in various regions worldwide. S9 was mainly included in the weak convection process area with log10Nw higher than 4.5 mm−1 m−3 and lower than Dm, and all other sites had a log10Nw lower than 4.0 mm−1 m−3. At S6 and S7, all distribution values were located in the vapor deposition box. Although the distribution at S2 and S4 overlapped somewhat in the vapor deposition regime, they showed a distribution characteristic closer to the aggregation box due to having a larger Dm distribution than the other sites.
3.4. Relation of DSD Parameters with Rain Rate
Figure 14 shows the rain rate, NT and reflectivity regression lines, and regression equation coefficients at the observation sites. At S8 and S9, the number of raindrops was very high when α had a value of 2.55 or more at the same rain rate. As the rain rate increased, the concentration of raindrops in the S5, S8, and S9 sites increased more compared to the other sites. When the rain rate is 60 mm h−1, NT at sites S5, S8, and S9 were higher than 5000 m−3, but other sites had NT less than 3000 m−3. As shown in the blue (S8) and green (S9) solid lines in Figure 14b, the increase in reflectivity is not significant even at the same rain rate. Even the α value of the Z–R relationship had a lower value than 150. In the R–NT relationship at the S7 site, the α value (sky blue) is about 2.49, which is a higher value than sites on the windward slope and lower than S8 and S9.
The increase in the rain rate at the site of the windward mountain slope mainly occurs with the increase in the raindrop size rather than the increase in NT (having an α value of less than 2.43 in Figure 14a). Conversely, a high proportion of raindrop size increase to the increase in rain rate may cause an increase in α in the Z–R relationship (having α high value over 200 in Figure 14b).
Figure 15 is the result of comparing the rate of change over time of the ZH and ZDR values retrieved through the disdrometer data. The characteristics of the increase in raindrop size due to the increase in rain rate on the windward slope area mentioned above can be seen in the degree of ZDR increase with the ZH increase. Compared to the increase in the ZH value, the increase in the ZDR value is large, and this means that the microphysical rainfall development characteristics on the windward side are more likely to be influenced by processes such as vapor deposition and aggregation related to particle growth when compared to the leeward side.
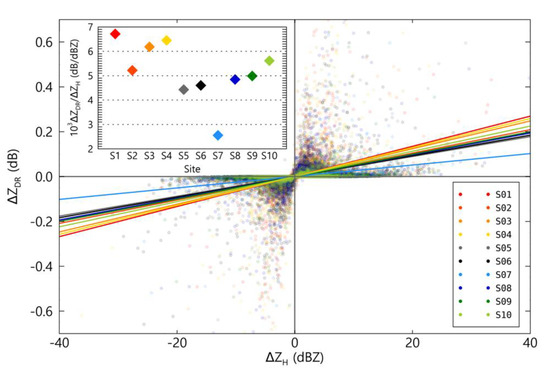
Figure 15.
The fitting lines for ΔZDR versus ΔZH. The inside graphs show the parameters of the relationships. The colored solid lines indicate each Parsivel site.
In particular, considering that the difference between the ΔZDR and ΔZH ratio values at S1 and S6 is large, about 3000 dB/dBZ, the rainfall estimation relationship generated using rainfall data collected in a specific region is not suitable for mountainous areas with complex regional differences in precipitation development characteristics. Therefore, an analysis using data collected from various mountain regions is necessary to improve the quantitative precipitation estimation of orographic rainfall.
4. Discussion
To analyze the microphysical characteristics of orographic rainfall, 10 Parsivel disdrometers installed along the long axis of Mt. Halla were installed and observed during the summer in 2012–2014. The raindrop size distribution obtained through observation was used to analyze the mountain region’s precipitation characteristics. To filter the non-meteorological echo, only the data that passed the filtering process through the relationship [46,47] of the fall velocity versus diameter were used for analysis.
During the observation period, there was a difference in raindrop size distribution characteristics depending on the altitude of the site and its position from the center of the mountain (windward and leeward) in the Jeju area. In the coastal region, which is the closest to the sea, the altitude is relatively low and the number of small raindrops less than 1 mm compared to the mountain area is low (about 1000 mm−1 m−3), regardless of the rain rate intensity. Both the windward and leeward coastal areas show similar characteristics. The low N(D) and the high proportion of rain rate of raindrops larger than 3 mm in the coastal area were similar to the result of Kim et al. [41]. They investigated that the reflectivity and LWC (liquid water contents) could be higher than those on mountain slopes due to the high proportion of large raindrops. In addition, it has a high reflectivity value due to the influence of an upward wind developed over 1 km altitude. The development of precipitation in coastal areas was similar to the results of Lee et al. [64]. They revealed that local updraft by forcible topographical upflow occurs in coastal areas and precipitation develops due to a moist upward wind by using numerical model simulation results.
The coastal area of the leeward side has a higher number of distribution characteristics for drops larger than 3 mm compared to the coastal area of the windward side. On the other hand, compared to the coastal area, the slope of the mountain area had a higher concentration of smaller drops than 1 mm. In particular, S3 and S9 sites located at an altitude of 320 to 340 m ASL, which is higher than LCL altitude, had much higher N(D) values compared to other sites. Rosenfeld and Ulbrich [13] noted that the high N(D) characteristic with small raindrops developed in the mountainous regions is the characteristic of orographic rainfall development by the supply of inflow water vapor from the lower layer. The characteristics of small raindrops generated and developed in the mountainous region above LCL (lifting condensation level) altitude were analyzed by Kim et al. [41] using disdrometer data analysis. In addition, Feng and Wang [42] showed that orographically–enhanced ascending flow activates the microphysical interactions of small-drop hydrometeors when a precipitation system passes over a mountain. From the results of this study, it was found that the fall velocity of a middle raindrop on the mountain slope was low, and the fall velocity of raindrops larger than 3 mm had a larger value compared to other regions. It can be seen that the updraft strengthened by the topography increases the floating time of small rainfall particles, and the interaction with the falling large raindrops can induce increased activation. In particular, through the wide spectrum characteristics of the fall velocity of raindrops on the windward side, the interaction potential with warm precipitation development such as collision and coalescence for raindrops could be seen.
The mountain slope area of the leeward side had a very high density of raindrops compared to other sites, even at a weak rain rate of less than 10 mm h−1; as the rain rate increased to 30 mm h−1 or more, the N(D) value for diameters larger than 3 mm increased significantly. The rapid increase in raindrop diameter with an increasing rain rate results from the growth and development of raindrops and rainfall on the leeward side. The increase in Dm and decrease in Nw with the increase in rain rate at the S9 site can be seen as the developmental characteristics of the continental convective system mentioned by Bringi et al. [14]. It has the same characteristics as inland precipitation development due to convergence on the slope of the leeward side [43,44,45]. On both the windward and leeward sides, Dm increased with increasing rain rate. On the windward side, Nw increased with increasing rain rate; however, the Nw was maintained or decreased gradually on the leeward side. Feng and Wang [42] studied that a strong terrain-induced upward motion could increase the supply of more vapor from the lower layer and develop condensation into droplets and small raindrops. The increase in diameter and concentration of these raindrops was considered as a result to be similar to the effect of the seeder–feeder mechanism in mountainous areas. Because Mt. Halla is close to the sea, has a low LCL, and has geographical requirements to receive a continuous water vapor supply at a low level from the sea, precipitation development by a similar mechanism may occur at the low level of the mountain slopes.
Due to the high Dm and Nw values, the developmental characteristics of a weak convection process that were proposed by Dolan et al. [9] are similar to what we have found. The major microphysical development characteristics of raindrops on the slope of the Jeju Island were different for the windward and leeward sides. These regional differences can be seen as differences in the regional microphysical development characteristics of orographic rainfall.
According to our PCA results, the main factors accounting for these differences were the development of raindrops by vapor deposition on the windward side and by weak convection on the leeward side. The main factors involved in precipitation development in low-elevation and mountain slope locations were raindrop size increases and raindrop number concentration increases, respectively. The PCA analysis results showed the characteristics of the development of small raindrops due to the supply of water vapor on the windward slope of the mountainous region and the development of precipitation due to the regional updraft on the leeward slope. Therefore, it is thought that the microphysical characteristics of precipitation can be identified through PCA analysis by using in situ data.
5. Conclusions
The main factors involved in precipitation development in the low-altitude and mountain slope areas are the size development and density increase in raindrops, respectively. This difference in characteristics also affects the relationship between rain rate and reflectivity. As a result, on the windward slope, where an increase in the N(D) of raindrops was a significant factor in the increase in rain rate, the reflectivity increase rate according to the increase in rain rate was lower than in the leeward slope. If the rainfall estimation relationship calculated using the drop size distribution data observed on the windward slope is used for rainfall estimation for orographic rainfall, it can cause underestimated results in coastal areas and leeward slopes.
This means that the rainfall estimation relation calculated through ground disdrometer observation data observed in a specific area can cause spatial and quantitative errors in mountainous areas. A summary of the results of this study is as follows.
- (1)
- On the windward slope, the concentration of small raindrops increases due to the influence of the forcible topographical rise of water vapor flowing from the sea at a low level, which can affect the increase in the rain rate. The high N(D) characteristics of small raindrops appeared at higher altitudes than LCL in mountainous terrain.
- (2)
- On the leeward slope, the concentration of large raindrops over 3 mm was lower, and the Nw was relatively high compared to the windward slope. These characteristics can be seen as a result of the weak convection of the low level. On the leeward slope, as the rain rate increased, the N(D) of raindrops decreased, and the diameter increased.
- (3)
- In the coastal area, large raindrops could develop at a low level due to the influence of the updraft developed over the coastline, and a low N(D) of small raindrops and relatively high concentration of large raindrops were shown on the ground.
This study revealed the influence of microphysical characteristics on the difference in regional DSD characteristics and rainfall estimation relationships in mountainous areas based on ground disdrometer observation data. In addition, the results of this study can be used for research on floods and landslides in mountainous areas caused by orographic development occurring in a short time and for improving disaster prevention capabilities.
Author Contributions
Conceptualization, H.-J.K. and W.J.; investigation, H.-J.K. and S.-H.S.; writing—original draft preparation, H.-J.K.; writing—review and editing, C.-H.Y. and D.-I.L.; funding acquisition, C.-H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2020R1I1A3066504).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ryzhkov, A.V.; Zrnić, D.S. Comparison of dual-polarization radar estimators of rain. J. Atmos. Ocean. Technol. 1995, 12, 249–256. [Google Scholar] [CrossRef]
- Abel, S.J.; Boutle, I.A. An improved representation of the raindrop size distribution for single-moment microphysics schemes. Q. J. R. Meteorol. Soc. 2012, 138, 2151–2162. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Hsieh, T.L.; Freer, M.; Mascio, J.; Jewett, B.F. The characterization of ice hydrometeor gamma size distributions as volumes in N0–λ–μ phase space: Implications for microphysical process modeling. J. Atmos. Sci. 2015, 72, 892–909. [Google Scholar] [CrossRef]
- Saleeby, S.M.; Cotton, W.R. A large-droplet mode and prognostic number concentration of cloud droplets in the Colorado State University Regional Atmospheric Modeling System (RAMS). Part I: Module descriptions and supercell test simulations. J. Appl. Meteorol. 2004, 43, 182–195. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Steiner, M.; Smith, J.A. Variability of raindrop size distributions in a squall line and implications for radar rainfall estimation. J. Hydrometeorol. 2003, 4, 43–61. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Quantification of the small-scale spatial structure of the raindrop size distribution from a network of disdrometers. J. Appl. Meteorol. Climatol. 2012, 51, 941–953. [Google Scholar] [CrossRef]
- Munchak, S.J.; Kummerow, C.D.; Elsaesser, G. Relationships between the raindrop size distribution and properties of the environment and clouds inferred from TRMM. J. Clim. 2012, 25, 2963–2978. [Google Scholar] [CrossRef]
- Cotton, W.R.; Bryan, G.; van den Heever, S.C. Cumulonimbus clouds and severe convective storms. Int. Geophys. 2011, 99, 87–142. [Google Scholar]
- Dolan, B.; Fuchs, B.; Rutledge, S.A.; Barnes, E.A.; Thompson, E.J. Primary modes of global drop size distributions. J. Atmos. Sci. 2018, 75, 1453–1476. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. The impact of size sorting on the polarimetric radar variables. J. Atmos. Sci. 2012, 69, 2042–2060. [Google Scholar] [CrossRef]
- Rutledge, S.A.; Houze, R.A., Jr. A diagnostic modelling study of the trailing stratiform region of a midlatitude squall line. J. Atmos. Sci. 1987, 44, 2640–2656. [Google Scholar] [CrossRef][Green Version]
- Houze, R.A., Jr. Stratiform precipitation in regions of convection: A meteorological paradox? Bull. Amer. Meteor. 1997, 78, 2179–2196. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Ulbrich, C.W. Cloud microphysical properties, processes, and rainfall estimation opportunities. In Radar and Atmospheric Science: A Collection of Essays in Honor of David Atlas; American Meteorological Society: Boston, MA, USA, 2003; pp. 237–258. [Google Scholar]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. An observationally based conceptual model of warm oceanic convective rain in the tropics. J. Appl. Meteorol. 2000, 39, 2165–2181. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Microphysics of raindrop size spectra: Tropical continental and maritime storms. J. Appl. Meteorol. Climatol. 2007, 46, 1777–1791. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; May, P.T. CPOL radar-derived drop size distribution statistics of stratiform and convective rain for two regimes in Darwin, Australia. J. Atmos. Ocean. Technol. 2010, 27, 932–942. [Google Scholar] [CrossRef]
- You, C.H.; Lee, D.I.; Jang, S.M.; Jang, M.; Uyeda, H.; Shinoda, T.; Kobayashi, F. Characteristics of rainfall systems accompanied with Changma front at Chujado in Korea. Asia-Pac. J. Atmos. Sci. 2010, 46, 41–51. [Google Scholar] [CrossRef]
- Yu, T.; Chandrasekar, V.; Xiao, H.; Joshil, S.S. Characteristics of Snow Particle Size Distribution in the PyeongChang Region of South Korea. Atmosphere 2020, 11, 1093. [Google Scholar] [CrossRef]
- Janapati, J.; Seela, B.K.; Lin, P.L.; Lee, M.T.; Joseph, E. Microphysical features of typhoon and non-typhoon rainfall observed in Taiwan, an island in the northwestern Pacific. Hydrol. Earth Syst. Sci. 2021, 25, 4025–4040. [Google Scholar] [CrossRef]
- Jung, S.A.; Lee, D.I.; Jou, B.J.D.; Uyeda, H. Microphysical properties of maritime squall line observed on June 2, 2008 in Taiwan. J. Meteorol. Soc. Jpn. Ser. II 2012, 90, 833–850. [Google Scholar] [CrossRef]
- Seela, B.K.; Janapati, J.; Lin, P.L.; Wang, P.K.; Lee, M.T. Raindrop size distribution characteristics of summer and winter season rainfall over north Taiwan. J. Geophys. Res. Atmos. 2018, 123, 11–602. [Google Scholar] [CrossRef]
- Chang, W.Y.; Wang, T.C.C.; Lin, P.L. Characteristics of the raindrop size distribution and drop shape relation in typhoon systems in the western Pacific from the 2D video disdrometer and NCU C-band polarimetric radar. J. Atmos. Ocean. Technol. 2009, 26, 1973–1993. [Google Scholar] [CrossRef]
- Oue, M.; Uyeda, H.; Lee, D.I. Raindrop size distribution parameters estimated from polarimetric radar variables in convective cells around Okinawa Island during the Baiu period. Asia-Pac. J. Atmos. Sci. 2011, 47, 33–44. [Google Scholar] [CrossRef]
- Hashimoto, A.; Harimaya, T. Characteristics of raindrop size distribution dependent on the life stage of a convective precipitation cloud in the Baiu season. J. Meteorol. Soc. Jpn. Ser. II 2005, 83, 641–649. [Google Scholar] [CrossRef][Green Version]
- Chen, G.; Zhao, K.; Wen, L.; Wang, M.; Huang, H.; Wang, M.; Yang, Z.; Zhang, G.; Zhang, P.; Lee, W.C. Microphysical characteristics of three convective events with intense rainfall observed by polarimetric radar and disdrometer in eastern China. Remote Sens. 2019, 11, 2004. [Google Scholar] [CrossRef]
- Ji, L.; Chen, H.; Li, L.; Chen, B.; Xiao, X.; Chen, M.; Zhang, G. Raindrop size distributions and rain characteristics observed by a PARSIVEL disdrometer in Beijing, Northern China. Remote Sens. 2019, 11, 1479. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, K.; Wang, M.; Zhang, G. Seasonal variations of observed raindrop size distribution in East China. Adv. Atmos. Sci. 2019, 36, 346–362. [Google Scholar] [CrossRef]
- Bringi, V.N.; Williams, C.R.; Thurai, M.; May, P.T. Using dual-polarized radar and dual-frequency profiler for DSD characterization: A case study from Darwin, Australia. J. Atmos. Ocean. Technol. 2009, 26, 2107–2122. [Google Scholar] [CrossRef]
- Maeso, J.; Bringi, V.N.; Cruz-Pol, S.; Chandrasekar, V. DSD characterization and computations of expected reflectivity using data from a two-dimensional video disdrometer deployed in a tropical environment. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS’05, Seoul, Korea, 29 July 2005; Volume 7, pp. 5073–5076. [Google Scholar]
- Tokay, A.; Bashor, P.G.; Habib, E.; Kasparis, T. Raindrop size distribution measurements in tropical cyclones. Mon. Weather Rev. 2008, 136, 1669–1685. [Google Scholar] [CrossRef]
- Le Loh, J.; Lee, D.I.; You, C.H. Inter-comparison of DSDs between Jincheon and Miryang at South Korea. Atmos. Res. 2019, 227, 52–65. [Google Scholar] [CrossRef]
- Suh, S.H.; Kim, H.J.; Lee, D.I.; Kim, T.H. Geographical characteristics of raindrop size distribution in the southern parts of South Korea. J. Appl. Meteorol. Climatol. 2021, 60, 157–169. [Google Scholar] [CrossRef]
- Ma, Y.; Ni, G.; Chandra, C.V.; Tian, F.; Chen, H. Statistical characteristics of raindrop size distribution during rainy seasons in the Beijing urban area and implications for radar rainfall estimation. Hydrol. Earth Syst. Sci. 2019, 23, 4153–4170. [Google Scholar] [CrossRef]
- Krishna, U.M.; Reddy, K.K.; Seela, B.K.; Shirooka, R.; Lin, P.L.; Pan, C.J. Raindrop size distribution of easterly and westerly monsoon precipitation observed over Palau islands in the Western Pacific Ocean. Atmos. Res. 2016, 174, 41–51. [Google Scholar] [CrossRef]
- Suh, S.H.; You, C.H.; Lee, D.I. Climatological characteristics of raindrop size distributions in Busan, Republic of Korea. Hydrol. Earth Syst. Sci. 2016, 20, 193–207. [Google Scholar] [CrossRef]
- Jwa, M.; Jin, H.G.; Lee, J.; Moon, S.; Baik, J.J. Characteristics of raindrop size distribution in Seoul, South Korea according to rain and weather types. Asia-Pac. J. Atmos. Sci. 2021, 57, 605–617. [Google Scholar] [CrossRef]
- Loh, J.L.; Lee, D.I.; Kang, M.Y.; You, C.H. Classification of rainfall types using parsivel disdrometer and S-band polarimetric radar in central Korea. Remote Sens. 2020, 12, 642. [Google Scholar] [CrossRef]
- Kozu, T.; Reddy, K.K.; Mori, S.; Thurai, M.; Ong, J.T.; Rao, D.N.; Shimomai, T. Seasonal and diurnal variations of raindrop size distribution in Asian monsoon region. J. Meteorol. Soc. Jpn. Ser. II 2006, 84, 195–209. [Google Scholar] [CrossRef]
- You, C.H.; Lee, D.I. Decadal variation in raindrop size distributions in Busan, Korea. Adv. Meteorol. 2015, 2015, 329327. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, K.O.; You, C.H.; Uyeda, H.; Lee, D.I. Microphysical characteristics of a convective precipitation system observed on July 04, 2012, over Mt. Halla in South Korea. Atmos. Res. 2019, 222, 74–87. [Google Scholar] [CrossRef]
- Feng, Y.C.; Wang, T.C.C. Precipitation characteristics of an autumn torrential rainfall event in northern Taiwan as determined from dual-polarization radar data. J. Meteorol. Soc. Jpn. Ser. II 2011, 89, 133–150. [Google Scholar] [CrossRef]
- Lee, K.O.; Shimizu, S.; Maki, M.; You, C.H.; Uyeda, H.; Lee, D.I. Enhancement mechanism of the 30 June 2006 precipitation system observed over the northwestern slope of Mt. Halla, Jeju Island, Korea. Atmos. Res. 2010, 97, 343–358. [Google Scholar] [CrossRef]
- Lee, K.O.; Uyeda, H.; Shimizu, S.; Lee, D.I. Dual-Doppler radar analysis of the enhancement of a precipitation system on the northern side of Mt. Halla, Jeju Island, Korea on 6 July 2007. Atmos. Res. 2012, 118, 133–152. [Google Scholar] [CrossRef]
- Lee, K.O.; Uyeda, H.; Lee, D.I. Microphysical structures associated with enhancement of convective cells over Mt. Halla, Jeju Island, Korea on 6 July 2007. Atmos. Res. 2014, 135, 76–90. [Google Scholar] [CrossRef]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
- Bao, X.; Wu, L.; Tang, B.; Ma, L.; Wu, D.; Tang, J.; Chen, H.; Wu, L. Variable raindrop size distributions in different rainbands associated with Typhoon Fitow (2013). J. Geophys. Res. Atmos. 2019, 124, 12262–12281. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Experimental quantification of the sampling uncertainty associated with measurements from PARSIVEL disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An optical disdrometer for measuring size and velocity of hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Beard, K.V. Terminal velocity and shape of cloud and precipitation drops aloft. J. Atmos. Sci. 1976, 33, 851–864. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Marshall, J.S. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zhang, G.; Brandes, E. Polarimetric radar estimators based on a constrained gamma drop size distribution model. J. Appl. Meteorol. 2004, 43, 217–230. [Google Scholar] [CrossRef]
- Smith, P.L. Raindrop size distributions: Exponential or gamma—Does the difference matter? J. Appl. Meteorol. Climatol. 2003, 42, 1031–1034. [Google Scholar] [CrossRef]
- Yuter, S.E.; Houze, R.A., Jr. Measurements of raindrop size distributions over the Pacific warm pool and implications for Z–R relations. J. Appl. Meteorol. 1997, 36, 847–867. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation. J. Appl. Meteorol. Climatol. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteorol. Climatol. 1996, 35, 355–371. [Google Scholar] [CrossRef]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized” distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Waterman, P.C. Symmetry, unitarity, and geometry in electromagnetic scattering. Phys. Rev. D 1971, 3, 825. [Google Scholar] [CrossRef]
- Leinonen, J. High-level interface to T-matrix scattering calculations: Architecture, capabilities and limitations. Opt. Express 2014, 22, 1655–1660. [Google Scholar] [CrossRef]
- Thurai, M.; Huang, G.J.; Bringi, V.N.; Randeu, W.L.; Schönhuber, M. Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain. J. Atmos. Ocean. Technol. 2007, 24, 1019–1032. [Google Scholar] [CrossRef]
- Testik, F.Y.; Pei, B. Wind effects on the shape of raindrop size distribution. J. Hydrometeorol. 2017, 18, 1285–1303. [Google Scholar] [CrossRef]
- Lee, K.O.; Uyeda, H.; Lee, D.I. Effect of an isolated elliptical terrain (Jeju Island) on rainfall enhancement in a moist environment. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 20484. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).