Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks
Abstract
:1. Introduction
1.1. Our Contribution
- To the best of the authors’ knowledge, this is the first time a UAV-assisted radar-communication network has been investigated where several buoys conduct uplink NOMA data transmission with the UAV while cooperatively sensing the radar target. In order to improve the data collection performance, we exploit the flexible mobility of the UAV and the efficiency of NOMA. Meanwhile, the buoy transmit power is optimized to meliorate the data collection performance and radar target localization simultaneously.
- In order to maximize the system throughput and minimize the CRB of localization, we formulate a two-objective optimization problem of the UAV location and the transmit power of the buoys. To tackle the NP-hard problem, we proposed a joint communication and radar-sensing many-objective optimization (CRMOP) algorithm that achieves a superior balance of data collection and radar target sense.
- In order to facilitate a better comparison with the CRMOP algorithm proposed in this paper, we consider a baseline and propose a CRBC algorithm based on the traditional optimization method where the CRB is regarded as a constraint to maximize the system throughput. Through comprehensive simulations, we demonstrate that our proposed algorithm not only achieves significantly higher throughput but also ensures reliable target localization accuracy.
1.2. Paper Organization
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Method
3.1. Overall Process of the Proposed Algorithm
| Algorithm 1 Overall Process of the Proposed Algorithm |
|
| Algorithm 2 Initial Parameter Determination | |
| Output: | |
| Intial UAV’s location , buoy transmit power , weight vectors and neighborhood set of weight vectors . | |
| Process: | |
| 1: | Randomly generate the initial parent population and following the uniform distribution. |
| 2: | Use Das and Dennis’s method to generate weight vectors . |
| 3: | while do |
| 4: | Generate M closest neighborhood weight vectors to . |
| 5: | end while |
| 6: | Divide and to several non-domination levels by non-dominated sorting method. |
| 7: | Associate each value in and with unique sub-region. |
| Algorithm 3 Offspring Parameter Generation |
| Output: |
| Offspring solutions and . |
|
3.2. Parameter Initialization
| Algorithm 4 Constraint Operation |
|
3.3. Offspring Parameter Generation
| Algorithm 5 Update Parent Population of Parameters |
| Output: Parent populations of and . |
|
3.4. Update Parent Population Parameter
3.4.1. Case with Only One Non-domination Level
3.4.2. Case with More than One Nondomination Level
3.5. Convergency and Complexity Analysis
3.6. CRBC Optimization (Baseline)
4. Results and Discussion
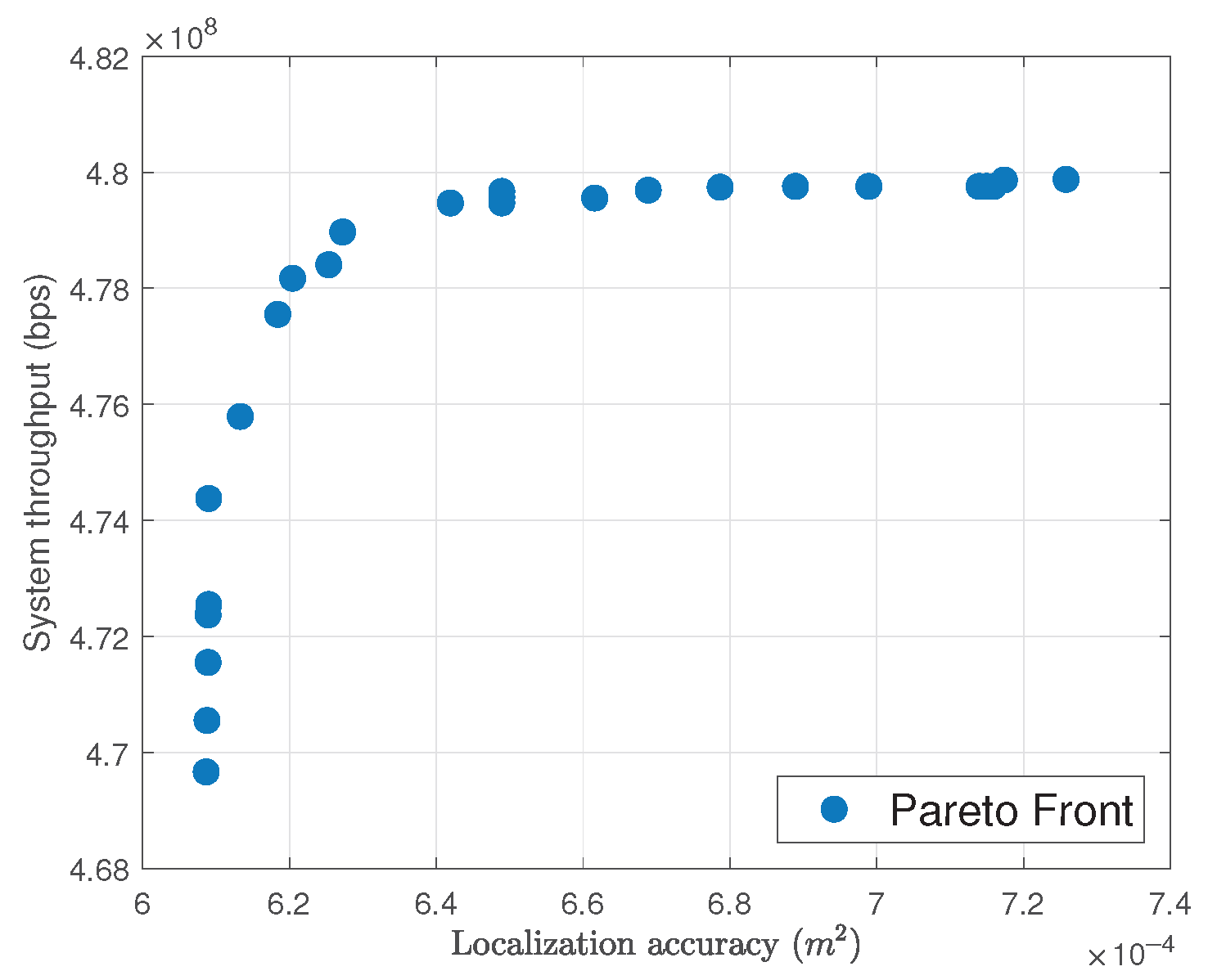
4.1. Nondominated Front Generation
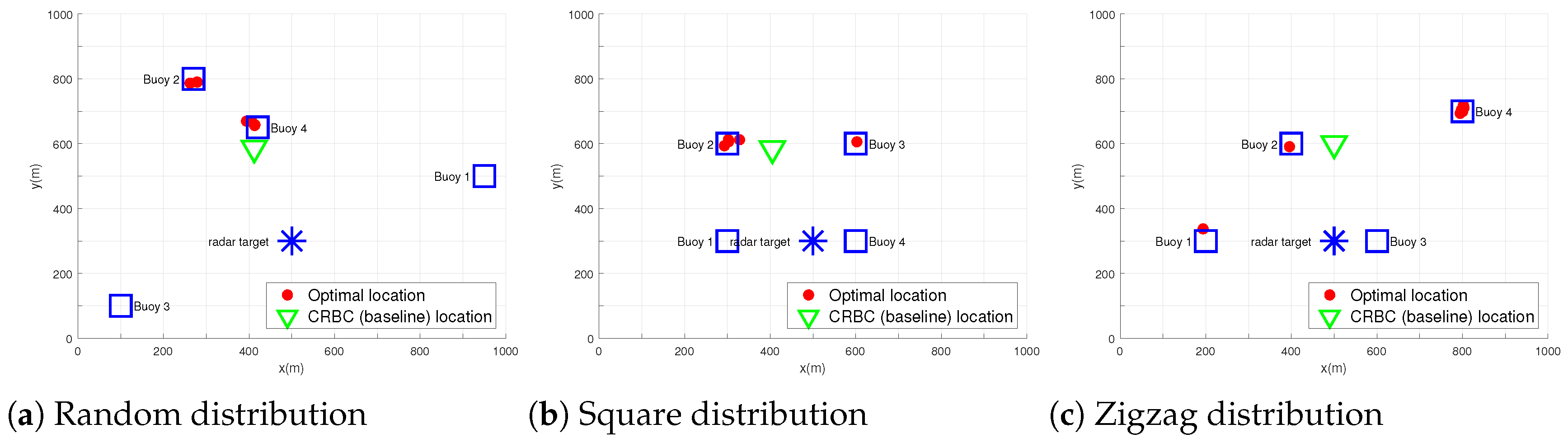
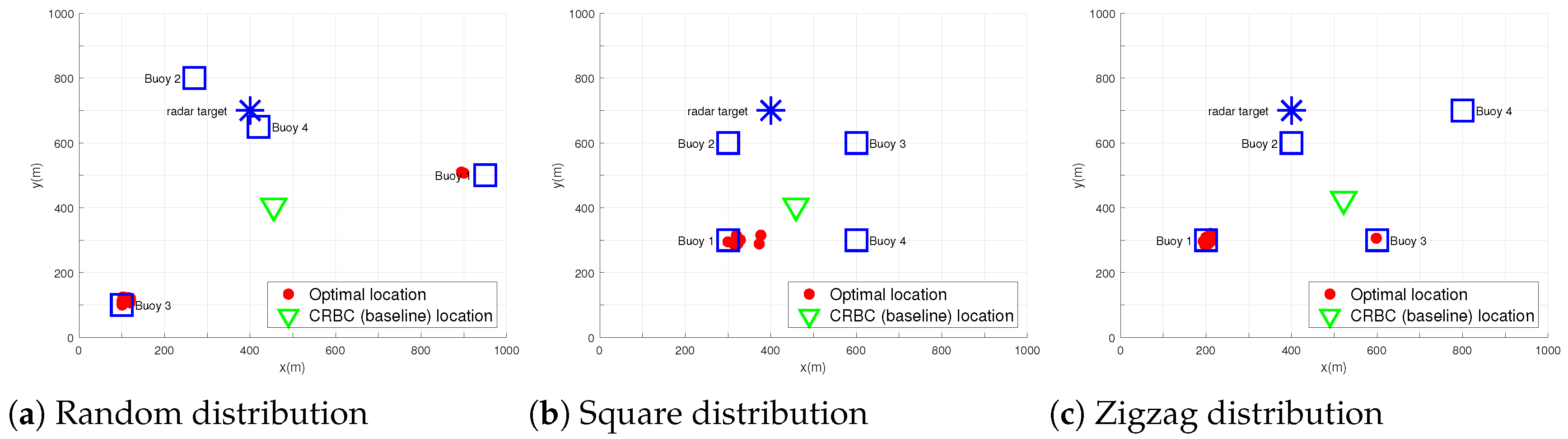
4.2. UAV Optimal Location
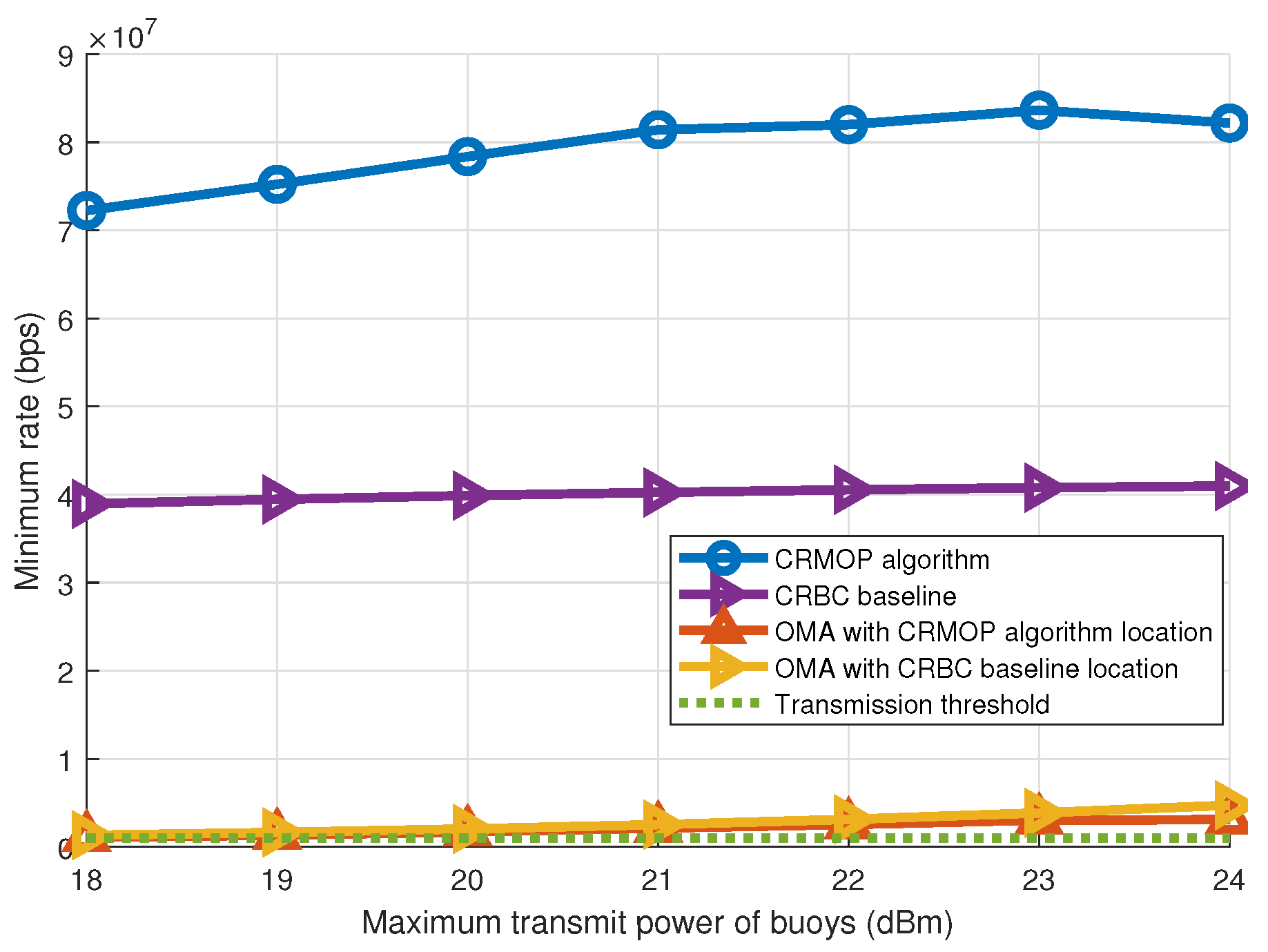
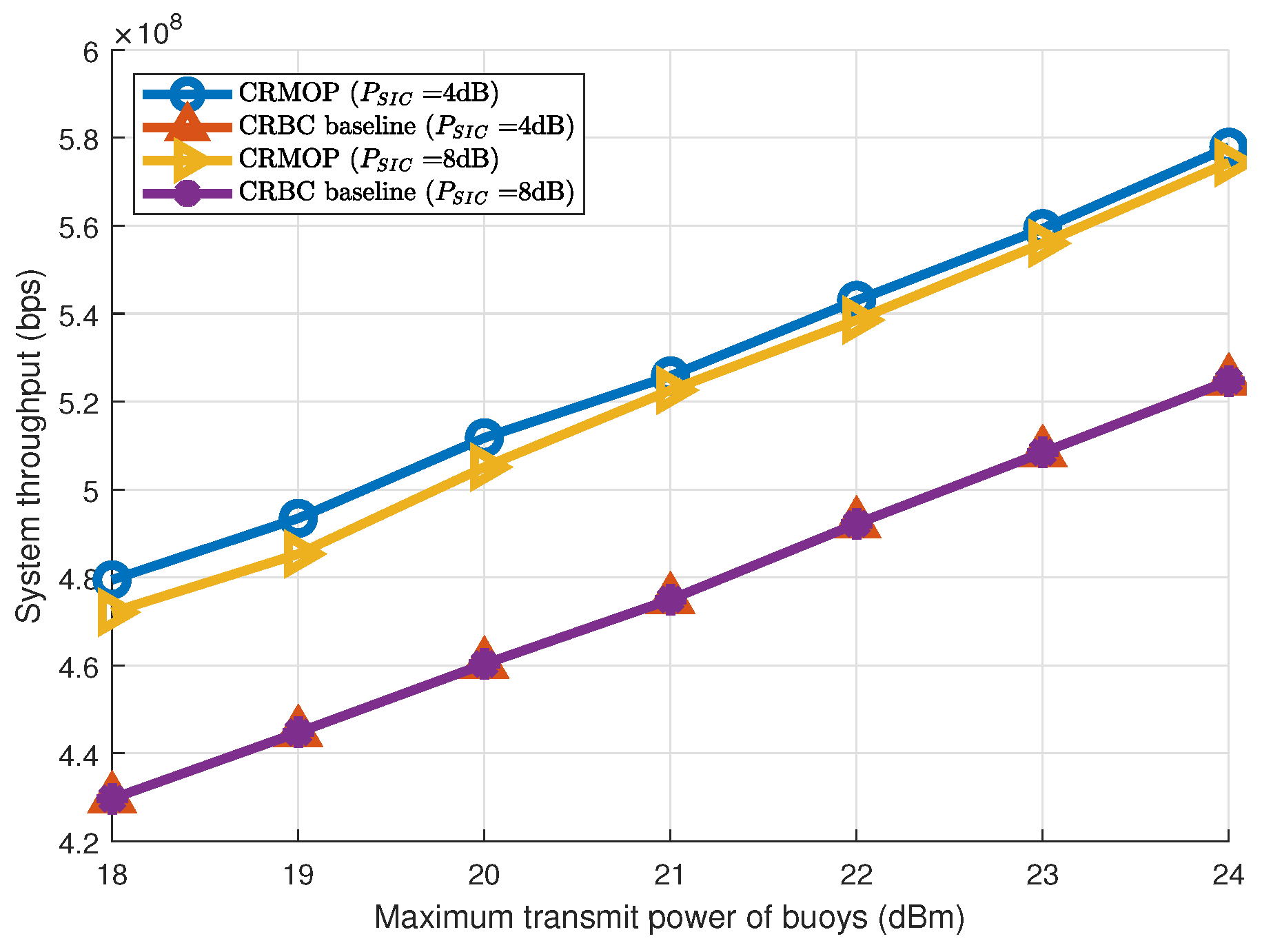
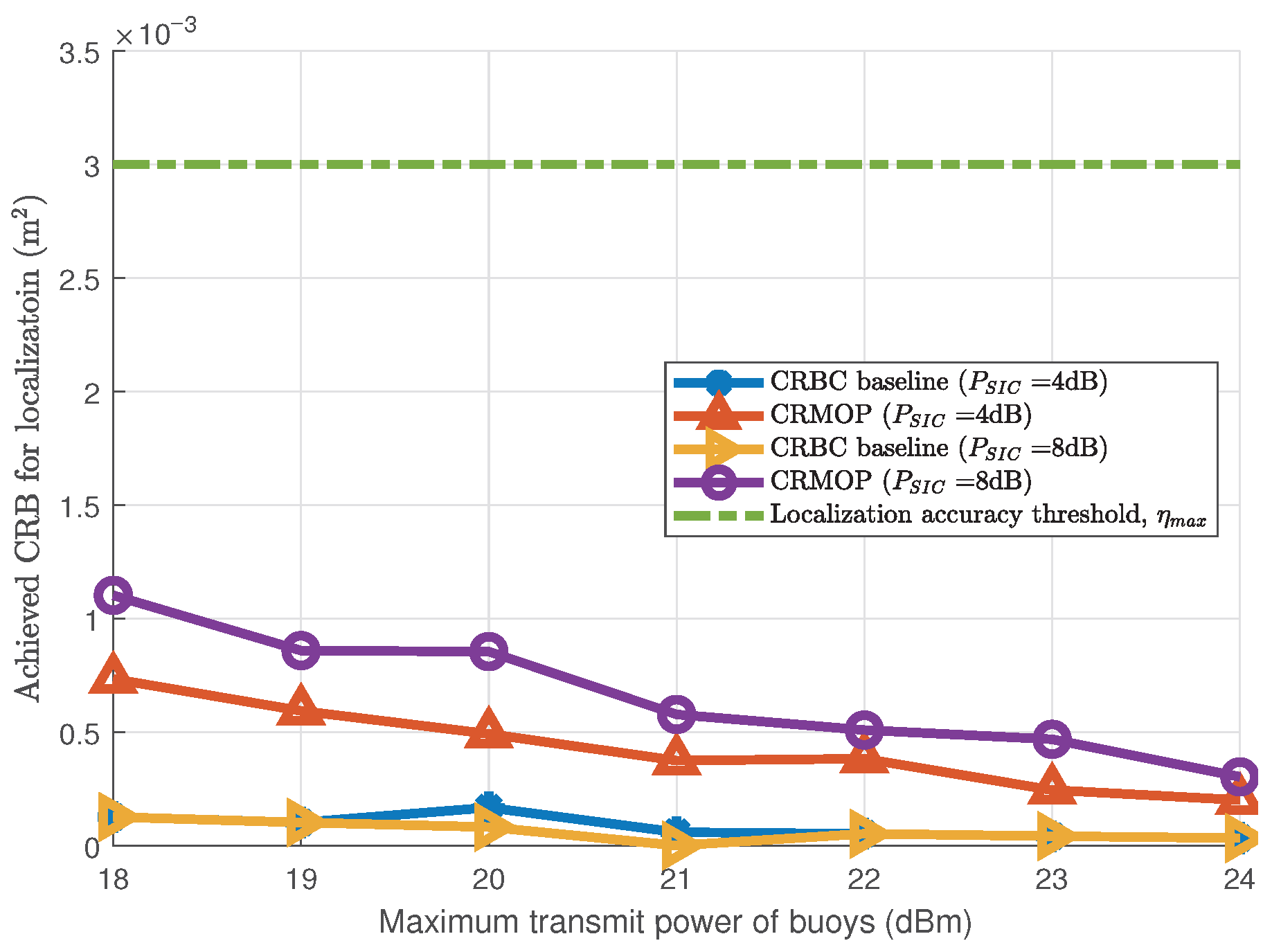
4.3. Performance Comparisons between CRMOP Algorithm and the CRBS Baseline
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.; Song, Y.; Jiang, N.; Xie, Z.; Fan, C.; Huang, X. Enhanced Doppler Resolution and Sidelobe Suppression Performance for Golay Complementary Waveforms. Remote Sens. 2023, 15, 2452. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Meng, X.; Zhou, B.; Fang, G.; Spencer, B.F. Discrimination Between Dry and Water Ices by Full Polarimetric Radar: Implications for China’s First Martian Exploration. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5100111. [Google Scholar] [CrossRef]
- Mao, Y.; Sun, R.; Wang, J.; Cheng, Q.; Kiong, L.C.; Ochieng, W.Y. New time-differenced carrier phase approach to GNSS/INS integration. GPS Solut. 2022, 26, 122. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Kak, A.; Nie, S. 6G and Beyond: The Future of Wireless Communications Systems. IEEE Access 2020, 8, 133995–134030. [Google Scholar] [CrossRef]
- Jiang, H.; Mukherjee, M.; Zhou, J.; Lloret, J. Channel Modeling and Characteristics for 6G Wireless Communications. IEEE Netw. 2021, 35, 296–303. [Google Scholar] [CrossRef]
- Wang, Q.; Dai, H.N.; Wang, Q.; Shukla, M.K.; Zhang, W.; Soares, C.G. On Connectivity of UAV-Assisted Data Acquisition for Underwater Internet of Things. IEEE Internet Things J. 2020, 7, 5371–5385. [Google Scholar] [CrossRef]
- Wang, X.; Fu, L.; Chen, N.; Sun, R.; Luan, T.H.; Quan, W.; Aldubaikhy, K. Joint Flying Relay Location and Routing Optimization for 6G UAV-IoT Networks: A Graph Neural Network-Based Approach. Remote Sens. 2022, 14, 4377. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Beatty, S. Cellular Communications in Ocean Waves for Maritime Internet of Things. IEEE Internet Things J. 2020, 7, 9965–9979. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Rotary-Wing UAV Enabled Wireless Network: Trajectory Design and Resource Allocation. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, Saudi Arabia, 9–13 December 2018. [Google Scholar]
- Zheng, Q.; Zhao, P.; Li, Y.; Wang, H.; Yang, Y. Spectrum interference-based two-level data augmentation method in deep learning for automatic modulation classification. Neural Comput. Appl. 2021, 33, 7723–7745. [Google Scholar] [CrossRef]
- Lian, Z.; Ji, P.; Wang, Y.; Su, Y.; Jin, B.; Zhang, Z.; Xie, Z.; Li, S. Geometry-Based UAV-MIMO Channel Modeling Assisted by Intelligent Reflecting Surface. IEEE Trans. Veh. Technol. 2022, 71, 6698–6703. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Zhang, M.; Cumanan, K.; Kwan Ng, D.W.; Zhang, G.; Tang, J.; Dobre, O.A. Energy-Constrained UAV-Assisted Secure Communications With Position Optimization and Cooperative Jamming. IEEE Trans. Commun. 2020, 68, 4476–4489. [Google Scholar] [CrossRef]
- Xie, L.; Xu, J.; Zhang, R. Throughput Maximization for UAV-Enabled Wireless Powered Communication Networks. IEEE Internet Things J. 2019, 6, 1690–1703. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutorials 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Ma, R.; Wang, R.; Liu, G.; Chen, H.H.; Qin, Z. UAV-Assisted Data Collection for Ocean Monitoring Networks. IEEE Netw. 2020, 34, 250–258. [Google Scholar] [CrossRef]
- Mei, W.; Zhang, R. Uplink Cooperative NOMA for Cellular-Connected UAV. IEEE J. Sel. Top. Signal Process. 2019, 13, 644–656. [Google Scholar] [CrossRef]
- Zhao, N.; Pang, X.; Li, Z.; Chen, Y.; Li, F.; Ding, Z.; Alouini, M.S. Joint Trajectory and Precoding Optimization for UAV-Assisted NOMA Networks. IEEE Trans. Commun. 2019, 67, 3723–3735. [Google Scholar] [CrossRef]
- Wang, N.; Li, F.; Chen, D.; Liu, L.; Bao, Z. NOMA-Based Energy-Efficiency Optimization for UAV Enabled Space-Air-Ground Integrated Relay Networks. IEEE Trans. Veh. Technol. 2022, 71, 4129–4141. [Google Scholar] [CrossRef]
- De Lima, C.; Belot, D.; Berkvens, R.; Bourdoux, A.; Dardari, D.; Guillaud, M.; Isomursu, M.; Lohan, E.S.; Miao, Y.; Barreto, A.N.; et al. Convergent Communication, Sensing and Localization in 6G Systems: An Overview of Technologies, Opportunities and Challenges. IEEE Access 2021, 9, 26902–26925. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Li, L.; Ma, Y.; Zhou, C.; Zhang, D. A New Method of Inland Water Ship Trajectory Prediction Based on Long Short-Term Memory Network Optimized by Genetic Algorithm. Appl. Sci. 2022, 12, 4073. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, F.; Li, B.; Yang, Z.; Wu, Y.; Zhu, H. Placement optimization of caching UAV-assisted mobile relay maritime communication. China Commun. 2020, 17, 209–219. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Wang, G.; Niu, Y.; Yang, M.; Wang, J.; Li, Y.; Zhong, Z. Impact of UAV Rotation on MIMO Channel Characterization for Air-to-Ground Communication Systems. IEEE Trans. Veh. Technol. 2020, 69, 12418–12431. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.X.; Chang, H.; He, Y.; Bian, J. A Novel Non-Stationary 6G UAV Channel Model for Maritime Communications. IEEE J. Sel. Areas Commun. 2021, 39, 2992–3005. [Google Scholar] [CrossRef]
- Yin, J.; Hoogeboom, P.; Unal, C.; Russchenberg, H.; van der Zwan, F.; Oudejans, E. UAV-Aided Weather Radar Calibration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10362–10375. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Zhang, J.A.; Liu, F.; Masouros, C.; Heath, R.W.; Feng, Z.; Zheng, L.; Petropulu, A. An Overview of Signal Processing Techniques for Joint Communication and Radar Sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1295–1315. [Google Scholar] [CrossRef]
- Wen, C.; Huang, Y.; Zheng, L.; Liu, W.; Davidson, T.N. Transmit Waveform Design for Dual-Function Radar-Communication Systems via Hybrid Linear-Nonlinear Precoding. IEEE Trans. Signal Process. 2023, 71, 2130–2145. [Google Scholar] [CrossRef]
- Ma, D.; Shlezinger, N.; Huang, T.; Liu, Y.; Eldar, Y.C. Joint Radar-Communication Strategies for Autonomous Vehicles: Combining Two Key Automotive Technologies. IEEE Signal Process. Mag. 2020, 37, 85–97. [Google Scholar] [CrossRef]
- Liu, R.; Li, M.; Liu, Y.; Wu, Q.; Liu, Q. Joint Transmit Waveform and Passive Beamforming Design for RIS-Aided DFRC Systems. IEEE J. Sel. Top. Signal Process. 2022, 16, 995–1010. [Google Scholar] [CrossRef]
- Wang, X.; Hassanien, A.; Amin, M.G. Dual-Function MIMO Radar Communications System Design Via Sparse Array Optimization. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1213–1226. [Google Scholar] [CrossRef]
- Ma, D.; Shlezinger, N.; Huang, T.; Shavit, Y.; Namer, M.; Liu, Y.; Eldar, Y.C. Spatial Modulation for Joint Radar-Communications Systems: Design, Analysis, and Hardware Prototype. IEEE Trans. Veh. Technol. 2021, 70, 2283–2298. [Google Scholar] [CrossRef]
- Wang, X.; Fei, Z.; Zhang, J.A.; Huang, J.; Yuan, J. Constrained Utility Maximization in Dual-Functional Radar-Communication Multi-UAV Networks. IEEE Trans. Commun. 2021, 69, 2660–2672. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.; da Fonseca, V. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, J.; Leung, H.; Wang, W. Adaptive Weighted Optimization Framework for Multiobjective Long-Term Planning of Concentrate Ingredients in Copper Industry. IEEE Trans. Instrum. Meas. 2022, 71, 2508913. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, S.; Shi, M.; Guo, Y. Angle-Based Multi-Objective Evolutionary Algorithm Based On Pruning-Power Indicator for Game Map Generation. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 341–354. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, S.; Wang, H.; Savić, D.A. Multi-Objective Cuckoo Search for the Optimal Design of Water Distribution Systems. In Civil Engineering and Urban Planning; ASCE: Reston, VA, USA, 2012. [Google Scholar]
- Wagner, T.; Beume, N.; Naujoks, B. Pareto-, Aggregation-, and Indicator-Based Methods in Many-Objective Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An Evolutionary Many-Objective Optimization Algorithm Based on Dominance and Decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Huang, X.; Suvorova, S.; Moran, B. Detection of moving targets in sea clutter using complementary waveforms. Signal Process. 2018, 146, 15–21. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Liu, T.; Chen, H.; Wang, Y.L. Detector Design and Performance Analysis for Target Detection in Subspace Interference. IEEE Signal Process. Lett. 2023, 30, 618–622. [Google Scholar] [CrossRef]
- Ruan, Y.; Jiang, L.; Li, Y.; Zhang, R. Energy-Efficient Power Control for Cognitive Satellite-Terrestrial Networks With Outdated CSI. IEEE Syst. J. 2021, 15, 1329–1332. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for Multi-UAV Enabled Wireless Networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Liu, Y.; Han, F.; Zhao, S. Flexible and Reliable Multiuser SWIPT IoT Network Enhanced by UAV-Mounted Intelligent Reflecting Surface. IEEE Trans. Reliab. 2022, 71, 1092–1103. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Power Allocation Strategies for Target Localization in Distributed Multiple-Radar Architectures. IEEE Trans. Signal Process. 2011, 59, 3226–3240. [Google Scholar] [CrossRef]
- Guerra, A.; Dardari, D.; Djuric, P.M. Dynamic Radar Networks of UAVs: A Tutorial Overview and Tracking Performance Comparison With Terrestrial Radar Networks. IEEE Veh. Technol. Mag. 2020, 15, 113–120. [Google Scholar] [CrossRef]
- Meikle, H. Modern Radar Systems; Artech House: London, UK, 2008. [Google Scholar]
- Hassani, S.A.; Guevara, A.; Parashar, K.; Bourdoux, A.; van Liempd, B.; Pollin, S. An In-Band Full-Duplex Transceiver for Simultaneous Communication and Environmental Sensing. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 1389–1394. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. Siam J. Optim. 1996, 8, 631–657. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems With Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Zhang, Q. Efficient Nondomination Level Update Method for Steady-State Evolutionary Multiobjective Optimization. IEEE Trans. Cybern. 2017, 47, 2838–2849. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A New Dominance Relation-Based Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 16–37. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Zhao, N.; Chen, Y.; Zhang, S.; Ding, Z.; Yu, F.R. Placement and Power Allocation for NOMA-UAV Networks. IEEE Wirel. Commun. Lett. 2019, 8, 965–968. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs. In Recent Advances in Learning and Control; Blondel, V., Boyd, S., Kimura, H., Eds.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2008; pp. 95–110. Available online: https://web.stanford.edu/~boyd/papers/graph_dcp.html (accessed on 22 June 2023).
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]


| Acronym | Definitions |
|---|---|
| UAV | Unmanned Aerial Vehicle |
| LoS | Line-of-sight |
| NOMA | Non-orthogonal Multiple Access |
| BS | Base Station |
| DFRC | Dual-functional Radar-communication |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| MOEA/DD | Many-objective Optimization Algorithm Based on Dominance and Decomposition |
| CRB | Cramer–Rao Bound |
| CRBC | CRB Constrained |
| CRMOP | Communication and Radar-Sensing Many-objective Optimization |
| AP | Access Point |
| 3D | Three-dimensional |
| CSI | Channel State Information |
| AWGN | Additive White Gaussian Noise |
| RCS | Radar Cross-section |
| MSE | Mean Square Error |
| PBI | Penalty-based Boundary Intersection |
| SBX | Simulated Binary Crossover |
| PF | Pareto Front |
| OMA | Orthogonal Multiple Access |
| Parameters | Values |
|---|---|
| Height of the UAV | 100 m |
| Target Location 1 | m |
| Target Location 2 | m |
| Minimum data rate requirement | 1 Mbps |
| Reference channel gain | −60 dB |
| AWGN power | −110 dBm |
| Probability of mating parents selection | 0.9 |
| Localization accuracy threshold | 3 |
| Minimum distance between UAV and target | 300 m |
| Distribution Type | Target Location | Algorithm | UAV Location | Buoy 1 Power (W) | Buoy 2 Power (W) | Buoy 3 Power (W) | Buoy 4 Power (W) | Throughput ( bps) | CRB for Localization ( m) |
|---|---|---|---|---|---|---|---|---|---|
| Random | 1 | CRMOP | [414.4384;662.3422] | 0.0630 | 0.0631 | 0.0631 | 0.0053 | 4.792 | 8.67 |
| [274.2414;787.6419] | 0.0626 | 0.0629 | 0.0607 | 0.0337 | 4.784 | 6.796 | |||
| CRBC | [412.0546;586.8216] | 0.0424 | 0.0433 | 0.0352 | 0.0518 | 4.2967 | 1.26 | ||
| 2 | CRMOP | [100.0000;109.5802] | 0.0630 | 0.0569 | 0.0324 | 0.0122 | 4.6683 | 1.976 | |
| [894.3048;509.9927] | 0.0614 | 0.0606 | 0.0428 | 0.0366 | 4.487 | 1.140 | |||
| CRBC | [455.3978;405.1585] | 0.0315 | 0.0313 | 0.0356 | 0.0524 | 3.2945 | 0.59 | ||
| Square | 1 | CRMOP | [305.7863;603.6381] | 0.0631 | 0.0622 | 0.0367 | 0.0075 | 4.7591 | 1.1316 |
| [610.1607;599.8689] | 0.0612 | 0.0630 | 0.0322 | 0.0174 | 4.734 | 1.035 | |||
| CRBC | [405.1476;584.6103] | 0.0364 | 0.0427 | 0.0463 | 0.0418 | 4.2008 | 0.946 | ||
| 2 | CRMOP | [328.6521;300.8771] | 0.0629 | 0.0631 | 0.0416 | 0.0078 | 4.729 | 1.05 | |
| [322.7507;288.2979] | 0.0630 | 0.0631 | 0.0402 | 0.0078 | 4.732 | 0.903 | |||
| CRBC | [458.8498;405.8288] | 0.0384 | 0.0479 | 0.0421 | 0.0377 | 4.141 | 0.79 | ||
| Zigzag | 1 | CRMOP | [794.4881;693.4549] | 0.0628 | 0.0602 | 0.0358 | 0.0155 | 4.624 | 3.24 |
| [395.6543;590.6740] | 0.0631 | 0.0606 | 0.0330 | 0.0029 | 4.751 | 1.74 | |||
| CRBC | [499.9866;600.0000] | 0.0349 | 0.0487 | 0.0428 | 0.0384 | 4.0625 | 1.245 | ||
| 2 | CRMOP | [196.9071;285.9520] | 0.0602 | 0.0631 | 0.0300 | 0.0492 | 4.62 | 2.12 | |
| [210.7754;320.6452] | 0.0631 | 0.0581 | 0.0264 | 0.0426 | 4.68 | 2.10 | |||
| CRBC | [521.8621;425.8656] | 0.0358 | 0.0519 | 0.0353 | 0.0323 | 3.995 | 1.587 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, S.; Han, F.; Chai, M.; Jiang, H.; Zhang, H. Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks. Remote Sens. 2023, 15, 5126. https://doi.org/10.3390/rs15215126
Liu Y, Zhao S, Han F, Chai M, Jiang H, Zhang H. Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks. Remote Sensing. 2023; 15(21):5126. https://doi.org/10.3390/rs15215126
Chicago/Turabian StyleLiu, Yuan, Shengjie Zhao, Fengxia Han, Mengqiu Chai, Hao Jiang, and Hongming Zhang. 2023. "Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks" Remote Sensing 15, no. 21: 5126. https://doi.org/10.3390/rs15215126
APA StyleLiu, Y., Zhao, S., Han, F., Chai, M., Jiang, H., & Zhang, H. (2023). Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks. Remote Sensing, 15(21), 5126. https://doi.org/10.3390/rs15215126








