Airborne Radio-Echo Sounding Data Denoising Using Particle Swarm Optimization and Multivariate Variational Mode Decomposition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Principles of MVMD
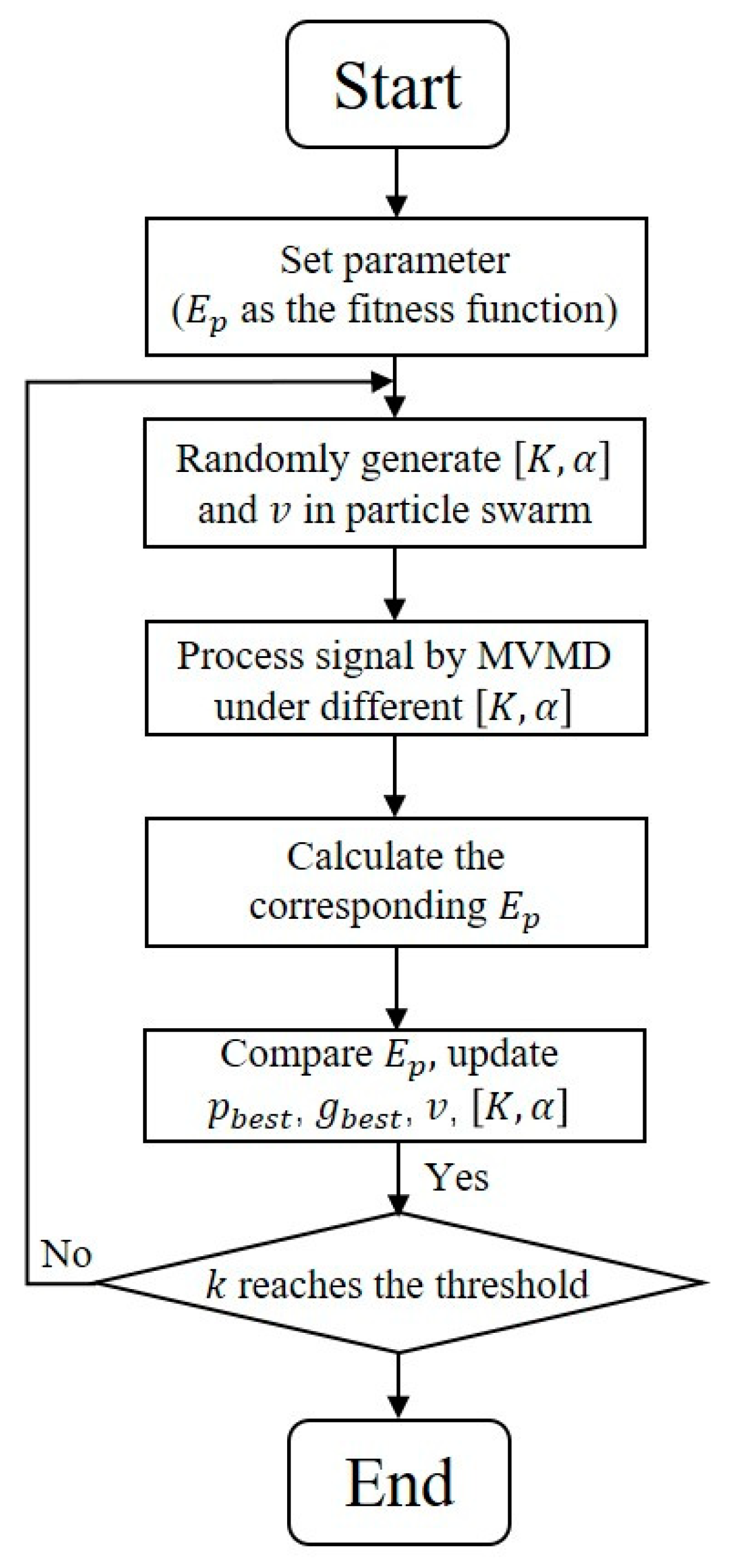
2.2. The PSO–MVMD Algorithm for Optimal Parameters of
2.3. Energy Entropy Used to Select the Effective IMF
2.4. The SNR, PSNR, and RMSE for the Evaluation of the Denoising Effect
3. Results
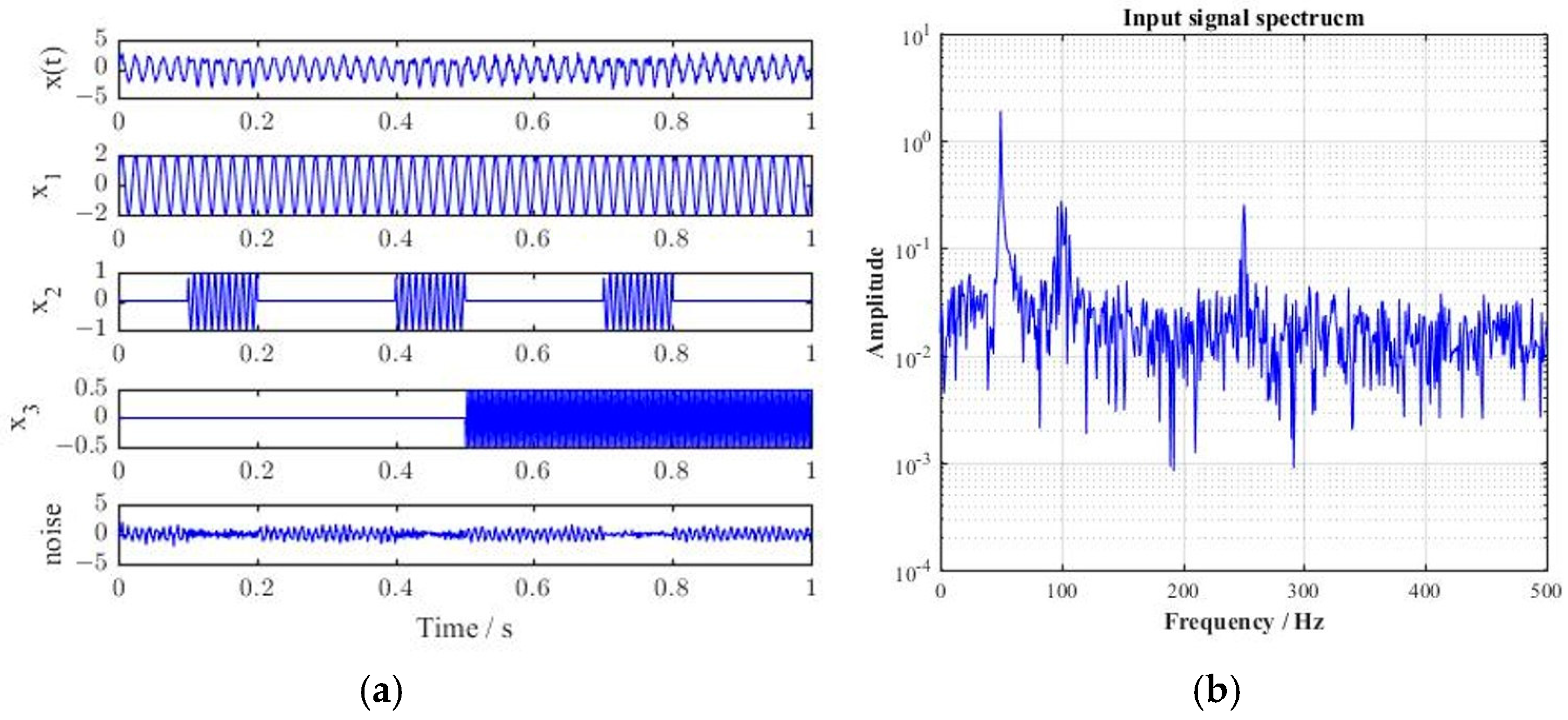
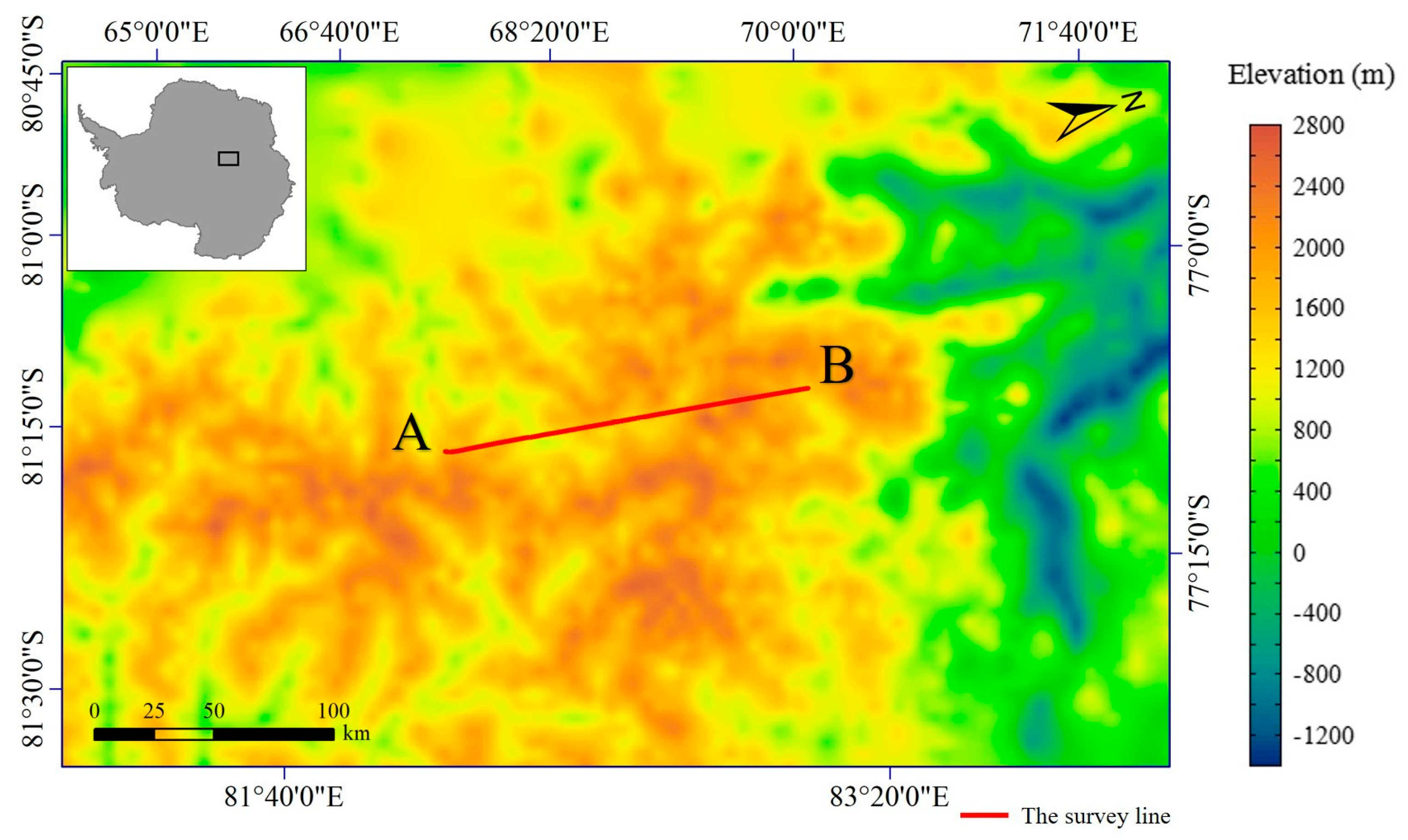
3.1. Radio-Echo Sounding Data
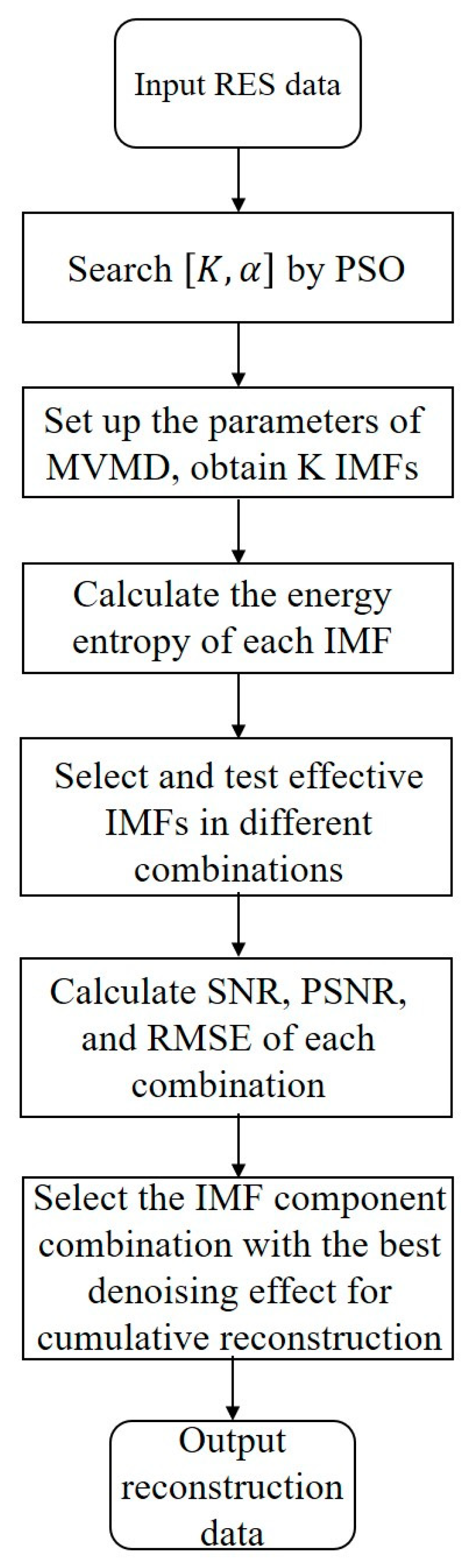
3.2. Data-Processing Procedure
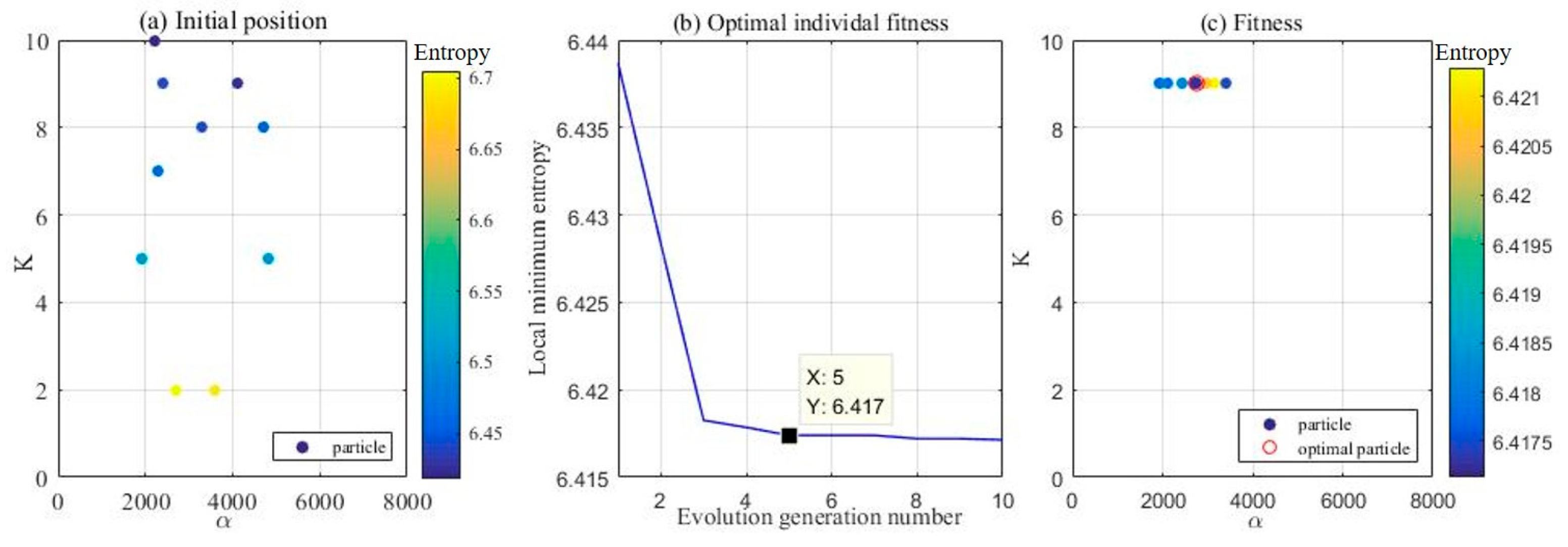
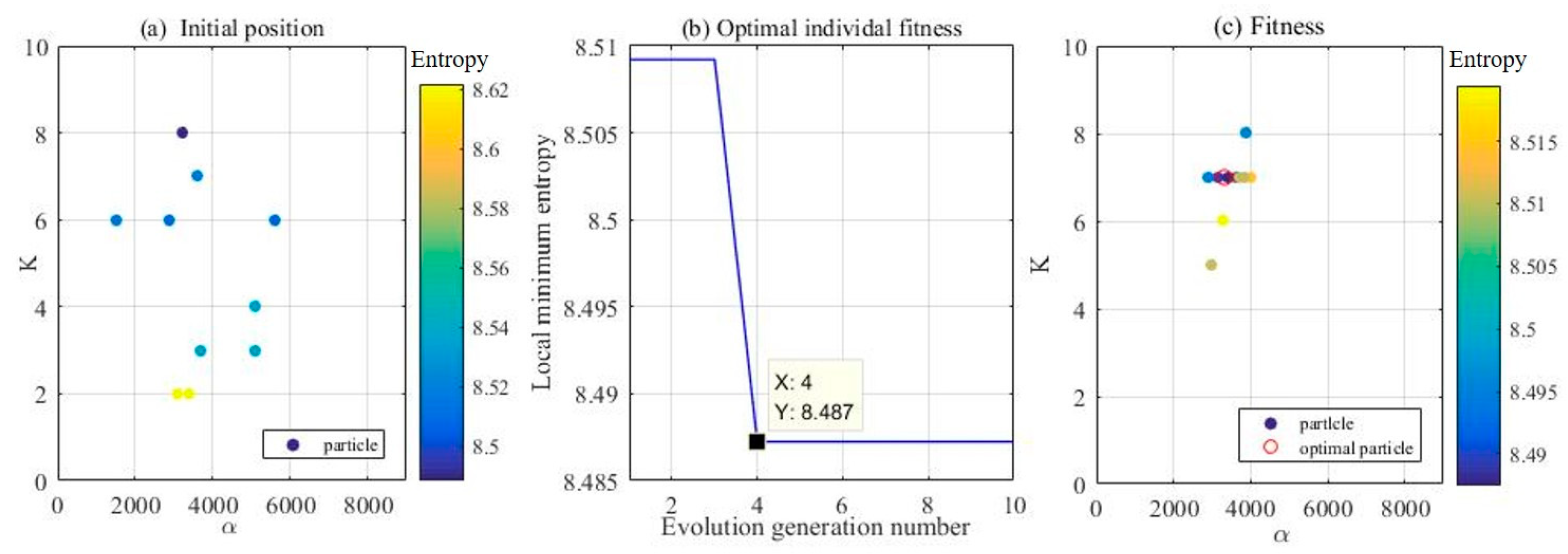
3.3. Parameter Settings
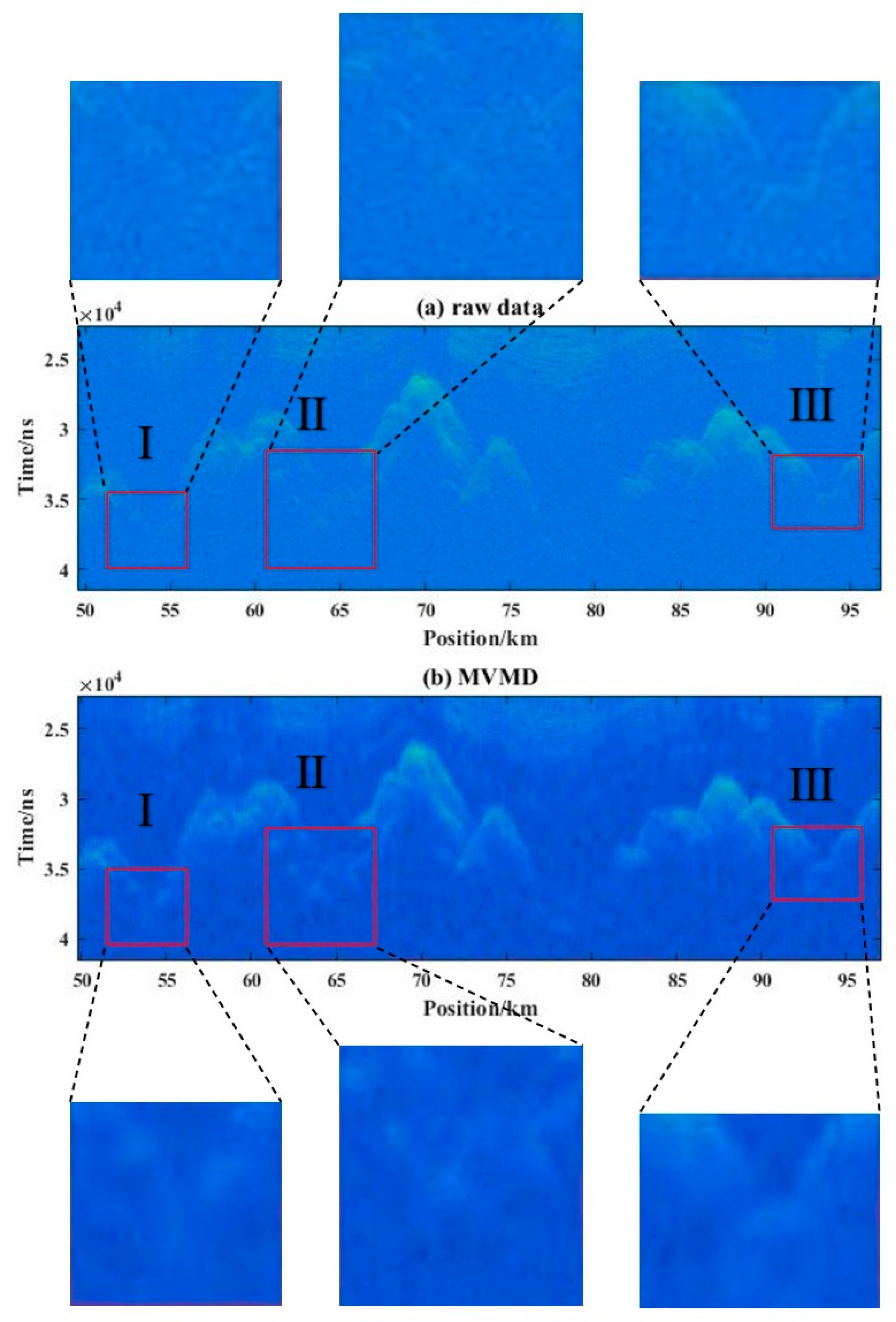
3.4. Data Reconstruction
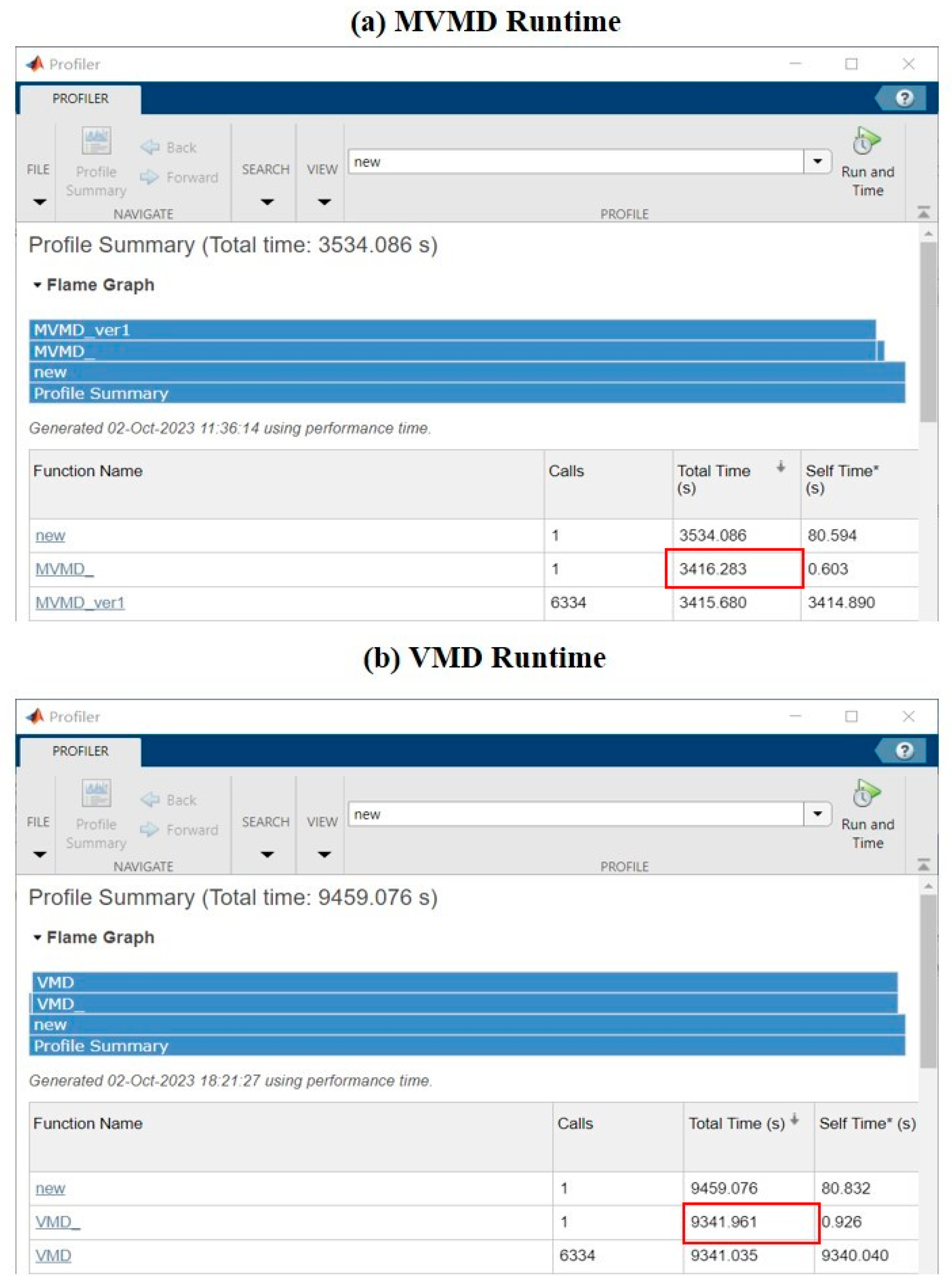
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mas E Braga, M.; Selwyn Jones, R.; Newall, J.C.H.; Rogozhina, I.; Andersen, J.L.; Lifton, N.A.; Stroeven, A.P. Nunataks as Barriers to Ice Flow: Implications for Palaeo Ice Sheet Reconstructions. Cryosphere 2021, 15, 4929–4947. [Google Scholar] [CrossRef]
- Gulick, S.P.S.; Shevenell, A.E.; Montelli, A.; Fernandez, R.; Smith, C.; Warny, S.; Bohaty, S.M.; Sjunneskog, C.; Leventer, A.; Frederick, B.; et al. Initiation and Long-Term Instability of the East Antarctic Ice Sheet. Nature 2017, 552, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Aitken, A.R.A.; Roberts, J.L.; Ommen, T.D.V.; Young, D.A.; Golledge, N.R.; Greenbaum, J.S.; Blankenship, D.D.; Siegert, M.J. Repeated Large-Scale Retreat and Advance of Totten Glacier Indicated by Inland Bed Erosion. Nature 2016, 533, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Stokes, C.R.; Abram, N.J.; Bentley, M.J.; Edwards, T.L.; England, M.H.; Foppert, A.; Jamieson, S.S.R.; Jones, R.S.; King, M.A.; Lenaerts, J.T.M.; et al. Response of the East Antarctic Ice Sheet to Past and Future Climate Change. Nature 2022, 608, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Ashmore, D.W.; Bingham, R.G.; Ross, N.; Siegert, M.J.; Jordan, T.A.; Mair, D.W.F. Englacial Architecture and Age-Depth Constraints Across the West Antarctic Ice Sheet. Geophys. Res. Lett. 2020, 47, e2019GL086663. [Google Scholar] [CrossRef]
- Sutter, J.; Fischer, H.; Eisen, O. Investigating the Internal Structure of the Antarctic Ice Sheet: The Utility of Isochrones for Spatiotemporal Ice-Sheet Model Calibration. Cryosphere 2021, 15, 3839–3860. [Google Scholar] [CrossRef]
- Frémand, A.C.; Fretwell, P.; Bodart, J.A.; Pritchard, H.D.; Aitken, A.; Bamber, J.L.; Bell, R.; Bianchi, C.; Bingham, R.G.; Blankenship, D.D.; et al. Antarctic Bedmap Data: Findable, Accessible, Interoperable, and Reusable (FAIR) Sharing of 60 Years of Ice Bed, Surface, and Thickness Data. Earth Syst. Sci. Data 2023, 15, 2695–2710. [Google Scholar] [CrossRef]
- Sime, L.C.; Karlsson, N.B.; Paden, J.D.; Prasad Gogineni, S. Isochronous Information in a Greenland Ice Sheet Radio Echo Sounding Data Set. Geophys. Res. Lett. 2014, 41, 1593–1599. [Google Scholar] [CrossRef]
- Morlighem, M.; Rignot, E.; Binder, T.; Blankenship, D.; Drews, R.; Eagles, G.; Eisen, O.; Ferraccioli, F.; Forsberg, R.; Fretwell, P.; et al. Deep Glacial Troughs and Stabilizing Ridges Unveiled beneath the Margins of the Antarctic Ice Sheet. Nat. Geosci. 2020, 13, 132–137. [Google Scholar] [CrossRef]
- Frémand, A.C.; Bodart, J.A.; Jordan, T.A.; Ferraccioli, F.; Robinson, C.; Corr, H.F.J.; Peat, H.J.; Bingham, R.G.; Vaughan, D.G. British Antarctic Survey’s Aerogeophysical Data: Releasing 25 Years of Airborne Gravity, Magnetic, and Radar Datasets over Antarctica. Earth Syst. Sci. Data 2022, 14, 3379–3410. [Google Scholar] [CrossRef]
- Bingham, R.G.; Rippin, D.M.; Karlsson, N.B.; Corr, H.F.J.; Ferraccioli, F.; Jordan, T.A.; Le Brocq, A.M.; Rose, K.C.; Ross, N.; Siegert, M.J. Ice-flow Structure and Ice Dynamic Changes in the Weddell Sea Sector of West Antarctica from Radar-imaged Internal Layering. J. Geophys. Res. Earth Surf. 2015, 120, 655–670. [Google Scholar] [CrossRef]
- Bell, R.E.; Seroussi, H. History, Mass Loss, Structure, and Dynamic Behavior of the Antarctic Ice Sheet. Science 2020, 367, 1321–1325. [Google Scholar] [CrossRef] [PubMed]
- Rose, K.C.; Ferraccioli, F.; Jamieson, S.S.R.; Bell, R.E.; Corr, H.; Creyts, T.T.; Braaten, D.; Jordan, T.A.; Fretwell, P.T.; Damaske, D. Early East Antarctic Ice Sheet Growth Recorded in the Landscape of the Gamburtsev Subglacial Mountains. Earth Planet. Sci. Lett. 2013, 375, 1–12. [Google Scholar] [CrossRef]
- Franke, S.; Eisermann, H.; Jokat, W.; Eagles, G.; Asseng, J.; Miller, H.; Steinhage, D.; Helm, V.; Eisen, O.; Jansen, D. Preserved Landscapes underneath the Antarctic Ice Sheet Reveal the Geomorphological History of Jutulstraumen Basin. Earth Surf. Processes Landf. 2021, 46, 2728–2745. [Google Scholar] [CrossRef]
- Winter, A.; Steinhage, D.; Creyts, T.T.; Kleiner, T.; Eisen, O. Age Stratigraphy in the East Antarctic Ice Sheet Inferred from Radio-Echo Sounding Horizons. Earth Syst. Sci. Data 2019, 11, 1069–1081. [Google Scholar] [CrossRef]
- Tang, X.; Sun, B.; Wang, T. Radar Isochronic Layer Dating for a Deep Ice Core at Kunlun Station, Antarctica. Sci. China Earth Sci. 2020, 63, 303–308. [Google Scholar] [CrossRef]
- Dong, S.; Tang, X.; Guo, J.; Fu, L.; Chen, X.; Sun, B. EisNet: Extracting Bedrock and Internal Layers From Radiostratigraphy of Ice Sheets With Machine Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Tang, X.; Luo, K.; Dong, S.; Zhang, Z.; Sun, B. Quantifying Basal Roughness and Internal Layer Continuity Index of Ice Sheets by an Integrated Means with Radar Data and Deep Learning. Remote Sens. 2022, 14, 4507. [Google Scholar] [CrossRef]
- Cavitte, M.G.P.; Blankenship, D.D.; Young, D.A.; Schroeder, D.M.; Parrenin, F.; Lemeur, E.; Macgregor, J.A.; Siegert, M.J. Deep Radiostratigraphy of the East Antarctic Plateau: Connecting the Dome C and Vostok Ice Core Sites. J. Glaciol. 2016, 62, 323–334. [Google Scholar] [CrossRef]
- Glen, J.W.; Paren, J.G. The Electrical Properties of Snow and Ice. J. Glaciol. 1975, 15, 15–38. [Google Scholar] [CrossRef]
- Fujita, S.; Mae, S.; Matsuoka, T. Dielectric Anisotropy in Ice Ih at 9.7 GHz. Ann. Glaciol. 1993, 17, 276–280. [Google Scholar] [CrossRef]
- Steinhage, D.; Kipfstuhl, S.; Nixdorf, U.; Miller, H. Internal Structure of the Ice Sheet between Kohnen Station and Dome Fuji, Antarctica, Revealed by Airborne Radio-Echo Sounding. Ann. Glaciol. 2013, 54, 163–167. [Google Scholar] [CrossRef]
- Johari, G.P.; Charette, P.A. The Permittivity and Attenuation in Polycrystalline and Single-Crystal Ice Ih at 35 and 60 MHz. J. Glaciol. 1975, 14, 293–303. [Google Scholar] [CrossRef]
- Volkov, A.A.; Vasin, A.A.; Volkov, A.A. Dielectric Properties of Water and Ice: A Unified Treatment. Ferroelectrics 2019, 538, 83–88. [Google Scholar] [CrossRef]
- King, E.C. The Precision of Radar-Derived Subglacial Bed Topography: A Case Study from Pine Island Glacier, Antarctica. Ann. Glaciol. 2020, 61, 154–161. [Google Scholar] [CrossRef]
- Lin, L. The Research on Subglacial Geophysical Characteristics of Princess Elizabeth Land in East Antarctic; Jilin University: Changchun, China, 2016. [Google Scholar]
- Cheng, S.; Liu, S.; Guo, J.; Luo, K.; Zhang, L.; Tang, X. Data Processing and Interpretation of Antarctic Ice-Penetrating Radar Based on Variational Mode Decomposition. Remote Sens. 2019, 11, 1253. [Google Scholar] [CrossRef]
- Scanlan, K.M.; Rutishauser, A.; Young, D.A.; Blankenship, D.D. Interferometric Discrimination of Cross-Track Bed Clutter in Ice-Penetrating Radar Sounding Data. Ann. Glaciol. 2020, 61, 68–73. [Google Scholar] [CrossRef]
- Lilien, D.A.; Hills, B.H.; Driscol, J.; Jacobel, R.; Christianson, K. ImpDAR: An Open-Source Impulse Radar Processor. Ann. Glaciol. 2020, 61, 114–123. [Google Scholar] [CrossRef]
- Liu, S.C.; Gao, E.G.; Xun, C. Seismic Data Denoising Simulation Research Based on Wavelet Transform. AMM 2014, 490–491, 1356–1360. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Chandran, D.; Burman, S. Subsurface Imaging and Interpretation Using Ground Penetrating Radar (GPR) and Fast Fourier Transformation (FFT). In Information Technology in Geo-Engineering: Proceedings of the 2nd International Conference (ICITG) Durham, UK; IOS Press: Amsterdam, The Netherlands, 2014; Volume 3. [Google Scholar]
- Anvari, R.; Mohammadi, M.; Kahoo, A.R.; Khan, N.A.; Abdullah, A.I. Random Noise Attenuation of 2D Seismic Data Based on Sparse Low-Rank Estimation of the Seismic Signal. Comput. Geosci. 2020, 135, 104376. [Google Scholar] [CrossRef]
- Xu, P.; Lu, W.; Wang, B. Seismic Interference Noise Attenuation by Convolutional Neural Network Based on Training Data Generation. IEEE Geosci. Remote Sens. Lett. 2021, 18, 741–745. [Google Scholar] [CrossRef]
- Nazari Siahsar, M.A.; Gholtashi, S.; Kahoo, A.R.; Marvi, H.; Ahmadifard, A. Sparse Time-Frequency Representation for Seismic Noise Reduction Using Low-Rank and Sparse Decomposition. Geophysics 2016, 81, V117–V124. [Google Scholar] [CrossRef]
- R Long, S.R.; Huang, N.E.; Tung, C.C.; Wu, M.L.; Lin, R.Q.; Mollo-Christensen, E.; Yuan, Y. The Hilbert techniques: An alternate approach for non-steady time series analysis. IEEE Geosci. Remote Sens. Soc. Lett. 1995, 3, 6–11. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A NEW VIEW OF NONLINEAR WATER WAVES: The Hilbert Spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Hwang, P.A.; Huang, N.E.; Wang, D.W. A Note on Analyzing Nonlinear and Nonstationary Ocean Wave Data. Appl. Ocean. Res. 2003, 25, 187–193. [Google Scholar] [CrossRef]
- Love, B.S.; Matthews, A.J.; Janacek, G.J. Real-Time Extraction of the Madden–Julian Oscillation Using Empirical Mode Decomposition and Statistical Forecasting with a VARMA Model. J. Clim. 2008, 21, 5318–5335. [Google Scholar] [CrossRef]
- Battista, B.M.; Knapp, C.; McGee, T.; Goebel, V. Application of the Empirical Mode Decomposition and Hilbert-Huang Transform to Seismic Reflection Data. Geophysics 2007, 72, H29–H37. [Google Scholar] [CrossRef]
- Battista, B.M.; Addison, A.D.; Knapp, C.C. Empirical Mode Decomposition Operator for Dewowing GPR Data. JEEG 2009, 14, 163–169. [Google Scholar] [CrossRef]
- Loutridis, S.J. Damage Detection in Gear Systems Using Empirical Mode Decomposition. Eng. Struct. 2004, 26, 1833–1841. [Google Scholar] [CrossRef]
- Liang, H.; Bressler, S.L.; Desimone, R.; Fries, P. Empirical Mode Decomposition: A Method for Analyzing Neural Data. Neurocomputing 2005, 65–66, 801–807. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Z.; McCallum, R.W. Artifact Reduction in Electrogastrogram Based on Empirical Mode Decomposition Method. Med. Biol. Eng. Comput. 2000, 38, 35–41. [Google Scholar] [CrossRef]
- Lei, T.; Liang, Q.; Tan, Q. A New Ground Penetrating Radar Signal Denoising Algorithm Based on Automatic Reversed-phase Correction and Kurtosis Value Comparison. J. Radars 2018, 7, 294–302. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Rehman, N.U.; Aftab, H. Multivariate Variational Mode Decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate Empirical Mode Decomposition. Proc. R. Soc. A. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Kennedy, J.; Elberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Net-works, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Mezura-Montes, E.; Coello Coello, C.A. Constraint-Handling in Nature-Inspired Numerical Optimization: Past, Present and Future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.; Wang, Q.; Han, K. Fault Feature Extraction and Diagnosis of Rolling Bearings Based on Wavelet Thresholding Denoising with CEEMDAN Energy Entropy and PSO-LSSVM. Measurement 2021, 172, 108901. [Google Scholar] [CrossRef]
- Liu, S.; Chen, Y.; Luo, C.; Jiang, H.; Li, H.; Li, H.; Lu, Q. Particle Swarm Optimization-Based Variational Mode Decomposition for Ground Penetrating Radar Data Denoising. Remote Sens. 2022, 14, 2973. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, Y.; Li, Y.; Feng, X.; Li, B.; Hu, X.; Song, Z. A GPR 2D Teager-Kaiser Energy Operator Based on the Multivariate Variational Mode Decomposition. Remote Sens. Lett. 2023, 14, 30–38. [Google Scholar] [CrossRef]
- Bie, F.; Miao, Y.; Lyu, F.; Peng, J.; Guo, Y. An Improved CEEMDAN Time-Domain Energy Entropy Method for the Failure Mode Identification of the Rolling Bearing. Shock. Vib. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- He, D.; Liu, C.; Jin, Z.; Ma, R.; Chen, Y.; Shan, S. Fault Diagnosis of Flywheel Bearing Based on Parameter Optimization Variational Mode Decomposition Energy Entropy and Deep Learning. Energy 2022, 239, 122108. [Google Scholar] [CrossRef]
- Liu, Z.; Lv, K.; Zheng, C.; Cai, B.; Lei, G.; Liu, Y. A Fault Diagnosis Method for Rolling Element Bearings Based on ICEEMDAN and Bayesian Network. J. Mech. Sci. Technol. 2022, 36, 2201–2212. [Google Scholar] [CrossRef]
- Shaw, R.; Srivastava, S. Particle Swarm Optimization: A New Tool to Invert Geophysical Data. Geophysics 2007, 72, F75–F83. [Google Scholar] [CrossRef]
- Li, F.; Ma, G.; Chen, S.; Huang, W. An Ensemble Modeling Approach to Forecast Daily Reservoir Inflow Using Bidirectional Long- and Short-Term Memory (Bi-LSTM), Variational Mode Decomposition (VMD), and Energy Entropy Method. Water Resour Manag. 2021, 35, 2941–2963. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-Organizing Hierarchical Particle Swarm Optimizer With Time-Varying Acceleration Coefficients. IEEE Trans. Evol. Computat. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Cui, X.; Jeofry, H.; Greenbaum, J.S.; Guo, J.; Li, L.; Lindzey, L.E.; Habbal, F.A.; Wei, W.; Young, D.A.; Ross, N.; et al. Bed Topography of Princess Elizabeth Land in East Antarctica. Earth Syst. Sci. Data 2020, 12, 2765–2774. [Google Scholar] [CrossRef]
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.L.; Barrand, N.E.; Bell, R.; Bianchi, C.; Bingham, R.G.; Blankenship, D.D.; Casassa, G.; et al. Bedmap2: Improved Ice Bed, Surface and Thickness Datasets for Antarctica. Cryosphere 2013, 7, 375–393. [Google Scholar] [CrossRef]
- Kun, L. Study on Characteristics and Significance of the Internal Layering and Subglacial Topography of the Ice Sheet in Princess Elizabeth Land, East Antarctica Based on Ice-Penetrating Radar Data; Jilin University: Changchun, China, 2022. [Google Scholar]
- Wright, A.; Siegert, M. A Fourth Inventory of Antarctic Subglacial Lakes. Antarct. Sci. 2012, 24, 659–664. [Google Scholar] [CrossRef]
- Oswald, G.K.A.; Robin, G.D.Q. Lakes Beneath the Antarctic Ice Sheet. Nature 1973, 245, 251–254. [Google Scholar] [CrossRef]
- Jamei, M.; Ali, M.; Karbasi, M.; Xiang, Y.; Ahmadianfar, I.; Yaseen, Z.M. Designing a Multi-Stage Expert System for Daily Ocean Wave Energy Forecasting: A Multivariate Data Decomposition-Based Approach. Appl. Energy 2022, 326, 119925. [Google Scholar] [CrossRef]
- Huang, C.; Song, H. Fault Feature Extraction Method for Rolling Bearing Based on MVMD and Complex Fourier Transform. J. Vibroeng. 2023, 25, 269–289. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, J.; Wang, D. Improving Seismic Resolution Based on Enhanced Multi-Channel Variational Mode Decomposition. J. Appl. Geophys. 2022, 199, 104592. [Google Scholar] [CrossRef]
- Guang, L.; Hao, Z.; Zhu, C.; Jian, C.; Sheng, F.; Lin, G. Multi-channel geomagnetic signal processing based on deep residual network and MVMD. Chin. J. Geophys. 2023, 66, 3540–3556. [Google Scholar]
- Liu, J.-Z.; Xue, Y.; Shi, L.; Han, L. Seismic Attenuation Estimation Using Multivariate Variational Mode Decomposition. Front. Earth Sci. 2022, 10, 917747. [Google Scholar] [CrossRef]

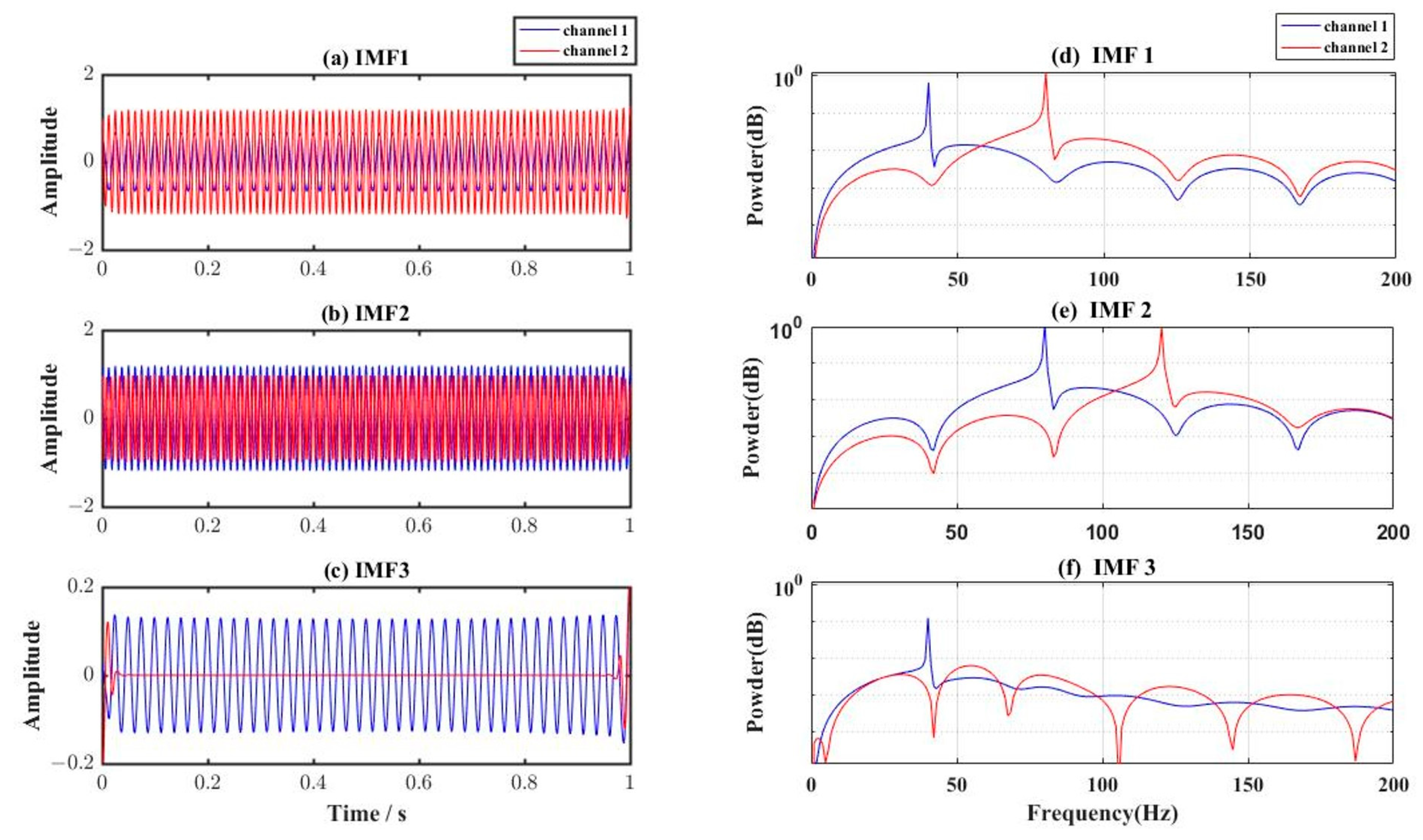
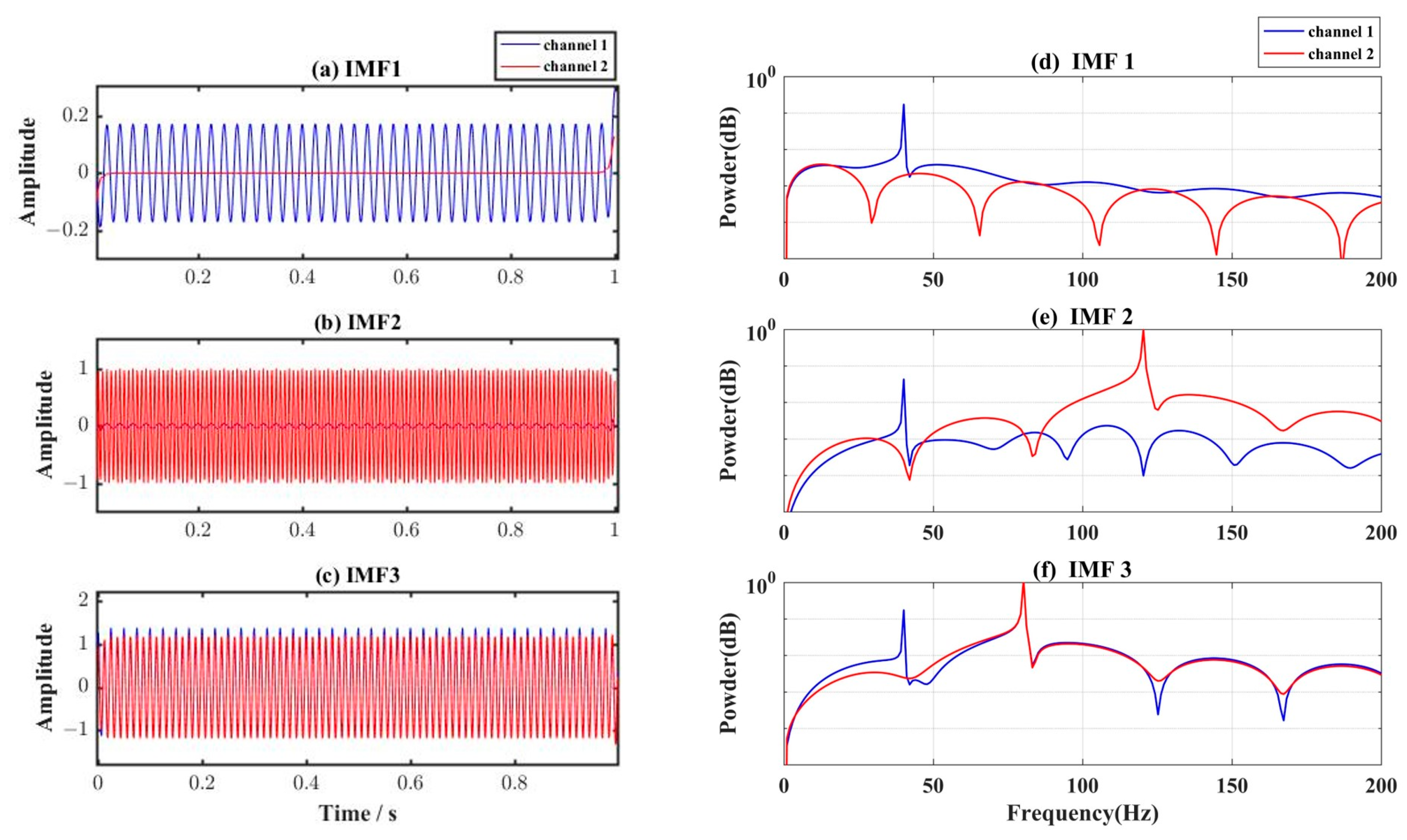


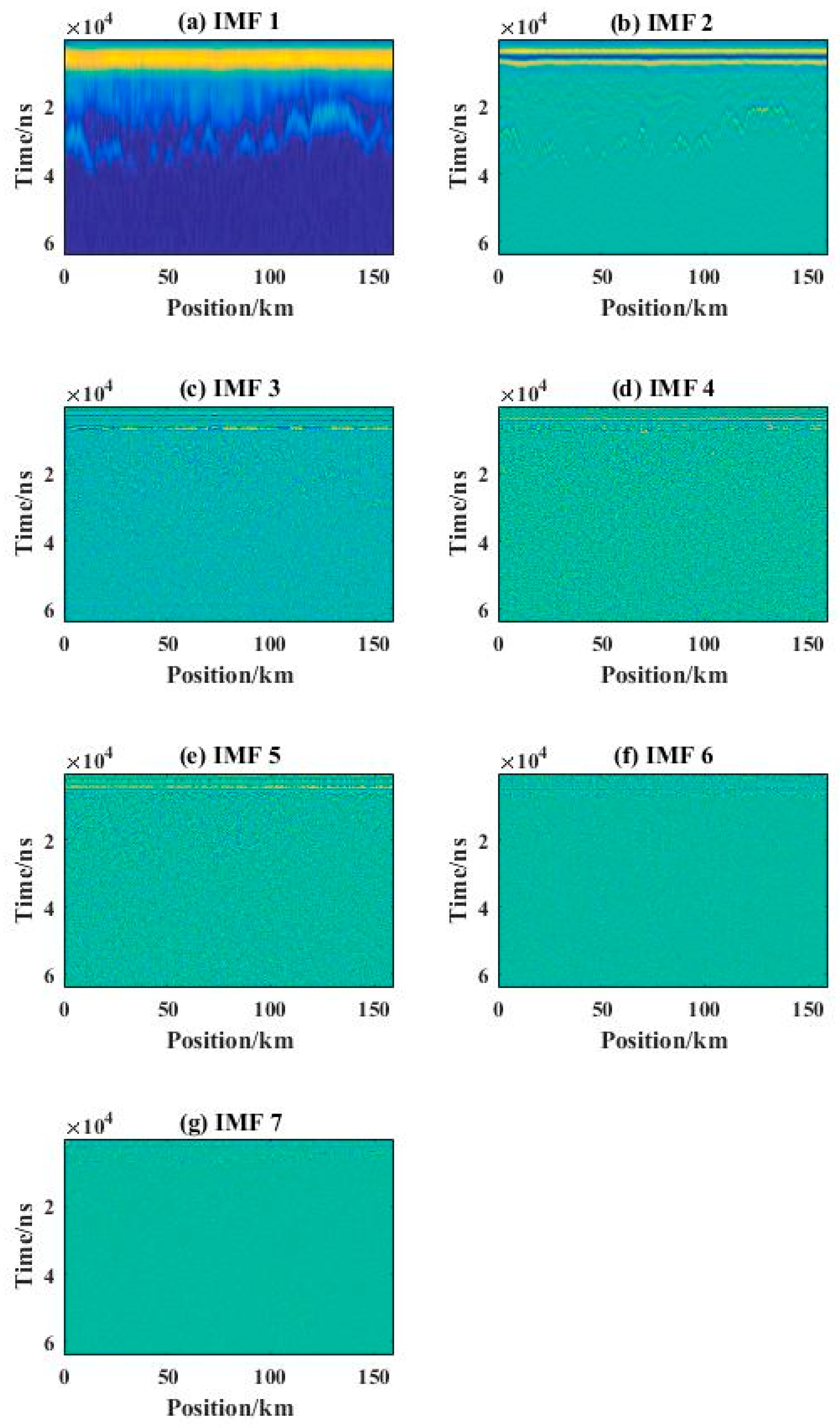
| IMF | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 |
|---|---|---|---|---|---|---|---|
| Energy entropy | 0.2777 | 0.2776 | 0.2784 | 0.2777 | 0.2780 | 0.2781 | 0.2784 |
| No. | IMFs | SNR | RMSE | PSNR | Note |
|---|---|---|---|---|---|
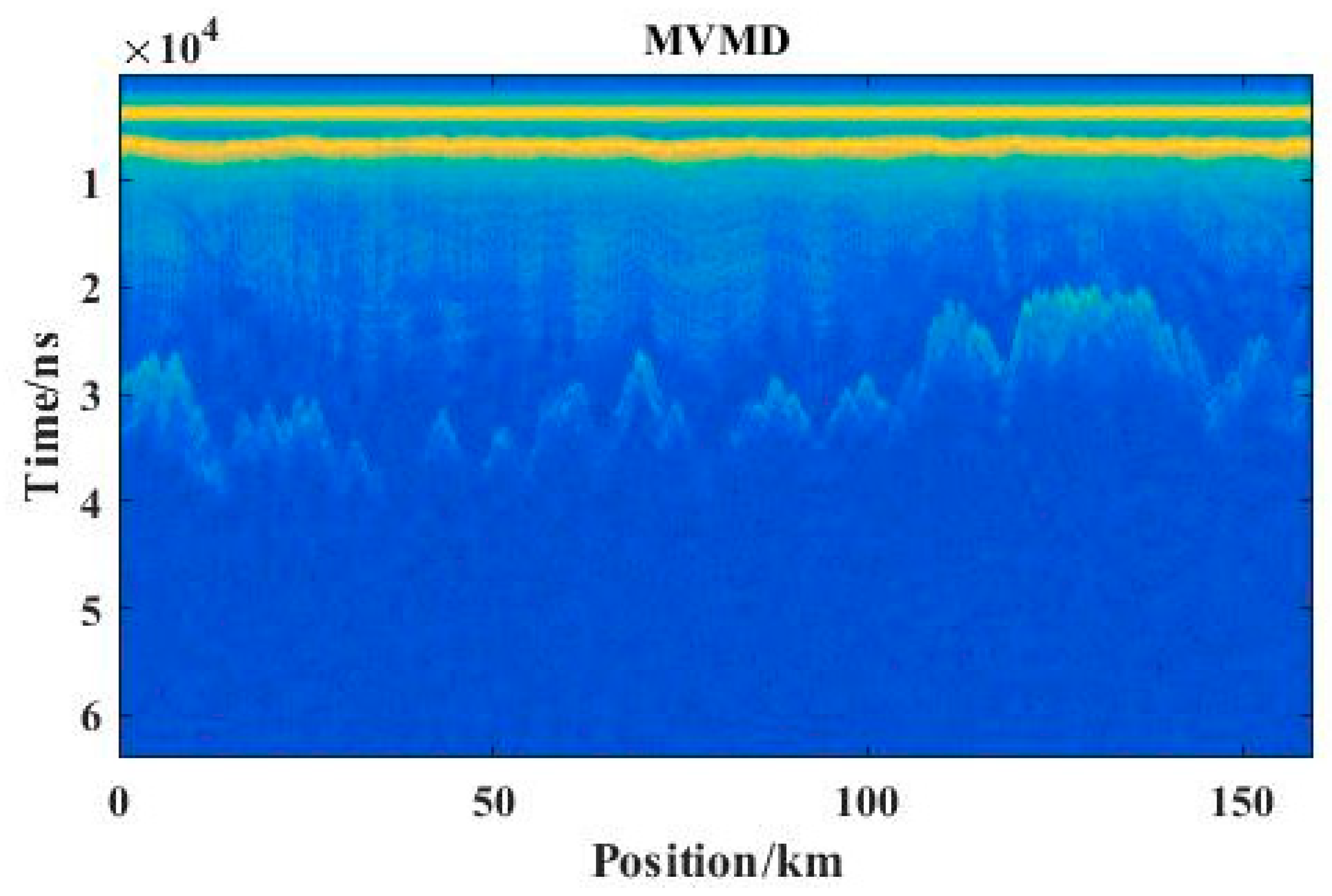
| 1 | 1, 2, and 4 | 77.89 | 2096.91 | 11.35 | Selected |
| 2 | 2 and 4 | 0.05 | 102,490.64 | 10.21 | |
| 3 | 1 and 2 | 73.80 | 2571.34 | 11.08 | |
| 4 | 1 and 4 | 56.80 | 6020.48 | 10.24 |
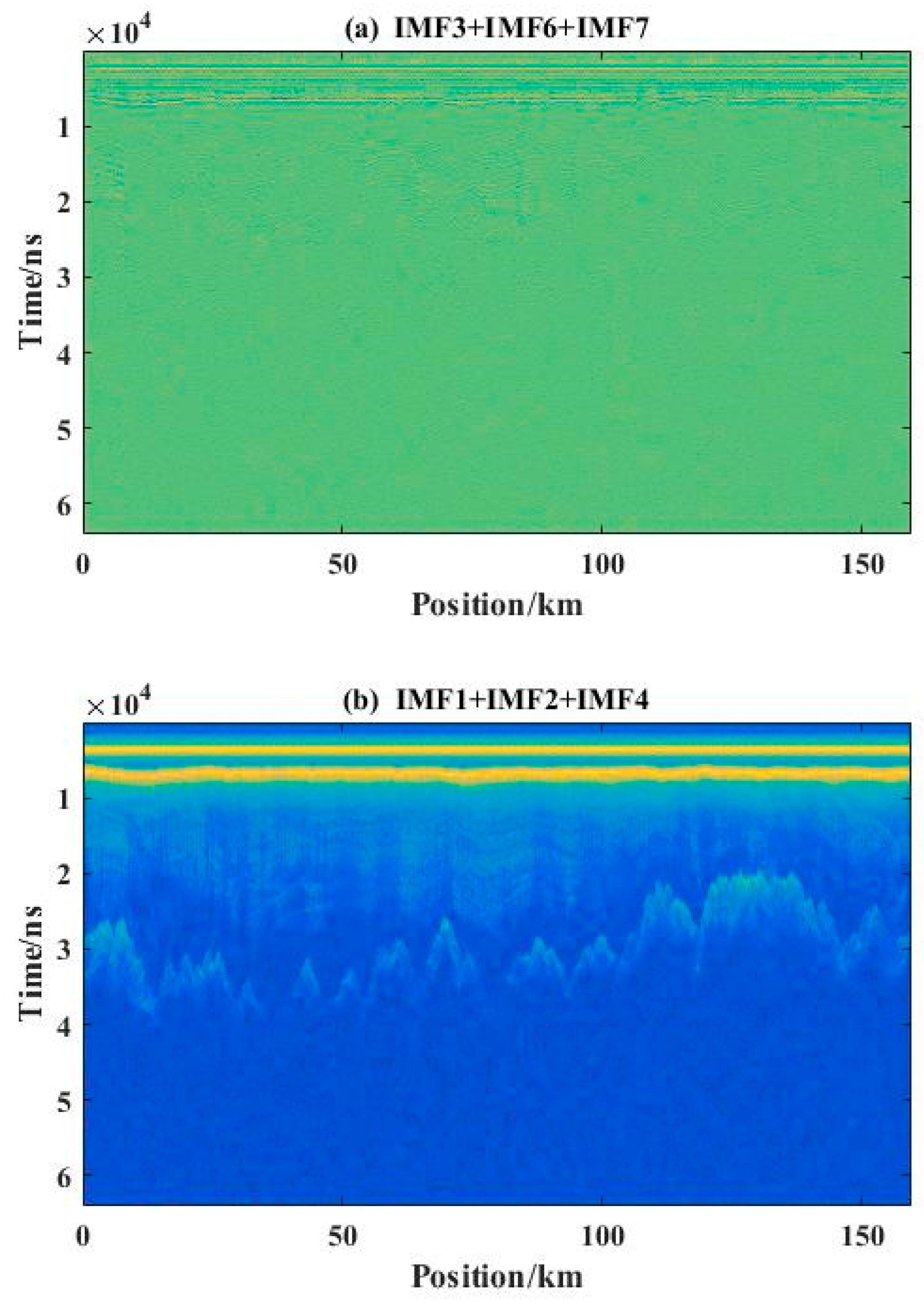
| Combination | SNR | RMSE | PSNR |
|---|---|---|---|
| IMF3, IMF6, and IMF7 | 0.01 | 102,720.86 | 9.16 |
| IMF1, IMF2, and IMF4 | 77.89 | 2096.91 | 11.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, S.; Luo, K.; Wang, L.; Tang, X. Airborne Radio-Echo Sounding Data Denoising Using Particle Swarm Optimization and Multivariate Variational Mode Decomposition. Remote Sens. 2023, 15, 5041. https://doi.org/10.3390/rs15205041
Chen Y, Liu S, Luo K, Wang L, Tang X. Airborne Radio-Echo Sounding Data Denoising Using Particle Swarm Optimization and Multivariate Variational Mode Decomposition. Remote Sensing. 2023; 15(20):5041. https://doi.org/10.3390/rs15205041
Chicago/Turabian StyleChen, Yuhan, Sixin Liu, Kun Luo, Lijuan Wang, and Xueyuan Tang. 2023. "Airborne Radio-Echo Sounding Data Denoising Using Particle Swarm Optimization and Multivariate Variational Mode Decomposition" Remote Sensing 15, no. 20: 5041. https://doi.org/10.3390/rs15205041
APA StyleChen, Y., Liu, S., Luo, K., Wang, L., & Tang, X. (2023). Airborne Radio-Echo Sounding Data Denoising Using Particle Swarm Optimization and Multivariate Variational Mode Decomposition. Remote Sensing, 15(20), 5041. https://doi.org/10.3390/rs15205041









