Abstract
Few-shot semantic segmentation (FSS) is committed to segmenting new classes with only a few labels. Generally, FSS assumes that base classes and novel classes belong to the same domain, which limits FSS’s application in a wide range of areas. In particular, since annotation is time-consuming, it is not cost-effective to process remote sensing images using FSS. To address this issue, we designed a feature transformation network (FTNet) for learning to few-shot segment remote sensing images from irrelevant data (FSS-RSI). The main idea is to train networks on irrelevant, already labeled data but inference on remote sensing images. In other words, the training and testing data neither belong to the same domain nor category. The FTNet contains two main modules: a feature transformation module (FTM) and a hierarchical transformer module (HTM). Among them, the FTM transforms features into a domain-agnostic high-level anchor, and the HTM hierarchically enhances matching between support and query features. Moreover, to promote the development of FSS-RSI, we established a new benchmark, which other researchers may use. Our experiments demonstrate that our model outperforms the cutting-edge few-shot semantic segmentation method by 25.39% and 21.31% in the one-shot and five-shot settings, respectively.
1. Introduction
Deep learning-based semantic segmentation is widely used in remote sensing [1,2]. Generally, semantic segmentation provides pixel-level classification for downstream applications, which is a fundamental computer vision task. Many models have been built by adopting fully convolutional networks and have achieved satisfactory results [3,4,5]. On this basis, novel modules such as encoder–decoder [6,7], dilated convolution [8], and atrous spatial pyramid pooling [9] have been proven to be effective. Indeed, pre-trained backbones, such as the ResNet [10] and VGG [11], have been utilized in various semantic segmentation models [8,9,10] for feature extraction, which has gradually become a stereotype. By contrast, VIT [12], SETR [13], and SegFormer [14] divide images into a patch sequence. In these works, transformers were used to extract image features [15,16], and their results surpassed traditional methods to some extent.
However, a large dataset is needed during training, thus limiting semantic segmentation’s application in a broader field. FSS has been proposed [17,18] to solve this limitation. Unlike supervised learning-based methods, FSS requires only a few annotations to segment new classes.
There are no overlap categories between training and inference for FSS [19], which is the main difference between few-shot semantic segmentation and semantic segmentation. Most FSS methods follow meta-learning [20], where episodes are formed by image and label pairs [17,21,22] to mimic few-shot scenes. Currently, FSS is mainly divided into two groups: relation-based methods and metric-based methods. Among them, relation-based methods [18,19,22,23,24] share the same backbone and freeze their parameters during training. The main idea is to design a practical decoder to compare the query and support data. In contrast, metric-based methods [21,25] tend to develop effective encoders to separate foreground and background classes. Furthermore, some works [26,27] bring transformers into FSS tasks with excellent results. As for remote sensing, it is time-consuming to obtain numerous annotated data. Therefore, some works [28,29,30] have aimed to reduce the need for annotations or use semi-supervised methods [31] to handle unknown categories.
Generally, FSS is conducted in a cross-validation manner with four splits [32]. Although there is no class overlap between the training and testing sets, they belong to the same domain. For example, there are 20 categories in PASCAL-5i [17], but each class’s pixel distribution is similar, called the in-domain dataset. Additionally, although FSS is named “few-shot”, a large, labeled dataset is still needed during training, which is inconvenient for remote sensing. We aim to train such a network on a large but irrelevant dataset and to predict masks on remote sensing images.
This work extends few-shot semantic segmentation to a new task called FSS-RSI. As we know, FSS’s training and testing sets contain different categories within the same domain. By contrast, FSS-RSI’s data differ not only in classes but also in image acquisition sensor and pixel distributions, which belong to irrelevant/cross-domain data.
To achieve the goal of FSS-RSI, the FTNet was designed. The meta-learning method [20] was adopted to train our network. Specifically, the FTNet transforms the support and query features into a domain-agnostic space with the learnable FTM. In this way, the gap between the support data and the query data is narrowed. In addition, the HTM is used to parse the correlations between the support and query features, which fully promotes the fitting capability of the support and query features.
To validate our network and provide convenience for other researchers, we established a new benchmark. The images used came from four different datasets, DeepGlobe [33], Potsdam [34], Vaihingen [35], and AISD [36], which were captured by satellites or drones. All four datasets are typical in remote sensing and contain commonly used categories in engineering. We combined these datasets into an FSS-format dataset and used them as a benchmark for FSS-RSI.
PASCAL-5i and our benchmark were used for our experiments. The FTNet achieves comparable accuracy to the cutting-edge method on the in-domain dataset. As for FSS-RSI, the FTNet performs at an absolute advantage. The mIoUs in the one-shot and five-shot settings were 25.39% and 21.31%, respectively, higher than the state-of-the-art (SOTA) method.
In summary, our main contributions lie in the following aspects:
- We extend the FSS to FSS-RSI, which aims to utilize irrelevant domain data to guide the segmentation of remote sensing images.
- A new benchmark is proposed. This benchmark may promote the development of FSS-RSI and serve as a tool for researchers.
- We propose an effective network with the FTM and the HTM. Our method significantly outperforms the cutting-edge few-shot semantic segmentation method in the FSS-RSI task.
2. Method
2.1. Problem Setting
Table 1 shows the differences between semantic segmentation (SS), FSS, and FSS-RSI. We define the training and testing data as domains and and their semantic categories as and , respectively.

Table 1.
Differences between SS, FSS, and FSS-RSI.
For SS, and belonged to the same domain, specifically remote sensing, in our task. The training and testing categories were the same. That is, SS only handles classes that have appeared in training. For FSS, both and were derived from remote sensing, but their categories did not overlap. That is, FSS can process classes with no appearance during training. FSS-RSI was the most challenging task, with and originating from different domains. The two domains have different classes and pixel distributions, which we call irrelevant data.
In the FSS-RSI task, episodes [18] were used to mimic few-shot scenes. Each episode consisted of a query set and a support set . In our study, represents image pairs consisting of RGB images and corresponding masks. denotes the RGB images. represents their masks. K means K pairs of images and masks were used, which we call the K-shot. and are the inputs during training. The proposed network predicts a binary mask to compute loss with . In the testing phase, the network predicted a new mask with and as the inputs. It should be noted that , and , respectively.
2.2. Model
The FTNet is designed to deal with FSS-RSI tasks. As shown in Figure 1, the network is built in a meta-learning manner [20]. Specifically, we used ResNet50 [10], which was pre-trained by ImageNet [37], as the backbone and froze its parameters during training. The query and support branches share the same backbone to extract multi-layered features. Furthermore, a prior mask [18] from high-level feature maps was introduced to strengthen the connection between the query and support data. It should be noted that support masks are important for FSS. Therefore, the FTNet adopted a support mask several times to enhance its guidance for the query images. In particular, the FTM is designed to transform the middle query feature, support feature, and prototype into a domain-independent, high-level feature space called the feature anchor. The FTNet achieves better performance when processing FSS-RSI tasks with the FTM. In addition, we input the fused query feature, support feature, and mask into the HTM, which enhanced information fusion within and between features. Figure 1 shows the model architecture of a one-shot structure, which can be easily expanded to a five-shot structure.
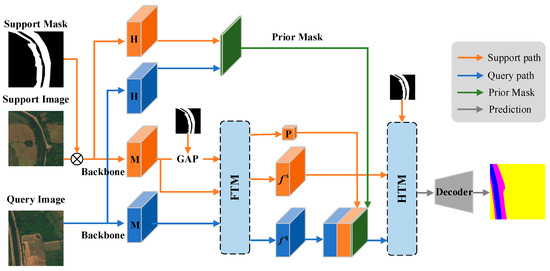
Figure 1.
The architecture of the FTNet. This network was built in a meta-learning manner with a prior mask [18]. The FTM and HTM are designed for better performance. H is the high-level feature, M is the middle-level feature, P is the prototype, is the support feature, is the query feature, ⊗ is the element-wise multiplication, and GAP denotes the global average pooling.
2.2.1. Feature Extraction
During the training phase, we froze the backbone’s parameters, which was the strategy employed by other methods [18,19,26]. There are five stages included in ResNet50. The FTNet mainly adopts feature maps for stage 3, stage 4, and stage 5, which are denoted as , , and . In order to enhance the performance of high-level feature maps, PPM [38] was used to refactor stage 5. Thus, we obtained as the following:
where means the average pooling and denotes the convolution, followed by the BatchNorm [39] and ReLU functions. is the upsampling and represents the concatenation. Pyramids with the sizes 1 × 1, 2 × 2, 3 × 3, and 6 × 6 were used, and is the level of pyramid. , , and were resized to be the same as .
According to [22,40,41,42], middle-level features contain more semantic information, such as the outline and color. Therefore, the FTNet concatenates and to obtain a middle-level feature map:
where and are the middle-level features of the support and query data. and are the same as in Function (1) with different parameters. Furthermore, we calculated the prototype using the support mask and as the following:
where means the Hadamard product, and represents the operation to reshape the initial query mask from to , with the same size as . is the global average pooling to reshape the feature map from to .
In addition, the prior mask generated by the high-level feature boosts performance in a training-class-insensitive way [18]. We used and to generate prior masks and merge them as the following:
where denotes the generation of a prior mask .
2.2.2. Feature Transformation Module
Motivation. Features extracted by convolutions have an excellent characterization within category and domain. As for FSS-RSI, the parameters learned during training tend to segment the categories that appear during training. Therefore, the FTNet transforms features into a space independent of classes and domains. This strategy reduces the influence of the source domain and training data. Inspired by a task-adaptive feature transformer (TAF) [43], we propose a simple learnable transformation matrix that transforms , , and to a domain-agnostic space.
For the feature matrix , the goal was to find a matrix that transforms to a domain-independent feature matrix , called the feature anchor, as the following:
In general, is a non-square matrix with no inverse. One solution is to calculate the pseudo-inverse [43] of is . Thus, the transformation matrix was obtained as the following:
The parameters of were initialized randomly and changed with the gradient’s backpropagation; therefore, the matrix was constantly optimized.
Specifically, for the prototype , we obtained . As for , we needed to transform it as the following:
where represents the reshape operation: . We used the transformation matrix to multiply Formula (8) to obtain . Furthermore, was transformed to the original shape as , that is,
where the inverse reshape is included. The same operation was performed for . Finally, , , and were obtained. They are domain-agnostic features. In other words, the gap between and and the gap between and were significantly reduced. We provide a more detailed explanation in Appendix A.
We further merged , , and to obtain as the following:
where is the repeat operation: . It should be noted that only the parameters of were learnable. The transformation matrix was calculated directly. This method does not add too many parameters.
2.2.3. Hierarchical Transformer Module
Motivation. A transformer is used in many works to extract features [12,13,14]. It establishes relationships within and between features to mine the connections between image blocks. As illustrated in [27], prototype-based FSS models are committed to providing class-wise clues rather than pixel-wise clues. We adopted self- and cross-attention paradigms to mine deep matching correlations.
To strengthen the support data’s performance, we again used support masks. We define , , and . We followed the usual transformer calculation, which is formulated as the following:
where , , and are the learnable parameters, and is the hidden dimension. Equation (11) is a general form of cross-attention. As shown in Figure 2, when the features in and are replaced with , Equation (11) represents the self-attention manner, which represents the relationship among query features. The main task of the HTM is to calculate an informative query feature. Thus, we only performed self-attention within the query path in a standard multi-head manner [12]. In addition, a cross-attention layer follows self-attention. Similar to [27], was obtained from the query features, and and were obtained from the support features. Inspired by the ResNet [10] and SegFormer [14], we design a hierarchical architecture with four scale blocks. Each block contains self- and cross-attention, followed by downsampling. At the end of the HTM process, we concatenated the four blocks after scaling them to the same resolution. In a nutshell, our model extracts abundant information within query features and obtains pixel-wise matching correlations using a cross-attention layer. We demonstrate the role of the HTM in mining this matching relationship, as detailed in Appendix B.
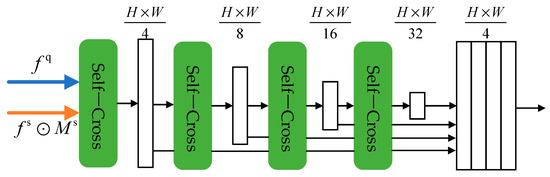
Figure 2.
The architecture of the HTM used in our network.
Finally, the FTNet adopts a simple decoder to generate predictions, mainly including stacked convolutional layers and upsampling. Because FSS is a binary classification task, binary cross-entropy loss (BCE) was used to optimize our model, which is formulated as the following:
where is the number of episodes in each batch and is the prediction of the query image.
2.2.4. Extension to K-Shot
Extending our model to K-shot (K > 1) format was straightforward. The K-shot setting means that there are K support pairs in one episode. Specifically, the support pair is and the query pair is still . In order not to change the model’s settings, we concatenated the K groups in the channel dimension directly as the following:
Therefore, the FTNet obtained an input with the same structure as a one-shot structure with simple convolutions.
2.3. Benchmark
The FSS-RSI benchmark was derived from four datasets of remote sensing, including DeepGlobe [33], Potsdam [34], Vaihingen [35], and AISD. These datasets differ from the commonly used FSS datasets regarding their pixel distributions and categories.
DeepGlobe [33] consists of natural landscape images taken by satellites. This dataset is annotated into seven categories: unknown, urban, aquatic, agricultural, forested, barren, and rangeland areas. The ground sampling distance was 50 cm. However, only 803 training images were labeled with a size of 2448 × 2448. Fortunately, this dataset was adopted as a tool for FSS-RSI, so DeepGlobe’s training set could meet the need. Specifically, we divided each image into 36 equal blocks and resized them to 400 × 400. The category “unknown” was set as the background. Images that contained only a single category were filtered out. Finally, we obtained 9175 pairs containing six categories. We named this dataset FSS-RSI-DeepGlobe; some samples are shown in Figure 3a.

Figure 3.
Some images and their corresponding masks of our benchmark: (a) data from DeepGlobe; (b) data from Potsdam; (c) data from Vaihingen; and (d) data from AISD.
Potsdam [34] was captured over Potsdam in Germany by aerial cameras. This dataset is annotated into six categories: clutter, tree, low vegetation, building, car, and impervious surface. The ground sampling distance of the images was 5 cm. We removed the category “car” because of the overlap with the source domain used in our work. The buildings in Potsdam are scattered and the category distribution is more balanced. Potsdam contains 38 image patches. The size of all images is 6000 × 6000. Each image was divided into 225 equal pieces. Similar to the DeepGlobe dataset, we removed pairs with a single category. Finally, we obtained 1896 pairs containing five categories. We named this dataset FSS-RSI-Potsdam; some samples are shown in Figure 3b.
Vaihingen [35] was captured over Vaihingen in Germany by aerial cameras and includes five categories (after removing “car”), like Potsdam. The ground sampling distance of the images was 9 cm. Unlike Potsdam, the class distribution is more compact, with dense settlement structures, narrow streets, and large buildings. Vaihingen contains 33 patches of different sizes. We resized the images to 2800 × 2000 pixels and divided each image into 35 equal pieces. We removed images with a single category. As already known, episodes needed to be built in each category. However, the filtered Vaihingen dataset contains only 6 “clutter” samples, which was insufficient to build a rich episode. Thus, images containing the category “clutter” were discarded. Finally, we obtained 308 pairs containing four categories. We named this dataset FSS-RSI-Vaihingen; some images are shown in Figure 3c.
AISD [36] is an aerial image segmentation dataset obtained using the OpenStreetMap [44,45,46] and Google Maps [47]. AISD covers parts of different cities, of which Berlin was selected for our experiment. There are only two categories in AISD: road and building. However, their appearance is very similar within and between the two categories. Thus, we believe AISD is a challenging task for FSS. AISD contains 200 patches of the same size, at 2611 × 2453. We resized the images with 2800 × 2400 pixels and divided each image into 42 equal pieces. We removed images with a single category similar to the other three datasets. Finally, we obtained 5640 pairs containing two categories. We named this dataset FSS-RSI-AISD; some samples are shown in Figure 3d. Table 2 provides a detailed description of PASCAL-5i and our benchmark.

Table 2.
Details of our benchmark. The FID was calculated between each dataset and PASCAL-5i.
As shown in Figure 4, we further calculated the pixel distribution of each category. The pixel distribution was relatively balanced, except for “urban areas” in FSS-RSI-DeepGlobe. Because of the richness of this dataset, we kept the class “urban areas”.
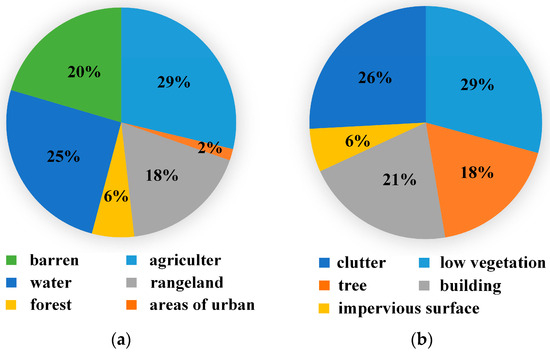
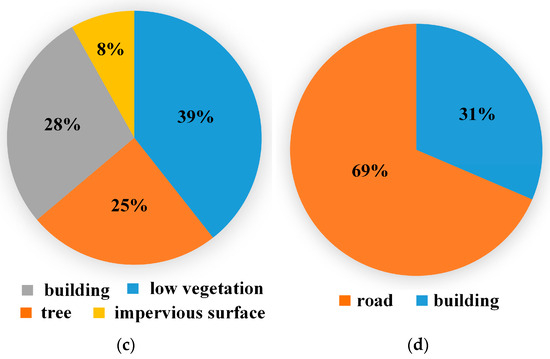
Figure 4.
Pixel distributions of our benchmark: (a) FSS-RSI-DeepGlobe; (b) FSS-RSI-Potsdam; (c) FSS-RSI-Vaihingen; and (d) FSS-RSI-AISD.
As shown in Table 2, the Fréchet inception distance (FID) [48] was reported to measure the different data distributions between our benchmark and PASCAL-5i. The FID is the Fréchet inception distance between the Gaussians obtained from the distributions of two datasets:
where and are means and covariances of the two distributions, and Tr is the matrix trace. The larger the FID, the greater the difference between the datasets, and vice versa.
As shown in Table 3, the same method was used to calculate the FID within PASCAL-5i. We followed the strategy of FSS, that is, using a standard cross-training manner. Specifically, the FID was calculated between each fold and the other three folds. Compared to the data within PASCAL-5i, the distribution gaps between our benchmark and PASCAL-5i were vast, where the FID was more than twice that of the in-domain data. In particular, the FID of FSS-RSI-Vaihingen was 328.08. Therefore, it is further proven that our benchmark and PASCAL-5i belong to different domains.

Table 3.
FIDs of different PASCAL-5i splits.
2.4. Experiments
2.4.1. Datasets and Metric
Datasets. PASCAL-5i is the irrelevant domain training set created from PASCAL VOC 2012 [49] with SDS [50] augmentation. The benchmark we proposed is the testing set in the remote sensing domain.
Metric. The mean intersection over union (mIoU) [19,26] was adopted in our experiment, as a standard metric in semantic segmentation. The IoU is defined as the following:
where ,, represent the number of false negatives, false positives, and true positives of the predictions, respectively. Furthermore, the mIoU is the average IoU of all categories.
2.4.2. Training and Testing Strategy
We used a generic meta-learning manner for training and testing. That is, each batch contained an episode. Unlike FSS, the entire PASCAL-5i dataset with all four splits was used as the training data. Indeed, we use a supervised learning strategy and fixed the backbone’s pre-training parameters during training. The Adam optimizer was adopted with a learning rate of 10−4, and the weight decay was 0.01. Furthermore, the size of the images was reshaped to 400 × 400 pixels, which was followed by random scaling, rotation, and cropping. A mini-batch of 16 was utilized in the experiment. We trained each model on four 2080 Ti GPUs with 50 epochs.
The test was performed on a single GPU. It should be noted that we tested the benchmark with the model trained on the PASCAL-5i without transfer. The mIoU was calculated for each dataset based on the average of 5 runs with different random seeds. A total of 600 tasks were contained in each run.
3. Result
3.1. Models for Comparison
To prove the performance of the FTNet, we selected several representative FSS models, including RPMMs [23], the PFENet [18], HSNet [24], BAM [19], and HDMNet [26]. Among them, RPMMs and the PFENet are classic prototype-based architectures, especially the PFENet, which is the most similar model to the FTNet. The HSNet uses 4D convolution to push meta-learning-based FSS to new heights. BAM and the HDMNet are cutting-edge in-domain FSS methods based on meta-learning and base-learning. For the RPMMs, PFENet, and HSNet, their released codes were used with the same settings. For BAM and the HDMNet, their meta paths were adopted, as there were no base classes in our benchmark. The testing method was exactly the same as ours.
3.2. Main Results
The results are shown in Table 4. The mIoU of the FTNet significantly exceeded that of the existing FSS model, including the SOTA model. Specifically, on the FSS-RSI-DeepGlobe dataset, the FTNet outperformed the suboptimal HSNet by 30.18% and 25.98% in the one-shot and five-shot settings, respectively. On the FSS-RSI-Potsdam dataset, the FTNet outperformed the suboptimal method by 37.57% and 8.90% in the one-shot and five-shot settings, respectively. On the FSS-RSI-AISD dataset, the FTNet outperformed the suboptimal methods by 17.48% and 13.61% in the one-shot and five-shot, respectively. In addition, our one-shot result was 13.53% higher than the HDMNet on the FSS-RSI-Vaihingen dataset. But the FTNet obtained a value that was 2.00% lower than BAM in the five-shot setting. For the mean results of all datasets, the mIoU significantly exceeded the suboptimal model, which was 25.39% and 21.31% higher than the HSNet in the one-shot and five-shot settings, respectively.

Table 4.
The mIoUs (%) of different methods experimented on our benchmark. The best results are denoted in bold. Suboptimal results are underlined.
As can be seen, the PFENet achieved an mIoU that was 10% lower on the FSS-RSI-DeepGlobe and FSS-RSI-Potsdam datasets, especially for the value of only 2.42% in the FSS-RSI-DeepGlobe’s five-shot setting. This proves that the PFENet had no FSS-RSI performance on these two datasets. However, as illustrated in Appendix C, the PFENet’s performance within the domain was good. The same is true for RPMMs on the FSS-RSI-Potsdam dataset. As already known, the HDMNet is a cutting-edge FSS model, even with only its meta branch. The results can be seen in Appendix C. However, for the FSS-RSI task, the HDMNet did not perform well. The obtained mIoUs were 17.70 and 23.08 in the one-shot and five-shot settings, which were 41.16% and 17.56% lower than the FTNet, respectively. Performing slightly worse than our method, the HSNet performed suboptimally on FSS-RSI-DeepGlobe’s one-shot and five-shot settings and on FSS-RSI-Potsdam’s one-shot setting. We found that except for the PFENet, the five-shot results of all models were better than the one-shot results. This phenomenon indicates that when there are more support data, FSS-RSI performs better, which is similar to FSS. This experiment showed that the FTNet achieved the best result in FSS-RSI with absolute advantages over the other cutting-edge FSS methods.
Some qualitative results of our methods are shown in Figure 5. Classes with regular shapes, such as buildings in the FSS-RSI-Potsdam and FSS-RSI-Vaihingen datasets, obtained better results. However, FSS-RSI is challenging for irregular categories, such as trees and low vegetation. In particular, FSS-RSI did not work well for categories with similar appearances, such as the barren and rangeland areas in the FSS-RSI-DeepGlobe dataset and all categories in the FSS-RSI-AISD dataset. These challenging cases also need to be solved using semantic segmentation. Indeed, compared to commonly handled categories, such as cars, people, and animals, it is more difficult to segment remote sensing images. This issue is exactly the intractable part that FSS needs to solve.


Figure 5.
Qualitative results of the FTNet: (a) FSS-RSI-DeepGlobe; (b) FSS-RSI-Potsdam; (c) FSS-RSI-Vaihingen; and (d) FSS-RSI-AISD.
4. Discussion
4.1. Ablation Study
To prove the effectiveness of the FTNet, we carried out an ablation study. The mIoU was selected as the metric. Our baseline was that the architecture removed the HTM and FTM. To further justify the effectiveness of our HTM, we adopted a vanilla transformer module (VTM) for comparison. There were four repeat blocks in the VTM without concatenation; each block was the same as the first in the HTM.
Effects of the HTM and FTM. Table 5 shows the results of the five forms. They were the baseline, adding the FTM, adding the HTM, adding the VTM, and adding both the HTM and FTM. As illustrated, the mIoU of the baseline was similar to that of BAM [19] and the HDMNet [26]. After adding our tailored modules, the FTNet’s performance was significantly boosted.

Table 5.
The mIoUs (%) of the ablation study. The best results are denoted in bold. The baseline is the architecture that removed the FTM and HTM.
Compared to the baseline, the mIoUs in the one-shot and five-shot settings were improved by 50.26% and 17.33%, respectively, after adding the FTM. Furthermore, adding the HTM improved the result by 61.34% and 32.35%, respectively. What surprised us the most is that our complete structure with both the FTM and HTM achieved the highest mIoUs, which were 72.87% and 37.78% higher than the baseline in the one-shot and five-shot settings, respectively. We note that adding the FTM obtained a result comparable to our complete architecture in the one-shot setting and a higher result in the five-shot setting on the FSS-IRS-Vaihingen dataset. These results prove the effectiveness of the proposed modules.
As illustrated in the HDMNet [26], a transformer module follows a backbone similar to ours. Unlike the HDMNet, we added the HTM to fuse low- and high-level information after the prior mask and prototype. Thus, our model’s performance was improved. As shown in Table 5, adding the VTM raised the mIoU from 17.51 to 21.55 in the one-shot setting. However, our HTM’s result was 31.09% higher than the VTM’s result in the one-shot setting. Furthermore, our device was out of memory when we trained the architecture with the VTM in the five-shot setting. Therefore, we could not collect the five-shot result using the VTM. The experimental results justify that our HTM is more effective than the VTM.
The visualization results of the five forms are shown in Figure 6. They are the results based on FSS-RSI-DeepGlobe in the one-shot setting. It is important to note that these qualitative results were unstable across different test rounds, and we consider the quantitative results in Table 5 on the entire dataset to be more reliable.

Figure 6.
Qualitative results of the ablation study.
Effects of different classes. We counted the mIoUs of each class on the whole benchmark, and the results are shown in Figure 7. To sum up, the FTNet had an unbalanced accuracy for each category. On the FSS-RSI-DeepGlobe dataset, the FTNet had a higher mIoU for agricultural, forested, and barren but a lower mIoU for the remaining three categories. On the FSS-RSI-Potsdam dataset, the category with the highest mIoU was “building”, which was 156.40% higher than “clutter”. On the FSS-RSI-Vaihingen dataset, the best class was “tree”, which was 206.92% higher than the categories of “impervious surface”. On the FSS-RSI-AISD dataset, the mIoU of “building” was higher. We believe that “building” had a more regular shape relative to “road”, which was more conducive to the prediction of the network.
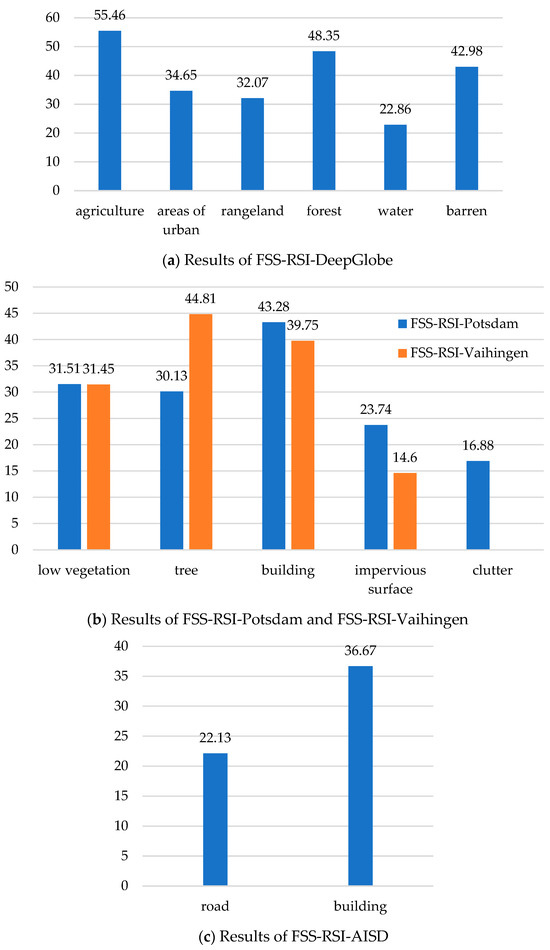
Figure 7.
The mIoUs (%) of different categories: (a) FSS-RSI-DeepGlobe; (b) FSS-RSI-Potsdam and FSS-RSI-Vaihingen; and (c) FSS-RSI-AISD.
When combined with the pixel distribution in each category in Figure 4, the segmentation results of FSS-RSI-DeepGlobe and FSS-RSI-Potsdam are independent of the number of pixels. On the FSS-RSI-Vaihingen dataset, the smallest pixel ratio was obtained for “impervious surface”, and the mIoU in this category was also the smallest. On the FSS-RSI-AISD dataset, the ratio of pixels was the opposite of the ratio of mIoUs. We do not have enough evidence to prove that the accuracy was related to the pixel ratio. Balancing the number of pixels in our benchmark and improving the semantic segmentation accuracy of each category will need to be considered in the future.
4.2. Limitations
This work introduces FSS into the field of remote sensing image segmentation. Our model achieved an absolute advantage over other SOTA methods, as our experiment shows. The results prove the effectiveness of our approach. However, we need to note that in the FSS-RSI task, the mIoU was only about 30%, which is still far from actual application needs. On the one hand, this phenomenon is attributable to the fact that FSS-RSI is a very challenging task. The training data and the test data were irrelevant. On the other hand, most of the categories in our benchmark did not have fixed shapes, such as low vegetation, impervious surface, and agriculture, which were difficult even for generic semantic segmentation [5,9]. In addition, FSS-RSI did not work well with categories with similar appearances, such as the barren and rangeland areas in the FSS-RSI-DeepGlobe dataset and all categories in the FSS-RSI-AISD dataset.
Some previous works on remote sensing images using FSS have achieved high accuracy [51,52]. Their training and testing data came from the same remote sensing dataset, which was different from our task. And the categories they contained were common categories with fixed shapes, such as airplanes, ships, or cars. In order to extend FSS-RSI to a broader range of applications, some innovative works need to be proposed. For example, tailored models must be designed for categories with no fixed shape to improve their segmentation accuracy. Moreover, FSS-RSI combined with the usual semantic segmentation, which simultaneously segments novel and known categories, would be promising future work.
5. Conclusions
To address the limitations of FSS for remote sensing, we extended the task to a new field called FSS-RSI. Specifically, we established a novel benchmark for evaluating FSS-RSI, which may be useful for other researchers. Moreover, we propose the FTNet with an FTM and an HTM. The FTM transforms the support feature, query feature, and prototype into a domain-agnostic space called the feature anchor. The HTM establishes abundant matching correlations between the support and query patches. In this way, our model can process remote sensing data with data from irrelevant domains.
Experiments were conducted on PASCAL-5i and our benchmark. The FTNet achieved comparable accuracy to the cutting-edge methods on the in-domain data but obtained an absolute advantage on the FSS-RSI data. The proposed method outperformed the suboptimal model by 25.39% and 21.31% in the one-shot and five-shot settings, respectively. We hope our method will be helpful for few-shot semantic segmentation for remote sensing. For future work, we will focus on two interesting aspects: (1) designing tailored models to improve the accuracy of the FSS-RSI and (2) dealing with FSS problems in some exceptional cases, such as object occlusion, light changes, and similar appearance.
Author Contributions
Conceptualization, Q.S. and J.C.; Methodology, Q.S.; Software, Q.S.; Validation, Z.X. and W.C.; Formal analysis, Z.X.; Investigation, W.L. and N.H.; Writing—original draft, Q.S.; Writing—review & editing, J.C., W.L. and N.H.; Visualization, Z.X. and W.C.; Supervision, J.C.; Funding acquisition, W.L. and N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Work Enhancement Based on Visual Scene Perception] and [National Key Laboratory Foundation of Human Factors Engineering] grant number [GJSD22007]. The APC was funded by [Work Enhancement Based on Visual Scene Perception].
Data Availability Statement
The PASCAL VOC dataset is available at http://host.robots.ox.ac.uk/pascal/VOC/voc2012 (accessed on 25 June 2012). The Deepglobe dataset is available at https://www.kaggle.com/datasets/balraj98/deepglobe-road-extraction-dataset (accessed on June 2018). The Potsdam dataset is available at https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-label-potsdam.aspx (accessed on February 2015). The Vaihingen dataset is available at https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-labelvaihingen.aspx (accessed on February 2015). The AISD dataset is available at https://zenodo.org/record/1154821#.XH6HtygzbIU (accessed on July 2017).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We indicated in Section 2.2.2 that the gaps between and and between and were significantly reduced after using the FTM. To confirm this, we compared the distance between the support and query features before and after using the FTM.
Specifically, for features and before the use of the FTM, we applied the global averaging pooling operation to change their shape from to , which is the same shape as . B, C, H, and W indicate the tensor’s batch, channel, height, and width, respectively. We defined B = 1 for convenience. The same operation was conducted on and . Thus, , , , , , and were all vectors with the shape of . The main purpose of the FTM was to transform the features into a domain-agnostic space. We could not directly describe this domain-agnostic space. However, we demonstrated this point by comparing the distance between the support and query features as an alternative. This was plausible because the most important purpose of FSS is to reduce the gap between these two features.
Indeed, the L2 norm was adopted as a metric. We calculated the distance , , , and , respectively. We collected 600 samples from the above four distances when testing on the FSS-RSI-DeepGlobe dataset. In Figure A1, we present a visualization of the whole results.
Figure A1a,b presents the distances before the use of the FTM with average distances of 3.40 and 75.85, respectively. Figure A1c,d presents the distances after the use of the FTM, with average distances of 0.47 and 0.88, respectively. The feature distances after the FTM are much smaller than those before the FTM. Thus, we further prove that the FTM is a useful module to reduce the gap between the support and query features.
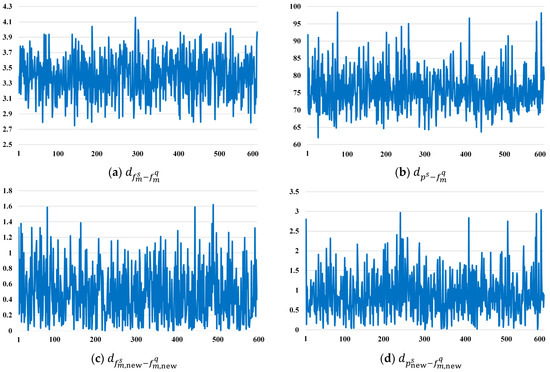
Figure A1.
Distances between support and query features: (a) and ; (b) and ; (c) and ; and (d) and .
Appendix B
To clarify that the HTM hierarchically enhances matching between the support and query features, the Frobenius norm was adopted as a metric. We denoted features before the HTM as and . That is, and , where are the features presented in Figure 2. Moreover, we denoted features after each transformer block as , , , , , , , and , respectively. The features after merging the four transformer blocks were denoted as and . Our purpose was to calculate the Frobenius norms as , , , , , and , respectively. Similar to the information presented in Appendix A, we collected 600 samples from the above six distances when testing on the FSS-RSI-DeepGlobe dataset. In Figure A2, we present a visualization of the results.
As shown in Figure A2a–f, the Frobenius norms decreased gradually, and their average values were reduced from 244.03 to 91.40. Indeed, the transformer is a dense image extraction and matching structure, which is difficult to explain using precise theory. We hope that Figure A2. will justify that the HTM can hierarchically enhance matching between the support and query features. Moreover, our ablation study, as presented in Section 4.1, can further prove the effectiveness of the HTM.
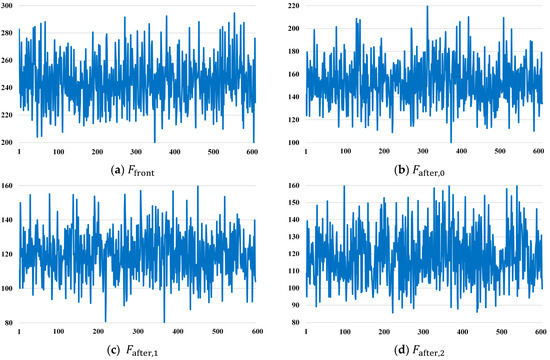
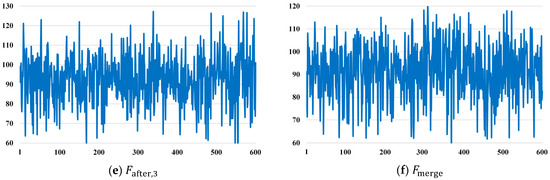
Figure A2.
Frobenius norms between support and query features: (a) and ; (b) and ; (c) and ; (d) and ; (e) and ; and (f) and .
Appendix C
Apart from the FSS-RSI, we further proved the performance of the FTNet on the in-domain dataset. The experiment was performed on PASCAL-5i, and we followed the commonly used data division of four folds, but we reported only the results in the one-shot setting. The results are shown in Table A1. As already known, a trick is used in the BAM and HDMNet. That is, the image pairs containing novel classes during training are removed. But in other works, novel classes are set as the background. This trick improves the performance of the BAM and HDMNet. We did not use this trick for fairness, i.e., we adopted the same strategy as for the other methods such as the HSNet and PFENet. Thus, we retrained the BAM and HDMNet according to their official settings. The results of their meta branches are shown in Table A1.

Table A1.
The mIoUs (%) of different methods on the in-domain dataset. The best results are denoted in bold. Suboptimal results are underlined.
Table A1.
The mIoUs (%) of different methods on the in-domain dataset. The best results are denoted in bold. Suboptimal results are underlined.
| Method | Fold0 | Fold1 | Fold2 | Fold3 | Average |
|---|---|---|---|---|---|
| PFENet | 63.23 | 70.79 | 53.28 | 57.25 | 61.14 |
| RPMMs | 59.50 | 71.58 | 55.40 | 51.96 | 59.61 |
| HSNet | 63.03 | 69.50 | 59.64 | 59.88 | 63.01 |
| BAM | 60.94 | 70.75 | 61.77 | 59.45 | 63.23 |
| HDMNet | 66.92 | 75.83 | 67.79 | 69.37 | 69.98 |
| FTNet | 62.42 | 71.06 | 58.00 | 58.91 | 62.60 |
As can be seen, the HDMNet is the best model, reaching the highest mIoU on three folds. And its average mIoU on all four folds was the highest, reaching 69.98. The PFENet and RPMMs also achieved good results on PASCAL-5i, reaching 61.14 and 59.61, respectively. The FTNet obtained a suboptimal result on Fold1, which was 10.54% lower than the HDMNet on all folds. However, our primary goal was FSS-RSI. The results in Table A1 further demonstrate the effectiveness of our model on FSS-RSI tasks. Figure A3 illustrates our model’s qualitative results on PASCAL-5i.

Figure A3.
Results of the FTNet on PASCAL-5i.
References
- Wang, Z.; Wang, B.; Zhang, C.; Liu, Y.; Guo, J. Defending against Poisoning Attacks in Aerial Image Semantic Segmentation with Robust Invariant Feature Enhancement. Remote Sens. 2023, 15, 3157. [Google Scholar] [CrossRef]
- He, Y.; Jia, K.; Wei, Z. Improvements in Forest Segmentation Accuracy Using a New Deep Learning Architecture and Data Augmentation Technique. Remote Sens. 2023, 15, 2412. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef]
- Noh, H.; Hong, S.; Han, B. Learning Deconvolution Network for Semantic Segmentation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Piscataway, NJ, USA, 7–13 December 2015; pp. 1520–1528. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-path Refinement Networks for High-Resolution Semantic Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5168–5177. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2016, arXiv:1511.07122. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.S.; et al. Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 6877–6886. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. arXiv 2016, arXiv:2105.15203. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2016, arXiv:1810.04805. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Shaban, A.; Bansal, S.; Liu, Z.; Essa, I.; Boots, B. One-Shot Learning for Semantic Segmentation. arXiv 2017, arXiv:1709.03410. [Google Scholar]
- Tian, Z.; Zhao, H.; Shu, M.; Yang, Z.; Li, R.; Jia, J. Prior Guided Feature Enrichment Network for Few-Shot Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1050–1065. [Google Scholar] [CrossRef] [PubMed]
- Lang, C.; Cheng, G.; Tu, B.; Han, J. Learning What Not to Segment: A New Perspective on Few-Shot Segmentation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 8047–8057. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching Networks for One Shot Learning. arXiv 2016, arXiv:1606.04080. [Google Scholar]
- Wang, K.; Liew, J.H.; Zou, Y.; Zhou, D.; Feng, J. PANet: Few-Shot Image Semantic Segmentation with Prototype Alignment. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9196–9205. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, G.; Liu, F.; Yao, R.; Shen, C. CANet: Class-Agnostic Segmentation Networks With Iterative Refinement and Attentive Few-Shot Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5212–5221. [Google Scholar] [CrossRef]
- Yang, B.; Liu, C.; Li, B.; Jiao, J.; Ye, Q. Prototype Mixture Models for Few-shot Semantic Segmentation. arXiv 2020, arXiv:2008.03898. [Google Scholar]
- Min, J.; Kang, D.; Cho, M. Hypercorrelation Squeeze for Few-Shot Segmenation. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 6921–6932. [Google Scholar] [CrossRef]
- Siam, M.; Oreshkin, B. Adaptive Masked Weight Imprinting for Few-Shot Segmentation. arXiv 2019, arXiv:1902.11123. [Google Scholar]
- Peng, B.; Tian, Z.; Wu, X.; Wang, C.; Liu, S.; Su, J.; Jia, J. Hierarchical Dense Correlation Distillation for Few-Shot Segmentation. arXiv 2023, arXiv:2303.14652. [Google Scholar]
- Zhang, G.; Kang, G.; Yang, Y.; Wei, Y. Few-Shot Segmentation via Cycle-Consistent Transformer. arXiv 2021, arXiv:2106.02320. [Google Scholar]
- Zhang, J.; Liu, Y.; Wu, P.; Shi, Z.; Pan, B. Mining Cross-Domain Structure Affinity for Refined Building Segmentation in Weakly Supervised Constraints. Remote Sens. 2022, 14, 1227. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, Y.; Guo, P.; Sun, Z.; Chen, X.; Tang, Y. Cycle and Self-Supervised Consistency Training for Adapting Semantic Segmentation of Aerial Images. Remote Sens. 2022, 14, 1527. [Google Scholar] [CrossRef]
- Sun, L.; Cheng, S.; Zheng, Y.; Wu, Z.; Zhang, J. SPANet: Successive Pooling Attention Network for Semantic Segmentation of Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2022, 15, 4045–4057. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, C.; Wang, D.; Ji, C.; Li, B. Semi-Supervised Contrastive Learning for Few-Shot Segmentation of Remote Sensing Images. Remote Sens. 2022, 14, 4254. [Google Scholar] [CrossRef]
- Deng, R.; Shen, C.; Liu, S.; Wang, H.; Liu, X. Learning to Predict Crisp Boundaries. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 570–586. [Google Scholar] [CrossRef]
- Demir, I.; Koperski, K.; Lindenbaum, D.; Pang, G.; Huang, J.; Basu, S.; Hughes, F.; Tuia, D.; Raskar, R. DeepGlobe 2018: A Challenge to Parse the Earth through Satellite Images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 172–181. [Google Scholar] [CrossRef]
- ISPRS. Potsdam. Available online: https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-label-potsdam.aspx (accessed on 20 June 2023).
- ISPRS Vaihingen. Available online: https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-labelvaihingen.aspx (accessed on 20 June 2023).
- Kaiser, P.; Wegner, J.D.; Lucchi, A.; Jaggi, M.; Hofmann, T.; Schindler, K. Learning Aerial Image Segmentation from Online Maps. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6054–6068. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Kai, L.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Piscataway, NJ, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. BiSeNet: Bilateral Segmentation Network for Real-Time Semantic Segmentation. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 334–349. [Google Scholar] [CrossRef]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. BiSeNet V2: Bilateral Network with Guided Aggregation for Real-Time Semantic Segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Fan, M.; Lai, S.; Huang, J.; Wei, X.; Chai, Z.; Luo, J.; Wei, X. Rethinking BiSeNet For Real-time Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9711–9720. [Google Scholar] [CrossRef]
- Seo, J.; Park, Y.-H.; Yoon, S.W.; Moon, J. Task-Adaptive Feature Transformer with Semantic Enrichment for Few-Shot Segmentation. arXiv 2022, arXiv:2202.06498. [Google Scholar]
- Haklay, M.; Weber, P. OpenStreetMap: User-Generated Street Maps. IEEE Pervasive Comput. 2008, 7, 12–18. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plan. B-Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Girres, J.-F.; Touya, G. Quality Assessment of the French OpenStreetMap Dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Google Maps. Available online: https://support.google.com/mapcontentpartners/answer/144284?hl=en (accessed on 20 September 2023).
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. arXiv 2017, arXiv:1706.08500. [Google Scholar]
- Everingham, M.; Gool, L.V.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes (voc) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Hariharan, B.; Arbeláez, P.; Bourdev, L.; Maji, S.; Malik, J. Semantic contours from inverse detectors. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 991–998. [Google Scholar] [CrossRef]
- Lang, C.; Wang, J.; Cheng, G.; Tu, B.; Han, J. Progressive Parsing and Commonality Distillation for Few-Shot Remote Sensing Segmentation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5613610. [Google Scholar] [CrossRef]
- Li, R.; Li, J.; Gou, S.; Lu, H.; Mao, S.; Guo, Z. Multi-Scale Similarity Guidance Few-Shot Network for Ship Segmentation in SAR Images. Remote Sens. 2023, 15, 3304. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).











