Retrieval of Surface Soil Moisture over Wheat Fields during Growing Season Using C-Band Polarimetric SAR Data
Abstract
:1. Introduction
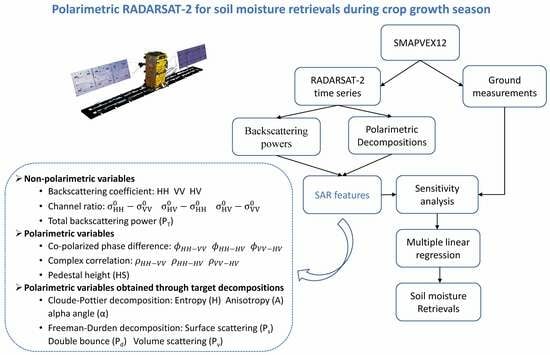
2. Materials and Methods
2.1. Materials
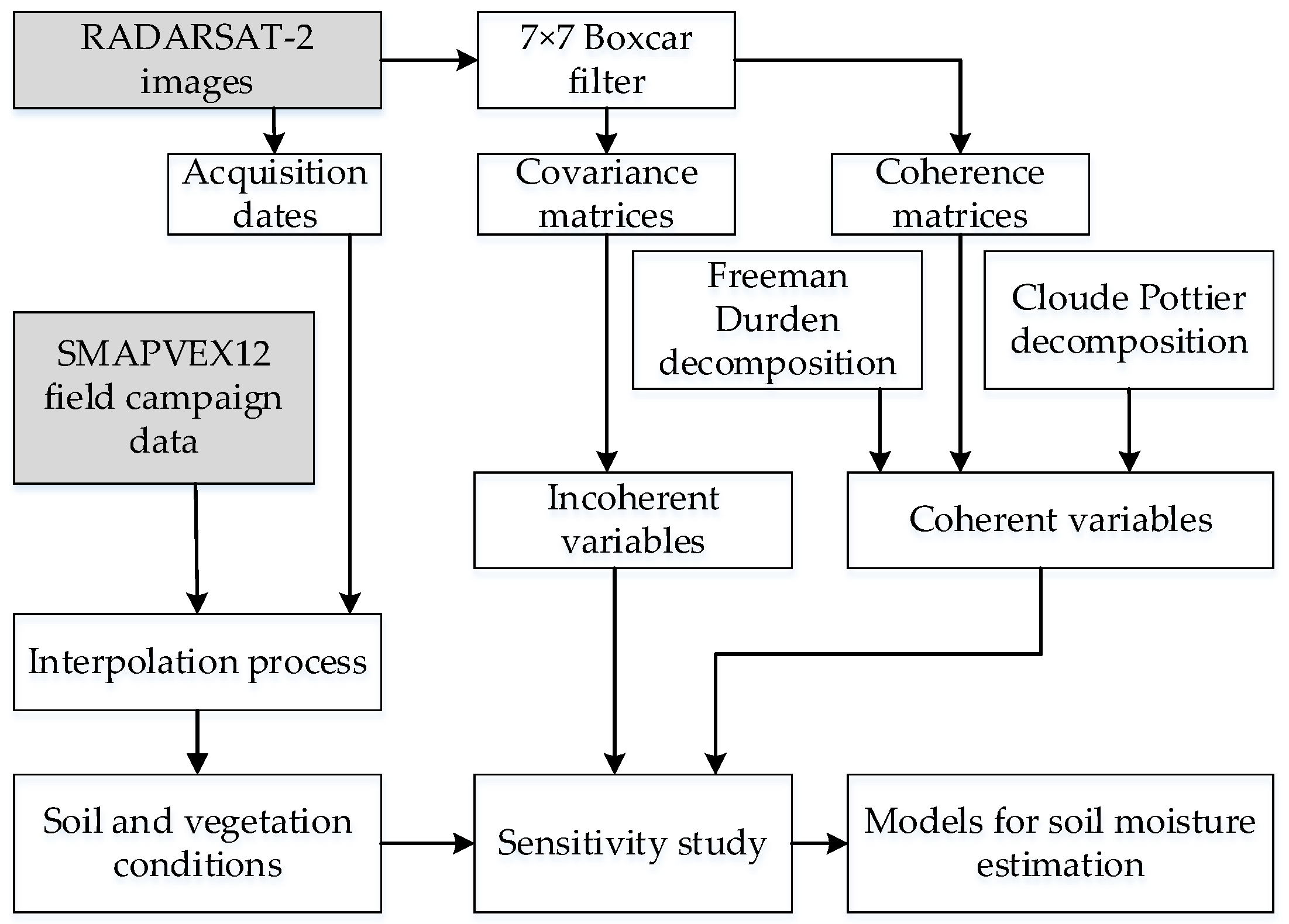
2.2. Methods
2.2.1. Temporal Interpolation of In Situ Measurements
2.2.2. Processing of RADARSAT-2 Images
2.2.3. Sensitivity Study and Modelling
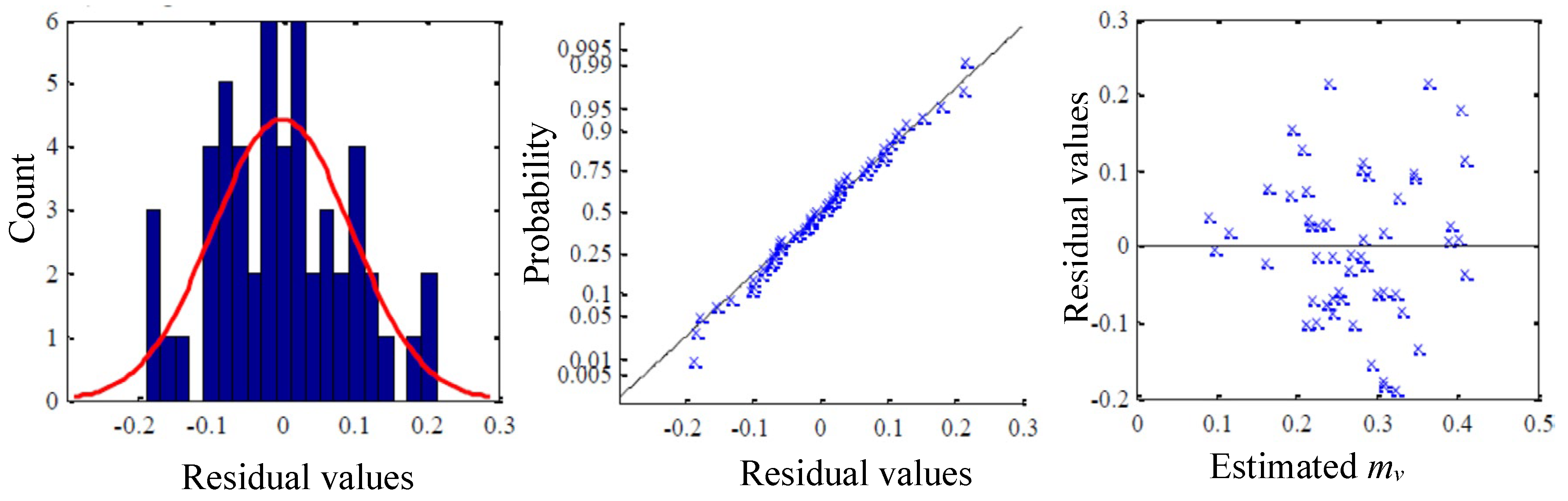
2.2.4. Calibration and Validation of the Models
3. Results
3.1. Temporal Interpolation
3.2. Sensitivity Analysis and Variable Selection
3.3. Non-Polarimetric Model
3.4. Models Based upon Non-Polarimetric and Polarimetric Variables
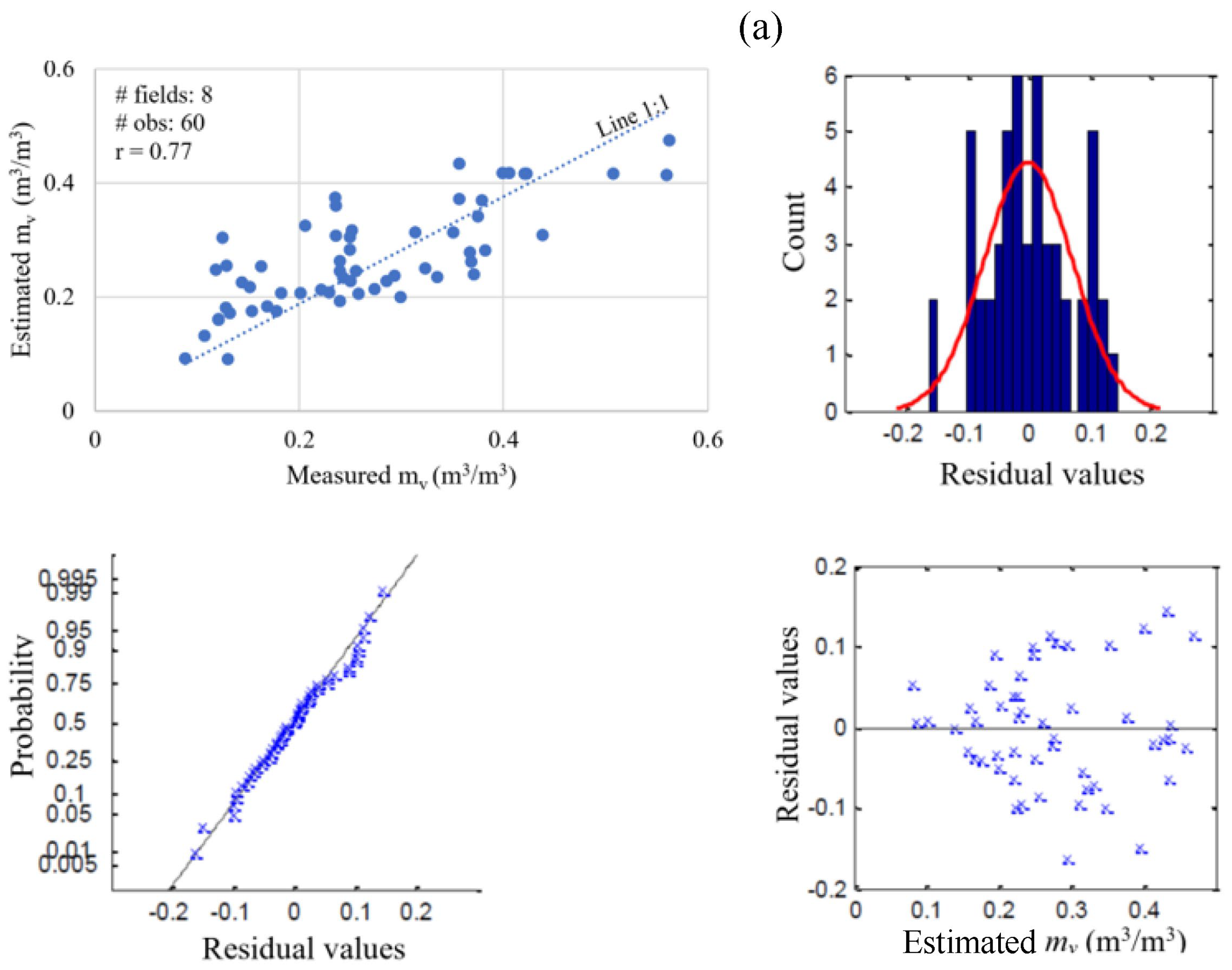
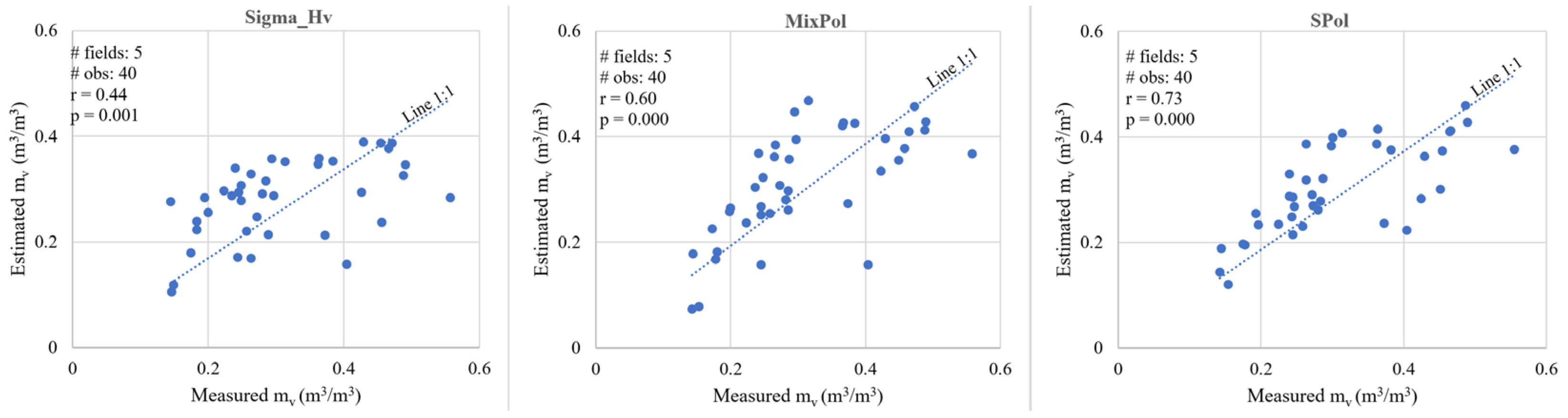
3.5. Validation of Models
4. Discussion
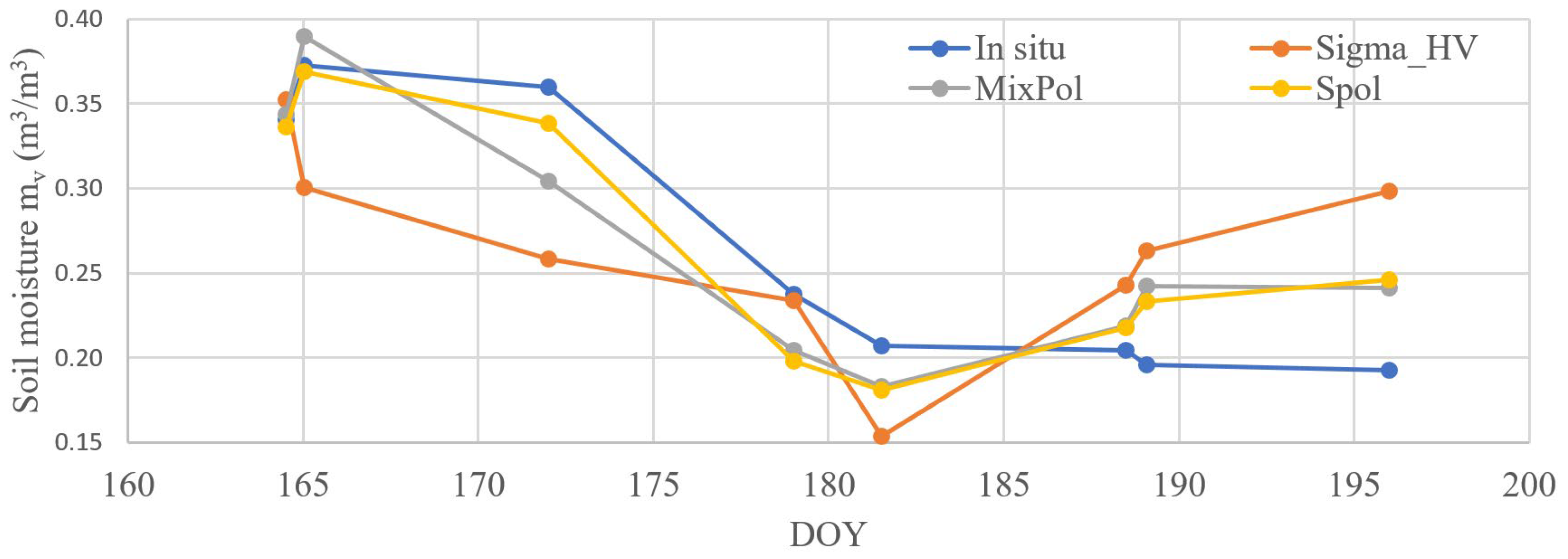
4.1. Match between Satellite Observation and Ground Measurements
4.2. Sensitivity Analysis
4.3. Selection of SAR Parameters for Empirical Models
4.4. Bias and Application of the Developed Models
4.5. Comparison with Recent Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Entekhabi, D.; Rodriguez-Iturbe, I.; Castelli, F. Mutual interaction of soil moisture state and atmospheric processes. J. Hydrol. 1996, 184, 3–17. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.J.; et al. A roadmap for high-resolution satellite soil moisture applications—Confronting product characteristics with user requirements. Remote Sens. Environ. 2021, 252, 112162. [Google Scholar] [CrossRef]
- Sakai, T.; Iizumi, T.; Okada, M.; Nishimori, M.; Grünwald, T.; Prueger, J.; Cescatti, A.; Korres, W.; Schmidt, M.; Carrara, A.; et al. Varying applicability of four different satellite-derived soil moisture products to global gridded crop model evaluation. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 51–60. [Google Scholar] [CrossRef]
- Flint, L.E.; Flint, A.L.; Mendoza, J.; Kalansky, J.; Ralph, F.M. Characterizing drought in California: New drought indices and scenario-testing in support of resource management. Ecol. Process. 2018, 7, 1. [Google Scholar] [CrossRef]
- Lahmers, T.M.; Kumar, S.V.; Locke, K.A.; Wang, S.; Getirana, A.; Wrzesien, M.L.; Liu, P.-W.; Ahmad, S.K. Interconnected hydrologic extreme drivers and impacts depicted by remote sensing data assimilation. Sci. Rep. 2023, 13, 3411. [Google Scholar] [CrossRef] [PubMed]
- McNairn, H.; Jackson, T.J.; Wiseman, G.; Belair, S.; Berg, A.; Bullock, P.; Colliander, A.; Cosh, M.H.; Kim, S.-B.; Magagi, R.; et al. The Soil Moisture Active Passive Validation Experiment 2012 (SMAPVEX12): Prelaunch calibration and validation of the SMAP soil moisture algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2784–2801. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Cappelletti, L.M.; Sörensson, A.A.; Salvia, M.; Ruscica, R.C.; Spennemann, P.; Fernandez-Long, M.E.; Jobbágy, E. Soil moisture estimates over sporadically flooded farmlands: Synergies and biases of remote sensing and in situ sources. Int. J. Remote Sens. 2022, 43, 6979–7001. [Google Scholar] [CrossRef]
- Cammalleri, C.; Vogt, J.V.; Bisselink, B.; de Roo, A. Comparing soil moisture anomalies from multiple independent sources over different regions across the globe. Hydrol. Earth Syst. Sci. 2017, 21, 6329–6343. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Bitar, A.A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- van der Schalie, R.; Kerr, Y.H.; Wigneron, J.P.; Rodríguez-Fernández, N.J.; Al-Yaari, A.; de Jeu, R.A.M. Global SMOS Soil Moisture Retrievals from The Land Parameter Retrieval Model. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 125–134. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Pan, M.; Wanders, N.; Kumar, D.N.; Wood, E.F. Four decades of microwave satellite soil moisture observations: Part 1. A review of retrieval algorithms. Adv. Water Resour. 2017, 109, 106–120. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Kerr, Y.; Rodriguez-Fernandez, N.; O’Neill, P.E.; Jackson, T.J.; De Lannoy, G.J.M.; Al Bitar, A.; Mialon, A.; Richaume, P.; et al. Evaluating soil moisture retrievals from ESA’s SMOS and NASA’s SMAP brightness temperature datasets. Remote Sens. Environ. 2017, 193, 257–273. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R.; Chaubell, J. SMAP L3 Radiometer Global Daily 36 km EASE-Grid Soil Moisture; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2019. [Google Scholar]
- Portal, G.; Jagdhuber, T.; Vall-llossera, M.; Camps, A.; Pablos, M.; Entekhabi, D.; Piles, M. Assessment of Multi-Scale SMOS and SMAP Soil Moisture Products across the Iberian Peninsula. Remote Sens. 2020, 12, 570. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Chen, N.; Zhang, X.; Cosh, M.H.; Wang, W. Satellite surface soil moisture from SMAP, SMOS, AMSR2 and ESA CCI: A comprehensive assessment using global ground-based observations. Remote Sens. Environ. 2019, 231, 111215. [Google Scholar] [CrossRef]
- Llamas, R.M.; Guevara, M.; Rorabaugh, D.; Taufer, M.; Vargas, R. Spatial Gap-Filling of ESA CCI Satellite-Derived Soil Moisture Based on Geostatistical Techniques and Multiple Regression. Remote Sens. 2020, 12, 665. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y. Advances in the Quality of Global Soil Moisture Products: A Review. Remote Sens. 2022, 14, 3741. [Google Scholar] [CrossRef]
- Boerner, W.; Mott, H.; Lueneburg, E.; Livingstone, C.; Brisco, B.; Brown, R.J.; Paterson, J.S. Polarimetry in Radar Remote Sensing: Basic and Applied Concepts; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Dobson, M.C.; Ulaby, F. Microwave Backscatter Dependence on Surface Roughness, Soil Moisture, and Soil Texture: Part III-Soil Tension. IEEE Trans. Geosci. Remote Sens. 1981, GE-19, 51–61. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T. Mapping Soil Moisture Distribution with Imaging Radar; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized Radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Gherboudj, I.; Magagi, R.; Berg, A.A.; Toth, B. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular RADARSAT-2 SAR data. Remote Sens. Environ. 2011, 115, 33–43. [Google Scholar] [CrossRef]
- Xing, M.; Chen, L.; Wang, J.; Shang, J.; Huang, X. Soil Moisture Retrieval Using SAR Backscattering Ratio Method during the Crop Growing Season. Remote Sens. 2022, 14, 3210. [Google Scholar] [CrossRef]
- Gao, L.; Gao, Q.; Zhang, H.; Li, X.; Chaubell, M.J.; Ebtehaj, A.; Shen, L.; Wigneron, J.-P. A deep neural network based SMAP soil moisture product. Remote Sens. Environ. 2022, 277, 113059. [Google Scholar] [CrossRef]
- Batchu, V.; Nearing, G.; Gulshan, V. A Deep Learning Data Fusion Model using Sentinel-1/2, SoilGrids, SMAP-USDA, and GLDAS for Soil Moisture Retrieval. J. Hydrometeorol. 2023. [Google Scholar] [CrossRef]
- Zhu, L.; Si, R.; Shen, X.; Walker, J.P. An advanced change detection method for time-series soil moisture retrieval from Sentinel-1. Remote Sens. Environ. 2022, 279, 113137. [Google Scholar] [CrossRef]
- Evans, D.L.; Farr, T.G.; van Zyl, J.J.; Zebker, H.A. Radar polarimetry: Analysis tools and applications. IEEE Trans. Geosci. Remote Sens. 1988, 26, 774–789. [Google Scholar] [CrossRef]
- Jiao, X.; McNairn, H.; Shang, J.; Pattey, E.; Liu, J.; Champagne, C. The sensitivity of RADARSAT-2 polarimetric SAR data to corn and soybean leaf area index. Can. J. Remote Sens. 2011, 37, 69–81. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- An, W.; Lin, M. An Incoherent Decomposition Algorithm Based on Polarimetric Symmetry for Multilook Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2383–2397. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Zou, B.; Gu, G. Polarimetric SAR Decomposition Method Based on Modified Rotational Dihedral Model. Remote Sens. 2023, 15, 101. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K. Comparison of different polarimetric decompositions for soil moisture retrieval over vegetation covered agricultural area. Remote Sens. Environ. 2017, 199, 120–136. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goïta, K.; Colliander, A. Multi-resolution soil moisture retrievals by disaggregating SMAP brightness temperatures with RADARSAT-2 polarimetric decompositions. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103114. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, L.; Yang, J.; Lopez-Sanchez, J.M.; Zhao, J.; Sun, W.; Shi, L.; Li, P. Soil moisture retrieval over agricultural fields from L-band multi-incidence and multitemporal PolSAR observations using polarimetric decomposition techniques. Remote Sens. Environ. 2021, 261, 112485. [Google Scholar] [CrossRef]
- Natural Resources Canada. Transition Guide NTDB to CanVec; Government of Canada, Natural Resources Canada, Earth and Sciences Sector: Ottawa, ON, Canada, 2013.
- Natural Resources Canada. Canadian Digital Elevation Model Product Specifications; Government of Canada, Natural Resources Canada, Map Information Branch: Ottawa, ON, Canada, 2016.
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging from Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Lee, J.S.; Ainsworth, T.L.; Kelly, J.P.; Lopez-Martinez, C. Evaluation and Bias Removal of Multilook Effect on Entropy/Alpha/Anisotropy in Polarimetric SAR Decomposition. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3039–3052. [Google Scholar] [CrossRef]
- López-Martínez, C.; Alonso-González, A.; Fàbregas, X. Perturbation Analysis of Eigenvector-Based Target Decomposition Theorems in Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2081–2095. [Google Scholar] [CrossRef]
- Toutin, T. Radarsat-2 DSM Generation With New Hybrid, Deterministic, and Empirical Geometric Modeling Without GCP. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2049–2055. [Google Scholar] [CrossRef]
- Mattia, F.; Toan, T.L.; Picard, G.; Posa, F.I.; Alessio, A.D.; Notarnicola, C.; Gatti, A.M.; Rinaldi, M.; Satalino, G.; Pasquariello, G. Multitemporal C-band radar measurements on wheat fields. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1551–1560. [Google Scholar] [CrossRef]
- Moran, M.S.; Alonso, L.; Moreno, J.F.; Pilar Cendrero Mateo, M.; Fernando de la Cruz, D.; Montoro, A. A RADARSAT-2 quad-polarized time series for monitoring crop and soil conditions in Barrax, Spain. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1057–1070. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H. Using multi-polarization C- and L-band synthetic aperture radar to estimate biomass and soil moisture of wheat fields. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 50–64. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Jagdhuber, T. An Approach to Extended Fresnel Scattering for Modeling of Depolarizing Soil-Trunk Double-Bounce Scattering. Remote Sens. 2016, 8, 818. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Volume III—Volume Scattering and Emission Theory, Advanced Systems and Applications; Artech House: Norwood, MA, USA, 1986; Volume 3. [Google Scholar]
- McNairn, H.; Duguay, C.; Brisco, B.; Pultz, T.J. The effect of soil and crop residue characteristics on polarimetric radar response. Remote Sens. Environ. 2002, 80, 308–320. [Google Scholar] [CrossRef]
- Cable, J.W.; Kovacs, J.M.; Jiao, X.; Shang, J. Agricultural Monitoring in Northeastern Ontario, Canada, Using Multi-Temporal Polarimetric RADARSAT-2 Data. Remote Sens. 2014, 6, 2343–2371. [Google Scholar] [CrossRef]
- Skriver, H.; Svendsen, M.T.; Thomsen, A.G. Multitemporal C- and L-band polarimetric signatures of crops. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2413–2429. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, T.; Qiu, J.; Zhao, X.; Li, R.; Wang, S. Microwave-based vegetation descriptors in the parameterization of water cloud model at L-band for soil moisture retrieval over croplands. GIScience Remote Sens. 2021, 58, 48–67. [Google Scholar] [CrossRef]
- He, L.; Panciera, R.; Tanase, M.A.; Walker, J.P.; Qin, Q. Soil moisture retrieval in agricultural fields using adaptive model-based polarimetric decomposition of SAR data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4445–4460. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, C.; Min, L.; Guo, Z.; Li, N. Retrieval of Farmland Surface Soil Moisture Based on Feature Optimization and Machine Learning. Remote Sens. 2022, 14, 5102. [Google Scholar] [CrossRef]
- Dong, L.; Wang, W.; Jin, R.; Xu, F.; Zhang, Y. Surface Soil Moisture Retrieval on Qinghai-Tibetan Plateau Using Sentinel-1 Synthetic Aperture Radar Data and Machine Learning Algorithms. Remote Sens. 2023, 15, 153. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Ngo, H.H.; Guo, W.; Chang, S.W.; Nguyen, D.D.; Nguyen, C.T.; Zhang, J.; Liang, S.; Bui, X.T.; Hoang, N.B. A low-cost approach for soil moisture prediction using multi-sensor data and machine learning algorithm. Sci. Total Environ. 2022, 833, 155066. [Google Scholar] [CrossRef]
- Singh, A.; Gaurav, K. Deep learning and data fusion to estimate surface soil moisture from multi-sensor satellite images. Sci. Rep. 2023, 13, 2251. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K.; Jagdhuber, T.; Hajnsek, I. Evaluation of simplified polarimetric decomposition for soil moisture retrieval over vegetated agricultural fields. Remote Sens. 2016, 8, 142. [Google Scholar] [CrossRef]
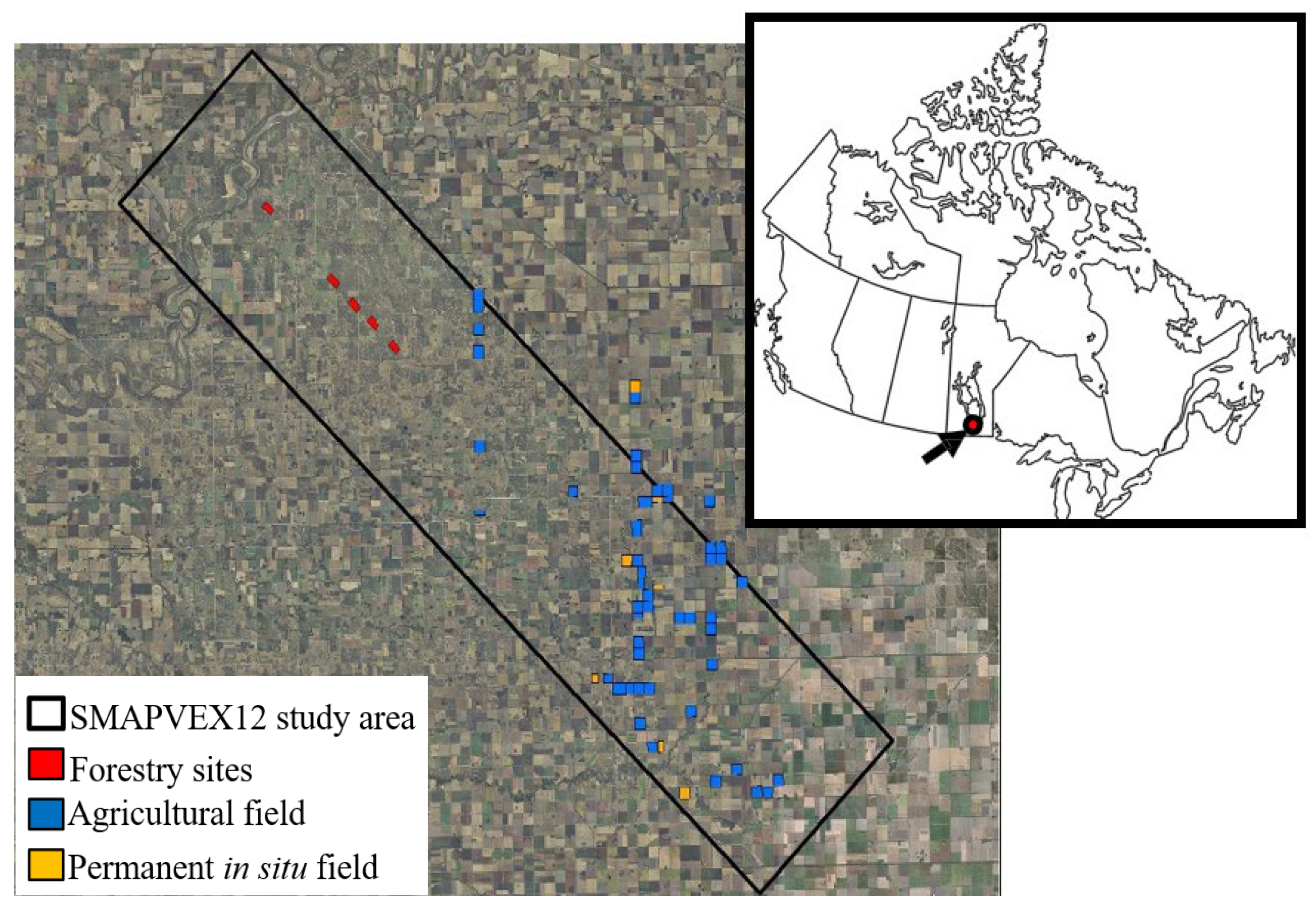



| Date (mm/dd) | Julian Day (DOY) | Local Time | Angle of Incidence (°) |
|---|---|---|---|
| 06/05 | 157 | 7:57 a.m. | 20–23.6 |
| 06/12 | 164 | 7:53 a.m. | 26.1–29.4 |
| 06/12 | 165 | 7:15 p.m. | 28.4–31.6 |
| 06/19 | 172 | 7:11 p.m. | 23.7–27.2 |
| 06/26 | 179 | 7:07 p.m. | 19–22.7 |
| 06/29 | 181 | 7:57 a.m. | 20–23.6 |
| 07/06 | 188 | 7:53 a.m. | 26.1–29.4 |
| 07/06 | 189 | 7:15 p.m. | 28.4–31.6 |
| 07/13 | 196 | 7:11 p.m. | 23.7–27.2 |
| Non-Polarimetric Variables (dB) |
|---|
| Backscattering coefficient HH (); Backscattering cross-coefficient HV (); Backscattering coefficient VV (); Channel ratio HH-VV (; Channel ratio HV-HH (); Channel ratio HV-VV (); Total backscattering power (PT). |
| Polarimetric Variables |
| Co-polarized phase difference (); Complex co-polarized channel correlation (); Cross-polarization phase differences (, ); Complex cross-polarization channels (, ); Pedestal height (HS). |
| Polarimetric Variables Obtained through Target Decomposition |
| Cloude–Pottier decomposition: Entropy (H), anisotropy (A), alpha-angle (α); Freeman–Durden decomposition: Surface component (Ps), Interaction component (Pd), Volume component (Pv). |
| Meteorological Station | |||||
|---|---|---|---|---|---|
| Field ID | Network | Distance (km) | r | p-Value | RMSE (m3/m3) |
| 73-1 | USDA | 1.0 | 0.871 | 0.00 | 0.018 |
| 74-1 | USDA | 0.0 | 0.929 | 0.00 | 0.015 |
| 104 | USDA | 0.0 | 0.971 | 0.00 | 0.027 |
| 105 | USDA | 0.8 | 0.974 | 0.00 | 0.018 |
| 31 | USDA | 0.0 | 0.912 | 0.00 | 0.033 |
| 32 | Sages | 0.0 | 0.774 | 0.00 | 0.062 |
| 44 | USDA | 0.8 | 0.885 | 0.00 | 0.036 |
| 45 | USDA | 0.0 | 0.875 | 0.00 | 0.044 |
| 55 | USDA | 0.0 | 0.888 | 0.00 | 0.037 |
| 81 | USDA | 0.0 | 0.911 | 0.00 | 0.018 |
| 85 | USDA | 3.7 | 0.716 | 0.01 | 0.037 |
| 91 | USDA | 0.0 | 0.910 | 0.00 | 0.020 |
| Non-Polarimetric Variables | |||||||
|---|---|---|---|---|---|---|---|
| PT | |||||||
| mv | 0.33 | 0.56 | 0.53 | 0.49 | −0.24 | 0.34 | 0.19 |
| s | 0.10 | −0.10 | 0.06 | 0.08 | 0.02 | −0.23 | −0.20 |
| l | −0.22 | 0.20 | 0.03 | −0.09 | −0.22 | 0.48 | 0.20 |
| VB | −0.07 | −0.18 | −0.25 | −0.15 | 0.20 | −0.10 | 0.10 |
| h | −0.27 | −0.35 | −0.52 | −0.42 | 0.28 | −0.10 | 0.13 |
| VWC | −0.15 | −0.30 | −0.34 | −0.25 | 0.20 | −0.12 | 0.06 |
| Non-Polarimetric Variables | |||||||
| HS | |||||||
| mv | 0.00 | −0.06 | −0.02 | −0.64 | −0.01 | 0.06 | 0.33 |
| s | −0.08 | −0.02 | 0.12 | 0.25 | 0.04 | 0.07 | −0.28 |
| l | 0.22 | 0.14 | −0.04 | −0.11 | 0.21 | −0.13 | 0.40 |
| VB | −0.25 | −0.03 | −0.16 | 0.41 | −0.15 | 0.13 | −0.10 |
| h | −0.26 | 0.09 | −0.24 | 0.53 | −0.17 | −0.01 | −0.04 |
| VWC | −0.19 | 0.05 | −0.17 | 0.14 | −0.23 | 0.08 | −0.10 |
| Variables from Target Decomposition | |||||||
| H | A | α | |||||
| mv | 0.29 | −0.34 | 0.01 | 0.13 | 0.50 | −0.14 | |
| s | −0.26 | 0.25 | −0.08 | 0.22 | −0.12 | 0.21 | |
| l | 0.35 | −0.21 | 0.09 | −0.42 | 0.19 | −0.26 | |
| VB | −0.07 | 0.10 | 0.36 | −0.12 | −0.12 | 0.03 | |
| h | −0.01 | 0.06 | 0.35 | −0.33 | −0.25 | 0.00 | |
| VWC | −0.07 | 0.16 | 0.24 | −0.09 | −0.22 | 0.01 | |
| Model | Number of Fields | Number of Observations | r | RMSE (m3/m3) | Variable | βi | Standard Error | p-Value |
|---|---|---|---|---|---|---|---|---|
| 3_Sigma | 8 | 60 | 0.59 | 0.096 | (Intercept) | 1.101 | 14% | 0.000 |
| 0.001 | 793% | 0.900 | ||||||
| 0.047 | 29% | 0.001 | ||||||
| −0.001 | −1426% | 0.944 | ||||||
| Sigma_HV | 8 | 60 | 0.60 | 0.095 | (Intercept) | 1.153 | 14% | 0.000 |
| 0.050 | 18% | 0.000 |
| Model | Number of Fields | Number of Observations | r | RMSE (m3/m3) | Variables | βi | Std. βi | Standard Error | p-Value |
|---|---|---|---|---|---|---|---|---|---|
| MixPol | 8 | 60 | 0.77 | 0.078 | 0.107 | 0.129 | 16% | 0.000 | |
| −0.117 | −0.177 | −23% | 0.000 | ||||||
| 0.057 | 0.076 | 34% | 0.005 | ||||||
| −0.003 | −0.057 | −24% | 0.000 | ||||||
| Hs | 2.072 | 0.082 | 15% | 0.000 | |||||
| A | −1.637 | −0.067 | −36% | 0.008 | |||||
| SPol | 8 | 60 | 0.71 | 0.084 | Intercept | 0.662 | 0.662 | 12% | 0.000 |
| 0.036 | 0.043 | 26% | 0.000 | ||||||
| −0.004 | −0.076 | −14% | 0.000 |
| Models Comparison | Statistical Metrics between Retrieved and Measured mv | References | |
|---|---|---|---|
| R2 | RMSE (m3/m3) | ||
| Our MLR | 0.54 | 0.074–0.087 | |
| Gradient-boosting regression | 0.891 | 0.0875 | Nguyen et al. [58] |
| ANN | 0.64 | 0.040 | Singh and Gaurav [59] |
| Random Forest | 0.64 | 0.0264 | Zhao et al. [56] |
| 0.753 (Asc)/0.671 (Des) | 0.045 (Asc)/0.049 (Des) | Dong et al. [57] | |
| Polarimetric decomposition | 0.49 | 0.12 | Wang et al. [60] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goïta, K.; Magagi, R.; Beauregard, V.; Wang, H. Retrieval of Surface Soil Moisture over Wheat Fields during Growing Season Using C-Band Polarimetric SAR Data. Remote Sens. 2023, 15, 4925. https://doi.org/10.3390/rs15204925
Goïta K, Magagi R, Beauregard V, Wang H. Retrieval of Surface Soil Moisture over Wheat Fields during Growing Season Using C-Band Polarimetric SAR Data. Remote Sensing. 2023; 15(20):4925. https://doi.org/10.3390/rs15204925
Chicago/Turabian StyleGoïta, Kalifa, Ramata Magagi, Vincent Beauregard, and Hongquan Wang. 2023. "Retrieval of Surface Soil Moisture over Wheat Fields during Growing Season Using C-Band Polarimetric SAR Data" Remote Sensing 15, no. 20: 4925. https://doi.org/10.3390/rs15204925
APA StyleGoïta, K., Magagi, R., Beauregard, V., & Wang, H. (2023). Retrieval of Surface Soil Moisture over Wheat Fields during Growing Season Using C-Band Polarimetric SAR Data. Remote Sensing, 15(20), 4925. https://doi.org/10.3390/rs15204925