Analysis of Electromagnetic Wave and Multipath Suppression from Overhead Perspective
Abstract
:1. Introduction
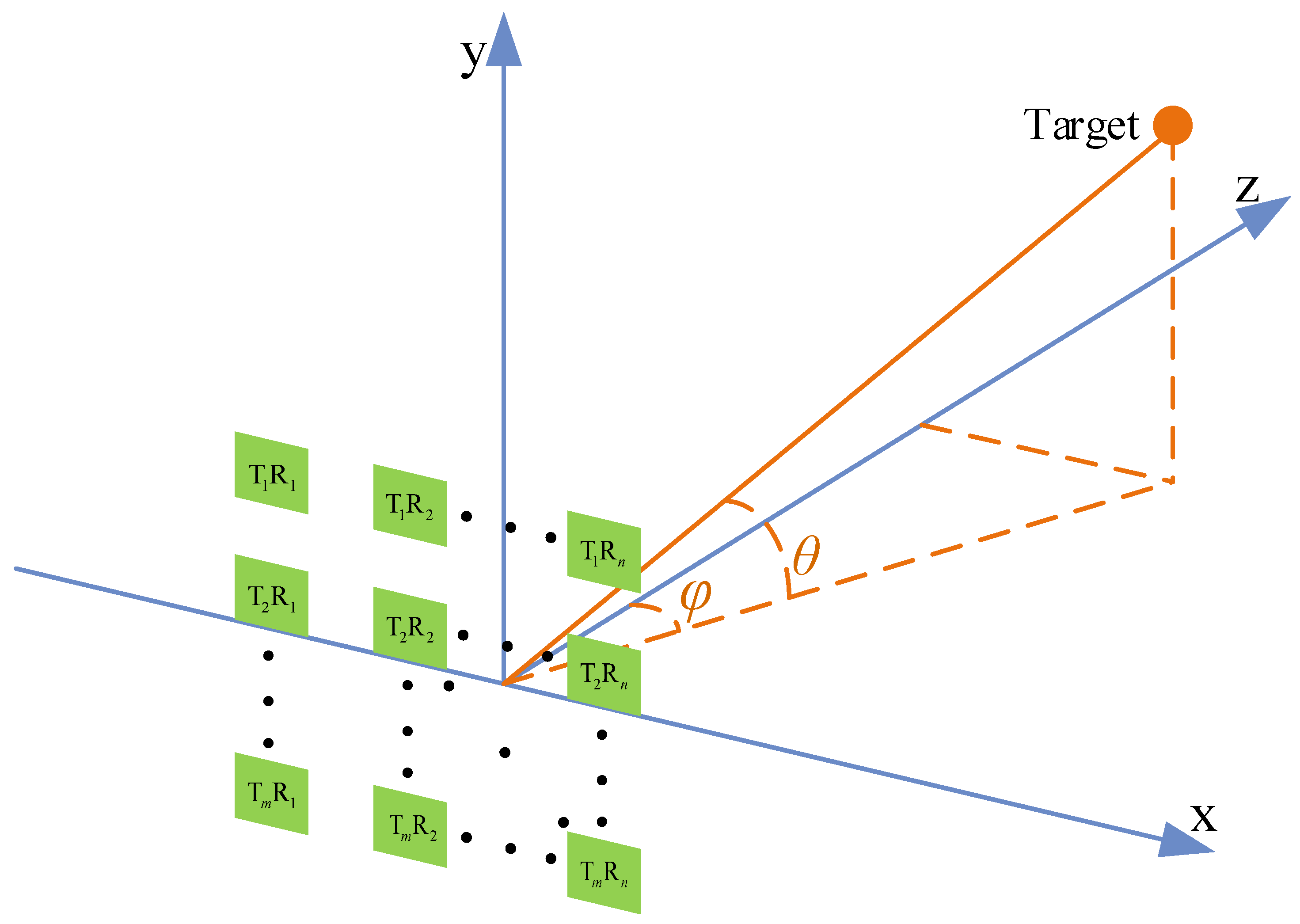
2. System Model of Overhead Perspective
2.1. The Model of EM Propagation for an Overhead Perspective
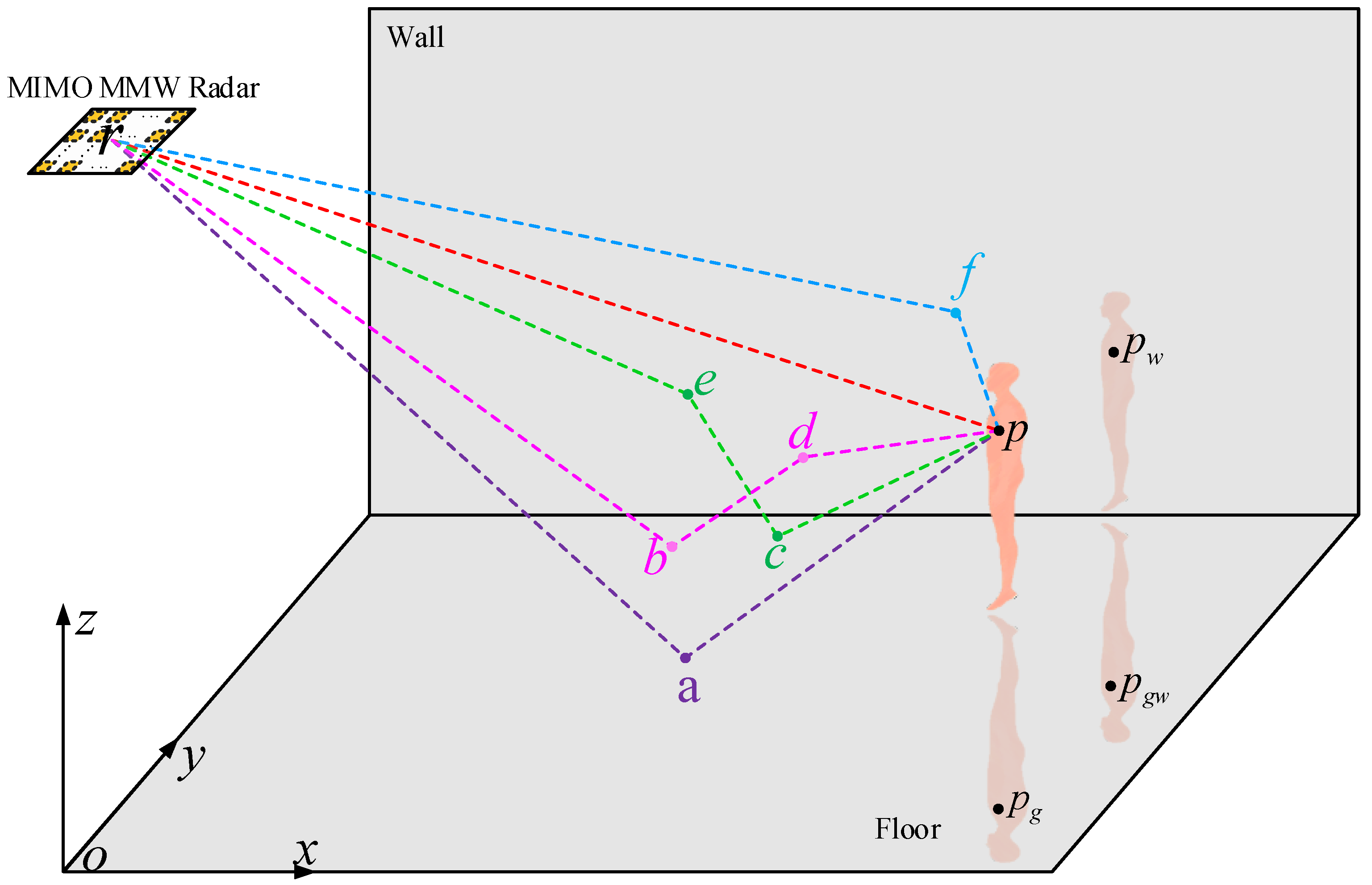
2.2. Received Signal in an Indoor Multipath Scenario
2.3. The 3D Point Cloud Generation Method
2.3.1. Data Preprocessing
2.3.2. Target Distance Estimation
2.3.3. Target Angle Estimation
2.3.4. Target Point Cloud Generation
3. Echo Component Analysis for Overhead MMW Radar
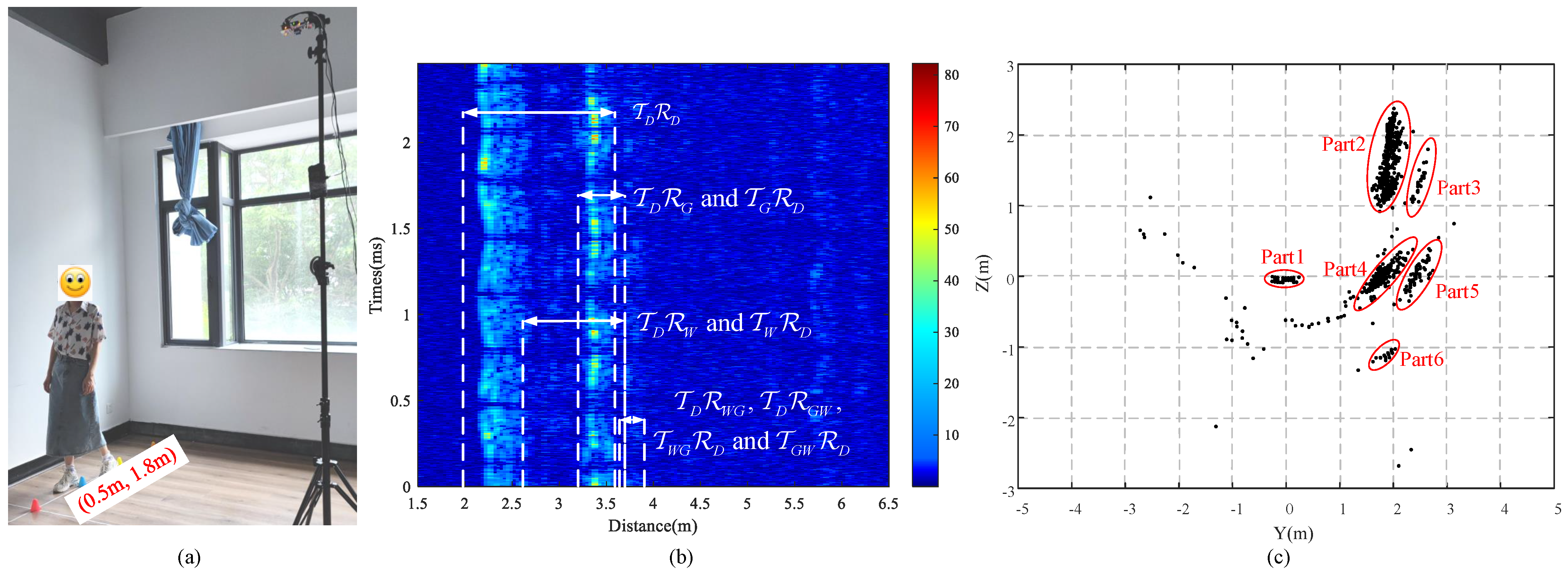
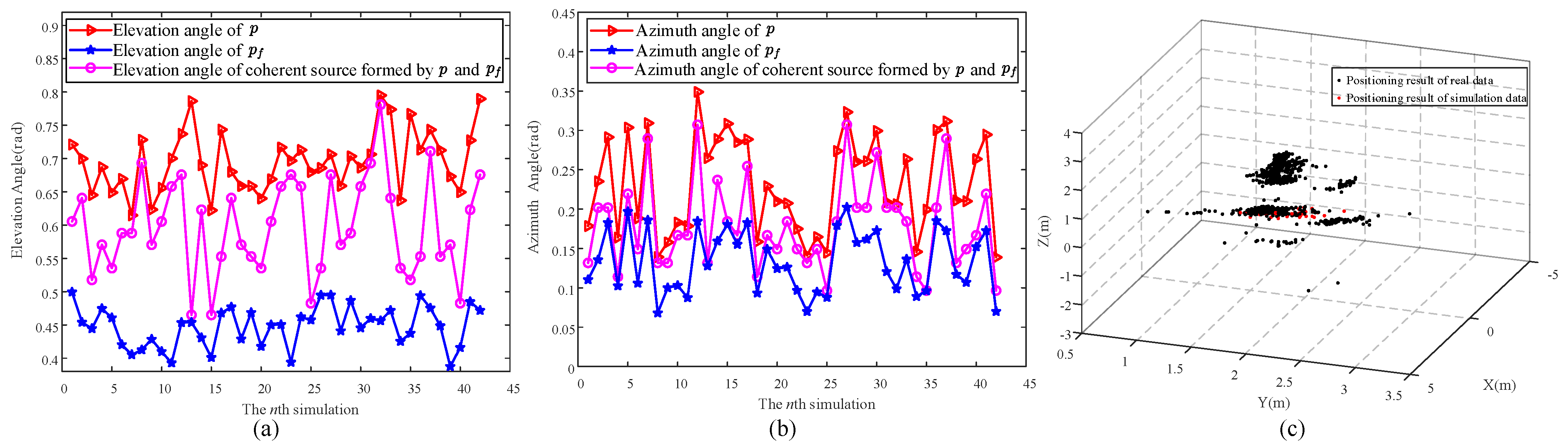
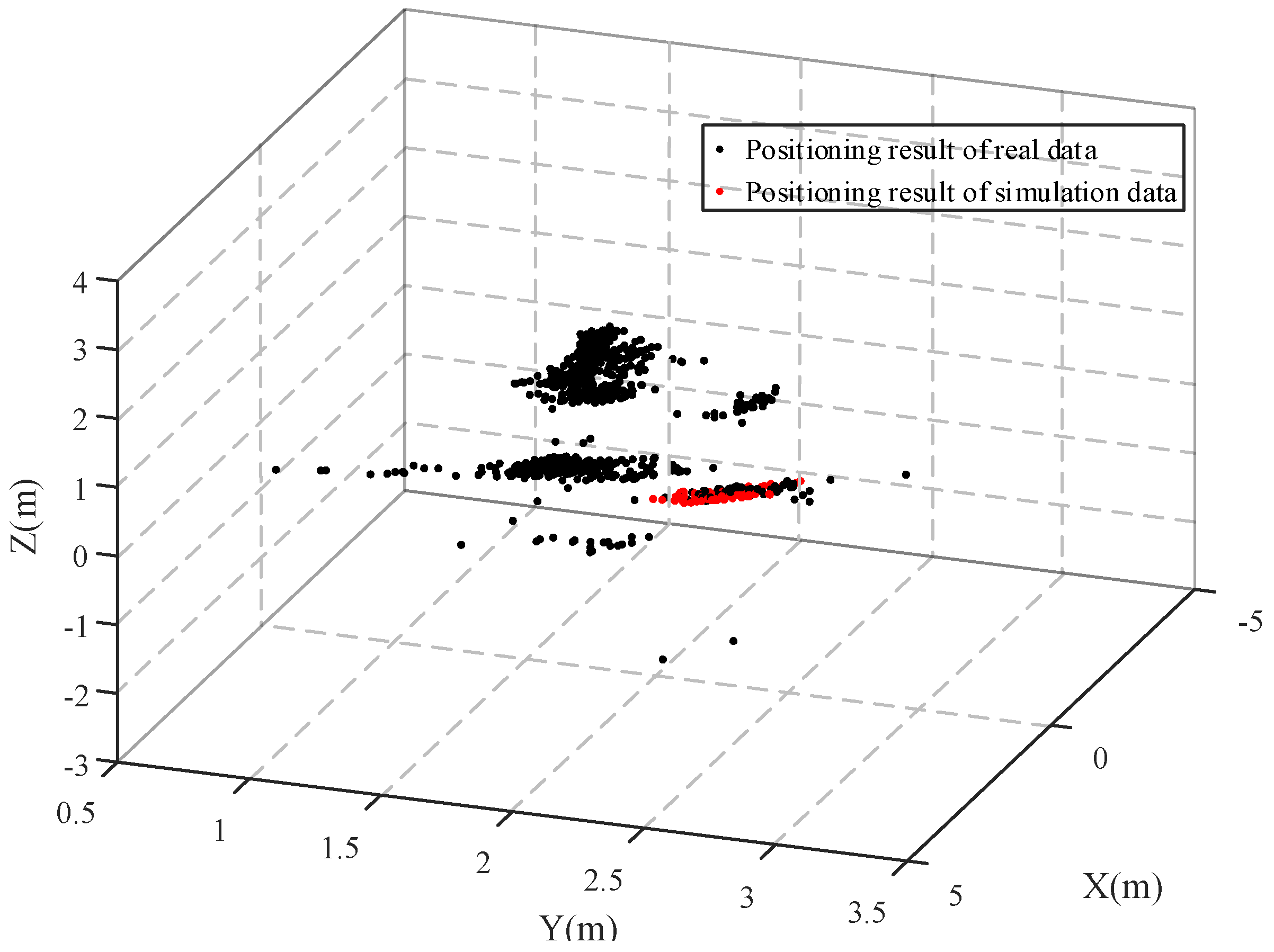
3.1. Detailed Analysis of Typical Data
3.2. Analysis of Data for Different Locations
4. Method of Suppressing Multipath Ghost Targets for an Overhead Perspective
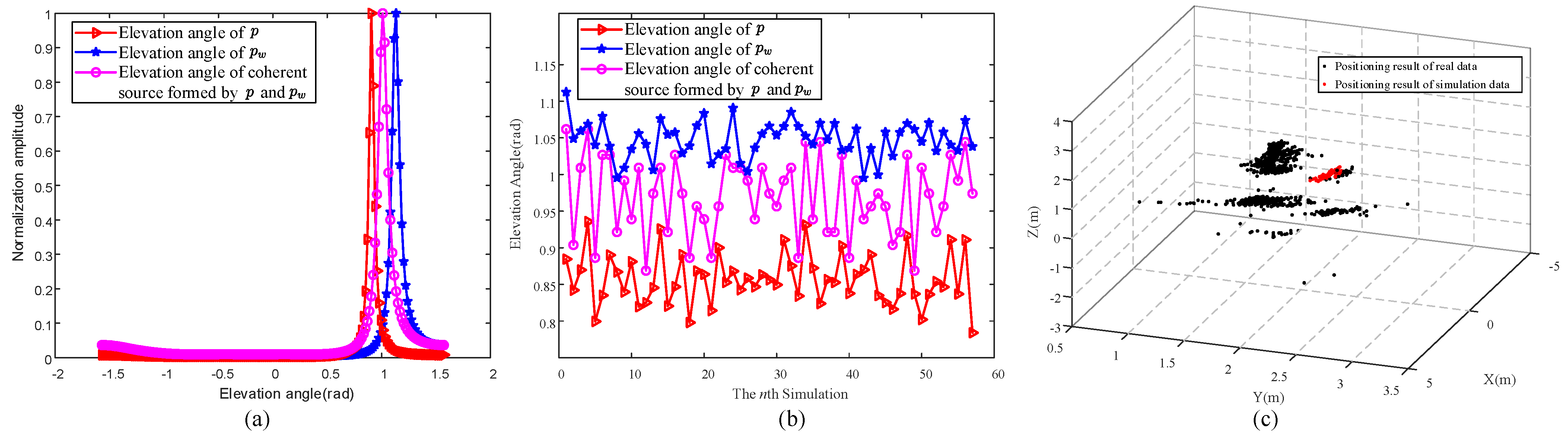
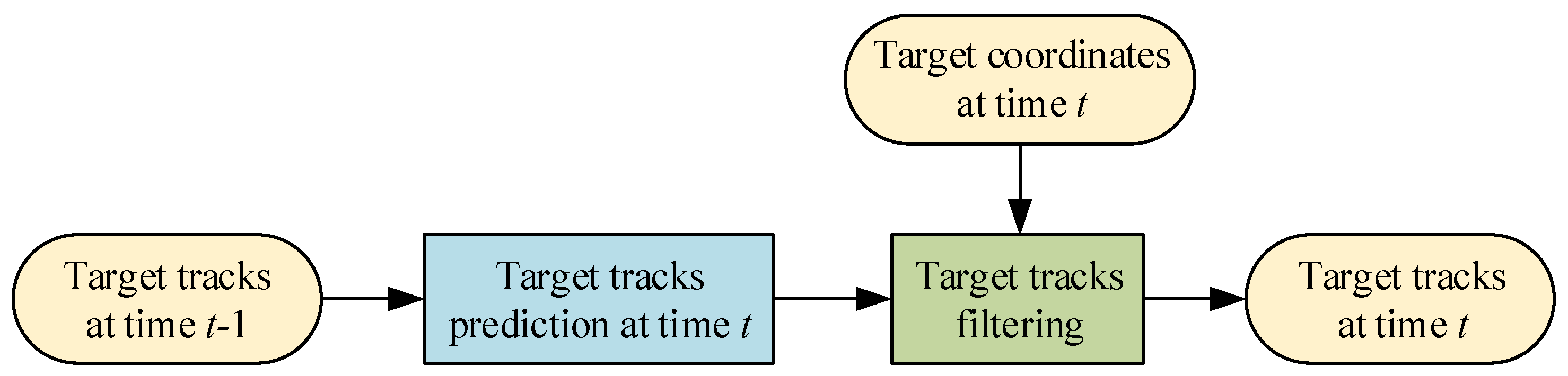
4.1. Multipath Ghost Suppression Method
| Algorithm 1: Multipath ghost target suppression algorithm |
 |
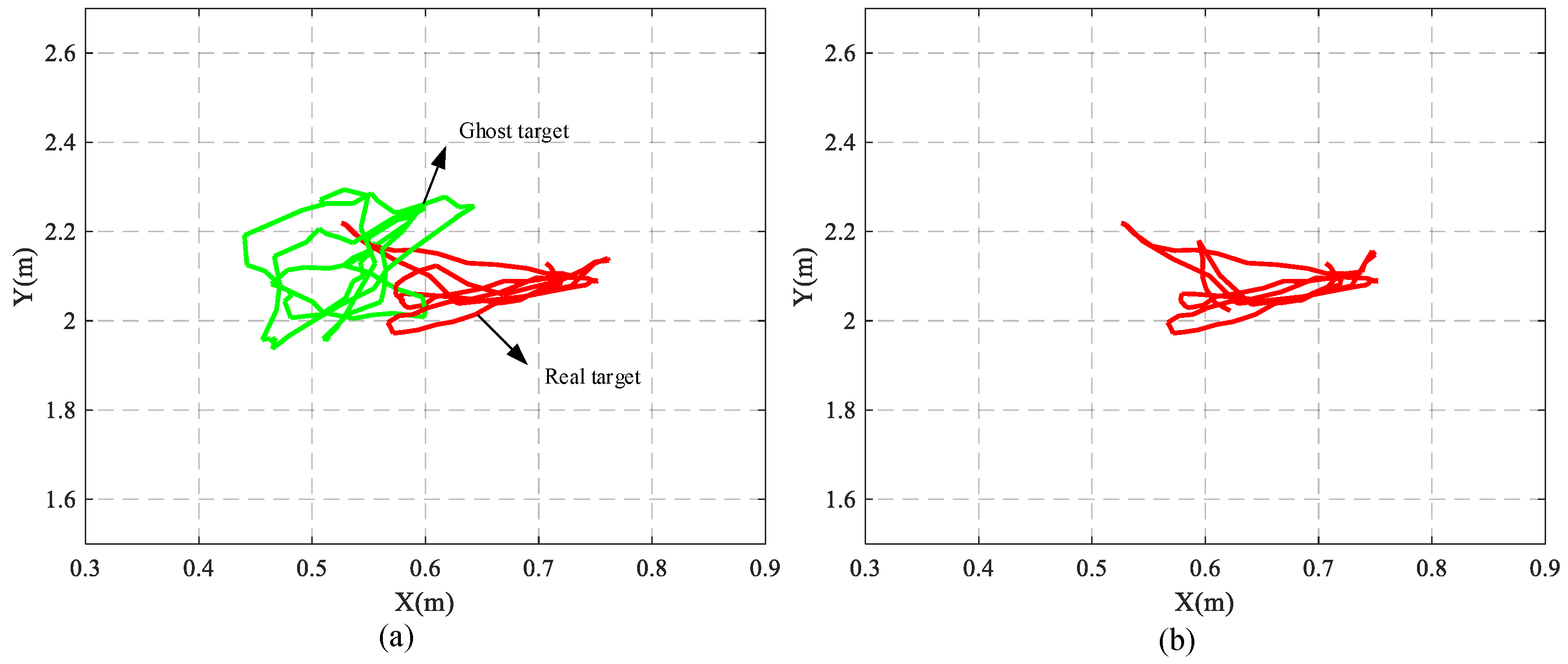
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xia, Z.; Luomei, Y.; Zhou, C.; Xu, F. Multidimensional feature representation and learning for robust hand-gesture recognition on commercial millimeter-wave radar. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4749–4764. [Google Scholar] [CrossRef]
- Zhang, W.; Li, G.; Wang, Z.; Wu, H. Non-contact monitoring of human heartbeat signals using mm-wave frequency-modulated continuous-wave radar under low signal-to-noise ratio conditions. IET Radar Sonar Navig. 2020, 16, 456–469. [Google Scholar] [CrossRef]
- Wang, B.; Guo, L.; Zhang, H.; Guo, Y.X. A millimeter-Wave radar-based fall detection method using line kernel convolutional neural network. IEEE Sens. J. 2020, 20, 13364–13370. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, F.; Wang, B.; Liu, K.R. mmTrack: Passive multi-person localization using commodity millimeter wave radio. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 2400–2409. [Google Scholar]
- Zhao, P.; Lu, C.X.; Wang, J.; Chen, C.; Wang, W.; Trigoni, N.; Markham, A. mID: Tracking and identifying people with millimeter wave radar. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems, Santorini, Greece, 29–31 May 2020; pp. 33–40. [Google Scholar]
- Pegoraro, J.; Rossi, M. Real-time people tracking and identification from sparse mm-Wave radar point-clouds. IEEE Access 2020, 9, 78504–78520. [Google Scholar] [CrossRef]
- Pegoraro, J.; Meneghello, F.; Rossi, M. Multiperson continuous tracking and identification from mm-wave micro-doppler signatures. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2994–3009. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Shi, Z.; Li, H.; Wu, P.; Li, S.; Cui, G.; Yang, X. Graph matching based image registration for multi-view through-the-wall imaging radar. IEEE Sens. J. 2022, 22, 1486–1494. [Google Scholar] [CrossRef]
- Ding, Y.; Huang, G.; Hu, J.; Li, Z.; Zhang, J.; Liu, X. Indoor target tracking using dual-frequency continuous-wave radar Based on the range-only measurements. IEEE Trans. Instrum. Meas. 2020, 69, 5385–5394. [Google Scholar] [CrossRef]
- Will, C.; Vaishnav, P.; Chakraborty, A.; Santra, A. Human target detection, tracking, and classification using 24-GHz FMCW radar. IEEE Sens. J. 2019, 17, 7283–7299. [Google Scholar] [CrossRef]
- Li, G.; Ge, Y.; Wang, Y.; Chen, Q.; Wang, G. Detection of human breathing in non-line-of-sight region by using mmWave FMCW radar. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Tang, Q.; Li, J.; Wang, L.; Jia, Y.; Cui, G. Multipath imaging for NLOS targets behind an L-Shaped corner with single-channel UWB radar. IEEE Sens. J. 2022, 22, 1531–1540. [Google Scholar] [CrossRef]
- Fujita, S.; Sakamoto, T.; Sato, T. An accurate UWB radar imaging method using indoor multipath echoes for targets in shadow regions. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–7. [Google Scholar]
- Li, L.; Krolik, J.L. Simultaneous target and multipath positioning. IEEE J. Sel. Top. Signal Process. 2014, 8, 153–165. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Guo, S.; Cui, G.; Wu, P.; Jia, C.; Kong, L. Joint estimation of NLOS building layout and targets via sparsity-driven approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Li, H.; Cui, G.; Guo, S.; Kong, L.; Yang, X. Target tracking and ghost mitigation based on multi-view through-the-wall radar imaging. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar]
- Copa, E.I.P.; Aziz, K.; Rykunov, M.; De Greef, E.; Bourdoux, A.; Horlin, F. Radar fusion for multipath mitigation in indoor environments. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar]
- Jia, Y.; Guo, Y.; Chen, S.; Song, R.; Wang, G.; Zhong, X.; Yan, C.; Cui, G. Multipath ghost and side/grating lobe suppression based on stacked generative adversarial nets in MIMO through-wall radar imaging. IEEE Access 2019, 7, 143367–143380. [Google Scholar] [CrossRef]
- Abdalla, A.T.; Muqaibel, A.H.; Al-Dharrab, S. Aspect dependent multipath ghost suppression in TWRI under compressive sensing framework. In Proceedings of the 2015 International Conference on Communications, Signal Processing, and Their Applications, Sharjah, United Arab Emirates, 17–19 February 2015; pp. 1–6. [Google Scholar]
- Cardillo, E.; Li, C.; Caddemi, A. Embedded heating, ventilation, and air-conditioning control systems: From traditional technologies toward radar advanced sensing. Rev. Sci. Instrum. 2021, 92, 061501. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, J.E.; Kim, K.T. Deep learning approach for radar-based people counting. IEEE Internet Things J. 2021, 9, 7715–7730. [Google Scholar] [CrossRef]
- Choi, J.W.; Yim, D.H.; Cho, S.H. People counting based on an IR-UWB radar sensor. IEEE Sens. J. 2017, 17, 5717–5727. [Google Scholar] [CrossRef]
- Antonucci, A.; Corrà, M.; Ferrari, A.; Fontanelli, D.; Fusari, E.; Macii, D.; Palopoli, L. Performance analysis of a 60-GHz radar for indoor positioning and tracking. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation, Pisa, Italy, 30 September–3 October 2019; pp. 1–7. [Google Scholar]
- Jia, Y.; Tian, H.; Fan, S.; Liu, B. Motion feature and millimeter wave multi-path AoA-ToA based 3D indoor positioning. In Proceedings of the 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Bologna, Italy, 9–12 September 2018; pp. 1–7. [Google Scholar]
- Lin, Z.; Lv, T.; Mathiopoulos, P.T. 3-D indoor positioning for millimeter-wave massive MIMO systems. IEEE Trans. Commun. 2018, 66, 2472–2486. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Z.; Guo, S.; Jia, Y.; Wang, L.; He, T.; Shao, H. MIMO through-wall-radar down-view imaging for moving target with ground ghost suppression. Digit. Signal Process. 2023, 134, 10386. [Google Scholar] [CrossRef]
- Hao, Z.; Yan, H.; Dang, X.; Ma, Z.; Jin, P.; Ke, W. Millimeter-wave wadar localization using indoor multipath effect. Sensors 2022, 22, 5671. [Google Scholar] [CrossRef]
- Yang, J.; Cui, G.; Yu, X.; Lu, S.; Kong, L. Passive location for coherent near-field sources with non-uniform sparse linear array. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1338–1343. [Google Scholar]
- Liu, C.; Liu, S.; Zhang, C.; Huang, Y.; Wang, H. Multipath propagation analysis and ghost target removal for FMCW automotive radars. In Proceedings of the IET International Radar Conference (IET IRC 2020), Online Conference, 4–6 November 2020; pp. 330–334. [Google Scholar]
- Kumbul, U.; Hayvaci, H.T. Multipath exploitation for knowledge-aided adaptive target detection. IET Radar Sonar Navigat. 2019, 13, 867–870. [Google Scholar] [CrossRef]
- Gui, L.; Yuan, W.; Xiao, F. CSI-based passive intrusion detection bound estimation in indoor NLoS scenario. Fundam. Res. 2022; in press. [Google Scholar] [CrossRef]
- Mercuri, M.; Lu, Y.; Polito, S.; Wieringa, F.; Liu, Y.H.; van der Veen, A.J.; Van Hoof, C.; Torfs, T. Enabling robust radar-based localization and vital signs monitoring in multipath propagation environments. IEEE Trans. Biomed. Eng. 2021, 68, 3228–3240. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO radar for advanced driver-assistance systems and autonomous driving: Advantages and challenges. IEEE Signal Process Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Jiang, M.; Guo, S.; Luo, H.; Yao, Y.; Cui, G. A robust target tracking method for crowded indoor environments using mmWave radar. Remote Sens. 2023, 15, 2425. [Google Scholar] [CrossRef]
- Zhang, G.; Geng, X.; Lin, Y.-J. Comprehensive mPoint: A method for 3D point cloud generation of human bodies utilizing FMCW MIMO mm-Wave radar. Sensors 2021, 21, 6455. [Google Scholar] [CrossRef] [PubMed]
- Rohling, H. Radar CFAR thresholding in clutter and multiple target situations. IEEE Trans. Aerosp. Electron. Syst. 1983, 4, 608–621. [Google Scholar] [CrossRef]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef] [PubMed]
- 60 GHz mmWave Sensor EVMs. 2020. Available online: https://www.ti.com/lit/ug/swru546e/swru546e.pdf (accessed on 19 August 2023).
- Guo, S.; Zhao, Q.; Cui, G.; Li, S.; Kong, L.; Yang, X. Behind corner targets location using small aperture millimeter wave radar in NLOS urban environment. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 460–470. [Google Scholar] [CrossRef]
- Granström, K.; Natale, A.; Braca, P.; Ludeno, G.; Serafino, F. Gamma gaussian inverse wishart probability hypothesis density for extended target tracking using X-Band marine radar data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6617–6631. [Google Scholar] [CrossRef]
- Clark, D.; Godsill, S. Group target tracking with the gaussian mixture probability hypothesis density filter. In Proceedings of the 2007 3rd International Conference on Intelligent Sensors, Sensor Networks and Information, Melbourne, VIC, Australia, 3–6 December 2007; pp. 149–154. [Google Scholar]
- Wahlstrom, N.; Ozkan, E. Extended target tracking using gaussian processes. IEEE Trans. Signal Process. 2015, 63, 4165–4178. [Google Scholar] [CrossRef]



| Transmitting Paths | Receiving Paths | ||
|---|---|---|---|
| Path Name | Propagation Process | Path Name | Propagation Process |
| Parameter | Tx Power | Angle Resolution | Maximum Angle | Maximum Range | Carried Frequency | Range Resolution | Chirp Cycle Time |
|---|---|---|---|---|---|---|---|
| Value | 12 dBm | 8.57 m | 60 GHz | 4.3 cm | 171 us |
| Target Position | (−0.5 m, 1.8 m) | (−1.5 m, 1.8 m) | (1 m, 1.3 m) | (−1 m, 1.3 m) | (0.5 m, 0.8 m) | (−1 m, 0.8 m) |
|---|---|---|---|---|---|---|
| CDD of type-1 (cm) | 14.76 | 4.79 | — | — | — | — |
| CDD of type-2 (cm) | 7.75 | 13.46 | 5.14 | 11.17 | 9.48 | 10.49 |
| CDD of type-3 (cm) | 14.27 | 12.5 | 10.47 | 10.13 | — | — |
| Target Position | (−0.5 m, 1.8 m) | (−1.5 m, 1.8 m) | (0.5 m, 1.3 m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Target Number | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| Before Suppression | 7.37% | 84.21% | 8.42% | 1.09% | 0% | 98.91% | 0% | 100% | 0% |
| After Suppression | 100% | 0% | 0% | 100% | 0% | 0% | 100% | 0% | 0% |
| Target Position | (−1 m, 1.3 m) | (0.5 m, 0.8 m) | (−1 m, 0.8 m) | ||||||
| Target Number | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| Before Suppression | 0% | 22.11% | 77.89% | 0% | 100% | 0% | 14.29% | 85.71% | 0% |
| After Suppression | 100% | 0% | 0% | 100% | 0% | 0% | 100% | 0% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Zhang, W.; Ren, Z.; Tang, C.; Ou, Y.; Cui, G.; Guo, S. Analysis of Electromagnetic Wave and Multipath Suppression from Overhead Perspective. Remote Sens. 2023, 15, 4903. https://doi.org/10.3390/rs15204903
Luo H, Zhang W, Ren Z, Tang C, Ou Y, Cui G, Guo S. Analysis of Electromagnetic Wave and Multipath Suppression from Overhead Perspective. Remote Sensing. 2023; 15(20):4903. https://doi.org/10.3390/rs15204903
Chicago/Turabian StyleLuo, Haolan, Wenqiang Zhang, Zhaoting Ren, Chuantian Tang, Yu Ou, Guolong Cui, and Shisheng Guo. 2023. "Analysis of Electromagnetic Wave and Multipath Suppression from Overhead Perspective" Remote Sensing 15, no. 20: 4903. https://doi.org/10.3390/rs15204903
APA StyleLuo, H., Zhang, W., Ren, Z., Tang, C., Ou, Y., Cui, G., & Guo, S. (2023). Analysis of Electromagnetic Wave and Multipath Suppression from Overhead Perspective. Remote Sensing, 15(20), 4903. https://doi.org/10.3390/rs15204903






