A Geometric Multigrid Method for 3D Magnetotelluric Forward Modeling Using Finite-Element Method
Abstract
1. Introduction
2. Methods
2.1. 3D MT Forward Modeling
2.2. Divergence Correction
2.3. Multigrid Algorithm
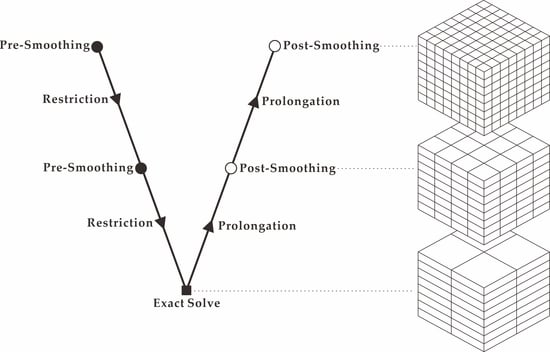
- Pre-smoothing: n1 times of smoothing iterations on the fine grid to obtain the approximate solution of Equation (13) . In this step, the high-frequency errors are eliminated, but the low-frequency errors remain.
- Compute residual: The residual vector corresponding to the approximate solution on the fine grid is calculated by .
- Restriction: Using the restriction matrix to project the residual vector onto the coarse grid, i.e., .
- Solve the residual equation: Solving the residual equation on a coarse grid and obtain .
- Prolongation: Using the prolongation matrix to project onto the fine grid (Prolongation matrix is the transposition of the restriction matrix).
- Coarse grid correction: Correcting the solution vector obtained on the fine grid in step 1) .
- Post-smoothing: The coarse grid correction brings new errors, so we use n2 times of smoothing iterations on to eliminate them.
| Algorithm 1. V-cycle multigrid method for the solution of Ae = b: MG(Ak,ek,bk,k) |
| 1: Input: level k, bk and initial guess ek, the coefficient matrix Ak−i(i = 0, 1, 2, …, k−1). |
| 2: Output: the updated solution ek |
| 3: if (k = 1) then |
| 4: Exactly solve by a direct solver |
| 5: else |
| 6: Pre-smoothing: n1 times of smoothing iterations on by complex BiCGStab |
| 7: Compute residual: |
| 8: Restriction: |
| 9: Recursion: MG(Ak−1, ek−1, bk−1, k−1) |
| 10: Prolongation: |
| 11: Correct: |
| 12: Post-smoothing: n2 times of smoothing iterations on by complex BiCGStab |
| 13: end if |
3. Numerical Experiments
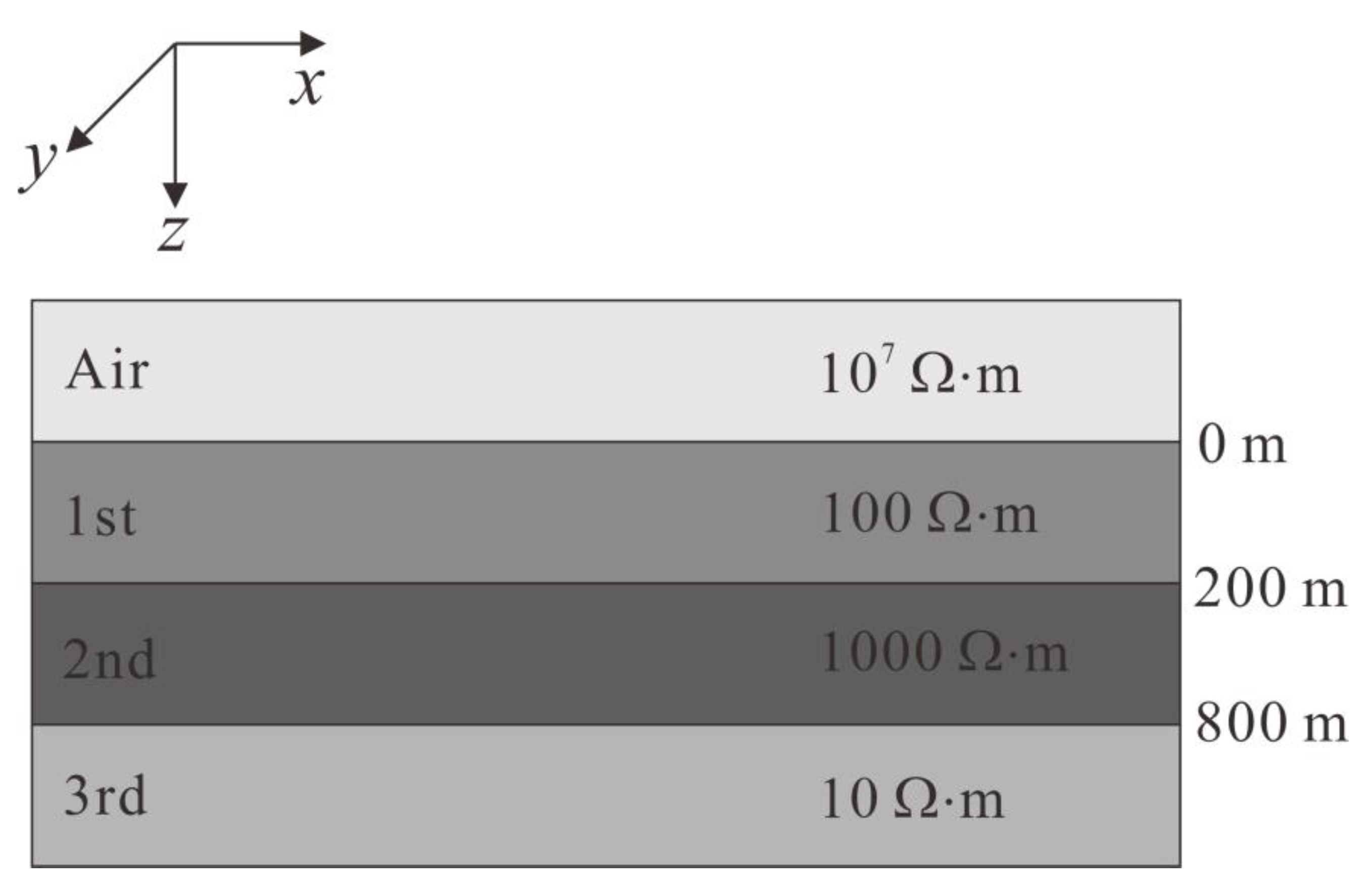
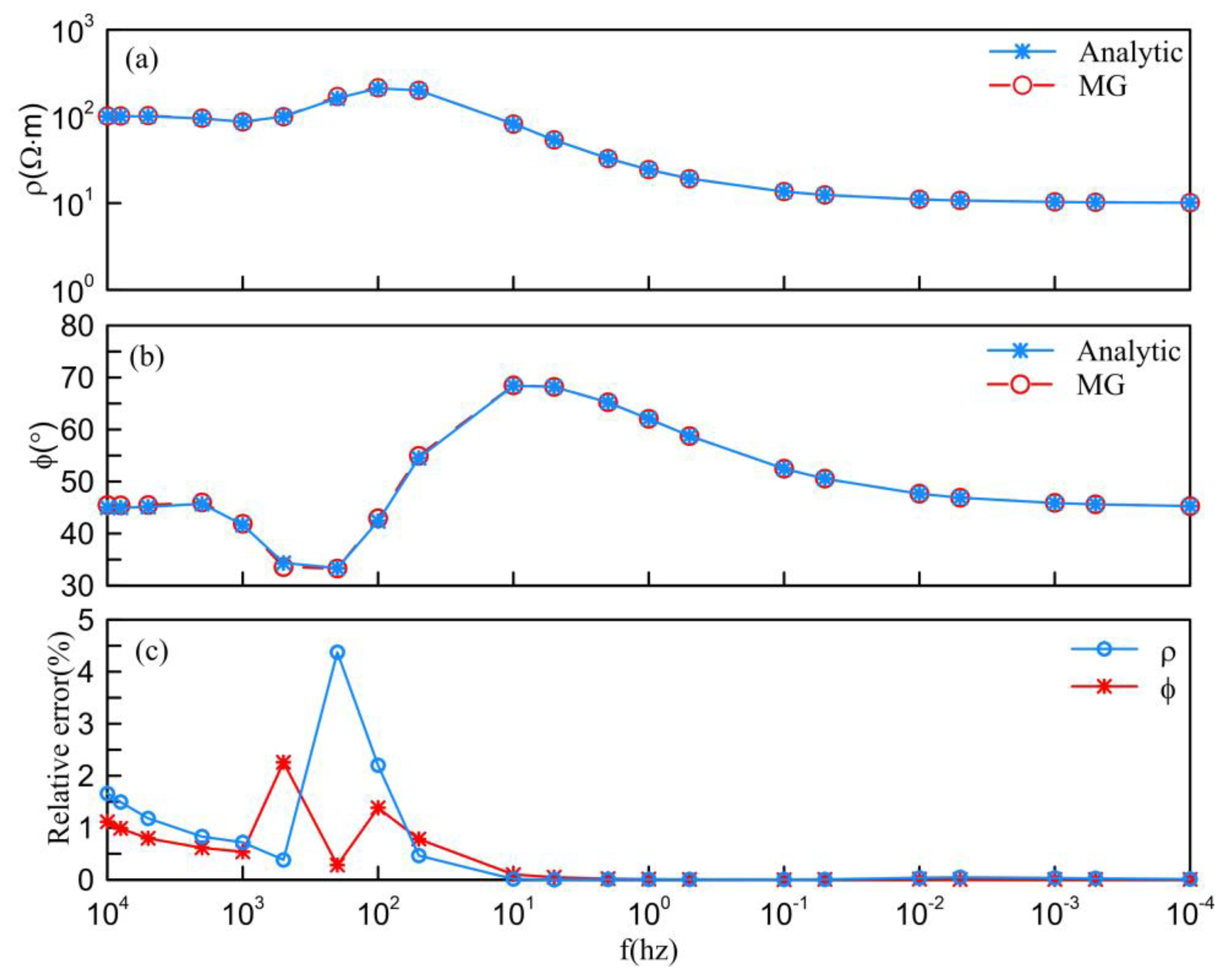
3.1. Algorithm Verification
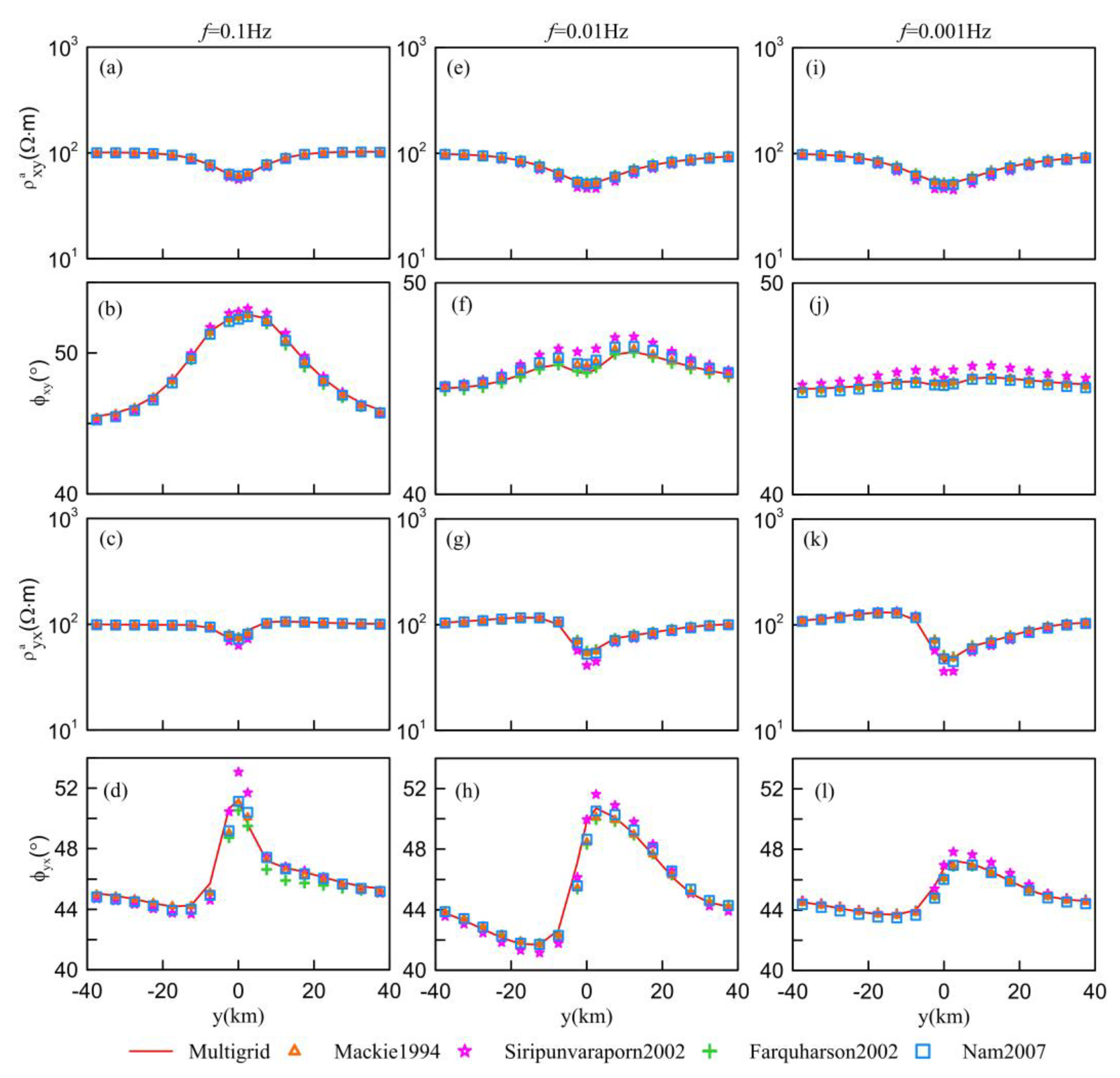
3.2. COMMEMI 3D-2 Model
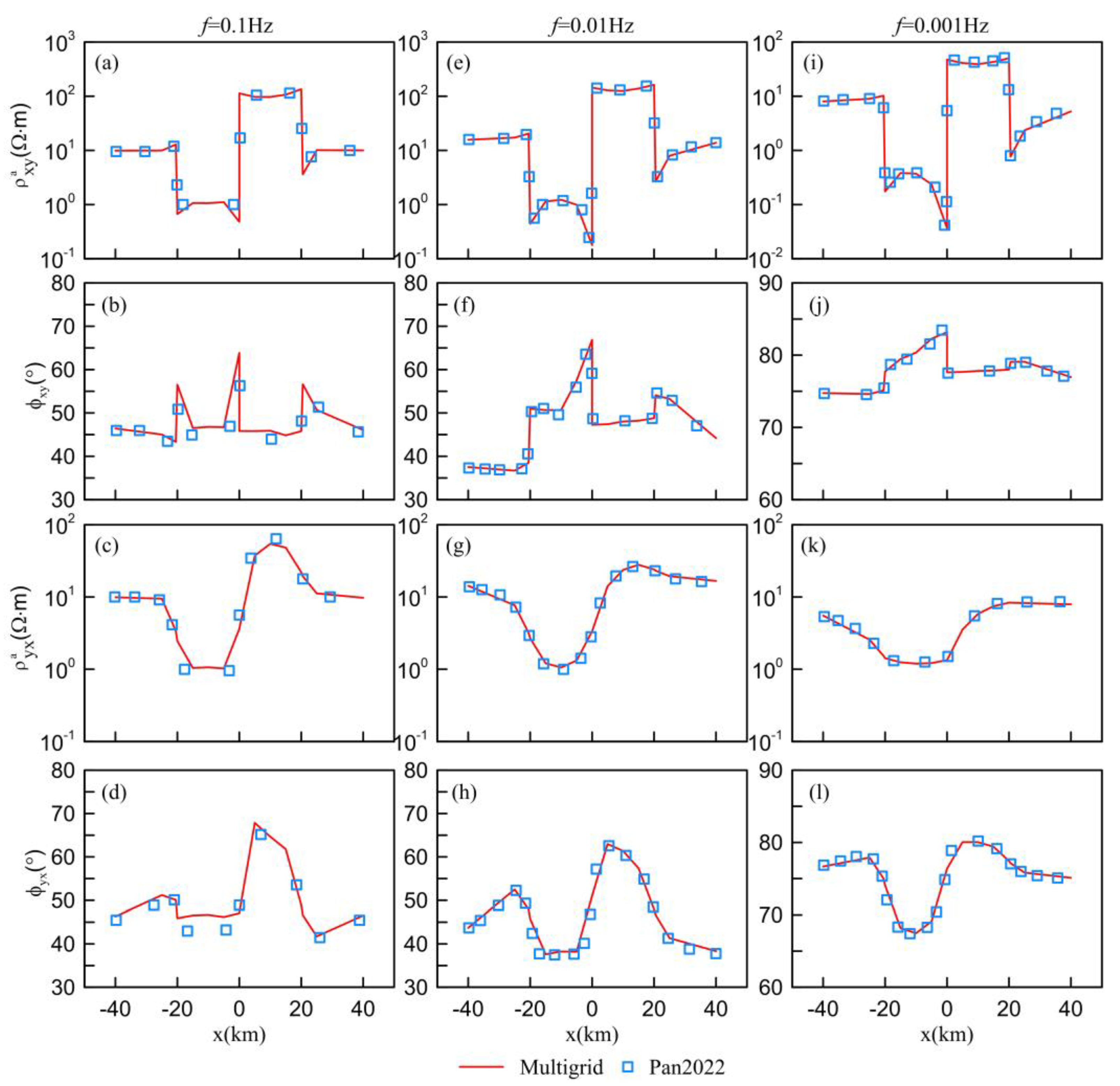
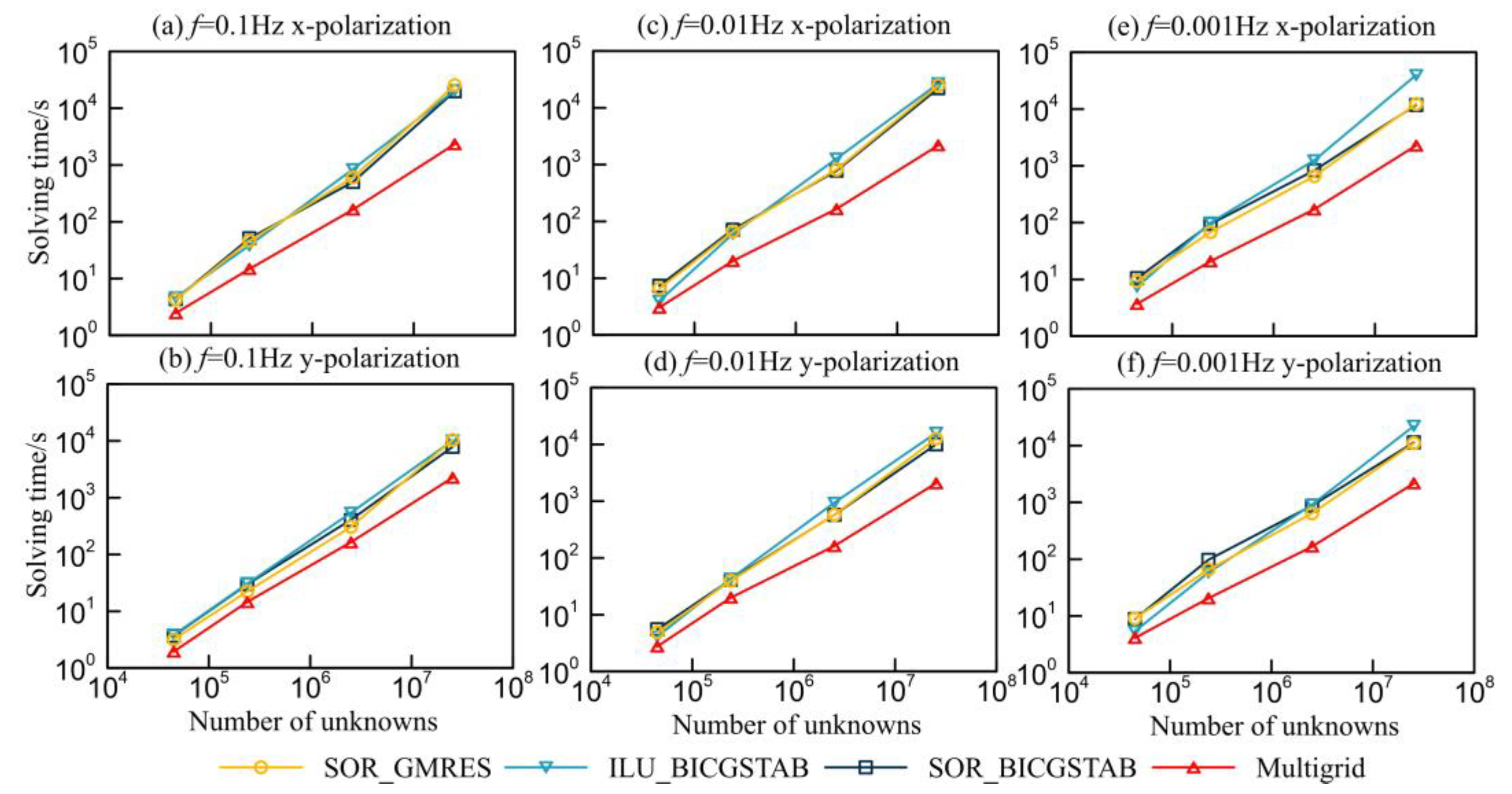
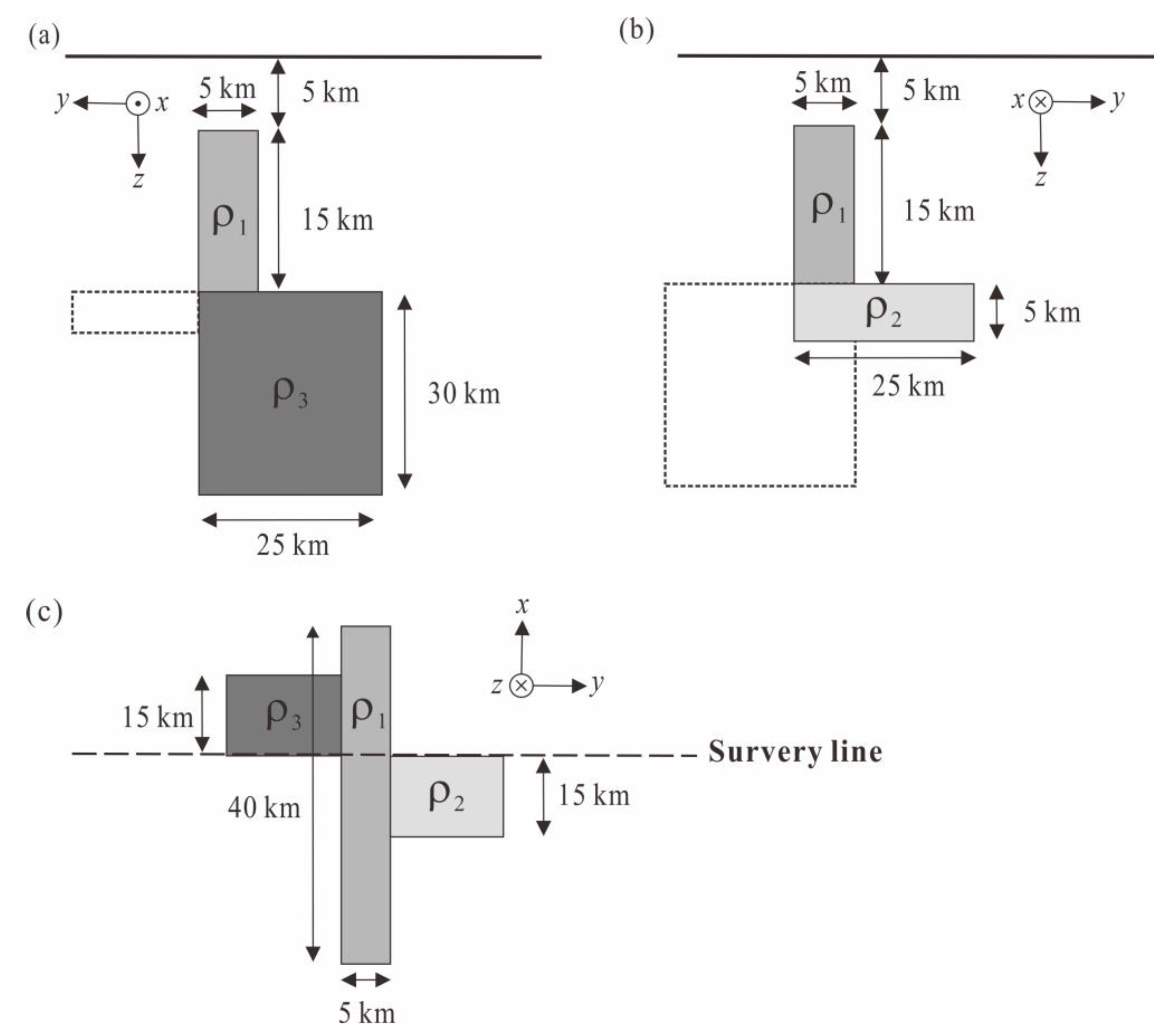
3.3. Dublin Test Model 1
3.4. Modified SEG/EAEG Salt Dome Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tikhonov, A. On determining electric characteristics of the deep layers of the Earth’s crust. Doklady 1950, 73, 295–297. [Google Scholar]
- Cagniard, L. Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics 1953, 18, 605–635. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Craven, J.A. Three-dimensional inversion of magnetotelluric data for mineral exploration: An example from the McArthur River uranium deposit, Saskatchewan, Canada. J. Appl. Geophys. 2009, 68, 450–458. [Google Scholar] [CrossRef]
- Jiang, W.; Duan, J.; Doublier, M.; Clark, A.; Schofield, A.; Brodie, R.C.; Goodwin, J. Application of multiscale magnetotelluric data to mineral exploration: An example from the east Tennant region, Northern Australia. Geophys. J. Int. 2022, 229, 1628–1645. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Wei, W.; Lu, Q.; Dong, H.; Li, Y. Theoretical assessment of 3-D magnetotelluric method for oil and gas exploration: Synthetic examples. J. Appl. Geophys. 2014, 106, 23–36. [Google Scholar] [CrossRef]
- Patro, P.K. Magnetotelluric studies for hydrocarbon and geothermal resources: Examples from the Asian region. Surv. Geophys. 2017, 38, 1005–1041. [Google Scholar] [CrossRef]
- Chandrasekhar, E.; Fontes, S.L.; Flexor, J.M.; Rajaram, M.; Anand, S. Magnetotelluric and aeromagnetic investigations for assessment of groundwater resources in Parnaiba basin in Piaui State of North-East Brazil. J. Appl. Geophys. 2009, 68, 269–281. [Google Scholar] [CrossRef]
- Hanekop, O.; Simpson, F. Error propagation in electromagnetic transfer functions: What role for the magnetotelluric method in detecting earthquake precursors? Geophys. J. Int. 2006, 165, 763–774. [Google Scholar] [CrossRef]
- Meqbel, N.M.; Egbert, G.D.; Wannamaker, P.E.; Kelbert, A.; Schultz, A. Deep electrical resistivity structure of the northwestern US derived from 3-D inversion of USArray magnetotelluric data. Earth Planet. Sci. Lett. 2014, 402, 290–304. [Google Scholar] [CrossRef]
- Wannamaker, P.E. Advances in three-dimensional magnetotelluric modeling using integral equations. Geophysics 1991, 56, 1716–1728. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Smith, R.B.; Gribenko, A.; Cuma, M.; Green, M. Three-dimensional inversion of large-scale EarthScope magnetotelluric data based on the integral equation method: Geoelectrical imaging of the Yellowstone conductive mantle plume. Geophys. Res. Lett. 2011, 38, L08307. [Google Scholar] [CrossRef]
- Mackie, R.L.; Madden, T.R.; Wannamaker, P.E. Three-dimensional magnetotelluric modeling using difference equations—Theory and comparisons to integral equation solutions. Geophysics 1993, 58, 215–226. [Google Scholar] [CrossRef]
- Mackie, R.L.; Smith, J.T.; Madden, T.R. Three-dimensional electromagnetic modeling using finite difference equations: The magnetotelluric example. Radio Sci. 1994, 29, 923–935. [Google Scholar] [CrossRef]
- Kelbert, A.; Meqbel, N.; Egbert, G.D.; Tandon, K. ModEM: A modular system for inversion of electromagnetic geophysical data. Comput. Geosci. 2014, 66, 40–53. [Google Scholar] [CrossRef]
- Haber, E.; Ascher, U.M. Fast finite volume simulation of 3D electromagnetic problems with highly discontinuous coefficients. SIAM J. Sci. Comput. 2001, 22, 1943–1961. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids. Geophysics 2014, 79, E287–E302. [Google Scholar] [CrossRef]
- Ren, Z.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophys. J. Int. 2013, 194, 700–718. [Google Scholar] [CrossRef]
- Cao, X.-Y.; Yin, C.-C.; Zhang, B.; Huang, X.; Liu, Y.-H.; Cai, J. 3D magnetotelluric inversions with unstructured finite-element and limited-memory quasi-Newton methods. Appl. Geophys. 2018, 15, 556–565. [Google Scholar] [CrossRef]
- Heagy, L.J.; Capriotii, J.; Kuttai, J.; Cowan, D.; Perez, F.; Hamman, J.; Banihirwe, A.; Paul, K. Advances in Magnetotelluric modelling and inversion with SimPEG. In Proceedings of the AGU Fall Meeting Abstracts, Online, 7–11 December 2020; p. GP005-04. [Google Scholar]
- Castillo-Reyes, O.; Modesto, D.; Queralt, P.; Marcuello, A.; Ledo, J.; Amor-Martin, A.; de la Puente, J.; García-Castillo, L.E. 3D magnetotelluric modeling using high-order tetrahedral Nédélec elements on massively parallel computing platforms. Comput. Geosci. 2022, 160, 105030. [Google Scholar] [CrossRef]
- Jin, J.-M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Da Silva, N.V.; Morgan, J.V.; MacGregor, L.; Warner, M. A finite element multifrontal method for 3D CSEM modeling in the frequency domain. Geophysics 2012, 77, E101–E115. [Google Scholar] [CrossRef]
- Schwarzbach, C.; Haber, E. Finite element based inversion for time-harmonic electromagnetic problems. Geophys. J. Int. 2013, 193, 615–634. [Google Scholar] [CrossRef]
- Kordy, M.; Wannamaker, P.; Maris, V.; Cherkaev, E.; Hill, G. 3-D magnetotelluric inversion including topography using deformed hexahedral edge finite elements and direct solvers parallelized on SMP computers–Part I: Forward problem and parameter Jacobians. Geophys. J. Int. 2016, 204, 74–93. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, B.; Liu, Y.; Cai, J. A goal-oriented adaptive finite-element method for 3D scattered airborne electromagnetic method modeling. Geophysics 2016, 81, E337–E346. [Google Scholar] [CrossRef]
- Zhang, B.; Yin, C.; Ren, X.; Liu, Y.; Qi, Y. Adaptive finite element for 3D time-domain airborne electromagnetic modeling based on hybrid posterior error estimation. Geophysics 2018, 83, WB71–WB79. [Google Scholar] [CrossRef]
- Han, X.; Yin, C.; Su, Y.; Zhang, B.; Liu, Y.; Ren, X.; Ni, J.; Farquharson, C.G. 3D Finite-Element Forward Modeling of Airborne EM Systems in Frequency-Domain Using Octree Meshes. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5912813. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. 3-D minimum-structure inversion of magnetotelluric data using the finite-element method and tetrahedral grids. Geophys. J. Int. 2017, 211, 1189–1205. [Google Scholar] [CrossRef]
- Xiong, B.; Luo, T.; Chen, L. Direct solutions of 3-D magnetotelluric fields using edge-based finite element. J. Appl. Geophys. 2018, 159, 204–208. [Google Scholar] [CrossRef]
- Liu, C.; Ren, Z.; Tang, J.; Yan, Y. Three-dimensional magnetotellurics modeling using edgebased finite-element unstructured meshes. Appl. Geophys. 2008, 5, 170–180. [Google Scholar] [CrossRef]
- Um, E.S.; Commer, M.; Newman, G.A. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the Earth: Finite-element frequency-domain approach. Geophys. J. Int. 2013, 193, 1460–1473. [Google Scholar] [CrossRef]
- Puzyrev, V.; Koldan, J.; de la Puente, J.; Houzeaux, G.; Vázquez, M.; Cela, J.M. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling. Geophys. J. Int. 2013, 193, 678–693. [Google Scholar] [CrossRef]
- Cai, H.; Xiong, B.; Han, M.; Zhdanov, M. 3D controlled-source electromagnetic modeling in anisotropic medium using edge-based finite element method. Comput. Geosci. 2014, 73, 164–176. [Google Scholar] [CrossRef]
- Xiao, T.; Liu, Y.; Wang, Y.; Fu, L.-Y. Three-dimensional magnetotelluric modeling in anisotropic media using edge-based finite element method. J. Appl. Geophys. 2018, 149, 1–9. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Miensopust, M.P. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction. J. Appl. Geophys. 2011, 75, 699–710. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, X.; Xiao, T.; Cai, H.; Li, J.; Peng, R.; Long, Z. Three-dimensional edge-based finite element modeling of magnetotelluric data in anisotropic media with a divergence correction. J. Appl. Geophys. 2021, 189, 104324. [Google Scholar] [CrossRef]
- Tang, W.; Li, Y.; Liu, J.; Deng, J. Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element with a divergence correction. Geophysics 2021, 86, E367–E382. [Google Scholar] [CrossRef]
- Trottenberg, U.; Oosterlee, C.W.; Schuller, A. Multigrid; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Mulder, W. A multigrid solver for 3D electromagnetic diffusion. Geophys. Prospect. 2006, 54, 633–649. [Google Scholar] [CrossRef]
- Mulder, W. Geophysical modelling of 3D electromagnetic diffusion with multigrid. Comput. Vis. Sci. 2008, 11, 129–138. [Google Scholar] [CrossRef]
- Jaysaval, P.; Shantsev, D.V.; de la Kethulle de Ryhove, S.; Bratteland, T. Fully anisotropic 3-D EM modelling on a Lebedev grid with a multigrid pre-conditioner. Geophys. J. Int. 2016, 207, 1554–1572. [Google Scholar] [CrossRef]
- Li, G.; Zhang, L.; Han, B. Stable electromagnetic modeling using a multigrid solver on stretching grids: The magnetotelluric example. IEEE Geosci. Remote Sens. Lett. 2016, 13, 334–338. [Google Scholar] [CrossRef]
- Guo, R.; Wang, Y.; Egbert, G.D.; Liu, J.; Liu, R.; Pan, K.; Li, J.; Chen, H. An efficient multigrid solver based on a four-color cell-block Gauss-Seidel smoother for 3D magnetotelluric forward modeling. Geophysics 2022, 87, E121–E133. [Google Scholar] [CrossRef]
- Pan, K.; Wang, J.; Hu, S.; Ren, Z.; Cui, T.; Guo, R.; Tang, J. An efficient cascadic multigrid solver for 3-D magnetotelluric forward modelling problems using potentials. Geophys. J. Int. 2022, 230, 1834–1851. [Google Scholar] [CrossRef]
- Koldan, J.; Puzyrev, V.; de la Puente, J.; Houzeaux, G.; Cela, J.M. Algebraic multigrid preconditioning within parallel finite-element solvers for 3-D electromagnetic modelling problems in geophysics. Geophys. J. Int. 2014, 197, 1442–1458. [Google Scholar] [CrossRef]
- Chen, H.; Deng, J.-Z.; Yin, M.; Yin, C.-C.; Tang, W.-W. Three-dimensional forward modeling of DC resistivity using the aggregation-based algebraic multigrid method. Appl. Geophys. 2017, 14, 154–164. [Google Scholar] [CrossRef]
- Codd, A.; Gross, L. Electrical Resistivity Tomography using a finite element based BFGS algorithm with algebraic multigrid preconditioning. Geophys. J. Int. 2018, 212, 2073–2087. [Google Scholar] [CrossRef]
- Yao, H.; Ren, Z.; Tang, J.; Lin, Y.; Yin, C.; Hu, X.; Huang, Q.; Zhang, K. 3D finite-element modeling of Earth induced electromagnetic field and its potential applications for geomagnetic satellites. Sci. China Earth Sci. 2021, 64, 1798–1812. [Google Scholar] [CrossRef]
- Briggs, W.L.; Henson, V.E.; McCormick, S.F. A Multigrid Tutorial; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Nédélec, J.-C. A new family of mixed finite elements in ℝ3. Numer. Math. 1986, 50, 57–81. [Google Scholar] [CrossRef]
- Smith, J.T. Conservative modeling of 3-D electromagnetic fields, Part II: Biconjugate gradient solution and an accelerator. Geophysics 1996, 61, 1319–1324. [Google Scholar] [CrossRef]
- Washio, T.; Oosterlee, C.W. Flexible multiple semicoarsening for three-dimensional singularly perturbed problems. SIAM J. Sci. Comput. 1998, 19, 1646–1666. [Google Scholar] [CrossRef]
- Riyanti, C.D.; Kononov, A.; Erlangga, Y.A.; Vuik, C.; Oosterlee, C.W.; Plessix, R.-E.; Mulder, W.A. A parallel multigrid-based preconditioner for the 3D heterogeneous high-frequency Helmholtz equation. J. Comput. Phys. 2007, 224, 431–448. [Google Scholar] [CrossRef]
- Watanabe, K.; Igarashi, H. Robustness of nested multigrid method for edge-based finite element analysis. IEEE Trans. Magn. 2009, 45, 1088–1091. [Google Scholar] [CrossRef]
- Zhdanov, M.; Varentsov, I.M.; Weaver, J.; Golubev, N.; Krylov, V. Methods for modelling electromagnetic fields results from COMMEMI—The international project on the comparison of modelling methods for electromagnetic induction. J. Appl. Geophys. 1997, 37, 133–271. [Google Scholar] [CrossRef]
- Miensopust, M.P.; Queralt, P.; Jones, A.G.; Modellers, D.M. Magnetotelluric 3-D inversion—A review of two successful workshops on forward and inversion code testing and comparison. Geophys. J. Int. 2013, 193, 1216–1238. [Google Scholar] [CrossRef]
- Siripunvaraporn, W.; Egbert, G.; Lenbury, Y. Numerical accuracy of magnetotelluric modeling: A comparison of finite difference approximations. Earth Planets Space 2002, 54, 721–725. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Oldenburg, D.W.; Haber, E.; Shekhtman, R. An algorithm for the three-dimensional inversion of magnetotelluric data. In SEG Technical Program Expanded Abstracts 2002; Society of Exploration Geophysicists: Houston, TX, USA, 2002; pp. 649–652. [Google Scholar]
- Nam, M.J.; Kim, H.J.; Song, Y.; Lee, T.J.; Son, J.S.; Suh, J.H. 3D magnetotelluric modelling including surface topography. Geophys. Prospect. 2007, 55, 277–287. [Google Scholar] [CrossRef]
- Aminzadeh, F.; Burkhard, N.; Nicoletis, L.; Rocca, F.; Wyatt, K. SEG/EAEG 3-D modeling project: 2nd update. Lead. Edge 1994, 13, 949–952. [Google Scholar] [CrossRef]





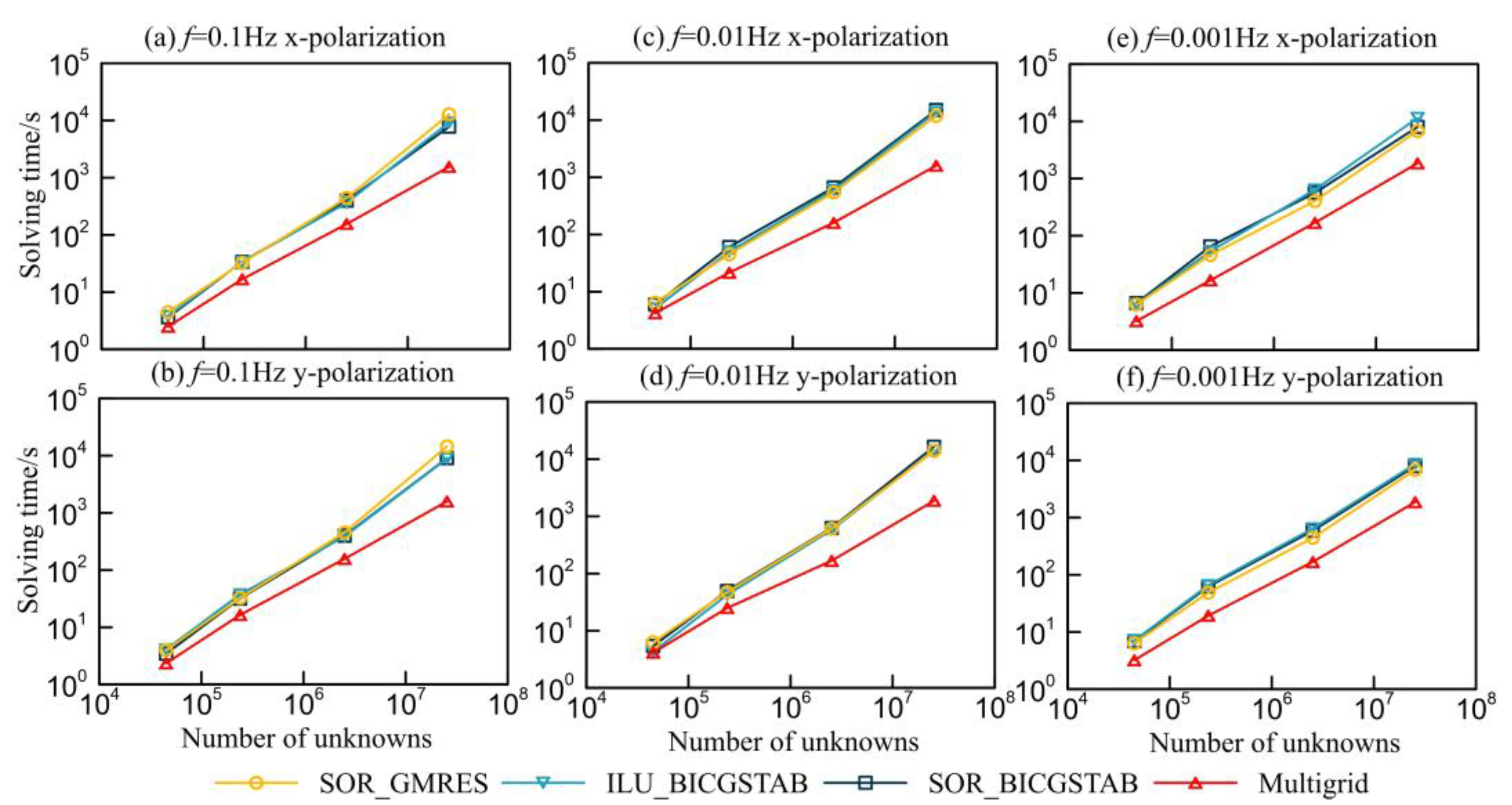



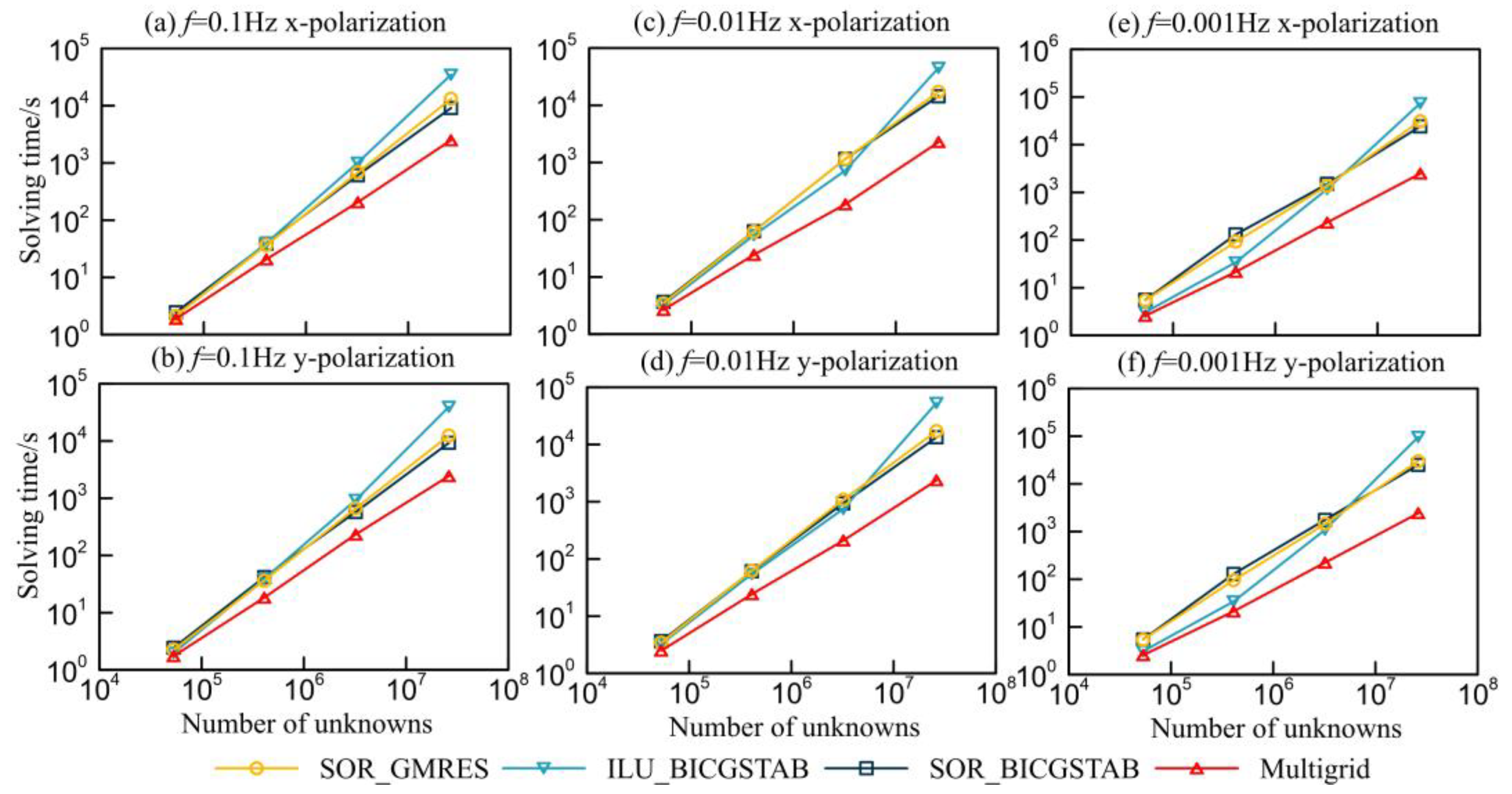
| Grid Size (DoFs) | Frequency (Hz) | Method | x-Polarization | y-Polarization | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Iterations | CPU Time(s) | Memory (GB) | Error | Iterations | CPU Time(s) | Memory (GB) | |||
| 128 × 128 × 64 (3,211,584) | 0.1 | SOR-GMRES | 9.9 × 10−8 | 896 | 827.73 | 8.8 | 9.8 × 10−8 | 504 | 456.86 | 8.8 |
| ILU-BICGSTAB | 1.0 × 10−7 | 1071 | 1073.77 | 9.3 | 9.6 × 10−8 | 597 | 591.95 | 9.3 | ||
| SOR-BICGSTAB | 9.9 × 10−8 | 483 | 692.75 | 7.6 | 9.3 × 10−8 | 473 | 658.21 | 7.6 | ||
| Multigrid | 4.4 × 10−8 | 8 | 191.96 | 12.4 | 6.2 × 10−8 | 8 | 188.56 | 12.4 | ||
| 0.01 | SOR-GMRES | 9.9 × 10−8 | 1266 | 1184.26 | 8.8 | 9.8 × 10−8 | 1011 | 918.75 | 8.8 | |
| ILU-BICGSTAB | 9.9 × 10−8 | 1278 | 1312.25 | 9.3 | 9.8 × 10−8 | 978 | 986.08 | 9.3 | ||
| SOR-BICGSTAB | 9.9 × 10−8 | 765 | 1115.31 | 7.6 | 9.8 × 10−8 | 831 | 1189.06 | 7.6 | ||
| Multigrid | 4.6 × 10−8 | 7 | 194.23 | 12.4 | 5.1 × 10−8 | 7 | 174.43 | 12.4 | ||
| 0.001 | SOR-GMRES | 9.9 × 10−8 | 1045 | 970.54 | 8.8 | 9.9 × 10−8 | 1031 | 933.31 | 8.8 | |
| ILU-BICGSTAB | 9.8 × 10−8 | 1612 | 1642.76 | 9.3 | 9.3 × 10−8 | 1064 | 1067.97 | 9.3 | ||
| SOR-BICGSTAB | 9.9 × 10−8 | 943 | 1365.88 | 7.6 | 9.4 × 10−8 | 766 | 1097.89 | 7.6 | ||
| Multigrid | 2.0 × 10−8 | 6 | 179.58 | 12.4 | 3.7 × 10−8 | 6 | 176.96 | 12.4 | ||
| Abnormal Body | x (km) | y (km) | z (km) | Resistivity (Ω⋅m) |
|---|---|---|---|---|
| Body1 | −20~20 | −2.5~2.5 | 5~20 | 10 |
| Body2 | −15~0 | −2.5~22.5 | 20~25 | 1 |
| Body3 | 0~15 | −22.5~2.5 | 20~50 | 10,000 |
| Grid Size (DoFs) | Frequency (Hz) | Method | x-Polarization | y-Polarization | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Iterations | CPU Time(s) | Memory (GB) | Error | Iterations | CPU Time(s) | Memory (GB) | |||
| 128 × 128 × 64 (3,211,584) | 0.1 | SOR-GMRES | 9.9 × 10−8 | 655 | 595.17 | 8.8 | 1.0 × 10−7 | 690 | 624.80 | 8.8 |
| ILU-BICGSTAB | 9.9 × 10−8 | 394 | 390.36 | 9.3 | 9.2 × 10−8 | 427 | 427.79 | 9.3 | ||
| SOR-BICGSTAB | 7.1 × 10−8 | 375 | 507.54 | 7.6 | 9.9 × 10−8 | 430 | 590.76 | 7.6 | ||
| Multigrid | 1.8 × 10−8 | 7 | 170.25 | 12.4 | 5.0 × 10−8 | 7 | 176.25 | 12.4 | ||
| 0.01 | SOR-GMRES | 9.9 × 10−8 | 876 | 802.80 | 8.8 | 9.9 × 10−8 | 930 | 860.56 | 8.8 | |
| ILU-BICGSTAB | 9.7 × 10−8 | 540 | 549.23 | 9.3 | 7.6 × 10−8 | 591 | 595.35 | 9.3 | ||
| SOR-BICGSTAB | 9.9 × 10−8 | 720 | 1007.60 | 7.6 | 9.7 × 10−8 | 924 | 1285.80 | 7.6 | ||
| Multigrid | 1.1 × 10−8 | 7 | 186.63 | 12.4 | 4.7 × 10−8 | 8 | 223.00 | 12.4 | ||
| 0.001 | SOR-GMRES | 9.9 × 10−8 | 649 | 597.36 | 8.8 | 1.0 × 10−7 | 711 | 661.19 | 8.8 | |
| ILU-BICGSTAB | 9.8 × 10−8 | 717 | 751.10 | 9.3 | 7.5 × 10−8 | 1101 | 1152.78 | 9.3 | ||
| SOR-BICGSTAB | 7.4 × 10−8 | 551 | 764.54 | 7.6 | 1.0 × 10−7 | 552 | 769.51 | 7.6 | ||
| Multigrid | 1.1 × 10−8 | 6 | 171.40 | 12.4 | 4.8 × 10−8 | 6 | 165.05 | 12.4 | ||
| Grid Size (DoFs) | Frequency (Hz) | Method | x-Polarization | y-Polarization | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Iterations | CPU Time(s) | Memory (GB) | Error | Iterations | CPU Time(s) | Memory (GB) | |||
| 128 × 128 × 88 (4,403,544) | 0.1 | SOR-GMRES | 9.9 × 10−8 | 774 | 1020.68 | 12 | 1.0 × 10−7 | 751 | 993.38 | 12 |
| ILU-BICGSTAB | 9.7 × 10−8 | 780 | 1146.60 | 12.6 | 9.8 × 10−8 | 820 | 1213.46 | 12.6 | ||
| SOR-BICGSTAB | 9.5 × 10−8 | 411 | 842.82 | 10.3 | 9.8 × 10−8 | 389 | 767.28 | 10.3 | ||
| Multigrid | 6.0 × 10−8 | 8 | 316.55 | 17 | 5.5 × 10−8 | 8 | 315.13 | 17 | ||
| 0.01 | SOR-GMRES | 1.0 × 10−7 | 1298 | 1736.92 | 12 | 1.0 × 10−7 | 1372 | 1841.99 | 12 | |
| ILU-BICGSTAB | 9.1 × 10−8 | 577 | 848.64 | 12.6 | 9.9 × 10−8 | 678 | 997.28 | 12.6 | ||
| SOR-BICGSTAB | 9.7 × 10−8 | 757 | 1545.95 | 10.3 | 9.7 × 10−8 | 708 | 1459.48 | 10.3 | ||
| Multigrid | 2.8 × 10−8 | 8 | 330.03 | 17 | 3.5 × 10−8 | 8 | 329.34 | 17 | ||
| 0.001 | SOR-GMRES | 1.0 × 10−7 | 1983 | 2651.39 | 12 | 1.0 × 10−7 | 1988 | 2634.64 | 12 | |
| ILU-BICGSTAB | 9.7 × 10−8 | 891 | 1345.04 | 12.6 | 9.6 × 10−8 | 738 | 1136.72 | 12.6 | ||
| SOR-BICGSTAB | 9.7 × 10−8 | 1283 | 2685.95 | 10.3 | 9.4 × 10−8 | 1175 | 2487.30 | 10.3 | ||
| Multigrid | 4.1 × 10−8 | 7 | 306.69 | 17 | 2.3 × 10−8 | 7 | 307.84 | 17 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yin, C.; Wang, L.; Liu, Y.; Zhang, B.; Ren, X.; Su, Y.; Li, J.; Chen, H. A Geometric Multigrid Method for 3D Magnetotelluric Forward Modeling Using Finite-Element Method. Remote Sens. 2023, 15, 537. https://doi.org/10.3390/rs15020537
Huang X, Yin C, Wang L, Liu Y, Zhang B, Ren X, Su Y, Li J, Chen H. A Geometric Multigrid Method for 3D Magnetotelluric Forward Modeling Using Finite-Element Method. Remote Sensing. 2023; 15(2):537. https://doi.org/10.3390/rs15020537
Chicago/Turabian StyleHuang, Xianyang, Changchun Yin, Luyuan Wang, Yunhe Liu, Bo Zhang, Xiuyan Ren, Yang Su, Jun Li, and Hui Chen. 2023. "A Geometric Multigrid Method for 3D Magnetotelluric Forward Modeling Using Finite-Element Method" Remote Sensing 15, no. 2: 537. https://doi.org/10.3390/rs15020537
APA StyleHuang, X., Yin, C., Wang, L., Liu, Y., Zhang, B., Ren, X., Su, Y., Li, J., & Chen, H. (2023). A Geometric Multigrid Method for 3D Magnetotelluric Forward Modeling Using Finite-Element Method. Remote Sensing, 15(2), 537. https://doi.org/10.3390/rs15020537