What Are We Missing? Occlusion in Laser Scanning Point Clouds and Its Impact on the Detection of Single-Tree Morphologies and Stand Structural Variables
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
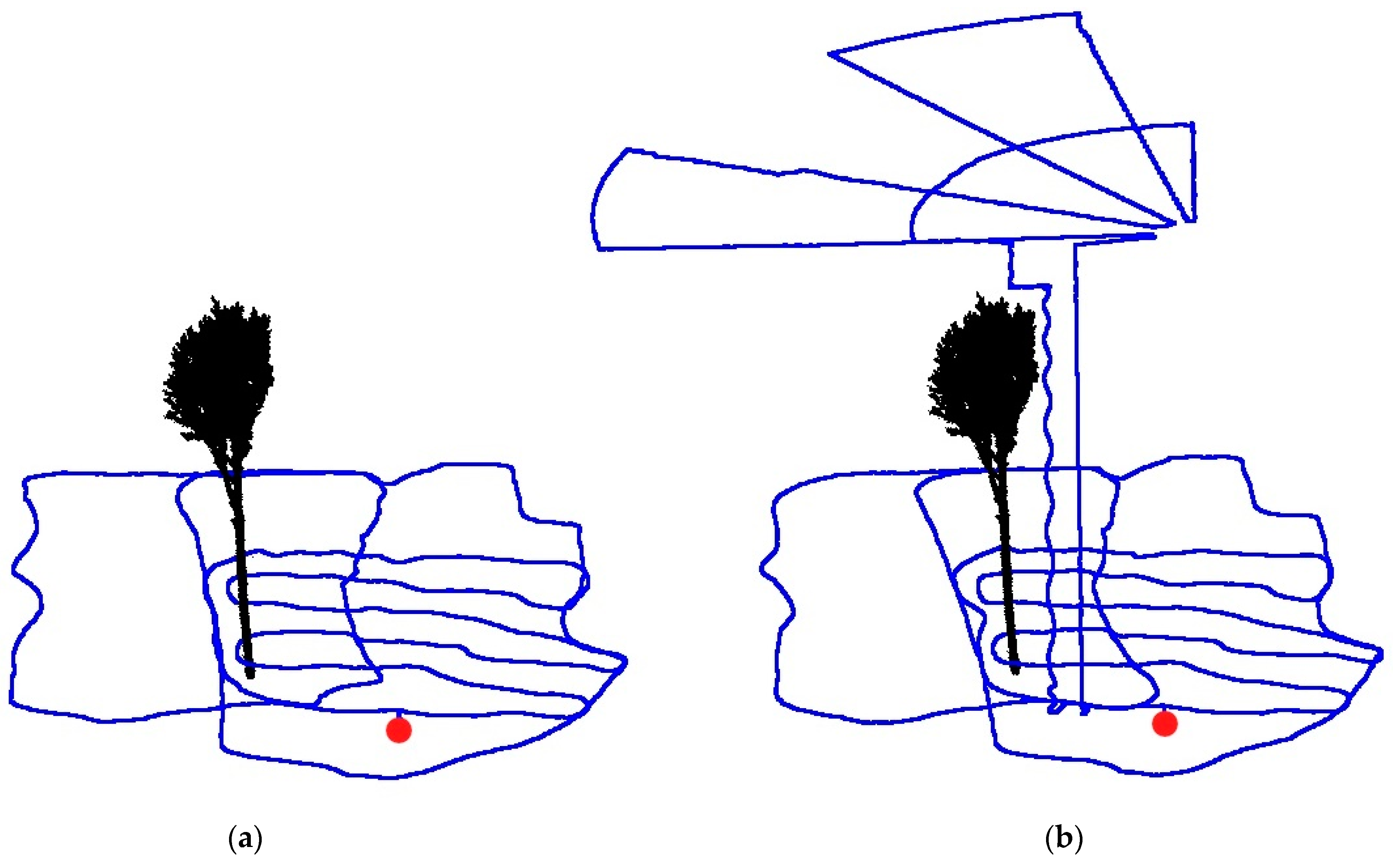
2.2. Data Collection
2.3. Data Processing
2.4. Data Analysis
3. Results
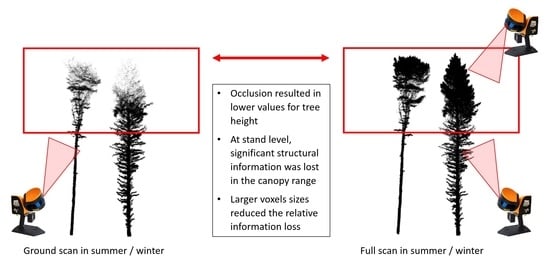
3.1. Visual Assessment of Single-Tree Point Clouds
3.2. Seasonal Comparison
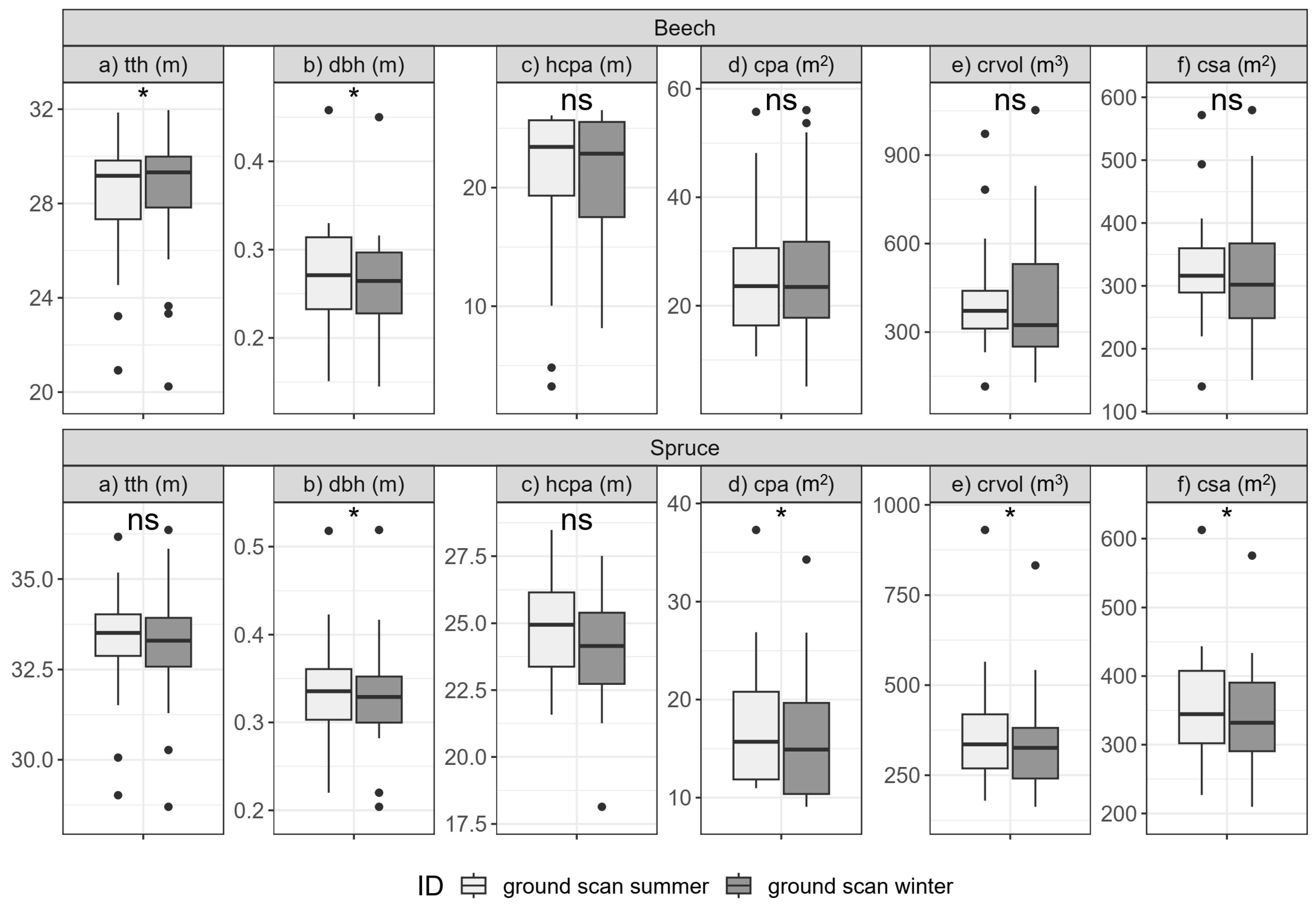
3.2.1. Single-Tree Morphologies (H1)
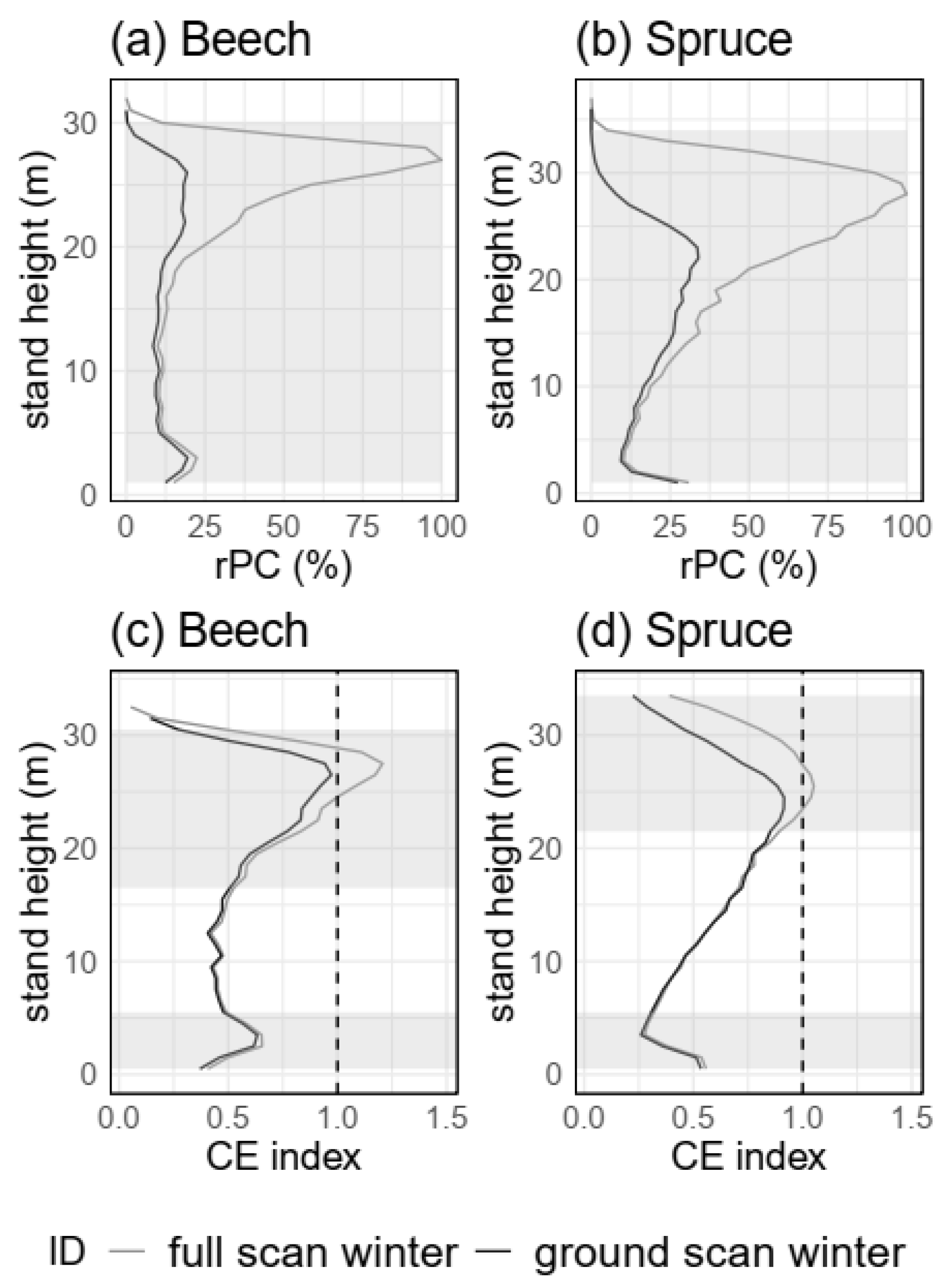
3.2.2. Stand Structure (H2)
3.3. Methodological Comparison
3.3.1. Single-Tree Morphologies (H3)
3.3.2. Stand structure (H4)
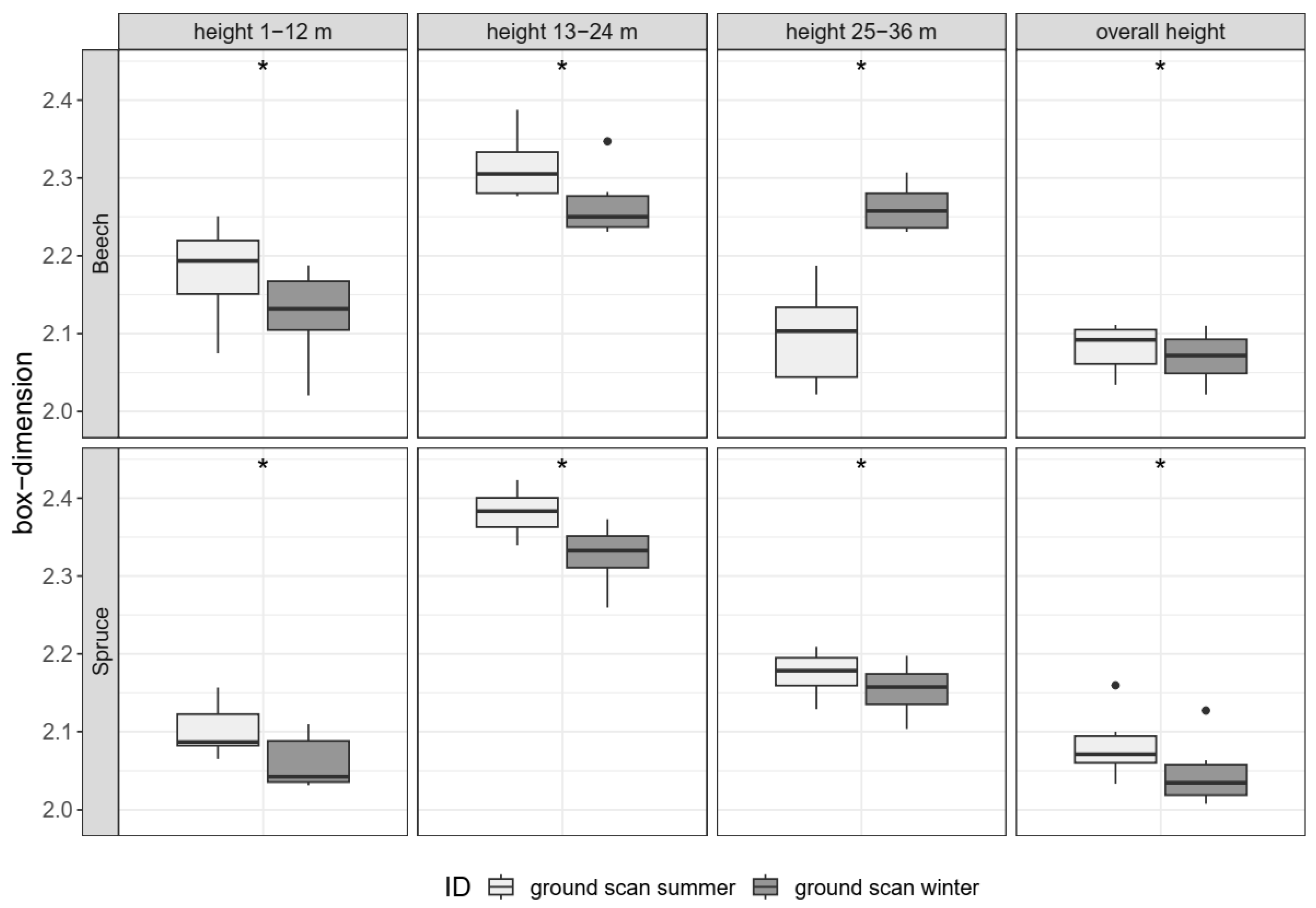
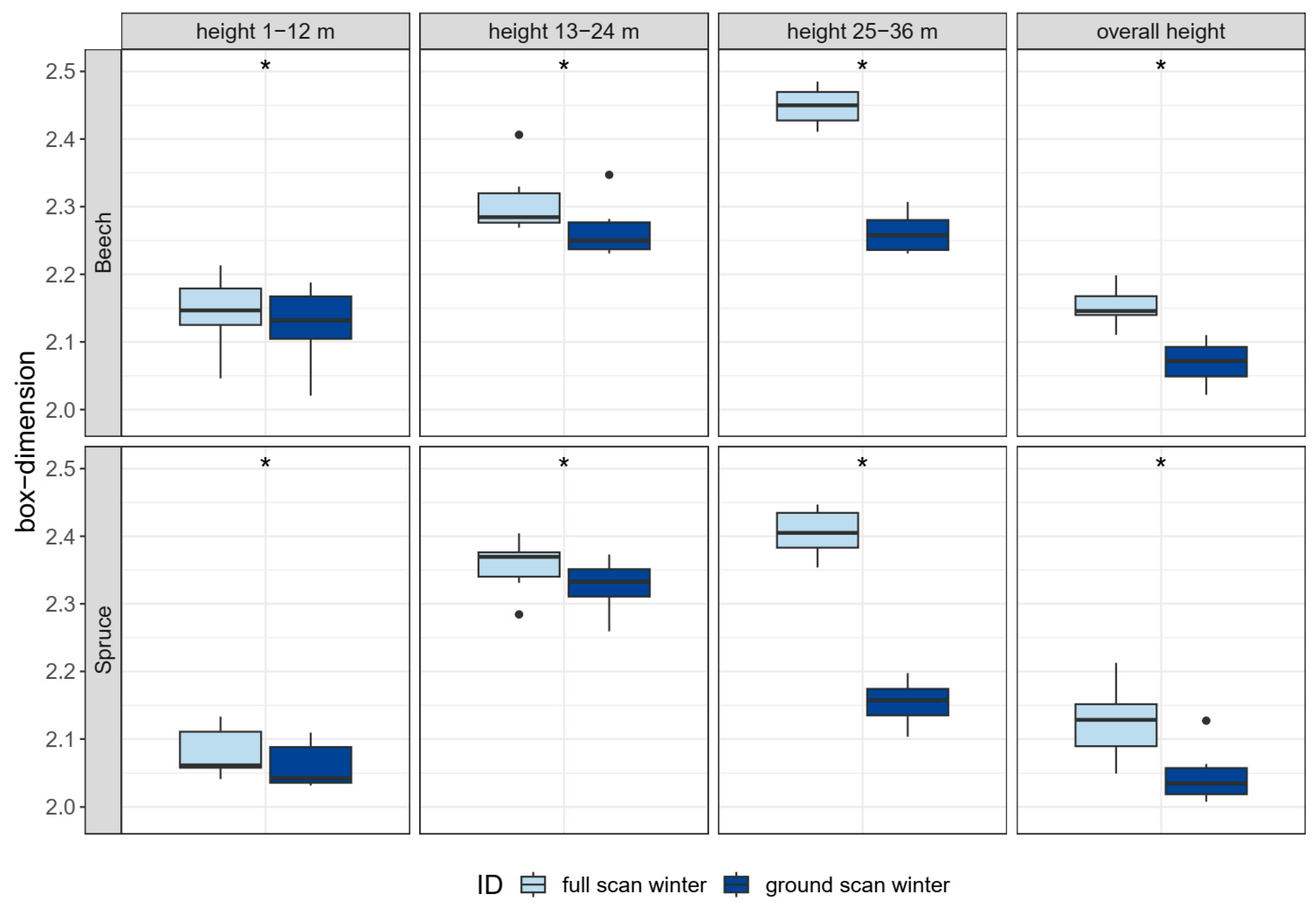
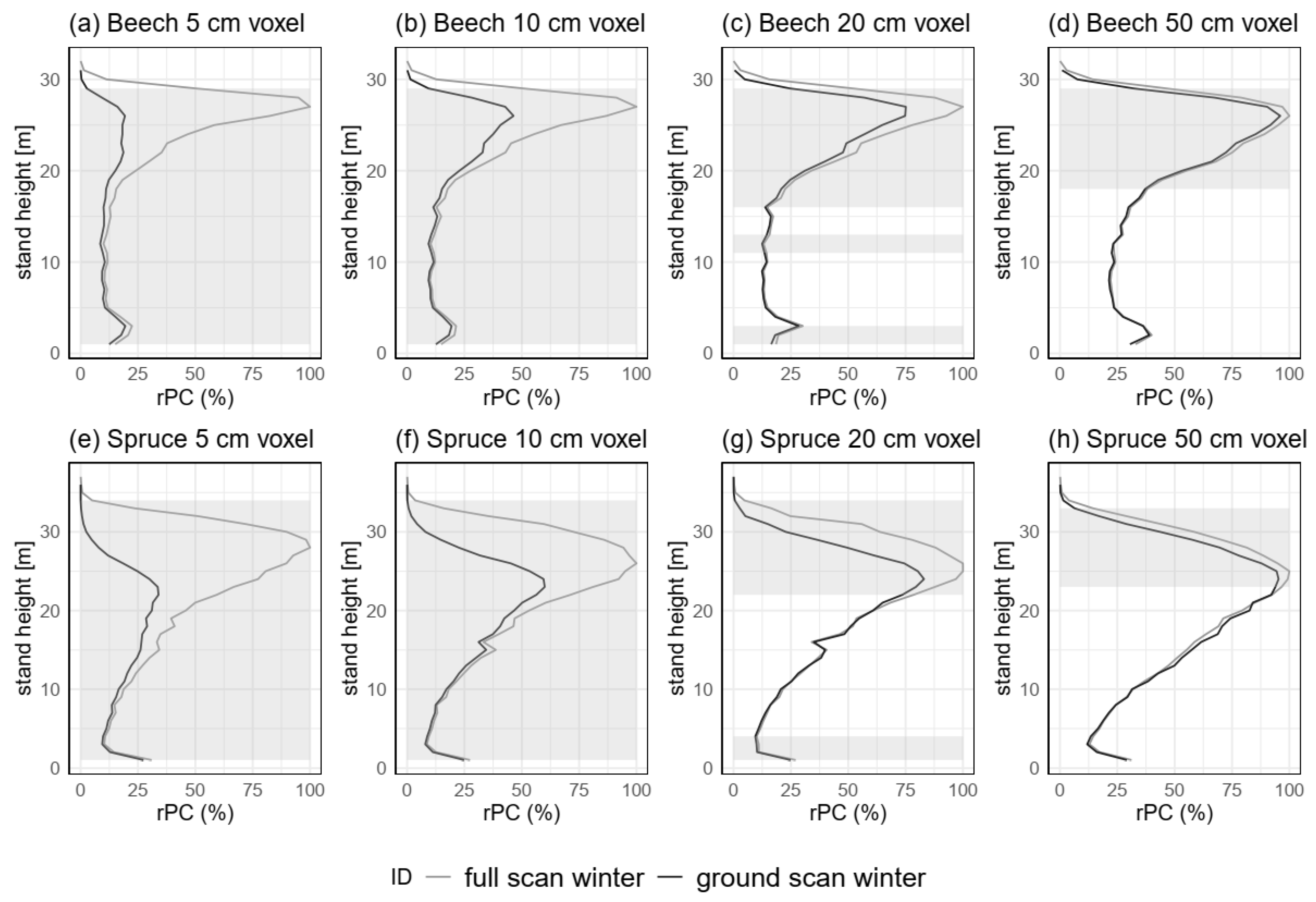
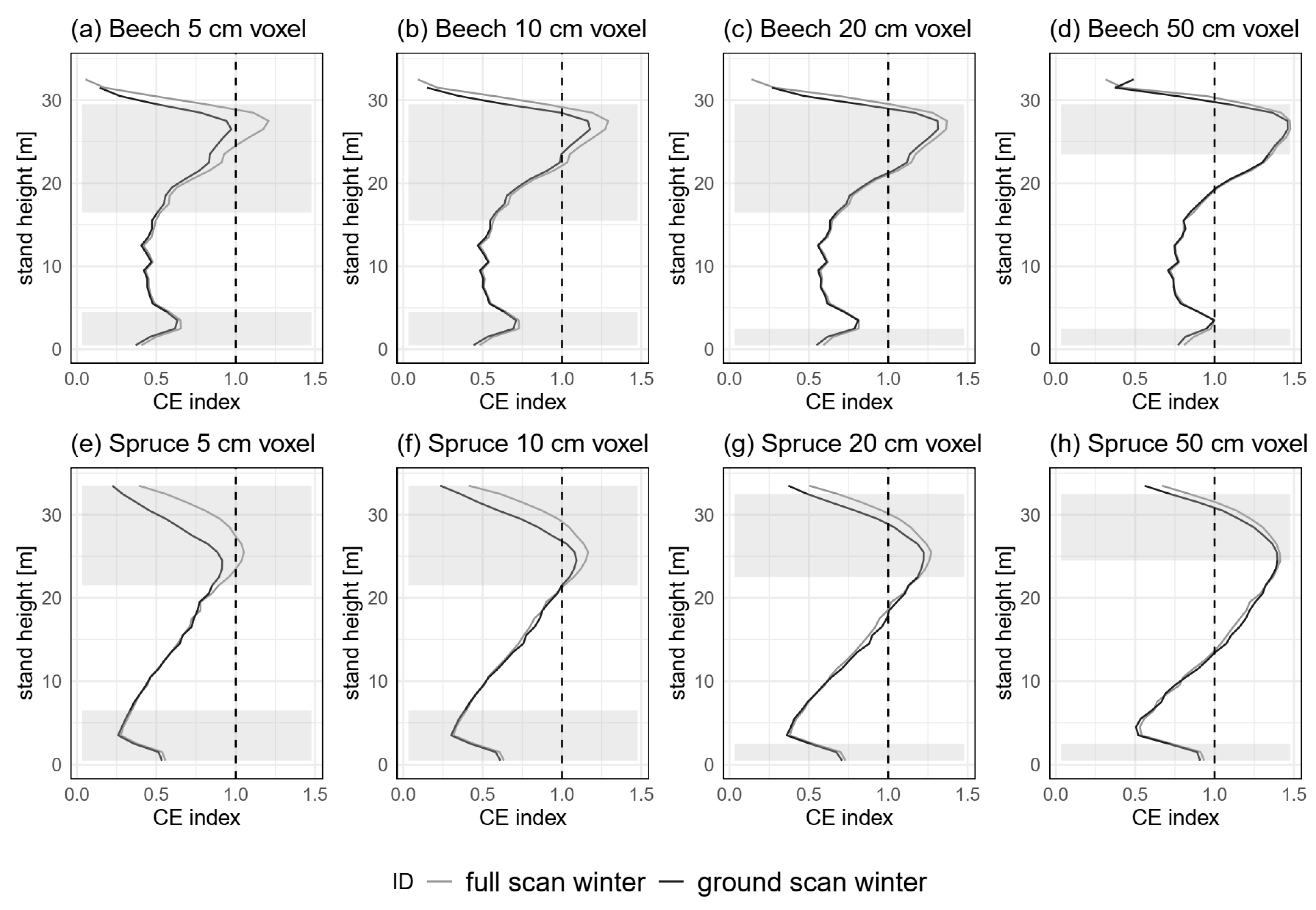
3.3.3. Spatial Resolution (H5)
4. Discussion
4.1. Seasonal Comparison
4.2. Methodological Comparison
4.2.1. Single-Tree Morphologies
4.2.2. Stand Structure
4.2.3. Spatial Resolution
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seidel, D.; Beyer, F.; Hertel, D.; Fleck, S.; Leuschner, C. 3D-laser scanning: A non-destructive method for studying above- ground biomass and growth of juvenile trees. Agric. For. Meteorol. 2011, 151, 1305–1311. [Google Scholar] [CrossRef]
- Seidel, D.; Ammer, C.; Puettmann, K. Describing forest canopy gaps efficiently, accurately, and objectively: New prospects through the use of terrestrial laser scanning. Agric. For. Meteorol. 2015, 213, 23–32. [Google Scholar] [CrossRef]
- Bayer, D.; Seifert, S.; Pretzsch, H. Structural crown properties of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica [L.]) in mixed versus pure stands revealed by terrestrial laser scanning. Trees 2013, 27, 1035–1047. [Google Scholar] [CrossRef]
- Pretzsch, H. Grundlagen der Waldwachstumsforschung; Springer: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-662-58154-4. [Google Scholar]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial Laser Scanning for Plot-Scale Forest Measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- Gough, C.M.; Atkins, J.W.; Fahey, R.T.; Hardiman, B.S. High rates of primary production in structurally complex forests. Ecology 2019, 100, e02864. [Google Scholar] [CrossRef]
- Bauhus, J.; Forrester, D.I.; Gardiner, B.; Jactel, H.; Vallejo, R.; Pretzsch, H. Ecological Stability of Mixed-Species Forests. In Mixed-Species Forests; Springer: Berlin/Heidelberg, Germany, 2017; pp. 337–382. [Google Scholar]
- Bohn, F.J.; Huth, A. The importance of forest structure to biodiversity-productivity relationships. R. Soc. Open Sci. 2017, 4, 160521. [Google Scholar] [CrossRef]
- Lelli, C.; Bruun, H.H.; Chiarucci, A.; Donati, D.; Frascaroli, F.; Fritz, Ö.; Goldberg, I.; Nascimbene, J.; Tøttrup, A.P.; Rahbek, C.; et al. Biodiversity response to forest structure and management: Comparing species richness, conservation relevant species and functional diversity as metrics in forest conservation. For. Ecol. Manag. 2019, 432, 707–717. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Schall, P.; Ammer, C.; Fischer, M.; Seidel, D. Effects of structural heterogeneity on the diurnal temperature range in temperate forest ecosystems. For. Ecol. Manag. 2019, 432, 860–867. [Google Scholar] [CrossRef]
- Kovács, B.; Tinya, F.; Ódor, P. Stand structural drivers of microclimate in mature temperate mixed forests. Agric. For. Meteorol. 2017, 234-235, 11–21. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Uhl, E.; Dahlhausen, J.; Rötzer, T.; Caldentey, J.; Koike, T.; van Con, T.; Chavanne, A.; Seifert, T.; et al. Crown size and growing space requirement of common tree species in urban centres, parks, and forests. Urban For. Urban Green. 2015, 14, 466–479. [Google Scholar] [CrossRef]
- Jacobs, M.; Rais, A.; Pretzsch, H. How drought stress becomes visible upon detecting tree shape using terrestrial laser scanning (TLS). For. Ecol. Manag. 2021, 489, 118975. [Google Scholar] [CrossRef]
- Lee, B.-U.; Jeon, H.-G.; Im, S.; Kweon, I.S. Depth Completion with Deep Geometry and Context Guidance. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3281–3287, ISBN 978-1-5386-6027-0. [Google Scholar]
- Lovell, J.L.; Jupp, D.; Newnham, G.J.; Culvenor, D.S. Measuring tree stem diameters using intensity profiles from ground-based scanning lidar from a fixed viewpoint. ISPRS J. Photogramm. Remote Sens. 2011, 66, 46–55. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Ryding, J.; Williams, E.; Smith, M.; Eichhorn, M. Assessing Handheld Mobile Laser Scanners for Forest Surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef]
- Choi, H.; Song, Y. Comparing tree structures derived among airborne, terrestrial and mobile LiDAR systems in urban parks. GIScience Remote Sens. 2022, 59, 843–860. [Google Scholar] [CrossRef]
- Neudam, L.; Annighöfer, P.; Seidel, D. Exploring the Potential of Mobile Laser Scanning to Quantify Forest Structural Complexity. Front. Remote Sens. 2022, 3, 861337. [Google Scholar] [CrossRef]
- Heidenreich, M.G.; Seidel, D. Assessing Forest Vitality and Forest Structure Using 3D Data: A Case Study from the Hainich National Park, Germany. Front. For. Glob. Chang. 2022, 5, 121. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Schall, P.; Juchheim, J.; Ammer, C.; Seidel, D. Effective number of layers: A new measure for quantifying three-dimensional stand structure based on sampling with terrestrial LiDAR. For. Ecol. Manag. 2016, 380, 212–223. [Google Scholar] [CrossRef]
- Abegg, M.; Kükenbrink, D.; Zell, J.; Schaepman, M.; Morsdorf, F. Terrestrial Laser Scanning for Forest Inventories—Tree Diameter Distribution and Scanner Location Impact on Occlusion. Forests 2017, 8, 184. [Google Scholar] [CrossRef]
- Li, L.; Mu, X.; Soma, M.; Wan, P.; Qi, J.; Hu, R.; Zhang, W.; Tong, Y.; Yan, G. An Iterative-Mode Scan Design of Terrestrial Laser Scanning in Forests for Minimizing Occlusion Effects. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3547–3566. [Google Scholar] [CrossRef]
- Matyssek, R.; Fromm, J.; Rennenberg, H.; Roloff, A. Biologie der Bäume: Von der Zelle zur Globalen Ebene; Verlag Eugen Ulmer: Stuttgart, Germany, 2010; ISBN 9783825284503. [Google Scholar]
- Stiers, M.; Annighöfer, P.; Seidel, D.; Willim, K.; Neudam, L.; Ammer, C. Quantifying the target state of forest stands managed with the continuous cover approach—revisiting Möller’s “Dauerwald” concept after 100 years. Trees For. People 2020, 1, 100004. [Google Scholar] [CrossRef]
- Willim, K.; Stiers, M.; Annighöfer, P.; Ehbrecht, M.; Ammer, C.; Seidel, D. Spatial Patterns of Structural Complexity in Differently Managed and Unmanaged Beech-Dominated Forests in Central Europe. Remote Sens. 2020, 12, 1907. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.-L.; Fournier, R.A. A model for deriving voxel-level tree leaf area density estimates from ground-based LiDAR. Environ. Model. Softw. 2014, 51, 184–189. [Google Scholar] [CrossRef]
- Pretzsch, H.; Rötzer, T.; Matyssek, R.; Grams, T.E.E.; Häberle, K.-H.; Pritsch, K.; Kerner, R.; Munch, J.-C. Mixed Norway spruce (Picea abies [L.] Karst) and European beech (Fagus sylvatica [L.]) stands under drought: From reaction pattern to mechanism. Trees 2014, 28, 1305–1321. [Google Scholar] [CrossRef]
- Pretzsch, H.; Bauerle, T.; Häberle, K.H.; Matyssek, R.; Schütze, G.; Rötzer, T. Tree diameter growth after root trenching in a mature mixed stand of Norway spruce (Picea abies [L.] Karst) and European beech (Fagus sylvatica [L.]). Trees 2016, 30, 1761–1773. [Google Scholar] [CrossRef]
- Grams, T.E.E.; Hesse, B.D.; Gebhardt, T.; Weikl, F.; Rötzer, T.; Kovacs, B.; Hikino, K.; Hafner, B.D.; Brunn, M.; Bauerle, T.; et al. The Kroof experiment: Realization and efficacy of a recurrent drought experiment plus recovery in a beech/spruce forest. Ecosphere 2021, 12, e03399. [Google Scholar] [CrossRef]
- Dritte Bundeswaldinventur—Ergebnisdatenbank. Available online: https://bwi.info (accessed on 19 June 2020).
- Pretzsch, H.; Grams, T.; Häberle, K.H.; Pritsch, K.; Bauerle, T.; Rötzer, T. Growth and mortality of Norway spruce and European beech in monospecific and mixed-species stands under natural episodic and experimentally extended drought. Results of the KROOF throughfall exclusion experiment. Trees 2020, 34, 957–970. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- GeoSLAM. GeoSLAM Hub; GeoSLAM: Nottingham, UK, 2020. [Google Scholar]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- GreenValley International, Ltd. LiDAR360 Software; GreenValley International, Ltd.: Berkeley, CA, USA, 2019. [Google Scholar]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Agostinelli, C.; Lund, U. R package Circular: Circular Statistics (Version 0.4-95). 2022. Available online: https://r-forge.r-project.org/projects/circular/ (accessed on 18 December 2022).
- Habel, K.; Grasman, R.; Gramacy, R.B.; Mozharovskyi, P.; Sterratt, D.C. _geometry: Mesh Generation and Surface Tessellation_. R Package Version 0.4.6.1. 2022. Available online: https://CRAN.R-project.org/package=geometry (accessed on 18 December 2022).
- Clark, P.J.; Evans, F.C. Distance to nearest neighbour as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Baddeley, A.; Turner, R. spatstat: An R Package for Analyzing Spatial Point Patterns. J. Stat. Softw. 2005, 12, 1–42. [Google Scholar] [CrossRef]
- Donnelly, K. Simulation to determine the variance and edge-effect of total nearest neighbour distances. In Simulation Methods in Archeology; Hodder, I., Ed.; Cambridge Press: London, UK, 1978; pp. 91–95. [Google Scholar]
- Pommerening, A.; Stoyan, D. Edge-correction needs in estimating indices of spatial forest structure. Can. J. For. Res. 2006, 36, 1723–1739. [Google Scholar] [CrossRef]
- Seidel, D. A holistic approach to determine tree structural complexity based on laser scanning data and fractal analysis. Ecol. Evol. 2018, 8, 128–134. [Google Scholar] [CrossRef]
- Sarkar, N.; Chaudhuri, B.B. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Trans. Syst. Man Cybern. 1994, 24, 115–120. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 18 December 2022).
- Dieler, J.; Pretzsch, H. Morphological plasticity of European beech (Fagus sylvatica L.) in pure and mixed-species stands. For. Ecol. Manag. 2013, 295, 97–108. [Google Scholar] [CrossRef]
- Masarovicová, E.; štefančík, L. Some ecophysiological features in sun and shade leaves of tall beech trees. Biol. Plant 1990, 32, 374–387. [Google Scholar] [CrossRef]
- Roloff, A.; Weisgerber, H.; Lang, U.M.; Stimm, B. (Eds.) Enzyklopädie der Holzgewächse: Handbuch und Atlas der Dendrologie/Begründet von Peter Schütt; Wiley-VCH: Weinheim, Germany, 2007; ISBN 9783527321414. [Google Scholar]
- Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of Backpack, Handheld, Under-Canopy UAV, and Above-Canopy UAV Laser Scanning for Field Reference Data Collection in Boreal Forests. Remote Sens. 2020, 12, 3327. [Google Scholar] [CrossRef]
- Trzeciak, M.; Brilakis, I. Comparison of accuracy and density of static and mobile laser scanners. In Proceedings of the 2021 European Conference on Computing in Construction, Ixia, Rhodes, Greece, 25–27 July 2021. [Google Scholar] [CrossRef]
- GeoSLAM. ZEB HORIZON User Guide V1.0; GeoSLAM: Nottingham, UK, 2020. [Google Scholar]
- Hunčaga, M.; Chudá, J.; Tomaštík, J.; Slámová, M.; Koreň, M.; Chudý, F. The Comparison of Stem Curve Accuracy Determined from Point Clouds Acquired by Different Terrestrial Remote Sensing Methods. Remote Sens. 2020, 12, 2739. [Google Scholar] [CrossRef]
- Seidel, D.; Ehbrecht, M.; Annighöfer, P.; Ammer, C. From tree to stand-level structural complexity—Which properties make a forest stand complex? Agric. For. Meteorol. 2019, 278, 107699. [Google Scholar] [CrossRef]
- Seidel, D.; Annighöfer, P.; Ehbrecht, M.; Magdon, P.; Wöllauer, S.; Ammer, C. Deriving Stand Structural Complexity from Airborne Laser Scanning Data—What Does It Tell Us about a Forest? Remote Sens. 2020, 12, 1854. [Google Scholar] [CrossRef]
- Guzmán, Q.J.A.; Sharp, I.; Alencastro, F.; Sánchez-Azofeifa, G.A. On the relationship of fractal geometry and tree–stand metrics on point clouds derived from terrestrial laser scanning. Methods Ecol. Evol. 2020, 11, 1309–1318. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, R.; Cheng, L.; Zhou, X.; Ruan, X.; Xiao, Y. A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data. Remote Sens. 2019, 11, 623. [Google Scholar] [CrossRef]
- Stereńczak, K.; Mielcarek, M.; Wertz, B.; Bronisz, K.; Zajączkowski, G.; Jagodziński, A.M.; Ochał, W.; Skorupski, M. Factors influencing the accuracy of ground-based tree-height measurements for major European tree species. J. Environ. Manag. 2019, 231, 1284–1292. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765, ISBN 978-1-5386-8094-0. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Robotics: Science and Systems X; 2014; ISBN 9780992374709. Available online: https://www.ri.cmu.edu/pub_files/2014/7/Ji_LidarMapping_RSS2014_v8.pdf (accessed on 18 December 2022).


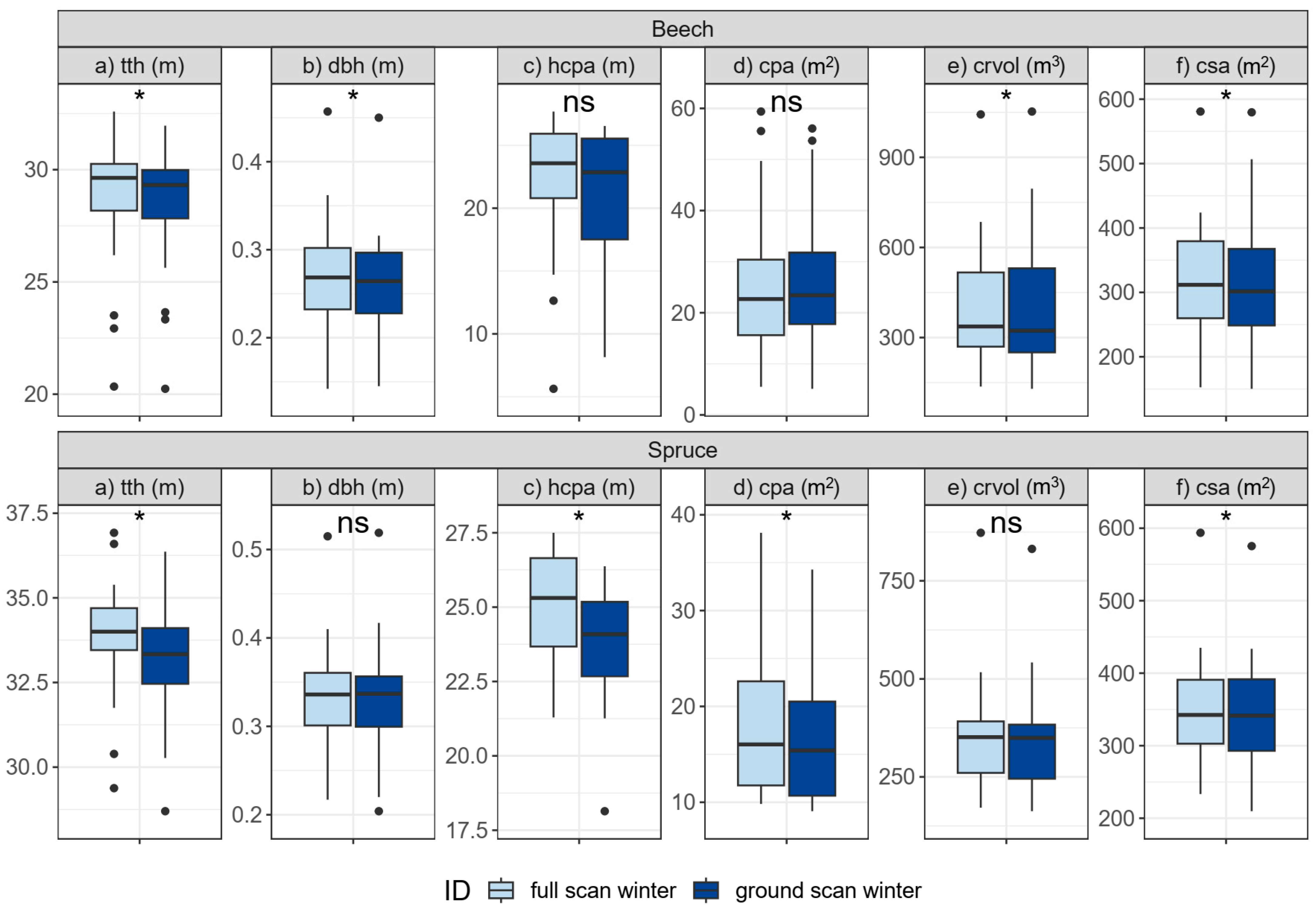
| Beech (abs.) | Beech (rel.) | Spruce (abs.) | Spruce (rel.) | p-Value | |
|---|---|---|---|---|---|
| tth (m) | −0.30 ± 0.34 | −1.04 ± 1.20 | −0.74 ± 0.45 | −2.19 ± 1.34 | 0.001 |
| dbh (m) | −0.01 ± 0.01 | −3.35 ± 5.02 | 0.00 ± 0.01 | −0.18 ± 2.42 | 0.025 |
| hcpa (m) | −0.88 ± 2.78 | −4.00 ± 12.68 | −1.24 ± 2.41 | −4.94 ± 9.58 | 0.685 |
| cpa (m2) | +0.43 ± 5.68 | +1.59 ± 21.16 | −1.12 ± 1.44 | −6.42 ± 8.23 | 0.602 |
| crvol (m3) | +4.85 ± 103.09 | +1.22 ± 26.00 | −3.88 ± 17.47 | −1.11 ± 4.98 | 0.052 |
| csa (m2) | −2.31 ± 41.29 | −0.73 ± 12.98 | −5.97 ± 13.31 | −1.72 ± 3.84 | 0.445 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathes, T.; Seidel, D.; Häberle, K.-H.; Pretzsch, H.; Annighöfer, P. What Are We Missing? Occlusion in Laser Scanning Point Clouds and Its Impact on the Detection of Single-Tree Morphologies and Stand Structural Variables. Remote Sens. 2023, 15, 450. https://doi.org/10.3390/rs15020450
Mathes T, Seidel D, Häberle K-H, Pretzsch H, Annighöfer P. What Are We Missing? Occlusion in Laser Scanning Point Clouds and Its Impact on the Detection of Single-Tree Morphologies and Stand Structural Variables. Remote Sensing. 2023; 15(2):450. https://doi.org/10.3390/rs15020450
Chicago/Turabian StyleMathes, Thomas, Dominik Seidel, Karl-Heinz Häberle, Hans Pretzsch, and Peter Annighöfer. 2023. "What Are We Missing? Occlusion in Laser Scanning Point Clouds and Its Impact on the Detection of Single-Tree Morphologies and Stand Structural Variables" Remote Sensing 15, no. 2: 450. https://doi.org/10.3390/rs15020450
APA StyleMathes, T., Seidel, D., Häberle, K.-H., Pretzsch, H., & Annighöfer, P. (2023). What Are We Missing? Occlusion in Laser Scanning Point Clouds and Its Impact on the Detection of Single-Tree Morphologies and Stand Structural Variables. Remote Sensing, 15(2), 450. https://doi.org/10.3390/rs15020450