Spatio-Temporal Dynamic Characteristics of Carbon Use Efficiency in a Virgin Forest Area of Southeast Tibet
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. MODIS GPP, NPP Dataset and Calculation of CUE
2.2.2. Land Cover Dataset
2.2.3. Climate Dataset
2.3. Analytical Methods
2.3.1. Theil-Sen Median Slope Estimator and Mann-Kendall Trend Analysis
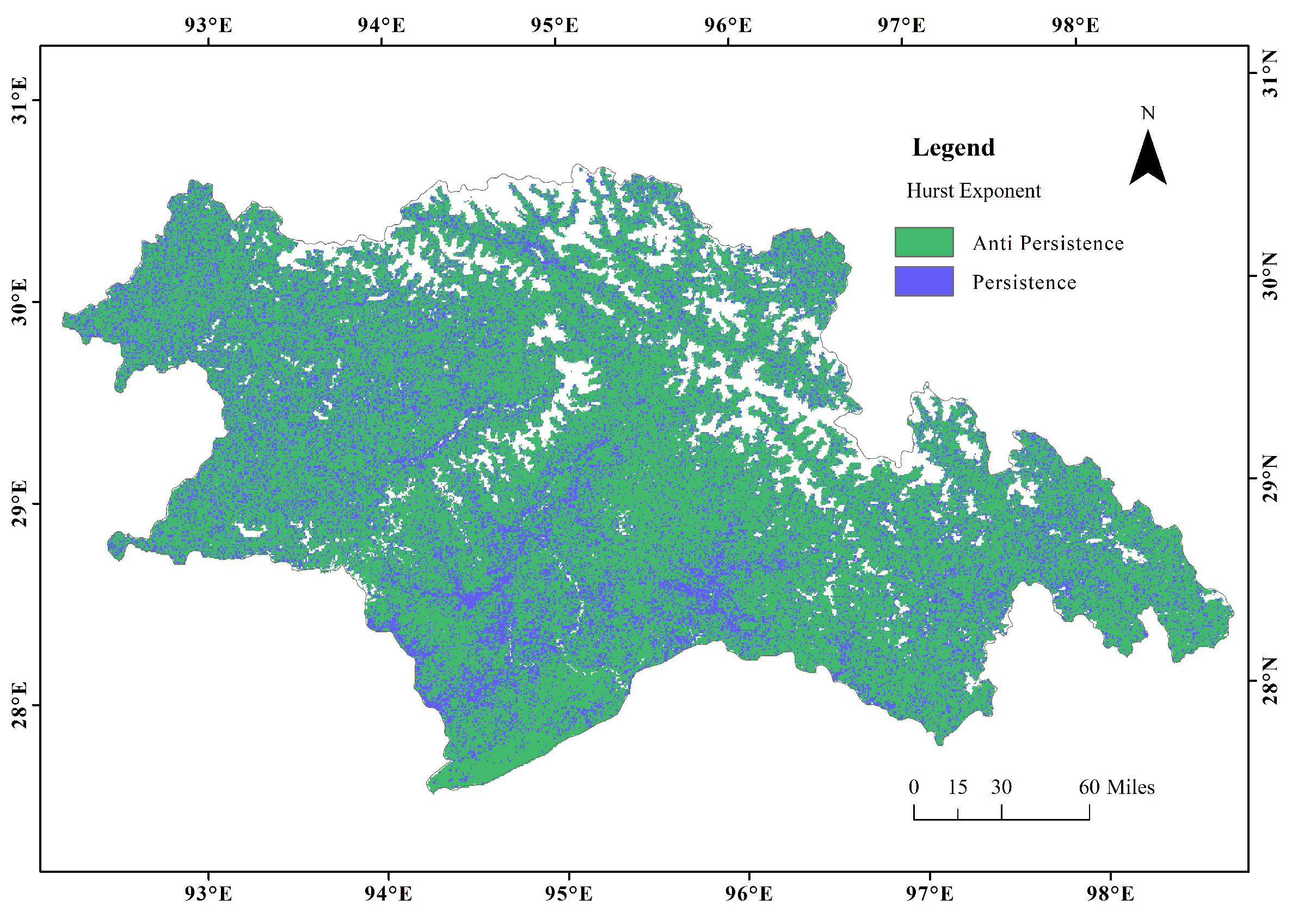
2.3.2. Spatiotemporal Stability Analysis
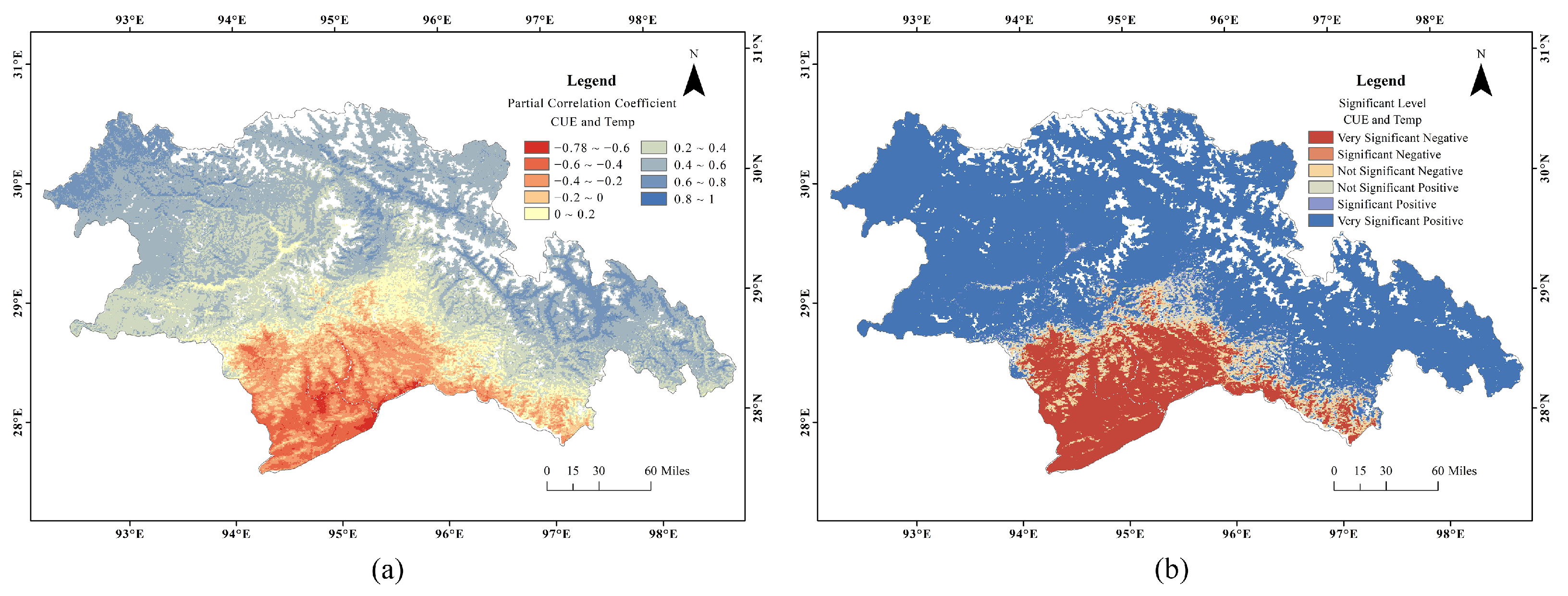
2.3.3. Correlation Analysis
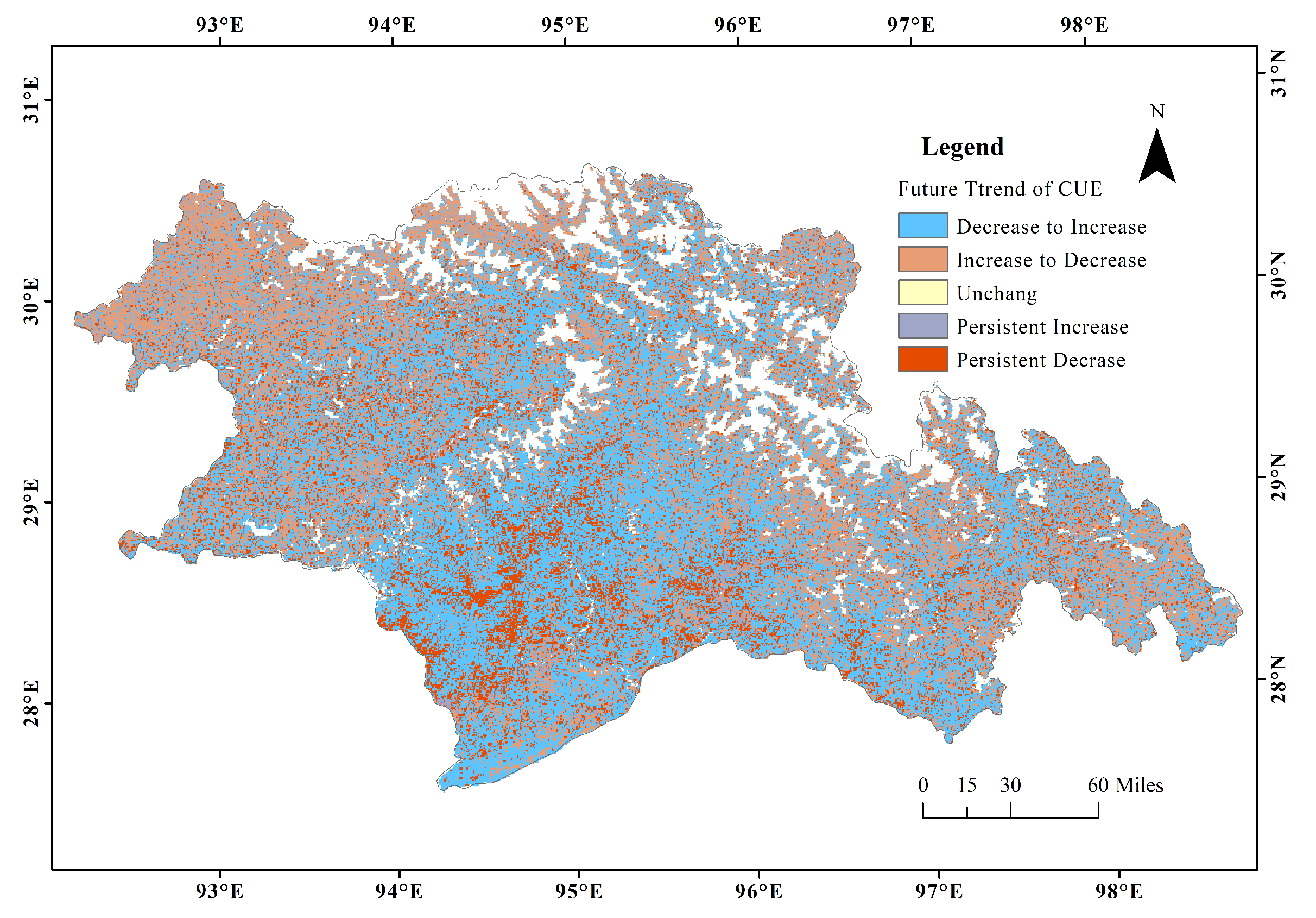
2.3.4. Future Trend Analysis
3. Results
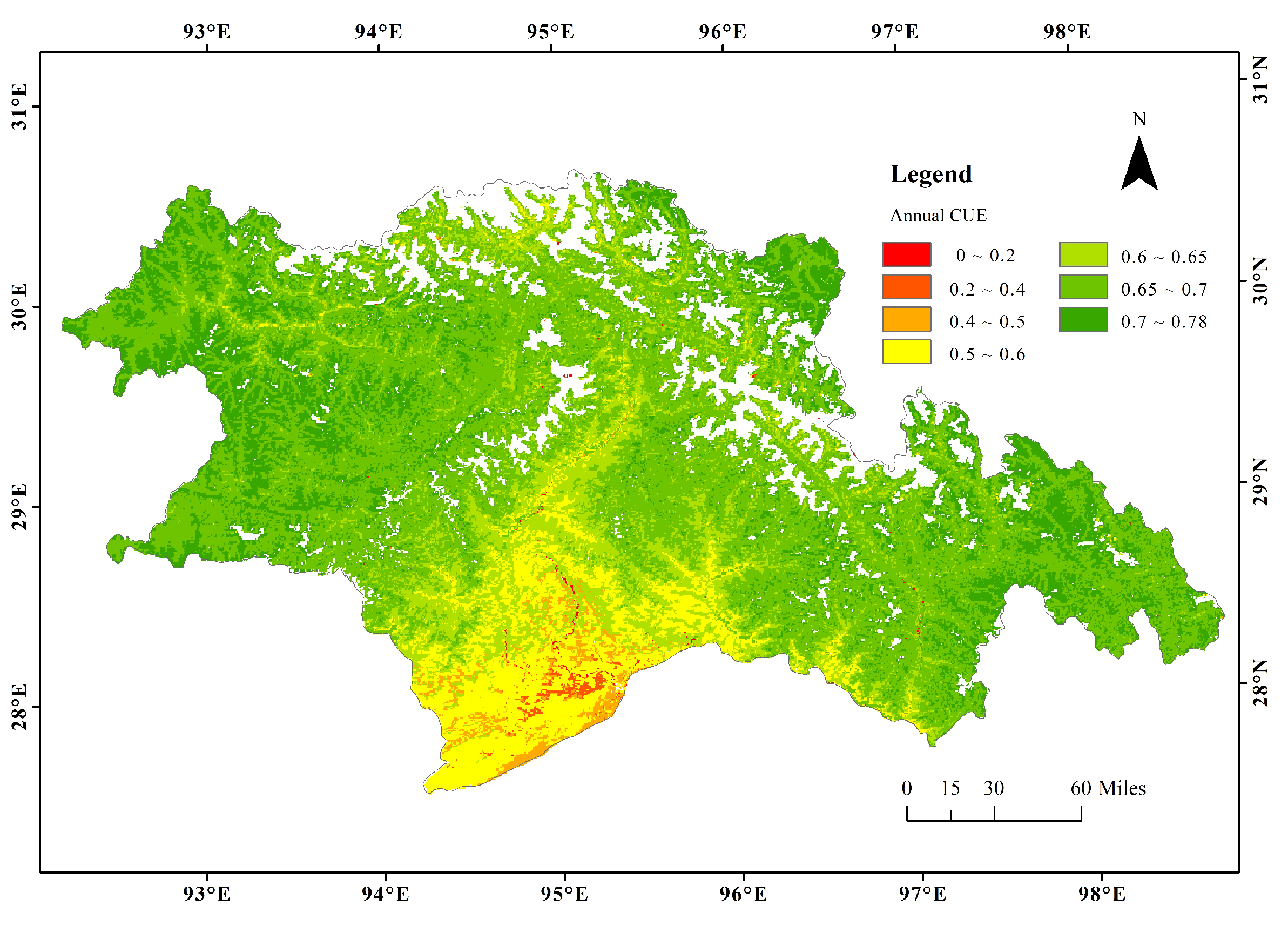
3.1. Spatial Patterns of CUE
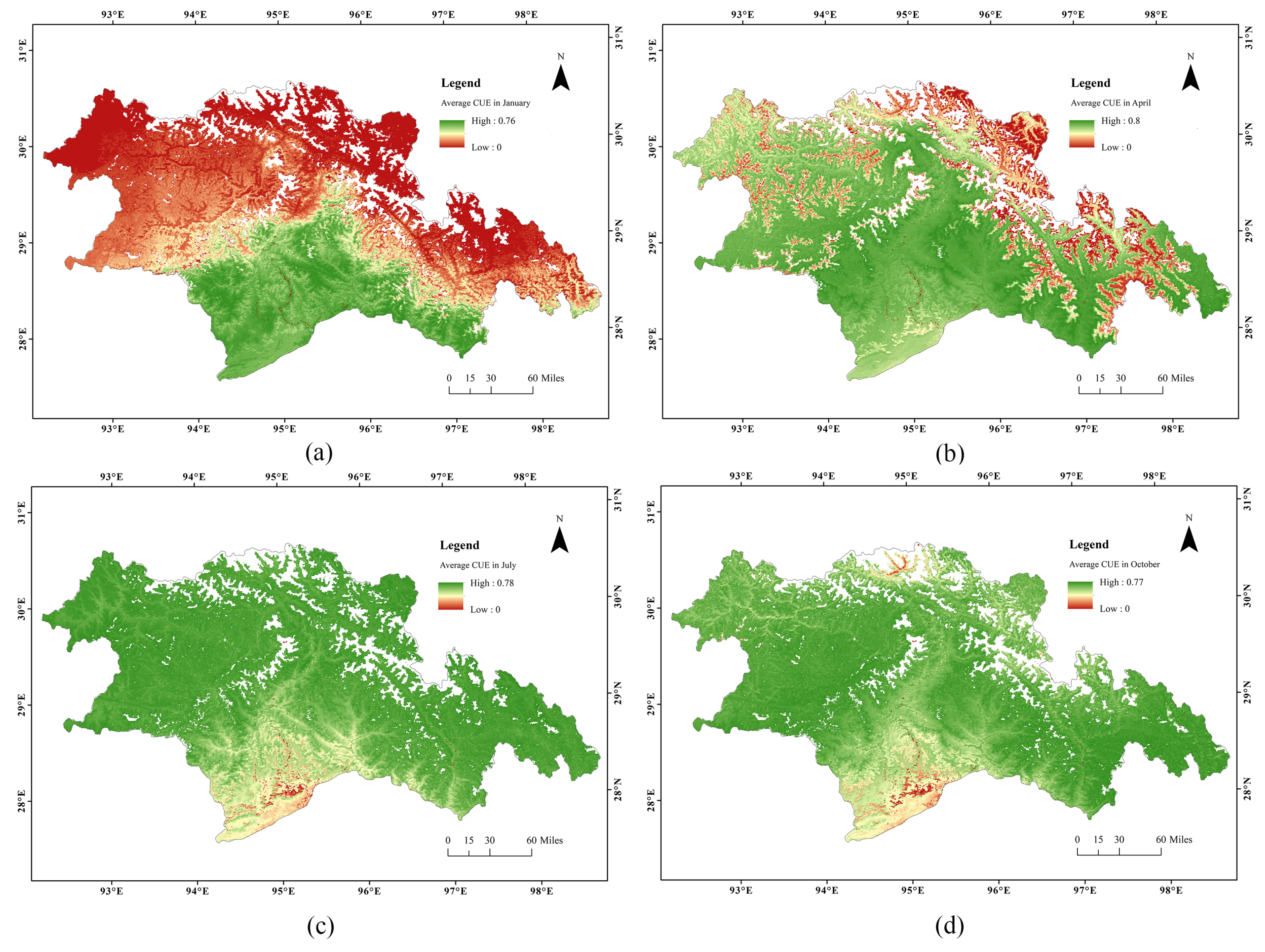
3.2. Intra-Annual and Inter-Annual Variation of CUE
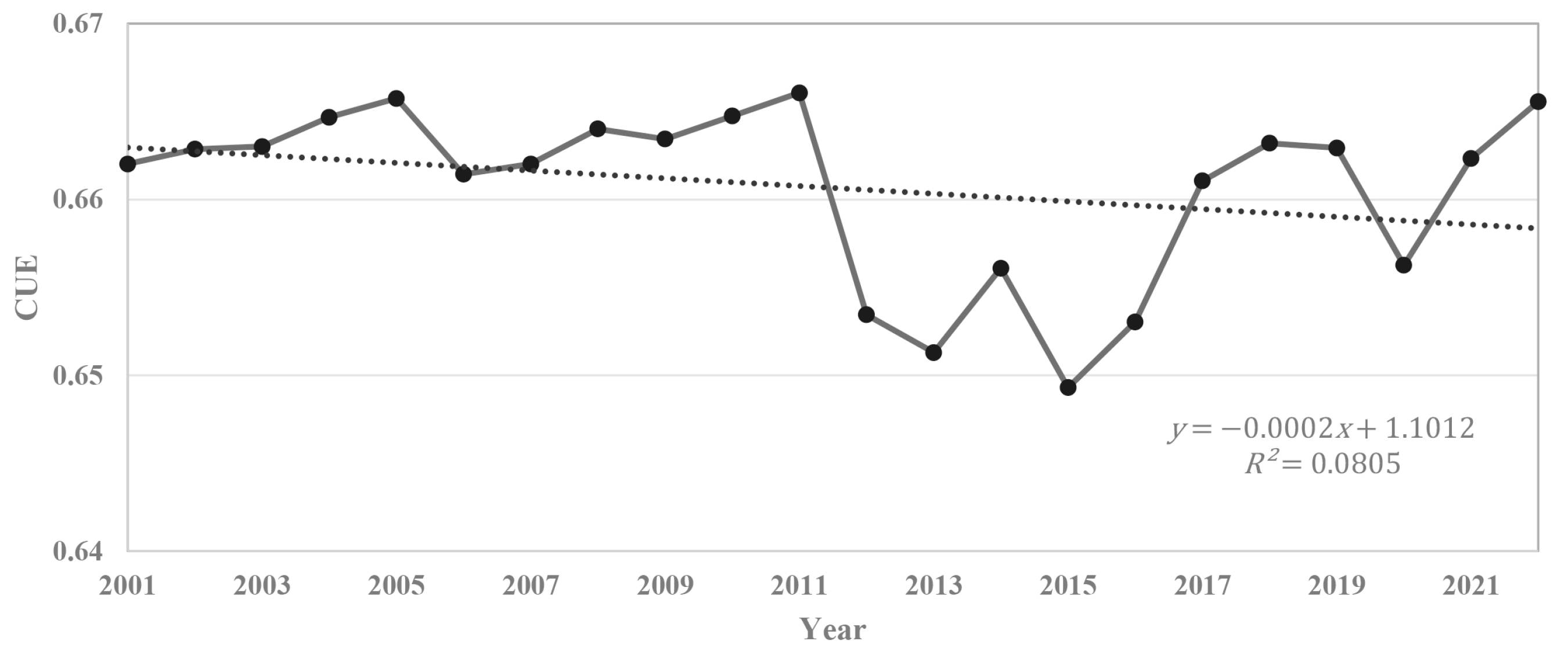
3.3. The Variation Trend of CUE
3.4. Variation of CUE with Temperature and Precipitation
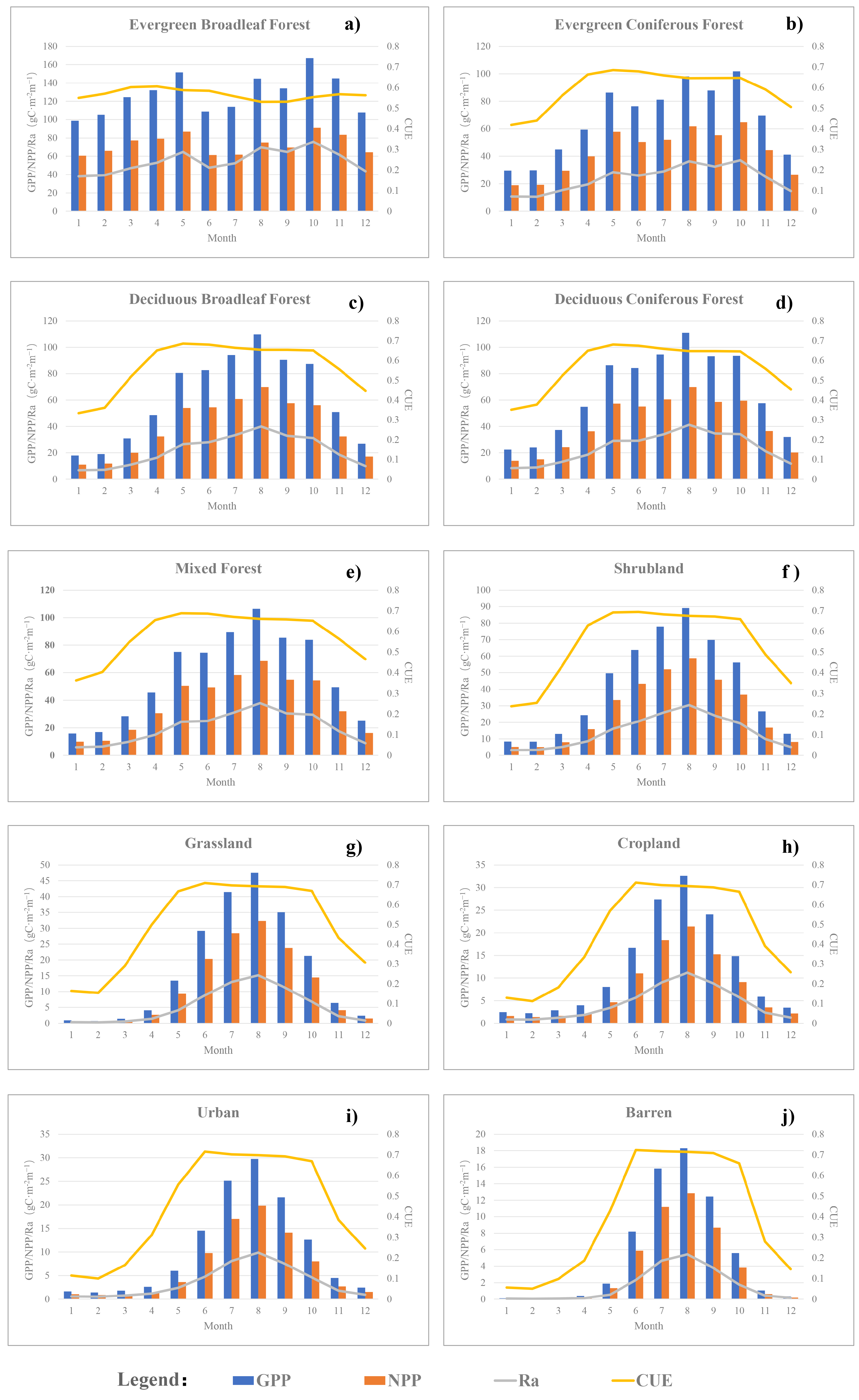
3.5. Cue Changes of Each Vegetation Type in Response to the Growth Process
4. Discussion
4.1. Influencing Factors of Forest CUE Variation
4.2. Reasons for High CUE in Low-Vegetation Areas and Limitations of MODIS Monitoring
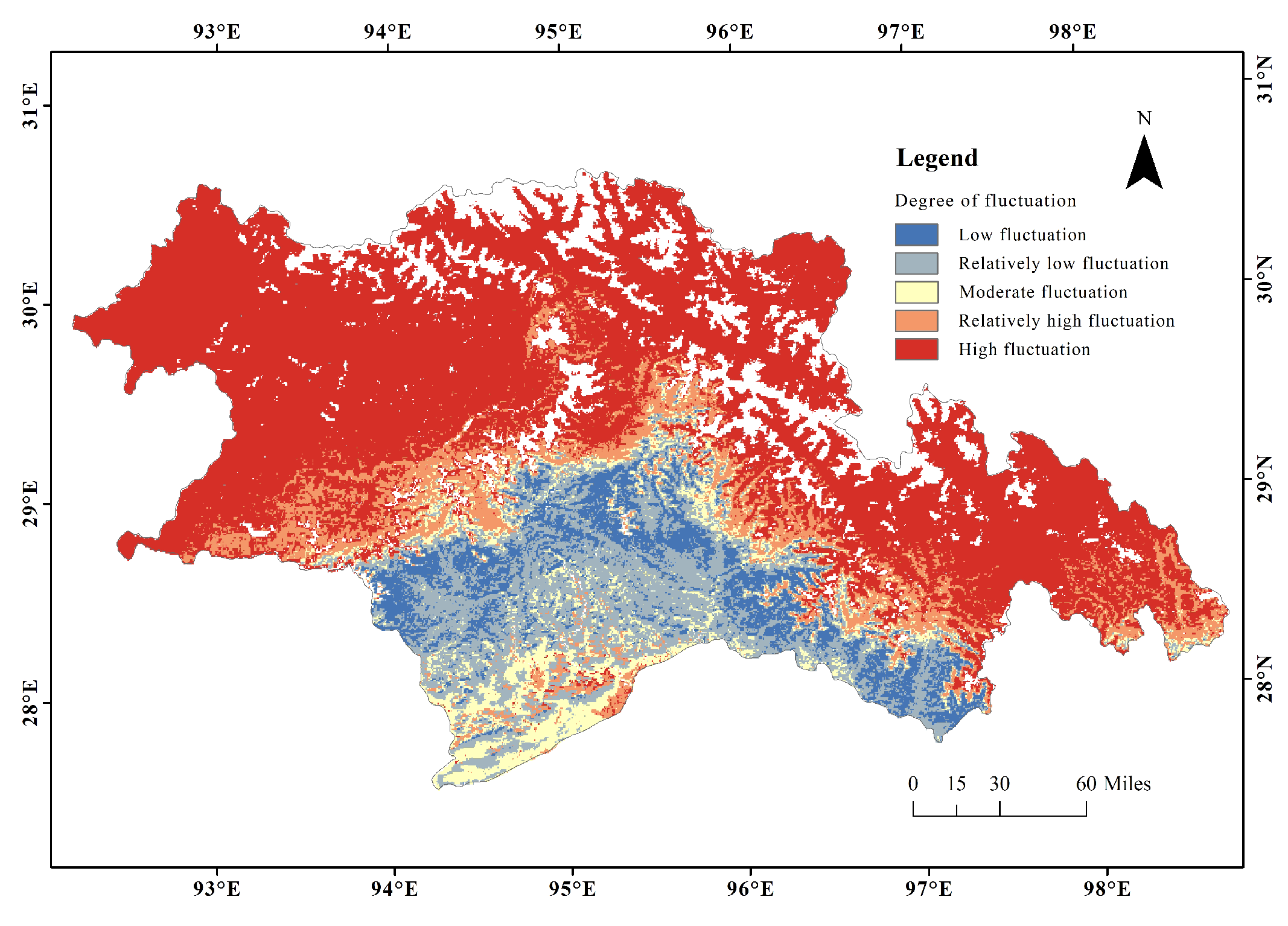
4.3. Reasons for the Increase in CUE Fluctuation in Recent Years
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
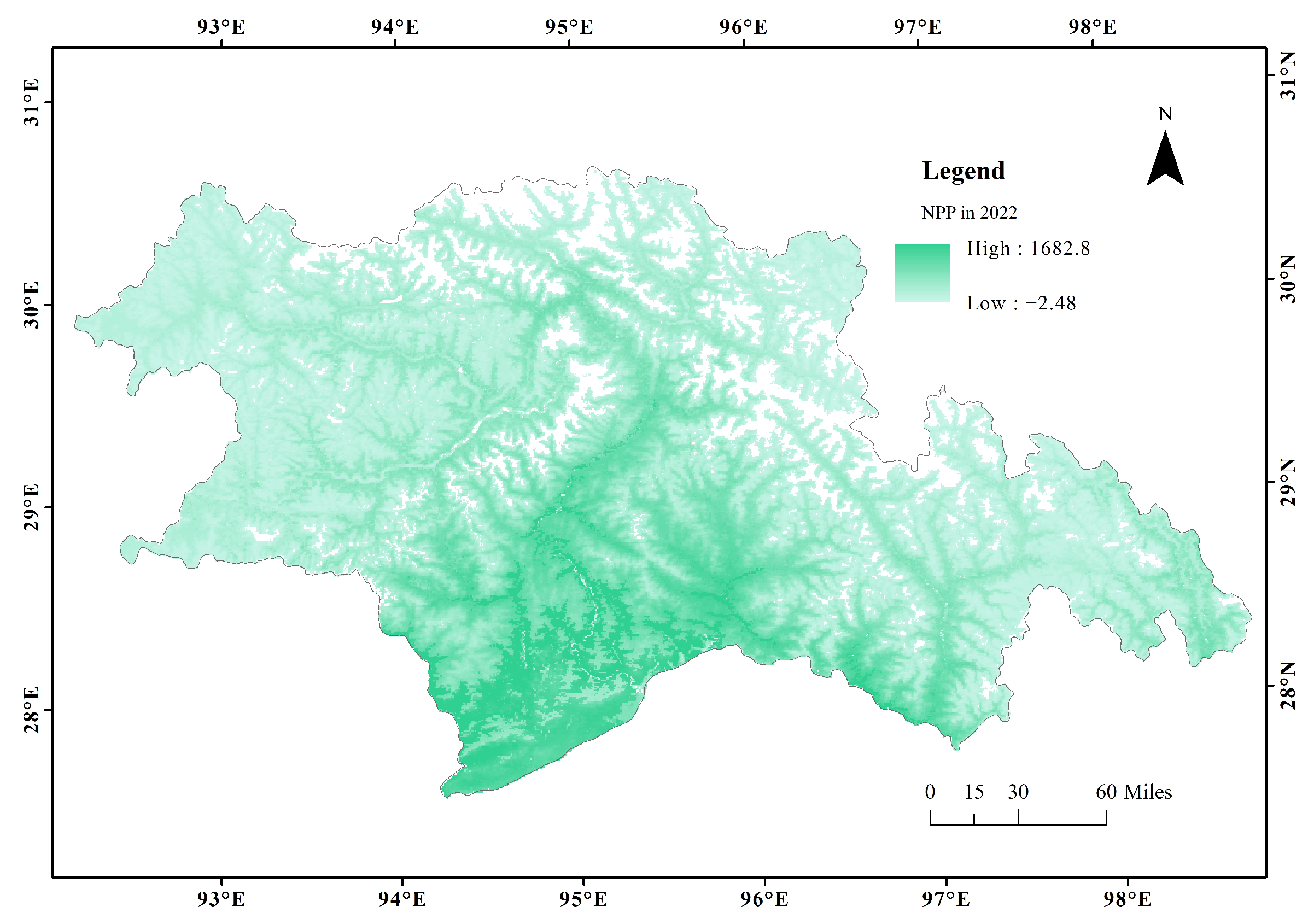
Appendix A.1
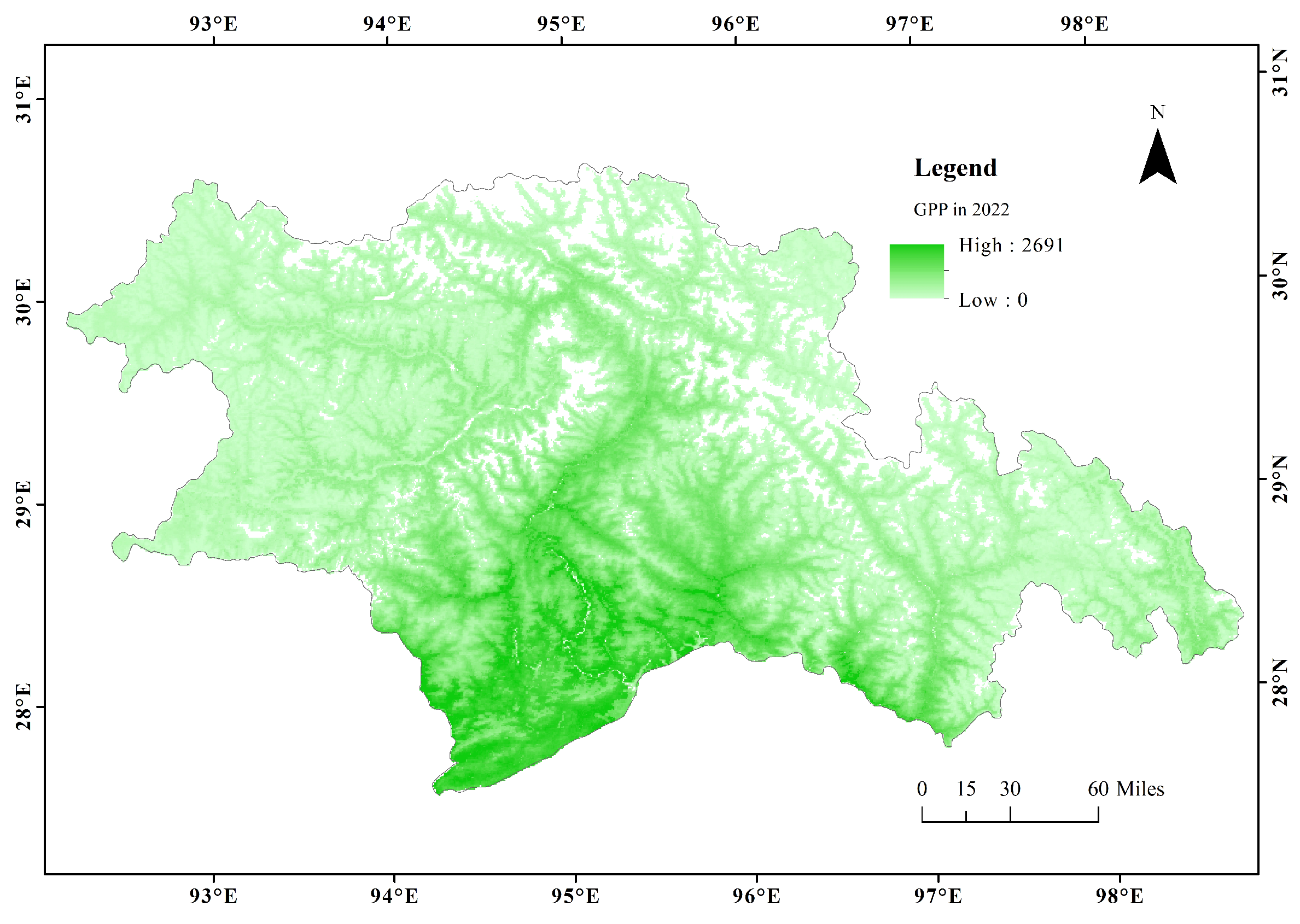
Appendix A.2
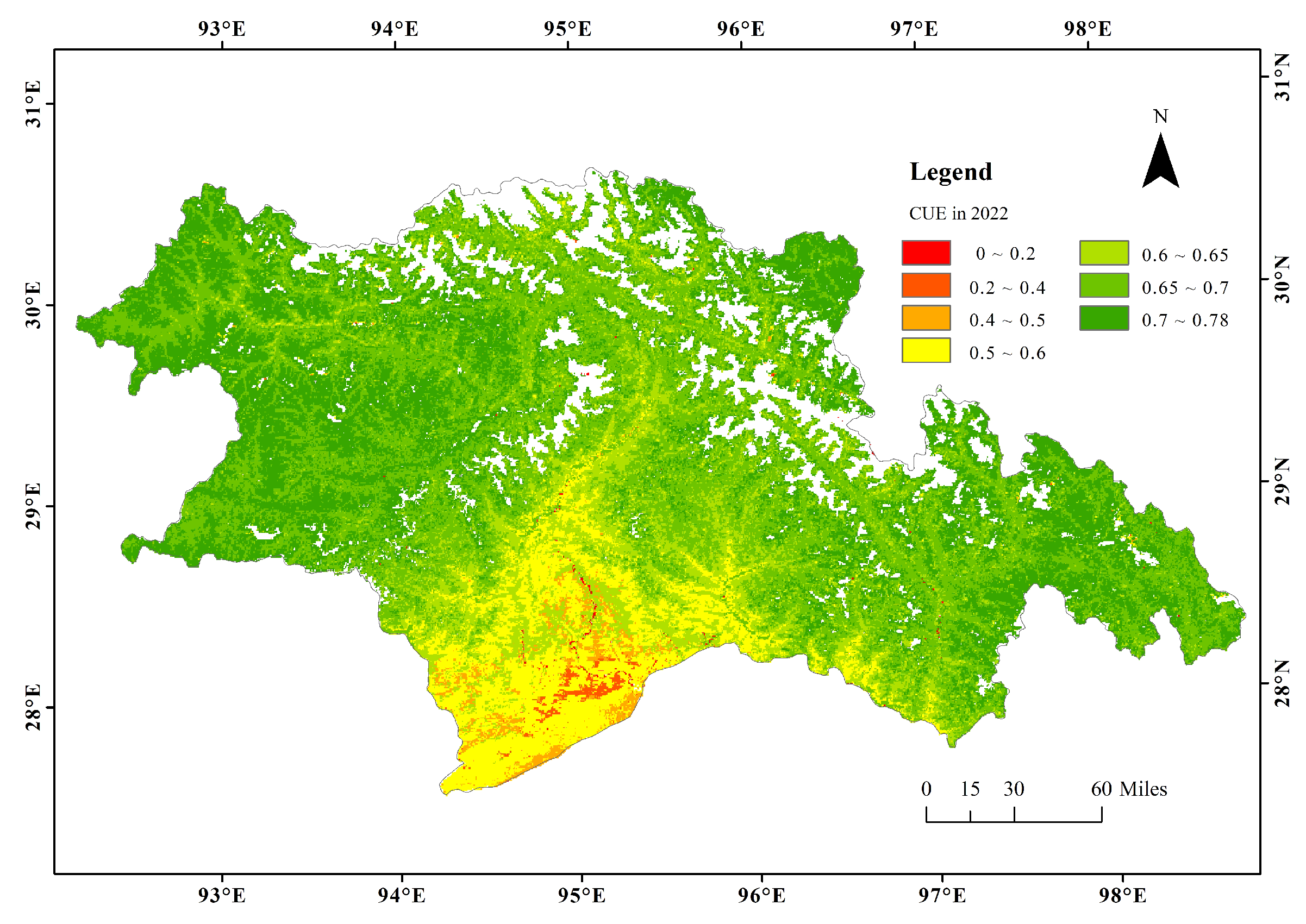
Appendix A.3
References
- Wang, M.; Wang, S.; Zhao, J.; Ju, W.; Hao, Z. Global positive gross primary productivity extremes and climate contributions during 1982–2016. Sci. Total Environ. 2021, 774, 145703. [Google Scholar] [CrossRef] [PubMed]
- Falkowski, P.; Scholes, R.J.; Boyle, E.; Canadell, J.; Canfield, D.; Elser, J.; Gruber, N.; Hibbard, K.; Högberg, P.; Linder, S.; et al. The global carbon cycle: A test of our knowledge of earth as a system. Science 2000, 290, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Yu, G.; Liu, L.; Hu, S.; Chapin, F.S., III. Climate change, human impacts, and carbon sequestration in China. Proc. Natl. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Shi, Y.; Sun, W.; Chang, J.; Zhu, J.; Chen, L.; Wang, X.; Guo, Y.; Zhang, H.; Yu, L.; et al. Terrestrial carbon sinks in China and around the world and their contribution to carbon neutrality. Sci. China Life Sci. 2022, 65, 861–895. [Google Scholar] [CrossRef]
- Adingo, S.; Yu, J.R.; Liu, X.; Li, X.; Sun, J.; Zhang, X. Variation of soil microbial carbon use efficiency (CUE) and its Influence mechanism in the context of global environmental change: A review. PeerJ 2021, 9, e12131. [Google Scholar] [CrossRef]
- Doughty, C.E.; Prŷs-Jones, T.; Abraham, A.J.; Kolb, T.E. Forest thinning in ponderosa pines increases carbon use efficiency and energy flow from primary producers to primary consumers. J. Geophys. Res. Biogeosci. 2021, 126, e2020JG005947. [Google Scholar] [CrossRef]
- Yu, G.; Ren, W.; Chen, Z.; Zhang, L.; Wang, Q.; Wen, X.; He, N.; Zhang, L.; Fang, H.; Zhu, X.; et al. Construction and progress of Chinese terrestrial ecosystem carbon, nitrogen and water fluxes coordinated observation. J. Geogr. Sci. 2016, 26, 803–826. [Google Scholar] [CrossRef]
- Zhu, W.Z. Advances in the carbon use efficiency of forest. Chin. J. Plant Ecol. 2013, 37, 1043–1058. [Google Scholar] [CrossRef]
- An, X.; Chen, Y.; Tang, Y. Factors affecting the spatial variation of carbon use efficiency and carbon fluxes in east Asia forest and grassland. Res. Soil Water Conserv. 2017, 24, 79–92. [Google Scholar]
- El, M.B.; Schwalm, C.; Huntzinger, D.N. Carbon and Water Use Efficiencies: A Comparative Analysis of Ten Terrestrial Ecosystem Models under Changing Climate. Sci. Rep. 2019, 9, 14680. [Google Scholar]
- Collalti, A.; Trotta, C.; Keenan, T.F. Thinning Can Reduce Losses in Carbon Use Efficiency and Carbon Stocks in Managed Forests Under Warmer Climate. J. Adv. Model. Earth Syst. 2018, 10, 2427–2452. [Google Scholar] [CrossRef]
- Chuai, X.; Guo, X.; Zhang, M.; Yuan, Y.; Li, J.; Zhao, R.; Yang, W.; Li, J. Vegetation and climate zones based carbon use efficiency variation and the main determinants analysis in China. Ecol. Indic. 2020, 111, 105967. [Google Scholar] [CrossRef]
- DeLucia, E.H.; Drake, J.E.; Thomas, R.B. Forest carbon use efficiency: Is respiration a constant fraction of gross primary production. Glob. Chang. Biol. 2007, 13, 1157–1167. [Google Scholar] [CrossRef]
- He, Y.; Piao, S.; Li, X.; Chen, A.; Qin, D. Global patterns of vegetation carbon use efficiency and their climate drivers deduced from MODIS satellite data and process-based models. Agric. For. Meteorol. 2018, 256, 150–158. [Google Scholar] [CrossRef]
- Li, B.; Huang, F.; Chang, S. The Variations of Satellite-Based Ecosystem Water Use and Carbon Use Efficiency and Their Linkages with Climate and Human Drivers in the Songnen Plain, China. Adv. Meteorol. 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Ye, X.; Liu, F.; Zhang, Z.; Xu, C.; Liu, J. Spatio-temporal variations of vegetation carbon use efficiency and potential driving meteorological factors in the Yangtze River Basin. J. Mt. Sci. 2020, 17, 1959–1973. [Google Scholar] [CrossRef]
- Cox, P.M. Description of the TRIFFID dynamic global vegetation model. Hadley Centre Tech. Note 2001, 21, 1–16. [Google Scholar]
- Clark, D.B.; Mercado, L.M.; Sitch, S.; Jones, C.D.; Gedney, N.; Best, M.J.; Pryor, M.; Rooney, G.G.; Essery, R.L.H.; Blyth, E.; et al. The Joint UK Land Environment Simulator (JULES), model description―Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Sands, P.J.; Landsberg, J. Physiological Ecology of Forest Production: Principles, Processes and Models; Elsevier/Academic Press: London, UK, 2011. [Google Scholar]
- Li, R.; Ye, C.; Wang, Y.; Han, G.D.; Sun, J. Carbon Storage Estimation and its Drivering Force Analysis Based on InVEST Model in the Tibetan Plateau. Acta Agrestia Sin. 2021, 29, 43. [Google Scholar]
- Chen, Z.; Yu, G. Spatial variations and controls of carbon use efficiency in China’s terrestrial ecosystems. Sci. Rep. 2019, 9, 19516. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.; Li, S.; Sun, W.; Shen, Z.X. Relationships between vegetation carbon use efficiency and climatic factors on the Tibetan Plateau. Can. J. Remote Sens. 2016, 42, 16–26. [Google Scholar] [CrossRef]
- Luo, X.; Jia, B.; Lai, X. Quantitative analysis of the contributions of land use change and CO2 fertilization to carbon use efficiency on the Tibetan Plateau. Sci. Total Environ. 2020, 728, 138607. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wei, J.; Zhou, J.; Yang, J.; Xu, Y.; Chen, Y.; Hao, J.; Cheng, W. Ecological Sensitivity Assessment of the Southeastern Qinghai-Tibet Plateau using GIS and AHP—A Case Study of the Nyingchi Region. J. Resour. Ecol. 2023, 14, 158–166. [Google Scholar]
- Du, L.; Gong, F.; Zeng, Y.; Ma, L.; Qiao, C.; Wu, H. Carbon use efficiency of terrestrial ecosystems in desert/grassland biome transition zone: A case in Ningxia province, northwest China. Ecol. Indic. 2021, 120, 106971. [Google Scholar] [CrossRef]
- Running, S.W.; Zhao, M. Daily GPP and annual NPP (MOD17A2/A3) products NASA Earth Observing System MODIS land algorithm. MOD17 User’s Guide 2015, 2015, 1–28. [Google Scholar]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Sun, G.; Liu, X.; Wang, X.; Li, S. Changes in vegetation coverage and its influencing factors across the Yellow River Basin during 2001–2020. J. Desert Res. 2021, 41, 205. [Google Scholar]
- Barbieri, L.F.P.; de Fatima Correia, M.; da Silva Aragão, M.R.; Vilar, R.D.A.A.; de Moura, M.S.B. Impact of climate variations and land use change: A Mann-Kendall Application. Rev. Geama 2017, 24, 127–135. [Google Scholar]
- Cai, Y.; Zhang, F.; Duan, P.; Jim, C.Y.; Chan, N.W.; Shi, J.; Liu, C.; Wang, J.; Bahtebay, J.; Ma, X. Vegetation cover changes in China induced by ecological restoration-protection projects and land-use changes from 2000 to 2020. Catena 2022, 217, 106530. [Google Scholar] [CrossRef]
- Liu, Y.; Li, L.; Chen, X.; Zhang, R.; Yang, J. Temporal-spatial variations and influencing factors of vegetation cover in Xinjiang from 1982 to 2013 based on GIMMS-NDVI3g. Glob. Planet. Chang. 2018, 169, 145–155. [Google Scholar] [CrossRef]
- Sun, S.; Song, Z.; Wu, X.; Wang, T.; Wu, Y.; Du, W.; Che, T.; Huang, C.; Zhang, X.; Ping, B.; et al. Spatio-temporal variations in water use efficiency and its drivers in China over the last three decades. Ecol. Indic. 2018, 94, 292–304. [Google Scholar] [CrossRef]
- Xie, P.; Chen, G.C.; Lei, H.F. Hydrological alteration analysis method based on Hurst coefficient. J. Basic Sci. Eng. 2009, 17, 32–39. [Google Scholar]
- Jiang, T.H.; Deng, L.T. Some problems in estimating a Hurst exponent-a case study of applicatings to climatic change. Sci. Geogr. Sin. 2004, 24, 177–182. [Google Scholar]
- Wang, G.-G.; Zhou, K.; Sun, L.; Qian, Y.-F.; Li, X.-M. Study on the vegetation dynamic change and R/S analysis in the past ten years in Xinjiang. Remote Sens. Technol. Appl. 2011, 25, 84–90. [Google Scholar]
- Yan, E.P.; Lin, H.; Dang, Y.F.; Xia, C.Z. The spatiotemporal changes of vegetation cover in Beijing-Tianjin sandstorm source control region during 2000–2012. Acta Ecol. Sin. 2014, 34, 5007–5020. [Google Scholar]
- Cannell, M.G.R.; Thornley, J.H.M. Modelling the components of plant respiration: Some guiding principles. Ann. Bot. 2000, 85, 45–54. [Google Scholar] [CrossRef]
- Gifford, R.M. Plant respiration in productivity models: Conceptualisation, representation and issues for global terrestrial carbon-cycle research. Funct. Plant Biol. 2003, 30, 171–186. [Google Scholar] [CrossRef]
- Ogawa, K. Mathematical analysis of change in forest carbon use efficiency with stand development: A case study on Abies veitchii Lindl. Ecol. Model. 2009, 220, 1419–1424. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, G.; Xue, B.; Yinglan, A. Changes in vegetation cover and its influencing factors in the inner Mongolia reach of the yellow river basin from 2001 to 2018. Environ. Res. 2022, 215, 114253. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, L.; Wang, W.; Cao, R.; Zhang, Y.; Shen, W. Spatio-temporal analysis of vegetation variation in the Yellow River Basin. Ecol. Indic. 2015, 51, 117–126. [Google Scholar] [CrossRef]
- Zhang, Q.; Lu, J.; Xu, X.; Ren, X.; Wang, J.; Chai, X.; Wang, W. Spatial and Temporal Patterns of Carbon and Water Use Efficiency on the Loess Plateau and Their Influencing Factors. Land 2022, 12, 77. [Google Scholar] [CrossRef]
- Piao, S.; Luyssaert, S.; Ciais, P.; Janssens, I.A.; Chen, A.; Cao, C.; Fang, J.; Friedlingstein, P.; Luo, Y.; Wang, S. Forest annual carbon cost: A global-scale analysis of autotrophic respiretion. Ecology 2010, 91, 652–661. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xu, M.; Chen, H.; Adams, J. Global pattern of NPP to GPP ratio derived from MODIS data: Effects of ecosystem type, geographical location and climate. Glob. Ecol. Biogeogr. 2009, 18, 280–290. [Google Scholar] [CrossRef]
- Lieth, H. Modeling the primary productivity of the world. In Primary Productivity of the Biosphere; Springer: Berlin/Heidelberg, Germany, 1975; pp. 237–263. [Google Scholar]
- Lieth, H. Primary productivity in ecosystems: Comparative analysis of global patterns. In Unifying Concepts in Ecology; van Dobben, W.H., Lowe-McConnell, R.H., Eds.; Publishers and Wageningen Center for Agricultural Publishing and Documentation: The Hague, The Netherlands, 1974; pp. 300–321. [Google Scholar]
- Canadell, J.G.; Mooney, H.A. Biological and ecological dimensions of global environmental change. In Encyclopedia of Global Environmental Change; John Wiley: Chichester, UK, 2002; pp. 1–9. [Google Scholar]
- Chen, Z.; Yu, G.; Wang, Q. Ecosystem carbon use efficiency in China: Variation and influence factors. Ecol. Indic. 2018, 90, 316–323. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Tribuzy, E.S.; Toledo, L.C.; Crispim, B.F.; Higuchi, N.; Santos, J.D.; Araújo, A.C.; Kruijt, B.; Nobre, A.D. Respiration from a tropical forest ecosystem: Partitioning of sources and low carbon use efficiency. Ecol. Appl. 2004, 14, 72–88. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, G.; Yang, J.; Wimberly, M.C.; Zhang, X.; Tao, J.; Jiang, Y.; Zhu, J. Climate-driven global changes in carbon use efficiency. Glob. Ecol. Biogeogr. 2014, 23, 144–155. [Google Scholar] [CrossRef]
- Bradford, M.A.; Crowther, T.W. Carbon use efficiency and storage in terrestrial ecosystems. New Phytol. 2013, 199, 7–9. [Google Scholar] [CrossRef]
- Crowther, T.W.; Bradford, M.A. Thermal acclimation in widespread heterotrophic soil microbes. Ecol. Lett. 2013, 16, 469–477. [Google Scholar] [CrossRef]
- Van Iersel, M.W. Carbon use efficiency depends on growth respiration, maintenance respiration, and relative growth rate. A case study with lettuce. Plant Cell Environ. 2003, 26, 1441–1449. [Google Scholar] [CrossRef]
- Gang, C.; Zhang, Y.; Guo, L.; Gao, X.; Peng, S.; Chen, M.; Wen, Z. Drought-induced carbon and water use efficiency responses in dryland vegetation of northern China. Front. Plant Sci. 2019, 10, 224. [Google Scholar] [CrossRef] [PubMed]
- Amthor, J.S. The McCree–de Wit–Penning de Vries–Thornley respiration paradigms: 30 years later. Ann. Bot. 2000, 86, 1–20. [Google Scholar] [CrossRef]
- Street, L.E.; Subke, J.A.; Sommerkorn, M.; Sloan, V.; Ducrotoy, H.; Phoenix, G.K.; Williams, M. The role of mosses in carbon uptake and partitioning in arctic vegetation. New Phytol. 2013, 199, 163–175. [Google Scholar] [CrossRef]
- Amthor, J.S. Respiration and Crop Productivity; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Huang, X.; Xiao, J.; Wang, X.; Ma, M. Improving the global MODIS GPP model by optimizing parameters with FLUXNET data. Agric. For. Meteorol. 2021, 300, 108314. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Liu, Z.; Che, M.; Chen, B. Evaluating parameter adjustment in the MODIS gross primary production algorithm based on eddy covariance tower measurements. Remote Sens. 2014, 6, 3321–3348. [Google Scholar] [CrossRef]
- Lin, X.; Chen, B.; Chen, J.; Zhang, H.; Sun, S.; Xu, G.; Guo, L.; Ge, M.; Qu, J.; Li, L.; et al. Seasonal fluctuations of photosynthetic parameters for light use efficiency models and the impacts on gross primary production estimation. Agric. For. Meteorol. 2017, 236, 22–35. [Google Scholar] [CrossRef]
- Dong, H.; Guo, H.; Yuan, Y. Estimation of Terrestrial Ecosystem GPP Based on Sun-induced Chlorophyll Fluorescence. Trans. Chin. Soc. Agric. Mach. 2019, 50, 205–211. [Google Scholar]
- Liu, X.; Liu, Z.; Liu, L.; Lu, X.; Chen, J.; Du, S.; Zou, C. Modelling the influence of incident radiation on the SIF-based GPP estimation for maize. Agric. For. Meteorol. 2021, 307, 108522. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, X.; Du, S.; Liu, X. Research Progress and Prospective of Global Satellite-based Solar-induced Chlorophyll Fluorescence Products. Remote Sens. Technol. Appl. 2021, 36, 1044–1056. [Google Scholar]
- Qiu, R.; Han, G.; Ma, X.; Xu, H.; Shi, T.; Zhang, M.A. comparison of OCO-2 SIF, MODIS GPP, and GOSIF data from gross primary production (GPP) estimation and seasonal cycles in North America. Remote Sens. 2020, 12, 258. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, T.; Kan, X.; Wang, J.; Tian, W. Spatial and temporal variation analysis of snow cover using MODIS over Qinghai-Tibetan Plateau during 2003–2014. J. Indian Soc. Remote Sens. 2017, 45, 887–897. [Google Scholar] [CrossRef]
- Huang, X.; Deng, J.; Wang, W.; Feng, Q.; Liang, T. Impact of climate and elevation on snow cover using integrated remote sensing snow products in Tibetan Plateau. Remote Sens. Environ. 2017, 190, 274–288. [Google Scholar] [CrossRef]
- Duan, H.; Xue, X.; Wang, T.; Kang, W.; Liao, J.; Liu, S. Spatial and temporal differences in alpine meadow, alpine steppe and all vegetation of the Qinghai-Tibetan Plateau and their responses to climate change. Remote Sens. 2021, 13, 669. [Google Scholar] [CrossRef]
- Onaindia, M.; de Manuel, B.F.; Madariaga, I.; Rodríguez-Loinaz, G. Co-benefits and trade-offs between biodiversity, carbon storage and water flow regulation. For. Ecol. Manag. 2013, 289, 1–9. [Google Scholar] [CrossRef]
- Xiang, W.; Xu, L.; Lei, P.; Ouyang, S.; Deng, X.; Chen, L.; Zeng, Y.; Hu, Y.; Zhao, Z.; Wu, H.; et al. Rotation age extension synergistically increases ecosystem carbon storage and timber production of Chinese fir plantations in southern China. J. Environ. Manag. 2022, 317, 115426. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Yu, Q.; Yang, Z.; Peng, A.; Zeng, Y.; Liu, W.; Zhao, J.; Yang, D. Spatio-Temporal Dynamic Characteristics of Carbon Use Efficiency in a Virgin Forest Area of Southeast Tibet. Remote Sens. 2023, 15, 2382. https://doi.org/10.3390/rs15092382
Yang Z, Yu Q, Yang Z, Peng A, Zeng Y, Liu W, Zhao J, Yang D. Spatio-Temporal Dynamic Characteristics of Carbon Use Efficiency in a Virgin Forest Area of Southeast Tibet. Remote Sensing. 2023; 15(9):2382. https://doi.org/10.3390/rs15092382
Chicago/Turabian StyleYang, Ziyan, Qiang Yu, Ziyu Yang, Anchen Peng, Yufan Zeng, Wei Liu, Jikai Zhao, and Di Yang. 2023. "Spatio-Temporal Dynamic Characteristics of Carbon Use Efficiency in a Virgin Forest Area of Southeast Tibet" Remote Sensing 15, no. 9: 2382. https://doi.org/10.3390/rs15092382
APA StyleYang, Z., Yu, Q., Yang, Z., Peng, A., Zeng, Y., Liu, W., Zhao, J., & Yang, D. (2023). Spatio-Temporal Dynamic Characteristics of Carbon Use Efficiency in a Virgin Forest Area of Southeast Tibet. Remote Sensing, 15(9), 2382. https://doi.org/10.3390/rs15092382






