Simple Summary
Excessive use of groundwater resources in the Central Valley in California has led to major land sinking over the years. In this study, we rely on satellite imagery to monitor and assess the extent of this sinking. Specifically, we use images from a satellite that emits microwaves which allows us to directly obtain the deformation at a specific time. Then, we apply a machine learning algorithm to the resulting data in an attempt to effectively predict short-term future deformation. We find that the algorithm applied has a low error when compared to the actual data. This shows that machine learning algorithms could be incorporated into models that assess potential hazards associated with land sinking.
Abstract
Land subsidence caused by excessive groundwater pumping in Central Valley, California, is a major issue that has several negative impacts such as reduced aquifer storage and damaged infrastructures which, in turn, produce an economic loss due to the high reliance on crop production. This is why it is of utmost importance to routinely monitor and assess the surface deformation occurring. Two main goals that this paper attempts to accomplish are deformation characterization and deformation prediction. The first goal is realized through the use of Principal Component Analysis (PCA) applied to a series of Interferomtric Synthetic Aperture Radar (InSAR) images that produces eigenimages displaying the key characteristics of the subsidence. Water storage changes are also directly analyzed by the use of data from the Gravity Recovery and Climate Experiment (GRACE) twin satellites and the Global Land Data Assimilation System (GLDAS). The second goal is accomplished by building a Long Short-Term Memory (LSTM) model to predict short-term deformation after developing an InSAR time series using LiCSBAS, an open-source InSAR time series package. The model is applied to the city of Madera and produces better results than a baseline averaging model and a one dimensional convolutional neural network (CNN) based on a mean squared error metric showing the effectiveness of machine learning in deformation prediction as well as the potential for incorporation in hazard mitigation models. The model results can directly aid policy makers in determining the appropriate rate of groundwater withdrawal while maintaining the safety and well-being of the population as well as the aquifers’ integrity.
1. Introduction
One of the most detrimental effects associated with excessive groundwater pumping is land subsidence [1]. Altered topography, reduced aquifer storages, and fractured infrastructures are one of the many consequences that follow land subsidence [2]. The removal of groundwater causes irreversible compaction in the aquifer leading to permanent land subsidence [3]. It is for these reasons that monitoring this phenomenon is important especially in the Central Valley which is a major agricultural region that accounts for 8% of the U.S. agriculture output [4].
Relying on traditional geodetic techniques, however, may prove unfruitful given their point-based measurements [5]. Since land subsidence in the Central Valley occurs over a large area [6], satellite geodesy is the more appropriate approach. In this study, the primary dataset that we rely on is interferometric synthetic aperture radar (InSAR). This geodetic technique is a method of combining two synthetic aperture radar (SAR) images over the same area that are temporally-separated resulting in a map displaying the deformation in the satellite’s line-of-sight (LOS) [7]. A brief summary of how InSAR works will be given in the Principal Component Analysis (PCA) section, but, for a more in-depth explanation of InSAR functionality, there are several articles and studies that rigorously discuss it [8,9]. Additionally, another form of satellite geodesy is employed using the Gravity Recovery and Climate Experiment (GRACE) along with the Follow-On (GRACE-FO) which is almost identical to its predecessor and launched in May 2018 after GRACE’s mission ended in October 2017 [10]. GRACE and GRACE-FO are twin satellites that are able to detect gravitational anomalies on Earth and, through repetitive orbits, are able to translate those anomalies into changes in mass [11]. In fact, this mass change can be directly linked to changes in Earth’s water distribution which allows the study of the terrestrial water cycle, sea level change, and even groundwater storage [12]. Similarly, a brief explanation of how GRACE/GRACE-FO works will be provided in the GRACE/GRACE-FO section, but, for a comprehensive discussion of GRACE functionality, the reader is referred to Kornfeld et al. [13].
The depletion of groundwater storage in the Central Valley along with the subsequent land subsidence is well-documented in the literature. For example, Famiglietti et al. [14] used GRACE data from 2003 to 2010 to measure the water loss rate that amounted to 30 km for that time period most of which was found to be attributed to groundwater loss specifically. Moreover, the groundwater loss rate that they computed using GRACE data was in agreement with rates found by Faunt et al. [15] who employed a hydrologic-based model instead. GRACE data have also been used over the Central Valley to create a drought index which is calculated using groundwater storage deviations [16]. The index exhibited a high correlation with standardized drought indices that are based on in-situ measurements and was able to effectively characterize groundwater drought. This showed the potential of remote sensing techniques in understanding hydrologic changes especially in areas with a lack of in-situ groundwater measurements.
The associated land subsidence started in the mid-1920’s [17], and, over the years, several researchers have attempted to characterize this deformation through different techniques [18,19,20,21,22]. To start with, traditional techniques such as leveling have been used to directly measure subsidence in the Central Valley and map out that deformation to some degree of certainty [17]. However, more recently, given the large areal nature of the problem, remote sensing techniques have been favored as a means of observing the bigger picture of subsidence [23,24,25]. In fact, since the launch of Sentinel-1, InSAR has been extensively used as a means to monitor land subsidence all around the world due to the large data availability. For example, InSAR analysis was performed on Las Vegas in order to understand the deformation that occurred between the years 1992 and 1997 [26]. It was found that draining aquifers was the leading cause for the observed deformation and, thus, showed that InSAR is able to acquire spatial and temporal information regarding land subsidence and aquifer systems which can immensely assist groundwater management models. Moreover, Chaussard et al. [27] utilize InSAR in order to characterize the subsidence over all of Central Mexico as opposed to the leveling surveys that are available only in Mexico City. After applying a time series InSAR analysis, they were able to identify a total of 21 areas that are suffering from land subsidence. The cause is similar to the Central Valley where groundwater is being excessively pumped to meet, in this case, 70% of the water needs of the inhabitants [27]. Finally, InSAR has also been applied to Mashhad Valley in northeast Iran where subsidence is also occurring due to excessive overdrafting of the groundwater storage [28]. Deformation calculated from the InSAR data showed agreement with the accurate leveling data as well as Global Positioning System (GPS) data. InSAR was also able to show the spatial distribution of the deformation along with the fault that governed its spatial extent [28].
Machine Learning (ML) algorithms have been on the rise in the past decade, and researchers from all different fields have been applying them to their work due to their efficiency in classification, pattern recognition, and prediction [29,30,31,32]. Unsurprisingly, geophysicists have also begun to apply ML algorithms with the intent of extracting even more valuable information from the available InSAR data. To begin with, Brengman et al. [33] applied a convolutional neural network with a synthetic InSAR dataset and trained it to identify the type of deformation as well as the location of the deformation. After training the network and applying it to a real InSAR dataset, an accuracy of 85.22% was achieved [33]. Similarly, a convolutional neural network was used to correctly distinguish volcanic surface deformation from atmospheric artifacts [34]. The network performed efficiently for large deformation which proves great potential for incorporation in automated volcanic InSAR processing and alert systems. Additionally, a susceptibility map was created from InSAR datasets using a multilayer perceptron (MLP) as well as ensemble machine learning algorithms over Jakarta, Indonesia [35]. The map showed a high prediction accuracy of 81.1% showing a promising use in hazard mitigation models associated with land subsidence.
Long short-term memory (LSTM) models have proved highly efficient when it comes to sequence prediction problems. They have been successfully applied in weather forecasting where results were shown to be on par with other state-of-the-art methods [36]. Furthermore, LSTMs are widely used in financial markets to predict fluctuating stock prices where they are able to remarkably beat several baseline measures [37,38,39].
Efforts to incorporate LSTMs with InSAR data to specifically predict land subsidence deformation have begun in the last couple of years. Chen et al. [40] applied LSTM to InSAR deformation data over the Beijing Capital International Airport and found the model to perform better than other baseline models such as MLP and recurrent neural networks (RNNs) and concluded that LSTMs show promise for adoption in early warning systems. Liu et al. [41] worked on applying a heterogeneous version of the LSTM algorithm over Cangzhou, China and discovered that it was able to effectively capture the spatial pattern of the deformation and shows great accuracy despite lacking relevant hydrological data. The model built is able to be extended to other areas as well by means of changing its different parameters [41]. Similar results were found by Li et al. [42] who developed a geographically weighted LSTM to predict land subsidence in the northeast Beijing Plain area that was capable of accurately modeling the temporal evolution of land subsidence and showed potential for use in conjunction with physically-based models especially when hydrogeological parameters are missing. To the authors’ knowledge, LSTM applied to predict land subsidence in the Central Valley has not been performed yet.
The purpose of this paper is to characterize and predict land subsidence deformation that is occurring in the Central Valley due to excessive groundwater pumping. First, we conduct a principal component analysis (PCA) on a series of InSAR images and obtain eigenimages displaying the spatial distribution of the associated deformation. Additionally, terrestrial water storage (TWS) and groundwater storage (GS) changes are visualized and analyzed using data from the GRACE twin satellites. Finally, an LSTM model is built and applied to the city of Madera and its results are compared to a baseline model and a one dimensional convolutional neural network (CNN) with the mean squared error being the main error metric used.
2. Materials and Methods
2.1. Area of Study
The study area where our analysis was performed is shown in Figure 1. The area covers a section of the Central Valley called the San Joaquin Valley which is California’s biggest agricultural hub and a major contributor to the U.S. food supply. It is bounded by the Sierra Nevada on the East, the Tehachapi Mountains on the South, and the Coast Ranges on the West [43]. The climate is semi-arid to arid with hot and dry summer months and cool and rainy winter months [44]. The region receives an average of 127–406 mm of annual rainfall [45]. There are nine dammed rivers (Fresno, Tuolumne, Kings, Stanislaus, San Joaquin, Merced, Kaweah, Kern, and Tule) that drain the Sierra Nevada, and their discharge is used for irrigation and public water supply [46]. Prior to agricultural development, groundwater was mainly charged through precipitation and streams lying on the valley margins, and it was discharged at the San Joaquin River in the North leaving the valley through the Sacramento-San Joaquin Delta [47]. After the development of groundwater systems for agricultural purposes, charge and discharge of groundwater primarily happens through irrigation return flow and groundwater withdrawal respectively [47]. Farmers have increasingly relied on groundwater pumping to meet their irrigation needs especially during the recent droughts [48] causing an increasing rate of induced land subsidence [49]. Given the low amount of ground-based measurements in relation to the large areal nature of land subsidence [50], we resort to remote sensing, specifically InSAR, to evaluate and characterize the problem. The flatness of the valley as well as the fact that the deformation is mostly vertical make InSAR a good candidate for use in analysis.
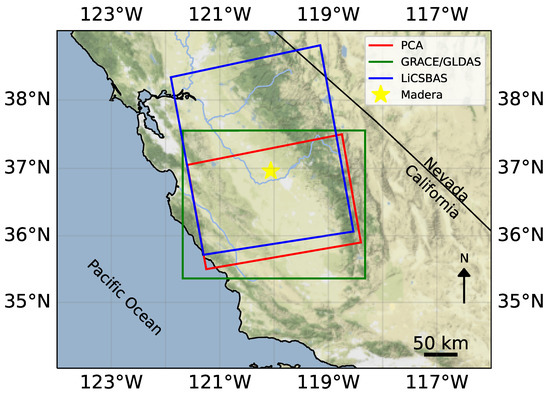
Figure 1.
Map showing the different areas of study. Red indicates the area where PCA was applied. Green indicates the area where the GRACE/GLDAS data were taken from. Blue indicates the area where the LiCSBAS time series analysis was applied. The yellow star pinpoints Madera’s location.
2.2. Principal Component Analysis
PCA is a method that condenses the main characteristics of the specific dataset which, in this case, is a series of InSAR images. This goal is accomplished by computing a set of linearly independent vectors such that the first vector captures the most variance in the dataset, while the second captures less variance, and the third even less up until the last vector that captures the least amount of variance [51]. Mathematically, this can be shown to be equivalent to finding the eigenvectors of the covariance matrix of the dataset:
where denotes the covariance matrix of the dataset X whose elements are the data variables. m is the dimensionality of the dataset. For example, for the case of , it is easy to visualize the dataset because we can project it on a 2-dimensional space, but for higher m values, as is our case working with high-dimensional images, it becomes much harder to visualize. The variances and covariances can be computed as such:
where and denote the associated means of and respectively. The eigenvectors V and eigenvalues can then be solved for.
When applied to images, PCA is capable of producing eigenimages through a simple reshaping of eigenvectors. Additionally, since the eigenvectors computed capture the most amount of variance in the dataset, the associated eigenimages will capture the leading and most important characteristics of the dataset [52]. In the case of applying PCA to InSAR images over the Central Valley, the eigenimages will reveal the key features of the deformation allowing the characterization of it.
Our area of study for PCA is shown in Figure 1. We form 48 interferograms (see Table 1) using Alaska Satellite Facility’s HyP3 which is a SAR image processor that is capable of producing InSAR images rapidly for analysis [53]. We use a reference SAR image that was taken on 4 May 2019 with an absolute orbit number of 16088, and all images used have an ascending flight path with 137 and 115 as the respective path and track number.

Table 1.
Secondary SAR images used for interferometric analysis using HyP3 software (InSAR product processed by ASF DAAC HyP3 2022 using GAMMA software. Contains modified Copernicus Sentinel data 2020, processed by ESA.)
In order to visualize the deformation that is occurring, we use the line-of-sight (LOS) displacement images for our analysis. We downsample the images from 2933 × 3683 to a more manageable 98 × 123 by running a set block size of 30 × 30 over the image pixels and taking the average of the pixel values in each block. This reduction in resolution will help accelerate the PCA algorithm while maintaining the same general features of the deformation observed in the images. After downsampling, each image is flattened into an array and stacked to form an input data matrix. This matrix is then fed into the PCA algorithm using the scikit-learn python package [54].
2.3. GRACE/GRACE-FO and GLDAS Data
We also utilize data from the GRACE twin satellites in order to assess and visualize the change in groundwater storage over the Central Valley. These satellites continuously orbit the Earth mapping its entire gravity field on a monthly basis and, as mentioned earlier, are designed to identify gravitational anomalies on Earth. They do so by measuring the minute changes to their 220 km separation which occur as the satellites pass over areas with a greater or weaker gravitational pull. A high-frequency microwave pulse goes back and forth between the two satellites, and the time it takes for the pulse to be received back to the satellite it was emitted from is used to calculate that minute change in distance. This change in distance is used to solve for the spherical harmonic coefficients of the exterior potential gravity field of Earth which is then transformed into a monthly mass change [55]. Since most monthly mass changes are attributed to changes in water storage, the unit of measurement of that mass change is in water equivalent height or water equivalent thickness (on the order of centimeters) which can be visualized as an increase or decrease of a thin layer of water thickness near the Earth’s surface. On the other hand, GLDAS is a system that combines satellite-based data and ground-based data through the use of various data assimilation techniques to obtain different land surface states and fluxes [56].
2.4. InSAR Time Series and Baseline Model
Forming an InSAR time series is accomplished using LiCSBAS [57,58,59] which is an open-source python package that uses InSAR products processed by an automatic InSAR processor called LiCSAR. These products are publicly available on the COMET-LiCS (Centre for the Observation and Modelling of Earthquakes, Volcanoes and Tectonics-Looking inside the Continents from Space) web portal [60,61]. We run LiCSBAS for a frame ID of 137A_05266_171717 using the default parameters from 2014 to 2021. After the interferograms are filtered through and the network is built, the small baseline inversion algorithm is applied producing a map of displacement time series for which the mean displacement velocity can be derived by least squares for each pixel resulting in a velocity map. This map is shown in Figure 2 where it is possible to see the overall subsidence occurring given the fact that most areas have a negative velocity.
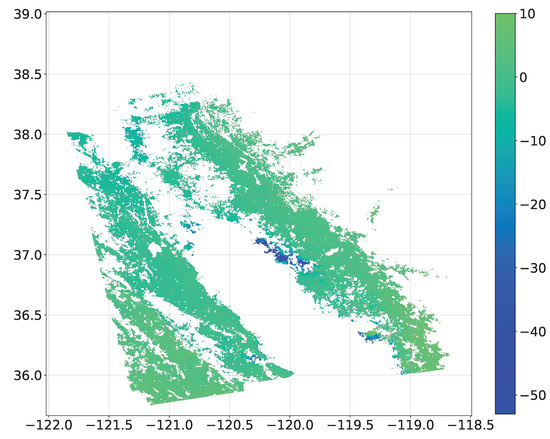
Figure 2.
Velocity map of the Central Valley formed using LiCSBAS (2014-2021). Color indicates the speed in units of mm/year. White areas indicate no value or masked value according to the default parameters of LiCSBAS.
Specifically, we divert our attention to the area in blue that is experiencing one of the most subsidence which is the city of Madera.
Line-of-sight displacement time series values over Madera are generally similar, so we take 121 displacement time series in a 11 × 11 grid over the area of Madera covering roughly 1 km and average them out into one time series. Additionally, since the time series values are not exactly temporally equidistant, linear interpolation is used to regularize the dataset to an interval of 6 days. This value was chosen due to Sentinel-1’s 6-day repeat cycle. Then, we smooth the resulting dataset using an exponential moving average (EMA) based on the following equation:
where and denote the displacements and smoothed displacements time series respectively. is a smoothing coefficient that ranges from 0 to 1 where higher values indicate older displacements being discarded quicker. We choose in such a way so as to maintain the general features of the time series as well as disposing of the roughness of the dataset, and we end up using a value of 0.17. Results of the smoothing can be seen in the top plot of Figure 3.
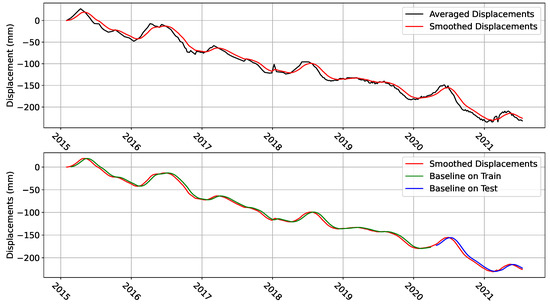
Figure 3.
Top plot shows the smoothed displacements compared to the averaged displacements after both have been regularized. Bottom plot shows the performance of the baseline model applied individually to the train and test datasets.
In preparation for applying the machine learning models on the dataset, we perform a train/test split with 80% of the data being used for training and the other 20% for testing. We also build a baseline model for predicting the deformation at the immediate next time step by averaging the previous 4 time steps. This is equivalent to looking at the deformation values in the last month and attempting to predict the future deformation in 6 days. Not only is the baseline model computationally efficient, but it also performs relatively well as can be seen in the bottom plot of Figure 3. In the context of this study, the primary purpose of the baseline model is to form a reference to which we can compare the machine learning models to. For this reason, we seek to quantify the performance of our models in predicting the value of deformation in the next time step using the mean squared error (MSE) metric as given by:
where and represent the actual smoothed displacements and the predicted displacements respectively with n being the number of data points being predicted.
2.5. CNN Model
Convolutional neural networks (CNNs) are generally applied in order to analyze two-dimensional images [62,63]. However, CNNs have also found great use in time series applications where they have been mainly utilized for classification or prediction purposes [64,65,66,67,68]. A more rigorous explanation of CNN functionality has been done by Albawi et al. [69], but typical CNN architectures mainly consist of three essential layers: convolutional, pooling, and fully connected layers [70]. The convolutional layer is the main layer that learns the different possible features of the dataset using kernels (filters) that run over the dataset in parts, while the pooling layer reduces the resolution of said features in order to achieve shift-invariance and reduce computational complexity [70,71]. Finally, a fully-connected layer combines all the features to come up with a reasonable classification or prediction [72].
We build the CNN architecture using TensorFlow [73] after normalizing the train and test datasets to a range of [0, 1] and splitting each into an input X and an output Y which correspond to an input of 4 values from the time series and an output of the 5th value sliding across the entire train and test dataset one time step at a time with no gaps. The model consists of a convolutional layer with 64 filters of size 3 and a rectified linear activation unit (ReLU). The output is then downsampled using a MaxPooling layer of size 2. The result of that is then flattened and connected to a Dense layer of size 50 with a ReLU activation function, and, finally, the last layer is a Dense layer of size 1. We train the model with a batch size of 90 over 5000 epochs and perform predictions over the train and test set.
2.6. LSTM Model
Long short-term memory (LSTM) networks are a type of recurrent neural networks that are capable of retaining critical information regarding the dataset over long time intervals making them ideal for processing and predicting time series data. This is accomplished through the use of gates that govern the flow of information into and out of the LSTM cell shown in Figure 4.
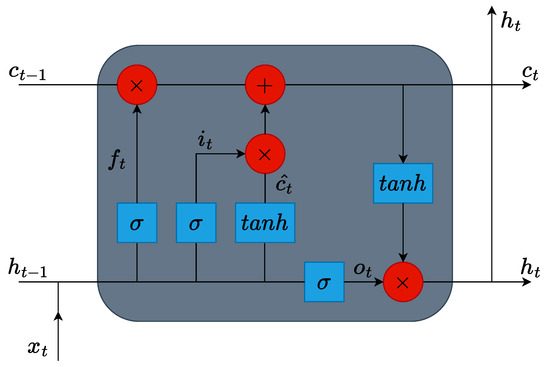
Figure 4.
LSTM cell showing the different connections within.
Specifically, traditional LSTMs have 3 gates, namely a forget gate, an input gate, and an output gate. The flow of information through these gates is governed by the following equations [74]:
where , , , and represent the forget, input, output, and cell activation vectors respectively. and are the cell state and hidden state vectors. W, U, and b are the weights of the input , weights of the hidden states , and biases for the different connections in the cell as indicated by the corresponding subscript. and are the sigmoid and hyperbolic tangent activation functions used in the LSTM cell. * denotes an element-wise multiplication.
In order to implement the LSTM model to our dataset, we use TensorFlow, an open-source python package built for machine learning [73]. We start off by normalizing our train and test datasets to a range of and splitting each into an input X and an output Y in a similar way to the CNN model. The input X is then reshaped into a 3D tensor to serve as the input layer to the LSTM layer that has an output dimensionality of 5. The next layer in the model is a Dense layer with an output dimensionality of 1. This is equivalent to a node that is fully connected to all the nodes in the previous layer and whose output is a scalar serving as the output layer which will be the prediction of that 5th value. We train the model with a batch size of 90 over 5000 epochs and perform predictions over the train and test set.
3. Results
3.1. PCA Study
In order to better understand the significance of the principal components, it is important to compute the fraction of variance captured by each principal component which can be found using [51]:
where n denotes the number of principal components.
The distribution of explained variance for the first few principal components is shown in Table 2.

Table 2.
Table showing the decreasing percentage of explained variance for the first 6 principal components.
We can see that the first principal component is able to explain around 67% of the variance in the dataset while the second component explains around 13% of the variance. Subsequent principal components account for less than 5% each. Theoretically, one would be able to re-project the dataset using the first two principal components without a great loss of information from the dataset. That is usually done for the purposes of dimensionality reduction. However, for our purposes, we seek to visualize and characterize the deformation, so we display the first two principal components after reshaping them in Figure 5.
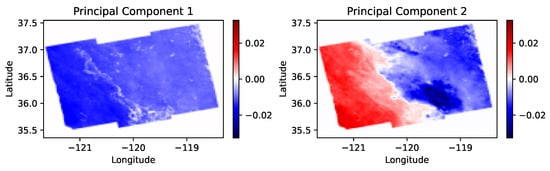
Figure 5.
The first 2 principal components from the PCA study. Colors represent LOS displacement in meters.
Most notably, the first principal component displays an all-negative displacement which is in line with what is expected given the subsidence occurring in the Central Valley. Additionally, the second principal component reveals a couple of concentrated regions of subsidence around the Tulare-Corcoran region as well as a streak of subsidence covering the city of Madera. Moreover, the region showing positive displacement in the second principal component falls outside the Central Valley to the East. Taking the weights of the principal components into account, this study not only visualizes the deformation taking place in the central valley, but it also identifies key areas that have experienced an even greater deformation over the study period.
It should be noted that the actual values of subsidence that the principal components present are not to be taken as an absolute measure of deformation namely because of the fact that the interferograms used did not share the same exact reference point. This study aims to give a rough preliminary analysis of the deformation occurring in the Central Valley using PCA as a way of visualizing and characterizing the key features of the subsidence.
3.2. GRACE/GLDAS Study
Using the GRACE Data Analysis Tool (DAT) by the National Aeronautics and Space Administration (NASA), we obtain the monthly water equivalent thickness data over the specified region indicated in Figure 1 [75]. These data have been processed by the Jet Propulsion Laboratory (JPL) at NASA and allow us to plot a time series showing the fluctuation of the water equivalent thickness over the period of April 2002 to June 2022 [76]. Additionally, we plot a line of best fit using least squares method in order to visualize the trend spanning that time period. The result is shown in Figure 6 where is taken to be the start of the dataset in April 2002.
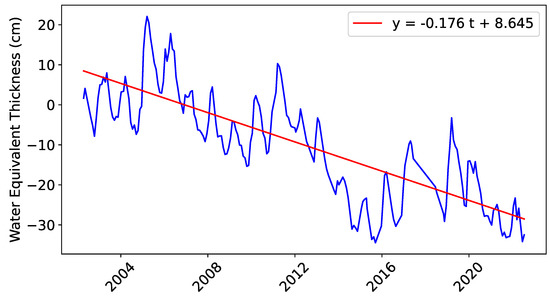
Figure 6.
Time−series of water equivalent thickness (Land: GRACE, GRACE−FO JPL) over the period of April 2002 to July 2022. Fitted line is included to visualize the trend ( defined at the start of the dataset).
It is clear that, over the years, there has been a decline in the water equivalent thickness over the Central Valley. This thickness can be thought of as the summation of all different sources of terrestrial water such as soil moisture, rivers, lakes, snow, ice, and groundwater. In order to isolate and assess groundwater levels in the Central Valley, we resort to data provided by the Global Land Data Assimilation System (GLDAS).
Groundwater storage is estimated after subtracting soil moisture, snow water equivalent, and canopy interception from the total terrestrial water storage obtained by GRACE. GLDAS data, specifically groundwater storage data [77], are accessed through Giovanni which is a web interface that allows access to many geophysical parameters for purposes of display as well as analysis [78]. We plot the groundwater time series that is averaged over the area of study in a similar fashion to the terrestrial water one as shown in Figure 7.
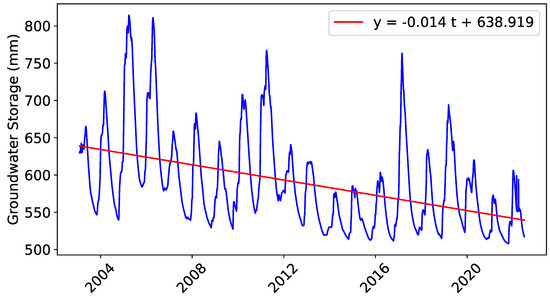
Figure 7.
Area−averaged groundwater storage time series over the period of February 2003 to July 2022. Fitted line is included to visualize the trend ( defined at the start of the dataset).
The fitted line correspondingly indicates a steady decrease in groundwater storage in the Central Valley over the years where is taken to be at the start of the dataset. Moreover, we build a time averaged map where each grid’s value is linearly averaged over time. Additionally, we perform a smoothing to the map’s values using matplotlib’s contourf function [79]. Results are displayed in Figure 8 where redder areas indicate lower values of groundwater storage and bluer areas indicate higher values.
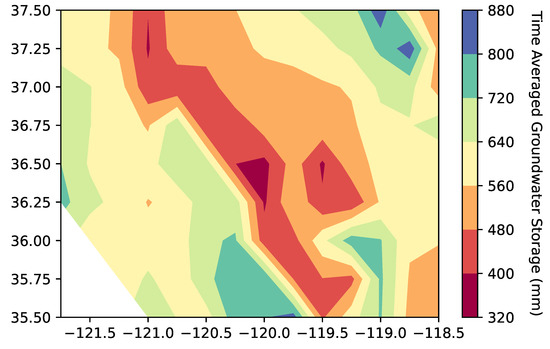
Figure 8.
Time averaged map of groundwater storage data over the period of February 2003 to July 2022.
Using the map, we are able to see that the red areas mainly run down the Central Valley showing how groundwater storage has been getting depleted over the years.
3.3. Machine Learning Study
We find that, for the baseline model, the MSE values are 11.89 and 19.85 for the train and test sets respectively. The top plot of Figure 9 shows the results of the LSTM prediction, while Figure 10 shows the results of the CNN prediction. When compared to the original smoothed displacements, one can see how effective both models are at predicting the next value of deformation due to the strong overlap with the smoothed displacements.
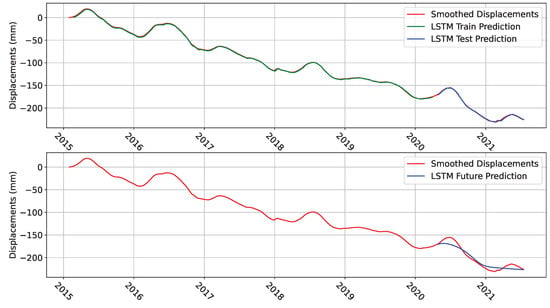
Figure 9.
Top plot shows LSTM prediction performance over the train and test datasets. Bottom plot shows LSTM future prediction performance when applied to the test set.
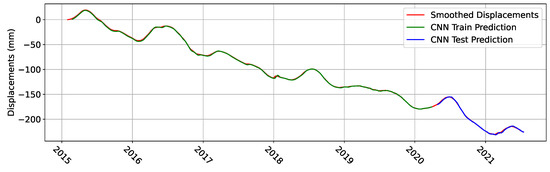
Figure 10.
CNN prediction performance over the train and test datasets.
Given the stochastic nature of the machine learning models, in order to quantify their performance, we run each model 20 times and average out the errors achieving a 0.47 ± 0.13 and 0.72 ± 0.15 MSE for the train and test sets of the LSTM model and a 0.64 ± 0.12 and 0.86 ± 0.15 MSE for the train and tests sets of the CNN model. The errors of all the models are shown in Table 3.

Table 3.
Table showing the errors of the different models built.
This indicates that the LSTM model performed much better than the baseline averaging model that was implemented previously as well as the CNN model.
It is important to note that the models are only being given true values at every prediction step, so the plots only show the performance of the models at predicting the next value given the last four true values of deformation. That is why, in the bottom plot of Figure 9, we attempt to make true future predictions by using the predictions of the best model, the LSTM model, as input for the next prediction, and we apply this method to the test set. Due to the compounding error at each time step, the prediction diverges rapidly from the expected true deformation. Although the prediction somewhat captures the shape of the deformation, the deviation from the smoothed displacements indicates a high error, and, if taken to even more time steps into the future, the resulting error would be even larger. This shows that, while the LSTM model excels at short-term predictions, care must be taken when attempting to predict deformations over the long-term.
4. Discussion
4.1. Eigenimages Analysis and GRACE Findings
Previous studies aimed at characterizing subsidence in the Central Valley have also found that the counties of Madera and Tulare have been experiencing subsidence over the years with maximums detected in 2010 and 2017 respectively due to the 2007–2010 and 2012–2017 droughts as well as the large density of groundwater wells in these areas [48]. The dominant agricultural crops in these regions are almonds in Madera county and fruits and nuts in Tulare county which ranks them in the highest water demand areas [48]. This high water demand results in a decreasing water table as more and more groundwater is pumped as evidenced by the GRACE plots. In our study, we used PCA to analyze 49 InSAR images and were able to produce eigenimages revealing the key areas experiencing land subsidence due to groundwater pumping. A similar approach has been taken before where Wang et al. used PCA on InSAR to identify coastal subsidence caused by brine mining [80]. Other studies have used PCA as a means to enhance InSAR data accuracy, such as Chen et al. who monitored deformation over Xuzhou, China after applying a PCA-based correction to the InSAR data [81]. However, to the authors’ best knowledge, PCA applied to identify key regions undergoing subsidence due to groundwater pumping in the Central Valley using InSAR data has not been performed yet.
4.2. Machine Learning Findings
Predicting deformation values using machine learning algorithms applied to InSAR data has been performed previously. For example, Chen et al. found that LSTM performed better than a multi-layer perceptron (MLP) and a recurrent neural network (RNN) at predicting future deformation values over the Beijing Capital International Airport using a root mean square error metric [40]. A similar approach was taken by Radman et al. who predicted subsidence over Lake Urmia, Iran by combining the forecasts of LSTM, CNN, and MLP to create a weighted ensemble after finding out that, individually, each model had its own strengths and weaknesses when applied to the InSAR data over that specific area [82]. In the Central Valley, LSTM combined with InSAR has only been used to estimate geologic composition [83]. In our study, we find that the LSTM machine learning model proves beneficial for predicting subsidence values when applied to InSAR data over the Central Valley, and it performs better than a baseline averaging model and a one-dimensional CNN model.
However, one must note that these LSTM results can be deceiving since the model could be achieving these low values of error by simply taking the deformation value at the previous time step and using that as the prediction for the next time step (persistence model) in which case, it would be unfruitful to resort to the complexity of the LSTM model. It is for this reason, that we test our model on the time-differenced data as well. Attempting to predict the differences in values instead of the values themselves is a stronger testament to the the model’s predictive potential.
In order to do this, we start by time-differencing our dataset using:
where is the time-differenced displacement. Then, we apply the same model in the same fashion as before. We display the results in Figure 11 where it can be seen that the scattered points follow a line on a predicted vs. actual value plot.
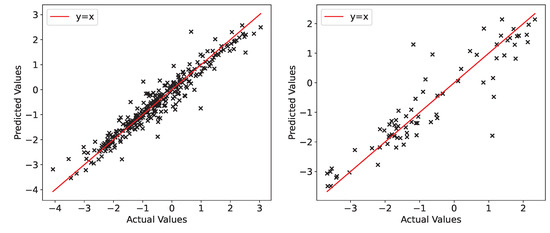
Figure 11.
Left plot shows the train scatter while the right plot shows the test scatter.
A model that is mimicking a persistence model would show a horizontal line with a value of 0 on this scatter plot. This shows that our model is doing more than just taking the last time step’s value and establishes its predicting power.
Future work with the LSTM model could be aimed at better optimizing the model’s parameters which would further decrease errors as well as make future predictions less prone to the compounding error effect. Additionally, another possibility to further understand the state of the Central Valley as it undergoes land subsidence is to incorporate more than just the deformation as observed through InSAR such as ground-based measurements as well. These data could then be used to train a multi-feature model that would be better equipped at predicting the ground state in the Central Valley. Moreover, one could also look at different machine learning techniques and see how they hold up against each other in terms of future deformation prediction.
4.3. Limitations
Given the fact that satellite data were the main dataset relied on in this study, there are some limitations to consider. To start with, InSAR is prone to errors from different sources such as topographical, orbital, tropospheric, as well as random noise [84]. Errors are reduced when a time series approach with filters is taken but not entirely. For example, tropospheric errors remain and can interfere with the true deformation signal. This error can be reduced by using atmospheric data from sources such as the Generic Atmospheric Correction Online Service for InSAR (GACOS). Moreover, machine learning algorithms generally perform better the more data there is to train on. As Sentinel-1 continues to orbit and capture more SAR images at a regularized 6-day interval, the better-equipped machine learning algorithms will be at predicting deformation values while also eliminating the need for manual interval regularization. Additionally, there are three different processing centers that provide slightly different solutions for GRACE data. These are the Jet Propulsion Laboratory (JPL), the German Research Center for Geosciences (GFZ), and the University of Texas Center for Space Research (CSR). They each have slightly different algorithms to obtain the spherical harmonic coefficients. The GRACE data used in this study were obtained from JPL. However, some studies show that using a combination of data from the different centers might be preferred for certain cases [85].
4.4. Recommendations
The results of this study show that the use of machine learning algorithms, specifically LSTM, can prove beneficial when it comes to predicting land subsidence in the Central Valley. Knowing deformation values in the near-future is central for mitigating land subsidence-related disasters such as infrastructure damage. The two main methods that are used for mitigating subsidence caused by excessive groundwater pumping are the reduction of groundwater withdrawal rates and the artificial recharge of aquifers [6]. Combined with other data sources such as field investigations and ground-based observations, future deformation values can help guide policy makers to dictate allowed groundwater withdrawal rates as well as when artificial recharge is necessary. Additionally, PCA proved to be an effective and quick method at identifying key areas undergoing subsidence in the Central Valley and could be used in future InSAR analyses aimed at uncovering areas of subsidence that cannot be easily identified using traditional ground-based techniques.
5. Conclusions
In this paper, we attempted to characterize and predict the subsidence occurring in the Central Valley due to excessive groundwater pumping. We started by conducting a rough preliminary analysis of the deformation using PCA. Results showed a general overall subsidence as expected with a couple of concentrated areas of subsidence, namely the Tulare-Corcoran region and the city of Madera. Additionally, we used data from GRACE to visualize the downward trend of terrestrial water storage as well as groundwater storage. A time-averaged map showcasing the low groundwater storage in the Central Valley over the period of 2003 to 2022 was also built to aid in visualizing the problem at hand. Then, we built an InSAR time series using LiCSBAS with the default parameters over the period of 2014 to 2021. The resulting velocity map also showed a concentrated region of subsidence over Madera which is where we attempted to predict future deformation.
First, a baseline averaging model was built with a mean squared error metric after splitting the dataset into a train and test set. Then, a LSTM and CNN machine learning models were built and trained on the dataset. The LSTM model performed much better than the baseline averaging model and the CNN model, so we used it for true future predictions. In that case, the LSTM model was able to generally capture the trend of the future deformation, but the error in further steps was high due to the compounding error effect. Additionally, the model was fitted to the time-differenced dataset in order to show its true predictive potential as evidenced by the scattered points following the line in Figure 11. All in all, this paper establishes the effectiveness of incorporating machine learning techniques, specifically LSTM, in predicting short-term deformation showing promise for use in hazard mitigation models dealing with land subsidence in the Central Valley.
Author Contributions
Conceptualization, J.Y. and J.B.R.; methodology, J.Y. and J.B.R.; software, J.Y.; validation, J.Y. and J.B.R.; formal analysis, J.Y.; investigation, J.Y.; resources, J.B.R.; data curation, J.Y.; writing—original draft preparation, J.Y.; writing—review and editing, J.Y.; visualization, J.Y.; supervision, J.B.R.; project administration, J.B.R.; funding acquisition, J.B.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded under DoE grant DE-SC0017324 to the University of California, Davis.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
InSAR data used for the PCA analysis were formed using HyP3 software provided by the Alaska Satellite Facility (ASF). ASF DAAC HyP3 2022 using the hyp3_gamma plugin version 5.1.2 running GAMMA release 20210701. Contains modified Copernicus Sentinel data 2019, processed by ESA. Data and plots of terrestrial water storage were formed using the NASA JPL Data Analysis Tool (DAT), while groundwater storage data and plots were formed using the Giovanni web environment which uses GLDAS data to estimate groundwater. GRACE land are available at http://grace.jpl.nasa.gov (accessed on 12 September 2022), supported by the NASA MEaSUREs Program. Analyses and visualizations used in this paper were produced with the Giovanni online data system, developed and maintained by the NASA GES DISC. InSAR time series was formed using LiCSBAS developed by Yu Morishita. The Madera data obtained from LiCSBAS were constrained to an 11 × 11 grid spanning from X/Y: 1945/2054 (36.96211, −120.07611) as the top left corner to X/Y: 1955/2064 (36.95211, −120.06611) as the bottom right corner.
Acknowledgments
LiCSAR contains modified Copernicus Sentinel data [2014–2021] analysed by the Centre for the Observation and Modelling of Earthquakes, Volcanoes and Tectonics (COMET). LiCSAR uses JASMIN, the UK’s collaborative data analysis environment (http://jasmin.ac.uk) (accessed on 15 October 2022).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| InSAR | Interferometric Synthetic Aperture Radar |
| PCA | Principal Component Analysis |
| GRACE | Gravity Recovery and Climate Experiment |
| GRACE-FO | Gravity Recovery and Climate Experiment-Follow On |
| GLDAS | Global Land Data Assimilation System |
| LSTM | Long Short-Term Memory |
| CNN | Convolutional Neural Network |
| LOS | Line-of-Sight |
| MSE | Mean Squared Error |
References
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A. Groundwater extraction, land subsidence, and sea-level rise in the Mekong Delta, Vietnam. Environ. Res. Lett. 2014, 9, 084010. [Google Scholar] [CrossRef]
- Holzer, T.L.; Galloway, D.L. Impacts of land subsidence caused by withdrawal of underground fluids in the United States. Humans Geol. Agents 2005, 16, 87–99. [Google Scholar]
- Xue, Y.Q.; Zhang, Y.; Ye, S.J.; Wu, J.C.; Li, Q.F. Land subsidence in China. Environ. Geol. 2005, 48, 713–720. [Google Scholar] [CrossRef]
- Nolan, B.T.; Gronberg, J.M.; Faunt, C.C.; Eberts, S.M.; Belitz, K. Modeling nitrate at domestic and public-supply well depths in the Central Valley, California. Environ. Sci. Technol. 2014, 48, 5643–5651. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Chen, J.; Zhang, X. Monitoring the land subsidence area in a coastal urban area with InSAR and GNSS. Sensors 2019, 19, 3181. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic aperture radar interferometry to measure Earth’s surface topography and its deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-Guarnieri, A.V.; Prati, C.M.; Rocca, F.; Massonnet, D. INSAR Principles B; ESA Publications: Paris, France, 2007. [Google Scholar]
- Kang, Z.; Bettadpur, S.; Nagel, P.; Save, H.; Poole, S.; Pie, N. GRACE-FO precise orbit determination and gravity recovery. J. Geod. 2020, 94, 1–17. [Google Scholar] [CrossRef]
- Ciracì, E.; Velicogna, I.; Swenson, S. Continuity of the mass loss of the world’s glaciers and ice caps from the GRACE and GRACE Follow-On missions. Geophys. Res. Lett. 2020, 47, e2019GL086926. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The gravity recovery and climate experiment follow-on mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Faunt, C.C.; Hanson, R.T.; Belitz, K.; Schmid, W.; Predmore, S.P.; Rewis, D.; McPherson, K. Chapter C. Numerical model of the hydrologic landscape and groundwater flow in California’s Central Valley. In Groundwater Availability of the Central Valley Aquifer of California; US Geological Survey: Reston, VA, USA, 2009. [Google Scholar]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE groundwater drought index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Poland, J.F.; Lofgren, B.; Ireland, R.; Pugh, R. Land Subsidence, in the San Joaquin Valley, California, as of 1972: A History of Land Subsidence Caused by Water-Level Decline in the San Joaquin Valley, from the 1920’s to 1972; US Government Printing Office: Washington, DC, USA, 1975; Volume 437. [Google Scholar]
- Lawson, A.C. Subsidence by thrusting: The discussion of a hypothetical fault. Bull. Geol. Soc. Am. 1939, 50, 1381–1394. [Google Scholar] [CrossRef]
- Ingerson, I.M. The hydrology of the Southern San Joaquin Valley, California, and its relation to imported water-supplies. Eos Trans. Am. Geophys. Union 1941, 22, 20–45. [Google Scholar] [CrossRef]
- Lofgren, B.E.; Klausing, R.L. Land Subsidence Due to Ground-Water Withdrawal, Tulare-Wasco Area, California; US Government Printing Office: Washington, DC, USA, 1969; Volume 437. [Google Scholar]
- Ireland, R.L.; Poland, J.F.; Riley, F.S. Land Subsidence in the San Joaquin Valley, California, as of 1980; US Government Printing Office: Washington, DC, USA, 1984; Volume 437. [Google Scholar]
- Wilson, A.M.; Gorelick, S. The effects of pulsed pumping on land subsidence in the Santa Clara Valley, California. J. Hydrol. 1996, 174, 375–396. [Google Scholar] [CrossRef]
- Aobpaet, A.; Cuenca, M.C.; Hooper, A.; Trisirisatayawong, I. InSAR time-series analysis of land subsidence in Bangkok, Thailand. Int. J. Remote Sens. 2013, 34, 2969–2982. [Google Scholar] [CrossRef]
- Gao, M.; Gong, H.; Chen, B.; Li, X.; Zhou, C.; Shi, M.; Si, Y.; Chen, Z.; Duan, G. Regional land subsidence analysis in eastern Beijing plain by insar time series and wavelet transforms. Remote Sens. 2018, 10, 365. [Google Scholar] [CrossRef]
- Aimaiti, Y.; Yamazaki, F.; Liu, W. Multi-sensor InSAR analysis of progressive land subsidence over the Coastal City of Urayasu, Japan. Remote Sens. 2018, 10, 1304. [Google Scholar] [CrossRef]
- Amelung, F.; Galloway, D.L.; Bell, J.W.; Zebker, H.A.; Laczniak, R.J. Sensing the ups and downs of Las Vegas: InSAR reveals structural control of land subsidence and aquifer-system deformation. Geology 1999, 27, 483–486. [Google Scholar] [CrossRef]
- Chaussard, E.; Wdowinski, S.; Cabral-Cano, E.; Amelung, F. Land subsidence in central Mexico detected by ALOS InSAR time-series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar] [CrossRef]
- Motagh, M.; Djamour, Y.; Walter, T.R.; Wetzel, H.U.; Zschau, J.; Arabi, S. Land subsidence in Mashhad Valley, northeast Iran: Results from InSAR, levelling and GPS. Geophys. J. Int. 2007, 168, 518–526. [Google Scholar] [CrossRef]
- Libbrecht, M.W.; Noble, W.S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef]
- Kan, A. Machine learning applications in cell image analysis. Immunol. Cell Biol. 2017, 95, 525–530. [Google Scholar] [CrossRef]
- Kwekha-Rashid, A.S.; Abduljabbar, H.N.; Alhayani, B. Coronavirus disease (COVID-19) cases analysis using machine-learning applications. Appl. Nanosci. 2021, 1–13. [Google Scholar] [CrossRef]
- Brengman, C.M.; Barnhart, W.D. Identification of surface deformation in InSAR using machine learning. Geochem. Geophys. Geosystems 2021, 22, e2020GC009204. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Hill, P.; Bull, D. Application of machine learning to classification of volcanic deformation in routinely generated InSAR data. J. Geophys. Res. Solid Earth 2018, 123, 6592–6606. [Google Scholar] [CrossRef]
- Hakim, W.L.; Achmad, A.R.; Lee, C.W. Land subsidence susceptibility mapping in jakarta using functional and meta-ensemble machine learning algorithm based on time-series InSAR data. Remote Sens. 2020, 12, 3627. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J.A. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Netw. 2020, 125, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liang, X.; Zhiyuli, A.; Zhang, S.; Xu, R.; Wu, B. AT-LSTM: An attention-based LSTM model for financial time series prediction. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 569, p. 052037. [Google Scholar]
- Yadav, A.; Jha, C.; Sharan, A. Optimizing LSTM for time series prediction in Indian stock market. Procedia Comput. Sci. 2020, 167, 2091–2100. [Google Scholar] [CrossRef]
- Kim, S.; Kang, M. Financial series prediction using Attention LSTM. arXiv 2019, arXiv:1902.10877. [Google Scholar]
- Chen, Y.; He, Y.; Zhang, L.; Chen, Y.; Pu, H.; Chen, B.; Gao, L. Prediction of InSAR deformation time-series using a long short-term memory neural network. Int. J. Remote Sens. 2021, 42, 6919–6942. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Wei, J.; Wu, H.; Deng, M. HLSTM: Heterogeneous Long Short-Term Memory Network for Large-Scale InSAR Ground Subsidence Prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8679–8688. [Google Scholar] [CrossRef]
- Li, H.; Zhu, L.; Dai, Z.; Gong, H.; Guo, T.; Guo, G.; Wang, J.; Teatini, P. Spatiotemporal modeling of land subsidence using a geographically weighted deep learning method based on PS-InSAR. Sci. Total Environ. 2021, 799, 149244. [Google Scholar] [CrossRef]
- Bandy, O.L.; Arnal, R.E. Middle Tertiary basin development, San Joaquin Valley, California. Geol. Soc. Am. Bull. 1969, 80, 783–820. [Google Scholar] [CrossRef]
- Smith, D.A.; Ralls, K.; Cypher, B.L.; Clark, H.O., Jr.; Kelly, P.A.; Williams, D.F.; Maldonado, J.E. Relative abundance of Endangered San Joaquin kit foxes (Vulpes macrotis mutica) based on scat–detection dog surveys. Southwest. Nat. 2006, 51, 210–219. [Google Scholar] [CrossRef]
- Galloway, D.; Riley, F.S. San Joaquin Valley, California. Land Subsid. United States US Geol. Surv. Circ. 1999, 1182, 23–34. [Google Scholar]
- Visser, A.; Moran, J.E.; Singleton, M.J.; Esser, B.K. Importance of river water recharge to the San Joaquin Valley groundwater system. Hydrol. Process. 2018, 32, 1202–1213. [Google Scholar] [CrossRef]
- Haugen, E.A.; Jurgens, B.C.; Arroyo-Lopez, J.A.; Bennett, G.L. Groundwater development leads to decreasing arsenic concentrations in the San Joaquin Valley, California. Sci. Total Environ. 2021, 771, 145223. [Google Scholar] [CrossRef]
- Jeanne, P.; Farr, T.G.; Rutqvist, J.; Vasco, D.W. Role of agricultural activity on land subsidence in the San Joaquin Valley, California. J. Hydrol. 2019, 569, 462–469. [Google Scholar] [CrossRef]
- Faunt, C.C.; Sneed, M.; Traum, J.; Brandt, J.T. Water availability and land subsidence in the Central Valley, California, USA. Hydrogeol. J. 2016, 24, 675–684. [Google Scholar] [CrossRef]
- Scudiero, E.; Skaggs, T.H.; Corwin, D.L. Regional scale soil salinity evaluation using Landsat 7, western San Joaquin Valley, California, USA. Geoderma Reg. 2014, 2, 82–90. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Friston, K.; Phillips, J.; Chawla, D.; Büchel, C. Revealing interactions among brain systems with nonlinear PCA. Hum. Brain Mapp. 1999, 8, 92–97. [Google Scholar] [CrossRef]
- Hogenson, K.; Arko, S.A.; Buechler, B.; Hogenson, R.; Herrmann, J.; Geiger, A. Hybrid Pluggable Processing Pipeline (HyP3): A cloud-based infrastructure for generic processing of SAR data. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 13 December 2016; Volume 2016, pp. IN21B–1740. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Cooley, S.S.; Landerer, F. Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) Level-3 Data Product User Handbook; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2019; 57p. [Google Scholar]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Morishita, Y.; Lazecky, M.; Wright, T.J.; Weiss, J.R.; Elliott, J.R.; Hooper, A. LiCSBAS: An open-source InSAR time series analysis package integrated with the LiCSAR automated Sentinel-1 InSAR processor. Remote Sens. 2020, 12, 424. [Google Scholar] [CrossRef]
- Morishita, Y. Nationwide urban ground deformation monitoring in Japan using Sentinel-1 LiCSAR products and LiCSBAS. Prog. Earth Planet. Sci. 2021, 8, 1–23. [Google Scholar] [CrossRef]
- Lazeckỳ, M.; Spaans, K.; González, P.J.; Maghsoudi, Y.; Morishita, Y.; Albino, F.; Elliott, J.; Greenall, N.; Hatton, E.; Hooper, A.; et al. LiCSAR: An automatic InSAR tool for measuring and monitoring tectonic and volcanic activity. Remote Sens. 2020, 12, 2430. [Google Scholar] [CrossRef]
- Wright, T.; Gonzalez, P.; Walters, R.; Hatton, E.; Spaans, K.; Hooper, A. LiCSAR: Tools for automated generation of Sentinel-1 frame interferograms. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 13 December 2016; Volume 2016, pp. G23A–1037. [Google Scholar]
- Lawrence, B.N.; Bennett, V.L.; Churchill, J.; Juckes, M.; Kershaw, P.; Pascoe, S.; Pepler, S.; Pritchard, M.; Stephens, A. Storing and manipulating environmental big data with JASMIN. In Proceedings of the 2013 IEEE International Conference on Big Data, Santa Clara, CA, USA, 6–9 October 2013; pp. 68–75. [Google Scholar]
- Zhao, L.; Bai, H.; Wang, A.; Zhao, Y. Multiple description convolutional neural networks for image compression. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 2494–2508. [Google Scholar] [CrossRef]
- Schlegl, T.; Waldstein, S.M.; Vogl, W.D.; Schmidt-Erfurth, U.; Langs, G. Predicting semantic descriptions from medical images with convolutional neural networks. In International Conference on Information Processing in Medical Imaging; Springer: Berlin/Heidelberg, Germany, 2015; pp. 437–448. [Google Scholar]
- Fukuoka, R.; Suzuki, H.; Kitajima, T.; Kuwahara, A.; Yasuno, T. Wind speed prediction model using LSTM and 1D-CNN. J. Signal Process. 2018, 22, 207–210. [Google Scholar] [CrossRef]
- Hussain, D.; Hussain, T.; Khan, A.A.; Naqvi, S.A.A.; Jamil, A. A deep learning approach for hydrological time-series prediction: A case study of Gilgit river basin. Earth Sci. Inform. 2020, 13, 915–927. [Google Scholar] [CrossRef]
- Hatami, N.; Gavet, Y.; Debayle, J. Classification of time-series images using deep convolutional neural networks. In Proceedings of the Tenth International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13–15 November 2017; SPIE: Bellingham, WA, USA, 2018; Volume 10696, pp. 242–249. [Google Scholar]
- Tang, W.; Long, G.; Liu, L.; Zhou, T.; Jiang, J.; Blumenstein, M. Rethinking 1d-cnn for time series classification: A stronger baseline. arXiv 2020, arXiv:2002.10061. [Google Scholar]
- Eren, L.; Ince, T.; Kiranyaz, S. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the IEEE 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- O’Shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. {TensorFlow}: A system for {Large-Scale} machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Landerer, N.F. CSR TELLUS GRACE Level-3 Monthly Land Water-Equivalent-Thickness Surface Mass Anomaly Release 6.0 version 04 in netCDF/ASCII/GeoTIFF Formats. 2021. Available online: https://podaac.jpl.nasa.gov/dataset/TELLUS_GRAC_L3_CSR_RL06_LND_v04 (accessed on 12 September 2022).
- Li, B.; Beaudoing, H.; Rodell, M. GLDAS Catchment Land Surface Model L4 Daily 0.25 × 0.25 Degree GRACE-DA1 V2.2. 2020. Available online: https://disc.gsfc.nasa.gov/datasets/GLDAS_CLSM025_DA1_D_2.2/summary (accessed on 18 September 2022).
- Acker, J.G.; Leptoukh, G. Online analysis enhances use of NASA earth science data. Eos Trans. Am. Geophys. Union 2007, 88, 14–17. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Wang, G.; Li, P.; Li, Z.; Liang, C.; Wang, H. Coastal subsidence detection and characterization caused by brine mining over the Yellow River Delta using time series InSAR and PCA. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103077. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, K.; Yan, S.; Zhang, K.; Zhang, H.; Liu, X.; Li, H.; Sun, Y. Monitoring land surface displacement over Xuzhou (China) in 2015–2018 through PCA-based correction applied to SAR interferometry. Remote Sens. 2019, 11, 1494. [Google Scholar] [CrossRef]
- Radman, A.; Akhoondzadeh, M.; Hosseiny, B. Integrating InSAR and deep-learning for modeling and predicting subsidence over the adjacent area of Lake Urmia, Iran. GIScience Remote Sens. 2021, 58, 1413–1433. [Google Scholar] [CrossRef]
- Yun, K.; Adams, K.; Reager, J.; Liu, Z.; Chavez, C.; Turmon, M.; Lu, T. Remote estimation of geologic composition using interferometric synthetic-aperture radar in California’s Central Valley. arXiv 2022, arXiv:2212.04813. [Google Scholar]
- Osmanoğlu, B.; Sunar, F.; Wdowinski, S.; Cabral-Cano, E. Time series analysis of InSAR data: Methods and trends. ISPRS J. Photogramm. Remote Sens. 2016, 115, 90–102. [Google Scholar] [CrossRef]
- Neves, M.C.; Nunes, L.M.; Monteiro, J.P. Evaluation of GRACE data for water resource management in Iberia: A case study of groundwater storage monitoring in the Algarve region. J. Hydrol. Reg. Stud. 2020, 32, 100734. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).