Dynamic Loss Reweighting Method Based on Cumulative Classification Scores for Long-Tailed Remote Sensing Image Classification

Abstract

Convolutional neural networks have been widely used in remote sensing classification and achieved quite good results. Most of these methods are based on datasets with relatively balanced samples, but such ideal datasets are rare in applications. Long-tailed datasets are very common in practice, and the number of samples among categories in most datasets is often severely uneven and leads to bad results, especially in the category with a small sample number. To address this problem, a novel remote sensing image classification method based on loss reweighting for long-tailed data is proposed in this paper to improve the classification accuracy of samples from the tail categories. Firstly, abandoning the general weighting approach, the cumulative classification scores are proposed to construct category weights instead of the number of samples from each category. The cumulative classification score can effectively combine the number of samples and the difficulty of classification. Then, the imbalanced information of samples from each category contained in the relationships between the rows and columns of the cumulative classification score matrix is effectively extracted and used to construct the required classification weights for samples from different categories. Finally, the traditional cross-entropy loss function is improved and combined with the category weights generated in the previous step to construct a new loss reweighting mechanism for long-tailed data. Extensive experiments with different balance ratios are conducted on several public datasets, such as HistAerial, SIRI-WHU, NWPU-RESISC45, PatternNet, and AID, to verify the effectiveness of the proposed method. Compared with other similar methods, our method achieved higher classification accuracy and stronger robustness.

1. Introduction

In recent years, with the rapid development of earth observation technology, remote sensing technology has reached an unprecedented new stage, and it is becoming easier and easier to obtain remote sensing images with high spatial, temporal, and spectral resolution [1]. This provides sufficient data for technological development from pixel-level or object-level classification to the semantic understanding of the overall scene. Semantic-based remote sensing image classification is widely used in many fields, such as urban planning [2], disaster monitoring [3], environmental protection [4], geographic image search [5], and other fields.

In the early years, remote sensing image classification was mainly based on low or medium-level visual features, such as the texture, shape, and spectrum of remote sensing images, and some traditional classifiers such as SVM (Support Vector Machine) [6] have been widely used to discriminate the different objects in remote sensing images [7]. With the rapid development of deep convolutional neural networks, a large number of classification methods based on convolutional neural networks [8,9] have been proposed in the literature and greatly improved the classification accuracy in applications.

Although methods based on deep convolutional neural networks have achieved remarkable performance, most of these methods are based on relatively balanced datasets, but such ideal datasets are rare in applications. In the practical application, long-tailed datasets are very common, and the number of samples among categories in most datasets is often severely uneven, i.e., a few head categories have most of the samples in the data, while the majority of tail categories contain only a few samples [10]. As shown in Figure 1, in the remote sensing images of urban scenes, roads and houses occupy 52.70% and 26.12% of the total image pixels, respectively, while cars and urban accumulations occupy only 2.34% and 0.97% of the image pixels, respectively. Thus, the imbalance of remote sensing data caused by the uneven distribution of remote sensing objects is the norm of data distribution in real situations. The direct result of the long-tailed distribution is to overfit samples from the head categories and underfit samples from the tail categories. However, for remote sensing image classification tasks, it is unexpected that the classification of samples is strongly influenced by the number of samples from each category [11], but rather that all categories can be effectively recognized.

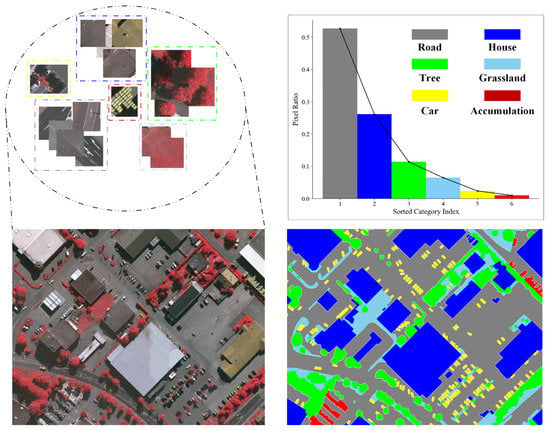
Figure 1. The distribution chart of the six main remote-sensing objects in the urban scenario. It can be seen from the figure that the percentages of different kinds of remote-sensing objects obviously obey a long-tailed distribution.

To solve the long-tailed problem, some methods have been proposed. Depending on the processing strategy, these methods can be divided into three categories, re-sampling, loss reweighting, and migration learning. The data re-sampling methods [12] need to reconstruct the distribution of the data, and the migration learning methods need to introduce some additional modules to realize the information migration between the source domain (samples from the head categories, pre-trained models) and the target domain (samples from the tail categories). In short, both of these methods will add more or less additional burdens, including structure design and model training. In contrast, the loss reweighting methods can achieve better performance than the above two kinds of methods by only weighting samples from each category. At the same time, it can maintain the original distribution of the data and the structure of the method. Currently, most of the loss reweighting methods utilize the number of samples from each category (NCS) to construct the weighting factors of samples from each category to coordinate the learning progress of head categories and tail categories [13,14,15]. However, the method based on the number of samples from each category only considers the effect of the number of samples from each category on the classification results of the method while ignoring the fact that the difficulty of classification varies among samples from different categories. Moreover, the training process of neural networks is dynamic, and the number of samples from each category as a static indicator does not reflect the actual training of the model. These defects easily cause some misalignment between the weight and the method by using the category weights generated from the number of samples from each category to guide the learning training of the model, as shown in Figure 2.

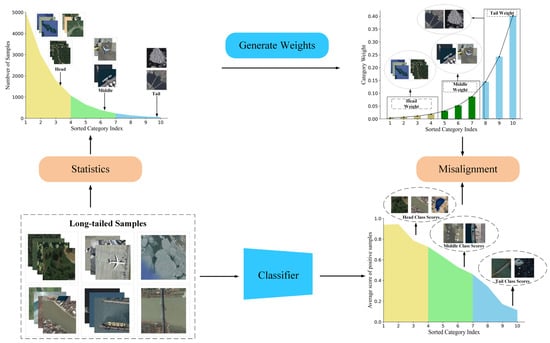
Figure 2. The loss reweighting method based on the number of samples from each category does not consider the difference in classification difficulty of samples from various categories and cannot adapt to the relatively dynamic training process of the model, which can easily cause the misalignment between the category weights and the real learning state of the model.

Based on the analysis above, a loss reweighting method based on the cumulative classification scores of categories (CCSMLW) is proposed to solve the long-tailed problem of remote sensing image classification. Different from constructing category weights based on the number of samples from each category, the proposed method uses cumulative classification scores of different categories to measure the degree of imbalance in samples from various categories and construct the required category weights for each category. Compared with previous methods, our proposed method more effectively coordinates the learning situation of the samples from the head categories and the samples from the tail categories of remote sensing data, and better improves the overall classification accuracy. To verify the performance of our proposed method, extensive comparison experiments are conducted on several datasets for remote sensing classification. The experimental results show that our proposed method achieves higher classification accuracy.

The main contributions of this paper can be summarized as follows.

(1)

We reveal the theoretical defects in most current remote sensing image classification methods based on the balanced category distribution and point out the fact that most samples for remote sensing image classification present a long-tailed distribution in real scenes.

(2)

We analyze the shortcomings of the current loss reweighting methods based on the number of samples from each category and propose a new approach to characterize the long-tailed distribution of remote sensing data by using the cumulative category classification scores instead of the number of samples from each category.

(3)

We propose an adaptive loss reweighting method using the accumulated classification scores of categories to automatically determine the weights required for different categories. This method improves the original cross-entropy loss function, effectively coordinates the learning progress of the head and tail categories and improves the overall classification accuracy of the classification network for remote sensing long-tailed data.

The rest of the paper is organized as follows. In Section 2, a brief review of the related literature on remote sensing image classification and deep long-tailed learning is presented. In Section 3, the theoretical basis and the implementation process of the method in this paper are described in detail. In Section 4, some details of the datasets, a thorough description of the implementation procedure of the comparison experiments, and the results of our and the other state-of-the-art methods are shown. In Section 5, the effectiveness of the submodules is discussed. In Section 6, the entire paper is summarized, and a very meaningful conclusion is given.

2. Related Works

Firstly, some recent developments in the fields of remote sensing image classification and deep long-tailed learning are summarized, and the deficiencies of some advanced methods in each field are analyzed. Then, it is pointed out that the effective combination of methods in both fields is important for improving the accuracy of remote sensing image scene classification tasks in real situations.

2.1. Remote Sensing Image Classification

For most vision tasks, it is very important to construct discriminative features that can effectively characterize the data samples, including remote sensing image classification. Over the past few decades, many studies have been undertaken to explore an effective discriminable feature. Early methods for remote sensing image classification mainly relied on artificial feature descriptors such as CH (Color Histograms) [16], SIFT (Scale-Invariant Feature Transform) [17], Gist [18], and HOG (Histograms of Oriented Gradients) [19] to construct the feature space of remote sensing data samples. These feature descriptors are mainly constructed based on the color, shape, texture, or spectral information of different objects in remote sensing images, thus possessing rich, shallow geometric information. After extensive feature extraction from remote sensing images, a good classifier such as SVMs (Support Vector Machine) is required to effectively classify the extracted features. For example, Yang et al. [20] compared the performance of SIFT features with Gabor texture features on IKONOS satellite images by using a MAP (Maximum A Posteriori) classifier. Santos et al. [21], on the other hand, evaluated a variety of global color descriptors and texture descriptors to perform remote sensing image classification.

In a real scene, the semantic information of the scene is usually the combination of various information, such as spectrum, color, texture, and shape. One type of information only represents one aspect of the remote sensing image, and a single type of feature descriptor is always unable to express the whole content of the remote sensing image. Therefore, the complementary combination of multiple features is applied to remote sensing image classification tasks as a new strategy. For example, Zhao et al. [22] proposed a Dirichlet-derived multitopic model that effectively combines three different kinds of features to perform remote sensing image classification. In contrast, Luo et al. [23] effectively combined six feature descriptors to form a multi-scale feature representation for remote sensing images to better describe different kinds of remote sensing images. Although the effective combination of various artificial feature descriptors can be helpful in improving the classification accuracy of remote sensing images, the manually constructed feature descriptors are only comprehensive representations of shallow information such as texture, shape, and spectrum and lack the participation of deep semantic information, so it is difficult for the manual feature descriptors to perform satisfactorily and robustly for the complex and variable remote sensing environment.

In recent years, with the rapid development of deep learning technology and the explosive increase in remote sensing data, a large number of methods based on deep learning has been applied to remote sensing image classification tasks. Among them, the deep convolutional neural network (CNN) has gradually become the main basic model for remote sensing image classification tasks due to its excellent design for image data. The method based on deep learning uses an efficient stacking of multi-layer neural network units to extract various features of an image adaptively compared to the traditional method based on manual features. The extracted features contain not only rich, shallow geometric information but also a large amount of deep discriminative semantic information. This makes the method based on deep learning more robust for complex and variable images than the traditional method based on artificial features. In addition, some studies [24,25] have shown that deep feature learning methods are excellent at discovering some semantic relationships hidden in high-dimensional data, which is very important and useful for the representation of relationships between different objects in remote sensing images. Based on this, many researchers started to improve the deep convolutional network effectively based on the remote sensing image characteristics to obtain excellent remote sensing image classification performance [26]. For example, Cheng et al. [27] added a metric learning regular term to the features extracted by CNN to optimize the training of CNN models and thus improve the accuracy of remote sensing image classification tasks.

However, both the methods based on traditional manual features and the methods based on deep learning are currently designed for datasets with relatively balanced distribution and do not consider the real distribution of remote sensing datasets in realistic scenarios. In real situations, remote sensing data mostly do not show a balanced distribution but an unbalanced long-tailed distribution. This leads to the fact that most of the current remote sensing image classification methods are difficult to apply to real applications. Therefore, it is important to introduce some excellent methods from the long-tailed learning field into the remote sensing image classification task to promote the overall development of the field.

2.2. Deep Long-Tailed Learning

Data resampling, loss reweighting, and migration learning are the three most common methods to solve the long tail problem. They address the long-tailed problem caused by uneven distribution from three different perspectives. Among them, the loss reweighting method does not require any changes to the original method and can improve the accuracy of the original method in a plug-and-play manner, which is well suited for remote sensing image classification tasks.

Data re-sampling is undoubtedly the simplest of the many methods of solving the long-tailed problem. This kind of method mainly transforms the original long-tailed distribution dataset into a balanced distribution dataset by a certain sampling strategy to improve the classification accuracy of the method for samples from the tail categories. Among many others, oversampling is one of the most common sampling strategies. This strategy is mainly used to obtain a relatively balanced distribution by randomly repeated sampling of the tail categories and then improve the classification accuracy of the method for samples from the tail categories. The oversampling strategy is effective in mitigating the long-tailed effect of remote sensing data, but this over-expansion of samples from the tail categories can easily cause the network to over-fit the samples from the tail categories. Corresponding to the oversampling strategy, under-sampling is another major sampling strategy. In contrast to the idea of oversampling, under-sampling mainly removes some samples randomly from the head categories to make the distribution of the dataset relatively balanced. Although the under-sampling strategy also enables the mitigation of the long-tailed effect of the data, discarding the available samples randomly undoubtedly reduces the diversity of the training samples. The method based on transfer learning [28,29,30] migrates the previously learned feature information or the feature information of the head categories to the learning process of samples from the tail categories to alleviate the problem of insufficient information in the tail categories due to insufficient training samples. According to the different transfer approaches, there are four main types of methods based on transfer learning: head-to-tail knowledge transfer, model pre-training, knowledge distillation, and self-training. However, no matter what type of migration approach these methods use, there are additional modules that need to be designed to assist in the implementation. This requires changes to the original method and adding some additional training parameters. This is not suitable for the remote sensing image classification task.

Loss reweighting is also an effective way to solve the long tail problem. Its main idea is to regulate the learning progress of the samples from the head and tail categories by assigning different loss weights to the samples from different categories, thus achieving the equalization training of the model. Currently, most of the reweighting methods construct loss weights based on the number of samples from each category, such as Huang et al. [31] and Wang et al. [32] directly utilize the inverse of the number of samples from each category as the loss weights for samples from each category. Cui et al. [33], on the other hand, observed that the number of samples from each category is not effective in describing the differences in the total amount of information between categories due to the overlap of information between samples, and thus proposed a concept called effective samples to construct loss weights instead of the number of samples from each category. Several studies in recent years [34,35] found that the large number of negative gradients generated by the samples from the head categories during the training of long-tailed data can have a serious inhibitory effect on the learning of samples from the tail categories. To solve this problem, Tan et al. and Wang et al. attenuated negative gradients of the head categories from two aspects based on the number of samples from each category, respectively, to eliminate the adverse effects of the above problem and improve the classification accuracy of the method for the samples from the tail categories. However, no matter how different the above methods are in terms of design ideas, they do not escape from the paradigm based on the number of samples from each category, and they do not consider the situation that the classification difficulty varies among samples from different categories and the defect that the number of samples from each category as a static indicator is difficult to effectively adapt to the dynamic training of the model.

3. Methodology

In this section, the overall framework of our proposed method is first described in detail. Then, the theoretical basis and algorithmic procedure of our proposed method are presented. Finally, the theoretical comparison is made between our improved loss function and the traditional cross-entropy loss function.

3.1. Overall Framework

In real situations, remote sensing data always show an unbalanced long-tailed distribution. This is a considerable challenge for many remote sensing image classification methods based on balanced data. This paper analyses the long-tailed problem in detail and proposes a novel loss reweighting method based on cumulative classification scores (CCSMLW) to solve the long-tailed problem without changing the original data distribution and the structure of the original method. The overall architecture of the proposed method is shown in Figure 3.

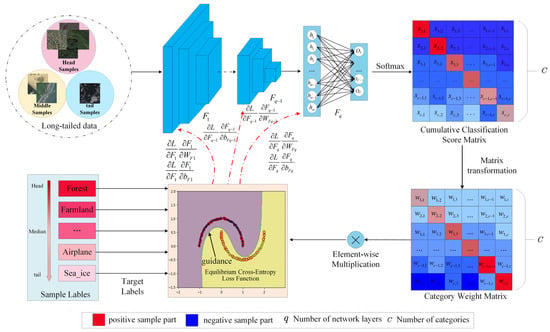
Figure 3. The overall structure of the proposed CCSMLW.

In the proposed method, a CNN-based feature extraction network and a fully connected network without bias terms are used to implement feature extraction and the scene classification of long-tailed remote sensing images, respectively. Then, the softmax function is used to normalize the output of the fully connected network to obtain the classification scores of the positive sample part and the negative sample part of each sample. Thirdly, the classification scores of each sample according to the category of the sample are accumulated to obtain a cumulative classification score matrix with $C$ rows and $C$ columns ($C$ denotes the number of categories in the dataset), where each row of the matrix represents the overall prediction of all samples from the category $i(i\le C)$, and each column represents the distribution of all samples classified as the category $i$. A specific matrix transformation is performed to generate the required weighting factors for each category based on the relationships between the rows and columns of the cumulative categorical score matrix. Finally, it is calculated by multiplying the generated category weighting factors with the improved loss function of this paper for loss calculation. The loss gradients of different categories are used to dynamically adjust the training process of the model so that the method can focus on the learning of weak samples from the tail categories. Compared with other methods, our proposed method does not require any change in the structure of the original method and is completely plug-and-play.

3.2. Category Weight Matrix Based on Category Cumulative Classification Score

In the multi-classification task, an instance sample corresponds to the $C$ output values. Each output represents the predicted probability that this sample belongs to a certain category after being normalized by the softmax function. For each instance sample, it is desired that only the classification score for the true category of this sample is the highest, and the classification scores for the other categories can be lower. That is, the classification scores of a sample include a positive sample classification score and $C-1$ negative sample classification scores. In the long-tailed remote sensing image classification task, the classification scores of the samples from different categories are seriously affected by the number of samples from each category. That is, the samples from the head categories often have higher positive sample classification scores and lower negative sample classification scores, and the opposite is true for samples from the tail categories. It can be used to generate category weights to guide the learning of samples from different categories by utilizing the differences in classification scores between the categories and thus solve the long-tailed problem. In this paper, the cumulative classification scores of different categories are used to generate the category weights.

Suppose there exists an instance sample $t$, whose corresponding network output value is $z^t=\left[z_1^t,\dots ,z_j^t,\dots ,z_C^t\right]$, whose category is $i(i\le C)$ and whose corresponding one-hot category label is $y^t$ ($y_{j=i}^t=1$ and $y_{j\ne i}^t=0$). Therefore, the “classification scores” of this instance sample (where the negative sample classification scores are equal to one minus the original negative sample classification scores) are shown in Equation (1).

$$p_{ij}^t=\{\begin{array}{l}\frac{e^{z_j^t}}{{\displaystyle \sum _{n=1}^C{e}^{z_n^t}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{y}_j^t=1\hfill \\ 1-\frac{e^{z_j^t}}{{\displaystyle \sum _{n=1}^C{e}^{z_n^t}}}\hspace{0.17em}\hspace{1em}\hspace{0.17em}{y}_j^t=0\hspace{1em}\hspace{1em}\hfill \end{array}$$

(1)

Based on Equation (1), the classification score of each instance sample can be calculated. After that, the cumulative classification scores $s_{ij}$ of each category can be calculated based on Equation (2).

$$s_{ij}={\displaystyle \sum _{k=1}^{N_i}{p}_{ij}^k}$$

(2)

where $p_{ij}^k$ denotes the classification score of the $k$-th instance sample and $N_i$ denotes the total number of samples in the category $i$.

After obtaining the cumulative classification score $s_{ij}$ for each category, a category classification state matrix $S$ is obtained. The size of this matrix is $C\times C$, where $C$ denotes the number of categories in the dataset. Equation (3) shows the definition of this state matrix.

$$S=\left[\begin{array}{cccc}{s}_{11}& s_{12}& \dots & s_{1C}\\ s_{21}& s_{22}& \dots & s_{2C}\\ \dots & \dots & \dots & \dots \\ s_{C1}& s_{C2}& \dots & s_{CC}\end{array}\right]$$

(3)

After the cumulative classification scores of each category are considered the cumulative number of some equivalent samples, the state matrix $S$ can be treated as a confusion matrix constructed from the equivalent samples. That is, each row of the matrix $S$ represents the overall classification of equivalent samples from a certain category, each column element represents the distribution of equivalent samples predicted to be in a certain category, and the diagonal elements represent the distribution of equivalent samples correctly classified that are from different categories. Therefore, the relationship between the rows and columns of the matrix $S$ can be used to construct the required category weights for samples from different categories. For the long-tailed remote sensing image classification task, the category weights are desired to apply higher weight factors to those categories with low cumulative classification scores (i.e., tail categories or categories that are difficult to classify) so that the method focuses more on the learning of samples from these categories. Therefore, a new matrix $M$ is obtained by performing the inverse operation for each element of the matrix $S$. Equation (4) shows the above operations.

$$M=\left[\begin{array}{cccc}\frac{1}{s_{11}}& \frac{1}{s_{12}}& \dots & \frac{1}{s_{1C}}\\ \frac{1}{s_{21}}& \frac{1}{s_{22}}& \dots & \frac{1}{s_{2C}}\\ \dots & \dots & \dots & \dots \\ \frac{1}{s_{C1}}& \frac{1}{s_{C2}}& \dots & \frac{1}{s_{CC}}\end{array}\right]=\left[\begin{array}{cccc}{m}_{11}& m_{12}& \dots & m_{1C}\\ m_{21}& m_{22}& \dots & m_{2C}\\ \dots & \dots & \dots & \dots \\ m_{C1}& m_{C2}& \dots & m_{CC}\end{array}\right]$$

(4)

After obtaining the matrix $M$, the relationship between the diagonal elements of the matrix is first used to generate the category weighting factors for the positive sample part. This is shown in Equations (5)–(8).

$$M^{pos}=M\ast I_C=\left[\begin{array}{cccc}{m}_{11}& 0& \dots & 0\\ 0& m_{22}& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & m_{CC}\end{array}\right]$$

(5)

$$M_{\alpha }^{pos}={(M^{pos})}^{\alpha }=\left[\begin{array}{cccc}{(m_{11})}^{\alpha }& 0& \dots & 0\\ 0& {(m_{22})}^{\alpha }& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & {(m_{CC})}^{\alpha }\end{array}\right]$$

(6)

$$d^{pos}={\displaystyle \sum _{i=1}^C{(m_{ii})}^{\alpha }}$$

(7)

$$R^{pos}=\frac{C}{d^{pos}}{M}_{\alpha }^{pos}=\left[\begin{array}{cccc}\frac{C}{d^{pos}}{(m_{11})}^{\alpha }& 0& \dots & 0\\ 0& \frac{C}{d^{pos}}{(m_{22})}^{\alpha }& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & \frac{C}{d^{pos}}{(m_{CC})}^{\alpha }\end{array}\right]$$

(8)

Secondly, each column element of the matrix $M$ (excluding the diagonal elements) is used to generate the weighting factors for the negative sample part. This is shown in Equations (9)–(13).

$$M^{neg}=M\ast (J_C-I_C)=\left[\begin{array}{cccc}0& m_{12}& \dots & m_{1C}\\ m_{21}& 0& \dots & m_{2C}\\ \dots & \dots & \dots & \dots \\ m_{C1}& m_{C2}& \dots & 0\end{array}\right]$$

(9)

$$M_{\beta }^{neg}=\left[\begin{array}{cccc}0& {(m_{12})}^{\beta }& \dots & {(m_{1C})}^{\beta }\\ {(m_{21})}^{\beta }& 0& \dots & {(m_{2C})}^{\beta }\\ \dots & \dots & \dots & \dots \\ {(m_{C1})}^{\beta }& {(m_{C2})}^{\beta }& \dots & 0\end{array}\right]$$

(10)

$$d^{neg}={\displaystyle \sum _{i=1,i\ne j}^C{(m_{ij})}^{\beta }}=\left[\begin{array}{ccc}\begin{array}{cc}{d}_1^{neg}& d_2^{neg}\end{array}& \dots & d_C^{neg}\end{array}\right]$$

(11)

$$D^{neg}=diag(d^{neg})=\left[\begin{array}{cccc}{d}_1^{neg}& 0& \dots & 0\\ 0& d_2^{neg}& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & d_C^{neg}\end{array}\right]$$

(12)

$$R^{neg}=(C-1)m_{\beta }^{neg}{(D^{neg})}^{-1}=\left[\begin{array}{cccc}0& \frac{C-1}{d_2^{neg}}{(m_{12})}^{\beta }& \dots & \frac{C-1}{d_C^{neg}}{(m_{1C})}^{\beta }\\ \frac{C-1}{d_1^{neg}}{(m_{21})}^{\beta }& 0& \dots & \frac{C-1}{d_C^{neg}}{(m_{2C})}^{\beta }\\ \dots & \dots & \dots & \dots \\ \frac{C-1}{d_1^{neg}}{(m_{C1})}^{\beta }& \frac{C-1}{d_2^{neg}}{(m_{C2})}^{\beta }& \dots & 0\end{array}\right]$$

(13)

Two hyperparameters of $\alpha$ and $\beta$ are introduced to exponentially weight the elements of the positive and negative sample parts of the matrix $M$ to make the category weights of the positive and negative sample parts more sensitive to the actual learning of the long-tail data.

Finally, the final category weight matrix $R$ is obtained by summing the category weights $R^{pos}$ of the positive sample part and the category weights $R^{neg}$ of the negative sample part according to the corresponding element positions. This is shown in Equation (14).

$$R=R^{pos}+R^{neg}=\left[\begin{array}{cccc}\frac{C}{d^{pos}}{(m_{11})}^{\alpha }& \frac{C-1}{d_2^{neg}}{(m_{12})}^{\beta }& \dots & \frac{C-1}{d_C^{neg}}{(m_{1C})}^{\beta }\\ \frac{C-1}{d_1^{neg}}{(m_{21})}^{\beta }& \frac{C}{d^{pos}}{(m_{22})}^{\alpha }& \dots & \frac{C-1}{d_C^{neg}}{(m_{2C})}^{\beta }\\ \dots & \dots & \dots & \dots \\ \frac{C-1}{d_1^{neg}}{(m_{C1})}^{\beta }& \frac{C-1}{d_2^{neg}}{(m_{C2})}^{\beta }& \dots & \frac{C}{d^{pos}}{(m_{CC})}^{\alpha }\end{array}\right]$$

(14)

3.3. Equilibrium Cross-Entropy Loss Function

Cross-Entroy (CE) Loss is a loss function applied to classification tasks, which is categorized into Sigmoid Cross-Entropy and Softmax Cross-Entropy according to the normalization operation of the input. The specific definitions are shown in Equations (15)–(18).

$$L_{BCE}=-{\displaystyle \sum _{j=1}^C\log ({\sigma }_j)}$$

(15)

$${\sigma }_j=\{\begin{array}{l}\frac{1}{1+e^{-z_j}}\hspace{1em}\hspace{1em}if\hspace{0.17em}{y}_j=1\\ 1-\frac{1}{1+e^{-z_j}}\hspace{1em}otherwise\end{array}$$

(16)

where $z_j\in Z$$Z=\left[z_1,\dots ,z_j,\dots ,z_C\right]$ denotes the output prediction of the model and $C$ denotes the number of categories of the data. $y_j\in \left\{0,1\right\}$, $1\le j\le C$ is the true label of one-hot encoding.

$$L_{SCE}=-{\displaystyle \sum _{j=1}^C{y}_j\log ({\sigma }_j)}$$

(17)

$${\sigma }_j=\frac{e^{z_j}}{{\displaystyle \sum _{n=1}^C{e}^{z_n}}}$$

(18)

here $z_j$, $C$ and $y_j$ have the same meaning as above.

In this paper, the above-mentioned Sigmoid Cross-Entropy loss function and Softmax Cross-Entropy loss function are effectively combined to propose a novel Equilibrium Cross-Entropy loss function. Firstly, an additional negative sample loss term is introduced to widen the gap between the positive and negative sample classification scores based on the original Softmax Cross-Entropy loss function so that the samples can be distinguished more effectively. Secondly, too many negative sample loss terms can seriously affect the learning of positive samples. This is especially obvious for long-tailed datasets with multiple categories. Based on this, a penalty factor is added before the negative sample loss term to make it no longer correlate with the number of categories. Finally, the two improvements mentioned above are effectively combined to obtain the final equilibrium loss function. The specific definitions are shown in Equations (19) and (20).

$$L_{EBCE}(z_j,y_j)=\{\begin{array}{l}-\log ({\sigma }_j)\hspace{1em}\hspace{1em}\hspace{1em}{y}_j=1\\ -\frac{1}{C-1}\log (1-{\sigma }_j)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{y}_j=0\end{array}$$

(19)

$${\sigma }_j=\{\begin{array}{l}\frac{e^{z_j}}{{\displaystyle \sum _{n=1}^C{e}^{z_n}}}\hspace{1em}{y}_j=1\\ \frac{1}{1+e^{z_j}}\hspace{1em}{y}_j=0\end{array}$$

(20)

4. Experiment and Results

In this section, some comparative experiments with the proposed method and several similar advanced methods are conducted on five challenging datasets to verify the effectiveness of our proposed method. To make the comparison results more convincing, both the proposed method and the comparison method in this paper use the same network structure and training parameters.

4.1. Dataset

The HistAerial dataset [36] is a high-resolution panchromatic remote sensing dataset created by the University of Lyon, France. It contains seven remote sensing scene categories. Three sizes of images are provided in the dataset, and the images with a size of $100\times 100$ are chosen as the experimental data for this paper. Meanwhile, each category in the original dataset contains a large number of images, and the images in each category are not balanced. Thus, 2000 images from each category are randomly selected for the subsequent experimental data in this paper. The spatial resolution is not provided in this dataset.

The SIRI-WHU dataset [37,38] is a high-resolution remote sensing dataset created by Wuhan University. It contains remote sensing images of different land types in four major categories and 12 subcategories. Each subcategory contains 200 remote sensing images with a size of $200\times 200$ and a spatial resolution of 2 m.

The NWPU-RESISC45 dataset [39] is a large remote sensing image classification dataset created by Northwestern Polytechnic University. It contains 45 remote-sensing scene categories. Each category contains 700 remote sensing images with a size of $256\times 256$. This data contains 31,500 remote sensing images with spatial resolutions ranging from 0.2 m to 30 m.

The PatternNet dataset [40] is a high-resolution remote sensing dataset created by Wuhan University. It contains 38 remote sensing scene categories. Each category contains 800 remote sensing images with the size of $256\times 256$ and spatial resolutions ranging from 0.06 m to 4.7 m.

The AID dataset [41] is a large dataset of aerial images created by Wuhan University. It contains 30 aerial scene categories. Each scene category contains 220 to 420 images. The size of the images is $600\times 600$. This dataset contains 10,000 remote sensing images with spatial resolutions ranging from 0.5 m to 8 m.

4.2. Data Processing

The above five datasets were collected and produced with the equalization of samples from each category, which could not meet the data distribution requirements needed for the comparison experiments in this paper. Thus, the above data were subjected to long-tailed processing to simulate the imbalanced distribution of samples from different categories under realistic situations. Firstly, the random data division of 7:3 was performed on the HistAerial dataset, SIRI-WHU dataset, NWPU-RESISC45 dataset, and PatternNet dataset, i.e., 70% of the data were used for training the model and 30% for testing the model. After that, the long tailing process is applied to the training data, i.e., the number of training samples from each category is decayed according to the following exponential formula:

$$n=n_i{u}_1{}^{\frac{i}{C-1}}$$

(21)

where $i$ denotes the category index. $n_i$ denotes the original number of training samples. $u_1\in (0,1)$ denotes the data imbalance ratio, i.e., $u_1={n^{\prime }}_{\min }/{n^{\prime }}_{\max }$, ${n^{\prime }}_{\max }$ denotes the maximum value of the number of samples from each category after long-tailed processing and ${n^{\prime }}_{\min }$ denotes the minimum value of the number of samples from each category after long-tailed processing. $C$ denotes the number of categories in the dataset. The sample distributions of the four datasets are shown in Figure 4.

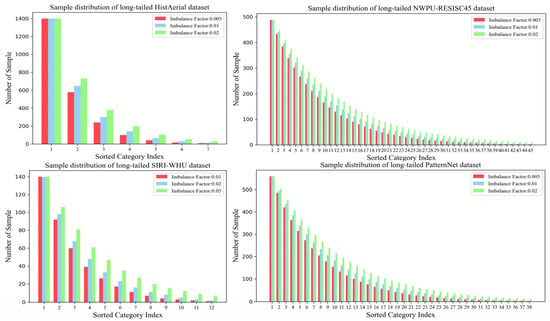
Figure 4. The distribution of the number of samples from each category after long-tailed processing for the HistAerial dataset, the SIRI-WHU dataset, the NWPU-RESISC45 dataset, and the PatternNet dataset.

The number of samples from each category in the AID dataset is not equal but only obeys a roughly balanced distribution; thus, another long-tailed approach is used for this dataset. Firstly, 100 images from each category are randomly selected as test images, and the rest of the images are used as candidate training data samples. After that, the dataset is divided into three parts according to the category index. The categories in the first part do not undergo sample size decay. The categories from the first part are not subjected to sample size decay, and the samples from the candidate training sample set are directly used as training samples. The categories from the second part are randomly discarded $\left(1-1/u_2\right)$ proportional samples, and the remaining samples in the candidate dataset are used as training samples. The categories from the third part discard $(1-1/u_2^2)$ the proportion of samples randomly, and the remaining samples in the candidate dataset are used as training samples, which $u_2$ denotes the decay factor. The sample distribution of the AID dataset is shown in Figure 5.

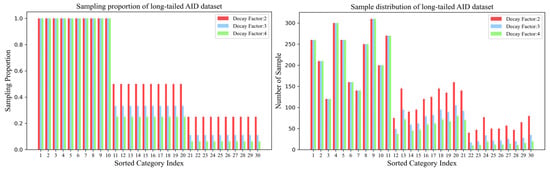
Figure 5. Long-tailed sampling percentage of the AID dataset and the distribution of the number of samples from each category after long-tailed processing.

In the comparison experiments, the imbalance ratios are set at 0.01, 0.02, and 0.05 for the SIRI-WHU dataset due to the small number of samples in each category. For the HistAerial dataset, the NWPU-RESISC45 dataset, and the PatternNet dataset, the imbalance ratios are set to 0.005, 0.01, and 0.02 because they have a relatively large number of samples per category to construct more imbalanced long-tailed data. For the AID dataset, three increasing decay factors $u_2$, which are 2, 3, and 4, are also set.

4.3. Implementation Detail

Extensive comparison experiments are conducted on the long-tailed processed HistAerial, SIRI-WHU, NWPU-RESISC45, PatternNet, and AID datasets. In the experiments, the randomly initialized ResNet32 network [42] is used as the backbone network for feature extraction, and a fully connected network without bias is utilized for the classification of remote-sensing images. For the training images, the images are first uniformly sized to $256\times 256$. After that, random horizontal and vertical flips are used to increase the diversity of the samples. Finally, a pixel-normalization operation is performed on the training images using the mean and variance. For the test images, the image size normalization and pixel normalization operations are performed. In the training process, the stochastic gradient descent (SGD) method is used to train the model with a momentum value of 0.9 and the weight-decay value of 0.2. The initial learning rate of the model is set to 0.08, and the learning rate decays by 0.1 at 40, 60, and 70 epochs, respectively. The discussion and settings of the hyperparameters $\alpha$ and $\beta$ in the comparison experiments are shown in Section 5.2. The hardware configuration used for the experiment is shown in Table 1.

Table 1. Experimental equipment configuration.

Item	Contents
Processor	Intel Core I9-12900K
Memory	64GB
Operating system	Ubuntu20.04
Gpu	3090ti
Pytorch	1.10.1

4.4. Evaluation Metrcics

To be able to effectively evaluate the performance between different methods, the overall accuracy (OA) and confusion Matrix are used as the main metrics to evaluate the methods. The OA value indicates the percentage of the number of correctly predicted samples in the test set to the total number of samples in the test set. The specific definition is shown in Equation (22):

$$OA=\frac{T}{T+F}$$

(22)

where $T$ denotes the number of samples correctly classified and $F$ denotes the number of samples incorrectly classified. The datasets are divided into three parts: head, middle, and tail, to evaluate the methods effectively and comprehensively, and the classification accuracy of the samples is calculated separately. Among them, categories with more than $2/3$ of the maximum number of samples from each category belong to the head part, categories with less than $1/3$ of the maximum number of samples from each category belong to the tail part, and the rest of the categories belong to the middle part. The confusion matrix can visually represent the classification results and is widely used to measure the performance of the method.

4.5. Comparison Experiments

To verify the effectiveness of our proposed method, the comparison experiments are conducted extensively on five datasets, HistAerial, SIRI-WHU, NWPU-RESISC45, PatternNet, and AID. Before the experiments, the long-tailed processing with various unbalanced proportions is performed on the above datasets so that they can be more effectively tested to determine whether the proposed method can effectively improve the classification accuracy of the samples from the weak category of tails and whether it can solve various problems brought by the data with long-tailed distribution in real situations for the remote sensing image classification tasks.

The methods used in the comparison experiments are based on the design idea of loss reweighting because such methods can be applied to the classification task of remote sensing long-tailed data in a plug-and-play way without changing the design structure of the original method or adding additional training parameters. According to the implementation, this kind of method is divided into three types, the first one is directly utilizing the number of samples from each category for category weighting, and its representative methods are Effective Number and Class Balanced. The second one is to adjust the positive and negative sample gradients to coordinate the learning progress of samples from the head categories and samples from the tail categories, which is represented by the SeeSaw and Equalization series [43]. The third one is our proposed method. Additionally, to make the comparison experiments more effective, Softmax cross-entropy, Focal loss [44], and GHM loss [45], which are loss functions commonly used in classification tasks to solve the sample imbalance problem, are introduced.

4.5.1. Experiment Results of the Long-Tailed HistAerial Dataset

The HistAerial dataset is a panchromatic remote sensing image dataset composed of seven remote sensing scenes. The images in this dataset contain only one band of remote sensing information, so the image quality is generally not high. In this paper, an extensive comparison experiment is conducted on this dataset to verify the effectiveness of our proposed method for panchromatic low-quality remote sensing data obeying a long-tailed distribution. The experimental results are shown in Table 2 and Figure 6.

Table 2. Comparison results of the proposed method with other similar advanced methods on the long-tailed HistAerial dataset with imbalance factors of 0.005, 0.01, and 0.02. The values in the table are the top1 OA (%).

Imbalance Factor	0.005	0.01	0.02
Softmax	57.18 ± 1.89	67.42 ± 0.54	72.27 ± 1.61
SeeSaw [35]	60.85 ± 1.43	68.75 ± 0.74	74.85 ± 1.00
Class Balanced	68.67 ± 0.66	74.59 ± 0.73	77.61 ± 0.52
Effective Number [33]	67.61 ± 0.87	74.91 ± 0.52	77.96 ± 0.29
Equalization [34]	56.59 ± 1.31	63.93 ± 1.03	74.32 ± 0.28
Equalizationv2 [43]	52.27 ± 0.64	62.67 ± 0.53	72.95 ± 0.21
Focal [44]	45.37 ± 1.08	57.94 ± 0.41	67.52 ± 1.01
GHM [45]	34.00 ± 0.83	38.87 ± 0.76	44.18 ± 2.82
ours	70.14 ± 0.63	75.60 ± 0.80	78.70 ± 0.74

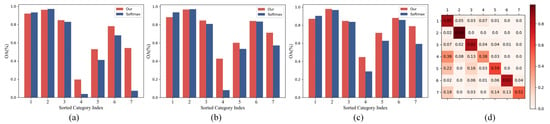
Figure 6. (a–c) show the classification accuracy of the proposed method and Softmax cross-entropy method for samples from each category in the long-tailed HistAerial dataset with imbalance ratios of 0.005,0.01, and 0.02, respectively. (d) shows the classification confusion matrix of the proposed method on the long-tailed HistAerial dataset with an imbalance ratio of 0.005.

The results in Table 2 show that our proposed method achieves the highest classification accuracy on the datasets with imbalance ratios of 0.005, 0.01, and 0.02. This fully verifies the effectiveness of our proposed method for long-tailed panchromatic remote sensing data. In particular, with an imbalance ratio of 0.005, the classification accuracy of our proposed method is 1.47% higher than that of the suboptimal method, which indicates that our proposed method can effectively mitigate the serious negative effects caused by the extremely imbalanced data distribution. It is also obvious from the table that the methods based on the number of samples from each category (e.g., Class Balanced and Effective Number) also have quite good performance for long-tailed remote sensing data. However, after deeper analysis, these methods sacrifice the classification accuracy of the samples from the head categories significantly in exchange for the improvement in the accuracy of the samples from the tail categories. This is unacceptable for real applications. In real applications, it is the effective detection of samples from the head categories that is the main requirement for many application tasks. Unlike the above methods, our proposed method can substantially improve the classification accuracy of the samples from the tail categories while maintaining the high classification accuracy of the samples from the head categories, thus solving the long-tailed problem of remote sensing data.

4.5.2. Experiment Results of the Long-Tailed SIRI-WHU Dataset

The SIRI-WHU dataset is a small remote sensing dataset containing 12 scene categories. An extensive comparison experiment is conducted on this dataset with the current state-of-the-art similar methods to verify the effectiveness of the proposed method for small long-tailed datasets in this paper. The experimental results are shown in Table 3 and Figure 7.

Table 3. Comparison results of the proposed method with other similar advanced methods on the long-tailed SIRI-WHU dataset with imbalance factors of 0.01, 0.02, and 0.05. The values in the table are the top1 OA (%).

Imbalance Factor	0.01	0.02	0.05
Softmax	47.8 ± 1.21	49.68 ± 1.00	62.01 ± 0.69
SeeSaw [35]	47.24 ± 0.81	49.62 ± 0.37	65.11 ± 0.35
Class Balanced	49.98 ± 1.24	54.09 ± 0.83	64.72 ± 1.29
Effective Number [33]	47.14 ± 0.33	54.12 ± 0.56	66.78 ± 0.42
Equalization [34]	48.27 ± 0.73	49.38 ± 0.54	61.75 ± 0.25
Equalizationv2 [43]	45.87 ± 0.36	50.83 ± 0.76	62.70 ± 0.40
Focal [44]	46.89 ± 2.38	50.55 ± 1.30	64.57 ± 0.59
GHM [45]	43.80 ± 1.54	45.40 ± 1.58	50.30 ± 1.77
ours	50.71 ± 1.07	54.91 ± 0.72	67.35 ± 0.36

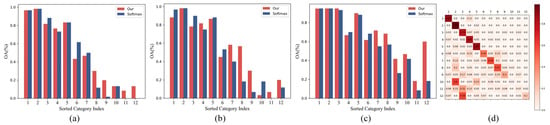
Figure 7. (a–c) show the classification accuracy of the proposed method and Softmax cross-entropy method for samples from each category in the long-tailed SIRI-WHU dataset with imbalance ratios of 0.01,0.02 and 0.05, respectively. (d) shows the classification confusion matrix of the proposed method on the long-tailed SIRI-WHU dataset with an imbalance ratio of 0.02.

The results in Table 3 show that our proposed method achieves the highest average classification accuracy on the datasets with imbalance ratios of 0.01, 0.02, and 0.05. This fully demonstrates that our proposed method has a fairly good classification performance for long-tailed datasets with a small number of samples. Meanwhile, the methods based on the number of samples from each category still achieve fairly good performance with the design mentioned above. Suboptimal classification accuracy was achieved on the datasets with all three imbalance ratios. In contrast, the Equalization series methods have worse classification accuracy, only higher than the Softmax cross-entropy. This kind of method may be better at handling long-tailed data with multiple categories. It can also be seen from Figure 7 that our proposed method can solve the long-tailed problem of remote sensing data by substantially improving the classification accuracy of the samples from the tail categories while maintaining the original classification accuracy of the samples from the head categories. Our proposed method is more in line with the needs of real application tasks than the method based on the number of samples from each category.

4.5.3. Experiment Results of the Long-Tailed NWPU-RESISC45 Dataset

The NWPU-RESISC45 dataset is a medium-sized remote sensing dataset containing 45 scene categories. An extensive comparison experiment is conducted on this dataset with the current advanced similar methods to verify the effectiveness of our proposed method for multi-category long-tailed datasets. The experimental results are shown in Table 4 and Figure 8.

Table 4. Comparison results of the proposed method with other similar advanced methods on the long-tailed NWPU-RESISC45 dataset with imbalance factors of 0.005, 0.01, and 0.02. The values in the table are the top1 OA (%).

Imbalance Factor	0.005	0.01	0.02
Softmax	49.29 ± 0.59	54.53 ± 0.50	59.79 ± 0.22
SeeSaw [35]	51.18 ± 0.97	56.15 ± 0.37	62.24 ± 0.68
Class Balanced	45.03 ± 0.36	52.88 ± 0.74	60.90 ± 0.46
Effective Number [33]	45.72 ± 0.69	53.87 ± 0.12	61.69 ± 0.20
Equalization [34]	50.73 ± 0.41	54.71 ± 0.34	61.49 ± 0.17
Equalizationv2 [43]	50.69 ± 0.08	56.29 ± 0.47	61.99 ± 0.18
Focal [44]	43.39 ± 1.02	46.66 ± 1.23	52.44 ± 1.52
GHM [45]	37.47 ± 0.25	40.58 ± 0.75	45.07 ± 0.23
ours	52.81 ± 0.53	57.21 ± 0.43	63.25 ± 0.27

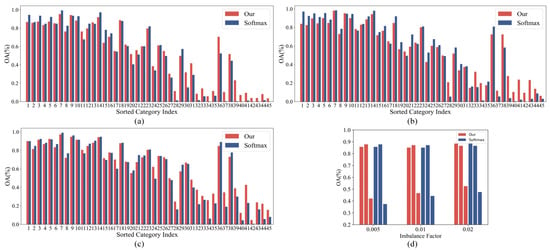
Figure 8. (a–c) show the classification accuracy of the proposed method and Softmax cross-entropy method for samples from each category in the long-tailed NWPU-RESISC45 dataset with imbalance ratios of 0.005,0.01, and 0.02, respectively. (d) shows the average classification accuracy of the proposed method and the Softmax cross-entropy on the long-tailed NWPU-RESISC45 data set with imbalance ratios of 0.005, 0.01, and 0.02 for samples from the head categories, middle categories, and tail categories, respectively.

The results in Table 4 show that our proposed method achieves the highest average classification accuracy on the datasets with imbalance ratios of 0.005, 0.01, and 0.02. Meanwhile, other similar methods (Seesaw, Equalization, and Equalizationv2) also have quite good performance, especially the Equalization series algorithm. This shows that the Equalization series methods are very effective for solving long-tailed data with a high number of categories. In contrast, the classification accuracy of methods based on the number of samples from each category decreases considerably, especially for the most unbalanced data. This shows that such methods have obvious shortcomings for long-tailed data with a large number of categories. As can be seen from Figure 8, our proposed method has a significant improvement in the classification accuracy for the samples from the tail categories compared to the Softmax cross-entropy, while it maintains a similar classification accuracy for the samples from the head and middle categories.

4.5.4. Experiment Results of the Long-Tailed PatternNet Dataset

The PatternNet dataset is a large dataset with 38 scene categories and has more samples than the above two datasets. An extensive comparison experiment is conducted on this dataset with current state-of-the-art similar methods to verify the effectiveness of the proposed method in this paper. The experimental results are shown in Table 5 and Figure 9.

Table 5. Comparison results of the proposed method with other similar advanced methods on the long-tailed PatternNet dataset with imbalance factors of 0.005, 0.01, and 0.02.

Methods	Imbalance Factor	Head Acc (%)	Middle Acc (%)	Tail Acc (%)	OA (%)
Softmax		98.14 ± 0.13	99.72 ± 0.04	79.20 ± 0.20	83.42 ± 0.14
SeeSaw [35]		98.04 ± 0.02	99.68 ± 0.11	79.56 ± 0.42	83.81 ± 0.27
Class Balanced		88.52 ± 0.98	97.66 ± 0.17	78.66 ± 0.99	81.94 ± 0.83
Effective Number [33]		89.58 ± 2.20	98.30 ± 0.21	80.37 ± 0.68	83.57 ± 0.49
Equalization [34]	0.005	98.60 ± 0.33	99.68 ± 0.07	78.97 ± 0.37	83.20 ± 0.36
Equalizationv2 [43]		98.94 ± 0.47	99.60 ± 0.03	78.27 ± 0.22	82.51 ± 0.33
Focal [44]		97.71 ± 0.39	99.21 ± 0.04	78.02 ± 1.73	82.46 ± 1.26
GHM [45]		98.21 ± 0.48	99.52 ± 0.14	67.75 ± 1.19	74.34 ± 0.89
Ours		97.54 ± 0.26	99.52 ± 0.11	81.64 ± 0.37	84.80 ± 0.89
Softmax		98.60 ± 0.05	99.41 ± 0.07	85.11 ± 0.51	88.26 ± 0.24
SeeSaw [35]		98.30 ± 0.05	99.30 ± 0.11	85.92 ± 0.30	88.99 ± 0.21
Class Balanced		91.14 ± 0.30	97.31 ± 0.30	86.60 ± 0.94	88.45 ± 0.71
Effective Number [33]		93.23 ± 0.37	98.13 ± 1.03	86.10 ± 0.21	88.77 ± 0.33
Equalization [34]	0.01	98.88 ± 0.26	99.16 ± 0.17	84.91 ± 0.38	88.26 ± 0.31
Equalizationv2 [43]		98.63 ± 0.23	99.35 ± 0.08	81.57 ± 0.44	85.70 ± 0.34
Focal [44]		97.90 ± 0.21	98.89 ± 0.49	82.72 ± 0.75	86.57 ± 0.53
GHM [45]		98.60 ± 0.19	99.26 ± 0.03	75.85 ± 0.42	81.40 ± 0.29
Ours		98.09 ± 0.30	99.10 ± 0.17	87.00 ± 0.36	89.76 ± 0.24
Softmax		98.46 ± 0.25	99.42 ± 0.12	88.55 ± 0.16	91.61 ± 0.15
SeeSaw [35]		97.70 ± 0.30	99.46 ± 0.04	88.96 ± 0.68	91.84 ± 0.49
Class Balanced		91.69 ± 0.27	98.02 ± 0.35	90.17 ± 0.63	91.94 ± 0.35
Effective Number [33]		93.43 ± 0.39	98.05 ± 0.27	90.75 ± 0.64	92.19 ± 0.42
Equalization [34]	0.02	98.36 ± 0.13	99.44 ± 0.06	89.20 ± 0.56	91.69 ± 0.20
Equalizationv2 [43]		98.71 ± 0.21	99.36 ± 0.18	86.35 ± 0.33	90.05 ± 0.24
Focal [44]		97.85 ± 0.25	98.86 ± 0.45	87.27 ± 0.66	90.52 ± 0.50
GHM [45]		98.05 ± 0.05	99.20 ± 0.46	86.68 ± 0.49	90.13 ± 0.34
ours		97.39 ± 0.45	99.28 ± 0.09	91.05 ± 0.27	93.37 ± 0.30

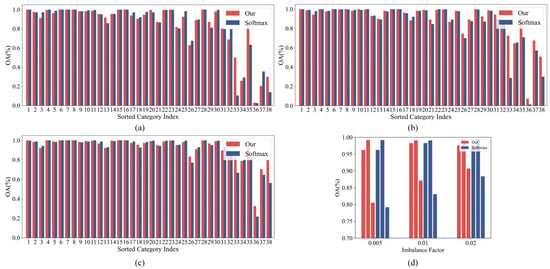
Figure 9. (a–c) show the classification accuracy of the proposed method and Softmax cross-entropy method for samples from each category in the long-tailed PatternNet dataset with imbalance ratios of 0.005, 0.01, and 0.02, respectively. (d) shows the average classification accuracy of the proposed method and the Softmax cross-entropy method on the long-tailed PatternNet dataset with imbalance ratios of 0.005, 0.01, and 0.02 for samples from the head categories, middle categories and tail categories, respectively.

From Table 5, it can be seen that our proposed method achieves the highest average classification accuracy on the datasets with imbalance ratios of 0.005, 0.01, and 0.02, as well as on the samples from the tail categories. This fully verifies the effectiveness of our proposed method for long-tailed data with a large number of samples. Although the methods based on the number of samples from each category have a fairly good classification accuracy, they also greatly sacrifice the classification accuracy of the samples from the head categories. Other similar methods, especially SeeSaw, also perform quite well. SeeSaw maintains a similar accuracy to Softamx cross-entropy for samples from the head categories and the middle categories, while the classification accuracy of the samples from the tail categories is improved, which fully proves the effectiveness of this method. The results in Figure 9 further reveal the greatest advantage of our proposed method. That is, the classification accuracy of samples from the tail categories is substantially improved while maintaining the accuracy of samples from the head categories.

4.5.5. Experiment Results of the Long-Tailed AID Dataset

Similar to the PatternNet dataset, AID is also a medium-sized dataset with 30 scene categories. An extensive comparison experiment is conducted on this dataset with current state-of-the-art similar methods to verify the effectiveness of our method for medium-sized long-tailed data. The experimental results are shown in Table 6 and Figure 10.

Table 6. Comparison results of the proposed method with other similar advanced methods on the long-tailed AID dataset with decay factors of 2, 3, and 4.

Methods	Decay Factor	Head Acc (%)	Middle Acc (%)	Tail Acc (%)	OA (%)
Softmax		93.26 ± 0.80	88.81 ± 0.37	73.35 ± 0.72	83.68 ± 0.21
SeeSaw [35]		92.93 ± 0.19	88.45 ± 0.64	74.13 ± 0.26	84.35 ± 0.25
Class Balanced		89.70 ± 1.93	86.39 ± 1.26	77.33 ± 1.91	83.65 ± 0.53
Effective Number [33]		88.83 ± 0.95	86.61 ± 0.21	78.57 ± 1.18	83.91 ± 0.53
Equalization [34]	2	93.59 ± 0.44	88.75 ± 0.26	72.90 ± 0.54	83.65 ± 0.33
Equalization2 [43]		92.94 ± 0.39	90.05 ± 1.92	69.97 ± 0.04	82.28 ± 0.26
Focal [44]		88.08 ± 0.48	81.96 ± 1.46	65.94 ± 2.83	76.57 ± 0.96
GHM [45]		87.42 ± 0.70	79.41 ± 0.86	57.85 ± 1.78	72.66 ± 1.08
Ours		91.90 ± 0.17	88.83 ± 0.21	77.73 ± 0.46	84.63 ± 0.09
Softmax		92.38 ± 0.36	88.66 ± 0.41	66.75 ± 0.52	76.35 ± 0.26
SeeSaw [35]		92.14 ± 0.60	87.66 ± 0.83	68.87 ± 0.52	77.36 ± 0.41
Class Balanced		85.71 ± 0.73	84.80 ± 0.75	69.93 ± 0.81	76.11 ± 0.60
Effective Number [33]		85.90 ± 1.10	85.20 ± 1.30	71.25 ± 0.58	77.01 ± 0.28
Equalization [34]	3	92.75 ± 0.66	87.40 ± 0.65	64.82 ± 0.35	75.11 ± 0.30
Equalization2 [43]		93.33 ± 0.29	87.46 ± 0.66	61.06 ± 1.04	73.11 ± 0.62
Focal [44]		87.71 ± 1.31	83.33 ± 0.37	56.06 ± 2.58	68.09 ± 1.95
GHM [45]		85.89 ± 2.20	82.09 ± 2.31	48.73 ± 2.56	62.95 ± 2.05
Ours		90.54 ± 0.77	88.06 ± 1.09	71.29 ± 0.49	78.43 ± 0.39
Softmax		92.54 ± 0.91	87.50 ± 1.97	61.12 ± 0.77	71.92 ± 0.65
SeeSaw [35]		91.75 ± 0.30	87.38 ± 0.64	62.03 ± 0.20	72.23 ± 0.13
Class Balanced		77.44 ± 1.12	79.23 ± 0.60	62.80 ± 1.84	68.21 ± 1.55
Effective Number [33]		81.18 ± 0.65	80.82 ± 0.42	62.78 ± 0.51	69.51 ± 0.44
Equalization [34]	4	92.68 ± 0.43	88.50 ± 0.93	60.72 ± 0.45	71.98 ± 0.25
Equalization2 [43]		92.33 ± 0.55	87.33 ± 1.03	58.26 ± 0.84	69.76 ± 0.42
Focal [44]		84.51 ± 2.09	81.56 ± 3.10	48.86 ± 4.28	61.52 ± 3.18
GHM [45]		85.89 ± 1.34	81.91 ± 1.37	41.57 ± 1.30	57.31 ± 1.00
ours		90.85 ± 0.93	87.57 ± 0.63	65.17 ± 0.86	74.25 ± 0.47

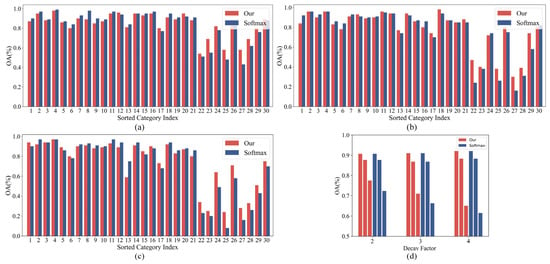
Figure 10. (a–c) show the classification accuracy of the proposed method and Softmax cross-entropy method for samples from each category in the long-tailed AID dataset with decay factors of 2, 3, and 4, respectively. (d) shows the average classification accuracy of the proposed method and the Softmax cross-entropy method on the long-tail AID dataset with decay factors of 2, 3, and 4 for the head categories, middle categories, and tail categories, respectively.

As can be seen from the results in Table 6, our proposed method achieves the highest average classification accuracy on the datasets with decay factors of 2, 3, and 4 for our proposed method, as well as for samples in the tail categories with decay factors of 3 and 4. This again demonstrates that our proposed method is very effective for long-tailed data with a large number of samples. Meanwhile, it can be seen that the methods based on the number of samples from each category (e.g., Class Balanced and Effective Number) also achieve quite good classification results. However, as shown above, this kind of method sacrifices too much classification accuracy for samples from the head categories. In the classification task of long-tailed data with a decay factor of 3, the Class Balanced achieves a 69.93% classification accuracy for the samples from the tail categories but only 85.71% for samples from the head categories, which is nearly 6.67% lower than the Softmax cross-entropy. Effective Number is similar, with a 6.48% decrease in classification accuracy for the samples from the head categories. In comparison, the performance of other similar methods, especially SeeSaw, is quite good. Figure 10 again reveals the greatest advantage of our proposed method, which is not repeated here.

5. Discussion

This research aims to solve the long-tailed problem in remote sensing image classification, and the experimental results show that our method has better performance than other similar methods. From the results of the comparison experiments in Section 4.5, it is found that although the loss reweighting methods based on the number of samples from each category are useful for alleviating the negative effects of the long-tailed problem, the static indicator can neither reflect the classification difficulty between categories nor adapt to the dynamic training process of the model. Thus, it can easily lead to over-weighting or under-weighting and then degrade the performance of the method.

To solve this problem, this paper proposes a loss reweighting method based on the category cumulative classification scores to improve the classification accuracy of samples from the tail categories. Meanwhile, to further optimize the classification results of long-tailed remote sensing data, this paper also improves the original cross-entropy and proposes a novel loss function named Equilibrium cross-entropy. To verify the effectiveness of these proposed modules and search for the optimal parameters, ablation experiments and parameter analysis experiments are conducted in this section.

5.1. Ablation Study

To verify the effectiveness of the modules in the proposed method in this paper, an extensive ablation experiment is conducted on the AID dataset. The experiment uses the same backbone network and training strategy as in the previous section. The results of the ablation experiment are shown in Table 7.

Table 7. Ablation study using long-tailed AID datasets with decay factors of 2 and 3.

Method	CWM	E-Loss	DF	Head Acc (%)	Middle Acc (%)	Tail Acc (%)	OA (%)
CCSMLW	Ⅹ	Ⅹ	2	92.99 ± 0.62	87.94 ± 0.89	72.89 ± 0.15	83.04 ± 0.30
	√	Ⅹ		92.71 ± 0.42	87.57 ± 0.54	75.77 ± 0.85	83.93 ± 0.46
	Ⅹ	√		93.33 ± 0.18	88.41 ± 0.33	74.75 ± 0.41	84.05 ± 0.20
	√	√		91.90 ± 0.17	88.83 ± 0.21	77.73 ± 0.46	84.63 ± 0.09
	Ⅹ	Ⅹ	3	91.47 ± 0.57	88.19 ± 0.28	65.73 ± 0.84	75.46 ± 0.71
	√	Ⅹ		91.16 ± 0.24	87.36 ± 0.52	69.03 ± 0.28	77.22 ± 0.08
	Ⅹ	√		92.61 ± 0.44	88.26 ± 0.83	67.62 ± 1.20	76.75 ± 0.31
	√	√		90.54 ± 0.77	88.06 ± 1.09	71.29 ± 0.49	78.43 ± 0.39

The results in Table 7 fully demonstrate the effectiveness of the modules in the proposed method in this paper. The Equilibrium Cross-Entroy loss function has all the improvements in classification accuracy on the head categories, middle category, and tail categories compared to the traditional Cross-Entroy loss function, which fully demonstrates that the effective combination of the sigmoid function with the softmax function can improve the overall performance of the method. It also indicates that for long-tailed datasets with multiple categories, appropriately reducing the proportion of their negative gradient loss is beneficial to improving the performance of the method. The loss reweighting method based on the cumulative category classification scores has a slight decrease in classification accuracy in the head categories and middle category (the average decrease is 0.455%), but the classification accuracy in the tail categories is greatly improved (the average improvement is 3.09%). This fully demonstrates that this loss reweighting method is very effective in improving the average classification accuracy of the samples from the tail categories in the long-tailed dataset. The effective combination of these two modules constitutes the method proposed in this paper. From the results in the table, it can be seen that the method proposed in this paper can greatly improve the classification accuracy of the samples from the tail categories (the average improvement is 5.20%) while approximately maintaining the same classification accuracy of the samples from the head categories and the samples from the middle category.

5.2. Parmeter Analysis

A suitable hyper-parameter is very important for the overall performance of the method. Thus, the parameter sensitivity experiments are conducted on the SIRI dataset with an imbalance ratio of 0.02 to search for the best combination of hyper-parameters. The experimental results are shown in Table 8 and Figure 11.

Table 8. Parametric analysis experiments using the long-tailed SIRI-WHU dataset with the imbalance ratio of 0.02.

$\mathit{\alpha }$	$\mathit{\beta }$	OA (%)	$\mathit{\alpha }$	$\mathit{\beta }$	OA (%)	$\mathit{\alpha }$	$\mathit{\beta }$	OA (%)
0.2	0.2	52.36 ± 0.40	0.4	0.2	53.29 ± 0.45	0.6	0.2	54.21 ± 0.82
	0.4	53.51 ± 1.35		0.4	54.36 ± 1.04		0.4	54.91 ± 0.72
	0.6	51.79 ± 1.50		0.6	54.25 ± 0.71		0.6	54.09 ± 0.24
	0.8	51.38 ± 0.59		0.8	52.08 ± 0.43		0.8	52.84 ± 0.35
	1.0	50.02 ± 0.35		1.0	51.57 ± 0.45		1.0	52.93 ± 0.21
$\alpha$	$\beta$	OA (%)	$\alpha$	$\beta$	OA (%)	$\alpha$	$\beta$	OA (%)
0.8	0.2	52.66 ± 0.94	1.0	0.2	50.69 ± 1.48	1.2	0.2	50.38 ± 1.47
	0.4	53.37 ± 0.62		0.4	51.31 ± 1.22		0.4	50.15 ± 1.22
	0.6	52.58 ± 0.97		0.6	52.21 ± 0.50		0.6	49.45 ± 0.65
	0.8	52.78 ± 0.66		0.8	51.62 ± 0.94		0.8	49.30 ± 0.96
	1.0	52.19 ± 0.82		1.0	50.73 ± 0.50		1.0	49.14 ± 1.32

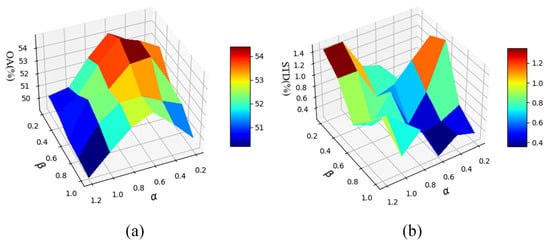
Figure 11. (a) shows the effect of hyperparameters $\alpha$ and $\beta$ on the average accuracy of our proposed method. (b) shows the effect of hyperparameters $\alpha$ and $\beta$ on the stability of our proposed method.

The hyperparameters of $\alpha$ and $\beta$ are used to exponentially weight the elements of the positive and negative sample parts of the category weight matrix, respectively. Larger values indicate that the category weight matrix is more sensitive to the imbalance of the data. This can also be seen from the results in Table 8 and Figure 11. As the values of hyper-parameters $\alpha$ and $\beta$ gradually increase, the classification accuracy of our proposed method experiences a gradual increase to a slight decrease, which fully indicates that proper hyperparameter settings can make the category weight matrix more effective in responding to the imbalance of the long-tailed data while inappropriate parameter settings may bring about under-weighting or over-weighting of the samples from various categories. Of course, the above results also indicate that our proposed method is not too sensitive to these two hyperparameters. Figure 11b shows the effect of different hyperparameter settings on the stability of the classification accuracy of our proposed method. The stability of the method is higher for $\alpha =0.4$ or $\alpha =0.6$. In summary, for the long tail SIRI-WHU dataset with an imbalance ratio of 0.02, $\alpha$ is taken as 0.6, and $\beta$ is taken as 0.4.

Parameter sensitivity experiments were also conducted on other long-tailed datasets, and the hyperparameters $\alpha$ and $\beta$ were found to correlate with the degree of imbalance in the remotely sensed data. That is, the greater the level of imbalance in the dataset, the hyperparameters $\alpha$ and $\beta$ should instead be taken smaller appropriately. That is, the more unbalanced the data are, the greater the difference between the category weights constructed above and the more unstable the training of the method is. Based on this, the hyperparameters of $\alpha$ and $\beta$ are taken as 0.4 when the imbalance ratio is 0.005 for the HistAerial dataset, NWPU-RESISC45 dataset, PatternNet dataset, 0.01 for the SIRI-WHU dataset, and 4 for the AID dataset as the decay factor, respectively. The hyperparameters $\alpha$ and $\beta$ are 0.6 and 0.4 for the imbalance ratio of 0.01 for the first three datasets, 0.02 for the SIRI-WHU dataset, and a decay factor of 3 for the AID dataset, respectively. The hyperparameters of $\alpha$ and $\beta$ are 0.6 for the imbalance ratio of 0.02 for the first three datasets, 0.05 for the SIRI-WHU dataset, and a decay factor of 2 for the AID dataset, respectively.

5.3. Comparative Analysis

In the comparison experiments, the comparison methods used all belong to the category of loss reweighting methods. This is because one of the biggest advantages of this kind of method is plug-and-play. That is, the classification accuracy of long-tailed remote sensing data can be substantially improved without changing the design structure of the original method and without increasing any training parameters. Such methods can also be divided into three types according to different design ideas. The first one is to solve the long-tailed problem by directly using the number of samples from each category for category weighting. The representative methods are Class Balanced and Effective Number. The second one is to improve the overall classification accuracy of the long-tailed data by adjusting the positive and negative sample gradients. The representative methods are the Seesaw and Equalization series. The third one is our proposed methodological idea. In this section, the experimental results on the HistAerial dataset with an imbalance ratio of 0.005 are used to analyze the advantages and disadvantages of these three kinds of methods, as shown in Figure 12.

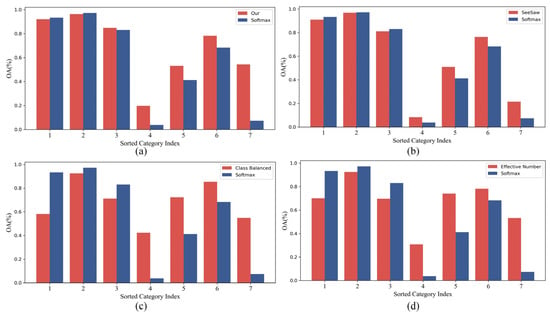
Figure 12. (a–d) show the classification accuracy of our proposed methods, SeeSaw, Class Balanced, Effective Number with Softmax cross-entropy for samples from each category on the long-tailed HistAerial dataset, respectively.

From the results in Figure 12, it can be seen that the method that directly utilizes the number of samples from each category for weighting (Effective Number and Class Balanced) has a significant accuracy decline in the classification of samples from the head categories (e.g., categories 1, 2, and 3). For example, the classification accuracy of Effective Number for category 1 with the largest number of samples is only 70.0%, which is 23.3% lower than the classification accuracy of Softmax cross-entropy. The improvement in classification accuracy precision of such methods is evident for samples from the tail categories. For example, Effective Number has a classification accuracy of 53.2% for category 7, which has the smallest number of samples, while Softmax cross-entropy has a classification accuracy of 7.3%. In summary, such methods can solve the long-tailed problem effectively, but it is completely unacceptable for the excessive sacrifice of the classification accuracy of samples from the head categories. After all, in real applications, it is the samples from the head categories that are the primary objects of classification for the classification task.

Such methods, represented by SeeSaw, basically maintain a similar classification accuracy to Softmax cross-entropy for samples from the head categories and have some improvement in classification accuracy for samples from the tail categories. However, the improvement to such methods is relatively small, and even for samples from some categories, there is no improvement in accuracy.

Unlike the above two kinds of methods, our proposed method has good classification accuracy not only for samples from the head categories but also for samples from the tail categories. For example, for category 7, which has the smallest number of samples, the classification accuracy of our proposed method is 54.3%, which is nearly 47% improvement over Softmax cross-entropy. In summary, our proposed method avoids the drawback that the methods represented by Effective Number sacrifice too much for the classification accuracy of samples from the head categories and has a higher classification accuracy of samples from the tail categories than the methods represented by SeeSaw.

6. Conclusions

In this paper, we first analyze in detail the long-tailed problem caused by the uneven distribution of samples in the remote sensing image classification and reveal the various defects of the current classification methods based on balanced data distribution for the long-tailed problem. Based on these, we propose a novel loss reweighting method using cumulative classification scores to solve the long-tailed problem of remote sensing image classification. Unlike the current approach of using the number of samples from each category to weight samples from different categories, our proposed method uses the cumulative classification scores of different categories to automatically construct category weights for samples from different categories adaptively and dynamically coordinate the learning progress of samples from the head and tail categories in combination with the improved equilibrium cross-entropy loss function, thus improving the overall classification accuracy. Compared with the traditional loss reweighting method based on the number of samples from each category, the method proposed in this paper effectively combines the number of samples from each category and the difficulty of category classification and can guide the training learning of the model in a relatively dynamic way, thus having more flexibility and robustness. Extensive comparison experiments are conducted on the five datasets of HistAerial, SIRI-WHU, NWPU-RESISC45, PatternNet, and AID after long-tailed processing, and the performance of the proposed method in this paper outperforms other similar methods, which indicates that our proposed method is effective to deal with the long-tailed problem of remote sensing image classification.