A Case Study on the Convection Initiation Mechanisms over the Northern Edge of Tarim Basin, Xinjiang, Northwest China
Abstract
:1. Introduction
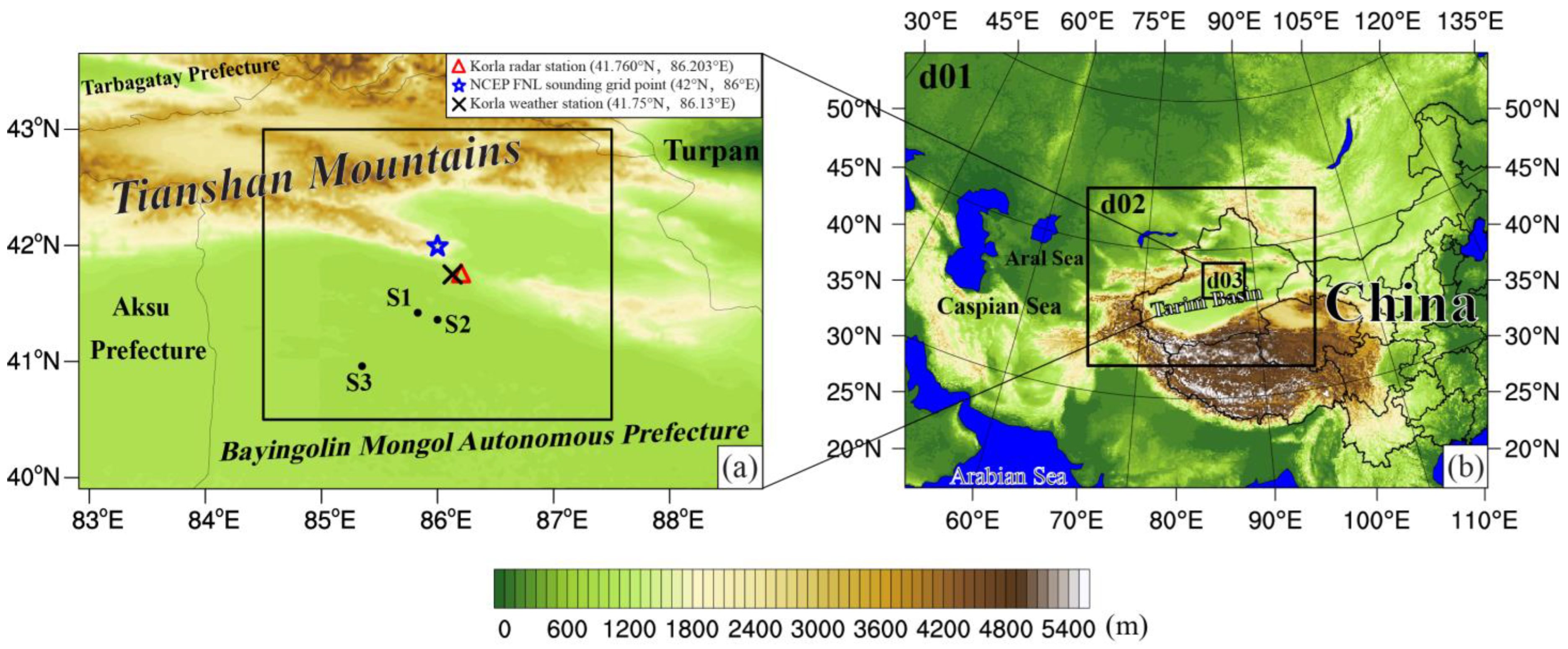
2. Data and Methodology
2.1. Dataset
2.2. Methods
3. Results
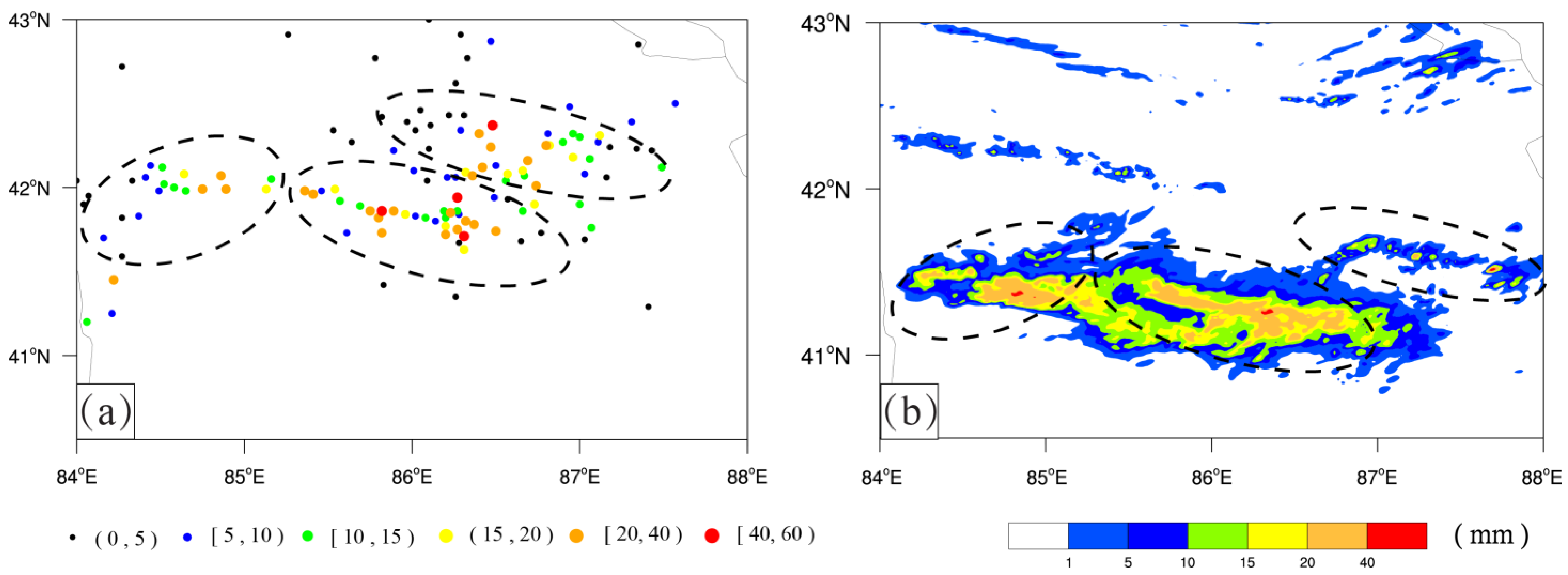
3.1. Case Overview
3.2. Setup of Numerical Experiment
3.3. Evaluation of Simulation
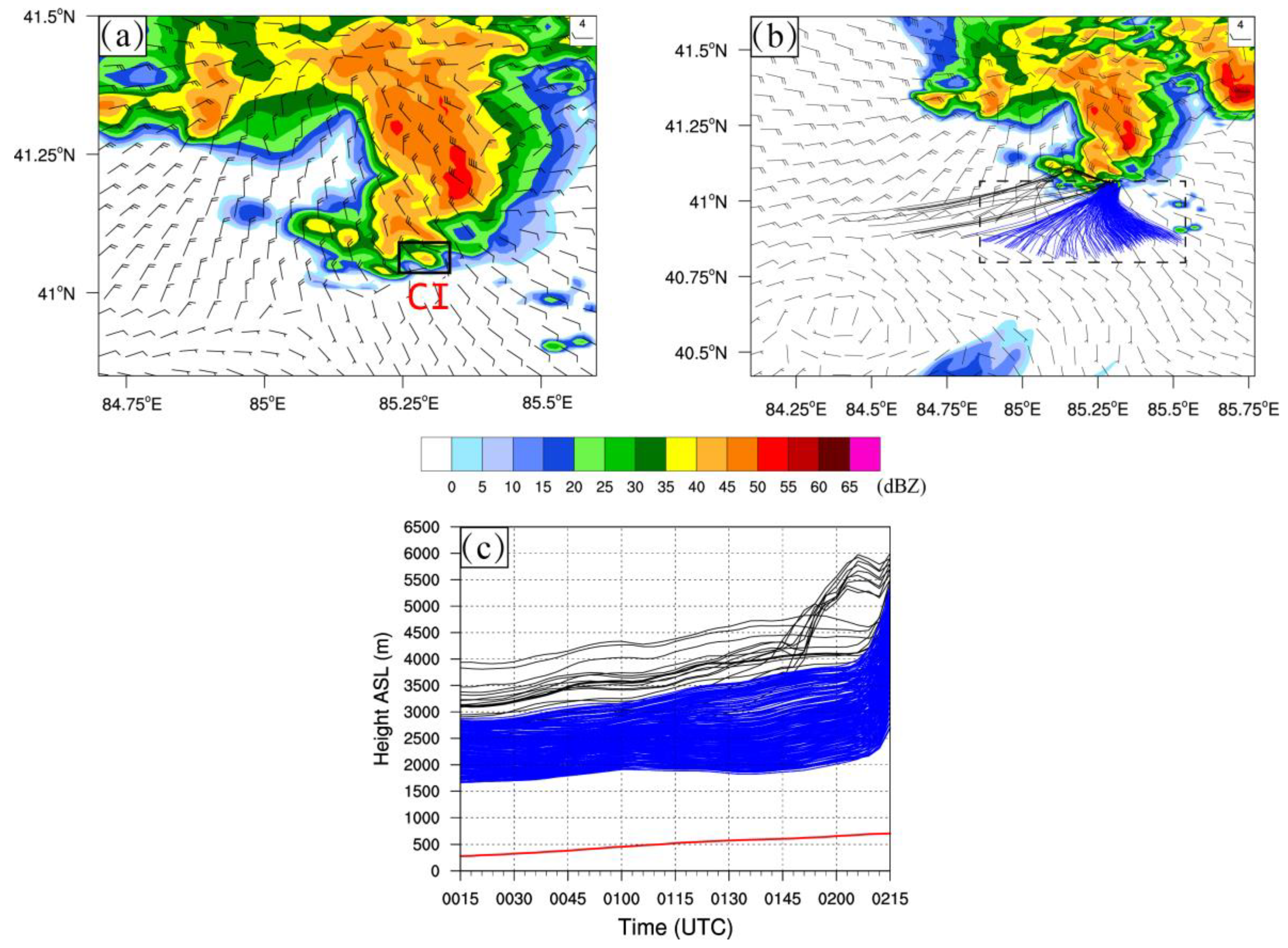
3.4. Convection Initiation
4. Discussion
5. Conclusions
- (1)
- This severe convective weather process occurred in favorable conditions with the southwesterly airflow ahead of the Central Asian Trough (CAT) at 500 hPa and the warm and humid southwesterly airflows at 700 hPa. In addition, there was relatively high convective effective potential energy before the occurrence of the rainstorm, and the warm advection at the lower level also provided a favorable condition for the CI.
- (2)
- The high-resolution WRF model reproduced the severe convective weather and the CI process associated with the GF well. Further analysis based on the vertical momentum budget along the Lagrangian backward trajectories showed that all of the air parcels came from above the planetary boundary layer height; therefore, the convection belonged to “elevated convection”.
- (3)
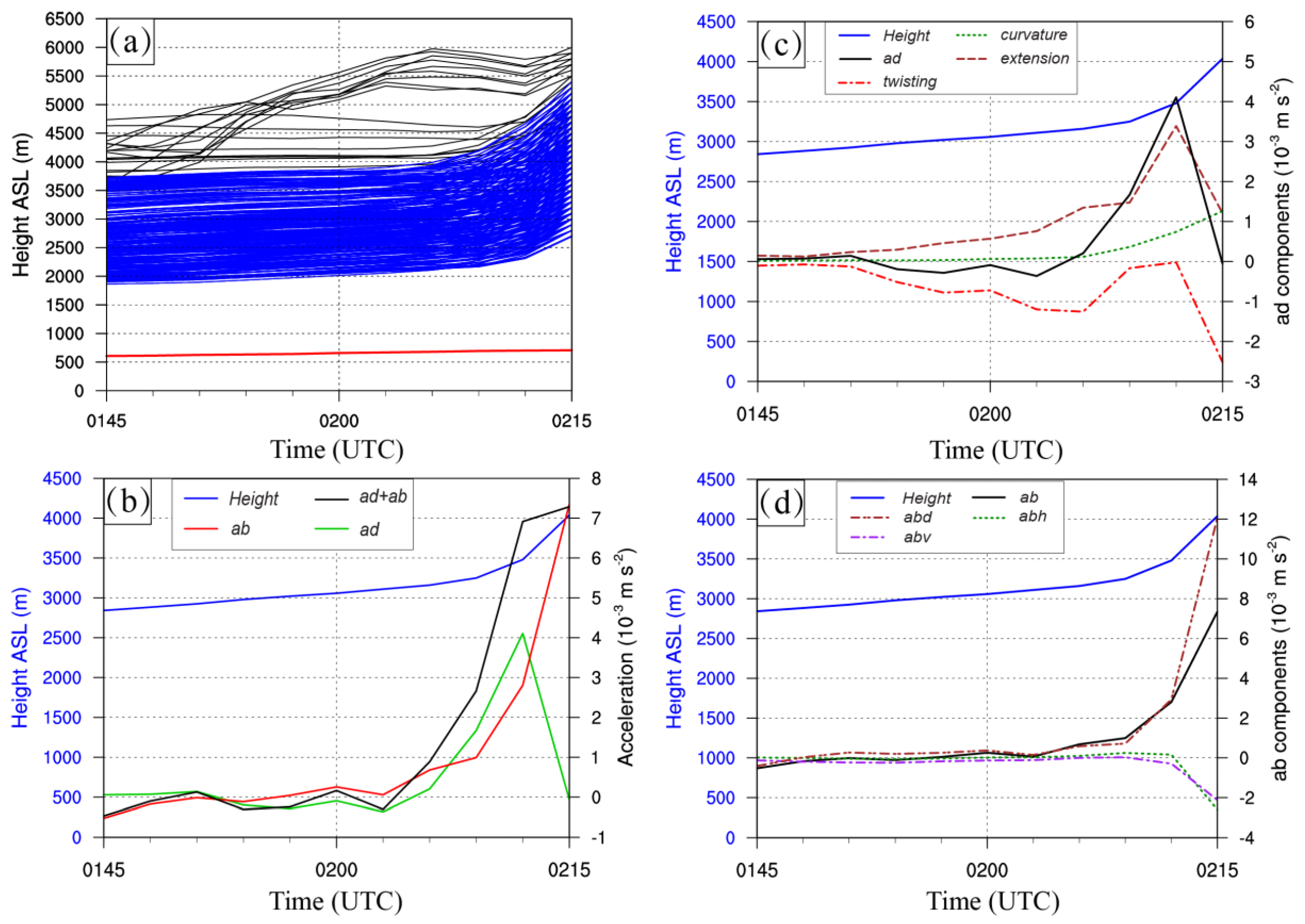
- The vertical acceleration of the air parcels during the CI process was decomposed into dynamic acceleration () and buoyant acceleration (), and both of them positively contributed almost in similar strength to the vertical acceleration. The further decomposition of the showed that it was mainly dominated by the extension term, while the curvature provides a small positive contribution. However, the twisting term provided a negative contribution to the . The is mainly controlled by the buoyant acceleration generated due to the release of latent heat with the ascending of the air parcels.
- (4)
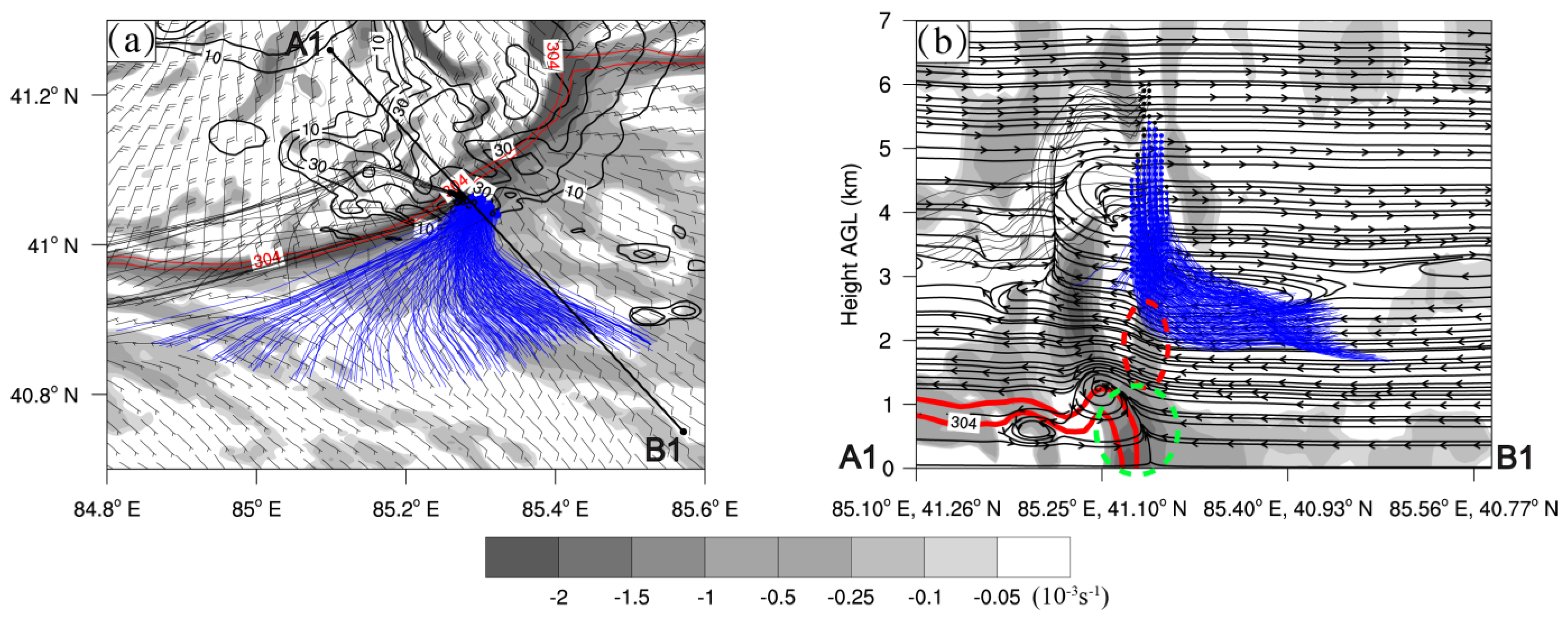
- Further investigations showed that the elevated convergence above the GF in the level about 1.5–3.2 km AGL was the intuitional physical meaning of the extension term which had dominated the . This elevated convergence was generated due to the convergent effect of these two airflows: one was the updraft generated due to the convergence in the low level (below 1.5 km AGL) near the leading edge of the GF, while the other one was the lower branch flow of the mid-level horizontal convective rolls (MHCRs) which centered at about 3–3.5 km AGL ahead of the GF. The MHCRs were generated due to the vertical shear of the horizontal winds in that level in front of the GF.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marengo, J.A.; Alcantara, E.; Cunha, A.P.; Seluchi, M.; Nobre, C.A.; Dolif, G.; Goncalves, D.; Assis Dias, M.; Cuartas, L.A.; Bender, F.; et al. Flash Floods and Landslides in the City of Recife, Northeast Brazil after Heavy Rain on May 25–28, 2022: Causes, Impacts, and Disaster Preparedness. Weather. Clim. Extrem. 2023, 39, 100545. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I. Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2021; Volume 2. [Google Scholar]
- Nanditha, J.S.; Kushwaha, A.P.; Singh, R.; Malik, I.; Solanki, H.; Chuphal, D.S.; Dangar, S.; Mahto, S.S.; Vegad, U.; Mishra, V. The Pakistan Flood of August 2022: Causes and Implications. Earths Future 2023, 11, e2022EF003230. [Google Scholar] [CrossRef]
- Li, Z.; Abulikemu, A.; Zhu, K.; Mamtimin, A.; Zeng, Y.; Li, J.; Abulimiti, A.; Kadier, Z.; Abuduaini, A.; Li, C.; et al. Diurnal Variation Characteristics of Summer Precipitation and Related Statistical Analysis in the Ili Region, Xinjiang, Northwest China. Remote Sens. 2023, 15, 3954. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, K.; Lu, Y.; Zheng, Y.; Xue, M.; Tan, Z.-M.; Xu, X.; Huang, H.; Chen, H.; Xu, F. Variability of Microphysical Characteristics in the “21· 7” Henan Extremely Heavy Rainfall Event. Sci. China Earth Sci. 2022, 65, 1861–1878. [Google Scholar] [CrossRef]
- Kong, M.; Abulikemu, A.; Zheng, J.; Aireti, M.; An, D. A Case Study on Convection Initiation Associated with Horizontal Convective Rolls over Ili River Valley in Xinjiang, Northwest China. Water 2022, 14, 1017. [Google Scholar] [CrossRef]
- He, X.; Abulikemu, A.; Mamtimin, A.; Li, R.; Abulimiti, A.; An, D.; Aireti, M.; Zhou, Y.; Sun, Q.; Li, Z.; et al. On the Mechanisms of a Snowstorm Associated with a Low-Level Cold Front and Low-Level Jet in the Western Mountainous Region of the Junggar Basin, Xinjiang, Northwest China. Atmosphere 2023, 14, 919. [Google Scholar] [CrossRef]
- Abulikemu, A.; Xu, X.; Wang, Y.; Ding, J.; Zhang, S.; Shen, W. A Modeling Study of Convection Initiation Prior to the Merger of a Sea-Breeze Front and a Gust Front. Atmos. Res. 2016, 182, 10–19. [Google Scholar] [CrossRef]
- Abulikemu, A.; Ming, J.; Xu, X.; Zhuge, X.; Wang, Y.; Zhang, Y.; Zhang, S.; Yu, B.; Aireti, M. Mechanisms of Convection Initiation in the Southwestern Xinjiang, Northwest China: A Case Study. Atmosphere 2020, 11, 1335. [Google Scholar] [CrossRef]
- Dalagnol, R.; Gramcianinov, C.B.; Crespo, N.M.; Luiz, R.; Chiquetto, J.B.; Marques, M.T.A.; Neto, G.D.; de Abreu, R.C.; Li, S.; Lott, F.C.; et al. Extreme Rainfall and Its Impacts in the Brazilian Minas Gerais State in January 2020: Can We Blame Climate Change? Clim. Resil. Sustain. 2022, 1, e15. [Google Scholar] [CrossRef]
- Sun, Q.; Abulikemu, A.; Yao, J.; Mamtimin, A.; Yang, L.; Zeng, Y.; Li, R.; An, D.; Li, Z. A Case Study on the Convection Initiation Mechanisms of an Extreme Rainstorm over the Northern Slope of Kunlun Mountains, Xinjiang, Northwest China. Remote Sens. 2023, 15, 4505. [Google Scholar] [CrossRef]
- Abulikemu, A.; Xu, X.; Wang, Y.; Ding, J.; Wang, Y. Atypical Occlusion Process Caused by the Merger of a Sea-Breeze Front and Gust Front. Adv. Atmos. Sci. 2015, 32, 1431–1443. [Google Scholar] [CrossRef]
- Zheng, J.; Abulikemu, A.; Wang, Y.; Kong, M.; Liu, Y. Convection Initiation Associated with the Merger of an Immature Sea-Breeze Front and a Gust Front in Bohai Bay Region, North China: A Case Study. Atmosphere 2022, 13, 750. [Google Scholar] [CrossRef]
- Abulikemu, A.; Wang, Y.; Gao, R.; Wang, Y.; Xu, X. A Numerical Study of Convection Initiation Associated With a Gust Front in Bohai Bay Region, North China. J. Geophys. Res. Atmos. 2019, 124, 13843–13860. [Google Scholar] [CrossRef]
- Hua, S.; Xu, X.; Chen, B. Influence of Multiscale Orography on the Initiation and Maintenance of a Precipitating Convective System in North China: A Case Study. J. Geophys. Res. Atmos. 2020, 125, e2019JD031731. [Google Scholar] [CrossRef]
- Wei, P.; Xu, X.; Xue, M.; Zhang, C.; Wang, Y.; Zhao, K.; Zhou, A.; Zhang, S.; Zhu, K. On the Key Dynamical Processes Supporting the 21.7 Zhengzhou Record-Breaking Hourly Rainfall in China. Adv. Atmos. Sci. 2023, 40, 337–349. [Google Scholar] [CrossRef]
- Kang, Y.; Peng, X.; Wang, S.; Hu, Y.; Shang, K.; Lu, S. Observational Analyses of Topographic Effects on Convective Systems in an Extreme Rainfall Event in Northern China. Atmos. Res. 2019, 229, 127–144. [Google Scholar] [CrossRef]
- Bai, L.; Meng, Z.; Huang, Y.; Zhang, Y.; Niu, S.; Su, T. Convection Initiation Resulting From the Interaction Between a Quasi-Stationary Dryline and Intersecting Gust Fronts: A Case Study. J. Geophys. Res. Atmos. 2019, 124, 2379–2396. [Google Scholar] [CrossRef]
- Wilhelmson, R.B.; Chen, C.-S. A Simulation of the Development of Successive Cells along a Cold Outflow Boundary. J. Atmos. Sci. 1982, 39, 1466–1483. [Google Scholar] [CrossRef]
- Harrison, S.J.; Mecikalski, J.R.; Knupp, K.R. Analysis of Outflow Boundary Collisions in North-Central Alabama. Weather Forecast 2009, 24, 1680–1690. [Google Scholar] [CrossRef]
- Wilson, J.W.; Schreiber, W.E. Initiation of Convective Storms at Radar-Observed Boundary-Layer Convergence Lines. Mon. Weather Rev. 1986, 114, 2516–2536. [Google Scholar] [CrossRef]
- Grasmick, C.; Geerts, B.; Turner, D.D.; Wang, Z.; Weckwerth, T.M. The Relation between Nocturnal MCS Evolution and Its Outflow Boundaries in the Stable Boundary Layer: An Observational Study of the 15 July 2015 MCS in PECAN. Mon. Weather Rev. 2018, 146, 3203–3226. [Google Scholar] [CrossRef]
- Hirt, M.; Craig, G.C.; Schäfer, S.A.K.; Savre, J.; Heinze, R. Cold-pool-driven Convective Initiation: Using Causal Graph Analysis to Determine What Convection-permitting Models Are Missing. Q. J. R. Meteorol. Soc. 2020, 146, 2205–2227. [Google Scholar] [CrossRef]
- Xian, Z.; Pielke, R.A. The Effects of Width of Landmasses on the Development of Sea Breezes. J. Appl. Meteorol. 1991, 1280–1304. Available online: https://www.jstor.org/stable/26185605 (accessed on 23 September 2023). [CrossRef]
- Lee, O.; Shun, C.M. Observation of Sea Breeze Interactions at and near Hong Kong International Airport. Meteorol. Appl. 2003, 10, 1–9. [Google Scholar] [CrossRef]
- Bergemann, M.; Jakob, C.; Lane, T.P. Global Detection and Analysis of Coastline-Associated Rainfall Using an Objective Pattern Recognition Technique. J. Clim. 2015, 28, 7225–7236. [Google Scholar] [CrossRef]
- Wu, F.; Lombardo, K. Precipitation Enhancement in Squall Lines Moving over Mountainous Coastal Regions. J. Atmos. Sci. 2021, 78, 3089–3113. [Google Scholar] [CrossRef]
- Birch, C.E.; Roberts, M.J.; Garcia-Carreras, L.; Ackerley, D.; Reeder, M.J.; Lock, A.P.; Schiemann, R. Sea-Breeze Dynamics and Convection Initiation: The Influence of Convective Parameterization in Weather and Climate Model Biases. J. Clim. 2015, 28, 8093–8108. [Google Scholar] [CrossRef]
- Lock, N.A.; Houston, A.L. Empirical Examination of the Factors Regulating Thunderstorm Initiation. Mon. Weather Rev. 2014, 142, 240–258. [Google Scholar] [CrossRef]
- Markowski, P. Convective Storm Initiation and Organization. In Atmospheric Convection: Research and Operational Forecasting Aspects; Springer: Berlin/Heidelberg, Germany, 2007; pp. 23–28. [Google Scholar]
- Schumacher, R.S.; Clark, A.J.; Xue, M.; Kong, F.; Schumacher, R. Factors Influencing the Development and Maintenance of Nocturnal Heavy-Rain-Producing Convective Systems in a 2 Storm-Scale Ensemble. Mon. Weather. Rev. 2013, 141, 2778–2801. [Google Scholar] [CrossRef]
- Xiao, X.; Sun, J.; Chen, M.; Qie, X.; Ying, Z.; Wang, Y.; Ji, L. Comparison of Environmental and Mesoscale Characteristics of Two Types of Mountain-to-Plain Precipitation Systems in the Beijing Region, China. J. Geophys. Res. Atmos. 2019, 124, 6856–6872. [Google Scholar] [CrossRef]
- Xu Dr., W.; Zipser, E.E.; Chen, Y.L.; Liu, C.; Liou, Y.C.; Lee, W.C.; Jou, B.J.D. An Orography-Associated Extreme Rainfall Event during TiMREX: Initiation, Storm Evolution, and Maintenance. Mon. Weather Rev. 2012, 140, 2555–2574. [Google Scholar] [CrossRef]
- Jeong, J.H.; Lee, D.I.; Wang, C.C. Impact of the Cold Pool on Mesoscale Convective System-Produced Extreme Rainfall over Southeastern South Korea: 7 July 2009. Mon. Weather Rev. 2016, 144, 3985–4006. [Google Scholar] [CrossRef]
- Yu, C.-K.; Lin, C.-Y. Formation and Maintenance of a Long-Lived Taiwan Rainband during 1–3 March 2003. J. Atmos. Sci. 2017, 74, 1211–1232. [Google Scholar] [CrossRef]
- Schenkman, A.D.; Xue, M.; Dawson, D.T. The Cause of Internal Outflow Surges in a High-Resolution Simulation of the 8 May 2003 Oklahoma City Tornadic Supercell. J. Atmos. Sci. 2016, 73, 353–370. [Google Scholar] [CrossRef]
- Klemp, J.B.; Rotunno, R. A Study of the Tornadic Region within a Supercell Thunderstorm. J. Atmos. Sci. 1983, 40, 359–377. [Google Scholar] [CrossRef]
- Weisman, M.L.; Evans, C.; Bosart, L. The 8 May 2009 Superderecho: Analysis of a 3 Km WRF--ARW Realtime Forecast. In Proceedings of the 25th Conference on Severe Local Storms, Denver, CO, USA, 11–14 October 2010. [Google Scholar] [CrossRef]
- Xu, X.; Xue, M.; Wang, Y. Mesovortices within the 8 May 2009 Bow Echo over the Central United States: Analyses of the Characteristics and Evolution Based on Doppler Radar Observations and a High-Resolution Model Simulation. Mon. Weather Rev. 2015, 143, 2266–2290. [Google Scholar] [CrossRef]
- Li, Q.; Wang, B.; Xu, J. Energy Balance and Momentum Budgets Due to the Internal Tides Generated by a Group of Submarine Canyons. Ocean Model. 2023, 181, 102126. [Google Scholar] [CrossRef]
- Fu, S.; Rotunno, R.; Xue, H. Convective Updrafts near Sea-Breeze Fronts. Atmos. Chem. Phys. 2022, 22, 7727–7738. [Google Scholar] [CrossRef]
- Xu, X.; Xue, M.; Wang, Y.; Huang, H. Mechanisms of Secondary Convection within a Mei-Yu Frontal Mesoscale Convective System in Eastern China. J. Geophys. Res. 2017, 122, 47–64. [Google Scholar] [CrossRef]
- Du, Y.; Shen, Y.; Chen, G. Influence of Coastal Marine Boundary Layer Jets on Rainfall in South China. Adv. Atmos. Sci. 2022, 39, 782–801. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Q.; Chen, Y.L.; Zhao, Y.; Wang, X. Numerical Simulations of Spatial Distributions and Diurnal Variations of Low-Level Jets in China during Early Summer. J. Clim. 2014, 27, 5747–5767. [Google Scholar] [CrossRef]
- Marion, G.R.; Trapp, R.J. The Dynamical Coupling of Convective Updrafts, Downdrafts, and Cold Pools in Simulated Supercell Thunderstorms. J. Geophys. Res. Atmos. 2019, 124, 664–683. [Google Scholar] [CrossRef]
- Jeevanjee, N.; Romps, D.M. Effective Buoyancy, Inertial Pressure, and the Mechanical Generation of Boundary Layer Mass Flux by Cold Pools. J. Atmos. Sci. 2015, 72, 3199–3213. [Google Scholar] [CrossRef]
- Xu, K.-M.; Randall, D.A. Updraft and Downdraft Statistics of Simulated Tropical and Midlatitude Cumulus Convection. J. Atmos. Sci. 2001, 58, 1630–1649. [Google Scholar] [CrossRef]
- Thomsen, S.; Greatbatch, R.J.; Dengler, M.; Kanzow, T.; Krahmann, G. Near-Inertial Waves Interacting with a Coherent Anticyclone off Peru. In Proceedings of the Nergy Transfers in Atmosphere and Ocean, Hamburg, Germany, 20–22 April 2015. [Google Scholar]
- Xu, X.; Xue, M.; Wang, Y. The Genesis of Mesovortices within a Real-Data Simulation of a Bow Echo System. J. Atmos. Sci. 2015, 72, 1963–1986. [Google Scholar] [CrossRef]
- Torri, G.; Kuang, Z.; Tian, Y. Mechanisms for Convection Triggering by Cold Pools. Geophys. Res. Lett. 2015, 42, 1943–1950. [Google Scholar] [CrossRef]
- Duolaite, X. Formulation of Precipitation Intensity Standard of Xinjiang. Chin. J. Desert Oasis Meteorol. 2005, 28, 7–8. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M. A Description of the Advanced Research WRF Version 4. NCAR Tech. Note Ncar/Tn-556+ Str 2019, 145. [Google Scholar]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative Forcing by Long-lived Greenhouse Gases: Calculations with the AER Radiative Transfer Models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Adams, J.C. MUDPACK: Multigrid Portable FORTRAN Software for the Efficient Solution of Linear Elliptic Partial Differential Equations. Appl. Math. Comput. 1989, 34, 113–146. [Google Scholar] [CrossRef]
- Yin, J.; Gu, H.; Liang, X.; Yu, M.; Sun, J.; Xie, Y.; Li, F.; Wu, C. A Possible Dynamic Mechanism for Rapid Production of the Extreme Hourly Rainfall in Zhengzhou City on 20 July 2021. J. Meteorol. Res. 2022, 36, 6–25. [Google Scholar] [CrossRef]
- Luo, Y.; Du, Y. The Roles of Low-Level Jets in “21·7” Henan Extremely Persistent Heavy Rainfall Event. Adv. Atmos. Sci. 2023, 40, 350–373. [Google Scholar] [CrossRef]
- LeBel, L.J.; Markowski, P.M. An Analysis of the Impact of Vertical Wind Shear on Convection Initiation Using Large-Eddy Simulations- Importance of Wake Entrainment. Mon. Weather Rev. 2023, 151, 1667–1688. [Google Scholar] [CrossRef]
- Feng, Z.; Varble, A.; Hardin, J.; Marquis, J.; Hunzinger, A.; Zhang, Z.; Thieman, M. Deep Convection Initiation, Growth, and Environments in the Complex Terrain of Central Argentina during CACTI. Mon. Weather Rev. 2021, 150, 1135–1155. [Google Scholar] [CrossRef]
- Singh, I.; Nesbitt, S.W.; Davis, C.A. Quasi-Idealized Numerical Simulations of Processes Involved in Orogenic Convection Initiation over the Sierras de Córdoba. J. Atmos. Sci. 2022, 79, 1127–1149. [Google Scholar] [CrossRef]
- Su, L.; Sun, X.; Du, Y.; Fung, J.C.H.; Chen, G. The Roles of Local Convergences in the Convection Initiation of a Record-Breaking Rainfall Event at the Coastal Pearl River Delta in South China. J. Geophys. Res. Atmos. 2023, 128, e2022JD037234. [Google Scholar] [CrossRef]
- Fedorovich, E.; Gibbs, J.A.; Shapiro, A. Numerical Study of Nocturnal Low-Level Jets over Gently Sloping Terrain. J. Atmos. Sci. 2017, 74, 2813–2834. [Google Scholar] [CrossRef]
- Rao, X.; Zhao, K.; Chen, X.; Huang, A.; Hu, S.; Hu, D.; Liu, X. Roles of Multi-Scale Orography in Triggering Nocturnal Convection at a Summer Rainfall Hotspot Over the South China Coast: A Case Study. J. Geophys. Res. Atmos. 2022, 127, e2022JD036503. [Google Scholar] [CrossRef]
- Browning, K.A.; Blyth, A.M.; Clark, P.A.; Corsmeier, U.; Morcrette, C.J.; Agnew, J.L.; Ballard, S.P.; Bamber, D.; Barthlott, C.; Bennett, L.J.; et al. The Convective Storm Initiation Project. Bull. Am. Meteorol. Soc. 2007, 88, 1939–1956. [Google Scholar] [CrossRef]






| Rain | Snow (In Liquid Form) | ||||
|---|---|---|---|---|---|
| Rating | 12 h Standard | 24 h Standard | Rating | 12 h Standard | 24 h Standard |
| drizzle | 0.0~0.1 | 0.0~0.2 | flurries | 0.0~0.1 | 0.0~0.2 |
| light rain | 0.2~5.0 | 0.3~6.0 | light snow | 0.2~2.5 | 0.3~3.0 |
| medium rain | 5.1~10.0 | 6.1~12.0 | medium snow | 2.6~5.0 | 3.1~6.0 |
| heavy rain | 10.1~20.0 | 12.1~24.0 | heavy snow | 5.1~10.0 | 6.1~12.0 |
| rainstorm | 20.1~40.0 | 24.1~48.0 | blizzard | 10.1~20.0 | 12.1~24.0 |
| heavy rainstorm | 40.1~80.0 | 48.1~96.0 | heavy blizzard | 20.1~40.0 | 24.1~48.0 |
| torrential rainstorm | >80.0 | >96.0 | torrential blizzard | >40.0 | >48.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abulimiti, A.; Sun, Q.; Yuan, L.; Liu, Y.; Yao, J.; Yang, L.; Ming, J.; Abulikemu, A. A Case Study on the Convection Initiation Mechanisms over the Northern Edge of Tarim Basin, Xinjiang, Northwest China. Remote Sens. 2023, 15, 4812. https://doi.org/10.3390/rs15194812
Abulimiti A, Sun Q, Yuan L, Liu Y, Yao J, Yang L, Ming J, Abulikemu A. A Case Study on the Convection Initiation Mechanisms over the Northern Edge of Tarim Basin, Xinjiang, Northwest China. Remote Sensing. 2023; 15(19):4812. https://doi.org/10.3390/rs15194812
Chicago/Turabian StyleAbulimiti, Aerzuna, Qi Sun, Lin Yuan, Yongqiang Liu, Junqiang Yao, Lianmei Yang, Jie Ming, and Abuduwaili Abulikemu. 2023. "A Case Study on the Convection Initiation Mechanisms over the Northern Edge of Tarim Basin, Xinjiang, Northwest China" Remote Sensing 15, no. 19: 4812. https://doi.org/10.3390/rs15194812
APA StyleAbulimiti, A., Sun, Q., Yuan, L., Liu, Y., Yao, J., Yang, L., Ming, J., & Abulikemu, A. (2023). A Case Study on the Convection Initiation Mechanisms over the Northern Edge of Tarim Basin, Xinjiang, Northwest China. Remote Sensing, 15(19), 4812. https://doi.org/10.3390/rs15194812






