Leveraging High-Resolution Long-Wave Infrared Hyperspectral Laboratory Imaging Data for Mineral Identification Using Machine Learning Methods
Abstract
:1. Introduction
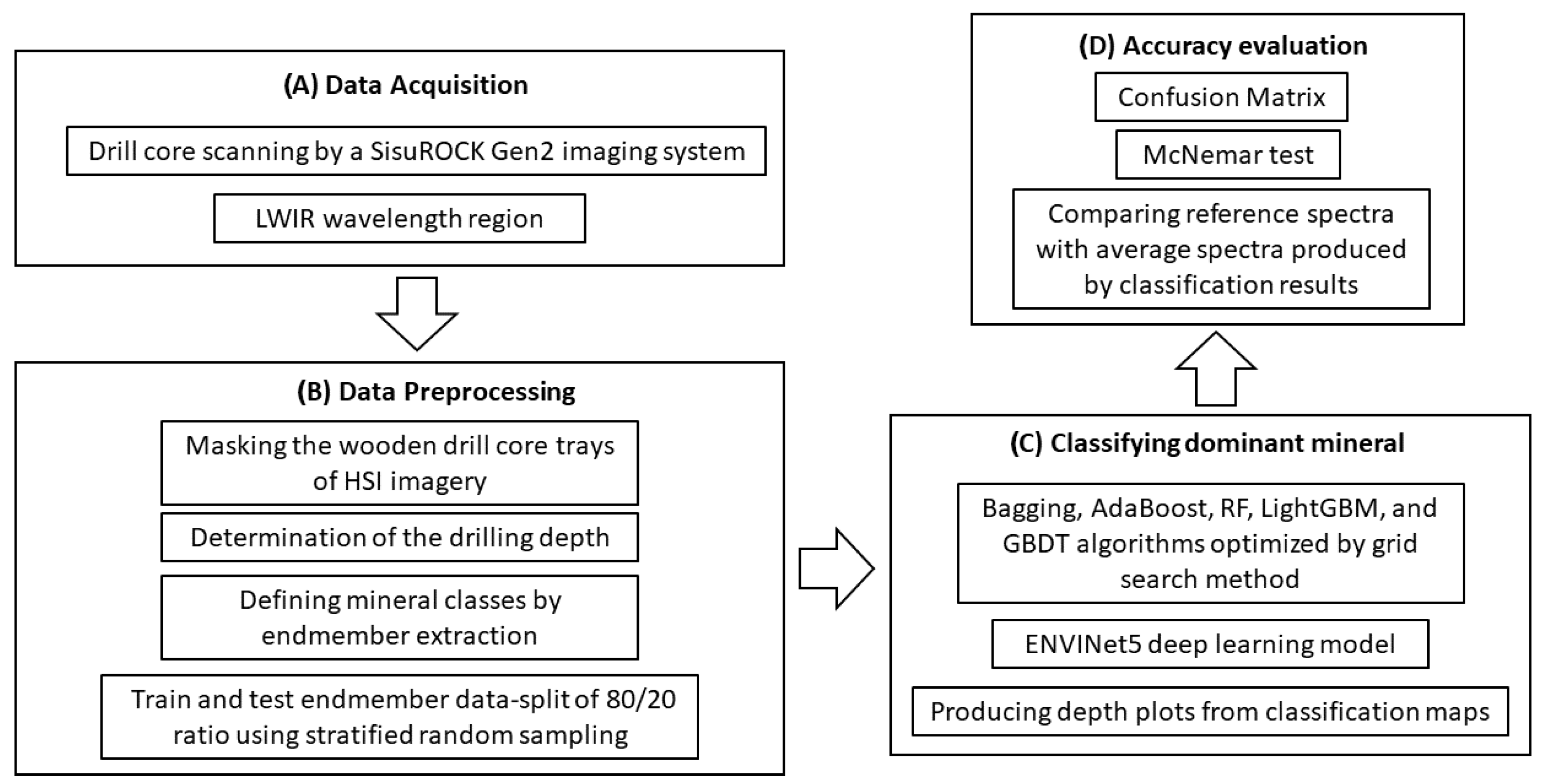
2. Materials and Methods
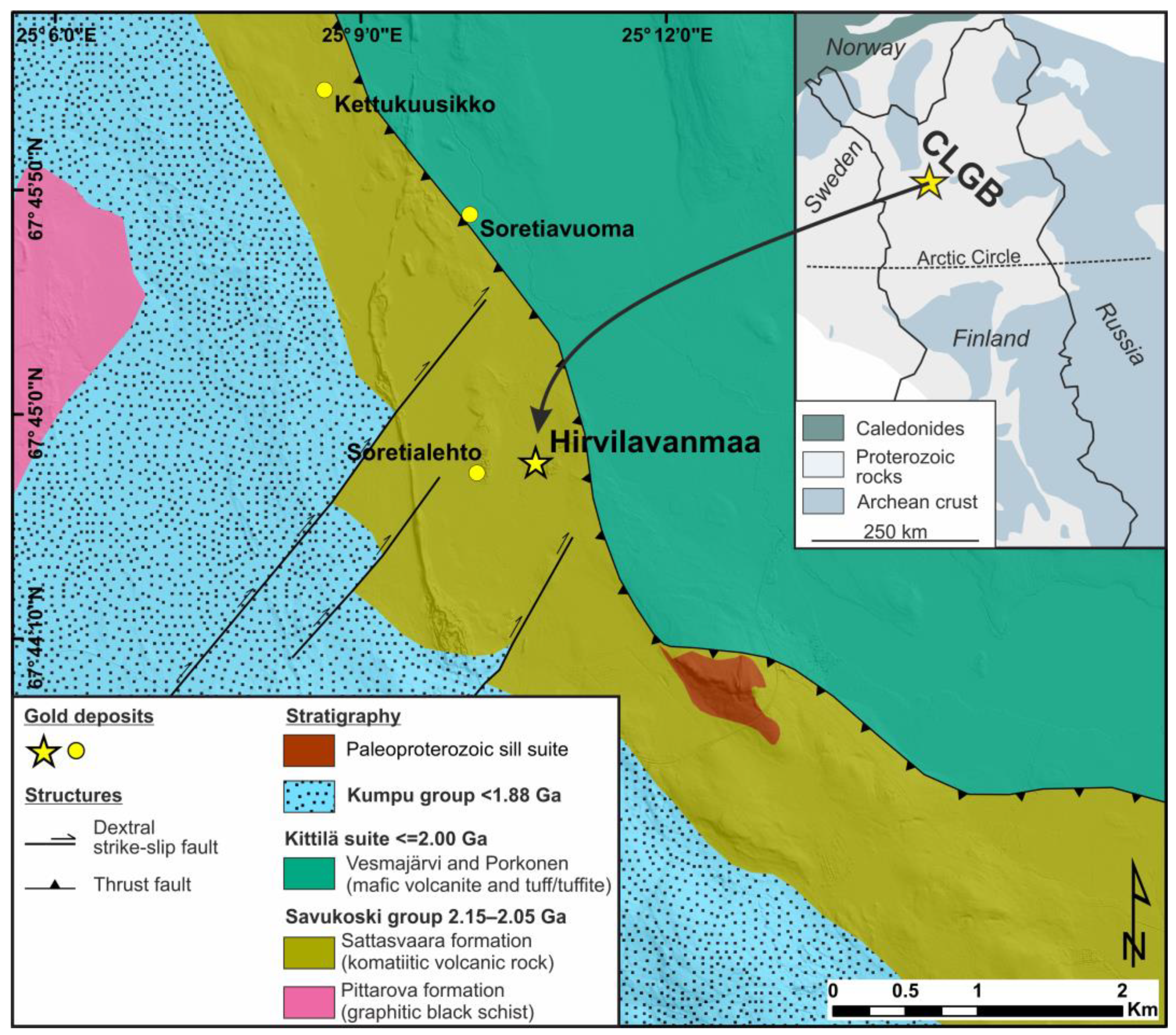
2.1. Drill Core Samples and Laboratory Hyperspectral Imaging Spectrometry
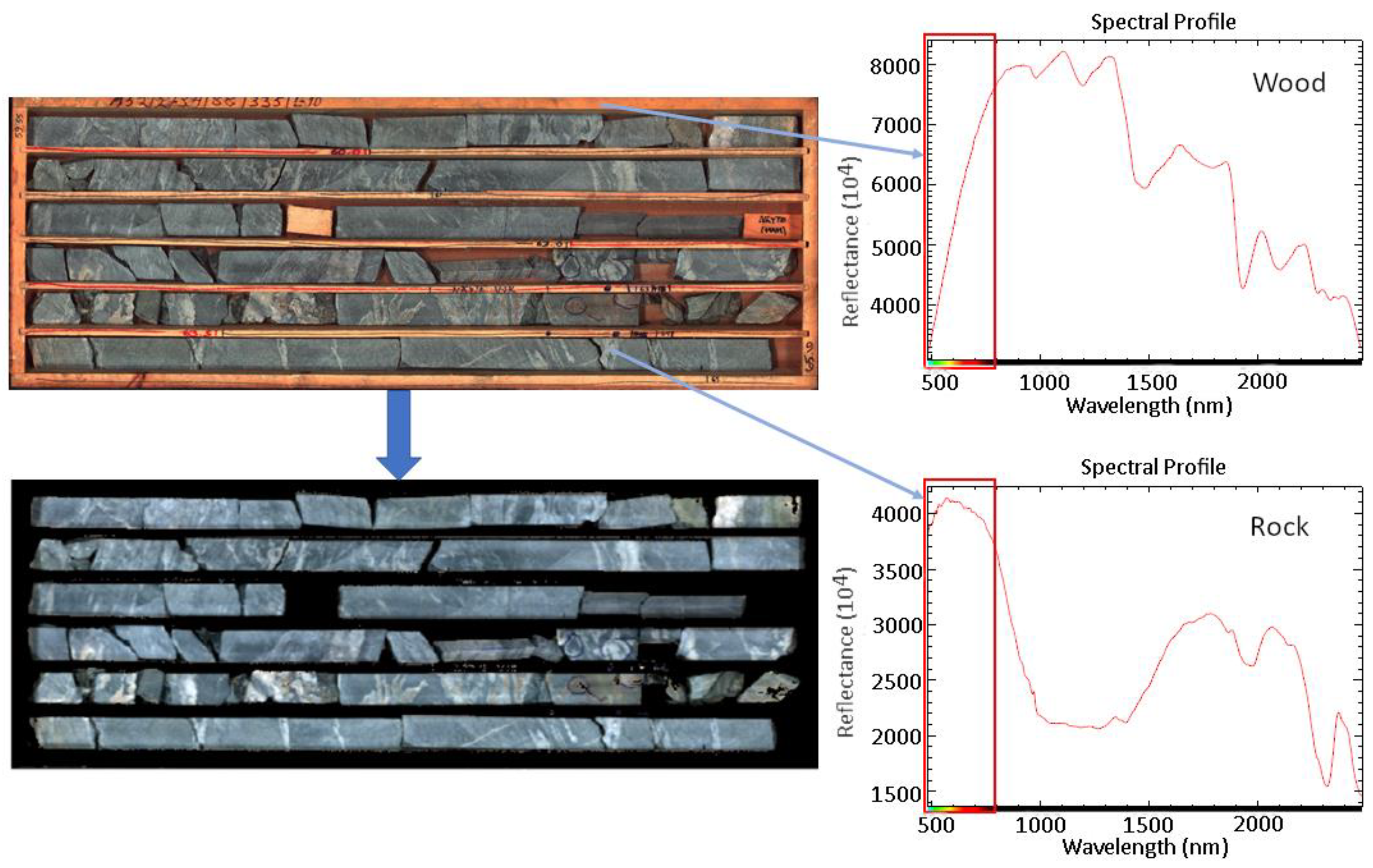
2.2. Pre-Processing of the Hyperspectral Image
2.3. Training and Testing Data Used in Classification Algorithms
2.4. Machine Learning Algorithms
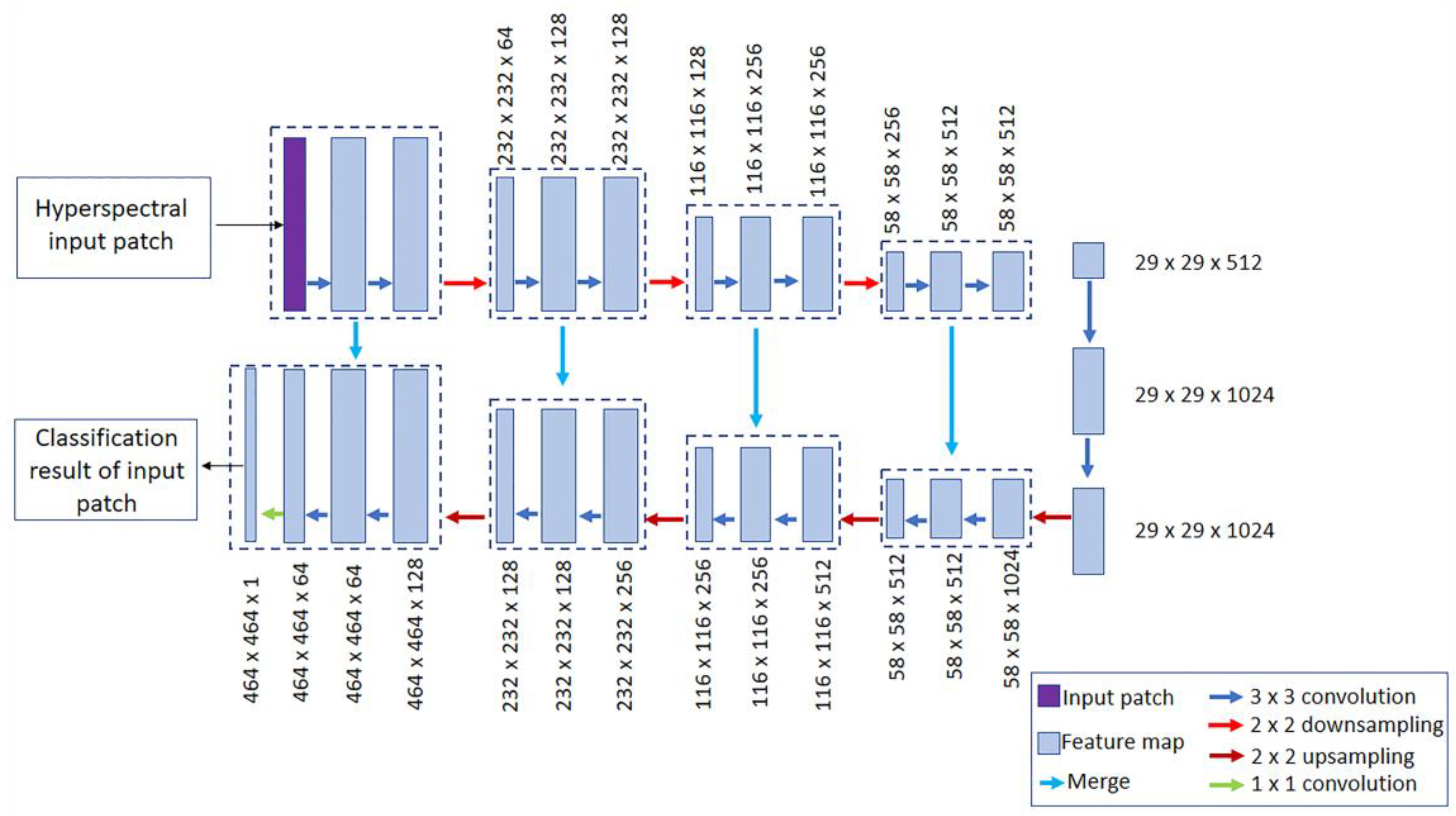
2.4.1. Deep Learning
2.4.2. Ensemble Machine Learning Models
Random Forest
Light Gradient-Boosting Machine (LightGBM)
Gradient-Boosting Decision Tree (GBDT)
AdaBoost
Bagging
Tuning Ensemble Algorithm Hyperparameters
2.5. Accuracy Assessment Methods
3. Results
Image Classification and Accuracy Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Z.; Hu, Y.; Liu, B.; Dai, K.; Zhang, Y. Development of Automatic Electric Drive Drilling System for Core Drilling. Appl. Sci. 2023, 13, 1059. [Google Scholar] [CrossRef]
- Acosta, I.C.C.; Khodadadzadeh, M.; Tusa, L.; Ghamisi, P.; Gloaguen, R. A Machine Learning Framework for Drill-Core Mineral Mapping Using Hyperspectral and High-Resolution Mineralogical Data Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4829–4842. [Google Scholar] [CrossRef]
- De La Rosa, R.; Tolosana-Delgado, R.; Kirsch, M.; Gloaguen, R. Automated Multi-Scale and Multivariate Geological Logging from Drill-Core Hyperspectral Data. Remote Sens. 2022, 14, 2676. [Google Scholar] [CrossRef]
- De La Rosa, R.; Khodadadzadeh, M.; Tusa, L.; Kirsch, M.; Gisbert, G.; Tornos, F.; Tolosana-Delgado, R.; Gloaguen, R. Mineral Quantification at Deposit Scale Using Drill-Core Hyperspectral Data: A Case Study in the Iberian Pyrite Belt. Ore Geol. Rev. 2021, 139, 104514. [Google Scholar] [CrossRef]
- Tuşa, L.; Kern, M.; Khodadadzadeh, M.; Blannin, R.; Gloaguen, R.; Gutzmer, J. Evaluating the Performance of Hyperspectral Short-Wave Infrared Sensors for the Pre-Sorting of Complex Ores Using Machine Learning Methods. Miner. Eng. 2020, 146, 106150. [Google Scholar] [CrossRef]
- Linton, P.; Kosanke, T.; Greene, J.; Porter, B. The Application of Hyperspectral Core Imaging for Oil and Gas. Geol. Soc. Lond. Spec. Publ. 2023, 527, SP527-2022. [Google Scholar] [CrossRef]
- Kruse, F.A. Identification and Mapping of Minerals in Drill Core Using Hyperspectral Image Analysis of Infrared Reflectance Spectra. Int. J. Remote Sens. 1996, 17, 1623–1632. [Google Scholar] [CrossRef]
- Okada, K. A Historical Overview of the Past Three Decades of Mineral Exploration Technology. Nat. Resour. Res. 2021, 30, 2839–2860. [Google Scholar] [CrossRef]
- Han, W.; Zhang, X.; Wang, Y.; Wang, L.; Huang, X.; Li, J.; Wang, S.; Chen, W.; Li, X.; Feng, R. A Survey of Machine Learning and Deep Learning in Remote Sensing of Geological Environment: Challenges, Advances, and Opportunities. ISPRS J. Photogramm. Remote Sens. 2023, 202, 87–113. [Google Scholar] [CrossRef]
- Van der Meer, F.D.; Van der Werff, H.M.A.; Van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Van Der Meijde, M.; Carranza, E.J.M.; De Smeth, J.B.; Woldai, T. Multi-and Hyperspectral Geologic Remote Sensing: A Review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Zaini, N.; Van der Meer, F.; Van der Werff, H. Determination of Carbonate Rock Chemistry Using Laboratory-Based Hyperspectral Imagery. Remote Sens. 2014, 6, 4149–4172. [Google Scholar] [CrossRef]
- Abdolmaleki, M.; Consens, M.; Esmaeili, K. Ore-Waste Discrimination Using Supervised and Unsupervised Classification of Hyperspectral Images. Remote Sens. 2022, 14, 6386. [Google Scholar] [CrossRef]
- Barton, I.F.; Gabriel, M.J.; Lyons-Baral, J.; Barton, M.D.; Duplessis, L.; Roberts, C. Extending Geometallurgy to the Mine Scale with Hyperspectral Imaging: A Pilot Study Using Drone-and Ground-Based Scanning. Mining, Metall. Explor. 2021, 38, 799–818. [Google Scholar] [CrossRef]
- Bedini, E. The Use of Hyperspectral Remote Sensing for Mineral Exploration: A Review. J. Hyperspectral Remote Sens. 2017, 7, 189–211. [Google Scholar] [CrossRef]
- Laukamp, C.; Rodger, A.; LeGras, M.; Lampinen, H.; Lau, I.C.; Pejcic, B.; Stromberg, J.; Francis, N.; Ramanaidou, E. Mineral Physicochemistry Underlying Feature-Based Extraction of Mineral Abundance and Composition from Shortwave, Mid and Thermal Infrared Reflectance Spectra. Minerals 2021, 11, 347. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Manolakis, D.; Pieper, M.; Truslow, E.; Lockwood, R.; Weisner, A.; Jacobson, J.; Cooley, T. Longwave Infrared Hyperspectral Imaging: Principles, Progress, and Challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 72–100. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine Learning Based Hyperspectral Image Analysis: A Survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A Review of Machine Learning in Processing Remote Sensing Data for Mineral Exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Asadzadeh, S.; de Souza Filho, C.R. A Review on Spectral Processing Methods for Geological Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 69–90. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A. Analysis of Imaging Spectrometer Data Using N-Dimensional Geometry and a Mixture-Tuned Matched Filtering Approach. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4138–4152. [Google Scholar] [CrossRef]
- Halder, A.; Ghosh, A.; Ghosh, S. Supervised and Unsupervised Landuse Map Generation from Remotely Sensed Images Using Ant Based Systems. Appl. Soft Comput. 2011, 11, 5770–5781. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Li, X.; Pan, X.; Li, L. Nondestructive Classification of Soybean Seed Varieties by Hyperspectral Imaging and Ensemble Machine Learning Algorithms. Sensors 2020, 20, 6980. [Google Scholar] [CrossRef] [PubMed]
- Jafarzadeh, H.; Mahdianpari, M.; Gill, E.; Mohammadimanesh, F.; Homayouni, S. Bagging and Boosting Ensemble Classifiers for Classification of Multispectral, Hyperspectral and PolSAR Data: A Comparative Evaluation. Remote Sens. 2021, 13, 4405. [Google Scholar] [CrossRef]
- Dev, V.A.; Eden, M.R. Formation Lithology Classification Using Scalable Gradient Boosted Decision Trees. Comput. Chem. Eng. 2019, 128, 392–404. [Google Scholar] [CrossRef]
- Qi, M.L. A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 2017 Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Lin, N.; Liu, H.; Li, G.; Wu, M.; Li, D.; Jiang, R.; Yang, X. Extraction of Mineralized Indicator Minerals Using Ensemble Learning Model Optimized by SSA Based on Hyperspectral Image. Open Geosci. 2022, 14, 1444–1465. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, K.; Wang, J.; Zhao, J. Identifying and Mapping Alteration Minerals Using HySpex Airborne Hyperspectral Data and Random Forest Algorithm. Front. Earth Sci. 2022, 10, 871529. [Google Scholar] [CrossRef]
- Lobo, A.; Garcia, E.; Barroso, G.; Martí, D.; Fernandez-Turiel, J.-L.; Ibáñez-Insa, J. Machine Learning for Mineral Identification and Ore Estimation from Hyperspectral Imagery in Tin–Tungsten Deposits: Simulation under Indoor Conditions. Remote Sens. 2021, 13, 3258. [Google Scholar] [CrossRef]
- Laakso, K.; Haavikko, S.; Korhonen, M.; Köykkä, J.; Middleton, M.; Nykänen, V.; Rauhala, J.; Torppa, A.; Torppa, J.; Törmänen, T. Applying Self-Organizing Maps to Characterize Hyperspectral Drill Core Data from Three Ore Prospects in Northern Finland. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications XIII, Berlin, Germany, 5–7 September 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12268, pp. 239–243. [Google Scholar]
- Torppa, J.; Chudasama, B.; Hautala, S.; Kim, Y. GisSOM for Clustering Multivariate Data. 2021. Available online: https://tupa.gtk.fi/raportti/arkisto/52_2021.pdf (accessed on 4 September 2023).
- Torppa, J.; Chudasama, B. Gissom Software for Multivariate Clustering of Geoscientific Data. Mineral Prospectivity and Exploration Targeting–MinProXT 2021 Webinar 31. Available online: https://tupa.gtk.fi/raportti/arkisto/57_2021.pdf#page=32 (accessed on 4 September 2023).
- Barker, R.D.; Barker, S.L.L.; Cracknell, M.J.; Stock, E.D.; Holmes, G. Quantitative Mineral Mapping of Drill Core Surfaces II: Long-Wave Infrared Mineral Characterization Using ΜXRF and Machine Learning. Econ. Geol. 2021, 116, 821–836. [Google Scholar] [CrossRef]
- Contreras Acosta, I.C.; Khodadadzadeh, M.; Gloaguen, R. Resolution Enhancement for Drill-Core Hyperspectral Mineral Mapping. Remote Sens. 2021, 13, 2296. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep Learning Classifiers for Hyperspectral Imaging: A Review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Bell, A.; del-Blanco, C.R.; Jaureguizar, F.; Jurado, M.J.; García, N. Automatic Mineral Recognition in Hyperspectral Images Using a Semantic-Segmentation-Based Deep Neural Network Trained on a Hyperspectral Drill-Core Database. SSRN 2022. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Meerdink, S.K.; Hook, S.J.; Roberts, D.A.; Abbott, E.A. The ECOSTRESS Spectral Library Version 1.0. Remote Sens. Environ. 2019, 230, 111196. [Google Scholar] [CrossRef]
- Goldfarb, R.J.; Groves, D.I. Orogenic Gold: Common or Evolving Fluid and Metal Sources through Time. Lithos 2015, 233, 2–26. [Google Scholar] [CrossRef]
- Hulkki, H.; Keinänen, V. The Alteration and Fluid Inclusion Characteristics of the Hirvilavanmaa Gold Deposit, Central Lapland Greenstone Belt, Finland. Geol. Surv. Finland, Spec. Pap. 2007, 44, 137–153. [Google Scholar]
- Gruninger, J.H.; Ratkowski, A.J.; Hoke, M.L. The Sequential Maximum Angle Convex Cone (SMACC) Endmember Model. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery X, Orlando, FL, USA, 12–15 April 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5425, pp. 1–14. [Google Scholar]
- Arroyo-Mora, J.P.; Kalacska, M.; Løke, T.; Schläpfer, D.; Coops, N.C.; Lucanus, O.; Leblanc, G. Assessing the Impact of Illumination on UAV Pushbroom Hyperspectral Imagery Collected under Various Cloud Cover Conditions. Remote Sens. Environ. 2021, 258, 112396. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Liu, L.-Y.; Wang, C.-K.; Huang, A.-T. A Deep Learning Approach for Building Segmentation in Taiwan Agricultural Area Using High Resolution Satellite Imagery. J. Photogramm. Remote Sens. 2022, 27, 1–14. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 2017. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Frġedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Bühlmann, P. Bagging, Boosting and Ensemble Methods; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 3642215505. [Google Scholar]
- Foody, G.M. Thematic Map Comparison: Evaluating the Statistical Significance of Differences in Classification Accuracy. Photogramm. Eng. Remote Sens. 2004, 70, 627–634. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2019; ISBN 0429629354. [Google Scholar]
- Stehman, S.V.; Czaplewski, R.L. Design and Analysis for Thematic Map Accuracy Assessment: Fundamental Principles. Remote Sens. Environ. 1998, 64, 331–344. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. In Proceedings of the Advances in Information Retrieval: 27th European Conference on IR Research, ECIR 2005, Santiago de Compostela, Spain, 21–23 March 2005; Proceedings 27. Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar]
- Salisbury, J.W.; Walter, L.S.; Vergo, N.; D’Aria, D.M. Mid-Infrared (2.1–25 Urn) Snectra of Minerals. 1987. Available online: https://pubs.usgs.gov/of/1987/0263/report.pdf (accessed on 4 September 2023).
- Salisbury, J.W.; D’Aria, D.M. Emissivity of Terrestrial Materials in the 8–14 Μm Atmospheric Window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Salisbury, J.W. Infrared (2.1–25 μm) Spectra of Minerals. Johns Hopkins Univ. Press 1991, 267. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Walter, L.S. Thermal Infrared (2.5–13.5 Μm) Spectroscopic Remote Sensing of Igneous Rock Types on Particulate Planetary Surfaces. J. Geophys. Res. Solid Earth 1989, 94, 9192–9202. [Google Scholar] [CrossRef]
- Tuşa, L.; Khodadadzadeh, M.; Contreras, C.; Rafiezadeh Shahi, K.; Fuchs, M.; Gloaguen, R.; Gutzmer, J. Drill-Core Mineral Abundance Estimation Using Hyperspectral and High-Resolution Mineralogical Data. Remote Sens. 2020, 12, 1218. [Google Scholar] [CrossRef]
- Pal, M. Support Vector Machine-based Feature Selection for Land Cover Classification: A Case Study with DAIS Hyperspectral Data. Int. J. Remote Sens. 2006, 27, 2877–2894. [Google Scholar] [CrossRef]
- Cracknell, M.J.; Reading, A.M. Geological Mapping Using Remote Sensing Data: A Comparison of Five Machine Learning Algorithms, Their Response to Variations in the Spatial Distribution of Training Data and the Use of Explicit Spatial Information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Jooshaki, M.; Nad, A.; Michaux, S. A Systematic Review on the Application of Machine Learning in Exploiting Mineralogical Data in Mining and Mineral Industry. Minerals 2021, 11, 816. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, F.; Xiao, F.; Chen, S.; Fang, Y. CBM Gas Content Prediction Model Based on the Ensemble Tree Algorithm with Bayesian Hyper-Parameter Optimization Method: A Case Study of Zhengzhuang Block, Southern Qinshui Basin, North China. Processes 2023, 11, 527. [Google Scholar] [CrossRef]
- Luo, C.; Chen, X.; Xu, J.; Zhang, S. Research on Privacy Protection of Multi Source Data Based on Improved Gbdt Federated Ensemble Method with Different Metrics. Phys. Commun. 2021, 49, 101347. [Google Scholar] [CrossRef]
- Li, G.; Gong, D.; Lu, X.; Zhang, D. Ensemble Learning Based Methods for Crown Prediction of Hot-Rolled Strip. ISIJ Int. 2021, 61, 1603–1613. [Google Scholar] [CrossRef]
- Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall Induced Landslide Susceptibility Mapping Based on Bayesian Optimized Random Forest and Gradient Boosting Decision Tree Models—A Case Study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Qin, R.; Liu, T. A Review of Landcover Classification with Very-High Resolution Remotely Sensed Optical Images—Analysis Unit, Model Scalability and Transferability. Remote Sens. 2022, 14, 646. [Google Scholar] [CrossRef]
- Al-Stouhi, S.; Reddy, C.K. Transfer Learning for Class Imbalance Problems with Inadequate Data. Knowl. Inf. Syst. 2016, 48, 201–228. [Google Scholar] [CrossRef] [PubMed]



| Classes | Training Set Size | Testing Set Size |
|---|---|---|
| Quartz | 19,797 | 4947 |
| Talc | 61,967 | 12,012 |
| Chlorite | 32,402 | 22,380 |
| Quartz–carbonate | 13,363 | 7084 |
| Aspectral | 8329 | 3094 |
| Hyperparameters | Values or Choices | Description/Function |
|---|---|---|
| Image patch sizes | 464 pixels × 464 pixels | HSI images were divided into equal-sized images, which were fed to the ENVINet5 model training and validation steps. |
| Number of epochs | 25 | The number of times an algorithm is run over all training samples. |
| Patches per epoch | 100 | The diversity of features needs to be learned, which ENVI can automatically identify or it can be achieved through trial and error. |
| Class weight | (2, 3) | The selected values are useful since the dataset contains sparse training samples. Class weight assists in extracting image patches that consist of more feature pixels [49]. |
| Loss weight | 0.9 | Assists in detecting feature pixels than categorizing the masked area from drill core wooden boxes. |
| Blur distance | (1, 6) | Assists in obtaining useful information about the border of mineral classes by blurring the edges. |
| Solid distance | - | Provides buffering around the training points and aids in providing neighborhood information to the training phase. |
| Classifier | Hyperparameter Search Space | Selected Hyperparameter Values via Grid Search |
|---|---|---|
| RF | n_estimators: [100, 150, 200] | 150 |
| max_depth: [3, 5, 8] | 8 | |
| min_samples_leaf: [1, 2, 4] | 1 | |
| min_samples_split: [2, 5, 10] | 10 | |
| GBDT | loss:[log_loss] | log_loss |
| learning_rate: [0.025, 0.05, 0.1] | 0.1 | |
| min_samples_split: [2, 5, 10] | 5 | |
| subsample: [0.15, 0.5, 1.0] | 1.0 | |
| max_depth: [3, 5, 8] | 8 | |
| max_features: [“log2”,”sqrt”] | log2 | |
| n_estimators: [100, 150, 200] | 150 | |
| LightGBM | n_estimators: [100, 150, 200] | 200 |
| max_depth: [3, 5, 8] | 8 | |
| learning_rate: [0.025, 0.05, 0.1] | 0.1 | |
| Bagging | max_depth: [3, 5, 8] | 8 |
| max_features: [“auto”,”sqrt”] | sqrt | |
| min_samples_split’: [2, 5, 10] | 2 | |
| n_estimators: [100, 150, 200] | 100 | |
| AdaBoost | max_depth: [3, 5, 8] | 5 |
| max_features: [“auto”,”sqrt”] | auto | |
| min_samples_split’: [2, 5, 10] | 10 | |
| n_estimators: [100, 150, 200] | 200 |
| A. GBDT | |||||||||
| Predicted class | |||||||||
| Class | Quartz | Talc | Aspectral | Chlorite | Quartz–carbonate | Total | R % | P % | F1-s % |
| Quartz | 4549 | 49 | 0 | 85 | 448 | 5131 | 91.95 | 88.66 | 90.35 |
| Talc | 65 | 10,810 | 3 | 1247 | 51 | 12,176 | 89.99 | 88.78 | 89.51 |
| Aspectral | 0 | 1 | 2814 | 358 | 19 | 3192 | 90.95 | 88.16 | 89.64 |
| Chlorite | 53 | 1110 | 272 | 20,178 | 689 | 22,302 | 90.16 | 90.48 | 90.43 |
| Quartz–carbonate | 280 | 42 | 5 | 512 | 5877 | 6716 | 82.96 | 87.51 | 85.27 |
| Total | 4947 | 12,012 | 3094 | 22,380 | 7084 | 49,517 | |||
| Overall Accuracy: 89.31%; Kappa Coefficient: 0.848 | |||||||||
| B. LightGBM | |||||||||
| Class | Quartz | Talc | Aspectral | Chlorite | Quartz–carbonate | Total | R % | P % | F1-s % |
| Quartz | 4537 | 54 | 0 | 86 | 448 | 5125 | 91.71 | 88.53 | 90.18 |
| Talc | 66 | 10,868 | 4 | 1339 | 64 | 12,341 | 90.48 | 88.06 | 89.39 |
| Aspectral | 1 | 3 | 2799 | 374 | 17 | 3194 | 90.47 | 87.63 | 89.13 |
| Chlorite | 54 | 1051 | 288 | 20,067 | 703 | 22,163 | 89.66 | 90.54 | 90.21 |
| Quartz–carbonate | 289 | 36 | 3 | 514 | 5852 | 6694 | 82.61 | 87.52 | 85.04 |
| Total | 4947 | 12,012 | 3094 | 22,380 | 7084 | 49,517 | |||
| Overall Accuracy: 89.10%; Kappa Coefficient: 0.845 | |||||||||
| C. RF | |||||||||
| Class | Quartz | Talc | Aspectral | Chlorite | Quartz–carbonate | Total | R % | P % | F1-s % |
| Quartz | 4589 | 50 | 0 | 81 | 501 | 5221 | 92.76 | 87.9 | 90.34 |
| Talc | 62 | 11,283 | 2 | 2011 | 13 | 13,371 | 93.93 | 84.38 | 88.91 |
| Aspectral | 0 | 1 | 2897 | 517 | 19 | 3434 | 93.63 | 84.36 | 88.78 |
| Chlorite | 81 | 671 | 189 | 19,095 | 1191 | 21,227 | 85.32 | 89.96 | 87.62 |
| Quartz–carbonate | 215 | 7 | 6 | 676 | 5360 | 6264 | 75.66 | 85.57 | 80.36 |
| Total | 4947 | 12,012 | 3094 | 22,380 | 7084 | 49,517 | |||
| Overall Accuracy: 87.29%; Kappa Coefficient: 0.82 | |||||||||
| D. Bagging | |||||||||
| Class | Quartz | Talc | Aspectral | Chlorite | Quartz–carbonate | Total | R % | P % | F1-s % |
| Quartz | 4597 | 52 | 0 | 77 | 502 | 5228 | 92.93 | 87.93 | 90.45 |
| Talc | 62 | 11,287 | 2 | 2000 | 14 | 13,365 | 93.96 | 84.45 | 88.97 |
| Aspectral | 0 | 1 | 2898 | 527 | 21 | 3447 | 93.67 | 84.07 | 88.60 |
| Chlorite | 76 | 664 | 189 | 19,106 | 1206 | 21,241 | 85.37 | 89.95 | 87.64 |
| Quartz–carbonate | 212 | 8 | 5 | 670 | 5341 | 6236 | 75.4 | 85.65 | 80.24 |
| Total | 4947 | 12,012 | 3094 | 22,380 | 7084 | 49,517 | |||
| Overall Accuracy: 87.30%; Kappa Coefficient: 0.82 | |||||||||
| E. ENVINet5 | |||||||||
| Class | Quartz | Talc | Aspectral | Chlorite | Quartz–carbonate | Total | R % | P % | F1-s % |
| Unclassified | 30 | 83 | 20 | 1104 | 110 | 1347 | |||
| Quartz | 4533 | 62 | 0 | 141 | 614 | 5350 | 91.63 | 84.73 | 88.04 |
| Talc | 61 | 11,512 | 3 | 2706 | 47 | 14,329 | 95.84 | 80.34 | 87.40 |
| Aspectral | 0 | 7 | 3003 | 808 | 35 | 3853 | 97.06 | 77.94 | 86.45 |
| Chlorite | 54 | 299 | 59 | 16,564 | 915 | 17,891 | 74.01 | 92.58 | 82.25 |
| Quartz–carbonate | 269 | 49 | 9 | 1057 | 5363 | 6747 | 75.71 | 79.49 | 77.55 |
| Total | 4947 | 12012 | 3094 | 22,380 | 7084 | 49,517 | |||
| Overall Accuracy: 82.74%; Kappa Coefficient: 0.764 | |||||||||
| F. AdaBoost | |||||||||
| Class | Quartz | Talc | Aspectral | Chlorite | Quartz–carbonate | Total | R % | P % | F1-s % |
| Quartz | 4396 | 73 | 0 | 104 | 547 | 5120 | 88.86 | 85.86 | 87.38 |
| Talc | 39 | 7755 | 1 | 1708 | 45 | 9548 | 64.56 | 81.22 | 71.92 |
| Aspectral | 1 | 3 | 3033 | 653 | 17 | 3707 | 98.03 | 81.82 | 89.14 |
| Chlorite | 46 | 4127 | 52 | 18,362 | 1253 | 23,840 | 82.05 | 77.02 | 79.51 |
| Quartz–carbonate | 465 | 54 | 8 | 1553 | 5222 | 7302 | 73.72 | 71.51 | 72.65 |
| Total | 4947 | 12,012 | 3094 | 22,380 | 7084 | 49,517 | |||
| Overall Accuracy: 78.29%; Kappa Coefficient: 0.689 | |||||||||
| Classification 1 | Classification 2 | χ2 | p-Value | Significant? |
|---|---|---|---|---|
| GBDT | LightGBM | 0.649 | 0.206 | No |
| GBDT | Bagging | 450.2 | 0 | Yes |
| GBDT | RF | 459 | 0 | Yes |
| GBDT | ENVINet5 | 2101.7 | 0 | Yes |
| GBDT | AdaBoost | 5055 | 0 | Yes |
| LightGBM | Bagging | 389.9 | 0 | Yes |
| LightGBM | RF | 398.3 | 0 | Yes |
| LightGBM | ENVINet5 | 2046 | 0 | Yes |
| LightGBM | AdaBoost | 4925 | 0 | Yes |
| Bagging | RF | 0.581 | 0.445 | No |
| Bagging | ENVINet5 | 1709 | 0 | Yes |
| Bagging | AdaBoost | 4206 | 0 | Yes |
| RF | ENVINet5 | 1729.2 | 0 | Yes |
| RF | AdaBoost | 4200 | 0 | Yes |
| ENVINet5 | AdaBoost | 830.8 | 0 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamedianfar, A.; Laakso, K.; Middleton, M.; Törmänen, T.; Köykkä, J.; Torppa, J. Leveraging High-Resolution Long-Wave Infrared Hyperspectral Laboratory Imaging Data for Mineral Identification Using Machine Learning Methods. Remote Sens. 2023, 15, 4806. https://doi.org/10.3390/rs15194806
Hamedianfar A, Laakso K, Middleton M, Törmänen T, Köykkä J, Torppa J. Leveraging High-Resolution Long-Wave Infrared Hyperspectral Laboratory Imaging Data for Mineral Identification Using Machine Learning Methods. Remote Sensing. 2023; 15(19):4806. https://doi.org/10.3390/rs15194806
Chicago/Turabian StyleHamedianfar, Alireza, Kati Laakso, Maarit Middleton, Tuomo Törmänen, Juha Köykkä, and Johanna Torppa. 2023. "Leveraging High-Resolution Long-Wave Infrared Hyperspectral Laboratory Imaging Data for Mineral Identification Using Machine Learning Methods" Remote Sensing 15, no. 19: 4806. https://doi.org/10.3390/rs15194806
APA StyleHamedianfar, A., Laakso, K., Middleton, M., Törmänen, T., Köykkä, J., & Torppa, J. (2023). Leveraging High-Resolution Long-Wave Infrared Hyperspectral Laboratory Imaging Data for Mineral Identification Using Machine Learning Methods. Remote Sensing, 15(19), 4806. https://doi.org/10.3390/rs15194806








