Integrated 1D, 2D, and 3D CNNs Enable Robust and Efficient Land Cover Classification from Hyperspectral Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Dataset
2.1.1. The Indian Pines Dataset
2.1.2. The Wuhan University Dataset
2.2. Related Works
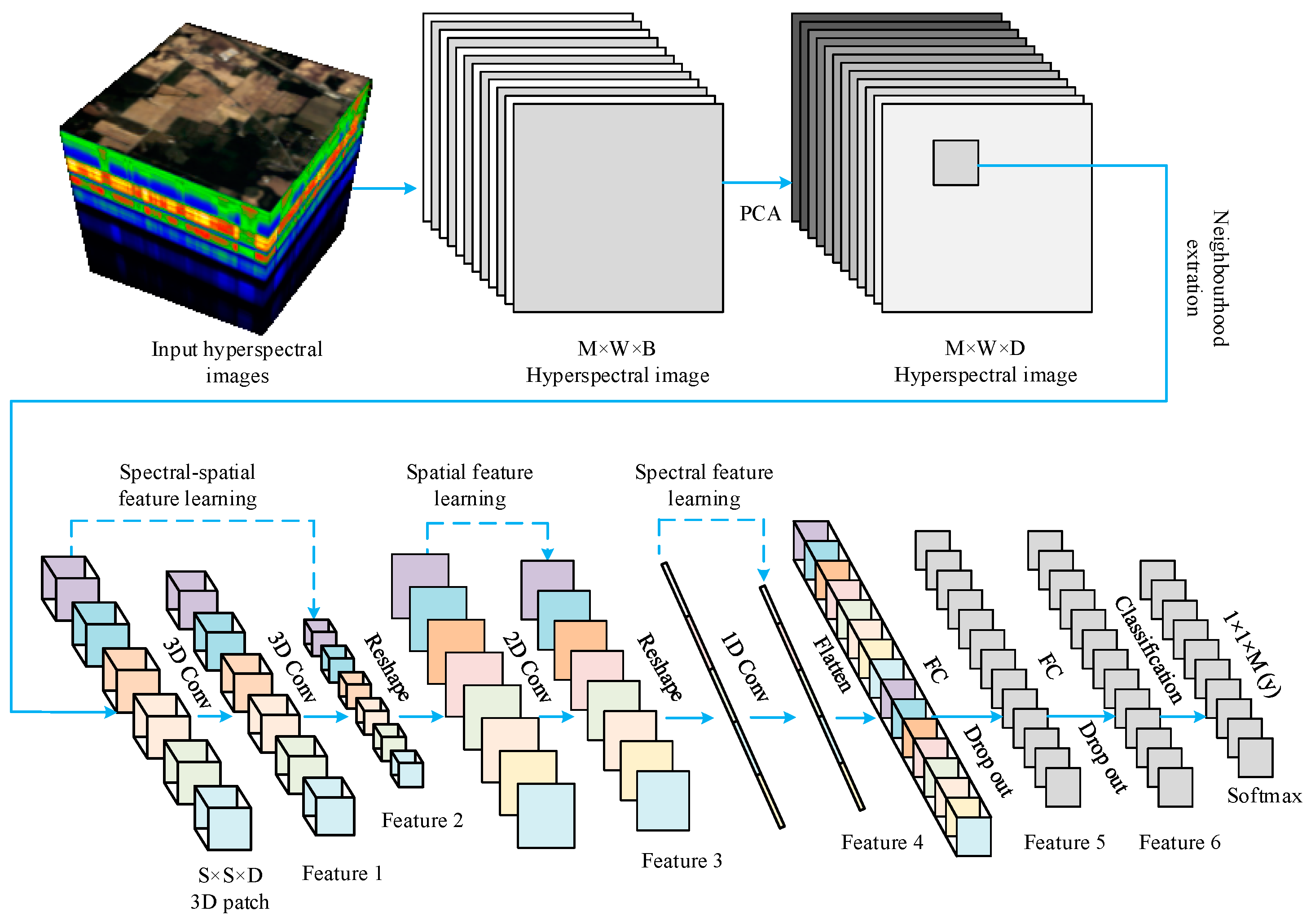
2.3. Proposed Integrated 1D, 2D and 3D CNNs (IntegratedCNNs)
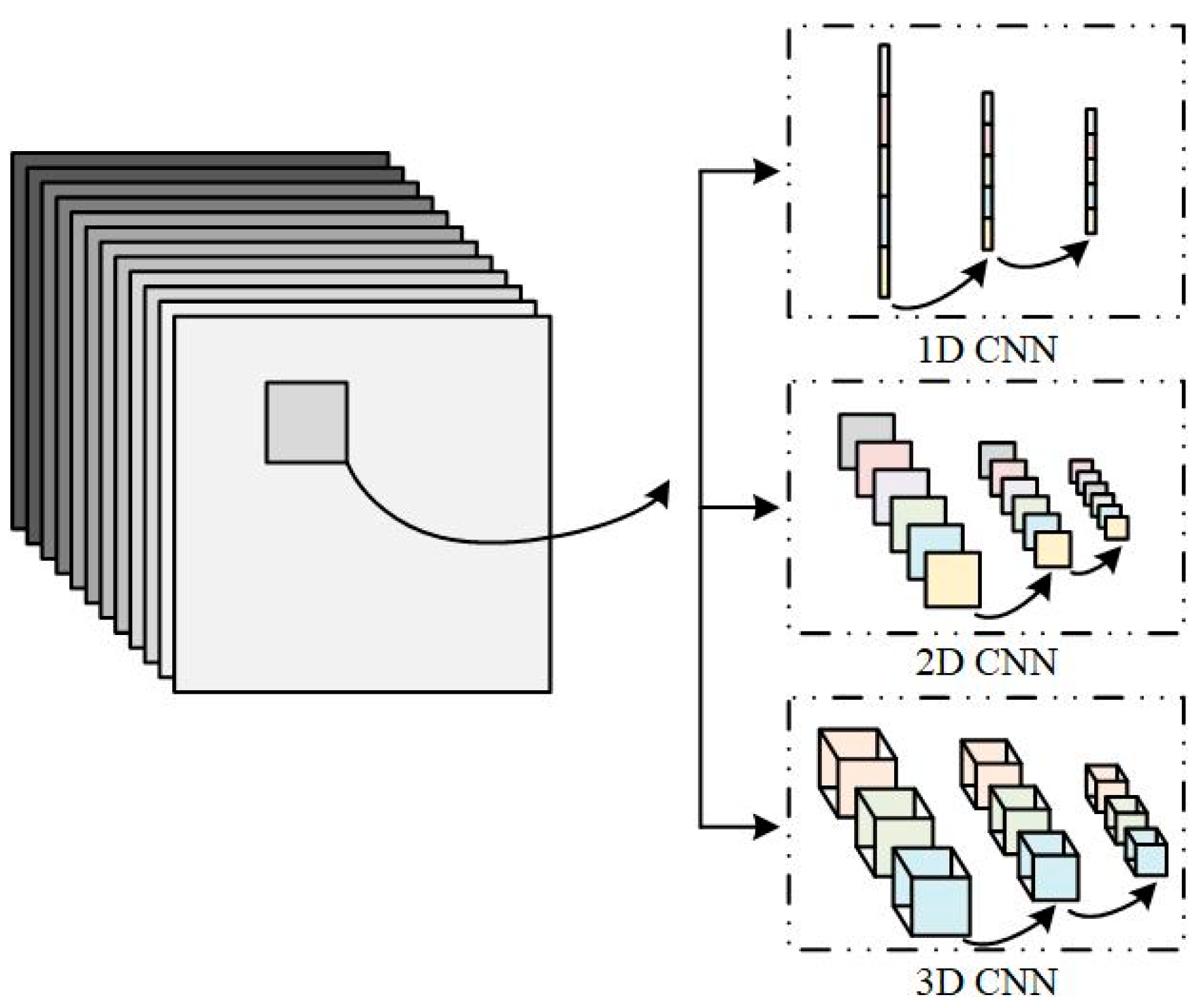
2.4. Conventional CNN Models
2.5. Computational Efficiency Assessment
2.6. Accuracy Assessment and Statistical Tests
3. Results
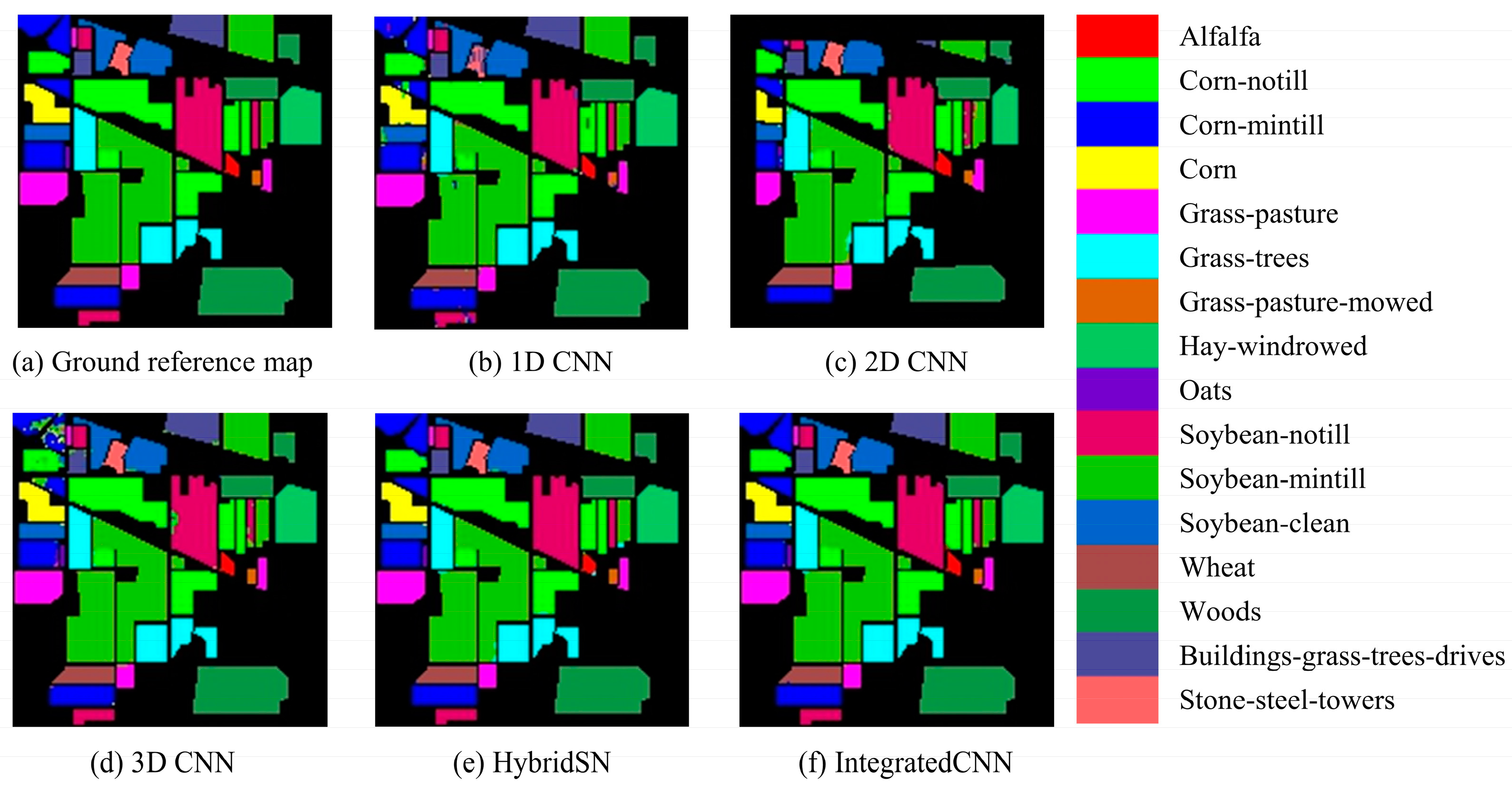
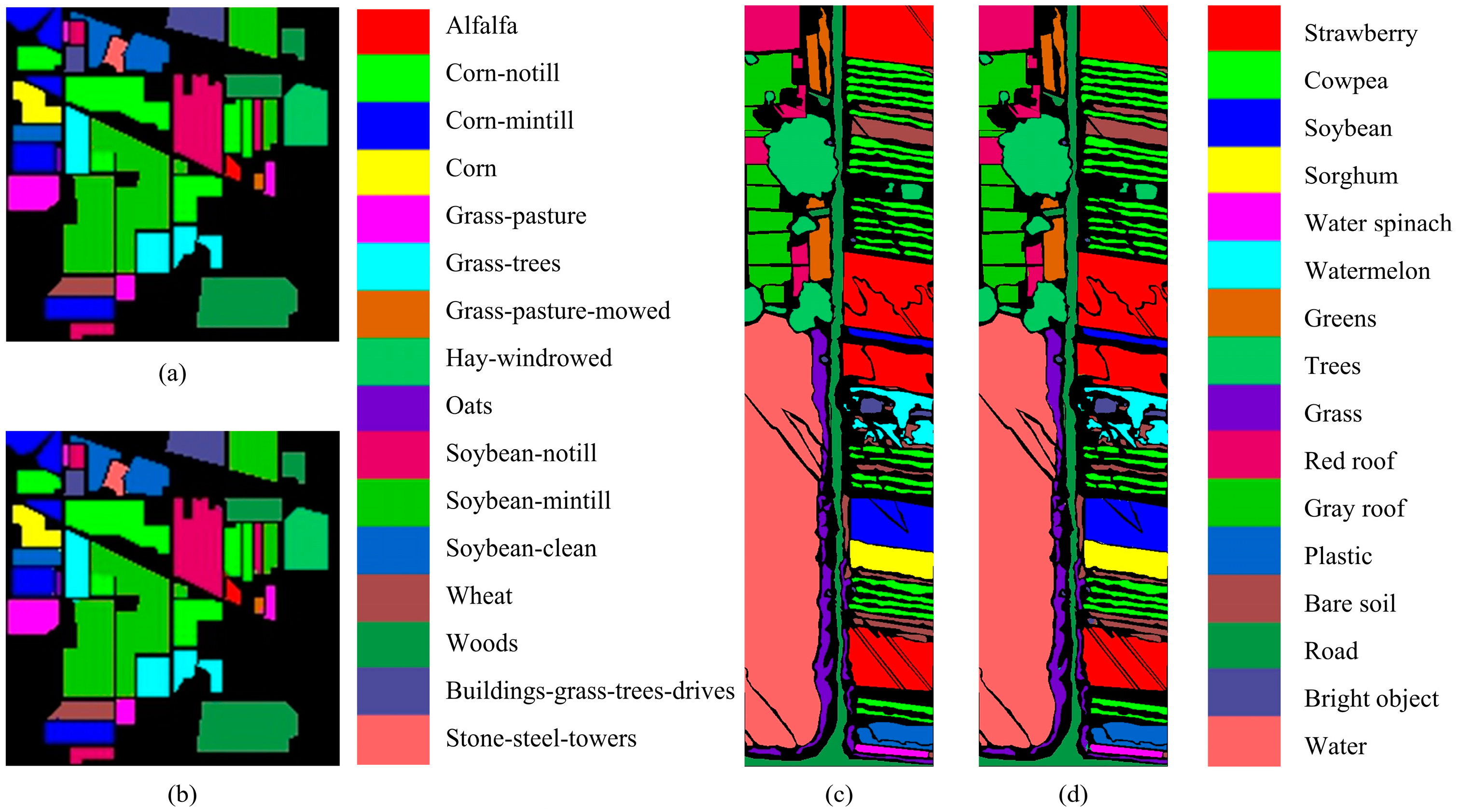
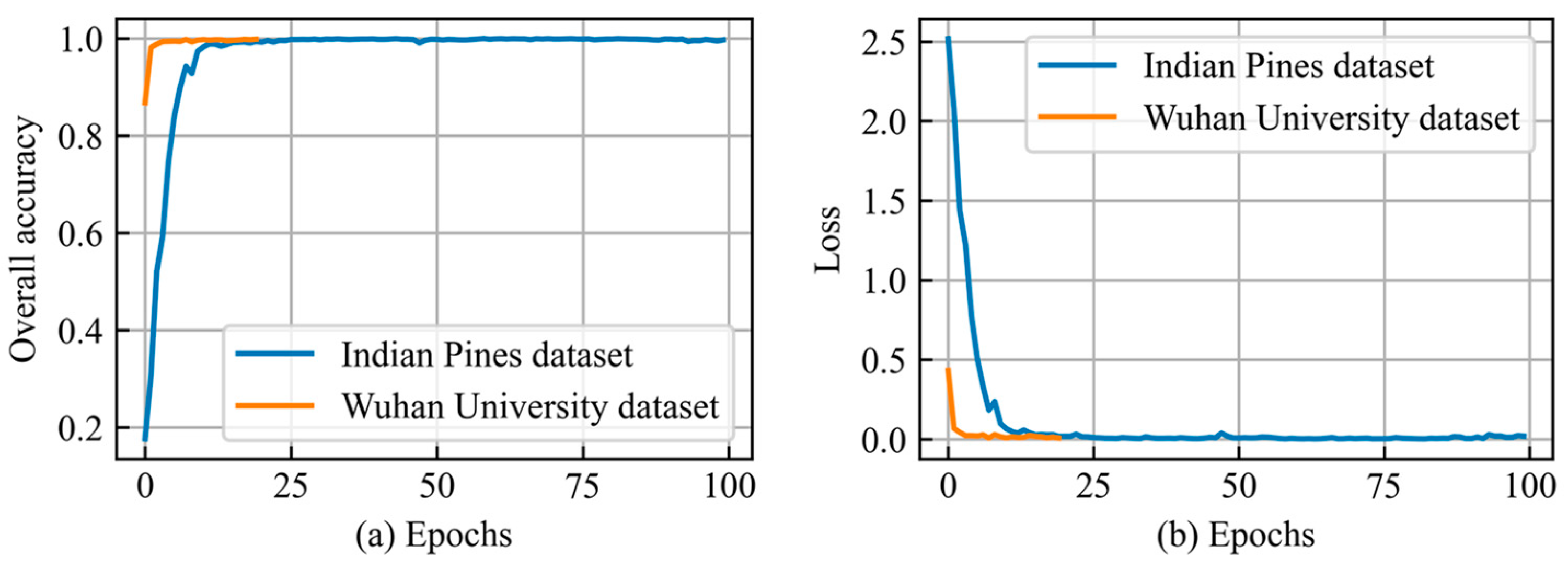
3.1. Performance of the IntegratedCNNs Model
3.2. Model Comparison
| Dataset | Testing Accuracy | 1D CNN | 2D CNN | 3D CNN | HybridSN | IntegratedCNNs |
|---|---|---|---|---|---|---|
| Indian Pines dataset | Overall accuracy (%) | 96.54 | 89.56 | 96.96 | 99.33 | 99.65 |
| Average accuracy (%) | 79.85 | 94.44 | 97.64 | 98.14 | 98.97 | |
| Kappa coefficient | 0.96 | 0.84 | 0.97 | 0.99 | 1.00 | |
| Wuhan University dataset | Overall accuracy (%) | 99.02 | 99.27 | 99.76 | 99.92 | 99.85 |
| Average accuracy (%) | 97.91 | 98.20 | 99.43 | 99.79 | 99.82 | |
| Kappa coefficient | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 |
3.3. Ablation Studies
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Layer | Output Shape | Parameter Count | Kernel |
|---|---|---|---|
| Input layer | (None, 25, 25, 30, 1) | 0 | |
| Conv3D (1) | (None, 23, 23, 24, 8) | 512 | 8 × (3 × 3 × 7) |
| Conv3D (2) | (None, 21, 21, 20, 16) | 5776 | 16 × (3 × 3 × 5) |
| Reshape (1) | (None, 21, 21, 320) | 0 | |
| Conv2D | (None, 19, 19, 32) | 92,192 | 32 × (3 × 3) |
| Reshape (2) | (None, 19, 608) | 0 | |
| Conv1D | (None, 17, 64) | 116,800 | 64 × (3) |
| Flatten | (None, 1088) | 0 | |
| Dense (1) | (None, 256) | 278,784 | |
| Dropout (1) | (None, 256) | 0 | |
| Dense (2) | (None, 128) | 32,896 | |
| Dropout (2) | (None, 128) | 0 | |
| Dense (3) | (None, 16) | 2064 | |
| Total number of parameters: 5,361,913 | |||
| No. | Land Cover Classes | 1D CNN | 2D CNN | 3D CNN | HybridSN | IntegratedCNNs |
|---|---|---|---|---|---|---|
| 1 | Alfalfa | 78.13 | 97.37 | 100.00 | 87.50 | 100.00 |
| 2 | Corn-notill | 96.70 | 98.21 | 96.70 | 98.50 | 99.60 |
| 3 | Corn-mintill | 97.07 | 99.32 | 81.93 | 100.00 | 100.00 |
| 4 | Corn | 94.58 | 100.00 | 100.00 | 100.00 | 98.80 |
| 5 | Grass-pasture | 95.86 | 97.41 | 98.23 | 100.00 | 99.41 |
| 6 | Grass-trees | 99.61 | 98.66 | 99.80 | 100.00 | 99.61 |
| 7 | Grass-pasture-mowed | 0.00 | 100.00 | 100.00 | 95.00 | 90.00 |
| 8 | Hay-windrowed | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 9 | Oats | 0.00 | 28.57 | 100.00 | 92.86 | 100.00 |
| 10 | Soybean-notill | 99.56 | 98.53 | 95.00 | 100.00 | 100.00 |
| 11 | Soybean-mintill | 98.84 | 98.84 | 99.77 | 99.01 | 99.77 |
| 12 | Soybean-clean | 92.53 | 97.44 | 97.83 | 98.31 | 99.28 |
| 13 | Wheat | 98.60 | 100.00 | 100.00 | 99.30 | 98.60 |
| 14 | Woods | 99.55 | 99.78 | 98.87 | 99.77 | 100.00 |
| 15 | Buildings-grass-trees-drives | 88.15 | 100.00 | 94.07 | 100.00 | 98.52 |
| 16 | Stone-steel-towers | 38.46 | 50.538 | 100.00 | 100.00 | 100.00 |
| No. | Land Cover Classes | 1D CNN | 2D CNN | 3D CNN | HybridSN | IntegratedCNNs |
|---|---|---|---|---|---|---|
| 1 | Strawberry | 99.58 | 99.68 | 99.96 | 99.99 | 99.99 |
| 2 | Cowpea | 99.46 | 99.57 | 99.96 | 99.92 | 99.97 |
| 3 | Soybean | 99.80 | 99.92 | 100.00 | 100.00 | 100.00 |
| 4 | Sorghum | 99.41 | 99.89 | 99.79 | 100.00 | 99.95 |
| 5 | Water spinach | 99.80 | 99.76 | 99.88 | 99.88 | 100.00 |
| 6 | Watermelon | 95.24 | 96.19 | 99.81 | 99.62 | 99.72 |
| 7 | Greens | 98.39 | 97.75 | 100.00 | 100.00 | 99.90 |
| 8 | Trees | 98.39 | 98.94 | 99.75 | 99.90 | 99.96 |
| 9 | Grass | 97.05 | 99.46 | 99.92 | 99.91 | 99.94 |
| 10 | Red roof | 98.40 | 99.01 | 99.69 | 99.99 | 99.93 |
| 11 | Gray roof | 98.70 | 99.21 | 99.98 | 100.00 | 99.47 |
| 12 | Plastic | 97.68 | 98.52 | 100.00 | 100.00 | 99.96 |
| 13 | Bare soil | 93.92 | 95.78 | 99.31 | 99.76 | 99.22 |
| 14 | Road | 99.44 | 98.71 | 100.00 | 99.99 | 99.38 |
| 15 | Bright object | 91.41 | 88.93 | 98.74 | 97.86 | 99.75 |
| 16 | Water | 99.94 | 99.96 | 100.00 | 100.00 | 99.93 |
| Testing Results | Indian Pines Dataset (Training with 5% of Samples) | Wuhan University Dataset (Training with 1% of Samples) | ||
|---|---|---|---|---|
| Train 20 Epochs | Train 100 Epochs | Train 20 Epochs | Train 100 Epochs | |
| Overall accuracy (%) | 85.14 | 93.12 | 95.53 | 97.69 |
| Average accuracy (%) | 60.84 | 86.77 | 87.34 | 93.95 |
| Kappa coefficient | 0.83 | 0.92 | 0.95 | 0.97 |

References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Dimitrovski, I.; Kitanovski, I.; Kocev, D.; Simidjievski, N. Current trends in deep learning for Earth Observation: An open-source benchmark arena for image classification. ISPRS J. Photogramm. Remote Sens. 2023, 197, 18–35. [Google Scholar] [CrossRef]
- Ran, R.; Deng, L.J.; Jiang, T.X.; Hu, J.F.; Chanussot, J.; Vivone, G. GuidedNet: A general CNN fusion framework via high-resolution guidance for hyperspectral image super-resolution. IEEE Trans. Cybern. 2023, 53, 4148–4161. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Jia, T.; Hu, X.; Zhao, J.; Wei, L.; Zhang, L. Mini-UAV-borne hyperspectral remote sensing: From observation and processing to applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]
- Osco, L.P.; Marcato Junior, J.; Marques Ramos, A.P.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A review on deep learning in UAV remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, J.; Zhang, L.; Zhang, G.; Li, X.; Wu, J. Geometric processing and accuracy verification of Zhuhai-1 hyperspectral satellites. Remote Sens. 2019, 11, 996. [Google Scholar] [CrossRef]
- Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G. Prisma: The Italian Hyperspectral Mission. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 175–178. [Google Scholar]
- Stuffler, T.; Kaufmann, C.; Hofer, S.; Förster, K.P.; Schreier, G.; Mueller, A.; Eckardt, A.; Bach, H.; Penné, B.; Benz, U.; et al. The EnMAP hyperspectral imager—An advanced optical payload for future applications in Earth observation programmes. AcAau 2007, 61, 115–120. [Google Scholar] [CrossRef]
- Qian, S.-E. Hyperspectral satellites, evolution, and development history. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 7032–7056. [Google Scholar] [CrossRef]
- Mou, L.; Saha, S.; Hua, Y.; Bovolo, F.; Bruzzone, L.; Zhu, X.X. Deep reinforcement learning for band selection in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Ang, L.-M.; Seng, K.P. Meta-scalable discriminate analytics for Big hyperspectral data and applications. Expert Syst. Appl. 2021, 176, 114777. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, H.; Zheng, K.; Gao, L.; Song, M. A novel classification framework for hyperspectral image classification based on multiscale spectral-spatial convolutional network. In Proceedings of the IGARSS 2021 IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 24–26 March 2021; pp. 1–5. [Google Scholar]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing 2021, 448, 179–204. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Yu, Z.Y.; Chanussot, J.; Zeeshan, Z.; Yuan, L.W.; Luo, W.; Nawaz, S.A.; Bhatti, M.A.; ul Ain, Q.; Mehmood, A. Local similarity-based spatial–spectral fusion hyperspectral image classification with deep CNN and Gabor filtering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Wu, S.; Shi, H.; Zhao, Y.; Sun, Y.; Zhuang, H.; Fu, E. An investigation of a multidimensional CNN combined with an attention mechanism model to resolve small-sample problems in hyperspectral image classification. Remote Sens. 2022, 14, 785. [Google Scholar] [CrossRef]
- Park, B.; Shin, T.; Cho, J.-S.; Lim, J.-H.; Park, K.-J. Improving blueberry firmness classification with spectral and textural features of microstructures using hyperspectral microscope imaging and deep learning. Postharvest Biol. Technol. 2023, 195, 112154. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on convolutional neural networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Ghosh, P.; Roy, S.K.; Koirala, B.; Rasti, B.; Scheunders, P. Hyperspectral unmixing using transformer network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5535116. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, L.; Dong, Y.; Huang, L.; Weng, S.; Zhang, D. A combination method of stacked autoencoder and 3D deep residual network for hyperspectral image classification. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102459. [Google Scholar] [CrossRef]
- Ahmad, M.; Khan, A.M.; Mazzara, M.; Distefano, S.; Ali, M.; Sarfraz, M.S. A fast and compact 3-D CNN for hyperspectral image classification. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 5502205. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Moreno-Álvarez, S.; Plaza, J.; Rico-Gallego, J.A.; Plaza, A. Distributed deep learning for remote sensing data interpretation. Proc. IEEE 2021, 109, 1320–1349. [Google Scholar] [CrossRef]
- Bera, S.; Shrivastava, V.K. Analysis of various optimizers on deep convolutional neural network model in the application of hyperspectral remote sensing image classification. Int. J. Remote Sens. 2020, 41, 2664–2683. [Google Scholar] [CrossRef]
- Mäyrä, J.; Keski-Saari, S.; Kivinen, S.; Tanhuanpää, T.; Hurskainen, P.; Kullberg, P.; Poikolainen, L.; Viinikka, A.; Tuominen, S.; Kumpula, T.; et al. Tree species classification from airborne hyperspectral and LiDAR data using 3D convolutional neural networks. Remote Sens. Environ. 2021, 256, 112322. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote. Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning deep hierarchical spatial–spectral features for hyperspectral image classification based on residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef] [PubMed]
- Jamali, A.; Mahdianpari, M.; Mohammadimanesh, F.; Brisco, B.; Salehi, B. 3-D hybrid CNN combined with 3-D generative adversarial network for wetland classification with limited training data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 8095–8108. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, L.; Zhang, X. Three-dimensional convolutional neural network model for tree species classification using airborne hyperspectral images. Remote Sens. Environ. 2020, 247, 111938. [Google Scholar] [CrossRef]
- Al-Kubaisi, M.A.; Shafri, H.Z.M.; Ismail, M.H.; Yusof, M.J.M.; Jahari bin Hashim, S. Attention-based multiscale deep learning with unsampled pixel utilization for hyperspectral image classification. GeoIn 2023, 38, 2231428. [Google Scholar] [CrossRef]
- Firat, H.; Asker, M.E.; Bayindir, M.İ.; Hanbay, D. 3D residual spatial–spectral convolution network for hyperspectral remote sensing image classification. Neural. Comput. Appl. 2023, 35, 4479–4497. [Google Scholar] [CrossRef]
- Wambugu, N.; Chen, Y.; Xiao, Z.; Tan, K.; Wei, M.; Liu, X.; Li, J. Hyperspectral image classification on insufficient-sample and feature learning using deep neural networks: A review. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102603. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Tulczyjew, L.; Kawulok, M.; Longépé, N.; Saux, B.L.; Nalepa, J. A multibranch convolutional neural network for hyperspectral unmixing. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 6011105. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature extraction for hyperspectral image classification: A review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Meng, Y.; Ma, Z.; Ji, Z.; Gao, R.; Su, Z. Fine hyperspectral classification of rice varieties based on attention module 3D-2DCNN. Comput. Electron. Agric. 2022, 203, 107474. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Pereira, N.S.; Plaza, J.; Plaza, A. Ghostnet for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10378–10393. [Google Scholar] [CrossRef]
- Huang, H.; Shi, G.; He, H.; Duan, Y.; Luo, F. Dimensionality reduction of hyperspectral imagery based on spatial–spectral manifold learning. IEEE T. Cybern. 2020, 50, 2604–2616. [Google Scholar] [CrossRef]
- Sellami, A.; Tabbone, S. Deep neural networks-based relevant latent representation learning for hyperspectral image classification. Pattern Recognit. 2022, 121, 108224. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Fung, T.; LeDrew, E. For change detection using various accuracy. Photogramm. Eng. Remote Sens. 1988, 54, 1449–1454. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Congalton, R.G.; Mead, R.A. A quantitative method to test for consistency and correctness in photointerpretation. Photogramm. Eng. Remote Sens. 1983, 49, 69–74. [Google Scholar]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral image classification with independent component discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]



| No. | Land Cover Classes | Total Samples | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Alfalfa | 46 | 14 | 32 |
| 2 | Corn-notill | 1428 | 428 | 1000 |
| 3 | Corn-mintill | 830 | 249 | 581 |
| 4 | Corn | 237 | 71 | 166 |
| 5 | Grass-pasture | 483 | 145 | 338 |
| 6 | Grass-trees | 730 | 219 | 511 |
| 7 | Grass-pasture-mowed | 28 | 8 | 20 |
| 8 | Hay-windrowed | 478 | 143 | 335 |
| 9 | Oats | 20 | 6 | 14 |
| 10 | Soybean-notill | 972 | 292 | 680 |
| 11 | Soybean-mintill | 2455 | 737 | 1719 |
| 12 | Soybean-clean | 593 | 178 | 415 |
| 13 | Wheat | 205 | 62 | 144 |
| 14 | Woods | 1265 | 380 | 886 |
| 15 | Buildings-grass-trees-drives | 386 | 116 | 270 |
| 16 | Stone-steel-towers | 93 | 28 | 65 |
| No. | Land Cover Classes | Total Samples | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Strawberry | 44,735 | 13,421 | 31,315 |
| 2 | Cowpea | 22,753 | 6826 | 15,927 |
| 3 | Soybean | 10,287 | 3086 | 7201 |
| 4 | Sorghum | 5353 | 1606 | 3747 |
| 5 | Water spinach | 1200 | 360 | 840 |
| 6 | Watermelon | 4533 | 1360 | 3173 |
| 7 | Greens | 5903 | 1771 | 4132 |
| 8 | Trees | 17,978 | 5393 | 12,585 |
| 9 | Grass | 9469 | 2841 | 6628 |
| 10 | Red roof | 10,516 | 3155 | 7361 |
| 11 | Gray roof | 16,911 | 5073 | 11,838 |
| 12 | Plastic | 3679 | 1104 | 2575 |
| 13 | Bare soil | 9116 | 2735 | 6381 |
| 14 | Road | 18,560 | 5568 | 12,992 |
| 15 | Bright object | 1136 | 341 | 795 |
| 16 | Water | 75,401 | 22,620 | 52,781 |
| Classifier | 1D CNN | 2D CNN | 3D CNN | HybridSN | IntegratedCNNs | |
|---|---|---|---|---|---|---|
| Indian Pines dataset | 1D CNN | - | ||||
| 2D CNN | 210.13 * | - | ||||
| 3D CNN | 472.20 * | 155.86 * | - | |||
| HybridSN | 896.06 * | 407.98 * | 84.67 * | - | ||
| IntegratedCNNs | 957.46 * | 459.58 * | 196.83 * | 32.50 * | - | |
| Wuhan University dataset | 1D CNN | - | ||||
| 2D CNN | 770.82 * | - | ||||
| 3D CNN | 1122.80 * | 70.45 * | - | |||
| HybridSN | 1618.20 * | 348.37 * | 128.30 * | - | ||
| IntegratedCNNs | 1706.59 * | 385.41 * | 137.54 * | 0.12 | - |
| Dataset | Efficiency | 1D CNN | 2D CNN | 3D CNN | HybridSN | IntegratedCNNs |
|---|---|---|---|---|---|---|
| Indian Pines dataset | Training time (s) | 44.06 | 901.20 | 1477.93 | 968.71 | 600.77 |
| Testing time (s) | 5.33 | 6.51 | 18.04 | 20.04 | 13.37 | |
| Wuhan University dataset | Training time (s) | 1108.34 | 4396.18 | 7935.22 | 5372.43 | 3228.42 |
| Testing time (s) | 76.02 | 27.30 | 148.71 | 149.47 | 114.47 |
| 3D CNN | 2D CNN | 1D CNN | Training Time (s) | Testing Times (s) | Overall Accuracy (%) | Average Accuracy (%) | Kappa Coefficient | |
|---|---|---|---|---|---|---|---|---|
| IntegratedCNNs | ✓ | ✓ | ✓ | 600.77 | 13.37 | 99.65 | 98.97 | 1.00 |
| 3D-2D CNN | ✓ | ✓ | 653.57 | 13.86 | 99.55 | 98.93 | 0.99 | |
| 3D-1D CNN | ✓ | ✓ | 663.51 | 13.81 | 99.45 | 97.05 | 0.99 | |
| 2D-1D CNN | ✓ | ✓ | 114.12 | 4.17 | 97.71 | 91.28 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, T.; Skidmore, A.; Sun, Y.; Jia, P.; Zhang, K. Integrated 1D, 2D, and 3D CNNs Enable Robust and Efficient Land Cover Classification from Hyperspectral Imagery. Remote Sens. 2023, 15, 4797. https://doi.org/10.3390/rs15194797
Liu J, Wang T, Skidmore A, Sun Y, Jia P, Zhang K. Integrated 1D, 2D, and 3D CNNs Enable Robust and Efficient Land Cover Classification from Hyperspectral Imagery. Remote Sensing. 2023; 15(19):4797. https://doi.org/10.3390/rs15194797
Chicago/Turabian StyleLiu, Jinxiang, Tiejun Wang, Andrew Skidmore, Yaqin Sun, Peng Jia, and Kefei Zhang. 2023. "Integrated 1D, 2D, and 3D CNNs Enable Robust and Efficient Land Cover Classification from Hyperspectral Imagery" Remote Sensing 15, no. 19: 4797. https://doi.org/10.3390/rs15194797
APA StyleLiu, J., Wang, T., Skidmore, A., Sun, Y., Jia, P., & Zhang, K. (2023). Integrated 1D, 2D, and 3D CNNs Enable Robust and Efficient Land Cover Classification from Hyperspectral Imagery. Remote Sensing, 15(19), 4797. https://doi.org/10.3390/rs15194797








