Abstract
Eucalyptus plantation forests in southern China provide not only the economic value of producing timber, but also the ecological value service of absorbing carbon dioxide and releasing oxygen. Based on the theory of spatial colonial modeling, this paper proposes a new method for 3D reconstruction of tree terrestrial LiDAR point clouds for determining the aboveground carbon stock of eucalyptus monocotyledons, which consists of the main steps of tree branch and trunk separation, skeleton extraction and optimization, 3D reconstruction, and carbon stock calculation. The main trunk and branches of the tree point clouds are separated using a layer-by-layer judgment and clustering method, which avoids errors in judgment caused by sagging branches. By optimizing and adjusting the skeleton to remove small redundant branches, the near-parallel branches belonging to the same tree branch are fused. The missing parts of the skeleton point clouds were complemented using the cardinal curve interpolation algorithm, and finally a real 3D structural model was generated based on the complemented and smoothed tree skeleton expansion. The bidirectional Hausdoff distance, average Hausdoff distance, and F distance were used as evaluation indexes, which were reduced by 0.7453 m, 0.0028 m, and 0.0011 m, respectively, and the improved spatial colonization algorithm enhanced the accuracy of the reconstructed tree 3D structural model. To verify the accuracy of our method to determine the carbon stock and its related parameters, we cut down 41 eucalyptus trees and destructively sampled the measurement data as reference values. The R2 of the linear fit between the reconstructed single-tree aboveground carbon stock estimates and the reference values was 0.96 with a CV(RMSE) of 16.23%, the R2 of the linear fit between the trunk volume estimates and the reference values was 0.94 with a CV(RMSE) of 19.00%, and the R2 of the linear fit between the branch volume estimates and the reference values was 0.95 with a CV(RMSE) of 38.84%. In this paper, a new method for reconstructing eucalyptus carbon stocks based on TLS point clouds is proposed, which can provide decision support for forest management and administration, forest carbon sink trading, and emission reduction policy formulation.
1. Introduction
Traditional plot survey methods can obtain accurate forest carbon stocks. However, these methods are time consuming, labor intensive, and costly, making them difficult to apply on a large scale [1,2,3]. Remote sensing can accurately and rapidly provide information on vegetation over large areas and has been widely used to estimate forest carbon stocks. Estimation of forest carbon stocks at different scales requires the application of specific techniques, including field surveys at the individual tree and plot level, terrestrial laser scanning (TLS), airborne LiDAR or regional-level radar, and satellite remote sensing at the national or global level [4,5]. All techniques have their associated uncertainties, and these are transferred to the next level. Forest carbon stock measurements at any scale are deeply affected by the accuracy of the methods used to determine carbon stocks in individual trees. Forest carbon stock estimates also require validation of ground survey products, and cutting and weighing trees is a direct method for accurately obtaining tree carbon stocks and biomass, which is commonly used to develop allometric growth models [5,6]. Allometric growth estimation is an indirect method for estimating carbon stocks and can verify the accuracy of remote sensing products at different spatial scales, but the uncertainty of the results is difficult to quantify or even unknown. Once allometric growth models are selected or constructed, field measurements are often used to predict individual tree biomass. However, they do not provide spatial distribution of biomass on a large scale, especially in countries and regions without well-established national forest inventory (NFI) or monitoring systems [7,8]. Remote sensing-based carbon estimates are often compared with field inventory-based assessments. However, almost all field-based carbon assessments are also estimates. Parameters such as survey data (i.e., tree diameter, height, wood density) are input into an isochronous growth model built by harvesting trees to predict biomass and carbon stocks [9]. The anisotropic growth equation provides the most probable value of statistically established biomass, rather than the actual biomass of the tree, which is standardized through destructive measurements. Large-scale mapping of forest carbon stocks requires validation and calibration of individual tree carbon stocks. Studies estimating biomass carbon stocks using Global Ecosystem Dynamics Investigation GEDI, ICESat-2, GLAS, optical satellite imagery, SAR data, and airborne laser scanning (ALS) data, either alone or in combination with parametric and non-parametric techniques, have been developed at a range of spatial resolutions, forest types, and ecosystems [8,10,11,12,13]. In addition, machine learning techniques can be combined to bring accurate measurements of forest canopy height and carbon stocks to large-scale, more efficient, and operational forest mitigation assessments. For example, airborne LiDAR has been shown to reduce errors in extrapolating aboveground biomass values to regional scales, but its calibration and validation still relies on ground-, individual-tree-level carbon stock data or products [13,14,15,16]. Therefore, accurate and non-destructive estimation of carbon stocks in individual tree level is important and challenging.
Obtaining accurate and detailed forest structural information was revolutionized with the advent of TLS, which initially focused on measuring traditional structural metrics such as height and diameter at breast height (DBH) but eventually evolved into more advanced applications such as individual modeling of branches and stems, habitat assessment, and tree species classification at both the single-tree and plot level of TLS [17,18]. TLS has been discussed as the preferred data source for forest aboveground biomass (AGB) validation and a potential new standard for assessing forest structure metrics [12]. Essentially, high-density point clouds are collected from the ground using TLS. From these point clouds, individual trees are segmented, and explicit geometric models are subsequently built. These models are used to estimate the volume of wood in individual trees, which in combination with wood density allows for the estimation of AGB [19,20,21,22]. Therefore, TLS is not a direct measure of tree AGB and should not be considered as such. Current shortcomings of TLS-based AGB estimation include uncertainty in the within-tree variability of wood density trees, the estimation of the volume of small tree limbs (<10 cm in diameter), the variability in wood density within individual trees, and the variability in the estimation of the automated variability in processing chain estimates. TLS can provide high-quality and high-density point clouds with obvious advantages in measuring forest 3D structure, providing new ideas and methods for carbon stock determination in individual trees [17,23,24]. TLS-based point clouds allow quantitative reconstruction of tree 3D structural models and provide basic topological, geometric, and volumetric properties of trees. These properties also include the total number of branches and the order of any branches, the parent–child relationships of branches, as well as the length, volume, and angle of individual branches, and the size distribution of branches. Theoretically these methods are independent of tree shape, size, and species, and allow direct reconstruction of tree volume, which in combination with wood density can be used to estimate tree biomass and carbon stocks.
For example, TreeQSM is a QSM method developed by Raumonen et al. to reconstruct the woody structure of trees (2013) and further developed by Calders, Newnham, and Raumonen et al. [20,25]. TreeQSM reconstructs the tree details using proximity relationships and geometric properties of the point set, which records the topological branching structure of the tree. The topology of the whole tree is fitted to the point clouds of a single tree by fitting cylindrical surfaces to it, and the volume of each cylindrical section is calculated, which in turn calculates the volume of the trunk and branches. Hackenberg et al. utilized the idea of pointing the point clouds of a tree through a spherical cut as a cylindrical section of a tree branch and further cylindrical fitting under the appropriate parameters of the center and radius of the circle [26]. Fan et al. updated and extended the AdTree method and proposed a new quantitative estimation method for tree attributes, AdQSM to extract DBH, tree height, volume, and AGB [19,27]. The calibration and validation of AGB products retrieved from satellite sensors requires accurate estimation of hectare (1 to 100 ha) AGB. Recent studies have recommended using non-destructive TLS-based techniques for individual tree AGB estimation to provide unbiased AGB predictors. Individual tree geometric models constructed based on TLS point clouds are used to estimate tree wood volume, which in combination with wood density can estimate AGB [28,29]. Some studies have shown that TLS can provide unbiased estimates of individual tree AGB with errors that are independent of tree size and low bias (±10%), while other studies show that the error increases with tree size [18,19,25,30]. In the absence of direct destructive measurements, TLS appears to be the best non-destructive estimate of individual tree AGB. Therefore, the 3D modeling method of single trees based on TLS point clouds brings new ideas for us to determine the carbon stock.
TLS point cloud reconstruction of tree 3D modeling is important for remote sensing estimation of aboveground carbon stock in single trees. By storing and displaying the real form of trees through computer modeling, it is possible to have a more comprehensive understanding of tree structure, growth, health status, and other aspects [31]. In general, the current computerized 3D reconstruction based on tree TLS point clouds mainly includes theories and methods such as clustering or segmentation, graph theory, iterative modeling, and spatial colonization [32]. The first three methods have now been proven to be used in TLS point clouds to measure tree biomass and carbon stock, while the spatial colonization algorithm originated from an algorithm proposed by Runions to solve leaf vein generation and was extended to tree modeling in subsequent studies, with the core idea of competing for the surrounding point clouds during the growth process and setting the deletion thresholds, influence radius, and step sizes to control the growth magnitude and direction, among other things [33]. The algorithm can utilize the principle of tree competition for space to reflect the branch growth trend and generate a continuous skeleton. Shi yi et al. introduced angular constraints in the spatial colonization algorithm based on the characteristics of trees’ phototropic upward growth [34]. Each point cloud searches for the nearest skeleton and influences it, excluding the interference of point clouds outside the angular constraints, and the set of points within a certain range jointly influences the direction of the tree skeleton, which is in line with plant phototropism and the characteristics of upward growth. The spatial colonization algorithm takes into account the complex and variable structure of trees and can make full use of the principle of tree competition in space to more accurately generate a continuous skeleton reflecting the trend of branches and trunks, and the algorithm has a wider scope of application. However, the algorithm can cause some topological errors in the skeleton growth due to the limitation of the field of view, and it is also less capable of handling the separation phenomenon between branches caused by the missing point clouds [35,36]. When the missing part of the point clouds is larger than the influence radius, the skeleton will stop growing in that direction, and, relying entirely on the Euclidean distance between the point clouds and expanding the influence radius, will result in topological or morphological errors. The skeleton growth process is more dependent on the field of view range; too large or too small field of view range will affect the accuracy of the skeleton, and the noise of fine branches inevitably occurs during the skeleton growth process [35]. Current spatial-colonization-based tree modeling methods are poor at reconstructing missing parts of the point clouds when growth stops in that direction when it reaches the missing part.
Our goal is to develop a single-tree-level aboveground carbon stock estimation method based on TLS point clouds. Specifically, we will propose a new method for 3D reconstruction of tree TLS point clouds for determining the aboveground carbon stock of Eucalyptus monocarps based on the idea of spatial colonial modeling, and develop a framework for reconstruction of Eucalyptus monocarps branches and trunks based on TLS point clouds, which includes the main steps of tree branch and trunk isolation, skeleton extraction and optimization, 3D reconstruction, and the calculation of carbon stock and related parameters. The reconstruction process generates a rough tree skeleton and then optimizes it and adjusts the unreasonable skeleton. It can reflect the structure and topological relationship of tree branches more accurately and propose effective strategies for the problem of incomplete tree skeleton due to the lack of point clouds. The main trunk and branches of the tree point clouds are separated using layer-by-layer judgment and clustering methods to avoid errors in judgment caused by sagging branches of trees. By optimizing and adjusting the skeleton to remove small redundant branches, near-parallel branches belonging to the same tree branch are fused. Curve interpolation algorithm will be used to complete the missing parts of the skeleton point clouds, generate a real 3D model of the tree based on the expansion of the smoothed tree skeleton, and realize the calculation of aboveground carbon stock based on the 3D model. We harvested 41 eucalyptus trees and used the measurement data of the felled trees to verify the accuracy of the calculation of carbon stock. For each tree, wood density values and carbon content were sampled and measured, combined with carbon stock calculations using tree 3D reconstruction. The aim of this study is to develop the utility of TLS in monitoring forest carbon stocks and to address the practical difficulties that limit the use of TLS for spatial colonization modeling of trees. This paper presents a new method for reconstructing eucalyptus carbon stocks based on TLS point clouds, which can provide decision support for forest management and management, forest carbon sink trading, and emission reduction policy formulation.
2. Materials and Methods
2.1. Terrestrial LiDAR Scanning of Eucalyptus Sample Trees
In this paper, a Pentax S-3180V 3D laser scanner (PENTAX, Saitama, Japan) was used to scan the plots. The measurement distance is 187.3 m, the minimum measurement range is 0.3 m, the resolution is 0.1 mm, the maximum data acquisition rate is 1,016,027 points/s, and the linear error at 50 m is less than 1 mm. The vertical field of view is 320° and the horizontal field of view is 360 °. Vertical resolution is 0.0004° and horizontal resolution is 0.0002°. The vertical accuracy and horizontal accuracy are 0.007°rms, and the scanning speed is less than 50 rps. A total of 41 eucalyptus sample trees were scanned in Guangxi Gaofeng State-Owned Forest Farm (22°49′–23°15′N, 108°8′–108°53′E). Among them, in the subordinate forest farms of Gaofeng Forest Farm, include Datang and Baise, 14 and 9 trees were scanned respectively, and 18 trees were scanned in the Wuming felling area of Nanning arboretum. At the center of each small plot, we set up a scanning station (height of about 1.5 m), and uniformly inserted flower poles and pasted target paper to the boundaries of the plots and the unobstructed areas of the sample trees to ensure that neighboring stations could see at least three common points, which was convenient for data splicing (Figure 1). The scanning quality and resolution of each station were set to a high level, the scanning time was approximately 3 min, and the density of the point clouds was approximately 53,000 pixel/m2. The data were denoised by Z + F Laser control, and then imported into LiDAR 360 software (https://www.lidar360.com/ (accessed on 1 May 2023))(Beijing GreenValley international, Ltd., Beijing, China) for pre-processing operations such as alignment and splicing, separation of ground points, and single-tree segmentation.

Figure 1.
Point clouds of sample trees using TLS (Terrestrial Laser Scanning). (The numbers in the figure are the target numbers).
2.2. Felling and Measurement of Sample Trees
To verify the accuracy of our method, felling was conducted after scanning the sample trees (Figure 2). First, the DBH and height of the felled trees were measured using circumference ruler and tape measure. The DBH measurements ranged from 6.3 cm to 28.6 cm and the tree height measurements ranged from 11.10 m to 31.90 m. The branches of the felled trees were then weighed and resolved to determine the tree weights, tree volumes, wood densities, and carbon contents. To determine the wood density, the fresh volume of the tree core and branches was measured using the drainage method, and then the samples were dried in an oven at 65 °C for 72 h, while the dry volume was measured at regular intervals until a constant weight was optimal. To determine the carbon storage in the branch and trunk samples, the carbon content was determined using the potassium dichromate oxidation external heating method, which was repeated three times for each sample.

Figure 2.
Cutting down of trees and the taking of destructive measurements.
2.3. Quantitative Reconstruction of Single-Tree Three-Dimensional Structure of Eucalyptus
2.3.1. Tree Point Cloud Preprocessing and Branch–Trunk Separation
The shape of the tree trunk is relatively regular, while the reconstruction of branches with complex structure requires more detailed information and will consume more computational resources. Therefore, the trunk of the tree was separated from the branches, which reduces the computation during the search process of the spatial colonization algorithm and also avoids the problem of the skeleton growing against the wall caused by the limitation of its field of view. After removing the outliers and noisy points of the trees, downsampling was performed using the neighborhood distance threshold homogenization method. A plane was fitted around the point clouds neighboring each point, and the point was removed if it was too far from the plane. If too high a neighborhood radius (or too low an error threshold) was used, it removed sharp corner sections. Removing noise while preserving detailed features such as branch tips repeated the operation with a smaller radius and a relatively high error threshold.
Based on the characteristic of compact growth of the trunk, the tree point clouds were segmented from bottom to top according to the Z-axis direction of the point clouds and divided into multiple level sets for processing. Due to the irregularity of tree growth, the trunk cannot be completely separated by height, as other segments (e.g., drooping branches) other than the trunk appear in the same level set. Each segment was divided by clustering using the density-based DBSCAN clustering method. In the trunk, point clouds were clustered into one class and in the branches point clouds were divided into multiple classes. At the same time, to avoid misjudgment of branches caused by sagging tree branches, the distance between each class of point clouds and the previous segment of trunk point clouds were used as a test basis. The separation effect of single trunk and branches is shown in Figure 3.
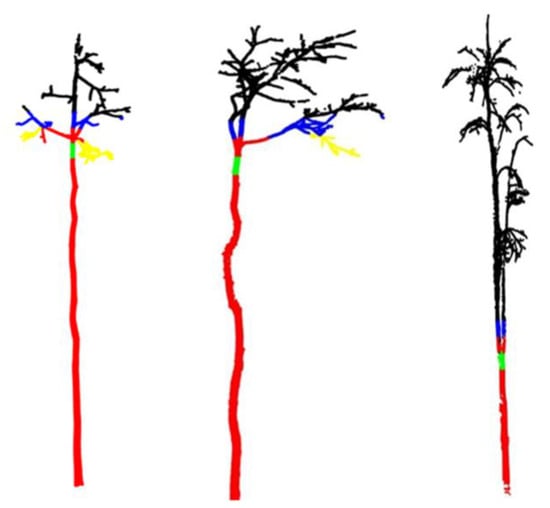
Figure 3.
Effect of separating the trunk and the branches. Red parts represent the trunk; Green parts indicate the separation points between the trunk and the crown; Blue and black parts represent branches.
The specific process is as follows:
- (1)
- The tree point clouds are uniformly divided into n segments in the order of Z-value from smallest to largest.
- (2)
- DBSCAN clustering method is carried out for a segment of point clouds according to the Z value from smallest to largest, clustered into k classes.
- (3)
- If k = 1, the segment point clouds are considered to still belong to the trunk part, step 2 is performed, and the judging of the next segment point cloud continues. If k > 1, the point clouds are divided into multiple classes according to the clustering of density, where the point clouds of class j in segment i is denoted as .
- (4)
- The closest distance between and each point of point clouds are determined, as in Equation (1):where , and .If the nearest distance is less than the point cloud neighbor threshold , then it is considered to be a branch caused by the extension of the trunk, and the number of branches is added to the count by one; otherwise, it is considered to be caused by the sagging of the end of the tree branch, and it is not counted in the number of branches, and, at the same time, the point clouds of the pseudo-branching portion of the tree cloud caused by the situation are deleted in the to eliminate the influence of the subsequent steps.
- (5)
- If the number of branches , the branch has not been generated, the search is continued, and step 2 is implemented; if , then the branch has been generated at this time, at the end of the search, and is selected as the end of the trunk position.
2.3.2. Improved Spatial Colonization Algorithm to Extract Tree Skeleton
Runions proposed a spatial colonization algorithm with open vein sequences for leaf vein point extraction was used for 3D reconstruction [35]. The core idea comes from the competition for space during tree growth, which gradually generates skeleton points according to the point cloud distribution. One cycle of the iteration of the spatial colonization algorithm is shown in Figure 4. As shown in Figure 4a, the initial position of growth (i.e., the initial skeleton points) was first determined. Each point cloud in each iteration was associated with the skeleton point closest to it (Figure 4b), and each skeleton point finds the point clouds associated with it. These point clouds collectively influenced the growth of the next skeleton point by finding the normalized vectors from the skeleton point to these points (Figure 4c). The sum of these vectors was used as the growth direction of the next skeleton point (Figure 4d), and the distance of the next skeleton point is determined by the growth step. At the end of the growth phase, for newly grown skeleton nodes, the points within the radius of their deletion threshold were deleted (Figure 4e). The next loop, as shown in Figure 4f,g, was then performed until the specified number of iterations was reached or no more new skeleton points were generated.
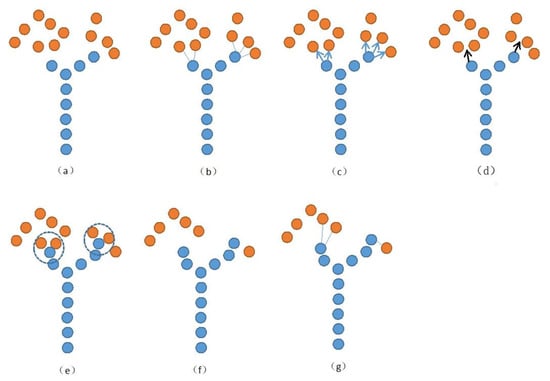
Figure 4.
(a–g) One cycle of skeleton growth of space colonization algorithm. Blue and orange indicate initial skeleton points and skeleton points to be searched, respectively.
In process (b), since searching the entire point clouds to find the nearest skeleton point will reach time complexity in each growth cycle, this paper uses a KD-Tree to establish the neighborhood relationship of the point clouds to achieve the effect of querying the neighboring points faster. During the skeleton growth process, the original input point clouds P was unchanged, and so there was no need to repeatedly construct or update the KD-Tree in each iteration. For the points to be deleted from P, an array of flag bits was used to record whether each point has been deleted or not, and the points marked for deletion were not used again in subsequent iterations.
The effectiveness of the spatial colonization algorithm depends on important parameters such as the growth step , the deletion threshold and the influence radius . The parameters can be adjusted appropriately if one expects to obtain skeleton points that accurately reflect the topology and direction of the tree’s branches and trunks. indicates the range of the field of view during the growth process, and when becomes smaller, the growth direction reflects the direction of the point clouds at the point closer to the current skeleton point. If the skeleton point slightly deviates from the main stem or the point clouds at that place are not uniformly distributed, it is easy to cause the problem of unstable growth direction. It is also possible that the point clouds in a certain part are sparse and the spacing is larger than the smaller influence radius leading to an early end of growth on that branch, which greatly increases the demand on the quality of the point clouds. When becomes large, the growth of the skeleton will prematurely encounter the bifurcation point of the branch, creating the problem of early bifurcation, which does not accurately reflect the structure of the skeleton.
Usually, it is difficult for a field of view range to satisfy the above requirements at the same time; to obtain the skeleton points more accurately, a small and a large influence radius () are set, and the skeleton direction is predicted by using the field of view ranges of the two regions to affect the growth direction of the skeleton points together. In this paper, the main steps for extracting the tree skeleton based on the improved spatial colonization algorithm are as follows:
- (1)
- Initialization phase: input the tree branch point clouds from step 2.3.1 and specify the initial node at the growth location, add it to the skeleton point set S, and create a KD-Tree for all point clouds sets P.
- (2)
- Finding the associated points: for each skeleton point in , corresponding to two sets and , and , denote the points associated with in the set P obtained by different influence radius . For a point v in or satisfying Equation (2),where cur is the number of currently existing skeleton points.Search for points in P within the influence radius and , respectively, and record the corresponding distances. For each skeleton point , find the point associated with it in P and add it to . Search for the points within the range of , and add the associated point to . Furthermore, to avoid anomalous branches due to the large angle of branches, the points in and that do not deviate more than 60° from the direction of the original skeleton are retained, and the rest of the points are discarded. Let the original growth vector formed by the skeleton point and its parent node be , then the retained point u satisfies Equation (3),
- (3)
- Growing node phase: for each skeleton point in , calculate the common influence of the points in on the next growth. The vectors of the points associated with it are normalized, and these vectors are summed up and normalized again to find the growth direction of the next skeleton node; when the set of the points associated with the corresponding is empty, the skeleton point ends its growth.For the points in , find the normalized vector , as in Equation (4):For the points in , find the normalized vector as in Equation (5):Add each vector obtained from the computation to the set , and similarly add to the set . Use the normalized vector of the sum of the vectors in the sets and as the growth direction of the skeleton points. The growth direction vectors and , for the affected influence radius and , respectively, are obtained, denoted as Equation (6):Determining the final growth direction by weighted averaging is expressed as Equation (7):
- (4)
- Deletion of nodes: after the generation of new skeleton points in the range of the deletion threshold is considered to complete the impact on the skeleton growth, and therefore delete the point clouds in the range of the deletion threshold of the new skeleton points.
- (5)
- Repeat steps (2) through (4) until no newer skeleton points are generated.
2.3.3. Optimization and Adjustment of the Skeleton
Due to the different settings of influence radius, growth step, and deletion threshold, the extraction of the skeleton will be different degrees of messy and unreasonable fine branches or near-parallel branches in the trunk (e.g., Figure 5), which affect the authenticity and accuracy of the tree structure and need to be further optimized and adjusted. In this paper, the weight of each skeleton point was used as the basis for the retention and deletion of fine branches, and the weight of each node was calculated after extracting the skeleton points, indicating its importance in the whole tree. When the skeleton point was closer to the root node in the graph and has more child nodes, the point was more important and less likely to be deleted in the fine branch deletion process. If the distance between two neighboring points in the skeleton is equal, the weight of the point is represented by the number of child nodes it possesses. Using recursion, starting from the root node, the recursion ends with the condition of traversing to the leaf nodes, and finding the weights of all the child nodes occurs before finding the weight of the parent node. To solve the unreasonable branching problem, this paper used the algorithmic strategy of reservation and pruning as follows:

Figure 5.
Near-parallel branches appearing during the growth of skeleton points.
- (1)
- For a branch node, iterate through all its child nodes. If the weight of the sub-node is less than reserve_threshold and the ratio of the weight of the sub-node to the weight of the current node is less than drop_ratio, it is considered to be a redundant extension branch, and so it is deleted from the sub-node. If the weight of this sub-node is less than the pending deletion threshold drop_threshold, then it belongs to the node to be deleted. If no other child nodes are reserved, the node with the maximum weight is reserved in the area to be deleted. This step is to prevent the original branch at the end of the branch from being deleted. In other cases, the skeleton points are directly retained, and the next round of processing is carried out.
- (2)
- After the removal of fine branches, there are also two skeleton lines extending approximately parallel in the thicker trunks due to field of view issues [27]. The AdTree modeling approach uses vertex fusion for skeleton simplification using a similarity metric α as a threshold for fusing vertices as in Equation (8):In the case of multiple child nodes, denote the distance from the current node C to the child nodes respectively, and denote the radius values of . denotes the angle formed by the two child nodes and the current node. The algorithm can simplify the skeleton to a greater extent in the case of tighter skeleton points. Since the angles of the near-parallel branches at the bifurcation may be larger, setting a larger threshold using the above method will change the normal branching, and so special treatment is needed. These near-parallel branches are characterized by the fact that the distance between the two lines always remains close in a longer distance of the skeleton bifurcation, based on which an algorithm is designed to solve the problem of near-parallel branches. The algorithm process is shown in Figure 6 as follows:
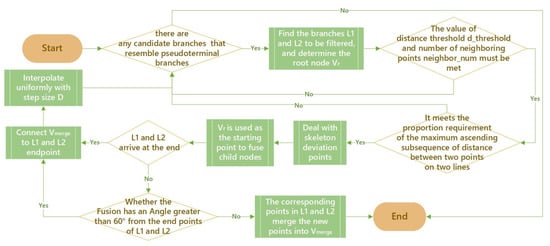 Figure 6. Algorithm flow chart.
Figure 6. Algorithm flow chart.
- ①
- The branch to be filtered is found. is a skeleton branch point, two child nodes of a skeleton branch point must be found, and depth-first traversal is used to extend backward to find two branches. If a branch is encountered again during depth traversal, the one with the closest Euclidean distance is chosen as the next node. , denote the ordered point sets on the two branches found to be screened. It is denoted as:where and have the same initial node .
- ②
- The branches to be screened are tested to see if they are subparallel branches. For true branches and near-parallel branches, the difference between the two is that near-parallel branches are usually close to each other over longer distances, and the change in distance is not significant as the points extend sequentially. Two criteria are set here, the number of neighboring points in two lines neighbor_num, and the maximum distance threshold of a branch d_threshold. If a point on a branch can see more points on another branch within the distance range of d_threshold, it is more likely to be a near-parallel branch. In addition, to better exclude the effect of ordinary branching, the distance is calculated for each point corresponding to a point on the two branches, and if the distance is basically gradually increasing, it is more likely to be a branch. The longest ascending subsequence of the sequence of distances to the corresponding points in the two lines is computed, and if the ratio of the length of this sequence to the minimum of the lengths of the two branches is too large, it is considered to be a branch.
- ③
- Treatment of skeleton deviation points and fusion of near-parallel branches: The fused branch is jointly influenced by two near-parallel branches. If a part of one branch deviates too much and is not within the d_threshold neighborhood of the other branch, i.e., there exists and Equation (9) is satisfied for any point ,then the point is deleted so as not to affect the deviation of the skeleton after fusion. Assuming that the skeleton points that are consecutively deleted in a segment arethen and are connected and interpolated uniformly with a step size D. Finally, the weighted average points of the corresponding points of L1 and L2 are taken and fused sequentially from the root to the tip. During the fusion process, to avoid the unreasonable visual effect of excessive fusion resulting in too large an angle, the angle between the newly generated points and the points outside the L1 and L2 lines is judged until the last point that makes the angle less than or equal to 60 degrees, thus ensuring a reasonable trend in the growth of tree branches.
2.3.4. Completing the Missing Point Clouds of the Tree Skeleton
We use the physiological and structural laws of trees to predict the position and direction of the skeleton lines in the missing parts. Section 2.3.1, Section 2.3.2 and Section 2.3.3 complete the extraction of the main skeleton. Since the skeleton points will stop growing where the point clouds are missing, there are still part of the point cloud clusters that are not used. To obtain a more accurate and complete skeleton, the remaining point clouds were subjected to DBSCAN clustering. After clustering, each class of point cloud clusters corresponds to a portion of untraversed branches. Each point cloud cluster is processed individually, and one point is selected as the starting point (the point corresponding to the minimum value in the Z-axis direction due to the bottom-up growth characteristic of trees) for skeleton extraction and optimization, and the skeleton is stored in the form of an undirected graph. The starting point selected above is not necessarily the root node of the branch; to determine the root node of the branch, the following method is used: for the branch with sub-branches, start from the node with degree 1 at any point in the undirected graph, and sum up the angles of all the bifurcations. If the point of departure is not the root node of the branch, the angle of the angle formed by the points passing from that point is more likely to contain an obtuse angle, and the sum of the angles is biased. The node with the smallest sum of angles is most likely to be the root node of the independent branch, and if there is no branch, the point with the smallest z-value is taken as the root node of the independent branch.
After establishing the root node of the independent branch, the skeleton extraction and adjustment process of the spatial colonization algorithm is redone with the root node. To connect the independent branch to the existing branch, the branch is gradually extended in the direction of the root node until it is within a certain distance threshold from the existing skeleton point, which is then selected for connection. To determine the extension direction of the branch at the root node, a polynomial function is fitted to the curve using the least squares method. Since the point clouds are three-dimensional, they are first projected onto the XOY plane. The number of fits is set as k. The polynomial is set to Equation (10):
The sum of squared errors is Equation (11):
To minimize the error squared, the partial derivative of is taken and = 0; the matrix form is simplified and used to represent, as in Equation (12):
Solving the matrix equation, i.e., obtaining a curve fit, defines y versus x as . Similarly, for XOZ plane solving for z versus x yields .
The obtained curve is extended along the direction of the root node, and, if an already existing skeleton point is searched within the distance threshold range , the independent branch is considered to be a new branch branch from the skeleton point. and are connected using a curve smoothing and interpolation algorithm.
In this experiment, the highest number of XOZ and XOY plane fitting functions were set to 1 or 2, respectively. The fitting results are shown in Figure 7. Since the points may be concentrated locally in the curves, there will be instability in fitting the quadratic curves when the direction of the branches deviates greatly from the original direction. Therefore, a fitting function with a maximum number of fits of 1, i.e., a more stable straight line, was chosen for judging the direction of the branch to determine the location of separation from the main branch. At the same time, the direction of the root extension must be obtained; in the obtained straight line to take a number of points , the root node of the independent branch is taken for , and is set as the starting point of the branch in the direction of the vector in the as , to find the closest point on the straight line to is recorded as , expressed in the Formula (13):
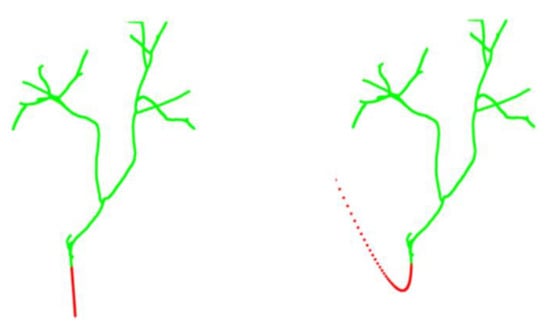
Figure 7.
When fitting a conic curve, the trend of the branches deviates greatly from the original direction. The red area indicates instability at quadratic fit.
The vectors from to the points on both sides of the line are calculated as and , respectively, and the one vector whose angle deviates greatly from is selected, i.e., as the extension direction of the root node as in Equation (14):
Taking as a point, in the direction of , taking points on the straight line with D as the spacing, until a point finds a point on the already existing branch in the θ-neighborhood for the first time, it is considered that is a branch extending from the skeleton point of , and is connected to . Meanwhile, combined with the characteristics of continuous growth of trees, to ensure the reasonableness of the connection process with the main trunk, the curve smoothing interpolation algorithm is used to interpolate at the original missing branches to achieve a more reasonable skeleton model.
We use cardinal curves to interpolate the skeleton points for the missing part of the point clouds, and, for the independent variable t, the interpolation points are as in Equation (15):
where denotes the point after cardinal curve interpolation and is the cubic cardinal matrix with the expression as in Equation (16):
where s is a parameter indicating the looseness or tightness of the shape of the control curve, expressed as Equation (17):
u is called the tension parameter. Two points are taken at each end of the missing point clouds as input points to the cardinal curve; the coordinates of the insertion points are computed and sequentially connected to generate new skeleton points, which connect the two parts of the point clouds that are segmented due to the missing point clouds.
2.3.5. Reconstructing the Three-Dimensional Structure of Trees
Cylinders proved to be robust for fitting tree-branch geometry elements. The skeleton and trunk point cloud portions of the tree branches were further processed to obtain realistic 3D structural models of single tree branches using cylinder fitting based on the skeleton line expansion radius and fitting.
Reconstructing the Trunk Structure
The morphology of tree branches and trunks is complex and irregular, but the trunk part is usually more regular. To better analyze and study the morphology of trees, a more stable cylindrical fitting algorithm is usually used, which can accurately reflect the morphological characteristics of trees, as well as simple and fast numerical calculations and related processing of tree trunks. The parameters of the cylinder can be divided into a point on the axis of the cylinder and the vector representing the direction of the axis, as well as the radius r totaling seven parameters. Segmentation in the direction of the z-axis was used in the main trunk section of the tree, and the least squares method was used to fit the columns to each segment of the point clouds (Eberly, 1999). The upper and lower bounds of the Z value of a segment of the point clouds were set to be and , respectively, and the intersections of the straight line formed by v through the point with z = and z = were the two endpoints of the center axis of the column. The cylindrical model of the multi-segment point clouds is obtained sequentially. The expression of the equation of each segment of the cylindrical surface is shown in Equation (18):
Reconstructing the Branches Structure
The structure of the branches is more complex and the point clouds in the fine branching section are not enough to fit the cylinder stably. Section 2.3.2 and Section 2.3.3 have extracted the skeleton of the tree branches, and so it is not necessary to use the surrounding point clouds for each section of the skeleton line to fit the cylinder. The radius of the tree branches is an important factor that affects the modeling results. This chapter obtains the radius of tree branches based on the allometric growth theory [37]. This theory considers that the radius of the parent node is equal to the sum of the radii of all child nodes, which is expressed as in Equation (19):
where denotes the radius of the current node, denotes the radius of the parent node, and is the value of a node weight indicating the importance of that node in the whole tree. The method used in this paper provides relatively fixed distances between skeleton nodes, using the number of a node with all its children to indicate that node’s weight.
2.4. Visualization of Single-Wood Branching Structures
We use python language in PyCharm 2018.3.7 for development and open-source algorithm libraries and mathematical toolkits such as VTK8.1.2 and NetworkX 2.2 for modeling. This section shows the tree geometry and topology, including the location of branches, extension direction, and the relationship between parent and child branches. We use a directed graph to store the coordinates and topological relationships of the skeleton points generated by the algorithm, and a round table to represent each segment of branches. The directed graph stores information about each node (including positional coordinates, weights, radii, and other attributes), and each edge is regarded as the center axis of the circular table. The center positions of the two bottom surfaces of the circular table correspond to the coordinates of the two points constituting this edge, and the radius of the two bottom surfaces corresponds to the radii of the points in the middle of these two points. At this point, the skeleton line composed of points and lines expands into a 3D model. Directly connecting multiple circular platforms results in a break at the connection, where a segment of connected points can be connected to form a non-breaking pipe. Since there are bifurcation points in the directed graph and only parent and child relationships between nodes are stored, there is no information about all sequentially connected points that can be used to generate a pipe, the algorithm is designed to extract the set of all sequentially connected points in the directed graph. When the search does not encounter a bifurcation point, the traversed points can be directly added to the array; when a bifurcation point P is encountered, the array is saved, and the search is repeated with P as the starting point. The effect before and after processing is shown in Figure 8.
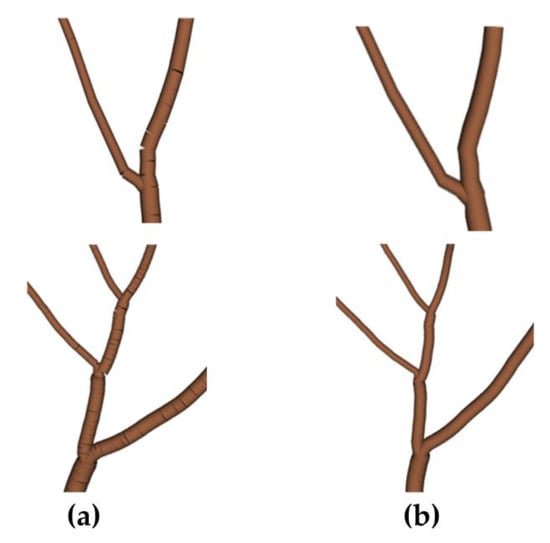
Figure 8.
Comparison of the effect before (a) and after (b) treatment.
The processed model solves the fracture problem at the joint, and the final 3D geometric reconstruction of the single tree is shown in Figure 9.

Figure 9.
Modeling effect.
The 3D geometric reconstruction of a single tree is shown in Figure 10a, comparing the method with AdTree (Figure 10b) and PypeTree (Figure 10c) modeling, respectively. It can be seen that the reconstructed branches of PypeTree are rough, which cannot reflect the complex structure, and the branches at the end of the branches are thicker, while AdTree can reflect the relatively complex branching structure, but it cannot guarantee the stability of the trunk, and there are some redundant small branches and inaccurate representation of the trunk trend. From the visual effect point of view, the improved algorithm proposed in this paper can reflect more details under the premise of maintaining the stability of the trunk.

Figure 10.
Different methods of single-tree model reconstruction. (a) The 3D geometric reconstruction of a single tree. (b) AdTree method. (c) PypeTree modeling method.
2.5. Single-Tree Parameter Extraction Based on 3D Geometric Structural Modeling
2.5.1. Tree Height and DBH
DBH and tree height are important single-tree factors that can be input into the equation as important parameters for carbon stock calculation. Although we developed a volume reconstruction method to directly calculate tree branch volume in Section 2.3, these two important factors are still extracted in this paper for subsequent applications. In this paper, the difference between the maximum value and the minimum value of the Z-axis in the single-tree point clouds are selected as the tree height. In Section 2.3.1, the trunk point clouds were obtained by segmentation, and the cylinder diameter was obtained as the DBH at the position of 1.3 m above the ground in the trunk model.
2.5.2. Determination of Carbon Stocks in Single Wood Based on Volumetric Reconstruction
Development of Tree-Volume 3D Reconstruction Algorithms
The tree volume in this paper includes the volume of branches and trunks; the volume of the main trunk part and branch part of the tree are taken at the same time and summed up to obtain the total volume of a single tree on the ground. The two points of each skeleton line in the tree model reconstructed in Section 2.3 have different radius attribute values. After expanding each skeleton line, the volume is calculated using a frustum as the abstract model. The volume of the tree branch is derived from Equation (20), where represent the radius of the skeleton points, respectively:
For the trunk, a segmented cylindrical fitting is used to find the volume for each segment of the cylinder, which is summed to obtain the volume of the trunk, as shown in Equation (21):
Summing the volumes of the trunk and branch sections yields the volume of the entire single log, as in Equation (22):
Calculation of Aboveground Carbon Stocks in Individual Trees
The most significant difference between the direct calculation of tree volume from the reconstructed single-tree model and the allometric growth equation is that there is no need to use tree height and DBH as parameter inputs to estimate volume. The aboveground carbon stocks of eucalyptus single trees studied in this paper consisted mainly of trunk and branch with carbon stocks. The average density of the trunk and branches (g/cm3) was obtained by combining the drainage method with weighing on a balance, and the volume of the trunk and branches of eucalyptus monocarps (cm3) was obtained by using Section 2.5.1 and multiplying the density of the trunk and branches with the volume to obtain the total dry volume of the branches and trunk of a monocarps (g), i.e., the biomass, and finally combining with the organic carbon stock in the samples of the tree cores and branches (g/kg) to obtain the carbon stock of the aboveground carbon in monocarps branches and trunks. The aboveground carbon stock of a single tree branch was finally combined with the organic carbon stock (g/kg) in the tree core and branch samples.
2.6. Accuracy Assessment
2.6.1. Evaluation of the Accuracy of 3D Structural Reconstruction of a Single Tree
The extracted skeleton line is an object representation of the topology, connectivity, and integrity of the original data, and the evaluation methods for it have not yet formed a universally uniform standard. Most of the studies on point clouds-based tree skeleton extraction are based on the analysis of visual effects, and there are also scholars who use the unidirectional Hausdoff distance or the bidirectional Hausdoff distance and the average Hausdoff distance as the judging standard of the skeleton [38]. We use a combination of visual effects and quantitative evaluation indexes to evaluate the skeleton accuracy. Hausdoff distance is used to describe the similarity or polygonal distance between two sets of point sets, which is expressed as the maximum value of the distance between the two points in the two sets of point sets that are closest to each other. The algorithm output of the skeleton point set is set to and the point set to of the standard skeleton, and the quantitative evaluation metrics are used, as in Equations (23)–(28). The one-way Hausdoff distances of the skeleton point sets and are denoted as Equations (23) and (24), respectively:
The bidirectional Hausdoff distance is expressed as Equations (3)–(19):
The average Hausdoff distance is expressed as Equations (3)–(20):
where
The position of the edges in the skeleton is important. Based on the extraction of the skeleton, the distance from the point to the line of the skeleton is used as an evaluation criterion. First, the distance from the point to the line segment is defined: the line segment AB and a point P are known, the point P is projected to the line where AB is located, and the projection point is . When is outside the line segment AB, the distance between the point P and the line segment AB is the minimum value of the distance between the point P and the two end points. When falls on AB, the distance between P and the line segment AB is the distance from P to the line AB. The formula for calculating the indicator of the setup is as follows (28):
where denotes the distance from point to edge in the above method.
2.6.2. Accuracy Assessment of Single-Tree Parameters
Tree height, DBH, trunk volume, and carbon stock measured after we felled the trees were used as reference values to validate the accuracy of our method. Bias, rBias, RMSE and RMSE% were used as metrics to evaluate the accuracy of our method for determining single-tree DBH, tree height, branch trunk volume, and aboveground carbon stock.
represents the estimated value from the ith tree of our method, represents the reference measurements, represents the average of the reference measurements, and n represents the number of trees.
3. Results
3.1. 3D Structure Reconstruction of Tree Level
To validate the effectiveness of the improved spatial colonization algorithm for extracting the tree skeleton, it was evaluated from two perspectives, including the visual effect and the proportion of the original point clouds being used for skeleton growth. The part of the extracted tree skeleton is demonstrated in Figure 11 and Figure 12 (black indicates the original point clouds and green indicates the skeleton points). A larger influence radius caused the growth to show changes in the branches earlier, especially at the forks (Figure 11), while a smaller influence radius caused some of the point clouds to stop growing in a certain direction due to the restricted growth field (Figure 12).
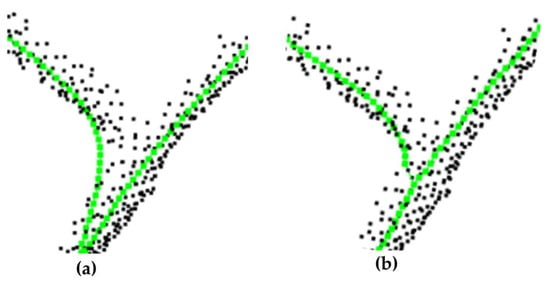
Figure 11.
Comparison between (a) larger influence radius and (b) the improved method. Black points are the point clouds, green points are the skeleton points.

Figure 12.
Comparison between (a) smaller influence radius and (b) the improved method. Black points are the point clouds, green points are the skeleton points.
For this experiment, we set the deletion threshold 0.05 m, the influence radius = 0.12 m, and = 0.20 m, to determine the proportion of preprocessed point clouds used in the growth process of this algorithm.
From the results in Table 1, it can be seen that the improved method used essentially the same number of point clouds or sacrifices only a small portion of them when compared with the original method using a larger influence radius. More points can be absorbed for growth compared with the original method using a smaller influence radius. The improved method in our study ensured the integrity of the branches to a certain extent, and, at the same time, it can achieve more accurate topology in the subsequent modelling process.

Table 1.
The proportion of single-tree point clouds used for spatial colonization growth.
Analysis of Experimental Parameters
The influence radius is an important parameter in the spatial colonization algorithm, which has a large impact on the extraction and modelling of the tree skeleton. In this paper, we set up controlled experiments to explore the role and influence of each parameter in the modelling process through the visual effects of modelling multiple branching sections of multiple trees. The improved algorithm used and to influence the radius, and so a controlled experiment was set up to determine the influence of the change of on skeleton extraction (Figure 13).
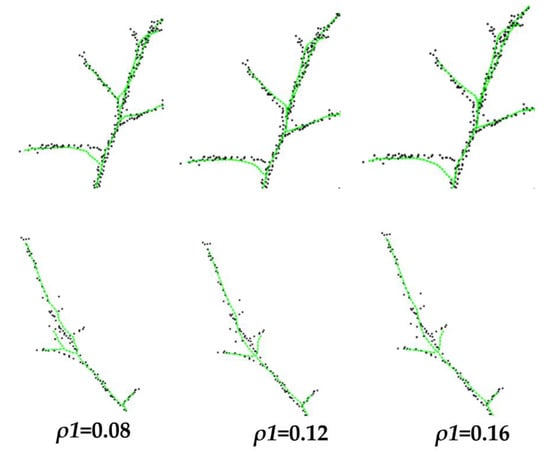
Figure 13.
Effect of different influence radius on skeleton growth. Black points are the point clouds, green points are the skeleton points.
From Figure 13, when the influence radius 2 remains unchanged, the smaller the value of , the more attention will be paid to the point cloud distribution in closer distance during the search of point clouds. In the process of growth, it is easy to be affected by the nearby point cloud, which produces unstable branches in the branches of the branches or the regions where the point cloud distribution is relatively scattered. The increase in will contain a large range of point clouds, and it is difficult to fit the branch direction at the fork.
The effect of different influence radius on the skeleton extraction is shown in Figure 14, where the skeleton aligns with = 0.12 m in the original method and with taking the values of 0.2 m, 0.3 m, and 0.4 m in the improved method were taken for comparison, respectively.
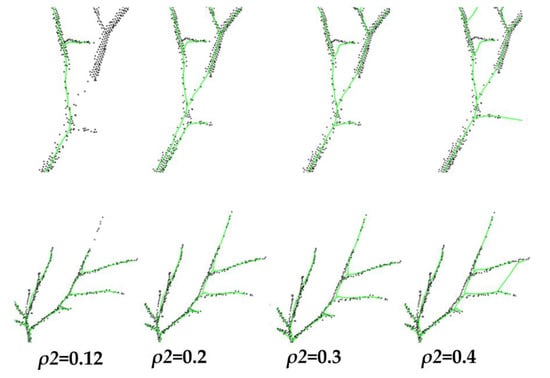
Figure 14.
Effect of different influence radius on skeleton extraction. Black points are the point clouds, green points are the skeleton points.
In the skeleton optimization and adjustment step, the effects of different skeleton edge removal ratios drop_ratio and to-be-removed thresholds drop_threshold on skeleton growth are explored, as shown in Figure 15 and Figure 16. As the threshold increased, more short edges were removed, ranging from initially discarding small noise-induced edges to erroneously excluding short edges belonging to genuine branches. By controlling the parameters appropriately, it was possible to preserve the correct skeleton points as much as possible while simultaneously removing small noise branches within the skeleton, achieving further optimization of the skeleton.
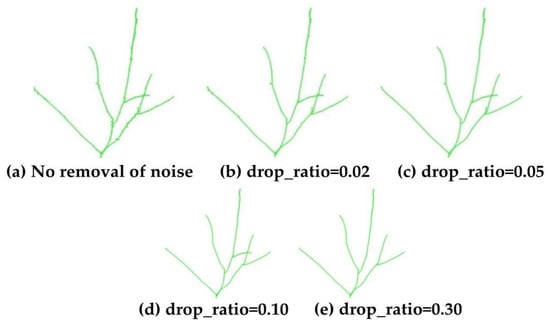
Figure 15.
Effect of different drop ratio on skeleton growth.
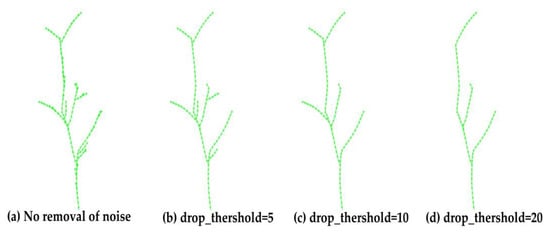
Figure 16.
Effect of different drop threshold on skeleton growth.
To verify the effectiveness of the improved algorithm on skeleton extraction, a controlled experiment was used to verify the accuracy of the skeleton. The improved algorithm was compared with PypeTree and AdTree. The results of the comparison experiments with the standard skeleton in terms of unidirectional Hausdoff distance, bidirectional Hausdoff distance, average Hausdoff distance, and distance are shown in Table 2, Table 3, Table 4 and Table 5.

Table 2.
The unidirectional Hausdoff distance of the skeleton extracted by different modeling.

Table 3.
The bidirectional Hausdoff distance of the skeleton extracted by different methods (m).

Table 4.
The average Hausdoff distance of the skeleton extracted by different methods (m).

Table 5.
The distance of the skeleton extracted by different methods (m).
According to the comparison of experimental results from Table 2, Table 3, Table 4 and Table 5, and in combination with the relevant evaluation indexes, the accuracy of skeleton extraction was improved by the improved algorithm proposed in this paper compared with the primitive spatial colonization algorithm. The average Hausdoff distance and F distance were reduced by 0.0025 and 0.0027 on average compared with the standard skeleton. The average Hausdoff distance and F distance were reduced by 0.065 and 0.0372 on average compared with PypeTree. The average Hausdoff distance and F distance were reduced by 0.0192 and 0.0312 on average compared with AdTree. The average Hausdoff distance and F distance were reduced by 0.0192 and 0.0312 on average compared with PypeTree. The unidirectional Hausdoff distance and bidirectional Hausdoff distance still had high errors because they reflected individual points rather than the whole, and a small number of discrete points can significantly increase the error values indicated by the above two metrics. Possibly due to the absence of skeleton points in the missing portion of the point clouds, complementary skeleton points would further improve the accuracy of the skeleton. The method in Section 3.3 was used to improve the algorithm based on the complete skeleton. The effect of skeleton complementation is shown in Figure 17 (red color indicates the complementary part of the skeleton).
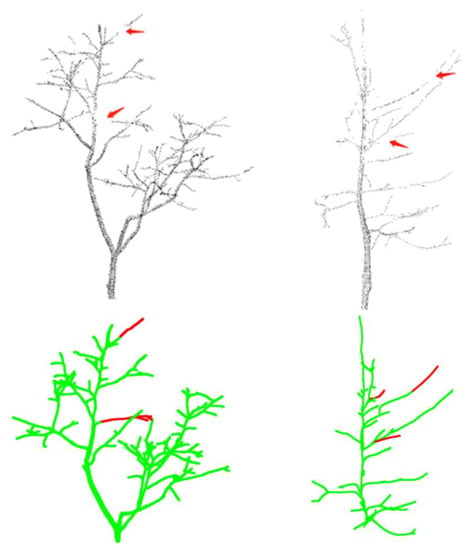
Figure 17.
Skeleton completion effect. Red parts are the skeleton repair effect; green parts are the skeleton points.
From the experiments, the bidirectional Hausdoff distance, the average Hausdoff distance, and the F-distance were found to be reduced by 0.9741, 0.0034, and 0.0019, respectively, for the first tree, and by 0.5166, 0.0023, and 0.0002, respectively, for the second tree. The two trees’ three metrics were reduced by an average of 0.7453, 0.0028, and 0.0011. Thus, the accuracy of the complemented skeleton was improved under the evaluation of several different metrics. The experimental results compared with the standard skeleton are shown in Figure 18.
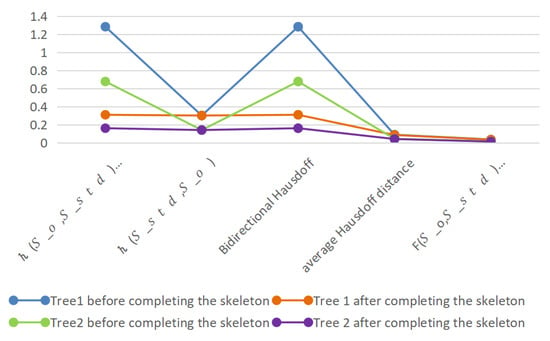
Figure 18.
Distance between standard skeleton and generated skeleton of tree.
The skeleton line extraction effect of different methods is shown in Figure 19. The skeleton extracted by AdTree based on the original point clouds had more noise of fine branches on the trunk, while PypeTree belongs to the clustering based on the level set, and the skeleton was in obvious segmentation, which was not natural and accurate enough. Our method can better show the natural bending state of tree branches and removed the noise of fine branches to a certain extent, which was better in the visual effect.

Figure 19.
Results of skeleton line extraction with different modeling methods: (a) our method; (b) original method; (c) AdTree; (d) PypeTree.
3.2. DBH and Tree Height
The DBH and tree height of 41 eucalyptus trees measured after felling will be used as reference values for reconstruction of our method. The DBH estimates of the reconstructed eucalyptus trees ranged from 6.7 cm to 30.9 cm, and the tree height estimates ranged from 10.19 m to 32.03 m. Figure 20a shows a linear fit of R2 of 0.9 from the 3D tree reconstruction to the reference value, and its slope was 0.83. The reconstructed DBH did not change significantly with the increase in DBH, and the estimated DBH fitted well with the reference value. Figure 20b shows that the R2 of the linear fit between the estimated height of the reconstructed tree and the reference value was 0.76, with a slope of 0.84. The reconstructed tree height underestimates the actual tree height. Overall, the TLS point clouds-based modelling approach did not have a large bias in estimating the DBH and tree height for tree size.
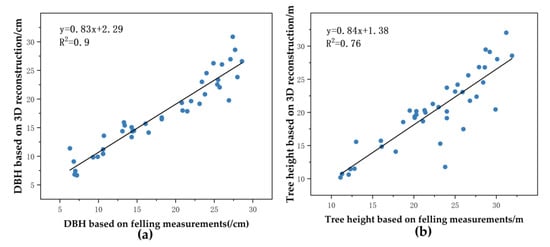
Figure 20.
Comparison of DBH and tree height based on 3D reconstruction of trees with reference values: (a) DBH; (b) tree height.
Figure 21a shows the distribution of residuals for DBH. Most of the residuals for DBH were between −3.0 cm and 3.0 cm, the range of residual distribution was not significantly different with increasing DBH, and they were uniformly distributed on both sides of the line y = 0. Figure 21b illustrates that most of the residuals for tree height were between −2 m and 2 m. There was no significant difference in the distribution range of residuals with increasing tree height, and the residuals were evenly distributed on both sides of the y = 0 line. The point cloud-based reconstruction of DBH and tree height performed similarly in all tree samples.
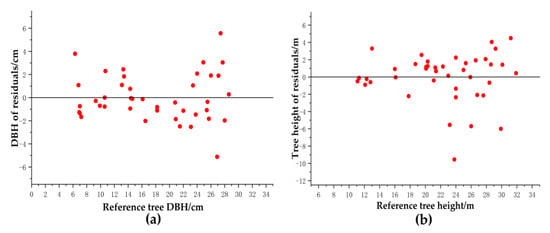
Figure 21.
Residual distribution of DBH and tree height. (a) the distribution of residuals for DBH. (b) the distribution of residuals for tree height.
The accuracy of point cloud-based reconstruction of eucalyptus trees for DBH and tree height is shown in Table 6. The Bias and RMSE of the breast diameter calculated by least squares were −0.56 cm and 2.38 cm, respectively. Among the 41 trees with DBH reference values ranging from 6.3 cm to 28.6 cm, the absolute value of DBH deviation less than 2.38 cm accounted for 70.7% of the total trees. The bias and RMSE of tree height were −2.24 m and 3.68 m, respectively. Among all the trees whose reference height ranges from 11.10 m to 31.90 m, 75.6% of the trees with absolute deviation of tree height was less than 3.68 m.

Table 6.
Comparison of the accuracy of DBH and tree height of eucalyptus determined based on point cloud reconstruction and destructive sampling.
3.3. Volume of Trunk and Branches
We used trunk and branch volumes from 41 trees sampled destructively as reference values for reconstructed trunk and branch volumes. The reference values for trunk volume from eucalyptus ranged from 0.01312 m3 to 0.80380 m3, and the reference values for branch volume ranged from 0.00047 m3 to 0.13049 m3. The estimates of the point cloud reconstructed trunk volume ranged from 0.00280 m3 to 0.79793 m3, and the estimates of the branch volume ranged from 0.00153 m3 to 0.17500 m3. Figure 22 shows the R2 of the linear fit of the estimates and reference trunk volumes of the point cloud reconstruction, respectively, was 0.94. Its slope was 0.95, indicating a slight underestimation of the trunk volume. The RMSE was 0.06222 m3, while the mean trunk volume was 0.32741 m3, resulting in a CV(RMSE) of 19.00%. The R2 of the linear fit of the estimated and reference values of the branch volume was 0.95. Its slope was 0.97, indicating an underestimation of the branch volume. The RMSE was 0.01615 m3 and the CV(RMSE) was 38.84%.
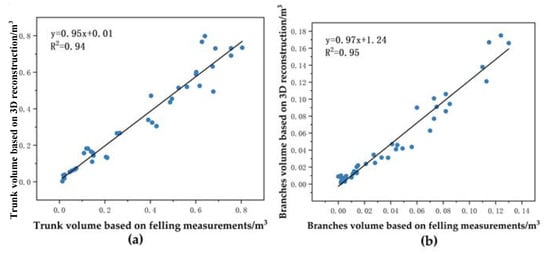
Figure 22.
Comparison of trunk and branch volume based on 3D reconstruction of trees with reference values: (a) trunk volume; (b) branch volume.
Figure 23 shows the residual distributions for the reconstructed trunk and branch volumes. Most of the trunk volume residuals were more evenly distributed on both sides of the y = 0 line and most of the residuals were between −0.1 m3 and 0.1 m3, with no significant difference in the range of residual distributions as the volume of the reference tree increases. Figure 23b provides the distribution of the residuals for the volume of the reconstructed tree branches. Most of the volume residuals were more evenly distributed on both sides of the y = 0 line, and most of the residuals were between −0.02 m3 and 0.02 m3. The range of residual distributions was not significantly different with increasing reference tree volume.
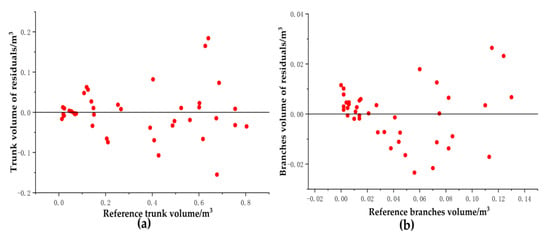
Figure 23.
Residual distribution of (a) trunk volume and (b) branch volume.
Table 7 provides the accuracy of the reconstructed trunk and branch volumes for the method in this paper. The Bias and rBias of the reconstructed trunk volume of the point clouds calculated by the least squares method were −0.00996 m3 and −3.04%, respectively. Of the 41 trees with trunk volume reference values ranging from 0.01312 m3 to 0.80380 m3, the absolute value of trunk volume deviation was less than 0.06222 m3 for 95.1% of the total number of trees. The Bias and rBias of branch volume were 0.00749 m3 and 18.02%, respectively, and the absolute value of branch volume deviation was less than 0.01615 m3 for 85.4% of the total number of trees.

Table 7.
Comparison of accuracy of eucalyptus branch and trunk volumes determined based on point clouds reconstruction and destructive sampling.
3.4. Aboveground Carbon Stocks
We used trunk and branch carbon stocks from 41 trees from destructive sampling as reference values for point cloud-based reconstruction of trunk and branch carbon stocks. The aboveground carbon stock reference values for a single tree from eucalyptus ranged from 4.98976 kg to 230.97258 kg, the trunk carbon stock reference values ranged from 4.82425 kg to 198.86840 kg, and the branches’ carbon stock reference values ranged from 0.16551 kg to 32.10418 kg. The point clouds reconstructed aboveground carbon stock estimates for single trees ranged from 7.14801 kg to 238.26647 kg, the estimated trunk carbon stock ranged from 1.03140 kg to 192.61373 kg, and the estimated branch carbon stock ranged from 0.51283 kg to 45.16920 kg. Figure 24 shows separately that the R2 of the linear fit of the point clouds reconstructed aboveground carbon stock estimates for single trees and the reference value was 0.96. Its slope of 0.98 indicated a slight underestimation of the aboveground carbon stock in individual trees. The RMSE was 14.94391 kg, while the average aboveground carbon stock in individual trees was 92.06388473 kg, resulting in a CV(RMSE) of 16.23%. The R2 of the linear fit of the trunk carbon stock estimate and the reference value was 0.94. Its slope was 0.94 indicating an underestimation of the trunk carbon stock. The RMSE was 15.03535 kg and the CV(RMSE) was 18.35%. The R2 of the linear fit of the estimated and reference values of the branch carbon stock was 0.95. Its slope was 0.97, indicating a slight underestimation of the branch carbon stock. The RMSE was 3.90454 kg and the CV(RMSE) was 38.39%.
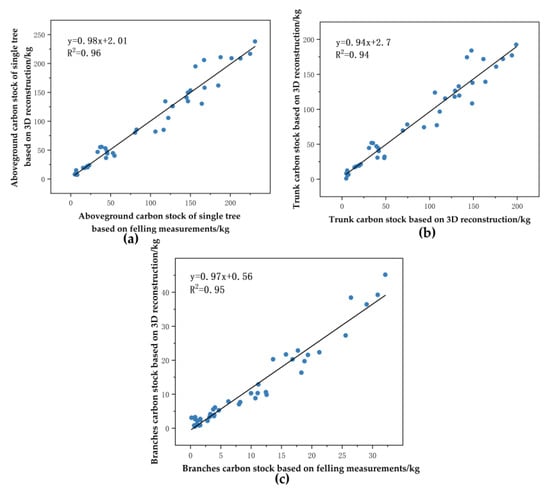
Figure 24.
Comparison of tree-level, trunk, and branch carbon stocks based on 3D reconstruction of trees with reference values: (a) tree-level; (b) trunk; (c) branches.
Figure 25 shows the distribution of residuals for the reconstructed carbon stocks for single trees, trunks, and branches, respectively. Most of the single-tree aboveground carbon stock residuals were more evenly distributed on either side of the y = 0 line, and most of the residuals were between −20 kg and 20 kg, with the range of residual distributions not differing significantly with increasing carbon stock in the reference trees. Figure 25b provides the distribution of carbon stock residuals for reconstructed tree branches. Most of the carbon stock residuals were more evenly distributed on both sides of the y = 0 line, and most of the residuals were between −5 kg and 5 kg, with no significant difference in the range of residual distributions as the reference tree carbon stock increases. Figure 25c provides the distribution of carbon stock residuals for the reconstructed tree trunks. Most of the carbon stock residuals were more evenly distributed on both sides of the y = 0 line and most of the residuals were between −20 kg and 20 kg, with no significant difference in the range of residual distributions as the reference tree carbon stock increases.
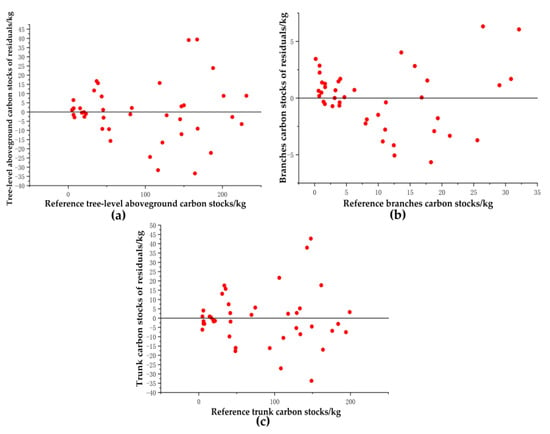
Figure 25.
Residual distribution of (a) tree-level, (b) trunk, and (c) branch carbon stocks.
Table 8 provides the accuracy of the reconstructed single-tree aboveground carbon stocks, and single-tree trunk and branch carbon stocks by the method in this paper. The Bias and rBias of the point cloud reconstruction of single-tree aboveground carbon stocks calculated by the least squares method were −0.09636 kg and −0.11%, respectively, and the absolute value of the deviation of single-tree aboveground carbon stocks was less than 14.94391 kg for 73.17% of the total number of trees. The Bias and rBias of trunk carbon stock were −2.33848 kg and −2.85%, respectively. Among the 41 trees in the range of the reference value of trunk carbon stock, the absolute value of the deviation of trunk carbon stock was less than 15.03535 kg for 75.6% of the total number of trees. The Bias and rBias of branch carbon stocks were 1.83295 kg and 18.02%, respectively, and the absolute value of the deviation of branch carbon stocks was less than 3.90454 kg for 87.8% of the total trees.

Table 8.
Comparison of the precision of aboveground, branch, and trunk carbon stocks of eucalyptus monocarps.
4. Discussion
4.1. Analysis of Results
The carbon sequestration capacity of forests plays an important role in offsetting carbon emissions and regulating climate change, and accurate measurement of carbon stocks in trees is essential for modelling the carbon dynamics of forest ecosystems [39,40,41,42]. Carbon stock estimation at the regional level involves continuous quantitative modelling at different scales. The development of aerial and satellite remote sensing has greatly reduced the uncertainty in scaling up plot-level biomass and carbon stock estimates to regional or national estimates [22]. When estimating carbon stocks per tree in a plot based on the establishment of allometric growth equation, a large amount of uncertainty is introduced into the system [18,43,44,45]. Currently, TLS point cloud reconstruction methods allow for direct determination of tree structure and are important for calibrating airborne and satellite-based remote sensing carbon stock estimates [46]. In this study, a method for reconstruction of eucalyptus carbon storage based on TLS point clouds was proposed, which mainly included steps such as branch separation, skeleton extraction, structural reconstruction, and carbon storage determination of eucalyptus single-tree point clouds based on an improved spatial colonization algorithm. In addition, 41 eucalyptus trees were felled for destructive measurement to verify the accuracy of our method.
During the process of eucalyptus tree structure reconstruction, a solution was proposed to address the limitations caused by the spatial colonization algorithm’s influence radius. This improvement method, which utilized dual perspectives, effectively resolved issues such as unstable growth direction due to a small field of view, premature termination of growth, and the premature impact of tree branching on skeleton point growth caused by an excessively large field of view. Simultaneously, adjustments and optimizations were made to the skeleton containing noisy branches, and a solution was proposed for the issue of nearly parallel branches on the skeleton, enhancing the correctness and rationality of the skeleton’s topological representation [23,32,33,34]. Furthermore, a completion strategy for the missing parts of the skeleton was designed. For point cloud data with partial scanning defects, the original branches were complemented by roughly predicting the direction of the branches. The root node of independent branches was determined based on the sum of bifurcation angles, and neighboring nodes were found through the extension of branches. The missing parts of the point clouds were interpolated using the Cardinal curve smoothing algorithm, resulting in the reconstruction of a realistic and detailed eucalyptus tree structure model [36]. Accuracy in eucalyptus tree structure reconstruction was evaluated based on visual effects and quantitative indicators. The results showed that the improved algorithm achieved higher accuracy compared with the original skeleton. Moreover, it exhibited significant improvements in accuracy compared to other methods. The average Hausdorff distance and F-distance were reduced by 0.0025 and 0.0027, respectively, compared with the standard skeleton. Compared with PypeTree, the average Hausdorff distance and F-distance were reduced by 0.065 and 0.0372, respectively. Compared with AdTree, the average Hausdorff distance and F-distance were reduced by 0.0192 and 0.0312, respectively. In the process of validating our method for determining carbon storage, we conducted an analysis of trees under destructive measurement conditions and measured the wood density and carbon content values of the samples in the laboratory.
Therefore, the carbon stock estimated by destructive measurements was estimated with minimal assumptions and was therefore used as a reference for comparing the performance of other methods [47,48]. Statistical results showed high agreement between the reconstructed carbon stock estimates and destructive measurements, with an R2 of 0.96 for the linear fit between the point cloud reconstructed single-tree aboveground carbon stock estimates and the reference values, an RMSE of 14.94391 kg, and a CV(RMSE) of 16.23%. The R2 of the linear fit of the trunk carbon stock estimate and the reference value was 0.94, the RMSE was 15.03535 kg, and the CV(RMSE) was 18.35%. The R2 of the linear fit of the branch carbon stock estimate to the reference value was 0.95, the RMSE was 3.90454 kg, and the CV(RMSE) was 38.39%. The biggest difference between this method and allometric equation is that it does not depend on DBH or tree height. We experimentally showed that the reconstruction results did not systematically overestimate or underestimate breast diameter, tree height, tree volume, and aboveground carbon stocks for tree size and shape.
4.2. Limitations and Application Potential
Our method needs to be made more robust to different raw point clouds in terms of eucalyptus structure reconstruction. Typically, the point clouds obtained by the LiDAR scanner are noisy, and subsequent optimization work can incorporate a more robust point cloud pre-processing function so that it can handle most of the noise problems [49,50]. In this paper, the skeleton-based modelling idea is used to reconstruct the tree structure, and so the accuracy of skeleton extraction affects the accuracy of the subsequent carbon stock determination. In addition, trees have different morphologies in nature, and there are few trees that do not exhibit universal growth patterns [51]. The modelling algorithm proposed in this paper is effective in reconstructing the sample trees, but there may be differences in the modelling results for trees with very complex branches, obscure branching, and branches with abnormal orientations. The algorithm in this paper needs to extract the skeleton points step by step in several iterations, which consumes more memory and computation time although accuracy is guaranteed. Whether it is for the structurally simple or complex part of a single-tree point clouds, it needs to iterate gradually according to fixed parameters (step size, influence radius, etc.). In the future, we can try to add a mechanism that can dynamically judge the current position and dynamically adjust the field of view, which can not only simplify calculation and improve efficiency, but also express the topological structure and branch direction of trees more concisely. Our approach has the potential to be applied to stand carbon stock calculations and to validate carbon stock monitoring by drones and satellites. However, we need to meet the forest TLS processing process, such as single-wood segmentation and ground filtering steps. Our current methods only support accurate calculations of carbon stock at tree level. In large-scale scenarios, if the computer memory and efficiency are guaranteed, the information of each tree in the stand level, including the location, species, and other parameters of the tree, our method will have the ability to calculate the carbon storage at the stand level. In this paper, our method was not able to estimate the carbon stock of tree leaves in terms of carbon stock estimation. Even though relevant studies have shown that the carbon stock in leaves is approximately 2–6% of the aboveground carbon stock in trees [19,52,53], reconstructing the carbon stock in leaves based on point clouds may require the development of new algorithms and models as well as the need for accuracy and validation with a large number of ground samples. When single values such as carbon content and wood density are applied to a particular tree, these values are assumed to be consistent across different parts of the tree’s branches. However, these values vary not only within a tree but also between trees. Assuming that these values are constant creates uncertainty in the final estimate. It is common to use local or global allometric growth equation to estimate the carbon content of a specific tree species [3,54]. Our method has the advantage of determining carbon stocks for different geographical locations and different tree species, with good generalizability and potential for wide application to different tree species, and is the same for all tree species. Our method determined aboveground carbon stocks in a single tree by reconstructing the 3D structure, and it also did not rely on a limited number of tree parameters. Our study specifically focuses on the accurate determination of single-tree aboveground carbon stocks, which is important for larger-scale carbon stock estimation and calibration based on aerial and satellite remote sensing. Our research is essential for the development of effective forest management strategies, providing new methods and techniques for high-precision, non-destructive measurements of aboveground carbon stocks in single trees in response to REDD+ policies aimed at reducing emissions from deforestation and forest degradation, sustainable management of forests and trading of conservation, enhancement of forest carbon stocks, and forest carbon sink projects in developing countries.
5. Conclusions
This study proposes a method to accurately determine the aboveground carbon stock of Eucalyptus monocarps from TLS point clouds, which develops an algorithmic framework for branch-trunk separation, skeleton extraction and optimization, 3D reconstruction, and carbon stock determination through an improved spatial colonization algorithm. The problem of different geometries and complexities of tree branches was solved during the method development process, effectively avoiding the problem of tree sagging branches leading to misjudgment. An accurate representation of the branch topology was established by optimizing and adjusting the modeling algorithm to remove small redundant branches. Function fitting was used to predict the direction of the branches in the independent branching part to complete the skeleton, and finally a smooth and realistic tree structure model was obtained. Destructive sampling experiments and laboratory measurements were carried out to validate the accuracy of the method and model in determining the aboveground carbon stock of eucalyptus monocarps, and this study provides a new method for non-destructive estimation of aboveground carbon stock in eucalyptus monocarps based on the TLS LiDAR point clouds, which provides technical support for forest carbon sink trading. To better evaluate the potential application of our method, we will use it for different tree species as much as possible in the future and optimize the modelling process to improve the accuracy of the method.
Author Contributions
Conceptualization, G.F.; data curation, F.L., H.C. and Z.X.; investigation, X.Z.; methodology, G.F.; resources, F.L., H.C., Z.X. and F.C.; software, G.F.; supervision, F.C.; validation, G.F.; visualization, F.C.; writing—review and editing, R.W.; funding acquisition, F.X. All authors have read and agreed to the published version of the manuscript.
Funding
Outstanding Youth Team Project of Central Universities (QNTD202308). Key Research and Development Project of Inner Mongolia Autonomous Region (2022YFHH0065-03); Tibet Autonomous Region Science and Technology Plan Project (XZ202301YD0043C); Provincial and Ministry Key Laboratory Opening Fund (2022076); and Guangxi Forestry Scientific Research [2022] No. 6.
Data Availability Statement
Data will be made available on request.
Acknowledgments
We would like to thank all those who contributed or indirectly contributed to this article for their work. We appreciate Zhenyu Xu’s contributions and work for this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qin, H.; Zhou, W.; Qian, Y.; Zhang, H.; Yao, Y. Estimating Aboveground Carbon Stocks of Urban Trees by Synergizing ICESat-2 LiDAR with GF-2 Data. Urban For. Urban Green. 2022, 76, 127728. [Google Scholar] [CrossRef]
- Thapa, R.B.; Watanabe, M.; Motohka, T.; Shiraishi, T.; Shimada, M. Calibration of Aboveground Forest Carbon Stock Models for Major Tropical Forests in Central Sumatra Using Airborne LiDAR and Field Measurement Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 661–673. [Google Scholar] [CrossRef]
- Singhal, J.; Srivastava, G.; Reddy, C.S.; Rajashekar, G.; Jha, C.S.; Rao, P.V.N.; Reddy, G.R.; Roy, P.S. Assessment of Carbon Stock at Tree Level Using Terrestrial Laser Scanning Vs. Traditional Methods in Tropical Forest, India. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5064–5071. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Estimating Aboveground Carbon Stock at the Scale of Individual Trees in Subtropical Forests Using UAV LiDAR and Hyperspectral Data. Remote Sens. 2021, 13, 4969. [Google Scholar] [CrossRef]
- Li, H.; Kato, T.; Hayashi, M.; Wu, L. Estimation of Forest Aboveground Biomass of Two Major Conifers in Ibaraki Prefecture, Japan, from PALSAR-2 and Sentinel-2 Data. Remote Sens. 2022, 14, 468. [Google Scholar] [CrossRef]
- Gou, Y.; Ryan, C.M.; Reiche, J. Large Area Aboveground Biomass and Carbon Stock Mapping in Woodlands in Mozambique with L-Band Radar: Improving Accuracy by Accounting for Soil Moisture Effects Using the Water Cloud Model. Remote Sens. 2022, 14, 404. [Google Scholar] [CrossRef]
- Bordoloi, R.; Das, B.; Tripathi, O.P.; Sahoo, U.K.; Nath, A.J.; Deb, S.; Das, D.J.; Gupta, A.; Devi, N.B.; Charturvedi, S.S.; et al. Satellite Based Integrated Approaches to Modelling Spatial Carbon Stock and Carbon Sequestration Potential of Different Land Uses of Northeast India. Environ. Sustain. Indic. 2022, 13, 100166. [Google Scholar] [CrossRef]
- Molina, P.X.; Asner, G.P.; Farjas Abadía, M.; Ojeda Manrique, J.C.; Sánchez Diez, L.A.; Valencia, R. Spatially-Explicit Testing of a General Aboveground Carbon Density Estimation Model in a Western Amazonian Forest Using Airborne LiDAR. Remote Sens. 2016, 8, 9. [Google Scholar] [CrossRef]
- Verly, O.M.; Vieira Leite, R.; da Silva Tavares-Junior, I.; José Silva Soares da Rocha, S.; Garcia Leite, H.; Marinaldo Gleriani, J.; Paula Miranda Xavier Rufino, M.; de Fatima Silva, V.; Moreira Miquelino Eleto Torres, C.; Plata-Rueda, A.; et al. Atlantic Forest Woody Carbon Stock Estimation for Different Successional Stages Using Sentinel-2 Data. Ecol. Indic. 2023, 146, 109870. [Google Scholar] [CrossRef]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. The Use of Fixed–Wing UAV Photogrammetry with LiDAR DTM to Estimate Merchantable Volume and Carbon Stock in Living Biomass over a Mixed Conifer–Broadleaf Forest. Int. J. Appl. Earth Obs. Geoinformation 2018, 73, 767–777. [Google Scholar] [CrossRef]
- Zhang, X. Quick Aboveground Carbon Stock Estimation of Densely Planted Shrubs by Using Point Cloud Derived from Unmanned Aerial Vehicle. Remote Sens. 2019, 11, 2914. [Google Scholar] [CrossRef]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.W.; et al. The Importance of Consistent Global Forest Aboveground Biomass Product Validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, M.M.; Al-Ali, Z.M.; Srinivasan, S. The Use of UAV-Based Remote Sensing to Estimate Biomass and Carbon Stock for Native Desert Shrubs. MethodsX 2021, 8, 101399. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zan, Q.; Yang, Q.; Zhu, D.; Chen, Y.; Yu, S. Remote Estimation of Mangrove Aboveground Carbon Stock at the Species Level Using a Low-Cost Unmanned Aerial Vehicle System. Remote Sens. 2019, 11, 1018. [Google Scholar] [CrossRef]
- Pereira, O.J.R.; Montes, C.R.; Lucas, Y.; Melfi, A.J. Use of Remote Sense Imagery for Mapping Deep Plant-Derived Carbon Storage in Amazonian Podzols in Regional Scale. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 3770–3772. [Google Scholar]
- Wang, B.; Waters, C.; Orgill, S.; Gray, J.; Cowie, A.; Clark, A.; Liu, D.L. High Resolution Mapping of Soil Organic Carbon Stocks Using Remote Sensing Variables in the Semi-Arid Rangelands of Eastern Australia. Sci. Total Environ. 2018, 630, 367–378. [Google Scholar] [CrossRef]
- Fang, R.; Strimbu, B.M. Comparison of Mature Douglas-Firs’ Crown Structures Developed with Two Quantitative Structural Models Using TLS Point Clouds for Neighboring Trees in a Natural Regime Stand. Remote Sens. 2019, 11, 1661. [Google Scholar] [CrossRef]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-Destructive Tree Volume Estimation through Quantitative Structure Modelling: Comparing UAV Laser Scanning with Terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Fan, G.; Nan, L.; Dong, Y.; Su, X.; Chen, F. AdQSM: A New Method for Estimating Above-Ground Biomass from TLS Point Clouds. Remote Sens. 2020, 12, 3089. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Georgopoulos, N.; Gitas, I.Z.; Stefanidou, A.; Korhonen, L.; Stavrakoudis, D. Estimation of Individual Tree Stem Biomass in an Uneven-Aged Structured Coniferous Forest Using Multispectral LiDAR Data. Remote Sens. 2021, 13, 4827. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Åkerblom, M.; Bartholomeus, H.; Disney, M.; Levick, S.; Origo, N.; Raumonen, P.; Verbeeck, H. Analysing Individual 3D Tree Structure Using the R Package ITSMe. Methods Ecol. Evol. 2023, 14, 231–241. [Google Scholar] [CrossRef]
- Li, X.; Zhou, X.; Xu, S. Individual Tree Reconstruction Based on Circular Truncated Cones From Portable LiDAR Scanner Data. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Brilli, L.; Chiesi, M.; Brogi, C.; Magno, R.; Arcidiaco, L.; Bottai, L.; Tagliaferri, G.; Bindi, M.; Maselli, F. Combination of Ground and Remote Sensing Data to Assess Carbon Stock Changes in the Main Urban Park of Florence. Urban For. Urban Green. 2019, 43, 126377. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive Estimates of Above-Ground Biomass Using Terrestrial Laser Scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly Accurate Tree Models Derived from Terrestrial Laser Scan Data: A Method Description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef]
- Du, S.; Lindenbergh, R.; Ledoux, H.; Stoter, J.; Nan, L. AdTree: Accurate, Detailed, and Automatic Modelling of Laser-Scanned Trees. Remote Sens. 2019, 11, 2074. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Barr, A.G.; Kljun, N.; Black, T.A.; McCaughey, J.H. Monitoring Boreal Forest Biomass and Carbon Storage Change by Integrating Airborne Laser Scanning, Biometry and Eddy Covariance Data. Remote Sens. Environ. 2016, 181, 82–95. [Google Scholar] [CrossRef]
- Poorazimy, M.; Shataee, S.; McRoberts, R.E.; Mohammadi, J. Integrating Airborne Laser Scanning Data, Space-Borne Radar Data and Digital Aerial Imagery to Estimate Aboveground Carbon Stock in Hyrcanian Forests, Iran. Remote Sens. Environ. 2020, 240, 111669. [Google Scholar] [CrossRef]
- Lau, A.; Martius, C.; Bartholomeus, H.; Shenkin, A.; Jackson, T.; Malhi, Y.; Herold, M.; Bentley, L.P. Estimating Architecture-Based Metabolic Scaling Exponents of Tropical Trees Using Terrestrial LiDAR and 3D Modelling. For. Ecol. Manag. 2019, 439, 132–145. [Google Scholar] [CrossRef]
- Su, Z.; Li, S.; Liu, H.; He, Z. Tree Skeleton Extraction From Laser Scanned Points. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6091–6094. [Google Scholar]
- Xu, Y.; Hu, C.; Xie, Y. An Improved Space Colonization Algorithm with DBSCAN Clustering for a Single Tree Skeleton Extraction. Int. J. Remote Sens. 2022, 43, 3692–3713. [Google Scholar] [CrossRef]
- Fu, Y.; Xia, Y.; Zhang, H.; Fu, M.; Wang, Y.; Fu, W.; Shen, C. Skeleton Extraction and Pruning Point Identification of Jujube Tree for Dormant Pruning Using Space Colonization Algorithm. Front. Plant Sci. 2023, 13, 1103794. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; He, P.; Hu, S.; Zhang, Z.; Geng, N.; He, D. Reconstruction Method of Tree Geometric Structures from Point Clouds Based on Angle-Constrained Space Colonization Algorithm. Trans. Chin. Soc. Agric. Mach. 2018, 49, 207–216. [Google Scholar] [CrossRef]
- Ratul, R.; Sultana, S.; Tasnim, J.; Rahman, A. Applicability of Space Colonization Algorithm for Real Time Tree Generation. In Proceedings of the 2019 22nd International Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 18–20 December 2019; pp. 1–6. [Google Scholar]
- Nuić, H.; Mihajlović, Ž. Algorithms for Procedural Generation and Display of Trees. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; pp. 230–235. [Google Scholar]
- Guo, J.; Xu, S.; Yan, D.-M.; Cheng, Z.; Jaeger, M.; Zhang, X. Realistic Procedural Plant Modeling from Multiple View Images. IEEE Trans. Vis. Comput. Graph. 2020, 26, 1372–1384. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Wang, Q.; Fan, X. An Optimized L1-Medial Skeleton Extraction Algorithm. In Proceedings of the 2021 IEEE International Conference on Industrial Application of Artificial Intelligence (IAAI), Harbin, China, 24–26 December 2021; pp. 460–466. [Google Scholar]
- Chinembiri, T.S.; Mutanga, O.; Dube, T. Carbon Stock Prediction in Managed Forest Ecosystems Using Bayesian and Frequentist Geostatistical Techniques and New Generation Remote Sensing Metrics. Remote Sens. 2023, 15, 1649. [Google Scholar] [CrossRef]
- Birungi, V.; Dejene, S.W.; Mbogga, M.S.; Dumas-Johansen, M. Carbon Stock of Agoro Agu Central Forest Reserve, in Lamwo District, Northern Uganda. Heliyon 2023, 9, e14252. [Google Scholar] [CrossRef]
- Lv, Y.; Han, N.; Du, H. Estimation of Bamboo Forest Aboveground Carbon Using the RGLM Model Based on Object-Based Multiscale Segmentation of SPOT-6 Imagery. Remote Sens. 2023, 15, 2566. [Google Scholar] [CrossRef]
- Pei, H.; Owari, T.; Tsuyuki, S.; Hiroshima, T. Identifying Spatial Variation of Carbon Stock in a Warm Temperate Forest in Central Japan Using Sentinel-2 and Digital Elevation Model Data. Remote Sens. 2023, 15, 1997. [Google Scholar] [CrossRef]
- Yi, L.; Li, H.; Guo, J.; Deussen, O.; Zhang, X. Tree Growth Modelling Constrained by Growth Equations. Comput. Graph. Forum 2018, 37, 239–253. [Google Scholar] [CrossRef]
- Marczak, P.T.; Van Ewijk, K.Y.; Treitz, P.M.; Scott, N.A.; Robinson, D.C.E. Predicting Carbon Accumulation in Temperate Forests of Ontario, Canada Using a LiDAR-Initialized Growth-and-Yield Model. Remote Sens. 2020, 12, 201. [Google Scholar] [CrossRef]
- Anurogo, W.; Lubis, M.Z.; Sari, L.R.; Mufida, M.K.; Prihantarto, W.J. Satellite-Based Estimation of Above Ground Carbon Stock Estimation for Rubber Plantation in Tembir Salatiga Central Java. In Proceedings of the 2018 4th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 August 2018; pp. 1–6. [Google Scholar]
- Fan, G.; Xu, Z.; Wang, J.; Nan, L.; Xiao, H.; Xin, Z.; Chen, F. Plot-Level Reconstruction of 3D Tree Models for Aboveground Biomass Estimation. Ecol. Indic. 2022, 142, 109211. [Google Scholar] [CrossRef]
- Gang, B.; Hasituya; Hugejiletu; Bao, Y. Remotely Sensed Estimate of Biomass Carbon Stocks in Xilingol Grassland Using MODIS NDVI Data. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shenyang, China, 20–22 December 2013; pp. 676–679.
- Li, M.; Im, J.; Quackenbush, L.J.; Liu, T. Forest Biomass and Carbon Stock Quantification Using Airborne LiDAR Data: A Case Study Over Huntington Wildlife Forest in the Adirondack Park. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3143–3156. [Google Scholar] [CrossRef]
- Pereira Coltri, P.; Zullo, J.; Ribeiro do Valle Gonçalves, R.; Romani, L.A.S.; Pinto, H.S. Coffee Crop’s Biomass and Carbon Stock Estimation With Usage of High Resolution Satellites Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1786–1795. [Google Scholar] [CrossRef]
- Bindu, G.; Rajan, P.; Jishnu, E.S.; Ajith Joseph, K. Carbon Stock Assessment of Mangroves Using Remote Sensing and Geographic Information System. Egypt. J. Remote Sens. Space Sci. 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Hui, Z.; Cai, Z.; Liu, B.; Li, D.; Liu, H.; Li, Z. A Self-Adaptive Optimization Individual Tree Modeling Method for Terrestrial LiDAR Point Clouds. Remote Sens. 2022, 14, 2545. [Google Scholar] [CrossRef]
- Chaddad, F.; Mello, F.A.O.; Tayebi, M.; Safanelli, J.L.; Campos, L.R.; Amorim, M.T.A.; Barbosa de Sousa, G.P.; Ferreira, T.O.; Ruiz, F.; Perlatti, F.; et al. Impact of Mining-Induced Deforestation on Soil Surface Temperature and Carbon Stocks: A Case Study Using Remote Sensing in the Amazon Rainforest. J. South Am. Earth Sci. 2022, 119, 103983. [Google Scholar] [CrossRef]
- Wicaksono, P.; Maishella, A.; Wahyudi, A.J.; Hafizt, M. Multitemporal Seagrass Carbon Assimilation and Aboveground Carbon Stock Mapping Using Sentinel-2 in Labuan Bajo 2019–2020. Remote Sens. Appl. Soc. Environ. 2022, 27, 100803. [Google Scholar] [CrossRef]
- Ojoatre, S.; Zhang, C.; Hussin, Y.A.; Kloosterman, H.E.; Ismail, M.H. Assessing the Uncertainty of Tree Height and Aboveground Biomass From Terrestrial Laser Scanner and Hypsometer Using Airborne LiDAR Data in Tropical Rainforests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4149–4159. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).