Slow Slip Events Associated with Seismic Activity in the Hikurangi Subduction Zone, New Zealand, from 2019 to 2022
Abstract
:1. Introduction
2. Data and Methodology
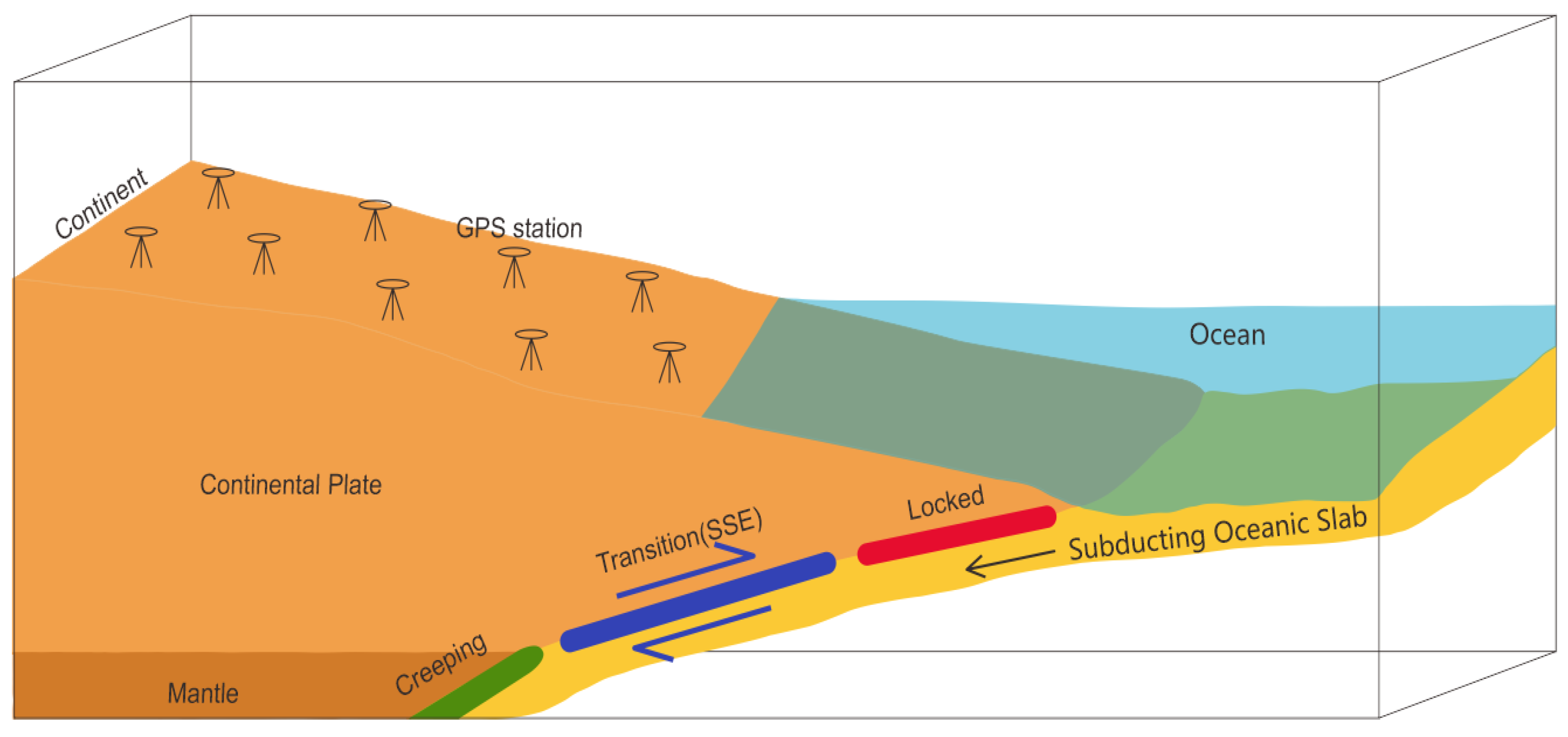
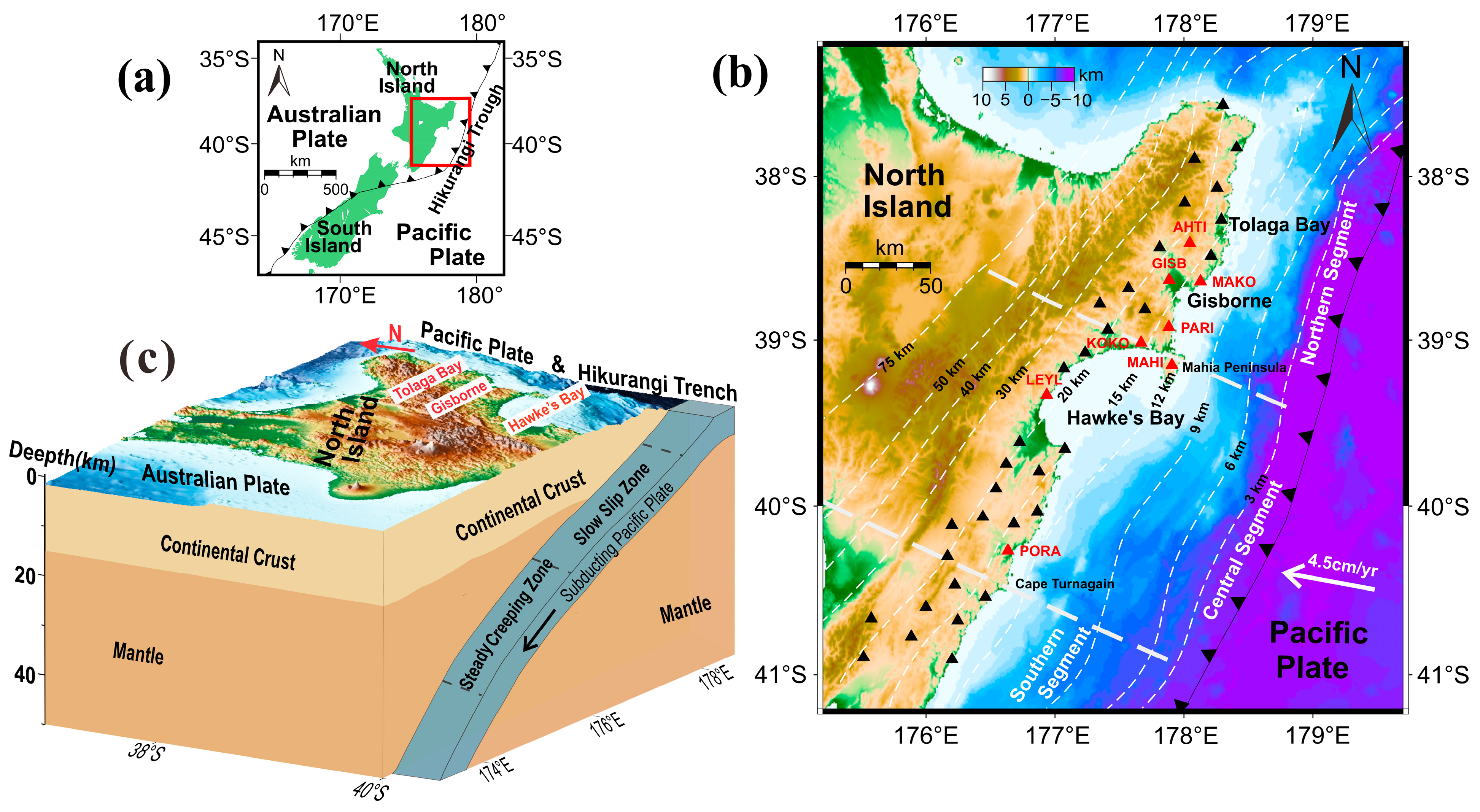
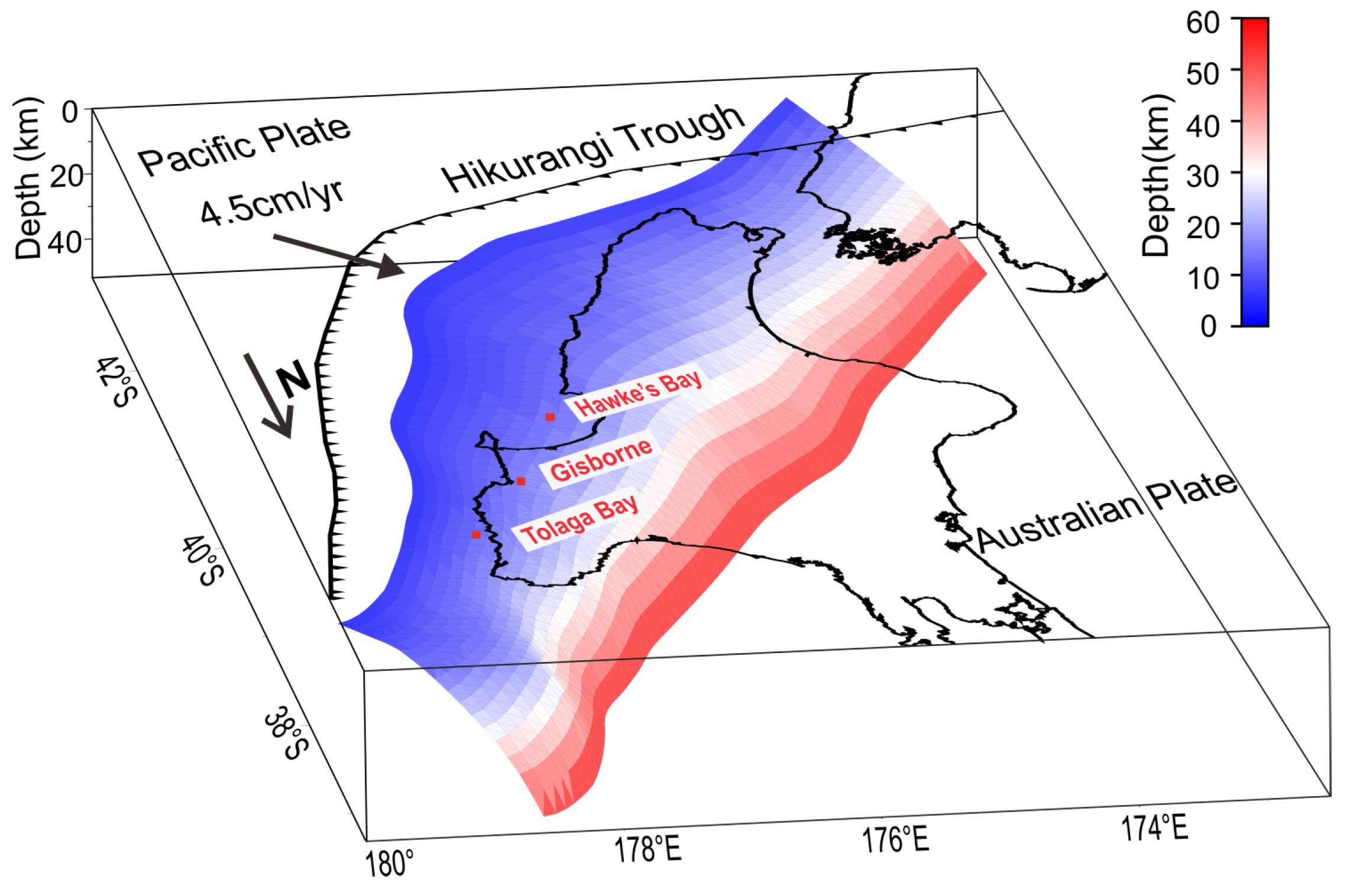
2.1. Regional Tectonic
2.2. Data Source
2.3. Methodology
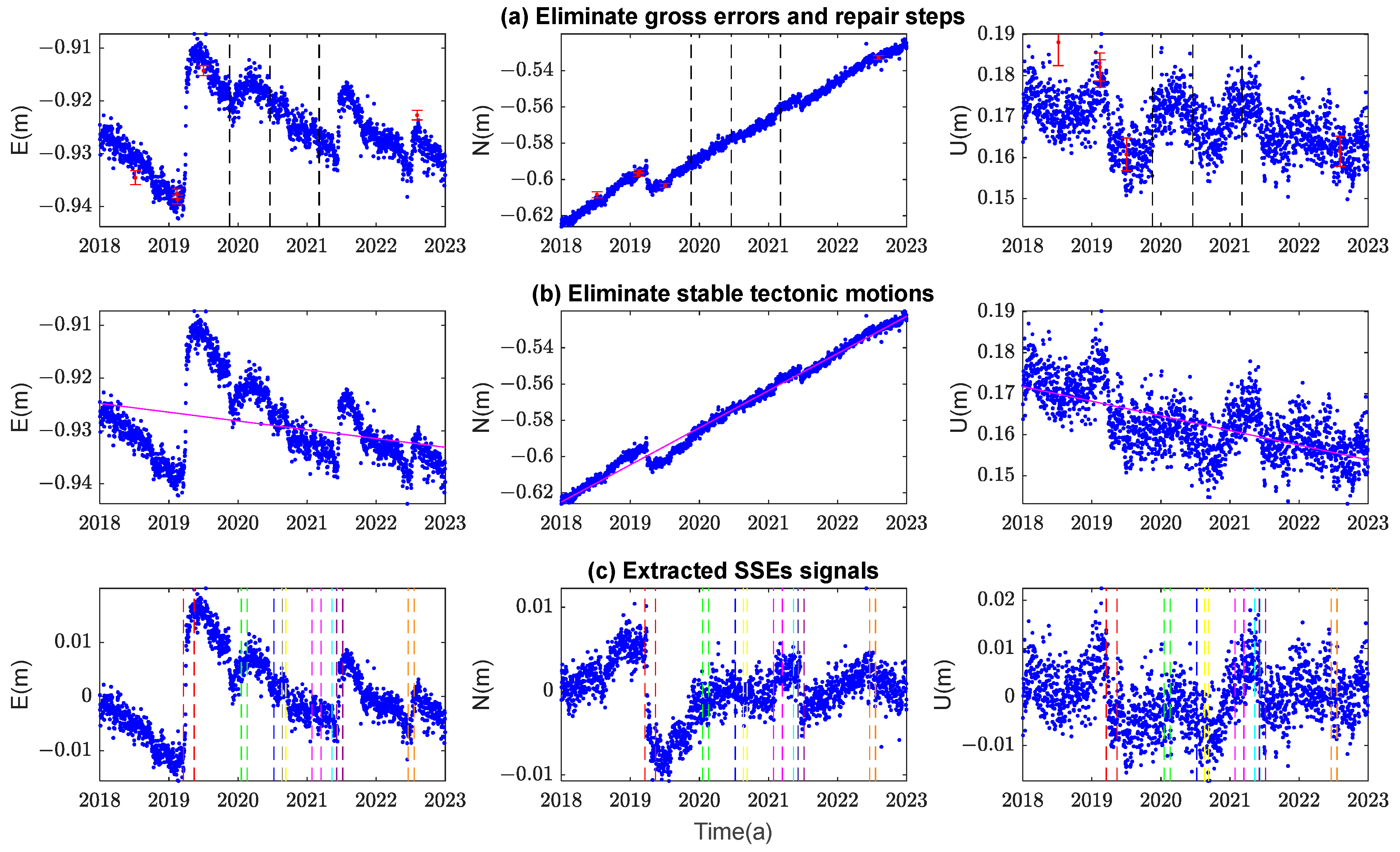
2.3.1. GPS Coordinate Time Series Modeling and SSEs Signals Extraction
2.3.2. NIF Inversion
3. Results
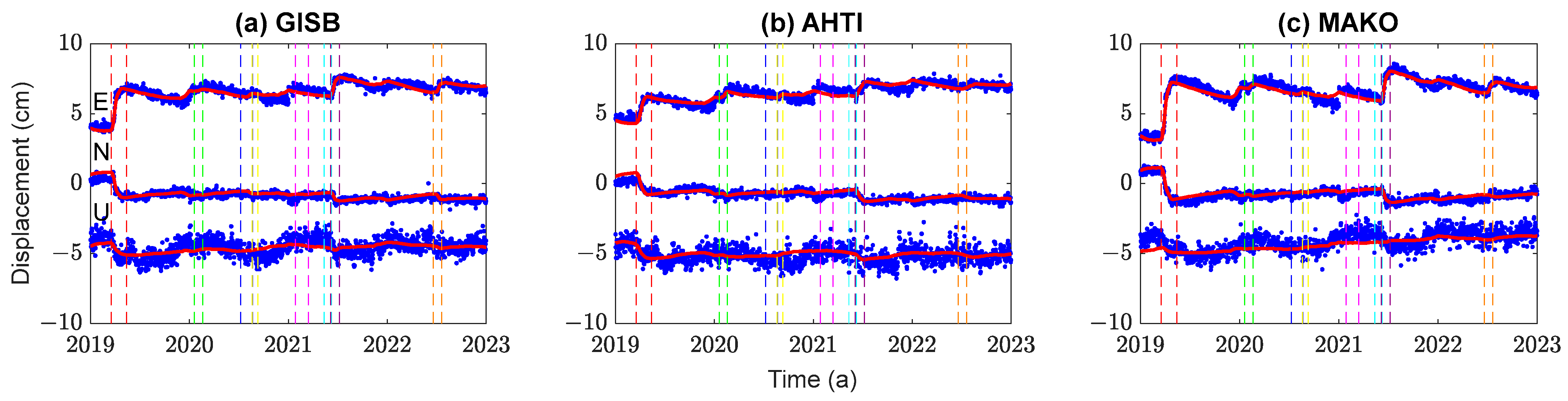
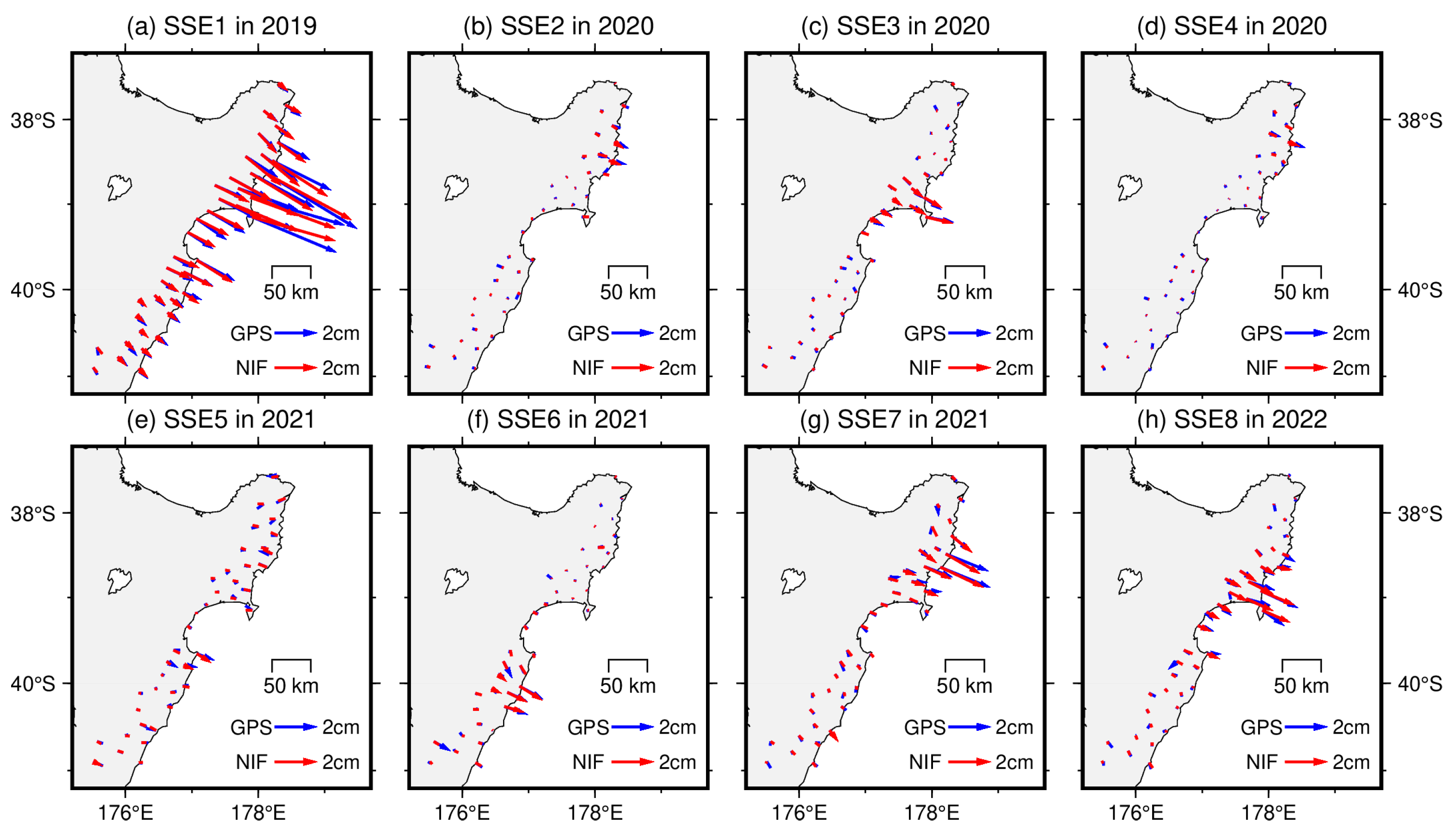
3.1. Surface Displacements
3.2. Cumulative Slip
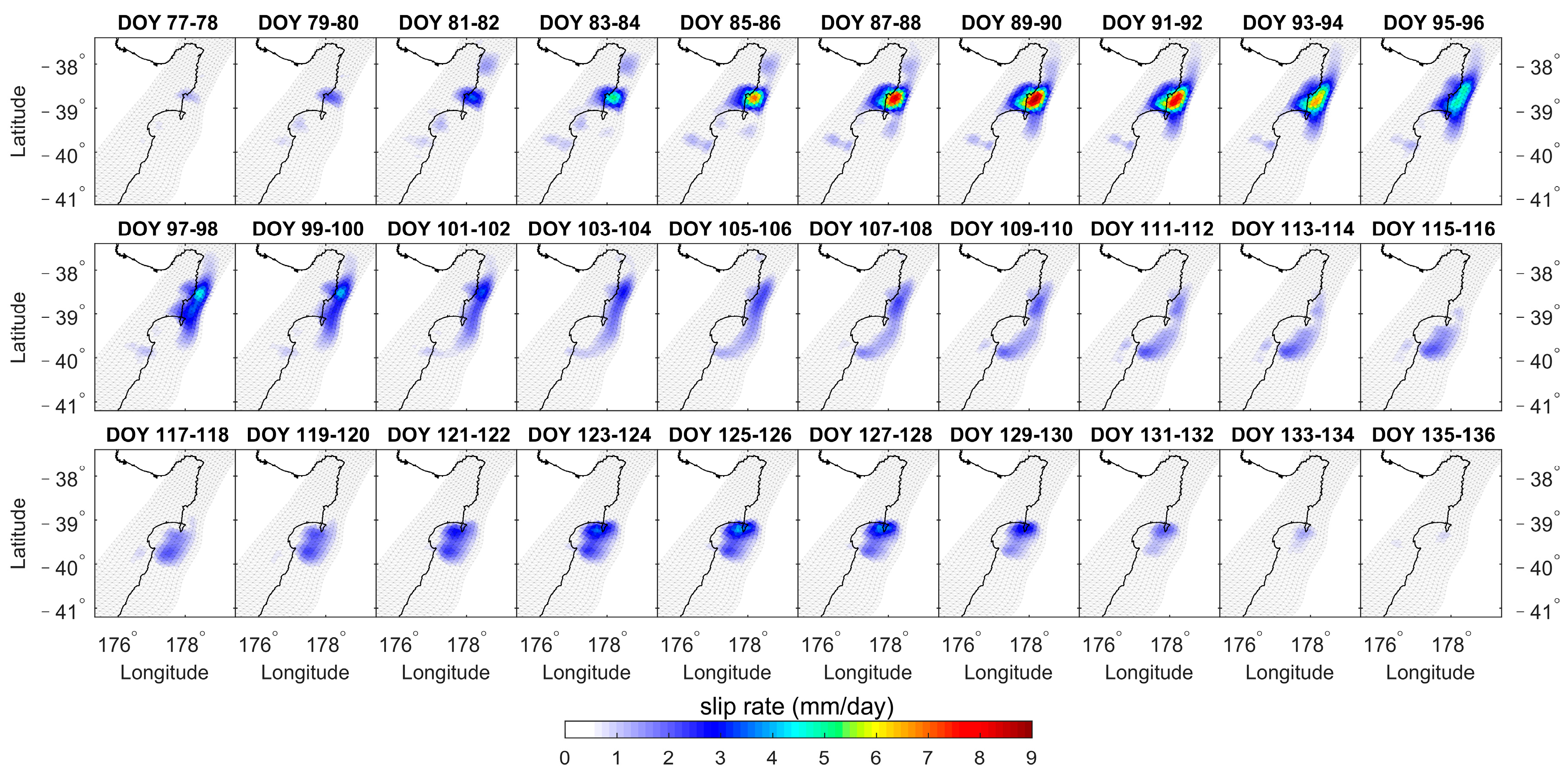
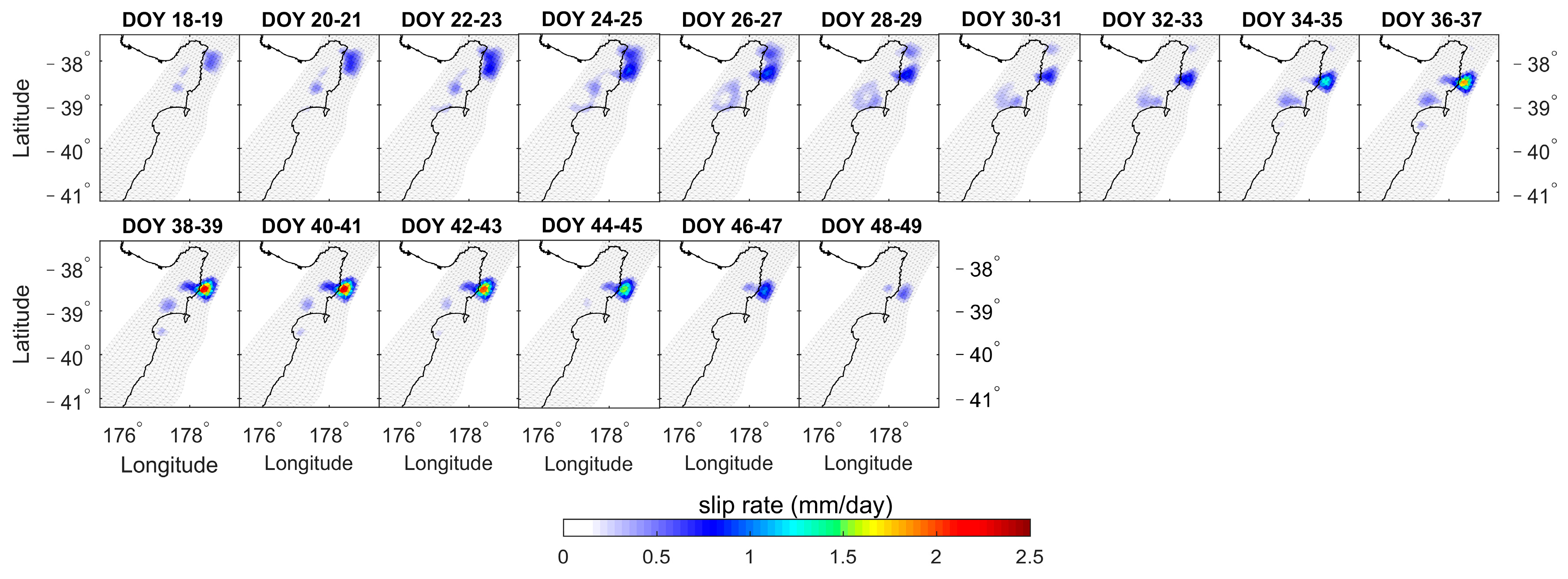
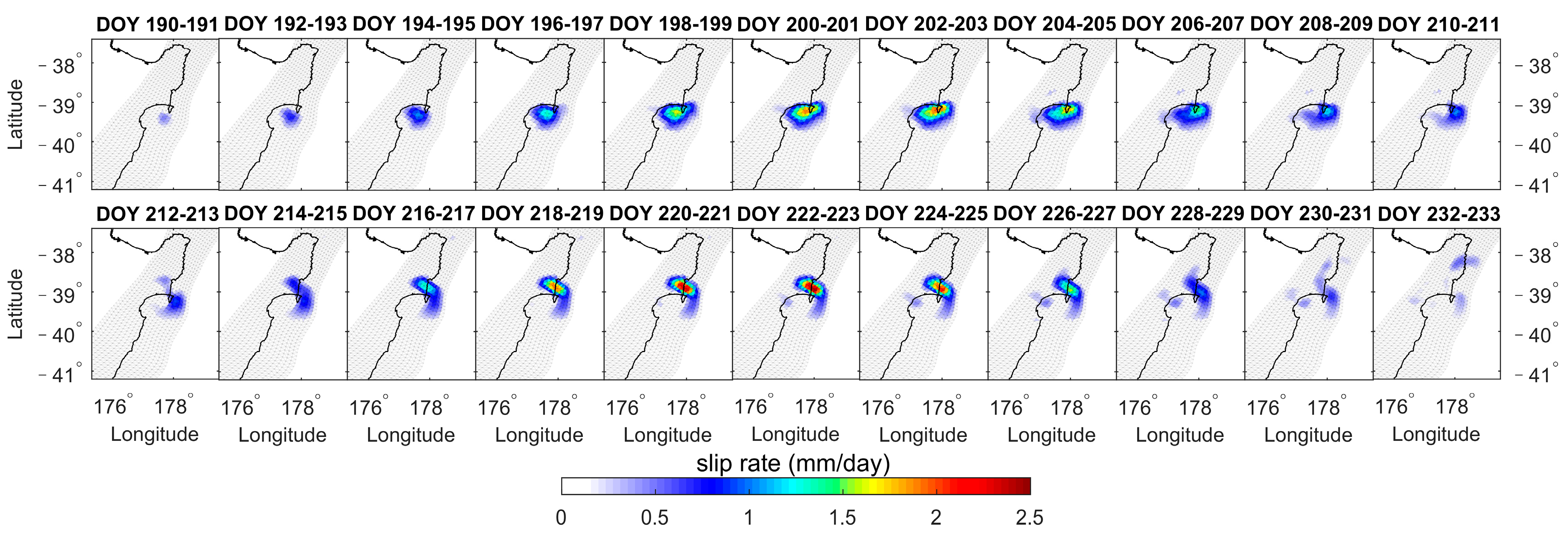
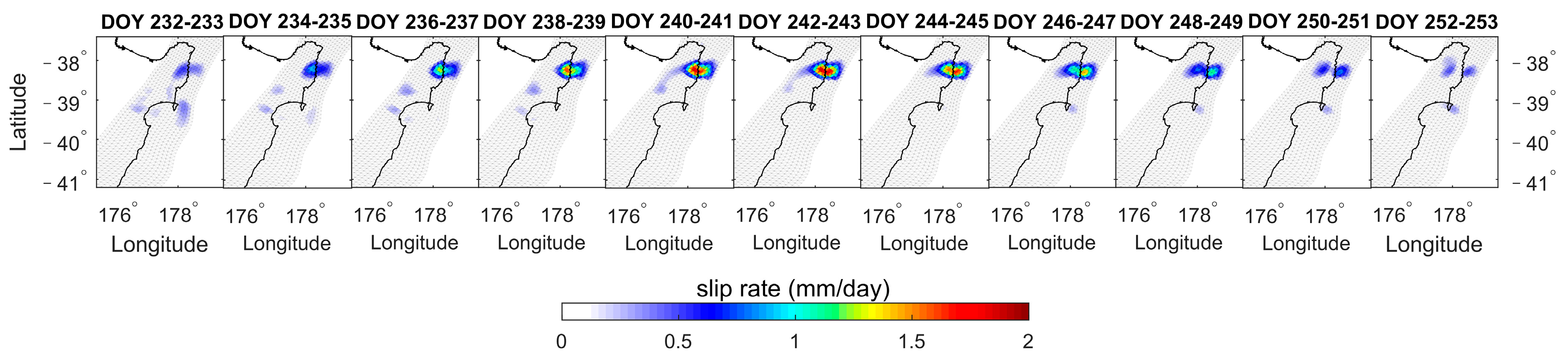
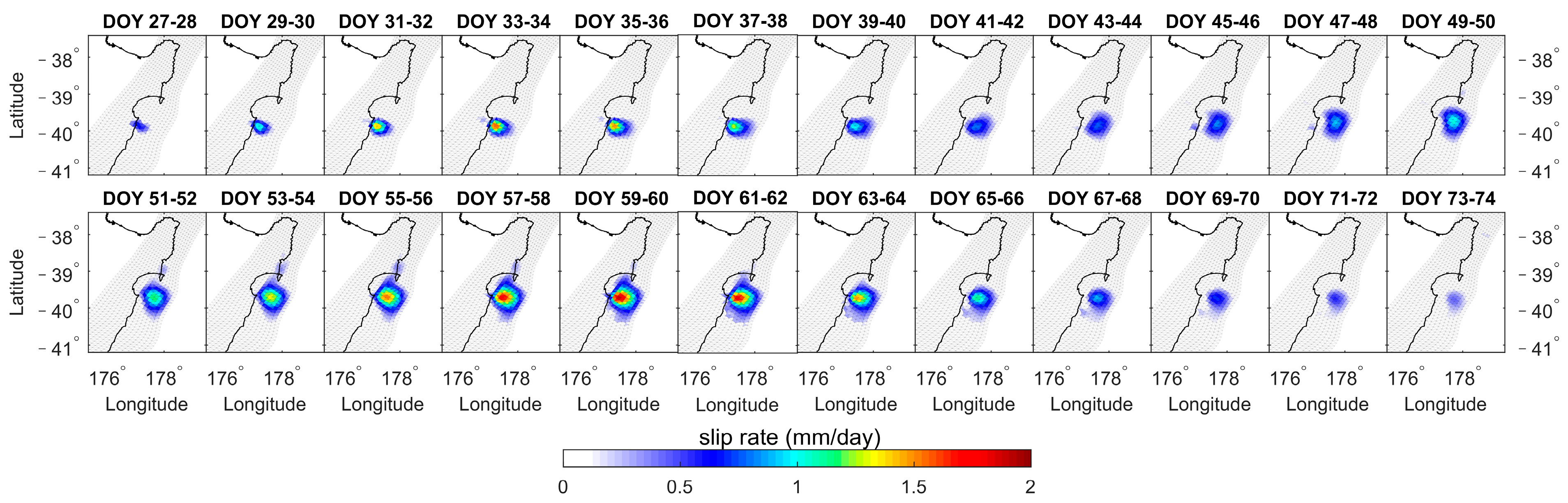
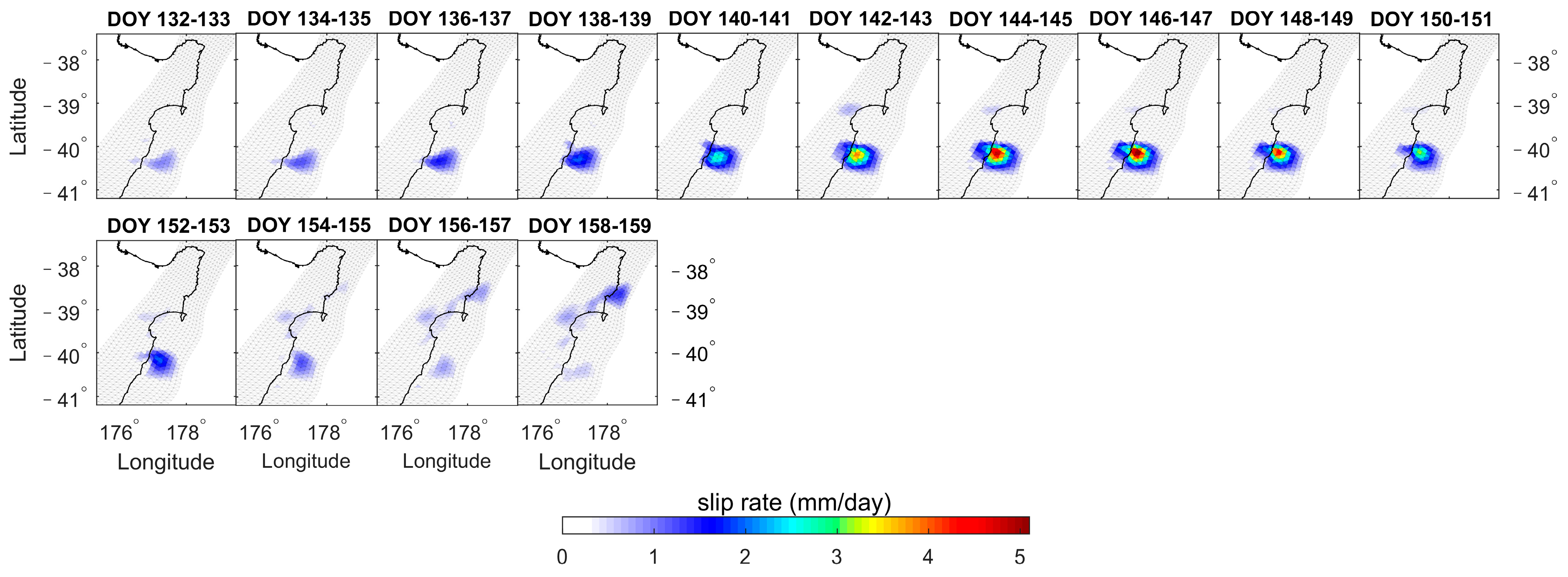
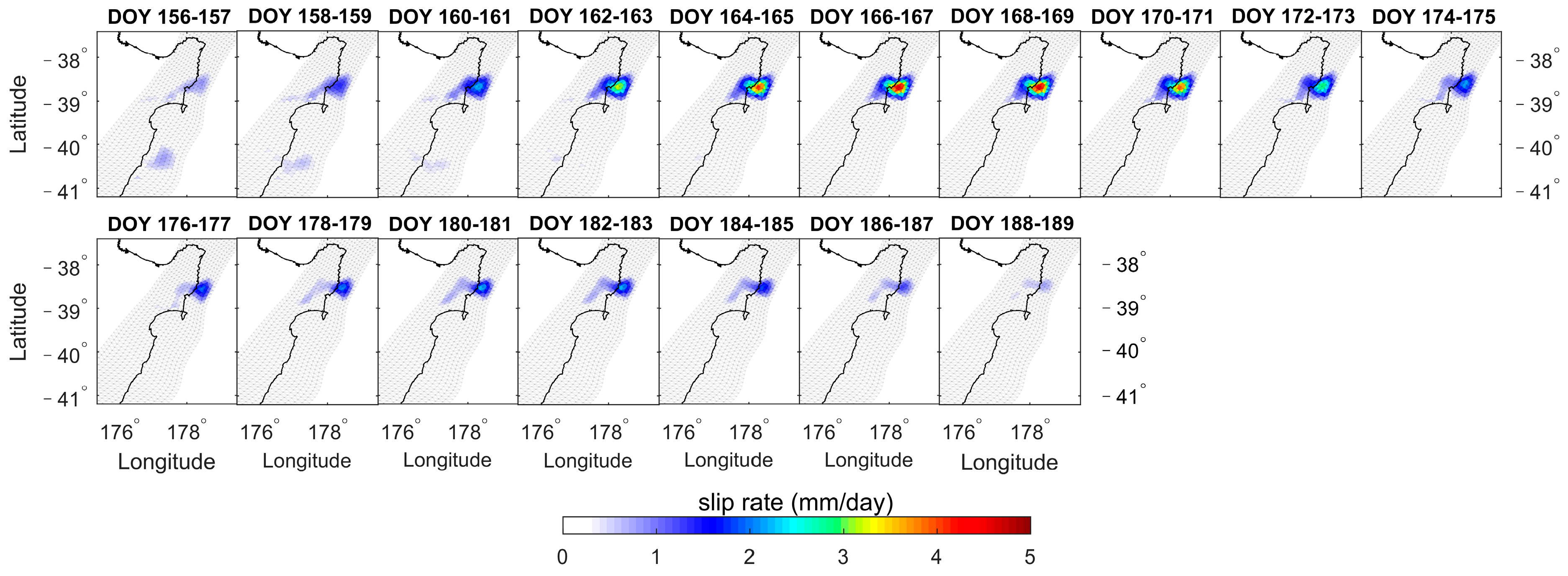
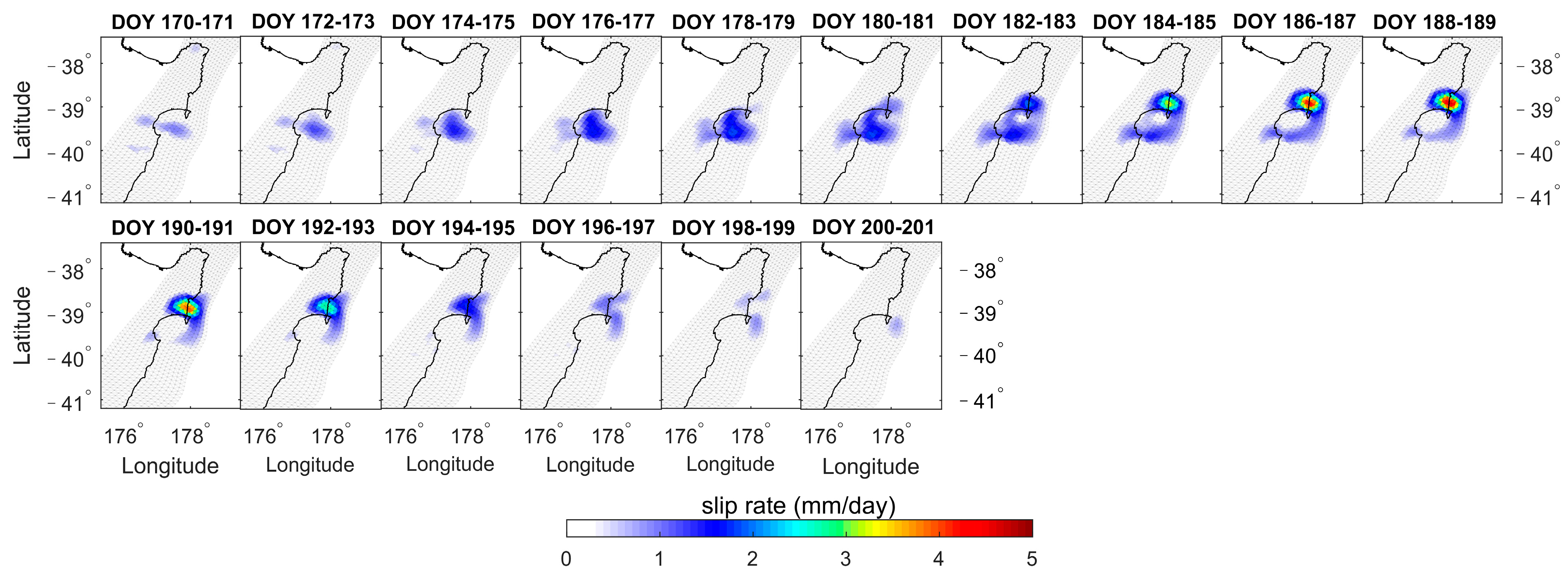
3.3. Slip Rate
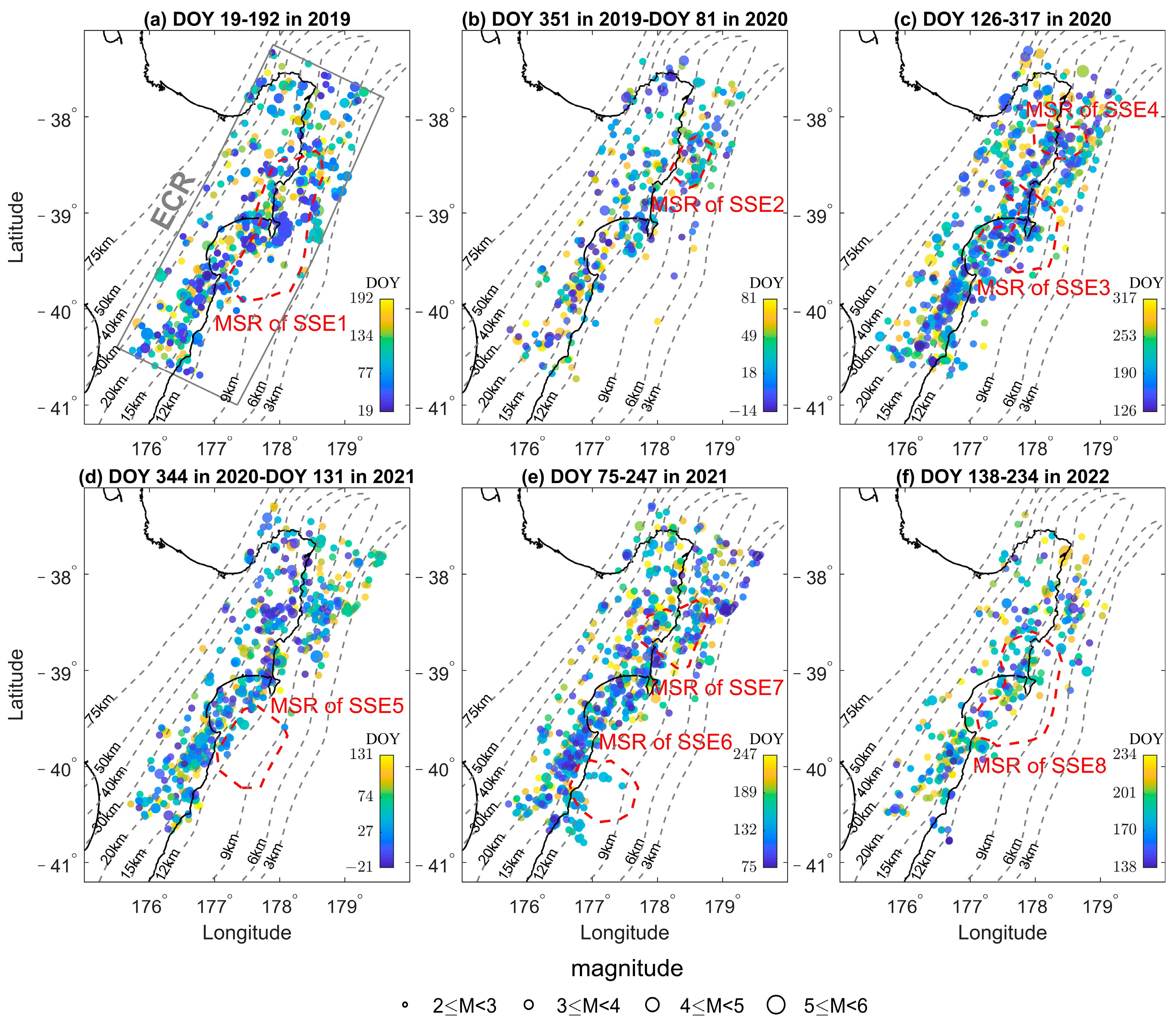
3.4. Relationship between SSEs and Seismic Activities
4. Discussion
5. Conclusions
- From 2019 to 2022, a total of eight shallow SSEs were identified in the central and northern margins of the Hikurangi Subduction Zone in New Zealand using GPS displacement time series. The maximum surface displacements of the eight SSEs observed by GPS are as follows: 4.97, 0.84, 1.33, 0.87, 0.88, 1.27, 2.53, and 1.92 cm.
- The fault slips of the eight SSEs are inverted by NIF. The cumulative slips vary from 2.39 to 14.35 cm, the daily slip rates range from 1.83 to 8.69 mm/day, the depths range of 6–20 km, and the duration ranges from 22 days to 58 days. SSE1, SSE2, SSE3, SSE5, and SSE8 exhibit significant biphasic behavior characterized by acceleration-deceleration-acceleration-deceleration patterns. However, SSE4, SSE6, and SSE7 exhibit only one acceleration-deceleration phase.
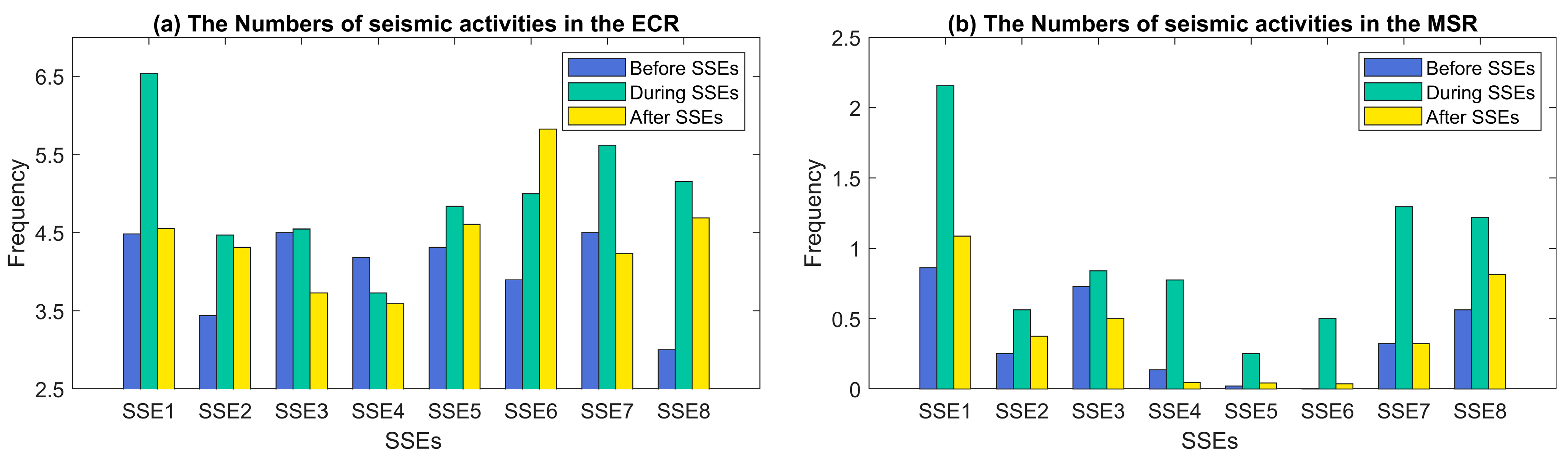
- By analyzing the spatial distribution and daily frequency of seismic activity before, during, and after the eight SSEs in New Zealand’s North Island’s Eastern Coastal Region (ECR), as well as in the Main Slip Regions (MSR) of the SSEs, it is evident that all eight SSEs bring about an increase in seismic frequency within their respective MSR, but only significant SSEs (SSE1 and SSE7, their cumulative slips are over 7 cm) trigger an elevated seismic frequency in the ECR of the New Zealand’s North Island.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Villafuerte, C.; Cruz-Atienza, V.M. Insights into the causal relationship between slow slip and tectonic tremor in Guerrero, Mexico. J. Geophys. Res. Solid Earth 2017, 122, 6642–6656. [Google Scholar] [CrossRef]
- Schwartz, S.Y.; Rokosky, J.M. Slow slip events and seismic tremor at circum-Pacific subduction zones. Rev. Geophys. 2007, 45, RG3004. [Google Scholar] [CrossRef]
- Song, S.; Hao, M.; Li, Y.; Wang, Q. Extraction of transient signal from GPS position time series by employing ICA. Geod. Geodyn. 2023; in press. [Google Scholar] [CrossRef]
- Li, M.; Yan, L.; Jiang, Z.; Xiao, G. Insights into spatio-temporal slow slip events offshore the Boso Peninsula in central Japan during 2011–2019 using GPS data. Geod. Geodyn. 2022, 13, 554–563. [Google Scholar] [CrossRef]
- Li, D.; Liu, Y. Spatiotemporal evolution of slow slip events in a nonplanar fault model for northern Cascadia subduction zone. J. Geophys. Res. Solid Earth 2016, 121, 6828–6845. [Google Scholar] [CrossRef]
- Fukuda, J.i. Variability of the Space-Time Evolution of Slow Slip Events Off the Boso Peninsula, Central Japan, from 1996 to 2014. J. Geophys. Res. Solid Earth 2018, 123, 732–760. [Google Scholar] [CrossRef]
- Li, Y.; Zhengdong, L.; Aiping, Z.; Meng, L.; Dingde, Y. NIF inversion and spatiotemporal analysis of GPS monitoring slow slip events. Geomat. Inf. Sci. Wuhan Univ. 2022, 1–13. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Z.; Davis, E.E.; Schwartz, S.Y.; Dixon, T.H.; Voss, N.; Malservisi, R.; Protti, M. Strain release at the trench during shallow slow slip: The example of Nicoya Peninsula, Costa Rica. Geophys. Res. Lett. 2017, 44, 4846–4854. [Google Scholar] [CrossRef]
- Wallace, L.M. Slow Slip Events in New Zealand. Annu. Rev. Earth Planet. Sci. 2020, 48, 175–203. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, D.; Shum, C.K.; Guo, R. The 2019 East Coast Slow Slip Event, New Zealand: Spatiotemporal Evolution and Associated Seismicity. Mar. Geod. 2022, 46, 195–215. [Google Scholar] [CrossRef]
- Romanet, P.; Ide, S. Ambient tectonic tremors in Manawatu, Cape Turnagain, Marlborough, and Puysegur, New Zealand. Earth Planets Space 2019, 71, 59. [Google Scholar] [CrossRef]
- Todd, E.K.; Schwartz, S.Y. Tectonic tremor along the northern Hikurangi Margin, New Zealand, between 2010 and 2015. J. Geophys. Res. Solid Earth 2016, 121, 8706–8719. [Google Scholar] [CrossRef]
- Douglas, A. Slow slip on the northern Hikurangi subduction interface, New Zealand. Geophys. Res. Lett. 2005, 32, 16305. [Google Scholar] [CrossRef]
- Wallace, L.M.; Beavan, J. A large slow slip event on the central Hikurangi subduction interface beneath the Manawatu region, North Island, New Zealand. Geophys. Res. Lett. 2006, 33, L11301. [Google Scholar] [CrossRef]
- Iwasaki, Y.; Mochizuki, K.; Ishise, M.; Todd, E.K.; Schwartz, S.Y.; Zal, H.; Savage, M.K.; Henrys, S.; Sheehan, A.F.; Ito, Y.; et al. Continuous Tremor Activity with Stable Polarization Direction Following the 2014 Large Slow Slip Event in the Hikurangi Subduction Margin Offshore New Zealand. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022161. [Google Scholar] [CrossRef]
- Segall, P.; Matthews, M. Time dependent inversion of geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 22391–22409. [Google Scholar] [CrossRef]
- Yohler, R.; Bartlow, N.; Wallace, L.M.; Williams, C. Time-Dependent Behavior of a Near-Trench Slow-Slip Event at the Hikurangi Subduction Zone. Geochem. Geophys. Geosystems 2019, 20, 4292–4304. [Google Scholar] [CrossRef]
- Miyazaki, S.i.; Segall, P.; McGuire, J.J.; Kato, T.; Hatanaka, Y. Spatial and temporal evolution of stress and slip rate during the 2000 Tokai slow earthquake. J. Geophys. Res. Solid Earth 2006, 111, B03409. [Google Scholar] [CrossRef]
- Bartlow, N.M.; Wallace, L.M.; Beavan, R.J.; Bannister, S.; Segall, P. Time-dependent modeling of slow slip events and associated seismicity and tremor at the Hikurangi subduction zone, New Zealand. J. Geophys. Res. Solid Earth 2014, 119, 734–753. [Google Scholar] [CrossRef]
- Mouslopoulou, V.; Bocchini, G.M.; Cesca, S.; Saltogianni, V.; Bedford, J.; Petersen, G.; Gianniou, M.; Oncken, O. Earthquake Swarms, Slow Slip and Fault Interactions at the Western-End of the Hellenic Subduction System Precede the Mw 6.9 Zakynthos Earthquake, Greece. Geochem. Geophys. Geosystems 2020, 21, e2020GC009243. [Google Scholar] [CrossRef]
- Wallace, L.M.; Kaneko, Y.; Hreinsdóttir, S.; Hamling, I.; Peng, Z.; Bartlow, N.; D’Anastasio, E.; Fry, B. Large-scale dynamic triggering of shallow slow slip enhanced by overlying sedimentary wedge. Nat. Geosci. 2017, 10, 765–770. [Google Scholar] [CrossRef]
- Wallace, L.M.; Bartlow, N.; Hamling, I.; Fry, B. Quake clamps down on slow slip. Geophys. Res. Lett. 2014, 41, 8840–8846. [Google Scholar] [CrossRef]
- Eijsink, A.M.; Ikari, M.J. Plate-Rate Frictional Behavior of Sediment Inputs to the Hikurangi Subduction Margin: How Does Lithology Control Slow Slip Events? Geochem. Geophys. Geosystems 2022, 23, e2022GC010369. [Google Scholar] [CrossRef]
- Leah, H.; Fagereng, Å.; Bastow, I.; Bell, R.; Lane, V.; Henrys, S.; Jacobs, K.; Fry, B. The northern Hikurangi margin three-dimensional plate interface in New Zealand remains rough 100 km from the trench. Geology 2022, 50, 1256–1260. [Google Scholar] [CrossRef]
- Woods, K. Investigation of Hikurangi Subduction Zoneslow Slip Events Using Onshore and Offshoregeodetic Data; Victoria University of Wellington: Wellington, New Zealand, 2022. [Google Scholar]
- Wang, W.; Savage, M.K.; Yates, A.; Zal, H.J.; Webb, S.; Boulton, C.; Warren-Smith, E.; Madley, M.; Stern, T.; Fry, B.; et al. Temporal velocity variations in the northern Hikurangi margin and the relation to slow slip. Earth Planet. Sci. Lett. 2022, 584, 117443. [Google Scholar] [CrossRef]
- Williams, C.A.; Eberhart-Phillips, D.; Bannister, S.; Barker, D.H.N.; Henrys, S.; Reyners, M.; Sutherland, R. Revised Interface Geometry for the Hikurangi Subduction Zone, New Zealand. Seismol. Res. Lett. 2013, 84, 1066–1073. [Google Scholar] [CrossRef]
- Okuwaki, R.; Hicks, S.P.; Craig, T.J.; Fan, W.; Goes, S.; Wright, T.J.; Yagi, Y. Illuminating a Contorted Slab with a Complex Intraslab Rupture Evolution During the 2021 Mw 7.3 East Cape, New Zealand Earthquake. Geophys. Res. Lett. 2021, 48, e2021GL095117. [Google Scholar] [CrossRef]
- Xie, Y.; Meng, L.; Zhou, T.; Xu, L.; Bao, H.; Chu, R. The 2021 Mw 7.3 East Cape Earthquake: Triggered Rupture in Complex Faulting Revealed by Multi-Array Back-Projections. Geophys. Res. Lett. 2022, 49, e2022GL099643. [Google Scholar] [CrossRef]
- Li, Y.; Zhengdong, L.; Meng, L. GPS coordinate time series common mode error extraction methods. GNSS World China 2022, 47, 54–59. [Google Scholar]
- Wallace, L.M. Subduction zone coupling and tectonic block rotations in the North Island, New Zealand. J. Geophys. Res. 2004, 109, B12406. [Google Scholar] [CrossRef]
- Wallace, L.M.; Barnes, P.; Beavan, J.; Van Dissen, R.; Litchfield, N.; Mountjoy, J.; Langridge, R.; Lamarche, G.; Pondard, N. The kinematics of a transition from subduction to strike-slip: An example from the central New Zealand plate boundary. J. Geophys. Res. Solid Earth 2012, 117, B02405. [Google Scholar] [CrossRef]
- Wallace, L.M.; Beavan, J. Diverse slow slip behavior at the Hikurangi subduction margin, New Zealand. J. Geophys. Res. 2010, 115, B12402. [Google Scholar] [CrossRef]
- Thomas, A.L. Poly3D: A Three-Dimensional, Polygonal Element, Displacement Discontinuity Boundary Element Computer Program with Applications to Fractures, Faults, and Cavities in the Earth’s Crust; Stanford University: Stanford, CA, USA, 1993. [Google Scholar]
- Bartlow, N.M.; Miyazaki, S.i.; Bradley, A.M.; Segall, P. Space-time correlation of slip and tremor during the 2009 Cascadia slow slip event. Geophys. Res. Lett. 2011, 38, L18309. [Google Scholar] [CrossRef]
- Ducellier, A.; Creager, K.C.; Schmidt, D.A. Detection of slow slip events using wavelet analysis of GNSS recordings. Geophysics 2022, 112, 2408–2424. [Google Scholar] [CrossRef]
- Jacobs, K.M.; Savage, M.K.; Smith, E.C.G. Quantifying seismicity associated with slow slip events in the Hikurangi margin, New Zealand. N. Z. J. Geol. Geophys. 2016, 59, 58–69. [Google Scholar] [CrossRef]
- Delahaye, E.J.; Townend, J.; Reyners, M.E.; Rogers, G. Microseismicity but no tremor accompanying slow slip in the Hikurangi subduction zone, New Zealand. Earth Planet. Sci. Lett. 2009, 277, 21–28. [Google Scholar] [CrossRef]
- Fukuda, J.i.; Kato, A.; Obara, K.; Miura, S.; Kato, T. Imaging of the early acceleration phase of the 2013-2014 Boso slow slip event. Geophys. Res. Lett. 2014, 41, 7493–7500. [Google Scholar] [CrossRef]
- Kano, M.; Fukuda, J.i.; Miyazaki, S.i.; Nakamura, M. Spatiotemporal Evolution of Recurrent Slow Slip Events Along the Southern Ryukyu Subduction Zone, Japan, From 2010 to 2013. J. Geophys. Res. Solid Earth 2018, 123, 7090–7107. [Google Scholar] [CrossRef]
- Liu, Y.; Rice, J.R.; Larson, K.M. Seismicity variations associated with aseismic transients in Guerrero, Mexico, 1995–2006. Earth Planet. Sci. Lett. 2007, 262, 493–504. [Google Scholar] [CrossRef]
- Wallace, L.M.; Hreinsdóttir, S.; Ellis, S.; Hamling, I.; D’Anastasio, E.; Denys, P. Triggered Slow Slip and Afterslip on the Southern Hikurangi Subduction Zone Following the Kaikōura Earthquake. Geophys. Res. Lett. 2018, 45, 4710–4718. [Google Scholar] [CrossRef]
- Ozawa, S.; Kawabata, R.; Kokado, K.; Yarai, H. Long-term slow slip events along the Nankai trough delayed by the 2016 Kumamoto earthquake, Japan. Earth Planets Space 2020, 72, 61. [Google Scholar] [CrossRef]
- Ozawa, S.; Yarai, H.; Kobayashi, T. Recovery of the recurrence interval of Boso slow slip events in Japan. Earth Planets Space 2019, 71, 78. [Google Scholar] [CrossRef]
- Obara, K.; Kato, A. Connecting slow earthquakes to huge earthquakes. Science 2016, 353, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Koulali, A.; McClusky, S.; Wallace, L.; Allgeyer, S.; Tregoning, P.; D’Anastasio, E.; Benavente, R. Slow slip events and the 2016 Te AraroaMw7.1 earthquake interaction: Northern Hikurangi subduction, New Zealand. Geophys. Res. Lett. 2017, 44, 8336–8344. [Google Scholar] [CrossRef]
- Radiguet, M.; Perfettini, H.; Cotte, N.; Gualandi, A.; Valette, B.; Kostoglodov, V.; Lhomme, T.; Walpersdorf, A.; Cabral Cano, E.; Campillo, M. Triggering of the 2014 Mw7.3 Papanoa earthquake by a slow slip event in Guerrero, Mexico. Nat. Geosci. 2016, 9, 829–833. [Google Scholar] [CrossRef]
- Chen, S.K.; Wu, Y.M.; Chan, Y.C. Episodic Slow Slip Events and Overlying Plate Seismicity at the Southernmost Ryukyu Trench. Geophys. Res. Lett. 2018, 45, 10369–10377. [Google Scholar] [CrossRef]
- Nishikawa, T.; Nishimura, T.; Okada, Y. Earthquake Swarm Detection Along the Hikurangi Trench, New Zealand: Insights into the Relationship Between Seismicity and Slow Slip Events. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020618. [Google Scholar] [CrossRef]
- Barnes, P.M.; Wallace, L.M.; Saffer, D.M.; Bell, R.E.; Underwood, M.B.; Fagereng, A.; Meneghini, F.; Savage, H.M.; Rabinowitz, H.S.; Morgan, J.K.; et al. Slow slip source characterized by lithological and geometric heterogeneity. Sci. Adv. 2020, 6, eaay3314. [Google Scholar] [CrossRef]
- Shreedharan, S.; Ikari, M.; Wood, C.; Saffer, D.; Wallace, L.; Marone, C. Frictional and Lithological Controls on Shallow Slow Slip at the Northern Hikurangi Margin. Geochem. Geophys. Geosystems 2022, 23, e2021GC010107. [Google Scholar] [CrossRef]
- Yarce, J.; Sheehan, A.F.; Nakai, J.S.; Schwartz, S.Y.; Mochizuki, K.; Savage, M.K.; Wallace, L.M.; Henrys, S.A.; Webb, S.C.; Ito, Y.; et al. Seismicity at the Northern Hikurangi Margin, New Zealand, and Investigation of the Potential Spatial and Temporal Relationships with a Shallow Slow Slip Event. J. Geophys. Res. Solid Earth 2019, 124, 4751–4766. [Google Scholar] [CrossRef]
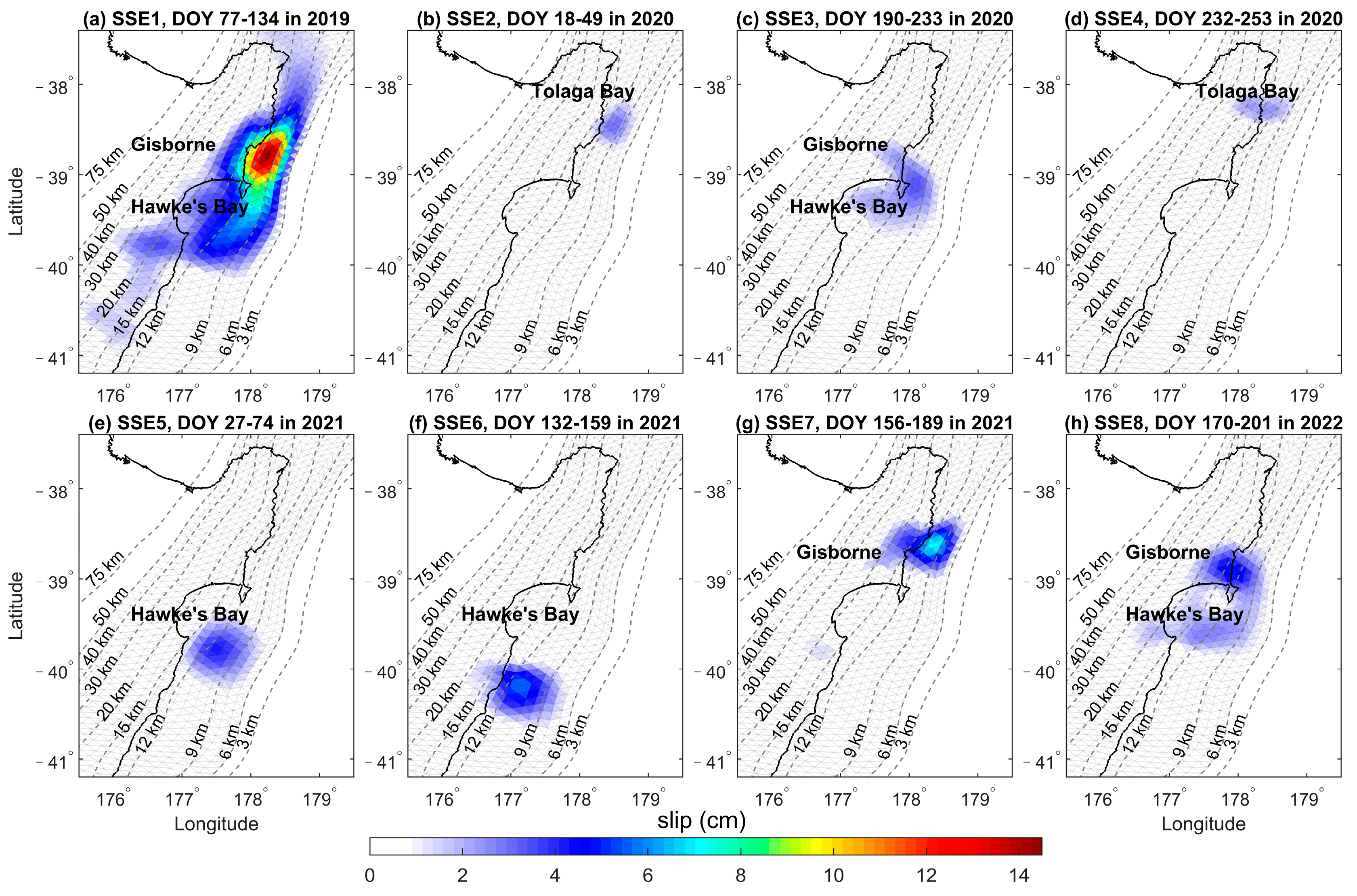
| Year | Event | Main Slip Region | Start and End Time | Maximum Surface Displacement | Cumulative Slip | Maximum Daily Slip Rate |
|---|---|---|---|---|---|---|
| (Duration/Day) | (cm) | (cm) | (mm/Day) | |||
| 2019 | SSE1 | Gisborne-Hawke’s Bay | 77~134 (58 days) | 4.97 | 14.35 | 8.69 |
| 2020 | SSE2 | Tolaga Bay | 18~49 (32 days) | 0.84 | 2.93 | 2.30 |
| SSE3 | Gisborne-Hawke’s Bay | 190~233 (44 days) | 1.33 | 3.37 | 1.98 | |
| SSE4 | Tolaga Bay | 232~253 (22 days) | 0.87 | 2.39 | 1.83 | |
| 2021 | SSE5 | Hawke’s Bay | 27~74 (48 days) | 0.88 | 4.12 | 1.89 |
| SSE6 | South of Hawke’s Bay | 132~159 (28 days) | 1.27 | 5.65 | 5.05 | |
| SSE7 | Gisborne | 156~189 (34 days) | 2.53 | 7.20 | 4.61 | |
| 2022 | SSE8 | Gisborne-Hawke’s Bay | 170~201 (32 days) | 1.92 | 4.87 | 1.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Sun, Y.; Li, M.; El-Mowafy, A.; Ma, L. Slow Slip Events Associated with Seismic Activity in the Hikurangi Subduction Zone, New Zealand, from 2019 to 2022. Remote Sens. 2023, 15, 4767. https://doi.org/10.3390/rs15194767
Yan L, Sun Y, Li M, El-Mowafy A, Ma L. Slow Slip Events Associated with Seismic Activity in the Hikurangi Subduction Zone, New Zealand, from 2019 to 2022. Remote Sensing. 2023; 15(19):4767. https://doi.org/10.3390/rs15194767
Chicago/Turabian StyleYan, Li, Yanling Sun, Meng Li, Ahmed El-Mowafy, and Lei Ma. 2023. "Slow Slip Events Associated with Seismic Activity in the Hikurangi Subduction Zone, New Zealand, from 2019 to 2022" Remote Sensing 15, no. 19: 4767. https://doi.org/10.3390/rs15194767
APA StyleYan, L., Sun, Y., Li, M., El-Mowafy, A., & Ma, L. (2023). Slow Slip Events Associated with Seismic Activity in the Hikurangi Subduction Zone, New Zealand, from 2019 to 2022. Remote Sensing, 15(19), 4767. https://doi.org/10.3390/rs15194767








