Monitoring Spatiotemporal Variation of Individual Tree Biomass Using Multitemporal LiDAR Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Plot Data
2.3. Remote Sensing Data Acquisition and Processing
2.4. Individual Tree Segmentation
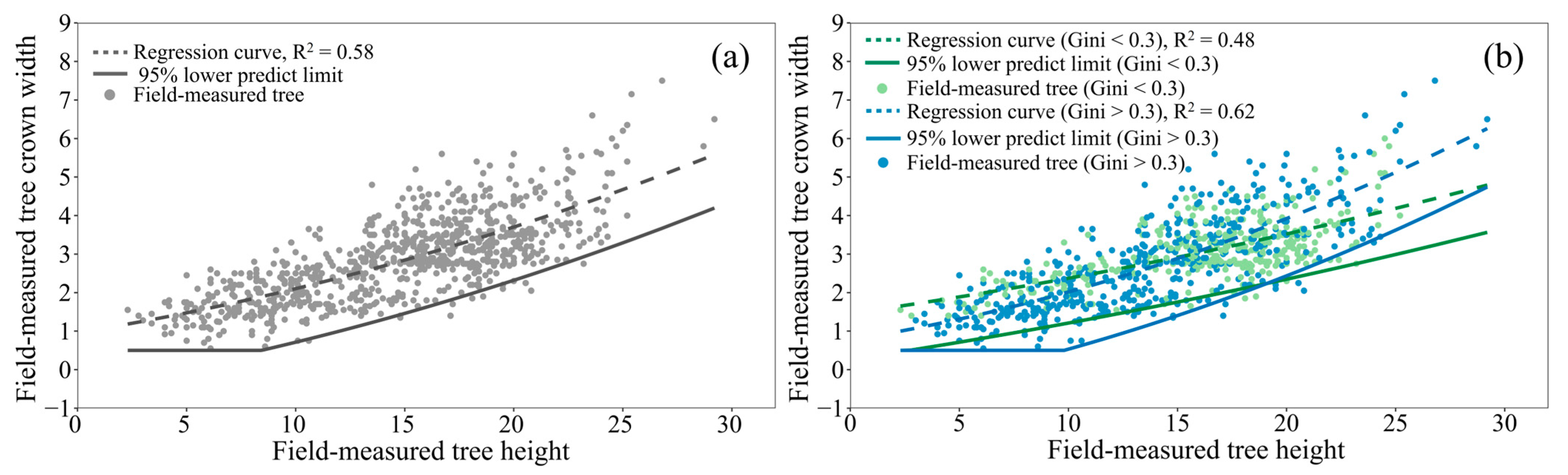
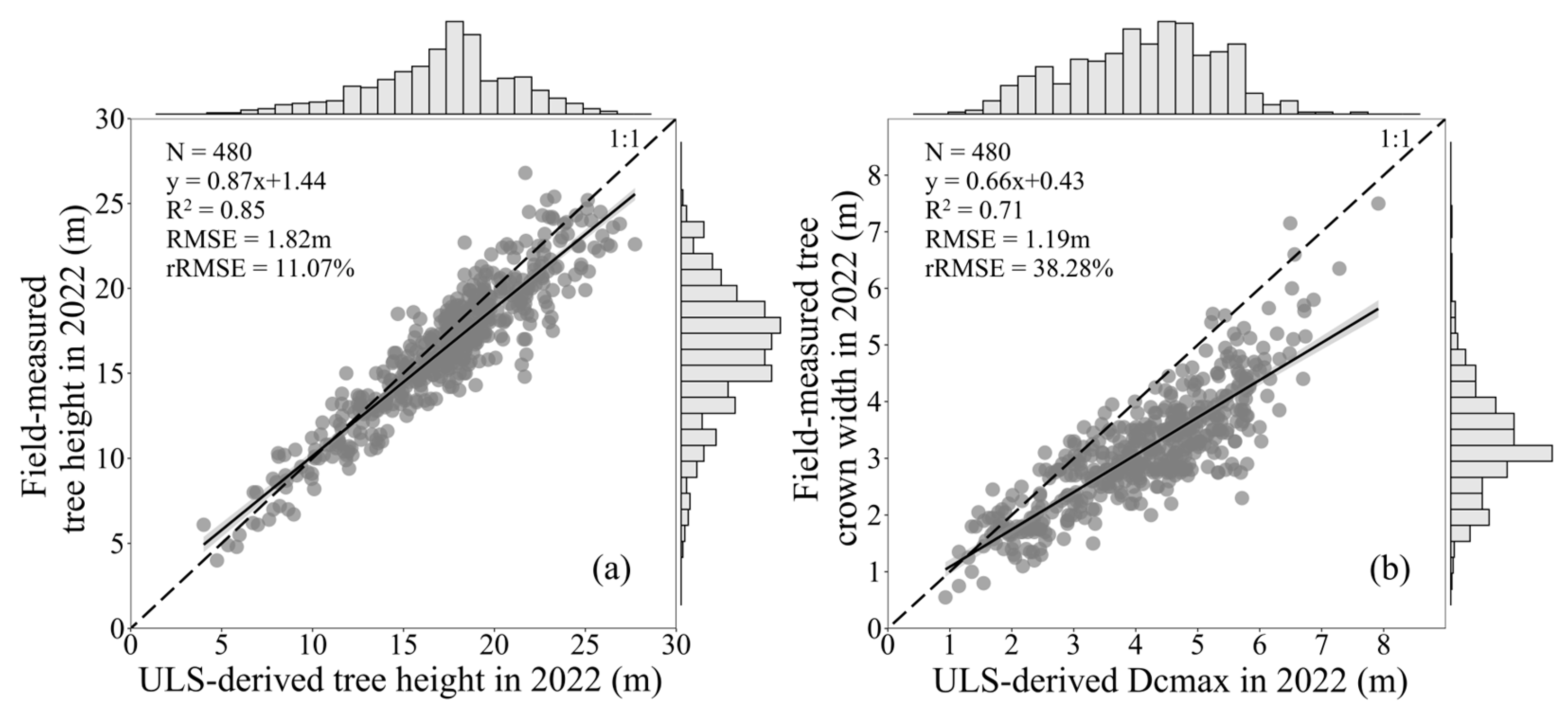
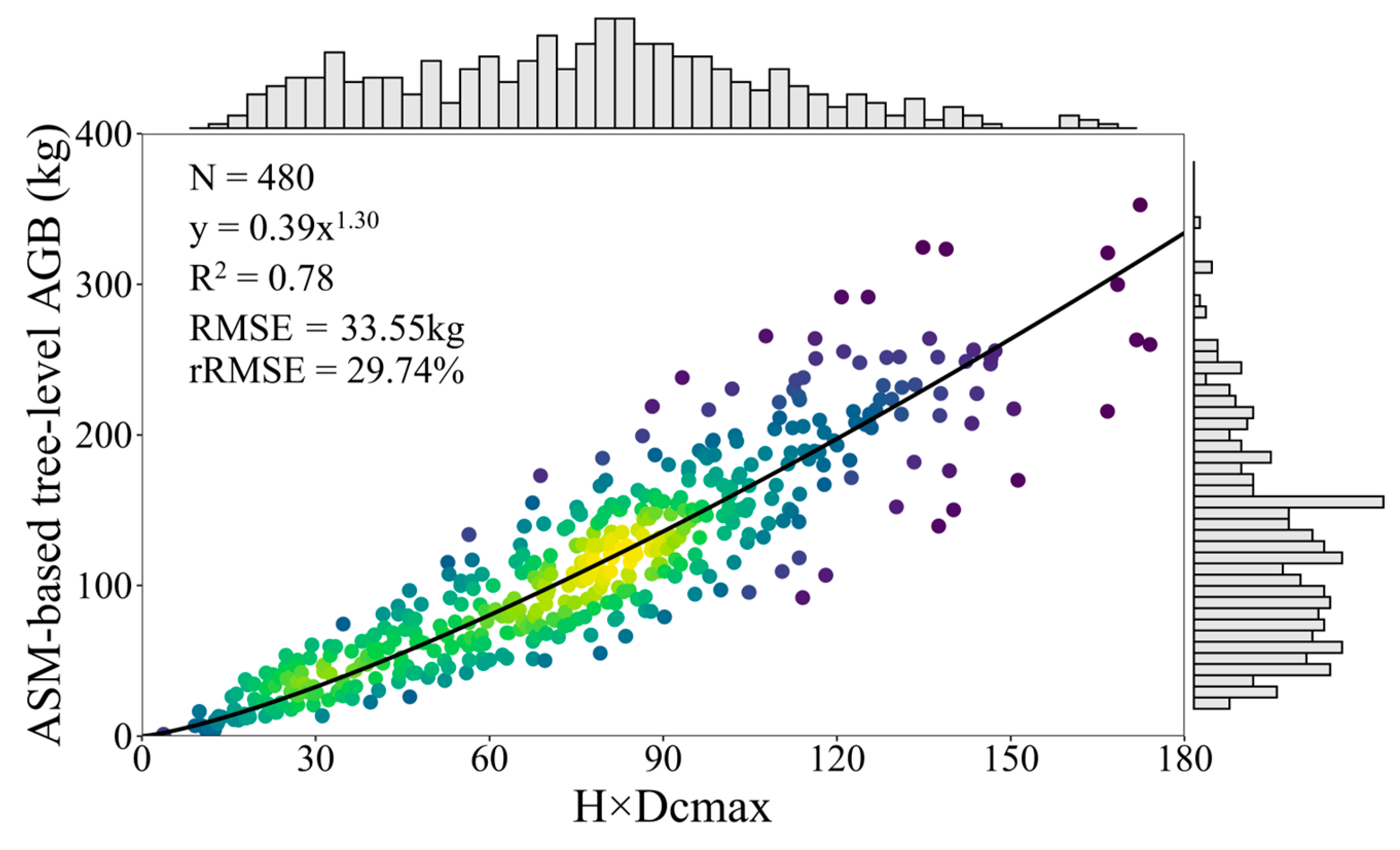
2.5. LiDAR-Based Tree AGB Model
- -
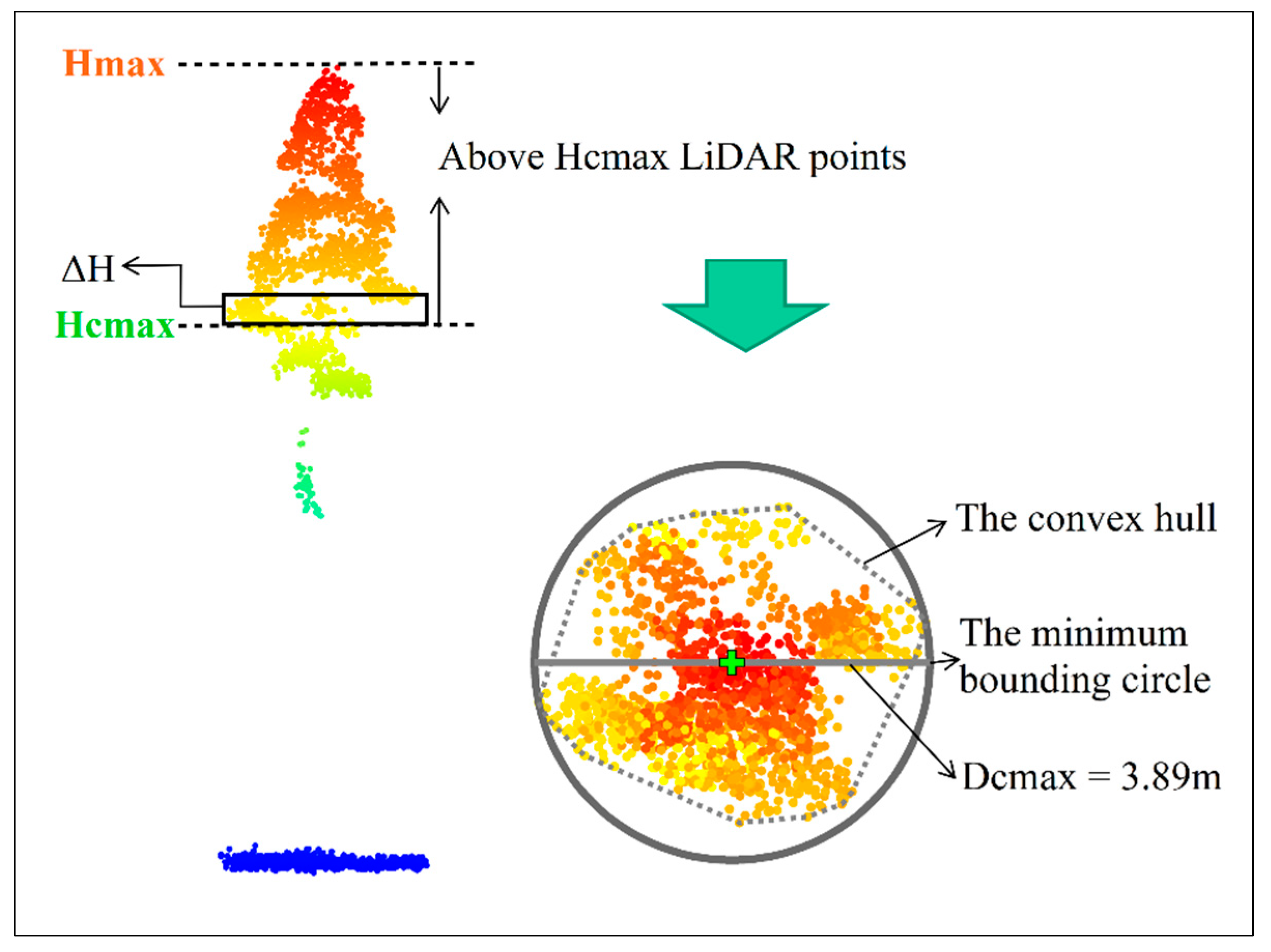
- First, the ULS2022 point cloud above 2 m of each tree was segmented into horizontal slices using a height interval (), which was set to 1 m heuristically.
- -
- For each slice, the points were projected onto a horizontal plane, and the alpha-shape method was used to obtain its convex hull. The area of the convex hull was then calculated.
- -
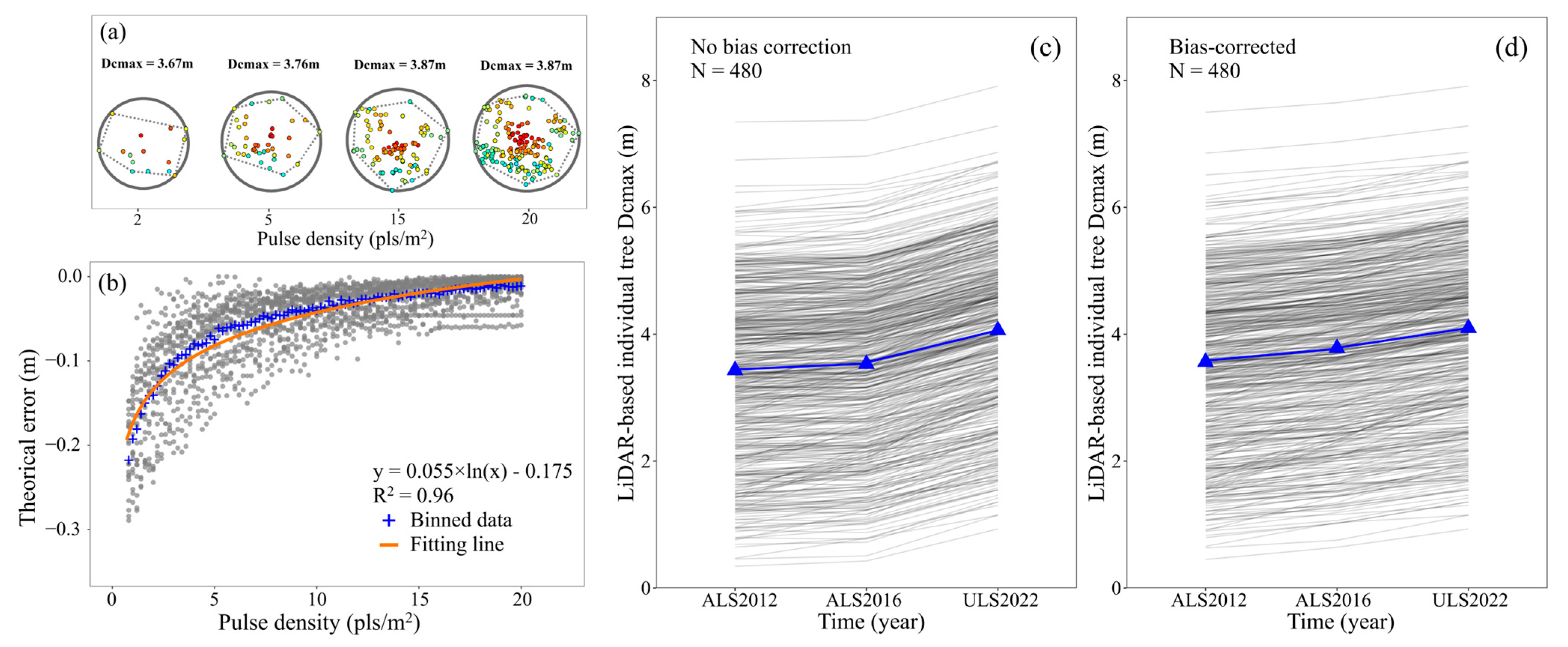
- The slice with the maximum area of the convex hull was identified, and its height above the ground (Hcmax) was determined. All the points above Hcmax were projected onto the horizontal plane. Similarly, a convex hull was generated for the projected points, and the diameter of the minimum bounding circle of this convex hull was viewed as Dcmax in 2022 (Figure 3).
- -
- The Hcmax was applied to each tree of ALS2012 and ALS2016, and the Dcmax in 2012 and 2016 is extracted according to the third step.
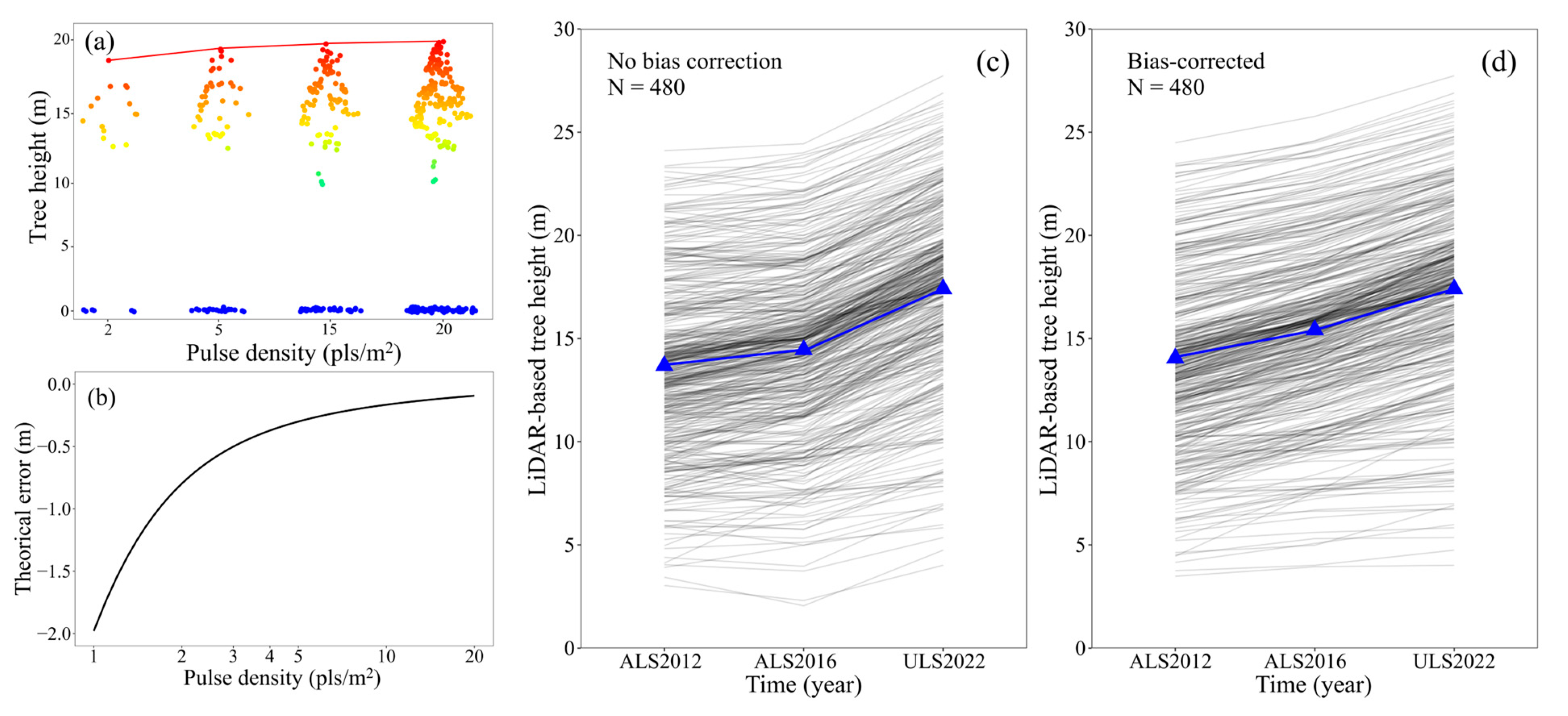
2.6. Correcting Biases for Tree Height and Dcmax
2.7. Spatial Extrapolation and AGB Dynamic Analysis
3. Results
3.1. ITS Algorithms Accuracy Comparison
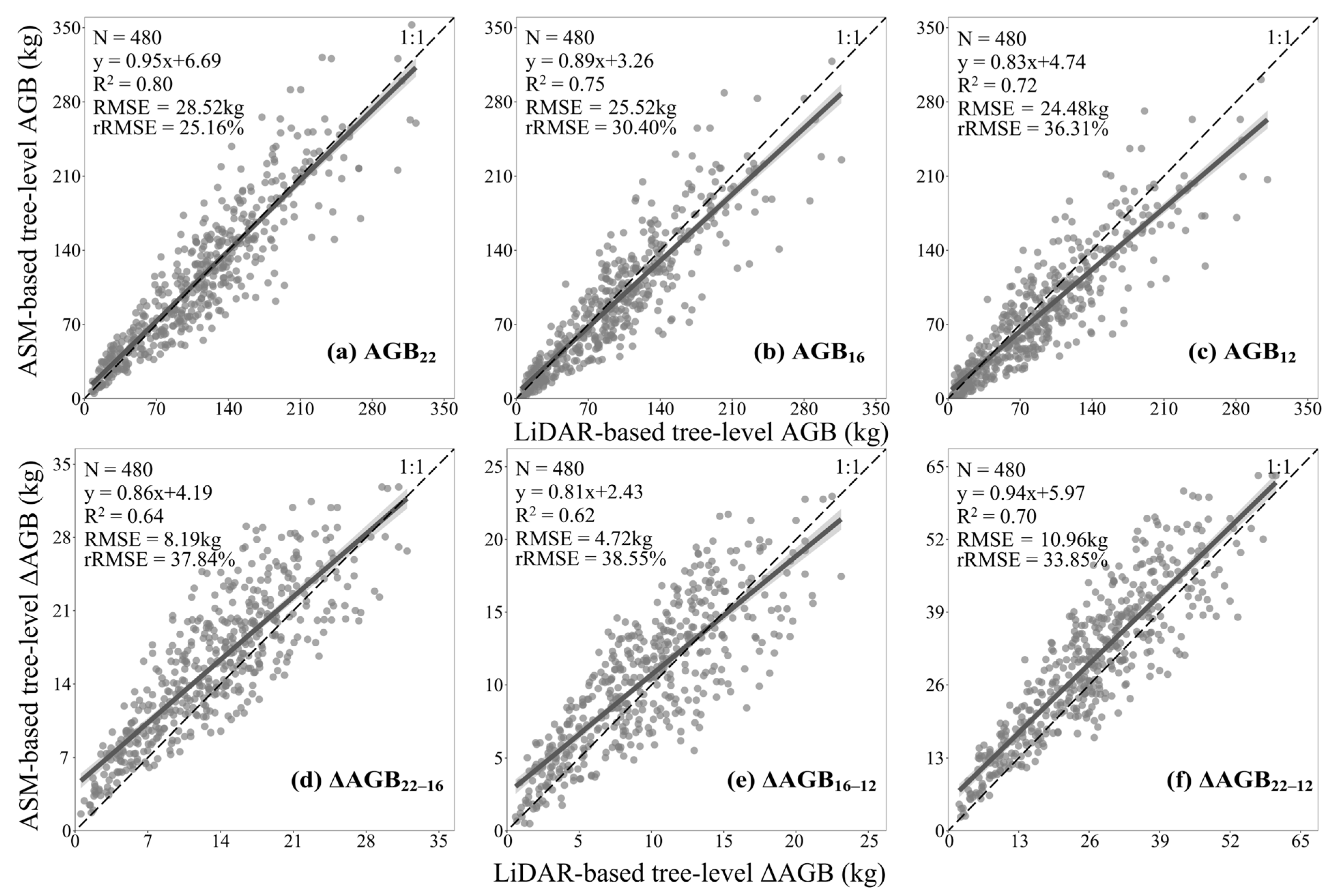
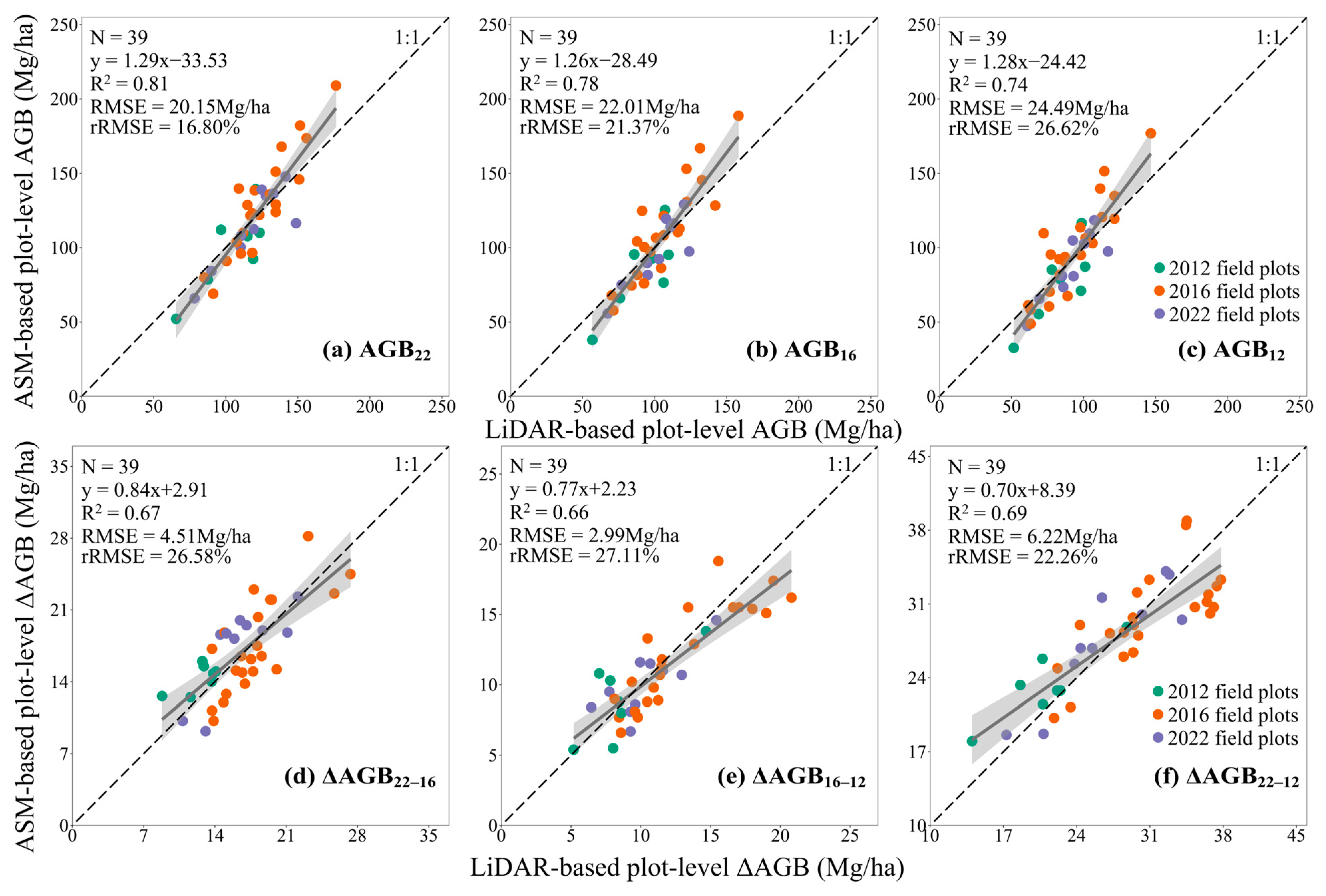
3.2. LiDAR-Based AGB Model Results and Accuracy Evaluation
3.3. H and Dcmax Correction Results
3.4. Assessment of AGB Changes at the Tree- and Plot-Level
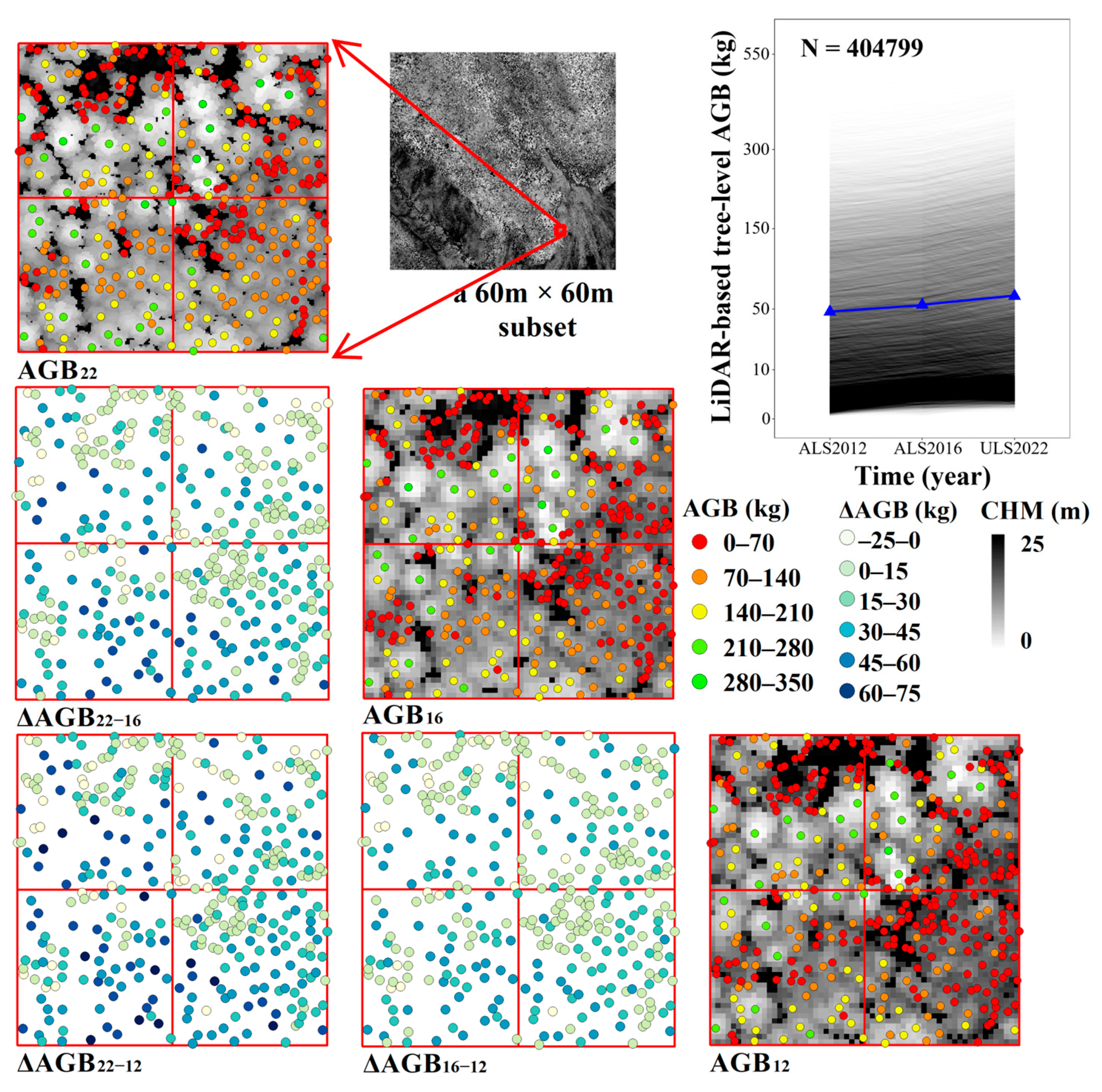
3.5. Spatiotemporal Variation in AGB
4. Discussion
4.1. Effectiveness and Applicability of ITS
4.2. Inconsistencies among Multitemporal LiDAR Data
4.3. Availability of LiDAR-Based Tree AGB Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Complete Parameters | Abbreviation |
| Aboveground biomass | AGB |
| Relative change rate of the aboveground biomass | ΔAGB% |
| Allometric scaling model | ASM |
| Tree height | H |
| Tree crown width | CW |
| Diameter at breast height | DBH |
| Light detection and ranging | LiDAR |
| Airborne laser scanning | ALS |
| Unmanned aerial vehicle | UAV |
| Unmanned aerial vehicle laser scanning | ULS |
| Area-based approach | ABA |
| Individual tree-based approach | ITA |
| Individual tree segmentation | ITS |
| Canopy height model | CHM |
| Digital terrain model | DTM |
| Gini coefficient | GC |
| Tree-level plot data | TPD |
| Plot-level plot data | PPD |
| Greater Khingan Mountains | GKM |
References
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Allouis, T.; Durrieua, S.; Véga, C.; Couteron, P. Exploiting fullwaveform lidar signals to estimate timber volume and above-ground biomass of individual trees. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1251–1254. [Google Scholar]
- Johnson, L.K.; Mahoney, M.J.; Bevilacqua, E.; Stehman, S.V.; Domke, G.M.; Beier, C.M. Fine-resolution landscape-scale biomass mapping using a spatiotemporal patchwork of LiDAR coverages. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103059. [Google Scholar] [CrossRef]
- Krofcheck, D.J.; Litvak, M.E.; Lippitt, C.D.; Neuenschwander, A. Woody biomass estimation in a southwestern US juniper savanna using lidar-derived clumped tree segmentation and existing allometries. Remote Sens. 2016, 8, 453. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Change Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Demol, M.; Verbeeck, H.; Gielen, B.; Armston, J.; Burt, A.; Disney, M.; Duncanson, L.; Hackenberg, J.; Kükenbrink, D.; Lau, A. Estimating forest above-ground biomass with terrestrial laser scanning: Current status and future directions. Methods Ecol. Evol. 2022, 13, 1628–1639. [Google Scholar] [CrossRef]
- Temesgen, H.; Affleck, D.; Poudel, K.; Gray, A.; Sessions, J. A review of the challenges and opportunities in estimating above ground forest biomass using tree-level models. Scand. J. For. Res. 2015, 30, 326–335. [Google Scholar] [CrossRef]
- Badreldin, N.; Sanchez-Azofeifa, A. Estimating Forest Biomass Dynamics by Integrating Multi-Temporal Landsat Satellite Images with Ground and Airborne LiDAR Data in the Coal Valley Mine, Alberta, Canada. Remote Sens. 2015, 7, 2832–2849. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest biomass mapping from lidar and radar synergies. Remote Sens. Environ. 2011, 115, 2906–2916. [Google Scholar] [CrossRef]
- Wulder, M.A.; Hermosilla, T.; White, J.C.; Coops, N.C. Biomass status and dynamics over Canada’s forests: Disentangling disturbed area from associated aboveground biomass consequences. Environ. Res. Lett. 2020, 15, 094093. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Wulder, M.A.; Bater, C.W.; Coops, N.C.; Hilker, T.; White, J.C. The role of LiDAR in sustainable forest management. For. Chron. 2008, 84, 807–826. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.H.; Martinuzzi, S.; Falkowski, M.J. Quantifying aboveground forest carbon pools and fluxes from repeat LiDAR surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Gregoire, T.G.; Ståhl, G. Model-assisted estimation of change in forest biomass over an 11year period in a sample survey supported by airborne LiDAR: A case study with post-stratification to provide “activity data”. Remote Sens. Environ. 2013, 128, 299–314. [Google Scholar] [CrossRef]
- Xu, D.; Wang, H.; Xu, W.; Luan, Z.; Xu, X. LiDAR applications to estimate forest biomass at individual tree scale: Opportunities, challenges and future perspectives. Forests 2021, 12, 550. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of multitemporal lidar for forest and carbon monitoring: Tree growth, biomass dynamics, and carbon flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Comparison of area-based and individual tree-based methods for predicting plot-level forest attributes. Remote Sens. 2010, 2, 1481–1495. [Google Scholar] [CrossRef]
- Økseter, R.; Bollandsås, O.M.; Gobakken, T.; Næsset, E. Modeling and predicting aboveground biomass change in young forest using multi-temporal airborne laser scanner data. Scand. J. For. Res. 2015, 30, 458–469. [Google Scholar] [CrossRef]
- Qi, Z.; Li, S.; Pang, Y.; Zheng, G.; Kong, D.; Li, Z. Assessing spatiotemporal variations of forest carbon density using bi-temporal discrete aerial laser scanning data in Chinese boreal forests. For. Ecosyst. 2023, 10, 100135. [Google Scholar] [CrossRef]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.R.P.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.-H. Area-based vs tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef]
- Dalponte, M.; Frizzera, L.; Ørka, H.O.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting stem diameters and aboveground biomass of individual trees using remote sensing data. Ecol. Indic. 2018, 85, 367–376. [Google Scholar] [CrossRef]
- Du, L.; Pang, Y.; Wang, Q.; Huang, C.; Bai, Y.; Chen, D.; Lu, W.; Kong, D. A LiDAR biomass index-based approach for tree-and plot-level biomass mapping over forest farms using 3D point clouds. Remote Sens. Environ. 2023, 290, 113543. [Google Scholar] [CrossRef]
- Knapp, N.; Huth, A.; Fischer, R. Tree Crowns Cause Border Effects in Area-Based Biomass Estimations from Remote Sensing. Remote Sens. 2021, 13, 1592. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Barbier, N.; Couteron, P.; Ploton, P.; Vincent, G.; Herold, M.; Mermoz, S.; Saatchi, S.; Chave, J.; de Boissieu, F.; et al. Upscaling Forest Biomass from Field to Satellite Measurements: Sources of Errors and Ways to Reduce Them. Surv. Geophys. 2019, 40, 881–911. [Google Scholar] [CrossRef]
- Dalponte, M.; Jucker, T.; Liu, S.; Frizzera, L.; Gianelle, D. Characterizing forest carbon dynamics using multi-temporal lidar data. Remote Sens. Environ. 2019, 224, 412–420. [Google Scholar] [CrossRef]
- Moura, Y.M.; Balzter, H.; Galvão, L.S.; Dalagnol, R.; Espírito-Santo, F.; Santos, E.G.; Garcia, M.; Bispo, P.D.; Oliveira, R.C.; Shimabukuro, Y.E. Carbon Dynamics in a Human-Modified Tropical Forest: A Case Study Using Multi-Temporal LiDAR Data. Remote Sens. 2020, 12, 430. [Google Scholar] [CrossRef]
- Brede, B.; Terryn, L.; Barbier, N.; Bartholomeus, H.M.; Bartolo, R.; Calders, K.; Derroire, G.; Moorthy, S.M.K.; Lau, A.; Levick, S.R. Non-destructive estimation of individual tree biomass: Allometric models, terrestrial and UAV laser scanning. Remote Sens. Environ. 2022, 280, 113180. [Google Scholar] [CrossRef]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gobakken, T.; Næsset, E. Assessing effects of laser point density, ground sampling intensity, and field sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2008, 38, 1095–1109. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between lidar pulse density and forest measurement accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
- Hastings, J.H.; Ollinger, S.V.; Ouimette, A.P.; Sanders-DeMott, R.; Palace, M.W.; Ducey, M.J.; Sullivan, F.B.; Basler, D.; Orwig, D.A. Tree species traits determine the success of LiDAR-based crown mapping in a mixed temperate forest. Remote Sens. 2020, 12, 309. [Google Scholar] [CrossRef]
- Stan, A.B.; Daniels, L.D. Growth releases across a natural canopy gap-forest gradient in old-growth forests. For. Ecol. Manag. 2014, 313, 98–103. [Google Scholar] [CrossRef]
- Meng, S.; Jia, Q.; Liu, Q.; Zhou, G.; Wang, H.; Yu, J. Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix gmelinii in the Western Daxing’anling Mountains, Northeastern China. Forests 2019, 10, 150. [Google Scholar] [CrossRef]
- Meng, S. The Aboveground Biomass of Main Tree Species in Daxing’anling Mountains. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2018. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.; Isenburg, M.; Hussin, Y. Generating Pit-free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Liu, Y.; You, H.; Tang, X.; You, Q.; Huang, Y.; Chen, J. Study on Individual Tree Segmentation of Different Tree Species Using Different Segmentation Algorithms Based on 3D UAV Data. Forests 2023, 14, 1327. [Google Scholar] [CrossRef]
- Minařík, R.; Langhammer, J.; Lendzioch, T. Automatic Tree Crown Extraction from UAS Multispectral Imagery for the Detection of Bark Beetle Disturbance in Mixed Forests. Remote Sens. 2020, 12, 4081. [Google Scholar] [CrossRef]
- Yang, Q.; Su, Y.; Jin, S.; Kelly, M.; Hu, T.; Ma, Q.; Li, Y.; Song, S.; Zhang, J.; Xu, G.; et al. The Influence of Vegetation Characteristics on Individual Tree Segmentation Methods with Airborne LiDAR Data. Remote Sens. 2019, 11, 2880. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Impact of tree-oriented growth order in marker-controlled region growing for individual tree crown delineation using airborne laser scanner (ALS) data. Remote Sens. 2014, 6, 555–579. [Google Scholar] [CrossRef]
- Valbuena, R.; Maltamo, M.; Mehtätalo, L.; Packalen, P. Key structural features of Boreal forests may be detected directly using L-moments from airborne lidar data. Remote Sens. Environ. 2017, 194, 437–446. [Google Scholar] [CrossRef]
- Adnan, S.; Maltamo, M.; Mehtätalo, L.; Ammaturo, R.N.L.; Packalen, P.; Valbuena, R. Determining maximum entropy in 3D remote sensing height distributions and using it to improve aboveground biomass modelling via stratification. Remote Sens. Environ. 2021, 260, 112464. [Google Scholar] [CrossRef]
- Glasser, G.J. Variance Formulas for the Mean Difference and Coefficient of Concentration. J. Am. Stat. Assoc. 1962, 57, 648–654. [Google Scholar] [CrossRef]
- Cao, Y.; Ball, J.G.C.; Coomes, D.A.; Steinmeier, L.; Knapp, N.; Wilkes, P.; Disney, M.; Calders, K.; Burt, A.; Lin, Y. Tree segmentation in airborne laser scanning data is only accurate for canopy trees. bioRxiv 2022, in press. [CrossRef]
- Roussel, J.-R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Sibona, E.; Vitali, A.; Meloni, F.; Caffo, L.; Dotta, A.; Lingua, E.; Motta, R.; Garbarino, M. Direct Measurement of Tree Height Provides Different Results on the Assessment of LiDAR Accuracy. Forests 2017, 8, 7. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Campbell, M.J.; Eastburn, J.F.; Mistick, K.A.; Smith, A.M.; Stovall, A.E.L. Mapping individual tree and plot-level biomass using airborne and mobile lidar in piñon-juniper woodlands. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103232. [Google Scholar] [CrossRef]
- Wang, Q.; Pang, Y.; Chen, D.; Liang, X.; Lu, J. Lidar biomass index: A novel solution for tree-level biomass estimation using 3D crown information. For. Ecol. Manag. 2021, 499, 119542. [Google Scholar] [CrossRef]
- Wedeux, B.; Dalponte, M.; Schlund, M.; Hagen, S.; Cochrane, M.; Graham, L.; Usup, A.; Thomas, A.; Coomes, D. Dynamics of a human-modified tropical peat swamp forest revealed by repeat lidar surveys. Glob. Change Biol. 2020, 26, 3947–3964. [Google Scholar] [CrossRef]
- Forzieri, G.; Guarnieri, L.; Vivoni, E.R.; Castelli, F.; Preti, F. Multiple attribute decision making for individual tree detection using high-resolution laser scanning. For. Ecol. Manag. 2009, 258, 2501–2510. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Li, W.; Guo, Q.; Kelly, M. Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches. Remote Sens. 2013, 5, 4163–4186. [Google Scholar] [CrossRef]
- Næsset, E. Effects of different sensors, flying altitudes, and pulse repetition frequencies on forest canopy metrics and biophysical stand properties derived from small-footprint airborne laser data. Remote Sens. Environ. 2009, 113, 148–159. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M. Automatic detection of harvested trees and determination of forest growth using airborne laser scanning. Remote Sens. Environ. 2004, 90, 451–462. [Google Scholar] [CrossRef]
- Hirata, Y. The effects of footprint size and sampling density in airborne laser scanning to extract individual trees in mountainous terrain. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Ploton, P.; Barbier, N.; Takoudjou Momo, S.; Réjou-Méchain, M.; Boyemba Bosela, F.; Chuyong, G.; Dauby, G.; Droissart, V.; Fayolle, A.; Goodman, R.C.; et al. Closing a gap in tropical forest biomass estimation: Taking crown mass variation into account in pantropical allometries. Biogeosciences 2016, 13, 1571–1585. [Google Scholar] [CrossRef]

| 2012 | 2016 | 2022 | ||||
|---|---|---|---|---|---|---|
| Range | Mean | Range | Mean | Range | Mean | |
| Tree-level Plot Data (TPD) | ||||||
| DBH/cm | 2.9–40.6 | 14.9 | 3.8–41.2 | 16.0 | 5.0–42.0 | 17.5 |
| Tree-level AGB/kg | 1.44–909.7 | 79.9 | 2.7–944.6 | 91.2 | 5.1–992.4 | 107.5 |
| Plot-level Plot Data (PPD) | ||||||
| DBH/cm | 8.6–16.2 | 11.1 | 9.4–16.9 | 11.8 | 10.6–18.0 | 13.0 |
| Plot-level AGB/(Mg/ha) | 32.6–176.9 | 91.9 | 38.1–188.7 | 103.0 | 50.6–209.0 | 119.9 |
| Parameters | ALS2012 | ALS2016 | ULS2022 |
|---|---|---|---|
| Acquisition time | 30 August 2012 | 28 August 2016 | 20 August 2022 |
| Sensor type | Leica ALS60 | Riegl LMS-Q680i | LiAir 1350 |
| Laser pulse frequency (kHz) | 300 | 200 | 350 |
| Flying altitude (m) | 2700 | 2200 | 200 |
| Scanning angle (°) | ±35 | ±30 | ±45 |
| Average pulse density(pulses/m2) | 5.2 | 2.6 | 146.2 |
| Wavelength (nm) | 1064 | 1550 | 1550 |
| ITS Methods | Recall | Precision | F-Score | Time (s) |
|---|---|---|---|---|
| li2012 | 0.45 | 0.53 | 0.49 | 18.8 |
| dalponte2016-FW | ||||
| Window size: 1.5 m | 0.58 | 0.55 | 0.56 | 4.8 |
| Window size: 2 m | 0.56 | 0.64 | 0.60 | 4.4 |
| Window size: 2.5 m | 0.47 | 0.72 | 0.57 | 3.9 |
| dalponte2016-VW | 0.66 | 0.68 | 0.67 | 5.5 |
| dalponte2016-GCVW | 0.80 | 0.73 | 0.76 | 5.8 |
| Environmental Factors | |||
|---|---|---|---|
| Forest stand age | 10% | 12% | 9% |
| Aspect | 3% | 2% | 4% |
| Elevation | 8% | 5% | 3% |
| Canopy density 2012 | 9% | 8% | |
| Canopy density 2016 | 5% | ||
| GC 2012 | 32% | 30% | |
| GC 2016 | 34% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Li, S.; Pang, Y.; Du, L.; Zhang, H.; Li, Z. Monitoring Spatiotemporal Variation of Individual Tree Biomass Using Multitemporal LiDAR Data. Remote Sens. 2023, 15, 4768. https://doi.org/10.3390/rs15194768
Qi Z, Li S, Pang Y, Du L, Zhang H, Li Z. Monitoring Spatiotemporal Variation of Individual Tree Biomass Using Multitemporal LiDAR Data. Remote Sensing. 2023; 15(19):4768. https://doi.org/10.3390/rs15194768
Chicago/Turabian StyleQi, Zhiyong, Shiming Li, Yong Pang, Liming Du, Haoyan Zhang, and Zengyuan Li. 2023. "Monitoring Spatiotemporal Variation of Individual Tree Biomass Using Multitemporal LiDAR Data" Remote Sensing 15, no. 19: 4768. https://doi.org/10.3390/rs15194768
APA StyleQi, Z., Li, S., Pang, Y., Du, L., Zhang, H., & Li, Z. (2023). Monitoring Spatiotemporal Variation of Individual Tree Biomass Using Multitemporal LiDAR Data. Remote Sensing, 15(19), 4768. https://doi.org/10.3390/rs15194768







