Abstract
Photon counting LiDAR can capture the 3D information of long-distance targets and has the advantages of high sensitivity and high resolution. However, the noise counts restrict improvements in the photon counting imaging quality. Therefore, how to make full use of the limited signal counts under noise interference to achieve efficient 3D imaging is one of the main problems in current research. To address this problem, in this paper, we proposes a 3D imaging method for undulating terrain depth estimation that combines constant false alarm probability detection with the Bayesian model. First, the new 3D cube data are constructed by adaptive threshold segmentation of the reconstructed histogram. Secondly, the signal photons are extracted in the Bayesian model, and depth estimation is realized from coarse to fine by the sliding-window method. The robustness of the method under intense noise is proven by sufficient undulating terrain simulations and outdoor imaging experiments. These results show that the proposed method is superior to typical existing methods.
1. Introduction
A 3D LiDAR imaging system based on single-photon detection technology can achieve picosecond time resolution, using the time-correlated single-photon counting (TCSPC) module to record the time-of-flight information of the echo photons [,,,]. Photon counting LiDAR also shows unique advantages in long-distance detection due to the single-photon detection sensitivity of the Geiger-mode avalanche photodiode (Gm-APD) [,]. It not only improves the detection ability of unit laser pulse energy and dramatically reduces the requirement of laser emission power but can also obtain more effective echo data by increasing the detection time. The above advantages make photon counting LiDAR able to solve the application limitations and technical problems of traditional linear detection within a specific range. Therefore, photon counting LiDAR is increasingly used in three-dimensional detection fields, such as topographic mapping, autonomous driving and underwater detection [,,].
When detecting the weak echo signal of a long-distance target, both the signal photons and the noise photons reaching the Gm-APD photosensitive surface may trigger the photoelectric conversion process and generate an electrical pulse signal [,]. Therefore, in addition to the effective information for the 3D reconstruction of the target, the weak echo photon counts also carry noise counts. The noise level is closely related to the background light and the detector’s dark counts. Although the use of a narrow-band filter module and the setting of the time gate can help to reduce the interference of background noise, the echo data still contain more noise data, which restricts the improvement of image reconstruction quality [,]. Aiming at this problem, the existing research methods generally only analyze the echo data of each pixel in the time dimension. Hence, the quality of image reconstruction decreases sharply at low signal-to-background ratio (SBR) values. In recent years, scholars have introduced image spatial correlation to algorithm design, improving the quality of photon counting imaging [,]. However, this kind of method is more suitable for the 3D reconstruction of static targets with less fluctuation of depth information. In particular, if the target’s depth information to be measured is in a state of continuous change at low SBR values, the corresponding signal counts are discretely distributed in multiple time bins of the histogram. At this time, the neighborhood data set constructed by image spatial correlation cannot show prominent aggregation characteristics on the time axis, which is not conducive to acquiring signal photon counts.
Therefore, for the problem of target imaging with varying depth fluctuations, the efficient extraction of signal photon counting data is still an urgent problem to be solved. Based on Bayesian inference, the relationship between the prior distribution and the parameters of the likelihood function is constructed []. We can obtain new information from the data; then, the prior probability is updated to obtain the posterior probability. Since the concept of Bayesian inference was established, many researchers have continuously improved it. It has been widely used in data processing in the fields of CCD, EMCCD, CMOS, multispectral radar and multisensor fusion, as shown in Table 1. The application of Bayesian statistical theory to different sensors indicates that the processing and analysis of data based on the Bayesian statistical approach are helpful in obtaining better estimation results.

Table 1.
Application classification of the Bayesian algorithm in different sensors.
Based on this, we propose a single-photon 3D imaging method for targets with depth fluctuations. The time bin position of each pixel where the signal counts are located can be obtained by combining constant false alarm probability detection with the Bayesian model. This method profoundly analyzes the statistical difference between noise and signal counts in the time dimension of the echo data and comprehensively considers the spatial correlation between the echo data of each pixel, aiming to mine more available information from the limited echo data and improve the 3D reconstruction performance of the target. The main contributions of the proposed method are as follows:
- Construction of a new 3D cube data model at a low time resolution scale by setting a constant false alarm probability, which greatly reduces the amount of data and the computational complexity of subsequent processing;
- Following the Bayesian framework, a posterior probability model of signal photon counts is established to solve the time bin position. The time bin position of a single-photon cluster can be updated by introducing the support point set;
- The extraction of signal counting data from coarse-scale to fine-scale is realized by the sliding-window method, and the depth information can be obtained while maintaining high precision;
- Simulation and experimental results show that the proposed method has a positive effect on the 3D imaging of targets with undulating depth information.
The remainder of this paper is structured as follows. In Section 2, typical existing research on target 3D reconstruction algorithms is reviewed. In Section 3, the theoretical knowledge of single-photon detection involved in this method is analyzed. In Section 4, the proposed method is described in detail. In Section 5, terrain detection simulation experiments with different depth fluctuations are carried out, and the reconstruction results are displayed and analyzed. In Section 6, an outdoor long-distance target imaging verification experiment is introduced, and the experimental results are analyzed. In Section 7, we discuss the advantages and disadvantages of the proposed algorithm. In Section 8, the work reported in this paper is summarized, and prospective future research directions are proposed.
2. Related Work
With the development of photon counting imaging technology, a series of photon counting 3D imaging algorithms have been developed [,,]. According to the distribution characteristics of echo photon data in the time and space dimensions, it can be divided into two estimation methods based on time and space–time correlation. The estimation method based on time correlation usually only uses the statistical difference of photon data in the time domain to distinguish signal counts and noise counts to achieve the purpose of filtering. The peak method is the most simple and intuitive time-of-flight information extraction algorithm []. This method solves the corresponding distance information by extracting the time bin position of the maximum counts in the photon statistical histogram. Nguyen et al. introduced and compared the performance of four different peak detection algorithms in []. The cross-correlation algorithm is another typical method. This method analyzes the matching characteristics between the echo response and the system instrument response function, which can obtain the target distance by calculating the cross correlation []. Feng et al. proposed a fast depth imaging denoising method using the temporal correlation of signal count data []. Based on the non-uniform Poisson probability model, this method extracts the signal response set of each pixel by setting an appropriate detection threshold. The above techniques can effectively filter out the interference of noise photon counts in the case of high SBR and sufficient pulse accumulation times. However, the detection time is usually limited in practical applications, and the reconstruction effect declines sharply as the number of signal photon counts in the echo data decreases.
Under weak echo detection or limited detection times, signal photon counts are easily submerged. Therefore, the spatial correlation of the image was introduced to improve the imaging quality. Kirmani et al. proposed the first photon imaging algorithm, which uses the first photon detected by each pixel for target imaging and reflectivity estimation []. This algorithm has a better reconstruction effect and can recover detailed information about the target at high SBR. However, the first photon count is likely to be generated by the background light, and the 3D reconstruction of the target could be worse in the intense noise background. Shin et al. proposed a sparse regularization target depth estimation algorithm for array detection under weak light conditions []. The depth and intensity information is estimated by establishing an accurate single-photon statistical detection model and combining the lateral smoothness and longitudinal sparsity in the detected scene space. In this method, the detection time of each pixel is the same, which is helpful in realizing the parallel detection of each pixel. Rapp et al. proposed an algorithm for unmixing signal and noise []. The acceptable minimum photon set is calculated by presetting the proper detection false alarm probability, and a suitable time window () is selected to find the time-of-flight dataset with the maximum photon count, where and represent the laser pulse width and the detection period, respectively. The time-of-flight information of the signal photon cluster is filtered by the sliding window method, and constructing superpixel and regularization constraints to smooth the image. Li et al. proposed a three-dimensional deconvolution computational imaging algorithm that abstracts the solution of the 3D information of the image into a deconvolution model []. The three-dimensional space–time matrix is used to solve the reflectivity and depth simultaneously, and the relationship between the reflectivity and depth of the target is also optimized. Hua et al. proposed the first signal photon unit (FSPU) imaging method []. The photon data sequence that meets the requirements is selected by setting the number of echo photon counts that can be accepted in a specific time range. The first signal photon unit data are used instead of the first photon in the FPI algorithm. In the case of increasing noise, the reconstruction effect of FSPU is significantly better than that of FPI. Chen et al. proposed a single-photon imaging method based on multiscale temporal resolution combined with adaptive threshold segmentation [,]. By constructing multiple histograms and pixel blocks with different temporal resolutions, the practical distinction between noise and signal is realized, but the quality of reconstruction in a noisy environment is degraded.
In addition, the deep learning algorithm can be applied to optimize single-photon 3D imaging algorithms. Lindell et al. proposed an image reconstruction algorithm suitable for sensor fusion detection []. By constructing a multiscale convolutional neural network to process photon counting data from a single-photon detector array and intensity images collected by the camera, the resolution of the target depth estimation is improved. Still, the imaging quality is significantly reduced in long-distance detection. Through the use of feature extraction and a non-local neural network, Peng et al. analyzed the correlation characteristics of echo photons in the space–time dimension in long-distance detection and combined the two loss terms of KL divergence and TV regularization to constrain the network training so as to complete the extraction of echo signal photon counts under intense noise []. Tan et al. established a multiscale convolutional neural network combined with a defined loss function for multiple returns, which converts the depth extraction into the removal of range ambiguity and can recover the detailed information of the target []. Peng et al. proposed an image reconstruction algorithm based on a unified deep neural network that can obtain better reconstruction fidelity under low SBR and severe blurring caused by multiple returns []. Although using deep learning algorithms improves the overall control of the image, it often requires a lot of sample training.
In short, based on the analysis of the time dimension, the use of spatial connections of pixels can make up for the lack of time sampling, which can improve the performance of photon counting imaging. However, if the target distance information fluctuates significantly, the imaging effect of the existing algorithm is non-ideal when the signal echo is weak. Therefore, in this paper, we propose a photon counting 3D imaging method for undulating terrain and verify the effectiveness of the proposed method in simulations of terrain detection and outdoor imaging experiments.
3. Basic Theory
3.1. Data Model
3.1.1. Time Characteristics
In this work, we assume that the emitted laser pulse shape is Gaussian (, where is the root mean square pulse width). As described in [], when the pixel is detected by a laser pulse, the output response of the Gm-APD detector is a non-homogeneous Poisson process with both noise and signal echo. The total intensity is
where is the distance to be measured, is the target reflectivity, denotes the background light level and is the detector dark counts. represents the photon detection efficiency, where and represent the avalanche efficiency and the quantum probability, respectively. In a detection period (), the total photon counts can be expressed as
where .
In photon counting imaging detection, as shown in Figure 1, the echo photon counting model can be obtained after the accumulation of four pulse detection cycles at pixel . It can be seen that the echo photon data of each pixel include two parts: signal counts and noise counts, which are represented by red and blue lines, respectively. Signal detection has the characteristics of slight variance. Therefore, the signal photon clusters can be considered to be concentrated near the depth of the target to be measured. However, compared with the signal data, it is generally believed that the noise data are constant or slightly changed in a specific time range, showing the characteristics of uniform distribution.
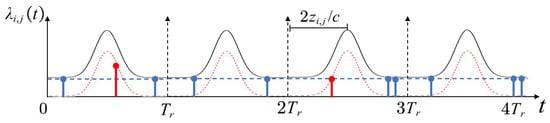
Figure 1.
Echo photon data observation model. Here, we show the generation process of echo photon data in four pulse detection cycles when there is only one target to be measured. When the first and third pulses are emitted, a signal count (red) is generated, and noise counts (blue) are generated after each pulse is emitted. (The red dashed line represents the signal response, the blue dashed line represents the noise response, and the black solid line represents the combined response.)
A detection period () can be divided into equal interval time bins (), where the time interval is defined as , that is, the time resolution of the histogram. represents the total number of time bins in a detection period (). After the accumulation of multiple pulse detections, the echo photon counts in each time bin are counted. Signal and noise can be distinguished by analyzing the different probability distribution characteristics of the echo data.
3.1.2. Spatial Characteristics
From the spatial correlation of the image, it can be seen that there is a correlation between the echo photon data of adjacent pixels in the photon counting LiDAR detection, that is, the photon counts of the pixel and its neighborhood pixels are very likely to come from a similar distance. Since pixels with similar lateral positions and reflectivity often belong to the same object and have similar depths, the method of echo photon data detection in similar pixels can be used to make the aggregation characteristics of signal photon clusters more apparent, as shown in Figure 2.
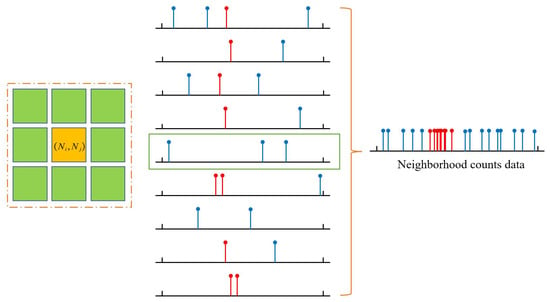
Figure 2.
Space sampling schematic diagram of photon counts. When there is no signal count in the echo photon data of the pixel , the count data of its 3 × 3 neighborhood pixels can be used to form a new dataset, which is helpful in solving the time range of the signal counts of the pixel (The red dashed line represents the signal response and the blue dashed line represents the noise response).
3.2. Probability Model
The single-photon detection model conforms to statistical optics theory. Since the echo signal reflected by the target is usually weak, the generation of signal and noise photoelectrons can be approximately considered to satisfy the Poisson random process, and the superposition model can also be modeled by Poisson distribution [,]. In single-pulse detection, the time bin () is used as the sampling unit, and the total photon counts in time bin are
where . Here, we define and , which represent signal counts and noise counts, respectively. The influence of dark counts () is obviously less than that of background light, which can be ignored in most daytime radiation analyses. The probability density function of producing k photoelectrons in time bin is
Based on this, the probability of at least one detection event is
where is the arm probability, is the noise count rate and is dead time of the detector.
If the response of the detector is triggered by noise photons, it is called a false alarm. If the noise photon triggers at least one avalanche event, the false-alarm probability of single-pulse detection can be obtained as
In actual detection, the SBR of the system is usually improved by multiple detections. We assume that the cumulative number of pulses is M, and the detection probability and false-alarm probability can be expressed as
where , and stands for the signal recognition threshold.
When the numbers of pulse accumulations and signal photon counts increase, the detection probability of the system increases. At the same time, the false-alarm probability increases with an increase in the number of noise photon counts. When the signal recognition threshold is set, the detection probability and the false-alarm probability are reduced, and the influence on the false-alarm probability is pronounced. Therefore, in practical applications, the appropriate signal recognition threshold () can be selected according to the expected detection probability () and the acceptable false-alarm probability ().
4. Methods
In the 3D imaging of the target, the echo photon data of each pixel are randomly generated by the scene attributes. We constructed a 3D echo data cube with time resolution of , which consists of the echo photon counts of the whole image, as shown in Figure 3a. Each pixel contains a photon statistical histogram, as shown in Figure 3b. Due to the interference of noise counts, the signal counts in the histogram are likely to be submerged, which not only increases the difficulty of practical information extraction but also leads to significant estimation error. In addition, the amount of data calculation for depth estimation also increases with the increase in noise interference.
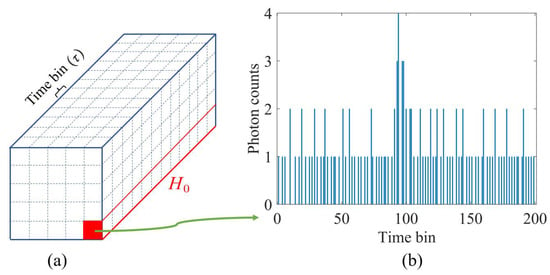
Figure 3.
Three-dimensional echo photon data schematic diagram. (a) The 3D echo data cube is composed of all pixels of the whole image when the time resolution is . (b) Photon statistical histogram of a single pixel in the cube, where the horizontal axis represents the position information of the time bin and the vertical axis represents the number of photons in each time bin.
In our previous work [], a single-photon imaging method with multiscale time resolution was proposed. This method clusters the signal counts into a time bin by generating multiple histograms with different time resolutions and adaptive threshold segmentation techniques, then separates them from the noise. Based on the idea of this method, we further propose a photon counting 3D undulating terrain depth estimation method based on the Bayesian model. The main ideas are shown in Figure 4.
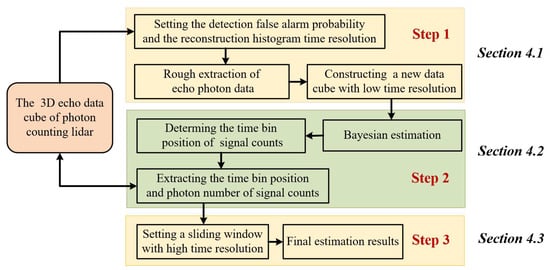
Figure 4.
Framework of our proposed method.
The overall idea of our method is to complete the rough extraction of signal photon counts at a low time resolution scale. Then, based on the obtained photon count data, a sliding window of appropriate width is set to accurately extract the time-of-flight information of each pixel at a high time resolution scale, and the target distance estimation process is realized from coarse to fine. The proposed method includes three main steps. In the first step, the histogram of each pixel is reconstructed by reducing the time resolution, and the constant false-alarm probability is set to adaptively adjust the signal recognition threshold to complete the rough screening of the data. In the second step, the support point set is introduced, and the Bayesian estimation model is constructed. The prior probability and likelihood probability of the Bayesian model are used to filter and discriminate the time bin position information of signal counts. In the third step, the photon counting data obtained by the above processing are processed by the sliding window method, and the distance information of each pixel can be obtained at a high time resolution scale.
4.1. Construction of the New Cube Data Model
We assume that the image size is , and each pixel is accumulated by M detection cycles. The 3D cube data with time resolution of can be expressed as , where , and represent the q-th time bin of pixel , the photon statistical histogram and the photon counts in the q-th time bin, respectively. Based on the theory discussed in Section 3.2, it can be concluded that the false-alarm probability is related to the noise counts and the signal recognition threshold. When the false-alarm probability is determined, the signal recognition threshold is adjusted adaptively according to the number of noise counts.
Therefore, when we set the acceptable false-alarm probability (), the signal recognition threshold () of each pixel is
where is the noise count rate. The time resolution of the reconstructed histogram can be expressed as , where represents the root mean square pulse width, and is the full width at half maximum of the laser pulse. is the reduction multiple of the time resolution when histogram reconstruction is performed for the first time. represents reduction multiple when the time resolution is continuously reduced for histogram reconstruction, where .
It is assumed that the reconstruction time resolution of the photon statistical histogram is , and that the total number of time bins in the detection period () is . Based on this, we can obtain the reconstructed 3D echo data () with time resolution () by performing histogram reconstruction on each pixel. Then, we can extract the photon counts (), which are higher than the signal recognition threshold (). The corresponding time bin position () in the reconstructed 3D echo data () of pixel can also be obtained, where .
The specific process of setting a constant false-alarm probability to extract the signal photon cluster is shown in Figure 5.
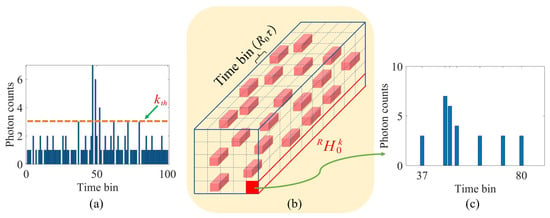
Figure 5.
Photon counting data extraction process under constant false-alarm probability. (a) The reconstructed histogram with a time resolution of . (b) The new cube data with a time resolution of obtained by constant false-alarm detection. (c) Subhistogram of a single pixel in the new cube composed of photon counts higher than the signal recognition threshold ().
Through the above preliminary screening processing, we can obtain the new cube data model (, where ). At this time, the subsequent data to be processed () are considerably reduced compared to the amount of data in . The specific calculation process of the method is shown in Algorithm 1.
| Algorithm 1: Adaptive threshold detection method under a constant false alarm |
| 1: Input , , , M, |
| 2: for |
| 3: for |
| 4: Initialize: |
| 5: compute : |
| 6: update |
| 7: if |
| 8: |
| 9: repeat the above steps |
| 10: end if |
| 11: end for |
| 12: end for |
| 13: |
| 14: Output: |
4.2. Bayesian Screening Process
Based on the new cube data , we introduce the support point set of pixel , which is composed of the photon counts of its eight adjacent pixels. Assuming that , the time bin position and the corresponding photon counts are respectively expressed as and , where , and respectively represent the time bin position and the number of photon counts.
When the support point set is given, the signal photon counts and the time bin position of each pixel can be obtained by using the preset time bin position detection threshold . The overall architecture of the Bayesian estimation is shown in Figure 6.
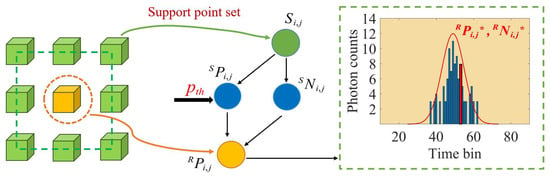
Figure 6.
The overall architecture of the Bayesian estimation method. When the support point set () is known, the preset time bin position detection threshold () is used to determine the position of the time bin where the signal photon cluster is located. Then, it is judged whether the photon counts at this position and the photon data of satisfy the Poisson distribution so as to obtain the time bin position () and the corresponding photon number () of pixel that satisfy the Bayesian model.
The the Bayesian model is mainly constructed to extract the time bin position with the most photon counts of each pixel. The time bin position of the signal photon cluster can be estimated in the Bayesian model, that is
where and are the prior distribution and likelihood probability, respectively. The denominator () is independent of the estimated value of , so it is ignored here.
The actual depths of pixel and its support point set are usually in a limited depth interval. Therefore, the time-of-flight information corresponding to these depth values is also within a limited range. Based on this feature, we assume that the prior probability of the time positions to be solved obeys the Gaussian distribution
where is the time bin position detection threshold, the specific selection rules of which are introduced in Section 5.2.
We accumulate the time bin position () of the echo photon data in the support point set () into the same coordinate system and define the time bin position with the most occurrences as the Gaussian distribution mean, as shown in Figure 7.
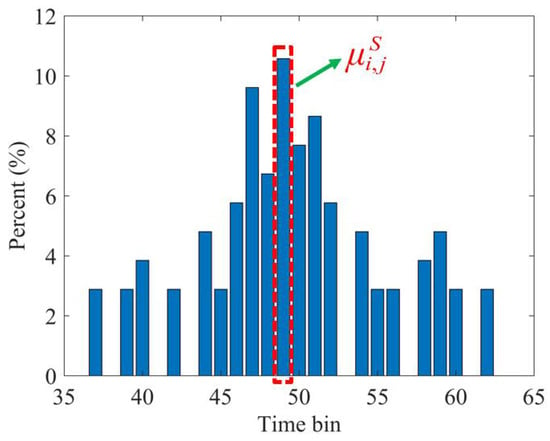
Figure 7.
The selection diagram of the Gaussian distribution mean (). The time bin position () of the echo photon data in the support point set () is accumulated into the same coordinate system, and the time bin position with the most occurrences is selected as the Gaussian distribution mean. The horizontal axis represents the position of the time bin, and the vertical axis represents the proportion of the position of each time bin.
Thus, the preliminary estimation of the position of the time bin where the signal photon cluster is located can be expressed as
Next, we need to solve the likelihood probability. The echo signal received by photon counting LiDAR is usually very weak. The generation of signal photon counts can be approximated to satisfy the Poisson random process. Therefore, we describe the likelihood probability as Poisson distribution
where is the mean value of the Poisson distribution of the support point set’s photon counts, and represents the number of photon counts corresponding to , where . A discriminant diagram of the Poisson distribution is shown in Figure 8.
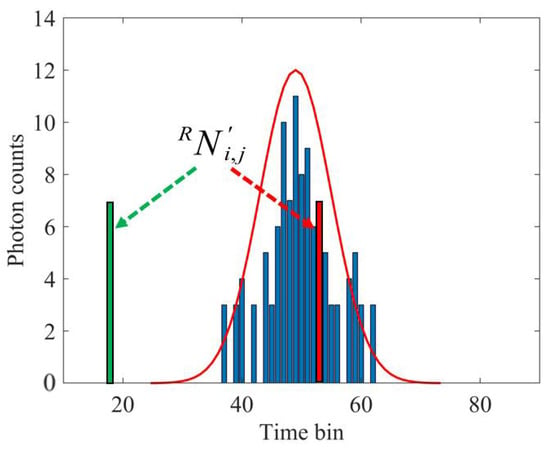
Figure 8.
Discriminant diagram of the Poisson distribution to judge whether the photon number () corresponding to the result obtained under the prior condition and the photon number () in the support point set () satisfy the Poisson distribution. The distribution of the photon counts that conform (green) and do not conform (red) to Poisson distribution in the histogram is shown.
Through the Bayesian screening process, we can estimate the time bin position and the number of signal photon counts:
The specific process is shown in Algorithm 2.
| Algorithm 2: Signal photon cluster extraction method based on the Bayesian model |
| 1: Input , , ,, |
| 2: Bayesian model: |
| 3: for |
| 4: for |
| 5: if |
| 6: |
| 7: update |
| 8: if |
| 9: update |
| 10: end if |
| 11: else |
| 12: , |
| 13: end if |
| 14: end for |
| 15: end for |
| 16: |
| 17: Output: H |
4.3. Depth Information Estimation
Based on the Bayesian estimation result (), the time bin position of the signal counts is obtained when . Otherwise, the time bin position information is not obtained, and we call these pixels “empty” pixels. It is necessary to construct the support point set of pixel again to find the time interval where the signal counts are located. The extraction of “empty” pixel photon count data and the sliding window diagram are shown in Figure 9.
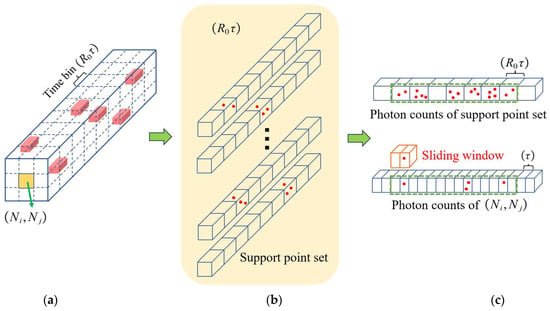
Figure 9.
The extraction of “empty” pixel photon count data and the sliding window diagram. (a) The 3D echo data cube composed of pixel and its 3 × 3 support point set after Bayesian estimation. (b) The number of signal counts of each pixel in the support point set. (c) The time interval of the signal counts in (b) when the time resolution is . We extract the photon count data in this time interval in the 3D echo data cube with a time resolution of and use a sliding window to slide through all the extracted data in turn.
According to the estimated time bin position information, the photon counts at the corresponding position of each pixel are extracted from the original data () with a time resolution of . Then, we use a window of size to slide through the extracted photon count data (, where ). The window position and the number of photons with the largest photon counts are recorded, and the time of flight () of each pixel can be obtained. The depth information can be calculated using the formula so as to reconstruct a 3D image of the target scene.
5. Simulations
5.1. Undulating Terrain Detection
We performed simulations of undulating terrain detection to verify the reconstruction effect of the proposed method. Here, the Monte Carlo method generates echo photon data obeying Poisson distribution. Echo data with different noise intensities are generated by setting different noise fluxes. In the simulation, the detection period is ms, the time resolution is ps, the photon detection efficiency is and the pulse accumulation time is . Based on the simulated data, the average count generated by each laser echo pulse is 0.16, so the photons per pixel (PPP) level are 3.2 when 20 pulses are accumulated.
We chose three kinds of terrain with different undulating degrees as the detection target. The position of the three terrains on the map, the terrain truth depth image and the point cloud map containing noise data are shown in Figure 10.
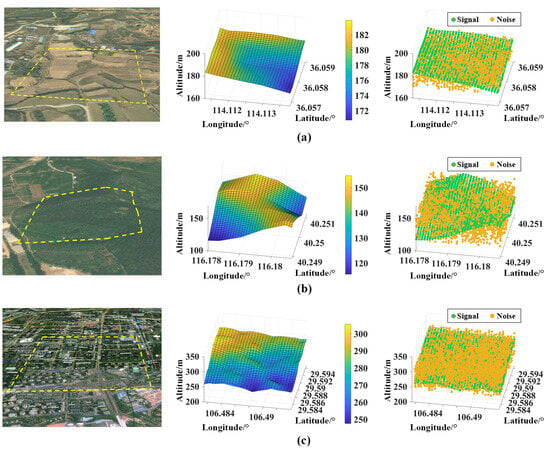
Figure 10.
Undulating terrain detected in three simulation experiments. From left to right: the position of the three terrains on the map, the true value of the depth and the three-dimensional scatter map of the terrain containing noise data. (a) Terrain 1 with a depth variation of 13.3 m. (b) Terrain 2 with a depth variation of 39.2 m. (c) Terrain 3 with a depth variation of 58.1 m.
5.2. Simulation Results
5.2.1. Algorithm Parameters and Evaluation Criteria
We must first determine the time bin position detection threshold used in our method. The specific steps are:
- Combined with the distribution characteristics of photon counts in the time and space dimensions, the data () selected by a constant false-alarm detection are equivalent to a detection period. Figure 11a shows the statistical result of data () in terrain 1. It can be seen that the photon counts show prominent aggregation characteristics within a certain range.
- The photon counts in the interval where the echo data are concentrated are extracted for Gaussian fitting. The results are shown in Figure 11b. It can be observed that the standard deviation of Gaussian fitting of terrain 1 is . Repeating the above steps, the Gaussian fitting results of terrain 2 and terrain 3 are and , respectively. The fitting curves are shown in Figure 11c,d.
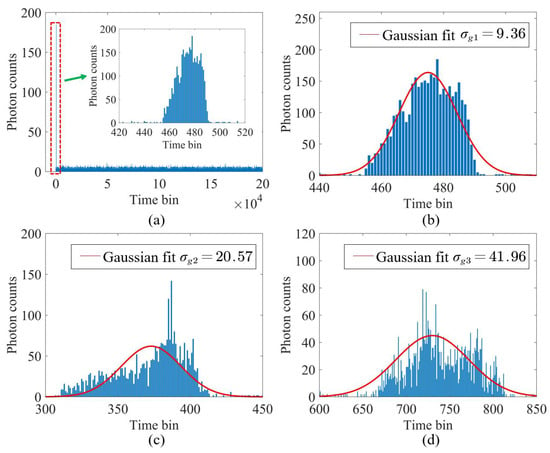
Figure 11.
The results of Gaussian fitting. The data used for Gaussian fitting are the new cube data () of the whole image, with an image size of 30 × 32 and a PPP level of 3.2. (a) Data () of Terrain 1 equivalent to a detection period. (b) Terrain 1 with a depth variation of 13.3 m. (c) Terrain 2 with a depth variation of 39.2 m. (d) Terrain 3 with a depth variation of 58.1 m.
The above Gaussian fitting is based on the data () of the entire detection area. Because the terrain depth information is continuously changing and the support point set only contains the terrain depth information in a small neighborhood, the terrain depth difference in the support point set can be considered to be smaller than the entire target detection area. Therefore, the dispersion of the position distribution of the time bin where the actual depth of each pixel in the support point set is lower than that of the entire image. In the Gaussian distribution, contains a probability of 68.3%. Therefore, we set the time bin position detection thresholds of the three terrains as , and , respectively.
To intuitively evaluate the 3D reconstruction ability of different methods, we use the root mean square error (RMSE) and the signal-to-reconstruction error ratio (SRE) as evaluation criteria []
5.2.2. Results of Undulating Terrain Detection
Current typical research methods of signal photon count adaptive screening using constant false-alarm probability include the Chen algorithm and the Rapp algorithm. The Chen algorithm uses the technique of reconstructing multiscale time resolution histograms to separate signal and noise. The selection of the reconstruction time resolution is usually more significant than the laser pulse width. The Rapp algorithm filters out the photon counts that meet the detection conditions by establishing a superpixel, and its data calculation amount is usually significant. In order to verify the reconstruction effect of the proposed method, several sets of undulating terrain reconstruction comparison experiments are carried out.
In the simulations, the noise count rates are set to 0.10 Mcps, 0.77 Mcps, 1.41 Mcps and 1.84 Mcps. We quantitatively compare the effects of terrain 3D reconstruction using the Rapp algorithm, the Chen algorithm and our method at different noise count rates. The histogram reconstruction parameter () and the sliding window width ( are used in our method.
The depth variation of undulating terrain 1 is 13.3 m. Figure 12 and Table 2 show the reconstruction results of different methods. The effect of the Chen algorithm is the worst among the three methods. The estimated depth information is more accurate when the noise count rate is lower than 0.77 Mcps. However, the reconstruction performance decreases sharply as the noise intensity increases. Compared with the reconstructed image results of the Rapp algorithm, the estimation results of the proposed method are closer to the undulating state of the actual terrain. The depth information estimated by the Rapp algorithm has fluctuations, and the performance is not as good as that of our method.
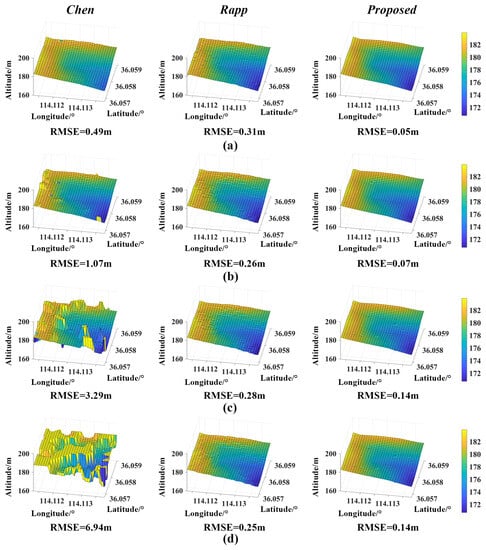
Figure 12.
Reconstruction results of undulating terrain 1. (a) Noise count rate @ 0.10 Mcps. (b) Noise count rate @ 0.77 Mcps. (c) Noise count rate @ 1.41 Mcps. (d) Noise count rate @ 1.84 Mcps.

Table 2.
The RMSE and SRE results of different methods on terrain 1 with a depth variation of 13.3 m.
It can be seen from the reconstruction results of terrain 1 that the depth estimation values obtained by our method are most consistent with the actual values under four noise count rates. The performance of terrain reconstruction using our method is significantly better than the other two methods. When the noise count rate is 0.10 Mcps, the RMSE and SRE obtained by the proposed method are 0.05 m and 71.52 dB, respectively. When the noise count rate increases to 1.84 Mcps, the RMSE increases to 0.14 m, and the SRE decreases to 62.38 dB. From the increment of RMSE and SRE, it can be seen that with the change in noise interference intensity, the proposed method still presents relatively superior terrain depth estimation results and better restores the undulating state of the terrain.
The depth variation of undulating terrain 2 is 39.2 m. Figure 13 and Table 3 show the reconstruction results of different methods. When the noise count rate is between 0.10 Mcps and 1.84 Mcps, the RMSE of terrain reconstruction using our method increases from 0.09 m to 0.28 m, the RMSE of the Rapp algorithm increases from 1.40 m to 2.13 m and the RMSE of the Chen algorithm increases from 1.23 m to 16.89 m. The variation range of the RMSE show that for the depth estimation of undulating terrain 2, the proposed method has a minor estimation error at the same noise count rate, and the effect is more significant.
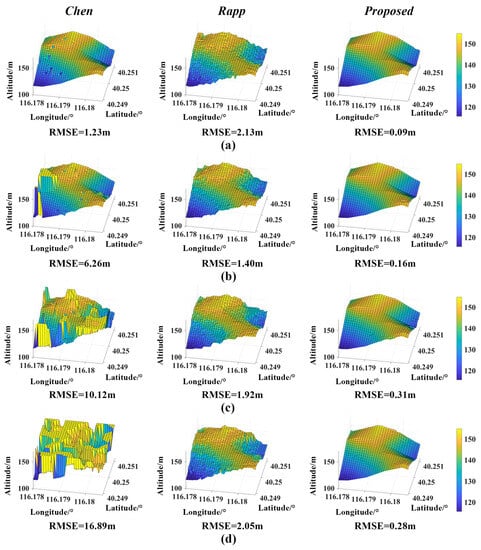
Figure 13.
Reconstruction results of undulating terrain 2. (a) Noise count rate @ 0.10 Mcps. (b) Noise count rate @ 0.77 Mcps. (c) Noise count rate @ 1.41 Mcps. (d) Noise count rate @ 1.84 Mcps.

Table 3.
The RMSE and SRE results of different methods on terrain 2 with a depth variation of 39.2 m.
Under the four noise counting rates, the SREs obtained using the proposed method are 64.23 dB, 59.01 dB, 53.05 dB and 53.82 dB, respectively. Figure 13 show that the 3D undulating terrain image reconstructed by our method is smoother and has a better visual presentation effect. Compared with the reconstruction result of low noise interference (0.10 Mcps), the influence of solid noise interference (1.84 Mcps) is increased. Still, our method and the Rapp algorithm both show acceptable results, and the method proposed in this paper is better. The maximum RMSE obtained by our method is 0.28 m. In comparison, the minimum RMSE of the Rapp algorithm is 1.40 m, which indicates that the method has superior depth information estimation performance for the echo photon data of undulating terrain 2.
The depth variation of undulating terrain 3 is 58.1 m. Figure 14 and Table 4 show the reconstruction results of different methods. The results show that when the noise count rate is higher than 1.41 Mcps, the depth information estimated by the Chen algorithm has a significant error, and almost no reliable information can be obtained. The maximum RMSE of the proposed method is 1 m. Rapp’s RMSE is between 3.26 m and 3.68 m due to the significant estimation error, and the estimation results are not as good as those obtained with our method. The proposed method can better restore the continuous depth fluctuation state of terrain 3.
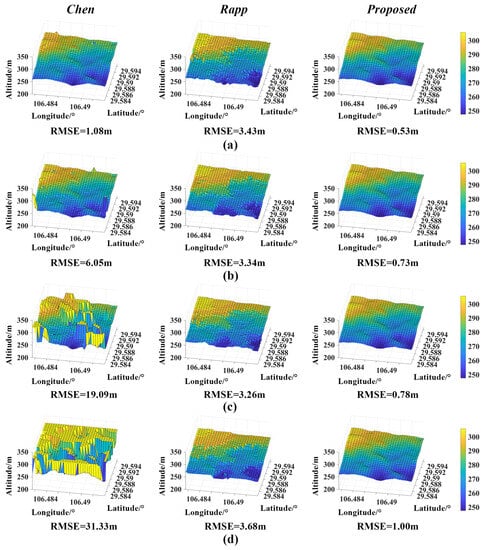
Figure 14.
Reconstruction results of undulating terrain 3. (a) Noise count rate @ 0.10 Mcps. (b) Noise count rate @ 0.77 Mcps. (c) Noise count rate @ 1.41 Mcps. (d) Noise count rate @ 1.84 Mcps.

Table 4.
The RMSE and SRE results of different methods on terrain 3 with a depth variation of 58.1 m.
Under the four noise count rates, the minimum RMSE values of terrain reconstruction using the Chen algorithm, the Rapp algorithm and the proposed method are 1.08 m, 3.43 m and 0.53 m, respectively. The RMSE obtained by the proposed method is at least 50.9% lower than that obtained by the other two methods. The SRE results presented in Table 4 show that the minimum SRE values of terrain reconstruction using the Chen algorithm, the Rapp algorithm and the proposed method are 19.60 dB, 37.54 dB and 48.84 dB, respectively. The proposed method has the best SRE at the same noise count rate. The reconstruction results of undulating terrain 3 further prove the robustness of the proposed method to the echo photon data generated by the target with depth fluctuation.
5.2.3. Summary of Simulation Detection Results of Undulating Terrain
Under different noise count rates, the RMSE and SRE change curves obtained using various methods to reconstruct the three undulating terrains are shown in Figure 15. Figure 15a shows the changing trend of RMSE, and Figure 15b shows the change in SRE. Compared with the Chen algorithm, our method can not only retain as many signal counts as possible but also reduce the interference of noise counts by setting the time resolution of histogram reconstruction in the range of . Therefore, the estimation results of the depth information of the terrain obtained by the proposed method are more consistent with the actual depth information. Compared with the Rapp algorithm, our method uses reconstructed histograms and adaptive signal segmentation technology for rough data extraction. Then, by introducing a support point set, data screening and discrimination are carried out in the Bayesian framework, which not only helps to reduce the amount of calculation but also dramatically improves the accuracy of data discrimination.
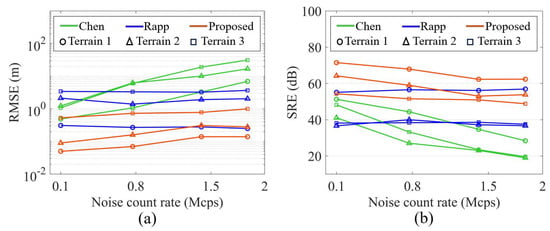
Figure 15.
The simulation results of three undulating terrains using different algorithms under different noise levels. (a) RMSE. (b) SRE.
From Figure 15a, it can be concluded that in the depth estimation of the three undulating terrains, the obtained RMSE values gradually increase as the noise intensity increases. However, the RMSE increment of the proposed method is significantly lower than that of the other two methods and has the slightest estimation error. The variation of undulating terrain depth also affects the quality of reconstruction. When the noise count rate is the same, the RMSE of reconstruction gradually increases with the increase of the variation of the three undulating terrains. Compared with the other two methods, the proposed method has the smallest RMSEs under the same noise interference for different undulating terrains, and the estimation error is within an acceptable range. It can be seen from Figure 15b that the SRE of terrain reconstruction decreases with increased terrain depth fluctuation. The SREs of the proposed method are higher than those of the other two methods at the same noise count rate, with better estimation results.
The proposed method shows promising results in reconstructing three different terrains. The minimum RMSEs for the reconstruction of undulating terrain 1, undulating terrain 2 and undulating terrain 3 are 0.05 m, 0.09 m and 0.53 m, respectively. The corresponding SREs are 71.52 dB, 64.23 dB and 54.32 dB, respectively. Although the reconstruction error of the proposed method gradually increases with the fluctuation of the noise count rate and undulating terrain depth information, it still has the best RMSE and SRE compared with the other two methods. By comparing the simulation results of the three groups of undulating terrain detection, our method has proven effective in 3D reconstructing of targets with depth fluctuation in high-noise scenarios.
6. Experiments
6.1. Experimental System
A schematic diagram and the main parameters of the photon counting LiDAR system are shown in Figure 16 and Table 5 []. In the laser emission unit, the pulse beam passes through the beam splitter (BS), the reflecting mirror (RM), the beam expander (BE) and the 45° perforated reflector (PM); then, it reaches the scanning module. After adjustment of the transmission direction of the laser pulse by the fast steering mirror (FSM) controlled by digital signal processing (DSP), it falls on different positions of the target to form a laser detection dot matrix in the detection area. The echo signal is filtered by a narrow-band filter (NBF) after passing through the FSM, the PM and the optical focusing lens (FL) and is transmitted to the photosensitive surface of the Gm-APD single-photon detector through multimode fiber. After the echo signal is photoelectrically converted, the time-of-flight information of the laser pulse is measured and recorded by the TCSPC module with a time resolution of ps. The distance information corresponding to a certain point of the target can be obtained. A 3D image reflecting the spatial information of the target can be obtained by performing space–time mapping transformation on the distance information of each point. The laser pulse emitted by the visible light laser is used as an indicator laser to facilitate visual observation of laser pointing.
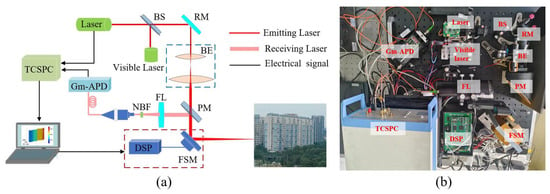
Figure 16.
Experimental setup of our photon counting LiDAR system. (a) Block diagram. (b) Physical image of the experimental device. BS, beam splitter; RM, reflecting mirror; BE, beam expander; PM, 45° perforated reflector; FL, optical focusing lens; NBF, narrow band-pass filter; FSM, fast steering mirror; DSP, digital signal processing; Gm-APD, Geiger mode avalanche photodiode.

Table 5.
Main parameters of the experimental system.
6.2. Building Imaging Results
To verify the performance of the proposed method in a real imaging environment, we carried out outdoor experiments. The wavelength of the pulsed laser is 1064 nm, the repetition frequency is 5.4 kHz and the image size is 60 × 60 pixels. The target scene we selected is an outdoor building, and the area indicated by the yellow dotted box is our detection range, as shown in Figure 17a. The imaging experiments are carried out in a long time mode and a short time mode. The single-pixel scanning dwell times corresponding to the two modes are 1 s and 100 ms, respectively. The aim of the long time mode is to accumulate enough pulse detection times to obtain the true depth image. The short time mode is mainly used to obtain echo photon data containing different noises for subsequent algorithm effect verification. Due to the system’s limited storage memory, the time gate of each pulse is set to 10 s.
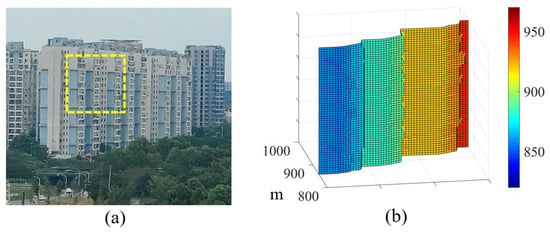
Figure 17.
(a) Image of the building in the visible light band in the range of 850–950 m. (b) Three-dimensional profile corresponding to the selected area shown in (a) (The yellow dashed frame indicates the range of the detection area).
A continuous-wave laser with a wavelength of 1064 nm is used as the noise source to simulate the noise environment of different intensities, and the noise level is changed by adjusting the output power. We use a 1 × 2 multimode fiber coupler with a splitting ratio of 1:99 to transmit the echo optical signal to the photosensitive surface of the Gm-APD, including the optical signal received by the receiving optical system and the noise signal generated by the continuous wave laser. Ports with splitting ratios 99% and 1% are connected to the optical receiving system and continuous wave laser, respectively.
When collecting the echo photon data of the true depth image, the long time mode is set, and the continuous-wave laser is turned off. The outdoor building imaging experiments are carried out at 5 p.m., and the TCSPC module collects data. In the data acquisition experiment of the true depth image, we set the scanning time of each pixel to 1 s, with a pulse accumulation number of each pixel of 5.4 K. At this time, we analyze the data and determine an average count generated by each laser pulse of 0.16. The results show that the number of signal counts generated by a single pulse in the designed outdoor imaging experiments is consistent with the setting in the simulations. Then, we use the peak and median filtering to obtain the building contour depth image, as shown in Figure 17b. Figure 18 shows that the distance of the building is between 850 m and 950 m.
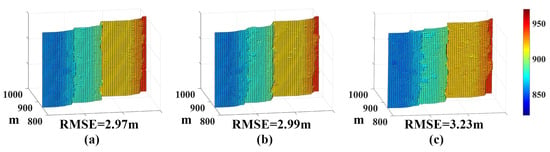
Figure 18.
The building depth estimation results obtained using the proposed method. (a) Noise count rate @ 0.23 Mcps. (b) Noise count rate @ 0.56 Mcps. (c) Noise count rate @ 1.02 Mcps.
We designed three sets of comparative experiments. Different noise environments are simulated by setting three different continuous-wave laser intensities. During the experiments, the intensity of the emitted laser signal of the pulsed laser is kept unchanged, and the short time mode is set. We turn on the continuous-wave laser and adjust its optical power to a lower level. The noise count rate is 0.23 Mcps, and the photon counting echo data generated by the outdoor building are collected. Then, we increase the optical power of the continuous-wave laser to moderate intensity, and the corresponding noise count rate is 0.56 Mcps. We collect the echo photon data of the building imaging. Finally, we continue to increase the optical power of the continuous-wave laser. When the noise count rate is about 1.02 Mcps, the echo photon data of building imaging detection under substantial noise interference is collected. The corresponding SBR levels can be obtained by the formula , which are 0.17, 0.06 and 0.03, respectively.
To be consistent with the PPP level of 3.2 in the simulations, we intercept the echo photon count data of 20 pulse cycles as the dataset for subsequent algorithm performance verification. Then, we use the proposed method to perform 3D imaging at three different noise count rates, where and . The 3D imaging results of the building are shown in Figure 18. At low noise intensity, the surface contour depth of the building reconstructed by the proposed method is relatively smooth. As the noise interference increases, the estimation error of some pixels increases, but it still shows the depth change of the target building, which is represented by different colors.
Furthermore, the Chen and Rapp algorithms are compared with our method. The RMSE and SRE results of the different methods on the outdoor building are shown in Table 6. At the three noise count rates, the RMSEs obtained by the proposed method are 2.97 m, 2.99 m and 3.23 m, and the SREs are 49.60 dB, 49.52 dB and 48.86 dB, respectively. The 3D imaging performance of the proposed method is significantly better than that of the other two methods. Although the imaging effect of our method is reduced in the case of noise interference enhancement, the obtained estimation results are still superior to those obtained with the Chen and Rapp algorithms. The results further reflect the effectiveness of the proposed method in 3D imaging under strong noise, which is consistent with the conclusions obtained in simulation experiments. The results of outdoor building imaging show that when the noise count rate is the same, the RMSE obtained using our method for 3D reconstruction is the lowest, and the SRE is the highest. The proposed method can achieve the best numerical results and the slightest depth estimation error on the echo dataset for long-distance outdoor building imaging.

Table 6.
The RMSE and SRE results of different methods on an outdoor building at a distance of 850–950 m.
7. Discussion
Photon counting LiDAR can achieve high-sensitivity detection at the single-photon level, but the noise counts are not conducive to the high-quality extraction of target information. Reasonable design of the signal processing algorithm is helpful in improving the imaging quality of photon counting LiDAR. However, the reconstruction effect is reduced for detection scenes in which the depth information changes continuously. Based on this, the method proposed in this paper has the following advantages:
- The reconstruction time resolution of the histogram is set within 6 times of the laser’s root mean square pulse width, which helps to filter out noise interference while retaining the signal data as much as possible. A new cube data model is constructed by adaptive threshold segmentation of the reconstructed histogram.
- In the Bayesian model, the position and the number of signal photon counts at the coarse time resolution scale can be extracted accurately by setting the time bin position detection threshold. Then, a sliding window is used to obtain estimation results with high time resolution.
- Based on the new cube data model constructed by adaptive threshold segmentation, it is helpful to introduce other advanced image algorithms to optimize the data filtering process.
- The amount of echo photon data of photon counting LiDAR is usually tremendous, and the extraction of signal counting requires a lot of computing resources. The proposed method shows a coarse-to-fine depth estimation process, which not only dramatically reduces the amount of subsequent data calculation through data preprocessing but also helps to improve imaging accuracy in actual detection. In view of the practical application requirements of existing photon counting LiDAR imaging technology, we plan to apply the proposed method to the data processing of airborne topographic surveys, urban digital 3D map drawing and glacier detection in future work.
Undulating terrain simulation and outdoor experiments show that our method achieves better results than the other tested methods. At the same time, our ideas can still be further optimized; the primary deficiencies are as follows:
- The time bin position detection threshold was selected from the global optimization perspective, which affects the data screening results. In the future, we will optimize the threshold selection process from the local echo data to obtain better performance.
- In actual detection, multiple surfaces with different depths may exist in a pixel. This factor is not considered in this paper. Multiple-surface recognition is a problem that needs to be solved in future work.
8. Conclusions
In this paper, the time–space characteristics of the photon counts are deeply analyzed, and a method for 3D undulating terrain depth estimation based on the Bayesian model is proposed. This method completes the adaptive coarse screening of photon counts by setting a constant false-alarm probability, which significantly reduces the complexity of subsequent processing. This rough screening method is also applicable in fluctuating noise environments. The Bayesian model is constructed to extract the position and number of signal photon counts, and depth estimation from coarse to fine is realized using a sliding window. We carried out sufficient simulations and outdoor target imaging experiments. The results show that the proposed method has a better effect and is superior to typical existing methods for 3D imaging of the target (long-distance building) with continuous change of depth information. The proposed method can achieve high-sensitivity and high-precision detection of the target under low false-alarm probability and is suitable for 3D imaging of the target with continuous change of depth information under intense noise interference. On this basis, future work will study the realization of 3D imaging of targets under substantial noise interference at lower signal photon counts and further improve the performance of the proposed method.
Author Contributions
Conceptualization, R.W., H.Y. and B.L.; methodology, R.W.; software, R.W.; validation, Z.C. and B.L.; formal analysis, R.W.; investigation, R.W.; resources, R.W.; data curation, R.W. and Z.L.; writing—original draft preparation, R.W.; writing—review and editing, R.W., H.Y., Z.C. and B.L.; visualization, R.W. and Z.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data underlying the results presented in this paper will be made available upon reasonable request.
Acknowledgments
The authors would like to thank the anonymous reviewers for their helpful advice.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krichel, N.J.; McCarthy, A.; Rech, I.; Ghioni, M.; Gulinatti, A.; Buller, G.S. Cumulative data acquisition in comparative photon-counting three-dimensional imaging. J. Mod. Opt. 2011, 58, 244–256. [Google Scholar] [CrossRef]
- Gariepy, G.; Krstajic, N.; Henderson, R.; Li, C.; Faccio, D. Single-photon sensitive light-in-flight imaging. Nat. Commun. 2015, 6, 6021. [Google Scholar] [CrossRef] [PubMed]
- Laurenzis, M. Single photon range, intensity and photon flux imaging with kilohertz frame rate and high dynamic range. Opt. Express 2019, 27, 38391–38403. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; McCarthy, A.; Ren, X.; Warburton, R.E.; Wallace, A.M.; Moffat, J.; Petillot, Y.; Buller, G.S. Underwater depth imaging using time-correlated single-photon counting. Opt. Express 2015, 23, 33911–33926. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Kong, W.; Huang, G.; Hou, J.; Jia, S.; Chen, T.; Shu, R. Design and Demonstration of a Novel Long-Range Photon-Counting 3D Imaging LiDAR with 32 × 32 Transceivers. Remote Sens. 2022, 14, 2851. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, B.; Wang, R.; Li, Z.; Chen, Z.; Zhao, B.; Guo, G.; Fan, W.; Huang, F.; Yang, Y. Photon counting lidar working in daylight. Opt. Laser Technol. 2023, 163, 109374. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Y.; Chen, Z.; Han, W. True random coded photon counting Lidar. Opto-Electron. Adv. 2020, 3, 190044. [Google Scholar] [CrossRef]
- Degnan, J.J. Scanning, Multibeam, Single Photon Lidars for Rapid, Large Scale, High Resolution, Topographic and Bathymetric Mapping. Remote Sens. 2016, 8, 958. [Google Scholar] [CrossRef]
- Rapp, J.; Tachella, J.; Altmann, Y.; McLaughlin, S.; Goyal, V.K. Advances in Single-Photon Lidar for Autonomous Vehicles: Working Principles, Challenges, and Recent Advances. IEEE Signal Process. Mag. 2020, 37, 62–71. [Google Scholar] [CrossRef]
- Gatt, P.; Johnson, S.; Nichols, T. Geiger-mode avalanche photodiode ladar receiver performance characteristics and detection statistics. Appl. Opt. 2009, 48, 3261–3276. [Google Scholar] [CrossRef]
- Simple approach to predict APD/PMT lidar detector performance under sky background using dimensionless parametrization. Opt. Laser Eng. 2006, 44, 779–796. [CrossRef]
- Pawlikowska, A.M.; Halimi, A.; Lamb, R.A.; Buller, G.S. Single-photon three-dimensional imaging at up to 10 kilometers range. Opt. Express 2017, 25, 11919–11931. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.P.; Ye, J.T.; Huang, X.; Jiang, P.Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.Z.; et al. Single-photon imaging over 200 km. Optica 2021, 8, 344–349. [Google Scholar] [CrossRef]
- Kang, Y.; Li, L.; Liu, D.; Li, D.; Zhang, T.; Zhao, W. Fast Long-Range Photon Counting Depth Imaging with Sparse Single-Photon Data. IEEE Photonics J. 2018, 10, 1–10. [Google Scholar] [CrossRef]
- Chang, J.; Li, J.; Chen, K.; Liu, S.; Wang, Y.; Zhong, K.; Xu, D.; Yao, J. Dithered Depth Imaging for Single-Photon Lidar at Kilometer Distances. Remote Sens. 2022, 14, 5304. [Google Scholar] [CrossRef]
- Hernandez-Marin, S.; Wallace, A.M.; Gibson, G.J. Bayesian Analysis of Lidar Signals with Multiple Returns. IEEE T. Pattern. Anal. 2007, 29, 2170–2180. [Google Scholar] [CrossRef]
- Gan, Y.; Cong, X.; Yang, Y. Structure-aware interrupted SAR imaging method for change detection. IEEE Access 2019, 7, 136391–136398. [Google Scholar] [CrossRef]
- Qu, Y.; Zhang, Y.; Xue, H. Retrieval of 30-m-resolution leaf area index from China HJ-1 CCD data and MODIS products through a dynamic Bayesian network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 222–228. [Google Scholar] [CrossRef]
- Riutort-Mayol, G.; Gomez-Rubio, V.; Marques-Mateu, A.; Lerma, J.L.; Lopez-Quilez, A. Bayesian multilevel random-effects model for estimating noise in image sensors. IET Image Process. 2020, 14, 2737–2745. [Google Scholar] [CrossRef]
- Harpsoe, K.B.W.; Andersen, M.I.; Kjaegaard, P. Bayesian photon counting with electron-multiplying charge coupled devices (EMCCDs). Astron. Astrophys. 2012, 537, A50. [Google Scholar] [CrossRef]
- Halimi, A.; Maccarone, A.; A. Lamb, R.; S. Buller, G.; McLaughlin, S. Robust and guided Bayesian reconstruction of single-photon 3D lidar data: Application to multispectral and underwater imaging. IEEE Trans. Comput. Imaging 2021, 7, 961–974. [Google Scholar] [CrossRef]
- Tachella, J.; Altmann, Y.; Ren, X.; McCarthy, A.; Buller, G.S.; McLaughlin, S.; Tourneret, J.Y. Bayesian 3D reconstruction of complex scenes from single-photon lidar Data. SIAM J. Imaging Sci. 2019, 12, 521–550. [Google Scholar] [CrossRef]
- Altmann, Y.; Ren, X.; McCarthy, A.; Buller, G.S.; McLaughlin, S. Robust Bayesian target detection algorithm for depth imaging from sparse single-photon data. IEEE Trans. Comput. Imaging 2016, 2, 456–467. [Google Scholar] [CrossRef]
- Yang, Y.; Cong, X.; Long, K.; Luo, Y.; Xie, W.; Wan, Q. MRF model-based joint interrupted SAR imaging and coherent change detection via variational Bayesian inference. Signal Process. 2018, 151, 144–154. [Google Scholar] [CrossRef]
- Ravindran, R.; Santora, M.J.; Jamali, M.M. Camera, LiDAR, and Radar Sensor Fusion Based on Bayesian Neural Network (CLR-BNN). IEEE Sens. J. 2022, 22, 6964–6974. [Google Scholar] [CrossRef]
- Chen, G.; Wiede, C.; Kokozinski, R. Data Processing Approaches on SPAD-Based d-TOF LiDAR Systems: A Review. IEEE Sens. J 2021, 21, 5656–5667. [Google Scholar] [CrossRef]
- Songmao, C.; Wei, H.; Xiuqin, S.; Zhenyang, Z.; Weihao, X. Research Progress on Photon Counting Imaging Algorithms. Laser Optoelectron. 2021, 58, 1811010. [Google Scholar]
- Tachella, J.; Altmann, Y.; Mellado, N.; Mccarthy, A.; Mclaughlin, S. Real-time 3D reconstruction from single-photon lidar data using plug-and-play point cloud denoisers. Nat. Commun. 2019, 10, 4984. [Google Scholar] [CrossRef]
- Zhang, C.; Lindner, S.; Antolović, I.M.; Mata Pavia, J.; Wolf, M.; Charbon, E. A 30-frames/s, 252 × 144 SPAD Flash LiDAR with 1728 Dual-Clock 48.8-ps TDCs, and Pixel-Wise Integrated Histogramming. IEEE J. Solid-State Circuits 2019, 54, 1137–1151. [Google Scholar] [CrossRef]
- Nguyen, K.Q.K.; Fisher, E.M.D.; Walton, A.J.; Underwood, I. An experimentally verified model for estimating the distance resolution capability of direct time of flight 3D optical imaging systems. Meas. Sci. Technol. 2013, 24, 125001. [Google Scholar] [CrossRef]
- McCarthy, A.; Ren, X.; Frera, A.D.; Gemmell, N.R.; Krichel, N.J.; Scarcella, C.; Ruggeri, A.; Tosi, A.; Buller, G.S. Kilometer-range depth imaging at 1550 nm wavelength using an InGaAs/InP single-photon avalanche diode detector. Opt. Express 2013, 21, 22098–22113. [Google Scholar] [CrossRef]
- Feng, Z.; He, W.; Fang, J.; Gu, G.; Chen, Q.; Zhang, P.; Chen, Y.; Zhou, B.; Zhou, M. Fast Depth Imaging Denoising with the Temporal Correlation of Photons. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Kirmani, A.; Venkatraman, D.; Shin, D.; Colaço, A.; Wong, F.N.C.; Shapiro, J.H.; Goyal, V.K. First-Photon Imaging. Science 2014, 343, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.; Kirmani, A.; Goyal, V.K.; Shapiro, J.H. Photon-Efficient Computational 3-D and Reflectivity Imaging with Single-Photon Detectors. IEEE Trans. Comput. Imaging 2015, 1, 112–125. [Google Scholar] [CrossRef]
- Rapp, J.; Goyal, V.K. A few photons among many: Unmixing signal and noise for photon-efficient active imaging. IEEE Trans. Comput. Imaging 2017, 3, 445–459. [Google Scholar] [CrossRef]
- Li, Z.P.; Huang, X.; Cao, Y.; Wang, B.; Li, Y.H.; Jin, W.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.Z.; et al. Single-photon computational 3D imaging at 45km. Photonics Res. 2020, 8, 1532–1540. [Google Scholar] [CrossRef]
- Hua, K.; Liu, B.; Chen, Z.; Fang, L.; Wang, H. Efficient and Noise Robust Photon-Counting Imaging with First Signal Photon Unit Method. Photonics 2021, 8, 229. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, B.; Guo, G. Adaptive single photon detection under fluctuating background noise. Opt. Express 2020, 28, 30199–30209. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, B.; Guo, G.; He, C. Single photon imaging with multi-scale time resolution. Opt. Express 2022, 30, 15895–15904. [Google Scholar] [CrossRef]
- Lindell, D.B.; O’Toole, M.; Wetzstein, G. Single-Photon 3D Imaging with Deep Sensor Fusion. ACM Trans. Graph. 2018, 37, 113. [Google Scholar] [CrossRef]
- Peng, J.; Xiong, Z.; Huang, X.; Li, Z.P.; Liu, D.; Xu, F. Photon-Efficient 3D Imaging with A Non-local Neural Network. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; pp. 225–241. [Google Scholar]
- Tan, H.; Peng, J.; Xiong, Z.; Liu, D.; Huang, X.; Li, Z.P.; Hong, Y.; Xu, F. Deep Learning Based Single-Photon 3D Imaging with Multiple Returns. In Proceedings of the 2020 International Conference on 3D Vision (3DV), Virtually, 25–28 November 2020; pp. 1196–1205. [Google Scholar]
- Peng, J.; Xiong, Z.; Tan, H.; Huang, X.; Li, Z.P.; Xu, F. Boosting Photon-Efficient Image Reconstruction With A Unified Deep Neural Network. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 4180–4197. [Google Scholar] [CrossRef] [PubMed]
- Fouche, D.G. Detection and false-alarm probabilities for laser radars that use Geiger-mode detectors. Appl. Opt. 2003, 42, 5388–5398. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Lu, Y.; Li, H.; Mao, T.; Guan, Y.; Zhang, L.; He, W.; Wu, P.; Chen, Q. Intensity-guided depth image estimation in long-range lidar. Opt. Laser Eng. 2022, 155, 107054. [Google Scholar] [CrossRef]
- Li, Z.; Liu, B.; Wang, H.; Yi, H.; Chen, Z. Advancement on target ranging and tracking by single-point photon counting lidar. Opt. Express 2022, 30, 29907–29922. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).