HCM-LMB Filter: Pedestrian Number Estimation with Millimeter-Wave Radar in Closed Spaces
Abstract
:1. Introduction
2. Clutter Model in Closed Space
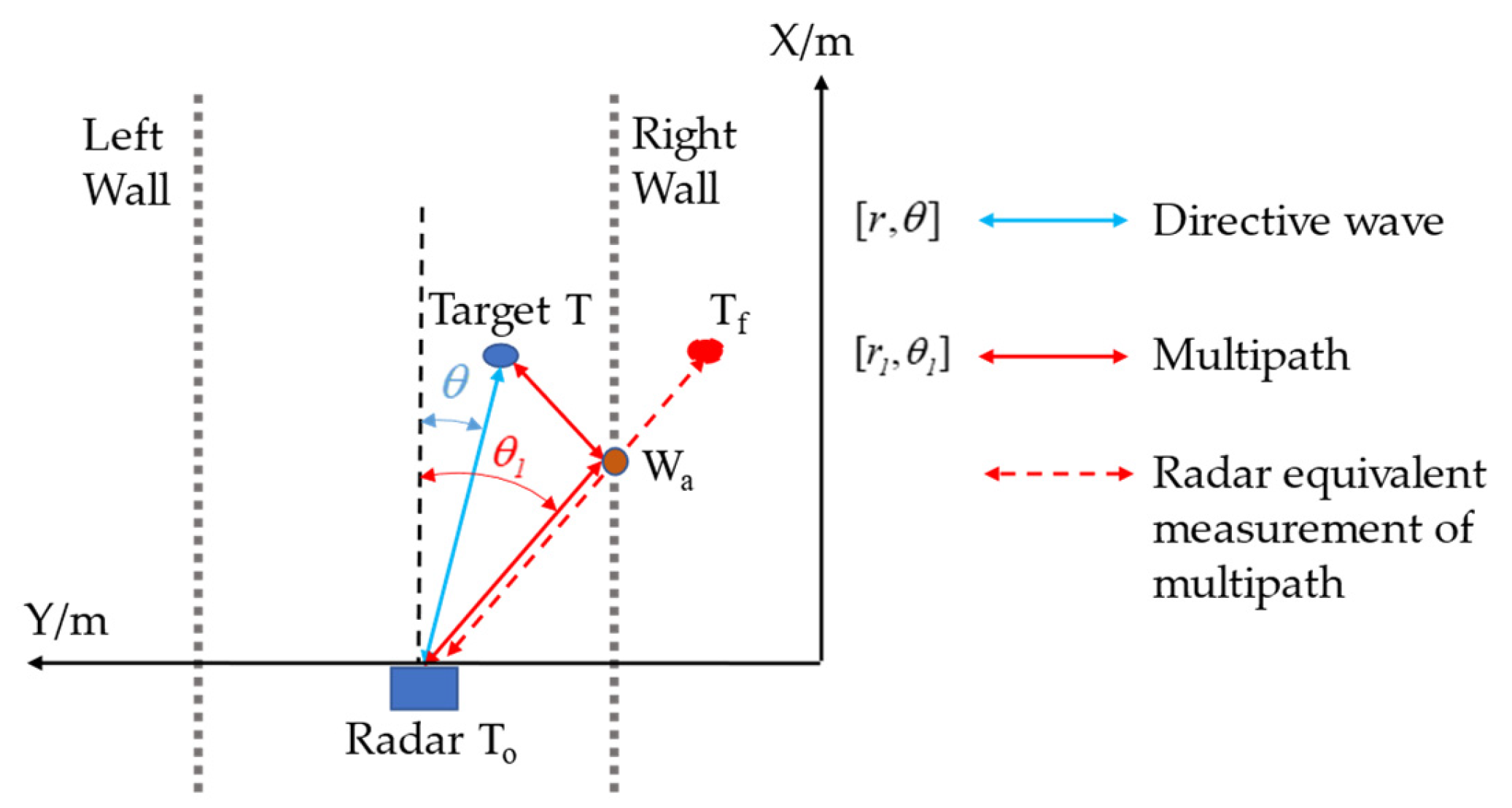
- Static clutter—points with zero velocity in the point cloud data—is generated by the environment or static targets. The Doppler frequency shift of stationary targets is close to zero, while the Doppler frequency shift of moving targets is related to the relative motion speed of the target and the radar, which is generally non-zero. Therefore, in the process of radar point cloud generation, since the relative motion speed between the radar and the wall cladding is zero, the multipath scattering of the wall has a Doppler frequency shift close to zero, which will be directly filtered out by the radar processor, and there is a low probability of generating such multipath point clouds. However, there is relative motion between the pedestrian and the radar, and both direct scattering point clouds and multipath point clouds will be retained by the radar processor.
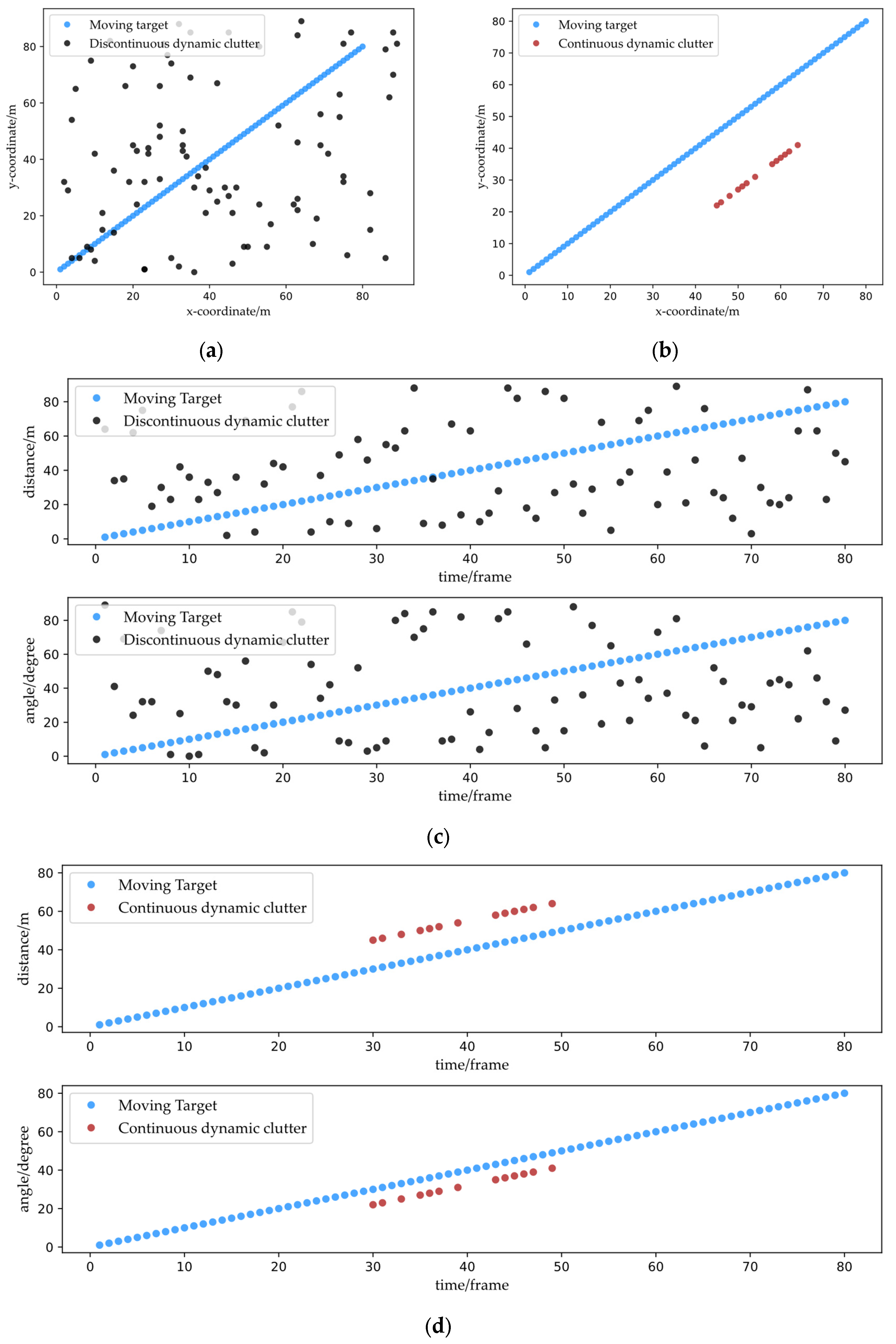
- Non-continuous dynamic clutter (abbreviated as “NCDC” in the following), with non-zero velocity, is generally multipath clutter generated by moving targets or noise generated by random environments. When comparing the spatial distribution of NCDC and moving target observations, NCDC is often distributed more scatteringly and can be regarded as independent of other NCDC or the moving targets. Its sequence also clearly shows discontinuity, making it more challenging to create a continuous sequence characteristic. Figure 1a,b, respectively, depict the simulation diagrams of the spatial and the spatial–temporal distributions of NCDC and moving target observations.
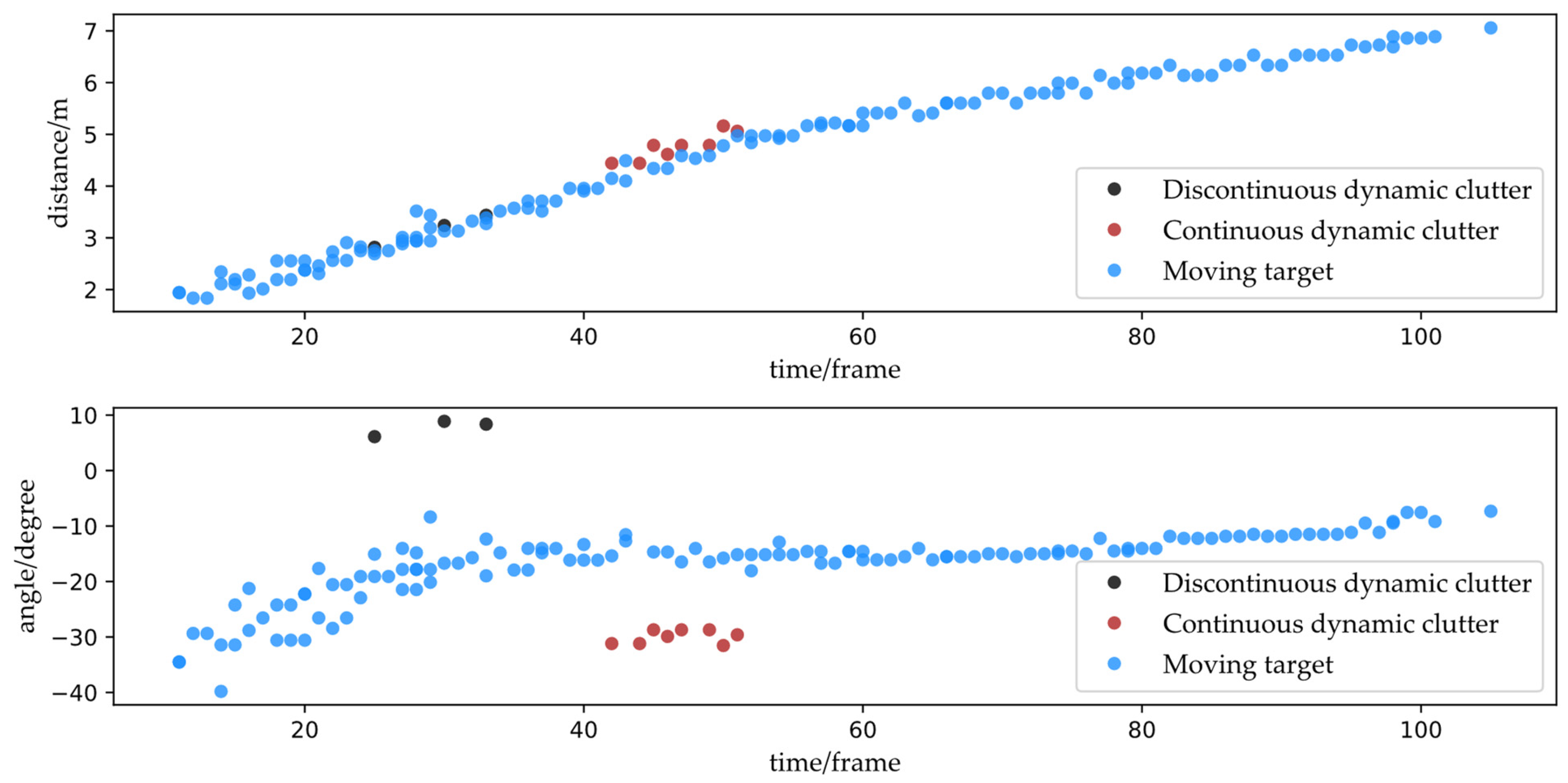
- Continuous dynamic clutter, caused by radar indoor multipath scattering (abbreviated as “CDC” in the following) with non-zero velocity, are points generated from a moving target by multipath wave. A moving target usually generates at most one CDC point in a frame, which may be because the power of the multipath wave is significantly lower than that of the direct wave power, so it is difficult to observe higher-order multipath scattering detected through the constant false-alarm rate (CFAR) detection of the radar. Although the CDC sequence shows a shorter duration and is sparser than the moving target sequence, it nevertheless displays continuity and similarity to the trajectory detected by the direct wave from the same moving target. Figure 1c,d show the simulation diagrams of the spatial–temporal distribution of the CDC and the moving target observations, respectively.
- CDC’s distance is related to the geometry of the moving target and the reflection point, and the value is greater than the direct wave observation related to it.
- The angle is related to the location of the moving target.
- A moving target does not generate or generates only one CDC passing through the same reflector at the same moment.
3. Influence of Continuous Dynamic Clutter on LMB Filter
3.1. Introduction of Labeled Multi-Bernoulli Filter
3.2. The Impact of Continuous Dynamic Clutter on Prediction of LMB Filter
3.3. The Impact of Continuous Dynamic Clutter on Update of LMB Filter
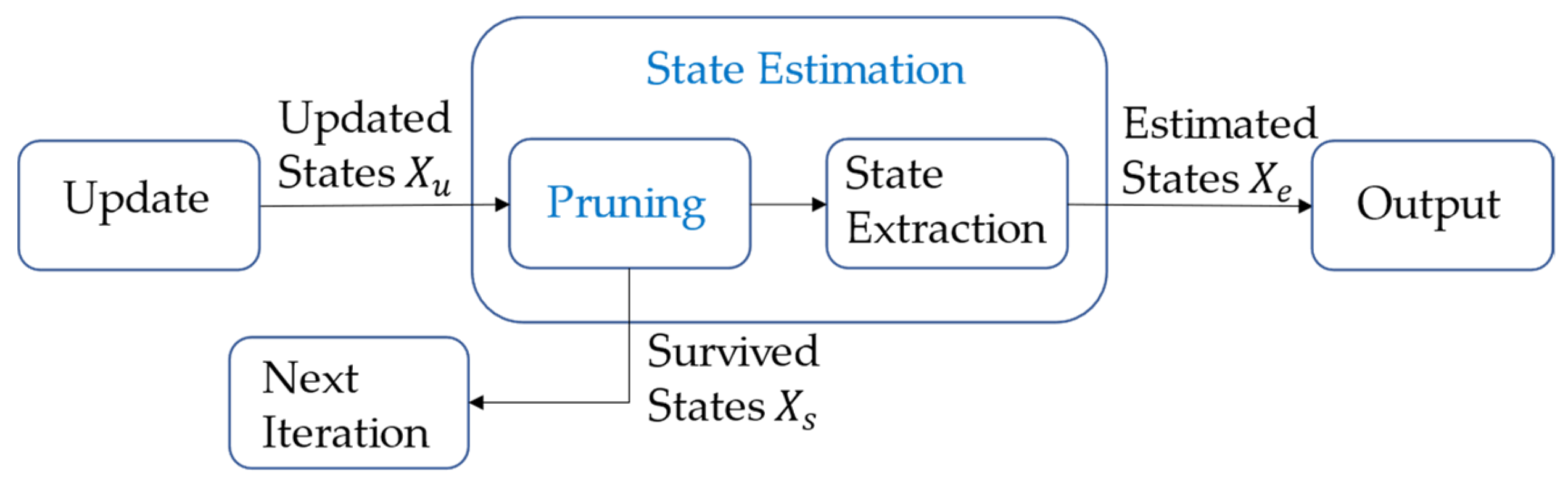
3.4. The Impact of Continuous Dynamic Clutter on State Estimation of LMB Filter
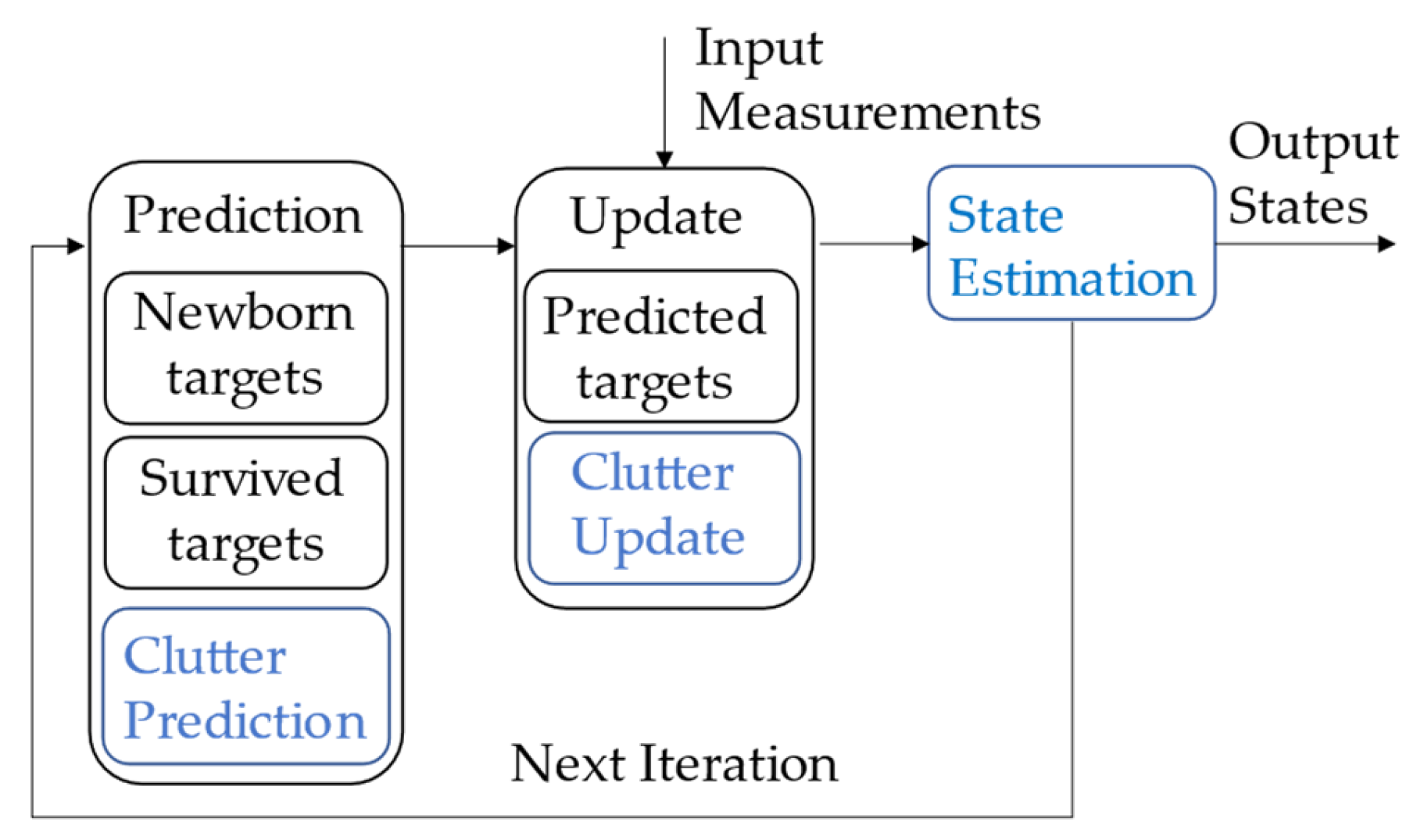
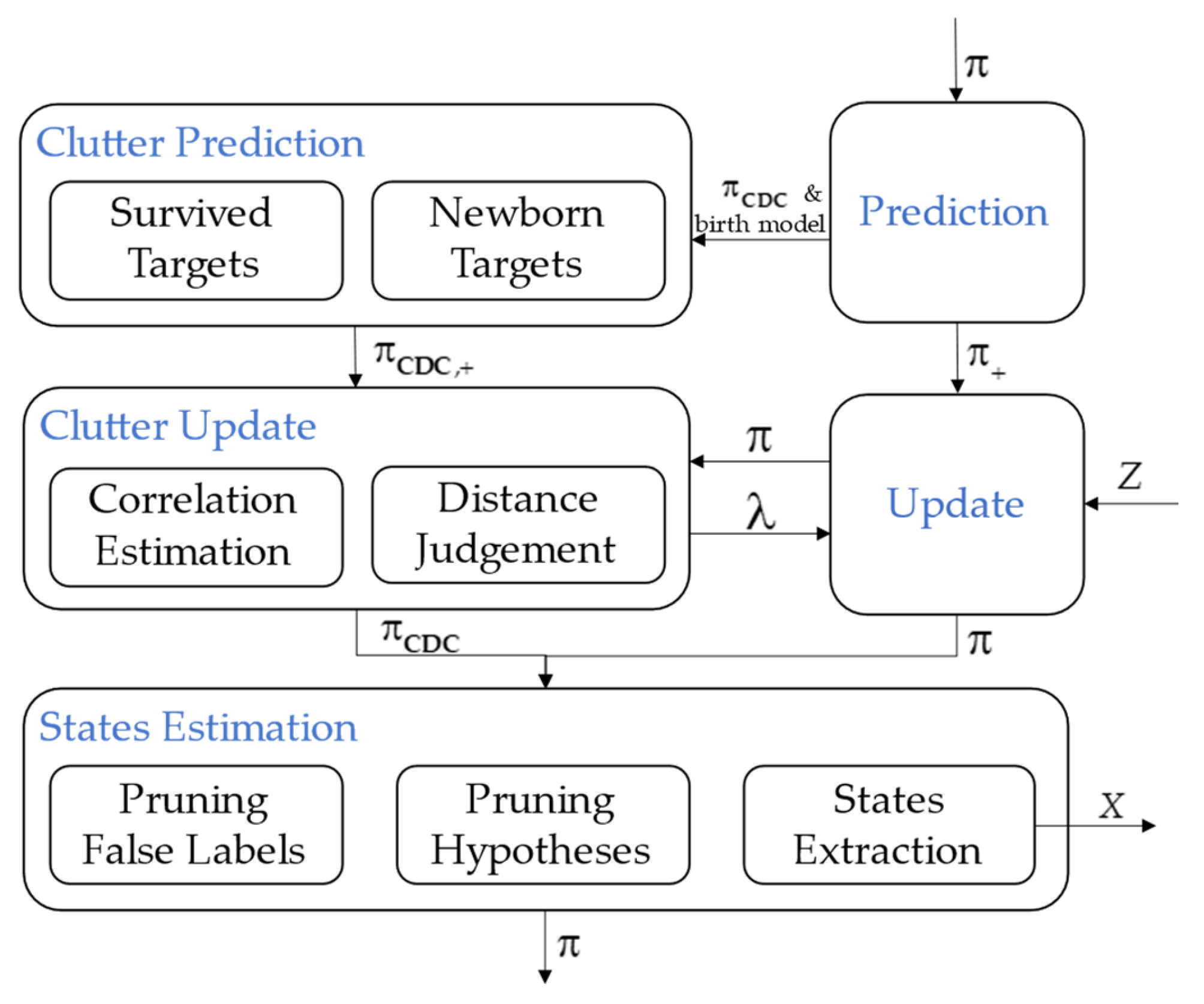
4. Hybrid Clutter Model LMB Filter
- Time-varying: clutter is a Poisson point process, but the intensity is time-varying.
- Continuity: CDC sequences’ detection rates are no higher than their corresponding sequences generated from the same moving targets.
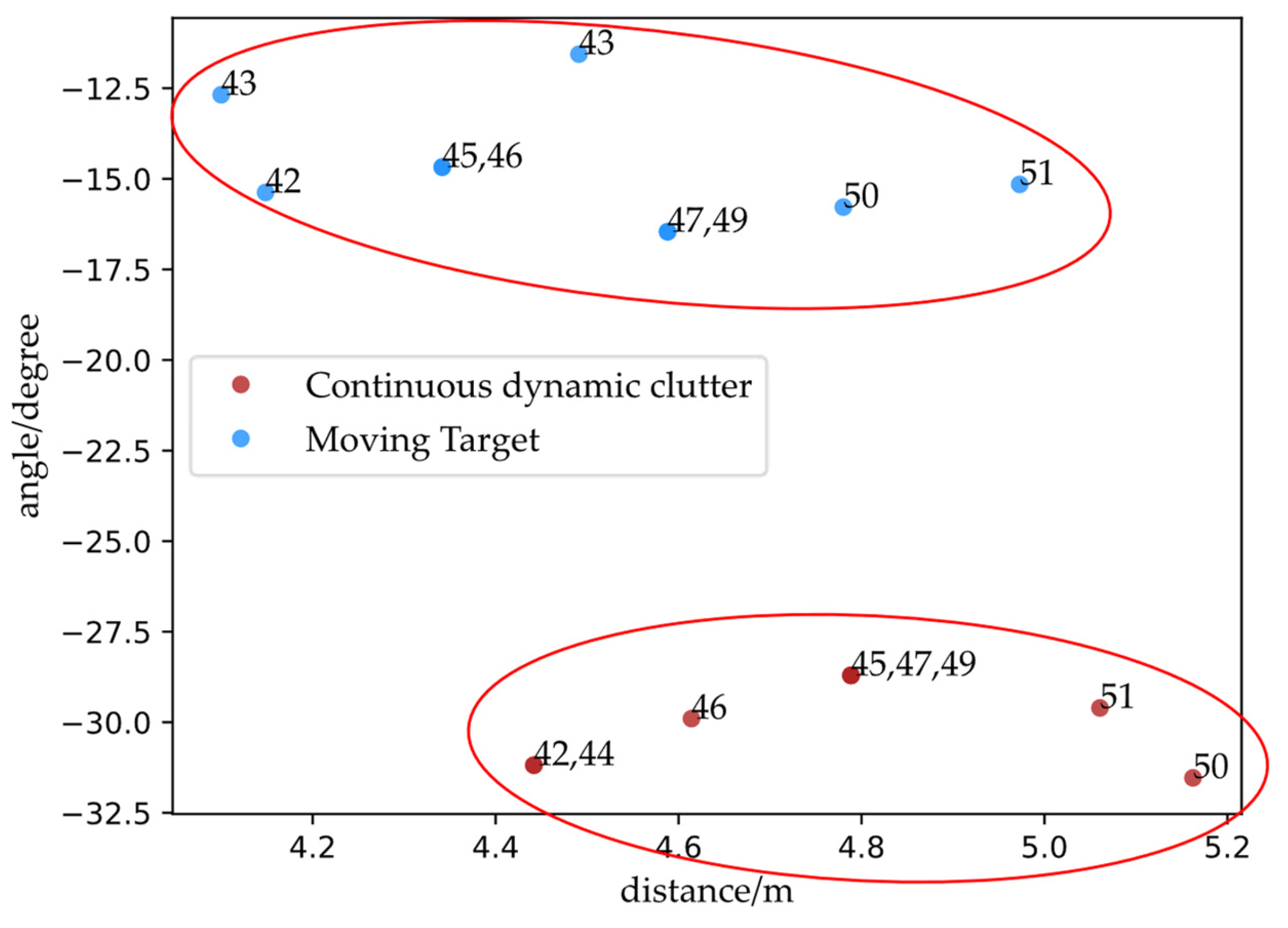
- Correlation: CDC is a clutter that is correlated with the moving target states, but they are independent of each other.
- Spatial distribution characteristics: the distance of CDC is always greater than the distance of its corresponding target state.
4.1. Clutter Prediction
4.2. Clutter Update
4.3. Management of False Labels
5. Experiments and Analysis
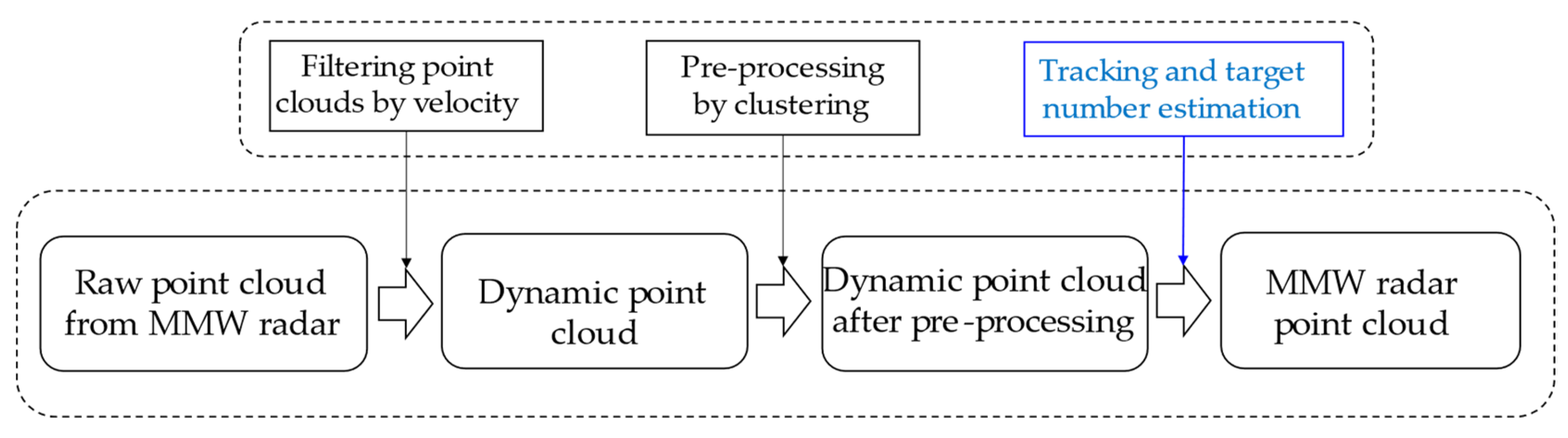
5.1. Experimental Data
5.2. Clutter Characteristics Model Validation with Real Data
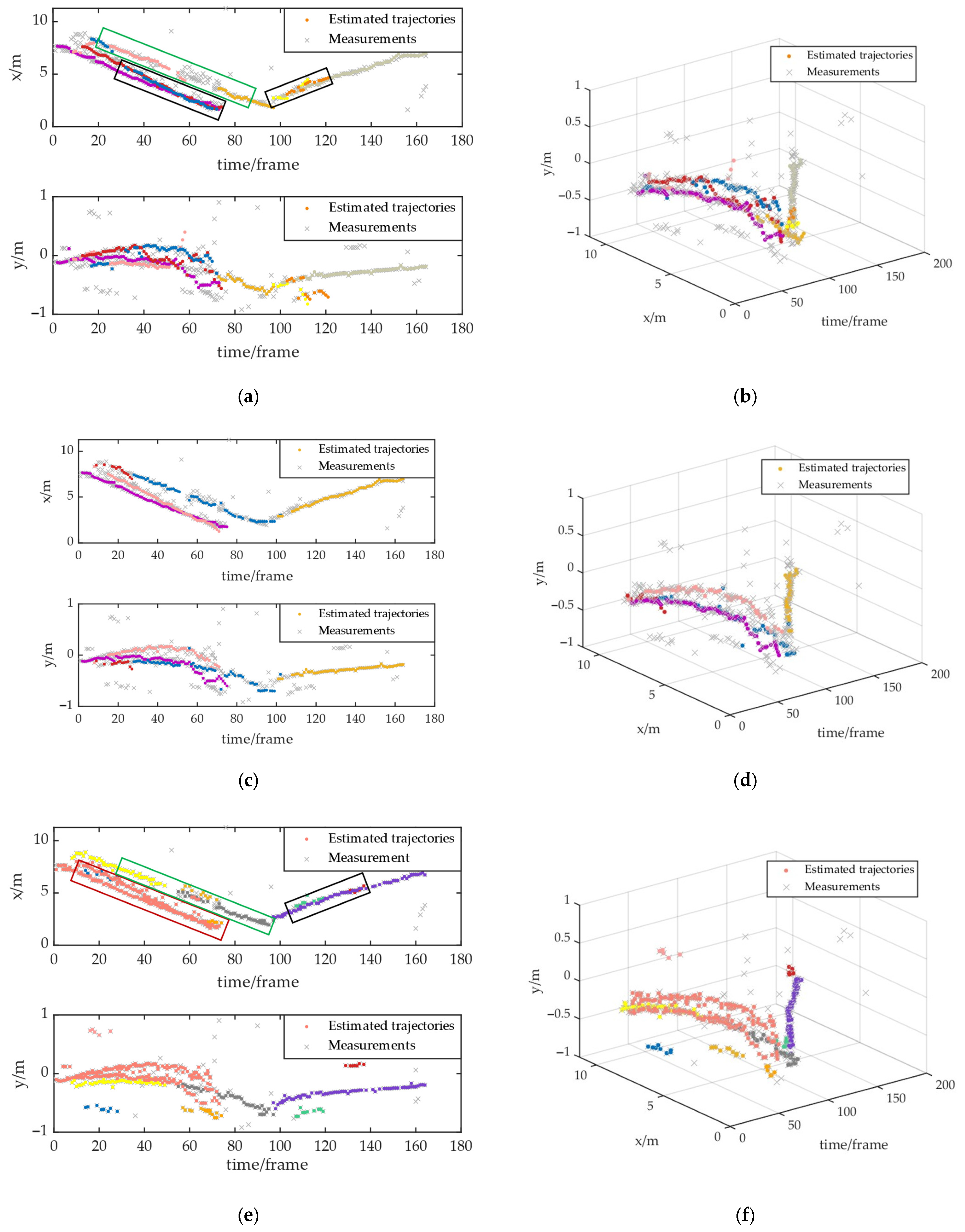
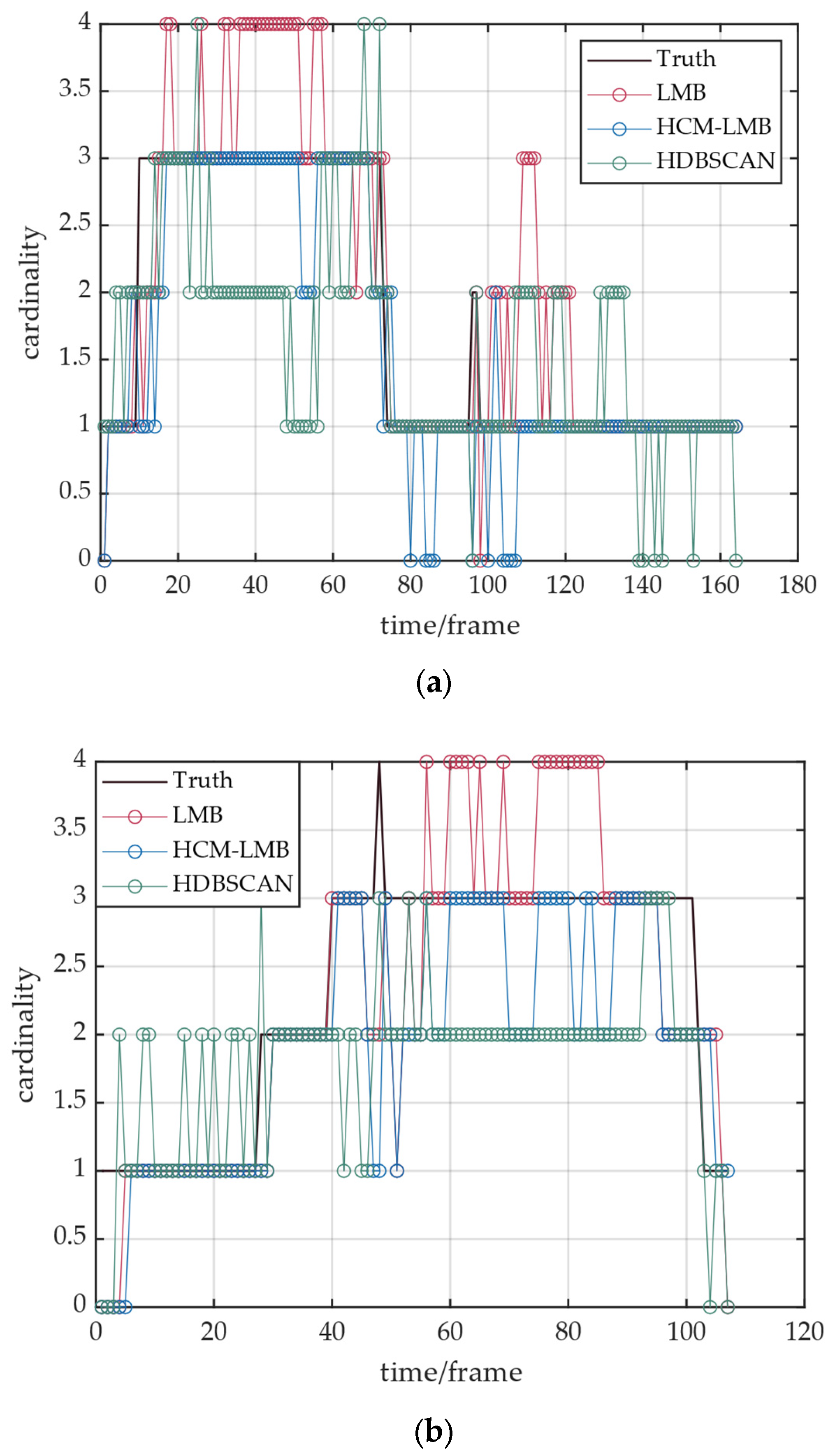
5.3. Performance Evaluation in Pedestrian Counting and Tracking
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, T.; Yang, M.; Jiang, K.; Wong, H.; Yang, D. MMW radar-based technologies in autonomous driving: A review. Sensors 2020, 20, 7283. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Dong, Y.; Hou, F.; Wu, J. Review on Millimeter-Wave Radar and Camera Fusion Technology. Sustainability 2022, 14, 5114. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.; Wang, Y.; Lin, Y.; Shen, W.; Jiang, W. False Detections Revising Algorithm for Millimeter Wave Radar SLAM in Tunnel. Remote Sens. 2023, 15, 277. [Google Scholar] [CrossRef]
- Cook, A.A.; Mısırlı, G.; Fan, Z. Anomaly Detection for IoT Time-Series Data: A Survey. IEEE Internet Things J. 2020, 7, 6481–6494. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. kdd 1996, 96, 34. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large databases. ACM Sigmod Rec. 1996, 25, 103–114. [Google Scholar] [CrossRef]
- Campello, R.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates in Advances in Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172. [Google Scholar]
- Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network Anomaly Detection: Methods, Systems and Tools. IEEE Commun. Surv. Tutor. 2014, 16, 303–336. [Google Scholar] [CrossRef]
- Zoubir, A.M.; Koivunen, V.; Chakhchoukh, Y.; Muma, M. Robust estimation in signal processing: A tutorial-style treatment of fundamental concepts. IEEE Signal Process. Mag. 2012, 29, 61–80. [Google Scholar] [CrossRef]
- Ross, S.M. Peirce’s criterion for the elimination of suspect experimental data. J. Eng. Technol. 2003, 20, 38–41. [Google Scholar]
- Blackman, S.S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Boston, MA, USA, 1999. [Google Scholar]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Ocean. Eng. 1983, 8, 173–184. [Google Scholar] [CrossRef]
- Reid, D. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.-N.; Ma, W.-K. The Gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007; Volume 685. [Google Scholar]
- Ristic, B.; Clark, D.; Vo, B.-N.; Vo, B.-T. Adaptive Target Birth Intensity for PHD and CPHD Filters. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1656–1668. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar] [CrossRef]
- Ristic, B.; Vo, B.-T.; Vo, B.-N.; Farina, A. A Tutorial on Bernoulli Filters: Theory, Implementation and Applications. IEEE Trans. Signal Process. 2013, 61, 3406–3430. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N. A random finite set conjugate prior and application to multi-target tracking. In Proceedings of the 2011 Seventh International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Adelaide, SA, Australia, 6–9 December 2011; pp. 431–436. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N. Labeled Random Finite Sets and Multi-Object Conjugate Priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.-N.; Vo, B.-T.; Phung, D. Labeled Random Finite Sets and the Bayes Multi-Target Tracking Filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Vo, B.-N.; Vo, B.-T.; Hoang, H.G. An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.-T.; Vo, B.-N.; Dietmayer, K. Multi-object tracking using labeled multi-Bernoulli random finite sets. In Proceedings of the 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014; pp. 1–8. [Google Scholar]
- Reuter, S.; Vo, B.-T.; Vo, B.-N.; Dietmayer, K. The Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar] [CrossRef]
- Suzuki, K.; Yamano, C.; Ikoma, N. Multiple Target Tracking in Automotive FCM Radar by Multi-Bernoulli Filter with Elimination of Other Targets. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 527–534. [Google Scholar] [CrossRef]
- Fröhle, M.; Granström, K.; Wymeersch, H. Decentralized Poisson Multi-Bernoulli Filtering for Vehicle Tracking. IEEE Access 2020, 8, 126414–126427. [Google Scholar] [CrossRef]
- Ishtiaq, N.; Gostar, A.K.; Bab-Hadiashar, A.; Palmer, J.; Hosseinezhad, R. Interaction-Aware Labeled Multi-Bernoulli Filter with Road Constraints. In Proceedings of the 2022 11th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 21–24 November 2022; pp. 248–254. [Google Scholar] [CrossRef]
- Ishtiaq, N.; Gostar, A.K.; Bab-Hadiashar, A.; Hoseinnezhad, R. Interaction-Aware Labeled Multi-Bernoulli Filter. Available online: https://arxiv.org/abs/2204.08655 (accessed on 19 April 2022).
- Bernardin, K.; Stiefelhagen, R. Evaluating multiple object tracking performance: The clear mot metrics. EURASIP J. Image Video Process. 2008, 2008, 1–10. [Google Scholar] [CrossRef]



| Measuring Performance | Value |
|---|---|
| Data rate | 17 Hz |
| Antenna channels | 4TX/2x6RX |
| Accuracy of distance measurement | 0.1 m |
| Distance range | 0.20 m to 250 m |
| Accuracy of azimuth angle | 0.1° |
| Range of azimuth angle | −60° to 60° |
| Sequence | Detection Probability, | Range–Angle Correlation Coefficient, | Time–Range Correlation Coefficient, | Time–Angle Correlation Coefficient, |
|---|---|---|---|---|
| Continuous dynamic clutter | 0.800 | 0.158 | 0.898 | 0.245 |
| Moving target 1 | 0.900 | 0.682 | 0.897 | 0.876 |
| Non-continuous dynamic clutter | 0.111 | −0.166 | 0.977 | −0.341 |
| Moving target 2 | 1.000 | 0.691 | 0.976 | 0.762 |
| Scene | Evaluation Indicators | LMB Filter | HCM-LMB Filter | HDBSCAN |
|---|---|---|---|---|
| Scene A | Number bias of pedestrians | 4 | 1 | 7 |
| MOTA | 0.669 | 0.819 | 0.666 | |
| Total cardinality bias | 58 | 37 | 36 | |
| False positives | 47 | 5 | 18 | |
| False negatives | 11 | 32 | 18 | |
| Scene B | Number bias of pedestrians | 1 | 0 | 3 |
| MOTA | 0.812 | 0.829 | 0.518 | |
| Total cardinality bias | 44 | 42 | 72 | |
| False positives | 21 | 2 | 10 | |
| False negatives | 23 | 40 | 62 |
| Evaluation Indicators | LMB Filter | HCM-LMB Filter |
|---|---|---|
| Average number bias of pedestrians | 2.4 | 0.8 |
| MOTA | 0.858 | 0.902 |
| Missed detection rate | 7.6% | 8.6% |
| False-alarm rate | 8.1% | 1.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Y.; Wang, Y.; Lin, Y.; Shen, W.; Jiang, W.; Sun, J. HCM-LMB Filter: Pedestrian Number Estimation with Millimeter-Wave Radar in Closed Spaces. Remote Sens. 2023, 15, 4698. https://doi.org/10.3390/rs15194698
Li Y, Li Y, Wang Y, Lin Y, Shen W, Jiang W, Sun J. HCM-LMB Filter: Pedestrian Number Estimation with Millimeter-Wave Radar in Closed Spaces. Remote Sensing. 2023; 15(19):4698. https://doi.org/10.3390/rs15194698
Chicago/Turabian StyleLi, Yang, You Li, Yanping Wang, Yun Lin, Wenjie Shen, Wen Jiang, and Jinping Sun. 2023. "HCM-LMB Filter: Pedestrian Number Estimation with Millimeter-Wave Radar in Closed Spaces" Remote Sensing 15, no. 19: 4698. https://doi.org/10.3390/rs15194698
APA StyleLi, Y., Li, Y., Wang, Y., Lin, Y., Shen, W., Jiang, W., & Sun, J. (2023). HCM-LMB Filter: Pedestrian Number Estimation with Millimeter-Wave Radar in Closed Spaces. Remote Sensing, 15(19), 4698. https://doi.org/10.3390/rs15194698







