1. Introduction
The state estimation problem has received widespread attention because of its existence in various fields such as target tracking [
1], navigation and positioning [
2], and signal processing [
3]. For target tracking, the state estimation is the most important step in its implementation process. When the maneuvering ability of the target is weak, its motion characteristics can be modeled by using the constant velocity (CV) model [
4] or the constant turn (CT) model [
5]. The Kalman filter (KF) or the extended Kalman filter (EKF) can be used to solve its state estimation problem. The KF is an optimal Bayesian state estimator of the single-model linear system in the Gaussian noise environment [
6,
7,
8], and the EKF is an approximate KF applied to the single-model nonlinear system. Both of these filters assume that the process noise and the measurement noise follow the Gaussian distribution, which means that the estimation performance of both filters will decrease in the non-Gaussian noise environment.
When the target has strong maneuverability, the single model methods have limited estimation ability and the multiple model methods need to be used for state estimation. Unfortunately, the optimal filter for a multiple-model linear system does not exist because the computational process of analytical solutions is very difficult. As a pseudo-Bayesian sub-optimal algorithm, the interactive multiple-model (IMM) filter [
9,
10,
11] is the most frequently used approach to solve the problem of multiple-model state estimation. Similar to the KF and EKF, the classic IMM filter [
9,
10,
11] also models the noise as the Gaussian distribution, which also causes its estimation performance to deteriorate under the non-Gaussian noise.
In practical applications, due to the low cost and instability of the sensor, the measurement is susceptible to outliers, which leads its noise to follow the non-Gaussian distribution. To improve the robustness, some filters based on the variational Bayesian (VB) method are proposed, such as the IMM-VB filter, the Gaussian–Pearson type VII mixture model-based robust VB-KF, and the inverse gamma model and generalized hyperbolic skew Student’s
t model-based VB-KF [
12,
13,
14]. Although the IMM-VB filter can effectively improve the state estimation accuracy of the multiple-model system under a non-Gaussian measurement noise environment, the computational burden is large, and an accurate non-Gaussian noise model needs to be required. Recently, a maximum correntropy criterion (MCC) method [
15] has been widely used to solve the problem of state estimation under outlier interference. Compared with the VB, the MCC has higher computational efficiency and does not need an accurate noise model. To solve the problem of state estimation under outlier interference, the MCC-based KF (MCCKF) [
16], cubature Kalman filter (MCCCKF) [
17], and unscented Kalman filter (MCCUKF) [
18] are successively proposed. Based on these filters, Ref. [
19] proposes an improved MCCCKF, which can adaptively estimate the kernel bandwidth to improve the positioning performance of a cooperative localization system. Ref. [
20] proposes an improved MCCUKF to overcome the problem of numerical instability under large shot noise, and Ref. [
21] proposes a distributed MCCKF to improve estimation performance in the presence of impulsive noise. In addition, a novel MCC-based Rauch–Tung–Striebel smoother [
22] is proposed to solve the state estimation problem under non-Gaussian process and measurement noises. For the maneuvering target tracking, the multiple-model-based filter is currently the mainstream method [
23,
24,
25]. Unfortunately, the above MCC-based filters are designed based on a single model, and they cannot solve the multiple-model state estimation problem under outlier interference. How to design multiple-model filters based on the maximum entropy criterion to improve the state estimation accuracy of maneuvering targets under outlier interference needs to be solved.
Currently, an MCC-based filter, which is called the IMM-MCC filter [
26], is designed based on the multiple model, and this filter can be considered as a combination of the IMM filter and MCCKF. To further improve the state estimation accuracy of a maneuvering target under outlier interference, a weighted MCC-based IMM (WMCC-IMM) filter is proposed. The proposed filter is also designed based on the multiple model. The main contributions of this article are as follows.
- (1)
Different from the IMM-MCC filter, the proposed filter adopts another Gaussian kernel function [
20] to construct the cost function. Based on this Gaussian kernel function, the weighted maximum correntropy criterion is defined, and a new cost function is given.
- (2)
The sub-model state update and state fusion steps are derived under the framework of WMCC, and the previous fusion state is used as the input of each sub-model to simplify the state interaction step.
- (3)
The difference between the IMM-MCC filter and WMCC-IMM filter is discussed, which reveals the superiority of the proposed filter in fusion strategy.
- (4)
To solve the state estimation problem of a maneuvering target in a radar system, the specific steps of the WMCC-IMM filter in radar maneuvering target tracking is given.
- (5)
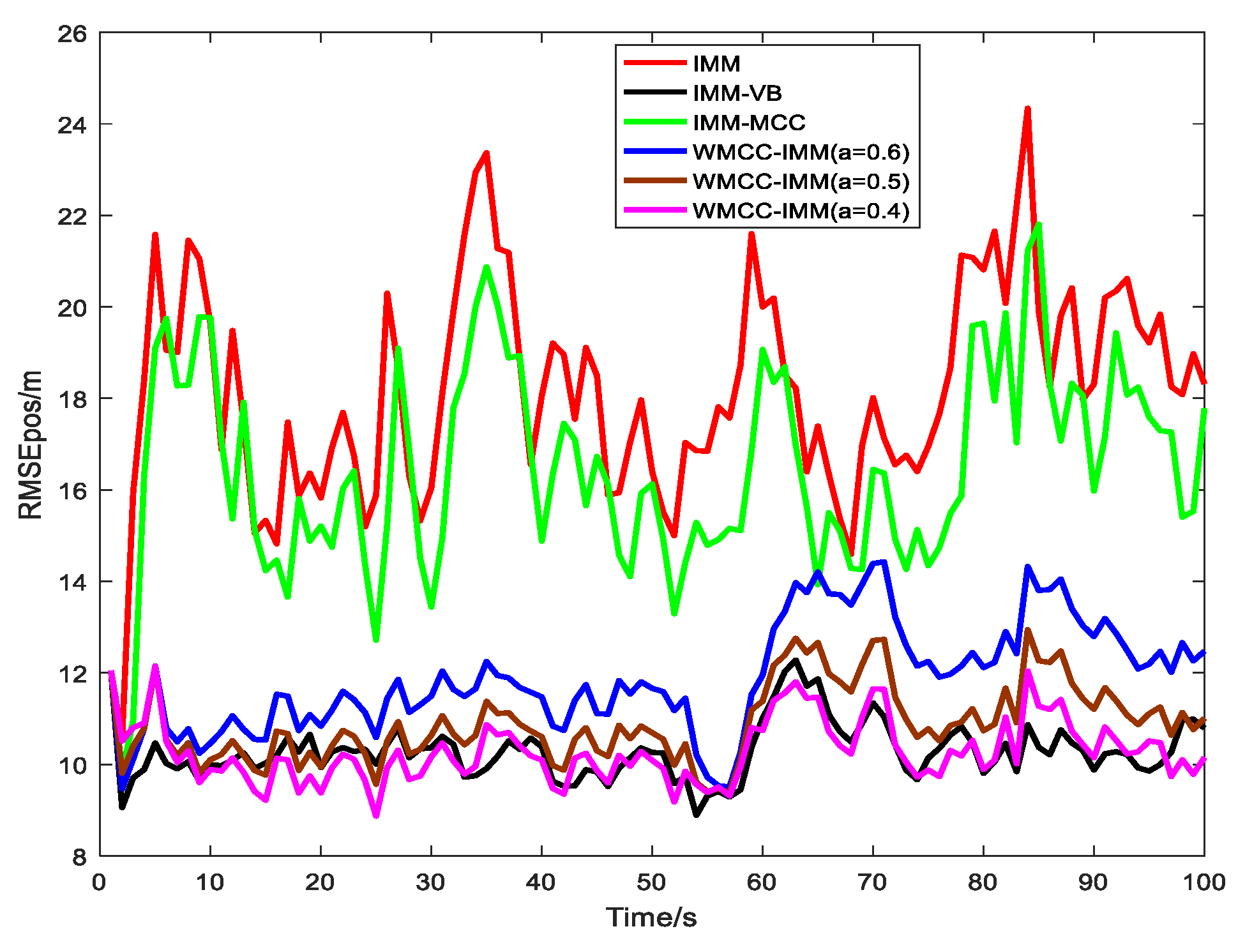
The effectiveness of the WMCC-IMM filter is tested using a set of simulation data and a set of actual test data. Simulation results show that the WMCC-IMM filter has better state estimation performance than the IMM-MCC filter. The great feedback from actual test data indicates that the proposed filter has potential value for practical engineering applications.
The structure of this article is as follows. In
Section 2, the problem under consideration is formulated, and the IMM filter is introduced. In
Section 3, the main results are presented, where the WMCC is defined, the WMCC-IMM filter is derived, the difference between the IMM-MCC filter and WMCC-IMM filter is discussed, and the specific steps of the WMCC-IMM filter in radar maneuvering target tracking is given. In
Section 4, two maneuvering target tracking cases are tested to verify the effectiveness of the WMCC-IMM filter. Lastly, the conclusion is drawn in
Section 5.
2. Problem Formulation
The discrete linear multiple-model system at time
can be represented by the following equations:
where Equations (1) and (2) are the state transition equation and measurement equation, respectively.
and
represent the state vector and measurement vector, respectively.
and
(
) represent the state transition matrix and the measurement matrix of the
i-th sub-model, respectively. It is assumed that the total number of sub-models is
.
and
represent the process noise and the measurement noise, respectively.
and
represent the corresponding nominal covariance matrix, respectively. For the above-mentioned system, the IMM filter can be used to implement the state estimation, and the IMM filter is divided into four steps:
2.1. State Interaction
It is assumed that the mean and covariance of state from the
i-th sub-model at time
are
and
, respectively.
is its weight, and
is the Markov transition matrix. The input state
and covariance
of the
i-th sub-model are formulated as
where
is the total number of sub-models,
is the transfer weight from
j-th sub-model to
i-th sub-model, and
is the Markov transition probability from
j-th sub-model to
i-th sub-model.
2.2. Sub-Model State Update
It is assumed that the state prior information and noises follow the Gaussian distribution. Using the KF to calculate the state posterior information, the state posterior information still follows the Gaussian distribution, and the following five equations can be obtained.
where
and
are the predicted state and covariance of the
i-th sub-model, respectively.
and
are the update state and covariance of the
i-th sub-model, respectively.
is the Kalman gain matrix.
2.3. Model Probability Update
Using the innovation
and covariance
of the
i-th sub-model to calculate the likelihood function
.
,
and
are formulated as
Using
to update the model weight, the model weight
is formulated as
2.4. State Fusion
The weighted fusion method is used to process the state and weight of each sub-model. The fusion state
and covariance
are formulated as
Due to the IMM filter, it is assumed that the process noise and measurement noise both follow the Gaussian distribution. Therefore, when the measurement is disturbed by outliers, the estimation performance of the IMM filter is degraded because of the mismatch of measurement noise modeling. How to design a robust filter to improve the state estimation accuracy of multiple-model systems under outlier interference is the purpose of this article.
3. Main Results
3.1. Weighted Maximum Correntropy Criterion
Due to the fact that the Gaussian kernel function of the IMM-MCC filter [
21] ignores the covariance of uncertain variables, to make full use of statistical information, another Gaussian kernel function [
20] is adopted in this article. Based on this function, the MCC realizes the calculation of uncertain variables by maximizing the following cost function.
where
represents the error vector,
is the kernel bandwidth, and
and
are the mean and covariance of the uncertain variable
.
is the Gaussian kernel function. It can be found from Equation (17) that the cost function of the MCC has the same weight for each Gaussian kernel function. When the system favors a certain set of statistical information, it is a simple and effective way to weigh each Gaussian kernel function to construct the cost function. Because of this, the WMCC is proposed to realize the calculation of
.
where
represents the weight of
, and
. In the state fusion step, the multiple-model system’s degree of dependence on the state statistics information obtained by each sub-model is different. At this time, the WMCC is more flexible than the MCC. Because of this, a novel IMM filter is derived under the framework of the WMCC to solve the multiple-model state estimation problem under outlier interference.
3.2. WMCC-IMM Filter
To improve the robustness of the multiple-model filter under outlier interference, in the initial plan, we intend to improve all four steps of the IMM filter in the framework of the WMCC. However, in the process of derivation, we find that there is reliable state information that can be used as the input of each sub-model in the state interaction step. Compared with using the WMCC to calculate the input of each sub-model, this way can effectively improve the computational efficiency. In addition, uncertain variables are not involved in the model probability update step. Therefore, the proposed WMCC-IMM filter only uses the WMCC in the sub-model state update and state fusion steps. The derivation process of the WMCC-IMM filter is as follows.
3.2.1. State Interaction
When the IMM filter is effective, the fusion state is close to the real state. Because of this, the fusion state can be used as reliable information for each sub-model. Therefore, in the WMCC-IMM filter, we directly use the fusion state as the input of each sub-model. This approach effectively improves the computational efficiency of state interaction because it avoids the calculation of the input of each sub-model. At this time, the input state
is formulated as
where
is the fusion state and covariance at time
. The input covariance
can be calculated by using Equation (4).
3.2.2. Sub-Model State Update
For each sub-model, based on the state transition equation, the predicted state
and covariance
can be calculated. Therefore, the following two sets of Gaussian kernel functions based on the state space system can be obtained.
where
and
are formulated as
where
and
are the useful information of state. Therefore, the Gaussian kernel functions from Equation (21) can be used to calculate the state. In Equation (21),
is an unknown variable, and it will be calculated by using the WMCC.
can be obtained through actual devices, therefore
is known. According to Equations (18) and (21), it can be found that
represents the likelihood of state and predicted information and
represents the likelihood of state and measurement information. It is assumed that the dependence of the sub-model on the state transition and measurement equations is the same. Based on the WMCC, the state update of each sub-model can be realized by maximizing the following cost function.
where
is the weight parameter. Firstly, the partial derivative of
in Equation (23) is considered to obtain the extreme point. The corresponding equation is as follows. In the sub-model state update step, the WMCC is essentially a maximum likelihood estimation method:
Let
, then we have
Using
to approximate
to calculate
and
, it can be found that the number of extreme points is one. Since Equation (23) is continuously differentiable and has the maximum value, the unique solution in Equation (25) is
, and we have
The derivation of
is shown in
Appendix A. According to Equation (26), the state estimation error
is formulated as
According to Equations (26), (27), and (29) and the framework of KF, it can be found that the measurement noise covariance of a sub-model is modified as
, and the estimation error covariance
is formulated as
Remark 1. According to Equations (21)–(30), it can be seen that the WMCC-based filter has the following features:
- (a)
The proposed filter is equivalent to the KF with Gaussian measurement noise covariance . When outlier interference occurs, the measurement usually deviates from the measurement prediction center . At this time, the proposed filter will reduce the trust degree of measurement and increase the measurement noise covariance. This is the main reason why the WMCC-based filter has better robustness than the KF under outlier interference. However, if the prediction center has bad estimation performance, the will be incorrect, which leads to further increase in the estimation error of state. Therefore, before using the WMCC-IMM filter, the target motion characteristics need to be accurately modeled.
- (b)
The different weight parameter means that the proposed filter works in different modes. When , the WMCC-based filter becomes the MCC-based filter. When , the WMCC-based filter only implements the state prediction step. When , the WMCC-based filter only uses the measurement to realize the sub-model state update.
- (c)
In terms of parameter setting, since is still less than 1 when the measurement is not disturbed by outliers, a value slightly less than 0.5 can be assigned to to compensate for the measurement noise covariance.
3.2.3. Model probability update
The model probability update step of the WMCC-IMM filter is similar to that of the IMM filter; the only difference is that the innovation covariance
is changed as
3.2.4. State Fusion
In the process of state fusion, the Gaussian kernel function can be obtained based on the state information sub-model as follows.
According to Equation (32), the WMCC realizes the state fusion by maximizing the following cost function.
where
,
is the updated weight of sub-model
i. The partial derivative of
in Equation (33) is considered to obtain the extreme point. The corresponding equation is as follows.
Using
to approximate
to calculate
, based on the similar principle from the sub-model state update step,
is formulated as
According to Equation (35), the fusion state estimation error
is formulated as
Using Equation (37), we can obtain that
According to Equation (38), the fusion state estimation error covariance
satisfies the following equation.
The state statistical information
from the
i-th sub-model is used to calculate the
i-th component of the right formula in Equation (39). At this time, we have
According to Equation (40),
is formulated as
Remark 2. It is worth noting that the fusion state statistics information obtained by the IMM filter can also be used to calculate . However, due to the existence of a large amount of cross-covariance information in , the corresponding computational complexity is large, while using the statistical information of sub-models to calculate can ignore the cross-covariance information and effectively improves the computational efficiency. At the same time, it can be found that due to the fact that the WMCC does not have the same constraint for the weights of each Gaussian kernel function, it can also be applied to the state fusion step, while the MCC cannot be used in this step
It is assumed that the total time is . For clarity, the pseudo-code of the WMCC-IMM filter is summarized in Algorithm 1.
| Algorithm 1: The pseudo-code of the WMCC-IMM filter |
for k = 0:L − 1
Input:
Using Equations (4) and (5) to calculate
Using Equation (22) to calculate
Using Equations (26)–(28) and (30) to calculate
Using Equations (11), (13), (14) and (31) to calculate
Using Equations (35), (36), and (41) to calculate
Output:
end |
3.3. Principle Analysis
In this section, the difference of state fusion between the WMCC-IMM filter and IMM-MCC filter is briefly discussed. The solution forms of the WMCC and MCC for state can be further summarized.
Theorem 1. According to Equation (35), the WMCC can be regarded as obtaining the fusion state by minimizing the following cost function. Proof . Calculate the partial derivative of
from Equation (42) to obtain the following equation. □
Based on Equation (43) to calculate the extreme point, the following equation can be obtained.
Since the loss function in (42) is continuously differentiable and has a minimum value, the only extreme point obtained in Equation (44) is
.
According to Equations (35) and (45), Theorem 1 is proven. It can be found from Equation (42) that the WMCC in the state fusion is equivalent to an adaptive weighted least square method.
Theorem 2. The IMM-MCC filter can be considered to obtain the fusion state by minimizing the following cost function Proof . Calculate the partial derivative of
from Equation (46) to obtain the following equation. □
Based on Equation (47) to calculate the extreme point, the following equation can be obtained.
Since the loss function in (46) is continuously differentiable and has a minimum value, the only extreme point obtained in Equation (48) is
.
According to the state fusion of the IMM and Equation (49), Theorem 2 is proven. It can be found that the IMM-MCC filter adopts the weighted average method to realize the state fusion.
Remark 3. According to Equations (18), (36), and (45), when the kernel bandwidth from tends to infinity and , the WMCC in state fusion becomes the weighted average method. In summary, the state fusion strategy adopted by the IMM-MCC filter is a special form of state fusion strategy adopted by the WMCC-IMM filter, which means that the data fusion strategy of the WMCC-IMM filter is a better choice than that of the IMM-MCC filter.
3.4. WMCC-IMM Filter Applied to Radar Maneuvering Target Tracking
In radar maneuvering target tracking, the state transition equation of a multiple-model system at time
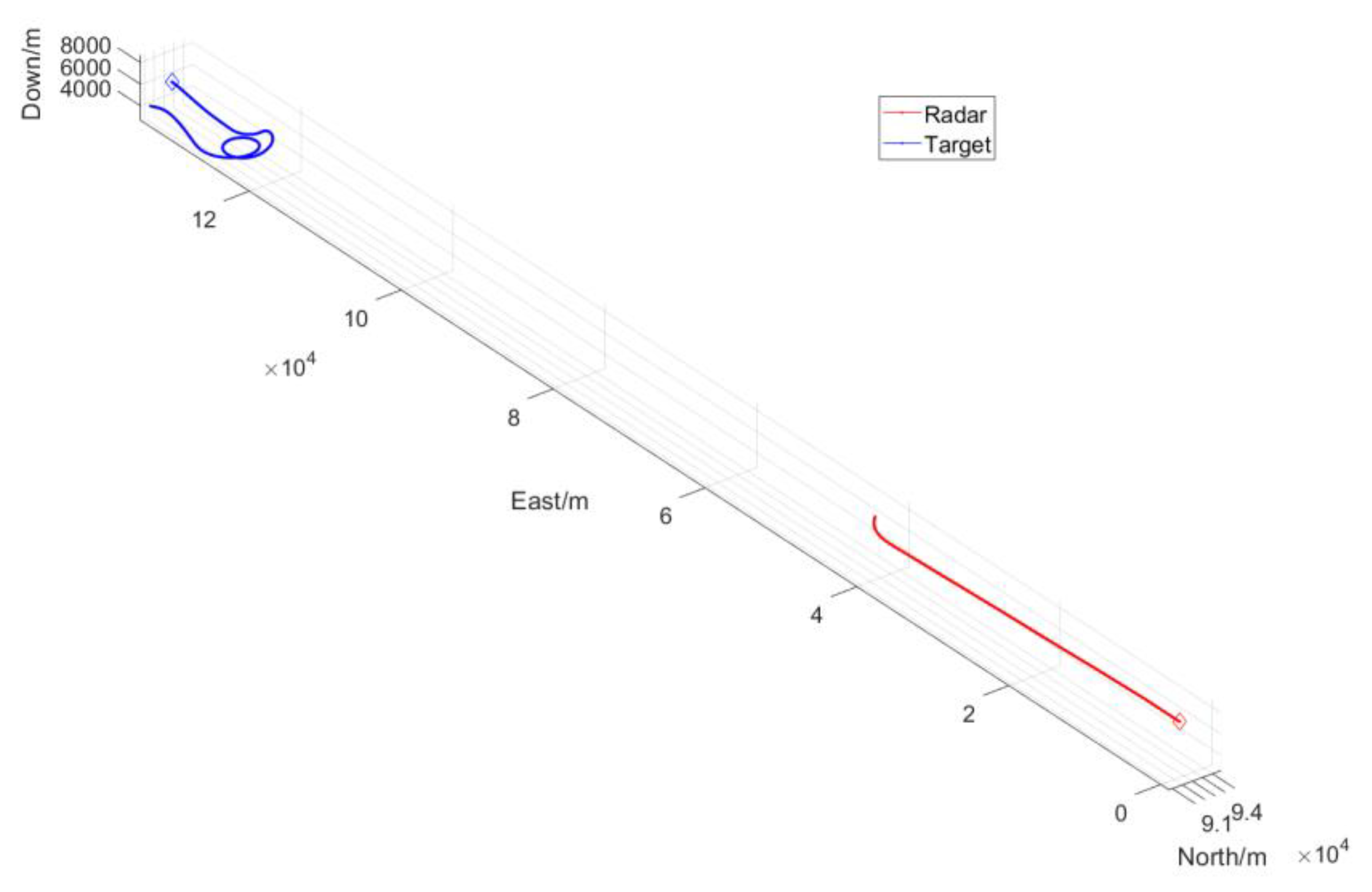
is the same as Equation (1), and the state of target consists of position, velocity, and acceleration in the North-East-Down coordinate system, where the initial position of the radar is its origin. Therefore, the specific form of the target state from the radar system is as follows.
where
,
, and
are the position, velocity, and acceleration of the target in the North-East-Down coordinate system, respectively.
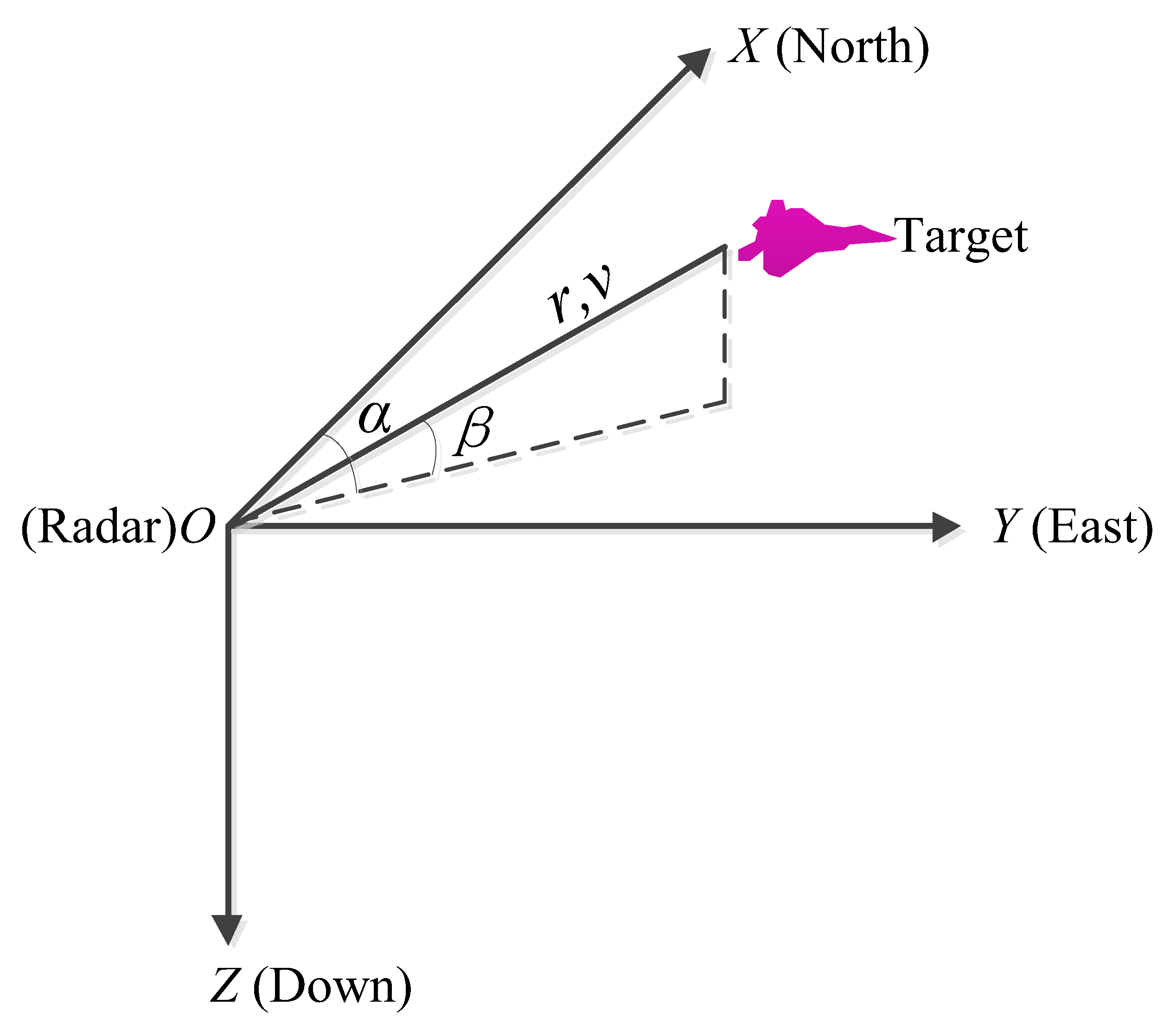
Based on the detection principle of radar, the geometric relationship of the target and radar is shown in
Figure 1. The measurement of the radar consists of radial distance, radial velocity, azimuth, and elevation. The measurement equation is formulated as
where
is the state of the radar at time
k+1.
and
are the position and velocity of the radar in the North-East-Down coordinate system, respectively.
is the measurement noise of the radar, and
is defined as its nominal covariance matrix. The state of the radar can be obtained through the navigation information. Based on this measurement equation, the Gaussian kernel function
from the sub-model state update step is changed as
According to Equation (53), Equation (24) is changed as
Let
, then we have
Based on the Taylor’s first-order expansion formula,
can be approximated as
According to Equations (55)–(57),
is formulated as
According to Equations (25) and (58), it can be found that the update state of
i-th sub-model from a radar system can be obtained by using
and
to replace
and
in Equations (26) and (27). Based on this,
is formulated as
According to Equation (59),
is formulated as
Similarly, the measurement noise covariance of a sub-model is modified as
, and the estimation error covariance
is formulated as
In the model probability update step, the innovation error
and covariance
is formulated as
Finally, the fusion state and covariance can be calculated by using Equations (35), (36), and (41). In summary, the pseudo-code of the WMCC-IMM filter in a radar system is summarized in Algorithm 2.
| Algorithm 2: The pseudo-code of the WMCC-IMM filter in a radar system |
for k = 0:L − 1
Input:
Using Equations (4) and (5) to calculate
Using Equation (22) to calculate
Using Equation (57) to calculate
Using Equations (60) and (61) to calculate
Using Equations (59) and (63)
Using Equations (64), (65), (13), and (14) (13), (14), (64) and (65) to calculate
Using Equations (35), (36), and (41) to calculate
Output:
end |