A Decompressed Spectral-Spatial Multiscale Semantic Feature Network for Hyperspectral Image Classification

Abstract

Convolutional neural networks (CNNs) have shown outstanding feature extraction capability and become a hot topic in the field of hyperspectral image (HSI) classification. However, most of the prior works usually focus on designing deeper or wider network architectures to extract spatial and spectral features, which give rise to difficulty for optimization and more parameters along with higher computation. Moreover, how to learn spatial and spectral information more effectively is still being researched. To tackle the aforementioned problems, a decompressed spectral-spatial multiscale semantic feature network (DSMSFNet) for HSI classification is proposed. This model is composed of a decompressed spectral-spatial feature extraction module (DSFEM) and a multiscale semantic feature extraction module (MSFEM). The former is devised to extract more discriminative and representative global decompressed spectral-spatial features in a lightweight extraction manner, while the latter is constructed to expand the range of available receptive fields and generate clean multiscale semantic features at a granular level to further enhance the classification performance. Compared with progressive classification approaches, abundant experimental results on three benchmark datasets prove the superiority of our developed DSMSFNet model.

1. Introduction

Hyperspectral image (HSI), generally captured by hyperspectral remote sensing sensors or imaging spectrometers, combines subdivisional spectroscopy with 2D imaging technology [1]. HSI utilizes subdivisional spectroscopy to decompose the total radiation of each pixel into the radiation spectrum of different bands and exploits 2D imaging technology to collect the spatial information of the surface, generating a 3D data cube containing rich spectrum, space, and radiation [2,3,4]. Owning to the abundant spatial and spectral information, HSI plays an important role in many practical applications, such as urban planning, land-cover investigation, precision agriculture, military detection, and environmental monitoring [5,6,7,8,9]. In the last few decades, HSI classification has been one of the most popular research fields [10] and attracted multitudinous scholars to devote great efforts to improving classification accuracy [11,12,13,14,15].

In the early period, plentiful HSI classification approaches based on machine learning (ML) utilizing spectral information were presented. Representative methods included support vector machine (SVM) [16], random forest (RF) [17], neural network [18], multinomial logistic regression (MLR) [19], and so on. Although these methods could obtain good classification results, the pure spectra contained much redundant information and noise, which were adverse to the classification performance. Therefore, researchers gave more attention to dimension reduction by using decomposition functions, for example, factor analysis (FA) [20], linear discriminant analysis (LDA) [21], principal component analysis (PCA) [22], and independent component analysis (ICA) [23]. The spatial features included the dependence between the central pixel and its neighborhood pixels, which were introduced into HSI classification to greatly improve the classification performance. An algorithm combining the band selection (BS) with a Markov random field (MRF) was proposed [24]. Jiang et al. designed a random label propagation algorithm (RLPA), which was based on spatial-spectral constraint knowledge, to cleanse the labelled noise [25]. The traditional classification approaches, whether spectral features-based or spatial-spectral features-based, all depended on handcraft features that lacked sufficient representation ability and poor generalization performance.

Of late, deep learning (DL) has developed rapidly and received a substantial amount of attention. Due to excellent performance, DL has been broadly applied to HSI classification. Chen et al. used an autoencoder to classify hyperspectral pixels, which was the first time DL was introduced into the field of HSI classification [26]. Hu et al. introduced 1D CNN into HSI classification for the first time, and the classification accuracy obtained by this method exceeded the traditional ML methods [27]. A 1D CNN model was designed by Li et al., which extracted pixel pairs from the raw HSI as the input data and obtained the spectral relationship between pixels [28]. Although these approaches could obtain good classification results, the input data of them needed to be flattened into a1Dvector, which seriously ignored the rich spatial information. Therefore, many methods integrated the spatial context with spectral information to improve classification accuracy. For example, Yang et al. presented a double-channel CNN to capture the spatial features and spectral features separately [29]. Li et al. developed a two-stream CNN with deep feature fusion to enhance spatial-spectral feature representative power [30]. An end-to-end residual spectral-spatial attention network without additional feature engineering was presented [31]. To reduce the computational complexity and obtain better classification results, Zhang et al. combined 2D CNN with spectral partition [32]. Considering the 3D characteristics of HSI data, plentiful classification algorithms based on 3DCNN were constructed. For example, Wang et al. [33] and Zhong et al. [34] devised spatial and spectral blocks under the construction of 3DCNN to obtain spectral-spatial information. To directly learn joint spatial-spectral features from the original HSI, Li et al. designed a 3D CNN algorithm [35]. To deal with the loss of vast initial information problems, Lin et al. constructed an attention-aware pseudo-3D CNN [36]. The 3D CNN framework was built to capture spatial-spectral joint features [37,38].

With the development of DL, many ancillary strategies have emerged, such as multiscale feature extraction, dense connection, multilayer feature fusion, and residual learning. For example, Gao et al. developed a network framework based on 3D convolution, which not only adopted multiscale blocks to extract spatial-spectral information at different scales but also introduced the dense connection to boost feature propagation and reuse [39]. Xue et al. utilized the shortcut connection structure to learn discriminative spatial-spectral features [40]. Safari et al. designed a multiscale DL learning approach to effectively capture spectral-spatial joint information over different scales [41]. To increase the network depth, Song et al. embedded residual learning into the built-deep feature fusion network [42]. To make full use of HSI’s data, Paoletti et al. presented a deep and dense 3DCNN framework [43]. To achieve complementary spatial-spectral information from different levels, Li et al. combined multilevel fusion with multiattention mechanisms [44].

Although the above-described CNN-based methods obtained promising classification accuracy, two challenging problems remain. The first challenge is that most of the prior works usually focus on wider or deeper network structures to invigorate the discrimination ability of CNNs to capture spatial-spectral features. However, wider or deeper network structures give rise to difficulty for optimization and more parameters along with higher computation, which critically influence the classification performance. The second challenge is how to learn spatial and spectral information more effectively. To resolve the problems mentioned above, this article proposes a decompressed spectral-spatial multiscale semantic feature network (DSMSFNet) for HSI classification. The designed DSMSFNet includes a decompressed spectral-spatial feature extraction module (DSFEM) and a multiscale semantic feature extraction module (MSFEM). The former is utilized to obtain more representative and discriminative global decompressed spectral-spatial features in a lightweight extraction manner, while the latter is constructed to capture clean multiscale semantic features at a granular level and further boost the classification performance. In conclusion, the contributions of this work are twofold as follows:

(1)

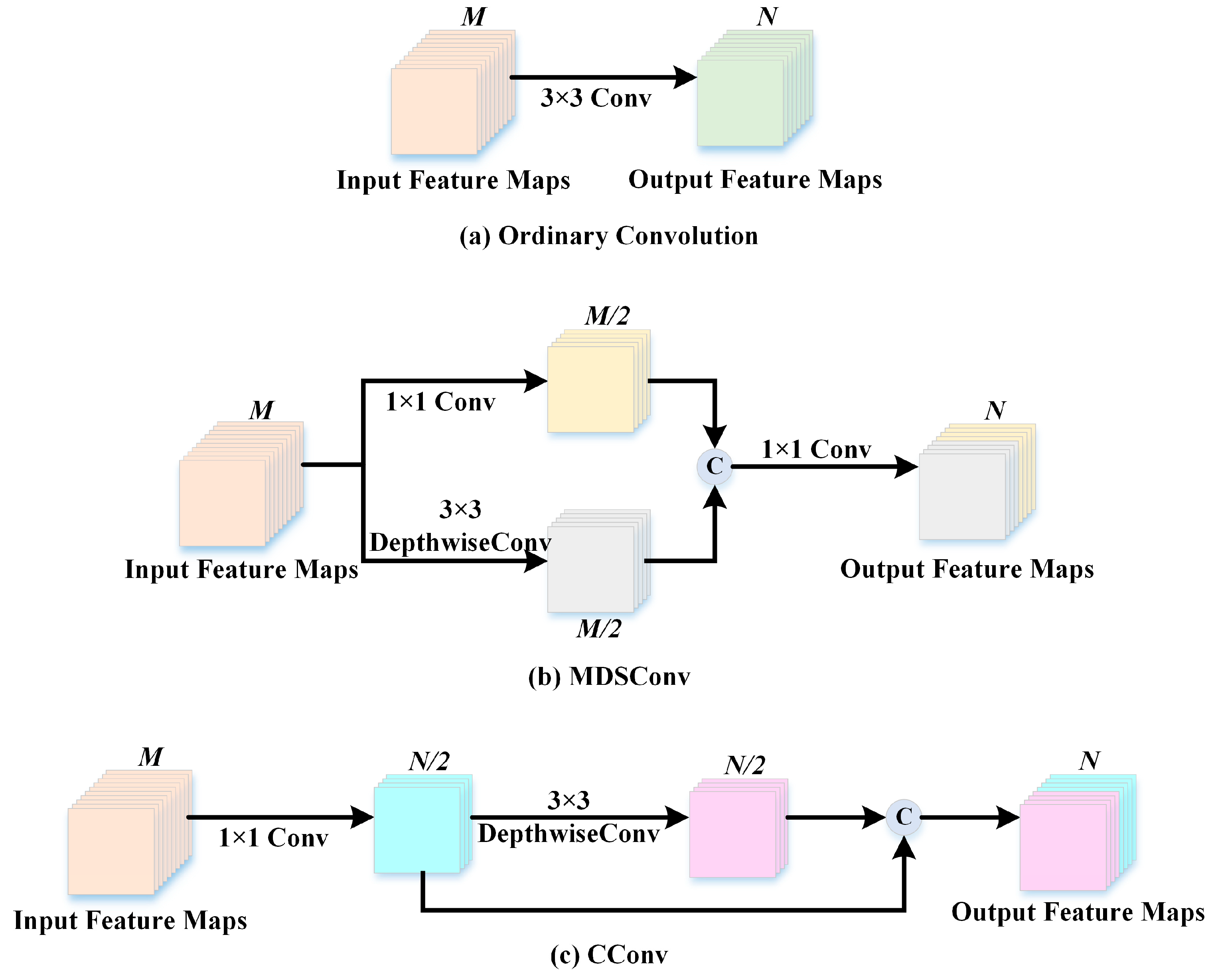
To decrease the training parameters and computational complexity, we devise a compressed-weight convolutional (CConv) layer, which takes the place of the traditional 2D convolutional layer, to extract spatial and spectral information through cheap operations.

(2)

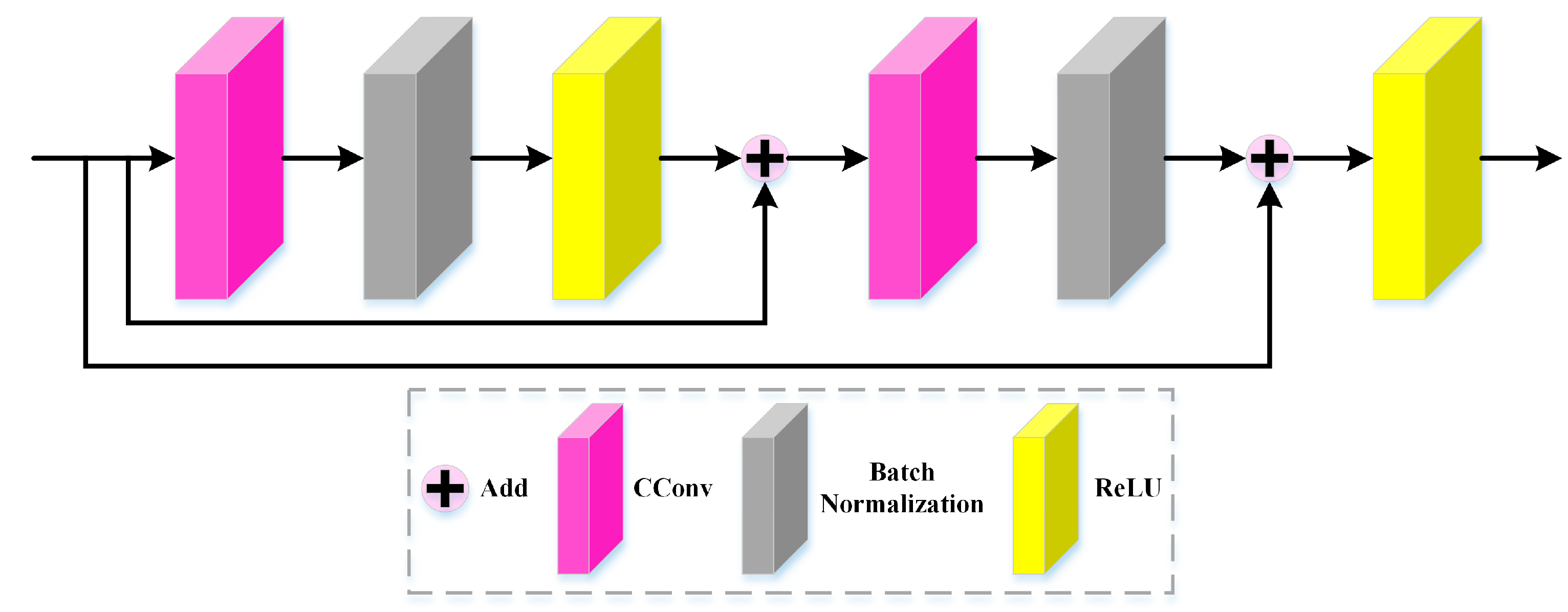
To conduct an efficient and lightweight spectral-spatial feature extraction, we construct a compressed residual block (CRB), embedding the CConv layer into a residual block, to alleviate the overfitting and achieve spectral-spatial feature reuse effectively.

(3)

To obtain more representative and discriminative global decompressed spectral-spatial features, we build a decompressed spectral-spatial feature extraction module (DSFEM) in a lightweight extraction manner. For one thing, DSFEM is composed of multiple decompressed dense blocks (DDBs), which provide abundant local decompressed spectral-spatial features. For another thing, the dense connection is introduced into DSFEM to integrate features from shallow and deep layers, thereby acquiring robust complementary information.

(4)

To further enhance the classification performance, we raise a multiscale semantic feature extraction module (MSFEM). The MSFEM can not only expand the range of available receptive fields but also generate clean multiscale semantic features for classification tasks at a granular level.

The remainder of this article is organized as follows: Section 2 provides an elaborate description of the developed HSI classification network model. Section 3 reports the experimental results and discussion. Section 4 summarizes the conclusion of this article and provides an outlook for future research.

2. Method

This article utilizes the Indian Pines dataset as an example to graphically describe the architecture of our constructed DSMSFNet, as exhibited in Figure 1. The developed method includes two main submodules: DSFEM to obtain more representative and discriminative global decompressed spectral-spatial features in a lightweight extraction manner and MSFEM to expand the range of available receptive fields and capture clean multiscale semantic features at a granular level for classification.

2.1. Decompressed Spectral-Spatial Feature Extraction Module

In this article, we devise a decompressed spectral-spatial feature extraction module (DSFEM) to obtain more representative and discriminative global decompressed spectral-spatial features. A DSFEM is composed of five decompressed dense blocks (DDBs) whose nuclear component is a compressed residual block (CRB). For the CRB, the compressed-weight convolutional (CConv) layer is the primary component, which can downgrade the number of training parameters and computational burden. Figure 2 gives the diagram of a DSFEM.

2.1.1. Compressed-Weight Convolution Layer

Recently, pointwise and depthwise convolution operations have attracted considerable attention and have been introduced into many computer vision tasks, such as MobileNet [45], Xception [46], and HSI classification [47]. Pointwise convolution is the standard convolution with a $1\times 1$ filter. Only one convolution kernel of depthwise convolution is responsible for one channel. Compared with standard convolution, depthwise convolution can reduce the number of network training parameters and improve the training speed. Figure 3a shows a standard convolution with $3\times 3$ filters. Gao et al. [47] presented a mixed depthwise convolution (MDSConv) to replace a $3\times 3$ ordinary depthwise separable convolution, as shown in Figure 3b. First, each feature map is divided equally into two parts: one is convoluted by the $1\times 1$ depthwise convolution, and the other is convoluted by the $3\times 3$ depthwise convolution. Then, the output feature maps of pointwise convolution and depthwise convolution are fused by a concatenation operation. Finally, the connected feature maps are sent into a pointwise convolution. Figure 3c is the architecture of our constructed CConv layer. Different from MDSConv, a $1\times 1$ point convolution is first performed to reduce the number of input channels. Then, we employ the $3\times 3$ depthwise convolution to take the place of the $3\times 3$ standard convolution. Finally, the feature maps from depthwise convolution are concatenated with the previous pointwise convolution feature maps.

Let $S_{in}$ and $S_{out}$ represent the number of input feature maps and output feature maps, respectively. The $3\times 3$ standard convolution requires $3\times 3\times S_{in}\times S_{out}$ parameters. For MDSConv, the number of parameters in this layer can be calculated as $3\times 3\times (S_{in}/2)+1\times 1\times (S_{in}/2)+1\times 1\times S_{in}\times S_{out}$. For CConv, the parameter number of this layer is $1\times 1\times S_{in}\times (S_{out}/2)+3\times 3\times (S_{out}/2)$. For example, we assume that both the number of input feature maps $S_{in}$ and output feature maps $S_{out}$ are 32, and then the parameter numbers of standard convolution, MDSConv, and CConv are 9216, 1184, and 656, respectively. As we can see, our designed CConv requires approximately $14\times$ fewer parameters than the $3\times 3$ standard convolution, and $2\times$ fewer parameters than MDSConv, demonstrating that the proposed CConv exhibits ascendant capability for reducing the number of network training parameters.

2.1.2. Compressed Residual Block

To capture discriminative spectral-spatial information in a lightweight feature extraction manner, we devise a compressed residual block (CRB), which embeds the CConv layer into a residual block. Figure 4 provides the structure of CRB. CRB is composed of two $3\times 3$ CConv layers to extract spatial and spectral information through cheap operations, two BN layers to accelerate the convergence of network, and two ReLU activation functions. In addition, we introduce skip transmission [48] into CRB to increase the network depth and achieve a good generalization performance. Each CRB can be expressed as follows:

$$Z(X)=\sigma (F(X)+H(X))$$

(1)

where $X$ and $Z(X)$ are the input and output of CRB, respectively. $\sigma$ denotes the ReLU activation function. $F(\bullet )$ represents a series of operations, including the CConv layer, BN layer, and ReLU. $H(X)$ is the identity operator, which is achieved by utilizing the skip transmission.

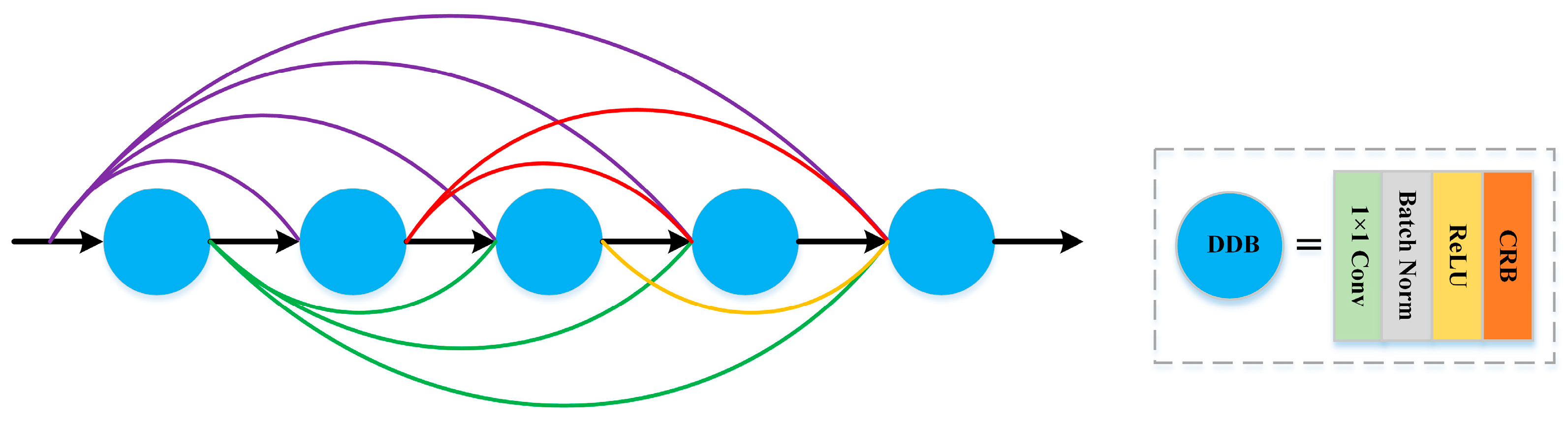
2.1.3. Decompressed Dense Block

As shown in Figure 2, each DDB comprises a $1\times 1$ convolution layer, a BN layer, a ReLU activation function, and a CRB. The $1\times 1$ convolution layer is used to reduce the channel numbers and boost the calculation efficiency in this block. CRB is adopted to learn more careful and representative spectral-spatial features. DDB can capture local spectral-spatial information while making the network converge faster. In addition, to obtain more comprehensive global decompressed spectral-spatial features and avoid gradient disappearance, the dense connection [49] is employed between each DDB.

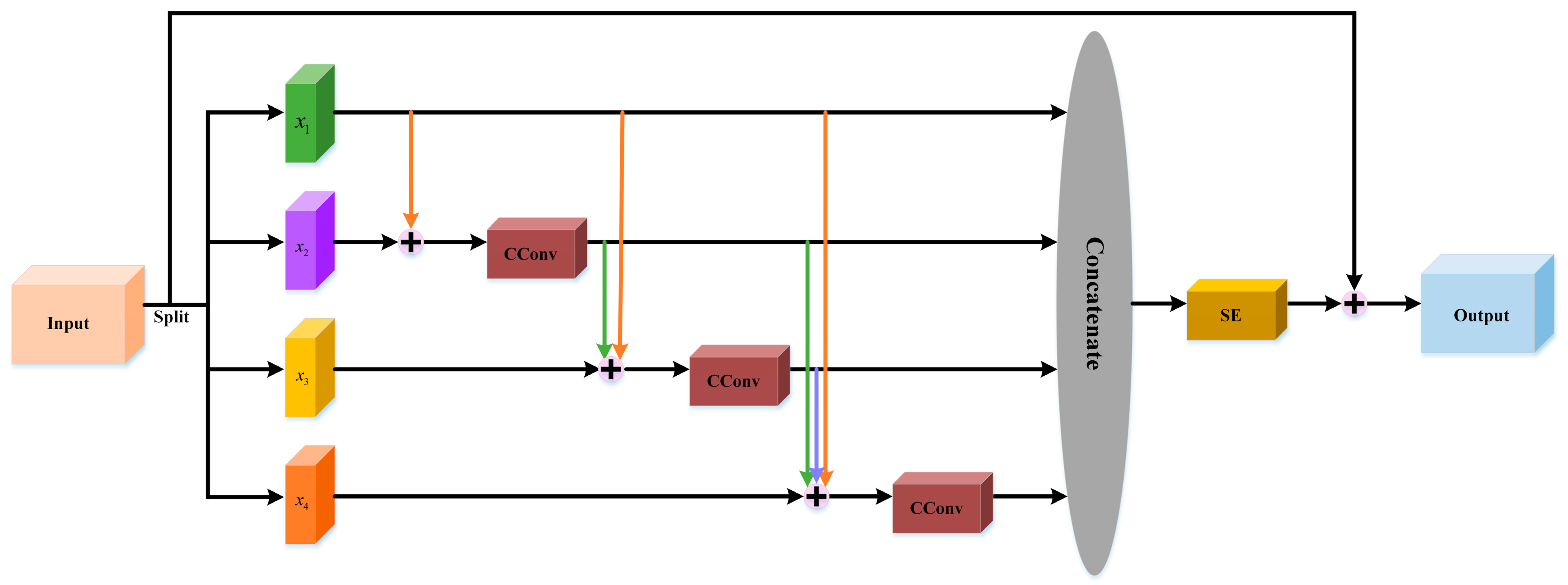
2.2. Multiscale Semantic Feature Extraction Module

During the training process, as the increase in network depth, spectral-spatial information will gradually disappear. The local decompressed spectral-spatial features generated by each DDB are conducive to HSI classification. Therefore, adequately utilizing these features can provide significant classification accuracy. However, only exploiting an ordinary concatenation operation to aggregate these locally decompressed spectral-spatial features may generate noise and redundant information, thereby downgrading the classification accuracies. In this section, we build a multiscale semantic feature extraction module (MSFEM), which can not only expand the range of available receptive fields but also extract clean multiscale high-level semantic features at a granular level to further boost the classification performance. The whole structure of the MSFEM is exhibited in Figure 5.

According to Figure 5, after aggerating all local decompressed spectral-spatial features generated by each DDB, the obtained global decompressed spectral-spatial features first are equally divided into four subsets, represented by $x_1$, $x_2$, $x_3$, and $x_4$. Except for $x_1$, the other subsets have a corresponding $3\times 3$ CConv layer following a BN layer and a ReLU function. Second, to enhance feature reuse of the previous layer, the output features of previous layers and current subset input features are added by elementwise summation. Then, these features are fed into the corresponding $3\times 3$ CConv layer to generate new subset features. Furthermore, we utilize the concatenation operation among four new subset features to obtain multiscale high-level semantic features for HSI classification. Finally, to achieve more comprehensive features and avoid information loss, we introduce a “squeeze-and-excitation” block [50] and skip transmission [48] into our devised MSFEM. Mathematically, MSFEM can be described as follows:

$$z_1=x_1$$

(2)

$$z_2=P(z_1+x_2)$$

(3)

$$z_3=P(z_1+z_2+x_3)$$

(4)

$$z_4=P(z_1+z_2+z_3+x_4)$$

(5)

$$z=Att([z_1,z_2,z_3,z_4])+X$$

(6)

where $X$ and $z$ are the input and output of MSFEM, respectively. $P$ denotes the $3\times 3$ CConv operation. $z_1$, $z_2$, $z_3$, and $z_4$ represent the output of each subset, respectively. $Att$ refers to the “squeeze-and-excitation” block. $[]$ stands for the concatenation operation.

2.3. The Overall Framework of the Proposed DSMSFNet

The main procedure of our presented DSMSFNet is exhibited in Figure 1. HSI contains hundreds of highly correlated spectral bands, which causes the Hughes effect and thereby impairs the classification performance. Therefore, the first PCA was performed on the original HSI to effectively reduce the spectral dimension and restrain the noisy bands. Second, we selected $w\times w$ sized neighborhoods around the target pixels to construct 3-D image cubes, which can fully exploit the property of HSI containing spatial and spectral information. Then, the 3-D image cubes of the size $19\times 19\times 25$ were sent to the DSFEM. The DSFEM is composed of five DDBs and each DDB can extract local decompressed spectral-spatial features of the size $19\times 19\times 48$ in a lightweight extraction manner. Additionally, we applied the dense connection to the designed DSFEM, which facilitated the local decompressed spectral-spatial features flow and achieved more discriminative global decompressed spectral-spatial features of the size $19\times 19\times 265$. Next, the obtained global decompressed spectral-spatial features were fed to a reduced dimension block, which consists of three $5\times 5$ 2-D convolutional layers, three BN layers, and three PReLU activation functions, acquiring reduced dimension features of the size $7\times 7\times 24$. Furthermore, we transmitted the reduced dimension features to MSFEM to generate clean multiscale semantic features of the size $7\times 7\times 24$ at a granular level, and, thereby, boosted the HSI classification performance. Finally, we utilized a 2D global average pooling layer, two fully connected layers and a softmax function to obtain the output classification maps. In addition, L2 regularization was also introduced into the developed DSMSFNet to improve the classification ability.

3. Experimental Results and Discussion

3.1. Datasets Description

We evaluate the classification performance of our presented approach on three commonly used hyperspectral datasets, including the Botswana (BOW) dataset, the Indian Pines (IP) dataset, and the Houston 2013 dataset.

The BOW dataset [51] was provided by the NASA EO-1 Hyperion sensor over the Okavango Delta. This scene contains 14 diverse land-cover categories and $1476\times 256$ hyperspectral pixels. After eliminating uncalibrated and noisy bands, 145 bands with a spatial resolution of 30 m per pixel ranging from 0.4 to 2.5 um remain.

The IP dataset [52] was gathered by the airborne visible/infrared imaging spectrometer (AVIRIS) in northwestern Indiana. This scene is made up of $145\times 145$ hyperspectral pixels and 16 different land-cover categories. After removing noisy bands, 200 spectral bands remained with a spatial resolution of 20 m per pixel ranging from 0.4 to 2.5 um.

The Houston 2013 dataset [53] was collected by the 2013 IEEE GRSS Data Fusion Competition. This scene involves $349\times 1905$ hyperspectral pixels and 15 different land-cover categories. It has 144 spectral bands with a spatial resolution of 2.5 m per pixel and the wavelength range is from 0.38 to 1.05 um.

Table 1. The information on the land-cover category of the BOW dataset.

No.	Color	Class	Train	Test
1		Water	10	85
2		Hippo grass	27	241
3		Floodplain grasses 1	19	162
4		Floodplain grasses 2	31	274
5		Reeds	25	223
6		Riparian	32	282
7		Fires car	21	182
8		Island interior	26	233
9		Acacia woodlands	27	242
10		Acacia shrub lands	27	242
11		Acacia grasslands	22	193
12		short mopane	26	225
13		Mixed mopane	11	90
14		Exposed soils	27	243
Total			331	2917

,

Table 2. The information on the land-cover category of the IP dataset.

No.	Color	Class	Train	Test
1		Alfalfa	10	36
2		Corn-notill	286	1142
3		Corn-mintill	166	664
4		Corn	48	189
5		Grass-pasture	97	386
6		Grass-trees	146	584
7		Grass-pasture-mowed	6	22
8		Hay-windrowed	96	382
9		Oats	4	16
10		Soybean-notill	195	777
11		Soybean-mintill	491	1964
12		Soybean-clean	119	474
13		Wheat	41	164
14		Woods	253	1012
15		Buildings-Grass-Tree	78	308
16		Stone-Steel-Towers	19	74
Total			2055	8194

and

Table 3. The information on the land-cover category of the Houston 2013 dataset.

No.	Color	Class	Train	Test
1		Healthy grass	239	1125
2		Stressed grass	126	1128
3		Synthetic grass	70	627
4		Trees	125	1119
5		Soil	125	1117
6		Water	33	292
7		Residential	127	1141
8		Commercial	125	1119
9		Road	126	1126
10		Highway	123	1104
11		Railway	124	1111
12		Parking Lot 1	124	1109
13		Parking Lot 2	47	422
14		Tennis Court	43	385
15		Running Track	66	594
Total			1510	13519

list landcover classes, colors, the numbers of randomly selected training samples, and testing samples.

3.2. Experimental Setup

TensorFlow 2.3.0 was utilized as the DL framework and all experiments were conducted on a PC with an Intel(R) Core(TM) i7-9700F CPU and NVIDIA GeForce RTX 2060 SUPER GPU.

Different hyperspectral datasets contain different annotated sample numbers and exist in the imbalanced data dilemma, so different training sample portions were used for three benchmark datasets. For the BOW, IP, and Houston 2013 datasets, we randomly chose 10%, 20%, and 10% annotated samples for training and the remaining 90%, 80%, and 90% annotated samples for testing, respectively. Adam was used to optimize the parameters and the learning rate was set to 0.001. Additionally, the epoch and batch size are 400 and 16, respectively.

We adopted the overall accuracy (OA), average accuracy (AA), and Kappa coefficient (Kappa) as criteria metrics to measure the classification performance of the proposed DSMSFNet.

3.3. Comparison Methods

The developed DSMSFNet was comprehensively compared with eleven advanced classification algorithms. These comparison approaches can be classified into two categories: one includes SVM, RF, KNN, and GuassianNB, which are based on traditional ML; the other includes HybridSN [54], MSRN_A [55], 3D_2D_CNN [56], RSSAN [31], MSRN_B [47], DMCN [57], and MSDAN [58], which are based on DL. Concretely, HybridSN and 3D_2D_CNN utilize 2D and 3D convolutional layers to extract spectral-spatial features. MSRN_A integrates a 2-D CNN stage involving a spatial attention module and a multiscale spatial feature extraction block with a 3-D CNN stage composed of a spatial-spectral attention module and a multiscale spectral feature extraction block to obtain salient spatial and spectral features. RSSAN utilizes a spectral-spatial attention learning module to find vital spatial and spectral parts and a spectral-spatial feature learning module to acquire important spectral-spatial information. MSRN_B proposes a multiscale residual network with mixed depthwise convolutions to generate discriminative spectral-spatial information. DMCN is composed of a grouped residual 2-D CNN, a dense 3-D CNN, and coordinate attention for acquiring spectral-spatial fusion features. MSDAN uses three multiscale dense connectivity blocks with three different scales to capture multiscale spectral-spatial features and embeds spectral-spatial-channel attention to boost feature representations. To ensure the reliability and authenticity of experimental results, for the BOW, IP, and Houston 2013 datasets, all experiments randomly chose 10%, 20%, and 10% annotated samples as the training set and the remaining 90%, 80%, and 90% annotated samples as the testing set, respectively.

Table 4. Results of classification for the BOW dataset.

No.	SVM	RF	KNN	GaussianNB	HybridSN	MSRN_A	3D_2D_CNN	RSSAN	MSRN_B	DMCN	MSDAN	DSMSFNet
1	100.00	97.89	99.59	98.37	87.82	96.05	92.75	100.00	98.78	91.01	95.29	97.59
2	98.11	98.81	92.13	67.74	100.00	100.00	96.77	100.00	100.00	88.24	100.00	100.00
3	78.65	90.25	93.62	80.58	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
4	100.00	83.64	87.25	65.02	98.47	100.00	99.47	100.00	100.00	96.48	96.41	100.00
5	80.59	72.66	82.33	71.90	88.24	97.05	95.90	87.08	92.37	100.00	96.54	100.00
6	50.00	76.34	60.00	57.23	97.78	100.00	97.51	93.53	100.00	100.00	97.10	100.00
7	100.00	98.67	99.55	97.00	100.00	100.00	100.00	100.00	100.00	99.57	100.00	100.00
8	84.90	88.02	77.53	82.84	99.44	100.00	100.00	100.00	91.92	94.49	100.00	100.00
9	68.48	80.14	78.23	71.43	98.26	100.00	100.00	97.45	100.00	100.00	100.00	100.00
10	75.62	76.83	88.02	67.83	98.67	100.00	98.67	98.22	96.96	97.80	100.00	100.00
11	86.24	89.53	91.49	88.85	97.51	96.48	99.64	99.27	100.00	99.63	100.00	100.00
12	89.60	91.57	93.49	91.61	97.59	100.00	100.00	97.44	46.55	96.41	100.00	100.00
13	90.77	79.76	93.06	70.97	100.00	100.00	100.00	94.88	100.00	98.77	97.97	100.00
14	100.00	98.80	97.59	93.62	100.00	97.70	100.00	95.31	83.33	97.18	100.00	100.00
OA (%)	82.05	85.98	87.04	78.83	96.95	99.01	98.53	97.15	91.50	97.57	98.66	99.79
AA (%)	81.82	86.95	87.87	81.06	95.87	99.12	98.13	96.16	92.21	97.02	98.71	99.82
Kappa × 100	80.53	84.81	85.96	77.10	96.69	98.92	98.40	96.92	90.81	97.36	98.55	99.78
Complexity (G)	—	—	—	—	0.0102	0.0011	0.0005	0.0002	0.0003	0.0045	0.0025	0.0003
Parameter (M)	—	—	—	—	9.2252	0.1965	0.2579	0.1159	0.1637	2.2292	1.2638	0.1628

The black bold highlights which mechanic works best.

,

Table 5. Results of classification for the IP dataset.

No.	SVM	RF	KNN	GaussianNB	HybridSN	MSRN_A	3D_2D_CNN	RSSAN	MSRN_B	DMCN	MSDAN	DSMSFNet
1	0.00	86.67	36.36	31.07	97.06	100.00	100.00	97.30	90.32	100.00	100.00	94.59
2	61.51	82.02	50.38	45.54	98.86	99.73	95.79	98.00	97.45	97.46	98.95	98.70
3	84.04	78.66	61.95	35.92	97.04	100.00	95.99	99.54	98.74	93.50	99.54	100.00
4	46.43	72.87	53.26	15.31	98.86	98.38	92.94	99.46	99.39	96.81	98.85	97.42
5	88.82	90.16	84.71	3.57	98.47	97.72	99.47	98.22	92.54	98.69	98.70	99.48
6	76.72	82.61	78.08	67.87	100.00	100.00	100.00	99.83	99.65	100.00	99.49	100.00
7	0.00	83.33	68.42	100.00	100.00	100.00	100.00	100.00	100.00	100.00	86.96	100.00
8	83.49	87.16	88.55	83.78	96.46	100.00	100.00	99.48	80.08	98.70	99.74	100.00
9	0.00	100.00	40.00	11.02	76.19	100.00	100.00	100.00	0.00	100.00	100.00	100.00
10	70.89	83.61	69.40	27.07	99.74	97.72	97.48	99.48	88.93	99.87	98.46	100.00
11	58.51	75.16	69.49	60.60	98.77	98.94	97.48	99.19	97.57	99.69	99.74	100.00
12	59.38	66.74	62.13	23.95	98.34	92.40	91.19	98.13	91.52	92.74	91.30	98.95
13	82.23	92.53	86.70	84.38	100.00	89.62	99.38	99.39	94.58	96.91	97.02	100.00
14	87.39	89.78	91.76	75.08	99.90	99.51	97.47	99.80	100.00	99.40	99.90	100.00
15	86.30	72.00	64.127	53.17	94.12	98.09	90.88	98.72	100.00	92.92	95.00	99.68
16	98.36	100.00	100.00	98.44	98.67	100.00	100.00	97.33	94.37	91.14	98.53	98.67
OA (%)	70.21	89.91	70.95	50.88	98.58	98.50	96.85	99.07	95.56	97.86	98.61	99.62
AA (%)	53.06	66.77	62.39	52.65	96.87	96.56	94.34	96.53	86.25	93.47	94.85	99.26
Kappa × 100	65.07	78.01	66.63	44.07	98.39	98.29	96.41	98.94	94.94	97.57	98.41	99.57
Complexity (G)	—	—	—	—	0.0102	0.0011	0.0005	0.0002	0.0003	0.0045	0.0025	0.0003
Parameter (M)	—	—	—	—	9.2258	0.1981	0.2582	0.1164	0.1642	2.2295	1.2640	0.1327

The black bold highlights which mechanic works best.

and

Table 6. Results of classification for the Houston 2013 dataset.

No.	SVM	RF	KNN	GaussianNB	HybridSN	MSRN_A	3D_2D_CNN	RSSAN	MSRN_B	DMCN	MSDAN	DSMSFNet
1	82.38	95.64	98.29	90.78	97.64	98.85	98.16	98.75	99.11	99.01	99.20	100.00
2	98.46	95.44	95.70	98.80	99.73	99.65	99.19	97.98	99.73	98.17	99.56	99.82
3	97.72	100.00	97.29	93.09	99.68	100.00	99.84	99.52	100.00	98.12	100.00	100.00
4	98.76	99.55	98.11	99.01	93.25	99.91	99.82	99.29	99.46	98.89	99.28	100.00
5	86.86	93.36	93.00	73.96	99.91	100.00	100.00	99.73	100.00	99.64	99.37	99.73
6	100.00	100.00	100.00	31.00	100.00	100.00	100.00	98.29	100.00	100.00	100.00	100.00
7	64.91	79.15	87.83	63.06	97.77	100.00	96.32	96.96	98.79	99.43	95.66	99.91
8	86.03	87.95	82.05	70.03	98.32	100.00	96.61	93.64	100.00	97.52	90.71	100.00
9	61.38	75.59	76.07	42.67	93.82	99.11	95.96	89.75	95.58	92.70	91.22	99.82
10	51.36	84.43	79.24	0.00	98.57	96.76	97.68	94.35	98.22	95.76	100.00	99.91
11	45.16	76.50	79.76	34.42	97.99	99.73	98.92	96.75	100.00	93.28	96.39	99.46
12	60.82	72.16	70.67	21.08	98.92	99.91	98.84	90.84	99.73	91.79	98.83	100.00
13	100.00	79.72	88.89	15.61	100.00	97.32	99.20	95.55	99.01	96.50	98.41	100.00
14	79.39	96.68	95.17	67.40	98.97	100.00	99.74	100.00	100.00	99.74	99.23	100.00
15	99.66	99.64	99.13	99.08	99.83	99.00	100.00	100.00	99.83	100.00	99.83	99.83
OA (%)	75.17	87.47	87.51	60.82	97.91	99.36	99.41	96.31	99.17	96.82	97.33	99.88
AA (%)	74.91	86.09	85.77	63.10	97.33	99.07	98.03	96.37	98.83	95.88	97.21	99.83
Kappa × 100	73.11	86.43	86.47	57.73	97.74	99.31	98.28	96.01	99.10	96.56	97.11	99.87
Complexity (G)	—	—	—	—	0.0102	0.0011	0.0005	0.0002	0.0003	0.0045	0.0025	0.0003
Parameter (M)	—	—	—	—	5.1220	0.1973	0.2580	0.1162	0.1639	2.2293	1.2639	0.1557

The black bold highlights which mechanic works best.

report land-cover class accuracy and three criteria metrics of all experiments on three public datasets. Additionally, to better display the superiority of our presented model for minority category classification, we define a noun named the minority category comparison (MCC), which is the training sample numbers of a category that is smaller than the average training sample numbers.

Table 4 reports each land-cover category and OA, AA, and Kappa accuracies of all comparison approaches for the BOW dataset. It is clear that our developed DSMSFNet obtains superb OA, AA, and Kappa, which demonstrates the stability and superiority of our constructed DSMSFNet. The GuassianNB has the lowest OA, AA, and Kappa, which are 20.96%, 18.66%, and 22.68% lower than those of the DSMSFNet, respectively. This is because the GuassianNB only extracts spectral features and ignores the abundant information in the spatial domain, which results in unsatisfactory classification accuracies. The MSRN_A achieves competitive OA, AA, and Kappa, which are 0.78%, 0.7%, and 0.86% lower than those of the DSMSFNet, respectively. This is because the MSRN_A devises multiscale spectral and spatial feature extraction blocks to acquire spectral-spatial information from diverse scales while utilizing spatial and spatial-spectral attention modules to emphasize the important information and suppress useless ones. In addition, the BOW dataset has five MCCs, including the 1st, 3rd, 7th, 11th, and 13th. Our proposed DSMSFNet acquires decent accuracy on the 3rd, 7th, 11th, and 13th CCMs, which indicates that the designed DSFEM and MSFEM can effectively capture global decompressed and clean semantic spectral-spatial features of the minority class. Similarly, the MSRN_B obtains optimal accuracy on the 3rd, 7th, 11th, and 13th CCMs. But the OA, AA, and Kappa of MSRN_B are 8.29%, 7.61%, and 8.97% lower than those of the DSMSFNet, respectively. This is because although both the MSRN_B and our developed DSMSFNet utilize mixed depthwise convolutions, the DSMSFNet needs fewer training parameters and provides more discriminative features for classification.

Table 5 presents each land-cover category and OA, AA, and Kappa accuracies of all comparison approaches for the IP dataset. We can obviously see that in terms of OA, AA, and Kappa, our proposed DSMSFNet outperforms eleven other comparison approaches. Concretely, the DSMDFNet classifies the most MCCs with high precision and obtains optimal accuracy on the 5th, 7th, 8th, 9th, 12th, and 13th ones, which verifies the effectiveness of the DSMSFNet in identifying the minority categories. Some similar observations can be found on the IP dataset. Among comparison methods, the GuassianNB achieves the most terrible OA, AA, and Kappa, which are 48.79%, 46.61%, and 55.50% lower than those of the DSMSFNet. This is because ML-based classification approaches need to count on prior knowledge, resulting in poor generalization ability. The RSSAN obtains suboptimal OA and AA accuracies, which are 0.55% and 1.47% lower than those of the DSMSFNet. But it does not show good classification performance on the CCMs. In addition, MSRN_A and 3D_2D_CNN have fine classification accuracy on the 1st, 7th, 8th, 9th, and 16th CCMs, which illustrates that they can effectively identify the minority categories. However, the three evaluation indices of MSRN_A and 3D_2D_CNN are not splendid. DSMSFNet achieves 99.62% OA, 99.26% AA, and 99.57% Kappa, which are 1.12%, 2.70%, and 3.16% higher than those of MSRN_A and 2.77%, 4.92%, and 3.16% higher than those of 3D_2D_CNN. These phenomena can adequately show the superiority and robustness of our proposed DSMSFNet.

Table 6 displays each land-cover category and OA, AA, and Kappa accuracies of all comparison approaches for the Houston 2013 dataset. Compared with eight DL-based classification approaches, SVM, RF, KNN, and GaussianNB obtain low criteria metrics. Specifically, our developed DSMSFNet again achieves splendid OA, AA, and Kappa and obtains excellent accuracy on the 3rd, 6th, 13th, and 14th CCMs. Uniformly, the GuassianNB produces unsatisfactory classification performance, and the three criteria metrics of it are 39.06%, 36.73%, and 42.14% lower than those of the DSMSFNet. This is because the eight DL-based approaches can utilize hierarchical feature extraction structures to capture automatically high-level features, thereby acquiring good classification results. Additionally, although the MSRN_A obtains encouraging classification accuracies, the three criteria metrics are 0.52%, 0.76%, and 0.56% lower than those of the DSMSFNet, and it only achieves worthy classification results on the 3rd, 6th, and 14th CCMs. The stabilized classification performance on the three benchmark datasets manifests that our presented DSMSFNet can fully excavate global decompressed spectral-spatial features and clean multiscale semantic features, which are conducive to enhancing the classification performance.

Moreover, the visual classification maps of all comparison approaches for the three benchmark datasets are depicted in Figure 6, Figure 7 and Figure 8, which are highly consistent with Table 4, Table 5 and Table 6. In Figure 6, Figure 7 and Figure 8, we can observe that the visual maps of four ML-based classification approaches are poor and contain a lot of noise; especially for the GuassianNB, the visual classification map has the most misclassified pixels and is the coarsest. By comparison, the visual classification results of the HybridSN, MSRN_A, 3D_2D_CNN, RSSAN, MSRN_B, DMCN, MSDAN, and DSMSFNet are relatively smooth and exhibit less noise. Among them, the visual classification map of the presented DSMSFNet is the smoothest and generates the least noise. To furthermore demonstrate the robust generalization performance of the DSMSFNet, the training sample proportions of eight DL-based classification algorithms are also changed, namely, 1%, 3%, 5%, 7%, and 10%. Figure 9 exhibits the matching classification results. As the number of training samples increases, the classification performance gap between diverse approaches gradually narrows. Our designed approach still acquires terrific classification results and demonstrates robust generalization performance.

3.4. Discussion

3.4.1. Influence of Different Spatial Sizes

The feature distributions and intrinsic structures of the three benchmark datasets are different, and the most suitable spatial sizes for them are different. Therefore, to investigate the impacts of different spatial sizes, we varied them in the grid of {$15\times 15$, $17\times 17$, $19\times 19$, $21\times 21$, $23\times 23$, $25\times 25$, $27\times 27$, $29\times 29$}; the results of the classification are given in Figure 10. In Figure 10, for the BOW and IP datasets, it is clear that the optimal spatial size is $19\times 19$. For the Houston 2013 dataset, when the spatial size is $23\times 23$, the accuracies of three criteria metrics are unexceptionable. This is because a small spatial size results in too little spatial context, while a large spatial size leads to too many pixels of different classes and noises, which indicate that the middle spatial sizes are appropriate for three benchmark datasets. Hence, for the BOW and IP datasets, the proper spatial size was set to $19\times 19$. For the Houston 2013 dataset, the proper spatial size was set to $23\times 23$.

3.4.2. Influence of Diverse Training Percentage

To analyze the classification performance of our constructed DSMSFNet under different training sample proportions on the three benchmark datasets, the labelled samples were chosen randomly in the grid of $\{1\%,3\%,5\%,7\%10\%,20\%,30\%\}$ as the training set and the corresponding remaining labelled samples as the testing set; the results of the classification are provided in Figure 11. In Figure 11, we can obviously see that for the three benchmark datasets, the accuracies of three criteria metrics gradually increase as the number of training samples increases. For the BOW and Houston 2013 datasets, when the training sample number exceeds 10%, the accuracies of OA, AA, and Kappa increase slowly and become gradually stable. For the IP dataset, when the training sample number exceeds 20%, the accuracies of OA, AA, and Kappa increase slowly and become gradually stable. This is because the IP dataset involves many continuous areas of the species; it needs more training samples to obtain excellent classification accuracies. While the other two datasets have many smaller areas of the species, they need fewer training samples to acquire decent classification results. Therefore, for the three public datasets, we set, respectively, the optimal training sample proportion to 10%, 20%, and 10%.

3.4.3. Influence of Different Numbers of Principal Components

The hyperspectral datasets consist of hundreds of continuous spectral bands with high correlation, which is adverse to the HSI classification. Therefore, before the DSMSFNet extracts decompressed global spectral-spatial features, we conducted PCA on the original hyperspectral datasets to reduce the training parameters of the model and abundant redundant information by lessening the dimension of the original hyperspectral datasets. To explore the relationship between the classification results and the number of principal components, we also conducted some experiments and varied the number of principal components in the grid of {5, 10, 15, 20, 25, 30, 35, 40}. The classification results are provided in Figure 12. In Figure 12, it can be easily found that for the three benchmark datasets, the three criteria metrics gradually increase as the number of principal components increases. For the BOW dataset, when the principal component number is 35, the three criteria metrics are optimal. When the principal component number is over 35, the three criteria metrics begin to decrease. For the IP and Houston 2013 datasets, when the principal component number is 25, the three criteria metrics are optimal. When the principal component number is over 25, the criteria metrics begin to descend. These phenomena partly explain that the principal component number is greater; the developed DSMSFNet can generate more discriminative spectral-spatial information from these principal components. But if the principal component number is too large, the three criteria metrics are not good, which is due to the interference of noise bands and excessive redundant information. Therefore, for the BOW, IP, and Houston 2013 datasets, we set the optimal principal component number to 35, 25, and 25, respectively.

3.4.4. Influence of Diverse Compressed Ratio in the MSFEM

We applied the “squeeze-and excitation” block to our constructed MSFEM to enhance the useful information and suppress other ones. The number of neurons in the first fully connected layer is determined by the compressed ratio $r$. We discuss the classification accuracies of our developed method under diverse compressed ratios $r$, which were set to {1, 2, 3, 4, 5, 6}. The classification results are provided in Figure 13. In Figure 13, we can clearly observe that for the three benchmark datasets, the optimal compressed ratio $r$ is 3, 4, and 6, respectively.

3.4.5. Influence of Different L2 Regularization Parameters

To avoid the overfitting problem, L2 regularization was also introduced into the proposed model. We analyzed the classification results under different L2 regularization parameters, including 0.0005, 0.002, 0.01, 0.02, 0.03, 0.1, and 1. The classification results are provided in Figure 14. In Figure 14, for the three benchmark datasets, as the L2 parameter increases, the three criteria metrics also gradually increase. For the BOW and Houston 2013 datasets, when the L2 parameter is 0.002, the three criteria metrics are superior. When the L2 parameter is over 0.002, the accuracies of OA, AA, and Kappa begin to decline. For the IP dataset, when the L2 parameter is 0.02, the three criteria metrics are optimal. When the L2 parameter is over 0.02, the accuracies of OA, AA, and Kappa begin to decrease. Therefore, for the three common datasets, we set the optimal L2 parameter to 0.002, 0.02, and 0.002, respectively.

3.4.6. Influence of Diverse Convolutional Kernel Numbers of DDBs

The DDB is composed of a $1\times 1$ convolutional layer, a BN layer, a ReLU activation function, and a CRB. Among them, the $1\times 1$ convolutional layer is utilized to reduce the dimension of local decompressed spectral-spatial features. The dimension of output local decompressed spectral-spatial features of each DDB directly influences the classification performance and computational complexity of the presented method. Therefore, we discuss the classification accuracies of our developed method under diverse convolutional kernel numbers of DDBs, which were set to {12, 24, 32, 48, 64}. Figure 15 provides the classification results. In Figure 15, for the BOW dataset, we can observe that when the convolutional kernel number is 64, the accuracies of three criteria metrics are first-rank. For the IP and Houston 2013 datasets, when the convolutional kernel number is 48, the accuracies of three criteria metrics are at their best and the classification performance of our developed DSMSFNet is excellent. Therefore, for the three benchmark datasets, we set the optimal convolutional kernel number to 64, 48, and 48, respectively.

3.4.7. Influence of Various Numbers of DDBs in the DSFEM

The DSFEM includes multiple DDBs and the number of DDBs directly affects the classification performance of our presented approach. If the number of DDBs is too low, the decompressed spectral-spatial features are inadequately extracted. If the number of DDBs is too high, the complexity and training parameters of the model increase. These are adverse to the HSI classification. Therefore, we conducted some experiments to investigate the impacts of various numbers of DDBs in the DSFEM in the grid of $\{2,3,4,5,6\}$. Figure 16 provides the results of the classification of the three public datasets. According to Figure 16, it is easy to see that for the IP datasets, when the number of DDBs is five, the accuracies of the three criteria metrics are obviously better than the other conditions. For the other two datasets, we can visibly see that the three evaluation indices gradually rise with the increase of DDB numbers. As the number of the DDBs is five, the three criteria metrics are excellent. As the number of the DDBs exceeds five, the accuracies of the three criteria metrics begin to decrease. Therefore, for the three benchmark datasets, we set the optimal number of DDBs to five, five, and five, respectively.

3.5. Ablation Study

3.5.1. The Effect of Constructed CConv Layer

To verify the validity of our constructed CConv layer, the ablation experiments were performed on the three benchmark datasets under six different conditions, named case1, case2, case3, case4, case5, and case6, where “×” represents each corresponding DDB that uses a conventional $3\times 3$ convolutional layer instead of CConv layers, and “√” refers to each corresponding DDB that uses CConv layers.

Table 7. The effect of the constructed CConv layer.

Datasets	Case	Location of DDB					Metrics
		DDB1	DDB2	DDB3	DDB4	DDB5	Parameters (M)	Time (s)	OA (%)
BOW	case1	×	×	×	×	×	0.522850	0.84	99.59
	case2	√	×	×	×	×	0.451093	0.82	98.97
	case3	√	√	×	×	×	0.389381	0.77	99.42
	case4	√	√	√	×	×	0.307669	0.77	99.42
	case5	√	√	√	√	×	0.235957	0.76	99.49
	case6	√	√	√	√	√	0.162785	0.72	99.79
IP	case1	×	×	×	×	×	0.319609	1.22	99.54
	case2	√	×	×	×	×	0.279361	1.19	98.89
	case3	√	√	×	×	×	0.240493	1.15	99.67
	case4	√	√	√	×	×	0.200149	1.12	98.77
	case5	√	√	√	√	×	0.159805	1.04	95.86
	case6	√	√	√	√	√	0.118369	1.02	99.62
Houston 2013	case1	×	×	×	×	×	0.356989	2.26	99.68
	case2	√	×	×	×	×	0.316650	2.20	99.64
	case3	√	√	×	×	×	0.276402	2.10	99.55
	case4	√	√	√	×	×	0.236154	1.99	99.56
	case5	√	√	√	√	×	0.195906	1.88	99.62
	case6	√	√	√	√	√	0.155658	1.78	99.88

The black bold highlights which mechanic works best.

shows the corresponding results on the three public datasets, including the training parameter number and testing time.

As shown in Table 7, it can be obviously seen that case 1 requires more parameters for training and a longer time for testing on the three benchmark datasets. This is because all cases utilize the CConv layer, except case 1. This means case 1 cannot reduce network parameters and computational complexity. Compared with the other cases, case 6 requires fewer parameters for training and a shorter time for testing on the three benchmark datasets. This is because the CConv layer is the primary component in the CRB. Each DDB can obtain representative local spectral-spatial information, where the main part of our designed DDB is CRB. DSFEM can capture more discriminative global spectral-spatial features and it comprises five DDBs through dense connection. This confirms that the CConv layer is effective and can effectively decrease the computational cost of our proposed model while enhancing the classification performance.

3.5.2. The Effect of the Designed DSMSFNet Model

To further discuss and demonstrate the importance of the DSFEM and MSFEM of our presented DSMSFNet on the three benchmark datasets, we conducted comparative experiments under three conditions, namely, network 1 (only using the DSFEM), network 2 (only using the MSFEM), and network 3 (using the DSFEM and MSFE, i.e., our proposed method). Figure 17 exhibits the corresponding classification results of the three benchmark datasets.

In Figure 17, for the three benchmark datasets, it is obvious that the three criteria metrics of network 2 are the lowest. For example, for the Houston 2013 dataset, the three criteria metrics are 6.66%, 7.26%, and 7.2% lower than those of network 3, respectively. For the IP dataset, the three criteria metrics are 32.06%, 59.25%, and 36.63% lower than those of network 3, respectively. For the BOW dataset, the three criteria metrics are 1.26%, 1.8%, and 1.37% lower than those of network 3, respectively. These experimental results certify that our designed DSFEM is conducive to the constructed DSMSFNet to not only capture adequately local decompressed spectral-spatial features of each DDB but also generate global decompressed spectral-spatial features by introducing dense connections, which further increase the diversity of spectral-spatial information. Compared with network 2, the three criteria metrics of network 1 are perceptibly raised. For example, for the Houston 2013 dataset, the three criteria metrics are 0.06%, 0.02%, and 0.06% lower than those of network 3, respectively. For the IP dataset, the three criteria metrics are 0.74%, 7.73%, and 0.85% lower than those of network 3, respectively. For the BOW dataset, the three criteria metrics are 0.2%, 0.28%, and 0.22% lower than those of network 3, respectively. These results indicate that the MSFEM can expand the range of available receptive fields while capturing multiscale high-level semantic features at a granular level to further boost the classification performance. Therefore, up to a point, the DSFEM and the MSFEM in our proposed model considerably boost the classification performance.

4. Conclusions

This article presents a decompressed spectral-spatial multiscale semantic feature network (DSMSFNet) for HSI classification. First, we design a CConv layer instead of conventional $3\times 3$ convolutional layer to decrease the training parameter number and computational complexity of our developed model. Second, taking the CConv layer as the dominating component, a CRB is constructed to capture spectral-spatial features in a lightweight feature extraction manner. Third, we devise a DDB, which is composed of a $1\times 1$ convolution layer, a BN layer, a ReLU activation function and a CRB, to generate local decompressed spectral-spatial features. In addition, to avoid gradient disappearance and obtain more comprehensive global decompressed spectral-spatial features, we also introduce the dense connection into our presented DSMSFNet. Furthermore, considering dispelling the redundant information and noise, we raise an MSFEM, which can not only expand the range of available receptive fields but also extract high-level clean multiscale semantic features at a granular level to further boost the classification performance. Finally, a 2D global average pooling layer, two fully connected layers, and a softmax function are utilized to acquire the output results. Additionally, L2 regularization is also introduced into the developed DSMSFNet to improve the classification ability. The experimental results on the three public datasets prove the superiority and effectiveness of our constructed model, while exhibiting competitive performance compared with the advanced classification algorithm.

Nevertheless, there is still room for improvement in our proposed framework. In future work, it is suggested to adaptively design the architecture of a DL model and not rely on specialized knowledge. Another important future avenue of exploration is integrating the semi-supervised or unsupervised training strategies into the presented model while maintaining high-quality classification results.