Determination of Crop Coefficients and Evapotranspiration of Potato in a Semi-Arid Climate Using Canopy State Variables and Satellite-Based NDVI
Abstract
1. Introduction
- to assess the relationship between GCC, LAI, and NDVI for potato variety Mondial, under southern African production conditions;
- to estimate Kc and ET of potato based on FAO-56, the Kcb-fraction of GCC (FGCC) and the Kcb-NDVI approaches;
- to compare ET values from the above three approaches with ET simulated by the LINTUL-Potato model.
2. Materials and Methods
2.1. Study Area, Field Selection and Crop Management
2.2. Field Data Measurements
2.2.1. Weather Information
2.2.2. Irrigation and Drainage
2.2.3. Soil Properties
2.2.4. Canopy Variables and Crop Yield
2.3. Sentinel-2 Satellite NDVI Acquisition
2.4. Crop Coefficients and Evapotranspiration
2.4.1. Crop Coefficients
2.4.2. Crop Evapotranspiration
2.5. Comparison of Crop Evapotranspiration with LINTUL Model Evapotranspiration
2.6. Water Use Efficiency
- WUE based on total water inputs (WUER+I kg ha−1 mm−1) (Equation (18));
- WUE based on water lost through ET (WUEET kg ha−1 mm−1) (Equation (19)).
3. Results
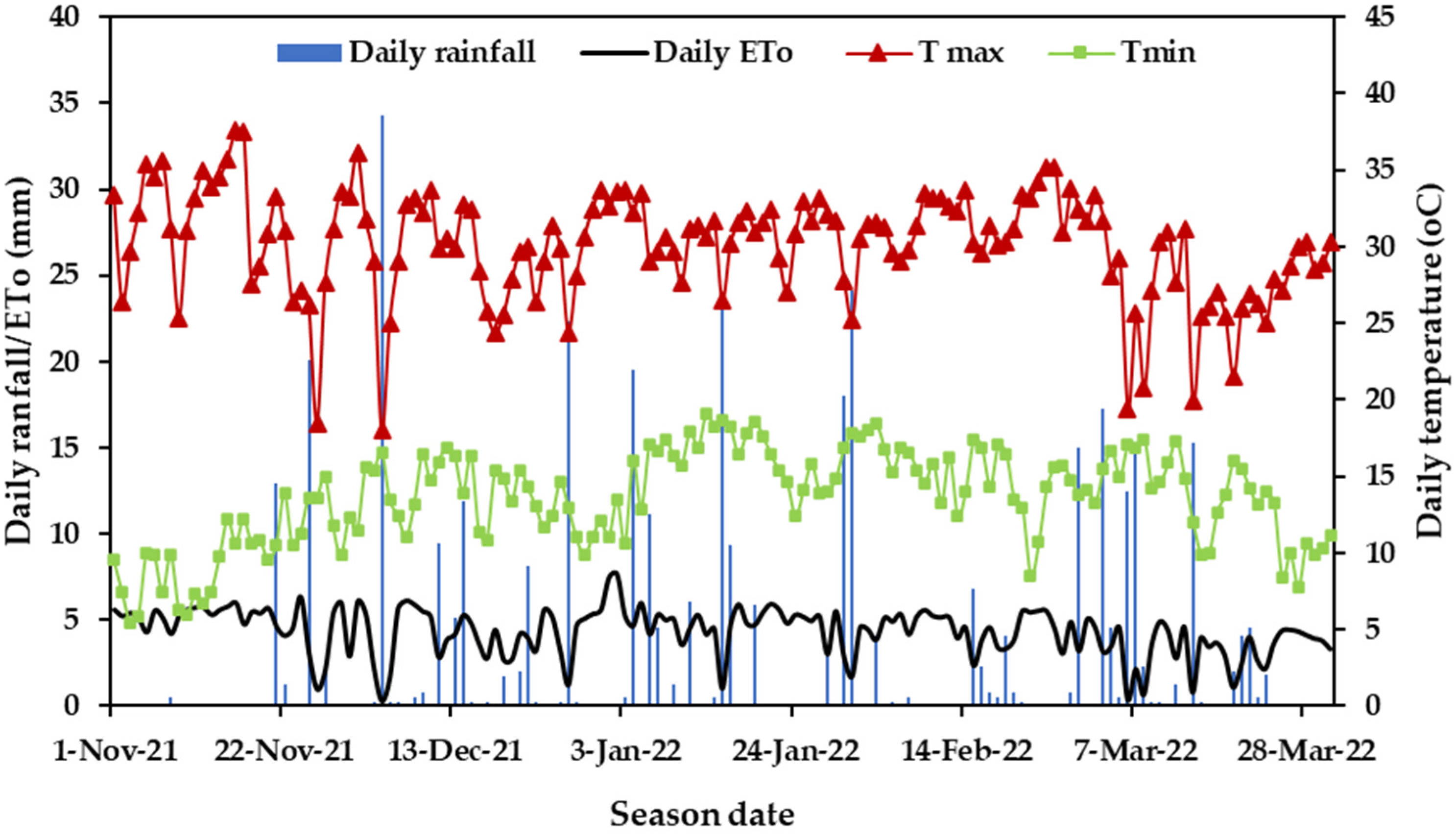
3.1. Weather Conditions during the Growing Season
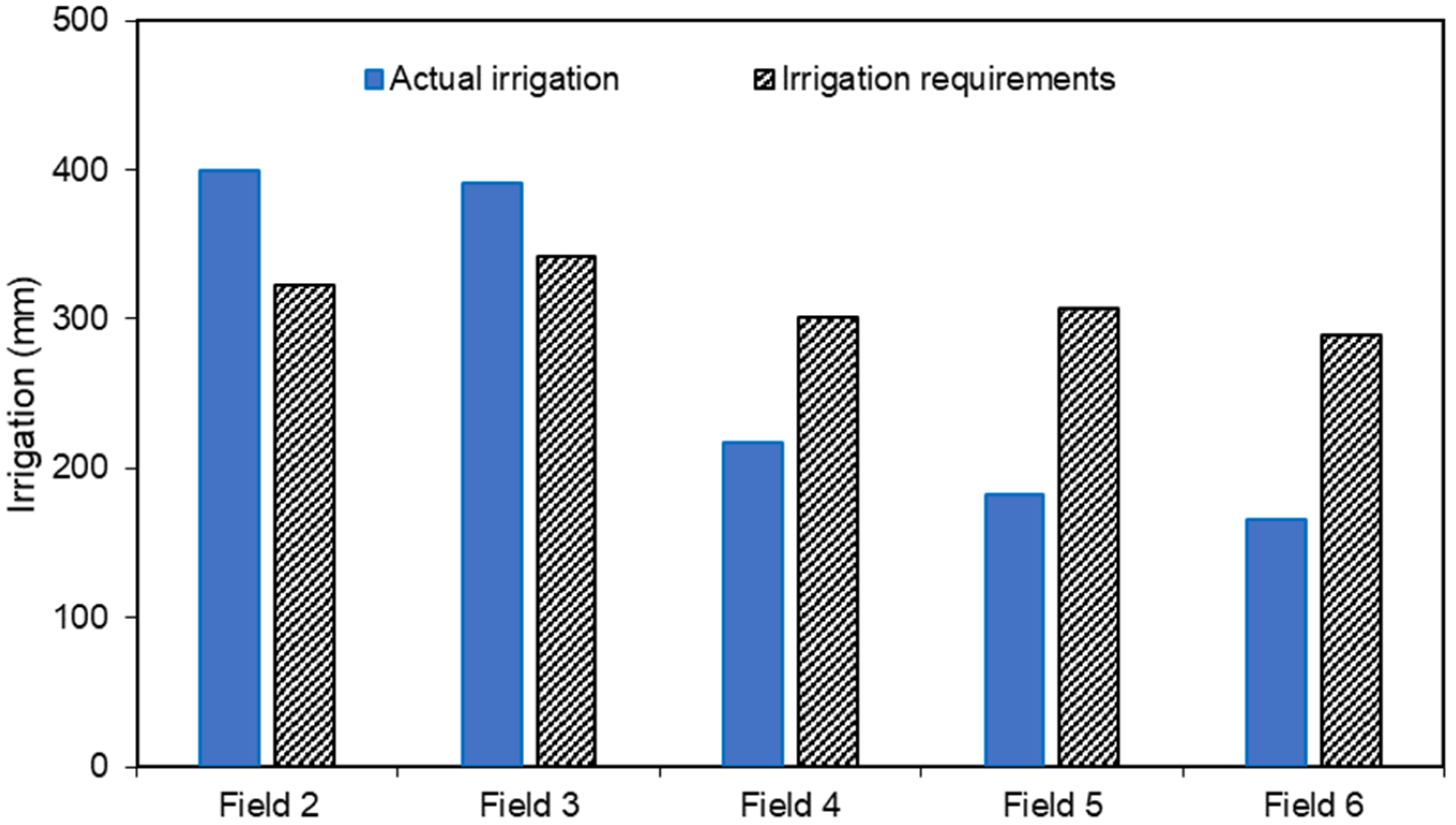
3.2. Growing Season Length, Rainfall, Irrigation, Drainage and Seasonal Reference Evapotranspiration
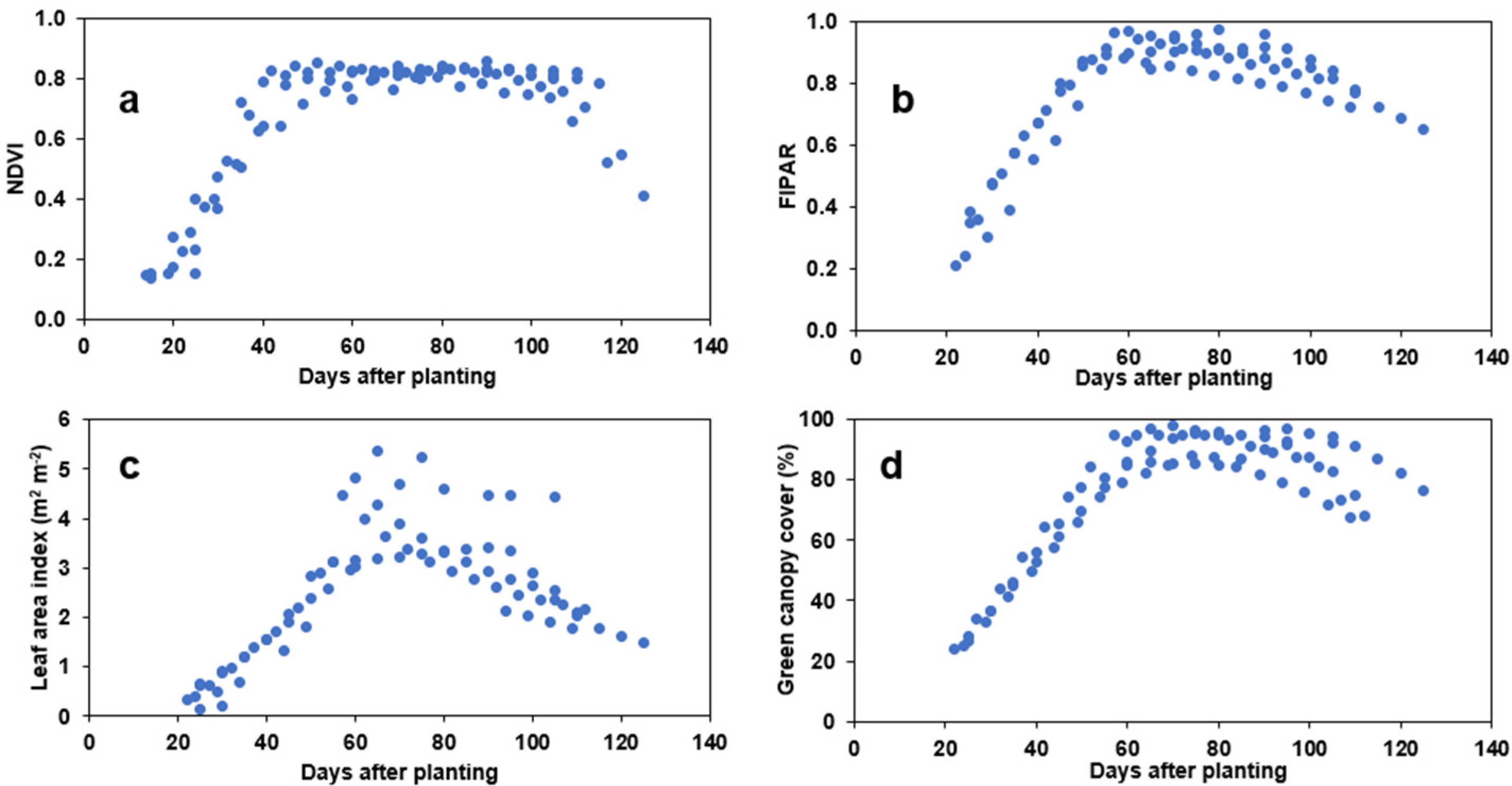
3.3. Crop Canopy Growth and Development
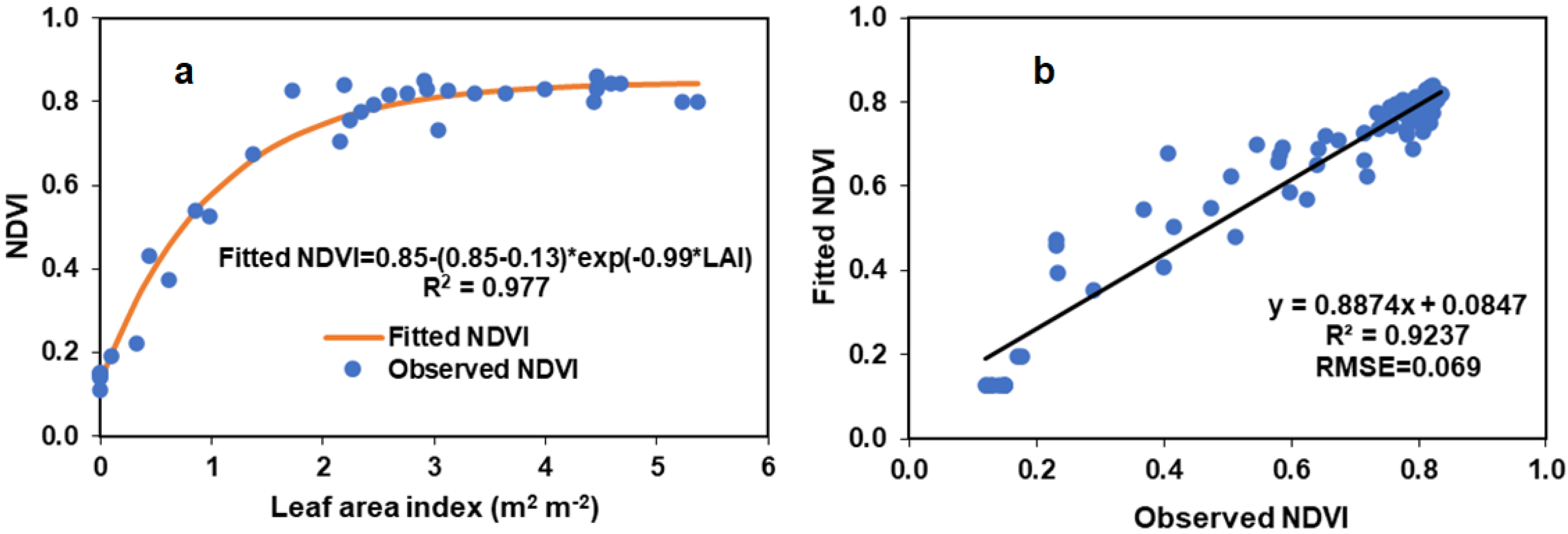
3.4. Relationship between Leaf Area Index and NDVI
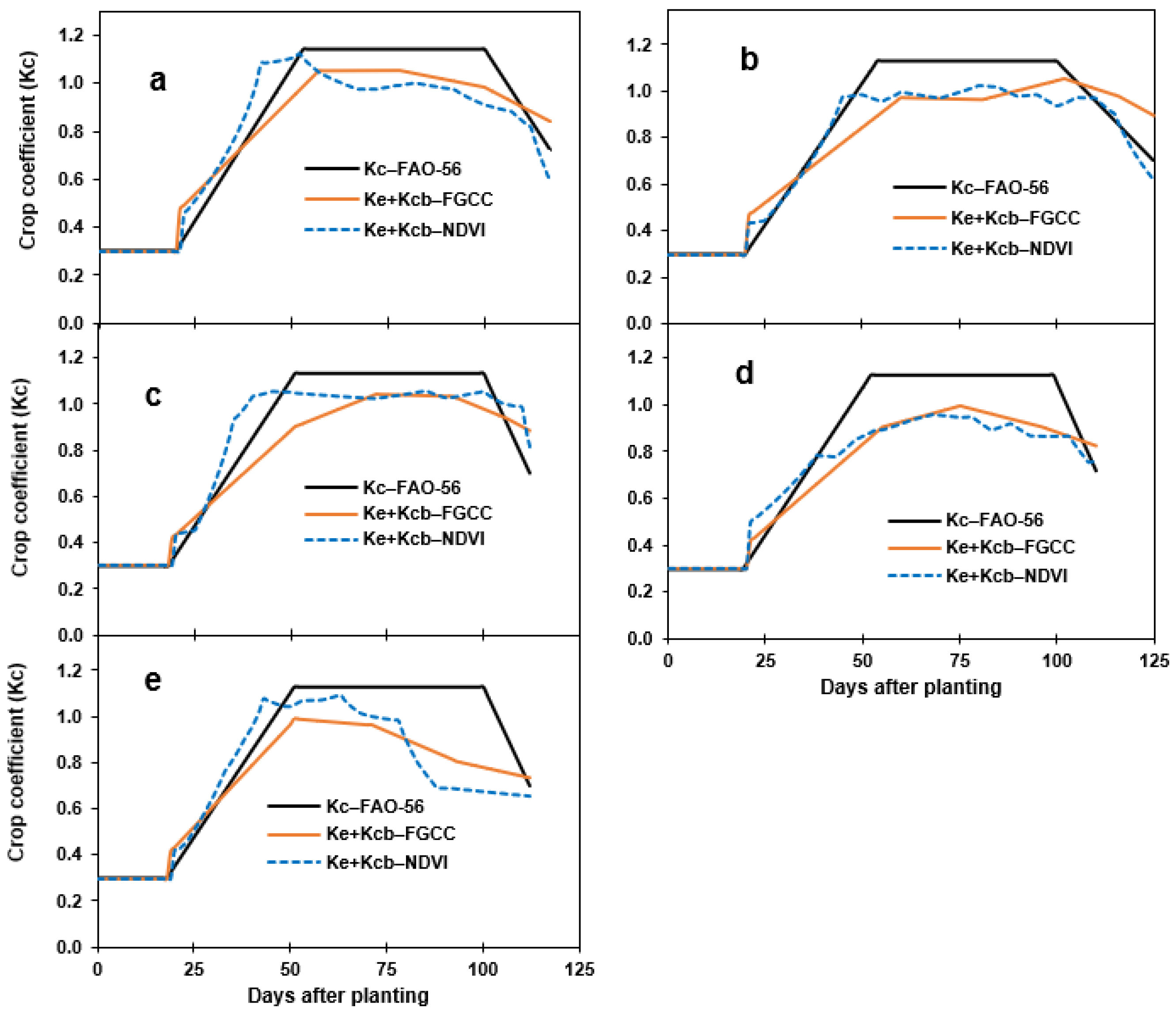
3.5. Comparison of Crop Coefficients for the Different Approaches
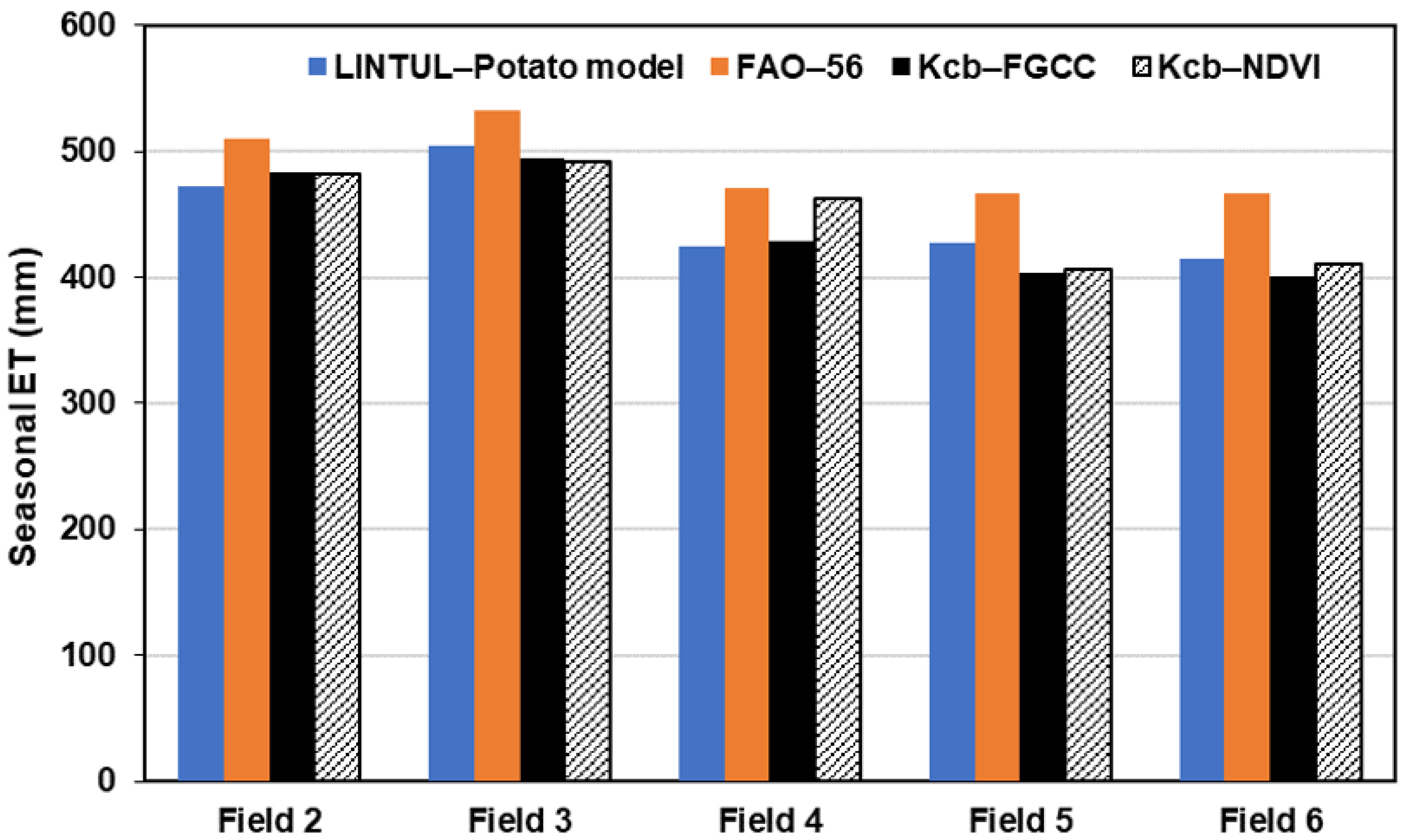
3.6. Evapotranspiration Estimate by the LINTUL Model
3.7. Yield and Water Use Efficiency
4. Discussion
5. Conclusions
- A close association between NDVI development over the season and the development of GCC and FIPAR suggest that NDVI can be successfully used to remotely monitor potato phenology during the season.
- Canopy variables (GCC, FIPAR and LAI) indicate that effective canopy cover was attained at GCC of 95%, FIPAR of 0.9, LAI of 3.5 m2 m−2 and NDVI of 0.85. The NDVI-LAI relationship was observed to saturate at LAI of about 3.5 m2 m−2.
- In comparison with the FAO-56 approach, Kc values based on FGCC and NDVI were slightly lower during the mid-season season growth stage. However, the Kc profiles based on FGCC and NDVI represented actual crop development and were therefore expected to be more accurate than the FAO-56 approach.
- Seasonal ET based on the Kcb-FGCC and Kcb-NDVI approaches compared well with ET simulated by the LINTUL-Potato model. This suggested that Kcb-FGCC and Kcb-NDVI approaches offer alternative ways of estimating crop ET using readily available ETo and NDVI or canopy variable information. These results reinforce the utility of the modified analytical approach proposed by Choudhury et al. [17] and modified by Campos et al. [24] for potato ET estimation to facilitate irrigation management.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stevens, J.; Sanewe, A.; Steyn, J.M.; Annandale, J.G.; Stirzaker, R.J. Improving On-Farm Irrigation Water and Solute Management Using Simple Tools and Adaptive Learning; Report No. TT821/20; Water Research Commission: Pretoria, South Africa, 2020; 188p. [Google Scholar]
- Basson, M.S. Water development in South Africa. In Proceedings of the Water in the Green Economy in Practice: Towards Rio+20, Zaragoza, Spain, 3–5 October 2011. [Google Scholar]
- Franke, A.C.; Steyn, J.M.; Ranger, K.S.; Haverkort, A.J. Developing environmental principles, criteria, indicators and norms for potato production in South Africa through field surveys and modelling. Agric. Syst. 2011, 104, 297–306. [Google Scholar] [CrossRef][Green Version]
- Steyn, J.M.; Franke, A.C.; van der Waals, J.E.; Haverkort, A.J. Resource use efficiencies as indicators of ecological sustainability in potato production: A South African case study. Field Crops Res. 2016, 199, 136–149. [Google Scholar] [CrossRef]
- Machakaire, A.T.B.; Steyn, J.M.; Caldiz, D.O.; Haverkort, A.J. Forecasting yield and tuber size of processing potatoes in South Africa using the LINTUL-Potato-DSS Model. Potato Res. 2016, 59, 195–206. [Google Scholar] [CrossRef]
- Charlesworth, P. Soil Water Monitoring. In Soil Water and Ground Water Sampling; CSIRO Land and Water: Canberra, Australia, 2000; 100p. [Google Scholar]
- Annandale, J.G.; Stirzaker, R.J.; Singels, A.; van der Laan, M.; Laker, M.C. Irrigation scheduling research: South African experiences and future prospects. Water SA 2011, 37, 751–764. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- De Jager, J.; Van Zyl, W. Atmospheric evaporative demand and evaporation coefficient concepts. Water SA 1989, 15, 103–110. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration (Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage Paper No.56; FAO: Rome, Italy, 1998; Volume 56, pp. 1–333. [Google Scholar]
- Pôças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficients: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233, 106081. [Google Scholar] [CrossRef]
- Mateos, L.; González-Dugo, M.P.; Testi, L.; Villalobos, F.J. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agric. Water Manag. 2013, 125, 81–91. [Google Scholar] [CrossRef]
- Neale, C.M.U.; Jayanthi, H.; Wright, J.L. Irrigation water management using high resolution airborne remote sensing. Irrig. Drain. Syst. 2005, 19, 321–336. [Google Scholar] [CrossRef]
- Bausch, W.C. Soil background effects on reflectance-based crop coefficients for corn. Remote Sens. Environ. 1993, 46, 213–222. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Mateos, L. Spectral vegetation indices for benchmarking water productivity of irrigated cotton and sugarbeet crops. Agric. Water Manag. 2008, 95, 48–58. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.C.B.; Kharrou, M.H.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci. 2005, 24, 1–14. [Google Scholar] [CrossRef]
- Barker, J.B.; Heeren, D.M.; Neale, C.M.U.; Rudnick, D.R. Evaluation of variable rate irrigation using a remote-sensing-based model. Agric. Water Manag. 2018, 203, 63–74. [Google Scholar] [CrossRef]
- Jayanthi, H.; Neale, C.M.U.; Wright, J.L. Development and validation of canopy reflectance-based crop coefficient for potato. Agric. Water Manag. 2007, 88, 235–246. [Google Scholar] [CrossRef]
- Er-Raki, S.; Rodriguez, J.C.; Garatuza-Payan, J.; Watts, C.J.; Chehbouni, A. Determination of crop evapotranspiration of table grapes in a semi-arid region of Northwest Mexico using multi-spectral vegetation index. Agric. Water Manag. 2013, 122, 12–19. [Google Scholar] [CrossRef]
- Jin, X.; Yang, G.; Xue, X.; Xu, X.; Li, Z.; Feng, H. Validation of two Huanjing-1A/B satellite-based FAO-56 models for estimating winter wheat crop evapotranspiration during mid-season. Agric. Water Manag. 2017, 189, 27–38. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Suyker, A.E.; Arkebauer, T.J.; Gonçalves, I.Z. Reflectance-based crop coefficients REDUX: For operational evapotranspiration estimates in the age of high producing hybrid varieties. Agric. Water Manag. 2017, 187, 140–153. [Google Scholar] [CrossRef]
- Moeletsi, M.E.; Walker, S. Rainy season characteristics of the Free State Province of South Africa with reference to rain-fed maize production. Water SA 2012, 38, 775–782. [Google Scholar] [CrossRef]
- Kruger, A.C.; Mbatha, S. Regional Weather and Climate of South Africa: Gauteng; South African Weather Service: Pretoria, South Africa, 2021.
- Kooman, P.L.; Haverkort, A.J. Modelling development and growth of the potato crop influenced by temperature and daylength: LINTUL-POTATO. In Potato Ecology and Modelling of Crops under Conditions Limiting Growth, 1st ed.; Haverkort, A.J., MacKerron, D.K.L., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; pp. 41–60. [Google Scholar]
- Alva, A.; Fan, M.; Qing, C.; Rosen, C.; Ren, H. Improving nutrient-use efficiency in chinese potato production: Experiences from the United States. J. Crop Improv. 2011, 25, 46–85. [Google Scholar] [CrossRef]
- Iwama, K. Physiology of the potato: New insights into root system and repercussions for crop management. Potato Res. 2008, 51, 333–353. [Google Scholar] [CrossRef]
- Djaman, K.; Koudahe, K.; Saibou, A.; Darapuneni, M.; Higgins, C.; Irmak, S. Soil water dynamics, effective rooting zone, and evapotranspiration of sprinkler irrigated potato in a sandy loam soil. Agronomy 2022, 12, 864. [Google Scholar] [CrossRef]
- Patrignani, A.; Ochsner, T.E. Canopeo: A powerful new tool for measuring fractional green canopy cover. Agron. J. 2015, 107, 2312–2320. [Google Scholar] [CrossRef]
- Haverkort, A.J. Potato Handbook: Crop of the Future; Aardappelwereld BV: The Hague, The Netherlands, 2018; p. 592. [Google Scholar]
- Er-Raki, S.; Chehbouni, A.; Duchemin, B. Combining satellite remote sensing data with the FAO-56 dual approach for water use mapping in irrigated wheat fields of a semi-arid region. Remote Sens. 2010, 2, 375–387. [Google Scholar] [CrossRef]
- Franke, A.C.; Haverkort, A.J.; Steyn, J.M. Climate change and potato production in contrasting South African agro-ecosystems 2. Assessing risks and opportunities of adaptation strategies. Potato Res. 2013, 56, 51–66. [Google Scholar] [CrossRef]
- Haverkort, A.J.; Franke, A.C.; Steyn, J.M.; Pronk, A.; Caldiz, D.; Kooman, P. A robust potato model: LINTUL-POTATO-DSS. Potato Res. 2015, 58, 313–327. [Google Scholar] [CrossRef]
- Prasad, R.; Hochmuth, G.J.; Boote, K.J. Estimation of nitrogen pools in irrigated potato production on sandy soil using the model SUBSTOR. PLoS ONE 2015, 1, e0117891. [Google Scholar] [CrossRef]
- Clément, C.C.; Cambouris, A.N.; Ziadi, N.; Zebarth, B.J.; Karam, A. Potato yield response and seasonal nitrate leaching as influenced by nitrogen management. Agronomy 2021, 11, 2055. [Google Scholar] [CrossRef]
- Gobin, A.; Sallah, A.H.M.; Curnel, Y.; Delvoye, C.; Weiss, M.; Wellens, J.; Piccard, I.; Planchon, V.; Tychon, B.; Goffart, J.P.; et al. Crop phenology modelling using proximal and satellite sensor data. Remote Sens. 2023, 15, 2090–2109. [Google Scholar] [CrossRef]
- Irmak, S.; Odhiambo, L.O.; Specht, J.E.; Djaman, K. Hourly and daily single and basal evapotranspiration crop coefficients as a function of growing degree days, days after emergence, leaf area index, fractional green canopy cover, and plant phenology for soybean. Trans. ASABE 2013, 56, 1785–1803. [Google Scholar]
- Bala, S.K.; Islam, A.S. Correlation between potato yield and MODIS-derived vegetation indices. Int. J. Remote Sens. 2009, 30, 2491–2507. [Google Scholar] [CrossRef]
- Johnson, D.M. A comprehensive assessment of the correlations between field crop yields and commonly used MODIS products. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 65–81. [Google Scholar] [CrossRef]
- Newton, I.H.; Tariqul Islam, A.F.M.; Saiful Islam, A.K.M.; Tarekul Islam, G.M.; Tahsin, A.; Razzaque, S. Yield prediction model for potato using Landsat time series images driven vegetation indices. Remote Sens. Earth Syst. Sci. 2018, 1, 29–38. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; López-Urrea, R.; Hunsaker, D.J.; Mota, M.; Mohammadi Shad, Z. Standard single and basal crop coefficients for vegetable crops, an update of FAO56 crop water requirements approach. Agric. Water Manag. 2021, 243, 106196. [Google Scholar] [CrossRef]
- Wright, J.L. New evapotranspiration crop coefficients. J. Irrig. Drain. Div. 1982, 108, 57–74. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.A.; Paredes, P.; Cunha, M.; Pereira, L.S. Estimation of actual crop coefficients using remotely sensed vegetation indices and soil water balance modelled data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef]
- Machakaire, A.T.B.; Steyn, J.M.; Franke, A.C. Assessing evapotranspiration and crop coefficients of potato in a semi-arid climate using Eddy Covariance techniques. Agric. Water Manag. 2021, 255, 107029. [Google Scholar] [CrossRef]
- Johnson, L.F.; Trout, T.J. Satellite NDVI assisted monitoring of vegetable crop evapotranspiration in california’s san Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef]
- Steyn, J.M.; Du Plessis, H.F. Soil, water and irrigation requirements of potatoes. In Guide to Potato Production in South Africa, 1st ed.; Denner, F.D., Venter, S., Niederwieser, J., Eds.; ARC-Roodeplaat, Vegetable and Ornamental Plants Institute: Pretoria, South Africa, 2012; pp. 123–134. [Google Scholar]
- Kadam, S.A.; Gorantiwar, S.D.; Mandre, N.P.; Tale, D.P. Crop coefficient for potato crop evapotranspiration estimation by field water balance method in semi-arid region, Maharashtra, India. Potato Res. 2021, 64, 421–433. [Google Scholar] [CrossRef]
- Gonzalez, T.F.; Pavek, M.J.; Holden, Z.J.; Garza, R. Evaluating potato evapotranspiration and crop coefficients in the Columbia Basin of Washington state. Agric. Water Manag. 2023, 286, 108371. [Google Scholar] [CrossRef]
- Unites States Bureau of Reclaimation (USBR). Agrinet Crop Coefficients: Potatoes. 2016. Available online: https://www.usbr.gov/pn/agrimet/cropcurves/POTAcc.html (accessed on 28 July 2023).
- Chakroun, H.; Zemni, N.; Benhamid, A.; Dellaly, V.; Slama, F.; Bouksila, F.; Berndtsson, R. Evapotranspiration in semi-arid climate:Remote sensing vs. soil water simulation. Sensors 2023, 23, 2823. [Google Scholar] [CrossRef]
- Steyn, J.M.; Kagabo, D.M.; Annandale, J.G. Potato growth and yield responses to irrigation regimes in contrasting seasons of a subtropical region. In Proceedings of the 8th African Crop Science Society Conference, El-Minia, Egypt, 27–31 October 2007; pp. 1647–1651. [Google Scholar]
- Ierna, A.; Mauromicale, G. Potato growth, yield and water productivity response to different irrigation and fertilization regimes. Agric. Water Manag. 2018, 201, 21–26. [Google Scholar] [CrossRef]
- Kiziloglu, F.M.; Sahin, U.; Tune, T.; Diler, S. The effect of deficit irrigation on potato evapotranspiration and tuber yield under cool season and semi-arid climatic conditions. J. Agron. 2006, 5, 284–288. [Google Scholar]
- French, A.N.; Hunsaker, D.J.; Sanchez, C.A.; Saber, M.; Gonzalez, J.R.; Anderson, R. Satellite-based NDVI crop coefficients and evapotranspiration with eddy covariance validation for multiple durum wheat fields in the US Southwest. Agric. Water Manag. 2020, 239, 106266. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Barnes, E.M.; Clarke, T.R.; Fitzgerald, G.J.; Pinter, P.J. Cotton irrigation scheduling using remotely sensed and FAO-56 basal crop coefficients. Trans. Am. Soc. Agric. Eng. 2005, 48, 1395–1407. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Barnes, E.M.; Kimball, B.A. Estimating cotton evapotranspiration crop coefficients with a multispectral vegetation index. Irrig. Sci. 2003, 22, 95–104. [Google Scholar] [CrossRef]
- Onder, S.; Caliskan, M.E.; Onder, D.; Caliskan, S. Different irrigation methods and water stress effects on potato yield and yield components. Agric. Water Manag. 2005, 73, 73–86. [Google Scholar] [CrossRef]
- Fandika, I.R.; Kemp, P.D.; Millner, J.P.; Horne, D.; Roskruge, N. Irrigation and nitrogen effects on tuber yield and water use efficiency of heritage and modern potato cultivars. Agric. Water Manag. 2016, 170, 148–157. [Google Scholar] [CrossRef]
- Djaman, K.; Irmak, S.; Koudahe, K.; Allen, S. Irrigation management in potato (Solanum tuberosum L.) production: A Review. Sustainability 2021, 13, 1504. [Google Scholar] [CrossRef]

| Field No. | Field Size (ha) | Planting Date | Vine Kill-Off Date | Monitoring | N-P-K (kg ha−1) |
|---|---|---|---|---|---|
| 1 | 14 | 04-Aug-21 | 17-Nov-21 | Less intensive | - |
| 2 | 22 | 08-Nov-21 | 05-Mar-22 | Intensive | 302-160-291 |
| 3 | 18 | 05-Nov-21 | 10-Mar-22 | Intensive | 229-281-287 |
| 4 | 36 | 15-Nov-21 | 07-Mar-22 | Intensive | 316-160-300 |
| 5 | 32 | 11-Nov-21 | 02-Mar-22 | Intensive | 311-171-295 |
| 6 | 20 | 17-Nov-21 | 09-Mar-22 | Intensive | 322-138-311 |
| Field No | I (mm day−1) | CU (%) | AE (%) |
|---|---|---|---|
| 1 | - | - | - |
| 2 | 8.6 | 81 | 91 |
| 3 | 8.9 | 93 | 89 |
| 4 | 8.5 | 88 | 86 |
| 5 | 8.8 | 95 | 93 |
| 6 | 9.8 | 92 | 92 |
| Field No. | Soil Layer (m) | pH (H2O) | Clay (%) | Silt (%) | Sand (%) | CEC (cmol + kg−1) | Available P (Bray 1) (mg kg−1) | Exchangeable Cations (mg kg−1) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| K+ | Ca2+ | Mg2+ | ||||||||
| 1 | - | - | - | - | - | - | - | - | - | - |
| 2 | 0–0.3 | 6.8 | 10 | 2 | 89 | 3.3 | 59 | 124 | 429 | 81 |
| 0.3–0.6 | 6.7 | 10 | 1 | 89 | 3.3 | 30 | 140 | 429 | 77 | |
| 3 | 0–0.3 | 6.0 | 10 | 1 | 89 | 2.7 | 103 | 133 | 334 | 70 |
| 0.3–0.6 | 6.0 | 9 | 2 | 89 | 2.9 | 87 | 219 | 326 | 83 | |
| 4 | 0–0.3 | 6.5 | 9 | 2 | 89 | 3.2 | 113 | 231 | 355 | 89 |
| 0.3–0.6 | 6.4 | 8 | 2 | 90 | 3.2 | 53 | 261 | 334 | 90 | |
| 5 | 0–0.3 | 6.4 | 10 | 2 | 88 | 3.1 | 62 | 251 | 325 | 94 |
| 0.3–0.6 | 6.5 | 10 | 2 | 88 | 3.3 | 80 | 280 | 331 | 103 | |
| 6 | 0–0.3 | 6.4 | 11 | 2 | 87 | 3.6 | 84 | 287 | 381 | 103 |
| 0.3–0.6 | 6.5 | 11 | 1 | 88 | 3.7 | 46 | 239 | 420 | 105 | |
| Field No. | Growing Season Length (days) | Rainfall (mm) | Effective Irrigation (mm) | Drainage (mm) | Seasonal ETo (mm) |
|---|---|---|---|---|---|
| 2 | 117 | 298 | 399 | 89 | 608 |
| 3 | 125 | 374 | 391 | 103 | 639 |
| 4 | 112 | 253 | 217 | 63 | 554 |
| 5 | 111 | 291 | 182 | 12 | 560 |
| 6 | 112 | 344 | 165 | 7 | 550 |
| Average | 115 | 312 | 271 | 55 | 582 |
| Field No. | Kc = FAO-56 | Kc = Kcb-FGCC | Kc = Kcb-NDVI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | Dev | Mid | Late | Initial | Dev | Mid | Late | Initial | Dev | Mid | Late | |
| 2 | 0.30 | 0.72 | 1.14 | 0.92 | 0.30 | 0.72 | 1.03 | 0.91 | 0.30 | 0.84 | 0.99 | 0.82 |
| 3 | 0.30 | 0.71 | 1.13 | 0.91 | 0.30 | 0.68 | 0.98 | 0.99 | 0.30 | 0.71 | 0.99 | 0.86 |
| 4 | 0.30 | 0.71 | 1.13 | 0.90 | 0.30 | 0.65 | 1.01 | 0.93 | 0.30 | 0.79 | 1.03 | 0.98 |
| 5 | 0.30 | 0.71 | 1.13 | 0.91 | 0.30 | 0.63 | 0.94 | 0.86 | 0.30 | 0.71 | 0.92 | 0.82 |
| 6 | 0.30 | 0.70 | 1.13 | 0.90 | 0.30 | 0.69 | 0.91 | 0.76 | 0.30 | 0.79 | 0.90 | 0.66 |
| Mean | 0.30 | 0.71 | 1.13 | 0.91 | 0.30 | 0.67 | 0.97 | 0.89 | 0.30 | 0.77 | 0.97 | 0.83 |
| Field No. | ET-FAO-56 (mm day−1) | ET-Kcb-FGCC (mm day−1) | ET-Kcb-NDVI (mm day−1) | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| 2 | 0.91 | 0.77 | 0.76 | 0.52 | 0.75 | 0.50 |
| 3 | 0.89 | 0.75 | 0.81 | 0.53 | 0.79 | 0.51 |
| 4 | 0.77 | 0.63 | 0.73 | 0.51 | 0.60 | 0.36 |
| 5 | 0.82 | 0.69 | 0.86 | 0.66 | 0.81 | 0.65 |
| 6 | 0.74 | 0.61 | 0.79 | 0.63 | 0.92 | 0.68 |
| All | 0.83 | 0.69 | 0.79 | 0.57 | 0.78 | 0.54 |
| Field No. | Fresh Tuber Yield (t ha−1) | WUER+I (kg ha−1 mm−1) | WUEET_FAO (kg ha−1 mm−1) | WUEET_FGCC (kg ha−1 mm−1) | WUEET_NDVI (kg ha−1 mm−1) | WUEET_LINTUL (kg ha−1 mm−1) |
|---|---|---|---|---|---|---|
| 2 | 91 | 130.3 | 178.0 | 188.0 | 188.4 | 192.4 |
| 3 | 110 | 144.3 | 207.5 | 223.5 | 224.4 | 218.6 |
| 4 | 114 | 241.9 | 241.4 | 265.0 | 246.1 | 267.5 |
| 5 | 94 | 199.2 | 202.1 | 233.7 | 232.0 | 220.6 |
| 6 | 69 | 136.3 | 148.9 | 173.1 | 169.3 | 167.2 |
| Mean | 95.7 | 170.4 | 195.6 | 216.7 | 212.0 | 213.3 |
| Study | Study Area | Climate | Methodology | Variety | Initial | Development | Mid- Season | Late- Season |
|---|---|---|---|---|---|---|---|---|
| This study [10] | South Africa | Semi-arid | FAO-56 | Mondial | 0.30 | 0.71 | 1.13 | 0.91 |
| This study | South Africa | Semi-arid | Kcb-FGCC | Mondial | 0.30 | 0.67 | 0.97 | 0.89 |
| This study | South Africa | Semi-arid | Kcb-NDVI | Mondial | 0.30 | 0.77 | 0.97 | 0.83 |
| [49] | South Africa | Semi-arid | Pan evap. | Up-to-Date | 0.45 | 0.65 | 0.83 | 0.60 |
| [47] | South Africa | Semi-arid | ECV | Mondial | - | 1.00 | 1.15 | 0.87 |
| [47] | South Africa | Semi-arid | ECV | Mondial | - | 0.45 | 0.86 | - |
| [50] | India | Semi-arid | SWB | Kufri Pukraj | - | 0.55 | 1.11 | 1.01 |
| [51] | USA | Arid | SWB | Russet varieties | 0.40 | - | 0.95 | 0.57 |
| [52] | USA | Arid | SWB | Russet Burbank | 0.30 | 0.69 | 0.93 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukiibi, A.; Franke, A.C.; Steyn, J.M. Determination of Crop Coefficients and Evapotranspiration of Potato in a Semi-Arid Climate Using Canopy State Variables and Satellite-Based NDVI. Remote Sens. 2023, 15, 4579. https://doi.org/10.3390/rs15184579
Mukiibi A, Franke AC, Steyn JM. Determination of Crop Coefficients and Evapotranspiration of Potato in a Semi-Arid Climate Using Canopy State Variables and Satellite-Based NDVI. Remote Sensing. 2023; 15(18):4579. https://doi.org/10.3390/rs15184579
Chicago/Turabian StyleMukiibi, Alex, Angelinus Cornelius Franke, and Joachim Martin Steyn. 2023. "Determination of Crop Coefficients and Evapotranspiration of Potato in a Semi-Arid Climate Using Canopy State Variables and Satellite-Based NDVI" Remote Sensing 15, no. 18: 4579. https://doi.org/10.3390/rs15184579
APA StyleMukiibi, A., Franke, A. C., & Steyn, J. M. (2023). Determination of Crop Coefficients and Evapotranspiration of Potato in a Semi-Arid Climate Using Canopy State Variables and Satellite-Based NDVI. Remote Sensing, 15(18), 4579. https://doi.org/10.3390/rs15184579






