Validation of Surface Waves Investigation and Monitoring Data against Simulation by Simulating Waves Nearshore and Wave Retrieval from Gaofen-3 Synthetic Aperture Radar Image
Abstract
:1. Introduction
2. Datasets
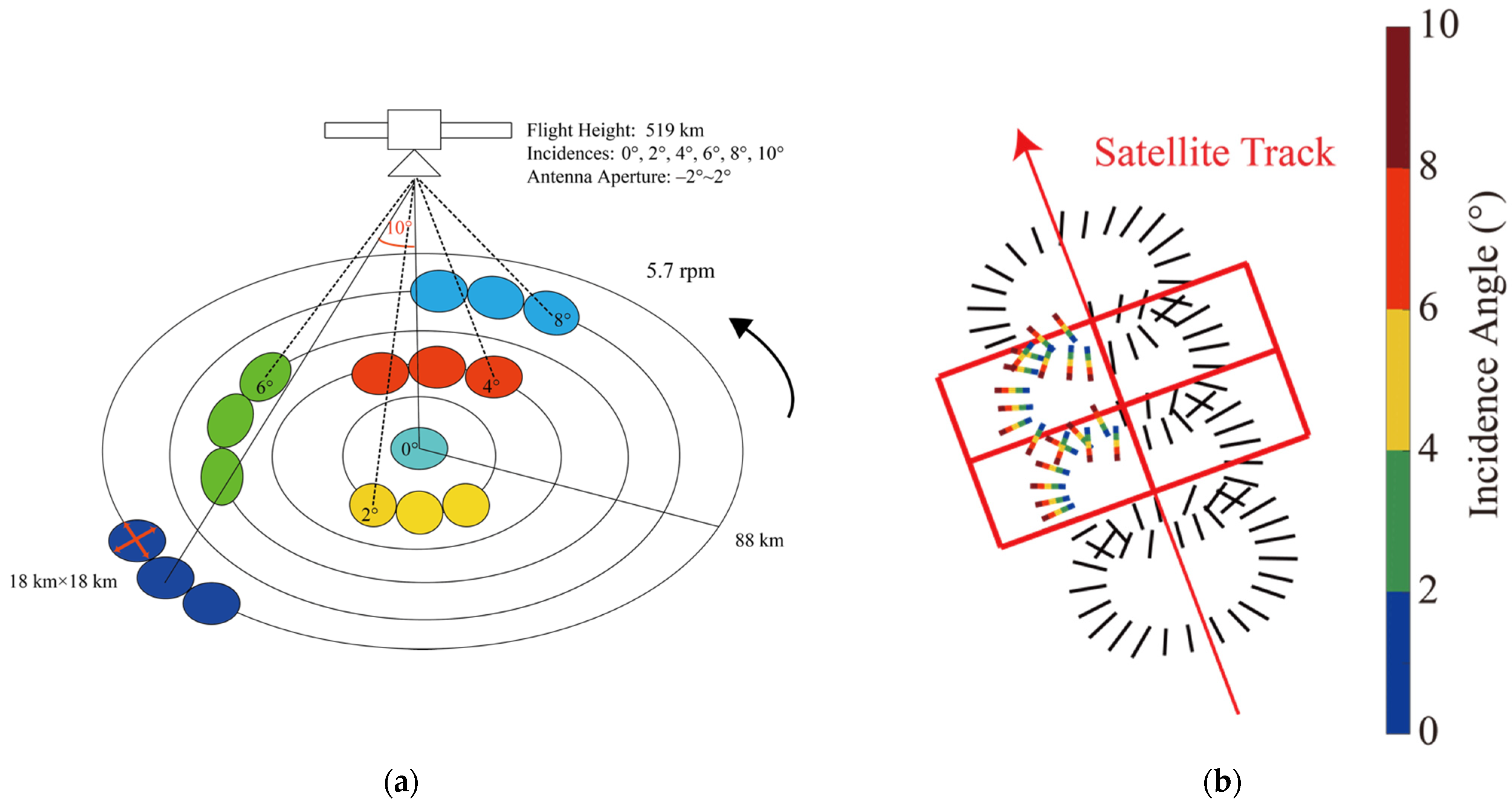
2.1. SWIM Data Onboard CFOSAT
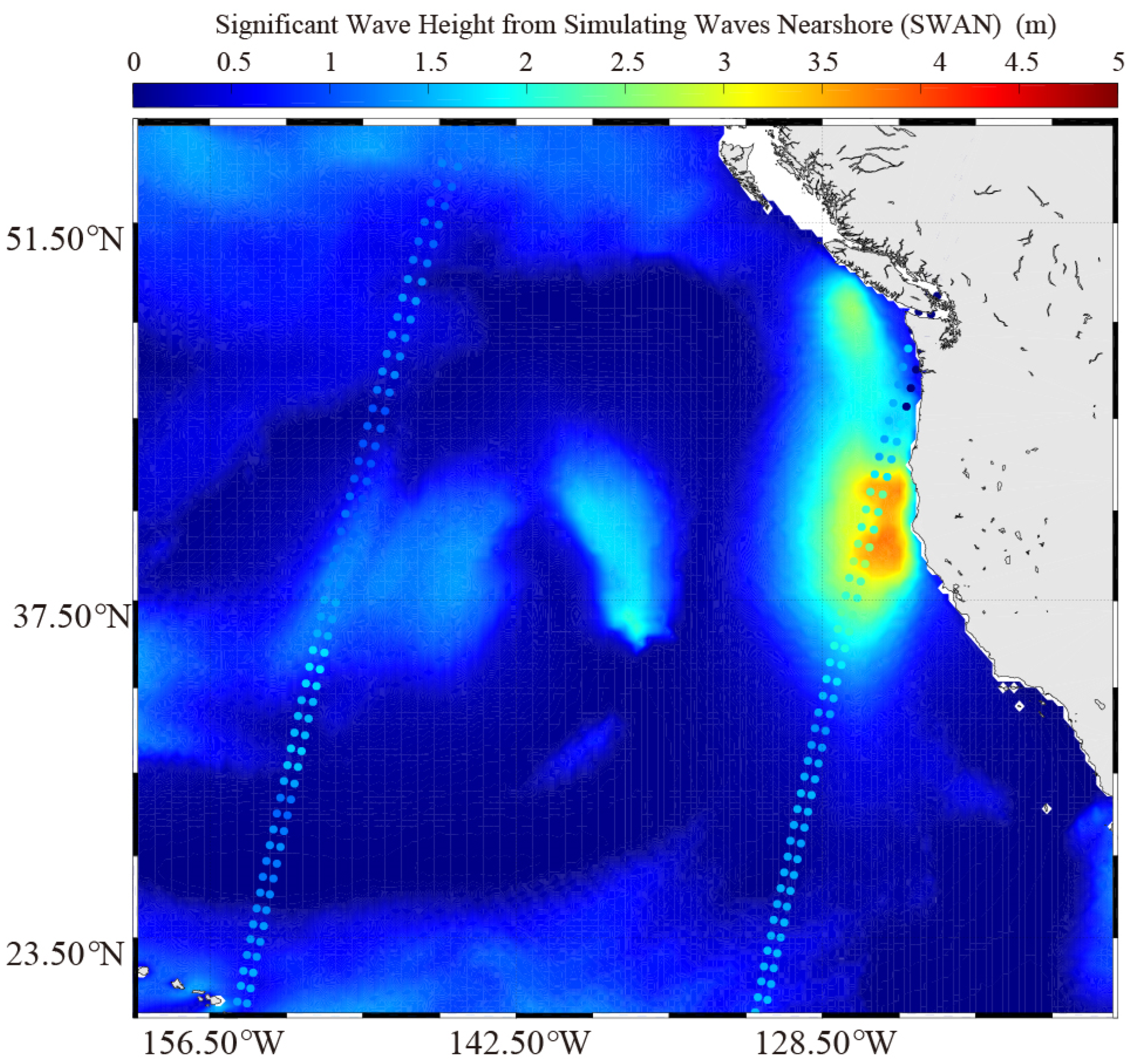
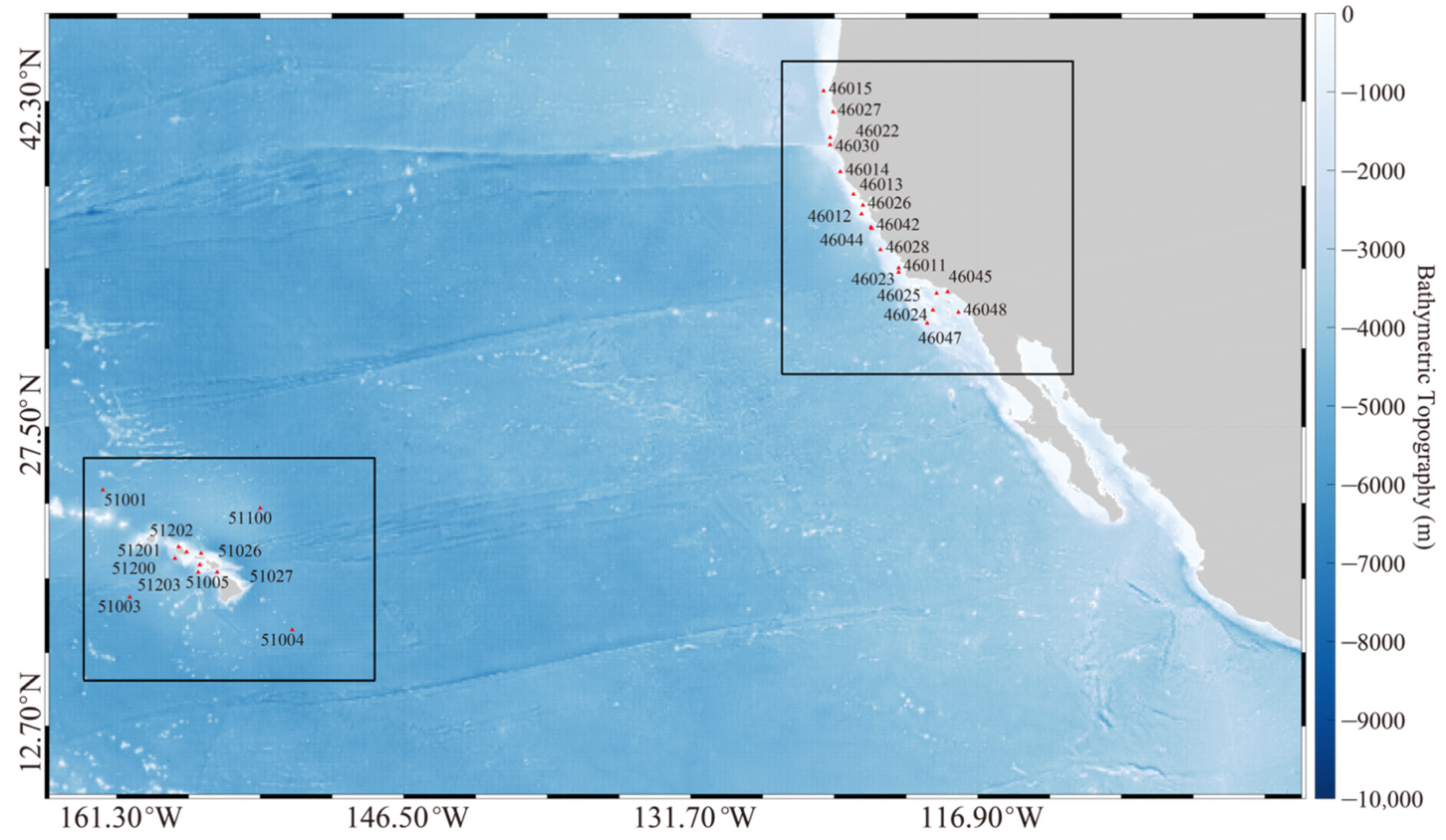
2.2. Model Settings of SWAN and NDBC Buoys
- The two-dimensional wave spectrum was resolved into 24 regular azimuthal directions with a 15° step;
- The frequency bins ranged logarithmically from 0 to 1, at an interval of Δf/f = 0.903;
- The spatial resolution of the simulated wave fields was a 0.1° grid with a 60 min temporal resolution;
- The input/dissipation terms were selected, referred to as nonlinear saturation-based white-capping combined with wind input (WESTH);
- The various physical processes included white-capping (WCAPping), nonlinear quadruplet wave interactions (QUADrupl), depth-induced wave breaking in shallow waters (BREaking), bottom friction (FRICtion) and triad wave–wave interactions (TRIad).
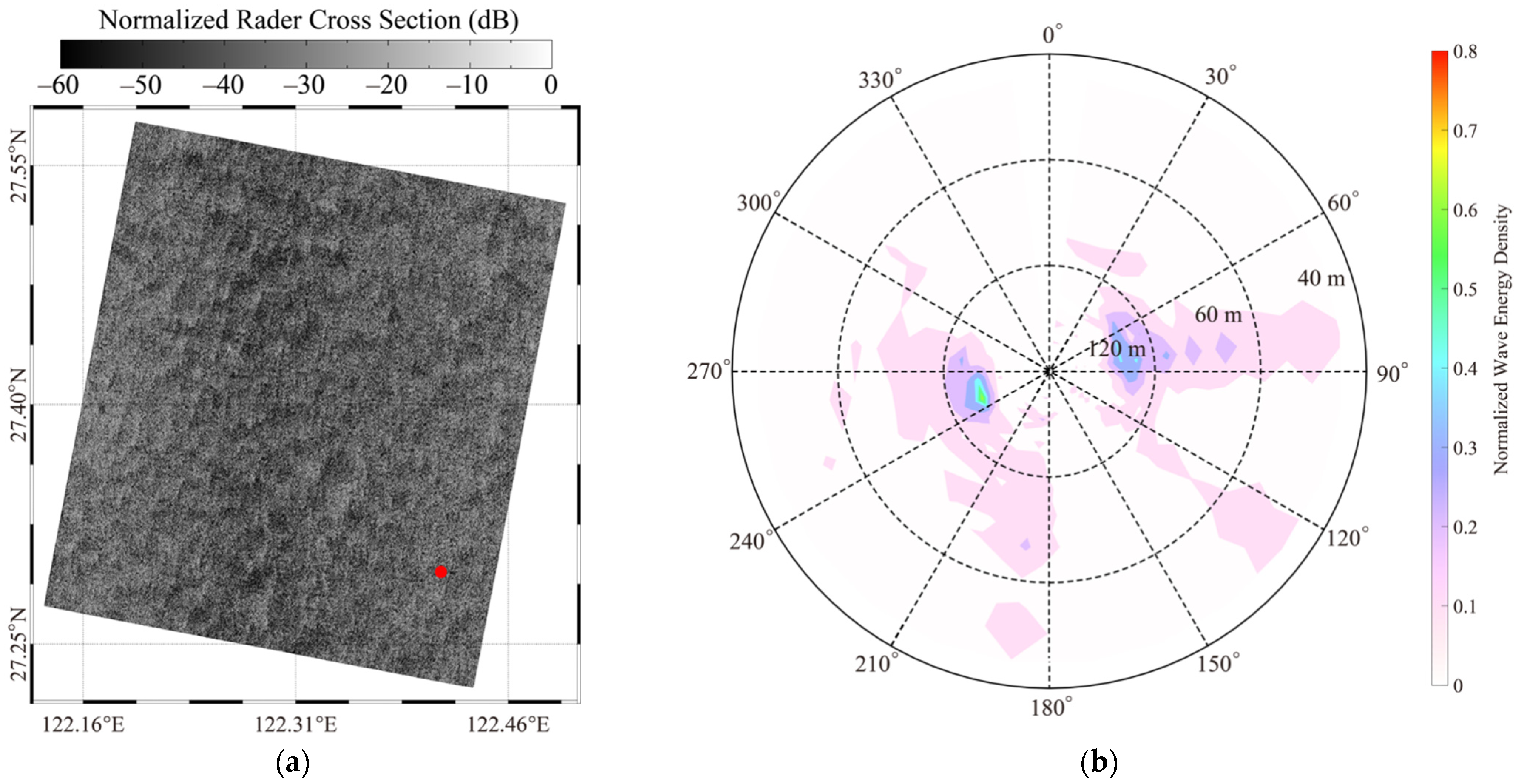
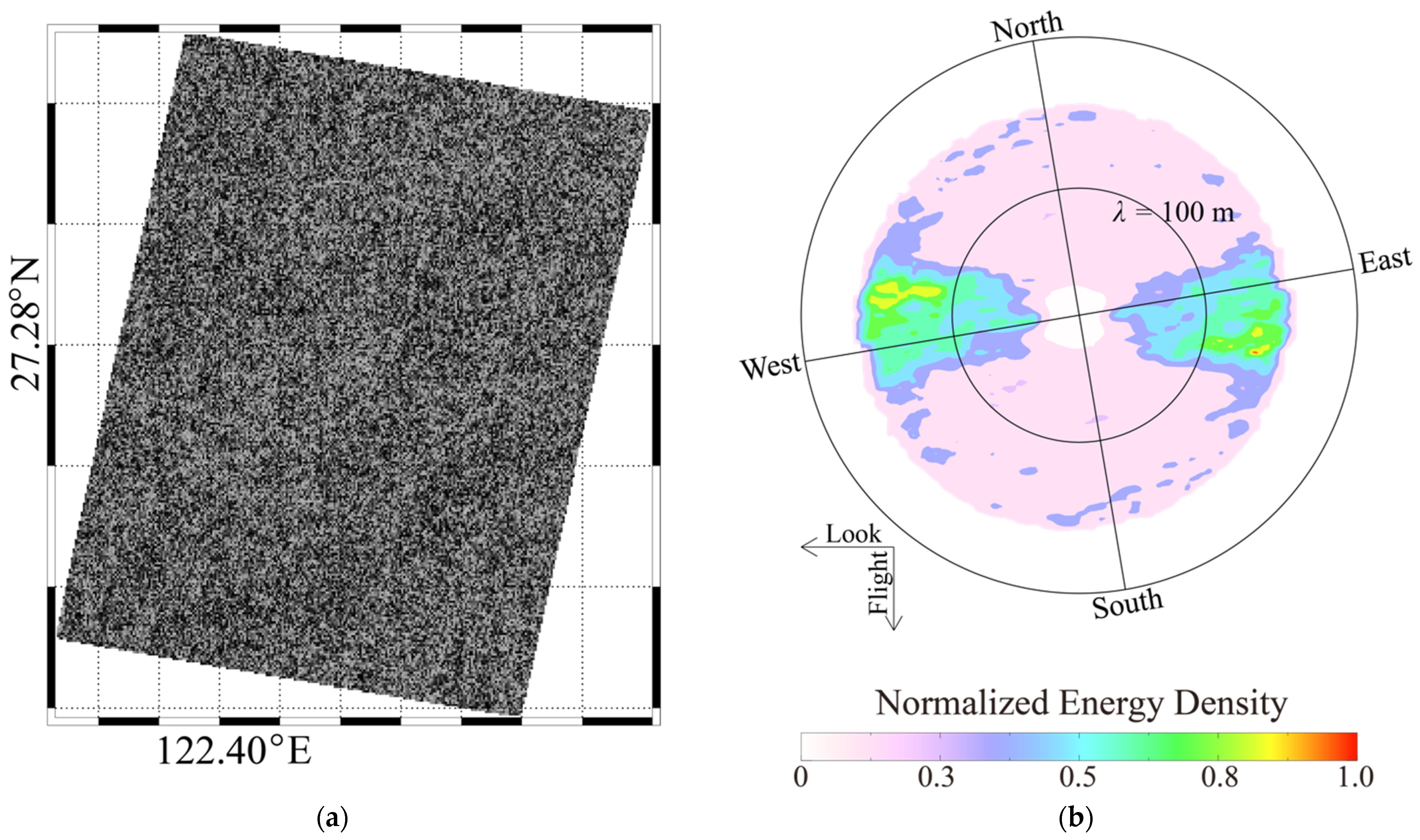
2.3. GF-3 Images
3. Methodology
4. Results
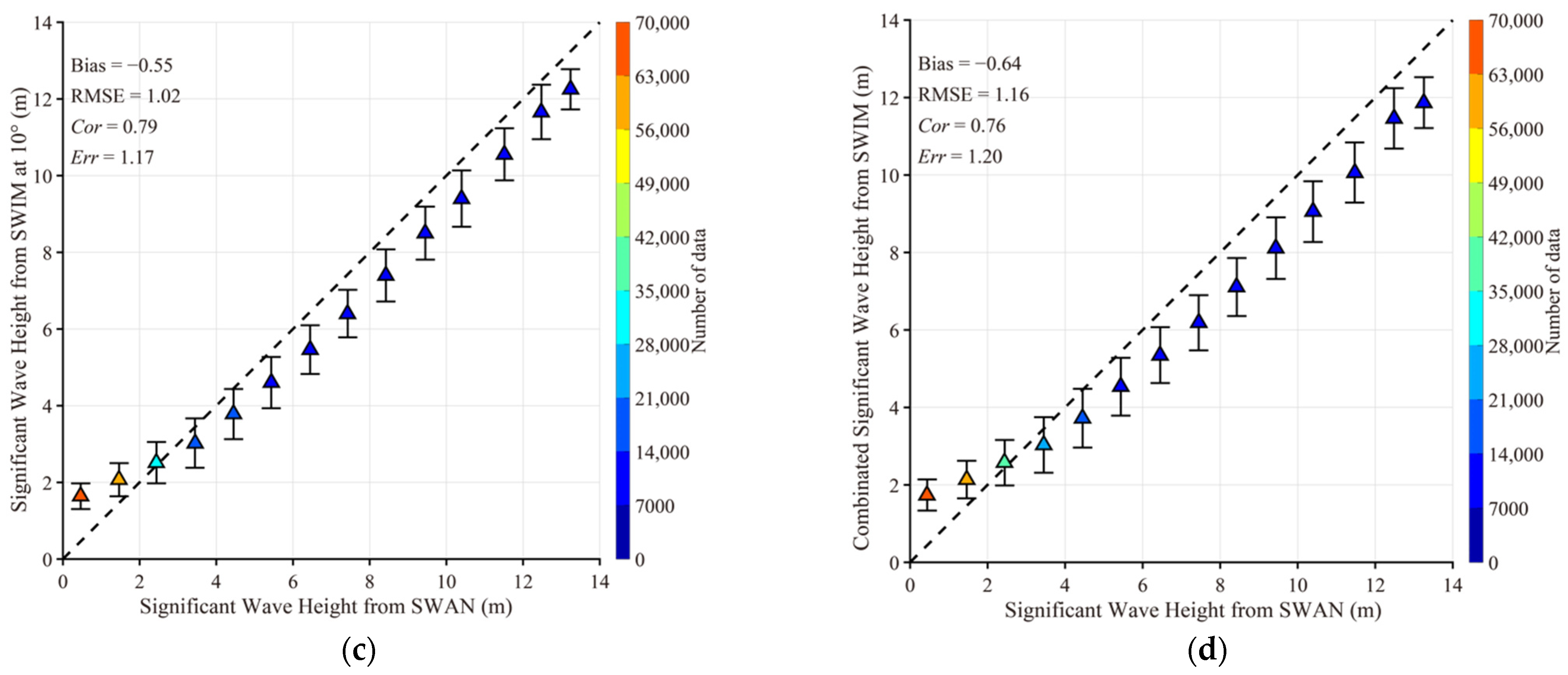
4.1. Comparison between SWIM Waves with SWAN-Simulated Results
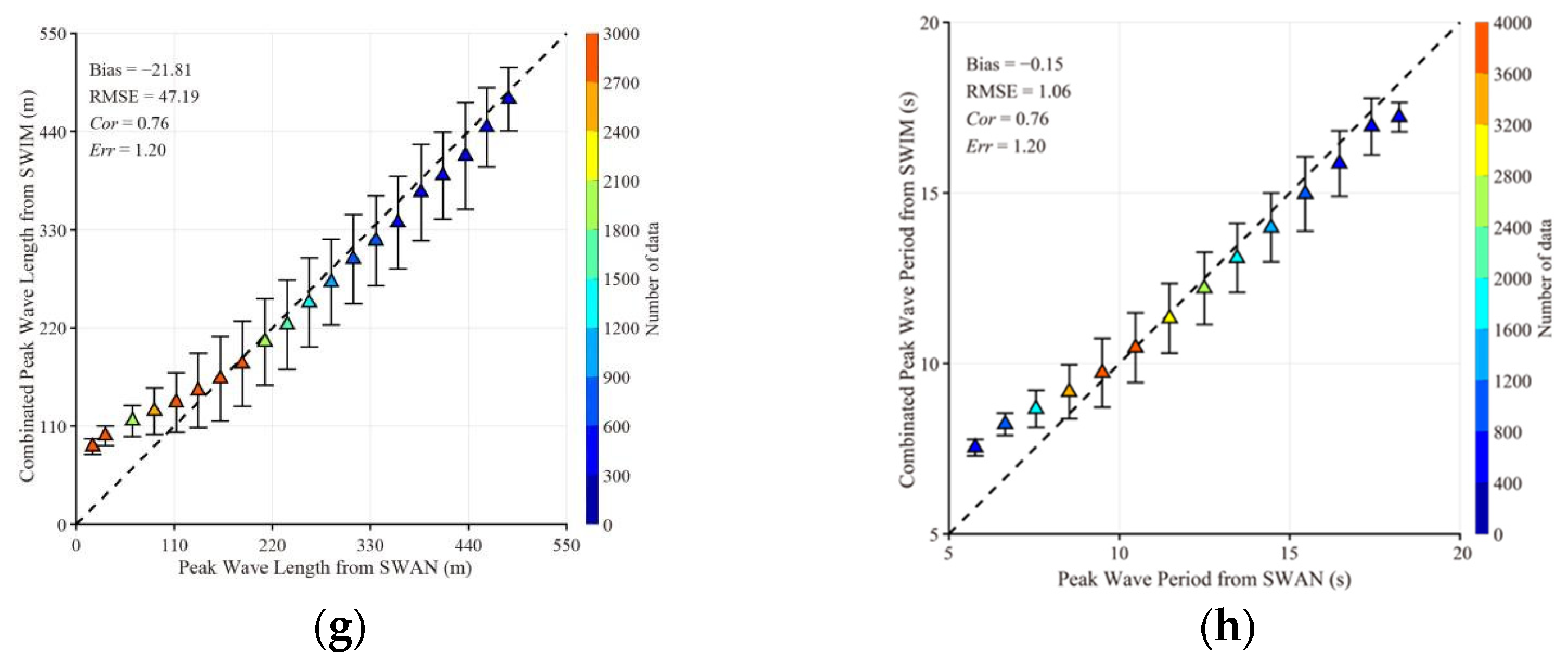
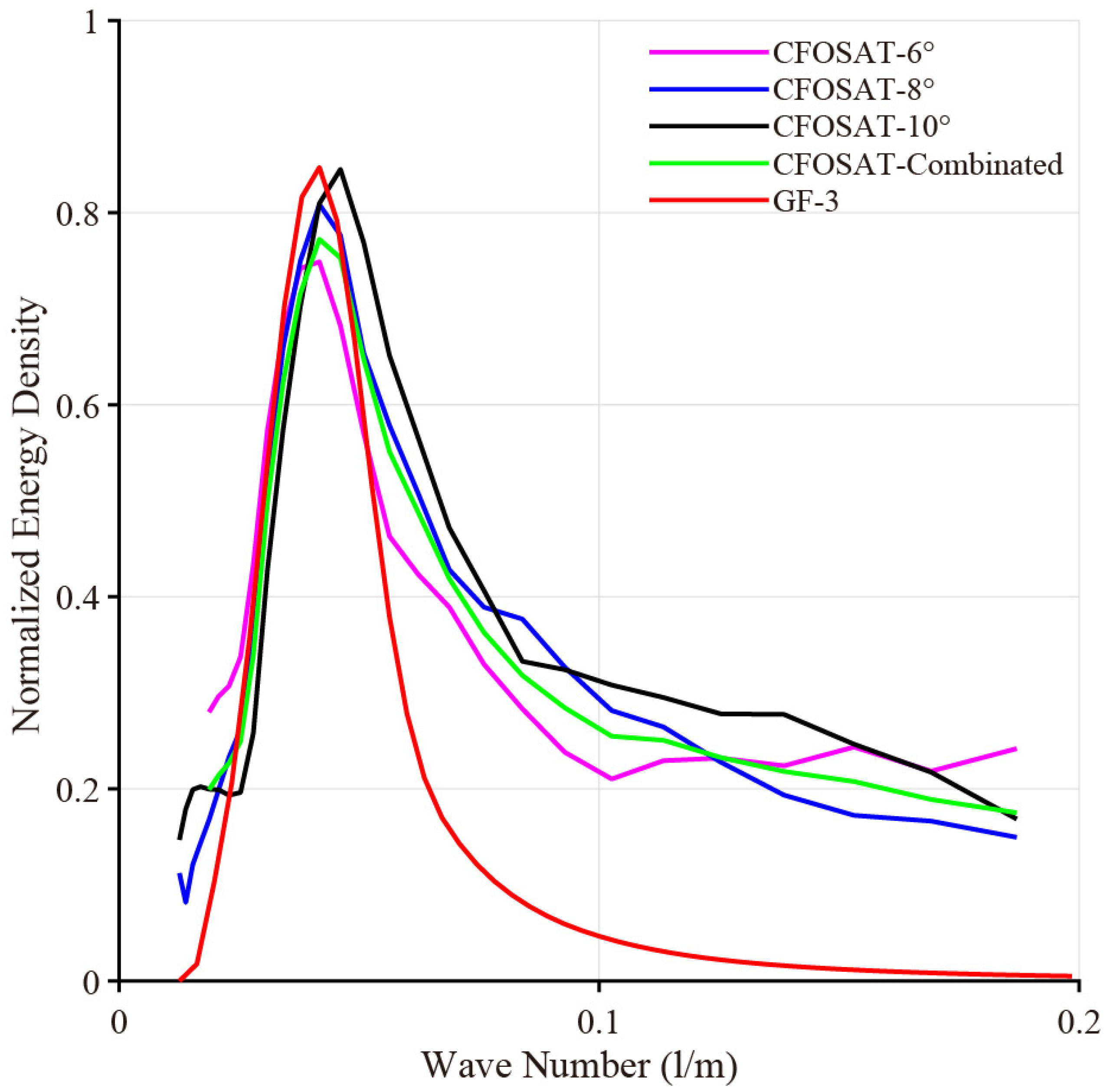
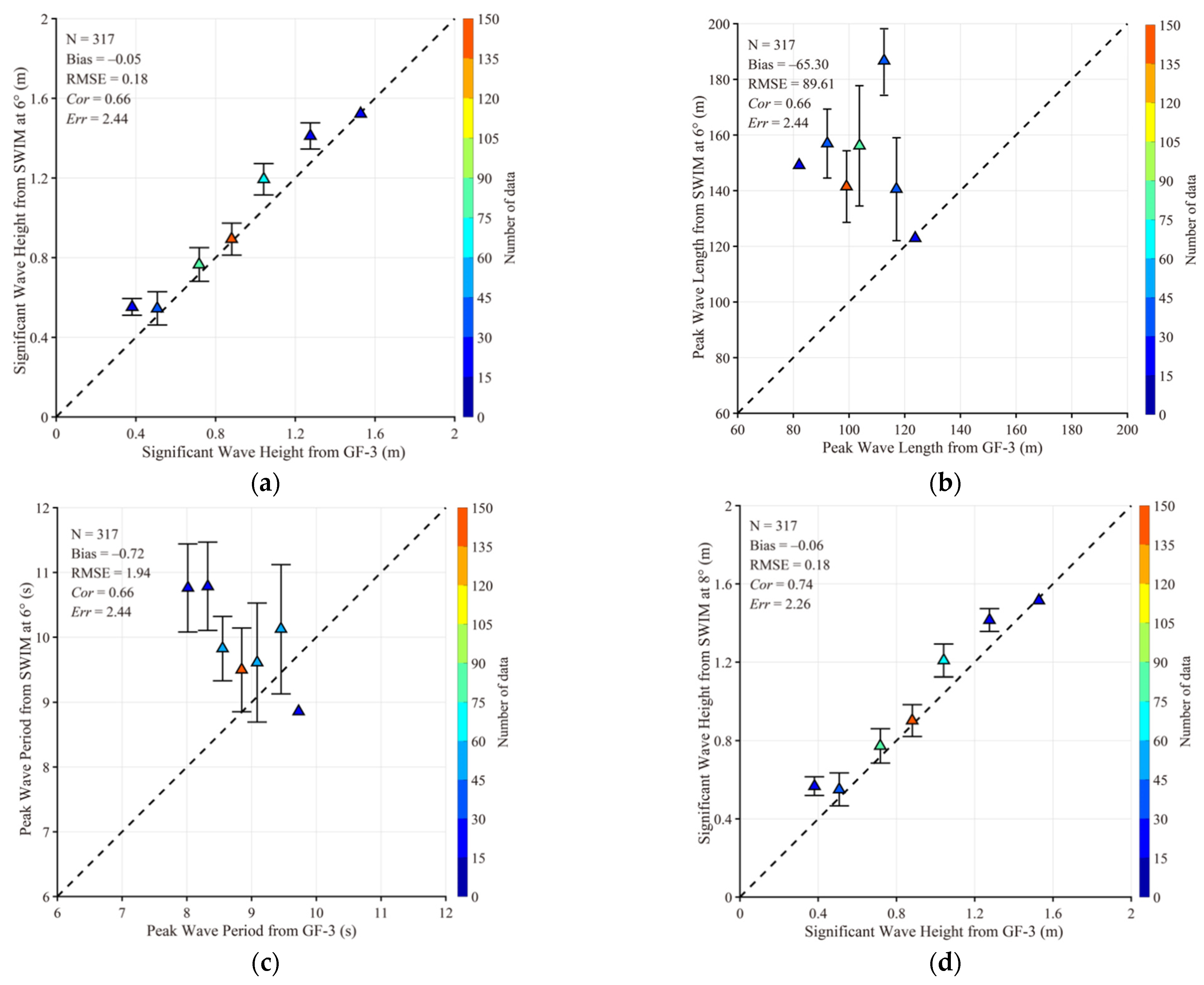
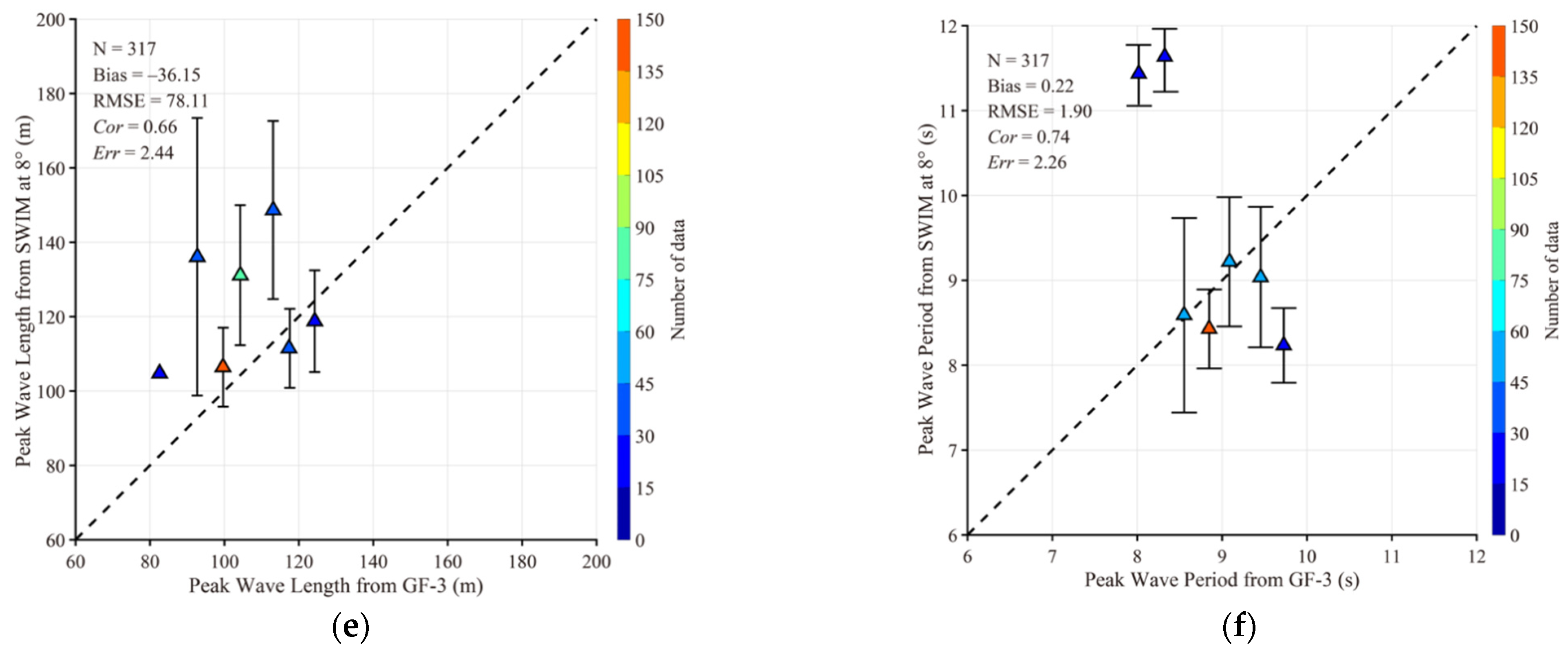
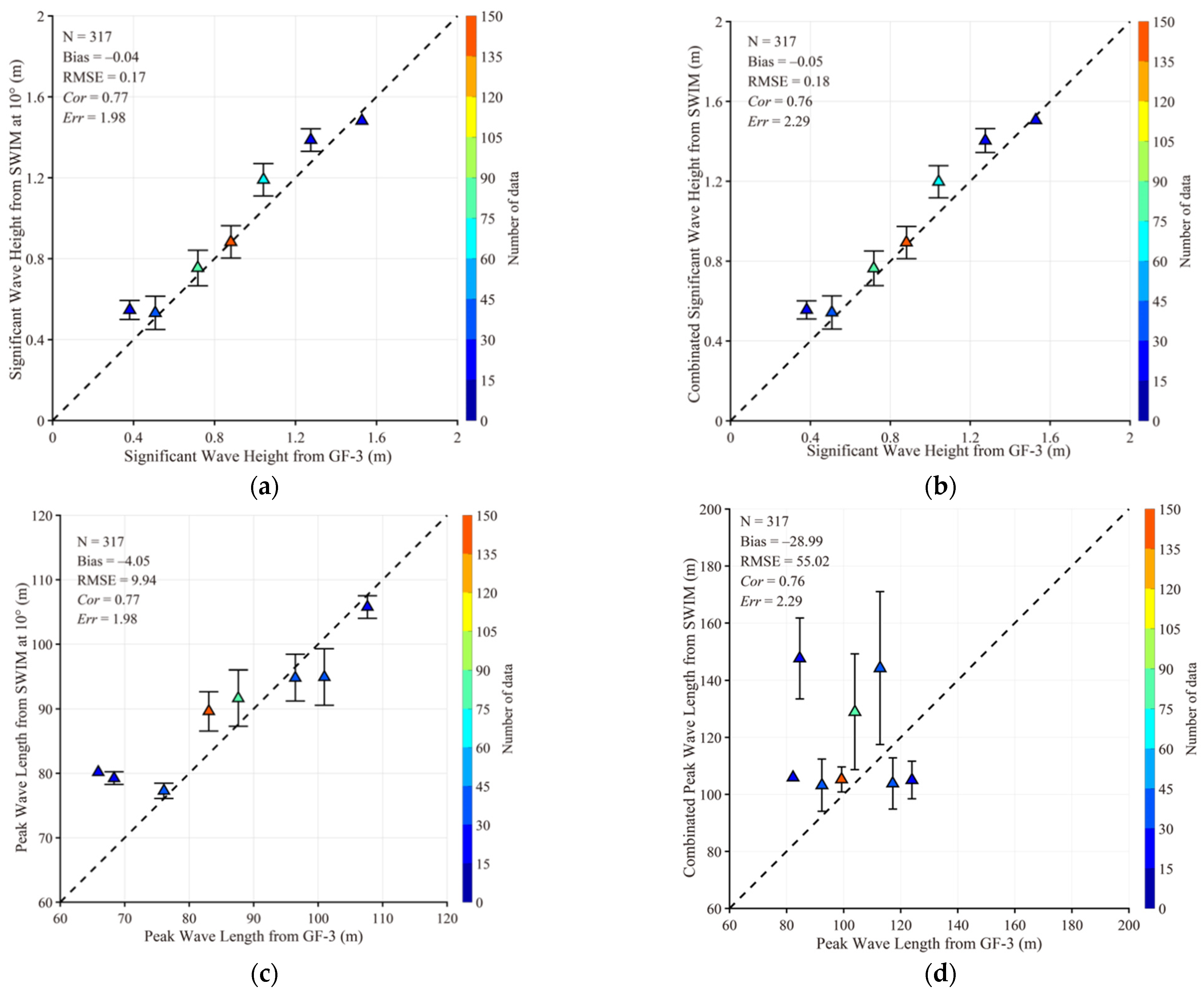
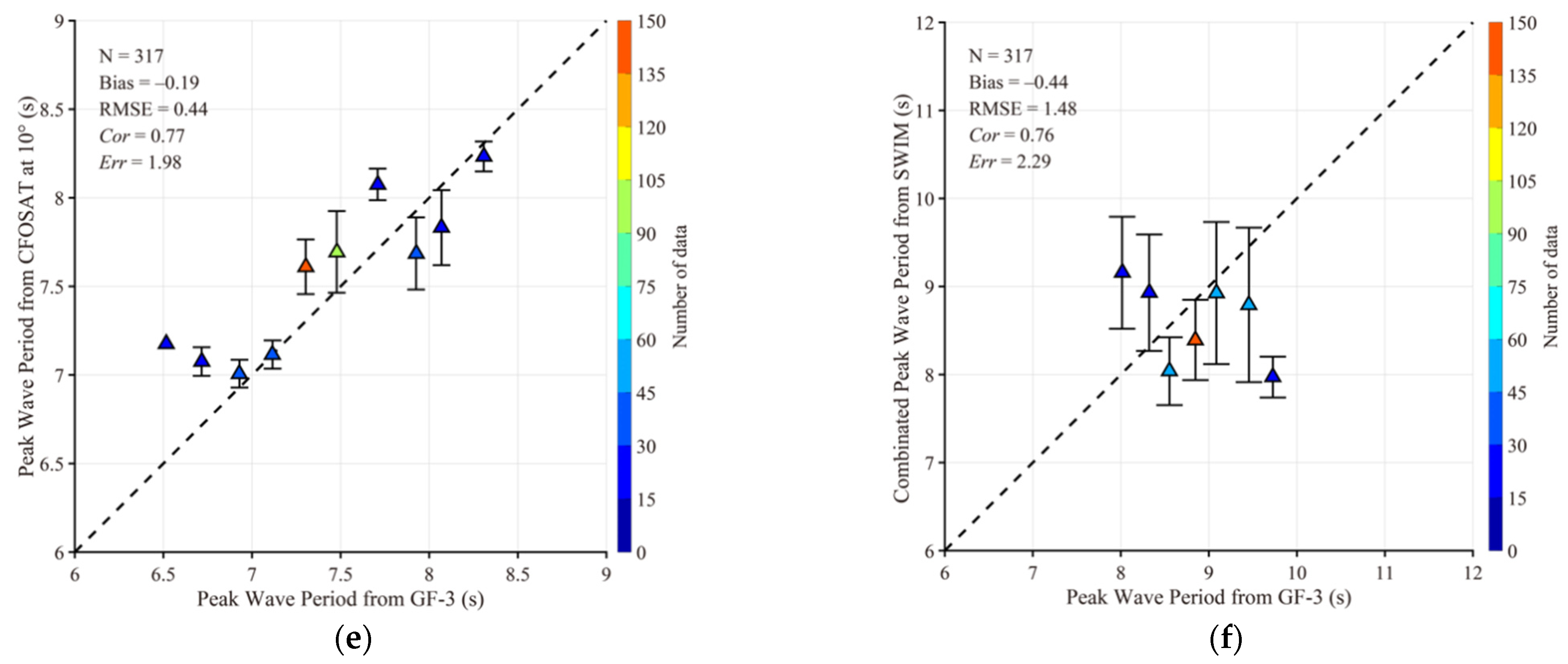
4.2. Comparison between SWIM Waves with GF-3 Retrievals
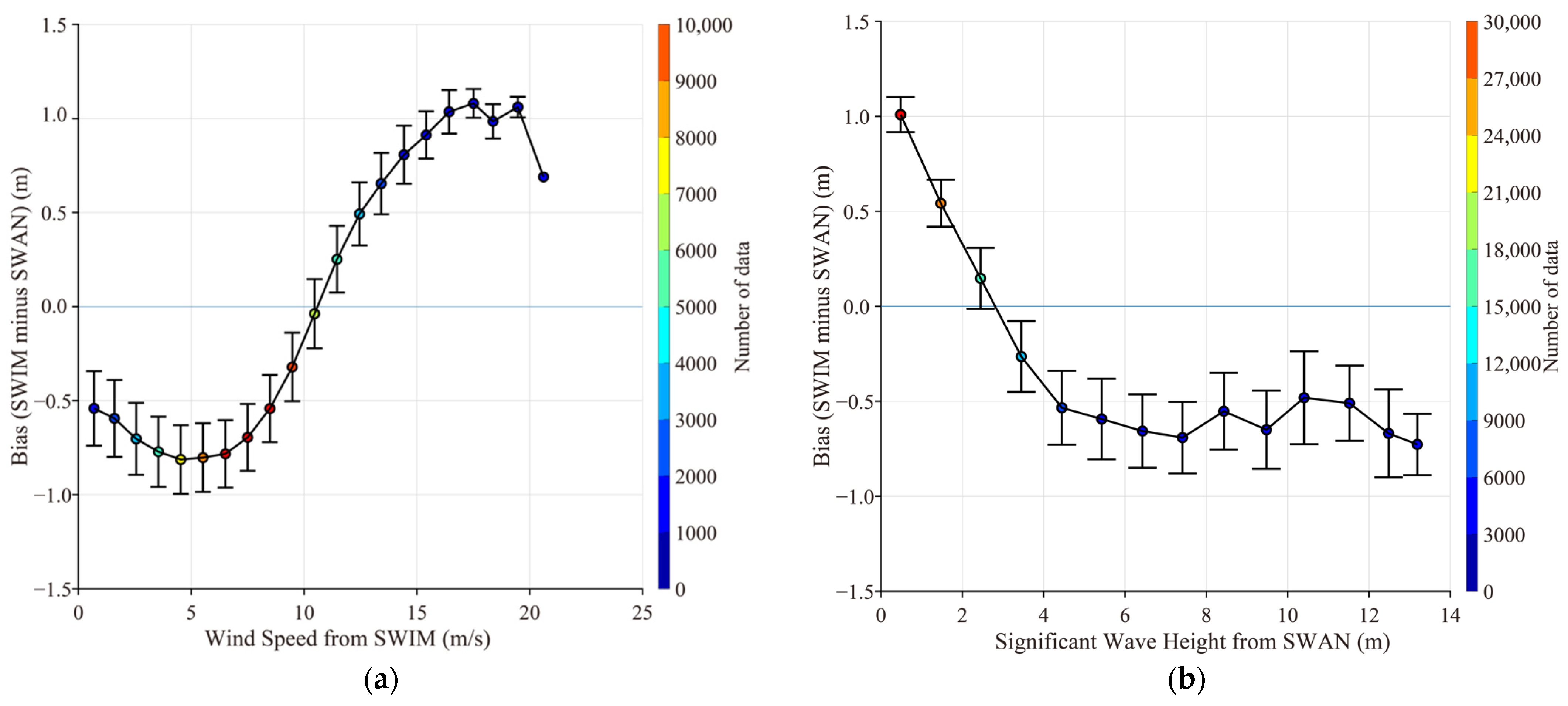
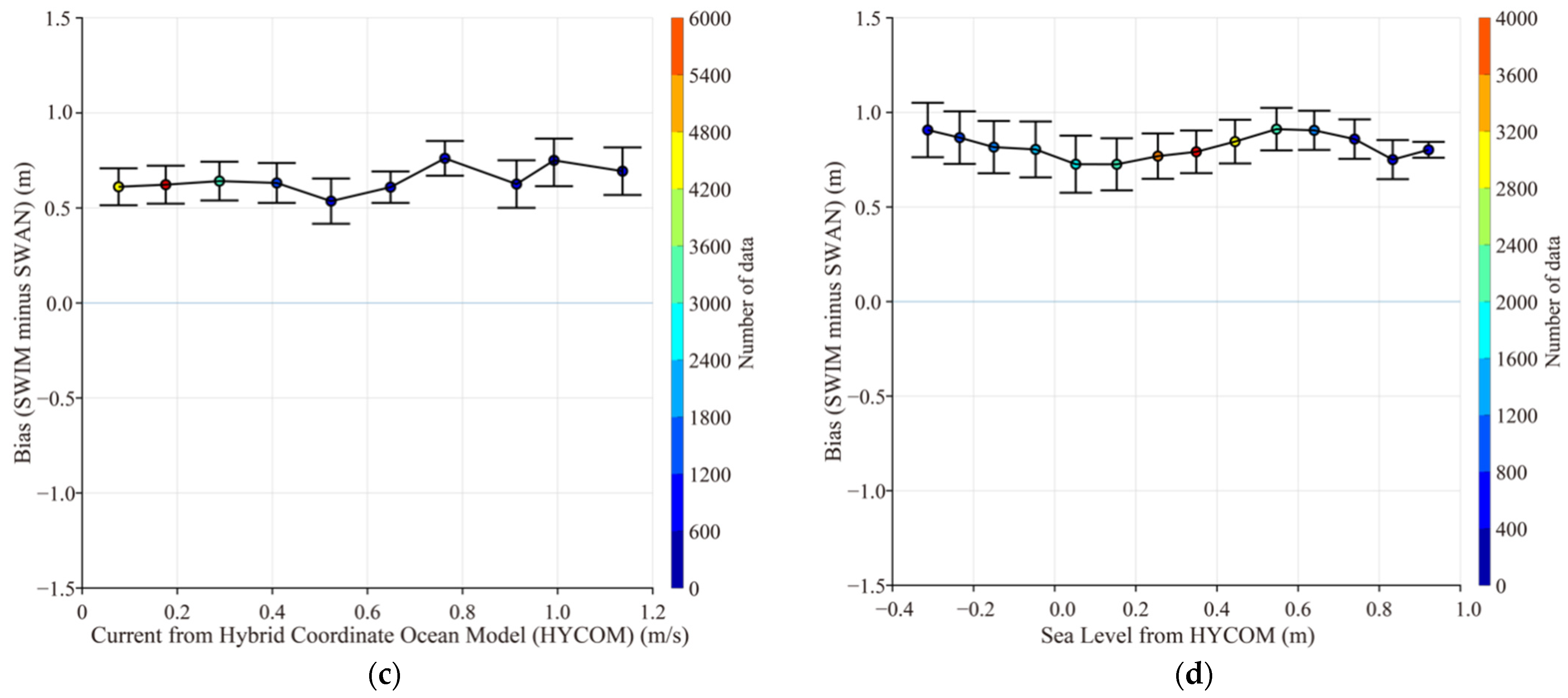
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.X.; Alexander, V.B.; Stefan, Z.; Young, L.R.; Guan, C.L. Wind and wave climate in the Arctic Ocean as observed by Altimeters. J. Climate 2016, 29, 7957–7975. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, C.L.; Sun, J.; Xie, L. Tropical cyclone wind speed retrieval from dual-polarization Sentinel-1 EW mode products. J. Atmos. Ocean. Technol. 2020, 3, 1713–1724. [Google Scholar] [CrossRef]
- Hauser, D.; Tison, C.; Amiot, T.; Delaye, L.; Corcoral, N.; Castillan, P. SWIM: The first spaceborne wave scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3000–3014. [Google Scholar] [CrossRef]
- Shao, W.Z.; Jiang, T.; Zhang, Y.; Shi, J.; Wang, W. Cyclonic wave simulations based on WAVEWATCH-III using a sea surface drag coefficient derived from CFOSAT SWIM data. Atmosphere 2021, 12, 1610. [Google Scholar] [CrossRef]
- Zhu, J.T.; Dong, X.L.; Lin, W.M.; Zhu, D. A preliminary study of the calibration for the rotating fan-beam scatterometer on CFOSAT. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 460–470. [Google Scholar] [CrossRef]
- Wang, L.L.; Ding, Z.Y.; Zhang, L.; Yan, C. CFOSAT-1 realizes first joint observation of sea wind and waves. Chin. J. Aeronaut. 2019, 20, 22–29. [Google Scholar]
- Wang, J.K.; Aouf, L.; Dalphinet, A.; Zhang, Y.G.; Xu, Y.; Hauser, D.; Liu, J.Q. The wide swath significant wave height: An innovative reconstruction of significant wave heights from CFOSAT SWIM and scatterometer using deep learning. Geophys. Res. Lett. 2021, 48, e2020GL091276. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.Q.; Xie, L.L.; Sun, C.R.; Liu, J.P.; Li, J.Y. China-France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields. Acta Oceanol. Sin. 2019, 38, 158–161. [Google Scholar] [CrossRef]
- Grigorieva, V.G.; Badulin, S.I.; Gulev, S.K. Global validation of SWIM/CFOSAT wind waves against voluntary observing ship data. Earth Space Sci. 2022, 9, e2021EA002008. [Google Scholar] [CrossRef]
- Lin, C.C.; Rommen, B.; Wilson, J.; Impagnatiello, F.; Park, P.S. An analysis of a rotating, range-gated, fanbeam spaceborne scatterometer concept. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2114–2121. [Google Scholar]
- Liu, J.Q.; Lin, W.M.; Dong, X.L.; Lang, S.Y.; Yun, R.S.; Zhu, D.; Zhang, K.; Sun, C.R.; Mu, B.; Ma, J.Y.; et al. First results from the rotating fan beam scatterometer onboard CFOSAT. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8793–8806. [Google Scholar] [CrossRef]
- Ebuchi, N. Evaluation of NSCAT-2 wind vectors by using statistical distributions of wind speeds and directions. J. Oceanogr. 2000, 56, 161–172. [Google Scholar] [CrossRef]
- Tsai, W.; Graf, J.E.; Winn, C.; Huddleston, J.N.; Dunbar, S.; Freilich, M.H.; Wentz, F.J.; Long, D.G.; Jones, W.L. Postlaunch sensor verification and calibration of the NASA scatterometer. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1517–1542. [Google Scholar] [CrossRef]
- Figa-Saldana, J.; Wilson, J.J.; Attema, E.; Gelsthorpe, R.; Drinkwater, M.R.; Stoffelen, A. The advanced scatterometer (ASCAT) on the meteorological operational (MetOp) platform: A follow on for European wind scatterometers. Can. J. Remote Sens. 2002, 28, 404–412. [Google Scholar] [CrossRef]
- Spencer, M.W.; Wu, C.; Long, D.G. Improved resolution backscatter measurements with the SeaWinds pencil-beam scatterometer. IEEE Trans. Geosci. Remote Sens. 2000, 38, 89–104. [Google Scholar] [CrossRef]
- Shao, W.Z.; Jiang, T.; Jiang, X.W.; Zhang, Y.G.; Zhou, W. Evaluation of sea surface winds and waves retrieved from the Chinese HY-2B data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2021, 14, 9624–9635. [Google Scholar] [CrossRef]
- He, J.N.; Guo, W.; Zhu, D.; Zhao, F. Analysis on calibration for flight experiments of CFOSAT scatterometer by return signal simulator. Remote Sens. Technol. App. 2015, 30, 731–736. [Google Scholar]
- Dong, X.L.; Zhu, D.; Lin, W.M.; Liu, H.G.; Jiang, J.S. Status and recent progresses of development of the scatterometer of CFOSAT. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 961–964. [Google Scholar]
- Alpers, R.; Bruening, C. On the relative importance of motion-related contributions to the SAR Imaging mechanism of ocean surface waves. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 873–885. [Google Scholar] [CrossRef]
- Ning, J.; Sun, L.N.; Cui, H.J.; Lu, K.X.; Wang, J. Study on characteristics of internal solitary waves in the Malacca Strait based on Sentinel-1 and GF-3 satellite SAR data. Acta Oceanol. Sin. 2020, 39, 151–156. [Google Scholar] [CrossRef]
- Alpers, R.; Ross, B.; Rufenach, L. On the detectability of ocean surface waves by real and synthetic aperture radar. J. Geophys. Res. Ocean. 1981, 86, 6481. [Google Scholar] [CrossRef]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. J. Geophys. Res. Ocean. 1991, 96, 10713. [Google Scholar] [CrossRef]
- Mastenbroek, C.; Valk, C. A semiparametric algorithm to retrieve ocean wave spectra from synthetic aperture radar. J. Geophys. Res. Ocean. 2000, 105, 3497–3516. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lehner, S.; Hoja, D. A parametric scheme for the retrieval of two-dimensional ocean wave spectra from synthetic aperture radar look cross spectra. J. Geophys. Res. Ocean. 2005, 110, C05004. [Google Scholar] [CrossRef]
- Sun, J.; Guan, C.L. Parameterized first-guess spectrum method for retrieving directional spectrum of swell-dominated waves and huge waves from SAR images. Chin. J. Oceanol. Limn. 2006, 24, 12–20. [Google Scholar]
- Jiang, T.; Shao, W.Z.; Hu, Y.Y.; Zheng, G.; Shen, W. L-band analysis of the effects of oil slicks on sea wave characteristics. J. Ocean Univ. China 2023, 22, 9–20. [Google Scholar] [CrossRef]
- Shao, W.Z.; Hu, Y.Y.; Jiang, X.W.; Zhang, Y.G. Wave retrieval from quad-polarized Chinese Gaofen-3 SAR image using an improved tilt modulation transfer function. Geo-Spat. Inf. Sci. 2023. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Konig, T.; Lehner, S. An empirical approach for the retrieval of integral ocean wave parameters from synthetic aperture radar data. J. Geophys. Res. Ocean. 2007, 42, 10182–10190. [Google Scholar] [CrossRef]
- Li, X.M.; Konig, T.; Schulz-Stellenfleth, J.; Lehner, S. Validation and intercomparison of ocean wave spectra inversion schemes using ASAR wave mode data. Int. J. Remote Sens. 2010, 31, 4969–4993. [Google Scholar] [CrossRef]
- Stopa, E.; Mouche, A. Significant wave heights from Sentinel-1 SAR: Validation and applications. J. Geophys. Res. Oceans 2017, 122, 1827–1848. [Google Scholar] [CrossRef]
- Pleskachevsky, A.; Jacobsen, S.; Tings, B.; Schwarz, E. Estimation of sea state from Sentinel-1 synthetic aperture radar imagery for maritime situation awareness. Int. J. Remote Sens. 2019, 40, 4104–4142. [Google Scholar] [CrossRef]
- Sheng, Y.X.; Shao, W.Z.; Zhu, S.; Sun, J.; Yuan, X.Z.; Li, S.Q.; Shi, J.; Zuo, J.C. Validation of significant wave height retrieval from co-polarization Chinese Gaofen-3 SAR imagery using an improved algorithm. Acta Oceanol. Sin. 2018, 37, 1–10. [Google Scholar] [CrossRef]
- Zhu, S.; Shao, W.Z.; Armando, M.; Shi, J.; Sun, J.; Yuan, X.Z.; Hu, J.C.; Yang, D.K.; Zuo, J.C. Evaluation of Chinese quad-polarization Gaofen-3 SAR wave mode data for significant wave height retrieval. Can. J. Remote Sens. 2019, 44, 588–600. [Google Scholar] [CrossRef]
- Hao, M.Y.; Shao, W.Z.; Yao, R.; Zhang, Y.G.; Jiang, X.W. Improvement of quad-polarized velocity bunching modulation transfer function by C-band Gaofen-3 SAR. Remote Sens. Lett. 2023, 14, 968–978. [Google Scholar] [CrossRef]
- Hauser, D.; Soussi, E.; Thouvenot, E.; Rey, L. SWIMSAT: A real-aperture radar to measure directional spectra of ocean waves from space–main characteristics and performance simulation. J. Atmos. Ocean. Technol. 2001, 18, 421–437. [Google Scholar] [CrossRef]
- Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New observations from the SWIM radar on-board CFOSAT: Instrument validation and ocean wave measurement assessment. IEEE Trans. Geosci. Remote 2021, 59, 5–26. [Google Scholar] [CrossRef]
- Ye, H.; Li, J.; Li, B.; Liu, J.; Tang, D.; Chen, W.; Yang, H.; Zhou, F.; Zhang, R.; Wang, S.; et al. Evaluation of CFOSAT scatterometer wind data in global oceans. Remote Sens. 2021, 13, 1926. [Google Scholar] [CrossRef]
- Tang, S.L.; Chu, X.Q.; Jia, Y.J.; Li, J.M.; Liu, Y.T.; Chen, Q.; Li, B.; Liu, J.L.; Chen, W.Y. An appraisal of CFOSAT wave spectrometer products in the South China Sea. Earth Space Sci. 2022, 9, e2021EA002055. [Google Scholar] [CrossRef]
- Zheng, K.W.; Osinowo, A.; Sun, J.; Hu, W. Long term characterization of sea conditions in the East China Sea using significant wave height and wind speed. J. Ocean. Univ. China 2018, 17, 733–743. [Google Scholar] [CrossRef]
- Holthuijsen, L. The continued development of the third-generation shallow water wave model ‘SWAN’. Tu Delft Dep. Hydraul. Eng. 2001, 32, 185–186. [Google Scholar]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Teng, C.C. Ocean observation from NOAA national data buoy center’s platforms. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 5–9 April 2010; Volume 7678, pp. 13–17. [Google Scholar]
- Shao, W.Z.; Nunziata, F.; Zhang, Y.G.; Corcione, V.; Migliaccio, M. Wind speed retrieval from the Gaofen-3 synthetic aperture radar for VV- and HH-polarization using a re-tuned algorithm. Eur. J. Remote Sens. 2021, 54, 318–337. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); UDC 551.466.31; Deutches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Shao, W.Z.; Jiang, X.W.; Sun, Z.F.; Hu, Y.Y.; Marino, A.; Zhang, Y.G. Evaluation of wave retrieval for Chinese Gaofen-3 synthetic aperture radar. Geo-Spat. Inf. Sci. 2022, 25, 229–243. [Google Scholar] [CrossRef]
- Shao, W.Z.; Li, X.F.; Sun, J. Ocean wave parameters retrieval from TerraSAR-X images validated against buoy measurements and model results. Remote Sens. 2015, 7, 12815–12828. [Google Scholar] [CrossRef]
- Merle, E.; Hauser, D.; Peureux, C.; Aouf, L.; Schippers, P.; Dufour, C.; Dalphinet, A. Directional and frequency spread of surface ocean waves from SWIM measurements. J. Geophys. Res. Oceans 2021, 126, e2021JC017220. [Google Scholar] [CrossRef]
- Li, X.M.; Lehner, S.; Bruns, T. Ocean wave integral parameter measurements using Envisat ASAR wave mode data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 155–174. [Google Scholar] [CrossRef]
- Yao, R.; Shao, W.Z.; Hao, M.Y.; Zuo, J.C.; Hu, S. The Respondence of wave on sea surface temperature in the context of global change. Remote Sens. 2023, 15, 1948. [Google Scholar] [CrossRef]
- Zhong, R.Z.; Shao, W.Z.; Zhao, C.; Jiang, X.W.; Zuo, J.C. Analysis of wave breaking on Gaofen-3 and TerraSAR-X SAR image and its effect on wave retrieval. Remote Sen. 2023, 15, 574. [Google Scholar] [CrossRef]
- Liu, M.; Yan, R.; Zhang, J.; Xu, Y.; Chen, P.; Shi, L.; Wang, J.; Zhong, S.; Zhang, X. Arctic sea ice classification based on CFOSAT SWIM data at multiple small incidence angles. Remote Sens. 2022, 14, 91. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Shao, W.Z.; Jiang, X.W.; Zhou, W.; Zuo, J.C. Improvement of VV-polarization tilt MTF for Gaofen-3 SAR data of a tropical cyclone. Remote Sens. Lett. 2023, 14, 461–468. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, M.; Shao, W.; Shi, S.; Liu, X.; Hu, Y.; Zuo, J. Validation of Surface Waves Investigation and Monitoring Data against Simulation by Simulating Waves Nearshore and Wave Retrieval from Gaofen-3 Synthetic Aperture Radar Image. Remote Sens. 2023, 15, 4402. https://doi.org/10.3390/rs15184402
Hao M, Shao W, Shi S, Liu X, Hu Y, Zuo J. Validation of Surface Waves Investigation and Monitoring Data against Simulation by Simulating Waves Nearshore and Wave Retrieval from Gaofen-3 Synthetic Aperture Radar Image. Remote Sensing. 2023; 15(18):4402. https://doi.org/10.3390/rs15184402
Chicago/Turabian StyleHao, Mengyu, Weizeng Shao, Shaohua Shi, Xing Liu, Yuyi Hu, and Juncheng Zuo. 2023. "Validation of Surface Waves Investigation and Monitoring Data against Simulation by Simulating Waves Nearshore and Wave Retrieval from Gaofen-3 Synthetic Aperture Radar Image" Remote Sensing 15, no. 18: 4402. https://doi.org/10.3390/rs15184402
APA StyleHao, M., Shao, W., Shi, S., Liu, X., Hu, Y., & Zuo, J. (2023). Validation of Surface Waves Investigation and Monitoring Data against Simulation by Simulating Waves Nearshore and Wave Retrieval from Gaofen-3 Synthetic Aperture Radar Image. Remote Sensing, 15(18), 4402. https://doi.org/10.3390/rs15184402







