A Multi-Channel Attention Network for SAR Interferograms Filtering Applied to TomoSAR
Abstract
:1. Introduction
2. Methodology
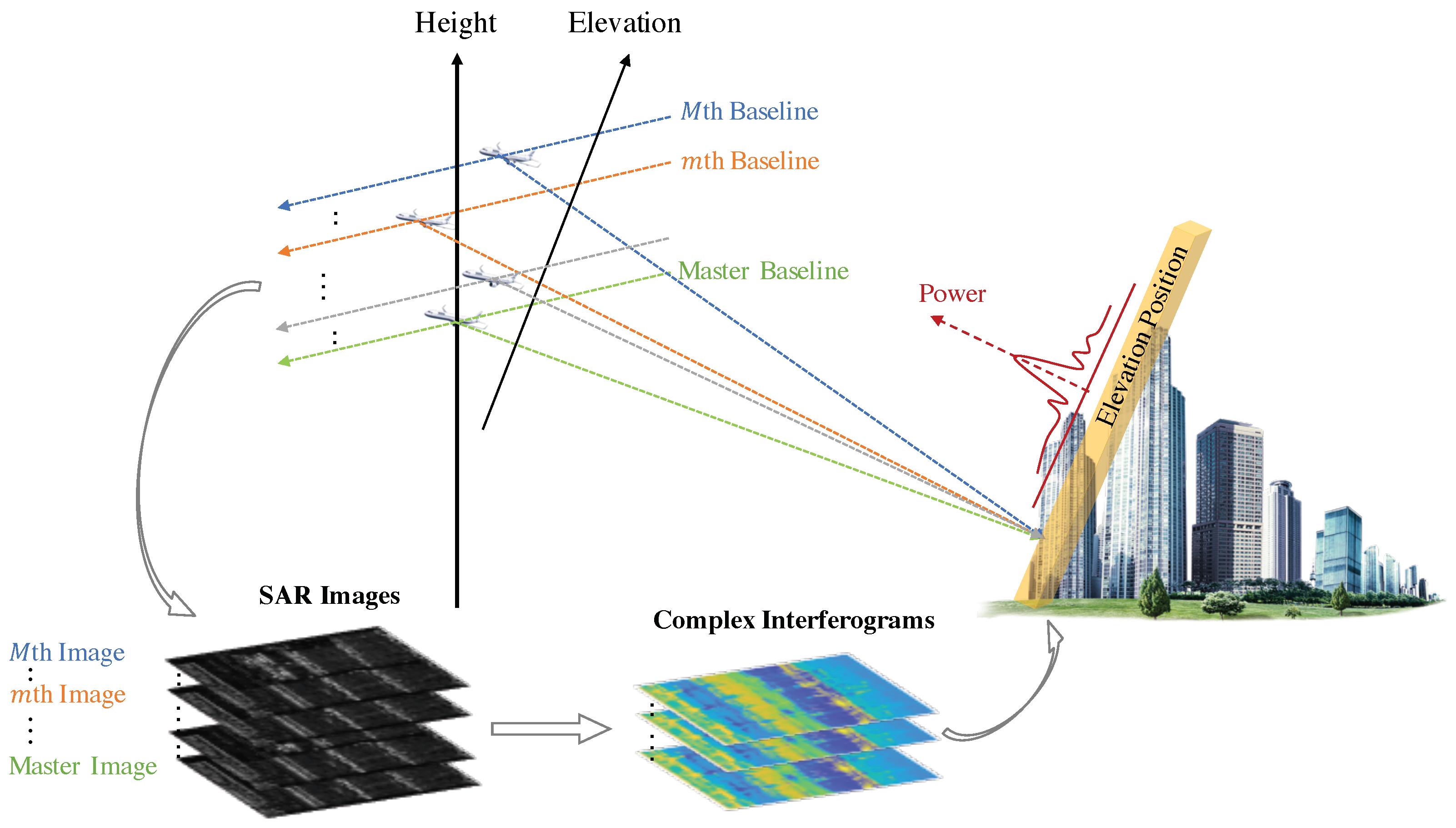
2.1. Tomographic SAR Interferograms
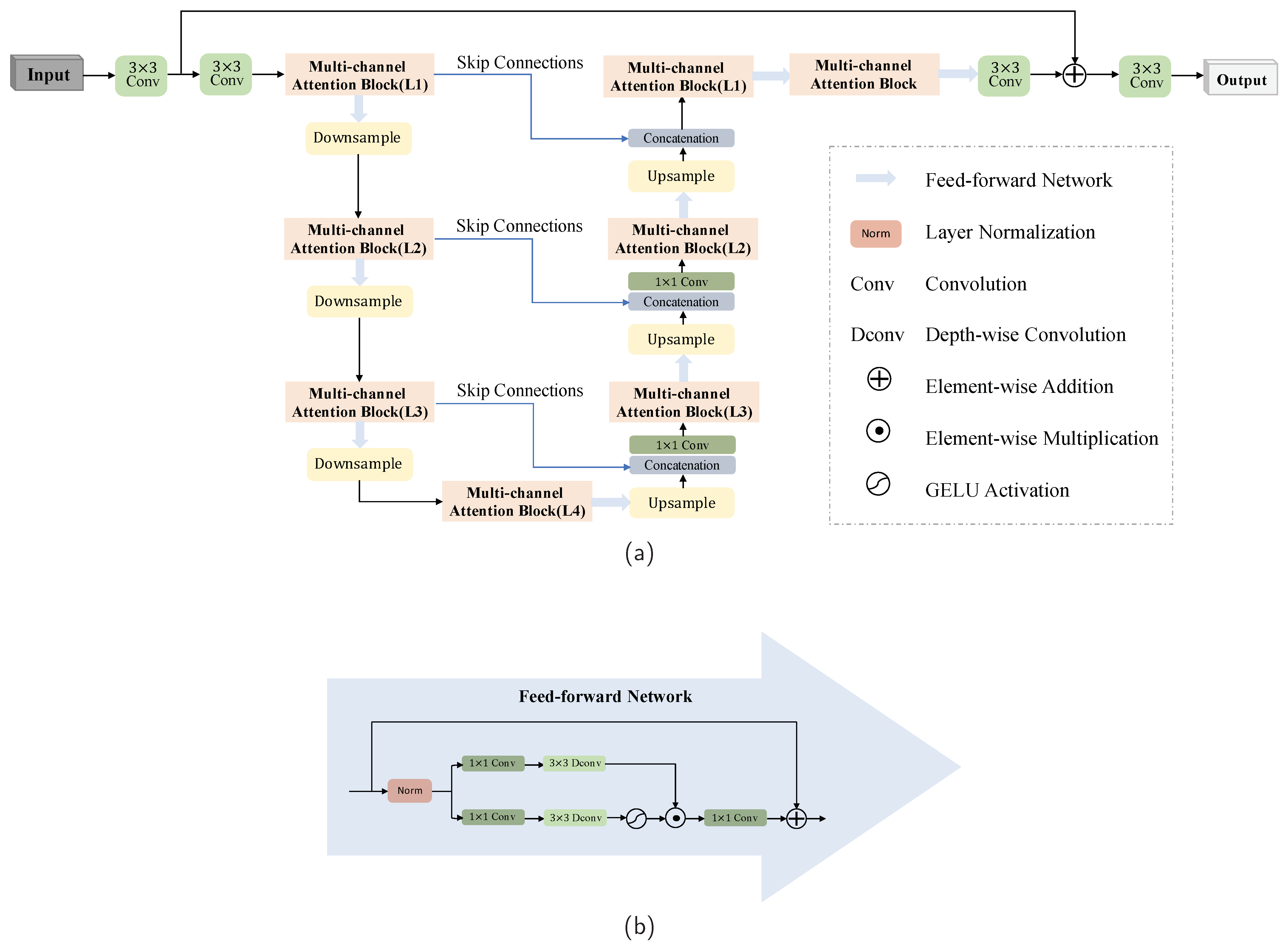
2.2. The Proposed Multi-Channel Attention Network
2.2.1. Overall Structure of the Proposed Framework
2.2.2. Multi-Channel Attention Block
- ;
- ;
- .
3. Experiment
3.1. Network Training
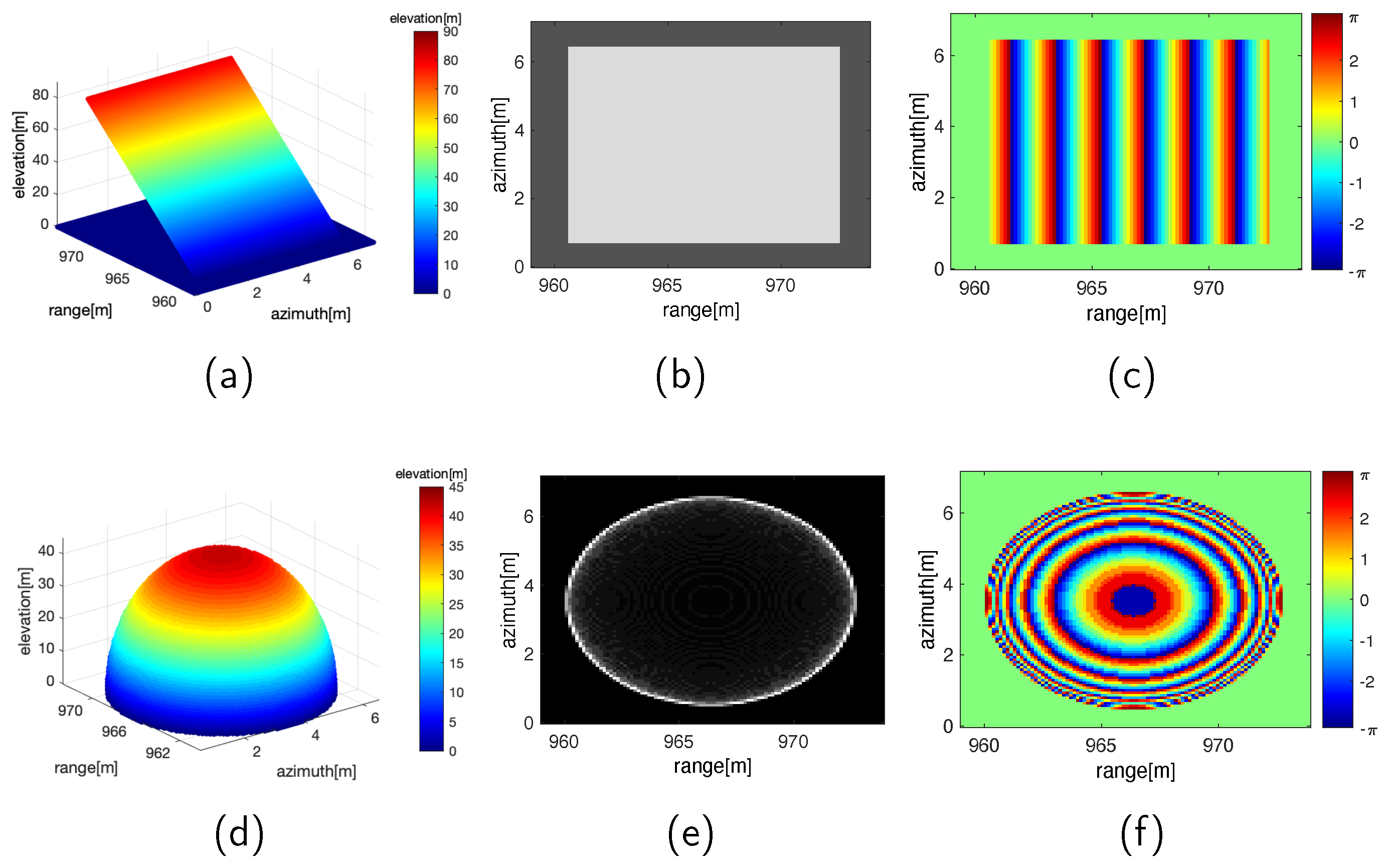
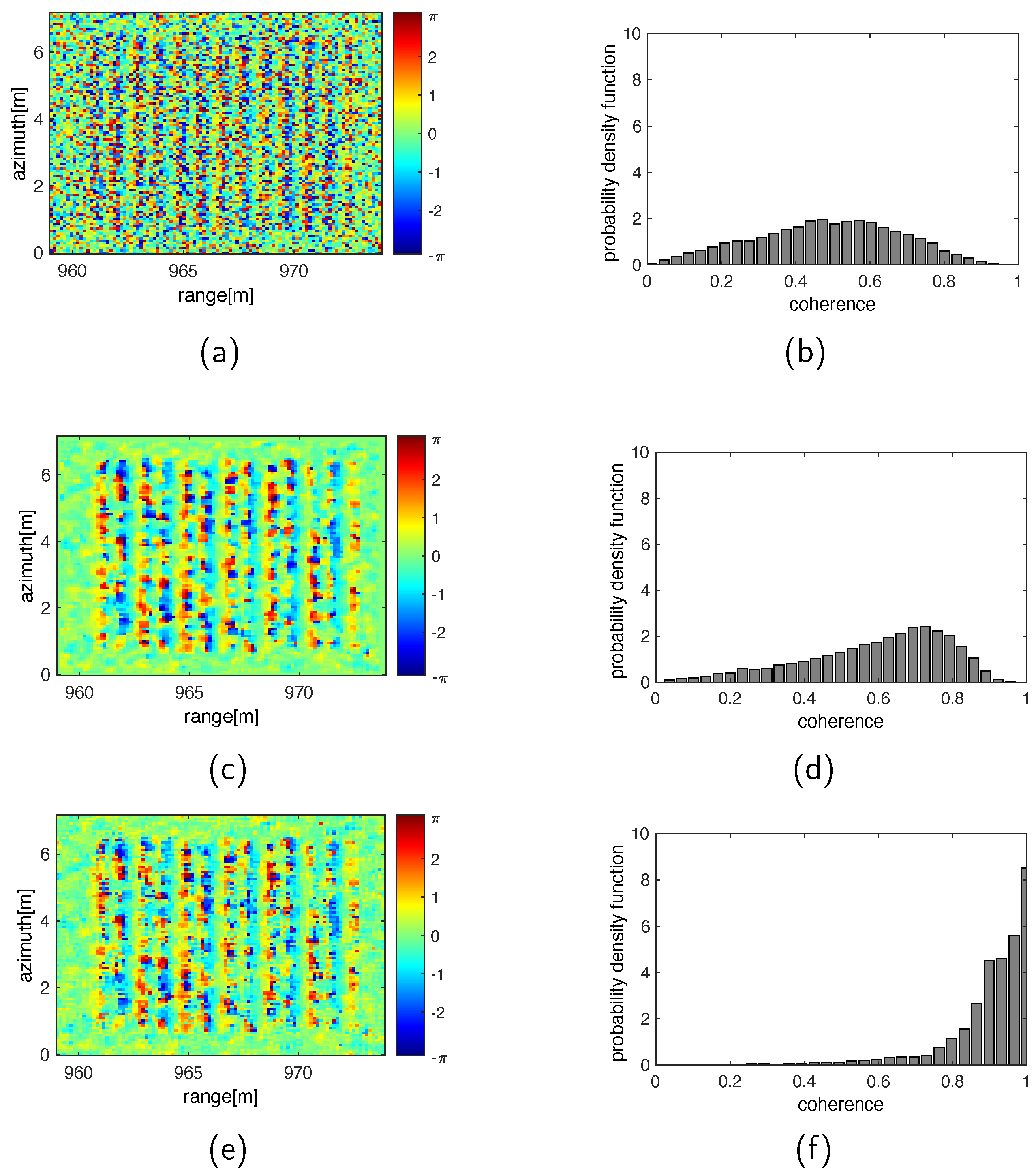
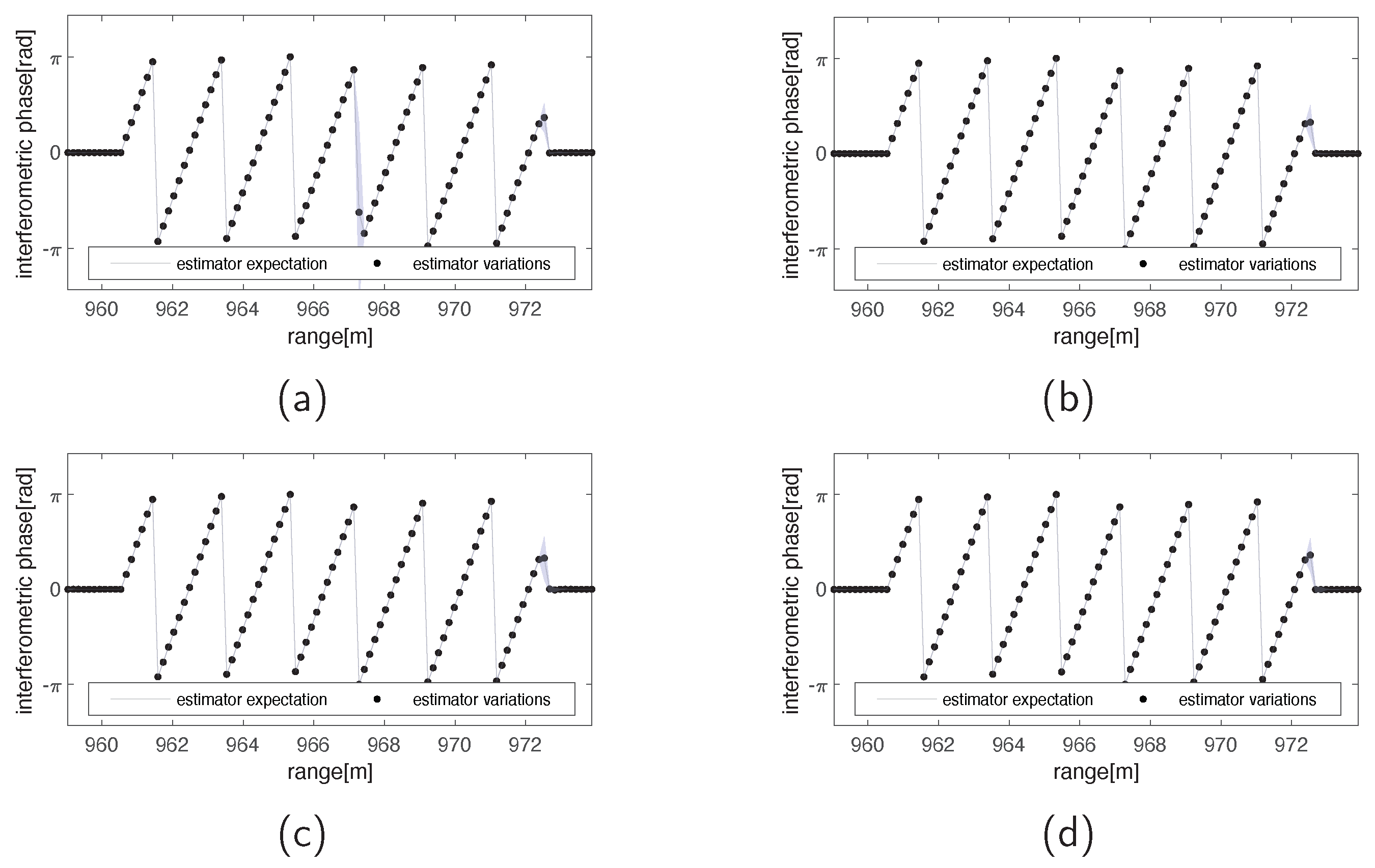
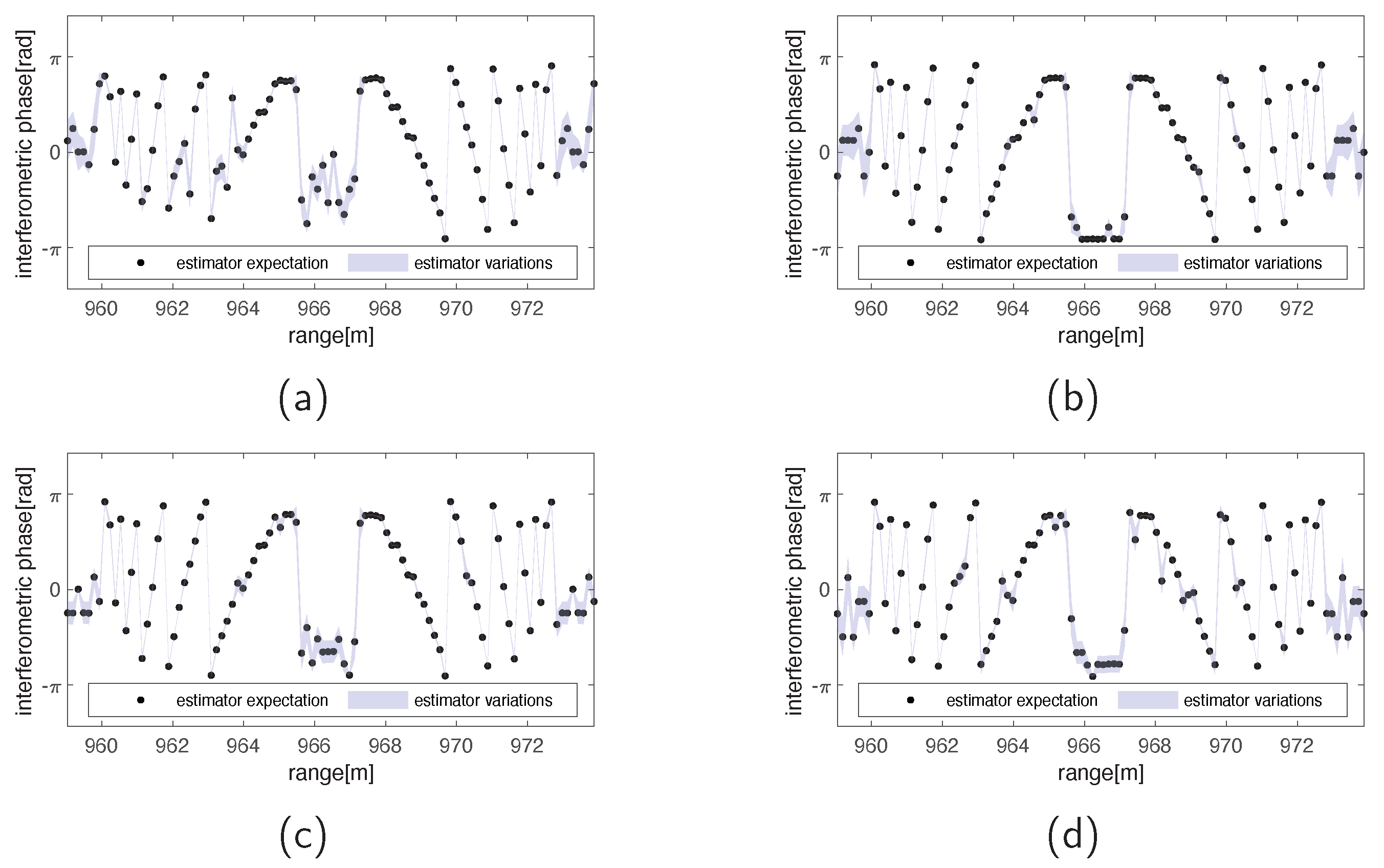
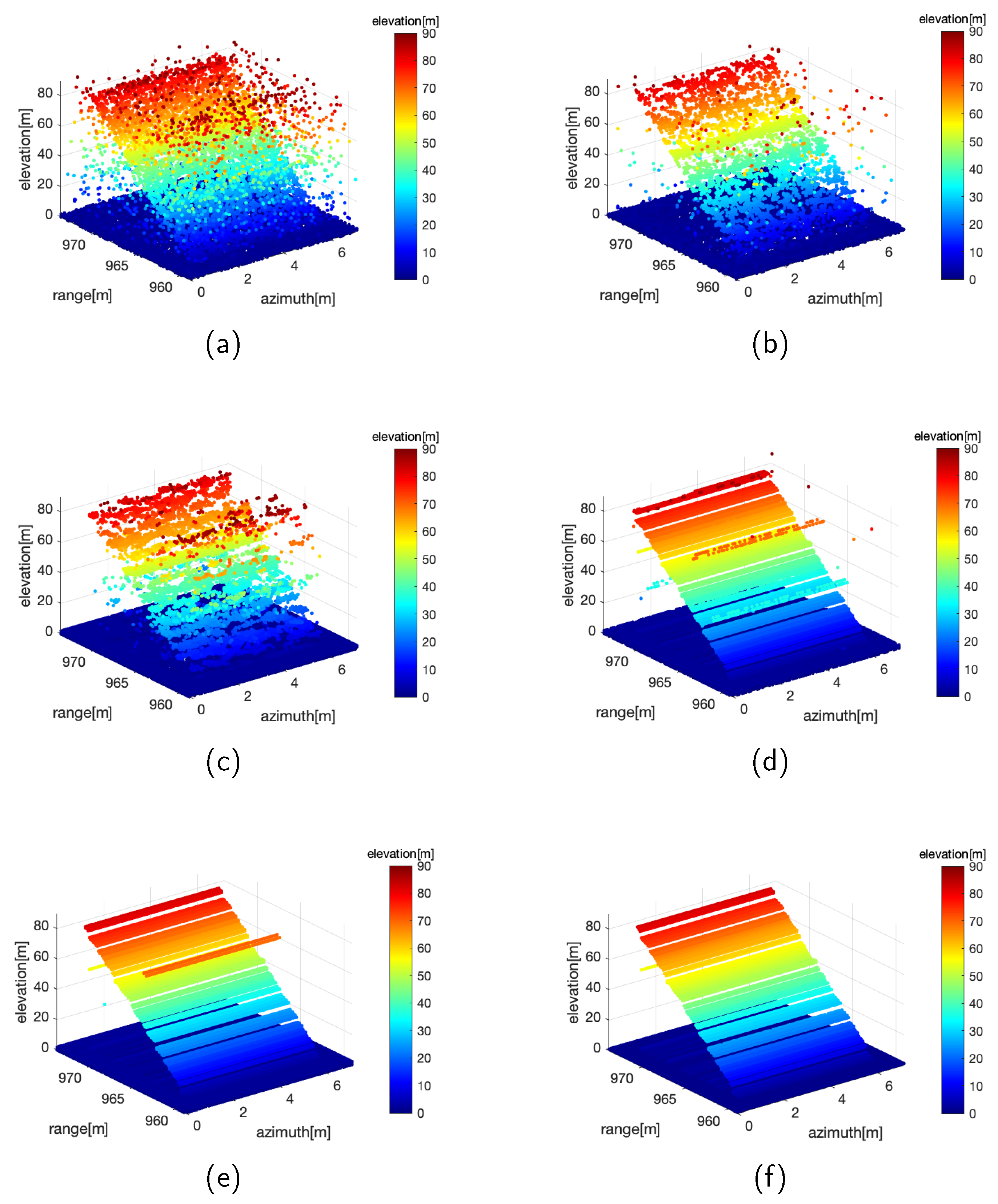
3.2. Simulated Data
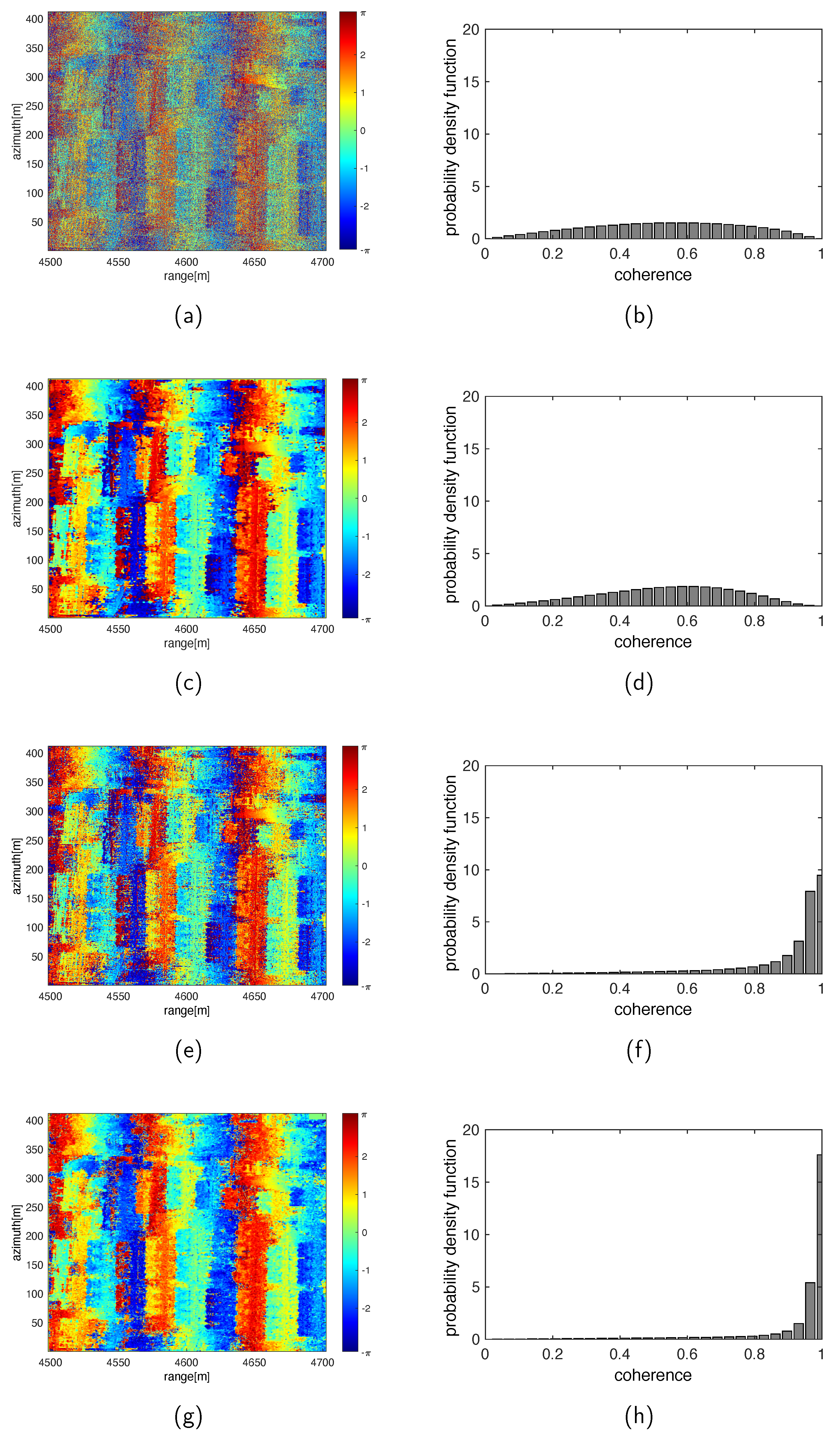
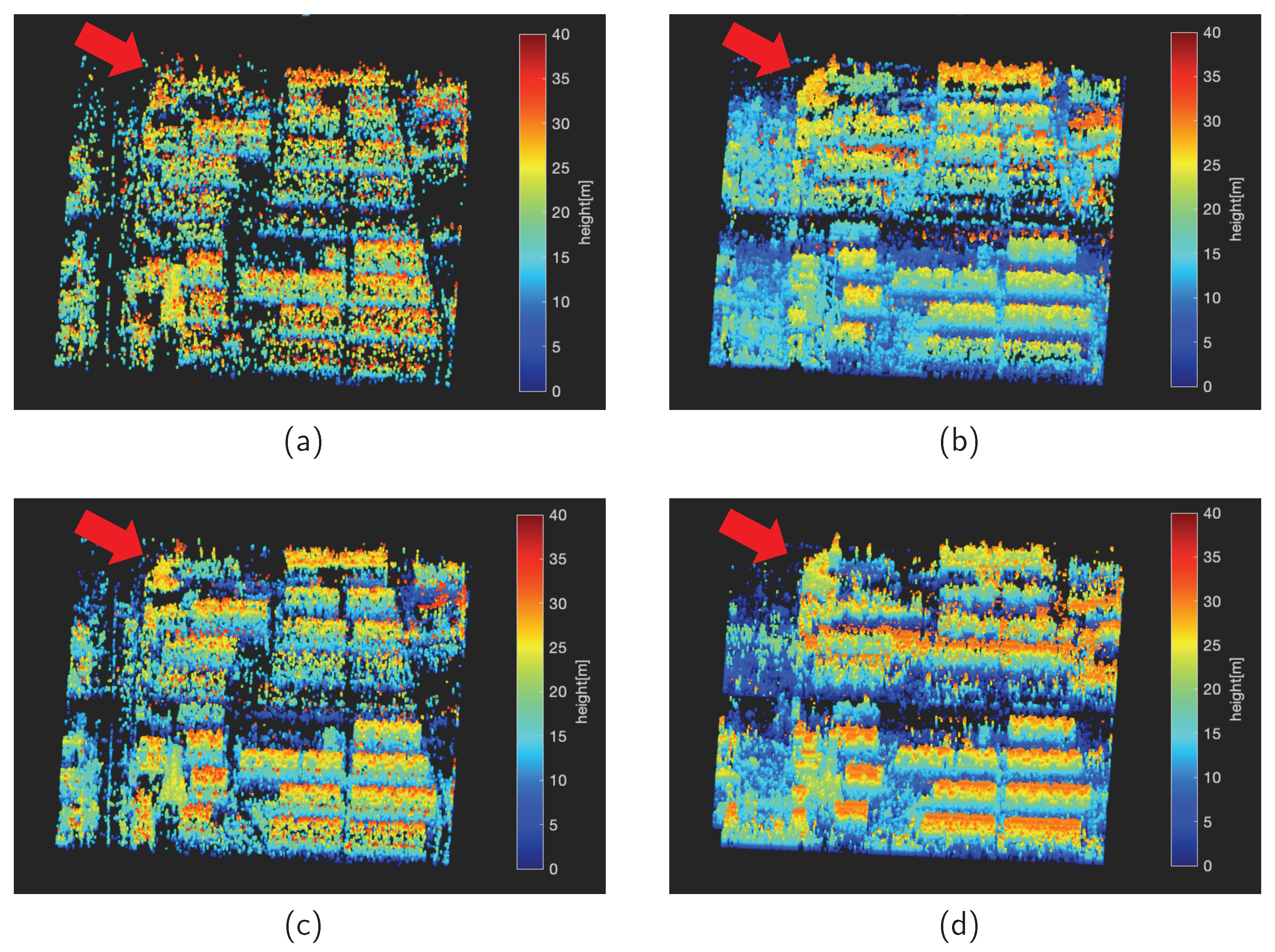
3.3. Real Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
- Rambour, C.; Budillon, A.; Johnsy, A.C.; Denis, L.; Tupin, F.; Schirinzi, G. From interferometric to tomographic SAR: A review of synthetic aperture radar tomography-processing techniques for scatterer unmixing in urban areas. IEEE Geosci. Remote Sens. Mag. 2020, 8, 6–29. [Google Scholar] [CrossRef]
- Goodman, J.W. Some fundamental properties of speckle. J. Opt. Soc. Am. 1976, 66, 1145–1150. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Denis, L.; Tupin, F.; Darbon, J.; Sigelle, M. Joint regularization of phase and amplitude of InSAR data: Application to 3-D reconstruction. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3774–3785. [Google Scholar] [CrossRef]
- D’Hondt, O.; López-Martínez, C.; Guillaso, S.; Hellwich, O. Nonlocal filtering applied to 3-D reconstruction of tomographic SAR data. IEEE Trans. Geosci. Remote Sens. 2017, 56, 272–285. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, X.; Bamler, R. Nonlocal compressive sensing-based SAR tomography. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3015–3024. [Google Scholar] [CrossRef]
- Li, J.; Xu, Z.; Li, Z.; Zhang, Z.; Zhang, B.; Wu, Y. An Unsupervised CNN-Based Multichannel Interferometric Phase Denoising Method Applied to TomoSAR Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3784–3796. [Google Scholar] [CrossRef]
- Xu, G.; Gao, Y.; Li, J.; Xing, M. InSAR phase denoising: A review of current technologies and future directions. IEEE Geosci. Remote Sens. Mag. 2020, 8, 64–82. [Google Scholar] [CrossRef]
- Lee, J.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar]
- Lee, J.; Papathanassiou, K.P.; Ainsworth, T.L.; Grunes, M.R.; Reigber, A. A new technique for noise filtering of SAR interferometric phase images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1456–1465. [Google Scholar]
- Ferraiuolo, G.; Pascazio, V.; Schirinzi, G. Maximum a posteriori estimation of height profiles in InSAR imaging. IEEE Geosci. Remote Sens. Lett. 2004, 1, 66–70. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Baran, I.; Stewart, M.P.; Kampes, B.M.; Perski, Z.; Lilly, P. A modification to the Goldstein radar interferogram filter. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2114–2118. [Google Scholar] [CrossRef]
- Lopez Martinez, C.; Fabregas, X. Modeling and reduction of SAR interferometric phase noise in the wavelet domain. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2553–2566. [Google Scholar] [CrossRef]
- Bian, Y.; Mercer, B. Interferometric SAR phase filtering in the wavelet domain using simultaneous detection and estimation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1396–1416. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tupin, F. NL-InSAR: Nonlocal interferogram estimation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1441–1452. [Google Scholar] [CrossRef]
- Sica, F.; Cozzolino, D.; Zhu, X.X.; Verdoliva, L.; Poggi, G. InSAR-BM3D: A nonlocal filter for SAR interferometric phase restoration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3456–3467. [Google Scholar] [CrossRef]
- Luo, X.; Wang, X.; Wang, Y.; Zhu, S. Efficient InSAR phase noise reduction via compressive sensing in the complex domain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1615–1632. [Google Scholar] [CrossRef]
- Ding, X.; Kang, J.; Zhang, Z.; Huang, Y.; Liu, J.; Yokoya, N. Coherence-guided complex convolutional sparse coding for interferometric phase restoration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Cai, J.; Meng, Z.; Ho, C.M. Residual channel attention generative adversarial network for image super-resolution and noise reduction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 454–455. [Google Scholar]
- Zhu, X.; Montazeri, S.; Ali, M.; Hua, Y.; Wang, Y.; Mou, L.; Shi, Y.; Xu, F.; Bamler, R. Deep learning meets SAR: Concepts, models, pitfalls, and perspectives. IEEE Geosci. Remote Sens. Mag. 2021, 9, 143–172. [Google Scholar] [CrossRef]
- Fracastoro, G.; Magli, E.; Poggi, G.; Scarpa, G.; Valsesia, D.; Verdoliva, L. Deep learning methods for synthetic aperture radar image despeckling: An overview of trends and perspectives. IEEE Geosci. Remote Sens. Mag. 2021, 9, 29–51. [Google Scholar] [CrossRef]
- Vitale, S.; Ferraioli, G.; Pascazio, V. Multi-objective CNN-based algorithm for SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9336–9349. [Google Scholar] [CrossRef]
- Yu, H.; Yang, T.; Zhou, L.; Wang, Y. PDNet: A Lightweight Deep Convolutional Neural Network for InSAR Phase Denoising. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Sun, X.; Zimmer, A.; Mukherjee, S.; Kottayil, N.K.; Ghuman, P.; Cheng, I. DeepInSAR—A deep learning framework for SAR interferometric phase restoration and coherence estimation. Remote Sens. 2020, 12, 2340. [Google Scholar] [CrossRef]
- Sica, F.; Gobbi, G.; Rizzoli, P.; Bruzzone, L. Φ-Net: Deep residual learning for InSAR parameters estimation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3917–3941. [Google Scholar] [CrossRef]
- Vitale, S.; Ferraioli, G.; Pascazio, V.; Schirinzi, G. InSAR-MONet: Interferometric SAR Phase Denoising Using a Multiobjective Neural Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Huang, Y.; Ferro Famil, L.; Reigber, A. Under-foliage object imaging using SAR tomography and polarimetric spectral estimators. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2213–2225. [Google Scholar] [CrossRef]
- Aghababaee, H.; Ferraioli, G.; Schirinzi, G.; Sahebi, M.R. The role of nonlocal estimation in SAR tomographic imaging of volumetric media. IEEE Geosci. Remote Sens. Lett. 2018, 15, 729–733. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Z.; Che, J.; Yang, Z.; Yang, Q.; Wong, K.K. Self-attention reinforcement learning for multi-beam combining in mmWave 3D-MIMO systems. Sci. China Inf. Sci. 2023, 66, 162304. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. CSUR 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Tang, H.; Xu, D.; Sebe, N.; Wang, Y.; Corso, J.J.; Yan, Y. Multi-channel attention selection GAN with cascaded semantic guidance for cross-view image translation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–19 June 2019; pp. 2417–2426. [Google Scholar]
- Tang, H.; Torr, P.H.; Sebe, N. Multi-channel attention selection GANs for guided image-to-image translation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 6055–6071. [Google Scholar] [CrossRef] [PubMed]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, New Orleans, LA, USA, 18–24 June 2021; pp. 568–578. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-trained image processing transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashvile, TN, USA, 20–25 June 2021; pp. 12299–12310. [Google Scholar]
- Wang, Z.; Cun, X.; Bao, J.; Zhou, W.; Liu, J.; Li, H. Uformer: A general u-shaped transformer for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17683–17693. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MICCAI 2015): 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Mukherjee, S.; Zimmer, A.; Sun, X.; Ghuman, P.; Cheng, I. An unsupervised generative neural approach for InSAR phase filtering and coherence estimation. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1971–1975. [Google Scholar] [CrossRef]
- Sohn, G.; Dowman, I. Data fusion of high-resolution satellite imagery and LiDAR data for automatic building extraction. ISPRS J. Photogramm. Remote Sens. 2007, 62, 43–63. [Google Scholar] [CrossRef]
- Zhu, X.X.; Shahzad, M. Facade reconstruction using multiview spaceborne TomoSAR point clouds. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3541–3552. [Google Scholar] [CrossRef]


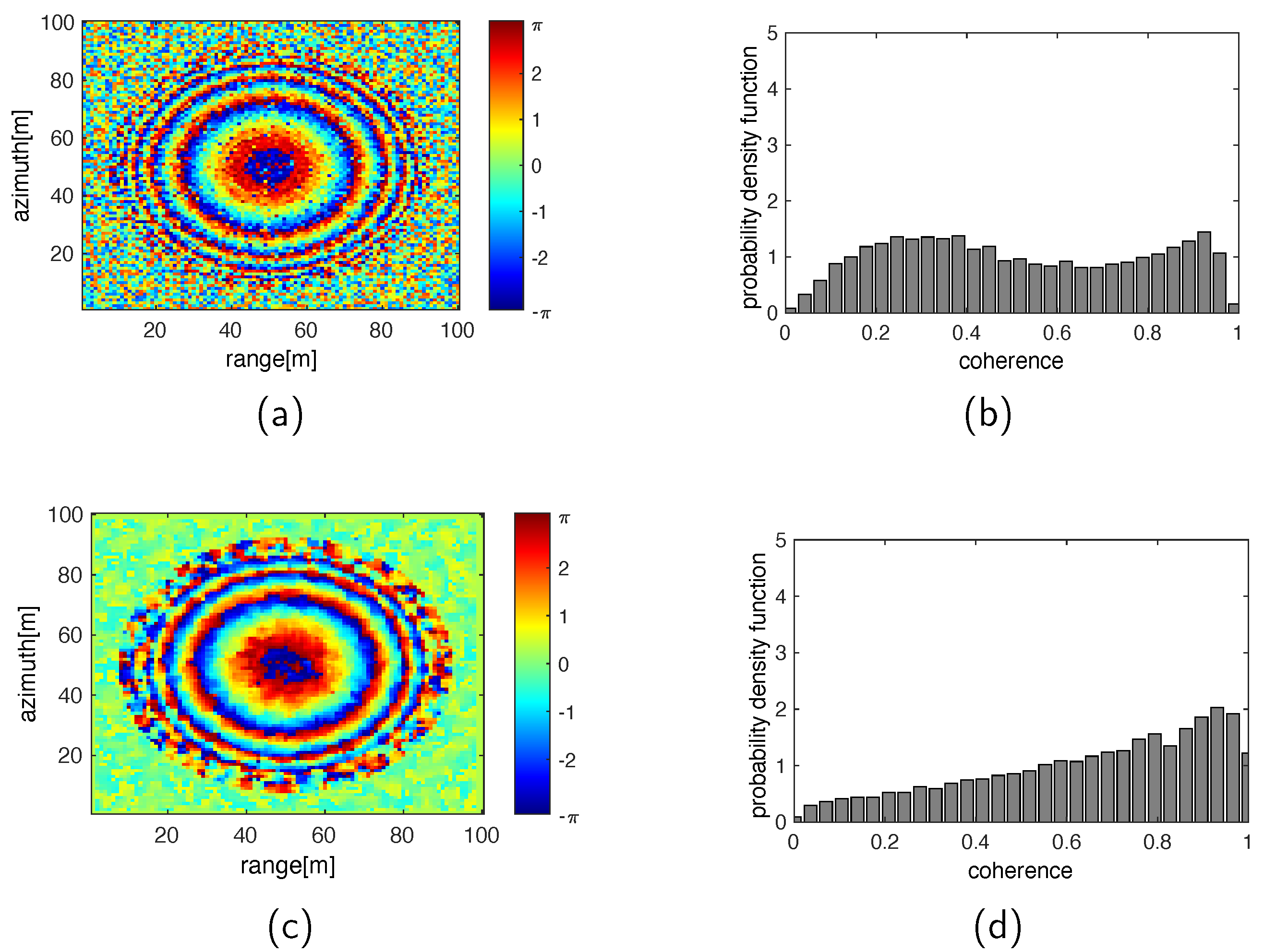

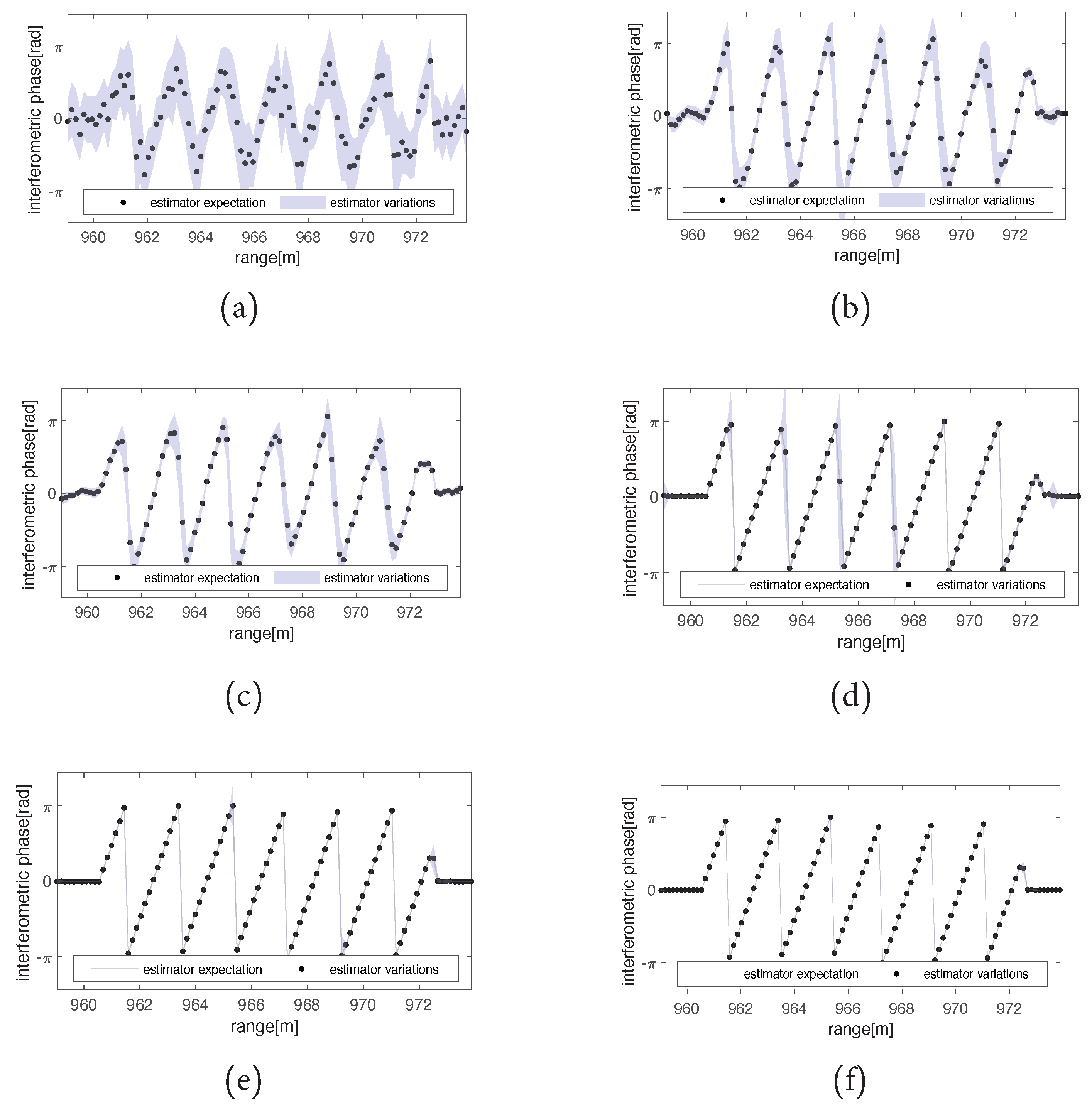
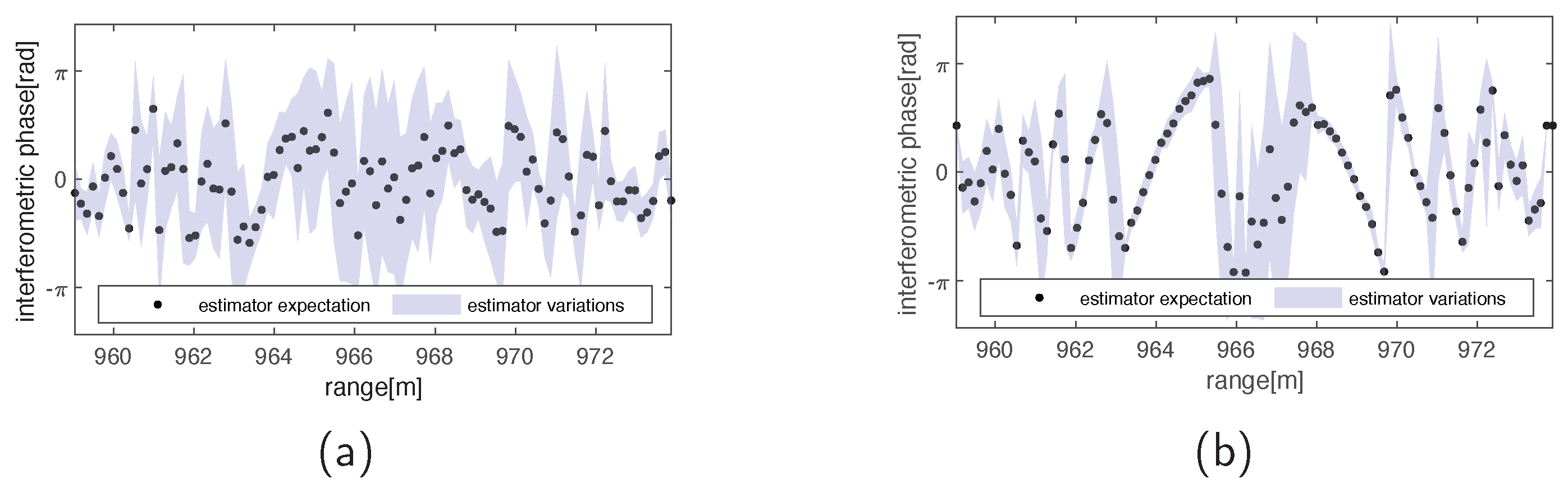

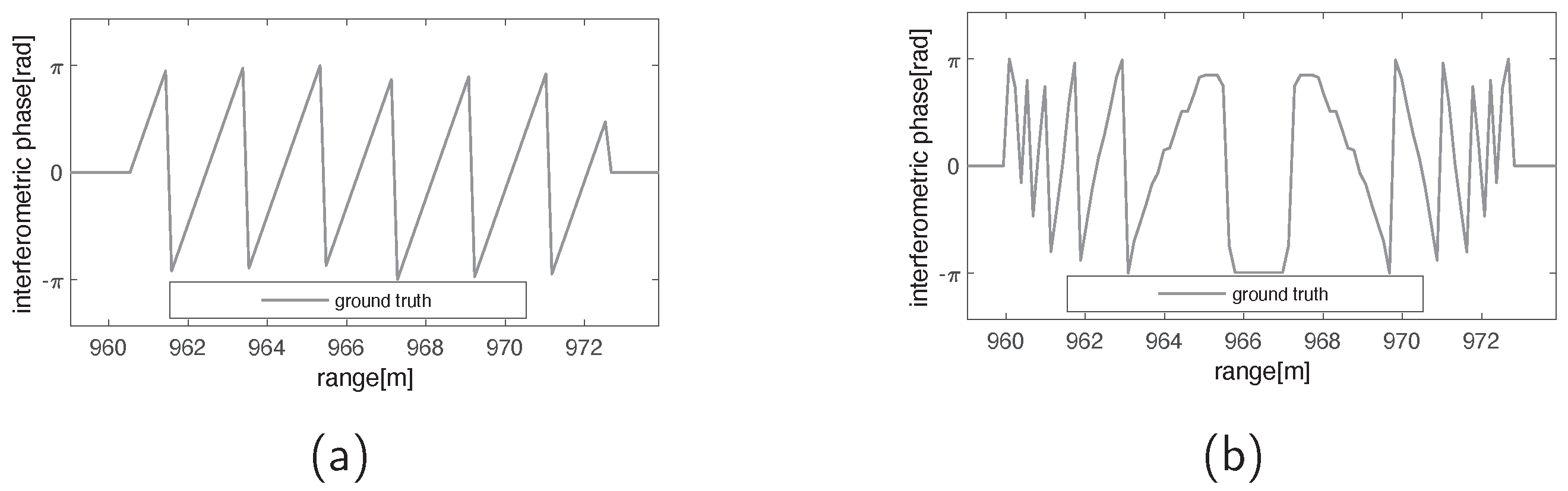





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, Z.; Zhang, B.; Wu, Y. A Multi-Channel Attention Network for SAR Interferograms Filtering Applied to TomoSAR. Remote Sens. 2023, 15, 4401. https://doi.org/10.3390/rs15184401
Li J, Li Z, Zhang B, Wu Y. A Multi-Channel Attention Network for SAR Interferograms Filtering Applied to TomoSAR. Remote Sensing. 2023; 15(18):4401. https://doi.org/10.3390/rs15184401
Chicago/Turabian StyleLi, Jie, Zhiyuan Li, Bingchen Zhang, and Yirong Wu. 2023. "A Multi-Channel Attention Network for SAR Interferograms Filtering Applied to TomoSAR" Remote Sensing 15, no. 18: 4401. https://doi.org/10.3390/rs15184401
APA StyleLi, J., Li, Z., Zhang, B., & Wu, Y. (2023). A Multi-Channel Attention Network for SAR Interferograms Filtering Applied to TomoSAR. Remote Sensing, 15(18), 4401. https://doi.org/10.3390/rs15184401





