Multiband Image Fusion via Regularization on a Riemannian Submanifold
Abstract
1. Introduction
1.1. Scope and Contributions
- An efficient multiband image fusion model utilizing the Riemannian submanifold regularization method is proposed. This model is characterized by rank equality constraints with matrix manifold, nonnegativity and sum-to-one constraints. This is a new problem formulation for investigating the latent structures across varying modalities and resolutions.
- An alternating minimization scheme is proposed to recover the latent structures of the subspace using the framework of the manifold alternating direction method of multipliers. An efficient projected Riemannian trust region method with guaranteed convergence is adopted to track the latent subspace.
- The proposed method is validated in two applications: (1) hyperspectral and panchromatic image fusion and (2) the fusion of hyperspectral, multispectral and panchromatic images. The experimental results show that the proposed method is more effective than the competitive state-of-the-art fusion methods.
1.2. Related Work
1.2.1. HS-PAN Image Fusion
1.2.2. HS-MS Image Fusion
2. Preliminaries for Riemannian Manifold Optimization
2.1. Riemannian Gradient and Tangent Space
2.2. Retractions
3. Problem Formulation
3.1. Degradation Model for Multiband Imaging
3.2. Proposed Fusion Model
3.3. Riemannian Submanifold Regularization
3.4. Nonnegativity and Sum-to-One Constraints
4. Proposed Method
4.1. Alternating Minimization Scheme
| Algorithm 1 Optimization procedures for the problem in Equation (6) |
|
4.2. Convergence Analysis
5. Performance Evaluation
5.1. Experimental Settings
5.2. Datasets and Quality Measures
- Botswana dataset: The HS image was collected by a Hyperion sensor over Okavango Delta, Botswana in 2001–2004. The number of bands in our experiment was 145. The spatial resolution is . The observed scene contains the land cover type information.
- Indian Pines dataset: The imaging sensor is the airborne visible infrared image spectrometer (AVIRS) airborne hyperspectral instrument. Images were captured over northern and western Indiana in the USA. The number of bands was 200. The dimensions of the HS images are . The scenery of this dataset includes housing, built structures, and forests.
- Kennedy Space Center dataset: This dataset was captured at Kennedy Space Center in Florida, United States by an AVIRIS. This dataset comprises 176 bands with an image size of . The content of the HS image contains various land cover types.
- Washington DC Mall dataset: This was collected by the hyperspectral digital image collection experiment (HYDICE) over the Washington DC Mall in the United States. A portion of the original data was used. The resolution of the HS image is . The number of spectral bands was 191.
5.3. Results
5.3.1. Hyperspectral and Panchromatic Image Fusion
5.3.2. Hyperspectral, Multispectral and Panchromatic Image Fusion
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Updating X
Appendix A.2. Updating ∧
Appendix B
Appendix B.1. Updating W
| Algorithm A1 Projected Riemannian trust region method for Equation (A6) |
| Algorithm A2 Retraction with projection |
|
Appendix B.2. Updating Z
References
- Leung, H.; Mukhopadhyay, S.C. Intelligent Environmental Sensing; Springer: Berlin/Heidelberg, Germany, 2015; Volume 13. [Google Scholar]
- Feng, X.; He, L.; Cheng, Q.; Long, X.; Yuan, Y. Hyperspectral and Multispectral Remote Sensing Image Fusion Based on Endmember Spatial Information. Remote Sens. 2020, 12, 1009. [Google Scholar] [CrossRef]
- Fauvel, M.; Chanussot, J.; Benediktsson, J.A. Decision Fusion for the Classification of Urban Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2828–2838. [Google Scholar] [CrossRef]
- Onana, V.D.P.; Koenig, L.S.; Ruth, J.; Studinger, M.; Harbeck, J.P. A Semiautomated Multilayer Picking Algorithm for Ice-Sheet Radar Echograms Applied to Ground-Based Near-Surface Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 51–69. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Loncan, L.; de Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simões, M.; et al. Hyperspectral Pansharpening: A Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, H.; Liu, S. Hyperspectral and Multispectral Image Fusion: From Model-Driven to Data-Driven. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 1256–1259. [Google Scholar]
- Xie, W.; Cui, Y.; Li, Y.; Lei, J.; Du, Q.; Li, J. HPGAN: Hyperspectral Pansharpening Using 3-D Generative Adversarial Networks. IEEE Trans. Geosci. Remote Sens. 2020, 59, 463–477. [Google Scholar] [CrossRef]
- Guan, P.; Lam, E.Y. Multistage Dual-Attention Guided Fusion Network for Hyperspectral Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5515214. [Google Scholar] [CrossRef]
- Arablouei, R. Fusing Multiple Multiband Images. J. Imaging 2018, 4, 118. [Google Scholar] [CrossRef]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing Hyperspectral and Multispectral Images via Coupled Sparse Tensor Factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Fang, L. Learning a Low Tensor-Train Rank Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2672–2683. [Google Scholar] [CrossRef]
- Veganzones, M.A.; Simões, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral Super-Resolution of Locally Low Rank Images From Complementary Multisource Data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.; Chen, M.; Godsill, S. Multiband Image Fusion Based on Spectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7236–7249. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, M.; Yang, S. Multispectral and Hyperspectral Image Fusion Based on Group Spectral Embedding and Low-Rank Factorization. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1363–1371. [Google Scholar] [CrossRef]
- Kanatsoulis, C.I.; Fu, X.; Sidiropoulos, N.D.; Ma, W. Hyperspectral Super-Resolution: A Coupled Tensor Factorization Approach. IEEE Trans. Signal Process. 2018, 66, 6503–6517. [Google Scholar] [CrossRef]
- Chen, Z.; Pu, H.; Wang, B.; Jiang, G.M. Fusion of Hyperspectral and Multispectral Images: A Novel Framework Based on Generalization of Pan-Sharpening Methods. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1418–1422. [Google Scholar] [CrossRef]
- Liao, W.; Huang, X.; Van Coillie, F.; Gautama, S.; Pižurica, A.; Philips, W.; Liu, H.; Zhu, T.; Shimoni, M.; Moser, G.; et al. Processing of Multiresolution Thermal Hyperspectral and Digital Color Data: Outcome of the 2014 IEEE GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2984–2996. [Google Scholar] [CrossRef]
- Yun, Z. Problems in the Fusion of Commercial High-Resolution Satellites Images as well as LANDSAT 7 Images and Initial Solutions. Geospat. Theory Process. Appl. 2002, 34, 587–592. [Google Scholar]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Otazu, X.; Gonzalez-Audicana, M.; Fors, O.; Nunez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Amolins, K.; Zhang, Y.; Dare, P. Wavelet based image fusion techniques: An introduction, review and comparison. Isprs J. Photogramm. Remote Sens. 2007, 62, 249–263. [Google Scholar] [CrossRef]
- Liu, J. Smoothing Filter-based Intensity Modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and Error-Based Fusion Schemes for Multispectral Image Pansharpening. IEEE Geosci. Remote Sens. Lett. 2014, 11, 930–934. [Google Scholar] [CrossRef]
- Xie, W.; Lei, J.; Cui, Y.; Li, Y.; Du, Q. Hyperspectral Pansharpening With Deep Priors. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1529–1543. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Huang, B.; Song, H.; Cui, H.; Peng, J.; Xu, Z. Spatial and Spectral Image Fusion Using Sparse Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1693–1704. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse Spatio-spectral Representation for Hyperspectral Image Super-resolution. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 63–78. [Google Scholar]
- Simões, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral Image Super-Resolution via Non-Negative Structured Sparse Representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef]
- Dian, R.; Fang, L.; Li, S. Hyperspectral Image Super-Resolution via Non-local Sparse Tensor Factorization. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3862–3871. [Google Scholar]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Spatial–Spectral-Graph-Regularized Low-Rank Tensor Decomposition for Multispectral and Hyperspectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1030–1040. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and Multispectral Image Fusion via Deep Two-Branches Convolutional Neural Network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Huang, T.; Dong, W.; Wu, J.; Li, L.; Li, X.; Shi, G. Deep Hyperspectral Image Fusion Network With Iterative Spatio-Spectral Regularization. IEEE Trans. Comput. Imaging 2022, 8, 201–214. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.; Zhao, Q.; Xu, Z.; Meng, D. MHF-Net: An Interpretable Deep Network for Multispectral and Hyperspectral Image Fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1457–1473. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and Multispectral Image Fusion Based on a Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3658–3668. [Google Scholar] [CrossRef]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2008; p. xvi+224. [Google Scholar]
- Boumal, N. An Introduction to Optimization on Smooth Manifolds; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Absil, P.A.; Malick, J. Projection-like Retractions on Matrix Manifolds. Siam J. Optim. 2012, 22, 135–158. [Google Scholar] [CrossRef]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F.H. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Bioucasdias, J.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral Unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Vogel, C.R. Computational Methods for Inverse Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Mishra, B.; Meyer, G.; Bonnabel, S.; Sepulchre, R. Fixed-rank matrix factorizations and Riemannian low-rank optimization. Comput. Stat. 2014, 29, 591–621. [Google Scholar] [CrossRef][Green Version]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Condat, L. Fast projection onto the simplex and the ℓ1 ball. Math. Program. 2016, 158, 575–585. [Google Scholar] [CrossRef]
- Nishihara, R.; Lessard, L.; Recht, B.; Packard, A.; Jordan, M.I. A General Analysis of the Convergence of ADMM. In Proceedings of the 32Nd International Conference on International Conference on Machine Learning, Lille, France, 7–9 July 2015; Volume 37, pp. 343–352. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Laben, C.; Brower, B. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 2000. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving Component Substitution Pansharpening Through Multivariate Regression of MS +Pan Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Psjr, C.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data: Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 265–303. [Google Scholar]
- Wei, Q.; Dobigeon, N.; Tourneret, J.; Bioucas-Dias, J.; Godsill, S. R-FUSE: Robust Fast Fusion of Multiband Images Based on Solving a Sylvester Equation. IEEE Signal Process. Lett. 2016, 23, 1632–1636. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A Regression-Based High-Pass Modulation Pansharpening Approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 984–996. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full Scale Regression-Based Injection Coefficients for Panchromatic Sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Wang, P.; Yao, H.; Li, C.; Zhang, G.; Leung, H. Multiresolution Analysis Based on Dual-Scale Regression for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5406319. [Google Scholar] [CrossRef]
- Xiao, J.L.; Huang, T.Z.; Deng, L.J.; Wu, Z.C.; Vivone, G. A New Context-Aware Details Injection Fidelity With Adaptive Coefficients Estimation for Variational Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5408015. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE Pan Sharpening of Very High Resolution Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Lee, J.; Lee, C. Fast and Efficient Panchromatic Sharpening. IEEE Trans. Geosci. Remote Sens. 2010, 48, 155–163. [Google Scholar]
- Remote Sensing Datasets. Available online: https://rslab.ut.ac.ir/data (accessed on 28 July 2023).
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Vandereycken, B. Low-Rank Matrix Completion by Riemannian Optimization. Siam J. Optim. 2013, 23, 1214–1236. [Google Scholar] [CrossRef]
- Absil, P.A.; Baker, C.G.; Gallivan, K.A. Trust-Region Methods on Riemannian Manifolds. Found. Comput. Math. 2007, 7, 303–330. [Google Scholar] [CrossRef]
- Jorge, N.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]


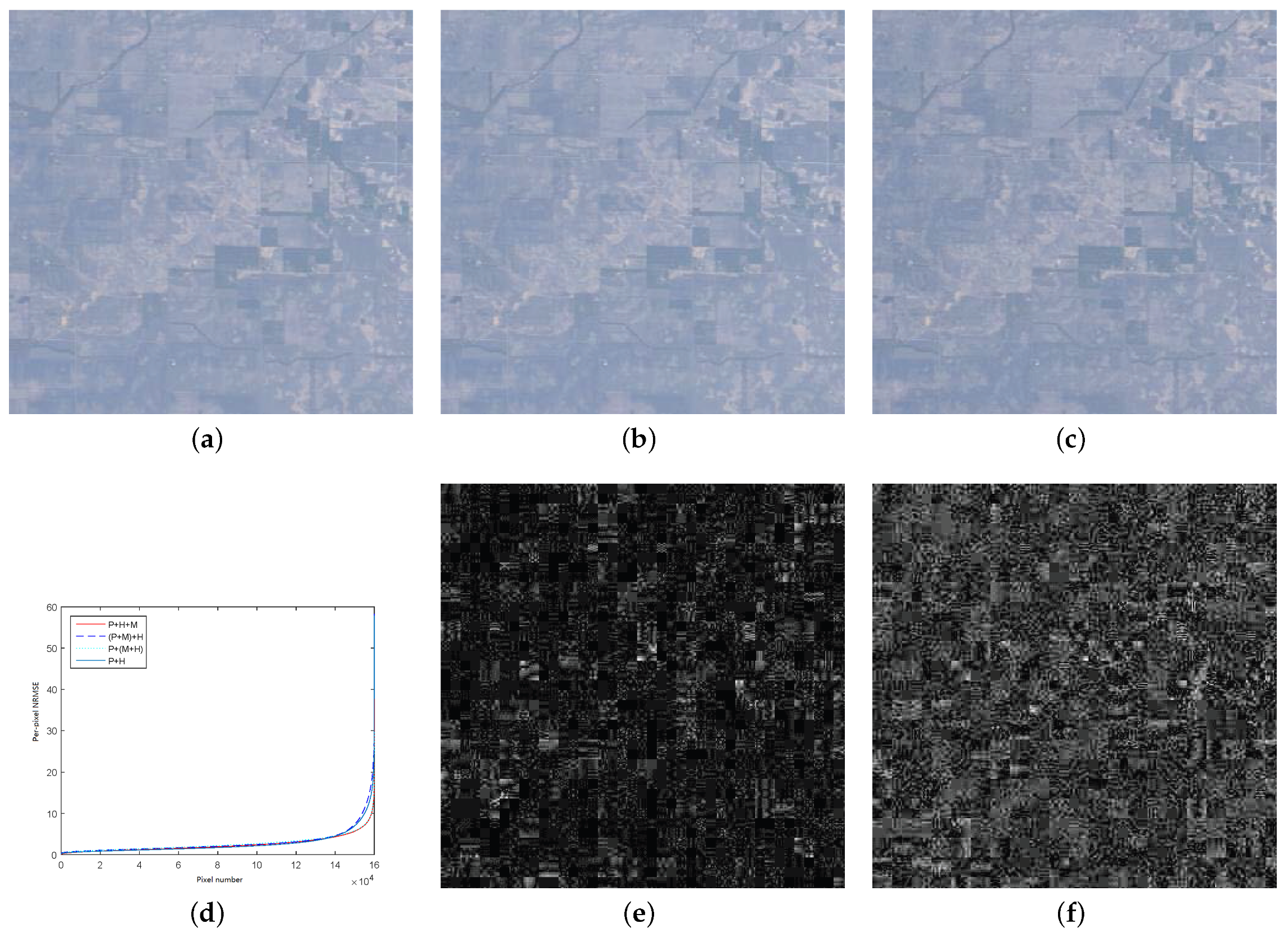

| Datasets | Botswana | Indian Pines | Washington DC Mall | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fusion Methods | ERGAS↓ | SAM↓ | UIQI (%)↑ | ERGAS↓ | SAM↓ | UIQI (%)↑ | ERGAS↓ | SAM↓ | UIQI (%)↑ |
| SFIM | 24.9670 | 2.6758 | 86.49 | 0.9583 | 1.2023 | 87.81 | 3.9752 | 2.6530 | 94.11 |
| MT | 3.0794 | 2.5482 | 90.02 | 0.9249 | 1.1800 | 88.83 | 3.3584 | 2.8864 | 95.76 |
| MT-HPM | 47.0230 | 2.6108 | 87.52 | 0.9722 | 1.2086 | 88.48 | 3.4854 | 2.5888 | 95.51 |
| GS | 2.8263 | 2.4166 | 91.25 | 1.3886 | 1.4620 | 81.38 | 5.7251 | 5.2996 | 84.39 |
| GSA | 3.1798 | 2.5806 | 90.06 | 0.8252 | 1.0897 | 89.76 | 3.5158 | 2.9546 | 95.87 |
| PCA | 2.9592 | 2.5074 | 90.42 | 1.8095 | 1.9336 | 76.61 | 3.8862 | 3.4006 | 91.50 |
| PCA-GF | 3.1833 | 3.1687 | 77.98 | 1.1607 | 1.6353 | 79.49 | 5.6117 | 2.8216 | 79.55 |
| RF | 1.8364 | 2.4047 | 94.65 | 1.0243 | 0.9509 | 91.41 | 3.5888 | 3.6285 | 93.21 |
| CF | 1.2706 | 2.5176 | 93.89 | 0.9441 | 1.7088 | 83.50 | 1.8495 | 3.5331 | 96.14 |
| HY | 1.7612 | 2.1741 | 91.97 | 1.0495 | 0.9555 | 90.94 | 2.7327 | 3.0719 | 96.33 |
| MT-R | 2.7732 | 3.1392 | 91.81 | 1.5811 | 1.4481 | 90.24 | 4.7134 | 2.1903 | 92.02 |
| MT-FSR | 2.7487 | 3.1581 | 91.90 | 1.5811 | 1.4594 | 90.21 | 4.7096 | 2.4774 | 91.85 |
| MT-DSR | 2.7728 | 3.1394 | 91.80 | 1.5822 | 1.4480 | 90.19 | 4.7108 | 2.1918 | 92.04 |
| CDIF | 2.2615 | 2.5503 | 93.15 | 1.2430 | 1.0518 | 93.88 | 4.0160 | 1.8530 | 95.85 |
| Proposed Method | 1.4321 | 1.9561 | 95.64 | 0.8025 | 0.9487 | 95.67 | 1.4122 | 2.3475 | 98.81 |
| Images | Fusion Methods | Botswana | Indian Pines | ||||||
| ERGAS↓ | SAM↓ | UIQI (%)↑ | Time (s)↓ | ERGAS↓ | SAM↓ | UIQI (%)↑ | Time (s)↓ | ||
| PAN + HS | HY | 1.8450 | 2.4035 | 94.49 | 48.34 | 0.8234 | 1.0494 | 87.17 | 86.45 |
| RF | 1.8364 | 2.4047 | 94.65 | 49.18 | 0.8191 | 1.0529 | 87.12 | 90.37 | |
| (PAN + MS) + HS | BD + HY | 3.0323 | 3.5445 | 93.61 | 49.17 | 0.7491 | 1.0801 | 87.16 | 86.26 |
| BD + RF | 3.0192 | 3.5324 | 93.69 | 51.54 | 0.7434 | 1.0846 | 87.20 | 86.40 | |
| MT + HY | 2.9706 | 3.5923 | 93.88 | 51.83 | 0.9252 | 1.1439 | 84.86 | 84.92 | |
| MT + RF | 2.9573 | 3.5786 | 93.95 | 51.06 | 0.9170 | 1.1519 | 84.89 | 86.25 | |
| CF | 1.8310 | 2.7891 | 89.96 | 38.93 | 0.9213 | 1.7485 | 86.83 | 73.48 | |
| PAN + (MS + HS) | HY + HY | 2.0442 | 2.1535 | 93.52 | 49.51 | 0.7789 | 0.9373 | 85.24 | 86.71 |
| RF + RF | 2.9769 | 3.6799 | 93.57 | 51.77 | 0.8110 | 0.9481 | 84.66 | 90.99 | |
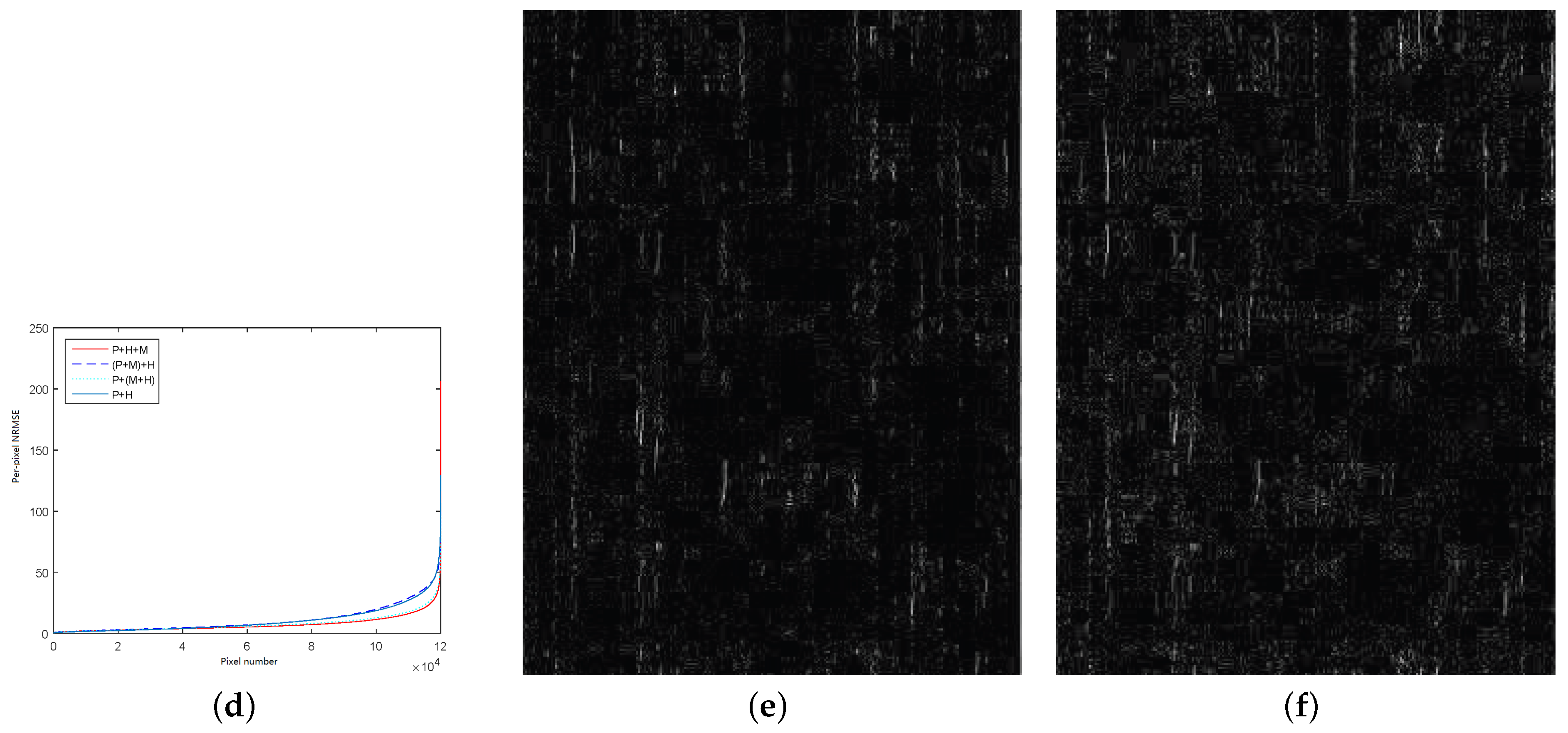
| PAN + MS + HS | Our Method | 1.6317 | 1.6408 | 98.52 | 38.01 | 0.5812 | 0.8850 | 95.18 | 65.51 |
| Images | Fusion Methods | Washington DC Mall | Kennedy Space Center | ||||||
| ERGAS↓ | SAM↓ | UIQI (%)↑ | Time (s)↓ | ERGAS↓ | SAM↓ | UIQI (%)↑ | Time (s)↓ | ||
| PAN + HS | HY | 3.9132 | 4.6076 | 92.63 | 83.29 | 3.9600 | 4.5045 | 94.55 | 111.47 |
| RF | 3.9207 | 4.6075 | 92.64 | 84.08 | 3.8971 | 4.2528 | 94.94 | 127.33 | |
| (PAN + MS) + HS | BD + HY | 4.0388 | 4.7666 | 92.32 | 83.91 | 3.6127 | 4.7748 | 95.42 | 110.40 |
| BD + RF | 4.1409 | 4.7867 | 92.06 | 87.09 | 3.4127 | 4.5649 | 95.94 | 110.49 | |
| MT + HY | 4.2401 | 4.8087 | 91.63 | 83.42 | 8.3050 | 5.3050 | 86.94 | 128.82 | |
| MT + RF | 4.3543 | 4.8267 | 91.29 | 84.47 | 8.2069 | 5.2489 | 87.24 | 121.36 | |
| CF | 4.0730 | 5.2249 | 82.12 | 57.11 | 3.6472 | 5.3522 | 86.37 | 88.72 | |
| PAN + (MS + HS) | HY + HY | 3.0955 | 3.6234 | 95.28 | 94.44 | 2.8052 | 5.6430 | 96.67 | 111.39 |
| RF + RF | 3.6510 | 3.8968 | 94.26 | 88.87 | 3.6730 | 6.1409 | 95.80 | 116.21 | |
| PAN + MS + HS | Our Method | 2.5503 | 2.8112 | 97.77 | 62.39 | 2.5044 | 4.2221 | 97.23 | 82.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Jing, Z.; Leung, H.; Peng, P.; Zhang, H. Multiband Image Fusion via Regularization on a Riemannian Submanifold. Remote Sens. 2023, 15, 4370. https://doi.org/10.3390/rs15184370
Pan H, Jing Z, Leung H, Peng P, Zhang H. Multiband Image Fusion via Regularization on a Riemannian Submanifold. Remote Sensing. 2023; 15(18):4370. https://doi.org/10.3390/rs15184370
Chicago/Turabian StylePan, Han, Zhongliang Jing, Henry Leung, Pai Peng, and Hao Zhang. 2023. "Multiband Image Fusion via Regularization on a Riemannian Submanifold" Remote Sensing 15, no. 18: 4370. https://doi.org/10.3390/rs15184370
APA StylePan, H., Jing, Z., Leung, H., Peng, P., & Zhang, H. (2023). Multiband Image Fusion via Regularization on a Riemannian Submanifold. Remote Sensing, 15(18), 4370. https://doi.org/10.3390/rs15184370








