Spatiotemporal Characteristics and Volume Transport of Lagrangian Eddies in the Northwest Pacific
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. SSH Eddy Detection Method
- (1)
- The daily ADT background fields are scanned with an output interval of 0.2 cm to ensure that each anticyclonic (cyclonic) eddy contains no more than one local ADT maximum (minimum). The extreme point is considered as the eddy center.
- (2)
- The amplitude is defined as the height difference between extreme point and the outermost closed contour.
- (3)
- The radius is determined as the standard circle radius with the same enclosed area as the contour. The overlapping area between the circle and the contour should be at least 30% of the eddy area.
- (4)
- The outermost contour is a single connected region containing at least 5 and at most 1000 pixels.
2.3. RCLV Detection Method
- (1)
- Selecting a finite time interval T = [t0, t1], the LAVD field is computed using Equation (4).
- (2)
- The center of the RCLVs is defined as the local maximum of LAVD.
- (3)
- The regions of RCLVs are grown by iterating through the nested contour field around the center. The boundaries of RCLVs are the outermost closed contour of LAVD.
- (4)
- The vorticity of RCLVs > 0 for anticyclonic eddies (ACEs), and else for cyclonic eddies (CEs) in the Northern Hemisphere.
- (5)
- The amplitude and the radius of RCLVs are determined in the same manner as SSH eddies.
- (6)
- The increment of the numerically calculated LAVD contour will distort the convex hull of the RCLV boundary. To ensure the coherence and convexity of the RCLV boundaries, the requirements of the Coherency Index (CI) and Convexity Deficiency (CD) are introduced:
- i.
- The CD is defined as the ratio of the difference in the area between the convex hull and the contour to the area enclosed by the contour’s area [45]. Higher CD values indicate more filamentary tails and less compact geometry. And the closer CD is to zero, the closer the eddy boundary is to become a convex curve.
- ii.
- The CI examines the change in the spatial compactness of particles inside the contour over a finite time interval T = [t0, t1], which is expressed from the variance of the particle positions (σ2(t)):
3. Results
3.1. Eddy Spatiotemporal Characteristics
3.2. Analysis of Eddy Transport
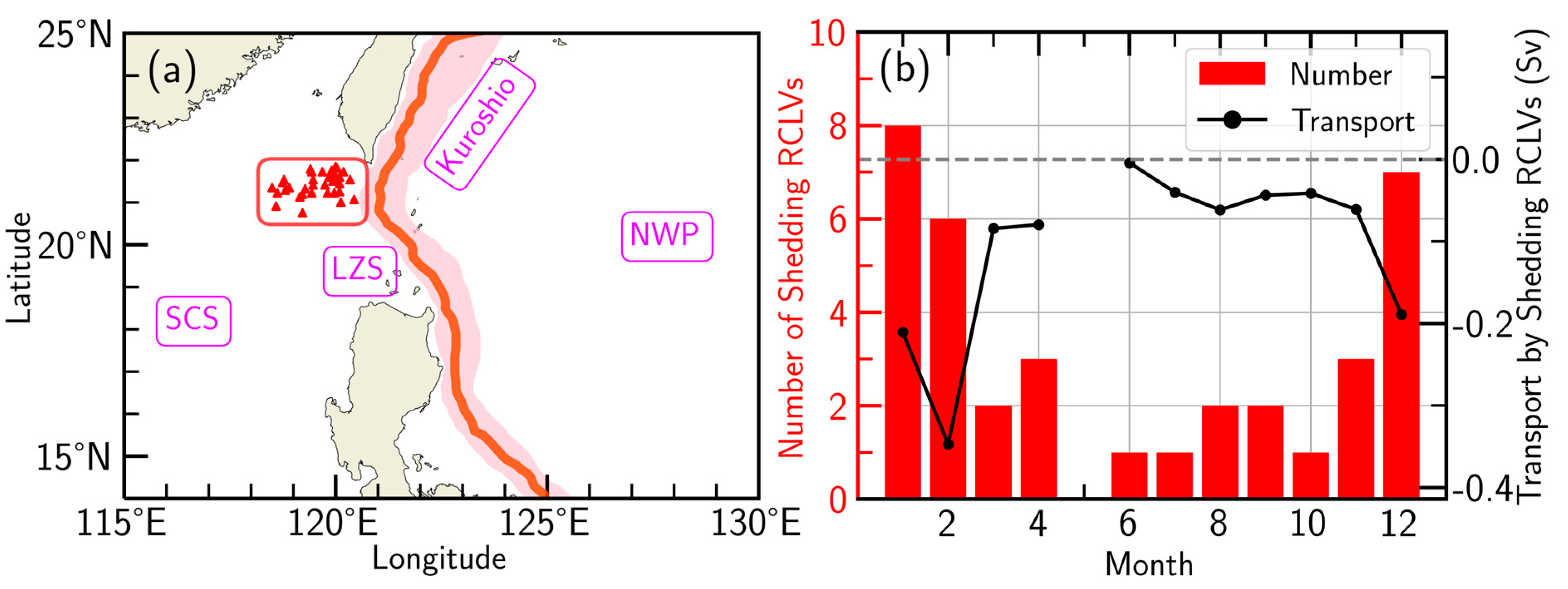
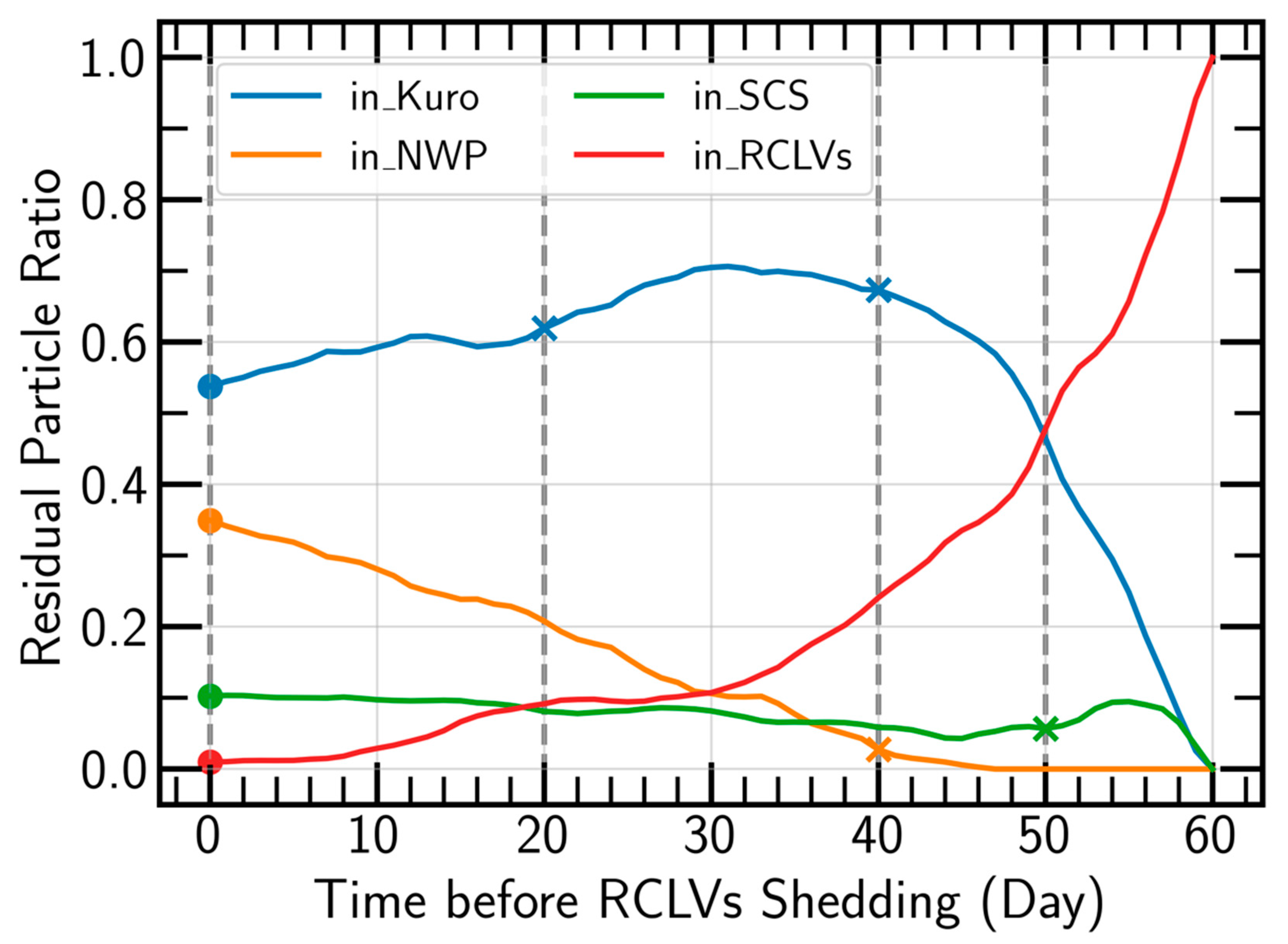
3.3. Features of Shedding RCLV in the Luzon Strait
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Qiu, B. Seasonal eddy field modulation of the North Pacific Subtropical Countercurrent: TOPEX/Poseidon observations and theory. J. Phys. Oceanogr. 1999, 29, 2471–2486. [Google Scholar] [CrossRef]
- Noh, Y.; Yim, B.Y.; You, S.H.; Yoon, J.H.; Qiu, B. Seasonal variation of eddy kinetic energy of the North Pacific Subtropical Countercurrent simulated by an eddy-resolving OGCM. Geophys. Res. Lett. 2007, 34, L07601. [Google Scholar] [CrossRef]
- Yoshida, S.; Qiu, B.; Hacker, P. Wind-generated eddy characteristics in the lee of the island of Hawaii. J. Geophys. Res. 2010, 115, C03019. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, C.; Guan, Y.; Chen, D.; McWilliams, J.; Nencioli, F. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 68, 54–67. [Google Scholar] [CrossRef]
- Ding, M.; Lin, P.; Liu, H.; Chai, F. Increased eddy activity in the Northeastern Pacific during 1993–2011. J. Clim. 2018, 31, 387–399. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, S.; Nowotarski, C.J.; Jiang, Y. Atmospheric responses to mesoscale oceanic eddies in the winter and summer North Pacific Subtropical Countercurrent region. Atmosphere 2020, 11, 816. [Google Scholar] [CrossRef]
- Sun, Z.; Hu, J.; Chen, Z.; Zhu, J.; Yang, L.; Chen, X.; Wu, X. A strong Kuroshio intrusion into the South China Sea and its accompanying cold-core anticyclonic eddy in winter 2020–2021. Remote Sens. 2021, 13, 2645. [Google Scholar] [CrossRef]
- Dufois, F.; Hardman-Mountford, N.J.; Greenwood, J.; Richardson, A.J.; Feng, M.; Matear, R.J. Anticyclonic eddies are more productive than cyclonic eddies in subtropical gyres because of winter mixing. Sci. Adv. 2016, 2, 5. [Google Scholar] [CrossRef]
- Kobashi, F.; Doi, H.; Iwasaka, N. Sea surface cooling induced by extratropical cyclones in the Subtropical North Pacific: Mechanism and interannual variability. J. Geophys. Res. Oceans 2019, 124, 2179–2195. [Google Scholar] [CrossRef]
- Sun, B.; Liu, C.; Wang, F. Global meridional eddy heat transport inferred from Argo and altimetry observations. Sci. Rep. 2019, 9, 1345. [Google Scholar] [CrossRef] [PubMed]
- Stammer, D. On Eddy characteristics, eddy transports, and mean flow properties. J. Phys. Oceanogr. 1998, 28, 727–739. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. Eddy transport of heat and thermocline waters in the North Pacific: A key to interannual/decadal climate variability? J. Phys. Oceanogr. 2001, 31, 675–687. [Google Scholar] [CrossRef]
- Jayne, S.R.; Marotzke, J. The oceanic eddy heat transport. J. Phys. Oceanogr. 2002, 32, 3328–3345. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, T.; Fu, L.-L. Eddy-induced meridional heat transport in the ocean. Geophys. Res. Lett. 2008, 35, L20601. [Google Scholar] [CrossRef]
- Chen, S.; Qiu, B. Interannual variability of the North Pacific Subtropical Countercurrent and its associated mesoscale eddy field. J. Phys. Oceanogr. 2010, 40, 213–225. [Google Scholar] [CrossRef]
- Kang, L.; Wang, F.; Chen, Y. Eddy generation and evolution in the North Pacific Subtropical Countercurrent (NPSC) zone. Chin. J. Oceanol. Limnol. 2010, 28, 968–973. [Google Scholar] [CrossRef]
- Yang, G.; Wang, F.; Li, Y.; Lin, P. Mesoscale eddies in the northwestern subtropical Pacific Ocean: Statistical characteristics and three-dimensional structures. J. Geophys. Res. Oceans 2013, 118, 1906–1925. [Google Scholar] [CrossRef]
- Cheng, Y.-H.; Ho, C.-R.; Zheng, Q.; Kuo, N.-J. Statistical characteristics of mesoscale eddies in the North Pacific derived from satellite altimetry. Remote Sens. 2014, 6, 5164–5183. [Google Scholar] [CrossRef]
- Kida, S.; Mitsudera, H.; Aoki, S.; Guo, X.; Ito, S.-I.; Kobashi, F.; Komori, N.; Kubokawa, A.; Miyama, T.; Morie, R.; et al. Oceanic fronts and jets around Japan: A review. J. Oceanogr. 2015, 71, 469–497. [Google Scholar] [CrossRef]
- Qu, T.; Mitsudera, H.; Yamagata, T. Intrusion of the North Pacific waters into the South China Sea. J. Geophys. Res. 2000, 105, 6415–6424. [Google Scholar] [CrossRef]
- Xue, H.; Chai, F.; Pettigrew, N.; Xu, D. Kuroshio intrusion and the circulation in the South China Sea. J. Geophys. Res. 2004, 109, C02017. [Google Scholar] [CrossRef]
- Caruso, M.J.; Gawarkiewicz, G.G.; Beardsley, R.C. Interannual variability of the Kuroshio intrusion in the South China Sea. J. Oceanogr. 2006, 62, 559–575. [Google Scholar] [CrossRef]
- Liang, W.-D.; Yang, Y.J.; Tang, T.Y.; Chuang, W.-S. Kuroshio in the Luzon Strait. J. Geophys. Res. 2008, 113, C08048. [Google Scholar] [CrossRef]
- Nan, F.; Xue, H.; Chai, F.; Shi, L.; Shi, M.; Guo, P. Identification of different types of Kuroshio intrusion into the South China Sea. Ocean Dyn. 2011, 61, 1291–1304. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.M. Eddy-induced heat transport in the subtropical North Pacific from Argo, TMI, and altimetry measurements. J. Phys. Oceanogr. 2005, 35, 458–473. [Google Scholar] [CrossRef]
- Souza, J.M.A.C.; de Boyer Montégut, C.; Cabanes, C.; Klein, P. Estimation of the Agulhas ring impacts on meridional heat fluxes and transport using ARGO floats and satellite data. Geophys. Res. Lett. 2011, 38, L21602. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhong, Y.; Tian, J.; Yang, Q.; Zhao, W. Estimation of eddy heat transport in the global ocean from Argo data. Acta Oceanol. Sin. 2014, 33, 42–47. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.; Han, W.; Hu, D. Surface Kuroshio path in the Luzon Strait area derived from satellite remote sensing data. J. Geophys. Res. 2006, 111, C11007. [Google Scholar] [CrossRef]
- He, Q.; Zhan, H.; Cai, S.; He, Y.; Huang, G.; Zhan, W. A new assessment of mesoscale eddies in the South China Sea: Surface features, three-dimensional structures, and thermohaline transports. J. Geophys. Res. Oceans 2018, 123, 4906–4929. [Google Scholar] [CrossRef]
- Jia, Y.L.; Liu, Q.Y. Eddy shedding from the Kuroshio bend at Luzon Strait. J. Oceanogr. 2004, 60, 1063–1069. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, Q.; Liu, W. Primary study of the mechanism of eddy shedding from the Kuroshio Bend in Luzon Strait. J. Oceanogr. 2005, 61, 1017–1027. [Google Scholar] [CrossRef]
- Nan, F.; Xue, H.; Xiu, P.; Chai, F.; Shi, M.; Guo, P. Oceanic eddy formation and propagation southwest of Taiwan. J. Geophys. Res. 2011, 116, C12045. [Google Scholar] [CrossRef]
- Wu, C.-R.; Chiang, T.-L. Mesoscale eddies in the northern South China Sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 2007, 54, 1575–1588. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Tian, J.; Liang, X. A mesoscale eddy pair southwest of Taiwan and its influence on deep circulation. J. Geophys. Res. Oceans 2013, 118, 6479–6494. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Qi, Y.; Han, G. Heat, salt and volume transports by eddies in the vicinity of the Luzon Strait. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 61, 21–33. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Qiu, B.; Tian, J. Anticyclonic eddy sheddings from Kuroshio Loop and the accompanying cyclonic eddy in the Northeastern South China Sea. J. Phys. Oceanogr. 2017, 47, 1243–1259. [Google Scholar] [CrossRef]
- Yang, Y.; Zeng, L.; Wang, Q. How much heat and salt are transported into the South China Sea by mesoscale eddies? Earth’s Future 2021, 9, e2020EF001857. [Google Scholar] [CrossRef]
- Froyland, G.; Padberg, K.; England, M.H.; Treguier, A.M. Detection of coherent oceanic structures via transfer operators. Phys. Rev. Lett. 2007, 98, 224503. [Google Scholar] [CrossRef] [PubMed]
- Olascoaga, M.J.; Wang, Y.; Beron-Vera, F.J.; Goni, G.J.; Haller, G. Objective detection of oceanic eddies and the Agulhas leakage. J. Phys. Oceanogr. 2013, 43, 1426–1438. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Haller, G.; Farazmand, M.; Trinanes, J.; Wang, Y. Dissipative inertial transport patterns near coherent Lagrangian eddies in the ocean. Chaos 2015, 25, 087412. [Google Scholar] [CrossRef]
- Haller, G.; Hadjighasem, A.; Farazmand, M.; Huhn, F. Defining coherent vortices objectively from the vorticity. J. Fluid. Mech. 2016, 795, 136–173. [Google Scholar] [CrossRef]
- Abernathey, R.; Haller, G. Transport by Lagrangian vortices in the Eastern Pacific. J. Phys. Oceanogr. 2018, 48, 667–685. [Google Scholar] [CrossRef]
- Xia, Q.; Li, G.; Dong, C. Global oceanic mass transport by coherent eddies. J. Phys. Oceanogr. 2022, 52, 1111–1132. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Coherent Lagrangian vortices: The black holes of turbulence. J. Fluid. Mech. 2013, 731, R4. [Google Scholar] [CrossRef]
- Chern, C.S.; Wang, J. Interactions of mesoscale eddy and western boundary current: A reduced-gravity numerical model study. J. Oceanogr. 2005, 61, 271–282. [Google Scholar] [CrossRef]
- Chen, X.; Qiu, B.; Chen, S.; Qi, Y.; Du, Y. Seasonal eddy kinetic energy modulations along the North Equatorial Countercurrent in the Western Pacific. J. Geophys. Res. Oceans 2015, 120, 6351–6362. [Google Scholar] [CrossRef]
- Jan, S.; Mensah, V.; Andres, M.; Chang, M.H.; Yang, Y.J. Eddy-Kuroshio interactions: Local and remote effects. J. Geophys. Res. Oceans 2017, 122, 9744–9764. [Google Scholar] [CrossRef]
- Yan, X.; Kang, D.; Curchitser, E.N.; Pang, C. Energetics of eddy–mean flow interactions along the western boundary currents in the North Pacific. J. Phys. Oceanogr. 2019, 49, 789–810. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Hadjighasem, A.; Xia, Q.; Olascoaga, M.J.; Haller, G. Coherent Lagrangian swirls among submesoscale motions. Proc. Natl. Acad. Sci. USA 2018, 116, 18251–18256. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Abernathey, R.; Sinha, A.; Chen, D. Quantifying Eulerian eddy leakiness in an idealized model. J. Geophys. Res. Oceans 2019, 124, 8869–8886. [Google Scholar] [CrossRef]
- Froyland, G.; Horenkamp, C.; Rossi, V.; van Sebille, E. Studying an Agulhas ring’s long-term pathway and decay with finite-time coherent sets. Chaos 2015, 25, 083119. [Google Scholar] [CrossRef]
- Wang, Y.; Beron-Vera, F.J.; Olascoaga, M.J. The life cycle of a coherent Lagrangian Agulhas ring. J. Geophys. Res. Oceans 2016, 121, 3944–3954. [Google Scholar] [CrossRef]
- Xia, Q.; Dong, C.; He, Y.; Li, G.; Dong, J. Lagrangian study of several long-lived Agulhas rings. J. Phys. Oceanogr. 2022, 52, 1049–1072. [Google Scholar] [CrossRef]
- Tian, F.; Wang, M.; Liu, X.; He, Q.; Chen, G. SLA-based orthogonal parallel detection of global rotationally coherent Lagrangian vortices. J. Atmos. Ocean. Technol. 2022, 39, 823–836. [Google Scholar] [CrossRef]
- He, Q.; Tian, F.; Yang, X.; Chen, G. Lagrangian eddies in the Northwestern Pacific Ocean. J. Oceanol. Limnol. 2021, 40, 66–77. [Google Scholar] [CrossRef]
- Liu, T.; He, Y.; Zhai, X.; Liu, X. Diagnostics of coherent eddy transport in the South China Sea based on satellite observations. Remote Sens. 2022, 14, 1690. [Google Scholar] [CrossRef]
- Peacock, T.; Haller, G. Lagrangian coherent structures: The hidden skeleton of fluid flows. Phys. Today 2013, 66, 41–47. [Google Scholar] [CrossRef]
- Serra, M.; Haller, G. Objective Eulerian coherent structures. Chaos 2016, 26, 053110. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhuang, W.; Hu, J.; Wu, Z.; Liu, C. Surface water exchanges in the Luzon Strait as inferred from Lagrangian coherent structures. Acta Oceanol. Sin. 2021, 39, 21–32. [Google Scholar] [CrossRef]
- Mason, E.; Pascual, A.; McWilliams, J.C. A new sea surface height—Based code for oceanic mesoscale eddy tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
- Pegliasco, C.; Delepoulle, A.; Mason, E.; Morrow, R.; Faugère, Y.; Dibarboure, G. META3.1exp: A new global mesoscale eddy trajectory atlas derived from altimetry. Earth Syst. Sci. Data 2022, 14, 1087–1107. [Google Scholar] [CrossRef]
- Liu, T.; Abernathey, R. A global Lagrangian eddy dataset based on satellite altimetry. Earth Syst. Sci. Data 2023, 15, 1765–1778. [Google Scholar] [CrossRef]
- Tarshish, N.; Abernathey, R.; Zhang, C.; Dufour, C.O.; Frenger, I.; Griffies, S.M. Identifying Lagrangian coherent vortices in a mesoscale ocean model. Ocean Model. 2018, 130, 15–28. [Google Scholar] [CrossRef]
- Hou, H.; Yu, F.; Nan, F.; Yang, B.; Guan, S.; Zhang, Y. Observation of near-inertial oscillations induced by energy transformation during typhoons. Energies 2018, 12, 99. [Google Scholar] [CrossRef]
- Guan, S.; Zhao, W.; Huthnance, J.; Tian, J.; Wang, J. Observed upper ocean response to typhoon Megi (2010) in the Northern South China Sea. J. Geophys. Res. Oceans 2014, 119, 3134–3157. [Google Scholar] [CrossRef]
- Sun, Z.; Hu, J.; Zheng, Q.; Li, C. Strong near-inertial oscillations in geostrophic shear in the northern South China Sea. J. Oceanogr. 2011, 67, 377–384. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, J.; Shang, X.; Xie, X.; Wu, X.; Gao, J.; Mei, H. Observation of near-inertial internal gravity waves in the Southern South China Sea. Remote Sens. 2023, 15, 368. [Google Scholar] [CrossRef]
- Byun, S.-S.; Park, J.J.; Chang, K.-I.; Schmitt, R.W. Observation of near-inertial wave reflections within the thermostad layer of an anticyclonic mesoscale eddy. Geophys. Res. Lett. 2010, 37, L01606. [Google Scholar] [CrossRef]
- Elipot, S.; Lumpkin, R.; Prieto, G. Modification of inertial oscillations by the mesoscale eddy field. J. Geophys. Res. 2010, 115, C09010. [Google Scholar] [CrossRef]
- Yang, B.; Hu, P.; Hou, Y. Observed near-inertial waves in the Northern South China Sea. Remote Sens. 2021, 13, 3223. [Google Scholar] [CrossRef]
- Cheng, Y.-H.; Ho, C.-R.; Zheng, Q.; Qiu, B.; Hu, J.; Kuo, N.-J. Statistical features of eddies approaching the Kuroshio east of Taiwan Island and Luzon Island. J. Oceanogr. 2017, 73, 427–438. [Google Scholar] [CrossRef]
- Tuo, P.; Yu, J.-Y.; Hu, J. The changing influences of ENSO and the Pacific meridional mode on mesoscale eddies in the South China Sea. J. Clim. 2019, 32, 685–700. [Google Scholar] [CrossRef]
- Wang, G.; Chen, D.; Su, J. Winter eddy genesis in the eastern South China Sea due to orographic wind jets. J. Phys. Oceanogr. 2008, 38, 726–732. [Google Scholar] [CrossRef]
- Kobashi, F.; Xie, S.-P. Interannual variability of the North Pacific Subtropical Countercurrent: Role of local ocean–atmosphere interaction. J. Oceanogr. 2011, 68, 113–126. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Tian, J.; Qiu, B.; Zhao, W.; Chang, P.; Wu, D.; Wan, X. Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci Rep. 2016, 6, 24349. [Google Scholar] [CrossRef]
- He, Y.; Feng, M.; Xie, J.; He, Q.; Liu, J.; Xu, J.; Chen, Z.; Zhang, Y.; Cai, S. Revisit the vertical structure of the eddies and eddy-induced transport in the Leeuwin Current system. J. Geophys. Res. Oceans 2021, 126, e2020JC016556. [Google Scholar] [CrossRef]
- Jia, Y.; Chassignet, E.P. Seasonal variation of eddy shedding from the Kuroshio intrusion in the Luzon Strait. J. Oceanogr. 2011, 67, 601–611. [Google Scholar] [CrossRef]
- Ambe, D.; Imawaki, S.; Uchida, H.; Ichikawa, K. Estimating the Kuroshio axis south of Japan using combination of satellite altimetry and drifting buoys. J. Oceanogr. 2004, 60, 375–382. [Google Scholar] [CrossRef]
- Sun, Z.; Hu, J.; Lin, H.; Chen, Z.; Zhu, J.; Yang, L.; Hu, Z.; Chen, X.; Wu, X. Lagrangian observation of the Kuroshio current by surface drifters in 2019. J. Mar. Sci. Eng. 2022, 10, 1027. [Google Scholar] [CrossRef]

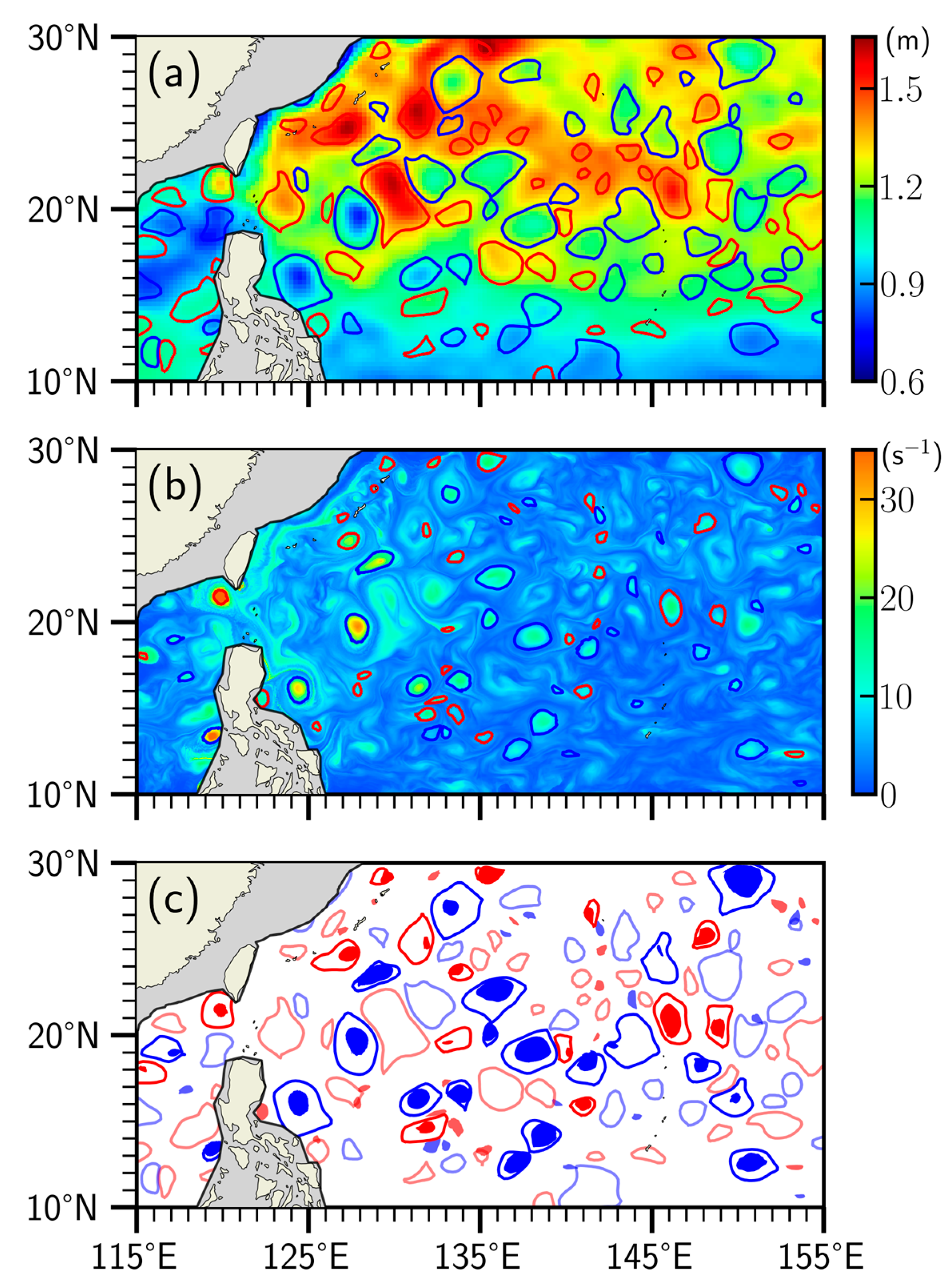
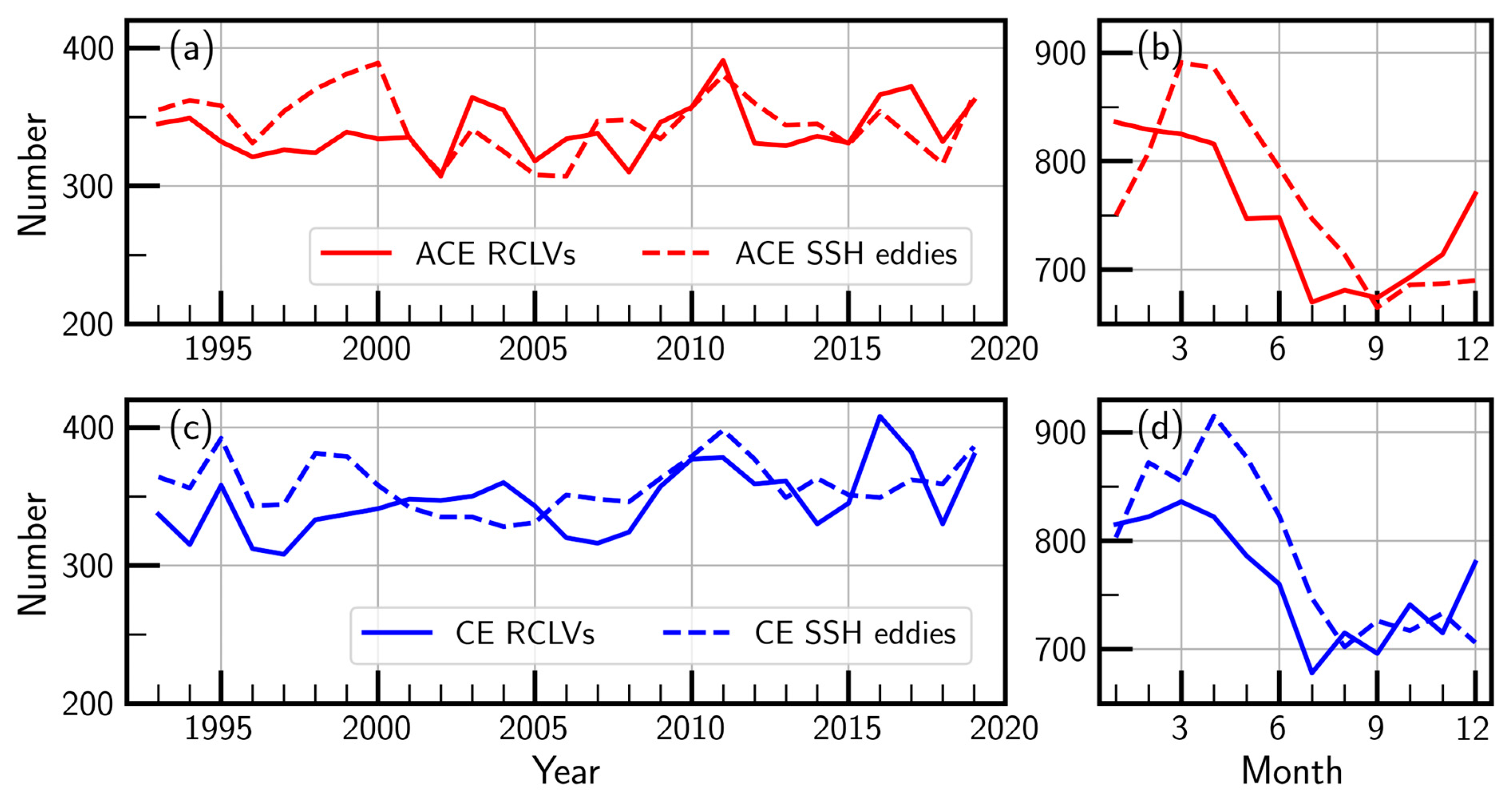

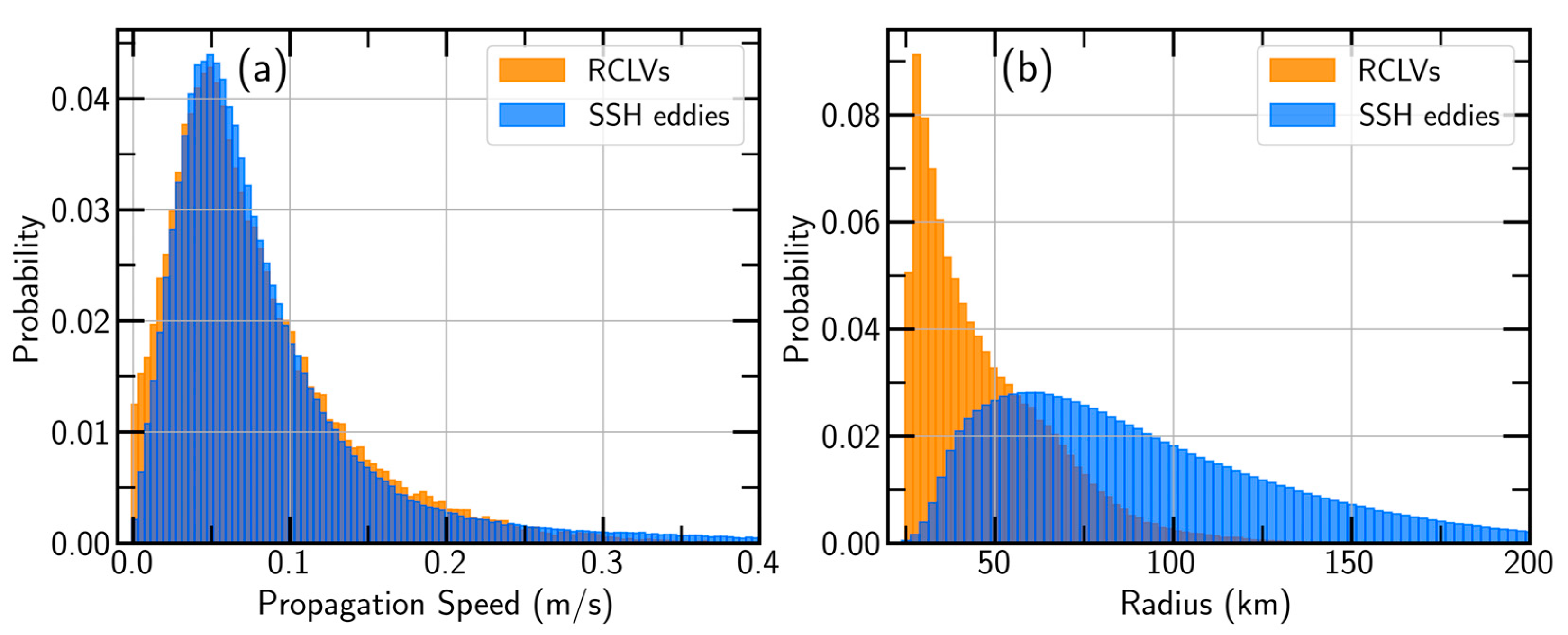
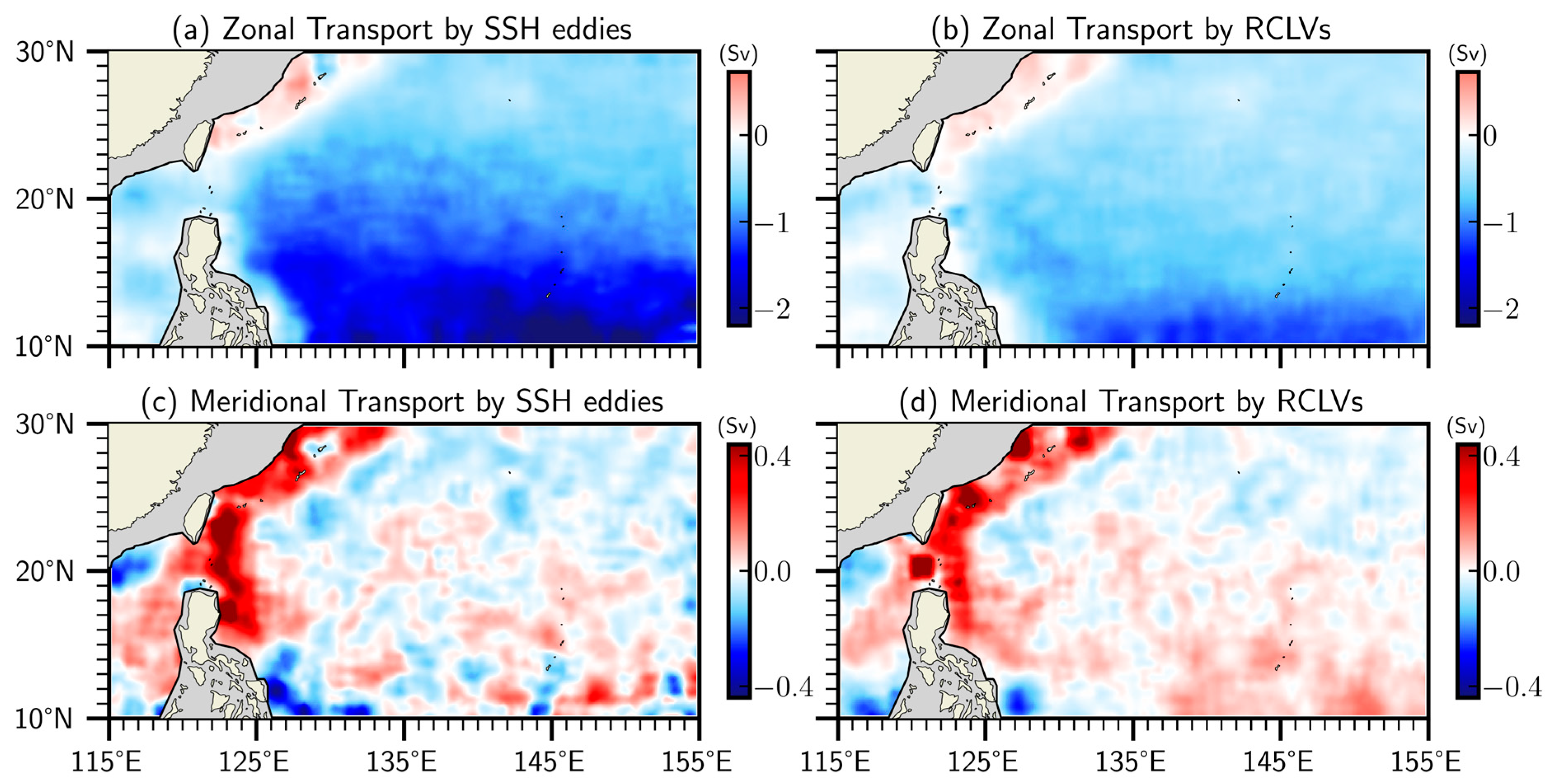



| Polarity | SSH Eddies | RCLVs | |
|---|---|---|---|
| Number/(N) | ACE | 9157 | 9003 |
| CE | 9476 | 9166 | |
| Amplitude/(m) | ACE | 6.9 × 10−2 | 6.9 × 10−2 |
| CE | 7.3 × 10−2 | 7.9 × 10−2 | |
| Radius/(m) | ACE | 9.08 × 104 | 4.69 × 104 |
| CE | 9.01 × 104 | 4.81 × 104 | |
| Zonal Propagation Speed/(m/s) | ACE | −6.7 × 10−2 | −8.6 × 10−2 |
| CE | −7.2 × 10−2 | −8.7 × 10−2 | |
| Meridional Propagation Speed/(m/s) | ACE | 0.20 × 10−2 | 0.03 × 10−2 |
| CE | 0.17 × 10−2 | 0.04 × 10−2 | |
| EKE/(m2/s2) | ACE | 3.65 × 10−2 | 2.87 × 10−2 |
| CE | 3.95 × 10−2 | 3.28 × 10−2 | |
| Vorticity/(s−1) | ACE | −1.39 × 10−6 | −5.64 × 10−6 |
| CE | 1.42 × 10−6 | 6.12 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Q.; Hu, J. Spatiotemporal Characteristics and Volume Transport of Lagrangian Eddies in the Northwest Pacific. Remote Sens. 2023, 15, 4355. https://doi.org/10.3390/rs15174355
Yuan Q, Hu J. Spatiotemporal Characteristics and Volume Transport of Lagrangian Eddies in the Northwest Pacific. Remote Sensing. 2023; 15(17):4355. https://doi.org/10.3390/rs15174355
Chicago/Turabian StyleYuan, Quanmu, and Jianyu Hu. 2023. "Spatiotemporal Characteristics and Volume Transport of Lagrangian Eddies in the Northwest Pacific" Remote Sensing 15, no. 17: 4355. https://doi.org/10.3390/rs15174355
APA StyleYuan, Q., & Hu, J. (2023). Spatiotemporal Characteristics and Volume Transport of Lagrangian Eddies in the Northwest Pacific. Remote Sensing, 15(17), 4355. https://doi.org/10.3390/rs15174355






