Polar Cap Patches Scaling Properties: Insights from Swarm Data
Abstract
:1. Introduction
2. Data and Methods
2.1. Swarm Data
2.1.1. Electron Density Measurements and RODI
2.1.2. The PCP Flag
2.2. The AE Index
2.3. Electron Density Scaling Exponents Estimation
- , is equivalent to a white noise;
- , has an antipersistent character meaning that it is more likely that its fluctuations will tend to change their sign;
- , is a completely uncorrelated time series as, for instance, a Brownian random motion;
- , has a persistent character meaning that it is more likely that its fluctuations will tend to keep a given sign;
- , is equivalent to a linear trend and hence completely predictable.
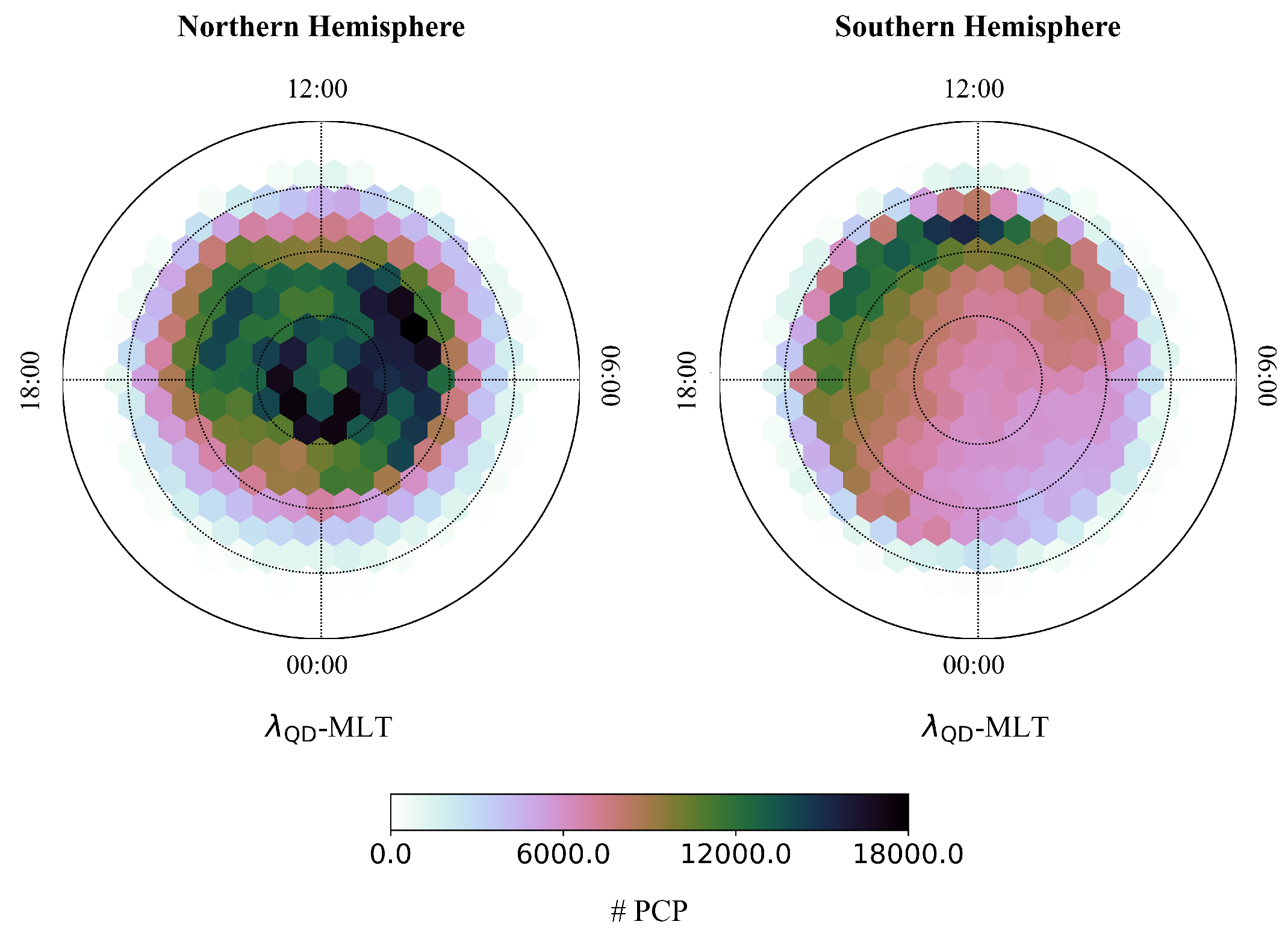
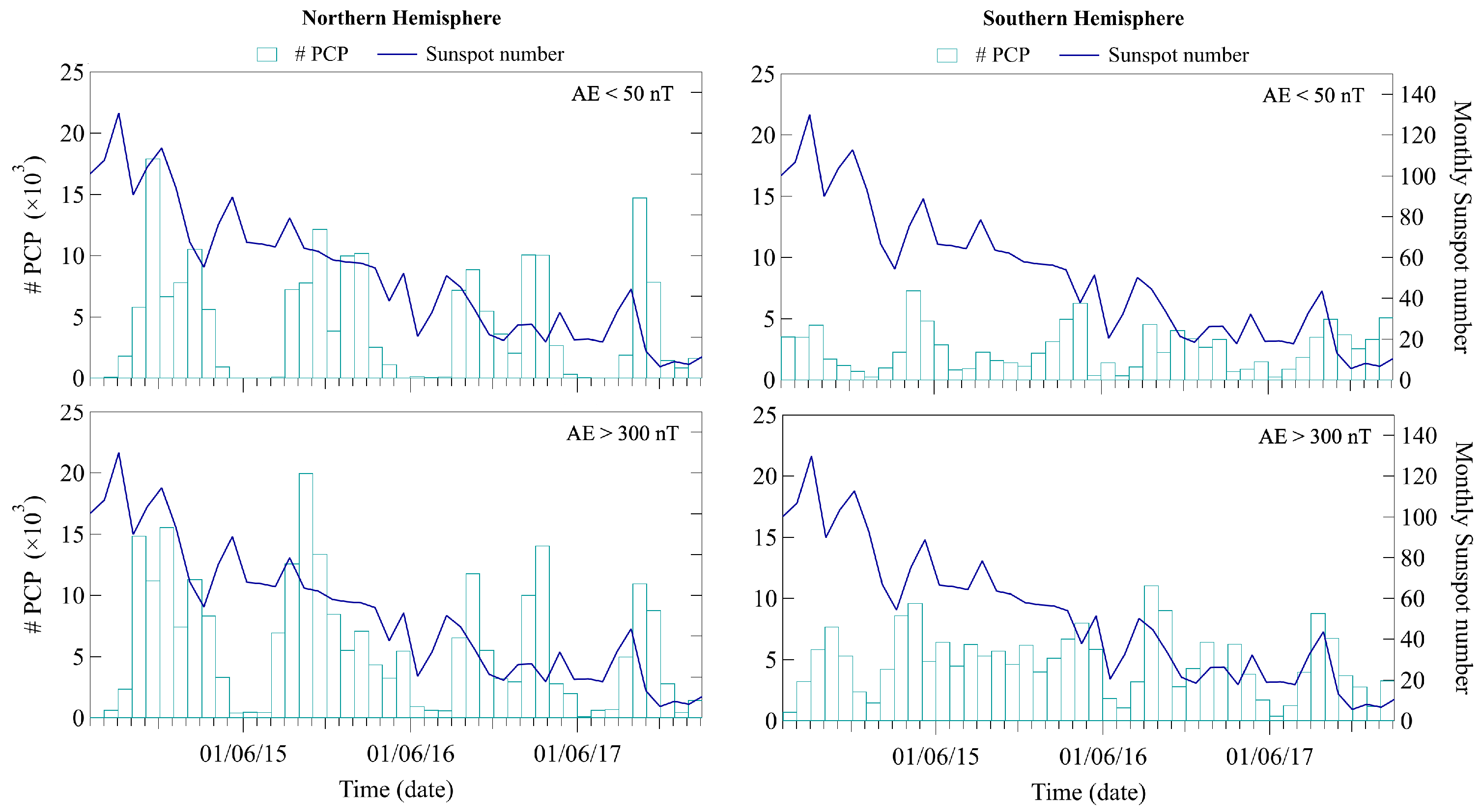
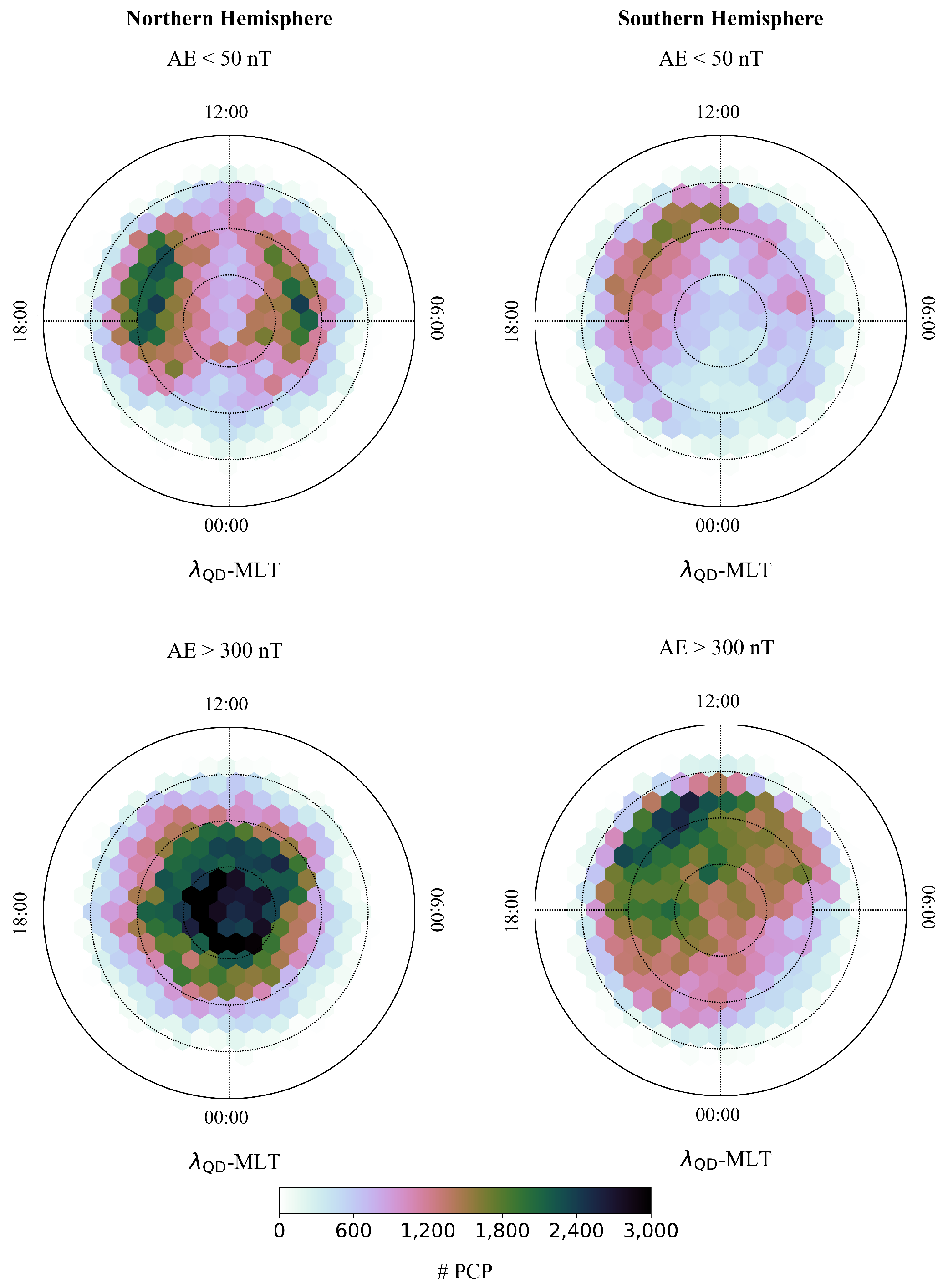
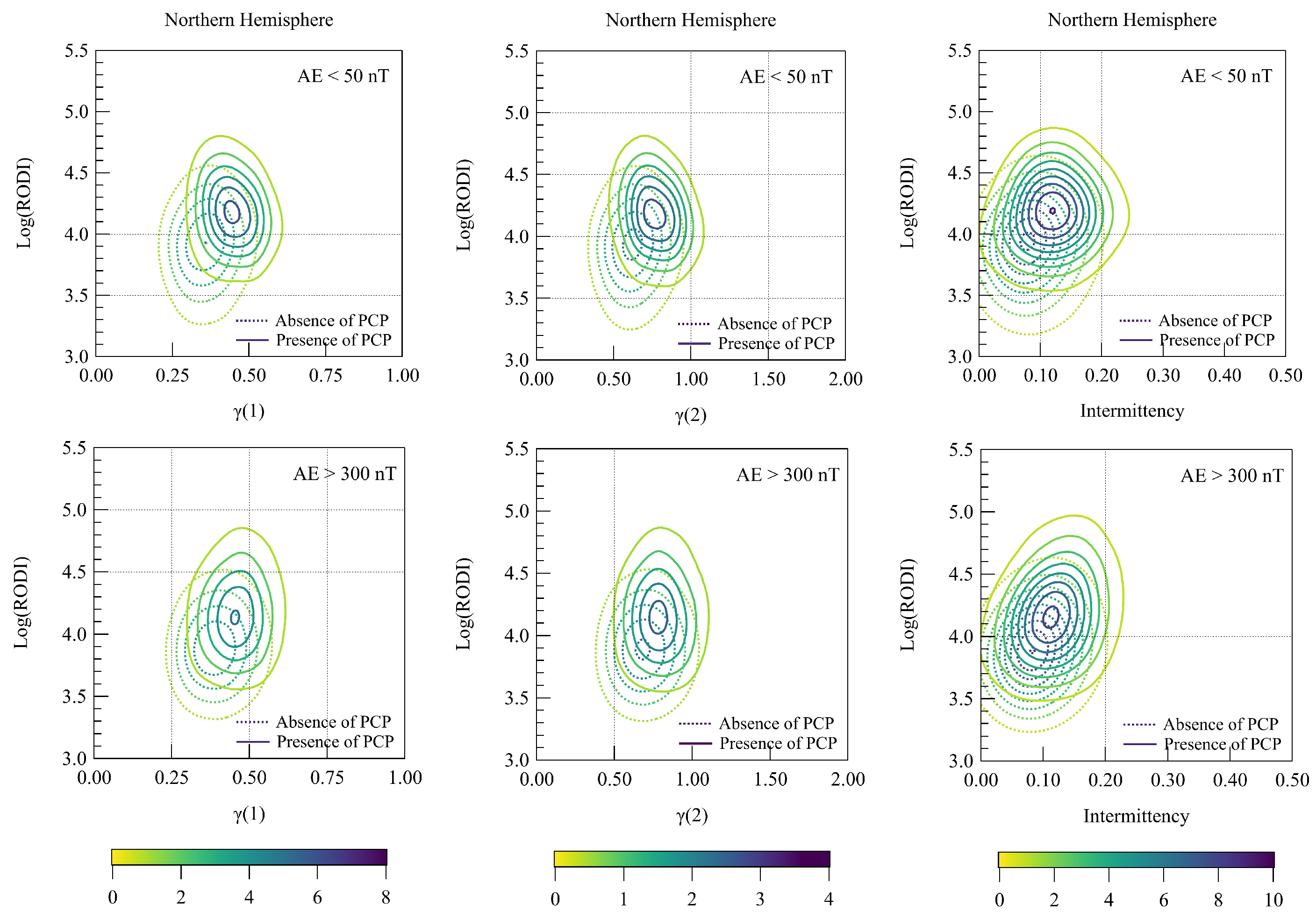
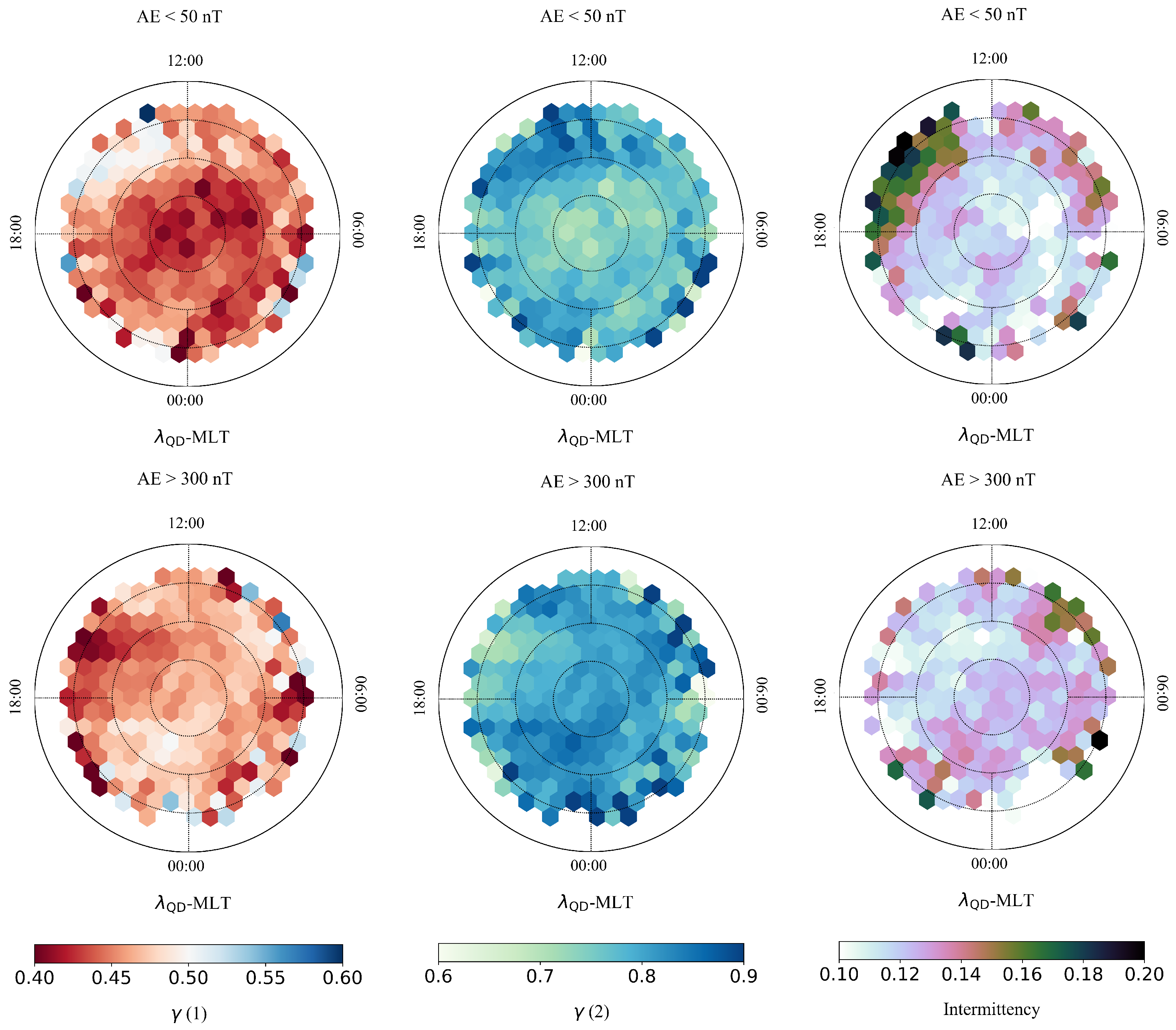
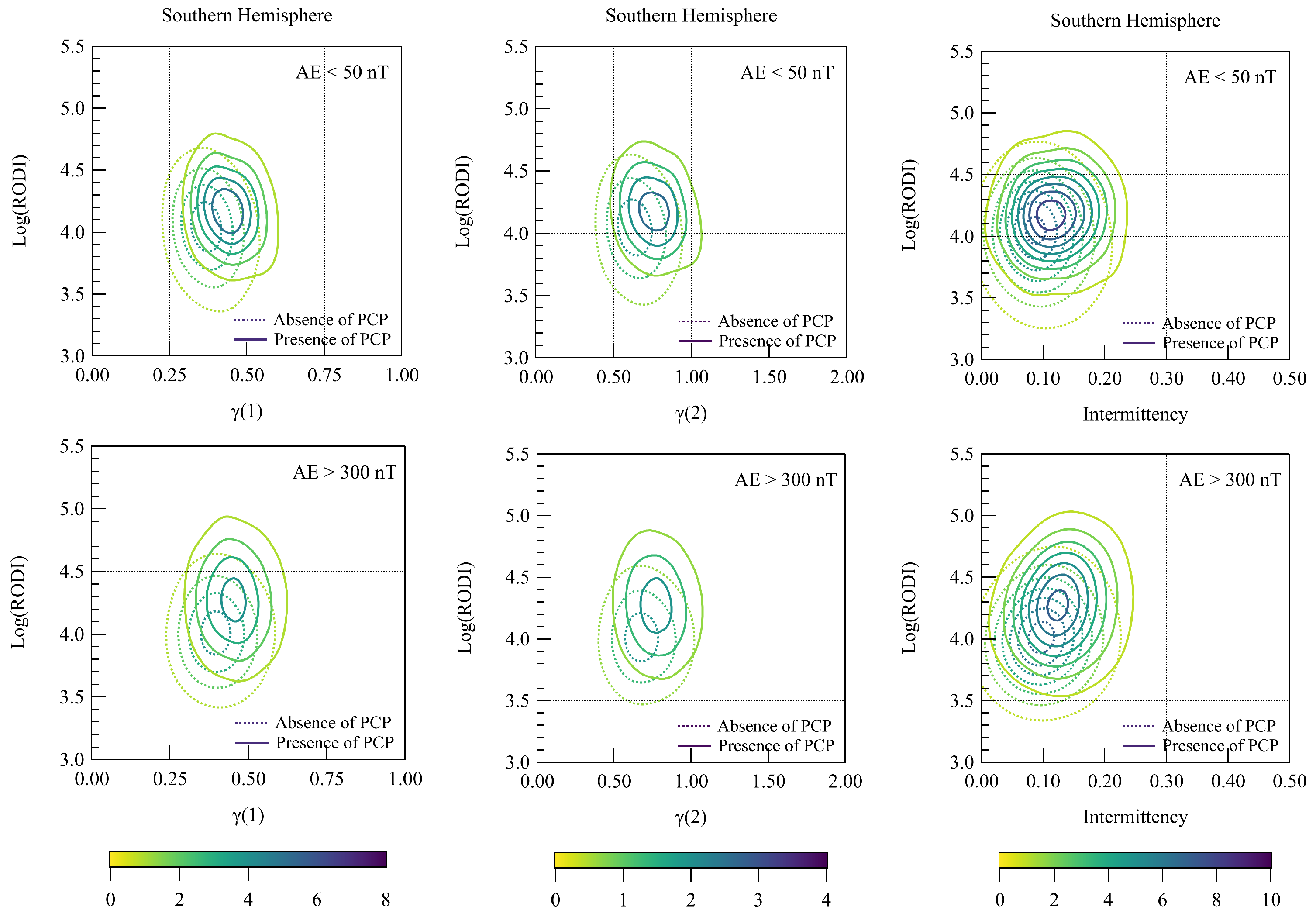
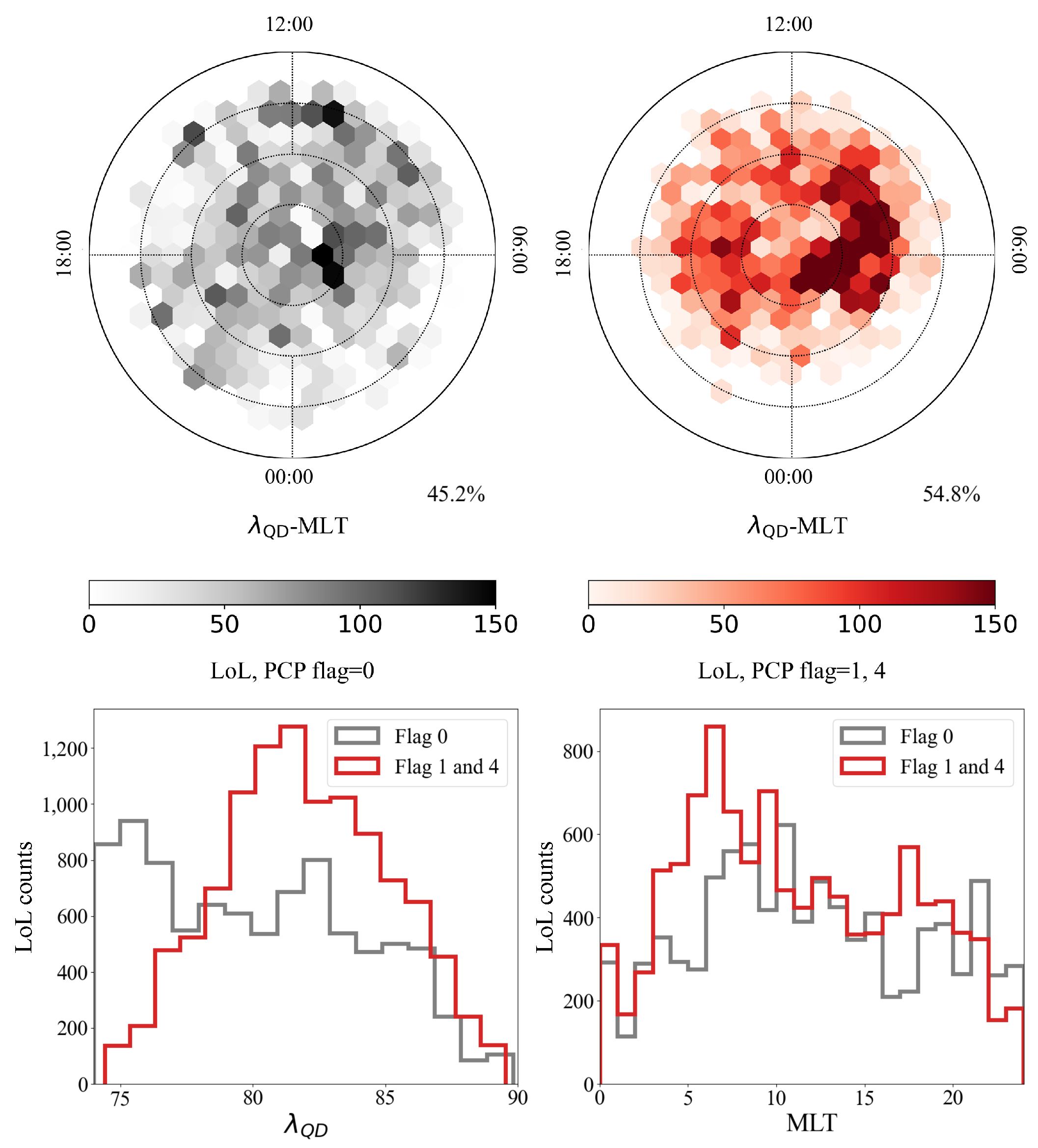
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Auroral Electrojet |
| CDF | Cumulative Distribution Function |
| CHAMP | Challenging Minisatellite Payload |
| DSFA | Detrended Structure Function Analysis |
| ESA | European Space Agency |
| EUV | Extreme Ultra Violet |
| GLONASS | Globalnaya Navigazionnaya Sputnikovaya Sistema |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| ICI-2 | Investigation of Cusp Irregularities-2 |
| INTERMAGNET | International Real-time Magnetic Observatory Network |
| ISGI | International Service of Geomagnetic Indices |
| LoL | Loss of Lock |
| MHD | Magnetohydrodynamics |
| MLT | Magnetic Local Time |
| PCP | Polar Cap Patch |
| Probability Density Function | |
| QD | Quasi-Dipole |
| RODI | Rate Of change of electron Density Index |
| sTEC | slant Total Electron Content |
| TITIPy | Topside Ionosphere Turbulence Indices with Python |
| WDC | World Data Center |
References
- Tsunoda, R.T. High-latitude F region irregularities: A review and synthesis. Rev. Geophys. 1988, 26, 719–760. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.; Le, H. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257. [Google Scholar] [CrossRef]
- Jin, Y.; Xiong, C.; Clausen, L.; Spicher, A.; Kotova, D.; Brask, S.; Kervalishvili, G.; Stolle, C.; Miloch, W. Ionospheric Plasma Irregularities Based on In Situ Measurements From the Swarm Satellites. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028103. [Google Scholar] [CrossRef]
- Bhattacharyya, A. Equatorial Plasma Bubbles: A Review. Atmosphere 2022, 13, 1637. [Google Scholar] [CrossRef]
- Carlson, H.C. Sharpening our thinking about polar cap ionospheric patch morphology, research, and mitigation techniques. Radio Sci. 2012, 47, 1–6. [Google Scholar] [CrossRef]
- Clausen, L.B.N.; Moen, J.I. Electron density enhancements in the polar cap during periods of dayside reconnection. J. Geophys. Res. Space Phys. 2015, 120, 4452–4464. [Google Scholar] [CrossRef]
- Lockwood, M.; Carlson, H.C., Jr. Production of polar cap electron density patches by transient magnetopause reconnection. Geophys. Res. Lett. 1992, 19, 1731–1734. [Google Scholar] [CrossRef]
- Dungey, J.W. Interplanetary Magnetic Field and the Auroral Zones. Phys. Rev. Lett. 1961, 6, 47–48. [Google Scholar] [CrossRef]
- Jin, Y.; Spicher, A.; Xiong, C.; Clausen, L.B.N.; Kervalishvili, G.; Stolle, C.; Miloch, W.J. Ionospheric Plasma Irregularities Characterized by the Swarm Satellites: Statistics at High Latitudes. J. Geophys. Res. Space Phys. 2019, 124, 1262–1282. [Google Scholar] [CrossRef]
- Basu, S.; Basu, S.; Chaturvedi, P.K.; Bryant, C.M., Jr. Irregularity structures in the cusp/cleft and polar cap regions. Radio Sci. 1994, 29, 195–207. [Google Scholar] [CrossRef]
- Lorentzen, D.A.; Moen, J.; Oksavik, K.; Sigernes, F.; Saito, Y.; Johnsen, M.G. In situ measurement of a newly created polar cap patch. J. Geophys. Res. Space Phys. 2010, 115, A12323. [Google Scholar] [CrossRef]
- Moen, J.; Oksavik, K.; Abe, T.; Lester, M.; Saito, Y.; Bekkeng, T.A.; Jacobsen, K.S. First in-situ measurements of HF radar echoing targets. Geophys. Res. Lett. 2012, 39, L07104. [Google Scholar] [CrossRef]
- Goodwin, L.V.; Iserhienrhien, B.; Miles, D.M.; Patra, S.; van der Meeren, C.; Buchert, S.C.; Burchill, J.K.; Clausen, L.B.N.; Knudsen, D.J.; McWilliams, K.A.; et al. Swarm in situ observations of F region polar cap patches created by cusp precipitation. Geophys. Res. Lett. 2015, 42, 996–1003. [Google Scholar] [CrossRef]
- Spicher, A.; Cameron, T.; Grono, E.M.; Yakymenko, K.N.; Buchert, S.C.; Clausen, L.B.N.; Knudsen, D.J.; McWilliams, K.A.; Moen, J.I. Observation of polar cap patches and calculation of gradient drift instability growth times: A Swarm case study. Geophys. Res. Lett. 2015, 42, 201–206. [Google Scholar] [CrossRef]
- Noja, M.; Stolle, C.; Park, J.; Lühr, H. Long-term analysis of ionospheric polar patches based on CHAMP TEC data. Radio Sci. 2013, 48, 289–301. [Google Scholar] [CrossRef]
- Burston, R.; Mitchell, C.; Astin, I. Polar cap plasma patch primary linear instability growth rates compared. J. Geophys. Res. Space Phys. 2016, 121, 3439–3451. [Google Scholar] [CrossRef]
- Spicher, A.; Clausen, L.B.N.; Miloch, W.J.; Lofstad, V.; Jin, Y.; Moen, J.I. Interhemispheric study of polar cap patch occurrence based on Swarm in situ data. J. Geophys. Res. Space Phys. 2017, 122, 3837–3851. [Google Scholar] [CrossRef]
- Keskinen, M.J.; Ossakow, S. Non-linear evolution of plasma enhancements in the auroral ionosphere 1. Long wavelength irregularities. J. Geophys. Res. Space Phys. 1982, 87, 144–150. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R.; Pignalberi, A.; Pezzopane, M.; Coco, I.; Giannattasio, F.; Marcucci, M.F. Ionospheric Turbulence and the Equatorial Plasma Density Irregularities: Scaling Features and RODI. Remote Sens. 2021, 13, 759. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Pignalberi, A.; Tozzi, R.; Coco, I.; Giannattasio, F.; Pezzopane, M.; Balasis, G. Looking for a proxy of the ionospheric turbulence with Swarm data. Sci. Rep. 2021, 11, 6183. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Pignalberi, A.; Lovati, G.; Pezzopane, M.; Tozzi, R.; Giannattasio, F.; Coco, I.; Marcucci, M.F. Ionospheric Turbulence: A Challenge for GPS Loss of Lock Understanding. Space Weather 2022, 20, e2022SW003129. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.E.; Åhlen, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys. Res. Space Phys. 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- Pezzopane, M.; Pignalberi, A.; Coco, I.; Consolini, G.; De Michelis, P.; Giannattasio, F.; Marcucci, M.F.; Tozzi, R. Occurrence of GPS Loss of Lock Based on a Swarm Half-Solar Cycle Dataset and Its Relation to the Background Ionosphere. Remote Sens. 2021, 13, 2209. [Google Scholar] [CrossRef]
- Lomidze, L.; Knudsen, D.J.; Burchill, J.; Kouznetsov, A.; Buchert, S.C. Calibration and Validation of Swarm Plasma Densities and Electron Temperatures Using Ground-Based Radars and Satellite Radio Occultation Measurements. Radio Sci. 2018, 53, 15–36. [Google Scholar] [CrossRef]
- Swarm L1b Product Definition. Available online: https://earth.esa.int/documents/10174/1514862/Swarm_L1b_Product_Definition (accessed on 31 August 2023).
- Zakharenkova, I.; Astafyeva, E. Topside ionospheric irregularities as seen from multisatellite observations. J. Geophys. Res. Space Phys. 2015, 120, 807–824. [Google Scholar] [CrossRef]
- De Michelis, P.; Pignalberi, A.; Consolini, G.; Coco, I.; Tozzi, R.; Pezzopane, M.; Giannattasio, F.; Balasis, G. On the 2015 St. Patrick’s Storm Turbulent State of the Ionosphere: Hints From the Swarm Mission. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027934. [Google Scholar] [CrossRef]
- Piersanti, M.; De Michelis, P.; Del Moro, D.; Tozzi, R.; Pezzopane, M.; Consolini, G.; Marcucci, M.F.; Laurenza, M.; Di Matteo, S.; Pignalberi, A.; et al. From the Sun to Earth: Effects of the 25 August 2018 geomagnetic storm. Ann. Geophys. 2020, 38, 703–724. [Google Scholar] [CrossRef]
- Pignalberi, A. TITIPy: A Python tool for the calculation and mapping of topside ionosphere turbulence indices. Comput. Geosci. 2021, 148, 104675. [Google Scholar] [CrossRef]
- Jin, Y.; Kotova, D.; Xiong, C.; Brask, S.M.; Clausen, L.B.N.; Kervalishvili, G.; Stolle, C.; Miloch, W.J. Ionospheric Plasma IRregularities-IPIR-Data product based on data from the Swarm satellites. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030183. [Google Scholar] [CrossRef] [PubMed]
- Swarm Product Specification for L2 Products and Auxiliary Products. Available online: https://earth.esa.int/eogateway/documents/20142/37627/swarm-level-2-product-specification.pdf/2979b351-b6a2-69b6-8539-9ed9f32984f0 (accessed on 31 August 2023).
- Swarm Handbook—Level 2 Product Definitions Introduction. Available online: https://swarmhandbook.earth.esa.int/article/introduction#:~:text=Level%202%20products%20are%20typically,well%20as%20ground%2Dbased%20observations (accessed on 31 August 2023).
- Coley, W.R.; Heelis, R.A. Adaptive identification and characterization of polar ionization patches. J. Geophys. Res. Space Phys. 1995, 100, 23819–23827. [Google Scholar] [CrossRef]
- Chartier, A.T.; Mitchell, C.N.; Miller, E.S. Annual Occurrence Rates of Ionospheric Polar Cap Patches Observed Using Swarm. J. Geophys. Res. Space Phys. 2018, 123, 2327–2335. [Google Scholar] [CrossRef]
- Kagawa, A.; Hosokawa, K.; Ogawa, Y.; Ebihara, Y.; Kadokura, A. Occurrence Distribution of Polar Cap Patches: Dependences on UT, Season and Hemisphere. J. Geophys. Res. Space Phys. 2020, 126, e2020JA028538. [Google Scholar] [CrossRef]
- David, M.; Sojka, J.; Schunk, R.; Coster, A. Hemispherical Shifted Symmetry in Polar Cap Patch Occurrence: A Survey of GPS TEC Maps From 2015–2018. Geophys. Res. Lett. 2019, 46, 10726–10734. [Google Scholar] [CrossRef]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785–801. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Hurst, H.E. Methods of using long-term storage in reservoirs. Proc. Inst. Civ. Eng. 1956, 5, 519–543. [Google Scholar] [CrossRef]
- Wiener, N. Time Series; M.I.T. Press: Cambridge, MA, USA, 1964; p. 42. [Google Scholar]
- De Michelis, P.; Consolini, G.; Tozzi, R. Magnetic field fluctuation features at Swarm’s altitude: A fractal approach. Geophys. Res. Lett. 2015, 42, 3100–3105. [Google Scholar] [CrossRef]
- Consolini, G.; Tozzi, R.; De Michelis, P.; Coco, I.; Giannattasio, F.; Pezzopane, M.; Marcucci, M.; Balasis, G. High-latitude polar pattern of ionospheric electron density: Scaling features and IMF dependence. J. Atmos. Sol.-Terr. Phys. 2021, 217, 105531. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 2013, 10, 2. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Alberti, T.; Tozzi, R.; Giannattasio, F.; Coco, I.; Pezzopane, M.; Pignalberi, A. Magnetic Field and Electron Density Scaling Properties in the Equatorial Plasma Bubbles. Remote Sens. 2022, 14, 918. [Google Scholar] [CrossRef]
- Kintner, P.M.; Seyler, C.E. The status of observations and theory of high latitude ionospheric and magnetospheric plasma turbulence. Space Sci. Rev. 1985, 41, 91–129. [Google Scholar] [CrossRef]
- Basu, S.; Basu, S.; MacKenzie, E.; Fougere, P.F.; Coley, W.R.; Maynard, N.C.; Winningham, J.D.; Sugiura, M.; Hanson, W.B.; Hoegy, W.R. Simultaneous density and electric field fluctuation spectra associated with velocity shears in the auroral oval. J. Geophys. Res. 1988, 93, 115–136. [Google Scholar] [CrossRef]
- Basu, S.; MacKenzie, E.; Basu, S.; Coley, W.R.; Sharber, J.R.; Hoegy, W.R. Plasma structuring by the gradient drift instability at high latitudes and comparison with velocity shear driven processes. J. Geophys. Res. 1990, 95, 7799–7818. [Google Scholar] [CrossRef]
- Dyson, P.L.; McClure, J.P.; Hanson, W.B. In situ measurements of the spectral characteristics of F region ionospheric irregularities. J. Geophys. Res. 1974, 79, 1497. [Google Scholar] [CrossRef]
- Cerisier, J.C.; Berthelier, J.J.; Beghin, C. Unstable density gradients in the high-latitude ionosphere. Radio Sci. 1985, 20, 755–761. [Google Scholar] [CrossRef]
- Zou, Y.; Nishimura, Y.; Lyons, L.R.; Shiokawa, K. Localized polar cap precipitation in association with nonstorm time airglow patches. Geophys. Res. Lett. 2017, 44, 609–617. [Google Scholar] [CrossRef]
- Spicher, A.; Miloch, W.J.; Clausen, L.B.N.; Moen, J.I. Plasma turbulence and coherent structures in the polar cap observed by the ICI-2 sounding rocket. J. Geophys. Res. Space Phys. 2015, 120, 10959–10978. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, R.; De Michelis, P.; Lovati, G.; Consolini, G.; Pignalberi, A.; Pezzopane, M.; Coco, I.; Giannattasio, F.; Marcucci, M.F. Polar Cap Patches Scaling Properties: Insights from Swarm Data. Remote Sens. 2023, 15, 4320. https://doi.org/10.3390/rs15174320
Tozzi R, De Michelis P, Lovati G, Consolini G, Pignalberi A, Pezzopane M, Coco I, Giannattasio F, Marcucci MF. Polar Cap Patches Scaling Properties: Insights from Swarm Data. Remote Sensing. 2023; 15(17):4320. https://doi.org/10.3390/rs15174320
Chicago/Turabian StyleTozzi, Roberta, Paola De Michelis, Giulia Lovati, Giuseppe Consolini, Alessio Pignalberi, Michael Pezzopane, Igino Coco, Fabio Giannattasio, and Maria Federica Marcucci. 2023. "Polar Cap Patches Scaling Properties: Insights from Swarm Data" Remote Sensing 15, no. 17: 4320. https://doi.org/10.3390/rs15174320
APA StyleTozzi, R., De Michelis, P., Lovati, G., Consolini, G., Pignalberi, A., Pezzopane, M., Coco, I., Giannattasio, F., & Marcucci, M. F. (2023). Polar Cap Patches Scaling Properties: Insights from Swarm Data. Remote Sensing, 15(17), 4320. https://doi.org/10.3390/rs15174320









