Reconstructing 42 Years (1979–2020) of Great Lakes Surface Temperature through a Deep Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
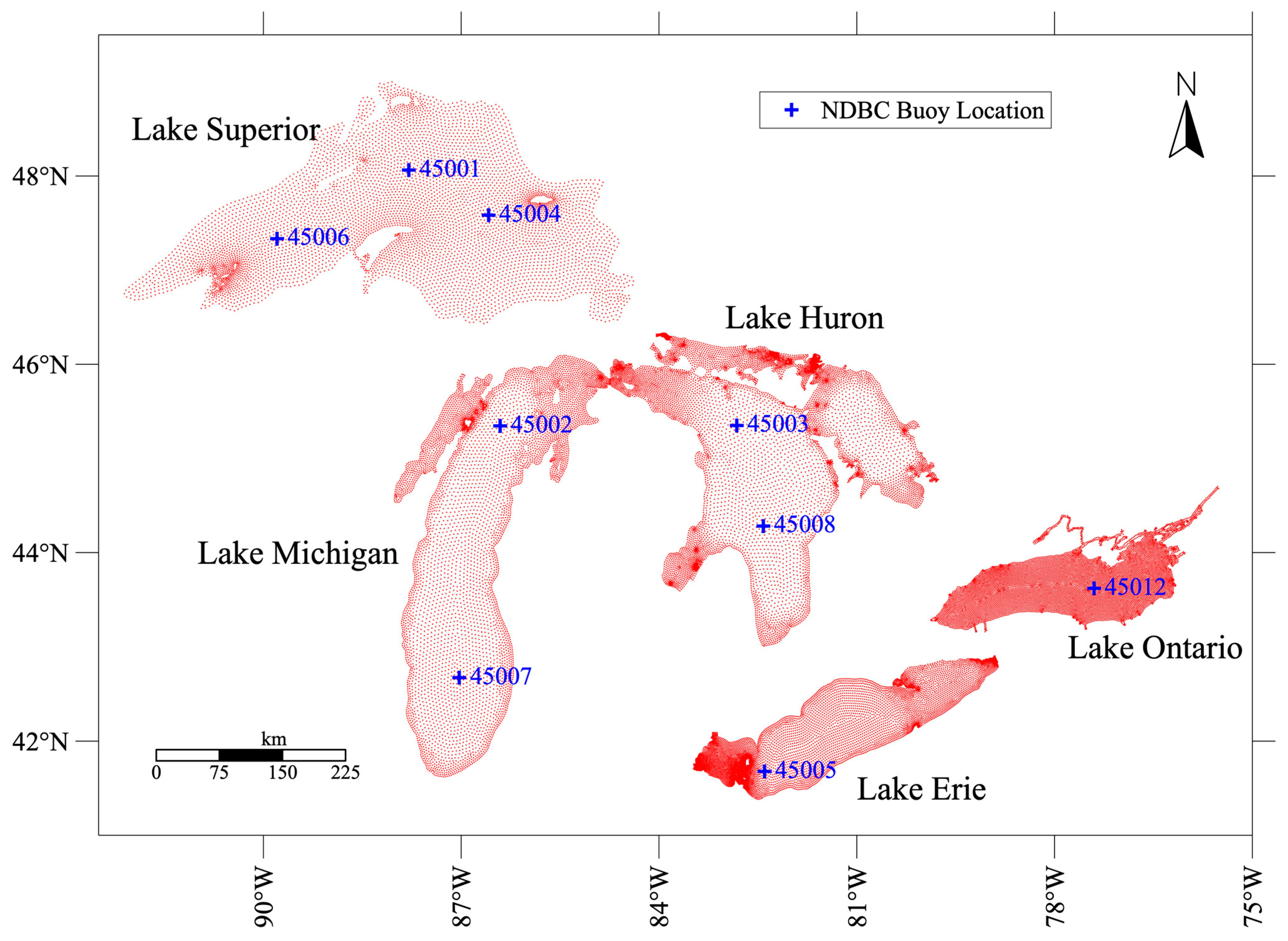
2.1. Study Area
2.2. Methodology
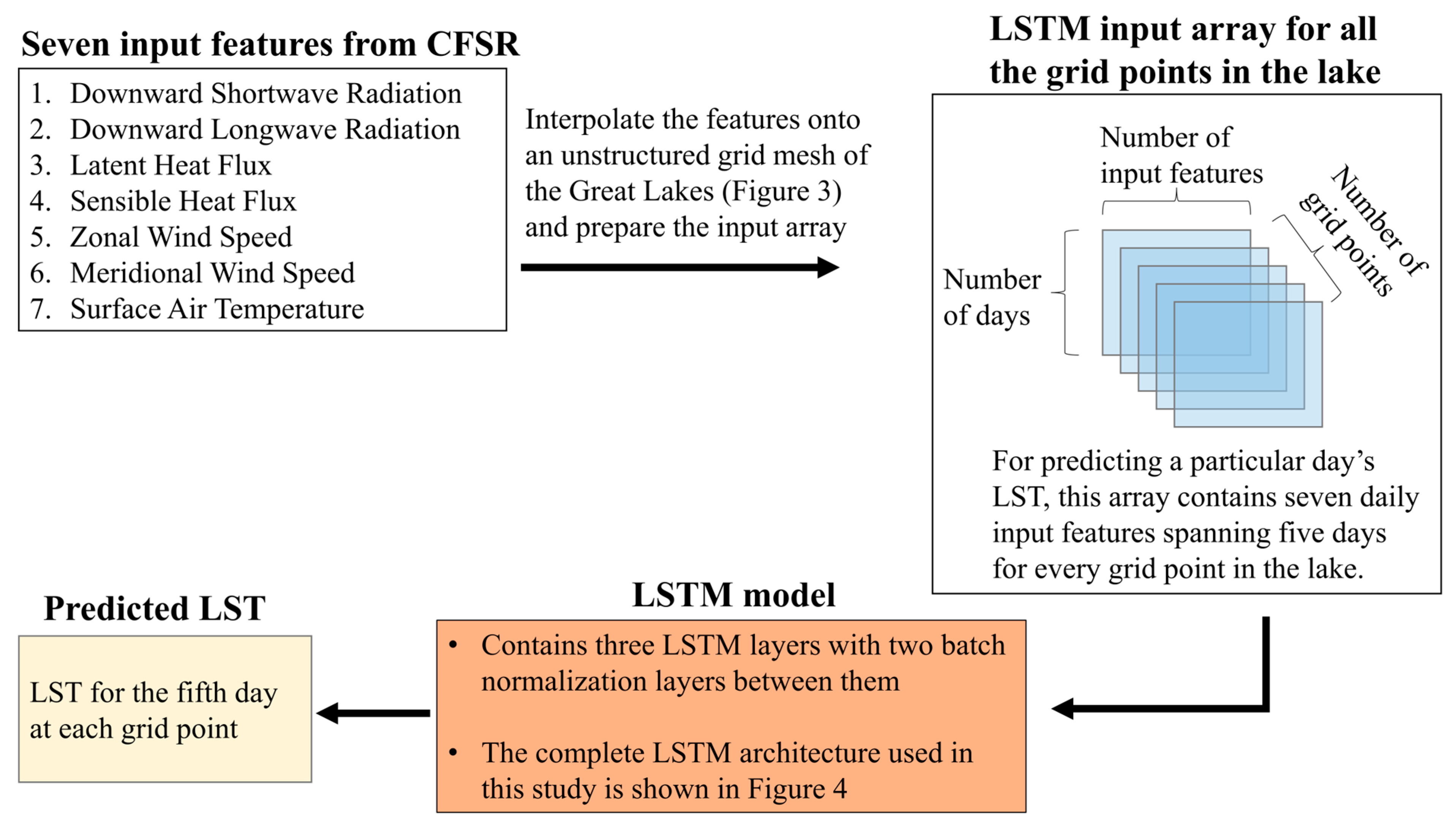
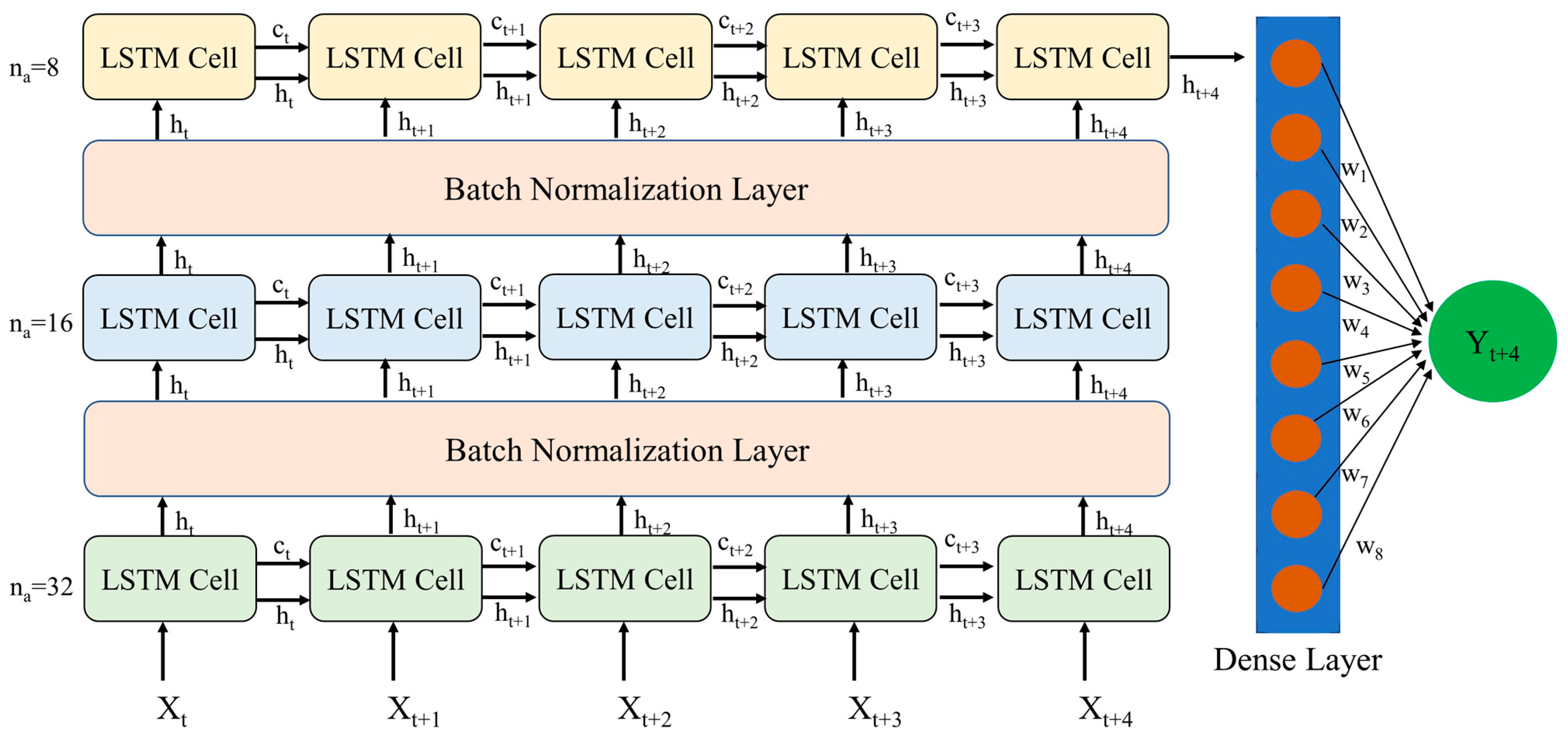
2.2.1. LSTM Architecture
2.2.2. Data Preprocessing
2.2.3. LSTM Training and Validation
3. Results
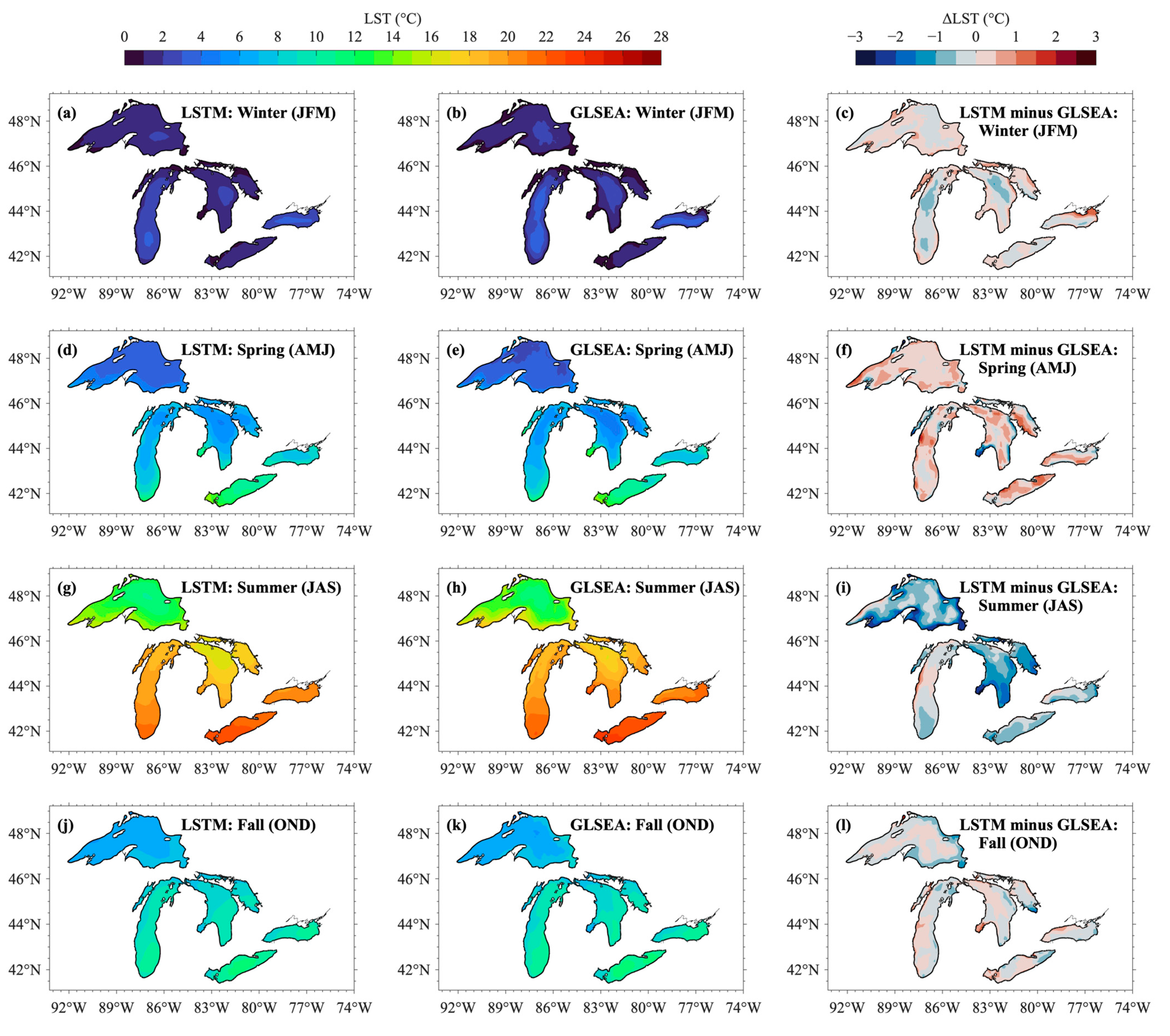
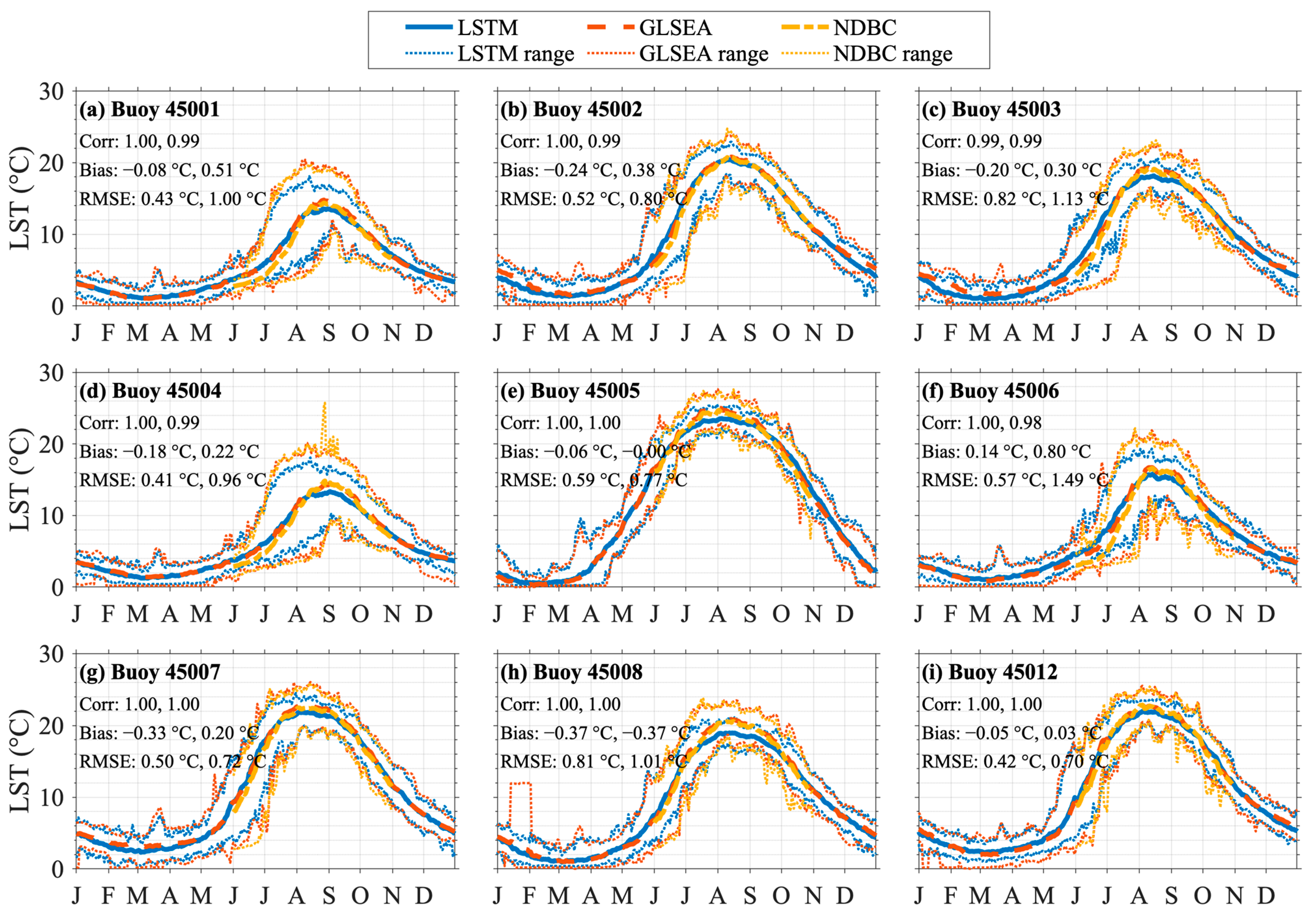
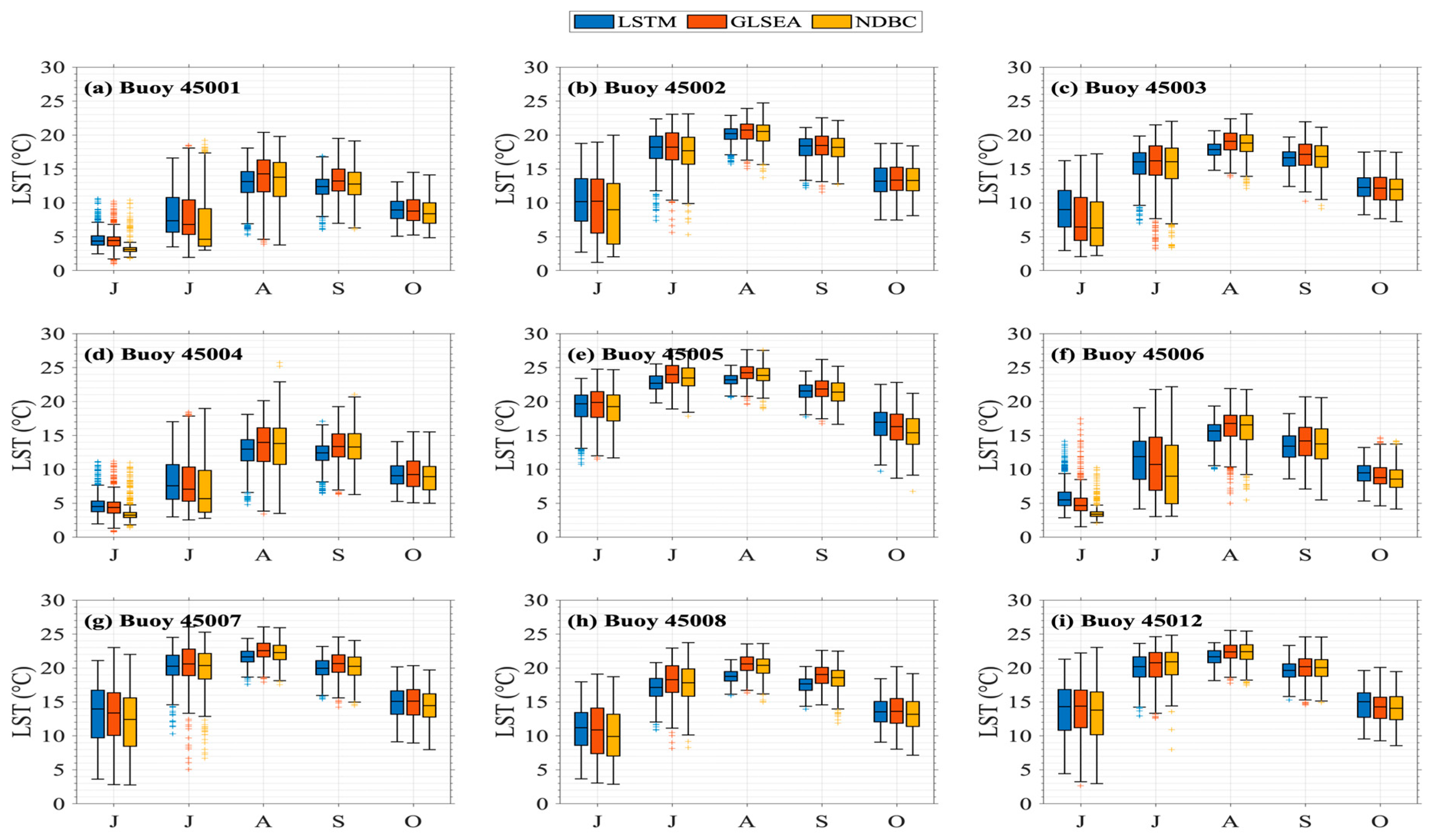
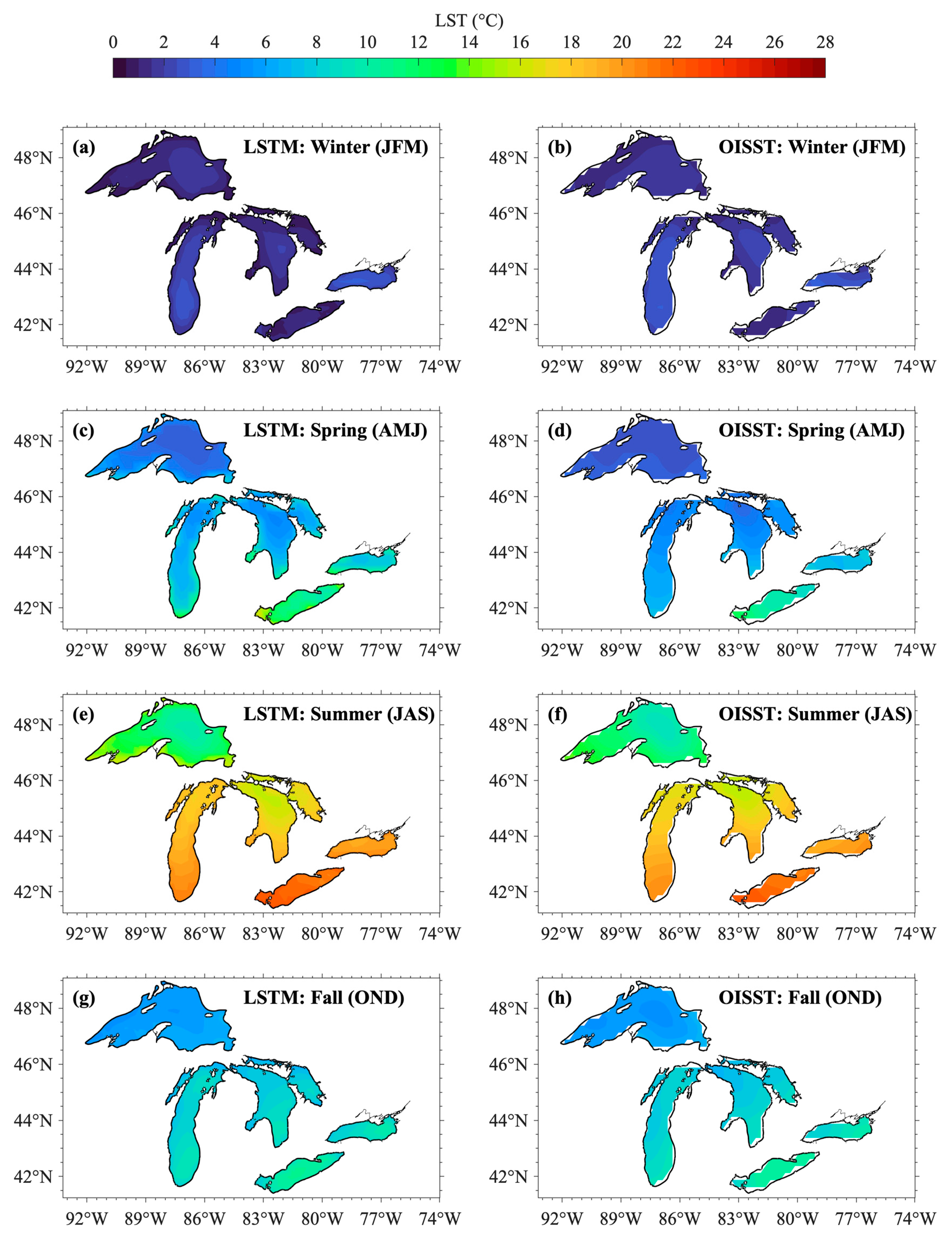
3.1. LSTM Prediction for 1995–2020 (Training Period)
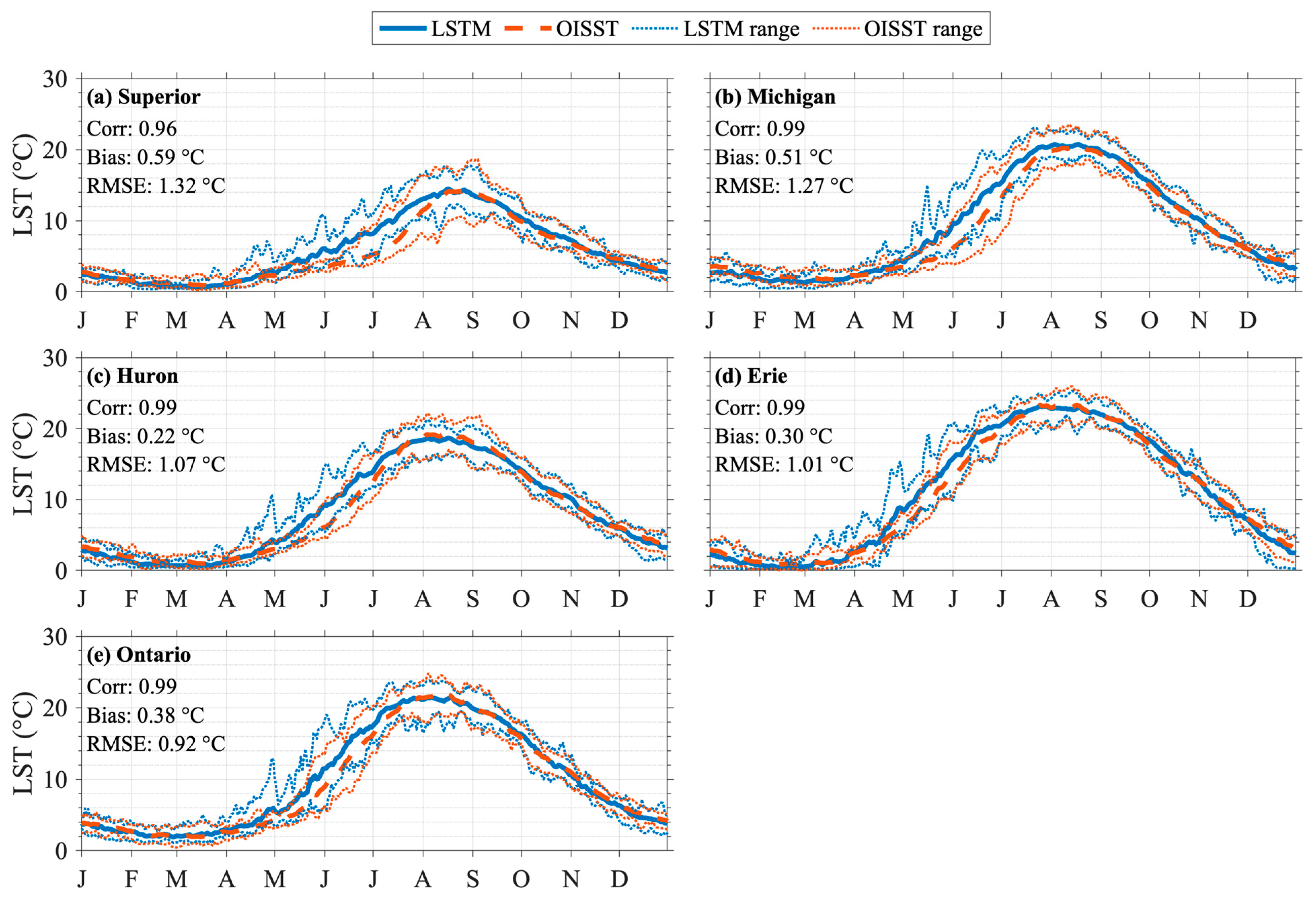
3.2. LSTM Prediction for 1979–1994 (Testing Period)
3.3. LSTM Prediction for the Change in LST Due to the 1997–1998 LST Regime Shift
4. Discussion
4.1. Necessity for an Extended High-Resolution LST Dataset for the Great Lakes
4.2. Uncertainty in Training LST (GLSEA) Data
4.3. Future Model Improvements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- U.S. Environmental Protection Agency (EPA); Government of Canada. The Great Lakes: An Environmental Atlas and Resource Book, 3rd ed.; Fuller, K., Shear, H., Eds.; EPA: Chicago, IL, USA, 1995.
- Changnon, S.A., Jr.; Jones, D.M.A. Review of the influences of the Great Lakes on weather. Water Resour. Res. 1972, 8, 360–371. [Google Scholar] [CrossRef]
- Scott, R.W.; Huff, F.A. Impacts of the Great Lakes on Regional Climate Conditions. J. Great Lakes Res. 1996, 22, 845–863. [Google Scholar] [CrossRef]
- Notaro, M.; Holman, K.; Zarrin, A.; Fluck, E.; Vavrus, S.; Bennington, V. Influence of the Laurentian Great Lakes on Regional Climate. J. Clim. 2013, 26, 789–804. [Google Scholar] [CrossRef]
- Notaro, M.; Zhong, Y.; Xue, P.; Peters-Lidard, C.; Cruz, C.; Kemp, E.; Kristovich, D.; Kulie, M.; Wang, J.; Huang, C.; et al. Cold Season Performance of the NU-WRF Regional Climate Model in the Great Lakes Region. J. Hydrometeorol. 2021, 22, 2423–2454. [Google Scholar] [CrossRef]
- Wang, J.; Xue, P.; Pringle, W.; Yang, Z.; Qian, Y. Impacts of Lake Surface Temperature on the Summer Climate over the Great Lakes Region. J. Geophys. Res. Atmos. 2022, 127, e2021JD036231. [Google Scholar] [CrossRef]
- Xue, P.; Ye, X.; Pal, J.S.; Chu, P.Y.; Kayastha, M.B.; Huang, C. Climate projections over the Great Lakes Region: Using two-way coupling of a regional climate model with a 3-D lake model. Geosci. Model Dev. 2022, 15, 4425–4446. [Google Scholar] [CrossRef]
- Shi, Q.; Xue, P. Impact of Lake Surface Temperature Variations on Lake Effect Snow over the Great Lakes Region. J. Geophys. Res. Atmos. 2019, 124, 12553–12567. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Do, H.X.; Mei, Y.; Stow, C.A. A tug-of-war within the hydrologic cycle of a continental freshwater basin. Geophys. Res. Lett. 2021, 48, e2020GL090374. [Google Scholar] [CrossRef]
- Kayastha, M.B.; Ye, X.; Huang, C.; Xue, P. Future rise of the Great Lakes water levels under climate change. J. Hydrol. 2022, 612, 128205. [Google Scholar] [CrossRef]
- Wagner, T.J.; Czarnetzki, A.C.; Christiansen, M.; Pierce, R.B.; Stanier, C.O.; Dickens, A.F.; Eloranta, E.W. Observations of the Development and Vertical Structure of the Lake-Breeze Circulation during the 2017 Lake Michigan Ozone Study. J. Atmos. Sci. 2022, 79, 1005–1020. [Google Scholar] [CrossRef]
- Xue, P.; Pal, J.S.; Ye, X.; Lenters, J.D.; Huang, C.; Chu, P.Y. Improving the Simulation of Large Lakes in Regional Climate Modeling: Two-Way Lake–Atmosphere Coupling with a 3D Hydrodynamic Model of the Great Lakes. J. Clim. 2017, 30, 1605–1627. [Google Scholar] [CrossRef]
- Bennington, V.; Notaro, M.; Holman, K.D. Improving Climate Sensitivity of Deep Lakes within a Regional Climate Model and Its Impact on Simulated Climate. J. Clim. 2014, 27, 2886–2911. [Google Scholar] [CrossRef]
- Sharma, S.; Gray, D.K.; Read, J.S.; O’reilly, C.M.; Schneider, P.; Qudrat, A.; Gries, C.; Stefanoff, S.; Hampton, S.E.; Hook, S. A global database of lake surface temperatures collected by in situ and satellite methods from 1985–2009. Sci. Data 2015, 2, 150008. [Google Scholar] [CrossRef] [PubMed]
- Lieberherr, G.; Wunderle, S. Lake Surface Water Temperature Derived from 35 Years of AVHRR Sensor Data for European Lakes. Remote Sens. 2018, 10, 990. [Google Scholar] [CrossRef]
- Willard, J.D.; Read, J.S.; Topp, S.; Hansen, G.J.A.; Kumar, V. Daily surface temperatures for 185,549 lakes in the conterminous United States estimated using deep learning (1980–2020). Limnol. Oceanogr. Lett. 2022, 7, 287–301. [Google Scholar] [CrossRef]
- Prats, J.; Reynaud, N.; Rebière, D.; Peroux, T.; Tormos, T.; Danis, P.-A. LakeSST: Lake Skin Surface Temperature in French inland water bodies for 1999–2016 from Landsat archives. Earth Syst. Sci. Data 2018, 10, 727–743. [Google Scholar] [CrossRef]
- Liu, B.; Wan, W.; Xie, H.; Li, H.; Zhu, S.; Zhang, G.; Wen, L.; Hong, Y. A long-term dataset of lake surface water temperature over the Tibetan Plateau derived from AVHRR 1981–2015. Sci. Data 2019, 6, 48. [Google Scholar] [CrossRef]
- Guo, L.; Zheng, H.; Wu, Y.; Fan, L.; Wen, M.; Li, J.; Zhang, F.; Zhu, L.; Zhang, B. An integrated dataset of daily lake surface water temperature over the Tibetan Plateau. Earth Syst. Sci. Data 2022, 14, 3411–3422. [Google Scholar] [CrossRef]
- Attiah, G.; Kheyrollah Pour, H.; Scott, K.A. Lake Surface Temperature Dataset in the North Slave Region Retrieved from Landsat Satellite Series–1984 to 2021. Earth Syst. Sci. Data Discuss. 2022, 2022, 1–37. [Google Scholar]
- Riffler, M.; Lieberherr, G.; Wunderle, S. Lake surface water temperatures of European Alpine lakes (1989–2013) based on the Advanced Very High Resolution Radiometer (AVHRR) 1 km data set. Earth Syst. Sci. Data 2015, 7, 1–17. [Google Scholar] [CrossRef]
- Pareeth, S.; Salmaso, N.; Adrian, R.; Neteler, M. Homogenised daily lake surface water temperature data generated from multiple satellite sensors: A long-term case study of a large sub-Alpine lake. Sci. Rep. 2016, 6, 31251. [Google Scholar] [CrossRef]
- Schwab, D.J.; Leshkevich, G.A.; Muhr, G.C. Automated Mapping of Surface Water Temperature in the Great Lakes. J. Great Lakes Res. 1999, 25, 468–481. [Google Scholar] [CrossRef]
- Woolway, R.I.; Anderson, E.J.; Albergel, C. Rapidly expanding lake heatwaves under climate change. Environ. Res. Lett. 2021, 16, 094013. [Google Scholar] [CrossRef]
- Notaro, M.; Bennington, V.; Lofgren, B. Dynamical Downscaling–Based Projections of Great Lakes Water Levels. J. Clim. 2015, 28, 9721–9745. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.-M. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L.; et al. ICOADS Release 3.0: A major update to the historical marine climate record. Int. J. Climatol. 2017, 37, 2211–2232. [Google Scholar] [CrossRef]
- Wong, A.P.S.; Wijffels, S.E.; Riser, S.C.; Pouliquen, S.; Hosoda, S.; Roemmich, D.; Gilson, J.; Johnson, G.C.; Martini, K.; Murphy, D.J.; et al. Argo Data 1999–2019: Two Million Temperature-Salinity Profiles and Subsurface Velocity Observations From a Global Array of Profiling Floats. Front. Mar. Sci. 2020, 7, 700. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Chin, T.M.; Liu, C.; Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling and environmental studies. Earth Syst. Sci. Data 2016, 8, 165–176. [Google Scholar] [CrossRef]
- Zhong, Y.; Notaro, M.; Vavrus, S.J. Spatially variable warming of the Laurentian Great Lakes: An interaction of bathymetry and climate. Clim. Dyn. 2019, 52, 5833–5848. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1940 to present. In Copernicus Climate Change Service (C3S) Climate Data Store (CDS); Copernicus: Göttingen, Germany, 2023. [Google Scholar] [CrossRef]
- Simmons, A.; Hersbach, H.; Muñoz-Sabater, J.; Nicolas, J.; Vamborg, F.; Berrisford, P.; de Rosnay, P.; Willett, K.; Woollen, J. Low Frequency Variability and Trends in Surface Air Temperature and Humidity from ERA5 and Other Datasets; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2021. [Google Scholar]
- Bryan, A.M.; Steiner, A.L.; Posselt, D.J. Regional modeling of surface-atmosphere interactions and their impact on Great Lakes hydroclimate. J. Geophys. Res. Atmos. 2015, 120, 1044–1064. [Google Scholar] [CrossRef]
- Mironov, D. Parameterization of Lakes in Numerical Weather Prediction: Description of a Lake Model; DWD: Offenbach, Germany, 2008. [Google Scholar]
- Sun, L.; Liang, X.-Z.; Xia, M. Developing the Coupled CWRF-FVCOM Modeling System to Understand and Predict Atmosphere-Watershed Interactions over the Great Lakes Region. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002319. [Google Scholar] [CrossRef]
- Yousefi, A.; Toffolon, M. Critical factors for the use of machine learning to predict lake surface water temperature. J. Hydrol. 2022, 606, 127418. [Google Scholar] [CrossRef]
- Heddam, S.; Ptak, M.; Zhu, S. Modelling of daily lake surface water temperature from air temperature: Extremely randomized trees (ERT) versus Air2Water, MARS, M5Tree, RF and MLPNN. J. Hydrol. 2020, 588, 125130. [Google Scholar] [CrossRef]
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.; Zwart, J.; Steinbach, M.; Kumar, V. Physics guided RNNs for modeling dynamical systems: A case study in simulating lake temperature profiles. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgery, AB, Canada, 2–4 May 2019; pp. 558–566. [Google Scholar]
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.S.; Zwart, J.A.; Steinbach, M.; Kumar, V. Physics-guided machine learning for scientific discovery: An application in simulating lake temperature profiles. ACM/IMS Trans. Data Sci. 2021, 2, 1–26. [Google Scholar] [CrossRef]
- Liu, W.-C.; Chen, W.-B. Prediction of water temperature in a subtropical subalpine lake using an artificial neural network and three-dimensional circulation models. Comput. Geosci. 2012, 45, 13–25. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2022, 34, 8501–8510. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Cai, Y.; Xu, L.; Chen, Z.; Gong, J. A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Environ. Model. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- Hou, S.; Li, W.; Liu, T.; Zhou, S.; Guan, J.; Qin, R.; Wang, Z. D2CL: A dense dilated convolutional LSTM model for sea surface temperature prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12514–12523. [Google Scholar] [CrossRef]
- Usharani, B. ILF-LSTM: Enhanced loss function in LSTM to predict the sea surface temperature. Soft Comput. 2022, 27, 1–13. [Google Scholar] [CrossRef]
- Pravallika, M.S.; Vasavi, S.; Vighneshwar, S. Prediction of temperature anomaly in Indian Ocean based on autoregressive long short-term memory neural network. Neural Comput. Appl. 2022, 34, 7537–7545. [Google Scholar] [CrossRef]
- Choi, H.-M.; Kim, M.-K.; Yang, H. Deep-learning model for sea surface temperature prediction near the Korean Peninsula. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2023, 208, 105262. [Google Scholar] [CrossRef]
- Sener, E.; Terzi, O.; Sener, S.; Kucukkara, R. Modeling of water temperature based on GIS and ANN techniques: Case study of Lake Egirdir (Turkey). Ekoloji 2012, 21, 44–52. [Google Scholar] [CrossRef]
- Zhu, S.; Ptak, M.; Choiński, A.; Wu, S. Exploring and quantifying the impact of climate change on surface water temperature of a high mountain lake in Central Europe. Environ. Monit. Assess. 2020, 192, 7. [Google Scholar] [CrossRef]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.A.; Hanson, P.C.; Watkins, W.; et al. Process-Guided Deep Learning Predictions of Lake Water Temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef]
- Liu, X.; Wilson, T.; Tan, P.-N.; Luo, L. Hierarchical LSTM framework for long-term sea surface temperature forecasting. In Proceedings of the 2019 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Washington, DC, USA, 5–8 October 2019; pp. 41–50. [Google Scholar]
- Hao, Z.; Li, W.; Wu, J.; Zhang, S.; Hu, S. A Novel Deep Learning Model for Mining Nonlinear Dynamics in Lake Surface Water Temperature Prediction. Remote Sens. 2023, 15, 900. [Google Scholar] [CrossRef]
- Mai, J.; Shen, H.; Tolson, B.A.; Gaborit, É.; Arsenault, R.; Craig, J.R.; Fortin, V.; Fry, L.M.; Gauch, M.; Klotz, D.; et al. The Great Lakes Runoff Intercomparison Project Phase 4: The Great Lakes (GRIP-GL). Hydrol. Earth Syst. Sci. 2022, 26, 3537–3572. [Google Scholar] [CrossRef]
- Feng, X.; Ma, G.; Su, S.-F.; Huang, C.; Boswell, M.K.; Xue, P. A multi-layer perceptron approach for accelerated wave forecasting in Lake Michigan. Ocean. Eng. 2020, 211, 107526. [Google Scholar] [CrossRef]
- Hu, H.; van der Westhuysen, A.J.; Chu, P.; Fujisaki-Manome, A. Predicting Lake Erie wave heights and periods using XGBoost and LSTM. Ocean. Model. 2021, 164, 101832. [Google Scholar] [CrossRef]
- Wu, C.; Li, B.; Xiong, N. An Effective Machine Learning Scheme to Analyze and Predict the Concentration of Persistent Pollutants in the Great Lakes. IEEE Access 2021, 9, 52252–52265. [Google Scholar] [CrossRef]
- Xue, P.; Wagh, A.; Ma, G.; Wang, Y.; Yang, Y.; Liu, T.; Huang, C. Integrating Deep Learning and Hydrodynamic Modeling to Improve the Great Lakes Forecast. Remote Sens. 2022, 14, 2640. [Google Scholar] [CrossRef]
- Kayastha, M.B.; Liu, T.; Titze, D.; Havens, T.C.; Huang, C.; Xue, P. Great Lakes Lake Surface Temperature for 1979–2020 Derived From LSTM; Zenodo: Genève, Switzerland, 2023. [Google Scholar] [CrossRef]
- Bai, X.; Wang, J.; Schwab, D.J.; Yang, Y.; Luo, L.; Leshkevich, G.A.; Liu, S. Modeling 1993–2008 climatology of seasonal general circulation and thermal structure in the Great Lakes using FVCOM. Ocean. Model. 2013, 65, 40–63. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Xue, P.; Schwab, D.J.; Hu, S. An investigation of the thermal response to meteorological forcing in a hydrodynamic model of Lake Superior. J. Geophys. Res. Ocean. 2015, 120, 5233–5253. [Google Scholar] [CrossRef]
- Huang, C.; Zhu, L.; Ma, G.; Meadows, G.A.; Xue, P. Wave Climate Associated With Changing Water Level and Ice Cover in Lake Michigan. Front. Mar. Sci. 2021, 8, 746916. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Zhong, Y.; Notaro, M.; Vavrus, S.J.; Foster, M.J. Recent accelerated warming of the Laurentian Great Lakes: Physical drivers. Limnol. Oceanogr. 2016, 61, 1762–1786. [Google Scholar] [CrossRef]
- Van Cleave, K.; Lenters, J.D.; Wang, J.; Verhamme, E.M. A regime shift in Lake Superior ice cover, evaporation, and water temperature following the warm El Niñ winter of 1997–1998. Limnol. Oceanogr. 2014, 59, 1889–1898. [Google Scholar] [CrossRef]
- Assel, R.A. The 1997 ENSO event and implication for North American Laurentian Great Lakes winter severity and ice cover. Geophys. Res. Lett. 1998, 25, 1031–1033. [Google Scholar] [CrossRef]
- Clites, A.H.; Wang, J.; Campbell, K.B.; Gronewold, A.D.; Assel, R.A.; Bai, X.; Leshkevich, G.A. Cold Water and High Ice Cover on Great Lakes in Spring 2014. Eos Trans. Am. Geophys. Union 2014, 95, 305–306. [Google Scholar] [CrossRef]
- Bronte, C.R.; Ebener, M.P.; Schreiner, D.R.; DeVault, D.S.; Petzold, M.M.; Jensen, D.A.; Richards, C.; Lozano, S.J. Fish community change in Lake Superior, 1970–2000. Can. J. Fish. Aquat. Sci. 2003, 60, 1552–1574. [Google Scholar] [CrossRef]
- Lynch, A.J.; Taylor, W.W.; Smith, K.D. The influence of changing climate on the ecology and management of selected Laurentian Great Lakes fisheries. J. Fish Biol. 2010, 77, 1764–1782. [Google Scholar] [CrossRef] [PubMed]
- Van Zuiden, T.M.; Sharma, S. Examining the effects of climate change and species invasions on Ontario walleye populations: Can walleye beat the heat? Divers. Distrib. 2016, 22, 1069–1079. [Google Scholar] [CrossRef]
- Collingsworth, P.D.; Bunnell, D.B.; Murray, M.W.; Kao, Y.-C.; Feiner, Z.S.; Claramunt, R.M.; Lofgren, B.M.; Höök, T.O.; Ludsin, S.A. Climate change as a long-term stressor for the fisheries of the Laurentian Great Lakes of North America. Rev. Fish Biol. Fish. 2017, 27, 363–391. [Google Scholar] [CrossRef]
- Alofs, K.; Lester, N.; Jackson, D. Ontario freshwater fish demonstrate differing range-boundary shifts in a warming climate. Divers. Distrib. 2014, 20, 123–136. [Google Scholar] [CrossRef]
- Cline, T.J.; Kitchell, J.F.; Bennington, V.; McKinley, G.A.; Moody, E.K.; Weidel, B.C. Climate impacts on landlocked sea lamprey: Implications for host-parasite interactions and invasive species management. Ecosphere 2014, 5, 1–13. [Google Scholar] [CrossRef]
- Arvola, L.; Palomäki, A.; Lehtinen, S.; Järvinen, M. Phytoplankton community structure and biomass in two basins of a boreal lake in relation to local weather conditions and North Atlantic oscillation. Int. Ver. Für Theor. Und Angew. Limnol. Verhandlungen 2002, 28, 700–704. [Google Scholar] [CrossRef]
- Jasser, I.; Arvola, L. Potential effects of abiotic factors on the abundance of autotrophic picoplankton in four boreal lakes. J. Plankton Res. 2003, 25, 873–883. [Google Scholar] [CrossRef]
- Arvola, L.; George, G.; Livingstone, D.M.; Järvinen, M.; Blenckner, T.; Dokulil, M.T.; Jennings, E.; Aonghusa, C.N.; Nõges, P.; Nõges, T.; et al. The Impact of the Changing Climate on the Thermal Characteristics of Lakes. In The Impact of Climate Change on European Lakes; George, G., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 85–101. [Google Scholar]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef]
- GLSEA_ACSPO_GCS. Available online: https://coastwatch.glerl.noaa.gov/erddap/files/GLSEA_ACSPO_GCS/ (accessed on 1 June 2023).
- Chen, R.; Wang, X.; Zhang, W.; Zhu, X.; Li, A.; Yang, C. A hybrid CNN-LSTM model for typhoon formation forecasting. GeoInformatica 2019, 23, 375–396. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Toffolon, M.; Majone, B. A simple lumped model to convert air temperature into surface water temperature in lakes. Hydrol. Earth Syst. Sci. 2013, 17, 3323–3338. [Google Scholar] [CrossRef]




| Lake | Elevation (m) | Average Depth (m) | Maximum Depth (m) | Volume (km3) | Water Surface Area (km2) |
|---|---|---|---|---|---|
| Superior | 183 | 149 | 406 | 12,232 | 82,097 |
| Michigan | 176 | 85 | 281 | 4918 | 57,753 |
| Huron | 176 | 59 | 229 | 3538 | 59,565 |
| Erie | 173 | 19 | 64 | 483 | 25,655 |
| Ontario | 74 | 86 | 244 | 1639 | 19,009 |
| Hyperparameters | Optimal Value |
|---|---|
| Optimizer | Adam |
| LSTM layers | 3 |
| Activation units | 32, 16, 8 |
| Activation function | tanh |
| Dropout | 0.2 |
| Learning rate | 0.001 |
| Epochs | 500 |
| Batch Size | 2048 |
| Lake | Number of Training Samples | Number of Validation Samples |
|---|---|---|
| Superior | 45,832,204 | 11,458,051 |
| Michigan | 43,781,716 | 10,945,429 |
| Huron | 60,299,536 | 15,074,884 |
| Erie | 46,401,784 | 11,600,446 |
| Ontario | 53,996,184 | 13,499,046 |
| Lake | Mean of Absolute Error (°C) | Mean of Squared Error (°C2) | Median of Absolute Error (°C) | R2 Score |
|---|---|---|---|---|
| Superior | 0.88 | 1.63 | 0.61 | 0.95 |
| Michigan | 0.99 | 1.8 | 0.76 | 0.97 |
| Huron | 0.94 | 1.83 | 0.65 | 0.97 |
| Erie | 0.85 | 1.3 | 0.65 | 0.98 |
| Ontario | 1.08 | 2.07 | 0.87 | 0.97 |
| Comparison with GLSEA | Comparison with NDBC | |||||
|---|---|---|---|---|---|---|
| Correlation | Bias (°C) | RMSE (°C) | Correlation | Bias (°C) | RMSE (°C) | |
| Superior | 0.99 | −0.19 | 0.76 | - | - | - |
| Michigan | 1.00 | 0.03 | 0.52 | - | - | - |
| Huron | 1.00 | −0.25 | 0.77 | - | - | - |
| Erie | 1.00 | −0.02 | 0.60 | - | - | - |
| Ontario | 1.00 | 0.02 | 0.58 | - | - | - |
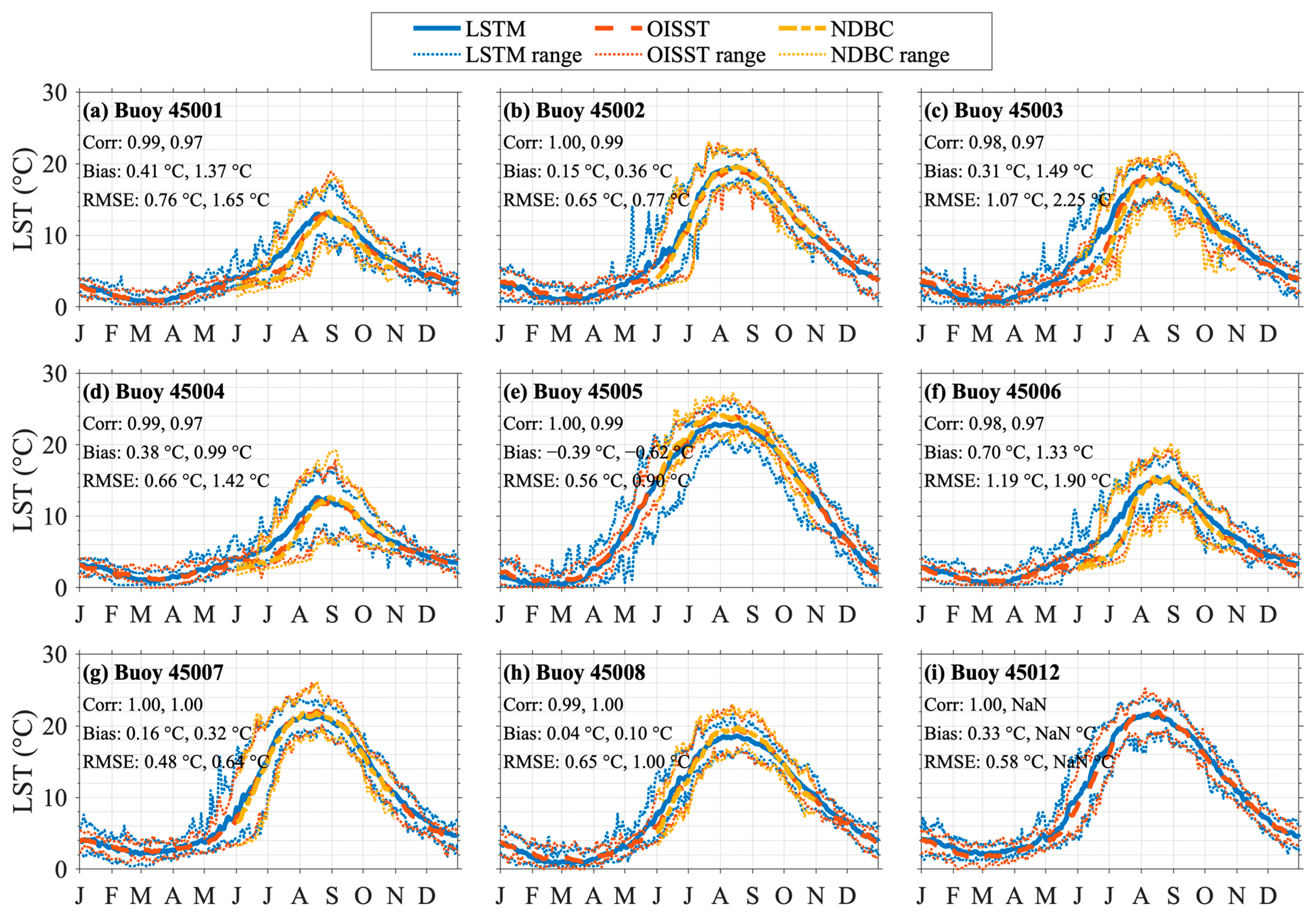
| 45001 | 0.98 | −0.08 | 0.91 | 0.98 | 0.43 | 1.42 |
| 45002 | 0.99 | −0.24 | 1.07 | 0.98 | 0.37 | 1.29 |
| 45003 | 0.98 | −0.20 | 1.28 | 0.97 | 0.28 | 1.65 |
| 45004 | 0.98 | −0.18 | 0.93 | 0.96 | 0.19 | 1.67 |
| 45005 | 0.99 | −0.06 | 1.02 | 0.98 | −0.08 | 1.02 |
| 45006 | 0.98 | 0.14 | 1.11 | 0.97 | 0.65 | 1.81 |
| 45007 | 0.99 | −0.33 | 1.02 | 0.98 | 0.18 | 1.14 |
| 45008 | 0.99 | −0.37 | 1.27 | 0.98 | −0.39 | 1.42 |
| 45012 | 0.99 | −0.05 | 0.97 | 0.97 | 0.16 | 1.22 |
| Comparison with OISST | Comparison with NDBC | |||||
|---|---|---|---|---|---|---|
| Correlation | Bias (°C) | RMSE (°C) | Correlation | Bias (°C) | RMSE (°C) | |
| Superior | 0.95 | 0.59 | 1.55 | - | - | - |
| Michigan | 0.98 | 0.51 | 1.50 | - | - | - |
| Huron | 0.98 | 0.22 | 1.31 | - | - | - |
| Erie | 0.99 | 0.30 | 1.36 | - | - | - |
| Ontario | 0.98 | 0.38 | 1.32 | - | - | - |
| 45001 | 0.97 | 0.35 | 1.04 | 0.93 | 1.36 | 2.03 |
| 45002 | 0.98 | 0.28 | 1.20 | 0.96 | 0.43 | 1.52 |
| 45003 | 0.98 | 0.26 | 1.32 | 0.93 | 1.42 | 2.66 |
| 45004 | 0.97 | 0.30 | 0.95 | 0.93 | 0.94 | 1.86 |
| 45005 | 0.99 | 0.04 | 1.03 | 0.92 | −0.40 | 1.49 |
| 45006 | 0.96 | 0.69 | 1.48 | 0.93 | 1.29 | 2.32 |
| 45007 | 0.99 | 0.30 | 1.07 | 0.98 | 0.54 | 1.32 |
| 45008 | 0.99 | 0.12 | 1.05 | 0.97 | 0.20 | 1.49 |
| 45012 | 0.99 | 0.25 | 0.98 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kayastha, M.B.; Liu, T.; Titze, D.; Havens, T.C.; Huang, C.; Xue, P. Reconstructing 42 Years (1979–2020) of Great Lakes Surface Temperature through a Deep Learning Approach. Remote Sens. 2023, 15, 4253. https://doi.org/10.3390/rs15174253
Kayastha MB, Liu T, Titze D, Havens TC, Huang C, Xue P. Reconstructing 42 Years (1979–2020) of Great Lakes Surface Temperature through a Deep Learning Approach. Remote Sensing. 2023; 15(17):4253. https://doi.org/10.3390/rs15174253
Chicago/Turabian StyleKayastha, Miraj B., Tao Liu, Daniel Titze, Timothy C. Havens, Chenfu Huang, and Pengfei Xue. 2023. "Reconstructing 42 Years (1979–2020) of Great Lakes Surface Temperature through a Deep Learning Approach" Remote Sensing 15, no. 17: 4253. https://doi.org/10.3390/rs15174253
APA StyleKayastha, M. B., Liu, T., Titze, D., Havens, T. C., Huang, C., & Xue, P. (2023). Reconstructing 42 Years (1979–2020) of Great Lakes Surface Temperature through a Deep Learning Approach. Remote Sensing, 15(17), 4253. https://doi.org/10.3390/rs15174253








