Author Contributions
Methodology, Software, Validation, Formal analysis, Investigation, Data Curation, Writing—Original Draft, Writing—Review and Editing, R.M.; Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data Curation, Writing—Original Draft, Writing—Review, Editing, Project administration and Funding acquisition, K.M.; Software, Validation, Formal analysis, Investigation and Data Curation, J.S.; Resource, Formal analysis & Investigation, J.N. and S.M.B.; Resource and Editing, F.M.; Resource and Editing, G.D. All authors have read and agreed to the published version of the manuscript.
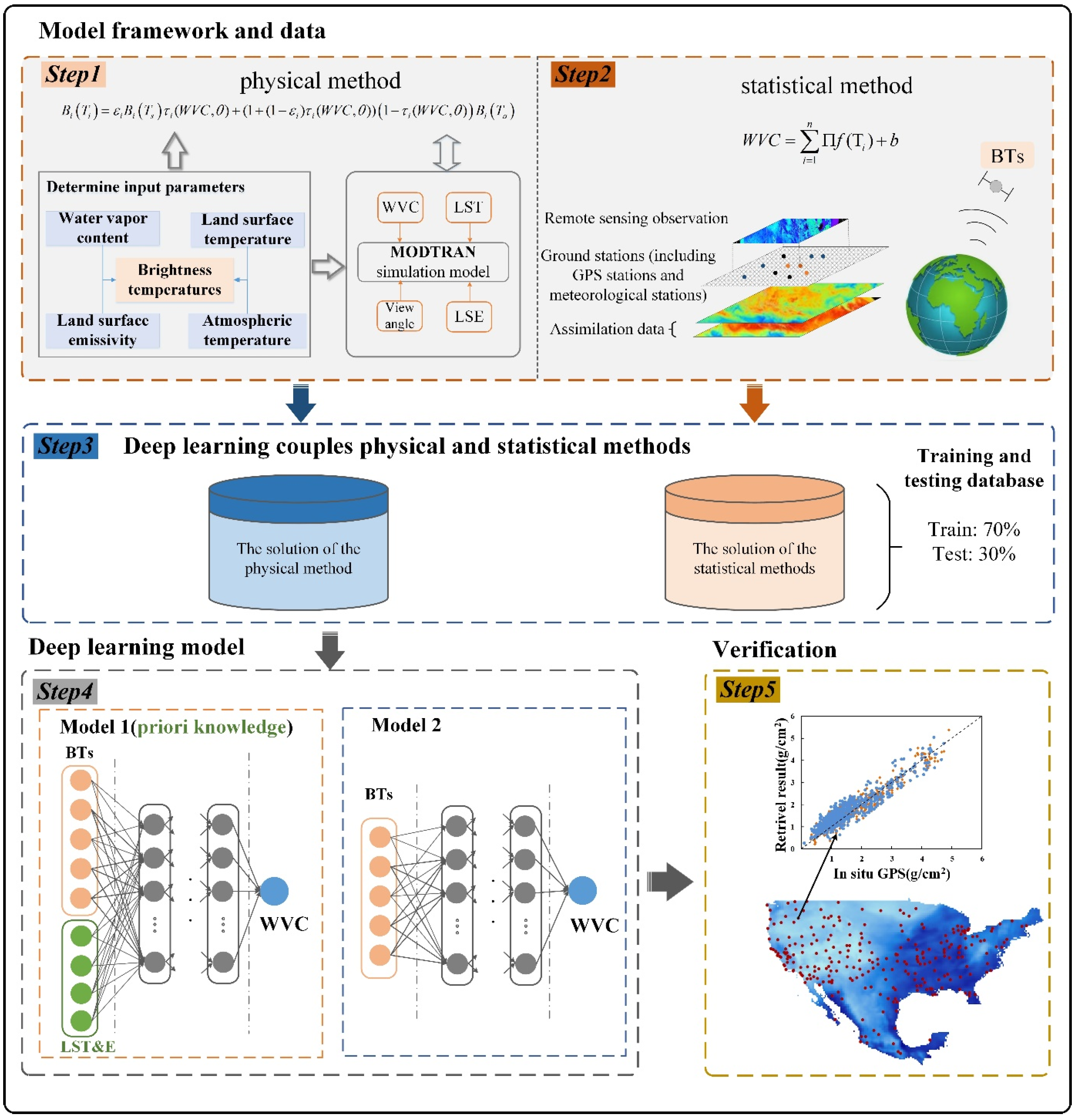
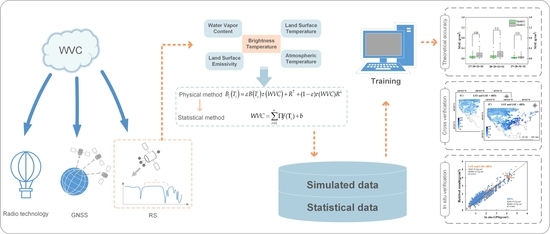
Figure 1.
A novel physics-statistical coupled deep learning paradigm for retrieving integrated water vapor content.
Figure 1.
A novel physics-statistical coupled deep learning paradigm for retrieving integrated water vapor content.
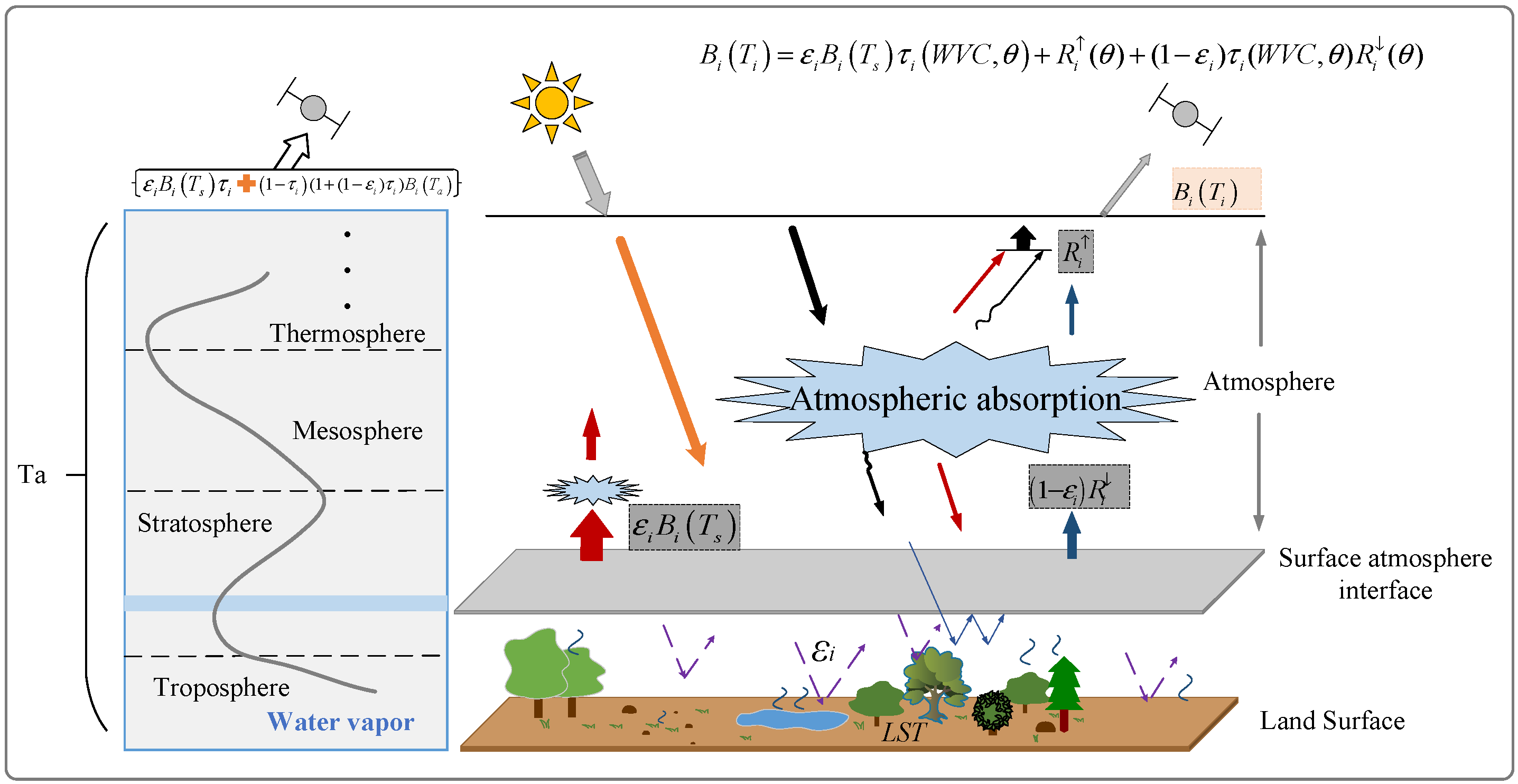
Figure 2.
Simplified diagram of radiative transfer modeling relating LST, LSE and WVC.
Figure 2.
Simplified diagram of radiative transfer modeling relating LST, LSE and WVC.
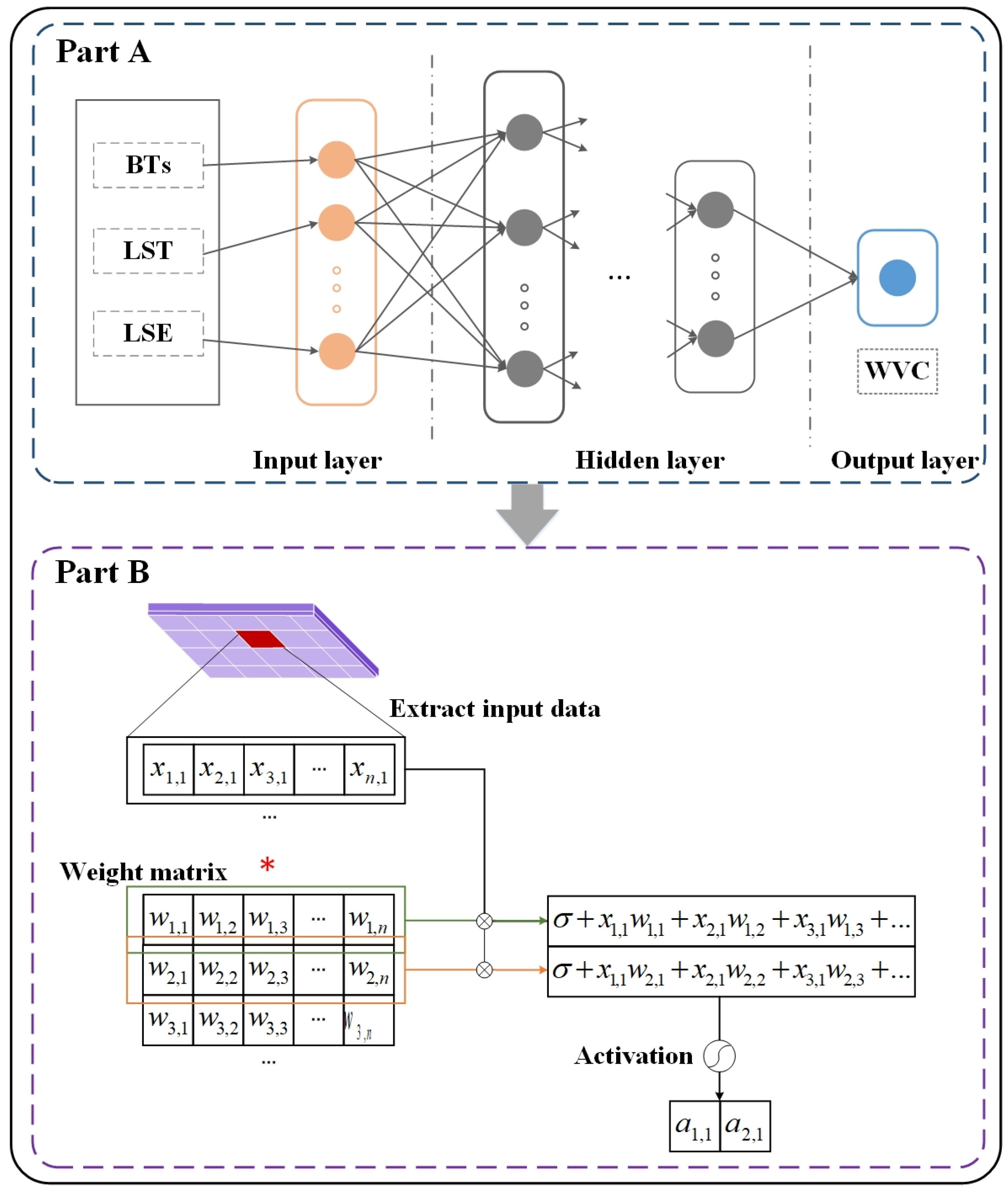
Figure 3.
DNN and schematic of neural network operation. ( is the number of input parameters, are the input parameters of the neural network, and WVC is the output parameter. is the weight of each neuron and is the bias. is the parameter input to the next layer of neurons after the activation function of the previous layer of neurons, indicates multiplication).
Figure 3.
DNN and schematic of neural network operation. ( is the number of input parameters, are the input parameters of the neural network, and WVC is the output parameter. is the weight of each neuron and is the bias. is the parameter input to the next layer of neurons after the activation function of the previous layer of neurons, indicates multiplication).
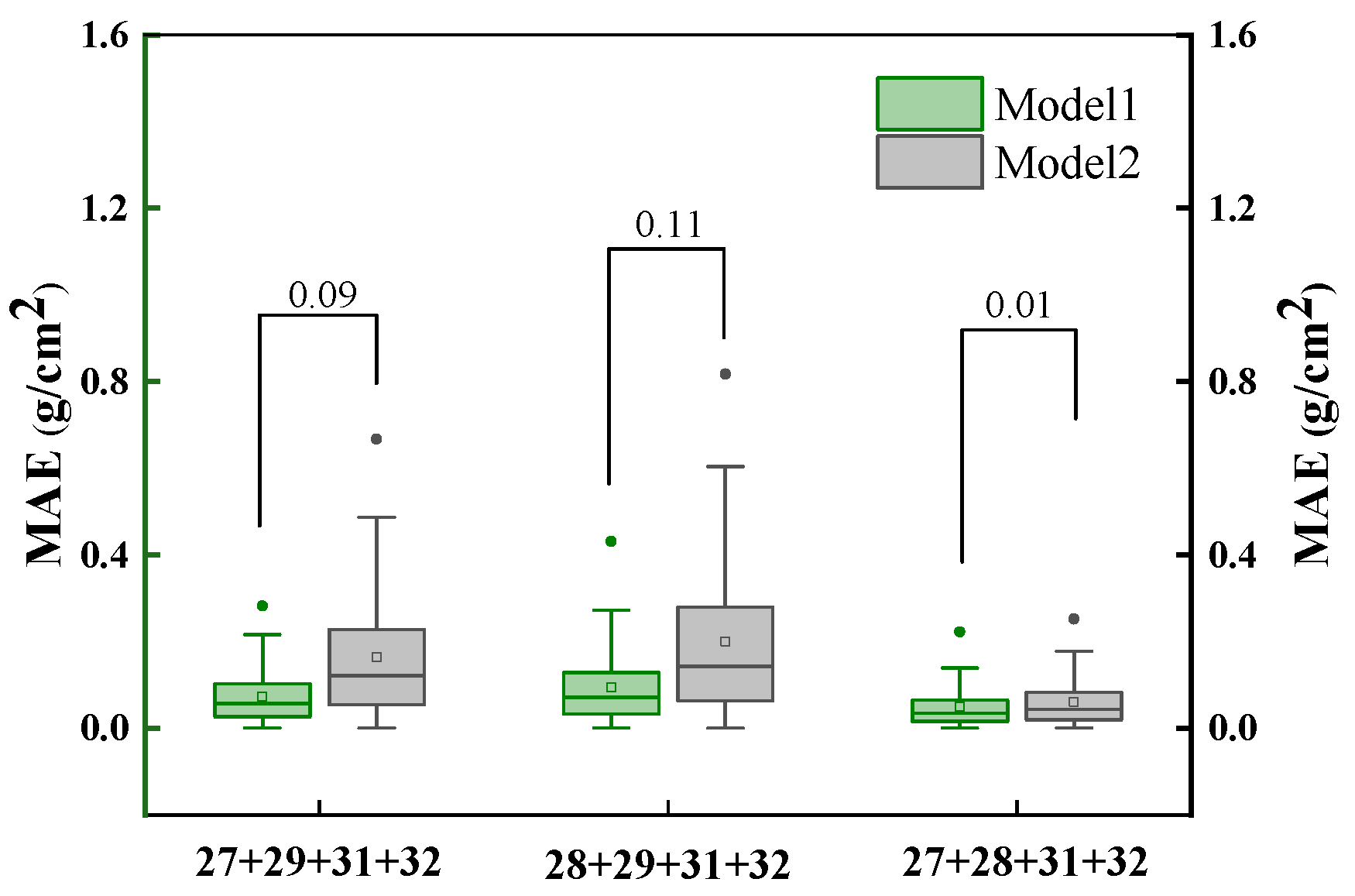
Figure 4.
Boxplot of absolute error of retrieval result. The left side of the connecting line shows the errors from model 1, while the right side shows the errors from model 2.
Figure 4.
Boxplot of absolute error of retrieval result. The left side of the connecting line shows the errors from model 1, while the right side shows the errors from model 2.
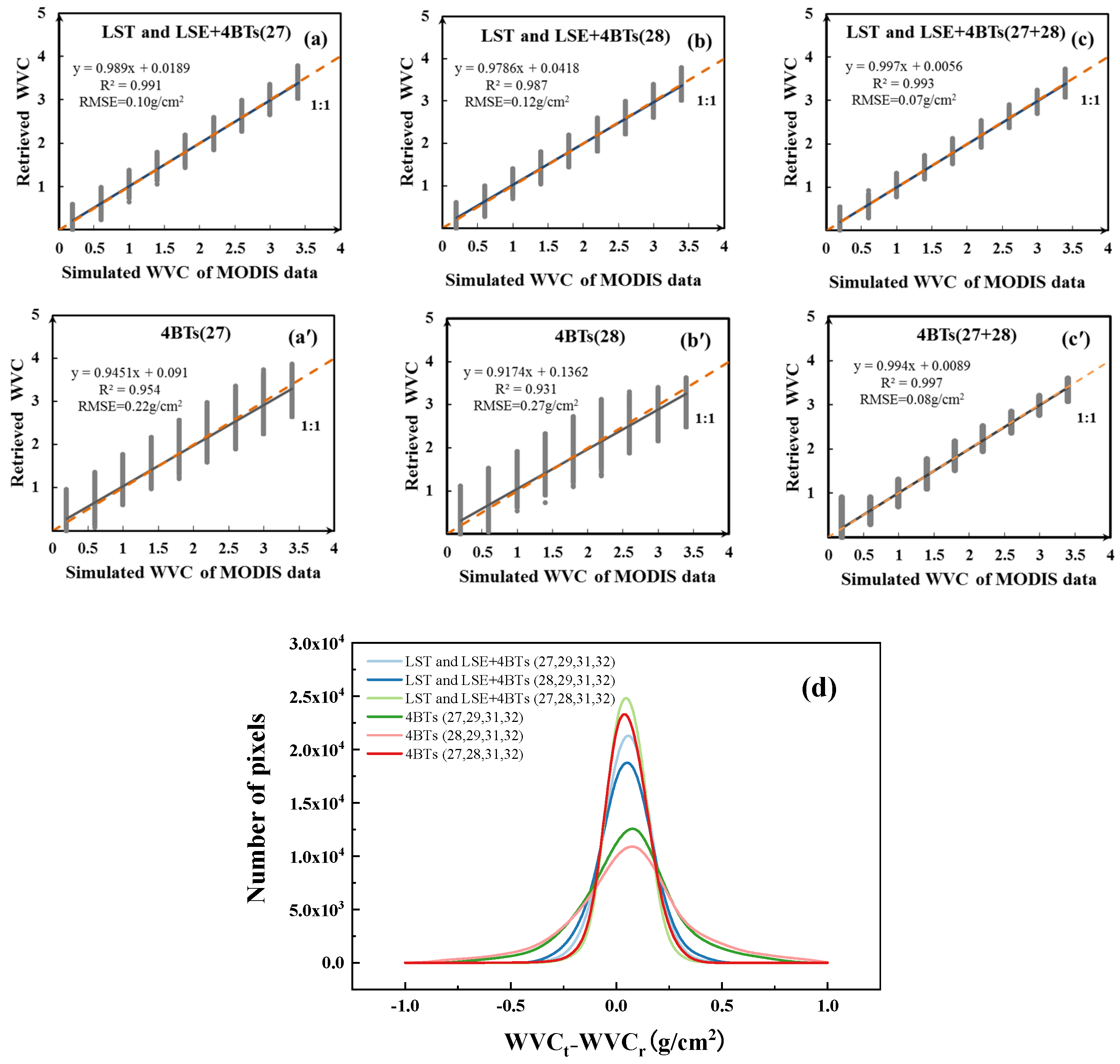
Figure 5.
Retrieval results of PSP–DL. WVCr shows retrieval results, WVCt is the MODTRAN simulation data. (a–c) are scatter plots of model 1 retrieval results and simulation data, (a) is the combination of prior knowledge and bands 27, 29, 31 and 32, (b) is the combination of prior knowledge and bands 28, 29, 31 and 32, (c) is the combination of prior knowledge and bands 27, 28, 31 and 32. (a′–c′) are scatter plots of model 1 retrieval results and simulation data, (a′) is the combination of bands 27, 29, 31 and 32, (b′) is the combination of bands 28, 29, 31 and 32, (c′) is the combination of bands 27, 28, 31 and 32, (d) is the error distribution of simulated data and retrieval data.
Figure 5.
Retrieval results of PSP–DL. WVCr shows retrieval results, WVCt is the MODTRAN simulation data. (a–c) are scatter plots of model 1 retrieval results and simulation data, (a) is the combination of prior knowledge and bands 27, 29, 31 and 32, (b) is the combination of prior knowledge and bands 28, 29, 31 and 32, (c) is the combination of prior knowledge and bands 27, 28, 31 and 32. (a′–c′) are scatter plots of model 1 retrieval results and simulation data, (a′) is the combination of bands 27, 29, 31 and 32, (b′) is the combination of bands 28, 29, 31 and 32, (c′) is the combination of bands 27, 28, 31 and 32, (d) is the error distribution of simulated data and retrieval data.
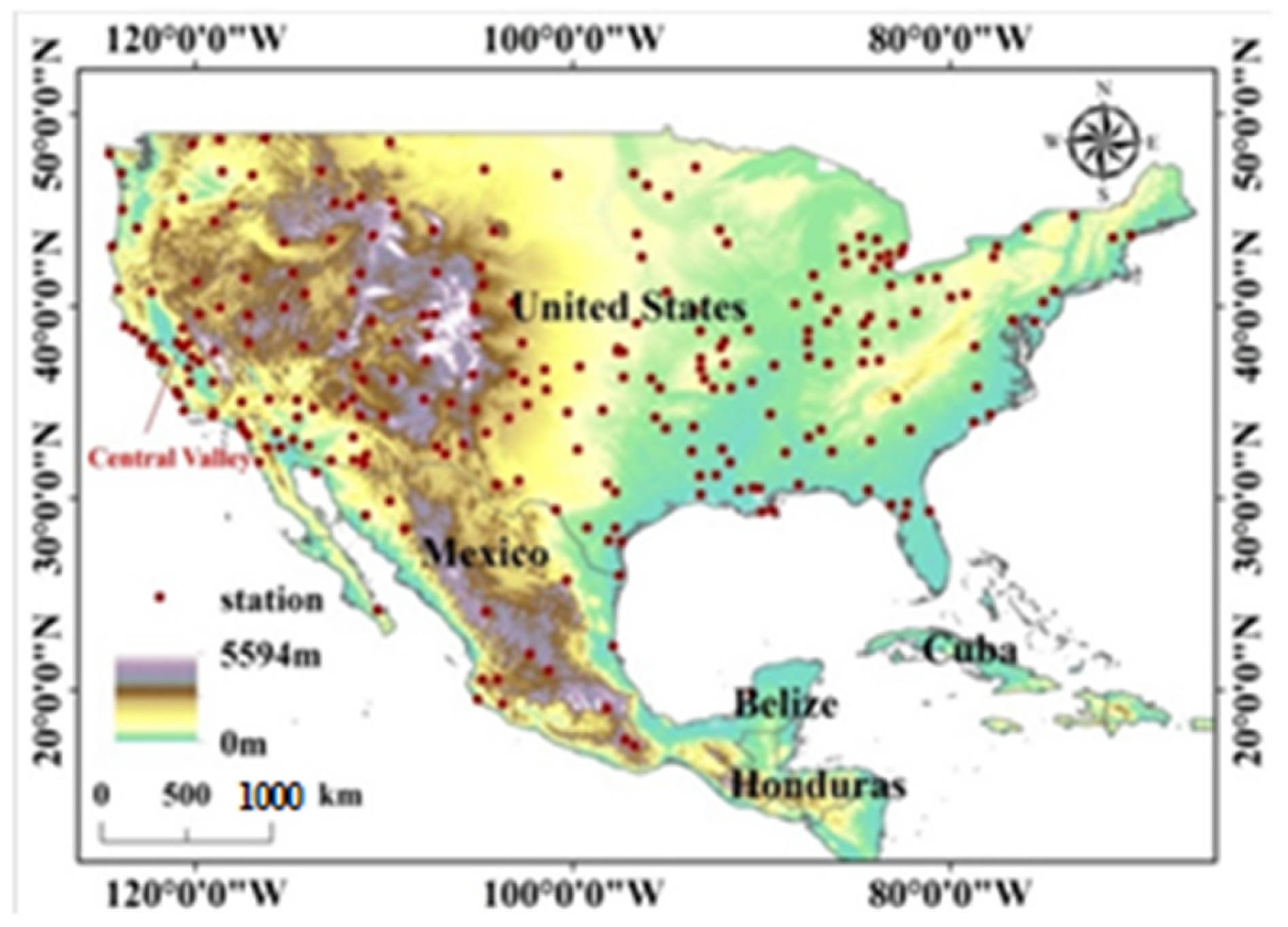
Figure 6.
A case study of southern North America (The United States and Mexico).
Figure 6.
A case study of southern North America (The United States and Mexico).
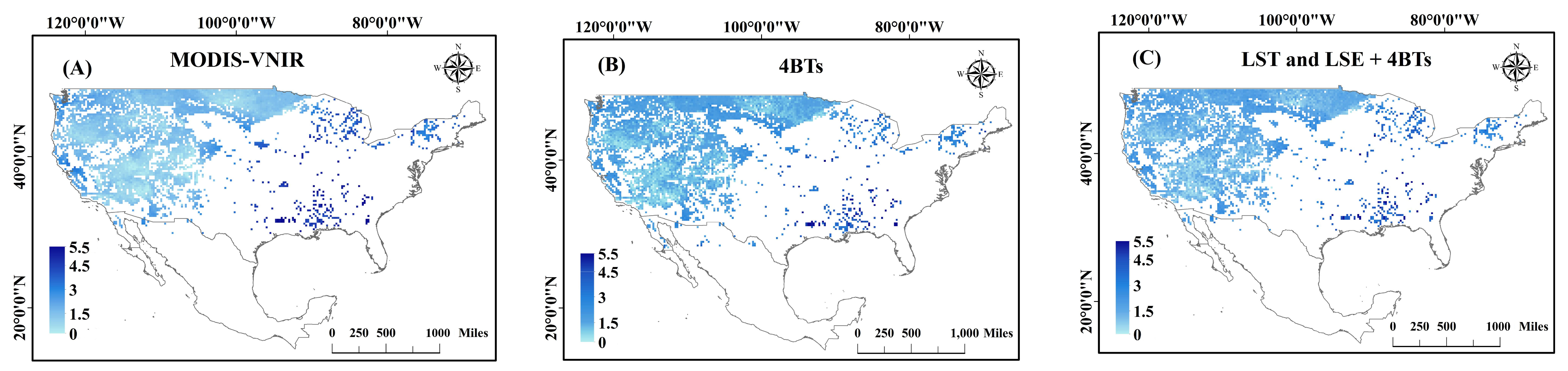
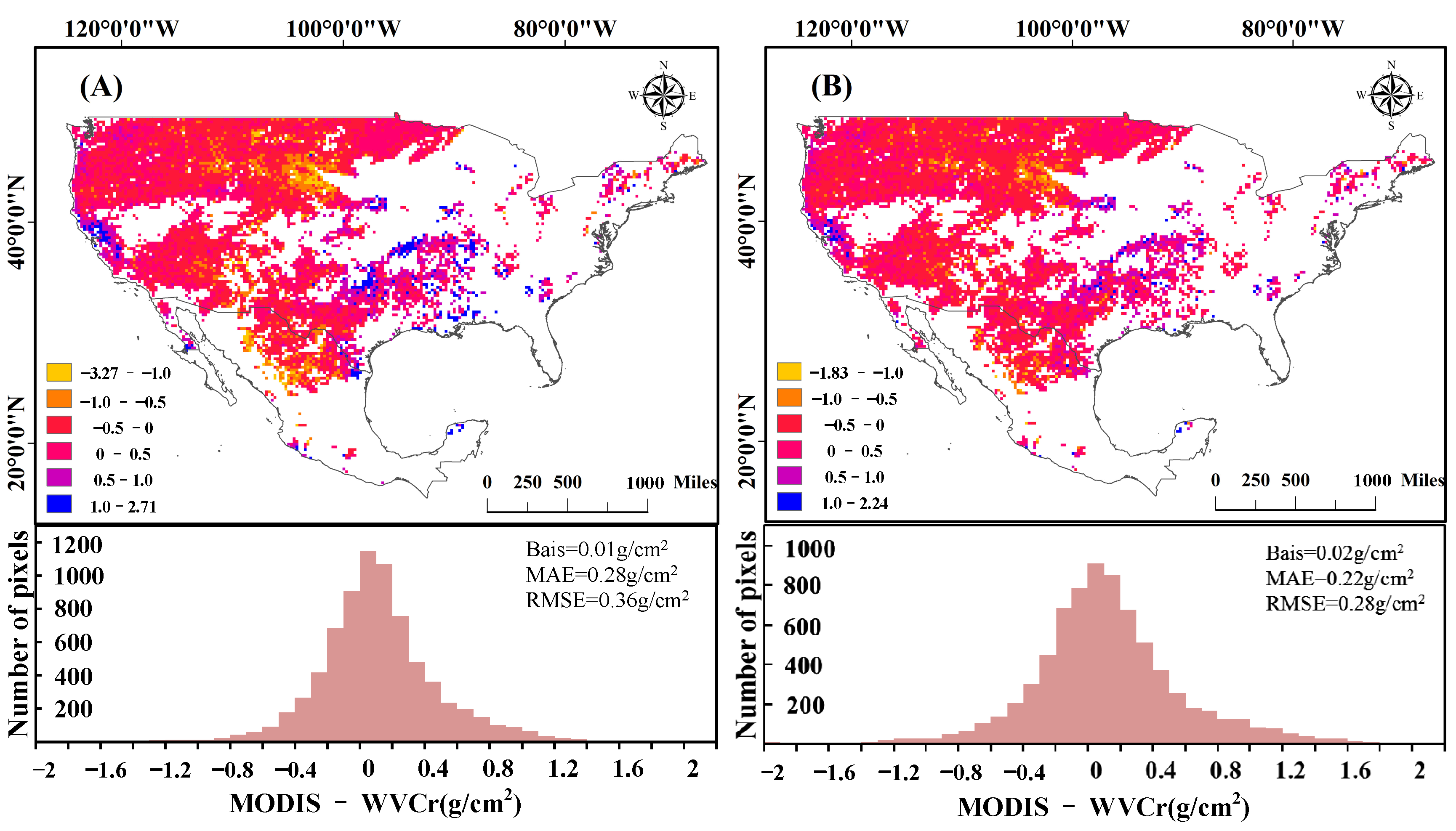
Figure 7.
WVC (g/cm2) retrieved by PSP–DL method. Integrated water vapor content products: (A) MODIS-VNIR, (B) WVC retrieved from MODIS bands 27, 28, 31 and 32, (C) WVC retrieved from MODIS bands 27, 28, 31 and 32 and MODIS LST and LSE products (MOD11). The white areas indicate invalid values.
Figure 7.
WVC (g/cm2) retrieved by PSP–DL method. Integrated water vapor content products: (A) MODIS-VNIR, (B) WVC retrieved from MODIS bands 27, 28, 31 and 32, (C) WVC retrieved from MODIS bands 27, 28, 31 and 32 and MODIS LST and LSE products (MOD11). The white areas indicate invalid values.
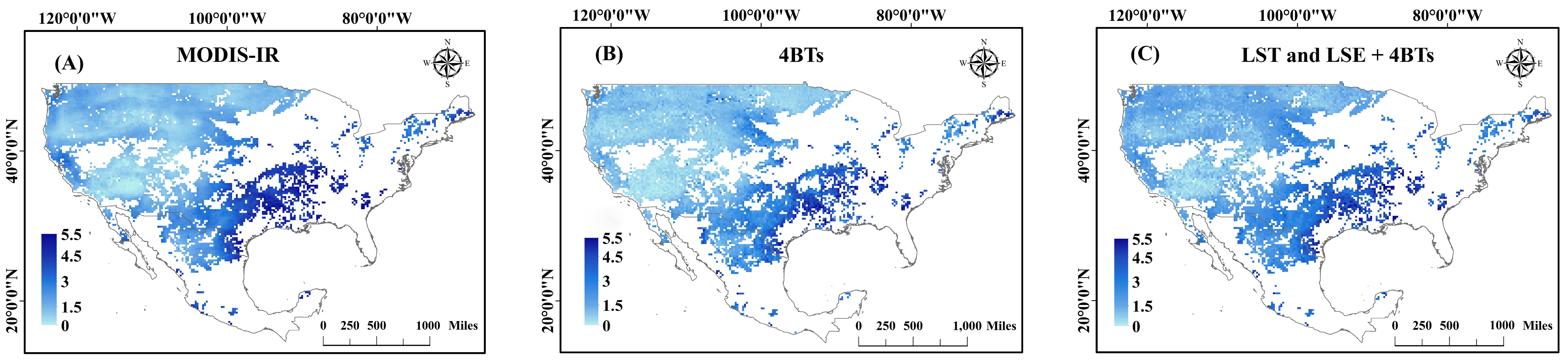
Figure 8.
WVC (g/cm2) retrieved by PSP–DL method. Integrated water vapor content products: (A) MODIS-TIR, (B) WVC retrieved from MODIS bands 27, 28, 31 and 32, (C) WVC retrieved from MODIS bands 27, 28, 31 and 32 and MODIS LST and LSE products (MOD11). The white areas indicate invalid values.
Figure 8.
WVC (g/cm2) retrieved by PSP–DL method. Integrated water vapor content products: (A) MODIS-TIR, (B) WVC retrieved from MODIS bands 27, 28, 31 and 32, (C) WVC retrieved from MODIS bands 27, 28, 31 and 32 and MODIS LST and LSE products (MOD11). The white areas indicate invalid values.
Figure 9.
Differences (g/cm2) between MODIS-VNIR products and WVC retrieved using PSP–DL method. (A) the difference between “MODIS-VNIR” and “4BTs”, (B) the difference between “MODIS-VNIR” and “LST and LSE + 4BTs”.
Figure 9.
Differences (g/cm2) between MODIS-VNIR products and WVC retrieved using PSP–DL method. (A) the difference between “MODIS-VNIR” and “4BTs”, (B) the difference between “MODIS-VNIR” and “LST and LSE + 4BTs”.
Figure 10.
Differences (g/cm2) between MODIS-TIR products and WVC retrieved using PSP–DL method. (A) the difference between “MODIS-TIR” and “4BTs”, (B) the difference between “MODIS-TIR” and “LST and LSE + 4BTs”. WVCr is the retrieval result of PSP–DL.
Figure 10.
Differences (g/cm2) between MODIS-TIR products and WVC retrieved using PSP–DL method. (A) the difference between “MODIS-TIR” and “4BTs”, (B) the difference between “MODIS-TIR” and “LST and LSE + 4BTs”. WVCr is the retrieval result of PSP–DL.
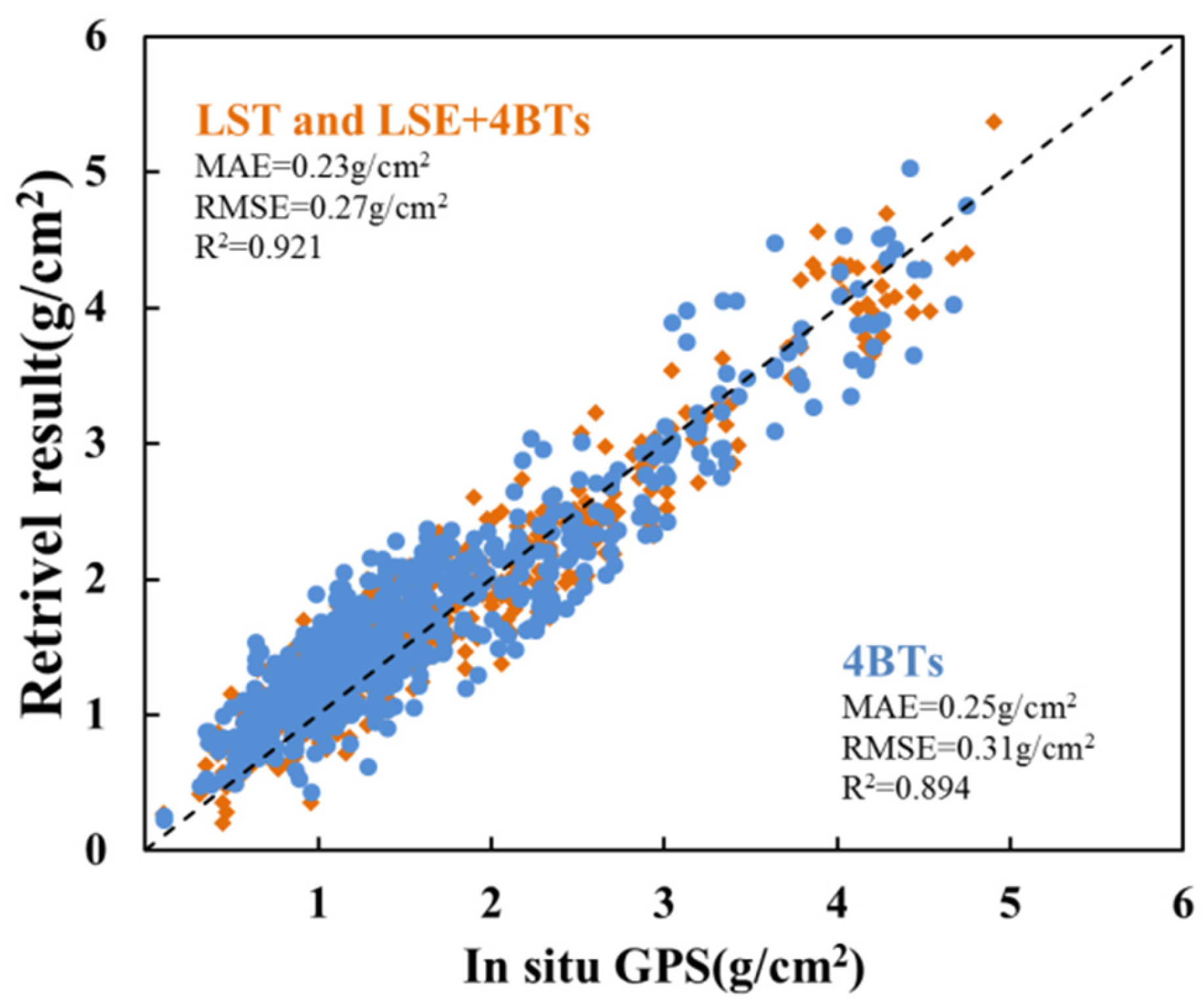
Figure 11.
Comparison between WVC retrieval by PSP–DL method and GPS data.
Figure 11.
Comparison between WVC retrieval by PSP–DL method and GPS data.
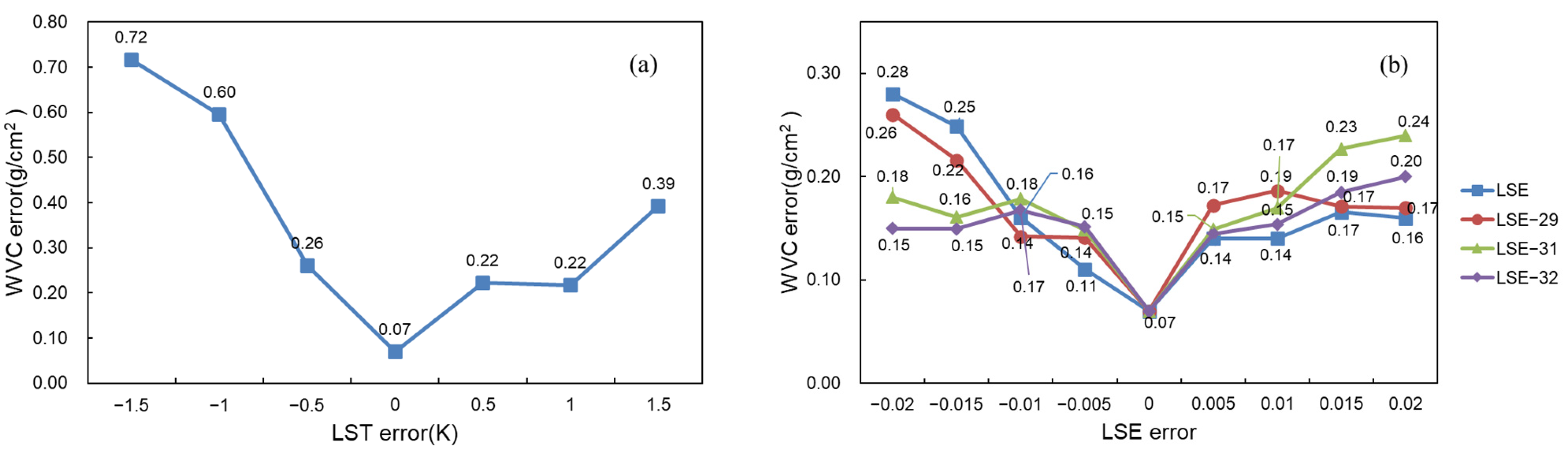
Figure 12.
The sensitivity analysis of parameters. (a) change of WVC error with the change of LST error, (b) change of WVC error with the change of LSE error.
Figure 12.
The sensitivity analysis of parameters. (a) change of WVC error with the change of LST error, (b) change of WVC error with the change of LSE error.
Table 1.
Datasets used in this study.
Table 1.
Datasets used in this study.
Table 2.
Band combinations used for retrieval of WVC.
Table 2.
Band combinations used for retrieval of WVC.
| Model | Situation | Variables |
|---|
| 1 | Use prior knowledge | BTs in thermal infrared band 27/28/29/31/32, LST and LSE of bands 29, 31, 32 |
| 2 | No prior knowledge used | BTs in thermal infrared band 27/28/29/31/32 |
Table 3.
WVC retrieval results using LST and LSE and bands 27, 29, 31, and 32.
Table 3.
WVC retrieval results using LST and LSE and bands 27, 29, 31, and 32.
| LST and LSE + 4BTs (from 27, 29, 31, 32) → WVC |
|---|
| | Nodes | 400 | 500 | 600 | 700 | 800 |
|---|
| Layers | | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 |
|---|
| 3 | 0.11 | 0.15 | 0.980 | 0.18 | 0.24 | 0.949 | 0.11 | 0.15 | 0.979 | 0.11 | 0.14 | 0.981 | 0.10 | 0.13 | 0.985 |
| 4 | 0.10 | 0.12 | 0.986 | 0.12 | 0.15 | 0.978 | 0.09 | 0.12 | 0.987 | 0.08 | 0.11 | 0.989 | 0.09 | 0.11 | 0.988 |
| 5 | 0.11 | 0.15 | 0.980 | 0.11 | 0.15 | 0.979 | 0.11 | 0.14 | 0.982 | 0.08 | 0.10 | 0.990 | 0.11 | 0.14 | 0.981 |
| 6 | 0.12 | 0.16 | 0.977 | 0.12 | 0.16 | 0.977 | 0.10 | 0.12 | 0.986 | 0.08 | 0.10 | 0.990 | 0.08 | 0.10 | 0.991 |
| 7 | 0.14 | 0.2 | 0.964 | 0.12 | 0.16 | 0.977 | 0.12 | 0.16 | 0.978 | 0.11 | 0.14 | 0.981 | 0.09 | 0.12 | 0.988 |
| 8 | 0.09 | 0.12 | 0.987 | 0.10 | 0.13 | 0.985 | 0.11 | 0.14 | 0.982 | 0.09 | 0.12 | 0.988 | 0.10 | 0.13 | 0.985 |
| 9 | 0.12 | 0.16 | 0.975 | 0.13 | 0.18 | 0.970 | 0.09 | 0.12 | 0.987 | 0.09 | 0.12 | 0.986 | 0.09 | 0.13 | 0.985 |
| 10 | 0.17 | 0.26 | 0.940 | 0.10 | 0.13 | 0.985 | 0.10 | 0.14 | 0.983 | 0.08 | 0.11 | 0.989 | 0.07 | 0.10 | 0.991 |
Table 4.
WVC retrieval results using LST and LSE and bands 28, 29, 31, and 32.
Table 4.
WVC retrieval results using LST and LSE and bands 28, 29, 31, and 32.
| LST and LSE + 4BTs (from 28, 29, 31, 32) → WVC |
|---|
| | Nodes | 400 | 500 | 600 | 700 | 800 |
|---|
| Layers | | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 |
|---|
| 3 | 0.12 | 0.15 | 0.978 | 0.15 | 0.20 | 0.964 | 0.11 | 0.15 | 0.979 | 0.12 | 0.16 | 0.977 | 0.12 | 0.15 | 0.978 |
| 4 | 0.13 | 0.17 | 0.974 | 0.13 | 0.17 | 0.974 | 0.14 | 0.19 | 0.969 | 0.10 | 0.13 | 0.985 | 0.12 | 0.15 | 0.979 |
| 5 | 0.13 | 0.17 | 0.972 | 0.13 | 0.17 | 0.972 | 0.10 | 0.13 | 0.983 | 0.14 | 0.19 | 0.963 | 0.11 | 0.15 | 0.978 |
| 6 | 0.14 | 0.18 | 0.966 | 0.11 | 0.14 | 0.980 | 0.09 | 0.12 | 0.987 | 0.11 | 0.14 | 0.981 | 0.11 | 0.14 | 0.981 |
| 7 | 0.24 | 0.32 | 0.906 | 0.13 | 0.17 | 0.974 | 0.13 | 0.17 | 0.974 | 0.14 | 0.18 | 0.967 | 0.11 | 0.14 | 0.981 |
| 8 | 0.13 | 0.18 | 0.970 | 0.11 | 0.14 | 0.978 | 0.13 | 0.18 | 0.972 | 0.13 | 0.16 | 0.973 | 0.11 | 0.15 | 0.978 |
| 9 | 0.17 | 0.23 | 0.951 | 0.15 | 0.20 | 0.962 | 0.11 | 0.14 | 0.982 | 0.11 | 0.14 | 0.980 | 0.09 | 0.12 | 0.984 |
| 10 | 0.11 | 0.14 | 0.980 | 0.11 | 0.14 | 0.980 | 0.12 | 0.16 | 0.978 | 0.10 | 0.13 | 0.983 | 0.10 | 0.13 | 0.983 |
Table 5.
WVC retrieval results using LST and LSE and bands 27, 28, 31, and 32.
Table 5.
WVC retrieval results using LST and LSE and bands 27, 28, 31, and 32.
| LST and LSE + 4BTs (from 27, 28, 31, 32) → WVC |
|---|
| | Nodes | 400 | 500 | 600 | 700 | 800 |
|---|
| Layers | | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 |
|---|
| 3 | 0.17 | 0.25 | 0.944 | 0.12 | 0.17 | 0.972 | 0.09 | 0.12 | 0.986 | 0.09 | 0.13 | 0.985 | 0.07 | 0.10 | 0.990 |
| 4 | 0.11 | 0.16 | 0.960 | 0.14 | 0.23 | 0.969 | 0.08 | 0.12 | 0.986 | 0.08 | 0.11 | 0.982 | 0.06 | 0.09 | 0.989 |
| 5 | 0.07 | 0.10 | 0.979 | 0.16 | 0.30 | 0.938 | 0.09 | 0.14 | 0.985 | 0.07 | 0.12 | 0.984 | 0.08 | 0.12 | 0.986 |
| 6 | 0.08 | 0.11 | 0.987 | 0.12 | 0.20 | 0.952 | 0.08 | 0.11 | 0.986 | 0.07 | 0.20 | 0.975 | 0.06 | 0.08 | 0.988 |
| 7 | 0.10 | 0.22 | 0.955 | 0.11 | 0.31 | 0.952 | 0.07 | 0.10 | 0.989 | 0.09 | 0.16 | 0.970 | 0.05 | 0.07 | 0.993 |
| 8 | 0.13 | 0.32 | 0.940 | 0.10 | 0.40 | 0.908 | 0.09 | 0.12 | 0.987 | 0.07 | 0.10 | 0.981 | 0.06 | 0.11 | 0.989 |
| 9 | 0.11 | 0.16 | 0.904 | 0.12 | 0.18 | 0.939 | 0.06 | 0.09 | 0.988 | 0.05 | 0.07 | 0.990 | 0.05 | 0.08 | 0.990 |
| 10 | 0.12 | 0.18 | 0.966 | 0.07 | 0.10 | 0.975 | 0.05 | 0.11 | 0.986 | 0.06 | 0.09 | 0.992 | 0.05 | 0.07 | 0.994 |
Table 6.
WVC retrieval results using bands 27, 29, 31, and 32.
Table 6.
WVC retrieval results using bands 27, 29, 31, and 32.
| 4BTs (from 27, 29, 31, and 32) → WVC |
|---|
| | Nodes | 400 | 500 | 600 | 700 | 800 |
|---|
| Layers | | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 |
|---|
| 3 | 0.19 | 0.25 | 0.943 | 0.18 | 0.24 | 0.948 | 0.17 | 0.23 | 0.952 | 0.17 | 0.23 | 0.952 | 0.17 | 0.23 | 0.950 |
| 4 | 0.19 | 0.25 | 0.941 | 0.17 | 0.22 | 0.953 | 0.17 | 0.23 | 0.950 | 0.17 | 0.23 | 0.95 | 0.17 | 0.23 | 0.952 |
| 5 | 0.17 | 0.23 | 0.950 | 0.20 | 0.29 | 0.921 | 0.20 | 0.28 | 0.926 | 0.18 | 0.25 | 0.942 | 0.17 | 0.22 | 0.953 |
| 6 | 0.17 | 0.23 | 0.951 | 0.17 | 0.23 | 0.950 | 0.16 | 0.22 | 0.953 | 0.18 | 0.25 | 0.941 | 0.17 | 0.23 | 0.950 |
| 7 | 0.17 | 0.24 | 0.946 | 0.17 | 0.23 | 0.948 | 0.19 | 0.27 | 0.934 | 0.18 | 0.24 | 0.947 | 0.18 | 0.24 | 0.945 |
| 8 | 0.19 | 0.25 | 0.942 | 0.18 | 0.23 | 0.949 | 0.18 | 0.25 | 0.939 | 0.17 | 0.23 | 0.950 | 0.17 | 0.23 | 0.952 |
| 9 | 0.19 | 0.25 | 0.941 | 0.16 | 0.22 | 0.954 | 0.17 | 0.22 | 0.953 | 0.17 | 0.24 | 0.947 | 0.17 | 0.24 | 0.944 |
| 10 | 0.19 | 0.26 | 0.936 | 0.17 | 0.23 | 0.949 | 0.18 | 0.23 | 0.949 | 0.18 | 0.24 | 0.945 | 0.18 | 0.25 | 0.944 |
Table 7.
WVC retrieval results using bands 28, 29, 31, and 32.
Table 7.
WVC retrieval results using bands 28, 29, 31, and 32.
| 4BTs (from 28, 29, 31, 32) → WVC |
|---|
| | Nodes | 400 | 500 | 600 | 700 | 800 |
|---|
| Layers | | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 |
|---|
| 3 | 0.22 | 0.30 | 0.918 | 0.21 | 0.29 | 0.924 | 0.20 | 0.28 | 0.927 | 0.21 | 0.28 | 0.925 | 0.21 | 0.28 | 0.927 |
| 4 | 0.21 | 0.28 | 0.926 | 0.22 | 0.29 | 0.921 | 0.21 | 0.28 | 0.926 | 0.20 | 0.28 | 0.929 | 0.20 | 0.28 | 0.927 |
| 5 | 0.20 | 0.28 | 0.928 | 0.22 | 0.29 | 0.921 | 0.20 | 0.27 | 0.930 | 0.20 | 0.28 | 0.929 | 0.21 | 0.28 | 0.925 |
| 6 | 0.21 | 0.28 | 0.926 | 0.20 | 0.28 | 0.928 | 0.20 | 0.28 | 0.927 | 0.20 | 0.28 | 0.929 | 0.21 | 0.30 | 0.917 |
| 7 | 0.20 | 0.27 | 0.931 | 0.21 | 0.29 | 0.924 | 0.20 | 0.28 | 0.928 | 0.20 | 0.27 | 0.931 | 0.21 | 0.28 | 0.926 |
| 8 | 0.25 | 0.33 | 0.896 | 0.20 | 0.28 | 0.927 | 0.21 | 0.29 | 0.923 | 0.21 | 0.28 | 0.926 | 0.21 | 0.28 | 0.926 |
| 9 | 0.22 | 0.29 | 0.920 | 0.20 | 0.28 | 0.928 | 0.23 | 0.32 | 0.907 | 0.21 | 0.28 | 0.925 | 0.21 | 0.28 | 0.925 |
| 10 | 0.21 | 0.28 | 0.926 | 0.21 | 0.28 | 0.928 | 0.21 | 0.28 | 0.928 | 0.22 | 0.29 | 0.921 | 0.20 | 0.27 | 0.930 |
Table 8.
WVC retrieval results using bands 27, 28, 31, and 32.
Table 8.
WVC retrieval results using bands 27, 28, 31, and 32.
| 4BTs (from 27, 28, 31, and 32) → WVC |
|---|
| | Nodes | 400 | 500 | 600 | 700 | 800 |
|---|
| Layers | | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 |
|---|
| 3 | 0.12 | 0.17 | 0.974 | 0.08 | 0.14 | 0.981 | 0.08 | 0.11 | 0.989 | 0.06 | 0.08 | 0.994 | 0.06 | 0.13 | 0.985 |
| 4 | 0.09 | 0.14 | 0.979 | 0.08 | 0.21 | 0.974 | 0.09 | 0.34 | 0.966 | 0.07 | 0.18 | 0.973 | 0.05 | 0.22 | 0.980 |
| 5 | 0.14 | 0.31 | 0.952 | 0.05 | 0.07 | 0.962 | 0.06 | 0.17 | 0.940 | 0.07 | 0.14 | 0.979 | 0.06 | 0.14 | 0.974 |
| 6 | 0.06 | 0.09 | 0.918 | 0.06 | 0.08 | 0.997 | 0.08 | 0.41 | 0.915 | 0.05 | 0.10 | 0.986 | 0.07 | 0.22 | 0.976 |
| 7 | 0.10 | 0.53 | 0.821 | 0.07 | 0.21 | 0.967 | 0.06 | 0.15 | 0.953 | 0.05 | 0.10 | 0.989 | 0.18 | 1.33 | 0.450 |
| 8 | 0.07 | 0.18 | 0.888 | 0.18 | 1.17 | 0.413 | 0.08 | 0.31 | 0.946 | 0.06 | 0.16 | 0.984 | 0.11 | 0.60 | 0.548 |
| 9 | 0.09 | 0.24 | 0.974 | 0.08 | 0.22 | 0.420 | 0.06 | 0.15 | 0.951 | 0.18 | 1.07 | 0.472 | 0.07 | 0.15 | 0.814 |
| 10 | 0.05 | 0.07 | 0.947 | 0.10 | 0.28 | 0.936 | 0.07 | 0.18 | 0.986 | 0.05 | 0.07 | 0.513 | 0.05 | 0.18 | 0.978 |