Differences Evaluation among Three Global Remote Sensing SDL Products
Abstract
1. Introduction
2. SDL Products and Evaluation Methods
2.1. SDL Products
2.1.1. CERES-SYN
2.1.2. ECMWF-SRB
2.1.3. GEWEX-SRB
2.2. Evaluation Methods
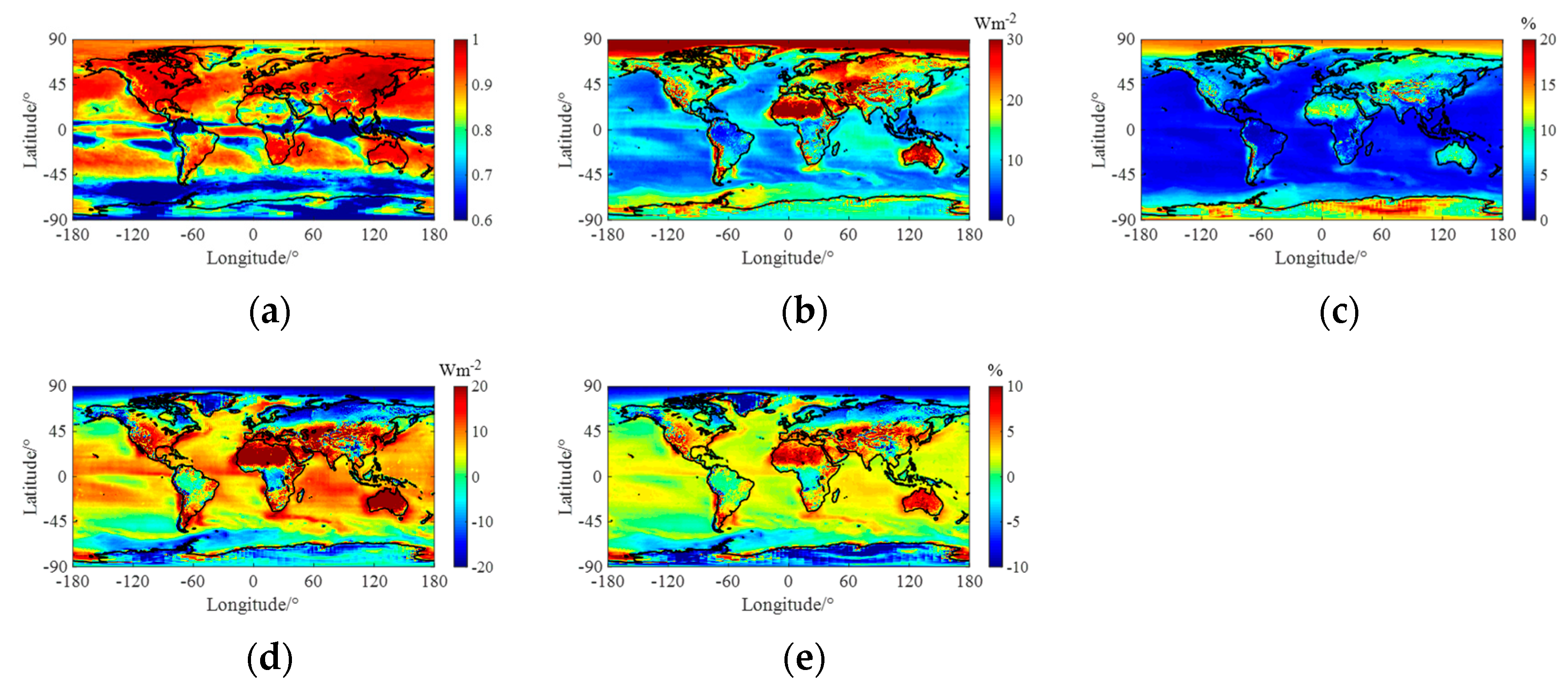
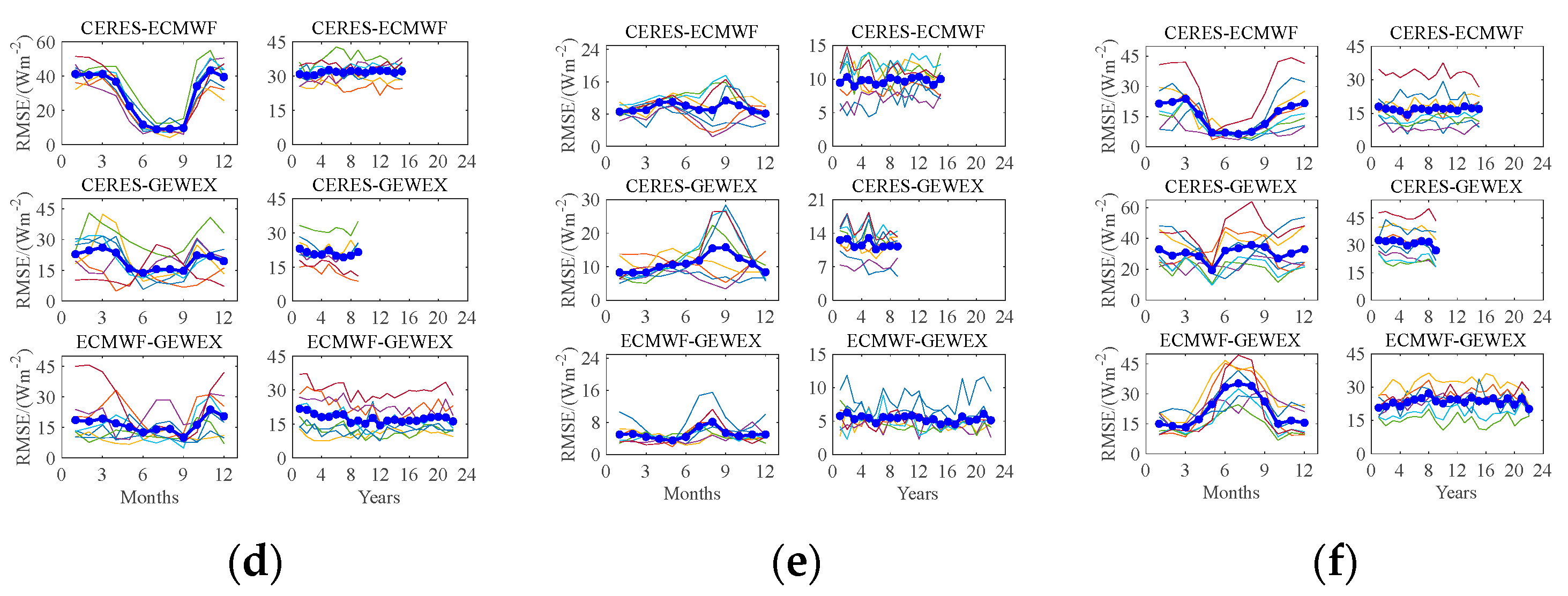
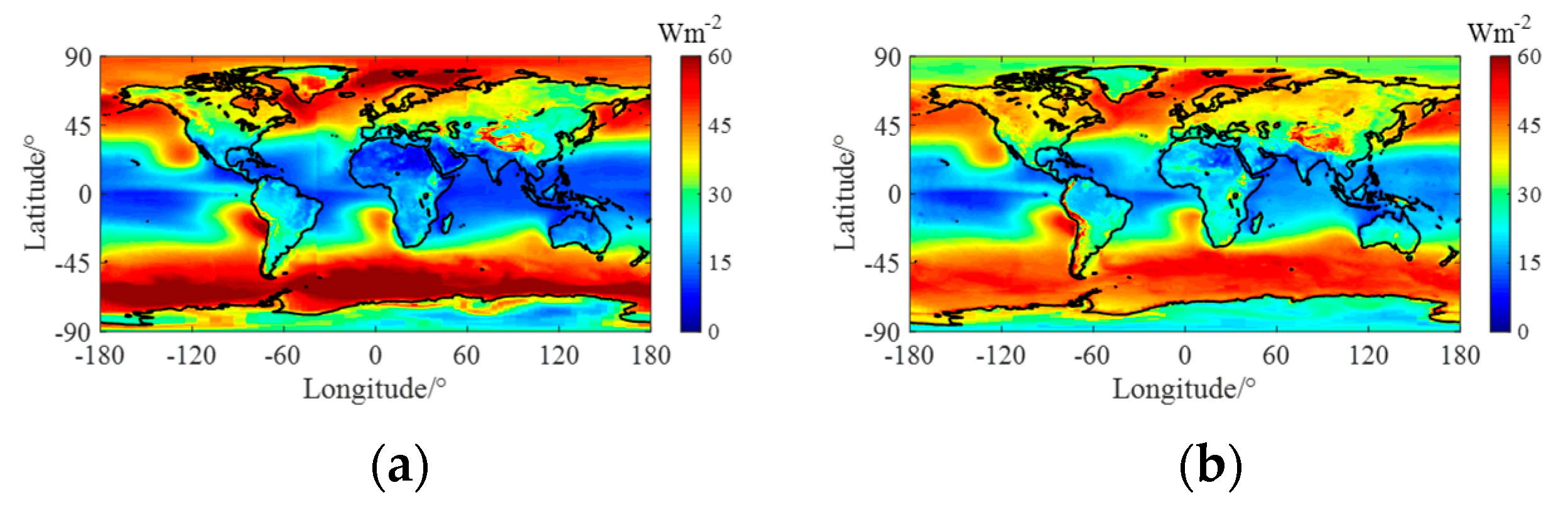
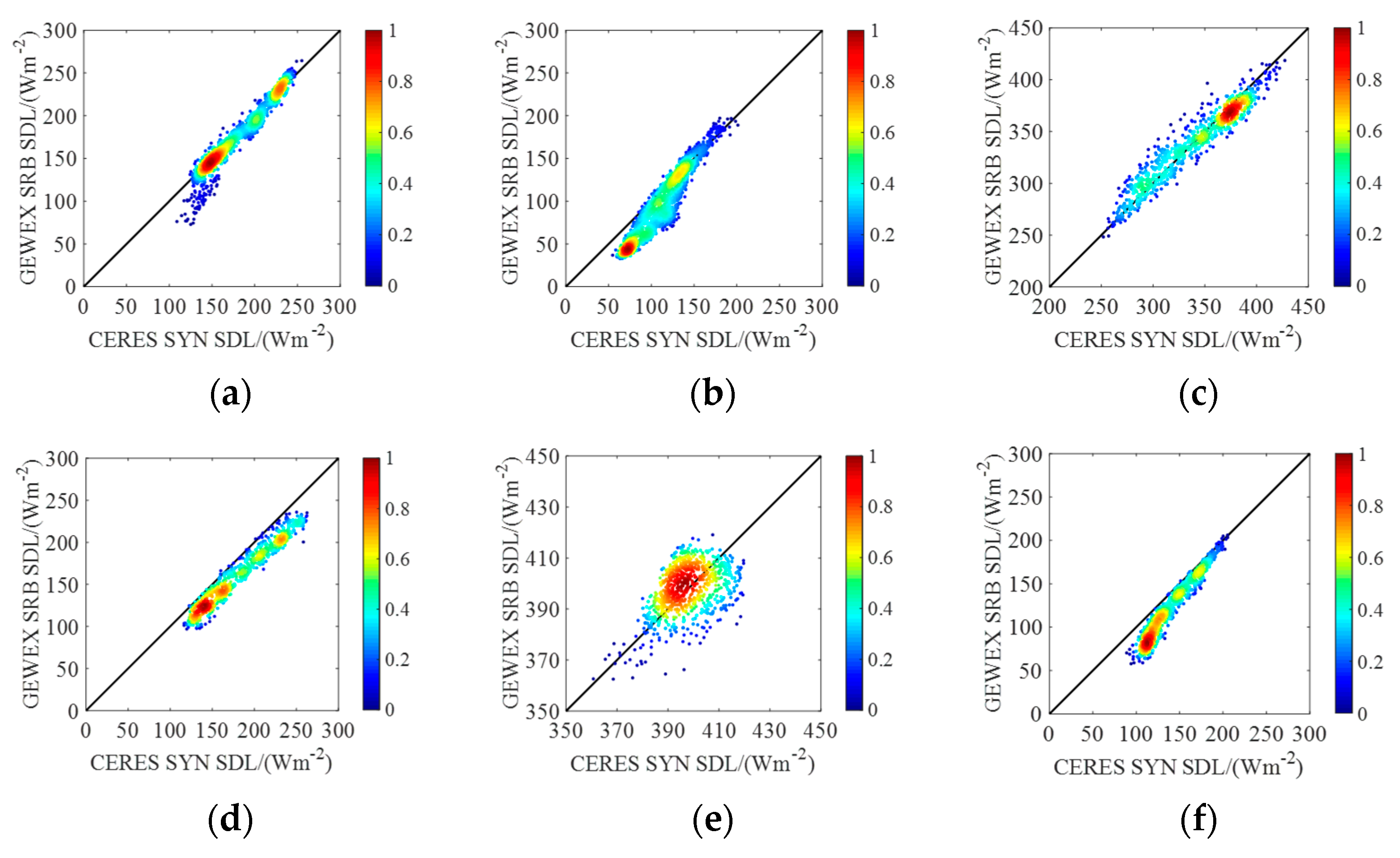
3. Differences Results
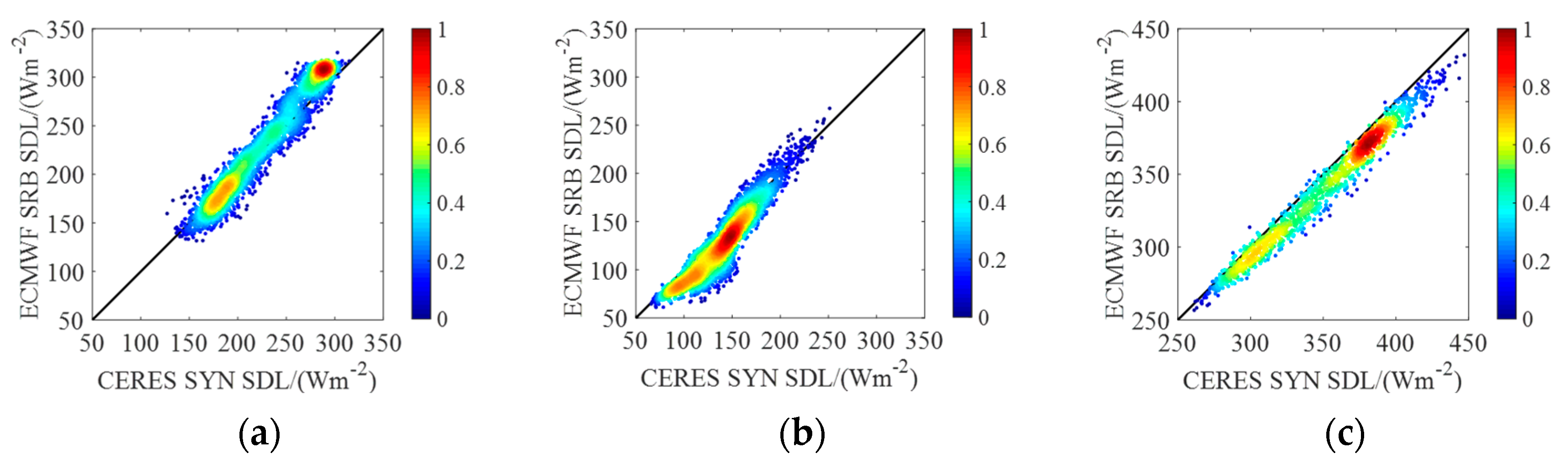
3.1. CERES-SYN vs. ECMWF-SRB
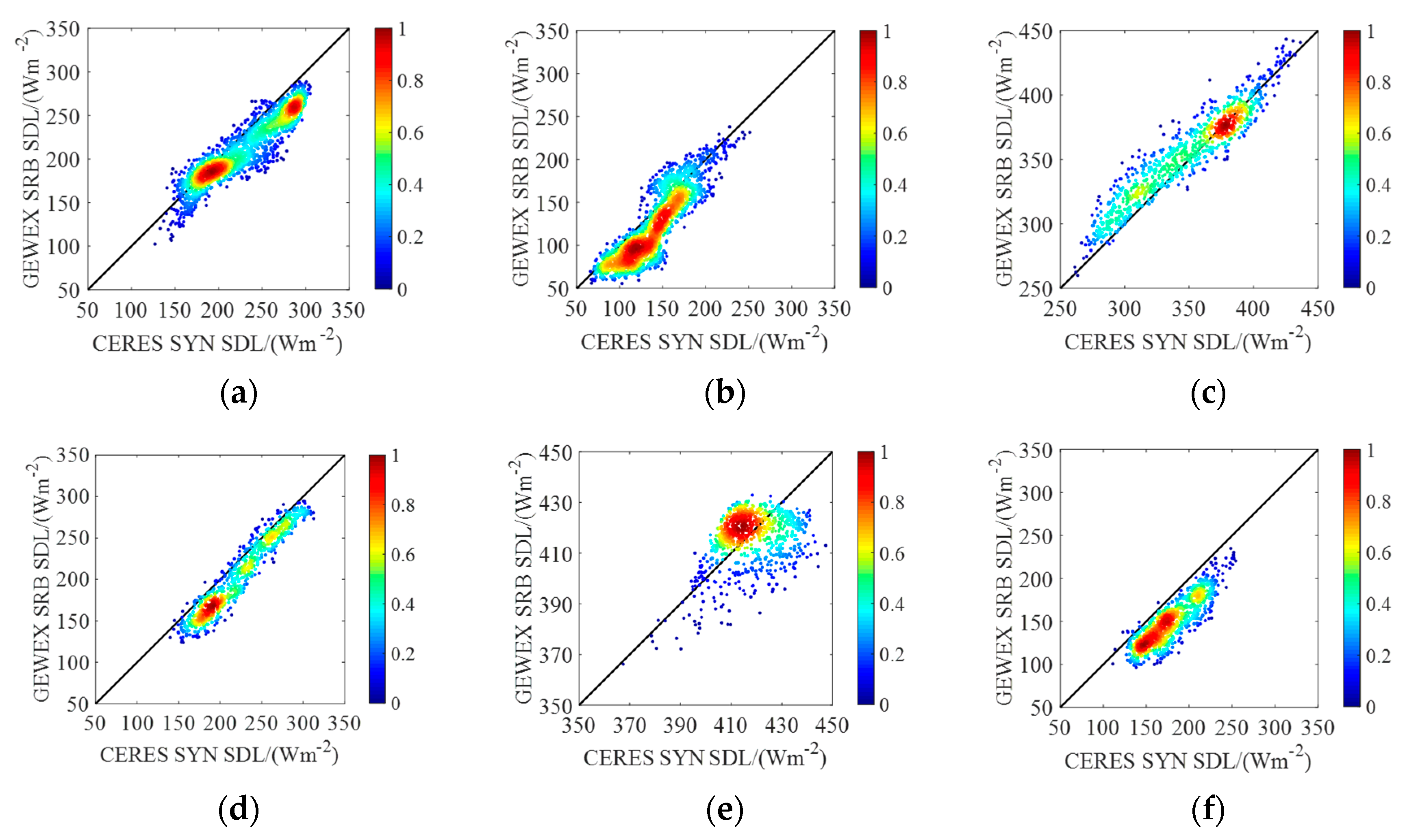
3.2. CERES-SYN vs. GEWEX-SRB
3.3. ECMWF-SRB vs. GEWEX-SRB
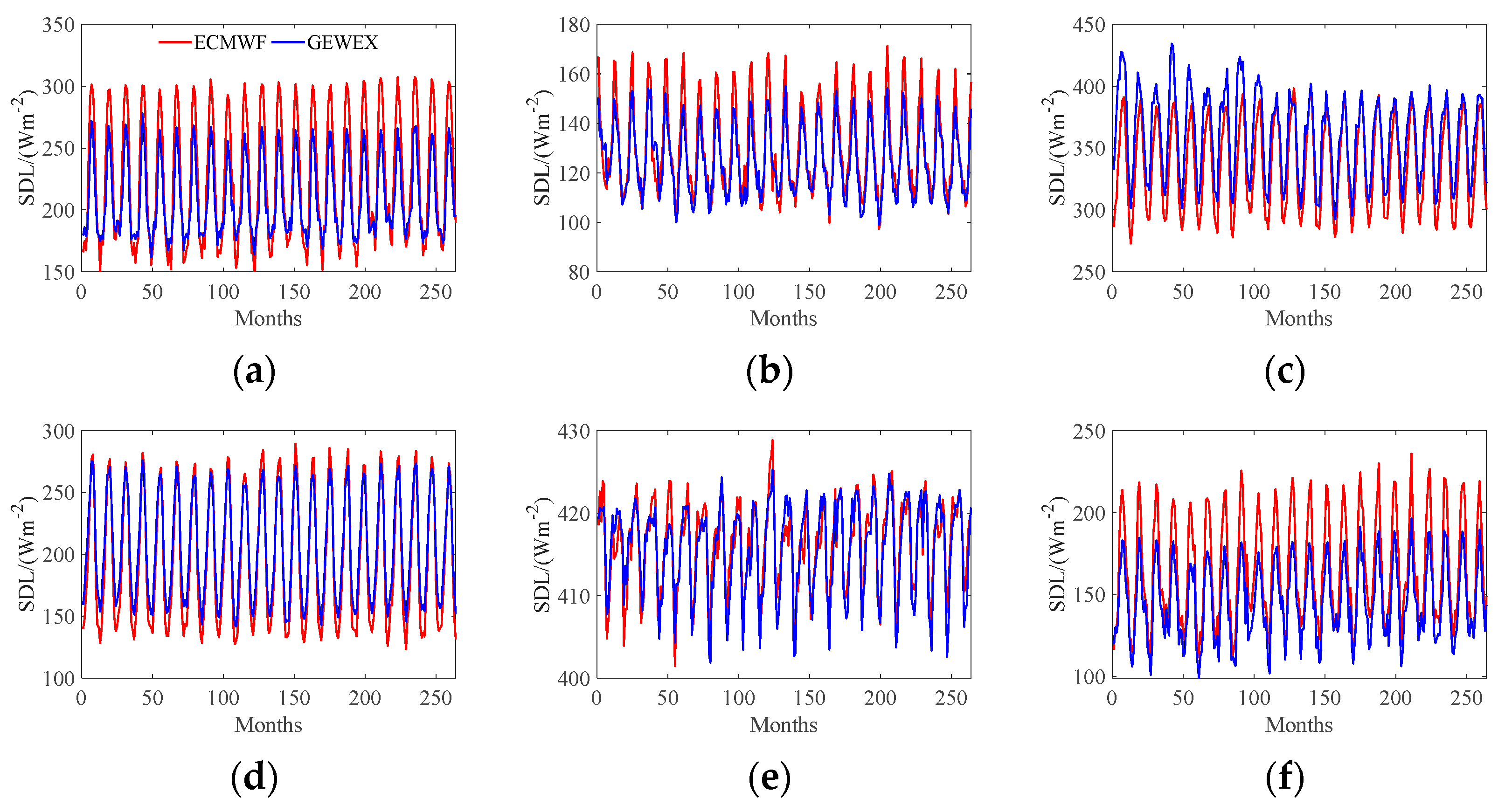
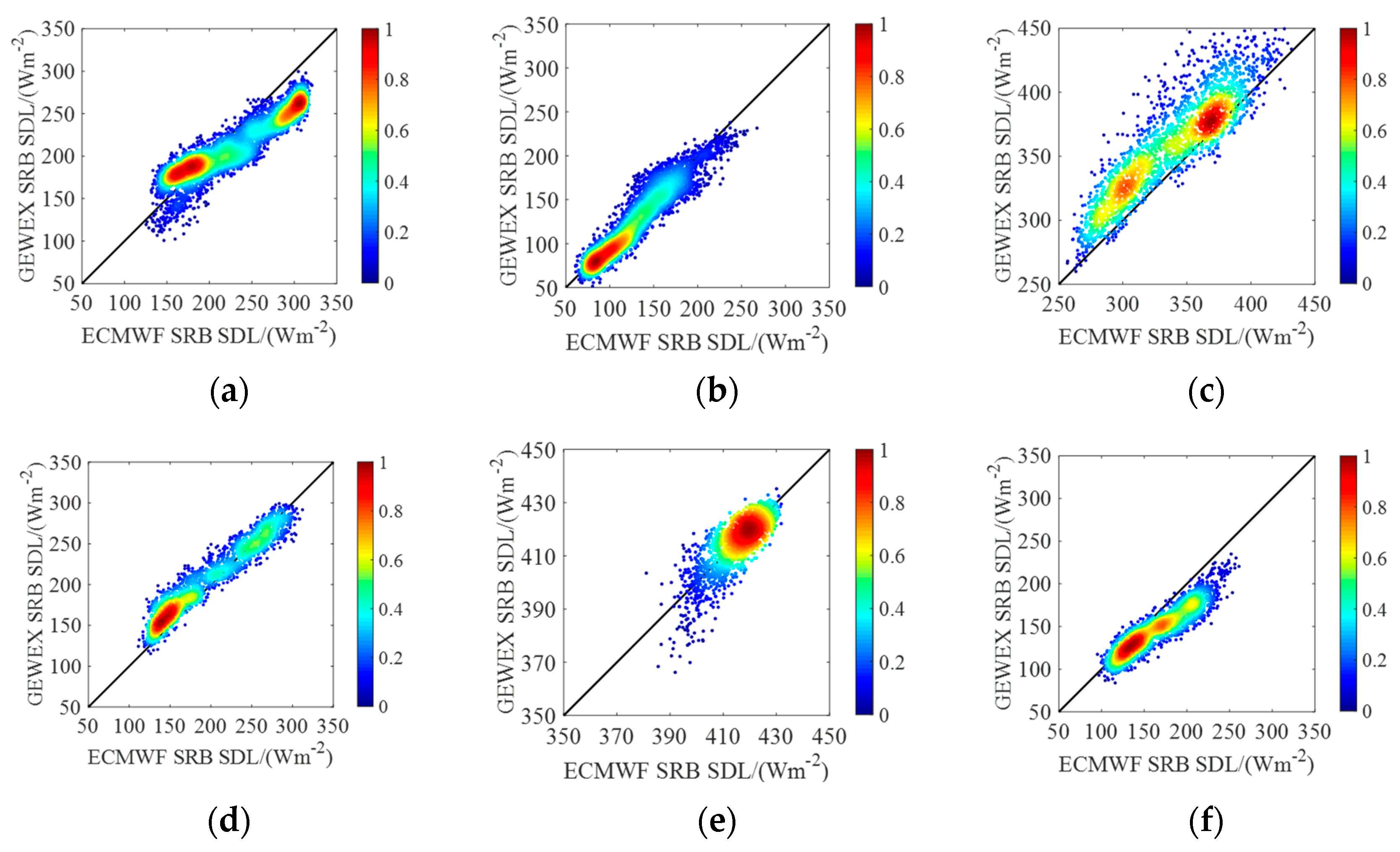
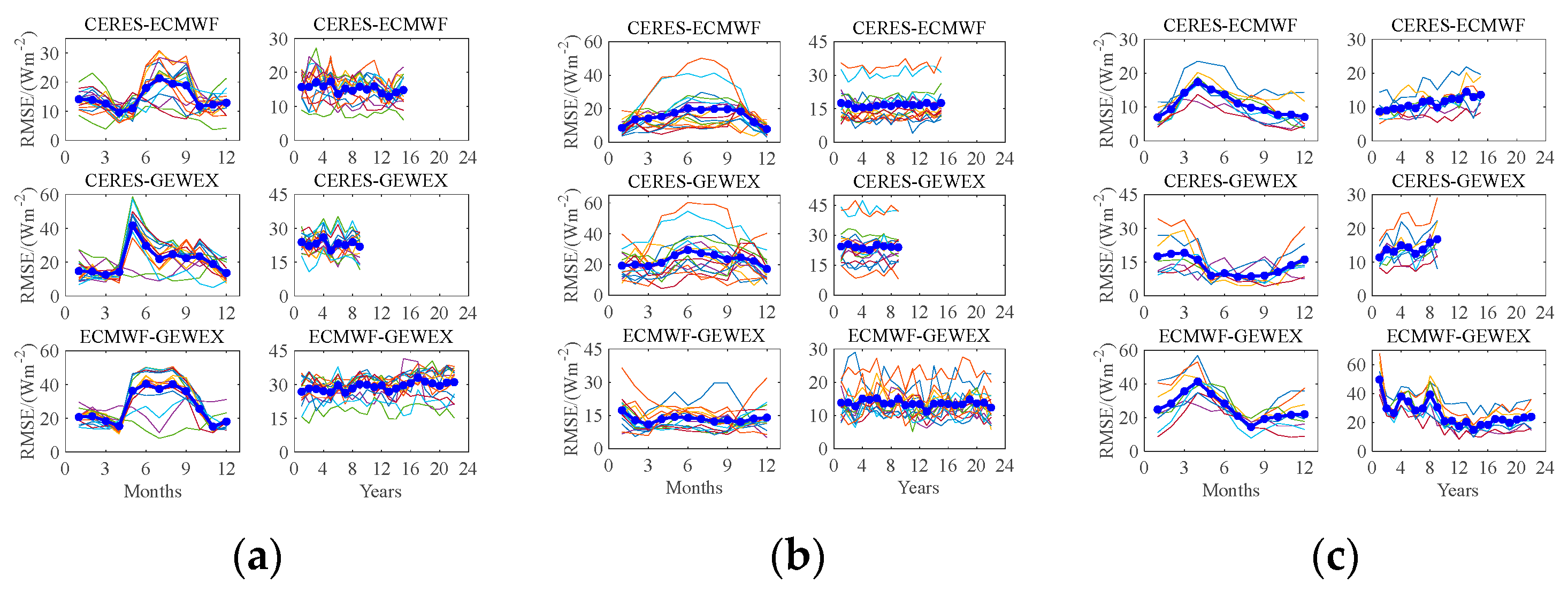
4. Experiment Results
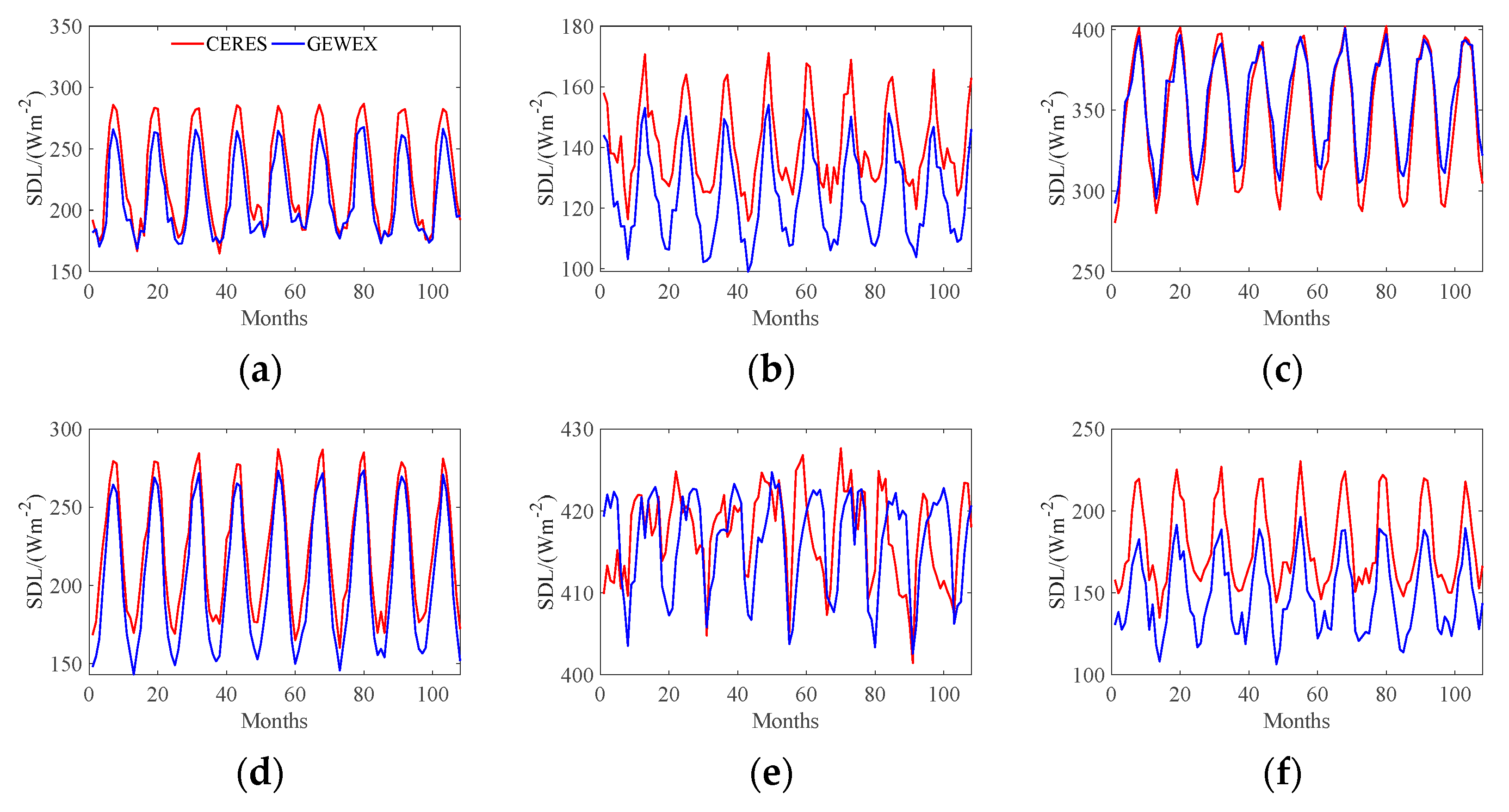
4.1. Time Series Analysis
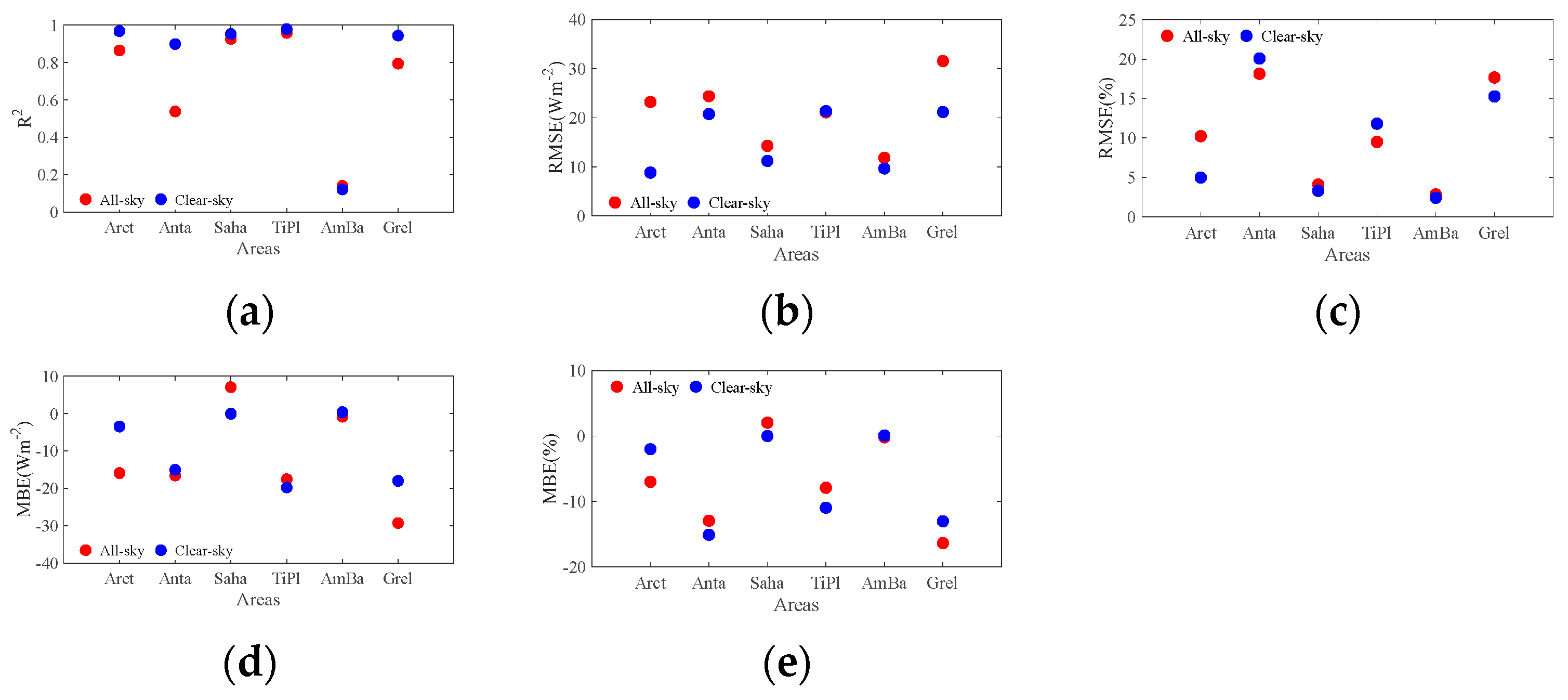
4.2. Impact of Clouds
4.3. Impact of Data Process
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Z.; Gebremichael, M.; Wang, Q.; Wang, J.; Sammis, T.W.; Nickless, A. Evaluation of Clear-Sky Incoming Radiation Estimating Equations Typically Used in Remote Sensing Evapotranspiration Algorithms. Remote Sens. 2013, 5, 4735–4752. [Google Scholar] [CrossRef]
- Ma, Y.; Yao, T.; Ishikawa, H.; Koike, T. Study of Land Surface Heat Fluxes and Water Cycle over the Tibetan Plateau. Dev. Earth Surf. Process. 2007, 10, 313–328. [Google Scholar]
- McDonald, K.R.; Enloe, Y.; Di, L.; Holloway, D. Data Integration Support to the Coordinated Enhanced Observing Period Project (CEOP). In Standard-Based Data and Information Systems for Earth Observation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 27–36. [Google Scholar]
- Zhang, H.; Dong, X.; Xi, B.; Xin, X.; Liu, Q.; He, H.; Xie, X.; Li, L.; Yu, S. Retrieving High-Resolution Surface Photosynthetically Active Radiation from the MODIS and GOES-16 ABI Data. Remote Sens. Environ. 2021, 260, 112436. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, X.; Wei, Y.; Zhang, W.; Hou, N.; Xu, J.; Yang, S.; Xie, X.; Jiang, B. Estimation of Long-Term Surface Downward Longwave Radiation over the Global Land from 2000 to 2018. Remote Sens. 2021, 13, 1848. [Google Scholar] [CrossRef]
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; König-Langlo, G.; McArthur, B.; Müller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New Precision Radiometry for Climate Research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J.; Zeng, Q. Validation of a Cloud-Base Temperature-Based Single-Layer Cloud Model for Estimating Surface Longwave Downward Radiation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Yu, S.; Li, L.; Cao, B.; Zhang, H.; Zhu, L.; Xin, X.; Liu, Q. Surface Downward Longwave Radiation Estimation from New Generation Geostationary Satellite Data. Atmos. Res. 2022, 276, 106255. [Google Scholar] [CrossRef]
- Wang, C.; Tang, B.-H.; Wu, H.; Tang, R.; Li, Z.-L. Estimation of Downwelling Surface Longwave Radiation under Heavy Dust Aerosol Sky. Remote Sens. 2017, 9, 207. [Google Scholar] [CrossRef]
- Gupta, S.K.; Darnell, W.L.; Wilber, A.C. A Parameterization for Longwave Surface Radiation from Satellite Data: Recent Improvements. J. Appl. Meteorol. Climatol. 1992, 31, 1361–1367. [Google Scholar] [CrossRef]
- Nussbaumer, E.A.; Pinker, R.T. Estimating Surface Long-Wave Radiative Fluxes at Global Scale. Q. J. R. Meteorol. Soc. 2012, 138, 1083–1093. [Google Scholar] [CrossRef]
- Dewitte, S.; Clerbaux, N. Measurement of the Earth Radiation Budget at the Top of the Atmosphere—A Review. Remote Sens. 2017, 9, 1143. [Google Scholar] [CrossRef]
- Lopes, F.M.; Dutra, E.; Trigo, I.F. Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation. Remote Sens. 2022, 14, 1704. [Google Scholar] [CrossRef]
- Cao, Y.; Li, M.; Zhang, Y. Estimating the Clear-Sky Longwave Downward Radiation in the Arctic from FengYun-3D MERSI-2 Data. Remote Sens. 2022, 14, 606. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Stackhouse, P.; Mikovitz, C.; Cox, S.J. An Assessment of Satellite Surface Radiation Products for Highlands with Tibet Instrumental Data. Geophys. Res. Lett. 2006, 33, L22403. [Google Scholar] [CrossRef]
- Gui, S.; Liang, S.; Li, L. Validation of Surface Radiation Data Provided by the CERES over the Tibetan Plateau. In Proceedings of the 2009 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; IEEE: New York, NY, USA, 2009; pp. 1–6. [Google Scholar]
- Gui, S.; Liang, S.; Li, L. Evaluation of Satellite-Estimated Surface Longwave Radiation Using Ground-Based Observations. J. Geophys. Res. Atmos. 2010, 115, D18214. [Google Scholar] [CrossRef]
- Zhang, T.; Stackhouse Jr, P.W.; Gupta, S.K.; Cox, S.J.; Mikovitz, J.C.; Hinkelman, L.M. The Validation of the GEWEX SRB Surface Shortwave Flux Data Products Using BSRN Measurements: A Systematic Quality Control, Production and Application Approach. J. Quant. Spectrosc. Radiat. Transf. 2013, 122, 127–140. [Google Scholar] [CrossRef]
- Gui, S.; Liang, S.; Wang, K.; Li, L.; Zhang, X. Assessment of Three Satellite-Estimated Land Surface Downwelling Shortwave Irradiance Data Sets. IEEE Geosci. Remote Sens. Lett. 2010, 7, 776–780. [Google Scholar] [CrossRef]
- Yan, H.; Huang, J.; Minnis, P.; Wang, T.; Bi, J. Comparison of CERES Surface Radiation Fluxes with Surface Observations over Loess Plateau. Remote Sens. Environ. 2011, 115, 1489–1500. [Google Scholar] [CrossRef]
- Sun, D.; Ji, C.; Sun, W.; Yang, Y.; Wang, H. Accuracy Assessment of Three Remote Sensing Shortwave Radiation Products in the Arctic. Atmos. Res. 2018, 212, 296–308. [Google Scholar] [CrossRef]
- Kratz, D.P.; Gupta, S.K.; Wilber, A.C.; Sothcott, V.E. Validation of the CERES Edition-4A Surface-Only Flux Algorithms. J. Appl. Meteorol. Climatol. 2020, 59, 281–295. [Google Scholar] [CrossRef]
- Mikovitz, J.C.; Stackhouse Jr, P.W.; Gupta, S.K.; Zhang, T.; Cox, S.J.; Doelling, D.R.; Keyes, D.F.; Hinkelman, L.M. A Comparison of Surface Flux Products from GEWEX Surface Radiation Budget with ECMWF ERA-40, NCEP/NCAR Reanalysis and CERES SRBAVG. In Proceedings of the 12th Conference on Atmospheric Radiation, Madison, WI, USA, 10–14 July 2006; pp. 10–14. [Google Scholar]
- Loeb, N.G.; Manalo-Smith, N.; Su, W.; Shankar, M.; Thomas, S. CERES Top-of-Atmosphere Earth Radiation Budget Climate Data Record: Accounting for in-Orbit Changes in Instrument Calibration. Remote Sens. 2016, 8, 182. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary Enhanced Temporal Interpolation for CERES Flux Products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Rutan, D.A.; Kato, S.; Doelling, D.R.; Rose, F.G.; Nguyen, L.T.; Caldwell, T.E.; Loeb, N.G. CERES Synoptic Product: Methodology and Validation of Surface Radiant Flux. J. Atmos. Ocean. Technol. 2015, 32, 1121–1143. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N. Parameterization of the Radiative Properties of Cirrus Clouds. J. Atmos. Sci. 1993, 50, 2008–2025. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.; Cribb, M.; Charlock, T.; Grossman, A. Multiple Scattering Parameterization in Thermal Infrared Radiative Transfer. J. Atmos. Sci. 1997, 54, 2799–2812. [Google Scholar] [CrossRef]
- Doelling, D.R.; Sun, M.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in Geostationary-Derived Longwave Fluxes for the CERES Synoptic (SYN1deg) Product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Karlsson, K.-G.; Riihelä, A.; Müller, R.; Meirink, J.; Sedlar, J.; Stengel, M.; Lockhoff, M.; Trentmann, J.; Kaspar, F.; Hollmann, R.; et al. CLARA-A1: A Cloud, Albedo, and Radiation Dataset from 28 Yr of Global AVHRR Data. Atmos. Chem. Phys. 2013, 13, 5351–5367. [Google Scholar] [CrossRef]
- Karlsson, K.-G.; Anttila, K.; Trentmann, J.; Stengel, M.; Fokke Meirink, J.; Devasthale, A.; Hanschmann, T.; Kothe, S.; Jääskeläinen, E.; Sedlar, J.; et al. CLARA-A2: The Second Edition of the CM SAF Cloud and Radiation Data Record from 34 Years of Global AVHRR Data. Atmos. Chem. Phys. 2017, 17, 5809–5828. [Google Scholar] [CrossRef]
- Sorooshian, S.; Lawford, R.; Try, P.; Rossow, W.; Roads, J.; Polcher, J.; Sommeria, G.; Schiffer, R. Water and Energy Cycles: Investigating the Links. World Meteorol. Organ. Bull. 2005, 54, 58–64. [Google Scholar]
- Pinker, R.T.; Tarpley, J.D.; Laszlo, I.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Lohmann, D.; Cosgrove, B.A.; et al. Surface Radiation Budgets in Support of the GEWEX Continental-Scale International Project (GCIP) and the GEWEX Americas Prediction Project (GAPP), Including the North American Land Data Assimilation System (NLDAS) Project. J. Geophys. Res. Atmos. 2003, 108, GCP5-1. [Google Scholar] [CrossRef]
- Randall, D.; Krueger, S.; Bretherton, C.; Curry, J.; Duynkerke, P.; Moncrieff, M.; Ryan, B.; Starr, D.; Miller, M.; Rossow, W.; et al. Confronting Models with Data: The GEWEX Cloud Systems Study. Bull. Am. Meteorol. Soc. 2003, 84, 455–469. [Google Scholar] [CrossRef][Green Version]
- Gupta, S.K.; Ritchey, N.A.; Wilber, A.C.; Whitlock, C.H.; Gibson, G.G.; Stackhouse Jr, P.W. A Climatology of Surface Radiation Budget Derived from Satellite Data. J. Clim. 1999, 12, 2691–2710. [Google Scholar] [CrossRef]
- Rossow, W.B.; Schiffer, R.A. Advances in Understanding Clouds from ISCCP. Bull. Am. Meteorol. Soc. 1999, 80, 2261–2288. [Google Scholar] [CrossRef]
- Wilber, A.C. Surface Emissivity Maps for Use in Satellite Retrievals of Longwave Radiation; NASA: Washington, WA, USA, 1999. [Google Scholar]
- Suarez, M.J.; daSilva, A.; Dee, D.; Bloom, S.; Bosilovich, M.; Pawson, S.; Schubert, S.; Wu, M.-L.; Sienkiewicz, M.; Stajner, I. Documentation and Validation of the Goddard Earth Observing System (GEOS) Data Assimilation System, Version 4; NASA: Washington, WA, USA, 2005. [Google Scholar]
- Li, J.; Wang, W.-C.; Chen, G.; You, Q. Characteristics of Top-of-Atmosphere Radiation Budget over the Tibetan Plateau and Its Bias Sources in Climate Models. Atmos. Res. 2022, 276, 106256. [Google Scholar] [CrossRef]
- Xin, X.; Yu, S.; Sun, D.; Zhang, H.; Li, L.; Zhong, B. Assessment of Three Satellite-Derived Surface Downward Longwave Radiation Products in Polar Regions. Atmosphere 2022, 13, 1602. [Google Scholar] [CrossRef]






| SDL Products | Spatial Scale | Spatial Resolution | Temporal Resolution | Versions |
|---|---|---|---|---|
| CERES-SYN | Global | 1° × 1° | Monthly | Edition4 |
| ECMWF-SRB | Global | 0.25° × 0.25° | Monthly | V2.0 |
| GEWEX-SRB | Global | 1° × 1° | Monthly | Release 4 |
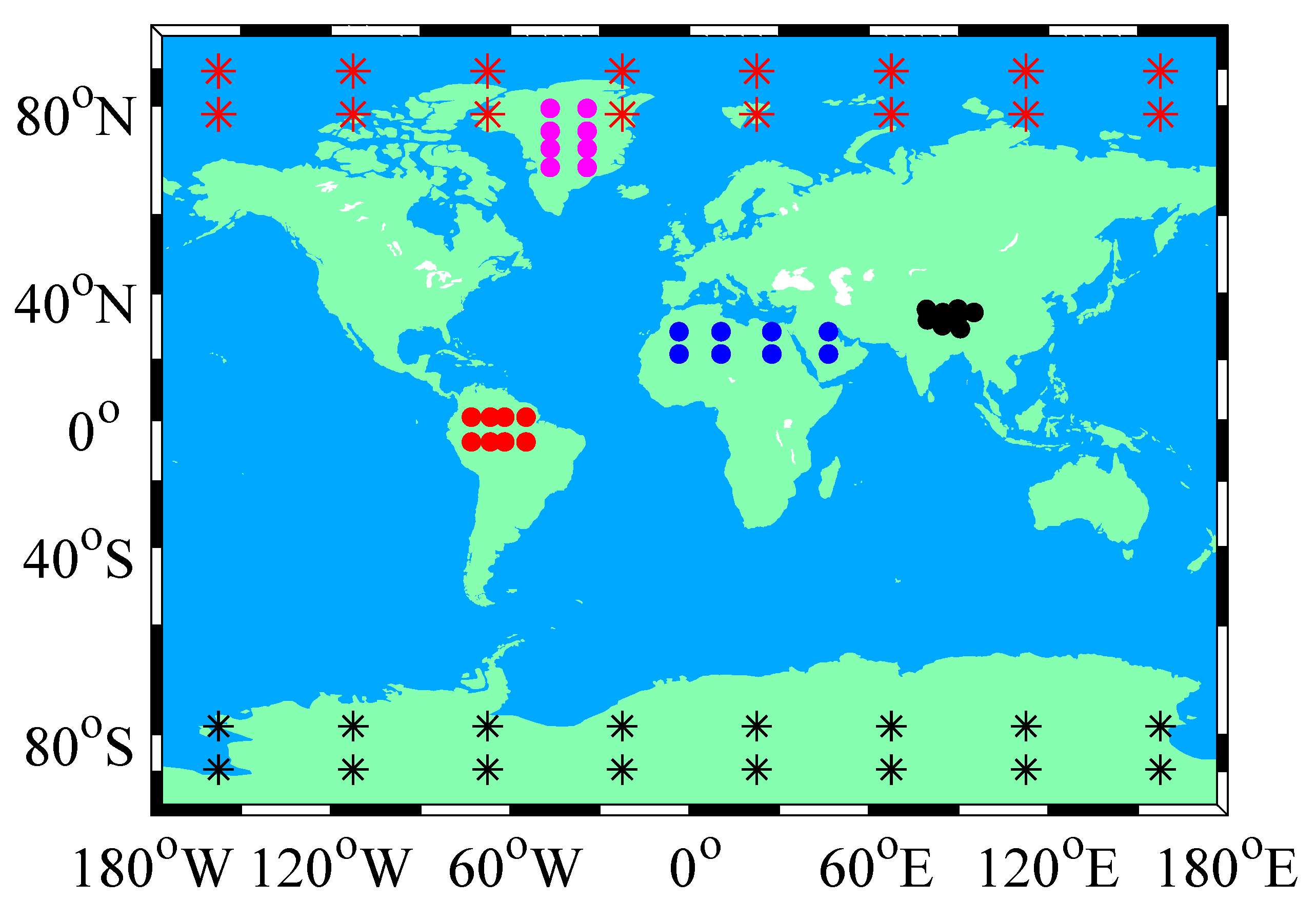
| Area | Symbols | N | Area | Symbols | N | Area | Symbols | N |
|---|---|---|---|---|---|---|---|---|
| Arctic | * (red) | 16 | Sahara | ● (blue) | 8 | Amazon Basin | ● (red) | 8 |
| Antarctic | * (black) | 16 | Tibet Plateau | ● (black) | 8 | Greenland | ● (purple) | 8 |
| Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) | Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) |
|---|---|---|---|---|---|---|---|
| Arctic | 0.94 | 15.48 (6.85) | 4.10 (1.86) | Tibet Plateau | 0.96 | 31.85 (14.30) | −26.39 (−11.82) |
| Antarctic | 0.74 | 16.81 (12.42) | −11.34 (−8.74) | Amazon Basin | 0.17 | 9.85 (2.37) | 2.66 (0.65) |
| Sahara | 0.98 | 11.47 (3.28) | −9.78 (−2.79) | Greenland | 0.88 | 17.04 (9.56) | −11.09 (−6.24) |
| Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) | Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) |
|---|---|---|---|---|---|---|---|
| Arctic | 0.86 | 23.20 (10.22) | −15.91 (−7.01) | Tibet Plateau | 0.96 | 21.08 (9.50) | −17.57 (−7.90) |
| Antarctic | 0.54 | 24.37 (18.12) | −16.59 (−12.95) | Amazon Basin | 0.14 | 11.84 (2.83) | −0.86 (−0.19) |
| Sahara | 0.93 | 14.26 (4.10) | 7.03 (2.03) | Greenland | 0.79 | 31.56 (17.66) | −29.29 (−16.37) |
| Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) | Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) |
|---|---|---|---|---|---|---|---|
| Arctic | 0.89 | 29.27 (13.03) | −15.29 (−6.84) | Tibet Plateau | 0.96 | 17.78 (8.98) | 8.93 (4.47) |
| Antarctic | 0.70 | 13.90 (10.99) | −4.51 (−4.23) | Amazon Basin | 0.62 | 5.53 (1.33) | −0.43 (−0.10) |
| Sahara | 0.80 | 27.36 (8.09) | 21.25 (6.28) | Greenland | 0.85 | 23.68 (14.42) | −18.09 (−10.93) |
| Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) | Area | R2 | RMSEab (RMSEre) | MBEab (MBEre) |
|---|---|---|---|---|---|---|---|
| Arctic | 0.97 | 8.85 (4.98) | −3.48 (−2.00) | Tibet Plateau | 0.98 | 21.36 (11.81) | −19.80 (−10.96) |
| Antarctic | 0.90 | 20.73 (20.06) | −15.05 (−15.10) | Amazon Basin | 0.12 | 9.65 (2.42) | 0.35 (0.10) |
| Sahara | 0.95 | 11.20 (3.29) | −0.07 (−0.01) | Greenland | 0.94 | 21.18 (15.28) | −18.01 (−13.01) |
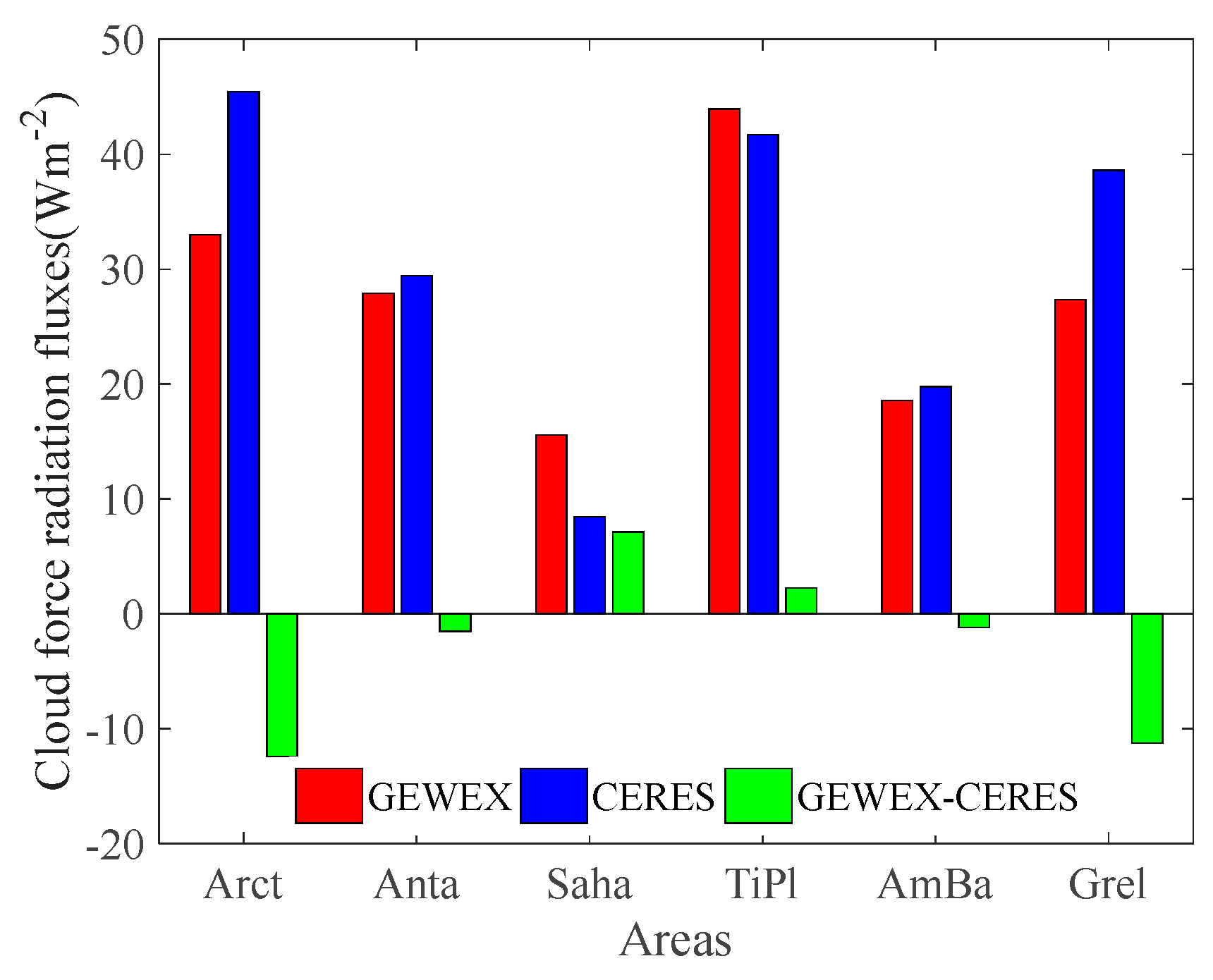
| Area | GE_F | CE_F | ΔF | Area | GE_F | CE_F | ΔF |
|---|---|---|---|---|---|---|---|
| Arctic | 33.00 | 45.43 | −12.43 | Tibet Plateau | 43.94 | 41.71 | 2.23 |
| Antarctic | 27.87 | 29.41 | −1.54 | Amazon Basin | 18.55 | 19.76 | −1.21 |
| Sahara | 15.54 | 8.44 | 7.10 | Greenland | 27.33 | 38.61 | −11.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Liu, G.; Zhang, R. Differences Evaluation among Three Global Remote Sensing SDL Products. Remote Sens. 2023, 15, 4244. https://doi.org/10.3390/rs15174244
Yu L, Liu G, Zhang R. Differences Evaluation among Three Global Remote Sensing SDL Products. Remote Sensing. 2023; 15(17):4244. https://doi.org/10.3390/rs15174244
Chicago/Turabian StyleYu, Laibo, Guoxiang Liu, and Rui Zhang. 2023. "Differences Evaluation among Three Global Remote Sensing SDL Products" Remote Sensing 15, no. 17: 4244. https://doi.org/10.3390/rs15174244
APA StyleYu, L., Liu, G., & Zhang, R. (2023). Differences Evaluation among Three Global Remote Sensing SDL Products. Remote Sensing, 15(17), 4244. https://doi.org/10.3390/rs15174244







