CE-RX: A Collaborative Cloud-Edge Anomaly Detection Approach for Hyperspectral Images
Abstract
1. Introduction
- We propose an algorithm called Cloud–Edge RX (CE-RX). This algorithm uses a new cloud–edge collaboration framework and takes full advantage of the characteristics of cloud and edge to improve detection accuracy at the edge.
- We introduce an edge-updating algorithm. This algorithm reduces the time spent updating data at the edge and the time of data transmission between the cloud and the edge.
- Following the proposed cloud–edge collaboration framework, we design a new computation latency model. By using this proposed computation latency model, we can further analyze which variables affect the real-time performance of the proposed CE-RX algorithm.
2. Related Work
2.1. RX Algorithm
2.2. CLP-RX Algorithm
2.3. Local-RX Algorithm
3. Proposed Algorithm
3.1. Cloud–Edge Collaboration Framework
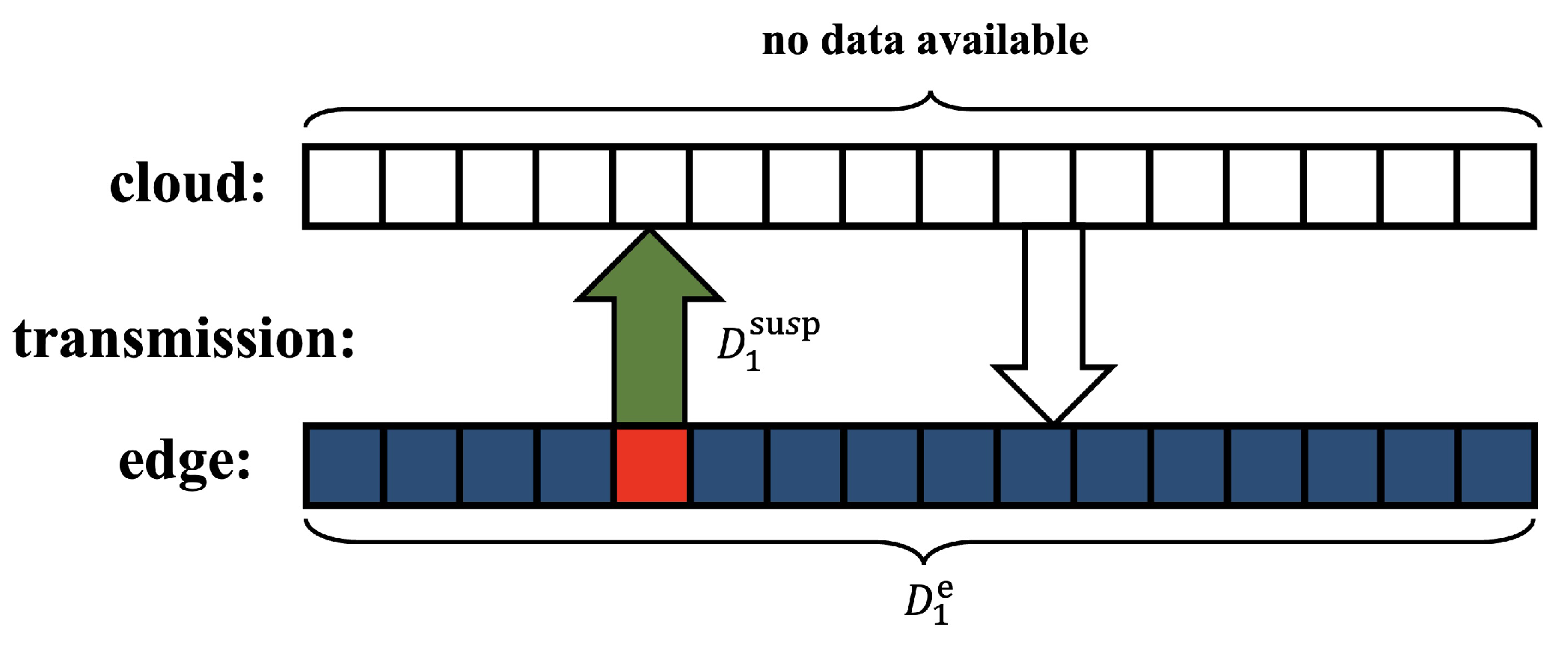
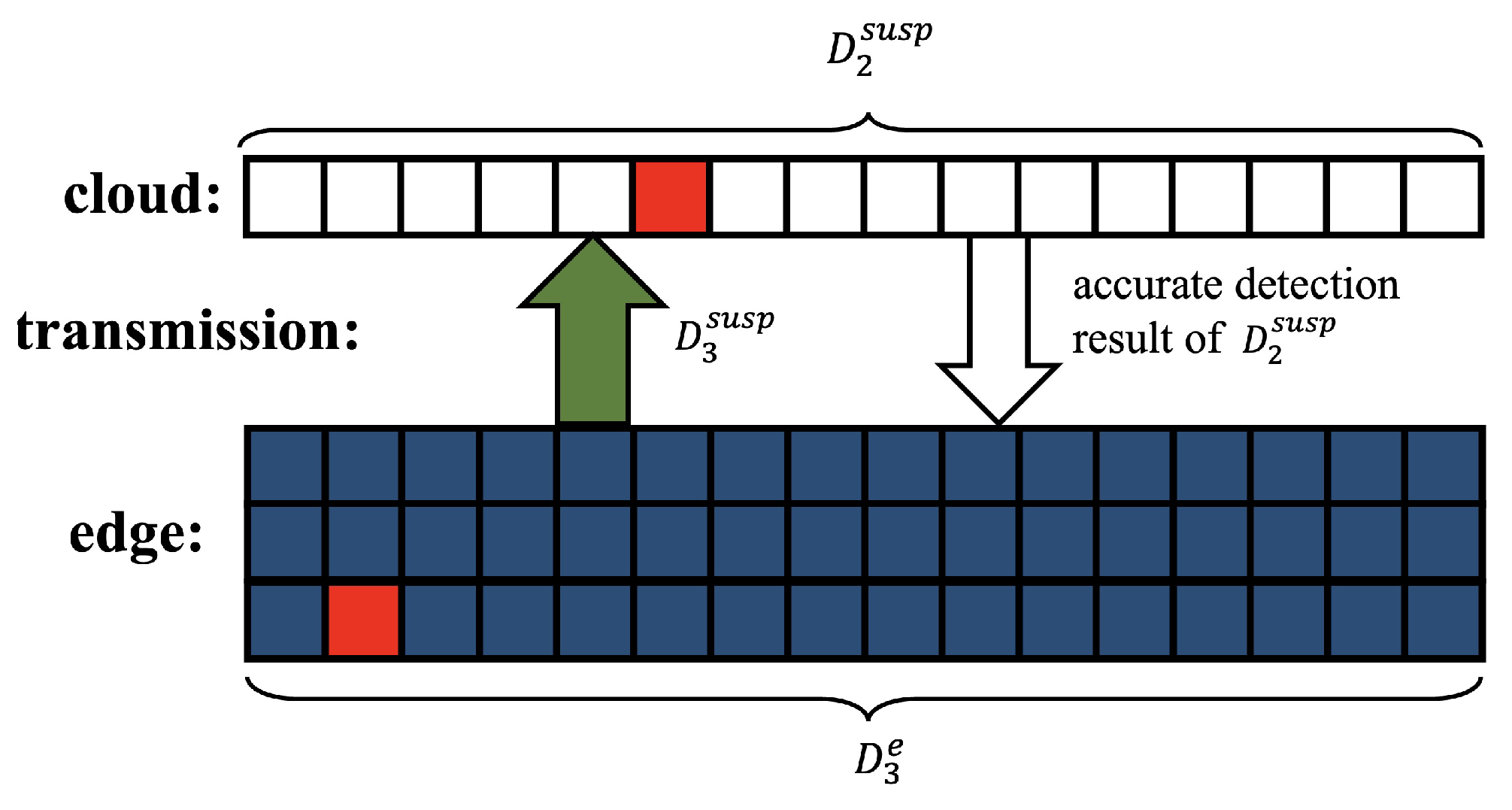
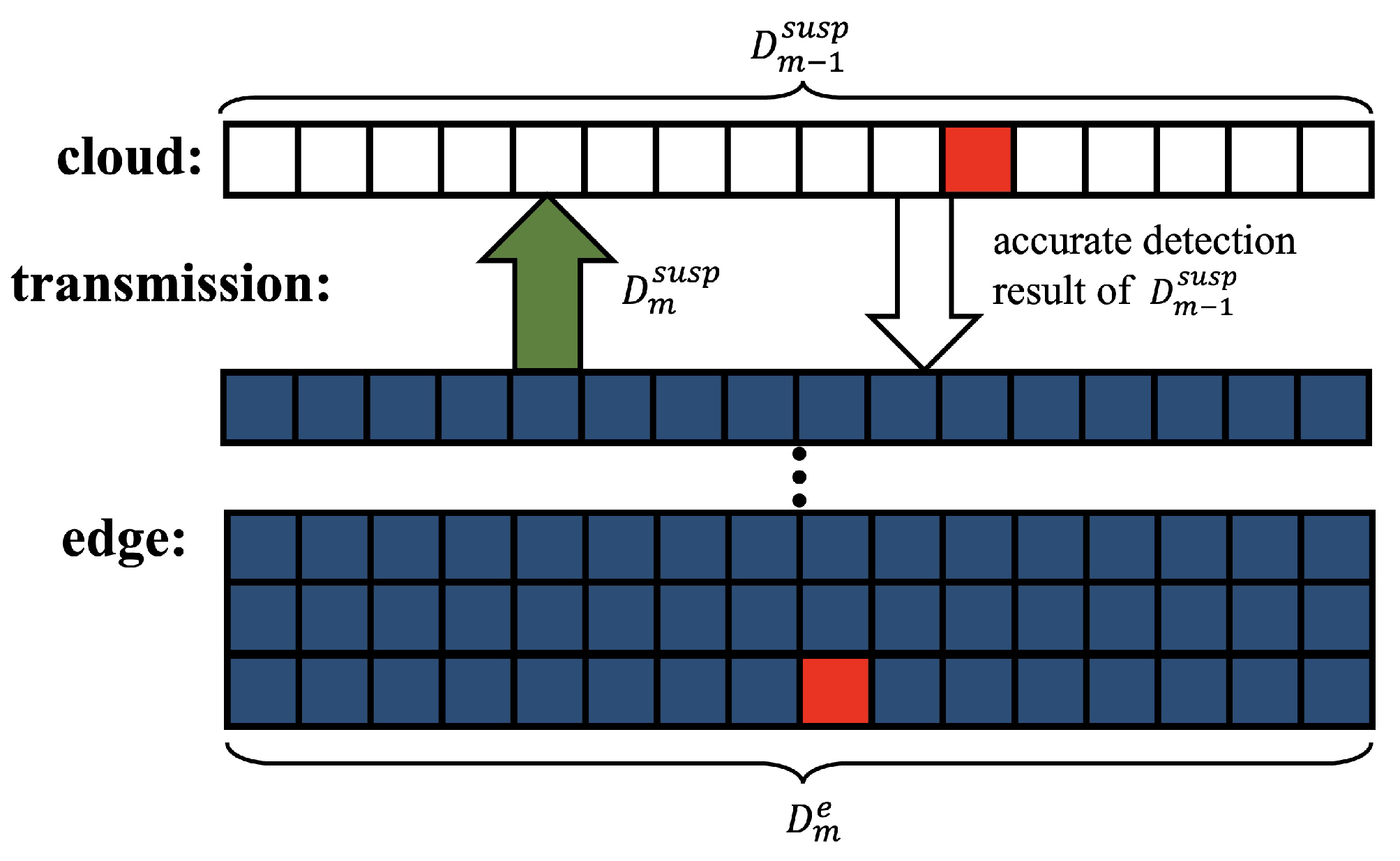
3.2. Edge Updating Algorithm
| Algorithm 1: Edge updating algorithm |
 |
| Algorithm 2: CE-RX algorithm |
 |
4. Time Latency Analysis of the Proposed Cloud–Edge Model
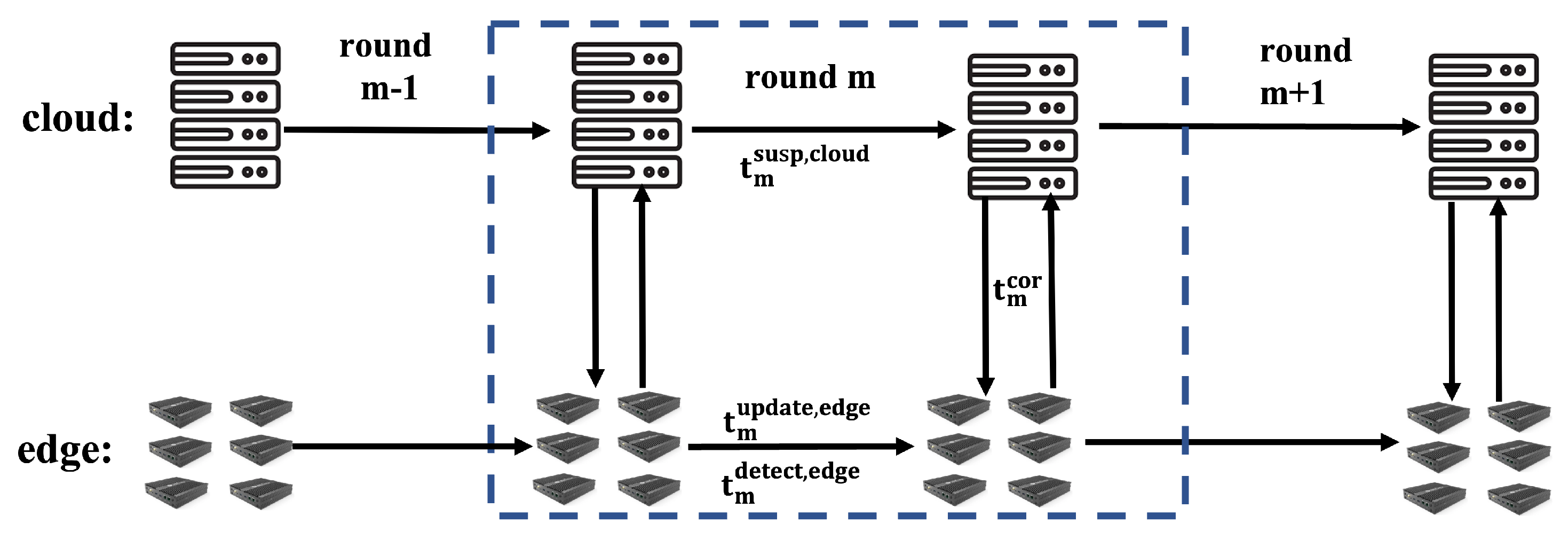
4.1. Computing Latency Model for the Cloud and for the Edge
4.2. System Latency Model
5. Experimental Results
5.1. Dataset Description
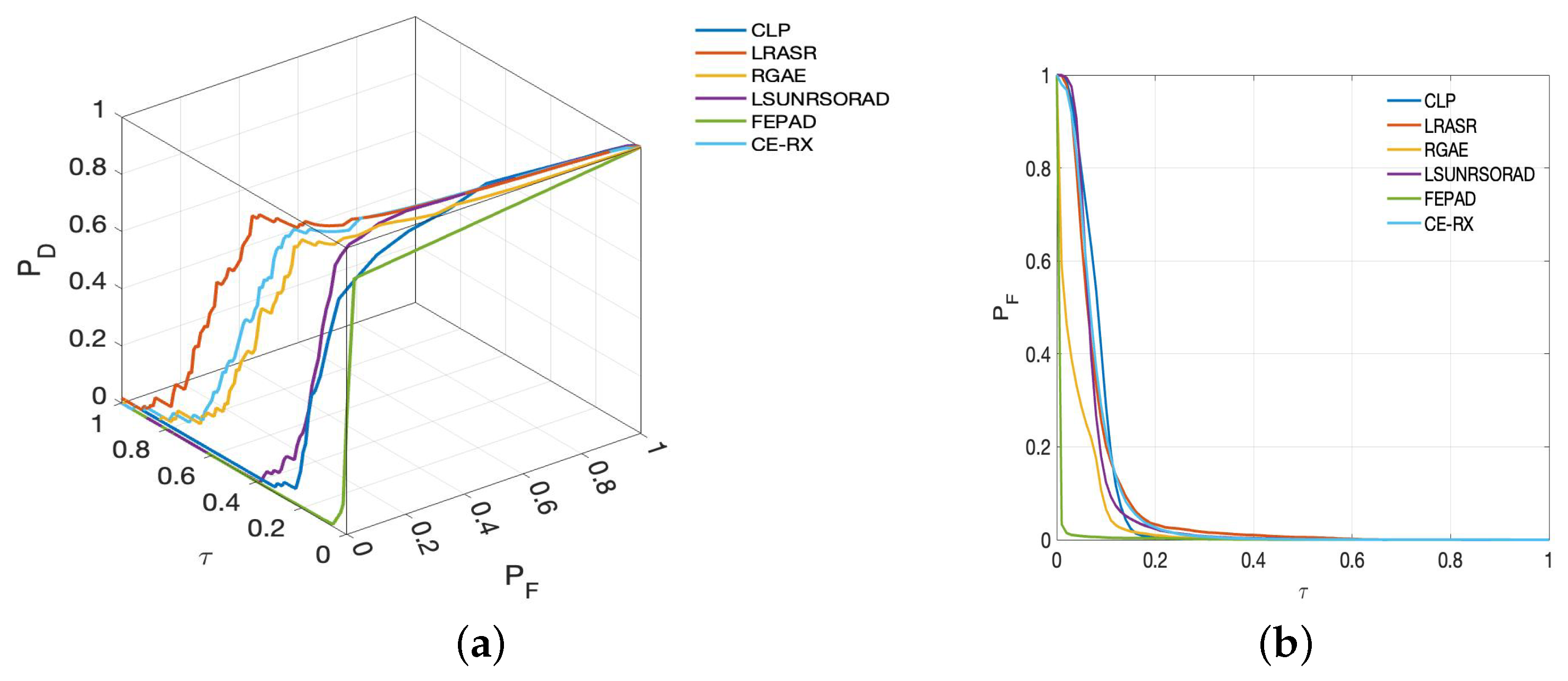
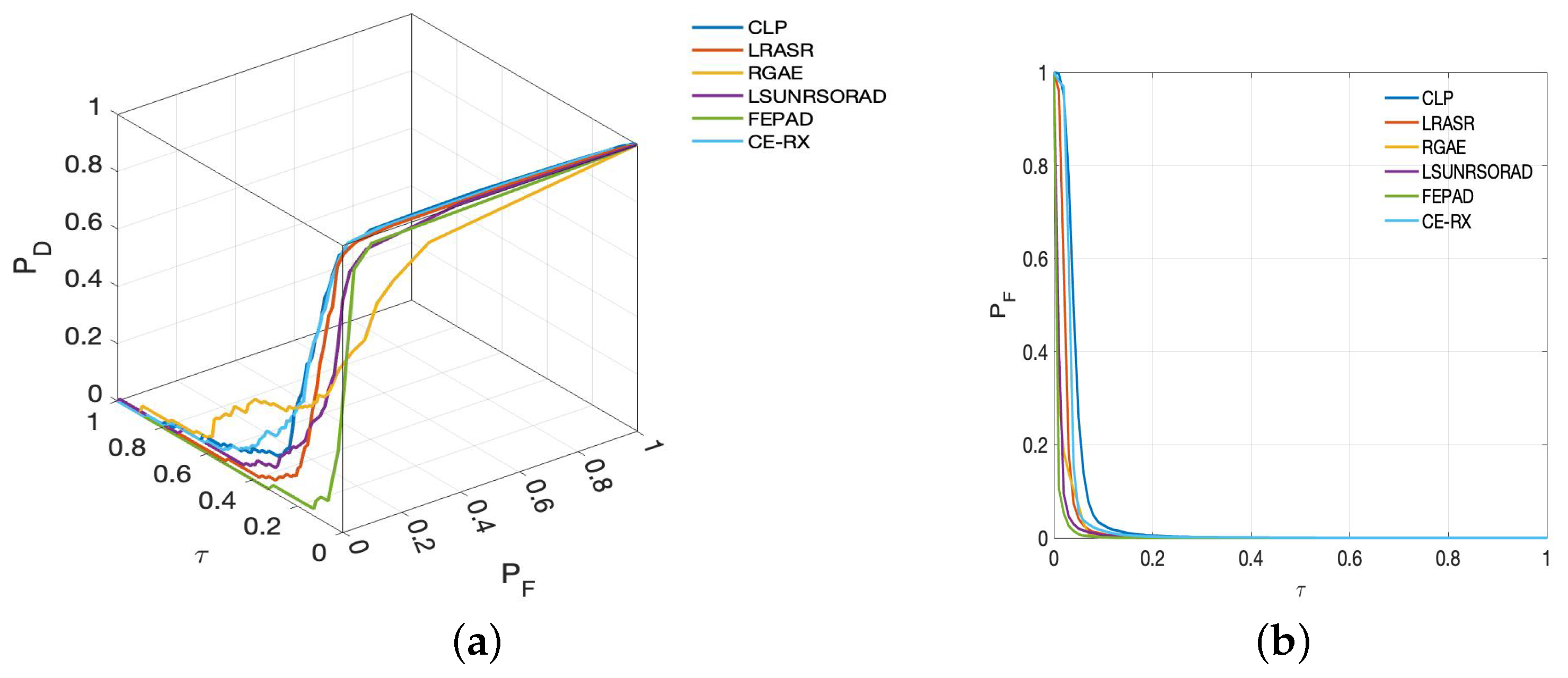
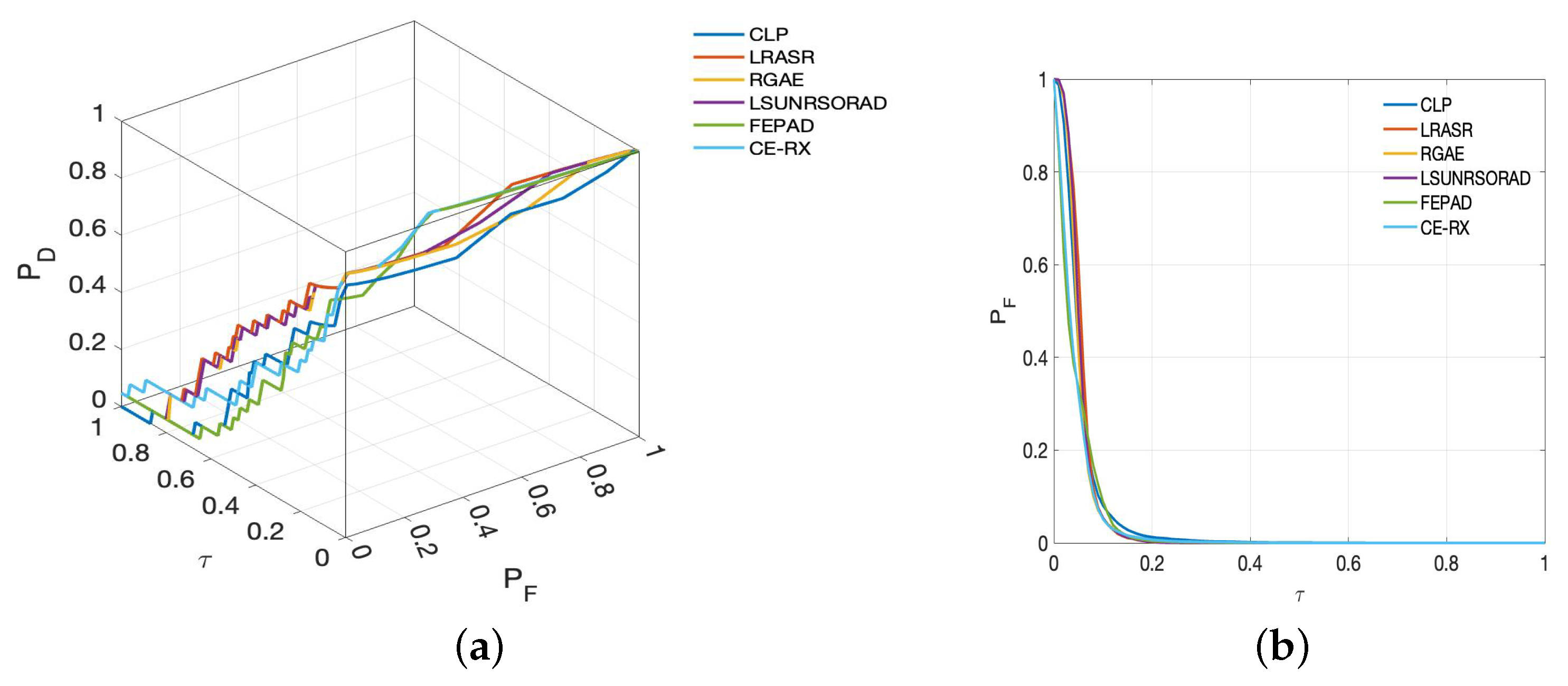
5.2. Detection Performance
5.3. Real-time Performance Analysis of Proposed Algorithms
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Sun, X.; Gao, L.; Yang, L. Endmember Extraction of Hyperspectral Remote Sensing Images Based on the Ant Colony Optimization (ACO) Algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2635–2646. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Zhang, W.; Gao, L.; Li, J.; Wang, J.; Li, X. Analysis of the proportion of surface reflected radiance in mid-infrared absorption bands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 2639–2646. [Google Scholar] [CrossRef]
- Gao, L.; Du, Q.; Zhang, B.; Yang, W.; Wu, Y. A Comparative Study on Linear Regression-Based Noise Estimation for Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 488–498. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Wang, F.; Song, M.; Yu, C. Meta-learning based hyperspectral target detection using Siamese network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5527913. [Google Scholar] [CrossRef]
- Song, M.; Liu, S.; Xu, D.; Yu, H. Multiobjective optimization-based hyperspectral band selection for target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5529022. [Google Scholar] [CrossRef]
- Chen, J.; Chang, C.I. Background-Annihilated Target-Constrained Interference-Minimized Filter (TCIMF) for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5540224. [Google Scholar] [CrossRef]
- Chen, Z.; Lu, Z.; Gao, H.; Zhang, Y.; Zhao, J.; Hong, D.; Zhang, B. Global to local: A hierarchical detection algorithm for hyperspectral image target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5544915. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Chen, Z.; Xu, S.; Hong, D.; Zhang, B. A Multidepth and Multibranch Network for Hyperspectral Target Detection Based on Band Selection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5506818. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Chen, Z.; Xu, F.; Hong, D.; Zhang, B. Hyperspectral Target Detection via Spectral Aggregation and Separation Network with Target Band Random Mask. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5515516. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing 2021, 448, 179–204. [Google Scholar] [CrossRef]
- Xie, H.; Chen, Y.; Ghamisi, P. Remote sensing image scene classification via label augmentation and intra-class constraint. Remote Sens. 2021, 13, 2566. [Google Scholar] [CrossRef]
- Liu, S.; Cao, Y.; Wang, Y.; Peng, J.; Mathiopoulos, P.T.; Li, Y. DFL-LC: Deep feature learning with label consistencies for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3669–3681. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1463–1474. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, X.; Li, Y.; Lei, J.; Li, J.; Du, Q. Weakly supervised low-rank representation for hyperspectral anomaly detection. IEEE Trans. Cybern. 2021, 51, 3889–3900. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Xie, W.; Li, Y.; Lei, J.; Du, Q. Weakly supervised discriminative learning with spectral constrained generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Neural Networks Learn. Syst. 2021, 33, 6504–6517. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Yu, X.; Reed, I.S.; Stocker, A.D. Comparative performance analysis of adaptive multispectral detectors. IEEE Trans. Signal Process. 1993, 41, 2639–2656. [Google Scholar] [CrossRef]
- Li, C.; Zhang, B.; Hong, D.; Yao, J.; Chanussot, J. LRR-Net: An Interpretable Deep Unfolding Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5513412. [Google Scholar] [CrossRef]
- Gao, L.; Sun, X.; Sun, X.; Zhuang, L.; Du, Q.; Zhang, B. Hyperspectral anomaly detection based on chessboard topology. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5505016. [Google Scholar] [CrossRef]
- Wang, M.; Hong, D.; Zhang, B.; Ren, L.; Yao, J.; Chanussot, J. Learning double subspace representation for joint hyperspectral anomaly detection and noise removal. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5507517. [Google Scholar] [CrossRef]
- Horstrand, P.; Díaz, M.; Guerra, R.; López, S.; López, J.F. A novel hyperspectral anomaly detection algorithm for real-time applications with push-broom sensors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4787–4797. [Google Scholar] [CrossRef]
- Báscones, D.; González, C.; Mozos, D. An FPGA accelerator for real-time lossy compression of hyperspectral images. Remote Sens. 2020, 12, 2563. [Google Scholar] [CrossRef]
- Li, C.; Gao, L.; Plaza, A.; Zhang, B. FPGA implementation of a maximum simplex volume algorithm for endmember extraction from remotely sensed hyperspectral images. J. Real-Time Image Process. 2019, 16, 1681–1694. [Google Scholar] [CrossRef]
- Du, Q.; Ren, H. Real-time constrained linear discriminant analysis to target detection and classification in hyperspectral imagery. Pattern Recognit. 2003, 36, 1–12. [Google Scholar] [CrossRef]
- Chang, C.I.; Ren, H.; Chiang, S.S. Real-time processing algorithms for target detection and classification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 760–768. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Qi, B.; Wang, J. Global and local real-time anomaly detectors for hyperspectral remote sensing imagery. Remote Sens. 2015, 7, 3966–3985. [Google Scholar] [CrossRef]
- Chen, S.Y.; Wang, Y.; Wu, C.C.; Liu, C.; Chang, C.I. Real-time causal processing of anomaly detection for hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1511–1534. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.Y.; Wu, C.C.; Liu, C.; Chang, C.I. Real-time causal processing of anomaly detection. In Proceedings of the High-Performance Computing in Remote Sensing II. SPIE, Edinburgh, UK, 26–27 September 2012; Volume 8539, pp. 50–57. [Google Scholar]
- Zhao, C.; Li, C.; Yao, X.; Li, W. Real-time kernel collaborative representation-based anomaly detection for hyperspectral imagery. Infrared Phys. Technol. 2020, 107, 103325. [Google Scholar] [CrossRef]
- Ndikumana, A.; Tran, N.H.; Ho, T.M.; Han, Z.; Saad, W.; Niyato, D.; Hong, C.S. Joint communication, computation, caching, and control in big data multi-access edge computing. IEEE Trans. Mob. Comput. 2019, 19, 1359–1374. [Google Scholar] [CrossRef]
- Pan, J.; McElhannon, J. Future edge cloud and edge computing for internet of things applications. IEEE Internet Things J. 2017, 5, 439–449. [Google Scholar] [CrossRef]
- Premsankar, G.; Di Francesco, M.; Taleb, T. Edge computing for the Internet of Things: A case study. IEEE Internet Things J. 2018, 5, 1275–1284. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, X.; Ren, J.; Cai, L. Efficient computing resource sharing for mobile edge-cloud computing networks. IEEE/ACM Trans. Netw. 2020, 28, 1227–1240. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Q.; Luo, Y.; Peng, K.; Zhang, X.; Meng, S.; Qi, L. A computation offloading method over big data for IoT-enabled cloud-edge computing. Future Gener. Comput. Syst. 2019, 95, 522–533. [Google Scholar] [CrossRef]
- Xu, X.; Gu, R.; Dai, F.; Qi, L.; Wan, S. Multi-objective computation offloading for internet of vehicles in cloud-edge computing. Wirel. Netw. 2020, 26, 1611–1629. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; He, Y.; Li, G.Y. Collaborative cloud and edge computing for latency minimization. IEEE Trans. Veh. Technol. 2019, 68, 5031–5044. [Google Scholar] [CrossRef]
- Jia, M.; Cao, J.; Yang, L. Heuristic offloading of concurrent tasks for computation-intensive applications in mobile cloud computing. In Proceedings of the 2014 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 27 April–2 May 2014; pp. 352–357. [Google Scholar]
- Zhang, X.; Hu, M.; Xia, J.; Wei, T.; Chen, M.; Hu, S. Efficient federated learning for cloud-based AIoT applications. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 40, 2211–2223. [Google Scholar] [CrossRef]
- Gu, H.; Ge, Z.; Cao, E.; Chen, M.; Wei, T.; Fu, X.; Hu, S. A collaborative and sustainable edge-cloud architecture for object tracking with convolutional siamese networks. IEEE Trans. Sustain. Comput. 2019, 6, 144–154. [Google Scholar] [CrossRef]
- Gamez, G.; Frey, D.; Michler, J. Push-broom hyperspectral imaging for elemental mapping with glow discharge optical emission spectrometry. J. Anal. At. Spectrom. 2012, 27, 50–55. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, B.; Zhang, F.; Wang, L.; Zhang, H.; Zhang, P.; Tong, Q. Fast real-time causal linewise progressive hyperspectral anomaly detection via cholesky decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4614–4629. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzon, E.M.; Garcia, I.; Plaza, A. Analysis and optimizations of global and local versions of the RX algorithm for anomaly detection in hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 801–814. [Google Scholar] [CrossRef]
- Chang, C.; Chiang, S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef]
- Chen, X.; Gu, C.; Zhang, Y.; Mittra, R. Analysis of partial geometry modification problems using the partitioned-inverse formula and Sherman–Morrison–Woodbury formula-based method. IEEE Trans. Antennas Propag. 2018, 66, 5425–5431. [Google Scholar] [CrossRef]
- Xu, X. Generalization of the Sherman–Morrison–Woodbury formula involving the Schur complement. Appl. Math. Comput. 2017, 309, 183–191. [Google Scholar] [CrossRef][Green Version]
- Chang, C.I. An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5131–5153. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1990–2000. [Google Scholar] [CrossRef]
- Fan, G.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Robust graph autoencoder for hyperspectral anomaly detection. In Proceedings of the ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 1830–1834. [Google Scholar]
- Tan, K.; Hou, Z.; Wu, F.; Du, Q.; Chen, Y. Anomaly detection for hyperspectral imagery based on the regularized subspace method and collaborative representation. Remote Sens. 2019, 11, 1318. [Google Scholar] [CrossRef]
- Ma, Y.; Fan, G.; Jin, Q.; Huang, J.; Mei, X.; Ma, J. Hyperspectral anomaly detection via integration of feature extraction and background purification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1436–1440. [Google Scholar] [CrossRef]







| Detection Algorithm | Detection Accuracy | Resource Utilization |
|---|---|---|
| RX algorithm (non-real-time) | Low accuracy detection; | Only runs on one device; |
| CLP algorithm (real-time) | Low accuracy detection at the previous detection stage; | Only runs on one device; |
| Local-RX algorithm (non-real-time) | High accuracy detection; | Only runs on one device; |
| Proposed algorithm (real-time) | Ability to perform accurate background suppression; | Use the cloud and the edge to run collaboratively; |
| Detector | ||
|---|---|---|
| CLP-RX (real-time) | 0.9225 | 0.0821 |
| LRASR (non-real-time) | 0.9948 | 0.0786 |
| RGAR (non-real-time) | 0.9887 | 0.0365 |
| LSUNRSOR (non-real-time) | 0.9579 | 0.0737 |
| FEBP (non-real-time) | 0.9791 | 0.0050 |
| CE-RX (real-time) | 0.9933 | 0.0783 |
| Experiment1 | Experiment2 | Experiment3 | Experiment4 | |
|---|---|---|---|---|
| AUC | 0.9591 | 0.9757 | 0.9933 | 0.9225 |
| Detector | ||
|---|---|---|
| CLP-RX (real-time) | 0.9070 | 0.0446 |
| LRASR (non-real-time) | 0.9826 | 0.0246 |
| RGAR (non-real-time) | 0.9767 | 0.0115 |
| LSUNRSOR (non-real-time) | 0.9753 | 0.0124 |
| FEBP (non-real-time) | 0.9690 | 0.0062 |
| CE-RX (real-time) | 0.9842 | 0.0348 |
| Experiment1 | Experiment2 | Experiment3 | Experiment4 | |
|---|---|---|---|---|
| AUC | 0.9206 | 0.9538 | 0.9842 | 0.9070 |
| Detector | ||
|---|---|---|
| CLP-RX (real-time) | 0.8567 | 0.0540 |
| LRASR (non-real-time) | 0.9438 | 0.0570 |
| RGAR (non-real-time) | 0.9311 | 0.0516 |
| LSUNRSOR (non-real-time) | 0.9553 | 0.0544 |
| FEBP (non-real-time) | 0.9590 | 0.0429 |
| CE-RX (real-time) | 0.9642 | 0.0418 |
| Experiment1 | Experiment2 | Experiment3 | Experiment4 | |
|---|---|---|---|---|
| AUC | 0.9362 | 0.9595 | 0.9642 | 0.8567 |
| Hyperspectral Data | |||||
|---|---|---|---|---|---|
| real-data1 | 54 ms | 87 ms | 21 ms | 4 ms | 91 ms |
| real-data2 | 45 ms | 85 ms | 20 ms | 5 ms | 90 ms |
| real-data3 | 42 ms | 79 ms | 20 ms | 5 ms | 84 ms |
| Hyperspectral Data | Real-Data1 | Real-Data2 | Real-Data3 |
|---|---|---|---|
| CLP-RX (real-time) | 0.087 s | 0.085 s | 0.079 s |
| LRASR (non-real-time) | 202 s | 131 s | 182 s |
| RGAR (non-real-time) | 436 s | 421 s | 401 s |
| LSUNRSOR (non-real-time) | 221 s | 232 s | 212 s |
| FEBP (non-real-time) | 11.2 s | 12.9 s | 10.1 s |
| CE-RX (real-time) | 0.091 s | 0.09 s | 0.084 s |
| Data Size | Latency | Latency Ratio |
|---|---|---|
| 1 GB | 34.52 s | 1 |
| 2 GB | 70.11 s | 2.03 |
| 4 GB | 142.64 s | 4.13 |
| 8 GB | 282.81 s | 8.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Cai, J.; Zhou, J.; Sun, J.; Xu, Y.; Zhang, Y.; Wei, Z.; Plaza, J.; Plaza, A.; Wu, Z. CE-RX: A Collaborative Cloud-Edge Anomaly Detection Approach for Hyperspectral Images. Remote Sens. 2023, 15, 4242. https://doi.org/10.3390/rs15174242
Wang Y, Cai J, Zhou J, Sun J, Xu Y, Zhang Y, Wei Z, Plaza J, Plaza A, Wu Z. CE-RX: A Collaborative Cloud-Edge Anomaly Detection Approach for Hyperspectral Images. Remote Sensing. 2023; 15(17):4242. https://doi.org/10.3390/rs15174242
Chicago/Turabian StyleWang, Yunchang, Jiang Cai, Junlong Zhou, Jin Sun, Yang Xu, Yi Zhang, Zhihui Wei, Javier Plaza, Antonio Plaza, and Zebin Wu. 2023. "CE-RX: A Collaborative Cloud-Edge Anomaly Detection Approach for Hyperspectral Images" Remote Sensing 15, no. 17: 4242. https://doi.org/10.3390/rs15174242
APA StyleWang, Y., Cai, J., Zhou, J., Sun, J., Xu, Y., Zhang, Y., Wei, Z., Plaza, J., Plaza, A., & Wu, Z. (2023). CE-RX: A Collaborative Cloud-Edge Anomaly Detection Approach for Hyperspectral Images. Remote Sensing, 15(17), 4242. https://doi.org/10.3390/rs15174242











