MOON: A Subspace-Based Multi-Branch Network for Object Detection in Remotely Sensed Images

Abstract

The effectiveness of training-based object detection heavily depends on the amount of sample data. But in the field of remote sensing, the amount of sample data is difficult to meet the needs of network training due to the non-cooperative imaging modes and complex imaging conditions. Moreover, the imbalance of the sample data between different categories may lead to the long-tail problem during the training. Given that similar sensors, data acquisition approaches, and data structures could make the targets in different categories possess certain similarities, those categories can be modeled together within a subspace rather than the entire space to leverage the amounts of sample data in different subspaces. To this end, a subspace-dividing strategy and a subspace-based multi-branch network is proposed for object detection in remotely sensed images. Specifically, a combination index is defined to depict this kind of similarity, a generalized category consisting of similar categories is proposed to represent the subspace, and a new subspace-based loss function is devised to address the relationship between targets in one subspace and across different subspaces to integrate the sample data from similar categories within a subspace and to balance the amounts of sample data between different subspaces. Furthermore, a subspace-based multi-branch network is constructed to ensure the subspace-aware regression. Experiments on the DOTA and HRSC2016 datasets demonstrated the superiority of our proposed method.

1. Introduction

Object detection in remotely sensed images is a challenging task due to the non-cooperative imaging mode and complex imaging conditions. Although, for natural images, learning-based object detection has acquired impressive advances in the last decade, such as Faster RCNN [1], YOLO [2], SSD [3], and RetinaNet [4], their applicability to remotely sensed images is limited. This limitation arises from the massive irrelevant backgrounds under the non-cooperative imaging mode and the diversity of targets under complex imaging conditions.

Indeed, early learning models for object detection in remotely sensed images were improved from the original models for object detection in natural images by adjusting the regression strategy, such as the FR-O [5], LR-O [6], and DCN [7], which were enlightening but suffered from poor detection accuracy at the same time.

Inspired by scene text detection, various object detection methods for remotely sensed images have been proposed, such as the R2CNN [8], RRPN [9], ICN [10], and CAD-Net [11], with a higher detection accuracy but also with an increase in computation complexity. Specifically, the R2CNN [8] utilized multi-scale features and inclined non-maximum suppression (NMS) to detect oriented objects. The RRPN [9] introduced the rotational region proposal network (RPN) and rotational region-of-interest (RoI) strategy to handle arbitrary-oriented proposals. The ICN [10] also applied the rotational RPN, multi-scale rotational RoI, and rotational NMS for the detection of oriented objects. CAD-Net [11] incorporated global and local features to improve the accuracy of object detection in remotely sensed images. However, these methods primarily emphasized the improvement of network structures for better feature expression rather than focusing on the properties of remotely sensed targets.

With further study of the properties of remotely sensed images, SCRDet [12], RT [13], Gliding Vertex [14], BBAvector [15], and HeatNet [16] were proposed to tackle certain characteristics of remotely sensed targets. In these methods, SCRDet [12] employed pixel and channel attention for the detection of small and cluttered objects. RT [13] designed a rotated RoI learner and a rotated position-sensitive RoI align module to extract rotation-invariant features. Gliding Vertex [14] utilized the gliding of the vertex of the horizontal bounding box on each side to denote an oriented object. BBAvector [15] detected the center keypoints and regressed the box-boundary-aware vectors to capture the oriented objects. HeatNet [16] addressed the cluster distribution problem of remotely sensed targets and refined an FFT-based heatmap to tackle the challenge of densely distributed targets. These methods concerned certain properties of remotely sensed targets, most of which focused on improving the representation of oriented bounding boxes. However, the relationship between the targets in different categories has not been taken into account, especially regarding the imbalance problem of sample data between different categories [17].

In recent years, transformers have also been introduced to object detection in remotely sensed images, such as the AO2-DETR [18], Gansformer [19], TRD [20], and TransConvNet [21], to deal with the small sample problem in network training [22]. Specifically, the AO2-DETR [18] generated oriented proposals to modulate cross-attention in the transformer decoder. Gansformer [19] employed a generative model to expand the sample data before the transformer backbone. The TRD [20] combined data augmentation with a transformer to improve the detection performance. TransConvNet [21] utilized an adaptive feature-fusion network to improve the representational ability for the remotely sensed targets. These methods focused on improving learning efficiency to deal with the small sample problem in network training [22]. However, nearly none of these methods concerned with the influence of the long-tail problem, which arises from the imbalance of sample data between different categories, as shown in Figure 1.

Moreover, almost all of the above learning models take the entire sample space as one space, which makes the high-dimensional nonlinearity for all of the possible categories cannot be neglected, whereby the high expressing ability, with more learning parameters for this kind of high-dimensional nonlinearity, must be considered. Additionally, more training samples are required to ensure the steady learning of the network. However, due to the non-cooperative imaging mode and complex imaging conditions, the amount of sample data is difficult to meet the needs of network training [23]. Training a universal network for the entire sample space has been confirmed by other application tasks to be much more difficult, or even impossible, compared to training several specific subnetworks for each subspace [24,25,26,27]. Specifically, to deal with this problem, GLRR [24] combined similar image patches into one group and removed the noise in the hyperspectral images by using a group-based reconstruction with a low-rank constraint, [25] divided the pixels in one sample image into different subspaces by using an unsupervised clustering, and learned the nonlinear relationship from the RGB to the high-spatial-resolution hyperspectral image by using a cluster-based multi-branch network for spectral super resolution. Furthermore, a fusion method for low-spatial-resolution hyperspectral and high-spatial-resolution multi-spectral images was also proposed [26]. Apart from these, [27] also utilized the subspace-dividing strategy for change detection in hyperspectral images. We realized that the similarity between the different categories should also be considered for the training of an object detection network. Especially, a similarity measurement method for different categories suitable for the object detection, a new subspace-dividing strategy especially for the imbalance problem between different categories, and a suitable network structure for the subspace-based object detection should be considered for remotely sensed images.

On the other hand, for the loss functions in object detection networks, two paradigms exist, i.e., learning from the sample data with category-level labels and learning from sample data with instance-level labels [28]. The former optimized the similarity between sample data and feature expression by using category-level loss functions, such as L2-softmax [29], large-margin softmax [30], and AM softmax [31]. The latter optimized the instance-level similarity through metric learning based loss functions, such as triplet loss [32], angular loss [33], and multi-similarity loss [34]. Among these methods, the category-level loss function is dominant for object detection in remotely sensed images, which follows the convention of object detection in natural images. On this basis, SCRDet [12] and RSDet [35] introduced constraints to the loss function, i.e., the IoU Smooth L1 Loss and Modulated Loss. DCL [36] utilized the angle distance and aspect-ratio-sensitive weighting to handle the boundary discontinuity of labels. Most of these methods primarily focused on the category-level loss function and the instance-level loss function, without thoroughly exploring the relationship between the targets of different categories.

Faced with the above problems, a subspace-dividing strategy and a subspace-based Multi-branch Object detectiOn Network (termed as MOON) is proposed in this paper to leverage the amounts of sample data in different subspaces and solve the long-tail problem for the remotely sensed images. In detail, a combination index is defined to depict this kind of similarity, a generalized category consisting of similar categories is proposed to represent the subspace by using the combination index, and a new subspace-based loss function is devised to take the relationship between targets in one subspace and across different subspaces into consideration to integrate the sample data from similar categories within a subspace and to balance the amounts of sample data between different subspaces. Moreover, a subspace-based multi-branch network is constructed to ensure the subspace-aware regression, combined with a specially designed module to decouple the shared features into a horizontal and rotated branch, and to enhance the rotated features. The novelties and the contributions of our proposed method can be summarized as follows:

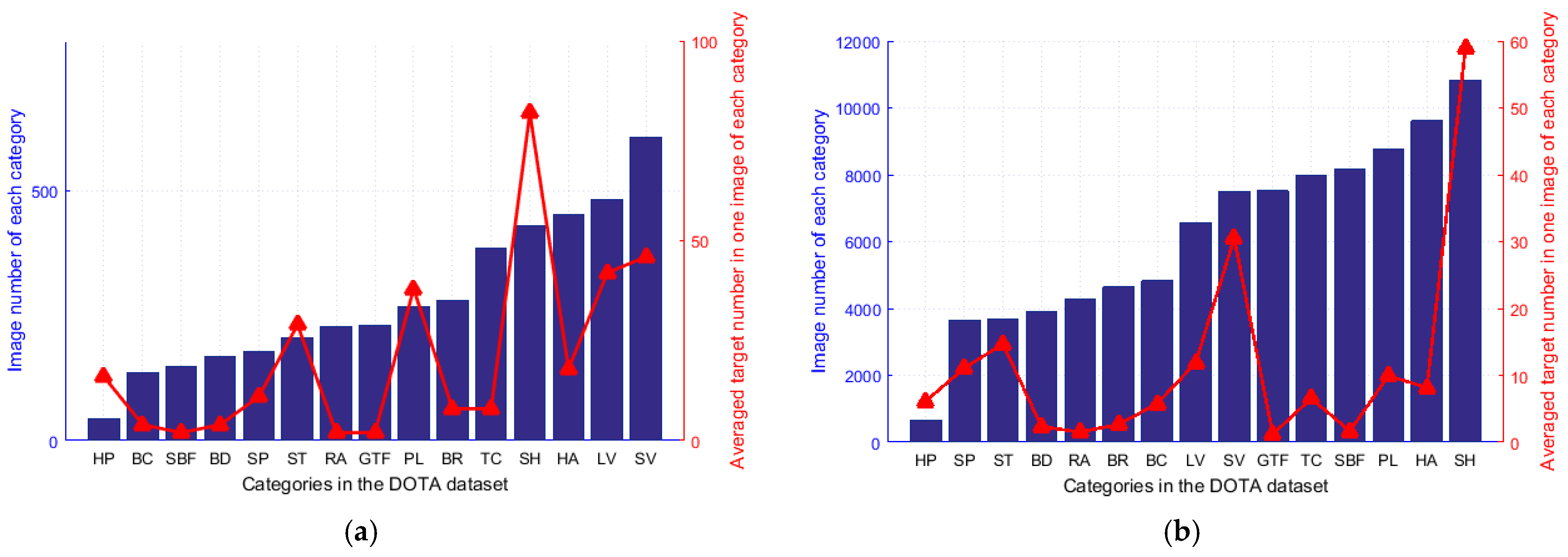
• To our best knowledge, this is the first time that the long-tail problem in object detection for remotely sensed images is focused to solve the high imbalance of sample data between different categories;
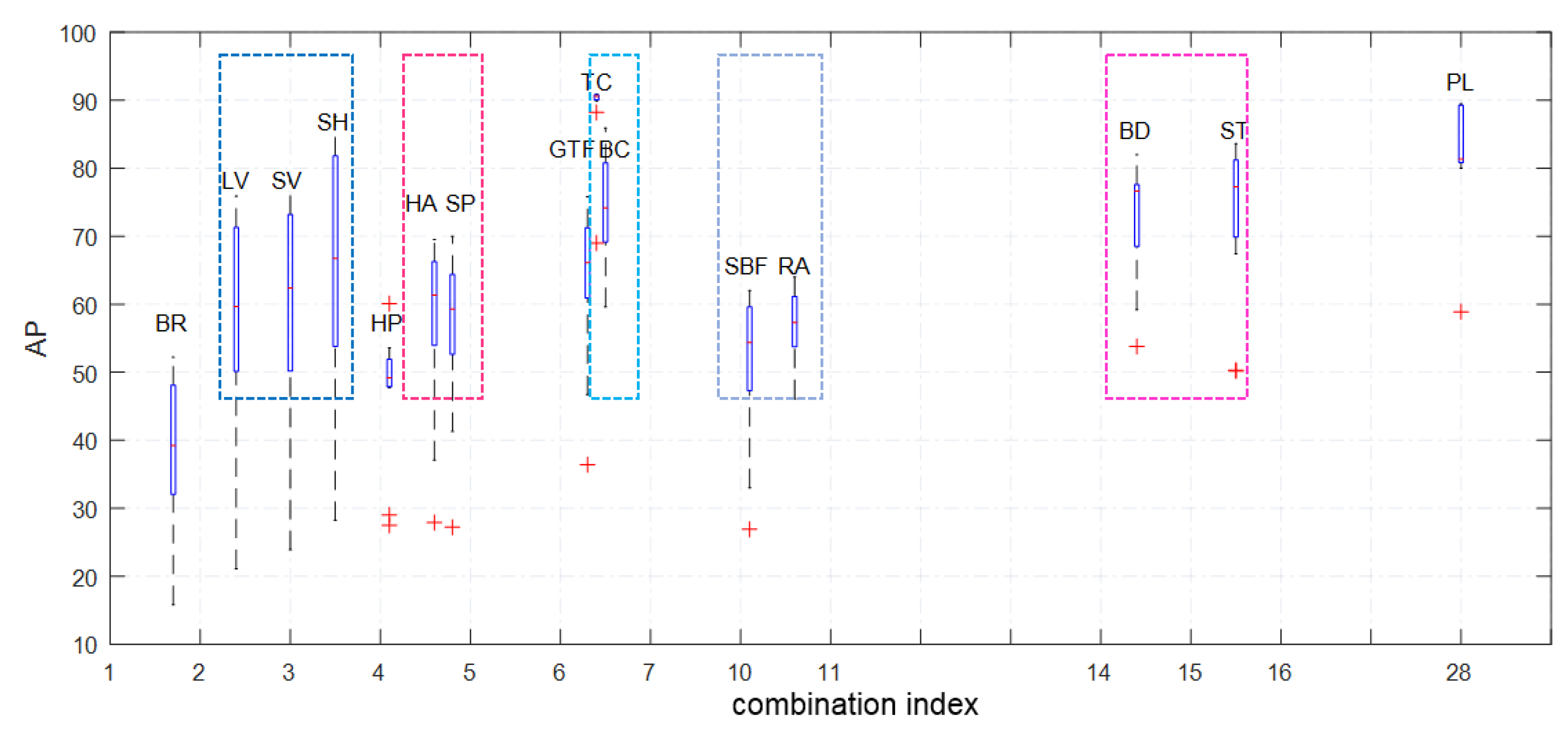
• A new framework of subspace-based object detection for remotely sensed images is proposed, in which a new combination index is defined to quantify certain similarities between different categories, and a new subspace-dividing strategy is also proposed to divide the entire sample space and balance the amounts of sample data between different subspaces;
• A new subspace-based loss function is designed to account for the relationship between targets in one subspace and across different subspaces, and a subspace-based multi-branch network is constructed to ensure the subspace-aware regression, combined with a specially designed module to decouple the learning of horizontal and rotated features.

2. Proposed Method

2.1. Problem Formulation

Theoretically, the process of object detection in remotely sensed images can be formulated as the learning of the posterior $P(C\mid B,I)$ [37], where $C=\{C_1,C_2,\dots ,C_K\}$ denotes the categories of remotely sensed targets, $B$ denotes the bounding boxes, and $I$ denotes the learned representation of the sample data [1]. The joint distribution of the sample data for object detection can be formulated as $P(C,B,I)$, which can be decomposed by the Bayes formulation:

$$P(C,B,I)=P(C\mid B,I)P(B,I)$$

(1)

If $P(B,I)$ is further decoupled into $P(B,I)=P(B\mid I)P\left(I\right)$, the conditional distribution $P(B\mid I)$, i.e., the bounding box prediction, will not formally involve the target properties of different categories for the remotely sensed targets. Furthermore, the prediction $P(C\mid B,I)$ contradicts the paradigm of object detection methods, as the bounding box regression of a target cannot be determined before the classification prediction. To accurately depict the process of object detection in remotely sensed images, Equation (1) should be rewritten into Equation (2), as follows:

$$P(C,B,I)=P(B\mid C,I)P(C,I)$$

(2)

where $P(C,I)$ can be further decoupled into $P(C,I)=P(C\mid I)P\left(I\right)$, which means the whole process is from sample data learning to classification prediction, and finally to bounding box regression. It is evident that, for the marginal distribution $P\left(I\right)$, if the amount of sample data is difficult to meet the needs of the network training, the learning models would suffer from the poor expression ability. For the classification prediction $P(C\mid I)$, the imbalance between the different categories of the targets would result in the long-tail problem, which arises from the imbalance of the sample data between different categories, as shown in Figure 1. This issue is exemplified by using the influential DOTA dataset [5] for remotely sensed object detection. From Figure 1, it can be seen that both the image number and the target number of each category exhibit a high imbalance. Even after applying the official data augmentation preprocessing for these sample images [13], i.e., cropping each sample image into multi-image patches with the same size, the long-tail problem has not been ameliorated. In addition, $P(B\mid C,I)$ reflects the implicit influence of classification prediction on the bounding box regression, which has not arisen much attention in current object detection approaches for remotely sensed images.

2.2. Combination Index and Subspace Division

To solve the long-tail problem, the similarity between different categories of remotely sensed targets should be considered. Concretely, as similar sensors, data acquisition approaches and data structures could make the targets in different categories possess certain similarities, and those categories should be modeled together in a subspace rather than the entire space to leverage the amounts of sample data in different categories. To depict this kind of similarity, which adopts a morphological similarity instead of the traditional feature similarity, for a category $C_K$, a combination index ${\Psi }_k$ of different impact factors is defined, including the averaged target size $\rho$, averaged aspect ratio $\nu$, target number $n$, and image number $N$:

$${\Psi }_k=\frac{{\sqrt{\rho }}_k}{{\nu }_k-\frac{1}{1/C\sum {\nu }_k}}\times log\left(\frac{n_k}{N_k}\right),k=1,\dots ,C_K$$

(3)

The consideration of image number $N$, target number $n$, and the averaged target size $\rho$ are motivated by the need to address the imbalance between different categories with different amounts of sample data, as shown in Figure 1. And the averaged aspect ratio $\nu$ is taken into account for the different difficulties of different categories influenced by the appearance of remotely sensed targets. The reason for selecting these impact factors is that, due to the non-cooperative imaging mode and complex imaging conditions of remotely sensed images, these properties are deemed more representative than the extracted features for the remotely sensed targets [17]. Moreover, these parameters can be directly acquired from the labels of the sample data before the network training, while the extracted features can usually only be available after the process of network training or even after the process of object detection, which is obviously contrary to the original intention of the network training.

Taking the DOTA dataset [5] as an example, the combination indexes ${\Psi }_k$ are calculated for 12 representative remotely sensed object detection methods from the Object Detection in Aerial Images (ODAI) challenge, including the RetinaNet [4], R2CNN [8], RRPN [9], LR-O [6], DCN [7], RT [13], ICN [10], Mask RCNN [38], HTC, R3Det [39], and BBAvector [15]. The relation between the combination index ${\Psi }_k$ (x-axis) and the accuracy of object detection (y-axis) is shown in Figure 2.

From Figure 2, it can be seen that, if the combination indexes of different categories are close, their prediction results are close as well, such as the three categories of the large vehicle (LV), small vehicle (SV), and ship (SH) in the dark blue box, as well as the two categories of the tennis court (TC) and basketball court (BC) in the light blue box. It is believed that these kinds of similar categories should be modeled together in one subspace rather than in the entire space to reduce the high-dimensional nonlinearity of the sample data in the entire space and to integrate the sample data within a subspace together for a steadier learning of the network. In light of this, as shown as Equation (4), the relationship of the absolute difference $\Psi$, the average precision AP, and their variance $\delta$ are taken as a new measurement ${\mathsf{\Omega }}_{s_{ij}}$ for the similarity between the two different categories $i$ and $j$. Then, a new subspace-division strategy is established, where, if ${\mathsf{\Omega }}_{s_{ij}}$ is small enough, then categories $i$ and $j$ will be grouped into one subspace. In the case of the DOTA dataset, all of the categories can be grouped into 6 subspaces, shown as Equation (5).

$${\mathsf{\Omega }}_{s_{ij}}:\parallel {\Psi }_i-{\Psi }_j\parallel <\parallel A{P}_i-A{P}_j\parallel +\parallel {\delta }_i-{\delta }_j\parallel$$

(4)

$$\mathsf{\Omega }=\{\begin{array}{cc}{\mathsf{\Omega }}_{s1}:& BR,HP,GTF,PL\\ {\mathsf{\Omega }}_{s2}:& LV,SV,SH\\ {\mathsf{\Omega }}_{s3}:& HA,SP\\ {\mathsf{\Omega }}_{s4}:& TC,BC\\ {\mathsf{\Omega }}_{s5}:& RA,SBF\\ {\mathsf{\Omega }}_{s6}:& BD,ST\end{array}\}$$

(5)

Therefore, the combination index ${\Psi }_k$ and its absolute difference are feasible to depict this kind of similarity between different categories, and the entire space can be divided into multiple subspaces for better learning effects. By applying subspace dividing, the inner property can be learned more efficiently for the categories within one specific subspace than for the entire space. As pointed out in paper [40], the learning models gradually focus from 200 classes to 50 classes and then to 29 classes, outperform the abrupt jump from 200 classes to 29 classes remarkably, which implicitly encodes the taxonomy information into the network training. Our proposed subspace-division strategy could automatically generate this kind of gradual focus, known as hierarchical learning, which sheds light on hierarchical learning, and which is effective for boosting the prediction accuracy of learning models.

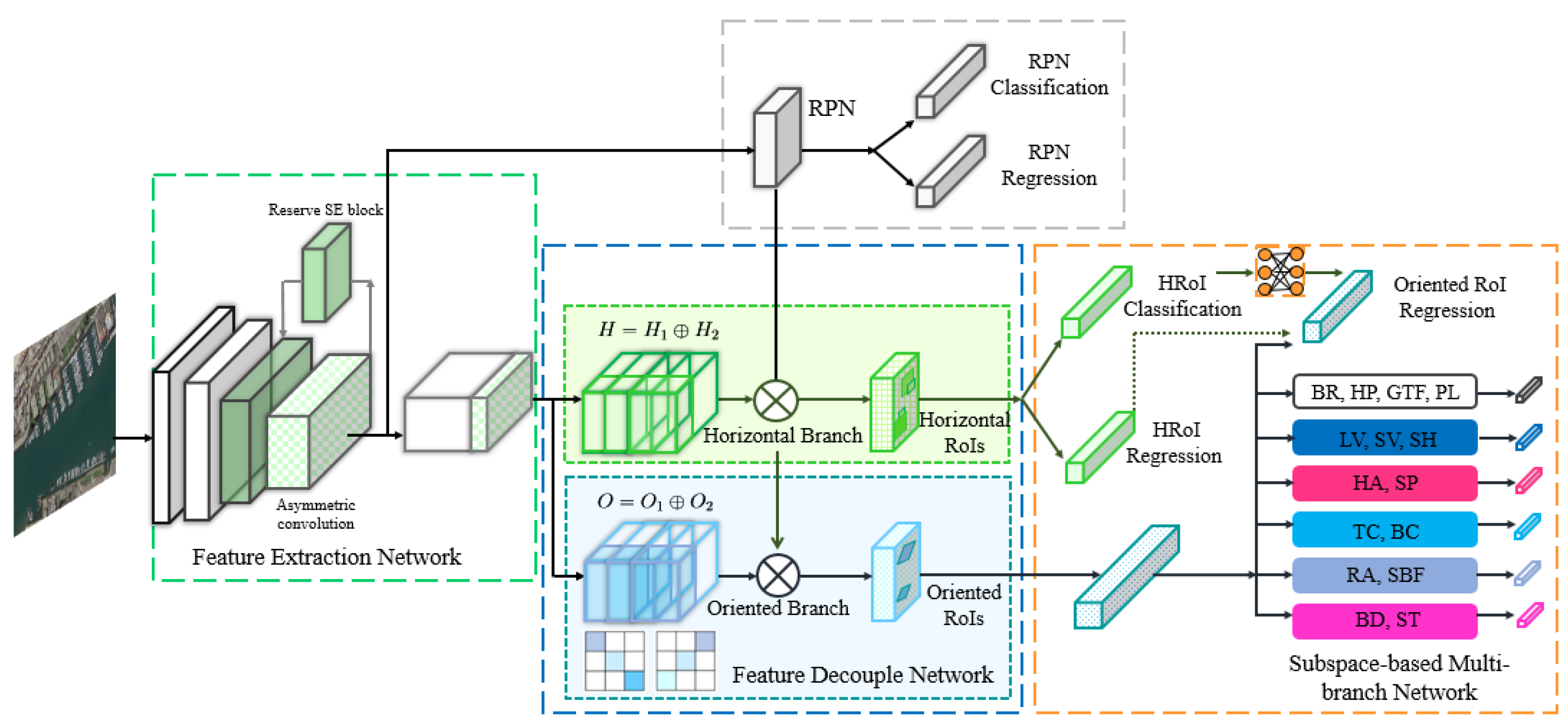
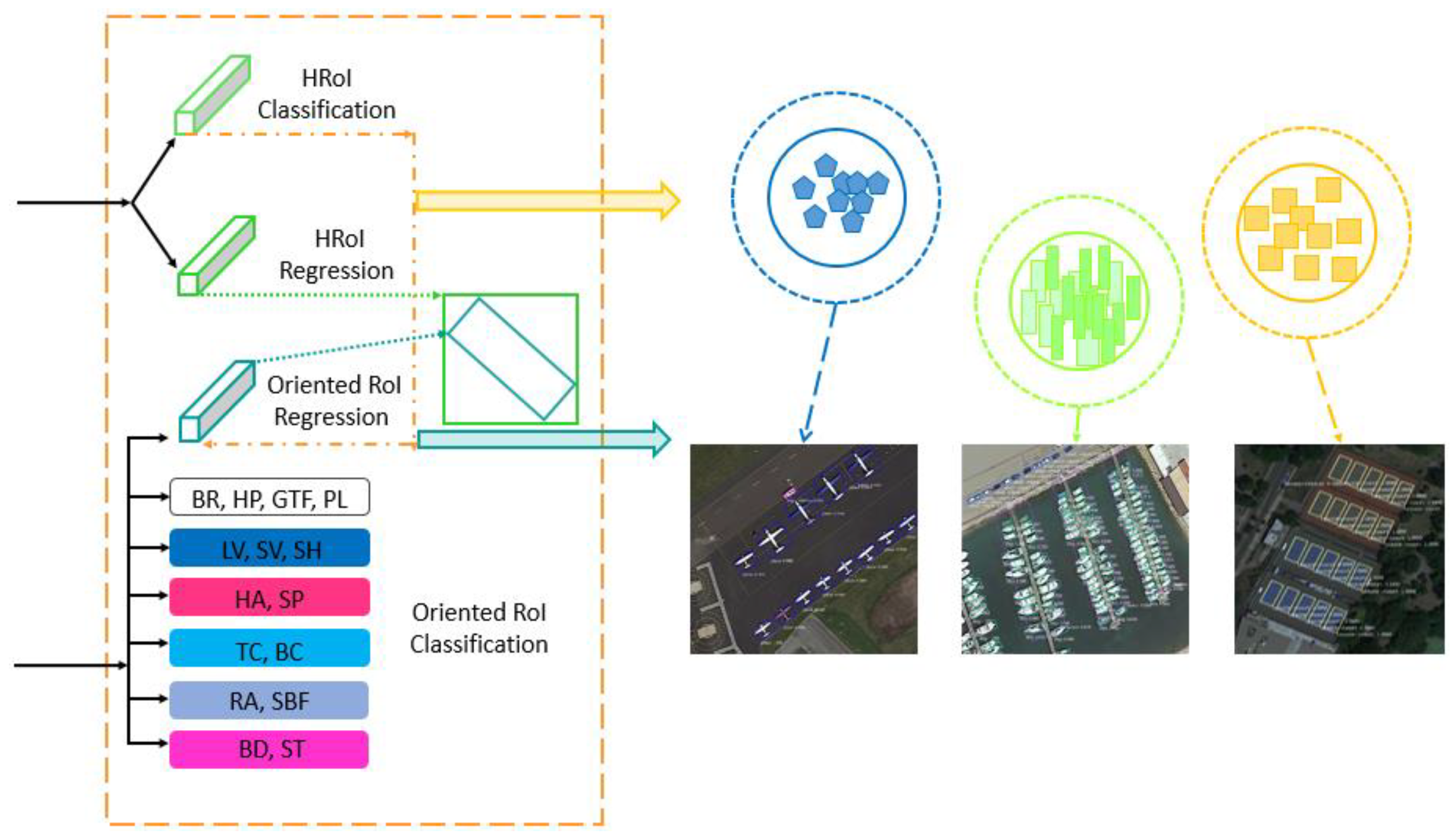
2.3. Subspace-Based Multi-branch Network

After a combination index ${\Psi }_k$ of different impact factors is defined and the entire space is divided into multiple subspaces for better learning effects, here, in this subsection, the overview of our proposed MOON method will be given, as shown in Figure 3, which decouples the shared features into the horizontal branch and the rotated branch and the subspace-based multi-branch network.

As discussed in the SCRDet [12], insufficient feature expression is one of the key obstacles for object detection in remotely sensed images, such as the bridge category and helicopter category in Figure 2. To address this issue, the extracted features are firstly enhanced from coarse to fine for better feature expression. The context information is firstly utilized to holistically enhance the features for the remotely sensed targets with different scales by adding the SE block [41] at the head of the Conv4x to the Conv3x, which proves to be simple but effective. On this basis, asymmetric convolution [42] is employed to enhance the aspect-ratio tolerance for the remotely sensed targets. After exploiting the context information from coarse to fine, feature expression can be enhanced efficiently.

Then, RPN provides coarse proposals for the targets, in which the horizontal anchors are utilized. The scales and ratios of the anchors are set to $\{4^2,8^2,{16}^2,{32}^2,{64}^2\}$ and $\{1:2,1:1,2:1\}$, respectively, considering the trade-off between being time-consuming and prediction-precision. There are 6000 RoIs from the RPN before the NMS, and there are 800 RoIs reserved after the NMS, with an intersection over union (IoU) set to 0.7.

As discussed in related works, the shared extracted features for the horizontal and rotated objects have a mutual influence on the learning of the orientation invariance for the classification and the orientation sensitiveness for the localization. The learning of the classification even impedes that of the localization. Therefore, the feature decouple network is facilitated after the RPN to decouple the shared features and acquire high-quality feature expression. Specifically, the shared features are decoupled into horizontal branch $H$ and oriented branch $O$, as in Figure 3. Then, both branches are divided into two sub-branches separately, i.e., $H=H_1\oplus H_2$ and $O=O_1\oplus O_2$.

Among the first sub-branches, $H_1$ and $O_1$, the separable convolutions are employed to reduce the computation [5]. Among the second sub-branches, the stack of asymmetric convolution is conducted on the horizontal sub-branch $H_2$, and the crisscross convolution is introduced to the oriented sub-branch $O_2$, which boosts the rotated features by introducing the crisscross convolution kernels, as in Figure 4. Then, these sub-branches are element-wise added separately. To the best of our knowledge, this study represents the initial introduction of the decouple learning approach for the horizontal and rotated features into the object detection explicitly. The learning of the orientation invariance for classification no longer interacts with the learning of the orientation sensitiveness for the localization, which is simple but significant for object detection in remotely sensed images. In addition, this is the first time that the crisscross convolution structure is introduced for the rotated features enhancement, which improves the pertinence of the remotely sensed targets.

Similar to the object detection in natural images, the horizontal branch $H$ proposes horizontal RoIs (HRoI) $\left\{{\nu }_i^H\right\}=\left\{\right(x_i,y_i,w_i,h_i\left)\right\}$, where $(x_i,y_i,w_i,h_i)$ denotes the center coordinates, the long side and the short side of a HRoI. To eliminate the misalignment between the RoIs and the oriented objects, the oriented RoIs $\left\{{\nu }_i^O\right\}=\left\{\right(x_i^p,y_i^p,w_i^p,h_i^p,{\theta }_i^p\left)\right\}$ are learned from the oriented branch and horizontal branch by the rotated RoI learner [13]. This process is equivalent to the position-sensitive RoI align, followed by the fully connected layers, to regress the offsets of the ground truth relative to the horizontal RoIs:

$$\begin{array}{c}{v}_x^g=1/w^p\left(\right(x^g-x^p)cos{\theta }^p+(y^g-y^p)sin{\theta }^p)\\ v_y^g=1/h^p\left(\right(y^g-y^p)cos{\theta }^p-(x^g-x^p)sin{\theta }^p)\\ v_w^g=log(w^g/w^p)\\ v_h^g=log(h^g/h^p)\\ v_{\theta }^g=\left(\right({\theta }^g-{\theta }^p\left)mod2\pi \right)/2\pi \end{array}$$

(6)

where $\left\{\right(x^p,y^p,w^p,h^p,{\theta }^p\left)\right\}$ represent the parameters of the oriented RoIs and $\left\{\right(x^g,y^g,w^g,h^g,{\theta }^g\left)\right\}$ represent the ground-truth bounding boxes, and $\left\{\right(v_x^g,v_y^g,v_w^g,v_h^g,v_{\theta }^g\left)\right\}$ denote the outputs of the fully connected layers [13].

After acquiring the rotated features and oriented RoIs, the rotated-position-sensitive RoI align, i.e., the RPS RoI Align [13], is applied to warp the features from H × W × (K × K × C) to K × K × C by using bilinear interpolation. Therefore, the orientation-robust RoI features can be acquired, which would be fed into fully connected layers for prediction. To match the oriented RoIs and ground-truth oriented RoIs, the polygon IoU is selected as the criteria.

2.4. Subspace-Based Loss Function

In this subsection, a subspace-aware classification will be introduced to form a new subspace-aware regression.

Generally speaking, to boost the learning of categories with few sample data, apart from the category-level cross-entropy loss function $L_{cls}$ [13] to penalize the mismatch between the prediction and ground truth in classification, to constrain the fine-grained relationships between targets in different categories is also a feasible strategy, with a metric learning based loss function [43,44] being an intuitive choice. However, for the remotely sensed images, as the target may change little crossing some different categories, such as the small vehicle category and the large vehicle category, while it may change a lot inside some particular category, such as the ship category in DOTA dataset, the metric learning based loss function cannot be introduced directly. To tackle this problem, a subspace-based loss function $L_{\Psi }$ is introduced to capture the relationship of different subspaces with certain similarities crossing different subspaces and within one subspace, which can be formulated by the intra-subspace loss and inter-subspace loss, respectively. The former maximizes the similarity of the subspaces with the inner-similarity property, denoted as $\left\{s_s^i\right\}(i=\mathrm{1,2},\dots ,M)$, while the latter minimizes the similarity of the subspaces with the inner-dissimilarity property, denoted as $\left\{s_d^i\right\}(j=\mathrm{1,2},\dots ,N)$. All of these constrains are evaluated by the cosine similarity metric. Therefore, the subspace-based loss function $L_{\Psi }$ can be formulated as:

$$\begin{array}{c}{L}_{\Psi }=log[1+{\sum }_{i=1}^M{\sum }_{j=1}^{N}exp(\lambda ({\alpha }_1^j{s}_d^j-{\alpha }_2^i{s}_s^i-m)\left)\right]\\ =log[1+{\sum }_{j=1}^{M}exp(\lambda {\alpha }_1^j(s_d^j-{\delta }_d)){\sum }_{i=1}^{N}exp(-\lambda {\alpha }_2^i(s_s^i-{\delta }_s)\left)\right]\end{array}$$

(7)

where $\lambda$ represents the scale factor, ${\delta }_d$ represents the inter-subspace margin, and ${\delta }_s$  represents the intra-subspace margin. In addition, ${\alpha }_1^j$ and ${\alpha }_2^i$ are non-negative factors to enhance the flexibility of the rescaling and optimization by measuring the distance from the optimum of their individual similarity scores [28], i.e., O_d for $s_d^j$ and O_s for $s_s^i$:

$$\begin{array}{cc}{\alpha }_1^j& =\mathrm{m}\mathrm{a}\mathrm{x}(0,s_d^j-O_d)\\ {\alpha }_2^i& =\mathrm{m}\mathrm{a}\mathrm{x}(0,O_s-s_s^i)\end{array}$$

(8)

To acquire a robust arc-like decision boundary, as in [28], the parameters are set to $O_s=1+m,O_d=-m,{\delta }_s=1-m,\mathrm{and}{\delta }_d=m$, in which the margin parameter $m$ controls the radius of the decision boundary, which can be viewed as a relaxation factor. By using the subspace-based loss function $L_{\Psi }$, the distribution of the categories with similar inner properties will be pulled together, while the distribution of the categories with dissimilar inner properties will be pushed apart, so the inner property of the categories with similar specificities can be efficiently learned through the training.

In accordance with the idea for the subspace-dividing approach, as the inner property of the similar categories within a subspace is more identical than that of the entire space, it is possible to form the regression process as a subspace-aware regression. Concretely, an orientation-invariant clustering for the horizontal branch, which involves the complexity, scale, appearance, and distribution information of different targets, is introduced into the oriented regression branch through the utilization of a self-expressive layer for each subspace. Concretely, given a data matrix $X=[x_1,x_2,\dots ,x_N]\in R^{d_x\times N}$, whose columns are drawn from a union of n subspaces, the self-expressiveness layer expresses each point $x_j\in R^{d_x}$ as a linear combination of other points, i.e.,

$$x_j={\sum }_{i\ne j}{c}_{ij}{x}_i$$

(9)

where ${\left\{c_{ij}\right\}}_{i\ne j}$ represent the self-expressive coefficients. An interesting characteristic of the self-expressiveness is that, the solution to Equation (9), which minimize a specific regularization function on the coefficients, exhibits a subspace-preserving property. This implies that the nonzero coefficients $c_{ij}$ only exist between $x_i$ and $x_j$ lying in the same subspace [45,46]. After applying the subspace clustering, subspace-aware regression can be acquired to assist and ensure accurate object location, as shown in Figure 5.

After acquiring the subspace-aware classification and the subspace-aware smooth L1 regression $L_{reg}={\sum }_{k\in \{x,y,w,h,\theta \}}{\mathit{smooth}}_{L1}\left(v_k^g\right)$, the overall loss function can be expressed as:

$$L=L_{cls}+L_{\Psi }+L_{reg}$$

(10)

3. Experiments and Discussion

3.1. Datasets and Implements

In the following experiments, two public datasets for object detection in remotely sensed images, i.e., the DOTA dataset [5] and HRSC2016 dataset [47], will be used to validate the effectiveness of our proposed MOON method. These datasets are very representative and influential in remotely sensed object detection, and the accuracy of the object detection in them can be directly compared from their official implements in the original papers for comparison.

The DOTA dataset is one of the largest aerial and satellite image datasets, which is collected from Google Earth and other platforms. There are 2806 images in this dataset, ranging from 800 × 800 to 4000 × 4000, which covers 15 categories. Here, the DOTA dataset is generally split into training (1/2), validation (1/6), and test (1/3).

The HRSC2016 dataset is an aerial image dataset, which is collected from the Google Earth. There are 1061 images in this dataset, ranging from 300 × 300 to 1500 × 900, which includes 20 categories of ships. There are 436 images, 181 images, and 444 images in the training, validation, and test set, respectively.

In the following experiments, the ResNet50 is selected as the backbone and the stochastic gradient descent (SGD) is selected as the network optimization method, with a mini-batch set to 100. The learning rate is set to 0.0025 with the moment set to 0.9. The average precision (AP) and the mean average precision (mAP) are selected as the evaluation criteria, which are consistent with and restricted by the online DOTA server.

3.2. Comparison with SOTA on the DOTA Dataset

In this section, our proposed MOON method will be compared with nine state-of-the-art methods for object detection in remotely sensed images, including the R2CNN [8], RRPN [9], FR-O, DCN, RT [13,48], ICN [10], Mask RCNN, HTC, R3Det [39], and BBAvector [15].

First of all, the comparison results on the public DOTA dataset are shown in the top 11 rows of

Table 1. Comparison results with the other methods on the DOTA dataset for different categories using the AP criterion.

Method	PL	BD	BR	GTF	SV	LV	SH	TC	BC	ST	SBF	RA	HA	SP	HC	mAP
R2CNN	88.5	71.2	31.7	59.3	51.9	56.2	57.3	90.8	72.8	67.4	56.7	52.8	53.1	51.9	53.6	60.7
RRPN	80.9	65.8	35.3	67.4	59.9	50.9	55.8	90.7	66.9	72.4	55.1	52.2	55.1	53.4	48.2	61.0
LR-O	81.1	77.1	32.3	72.6	48.5	49.4	50.5	89.9	72.6	73.7	61.4	58.7	54.8	59.0	48.7	62.0
DCN	80.8	77.7	37.2	75.8	58.8	51.1	63.5	88.2	75.5	78.0	57.8	64.0	57.9	59.5	49.7	65.0
Mask RCNN	89.2	76.3	50.8	66.2	78.2	75.9	86.1	90.2	81.0	81.9	45.9	57.4	64.8	63.0	47.7	70.3
HTC	89.3	77.0	52.2	66.0	77.9	75.6	86.9	90.5	80.6	80.5	48.7	57.2	69.5	64.6	52.5	71.3
R3Det	89.5	82.0	48.5	62.5	70.5	74.3	77.5	90.8	81.4	83.5	62.0	59.8	65.4	67.5	60.1	71.7
BBAvector	88.4	80.0	50.7	62.2	78.4	79.0	87.9	90.9	83.6	84.4	54.1	60.2	65.2	64.3	55.7	72.3
RT (baseline)	88.3	77.0	51.6	69.6	77.5	77.2	87.1	90.8	84.9	83.1	53.0	63.8	74.5	68.8	59.2	73.8
MOON	89.0	84.4	54.4	77.2	78.4	77.8	87.7	90.8	87.6	85.3	63.9	67.6	77.2	70.6	63.4	77.0
MOON (MS + RR)	89.1	85.7	56.6	80.3	79.1	84.9	88.0	90.9	87.6	87.6	69.5	70.7	78.3	78.4	69.4	79.8

, and the highest accuracy of each category is highlighted in bold, while the second-best is underlined. We should mention that, during the comparison, only the pure network structure is used, and the additional approaches, such as data augmentation, are not used. The results presented in the top 11 rows of Table 1 demonstrate that our proposed MOON method achieves a very competitive performance and outperforms the other compared methods both in terms of the final mAP and the AP for most categories, respectively, which has validated the effectiveness of our proposed method.

Secondly, as shown in the last row of Table 1, combining our proposed method with the Multi Scales (MS) [49] and Random Rotate (RR) [5] data augmentation methods, the final mAP can be further improved to 79.8.

3.3. Comparision for the Long-Tail Problem

In the following section, our proposed MOON method will be compared with the methods specially designed for addressing the long-tail problem, to assess the effectiveness of our proposed method. The influential RoI Transformer (RT) method is selected as the baseline method for its similar pipeline with our proposed method. And the methods for long-tail problem, i.e., the focal loss [4] and GHM loss [50], are selected as the compared methods. It can be seen from

Table 2. Comparison results with other methods for the long-tail problem using the AP criterion.

Method	PL	BD	BR	GTF	SV	LV	SH	TC	BC	ST	SBF	RA	HA	SP	HC	mAP
RT (baseline)	88.3	77.0	51.6	69.6	77.5	77.2	87.1	90.8	84.9	83.1	53.0	63.8	74.5	68.8	59.2	73.8
RT + focal loss	88.7	82.6	54.1	72.0	77.4	77.5	87.4	90.9	86.8	85.2	62.7	59.3	76.1	68.7	59.4	75.2
RT + GHM	88.7	77.4	53.9	77.4	77.6	77.6	87.7	90.8	86.8	85.6	61.9	60.1	76.1	70.5	64.3	75.8
MOON	89.0	84.4	54.4	77.2	78.4	77.8	87.7	90.8	87.6	85.3	63.9	67.6	77.2	70.6	63.4	77.0

that our proposed MOON method is superior to the other methods for the long-tail problem of remotely sensed images, particularly in the categories with few sample data, such as the soccer ball field (SBF) and roundabout (RA).

3.4. Ablation Studies

In this section, the effectiveness of each part, the multi-branch network (m-net) and the subspace-based loss function (s-loss), will be validated respectively. The ablation studies are conducted on the ship category, as in [16], which is representative and challenging for object detection in remotely sensed images due to its different scale, aspect ratio, arbitrary orientation, and dense distribution properties. Additionally, the RoI Transformer (RT) is selected as the baseline detection method for its high detection accuracy and similar feature-extraction pipeline with our proposed method. As shown in

Table 3. Results of ablation studies on our proposed method.

Method	m-net	s-loss	mAP
RT (Baseline)			72.9
RT + m-net	√		74.1
RT + s-loss		√	74.7
MOON (RT + m-net + s-loss)	√	√	75.2

, the effectiveness of each part of this proposed method has been verified, among which the s-loss takes the effect remarkably.

3.5. Effect of Each Part of the Multi-branch Network

To validate the effectiveness of each part of the multi-branch network in our proposed MOON method, the RT is selected as the baseline method as well. On this basis, the baseline method is compared with that of the shared feature decouple and the crisscross convolution separately. After that, the multi-branch network is compared, which contains both the shared feature decouple and the crisscross convolution. As shown in

Table 4. Effect of each part of our proposed multi-branch network.

Method	Decouple	Crisscross	mAP
RT (Baseline)			72.9
RT + Decouple	√		73.8
RT + Crisscross		√	73.3
MOON (RT + Decouple + Crisscross)	√	√	74.1

, the shared feature decouple improves the accuracy of the object detection by 0.9% through eliminating the interaction between the learning of the horizontal and rotated features, which is significant but generally ignored in the object detection of remotely sensed images. And the crisscross convolution structure improves the object detection accuracy by 0.4% through enhancing the rotated features. Consequently, the overall m-net improves the accuracy of the object detection by 1.2%, which validates the effectiveness of the multi-branch network.

3.6. Effect of Each Part of the Subspace-based Loss Function

To verify the effectiveness of each part of the subspace-based loss function in our proposed MOON method, the s-loss is divided into subspace-aware classification (SC), subspace-aware regression (SR), and the s-loss function. However, when the ablation study is conducted on the ship category exclusively, the subspace aware is difficult to apply for the very limited sample amount in this category. Therefore, the small vehicle category is added into this experiment. Both the baseline method and our proposed method are trained on the ship and small vehicle categories. As depicted in

Table 5. Effect of each part of our proposed subspace-based loss function.

Method	SC	SR	mAP
RT (Baseline)			72.9
RT + SC	√		73.9
RT + SR		√	73.8
MOON (RT + SC + SR)	√	√	74.7

, the s-loss improves the accuracy of the object detection by 1.8%, which validates the effectiveness of the subspace-based loss function.

3.7. Comparison on HRSC2016 Dataset

The comparison experiments are also conducted on the HRSC2016 dataset to verify the effectiveness and the universality of our proposed method. In order to assess its performance, our proposed method is compared with the official object detection methods of HRSC2016, i.e., the RC2, as shown in

Table 6. Results on the HRSC2016 dataset.

Method	mAP
RC2	75.7
R2PN	79.6
R2CNN	79.7
RT	80.1
BBAvector	82.8
MOON	84.9

. In the evaluation, the voc07 metric is used to remain consistent with that of the RT method. Since the HRSC2016 is exclusively focuses on the ship category, the subspace-aware classification of the s-loss has been removed. From Table 6, it can be seen that our proposed method outperforms the other object detection methods significantly.

4. Conclusions

To solve the sample data insufficiency problem and the long-tail problem in the object detection of remotely sensed images, a subspace-dividing strategy and a subspace-based multi-branch network is proposed. Specifically, a combination index is defined to depict the similarity between different categories, a subspace-dividing strategy is proposed based on this combination index, and a new subspace-based loss function is devised to integrate the sample data from similar categories within a subspace and to balance the amounts of sample data between different subspaces. Moreover, a subspace-based multi-branch network is constructed to ensure the subspace-aware regression. Experiments on the DOTA and HRSC2016 datasets demonstrated the superiority of our proposed method.