Laboratory Characterisation of a Commercial RGB CMOS Camera for Measuring Night Sky Brightness
Abstract
:1. Introduction
2. Materials
2.1. The Sky Quality Meter
2.2. The Analysed Camera
2.3. The Laboratory Spectroradiometer
2.4. The UV Radiometer
2.5. The Coloured LED Source
2.6. Measurements of Night Sky Spectral Radiance
3. Methods
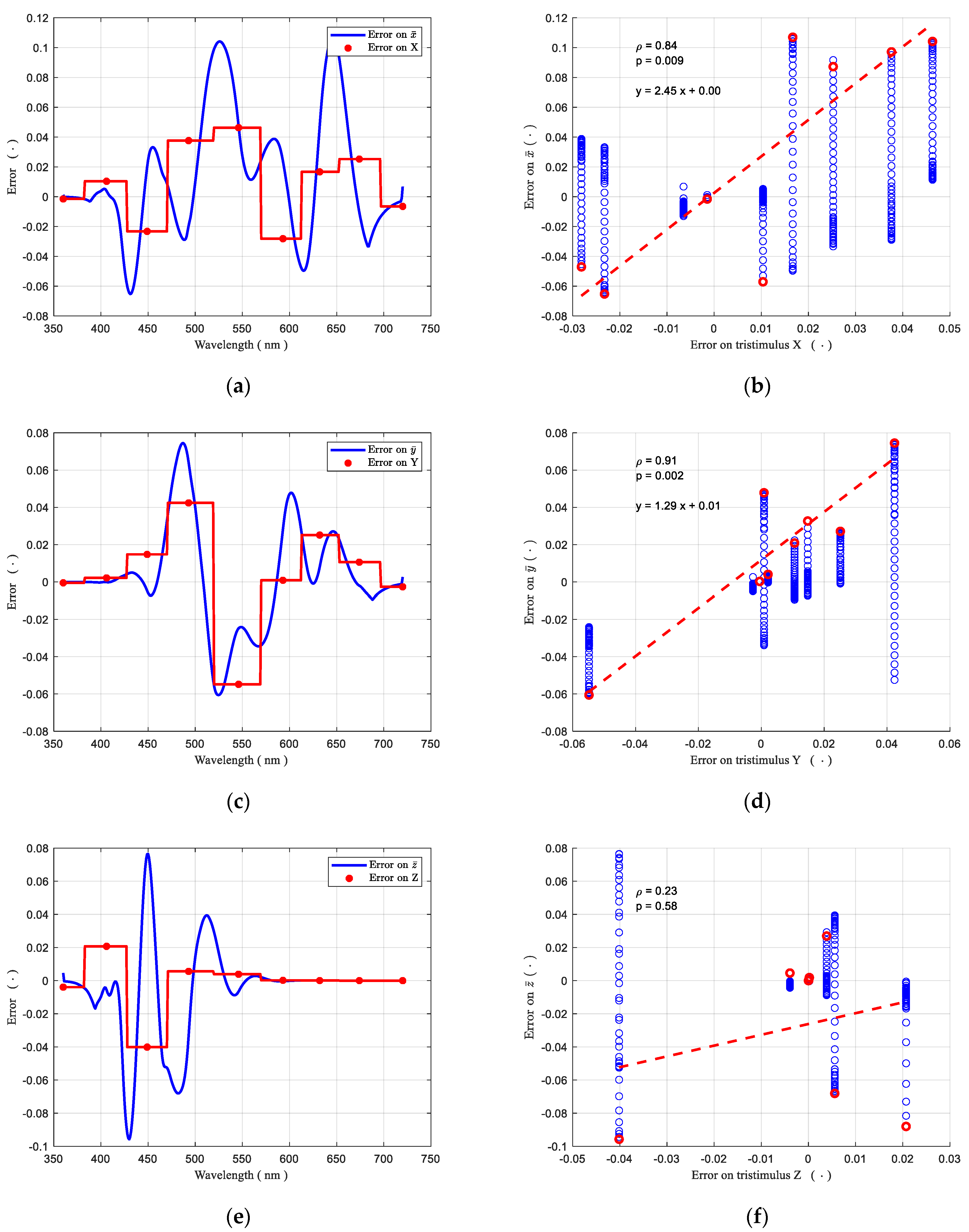
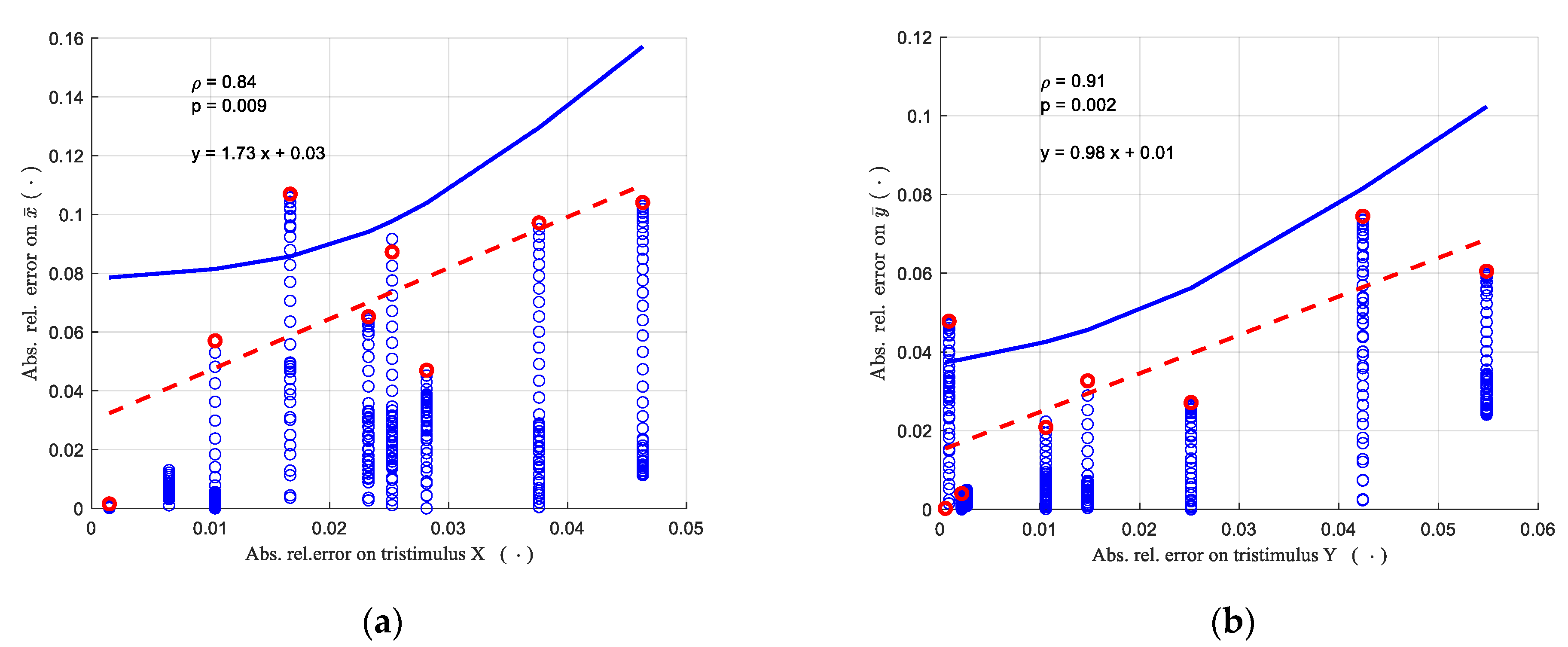
3.1. Measures for the Spectral Responsivity Estimate
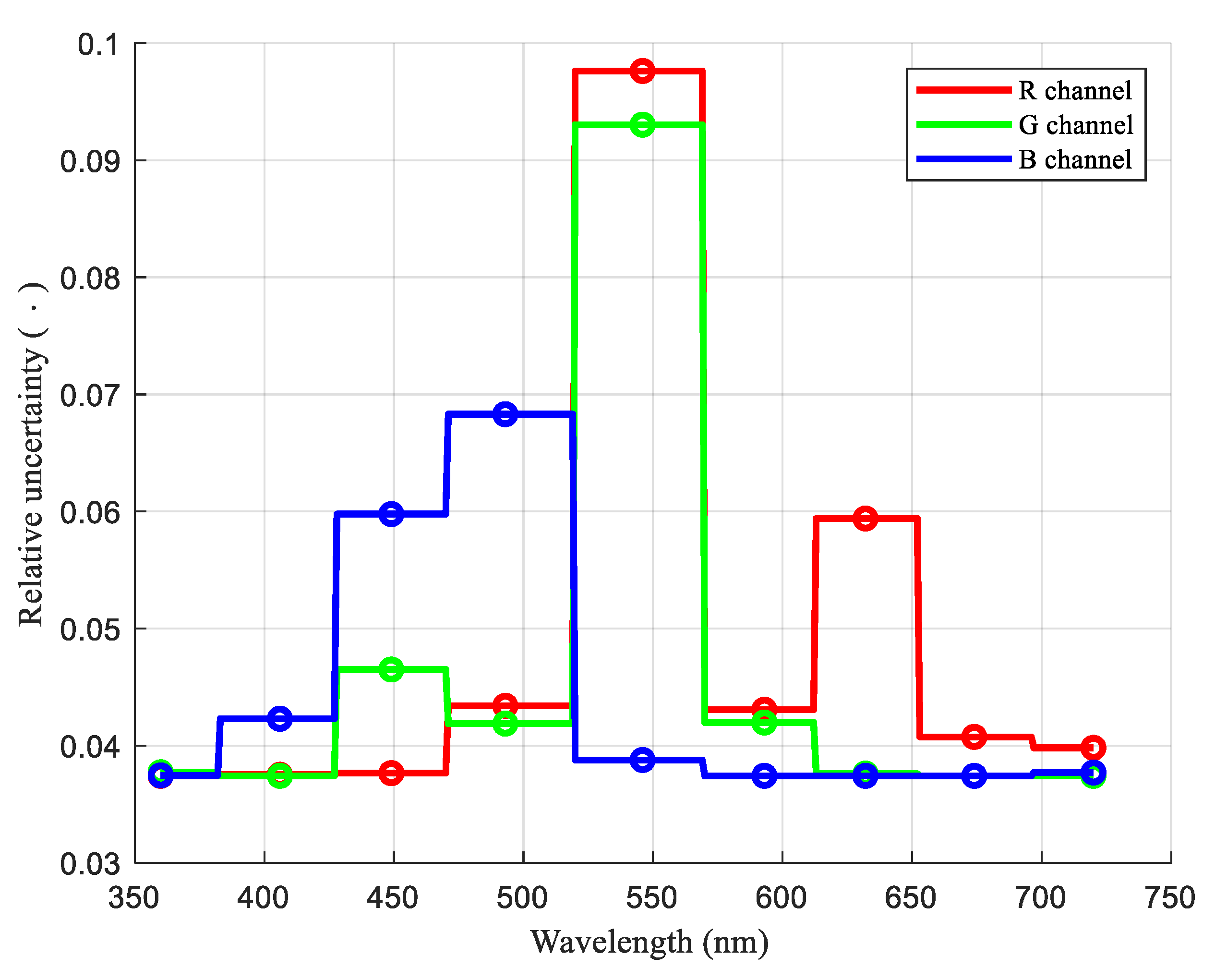
3.2. Uncertainty on the Spectral Responsivity Estimate
3.3. Analysis of the SQM Radiometer
3.4. Analysis of the Camera
4. Results
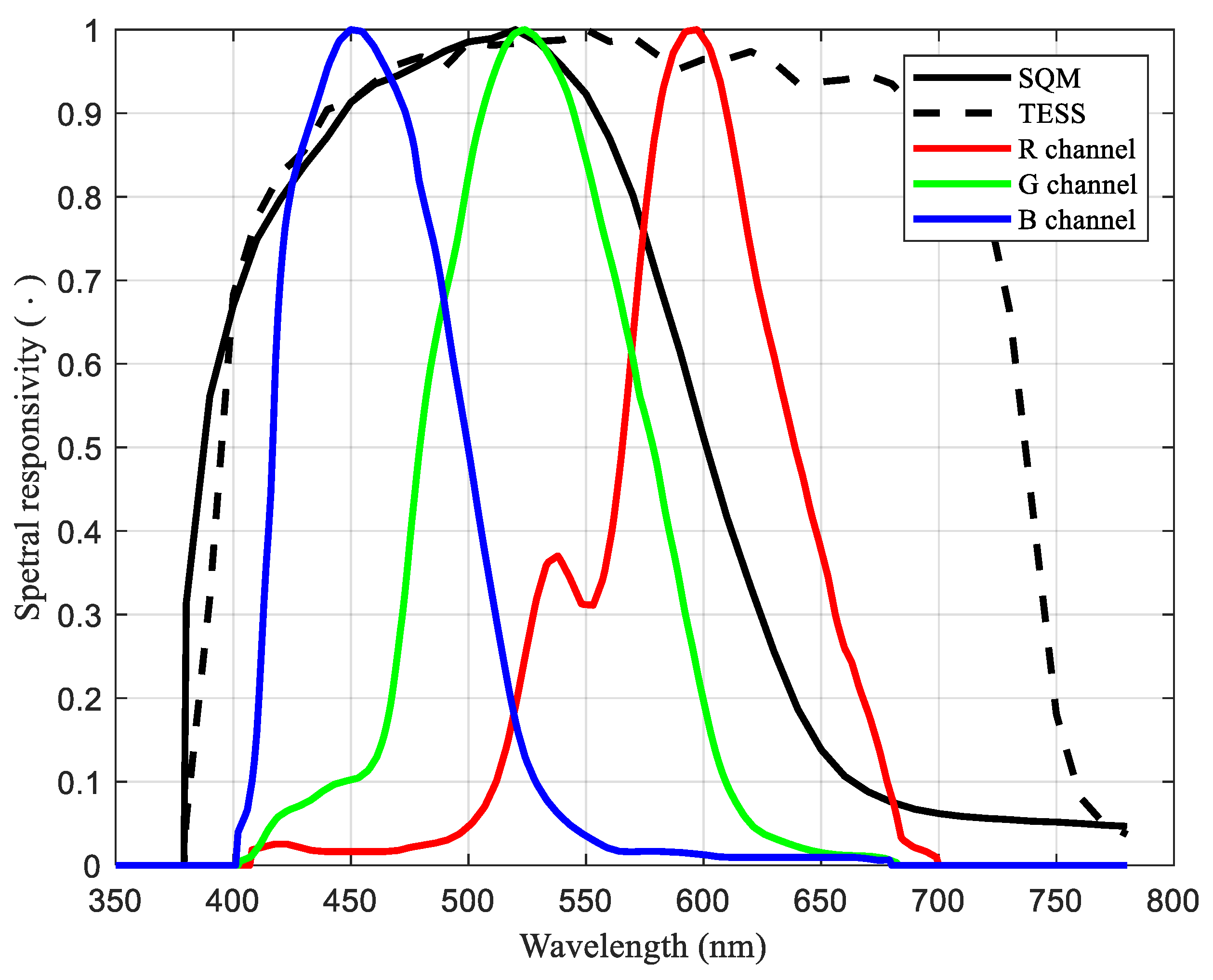
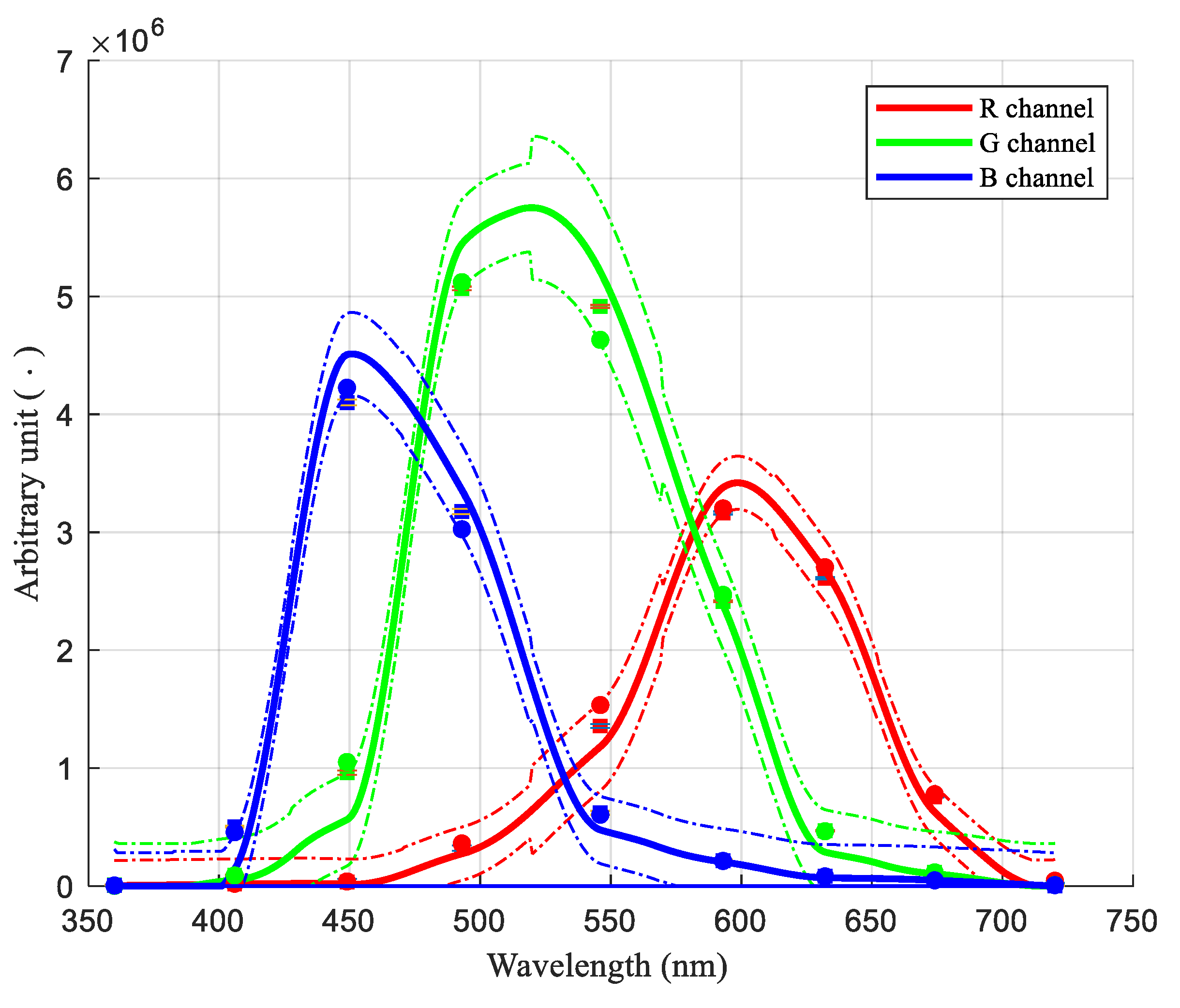
4.1. Spectral Sensitivity of the RGB Channels
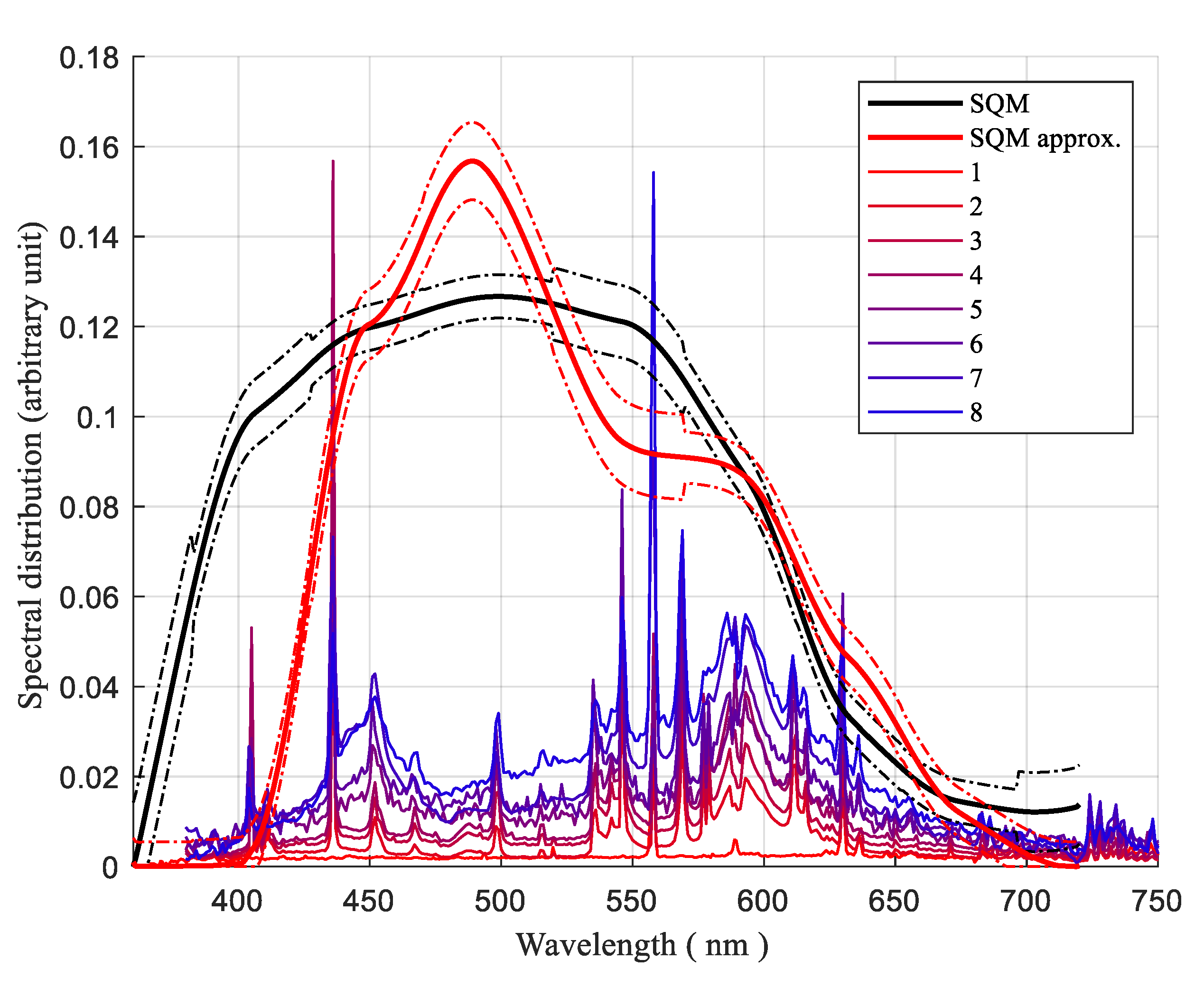
4.2. SQM Spectral Responsivity and Its Least Square Approximation
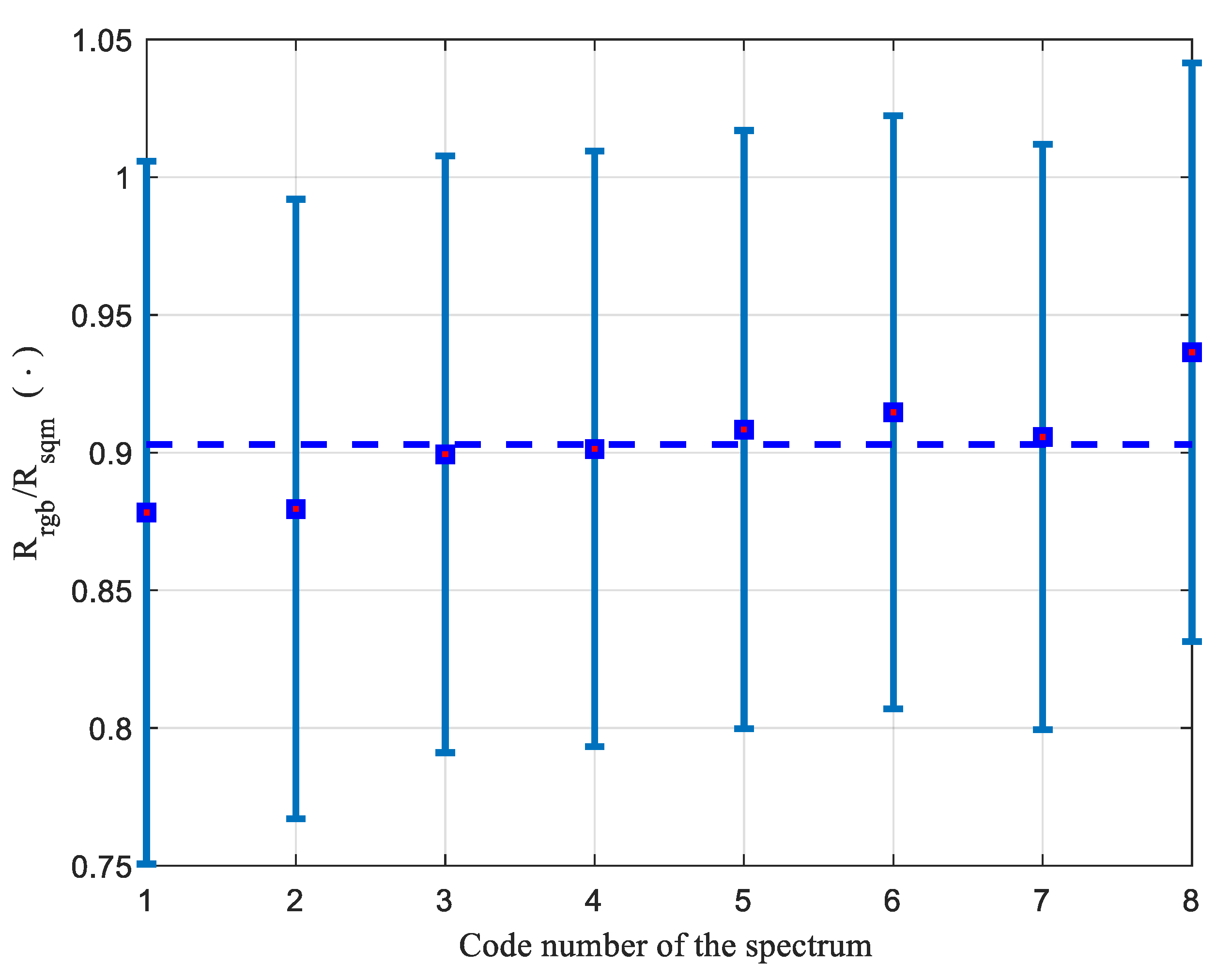
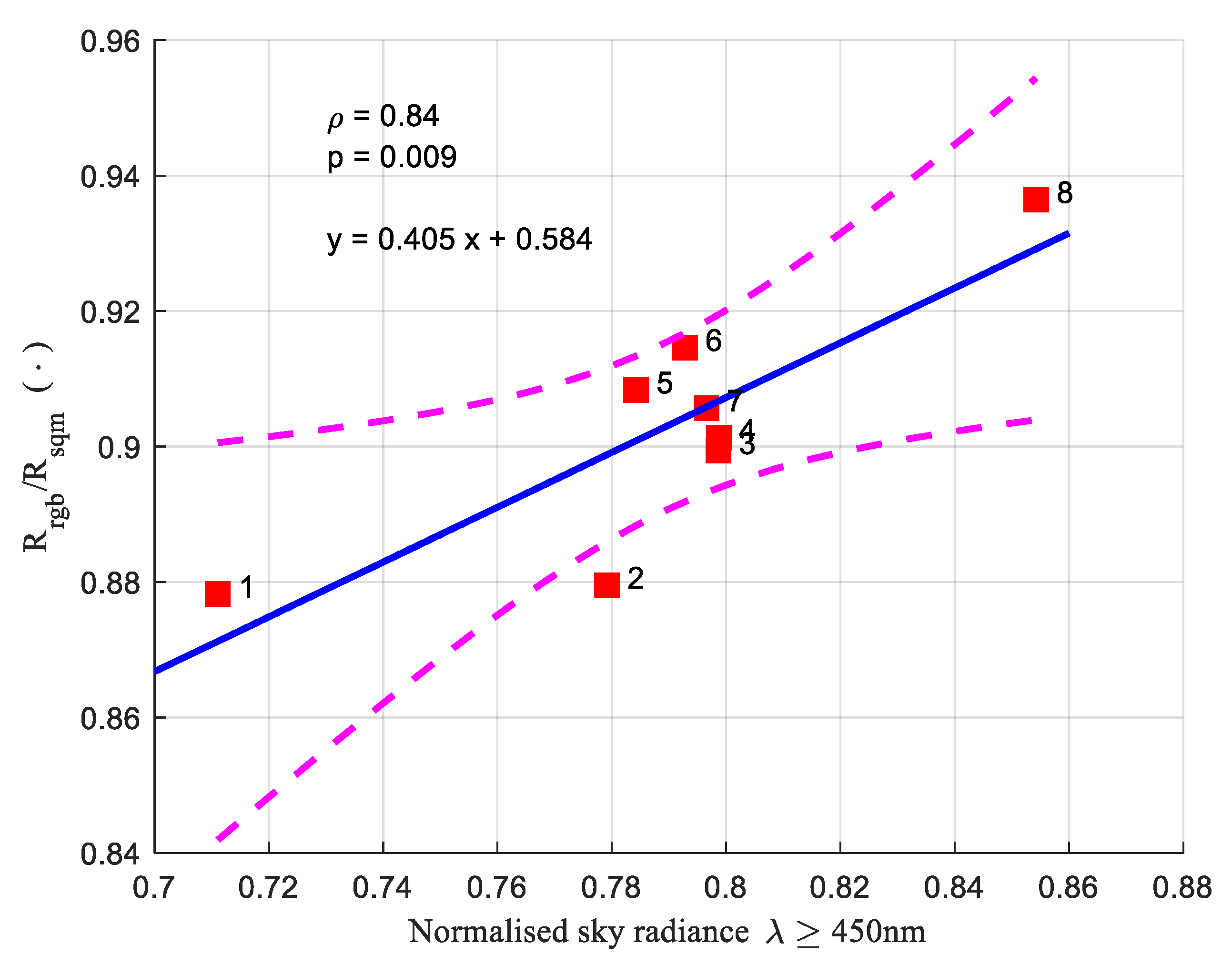
4.3. Cases of Real Night Sky Spectral Radiances
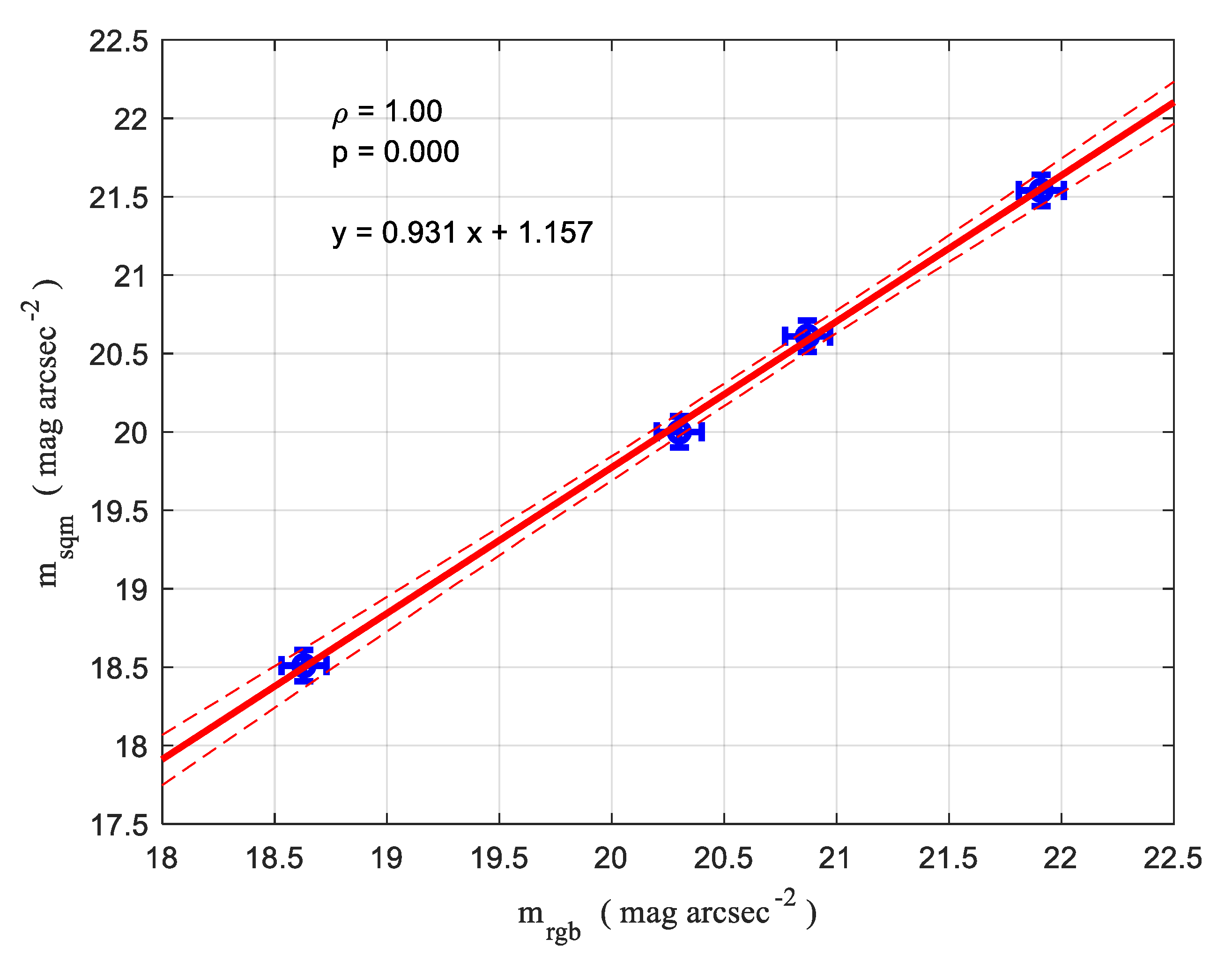
4.4. Comparison between Field Measures from Real SQMs and the Synthetic SQM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jechow, A.; Hölker, F.; Kolláth, Z.; Gessner, M.O.; Kyba, C.C. Evaluating the summer night sky brightness at a research field site on Lake Stechlin in northeastern Germany. J. Quant. Spectrosc. Radiat. Transf. 2016, 181, 24–32. [Google Scholar] [CrossRef]
- Jechow, A.; Kolláth, Z.; Lerner, A.; Hänel, A.; Shashar, N.; Hölker, F.; Kyba, C.C. Measuring Light Pollution with Fisheye Lens Imagery from A Moving Boat–A Proof of Concept. Int. J. Sustain. Light. 2017, 19, 15–25. [Google Scholar] [CrossRef]
- Hänel, A.; Posch, T.; Ribas, S.J.; Aubé, M.; Duriscoe, D.; Jechow, A.; Kollath, Z.; Lolkema, D.E.; Moore, C.; Schmidt, N.; et al. Measuring night sky brightness: Methods and challenges. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 278–290. [Google Scholar] [CrossRef]
- Fiorentin, P.; Bertolo, A.; Cavazzani, S.; Ortolani, S. Calibration of digital compact cameras for sky quality measures. J. Quant. Spectrosc. Radiat. Transf. 2020, 255, 107235. [Google Scholar] [CrossRef]
- Kolláth, Z.; Cool, A.; Jechow, A.; Kolláth, K.; Száz, D.; Tong, K.P. Introducing the dark sky unit for multi-spectral measurement of the night sky quality with commercial digital cameras. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107162. [Google Scholar] [CrossRef]
- Burggraaff, O.; Schmidt, N.; Zamorano, J.; Pauly, K.; Pascual, S.; Tapia, C.; Spyrakos, E.; Snik, F. Standardized spectral and radiometric calibration of consumer cameras. Opt. Express 2019, 27, 19075–19101. [Google Scholar] [CrossRef] [PubMed]
- Cardiel, N.; Zamorano, J.; Bará, S.; Sánchez de Miguel, A.; Cabello, C.; Gallego, J.; García, L.; González, R.; Izquierdo, J.; Pascual, S.; et al. Synthetic RGB photometry of bright stars: Definition of the standard photometric system and UCM library of spectrophotometric spectra. Mon. Not. R. Astron. Soc. 2021, 504, 3730–3748. [Google Scholar] [CrossRef]
- Bertolo, A.; Binotto, R.; Ortolani, S.; Sapienza, S. Measurements of night sky brightness in the Veneto region of Italy: Sky quality meter network results and differential photometry by digital single lens reflex. J. Imaging 2019, 5, 56. [Google Scholar] [CrossRef]
- Bará, S.; Lima, R.C.; Zamorano, J. Monitoring long-term trends in the anthropogenic night sky brightness. Sustainability 2019, 11, 3070. [Google Scholar] [CrossRef]
- Cinzano, P. Night Sky Photometry with Sky Quality Meter. ISTIL Int. Rep. 2005, 9, 1–14. [Google Scholar]
- Available online: http://www.unihedron.com/ (accessed on 17 May 2023).
- Zamorano, J.; García, C.; Tapia, C.; de Miguel, A.S.; Pascual, S.; Gallego, J. Stars4all night sky brightness photometer. Int. J. Sustain. Light. 2016, 18, 49–54. [Google Scholar] [CrossRef]
- Bará, S.; Tapia, C.E.; Zamorano, J. Absolute radiometric calibration of TESS-W and SQM night sky brightness sensors. Sensors 2019, 19, 1336. [Google Scholar] [CrossRef]
- Available online: http://astrosurf.com/buil/50d/test.htm (accessed on 1 August 2023).
- Cavazzani, S.; Ortolani, S.; Bertolo, A.; Binotto, R.; Fiorentin, P.; Carraro, G.; Zitelli, V. Satellite measurements of artificial light at night: Aerosol effects. Mon. Not. R. Astron. Soc. 2020, 499, 5075–5089. [Google Scholar] [CrossRef]
- Cavazzani, S.; Ortolani, S.; Bertolo, A.; Binotto, R.; Fiorentin, P.; Carraro, G.; Saviane, I.; Zitelli, V. Sky Quality Meter and satellite correlation for night cloud-cover analysis at astronomical sites. Mon. Not. R. Astron. Soc. 2020, 493, 2463–2471. [Google Scholar] [CrossRef]
- Puschnig, J.; Näslund, M.; Schwope, A.; Wallner, S. Correcting sky-quality-meter measurements for ageing effects using twilight as calibrator. Mon. Not. R. Astron. Soc. 2021, 502, 1095–1103. [Google Scholar] [CrossRef]
- Fiorentin, P.; Cavazzani, S.; Ortolani, S.; Bertolo, A.; Binotto, R. Instrument assessment and atmospheric phenomena in relation to the night sky brightness time series. Measurement 2022, 191, 110823. [Google Scholar] [CrossRef]
- Puschnig, J.; Wallner, S.; Schwope, A.; Näslund, M. Long-term trends of light pollution assessed from SQM measurements and an empirical atmospheric model. Mon. Not. R. Astron. Soc. 2023, 518, 4449–4465. [Google Scholar] [CrossRef]
- Fiorentin, P.; Binotto, R.; Cavazzani, S.; Bertolo, A.; Ortolani, S.; Saviane, I. Long-Time Trends in Night Sky Brightness and Ageing of SQM Radiometers. Remote Sens. 2022, 14, 5787. [Google Scholar] [CrossRef]
- Kolláth, Z.; Dömény, A. Night sky quality monitoring in existing and planned dark sky parks by digital cameras. Int. J. Sustain. Light. 2017, 19, 61–68. [Google Scholar] [CrossRef]
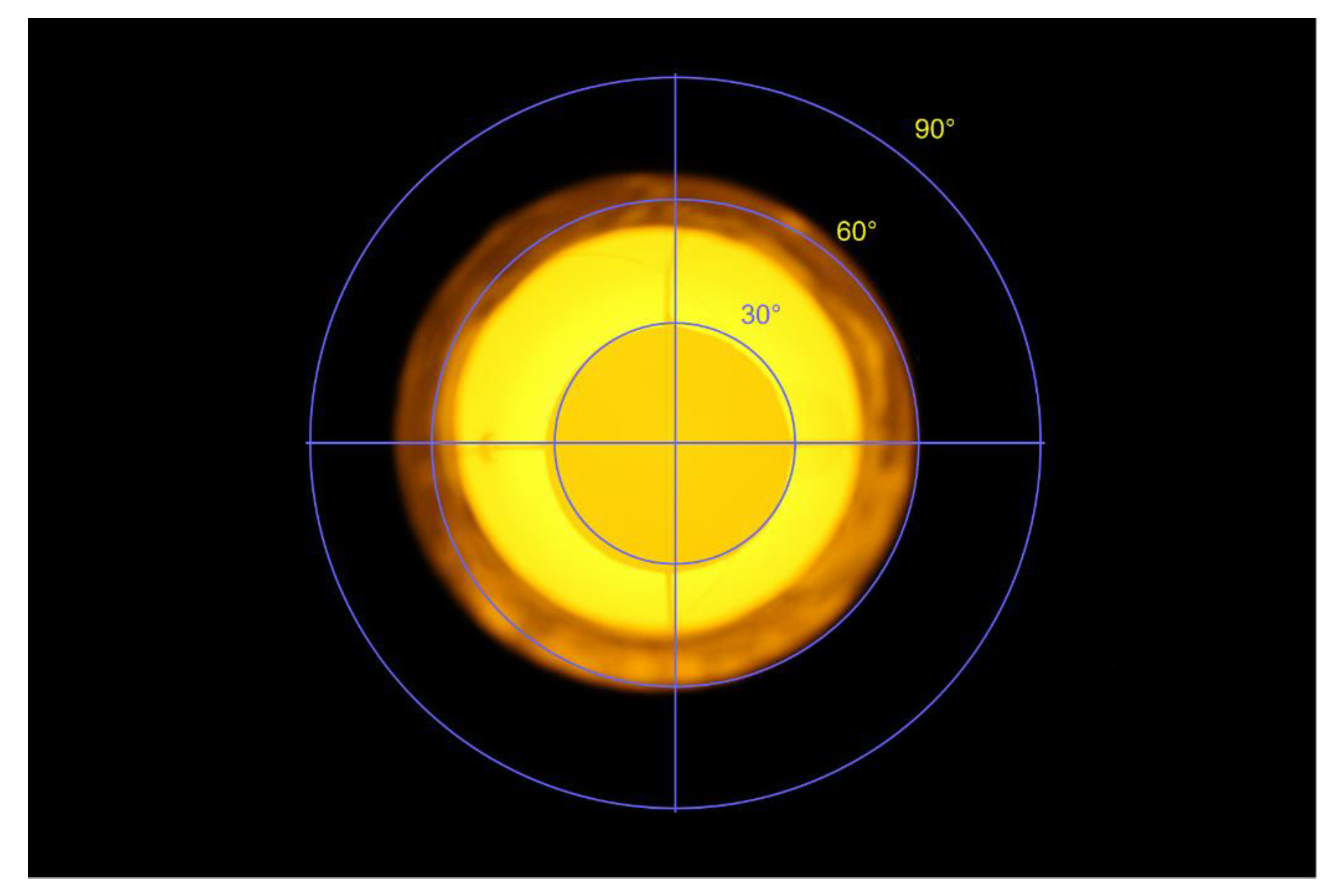
- Bartolomei, M.; Olivieri, L.; Bettanini, C.; Cavazzani, S.; Fiorentin, P. Verification of Angular Response of Sky Quality Meter with Quasi-Punctual Light Sources. Sensors 2021, 21, 7544. [Google Scholar] [CrossRef]
- Jechow, A.; Kyba, C.C.; Hölker, F. Beyond all-sky: Assessing ecological light pollution using multi-spectral full-sphere fisheye lens imaging. J. Imaging 2019, 5, 46. [Google Scholar] [CrossRef] [PubMed]
- Jechow, A.; Kyba, C.C.; Hölker, F. Mapping the brightness and color of urban to rural skyglow with all-sky photometry. J. Quant. Spectrosc. Radiat. Transf. 2020, 250, 106988. [Google Scholar] [CrossRef]
- Fiorentin, P.; Scroccaro, A. Detector-based calibration for illuminance and luminance meters—Experimental results. IEEE Trans. Instrum. Meas. 2010, 59, 1375–1381. [Google Scholar] [CrossRef]
- Manual of DeltaOhm Quantum-Photo-Radiometer HD 9021. Available online: http://www.deltaohm.co.kr/main/products/pdisplay.php?active=product&no=538&thiscode=100201 (accessed on 25 August 2023).
- Available online: https://c7076-control.chem.sfu.ca/interlock_monitoring_system_resources/usb6008.pdf (accessed on 22 May 2023).
- Available online: https://it.mathworks.com/help/matlab/learn_matlab/matrices-and-arrays.html?lang=en (accessed on 17 March 2023).
- Wyszecki, G.; Stiles, W.S. Color Science: Concepts and Methods, Quantitative Data and Formulae; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Coffin, D. Decoding Raw Digital Photos in Linux. Available online: https://www.dechifro.org/dcraw/ (accessed on 1 March 2023).





| Error (%) vs. Peak Wavelength (nm) | Average of Abs Error (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tristimulus Func. | 360 | 405 | 450 | 490 | 545 | 590 | 630 | 675 | 720 | ||
| 1st approx. | −0.2 | 1.1 | −2.5 | 4.0 | 5.0 | −3.0 | 1.8 | 2.7 | 0.7 | 2.3 | |
| 2nd approx. | 0.0 | −0.2 | 0.5 | 1.4 | 4.7 | 1.9 | 2.7 | 0.7 | 0.4 | 1.4 | |
| 1st approx. | 0.0 | 0.2 | 1.5 | 4.2 | −5.5 | 0.1 | 2.5 | 1.1 | −0.3 | 1.7 | |
| 2nd approx. | 0.0 | 0.0 | 0.40 | 3.3 | −2.9 | 1.7 | 1.1 | 0.1 | −0.2 | 1.1 | |
| 1st approx. | −0.1 | 3.7 | −7.2 | 1.0 | 0.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1.5 | |
| 2nd approx. | 0.0 | −1.1 | 1.7 | −1.6 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | |
| 1st Approx. Error | 2nd Approx Error | |||
|---|---|---|---|---|
| Tristimulus Function | Max Abs (%) | Std (%) | Max Abs (%) | Std (%) |
| 11 | 5.0 | 11 | 4.2 | |
| 8.4 | 3.8 | 7.5 | 2.8 | |
| 14 | 3.9 | 9.6 | 2.8 | |
| Error (%) vs. Peak Wavelength (nm) | Average of Abs Error (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Camera Channel | 360 | 405 | 450 | 490 | 545 | 590 | 630 | 675 | 720 | |
| R | 0.0 | 0.1 | 0.1 | 1.2 | 5.2 | 1.1 | 2.7 | 0.7 | 0.5 | 1.3 |
| G | 0.1 | 0.0 | 1.6 | 0.9 | −4.9 | 1.0 | −0.1 | 0.0 | 0.1 | 1.0 |
| B | −0.1 | −1.0 | 2.8 | −3.3 | −0.3 | 0.0 | 0.0 | 0.0 | 0.1 | 0.9 |
| Error (%) vs. Peak Wavelength (nm) | Average of Abs Error (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Instrument | 360 | 405 | 450 | 490 | 545 | 590 | 630 | 675 | 720 | |
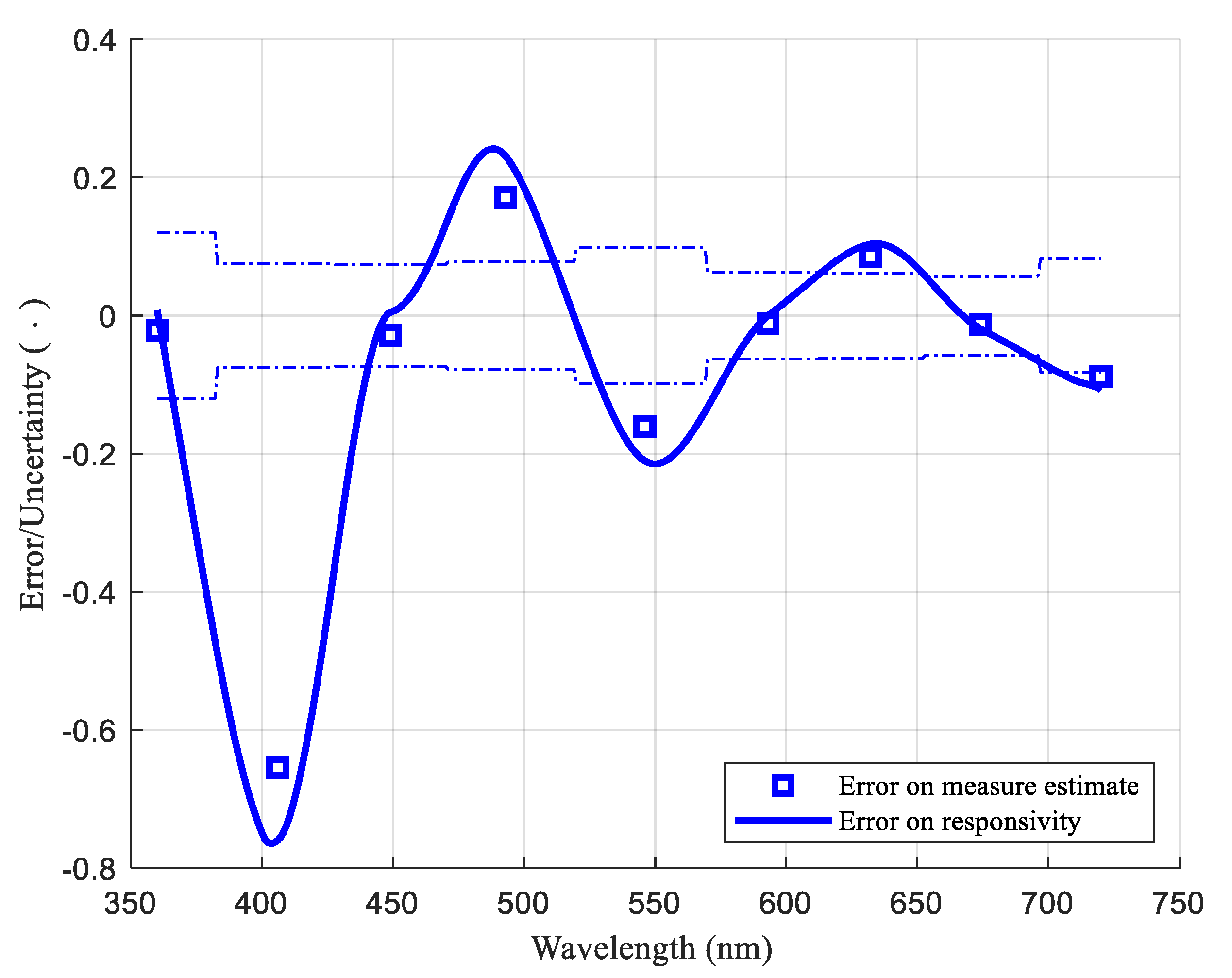
| SQM | 6.1 | 2.7 | 0.6 | −0.2 | −3.0 | 1.3 | 0.7 | 0.0 | −3.4 | 0.5 |
| Site | SQM | SQC sw (a) | Δ SQC sw | RGB | Δ RGB | Expected Δ RGB |
|---|---|---|---|---|---|---|
| Mößna (Austria) | 21.54 | 21.52 | −0.02 | 21.91 | 0.37 | 0.15 (0.31 (b)) |
| Asiago Ekar (Italy) | 20.61 | 20.53 | −0.08 | 20.87 | 0.26 | 0.11 (0.24 (b)) |
| Ca’ di Mezzo (Italy) | 20.00 | 19.95 | −0.05 | 20.30 | 0.30 | NA |
| Padova (Italy) | 18.51 (c) | 18.40 | −0.11 | 18.63 | 0.12 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorentin, P.; Bertolo, A.; Cavazzani, S.; Ortolani, S. Laboratory Characterisation of a Commercial RGB CMOS Camera for Measuring Night Sky Brightness. Remote Sens. 2023, 15, 4196. https://doi.org/10.3390/rs15174196
Fiorentin P, Bertolo A, Cavazzani S, Ortolani S. Laboratory Characterisation of a Commercial RGB CMOS Camera for Measuring Night Sky Brightness. Remote Sensing. 2023; 15(17):4196. https://doi.org/10.3390/rs15174196
Chicago/Turabian StyleFiorentin, Pietro, Andrea Bertolo, Stefano Cavazzani, and Sergio Ortolani. 2023. "Laboratory Characterisation of a Commercial RGB CMOS Camera for Measuring Night Sky Brightness" Remote Sensing 15, no. 17: 4196. https://doi.org/10.3390/rs15174196
APA StyleFiorentin, P., Bertolo, A., Cavazzani, S., & Ortolani, S. (2023). Laboratory Characterisation of a Commercial RGB CMOS Camera for Measuring Night Sky Brightness. Remote Sensing, 15(17), 4196. https://doi.org/10.3390/rs15174196






