Relationship between CO2 Fertilization Effects, and Stand Age, Stand Type, and Site Conditions
Abstract
:1. Introduction
2. Dataset
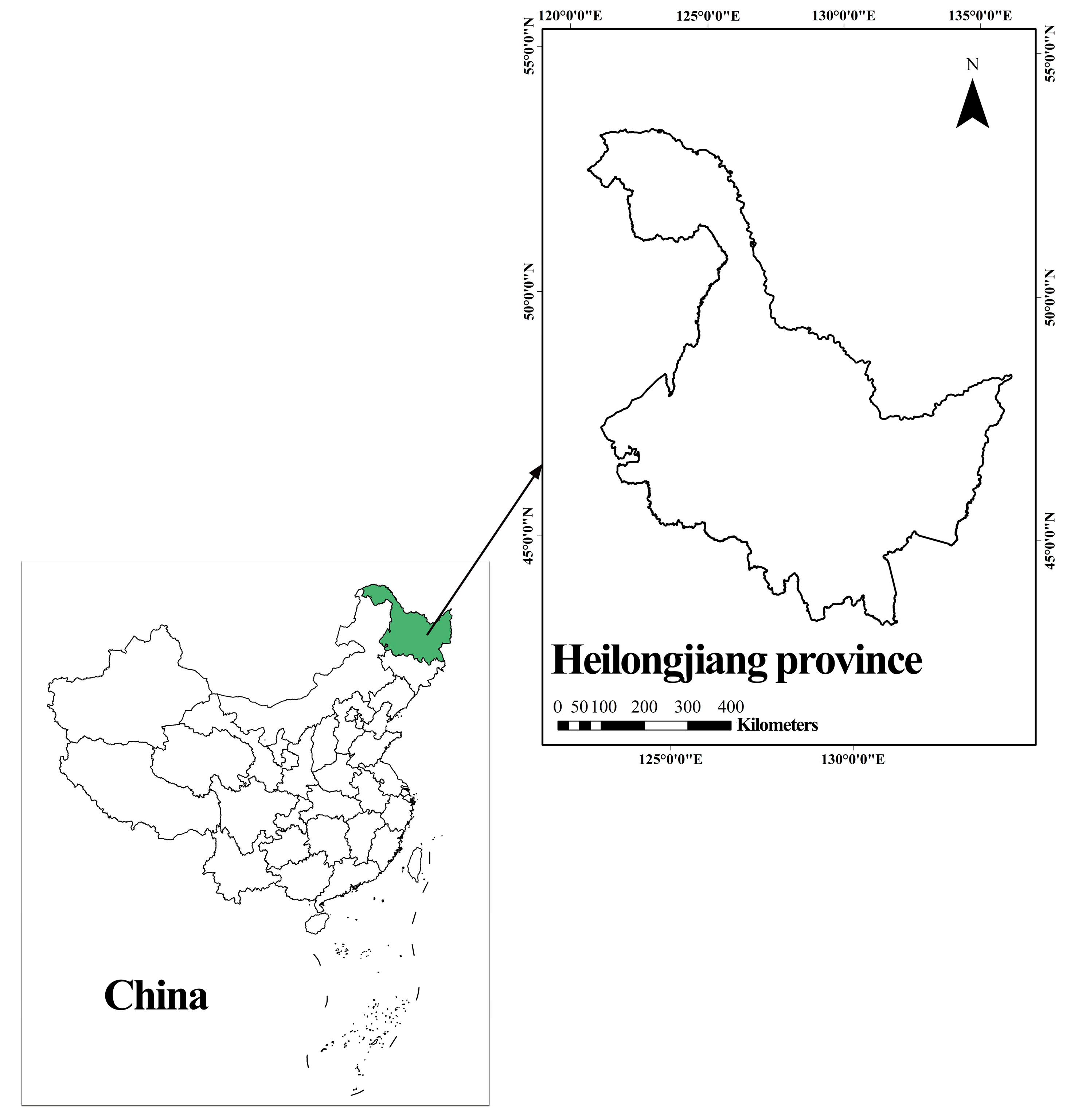
2.1. Study Region
2.2. Study Data
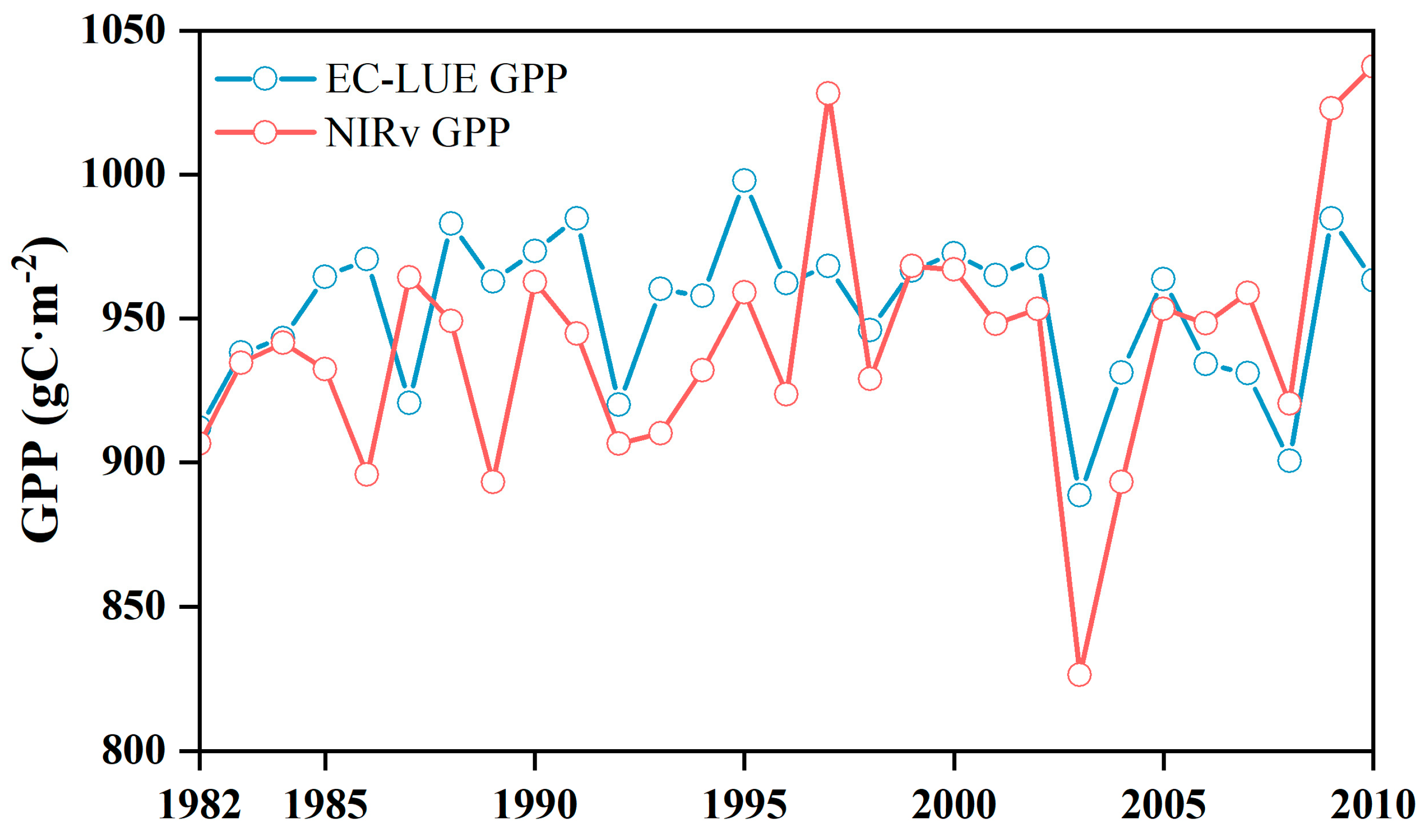
2.2.1. GPP Data
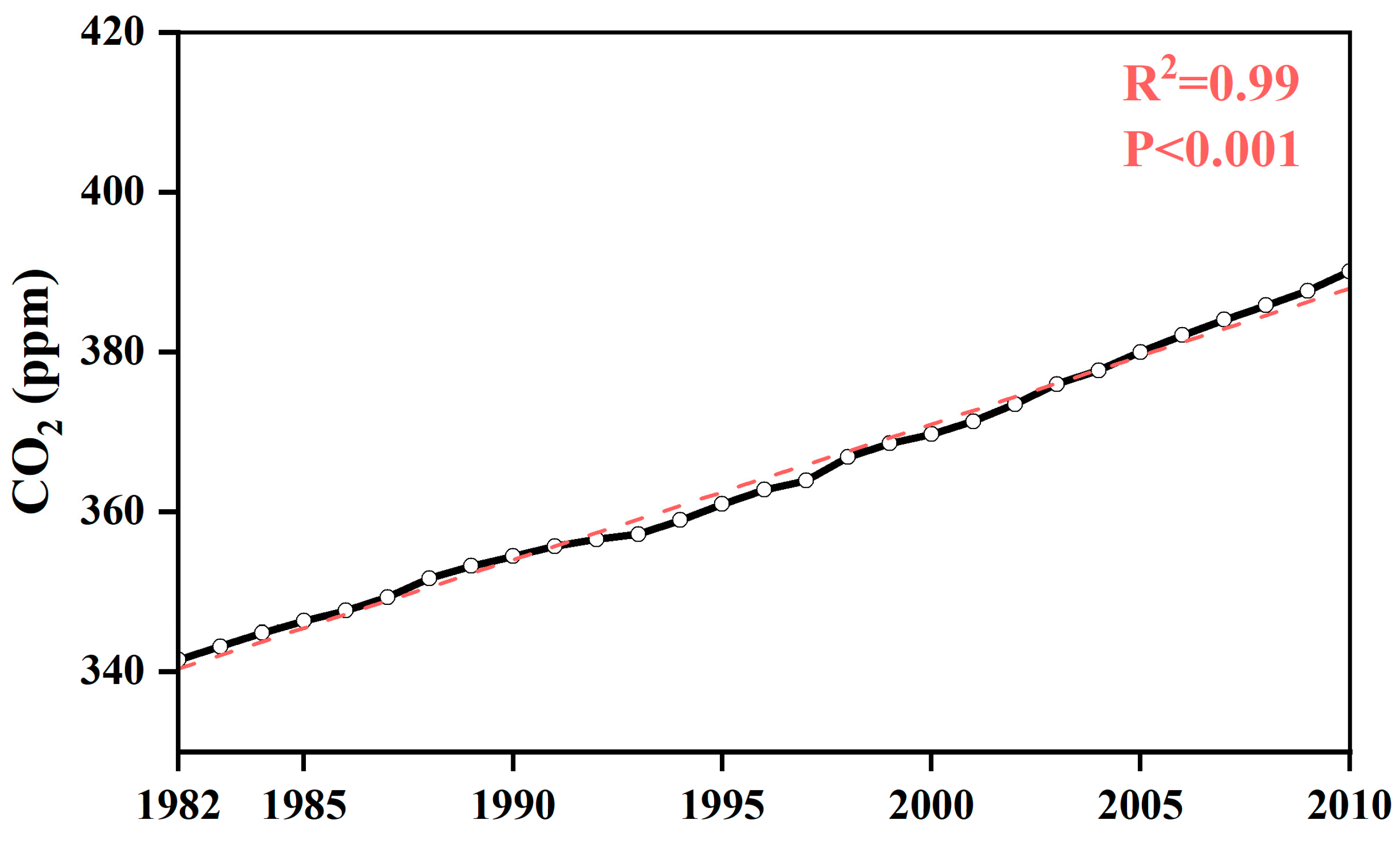
2.2.2. Environmental and Climatic Data
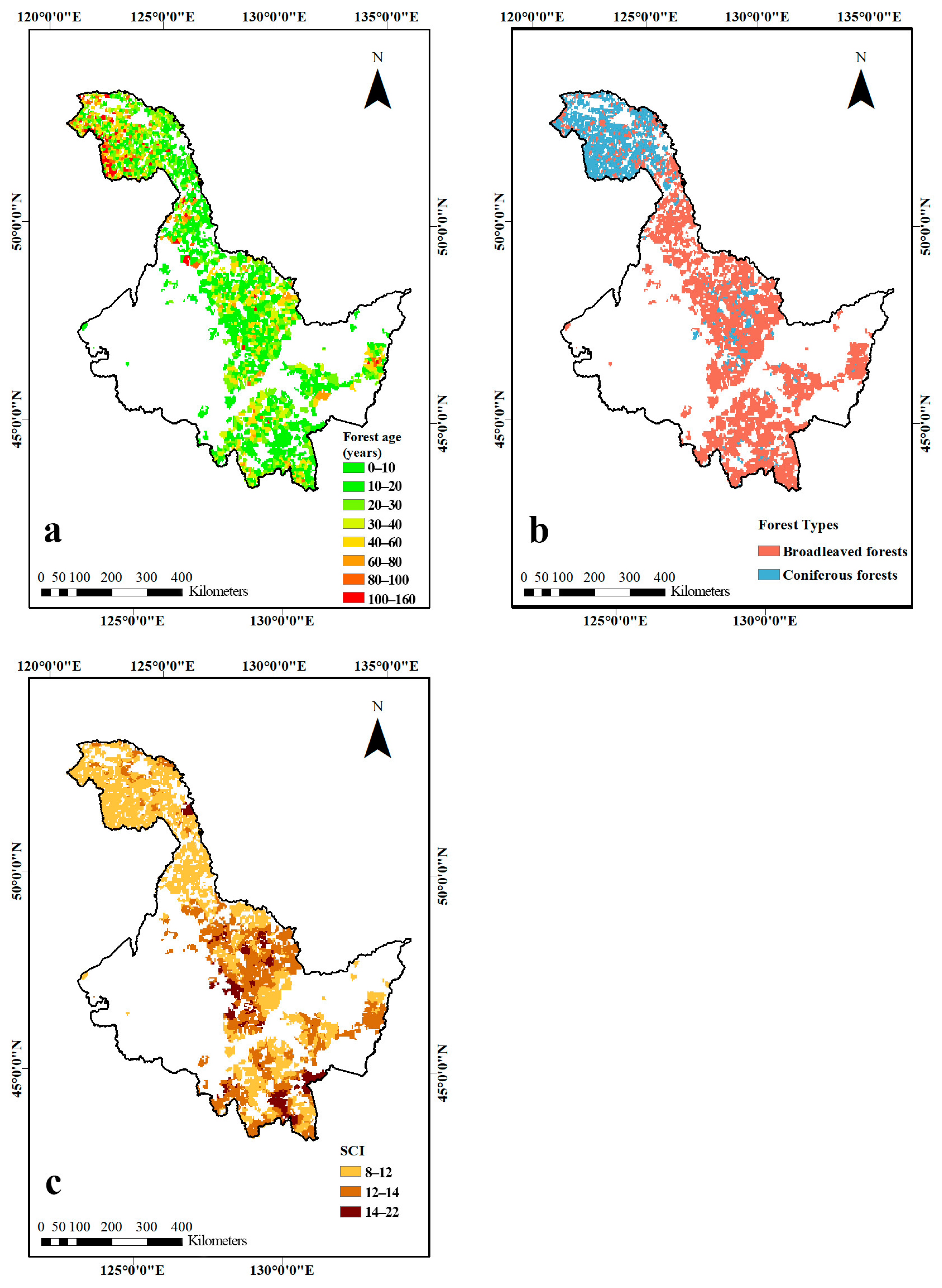
2.2.3. Stand Type, Stand Age, and Site Condition
3. Methods
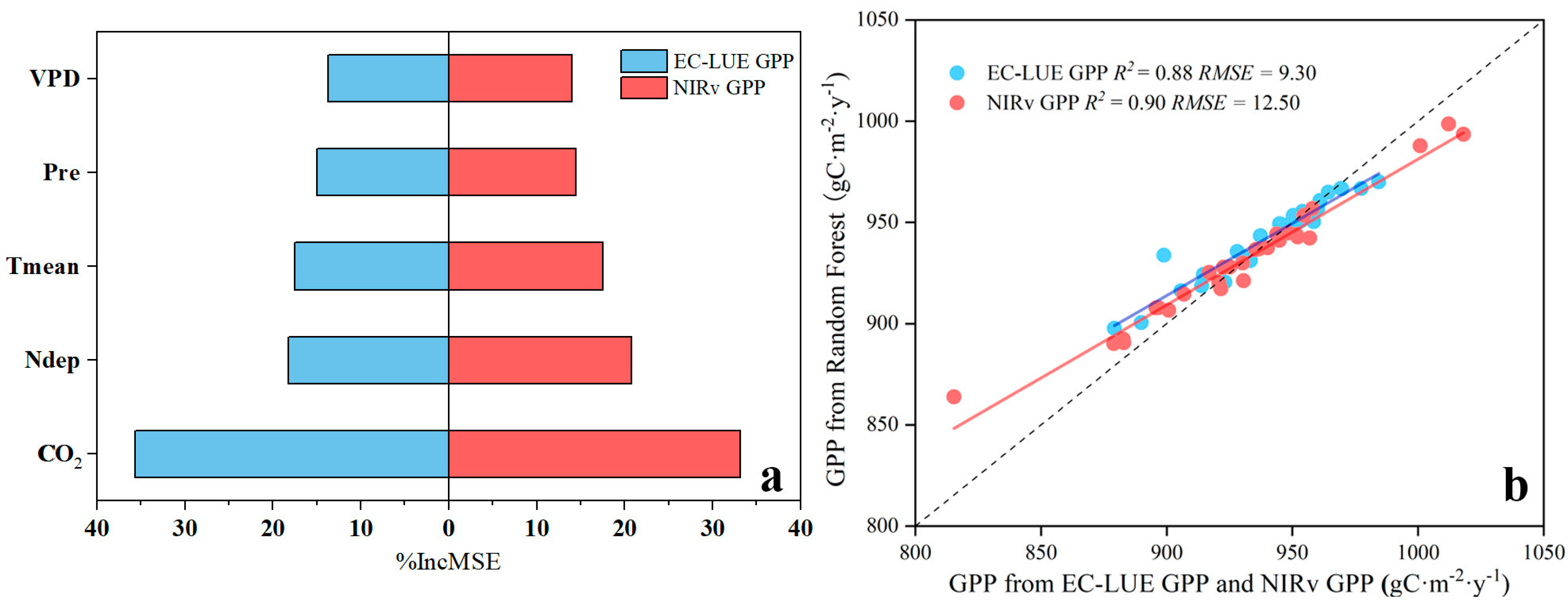
3.1. Variable Selection and Importance Analysis
3.2. Calculation of GPP Responses to Atmospheric CO2 Concentrations
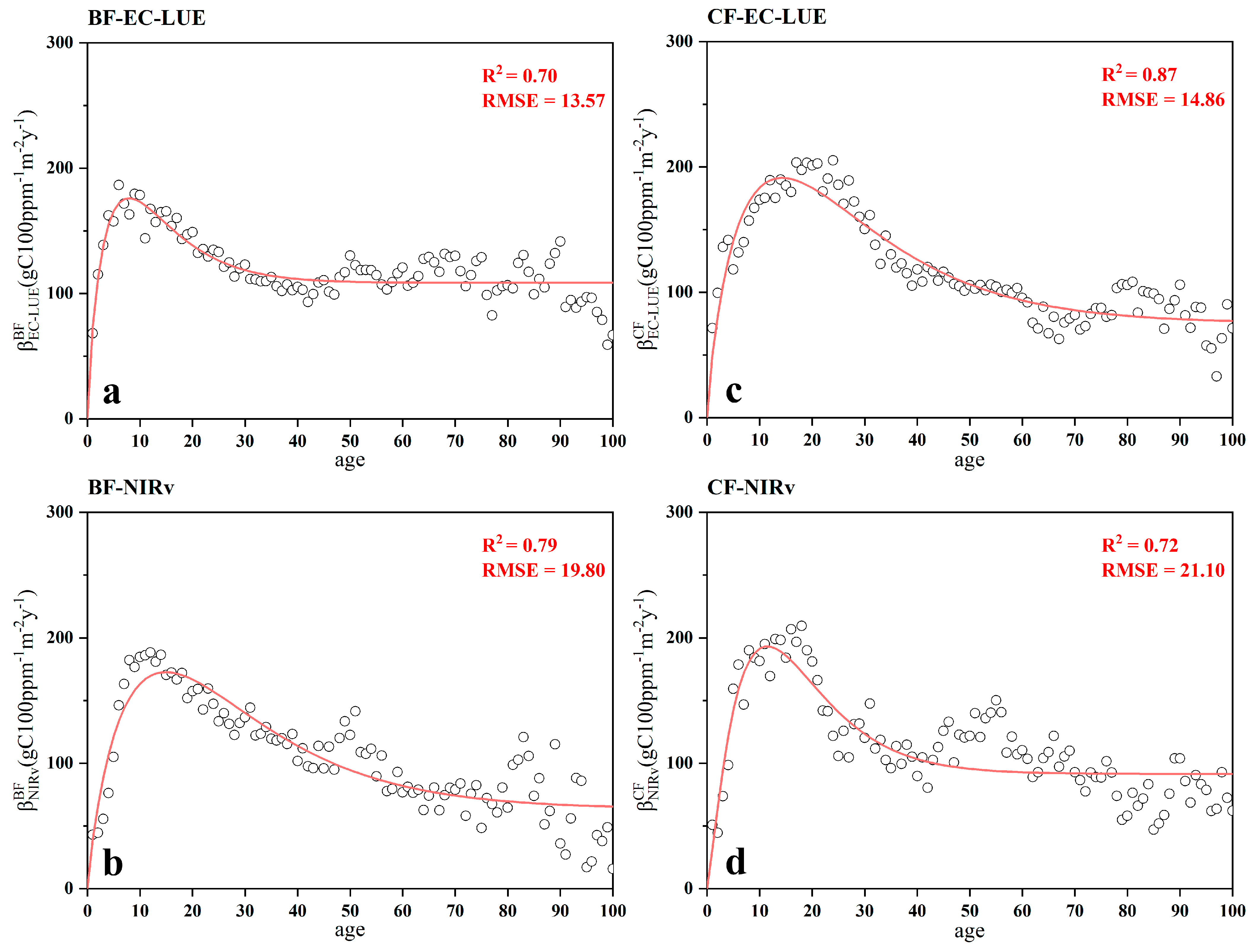
3.3. Analysis of the Variation of with Stand Age
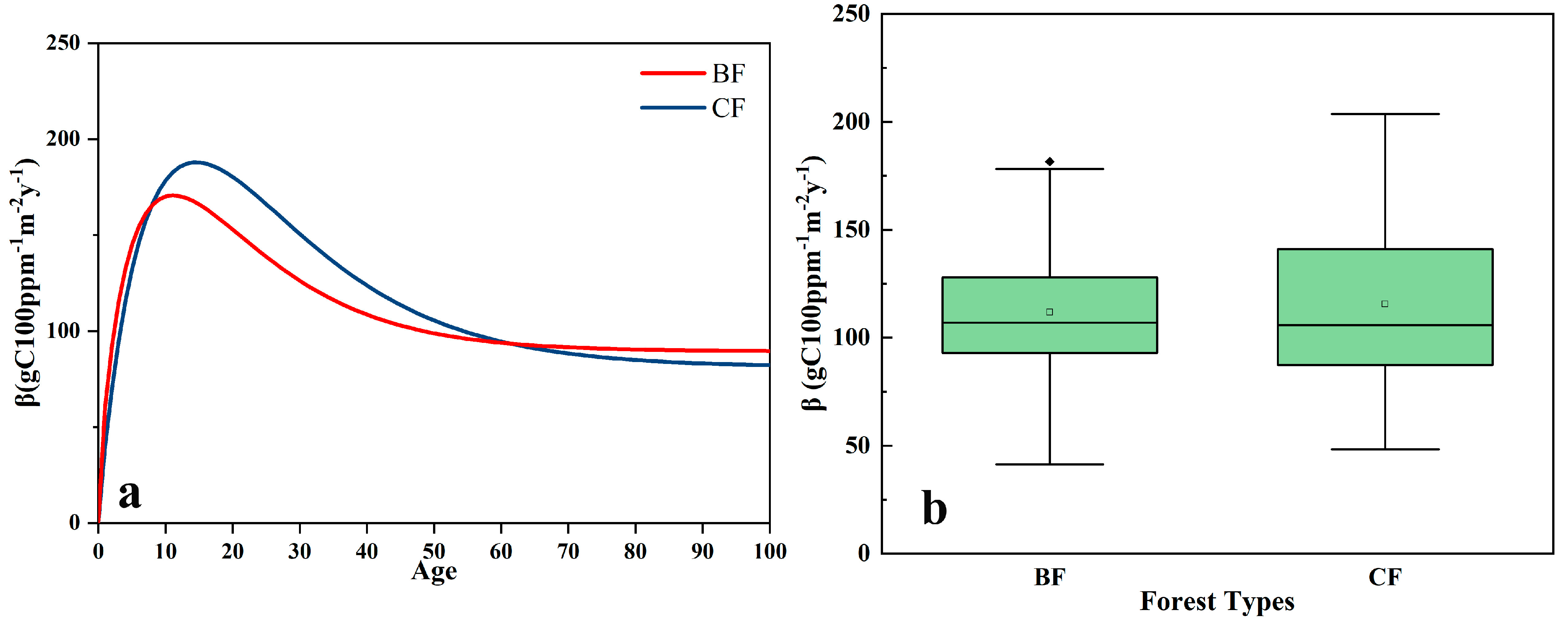
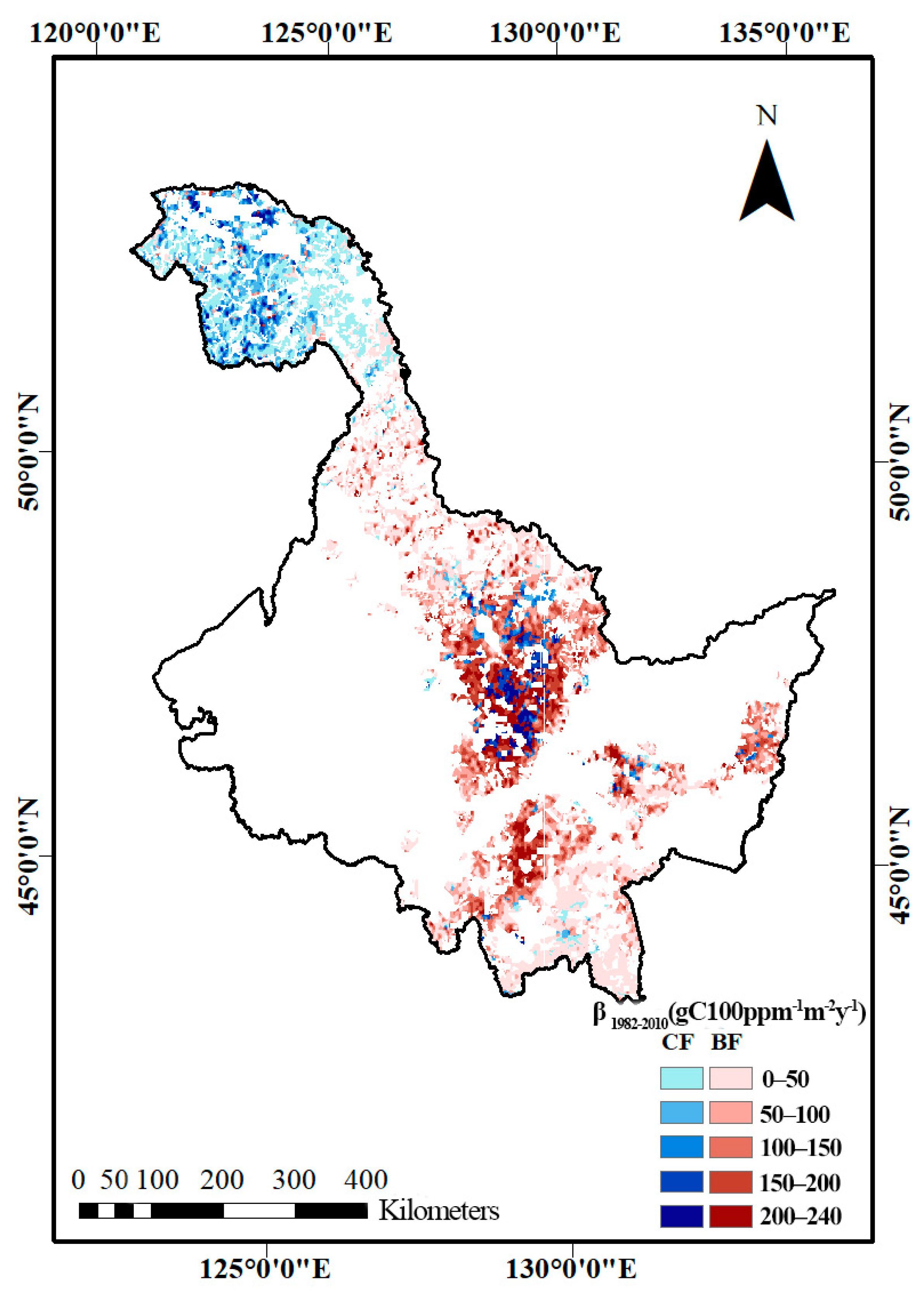
3.4. Comparison of the Differences in among Different Conditions
4. Results
4.1. Random Forest Model Validation
4.2. Variation of the CO2 Fertilization Effect (CFE) with Stand Age
4.3. Differences in CFE between Different Stand Types
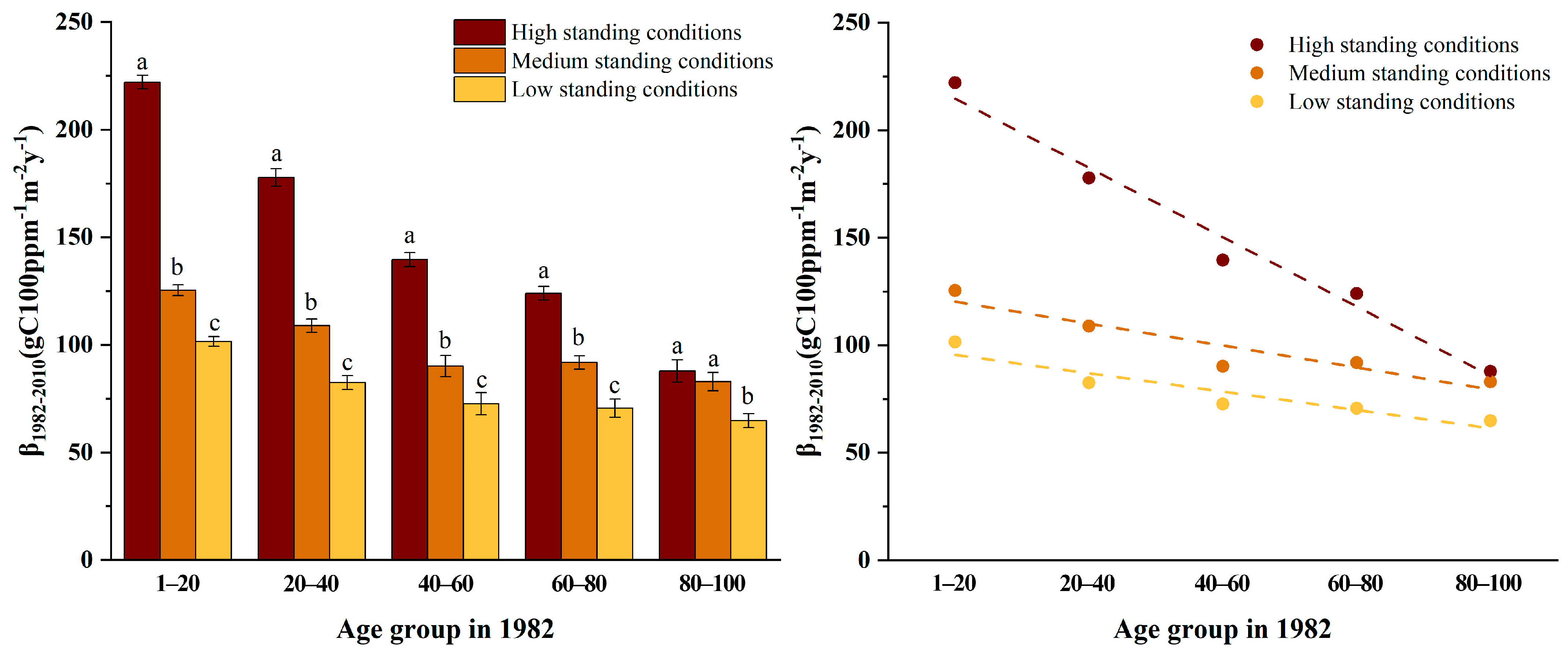
4.4. Differences in CFE among Different Site Conditions
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Etheridge, D.M.; Steele, L.P.; Langenfelds, R.L.; Francey, R.J.; Barnola, J.-M.; Morgan, V.I. Natural and anthropogenic changes in atmospheric CO2over the last 1000 years from air in Antarctic ice and firn. J. Geophys. Res. Atmos. 1996, 101, 4115–4128. [Google Scholar] [CrossRef]
- Keenan, T.F.; Luo, X.; De Kauwe, M.G.; Medlyn, B.E.; Prentice, I.C.; Stocker, B.D.; Smith, N.G.; Terrer, C.; Wang, H.; Zhang, Y.; et al. RETRACTED ARTICLE: A constraint on historic growth in global photosynthesis due to increasing CO2. Nature 2021, 600, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Canadell, J.G.; Monteiro, P.M.S.; Costa, M.H.; Cotrim da Cunha, L.; Cox, P.M.; Eliseev, A.V.; Henson, S.; Ishii, M.; Jaccard, S.; Koven, C.; et al. Global Carbon and other Biogeochemical Cycles and Feedbacks. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 923–1054. [Google Scholar] [CrossRef]
- Pei, Z.; Han, G.; Shi, T.; Ma, X.; Gong, W. A XCO Retrieval Algorithm Coupled Spatial Correlation for the Aerosol and Carbon Detection Lidar. Atmos. Environ. 2023, 309, 119933. [Google Scholar] [CrossRef]
- Shi, T.; Han, G.; Ma, X.; Mao, H.; Chen, C.; Han, Z.; Pei, Z.; Zhang, H.; Li, S.; Gong, W. Quantifying factory-scale CO2/CH4 emission based on mobile measurements and EMISSION-PARTITION model: Cases in China. Environ. Res. Lett. 2023, 18, 034028. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Mao, J.; Ribes, A.; Yan, B.; Shi, X.; Thornton, P.E.; Séférian, R.; Ciais, P.; Myneni, R.B.; Douville, H.; Piao, S.; et al. Human-induced greening of the northern extratropical land surface. Nat. Clim. Chang. 2016, 6, 959–963. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Gloor, M.; Gruber, N.; Beaulieu, C.; Jacobson, A.R.; Fletcher, S.E.M.; Pacala, S.; Rodgers, K. Trends and regional distributions of land and ocean carbon sinks. Biogeosciences 2010, 7, 2351–2367. [Google Scholar] [CrossRef]
- Ballantyne, A.; Smith, W.; Anderegg, W.; Kauppi, P.; Sarmiento, J.; Tans, P.; Shevliakova, E.; Pan, Y.; Poulter, B.; Anav, A.; et al. Accelerating net terrestrial carbon uptake during the warming hiatus due to reduced respiration. Nat. Clim. Chang. 2017, 7, 148–152. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global Carbon Budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Walker, A.P.; De Kauwe, M.G.; Bastos, A.; Belmecheri, S.; Georgiou, K.; Keeling, R.F.; McMahon, S.M.; Medlyn, B.E.; Moore, D.J.P.; Norby, R.J.; et al. Integrating the evidence for a terrestrial carbon sink caused by increasing atmospheric CO2. New Phytol. 2021, 229, 2413–2445. [Google Scholar] [CrossRef]
- Beedlow, P.A.; Tingey, D.T.; Phillips, D.L.; Hogsett, W.E.; Olszyk, D.M. Rising Atmospheric CO2 and Carbon Sequestration in Forests. Front. Ecol. Environ. 2004, 2, 315–322. [Google Scholar] [CrossRef]
- Huntzinger, D.N.; Michalak, A.M.; Schwalm, C.; Ciais, P.; King, A.W.; Fang, Y.; Schaefer, K.; Wei, Y.; Cook, R.B.; Fisher, J.B.; et al. Uncertainty in the response of terrestrial carbon sink to environmental drivers undermines carbon-climate feedback predictions. Sci. Rep. 2017, 7, 4765. [Google Scholar] [CrossRef] [PubMed]
- Ekdahl, C.A.; Keeling, C.K. Atmospheric carbon dioxide and radiocarbon in the natural carbon cycle: I. Quantitative deductions from records at Mauna Loa Observatory and at the South Pole. Brookhaven Symp. Biol. 1973, 24, 51–85. [Google Scholar]
- Wang, S.; Zhang, Y.; Ju, W.; Chen, J.M.; Ciais, P.; Cescatti, A.; Sardans, J.; Janssens, I.A.; Wu, M.; Berry, J.A.; et al. Recent global decline of CO2 fertilization effects on vegetation photosynthesis. Science 2020, 370, 1295–1300. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.A.; Buckley, T.N.; Turnbull, T.L. Diminishing CO2-driven gains in water-use efficiency of global forests. Nat. Clim. Chang. 2020, 10, 466–471. [Google Scholar] [CrossRef]
- Jiang, M.; Medlyn, B.E.; Drake, J.E.; Duursma, R.A.; Anderson, I.C.; Barton, C.V.M.; Boer, M.M.; Carrillo, Y.; Castañeda-Gómez, L.; Collins, L.; et al. The fate of carbon in a mature forest under carbon dioxide enrichment. Nature 2020, 580, 227–231. [Google Scholar] [CrossRef]
- Ciríaco da Silva, E.; Nogueira, R.J.; Silva, M.; Albuquerque, M. Drought Stress and Plant Nutrition. Plant Stress 2010, 5, 32–41. [Google Scholar]
- Hararuk, O.; Campbell, E.M.; Antos, J.A.; Parish, R. Tree rings provide no evidence of a CO2 fertilization effect in old-growth subalpine forests of western Canada. Glob. Change Biol. 2019, 25, 1222–1234. [Google Scholar] [CrossRef]
- Reich, P.B.; Hobbie, S.E.; Lee, T.; Ellsworth, D.S.; West, J.B.; Tilman, D.; Knops, J.M.H.; Naeem, S.; Trost, J. Nitrogen limitation constrains sustainability of ecosystem response to CO2. Nature 2006, 440, 922–925. [Google Scholar] [CrossRef]
- Wang, G.G.; Chhin, S.; Bauerle, W.L. Effect of natural atmospheric CO2 fertilization suggested by open-grown white spruce in a dry environment. Glob. Change Biol. 2006, 12, 601–610. [Google Scholar] [CrossRef]
- Ellsworth, D.S.; Anderson, I.C.; Crous, K.Y.; Cooke, J.; Drake, J.E.; Gherlenda, A.N.; Gimeno, T.E.; Macdonald, C.A.; Medlyn, B.E.; Powell, J.R.; et al. Elevated CO2 does not increase eucalypt forest productivity on a low-phosphorus soil. Nat. Clim. Change 2017, 7, 279–282. [Google Scholar] [CrossRef]
- Fernández-Martínez, M.; Vicca, S.; Janssens, I.A.; Ciais, P.; Obersteiner, M.; Bartrons, M.; Sardans, J.; Verger, A.; Canadell, J.G.; Chevallier, F.; et al. Atmospheric deposition, CO2, and change in the land carbon sink. Sci. Rep. 2017, 7, 9632. [Google Scholar] [CrossRef] [PubMed]
- Ainsworth, E.A.; Long, S.P. What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2. New Phytol. 2005, 165, 351–372. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.W.; Ball, J.T.; Walker, R.F. Effects of CO2 and nitrogen fertilization on vegetation and soil nutrient content in juvenile ponderosa pine. Plant Soil 1997, 190, 29–40. [Google Scholar] [CrossRef]
- Winter, K.; Aranda, J.; Garcia, M.; Virgo, A.; Paton, S.R. Effect of elevated CO2 and soil fertilization on whole-plant growth and water use in seedlings of a tropical pioneer tree, Ficus insipida Willd. Flora 2001, 196, 458–464. [Google Scholar] [CrossRef]
- Allen, L.H.; Drake, B.G.; Rogers, H.H.; Shinn, J.H. Field techniques for exposure of plants and ecosystems to elevated CO2and other trace gases. Crit. Rev. Plant Sci. 1992, 11, 85–119. [Google Scholar] [CrossRef]
- Smith, W.K.; Reed, S.C.; Cleveland, C.C.; Ballantyne, A.P.; Anderegg, W.R.L.; Wieder, W.R.; Liu, Y.Y.; Running, S.W. Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization. Nat. Clim. Chang. 2016, 6, 306–310. [Google Scholar] [CrossRef]
- Magnussen, S.; Köhl, M.; Olschofsky, K. Error propagation in stock-difference and gain–loss estimates of a forest biomass carbon balance. Eur. J. For. Res. 2014, 133, 1137–1155. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ju, W.; Qiu, B.; Zhang, Z. Tracking the seasonal and inter-annual variations of global gross primary production during last four decades using satellite near-infrared reflectance data. Sci. Total Environ. 2021, 755, 142569. [Google Scholar] [CrossRef]
- Zheng, Y.; Shen, R.; Wang, Y.; Li, X.; Liu, S.; Liang, S.; Chen, J.M.; Ju, W.; Zhang, L.; Yuan, W. Improved estimate of global gross primary production for reproducing its long-term variation, 1982–2017. Earth Syst. Sci. Data 2020, 12, 2725–2746. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, X.; Yamamoto, H.; Tani, H.; Zhong, G.; Yin, S. An attempt to introduce atmospheric CO2 concentration data to estimate the gross primary production by the terrestrial biosphere and analyze its effects. Ecol. Indic. 2018, 84, 218–234. [Google Scholar] [CrossRef]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z.; et al. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, X.; He, X.; Davi, N.K.; Cui, M.; Peng, J. Extension of summer (June–August) temperature records for northern Inner Mongolia (1715–2008), China using tree rings. Quat. Int. 2013, 283, 21–29. [Google Scholar] [CrossRef]
- Sheng, H.; Cai, T. Influence of Rainfall on Canopy Interception in Mixed Broad-Leaved—Korean Pine Forest in Xiaoxing’an Mountains, Northeastern China. Forests 2019, 10, 248. [Google Scholar] [CrossRef]
- National Forestry and Grassland Administration. 2015. Available online: http://www.forestry.gov.cn/ (accessed on 20 June 2022).
- Tans, P.; Keeling, R. Global Monitoring Laboratory–Carbon Cycle Greenhouse Gases: Trends in CO2. Available online: https://gml.noaa.gov/ccgg/trends/data.html (accessed on 20 June 2022).
- Hegglin, M.; Kinnison, D.; Lamarque, J.-F. CCMI nitrogen surface fluxes in support of CMIP6—version 2.0. Version 20160706. Earth Syst. Grid Fed. 2016. [Google Scholar] [CrossRef]
- Climatic Research Unit, Met Office. CRU TS Version 4.05. Available online: https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.05/ (accessed on 20 June 2022).
- FRSOC, Forest Resources Statistics of China (2009–2014); Department of Forest Resources Management State Forestry Administration: Beijing, China, 2016.
- Goldberger, A.S. Best Linear Unbiased Prediction in the Generalized Linear Regression Model. J. Am. Stat. Assoc. 1962, 57, 369–375. [Google Scholar] [CrossRef]
- Zhang, X.S.; Sun, S.Z.; Yong, S.P.; Zuo, Z.D.; Wang, R.Q. Vegetation Map of the People’s Republic of China; Geography Press: Beijing, China, 2007. [Google Scholar]
- Wang, B.; Li, M.; Fan, W.; Yu, Y.; Chen, J.M. Relationship between Net Primary Productivity and Forest Stand Age under Different Site Conditions and Its Implications for Regional Carbon Cycle Study. Forests 2018, 9, 5. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 2013, 499, 324–327. [Google Scholar] [CrossRef]
- Fatichi, S.; Leuzinger, S.; Paschalis, A.; Langley, J.A.; Barraclough, A.D.; Hovenden, M.J. Partitioning direct and indirect effects reveals the response of water-limited ecosystems to elevated CO2. Proc. Natl. Acad. Sci. USA 2016, 113, 12757–12762. [Google Scholar] [CrossRef]
- Trancoso, R.; Larsen, J.R.; McVicar, T.R.; Phinn, S.R.; McAlpine, C.A. CO2-vegetation feedbacks and other climate changes implicated in reducing base flow. Geophys. Res. Lett. 2017, 44, 2310–2318. [Google Scholar] [CrossRef]
- Ryan, M.G.; Binkley, D.; Fownes, J.H. Age-Related Decline in Forest Productivity: Pattern and Process. Adv. Ecol. Res. 1997, 27, 213–262. [Google Scholar] [CrossRef]
- Watson, F.G.R.; Vertessy, R.A.; Grayson, R.B. Large-Scale Modelling of Forest Hydrological Processes and Their Long-Term Effect on Water Yield. Hydrol. Process 1999, 13, 689–700. [Google Scholar] [CrossRef]
- Körner, C. Plant CO2 responses: An issue of definition, time and resource supply. New Phytol. 2006, 172, 393–411. [Google Scholar] [CrossRef] [PubMed]
- Oren, R.; Ellsworth, D.S.; Johnsen, K.H.; Phillips, N.; Ewers, B.E.; Maier, C.; Schäfer, K.V.R.; McCarthy, H.; Hendrey, G.; McNulty, S.G.; et al. Soil fertility limits carbon sequestration by forest ecosystems in a CO2-enriched atmosphere. Nature 2001, 411, 469–472. [Google Scholar] [CrossRef]
- Sigurdsson, B.D.; Medhurst, J.L.; Wallin, G.; Eggertsson, O.; Linder, S. Growth of mature boreal Norway spruce was not affected by elevated [CO2] and/or air temperature unless nutrient availability was improved. Tree Physiol. 2013, 33, 1192–1205. [Google Scholar] [CrossRef] [PubMed]
- Cotrufo, M.F.; Ineson, P.; Scott, A. Elevated CO2 reduces the nitrogen concentration of plant tissues. Glob. Chang. Biol. 1998, 4, 43–54. [Google Scholar] [CrossRef]
- Luo, Y.; Su, B.; Currie, W.S.; Dukes, J.S.; Finzi, A.; Hartwig, U.; Hungate, B.; Mc Murtrie, R.E.; Oren, R.; Parton, W.J.; et al. Progressive Nitrogen Limitation of Ecosystem Responses to Rising Atmospheric Carbon Dioxide. Bioscience 2004, 54, 731–739. [Google Scholar] [CrossRef]
- Norby, R.J.; Warren, J.M.; Iversen, C.M.; Medlyn, B.E.; McMurtrie, R.E. CO2 enhancement of forest productivity constrained by limited nitrogen availability. Proc. Natl. Acad. Sci. USA 2010, 107, 19368–19373. [Google Scholar] [CrossRef]
- Gunderson, C.A.; Wullschleger, S.D. Photosynthetic acclimation in trees to rising atmospheric CO2: A broader perspective. Photosynth. Res. 1994, 39, 369–388. [Google Scholar] [CrossRef]
- Gedalof, Z.; Berg, A.A. Tree ring evidence for limited direct CO2 fertilization of forests over the 20th century: Limited CO2 fertilization of forests. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Korner, C. Carbon limitation in trees. J. Ecol. 2003, 91, 4–17. [Google Scholar] [CrossRef]
- Nabuurs, G.-J.; Lindner, M.; Verkerk, P.J.; Gunia, K.; Deda, P.; Michalak, R.; Grassi, G. First signs of carbon sink saturation in European forest biomass. Nat. Clim. Change 2013, 3, 792–796. [Google Scholar] [CrossRef]
- Bader, M.K.-F.; Leuzinger, S.; Keel, S.G.; Siegwolf, R.T.W.; Hagedorn, F.; Schleppi, P.; Körner, C. Central European hardwood trees in a high-CO2 future: Synthesis of an 8-year forest canopy CO2 enrichment project. J. Ecol. 2013, 101, 1509–1519. [Google Scholar] [CrossRef]
- Callaway, R.M.; DeLucia, E.H.; Thomas, E.M.; Schlesinger, W.H. Compensatory responses of CO2 exchange and biomass allocation and their effects on the relative growth rate of ponderosa pine in different CO2 and temperature regimes. Oecologia 1994, 98, 159–166. [Google Scholar] [CrossRef]
- Fatichi, S.; Leuzinger, S. Reconciling observations with modeling: The fate of water and carbon allocation in a mature deciduous forest exposed to elevated CO2. Agric. For. Meteorol. 2013, 174–175, 144–157. [Google Scholar] [CrossRef]
- Chapin, F.S.; Kedrowski, R.A. Seasonal Changes in Nitrogen and Phosphorus Fractions and Autumn Retranslocation in Evergreen and Deciduous Taiga Trees. Ecology 1983, 64, 376–391. [Google Scholar] [CrossRef]
- Boerner, R.E.J. Foliar Nutrient Dynamics and Nutrient Use Efficiency of Four Deciduous Tree Species in Relation to Site Fertility. J. Appl. Ecol. 1984, 21, 1029. [Google Scholar] [CrossRef]
- Aerts, R.; Chapin, F.S., III. The mineral nutrition of wild plants revisited: A reevaluation of processes and patterns. Adv. Ecol. Res. 1999, 30, 1–67. [Google Scholar]
- Li, X.; Piao, S.; Wang, K.; Wang, X.; Wang, T.; Ciais, P.; Chen, A.; Lian, X.; Peng, S.; Peñuelas, J. Temporal trade-off between gymnosperm resistance and resilience increases forest sensitivity to extreme drought. Nat. Ecol. Evol. 2020, 4, 1075–1083. [Google Scholar] [CrossRef]
- Liu, C.; Berg, B.; Kutsch, W.; Westman, C.J.; Ilvesniemi, H.; Shen, X.; Shen, G.; Chen, X. Leaf litter nitrogen concentration as related to climatic factors in Eurasian forests: Leaf-Litter Nitrogen and Climate in Eurasian Forests. Glob. Ecol. Biogeogr. 2006, 15, 438–444. [Google Scholar] [CrossRef]
- McGroddy, M.E.; Daufresne, T.; Hedin, L.O. Scaling of C:N:P Stoichiometry in forests worldwide: Implications of terrestrial redfield-type ratios. Ecology 2004, 85, 2390–2401. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Allometry, Leaf Nitrogen and Phosphorus Stoichiometry, and Interspecific Trends in Annual Growth Rates. Ann. Bot. 2006, 97, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Chen, J.M.; Price, D.T.; Cihlar, J. Effects of stand age on net primary productivity of boreal black spruce forests in Ontario, Canada. Can. J. For. Res. 2002, 32, 833–842. [Google Scholar] [CrossRef]

| Dataset | Description | Resolution |
|---|---|---|
| EC-LUE GPP | 1982–2017 global GPP dataset corrected using the EC-LUE model | 0.05° × 0.05°; 8-day |
| NIRv GPP | 1982–2018 global GPP dataset estimated using novel vegetation index NIRv | 0.05° × 0.05°; monthly |
| CO2 concentration | Data on annual average atmospheric CO2 concentrations from 1982 to 2010 published by the Mauna Loa Observatory—ESRL Global Monitoring Laboratory | Yearly |
| Nitrogen deposition (Ndep) | The historical nitrogen deposition database (1850–2014) in the input4MIPs dataset | 0.5° × 0.5°; monthly |
| Climatic data | Calculated from the CRU TS (version 4.0.5) global meteorological data from 1901 to 2020 provided by the National Centre for Atmospheric Science | 0.5° × 0.5°; monthly |
| Stand age map | Constructed from forest inventory data in 2010 | 1 km × 1 km |
| Stand type map | Constructed from CAS in 2006 | 1 km × 1 km |
| Site class index map | Constructed from forest inventory data in 2010 | 1 km × 1 km |
| Stand Type—Remote Sensing Product | a | b | c | d |
|---|---|---|---|---|
| BF-EC-LUE | 108.52 | 2.67 | 6.93 | 0.76 |
| BF-NIRv | 63.66 | 5.66 | 14.52 | 0.85 |
| CF-EC-LUE | 75.30 | 5.19 | 14.58 | 0.79 |
| CF-NIRv | 91.59 | 3.44 | 7.51 | 1.36 |
| BF | 89.49 | 3.47 | 11.28 | 0.71 |
| CF | 81.25 | 4.53 | 12.87 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, S.; Wang, B.; Li, M.; Kong, X.; Shi, J.; Chen, Y.; Fan, W. Relationship between CO2 Fertilization Effects, and Stand Age, Stand Type, and Site Conditions. Remote Sens. 2023, 15, 4197. https://doi.org/10.3390/rs15174197
Bian S, Wang B, Li M, Kong X, Shi J, Chen Y, Fan W. Relationship between CO2 Fertilization Effects, and Stand Age, Stand Type, and Site Conditions. Remote Sensing. 2023; 15(17):4197. https://doi.org/10.3390/rs15174197
Chicago/Turabian StyleBian, Shaojie, Bin Wang, Mingze Li, Xiangqi Kong, Jinning Shi, Yanxi Chen, and Wenyi Fan. 2023. "Relationship between CO2 Fertilization Effects, and Stand Age, Stand Type, and Site Conditions" Remote Sensing 15, no. 17: 4197. https://doi.org/10.3390/rs15174197
APA StyleBian, S., Wang, B., Li, M., Kong, X., Shi, J., Chen, Y., & Fan, W. (2023). Relationship between CO2 Fertilization Effects, and Stand Age, Stand Type, and Site Conditions. Remote Sensing, 15(17), 4197. https://doi.org/10.3390/rs15174197





