Differences in Global Precipitation Regimes between Land and Ocean Areas Based on the GPM IMERG Product
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
3. Results
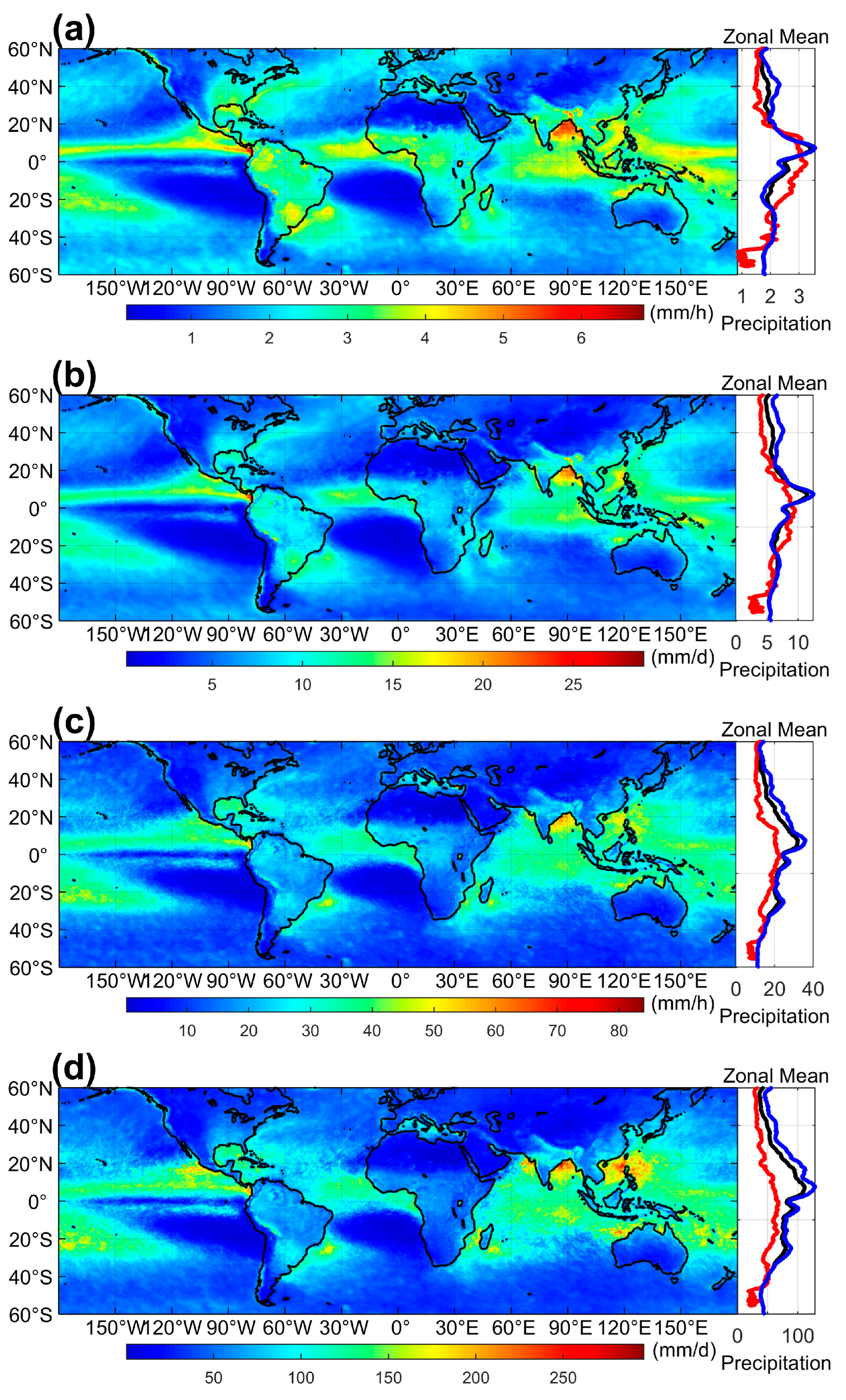
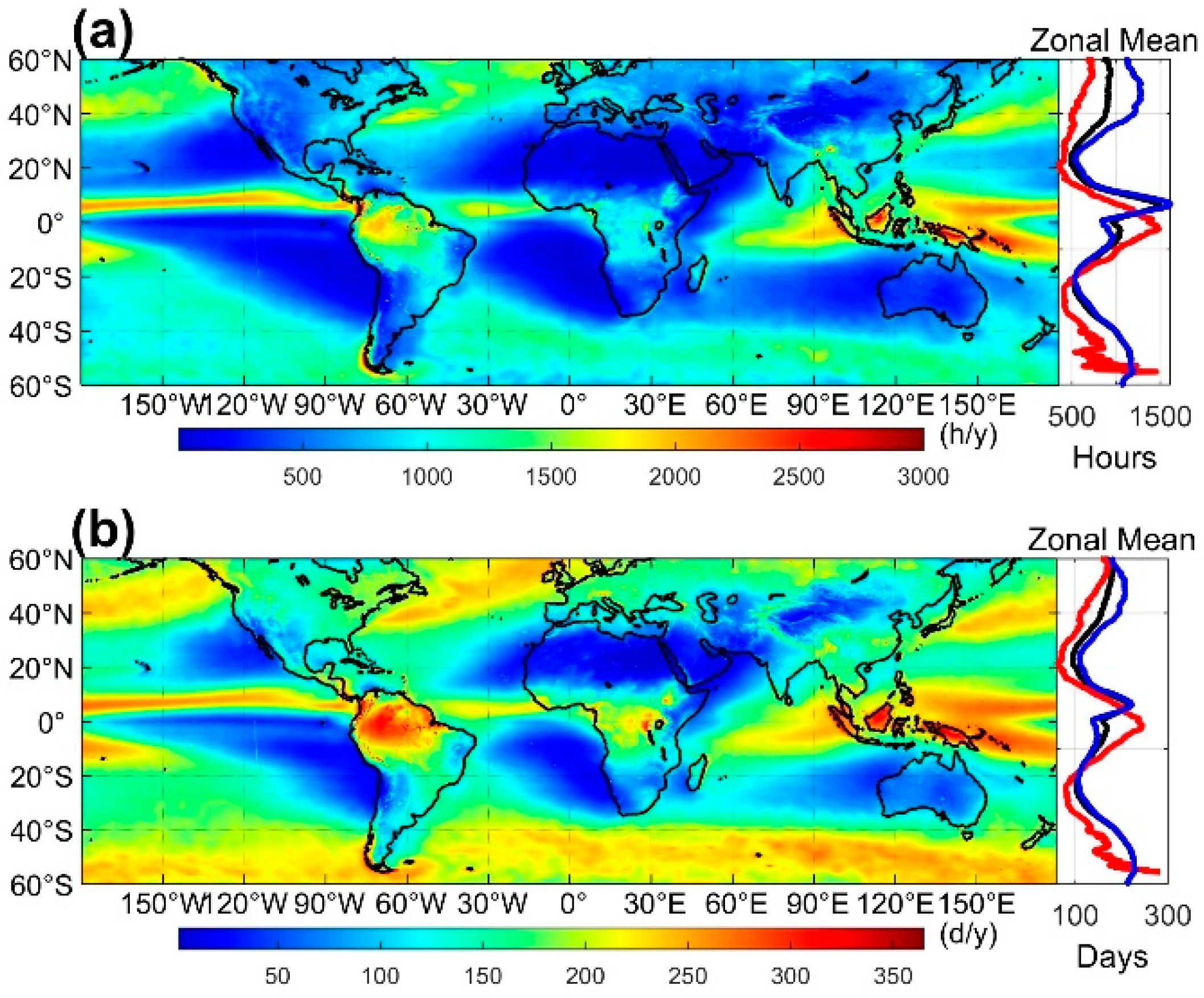
3.1. Global Distribution of Precipitation Based on the GPM IMERG Product
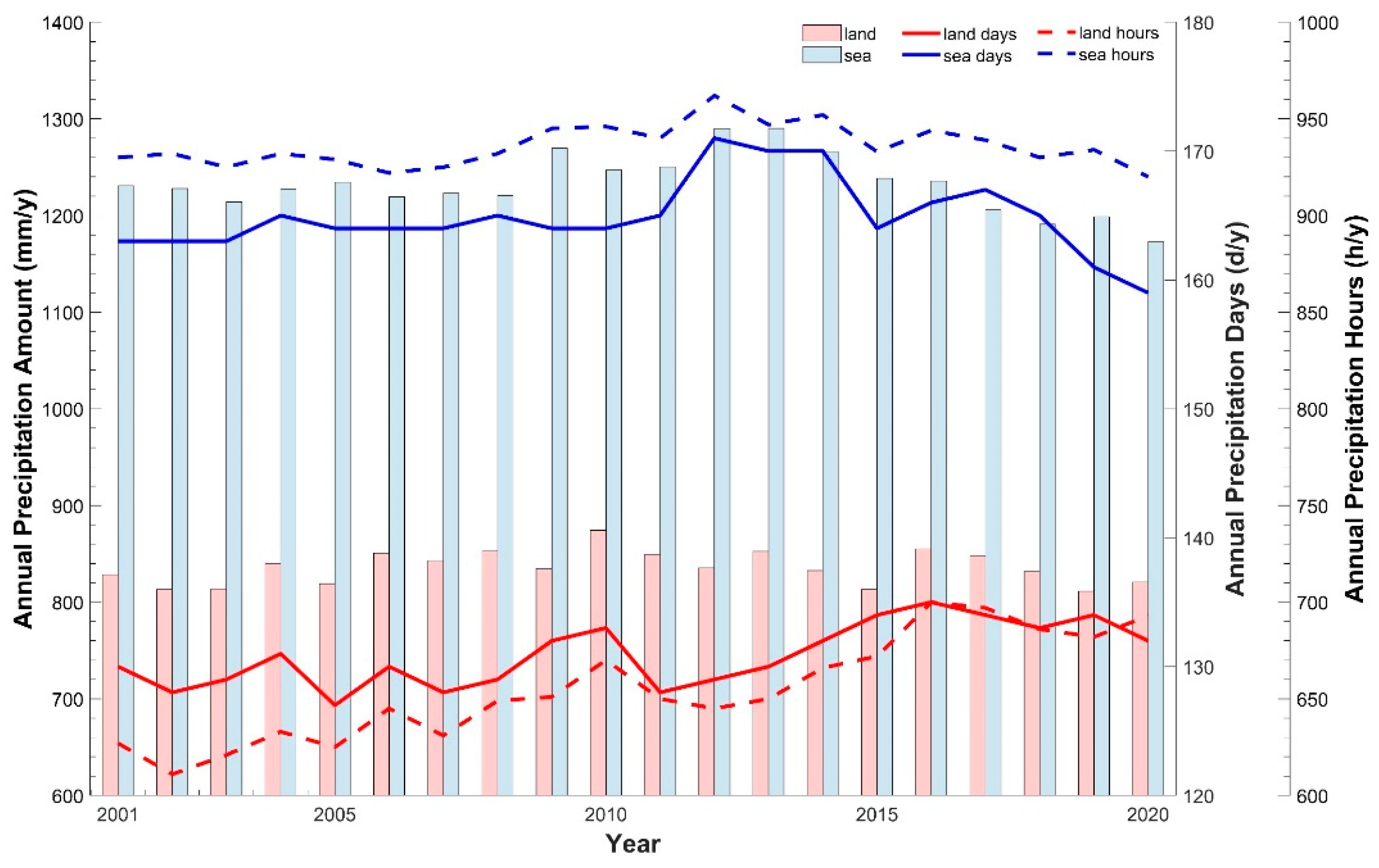
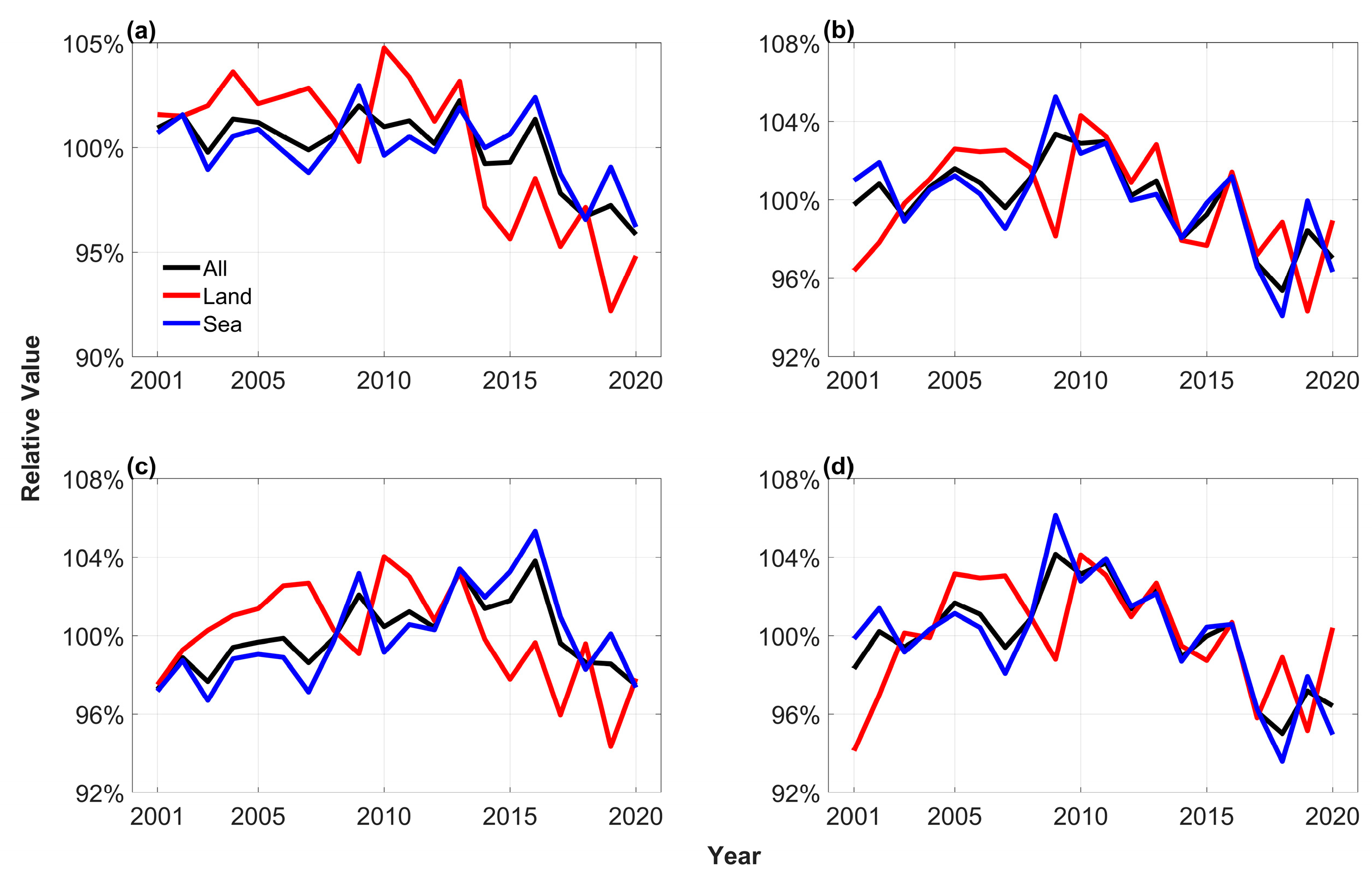
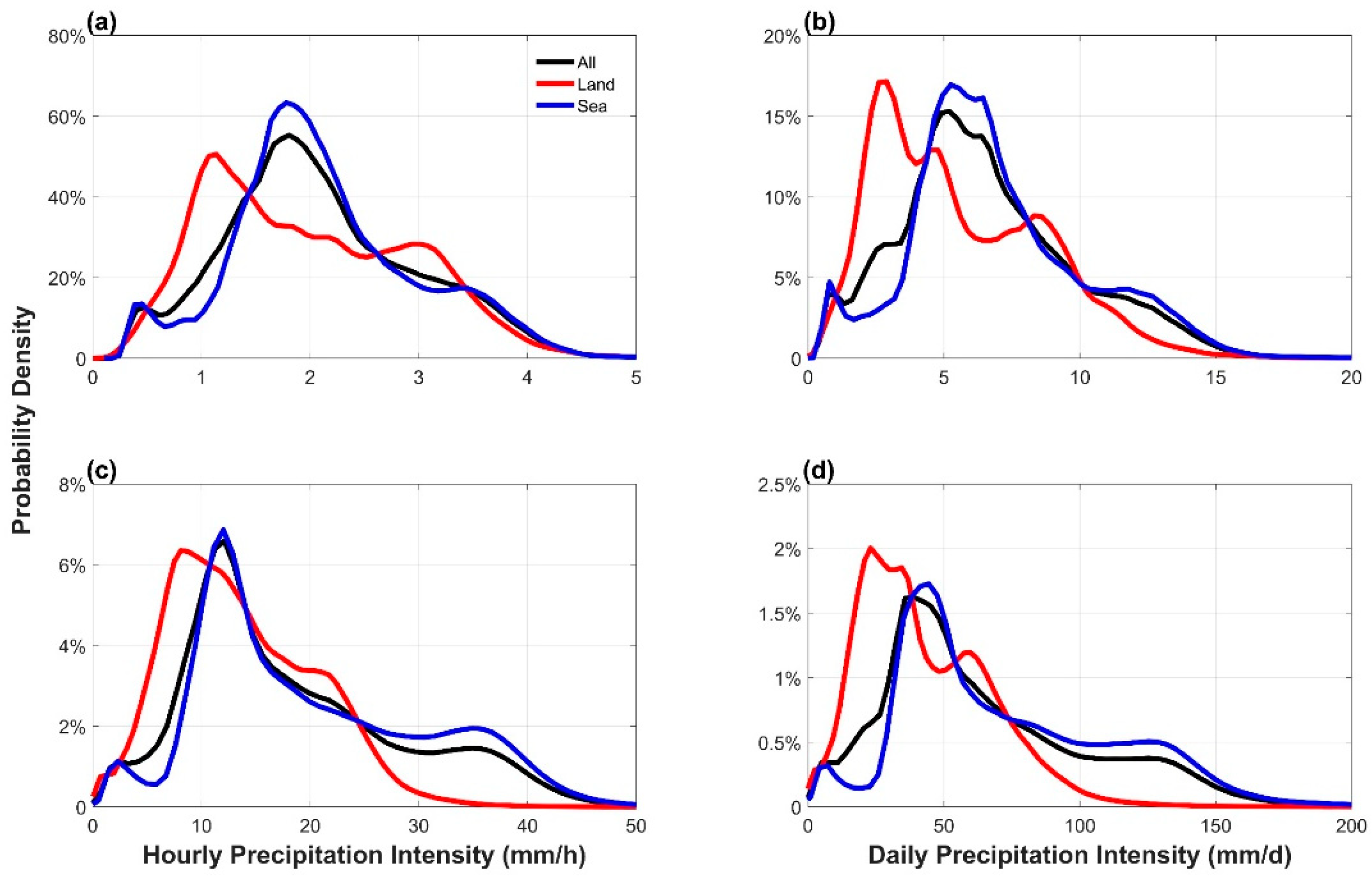
3.2. Discrepancy in Precipitation Regimes between Land and Ocean Areas
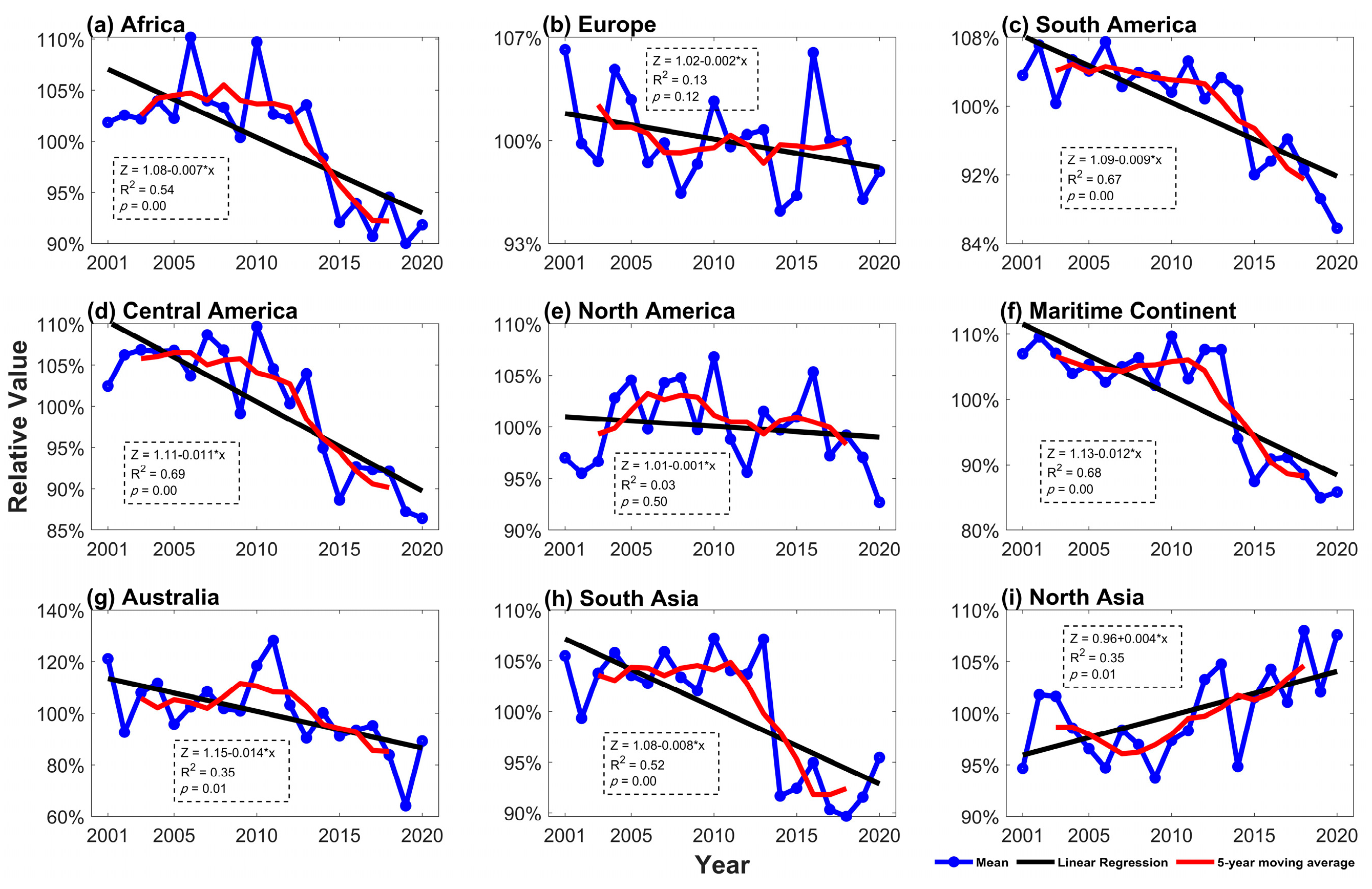
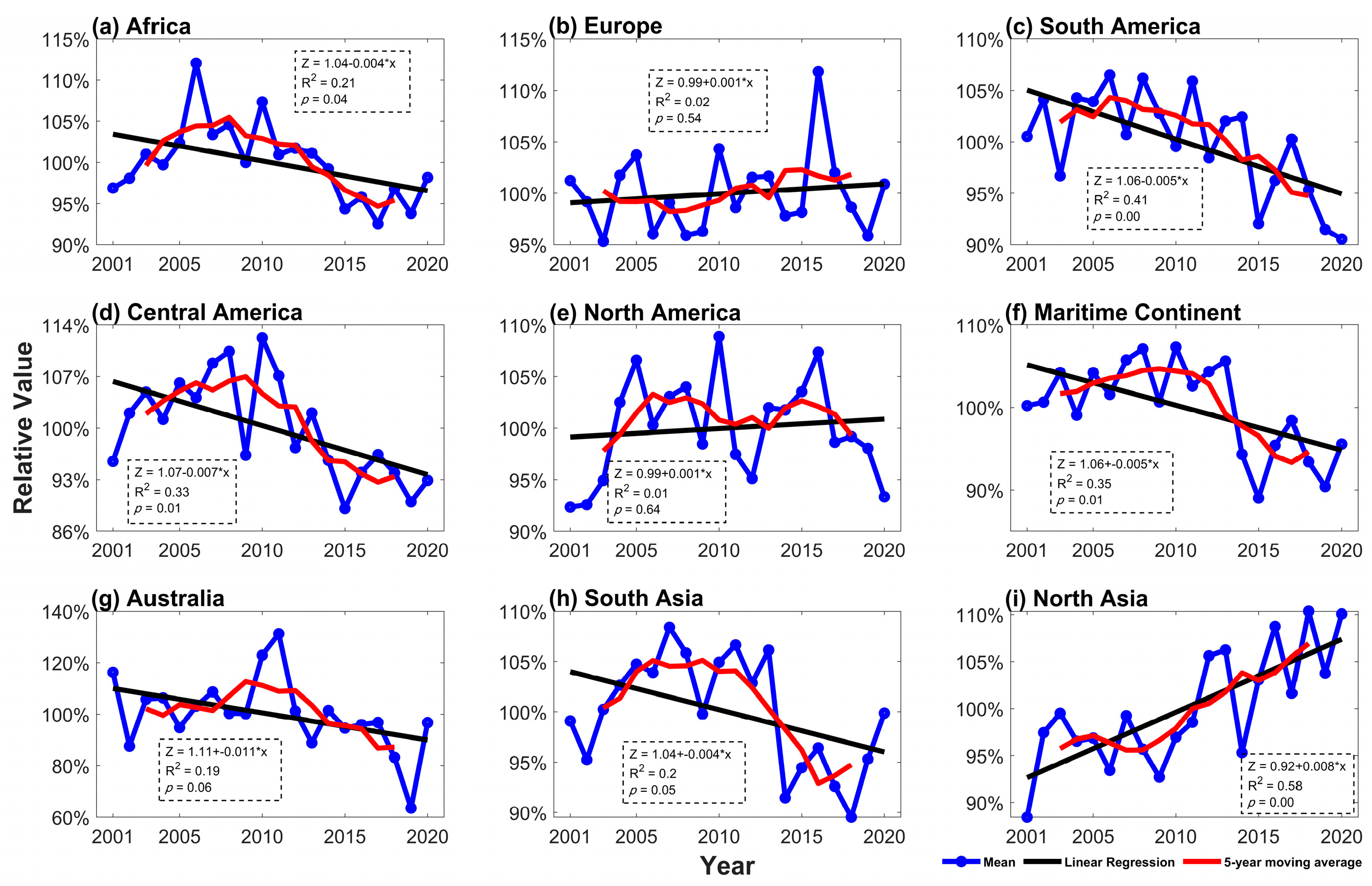
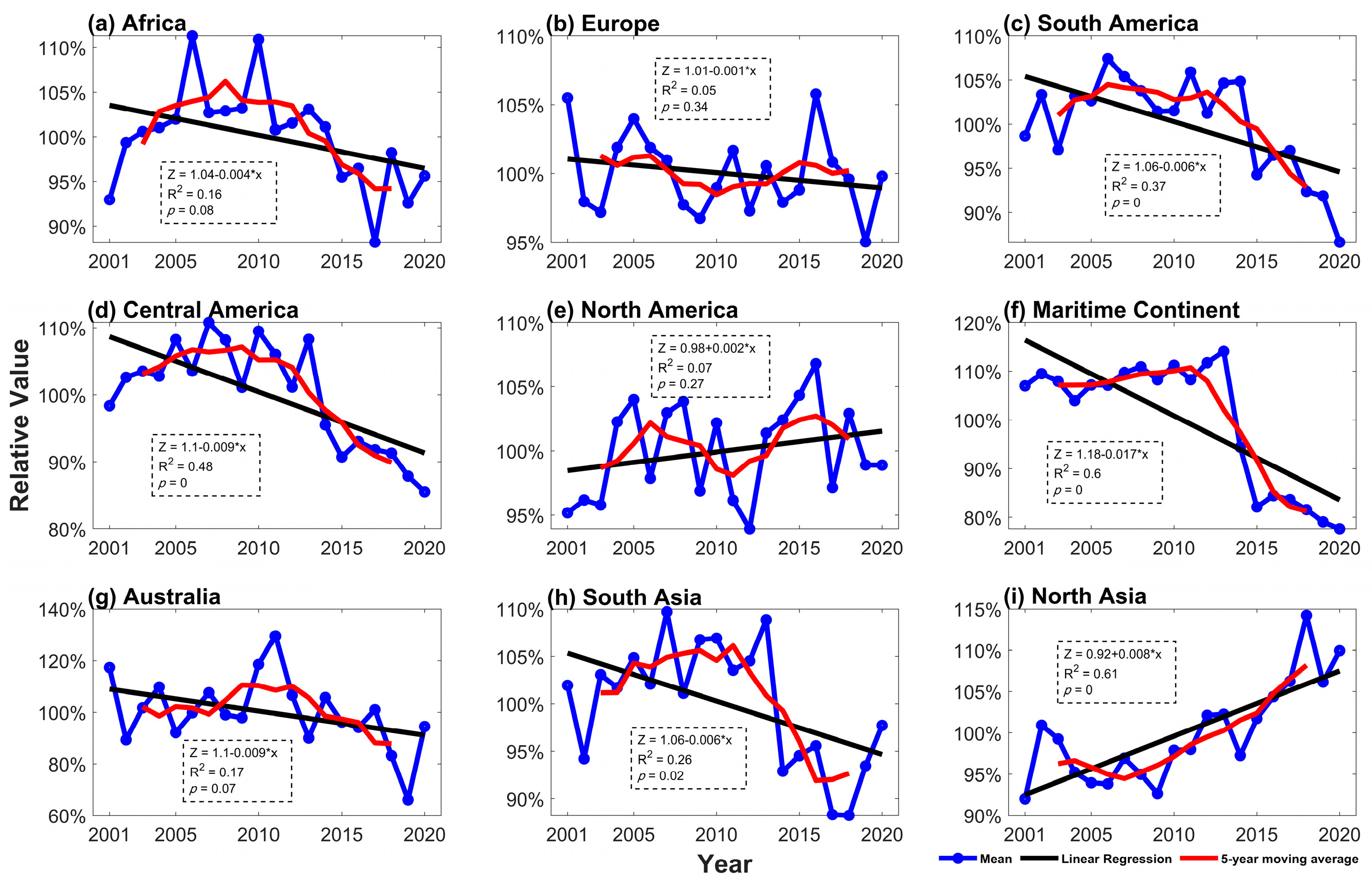
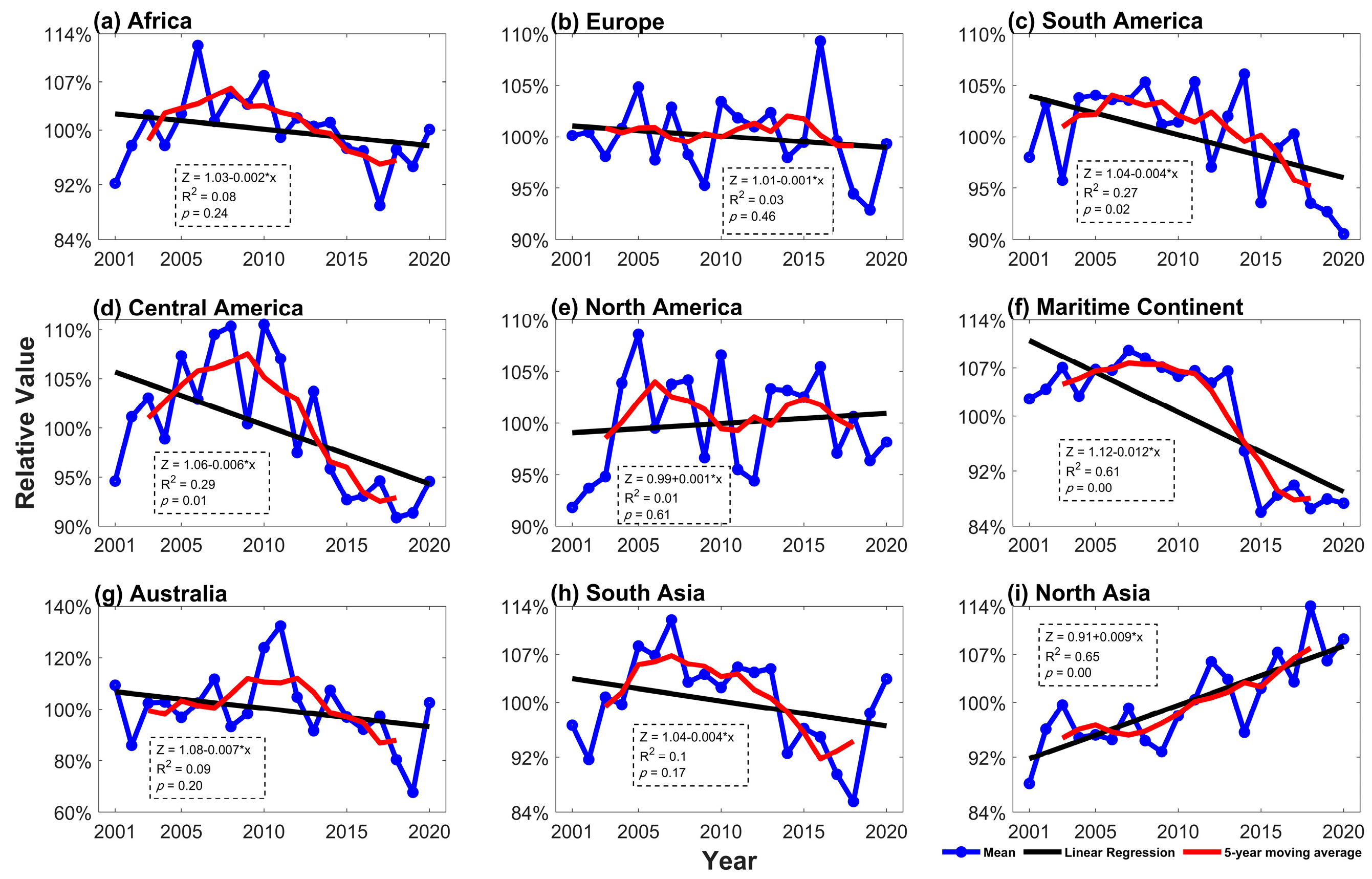
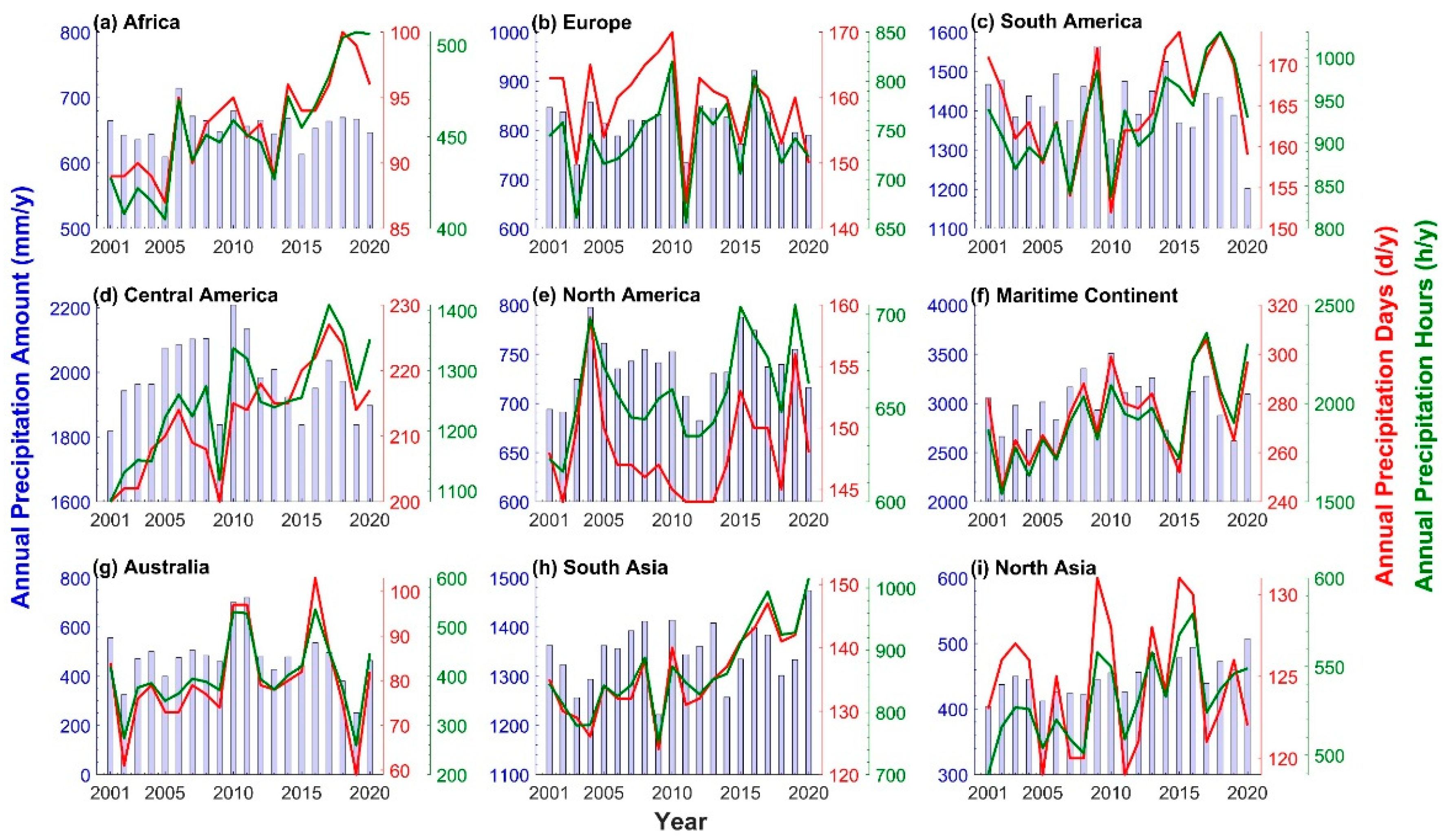
3.3. Variation in Extreme Precipitation in Nine Mainland Regions of the Globe
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ficklin, D.L.; Null, S.E.; Abatzoglou, J.T.; Novick, K.A.; Myers, D.T. Hydrological Intensification Will Increase the Complexity of Water Resource Management. Earth’s Future 2022, 10, e2021EF002487. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, Q.; Wang, Z.; Chiew, F.H.S.; Zhang, X.; Xiao, H. Different Precipitation Elasticity of Runoff for Precipitation Increase and Decrease at Watershed Scale. J. Geophys. Res. Atmos. 2019, 124, 11932–11943. [Google Scholar] [CrossRef]
- Fishman, R. More uneven distributions overturn benefits of higher precipitation for crop yields. Environ. Res. Lett. 2016, 11, 024004. [Google Scholar] [CrossRef]
- Song, X.-P.; Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Tyukavina, A.; Vermote, E.F.; Townshend, J.R. Global land change from 1982 to 2016. Nature 2018, 560, 639–643. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric water vapor, convenction and climate. Rev. Geophys. 2010, 48, RG2001. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T. Significant Increases in Extreme Precipitation and the Associations with Global Warming over the Global Land Monsoon Regions. J. Clim. 2019, 32, 8465–8488. [Google Scholar] [CrossRef]
- Neelin, J.D.; Sahany, S.; Stechmann, S.N.; Bernstein, D.N. Global warming precipitation accumulation increases above the current-climate cutoff scale. Proc. Natl. Acad. Sci. USA 2017, 114, 1258–1263. [Google Scholar] [CrossRef]
- Song, F.; Lu, J.; Leung, L.R.; Liu, F. Contrasting Phase Changes of Precipitation Annual Cycle Between Land and Ocean Under Global Warming. Geophys. Res. Lett. 2020, 47, e2020GL090327. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes Under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Martinez-Villalobos, C.; Neelin, J.D. Shifts in Precipitation Accumulation Extremes During the Warm Season Over the United States. Geophys. Res. Lett. 2018, 45, 8586–8595. [Google Scholar] [CrossRef]
- Fan, L.; Lu, C.; Yang, B.; Chen, Z. Long-term trends of precipitation in the North China Plain. J. Geogr. Sci. 2012, 22, 989–1001. [Google Scholar] [CrossRef]
- Arias, P.; Bellouin, N.; Coppola, E.; Jones, R.; Krinner, G.; Marotzke, J.; Zickfeld, K. Faculty Opinions recommendation of IPCC, 2021: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Cambridge, UK; New York, NY, USA, 2021; pp. 287–422. [Google Scholar] [CrossRef]
- Herold, N.; Alexander, L.V.; Donat, M.G.; Contractor, S.; Becker, A. How much does it rain over land? Geophys. Res. Lett. 2016, 43, 341–348. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Harrison, L.; Funk, C.; Peterson, P. Identifying changing precipitation extremes in Sub-Saharan Africa with gauge and satellite products. Environ. Res. Lett. 2019, 14, 085007. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Seamless Poleward Atmospheric Energy Transports and Implications for the Hadley Circulation. J. Clim. 2003, 16, 3706–3722. [Google Scholar] [CrossRef]
- Santer, B.D.; Po-Chedley, S.; Feldl, N.; Fyfe, J.C.; Fu, Q.; Solomon, S.; England, M.; Rodgers, K.B.; Stuecker, M.F.; Mears, C.; et al. Robust Anthropogenic Signal Identified in the Seasonal Cycle of Tropospheric Temperature. J. Clim. 2022, 35, 6075–6100. [Google Scholar] [CrossRef]
- Ali, H.; Peleg, N.; Fowler, H.J. Global Scaling of Rainfall With Dewpoint Temperature Reveals Considerable Ocean-Land Difference. Geophys. Res. Lett. 2021, 48, e2021GL093798. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Knutti, R. The Uneven Nature of Daily Precipitation and Its Change. Geophys. Res. Lett. 2018, 45, 11980–11988. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, R.; Wang, K. Climatology and changes in internal intensity distributions of global precipitation systems over 2001–2020 based on IMERG. J. Hydrol. 2023, 620, 129386. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K. Global precipitation system scale increased from 2001 to 2020. J. Hydrol. 2022, 616, 128768. [Google Scholar] [CrossRef]
- McErlich, C.; McDonald, A.; Schuddeboom, A.; Vishwanathan, G.; Renwick, J.; Rana, S. Positive correlation between wet-day frequency and intensity linked to universal precipitation drivers. Nat. Geosci. 2023, 16, 410–415. [Google Scholar] [CrossRef]
- Madakumbura, G.D.; Thackeray, C.W.; Norris, J.; Goldenson, N.; Hall, A. Anthropogenic influence on extreme precipitation over global land areas seen in multiple observational datasets. Nat. Commun. 2021, 12, 3944. [Google Scholar] [CrossRef] [PubMed]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Zhang, A.; Zhao, X. Changes of precipitation pattern in China: 1961–2010. Theor. Appl. Clim. 2022, 148, 1005–1019. [Google Scholar] [CrossRef]
- Mao, Y.; Wu, G.; Xu, G.; Wang, K. Reduction in Precipitation Seasonality in China from 1960 to 2018. J. Clim. 2022, 35, 227–248. [Google Scholar]
- Wu, G.; Li, Y.; Qin, S.; Mao, Y.; Wang, K. Precipitation unevenness in gauge observations and eight reanalyses from 1979 to 2018 over China. J. Clim. 2021, 35.1, 227–248. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global Increasing Trends in Annual Maximum Daily Precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Zwiers, F.; Westra, S.; Alexander, L.V. A Global, Continental, and Regional Analysis of Changes in Extreme Precipitation. J. Clim. 2021, 34, 243–258. [Google Scholar] [CrossRef]
- He, J.; Soden, B.J. A re-examination of the projected subtropical precipitation decline. Nat. Clim. Change 2017, 1, 53–57. [Google Scholar] [CrossRef]
- Lin, M.; Huybers, P. If Rain Falls in India and No One Reports It, Are Historical Trends in Monsoon Extremes Biased? Geophys. Res. Lett. 2019, 46, 1681–1689. [Google Scholar] [CrossRef]
- Rai, P.; Choudhary, A.; Dimri, A.P. Future precipitation extremes over India from the CORDEX-South Asia experiments. Theor. Appl. Clim. 2019, 137, 2961–2975. [Google Scholar] [CrossRef]
- Marelle, L.; Myhre, G.; Hodnebrog, Ø.; Sillmann, J.; Samset, B.H. The Changing Seasonality of Extreme Daily Precipitation. Geophys. Res. Lett. 2018, 45, 11352–11360. [Google Scholar] [CrossRef]
- Cattoën, C.; Robertson, D.E.; Bennett, J.C.; Wang, Q.J.; Carey-Smith, T.K. Calibrating Hourly Precipitation Forecasts with Daily Observations. J. Hydrometeorol. 2020, 21, 1655–1673. [Google Scholar] [CrossRef]
- Barbero, R.; Fowler, H.J.; Blenkinsop, S.; Westra, S.; Moron, V.; Lewis, E.; Chan, S.; Lenderink, G.; Kendon, E.; Guerreiro, S.; et al. A synthesis of hourly and daily precipitation extremes in different climatic regions. Weather Clim. Extrem. 2019, 26, 100219. [Google Scholar] [CrossRef]
- Barbero, R.; Fowler, H.J.; Lenderink, G.; Blenkinsop, S. Is the intensification of precipitation extremes with global warming better detected at hourly than daily resolutions? Geophys. Res. Lett. 2017, 44, 974–983. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.E.; Gourley, J.J.; Qi, Y.; Wang, J. Performance evaluation of radar and satellite rainfalls for Typhoon Morakot over Taiwan: Are remote-sensing products ready for gauge denial scenario of extreme events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Miao, C.; Zhao, X.; Zhang, Q.; Su, J. Evaluation of the GPM IMERG product at the hourly timescale over China. Atmos. Res. 2023, 285, 106656. [Google Scholar] [CrossRef]
- Li, R.; Qi, D.; Zhang, Y.; Wang, K. A new pixel-to-object method for evaluating the capability of the GPM IMERG product to quantify precipitation systems. J. Hydrol. 2022, 613, 128476. [Google Scholar] [CrossRef]
- Ding, M.; Yong, B.; Yang, Z. Extreme precipitation monitoring capability of the multi-satellite jointly retrieval precipitation products of Global Precipitation Measurement (GPM) mission. J. Remote Sens. 2022, 26, 657–671. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Kachi, M.; Oki, R.; Shimizu, S.; Kojima, M. Global Precipitation Measurement (GPM) Mission and Its Latest Progress: A Review. Remote Sens. Technol. Appl. 2015, 30, 607–615. [Google Scholar]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. Atmos. 2004, 109, 265–274. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Zhou, C.; Gao, W.; Hu, J.; Du, L.; Du, L. Capability of IMERG V6 Early, Late, and Final Precipitation Products for Monitoring Extreme Precipitation Events. Remote Sens. 2021, 13, 689. [Google Scholar] [CrossRef]
- Xu, F.; Guo, B.; Ye, B.; Ye, Q.; Chen, H.; Ju, X.; Guo, J.; Wang, Z. Systematical Evaluation of GPM IMERG and TRMM 3B42V7 Precipitation Products in the Huang-Huai-Hai Plain, China. Remote Sens. 2019, 11, 697. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A com-prehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Li, R.; Wang, K.; Qi, D. Event-Based Evaluation of the GPM Multisatellite Merged Precipitation Product From 2014 to 2018 Over China: Methods and Results. J. Geophys. Res. Atmos. 2021, 126, e2020JD033692. [Google Scholar] [CrossRef]
- Li, R.; Wang, K.; Qi, D. Validating the Integrated Multisatellite Retrievals for Global Precipitation Measurement in Terms of Diurnal Variability with Hourly Gauge Observations Collected at 50,000 Stations in China. J. Geophys. Res. Atmos. 2018, 123, 10423–10442. [Google Scholar] [CrossRef]
- Ramadhan, R.; Marzuki, M.; Yusnaini, H.; Ningsih, A.P.; Hashiguchi, H.; Shimomai, T.; Vonnisa, M.; Ulfah, S.; Suryanto, W.; Sholihun, S. Ground Validation of GPM IMERG-F Precipitation Products with the Point Rain Gauge Records on the Extreme Rainfall Over a Mountainous Area of Sumatra Island. J. Penelit. Pendidik. IPA 2022, 8, 163–170. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Godoy, M.R.V.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Pambianchi, G. Reliability of the IMERG product through reference rain gauges in Central Italy. Atmos. Res. 2022, 278, 106340. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K. Global precipitation system size. Environ. Res. Lett. 2021, 16, 054005. [Google Scholar] [CrossRef]
- Endres, D.; Schindelin, J. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Feng, X.; Thompson, S.E.; Woods, R.; Porporato, A. Quantifying Asynchronicity of Precipitation and Potential Evapotranspiration in Mediterranean Climates. Geophys. Res. Lett. 2019, 46, 14692–14701. [Google Scholar] [CrossRef]
- Dai, A. Global Precipitation and Thunderstorm Frequencies. Part II: Diurnal Variations. J. Clim. 2001, 14, 1112–1128. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Zhang, Y. How often does it really rain. Bull. Am. Meteorol. Soc. 2018, 99, 289–298. [Google Scholar] [CrossRef]
- Li, X.-F.; Blenkinsop, S.; Barbero, R.; Yu, J.; Lewis, E.; Lenderink, G.; Guerreiro, S.; Chan, S.; Li, Y.; Ali, H.; et al. Global distribution of the intensity and frequency of hourly precipitation and their responses to ENSO. Clim. Dyn. 2020, 54, 4823–4839. [Google Scholar] [CrossRef]
- Li, Y.; Guo, B.; Wang, K.; Wu, G.; Shi, C. Performance of TRMM Product in Quantifying Frequency and Intensity of Precipitation during Daytime and Nighttime across China. Remote Sens. 2020, 12, 740. [Google Scholar] [CrossRef]
- Markonis, Y.; Papalexiou, S.M.; Martinkova, M.; Hanel, M. Assessment of Water Cycle Intensification Over Land using a Multisource Global Gridded Precipitation DataSet. J. Geophys. Res. Atmos. 2019, 124, 11175–11187. [Google Scholar] [CrossRef]
- Cui, D.; Wang, C.; Santisirisomboon, J. Characteristics of extreme precipitation over eastern Asia and its possible con-nections with Asian summer monsoon activity. Int. J. Climatol. 2019, 39, 711–723. [Google Scholar] [CrossRef]
- Mtewele, Z.F.; Xu, X.; Jia, G. Heterogeneous Trends of Precipitation Extremes in Recent Two Decades over East Africa. J. Meteorol. Res. 2021, 35, 1057–1073. [Google Scholar] [CrossRef]
| Hourly | Daily | |
|---|---|---|
| Mean value | 0.0323 * | 0.0461 |
| Extreme value | 0.0149 * | 0.0474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, P.; Hao, H.; Wu, G. Differences in Global Precipitation Regimes between Land and Ocean Areas Based on the GPM IMERG Product. Remote Sens. 2023, 15, 4179. https://doi.org/10.3390/rs15174179
Lv P, Hao H, Wu G. Differences in Global Precipitation Regimes between Land and Ocean Areas Based on the GPM IMERG Product. Remote Sensing. 2023; 15(17):4179. https://doi.org/10.3390/rs15174179
Chicago/Turabian StyleLv, Pengfei, Hongfei Hao, and Guocan Wu. 2023. "Differences in Global Precipitation Regimes between Land and Ocean Areas Based on the GPM IMERG Product" Remote Sensing 15, no. 17: 4179. https://doi.org/10.3390/rs15174179
APA StyleLv, P., Hao, H., & Wu, G. (2023). Differences in Global Precipitation Regimes between Land and Ocean Areas Based on the GPM IMERG Product. Remote Sensing, 15(17), 4179. https://doi.org/10.3390/rs15174179







