Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping
Abstract
:1. Introduction
2. Related Work
2.1. Multi-Objective Imaging Satellite Task Planning Model
2.2. Particle Update Strategy in LMOCSO
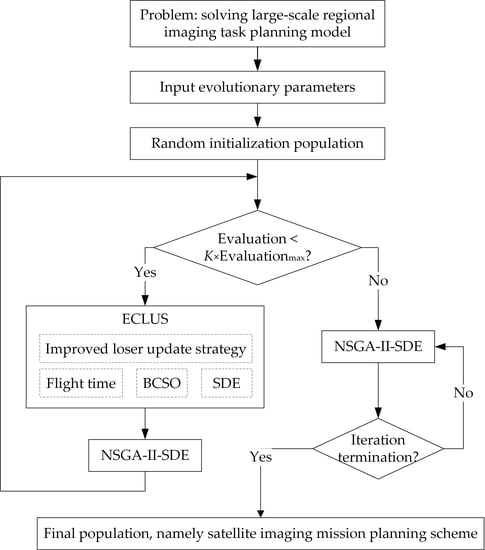
3. Proposed Method
3.1. Efficient Competition Learning Particle Update Strategy
3.1.1. Improved Loser Update Strategy
3.1.2. Flight Time
3.1.3. Binary Decision Variable Update Strategy
3.1.4. Winner Selection Based on SDE
3.1.5. Procedure of ECLUS
| Algorithm 1: Procedure of ECLUS |
| Input: Current population (even individual) |
| Output: New population |
| 1 Obtain the Pareto number of each individual by non-dominated sorting ; |
| 2 Calculate the SDE of each individual in each Pareto layer according to (24); |
| 3 Obtain competitive particle pairs by grouping individuals in pairs within ; |
| 4 Select the winner and the loser from each pair based on the Pareto number and SDE; |
| 5 Update the real and binary decision variables for all losers based on (14), (19), (21), (22), and (23); |
| 6 Generate the new population by combining updated losers and winners; |
| 7 return ; |
3.2. Procedure of ECL-INS-LMOA
4. Experiment and Analysis
4.1. Experimental Settings
4.1.1. Imaging Satellite
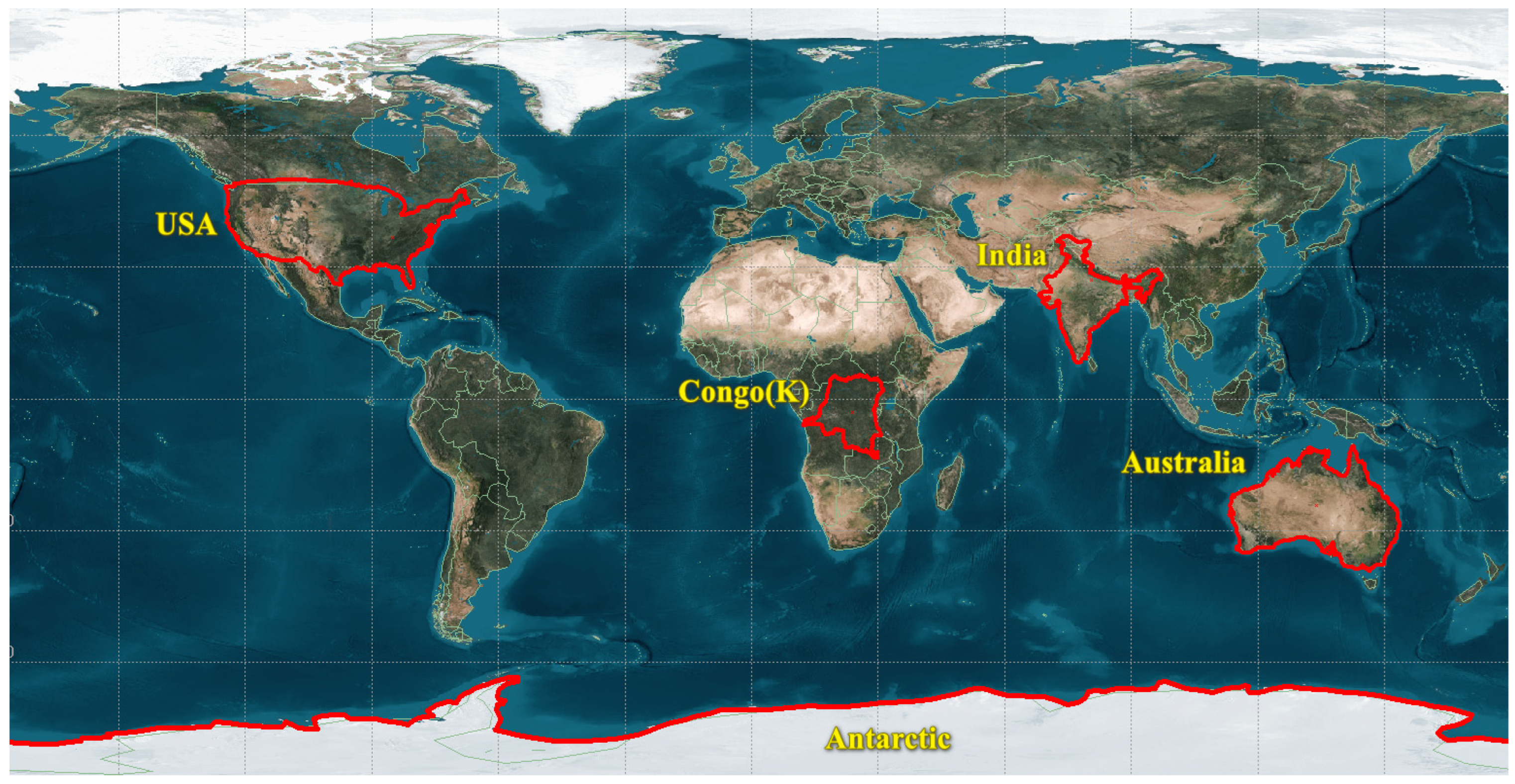
4.1.2. Imaging Regions
4.1.3. Candidate Strips for Each Region
4.1.4. Parameter Settings for MOEAs
4.2. Results and Analysis
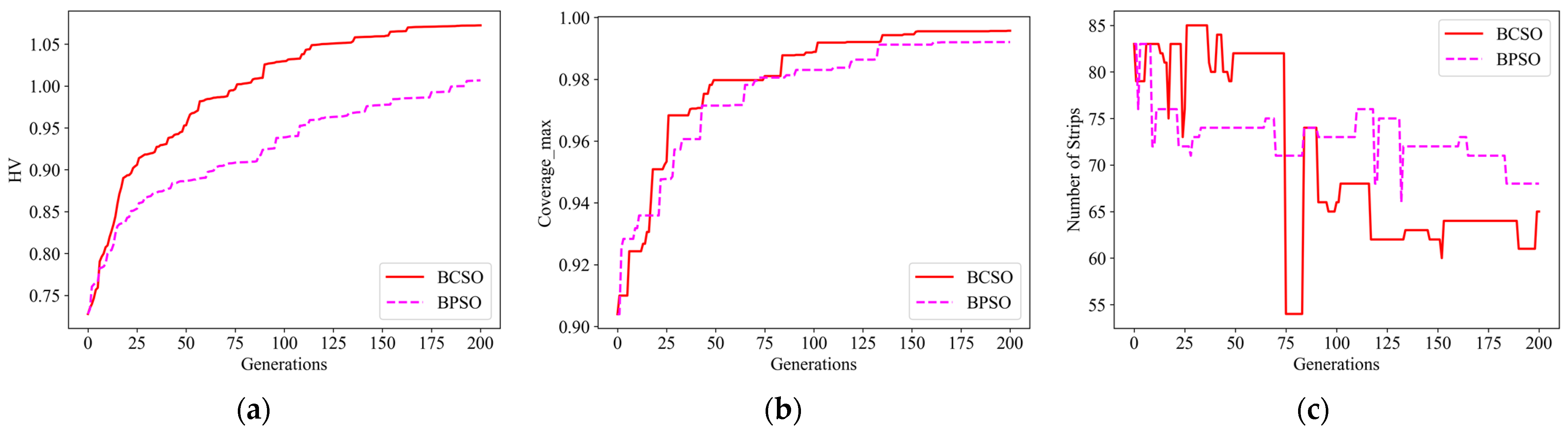
4.2.1. Verification of Particle Update Strategies in ECLUS
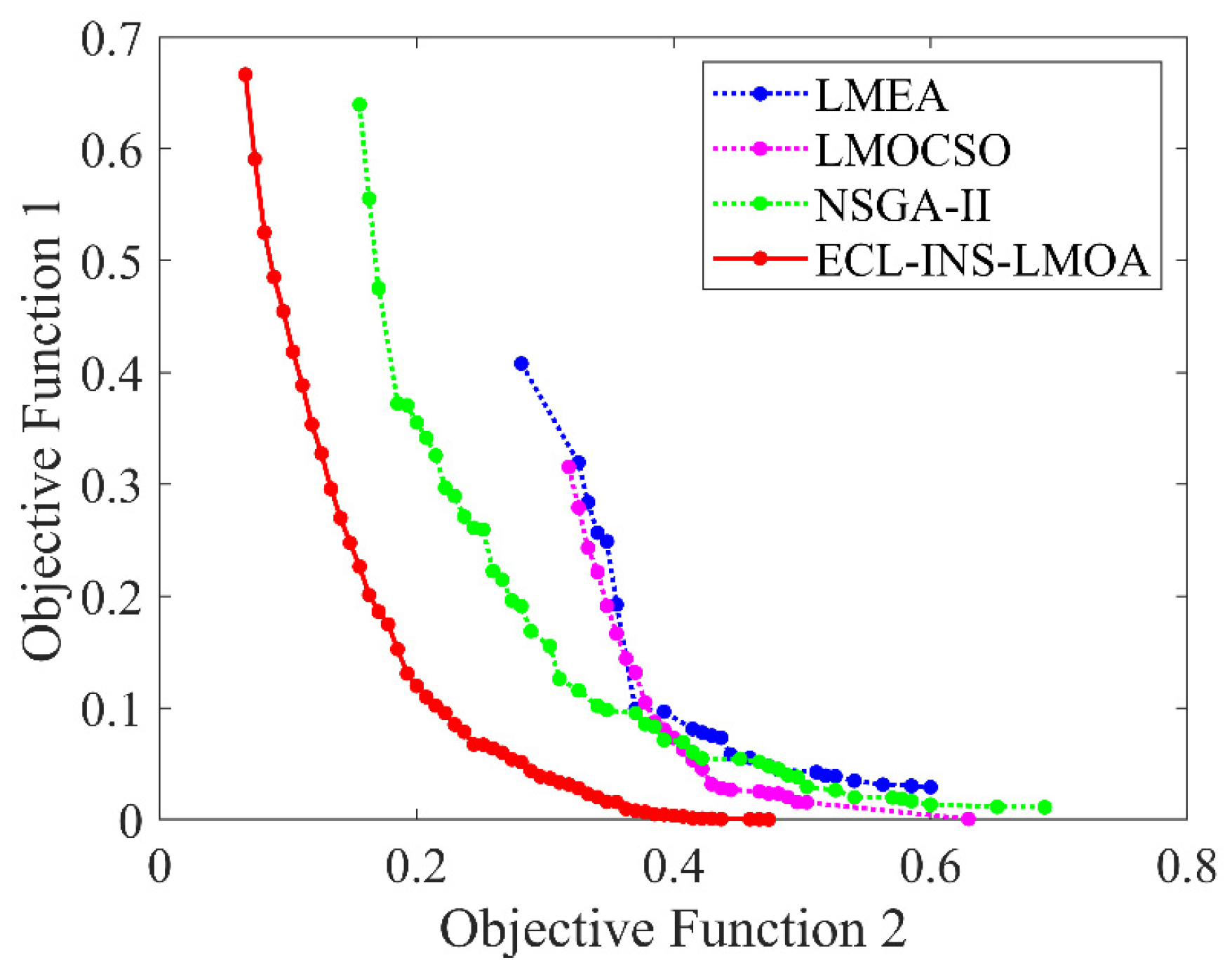
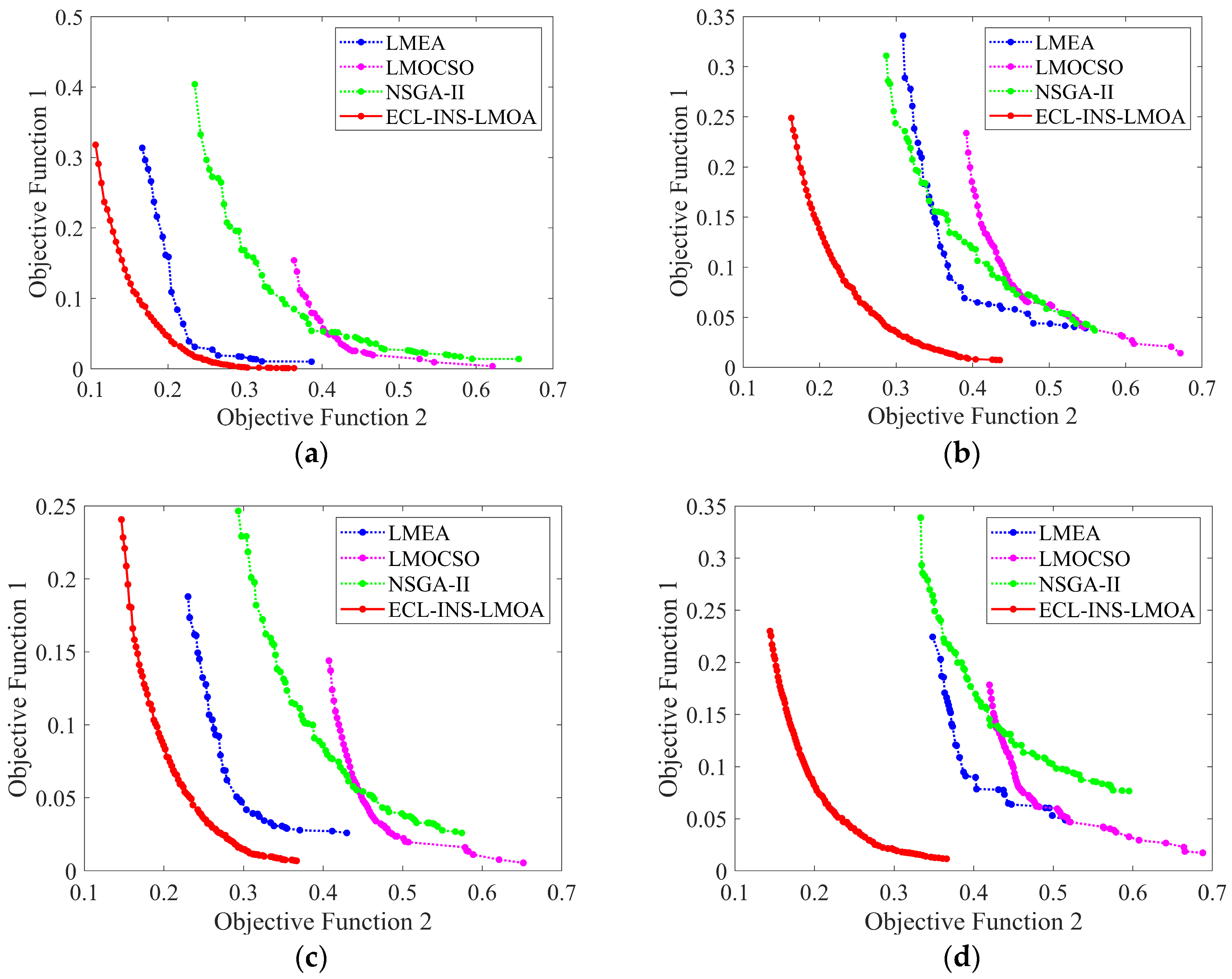
4.2.2. Comparison between ECL-INS-LMOA and Comparative Algorithms
- The distribution of solutions in the objective space
- 2.
- Regional coverage results
- 3.
- Runtime
4.2.3. Results of ECL-INS-LMOA for Larger Regions
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, X.; Jiao, J.; Zhong, Y.; Ma, A.; Xu, Y.; Sha, Z.; Huang, F.; Wan, Y.; Hu, W. The CNRIEEEMC: A communication-navigation-remote sensing-integrated ecological environment emergency monitoring chain for tailings areas. Int. J. Appl. Earth Obs. 2022, 108, 102710. [Google Scholar] [CrossRef]
- Zhang, G.; Cui, H.; Wang, T.; Li, Z.; Jiang, B.; Li, X.; Wang, H.; Zhu, Y. Random cross-observation intensity consistency method for large-scale SAR images mosaics: An example of Gaofen-3 SAR images covering China. ISPRS J. Photogramm. 2019, 156, 215–234. [Google Scholar] [CrossRef]
- Mi, W.; Fang, Y. Intelligent remote sensing satellite and remote sensing image real-time service. Acta Geod. Cartogr. Sin. 2019, 48, 1586–1594. [Google Scholar]
- Xu, Y.; Du, B.; Zhang, L. Assessing the Threat of Adversarial Examples on Deep Neural Networks for Remote Sensing Scene Classification: Attacks and Defenses. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1604–1617. [Google Scholar] [CrossRef]
- Richer-de-Forges, A.C.; Chen, Q.; Baghdadi, N.; Chen, S.; Gomez, C.; Jacquemoud, S.; Martelet, G.; Mulder, V.L.; Urbina-Salazar, D.; Vaudour, E.; et al. Remote Sensing Data for Digital Soil Mapping in French Research—A Review. Remote Sens. 2023, 15, 3070. [Google Scholar] [CrossRef]
- Zhu, B.; Bai, Y.; Zhang, Z.; He, X.; Wang, Z.; Zhang, S.; Dai, Q. Satellite Remote Sensing of Water Quality Variation in a Semi-Enclosed Bay (Yueqing Bay) under Strong Anthropogenic Impact. Remote Sens. 2022, 14, 550. [Google Scholar] [CrossRef]
- McCarthy, M.J.; Jessen, B.; Barry, M.J.; Figueroa, M.; McIntosh, J.; Murray, T.; Schmid, J.; Muller-Karger, F.E. Mapping hurricane damage: A comparative analysis of satellite monitoring methods. Int. J. Appl. Earth Obs. 2020, 91, 102134. [Google Scholar] [CrossRef]
- Xia, Z.; Li, Y.; Guo, X.; Chen, R. High-resolution mapping of water photovoltaic development in China through satellite imagery. Int. J. Appl. Earth Obs. 2022, 107, 102707. [Google Scholar] [CrossRef]
- Wang, Y.; Su, J.; Zhai, X.; Meng, F.; Liu, C. Snow Coverage Mapping by Learning from Sentinel-2 Satellite Multispectral Images via Machine Learning Algorithms. Remote Sens. 2022, 14, 782. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.; Chen, T.; Deng, W. Hyperspectral Image Classification Based on Fusing S3-PCA, 2D-SSA and Random Patch Network. Remote Sens. 2023, 15, 3402. [Google Scholar] [CrossRef]
- Lu, Z.; Shen, X.; Li, D.; Chen, Y.; Li, D. A Mission Planning Modeling Method of Multipoint Target Imaging within a Single Pass for Super-Agile Earth Observation Satellite. IEEE Syst. J. 2022, 16, 1921–1932. [Google Scholar] [CrossRef]
- Rainjonneau, S.; Tokarev, I.; Iudin, S.; Rayaprolu, S.; Pinto, K.; Lemtiuzhnikova, D.; Koblan, M.; Barashov, E.; Kordzanganeh, M.; Pflitsch, M. Quantum algorithms applied to satellite mission planning for Earth observation. arXiv 2023, arXiv:2302.07181. [Google Scholar] [CrossRef]
- Eddy, D.; Kochenderfer, M. Markov Decision Processes For Multi-Objective Satellite Task Planning. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–12. [Google Scholar]
- Tian, Y.; Si, L.; Zhang, X.; Cheng, R.; He, C.; Tan, K.C.; Jin, Y. Evolutionary Large-Scale Multi-Objective Optimization: A Survey. ACM Comput. Surv. 2021, 54, 1–34. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Rajani; Kumar, D.; Kumar, V. Impact of Controlling Parameters on the Performance of MOPSO Algorithm. Procedia Comput. Sci. 2020, 167, 2132–2139. [Google Scholar] [CrossRef]
- Antonio, L.M.; Coello CA, C.; Morales MA, R.; Brambila, S.G.; González, J.F.; Tapia, G.C. Co-evolutionary Operations for Large Scale Multi-objective Optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Li, M.; Wei, J. A cooperative co-evolutionary algorithm for large-scale multi-objective optimization problems: ACM. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 1716–1721. [Google Scholar]
- Cao, B.; Zhao, J.; Gu, Y.; Ling, Y.; Ma, X. Applying graph-based differential grouping for multi-objective large-scale optimization. Swarm Evol. Comput. 2020, 53, 100626. [Google Scholar] [CrossRef]
- Basu, S.; Mondal, A.; Basu, A. A Cooperative Co-evolutionary Approach for Multi-objective Optimization. In Recent Trends in Signal and Image Processing: ISSIP; Bhattacharyya, S., Mukherjee, A., Bhaumik, H., Das, S., Yoshida, K., Eds.; Springer: Singapore, 2019; pp. 57–65. [Google Scholar]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. A Decision Variable Clustering-Based Evolutionary Algorithm for Large-Scale Many-Objective Optimization. IEEE Trans. Evolut. Comput. 2018, 22, 97–112. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Q.; Tian, Y.; Tan, K.C. A Variable Importance-Based Differential Evolution for Large-Scale Multi-objective Optimization. IEEE Trans. Cybern. 2022, 52, 13048–13062. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Zhang, X. Improved SparseEA for sparse large-scale multi-objective optimization problems. Complex Intell. Syst. 2023, 9, 1127–1142. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, X.; Wang, C.; Jin, Y. An Evolutionary Algorithm for Large-Scale Sparse Multi-objective Optimization Problems. IEEE Trans. Evolut. Comput. 2020, 24, 380–393. [Google Scholar] [CrossRef]
- Zille, H.; Ishibuchi, H.; Mostaghim, S.; Nojima, Y. A Framework for Large-Scale Multi-objective Optimization Based on Problem Transformation. IEEE Trans. Evolut. Comput. 2018, 22, 260–275. [Google Scholar] [CrossRef]
- He, C.; Li, L.; Tian, Y.; Zhang, X.; Cheng, R.; Jin, Y.; Yao, X. Accelerating Large-Scale Multi-objective Optimization via Problem Reformulation. IEEE Trans. Evolut. Comput. 2019, 23, 949–961. [Google Scholar] [CrossRef]
- Liu, R.; Liu, J.; Li, Y.; Liu, J. A random dynamic grouping based weight optimization framework for large-scale multi-objective optimization problems. Swarm Evol. Comput. 2020, 55, 100684. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, M.; Lin, Q.; Tan, K.C. Evolutionary Large-Scale Multi-objective Optimization via Self-guided Problem Transformation. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Liu, R.; Ren, R.; Liu, J.; Liu, J. A clustering and dimensionality reduction based evolutionary algorithm for large-scale multi-objective problems. Appl. Soft Comput. 2020, 89, 106120. [Google Scholar] [CrossRef]
- Ji, W.; Yue, Y.; Wang, X.; Lin, P. Large-scale Multi-objective Natural Computation Based on Dimensionality Reduction and Clustering. J. Syst. Simul. 2023, 35, 41–56. [Google Scholar]
- Tan, Z.; Wang, H.; Liu, S. Multi-stage dimension reduction for expensive sparse multi-objective optimization problems. Neurocomputing 2021, 440, 159–174. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, C.; Zhang, X.; Tan, K.C.; Jin, Y. Solving large-scale multi-objective optimization problems with sparse optimal solutions via unsupervised neural networks. IEEE Trans. Cybern. 2020, 51, 3115–3128. [Google Scholar] [CrossRef]
- He, C.; Cheng, R.; Yazdani, D. Adaptive Offspring Generation for Evolutionary Large-Scale Multi-objective Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 786–798. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Y.; Wan, Z. Large-scale many-objective optimization driven by distributional adversarial networks. arXiv 2020, arXiv:2003.07013. [Google Scholar]
- He, C.; Huang, S.; Cheng, R.; Tan, K.C.; Jin, Y. Evolutionary multi-objective optimization driven by generative adversarial networks (GANs). IEEE Trans. Cybern. 2020, 51, 3129–3142. [Google Scholar] [CrossRef] [PubMed]
- Kropp, I.; Nejadhashemi, A.P.; Deb, K. Improved Evolutionary Operators for Sparse Large-Scale Multi-objective Optimization Problems. IEEE Trans. Intell. Transp. Syst. 2023, 1. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, L.; Sun, D.; Zhang, X. A multi-stage knowledge-guided evolutionary algorithm for large-scale sparse multi-objective optimization problems. Swarm Evol. Comput. 2022, 73, 101119. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Li, K.; Yeh, W.; Jian, M.; Dong, J. Enhancing MOEA/D with information feedback models for large-scale many-objective optimization. Inf. Sci. 2020, 522, 1–16. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, H.; Ma, H.; Zhang, X.; Tan, K.C.; Jin, Y. Integrating Conjugate Gradients Into Evolutionary Algorithms for Large-Scale Continuous Multi-Objective Optimization. IEEE/CAA J. Autom. Sin. 2022, 9, 1801–1817. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A Competitive Swarm Optimizer for Large Scale Optimization. IEEE Trans. Cybern. 2015, 45, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zheng, X.; Zhang, X.; Jin, Y. Efficient Large-Scale Multi-objective Optimization Based on a Competitive Swarm Optimizer. IEEE Trans. Cybern. 2020, 50, 3696–3708. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, M.; Shen, X.; Zhang, G.; Lu, Z.; Xu, J. A Multi-Objective Modeling Method of Multi-Satellite Imaging Task Planning for Large Regional Mapping. Remote Sens. 2020, 12, 344. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M. Test Problems for Large-Scale Multi-objective and Many-Objective Optimization. IEEE Trans. Cybern. 2017, 47, 4108–4121. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Shift-Based Density Estimation for Pareto-Based Algorithms in Many-Objective Optimization. IEEE Trans. Evolut. Comput. 2014, 18, 348–365. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; He, R.; Chen, Y. Multi-satellite scheduling framework and algorithm for very large area observation. Acta Astronaut. 2020, 167, 93–107. [Google Scholar] [CrossRef]
- Gu, Y.; Han, C.; Chen, Y.; Liu, S.; Wang, X. Large Region Targets Observation Scheduling by Multiple Satellites Using Resampling Particle Swarm Optimization. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1800–1815. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Zhang, Y.; Zheng, K. Research Progress and Prospect of Satellite Constellation Optimization Design. J. Phys. Conf. Ser. 2023, 2457, 12045. [Google Scholar] [CrossRef]
- Long, J.; Wu, S.; Han, X.; Wang, Y.; Liu, L. Autonomous Task Planning Method for Multi-Satellite System Based on a Hybrid Genetic Algorithm. Aerospace 2023, 10, 70. [Google Scholar] [CrossRef]
- Li, H.; He, F.; Chen, Y.; Pan, Y. MLFS-CCDE: Multi-objective large-scale feature selection by cooperative co-evolutionary differential evolution. Memetic Comput. 2021, 13, 1–18. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S. A multi-objective optimization algorithm for feature selection problems. Eng. Comput. 2022, 38, 1845–1863. [Google Scholar] [CrossRef]
- Mishra, V.; Kane, L. A survey of designing convolutional neural network using evolutionary algorithms. Artif. Intell. Rev. 2023, 56, 5095–5132. [Google Scholar] [CrossRef]
- Cao, B.; Li, M.; Liu, X.; Zhao, J.; Cao, W.; Lv, Z. Many-Objective Deployment Optimization for a Drone-Assisted Camera Network. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2756–2764. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Y.; Qu, D.; Chen, X.; Li, Y. Multi-Objective Optimization of Evacuation Route for Heterogeneous Passengers in the Metro Station Considering Node Efficiency. IEEE Trans. Intell. Transp. Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, T.; Ding, X. Large-Scale WSNs Resource Scheduling Algorithm in Smart Transportation Monitoring Based on Differential Ion Coevolution and Multi-Objective Decomposition. IEEE Trans. Intell. Transp. Syst. 2022, 1–10. [Google Scholar] [CrossRef]







| Satellite | Gaofen-3 |
|---|---|
| Launch Time | 10 August 2016 |
| Orbit Type | Repeat sun-synchronous orbit |
| Orbital Altitude (km) | 755 |
| Imaging Mode | Fine strip II |
| Swing Ability | 19–50° |
| Spatial Resolution (m) | 10 |
| Swath Width (km) | 100 |
| Band | C |
| Polarization | Dual polarization |
| Region | Congo (K) | India | Australia | USA | Antarctica |
|---|---|---|---|---|---|
| Area (10,000 square km) | 234.5 | 298.0 | 774.1 | 936.4 | 1424.5 |
| Ranking in world | 11 | 7 | 6 | 4 | - |
| Region | Sub-Region | Imaging Time | Number of Candidate Stripes | Number of Real/Binary Decision Variables |
|---|---|---|---|---|
| Congo (K) | 1 | 1 December 2019–31 December 2019 | 41 | 135 |
| 2 | 1 January 2020–31 January 2020 | 52 | ||
| 3 | 1 February 2020–29 February 2020 | 42 | ||
| India | 1 | 1 December 2019–31 December 2019 | 37 | 264 |
| 2 | 1 January 2020–31 January 2020 | 80 | ||
| 3 | 1 February 2020–29 February 2020 | 74 | ||
| 4 | 1 March 2020–31 March 2020 | 44 | ||
| 5 | 1 April 2020–30 April 2020 | 29 | ||
| Australia | 1 | 1 December 2019–31 December 2019 | 64 | 411 |
| 2 | 1 January 2020–31 January 2020 | 97 | ||
| 3 | 1 February 2020–29 February 2020 | 98 | ||
| 4 | 1 March 2020–31 March 2020 | 105 | ||
| 5 | 1 April 2020–30 April 2020 | 47 | ||
| The United States | 1 | 1 December 2019–31 December 2019 | 115 | 491 |
| 2 | 1 January 2020–31 January 2020 | 131 | ||
| 3 | 1 February 2020–29 February 2020 | 118 | ||
| 4 | 1 March 2020–31 March 2020 | 104 | ||
| 5 | 1 April 2020–20 April 2020 | 23 | ||
| Antarctica | 1 | 19 December 2019–20 December 2019 | 20 | 798 |
| 2 | 20 December 2019–26 December 2019 | 96 | ||
| 3 | 26 December 2019–1 January 2020 | 99 | ||
| 4 | 1 January 2020–7 January 2020 | 91 | ||
| 5 | 7 January 2020–13 January 2020 | 91 | ||
| 6 | 13 January 2020–23 January 2020 | 163 | ||
| 7 | 23 January 2020–3 February 2020 | 79 | ||
| 8 | 3 February 2020–16 February 2020 | 139 | ||
| 9 | 16 February 2020–28 February 2020 | 20 |
| Region | Number of Decision Variables | Evaluation Times of Objective Function | |||
|---|---|---|---|---|---|
| NSGA-II | LMOCSO | LMEA | ECL-INS-LMOA | ||
| Congo (K) | 135 | 48,000 | 48,000 | 160,000 | 48,000 |
| India | 264 | 70,000 | 70,000 | 1,320,000 | 70,000 |
| Australia | 411 | 100,000 | 100,000 | 2,000,000 | 100,000 |
| The United States | 491 | 130,000 | 130,000 | 2,000,000 | 130,000 |
| Antarctica | 798 | 160,000 | 160,000 | 2,100,000 | 160,000 |
| Algorithm | Objective Function 1 | Coverage Rate | Objective Function 2 | Number of Imaging Strips |
|---|---|---|---|---|
| LMEA | 0.02902 | 97.10% | 0.60000 | 81 |
| LMOCSO | 0.00067 | 99.93% | 0.62963 | 85 |
| NSGA-II | 0.01120 | 98.88% | 0.68889 | 93 |
| ECL-INS-LMOA | 0.00018 | 99.98% | 0.47407 | 64 |
| Algorithm | NSGA-II | LMOCSO | LMEA | ECL-INS-LMOA |
|---|---|---|---|---|
| Calculation time of objective functions | 1.2992 | |||
| Total optimization time | 7.7601 × 102 | 1.5365 × 103 | 1.0512 × 104 | 5.3960 × 102 |
| Region | Algorithm | Objective Function 1 | Coverage Rate | Objective Function 2 | Number of Imaging Strips |
|---|---|---|---|---|---|
| India | LMEA | 0.01037 | 98.96% | 0.38636 | 102 |
| LMOCSO | 0.00389 | 99.61% | 0.62121 | 164 | |
| NSGA-II | 0.01418 | 98.58% | 0.65530 | 173 | |
| ECSO-NSGA-II | 0.00113 | 99.89% | 0.36364 | 96 | |
| Australia | LMEA | 0.03913 | 96.09% | 0.54745 | 225 |
| LMOCSO | 0.01430 | 98.57% | 0.67153 | 276 | |
| NSGA-II | 0.03689 | 96.31% | 0.55961 | 230 | |
| ECSO-NSGA-II | 0.00736 | 99.26% | 0.43552 | 179 | |
| The United States | LMEA | 0.02598 | 97.40% | 0.42974 | 211 |
| LMOCSO | 0.00542 | 99.46% | 0.65173 | 320 | |
| NSGA-II | 0.02597 | 97.40% | 0.57434 | 282 | |
| ECSO-NSGA-II | 0.00688 | 99.31% | 0.36660 | 180 | |
| Antarctica | LMEA | 0.04870 | 95.13% | 0.51504 | 411 |
| LMOCSO | 0.01726 | 98.27% | 0.68797 | 549 | |
| NSGA-II | 0.07696 | 92.30% | 0.58647 | 468 | |
| ECSO-NSGA-II | 0.01158 | 98.84% | 0.36591 | 292 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Shen, X.; Zhang, G.; Lu, Z. Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping. Remote Sens. 2023, 15, 4178. https://doi.org/10.3390/rs15174178
Chen Y, Shen X, Zhang G, Lu Z. Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping. Remote Sensing. 2023; 15(17):4178. https://doi.org/10.3390/rs15174178
Chicago/Turabian StyleChen, Yaxin, Xin Shen, Guo Zhang, and Zezhong Lu. 2023. "Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping" Remote Sensing 15, no. 17: 4178. https://doi.org/10.3390/rs15174178
APA StyleChen, Y., Shen, X., Zhang, G., & Lu, Z. (2023). Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping. Remote Sensing, 15(17), 4178. https://doi.org/10.3390/rs15174178