Velocity-Related Magnetic Interference Compensation of Unmanned Underwater Vehicle

Abstract

Underwater magnetic detection based on unmanned underwater vehicles (UUVs) is an important approach for marine exploration and monitoring. Due to the interference of the carrier magnetic field, the detection accuracy is severely limited. To improve the performance of magnetic detection, various compensation methods have been developed. However, the compensation effectiveness of these methods is greatly diminished when UUVs sail at different velocities. In this paper, we propose a velocity-related interference magnetic compensation method that enhances the conventional Tolles–Lawson model. By introducing a velocity-related term and combining the ridge regression with the linear fitting algorithm, we determine the compensation parameters for various UUV velocities. Field experiments are conducted to verify the effectiveness of the proposed method. The results show that the root mean square error of the total magnetic field after compensation is reduced from 246.90 nT to 2.23 nT. Our study demonstrates that the velocity-related compensation method can significantly improve the accuracy of interference magnetic compensation under different UUV velocities, making it applicable to actual underwater magnetic detection.

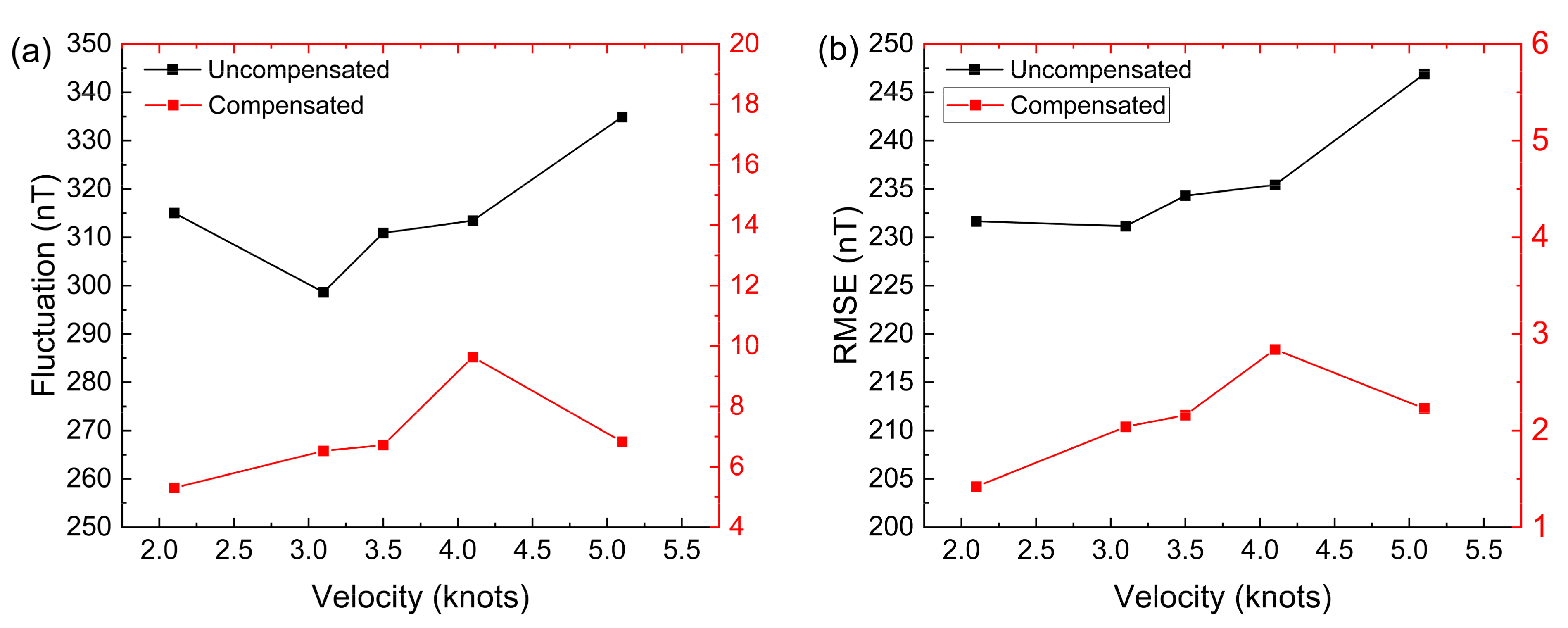
1. Introduction

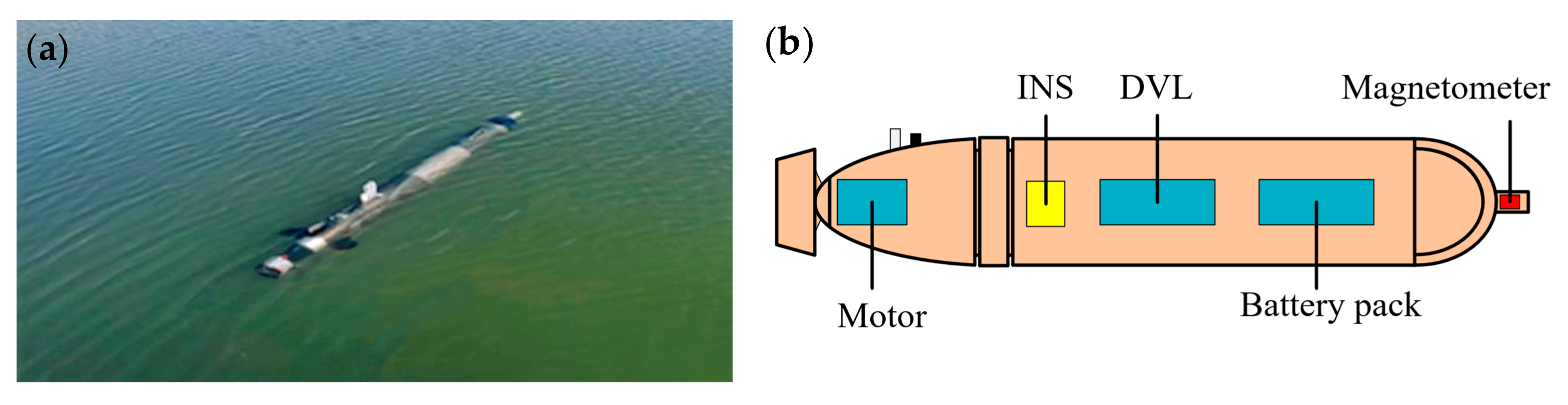
As a non-acoustic detection technology, underwater magnetic detection plays an irreplaceable role in geoscience, especially in oceanography [1,2]. With the rapid development of marine observation and exploration, unmanned underwater vehicles (UUVs) have become attractive underwater carriers for a variety of sensors and navigation equipment [3]. UUVs navigate underwater via remote or automatic control, and they have good performance in terms of adaptability, detection range, and operation efficiency [4]. UUVs equipped with magnetometers for underwater magnetic detection hold enormous promise for marine exploration and monitoring, including earthquake monitoring and research, benthonic geological research, marine mineral resource exploration, underwater salvage and search operations, investigation of undersea oil pipelines, detection of underwater magnetic targets, and autonomous underwater navigation of submersibles [5,6,7,8,9].

However, in addition to sensing the magnetic field of the target, the magnetometer on UUVs inevitably detects interference from the carrier, the local geomagnetic field, and other sources during actual detection [10]. The interference magnetic field generated by carriers can significantly distort underwater magnetic measurements. This field mainly consists of three components: the induced magnetic field, the permanent magnetic field, and the eddy current magnetic field, all of which are generated by ferromagnetic materials that are inevitably present in UUVs. It has been reported that on the surface of an underwater vehicle, the induced magnetic field can be of similar magnitude to the geomagnetic field and continuously changes with the vehicle’s attitude [11]. As stated in reference [12], any measurement error exceeding 30 nT can lead to the failure of underwater magnetic detection. In conclusion, the interference of UUVs can considerably affect the accuracy of underwater magnetic detection. Therefore, compensating for carrier magnetic interference is of critical importance.

Notably, the interference magnetic field of UUVs is also affected by their internal electromechanical system’s working state [13]. For instance, UUVs need to operate at various velocities during magnetic detection to adapt to the complex marine environment and control their heading and path [14]. This is achieved through changes in motor speed and battery current, resulting in fluctuations in the interference of the magnetic field [15]. Therefore, the magnetic field interference varies under different operating velocities of UUVs. Hence, it is necessary to compensate for velocity-related interference on the magnetic field to achieve high-precision measurements.

To reduce magnetic detection distortion, researchers have focused on studying carrier magnetic interference compensation [16,17,18,19]. In 1954, Tolles and Lawson analyzed the material composition and structure of aircraft to represent the interference as the sum of three field strengths: permanent field, induced field, and eddy current field, and proposed the Tolles–Lawson model [20]. Leliak et al. established a method to solve the compensation parameters in the interference magnetic model by representing the interference as 16 compensation functions, with each function composed of a fixed compensation coefficient and a base function [21]. Leach subsequently proposed the least squares method as a means to solve compensation model parameters while analyzing complex collinearity in the process [22]. Meanwhile, Gebre-Egziabher introduced a two-step calibration method that uses the least squares method to estimate intermediate variables and subsequently arrives at a solution for the model using those values [23]. However, Gebre-Egziabher’s calibration method falls short in addressing ill-condition problems [24], since its core algorithm still relies on the least squares method. As computational and mathematical solution methods continue to develop, more algorithms such as recursive least squares (RLS), truncated singular value decomposition, ridge regression, and neural networks have emerged as possible solutions [25,26,27,28]. Although these algorithms can improve computing accuracy, they cannot effectively improve the interference compensation accuracy as they are all based on the conventional Tolles–Lawson model. Currently, scholars studying geomagnetic compensation are increasingly focusing on the electromechanical interference of carriers, which the Tolles–Lawson model does not account for. In reference [29], the authors proposed a compensation method for the magnetic interference caused by the relative motion component and onboard current. In reference [30], the dynamic interference of various airborne equipment is considered, which is useful for reducing interference magnetic field. By studying the sources of these additional magnetic interferences and developing new compensation models, one can effectively improve the precision of magnetic interference compensation. However, available models have not taken the significant interference caused by variations in the velocity of UUV into account, and the compensation for this interference has yet to be addressed.

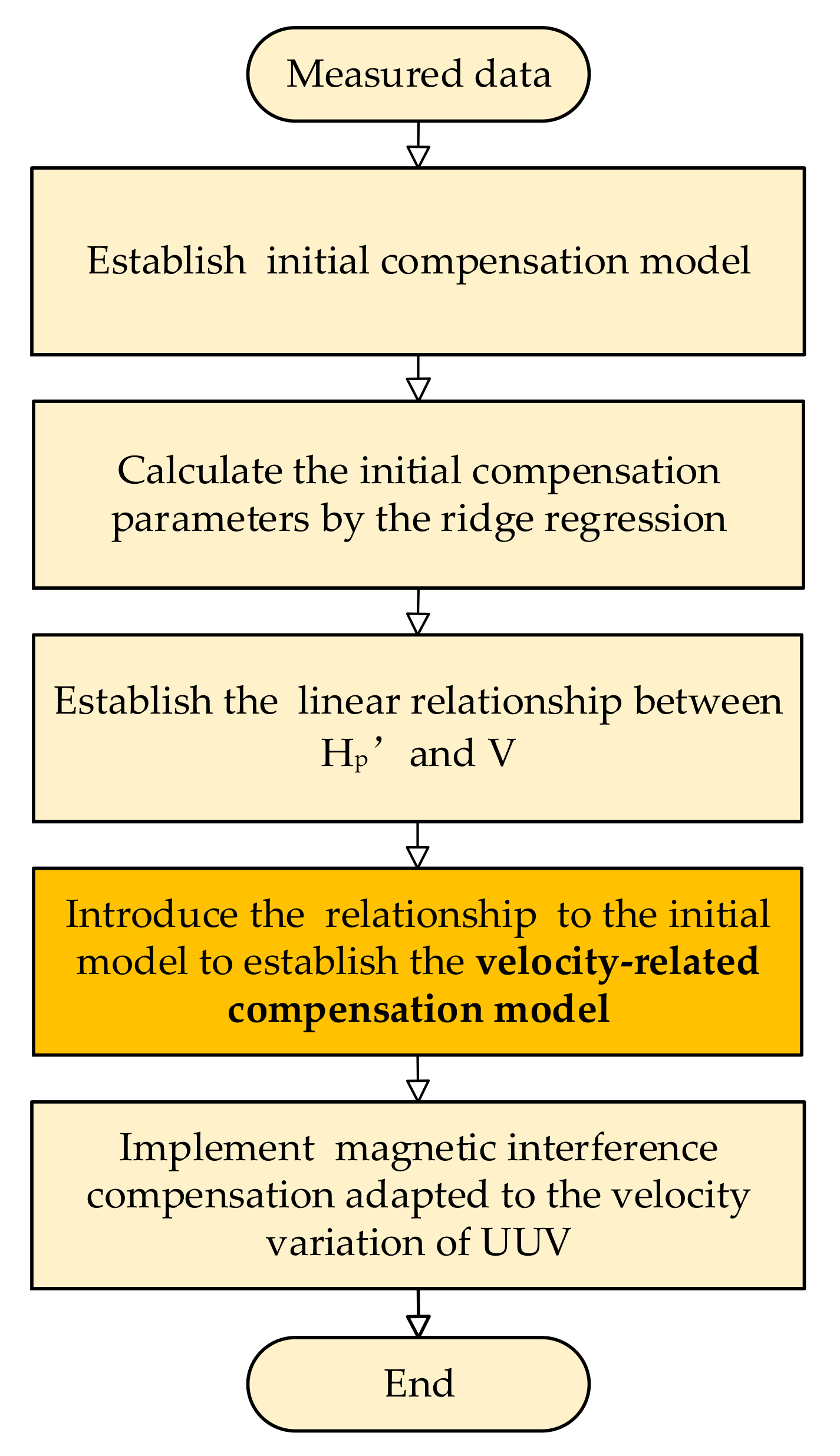
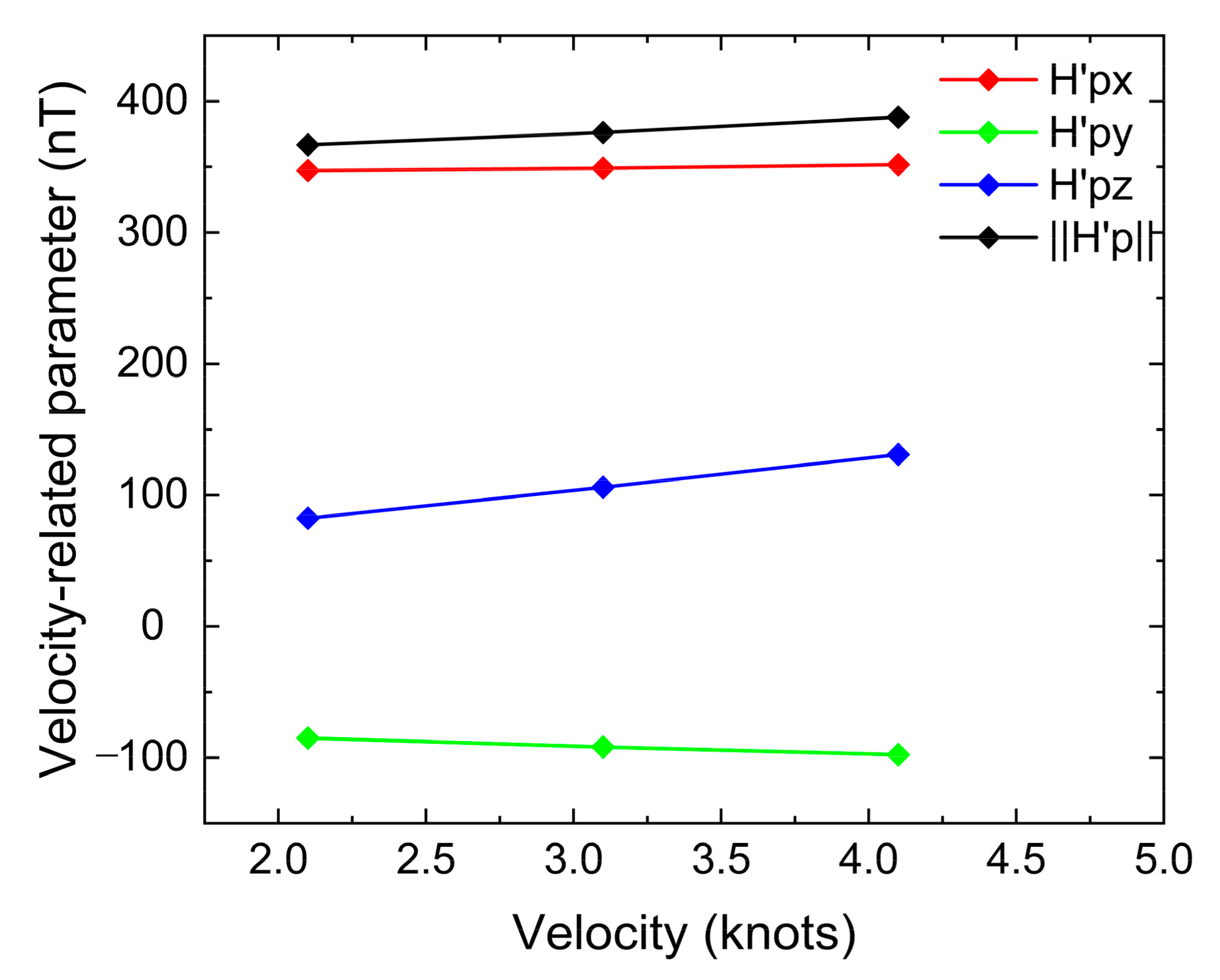
In this paper, a modified compensation method for UUV magnetic interference that takes velocity into account is proposed. We introduce a velocity-related term to improve the Tolles–Lawson model, which greatly expands the model’s application to UUV sailing at various velocities. We estimate the compensation parameters in two steps. First, we use the ridge estimation algorithm, which has certain advantages in fitting ill-conditioned data, to calculate the initial compensation parameters for several sets of constant velocities. Then, we use linear fitting to determine the functional relation between the initial compensation parameter and UUV velocity. By substituting the functional relation into the initial model, we establish a velocity-related compensation model. Finally, we verify the proposed compensation model’s practicability with a series of field experiments. The contributions made in this paper are as follows:

• The impact of UUV velocity variation on the accuracy of underwater magnetic detection has been considered. A velocity-related term is introduced to improve the compensation accuracy for carrier interference magnetic field.
• A two-step approach with ridge regression and linear fitting is employed to determine the compensation parameters, which has good operability. The ridge regression algorithm is applied to address the ill-conditioning of measured date to enhance the reliability of parameter estimation.
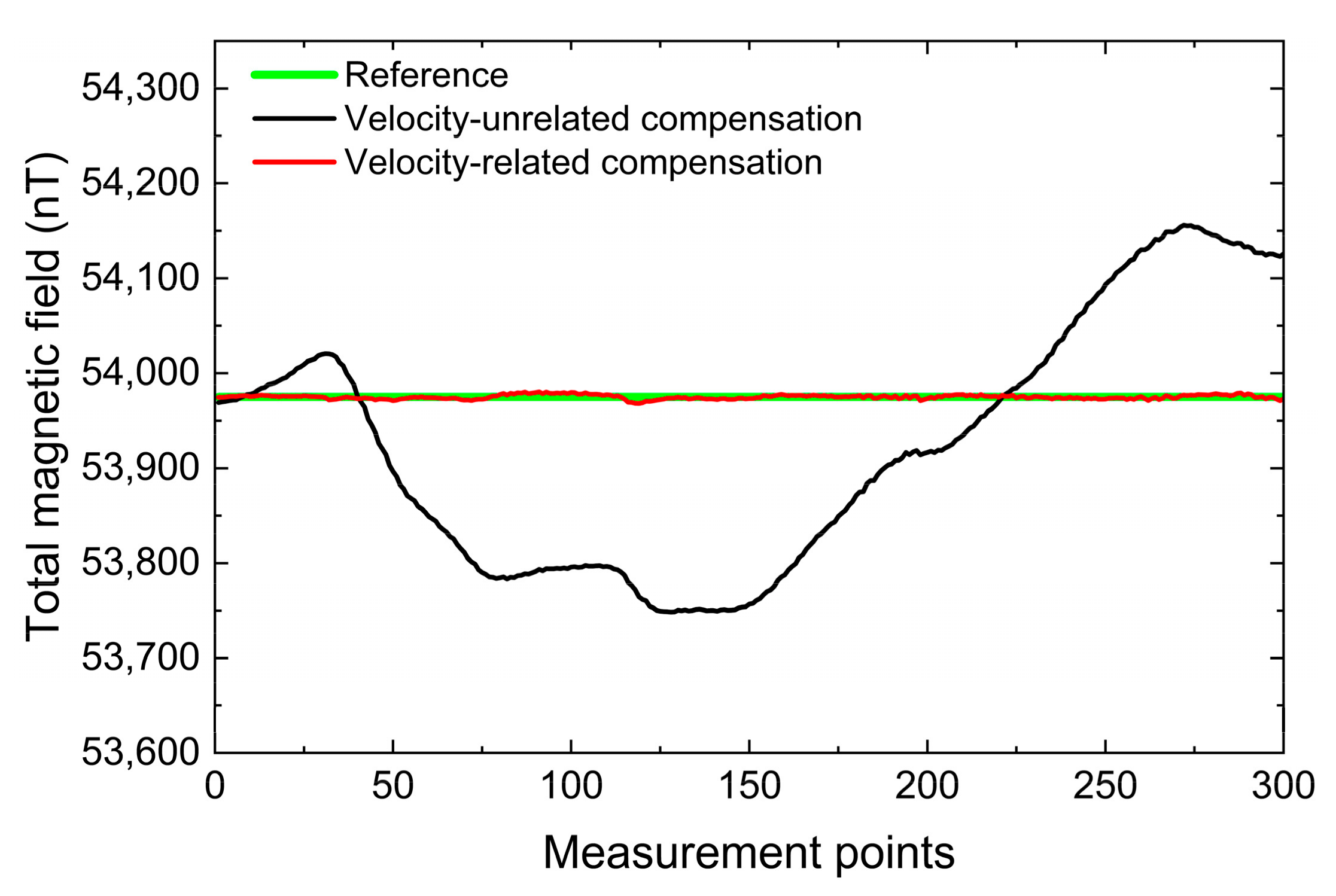
• The proposed compensation method achieves high-precision compensation in field experiments, and it is feasible and effective for underwater magnetic detection.

2. Velocity-Related Compensation Method for UUV Magnetic Interference

2.1. Interference Magnetic Field Model of UUVs

In the measurement system, a triaxial magnetometer is installed on the UUV to capture magnetic signals in real time. However, during practical measurement, these signals often contain interference from ferromagnetic materials present on the UUV. This interference can lead to distortion of underwater magnetic detection. Specifically, the interference typically includes the permanent magnetic field, induced magnetic field, and eddy current magnetic field. The eddy current magnetic field is mainly caused by conductive materials constantly cutting through the geomagnetic field. Since it consisted of high-frequency components, low-pass filtering is commonly employed for reducing its interference during data processing [31].

Moreover, the presence of hard magnetic materials on the UUV can generate a permanent magnetic field over a period of long-term exposure to a strong magnetic field. This field is continuous and typically does not weaken under most circumstances. Its expression is given as:

$$H_p={\left[\begin{array}{ccc}{H}_{px}& H_{py}& H_{pz}\end{array}\right]}^T,$$

(1)

where $H_{px}$, $H_{py}$, $H_{pz}$ denote the projections of the permanent magnetic field on the x, y, and z-axes of the triaxial magnetometer, respectively. Since the carrier is rigidly connected to the underwater magnetic vector measurement system, these projections are treated as constants.

The induced magnetic field is generated by the magnetization of soft magnetic materials due to an external magnetic field. A 3 × 3 matrix with nine parameters is utilized to represent the magnetization and interaction of each axis in the external magnetic field, which can be expressed as:

$$K=\left[\begin{array}{ccc}{k}_{xx}& k_{xy}& k_{xz}\\ k_{yx}& k_{yy}& k_{yz}\\ k_{zx}& k_{zy}& k_{zz}\end{array}\right]$$

(2)

Furthermore, based on Euler’s theorem [32], the geomagnetic field in the geographic coordinate system can be converted into the measurement field in the magnetometer coordinate system using the rotation matrix $R_m$ as shown below:

$$R_m=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& -\sin \alpha & \cos \alpha \end{array}\right]\left[\begin{array}{ccc}\cos \beta & 0& -\sin \beta \\ 0& 1& 0\\ \sin \beta & 0& \cos \beta \end{array}\right]\left[\begin{array}{ccc}\cos \gamma & \sin \gamma & 0\\ -\sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right],$$

(3)

where $\alpha$, $\beta$, $\gamma$ represent three Euler angles between the geographic coordinate system and the magnetometer coordinate system.

Hence, according to the Tolles–Lawson model [20], the interference magnetic field of UUVs can be expressed as follows:

$$H_{ex}=K{R}_m{H}_e+H_p,$$

(4)

where $H_e={\left[\begin{array}{ccc}{H}_{ex}& H_{ey}& H_{ez}\end{array}\right]}^T$ denotes the value of the geomagnetic field in the geographic coordinate system.

The measured magnetic field can be initially modeled as follows:

$$H_m=R_m{H}_e+H_{ex}=\left(K+E\right)R_m{H}_e+H_p,$$

(5)

where $E$ denotes the identity matrix.

2.2. Velocity-Related Compensation Model

2.2.1. The Mathematical Model

Based on the analysis in Section 2.1, we can derive the expression of the interference compensation model as follows:

$$\left\{\begin{array}{c}{H}_e=R_m^{-1}{M}_k^{-1}(H_m-H_p)\\ M_k^{}=(K+E)=\left[\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\right]\end{array}\right.$$

(6)

The internal elements of $M_k^{}$ are considered constant, as the magnetization parameters of soft magnetic materials on UUV remain unchanged in all directions.

Apart from the permanent magnetic field and the induced magnetic field, electromechanical devices can introduce extra interference while the UUV is operational. During underwater magnetic detection, changes in velocity are necessary and inevitable. The control of UUV velocity is achieved through changes in motor speed and battery current, which must lead to changes in the magnetic field. Therefore, this velocity-related magnetic field interference cannot be ignored. To confirm this, we secured the UUV with a non-magnetic truss and controlled the motor to run at different speeds during a shore-based experiment. Through spectral analysis, we found that the generated magnetic field interference contains both AC and DC components, where the AC signal can be filtered out by a low-pass filter, while the DC signal reveals a linear relationship with the motor speed. The target signals we need to detect are often low-frequency signals, so it is not sufficient to consider only the permanent magnetic interference in $H_p$.

To compensate for the interference resulting from velocity variations, we introduce a velocity-related term into the compensation model. Accordingly, we establish a linear function to describe the relationship between velocity and the interference it generates, and define the correlation coefficient as follows:

$$G={[\begin{array}{ccc}{g}_x& g_y& g_z\end{array}]}^T$$

(7)

The velocity-related term is expressed as:

$${H_p}^{\prime }=VG+H_p,$$

(8)

where $V$ is the scalar velocity of UUV, $H_p$ is related to the permanent magnetic field.

By substituting $H_p$ into Equation (6), we can derive the velocity-related compensation model as follows:

$$H_e=R_m^{-1}\cdot M_k^{-1}\cdot (H_m-H_p{}^{\prime })=R_m^{-1}\cdot M_k^{-1}\cdot (H_m-VG-H_p)$$

(9)

2.2.2. Compensation Principle

The parameter estimation procedure for total magnetic field compensation is mainly divided into two parts. First, we establish a parameter estimation method to solve the values of $M_k^{}$ and $H_p{}^{\prime }$ at different velocities of the UUV. Second, we obtain the coefficients related to $V$ in the linear model of $H_p{}^{\prime }$ through fitting.

By reorganizing Equation (9), we obtain the following equation:

$$\left\{\begin{array}{c}{‖H_e‖}^2=H_e{}^T\cdot H_e={(H_m-H_p{}^{\prime })}^T{(M_k^{-1})}^T{(R_m^{-1})}^T{R}_m^{-1}{M}_k^{-1}(H_m-H_p{}^{\prime })={(H_m-H_p{}^{\prime })}^{T}C(H_m-H_p{}^{\prime })\\ C={(M_k^{-1})}^T{M}_k^{-1}=\left[\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\\ c_{12}& c_{22}& c_{23}\\ c_{13}& c_{23}& c_{33}\end{array}\right]\end{array}\right.,$$

(10)

where ${(R_m^{-1})}^T{R}_m^{-1}=E$ for the rotation matrix is the orthogonal matrix, the value of ${‖H_e‖}^2$ can be acquired from the output of the magnetometer.

The above equation can be further expensed as follows:

$${‖H_e‖}^2-f(C,H_p{}^{\prime })=HP,$$

(11)

where $f(C,H_p{}^{\prime })=\left[c_{11}{H}_{\mathrm{p}x}^{\prime }{}^2+c_{22}{H}_{\mathrm{py}}^{\prime }{}^2+c_{33}{H}_{\mathrm{pz}}^{\prime }{}^2+2c_{12}{H}_{\mathrm{p}x}^{\prime }{H}_{\mathrm{py}}^{\prime }+2c_{13}{H}_{\mathrm{p}x}^{\prime }{H}_{\mathrm{pz}}^{\prime }+2c_{23}{H}_{\mathrm{py}}^{\prime }{H}_{\mathrm{pz}}^{\prime }\right]$, $H=\left[H_{mx}^2,H_{my}^2,H_{mz}^2,H_{mx}{H}_{my},H_{mx}{H}_{mz},H_{my}{H}_{mz},H_{mx},H_{my},H_{mz}\right]$, $P=\left[\begin{array}{c}\begin{array}{c}{p}_1\\ p_2\\ p_3\\ p_4\\ p_5\\ p_6\\ p_7\\ p_8\\ p_9\end{array}\end{array}\right]=\lceil \begin{array}{c}{c}_{11}\\ c_{22}\\ c_{33}\\ 2c_{12}\\ 2c_{13}\\ 2c_{23}\\ 2\left(-c_{11}{H}_{mx}-c_{12}{H}_{my}-c_{13}{H}_{mz}\right)\\ 2\left(-c_{22}{H}_{my}-c_{12}{H}_{mx}-c_{23}{H}_{mz}\right)\\ 2\left(-c_{33}{H}_{mz}-c_{13}{H}_{mx}-c_{23}{H}_{my}\right)\end{array}\rceil$.

$H$ contains only magnetic measured data and $P$ is the parameter vector that needs to be estimated. Since $f(C,H_p{}^{\prime })<<{‖H_e‖}^2$, it can be ignored during parameter estimation. Thus, the equation can be simplified to a linear form as ${‖H_e‖}^2=HP$. However, severe ill-conditioning often exists in the measured matrix due to the non-ergodicity of the UUV’s attitude during actual measurement. To address this issue, we use ridge regression [33] to estimate the parameter vector $P$ based on the linear equation:

$$\widehat{P}={\left[H^{T}H+\alpha E\right]}^{-1}{H}^T{‖H_0‖}^2,$$

(12)

where $\alpha$ is the ridge parameter used to suppress the ill-conditioning of the above equation.

As the parameters in $P$ are estimated, the value of $f(C,H_p{}^{\prime })$ can be calculated. Accordingly, iterators can be created to update $P$ in order to reduce the estimation error:

$${{\widehat{P}}^{\prime }}_i={\left[H^{T}H+\alpha E\right]}^{-1}{H}^T[{‖H_0‖}^2-f_{i-1}(C,H_p{}^{\prime })]$$

(13)

As mentioned earlier, compensation parameters $C$ and $H_p{}^{\prime }$ can be determined when the UUV sails at a certain velocity. Using the estimates of $H_p{}^{\prime }$ at various velocities of the UUV as shown in Equation (14), the optimal values of $G$ and $H_P$ can be obtained through linear fitting.

$$\left\{\begin{array}{c}{H}_{p1}{}^{\prime }=V_{1}G+H_p\\ H_{p2}{}^{\prime }=V_{2}G+H_p\\ H_{p3}{}^{\prime }=V_{3}G+H_p\\ \dots \end{array}\right.$$

(14)

Finally, the compensation for total magnetic field distortion can be achieved through the velocity-related compensation model expressed in Equation (10).

The system flowchart of the velocity-related compensation method is presented in Figure 1.

3. Field Experiment

3.1. Experimental Setup

The field experiment was conducted in an experimental reservoir in Hebei Province, which is undeveloped and far away from artificial construction. The intensity of the local geomagnetic field approximates the IGFR 2012 values monitored with a proton magnetometer. A 200 m caliber UUV with a non-magnetic aluminum alloy shell was used for the experiment, and its main construction is shown in Figure 2. A triaxial fluxgate magnetometer is used to detect the magnetic signal. To minimize stray magnetic fields generated by the motor system installed in the tail and interference from the battery pack, the magnetometer was mounted in a plastic watertight cabin extending from the head of the UUV. Additionally, a Doppler Velocity Log (DVL) and an Inertial Navigation System (INS) were served as the velocity sensor while functioning as the attitude sensor within the UUV, respectively.

The triaxial fluxgate magnetometer used in the experiment can provide highly precision measurements of triaxial static and alternating magnetic fields. Its main performance indicators are listed in

Table 1. Main performance indicators of the triaxial fluxgate magnetometer.

Performance	Parameter Value
Measurement range	±100,000 nT
Non-orthogonality error	<±0.1°
Linearity	<0.0015%
Noise	<10 pT RMS√Hz@1Hz
Maximum offset	±5 nT at ± 100 μT
Bandwidth	3 kHz
Frequency response	DC to 1 kHz

. Additionally, the magnetometer is sealed using poly-ether-ether-ketone (PEEK) with excellent pressure resistance and waterproofness, making it ideal for underwater measurements.

To reduce errors in the measured data, the UUV navigated at various headings, pitches, and roll angles whenever possible. Thus, it was controlled to sail along a typical circular trajectory submerged to a depth of 1.5 m underwater. The diameter of this trajectory was minimized to ensure a nearly constant intensity of the geomagnetic field. The underwater geomagnetic total field strength was measured at the center of the trajectory with a proton magnetometer and was found to be 53,975 nT, which was used as the true value for estimating compensation parameters. Before the field experiment, the magnetometer was calibrated with the method introduced in [34]. After calibration, measurement error was reduced from 43 nT to less than 1.2 nT. Moreover, the UUV sailed along a straight line to ensure the proper operation of the measurement system in the pre-experiment. The entire trajectory of the UUV is illustrated in Figure 3a and the attitude angles measured by the INS are shown in Figure 3b–d.

3.2. Estimation and Compensation

In accordance with the typical cruising velocity of UUVs for marine exploration [35], we set the UUV velocity at around 3 knots in the experiment. Initially, the velocity of UUV was set as 2.1 knots, which corresponded to 20% of its maximum. The actual velocity of UUV was monitored by DVL in real time, which fluctuated by around 2.1 knots as shown I Figure 4c. The measured data of magnetic field components and the calculated total magnetic field are presented in Figure 4a,b. As indicated in the figure, the maximum fluctuation of the total magnetic field calculated based on the true value is nearly 300 nT.

The measured data were subsequently used to calculate compensation parameters $C$ and $H_p{}^{\prime }$ according to Equation (11). For total magnetic field compensation, the exact value of $M_k^{}$ is not necessary. To simplify the calculation, we assume that $M_k^{}$ is a symmetric matrix, allowing the values of its elements to be calculated easily by matrix decomposition. The resulting solutions are as follows (

Table 2. Values of compensation parameters when UUV sails at 2.1 knots.

${\mathbf{M}}_{\mathbf{k}}^{}$	${\mathbf{H}}_{\mathbf{p}}{}^{\prime }$
$\left[\begin{array}{ccc}1.00626& 0.00006& 0.00203\\ 0.00006& 0.99632& 0.00057\\ 0.00203& 0.00057& 0.99457\end{array}\right]$	$\left[\begin{array}{c}347.13\\ -85.06\\ 82.39\end{array}\right]$

):

Finally, these parameters were used to compensate for the interference magnetic field. As demonstrated in Equation (10), the different attitudes of the UUV have no effect on the compensation of the total magnetic field.

Figure 5 compares the total magnetic field before and after compensation. To make the results more intuitive, the true value measured by the proton magnetometer was taken as a reference and presented as a green line. Two primary statistical indicators, maximum fluctuation and root mean square error (RMSE), were employed as evaluation indices of the compensation accuracy in

Table 3. Measuring accuracy of total magnetic field compensation at 2.1 knots.

	Fluctuation (nT)	RMSE (nT)
Uncompensation	315.05	231.66
Compensation	5.30	1.42

. After compensation, the fluctuation of the total magnetic field decreased from 315.05 nT to 5.30 nT (1.7% of the value before compensation), while the RMSE dropped from 231.30 nT to 1.61 nT (0.7% of the value before compensation).

In the same way, the compensation parameters when UUV sail at 3.1 knots (30%) and 4.1 knots (40%) can be obtained as follows (

Table 4. Values of compensation parameters when UUV sail at 3.1 and 4.1 knots.

Velocity	${\mathbf{M}}_{\mathbf{k}}^{}$	${\mathbf{H}}_{\mathbf{p}}{}^{\prime }$
3.1 knots	$\left[\begin{array}{ccc}1.00633& 0.00007& 0.00199\\ 0.00007& 0.99670& 0.00056\\ 0.00199& 0.00056& 0.99460\end{array}\right]$	$\left[\begin{array}{c}348.98\\ -91.80\\ 106.03\end{array}\right]$
4.1 knots	$\left[\begin{array}{ccc}1.00651& 0.00006& 0.00211\\ 0.00006& 0.99658& 0.00056\\ 0.00211& 0.00056& 0.99457\end{array}\right]$	$\left[\begin{array}{c}351.68\\ -97.71\\ 130.93\end{array}\right]$

):

The compensation results are presented in Figure 6. After compensation, the maximum fluctuation of the magnetic total field decreased from 298.64 nT to 6.53 nT (2.2%) at 3.1 knots and from 313.45 nT to 9.64 nT (3.1%) at 4.1 knots. The RMSE of the magnetic total field also decreased from 231.16 nT to 2.04 nT (0.9%) at 3.1 knots and from 235.43 nT to 2.84 nT (1.2%) at 4.1 knots (

Table 5. Measuring accuracy of total magnetic field compensation at 3.1 and 4.1 knots.

		Fluctuation (nT)	RMSE (nT)
3.1 knots	Uncompensation	298.64	231.16
	Compensation	6.53	2.04
4.1 knots	Uncompensation	313.45	235.43
	Compensation	9.64	2.84

). These results suggest that the compensation method has reliable performance at a certain velocity.

The estimation results for different velocities reveal that $H_p{}^{\prime }$ exhibits significant variation, while $M_k^{}$ remains nearly constant. Minor variations are believed to be caused by the non-uniformity of the magnetic field along the circular trajectory, with $M_k^{}$ primarily determined by inherent characteristics of the measurement system based on UUV, such as the magnetization coefficient of the soft magnetic material. Figure 7 provides the fitting results by the linear model based on the $H_p{}^{\prime }$ values at the velocities of 2.1, 3.1, and 4.1 knots.

The $G$ and $H_p$ in Equation (8) can be calculated as:

$$G={\left[\begin{array}{ccc}2.30& -6.40& 24.57\end{array}\right]}^T$$

$$H_p={[\begin{array}{ccc}341.99& 71.27& 28.78\end{array}]}^T$$

The reliability of the linearity assumption is supported by a goodness-of-fit level that approaches 0.99. Based on the linear relationship between $‖H_p{}^{\prime }‖$ and $V$, it can be concluded that changes in UUV velocity do interfere with the interference magnetic field.

3.3. Verification of Velocity-Related Compensation Method

To assess the effectiveness of the velocity-related compensation method, the UUV was operated to sail at 5.1 knots along the same circular trajectory in the reservoir.

In comparison, Figure 8 presents the velocity-unrelated compensation result. In this case, the parameters estimated from the measured data at 2.1 knots were directly employed to compensate for the interference magnetic field since the velocity-related term was not considered.

After compensation, both the fluctuation and RMSE remained at high levels (

Table 6. Measuring accuracy of velocity-unrelated compensation at 5.1 knots.

	Fluctuation (nT)	RMSE (nT)
Uncompensation	334.90	246.90
Compensation	226.52	141.15

). This indicates that this compensation method is not applicable for compensating interference when the velocity of the UUV varies.

Afterwards, the velocity-related model was employed for compensation. Given that the velocity of the UUV is known and that $G$ and $H_p$ were estimated in Section 3.2, $H_p{}^{\prime }$ at 5.1 knots could be calculated using Equation (8). Additionally, $M_k^{}$ was determined by averaging the estimates from the three sets of data mentioned above. Using $H_p{}^{\prime }$ and $M_k^{}$, the velocity-related compensation model was applied to achieve interference compensation at 5.1 knots. The resulting plot is presented in Figure 9.

Table 7. Measuring accuracy of velocity-related compensation at 5.1 knots.

	Fluctuation (nT)	RMSE (nT)
Uncompensation	334.90	246.90
Compensation	6.83	2.23

shows that after compensation, the fluctuation was reduced to 6.83 nT (2%), and the RMSE was reduced to 2.23 nT (0.9%).

In Figure 10, we present a comparison between the velocity-related compensation results and the velocity-unrelated compensation results. When the sailing velocity of UUV changes, the magnetic interference compensation ability of the initial method greatly diminishes, which highlights the necessity of accounting for velocity-related magnetic disturbances in actual UUV operations. Following the velocity-related compensation, the curve of the calibrated magnetic field closely approximates the reference curve with small fluctuation and RMSE, undoubtedly offering better compensation performance.

In order to further prove the reproducibility of the velocity-related compensation method proposed in this paper, the verification experiment when UUV sails at 3.5 knots is carried out in the same reservoir. The statistical indicators of the total magnetic field before and after compensation are presented in

Table 8. Measuring accuracy of velocity-related compensation at 3.5 knots.

	Fluctuation (nT)	RMSE (nT)
Uncompensation	310.9	234.3
Compensation	6.72	2.16

. It can be found that the compensation parameters estimated based on the velocity-related model are applicable to the measurement data at 3.5 knots. Additionally, Figure 11 shows the statistical indicators at different velocities, providing a validation of the consistency of the results and the effectiveness of the compensation method at varying sailing velocities.

The initial model primarily compensates for the permanent and induced interference magnetic fields, without considering the interference caused by carrier electromechanical equipment. It inevitably leads to inaccuracies in the compensation since the electromechanical interference is unavoidable and exerts a significant influence when the UUV measurement system detects abnormal magnetic field in concerned water areas. In practice, the velocity of UUVs is determined by the operating state of the motor and the battery. As UUV velocity changes, the disturbing magnetic field generated by the motor and battery changes. Hence, the introduction of the velocity-related term in the compensation model becomes necessary. The experiment results prove that the velocity-related compensation model can improve compensation accuracy.

4. Conclusions

In this paper, we present an improved method for compensating carrier interference magnetic fields. First, we establish an initial compensation model based on the Tolles–Lawson model. Next, we estimate the compensation parameters for the UUV at several velocities using the ridge estimation algorithm. We then develop the velocity-related term based on the relationship between the compensation parameters and the velocity and introduce it into the initial magnetic compensation model, achieving the establishment of the velocity-related model. Finally, we verify the compensation method through field experiments. The results show that the initial model based on the Tolles–Lawson model performs well only when the UUV sails at a constant velocity. By contrast, the velocity-related model has good applicability even when the velocity of the UUV varies, with the fluctuation reduced from 334.90 nT to 6.83 nT and the RMSE reduced from 246.90 nT to 2.23 nT after compensation. Additionally, the reproducibility of the compensation method has been proved. These experiment results demonstrate that the velocity-related compensation model can effectively reduce the influence of the variation of UUV velocity on the accuracy of interference magnetic field compensation. Thus, it presents a highly adaptable method for underwater magnetic detection.