Abstract
Constructing a surface representation from the sparse point cloud of a satellite is an important task for satellite on-orbit services such as satellite docking and maintenance. In related studies on surface reconstruction from point clouds, implicit neural representations have gained popularity in learning-based 3D object reconstruction. When aiming for a satellite with a more complicated geometry and larger intra-class variance, existing implicit approaches cannot perform well. To solve the above contradictions and make effective use of implicit neural representations, we built a NASA3D dataset containing point clouds, watertight meshes, occupancy values, and corresponding points by using the 3D models on NASA’s official website. On the basis of NASA3D, we propose a novel network called GONet for a more detailed reconstruction of satellite grids. By designing an explicit-related implicit neural representation of the Grid Occupancy Field (GOF) and introducing it into GONet, we compensate for the lack of explicit supervision in existing point cloud surface reconstruction approaches. The GOF, together with the occupancy field (OF), serves as the supervised information for neural network learning. Learning the GOF strengthens GONet’s attention to the critical points of the surface extraction algorithm Marching Cubes; thus, it helps improve the reconstructed surface’s accuracy. In addition, GONet uses the same encoder and decoder as ConvONet but designs a novel Adaptive Feature Aggregation (AFA) module to achieve an adaptive fusion of planar and volume features. The insertion of AFA allows for the obtained implicit features to incorporate more geometric and volumetric information. Both visualization and quantitative experimental results demonstrate that our GONet could handle 3D satellite reconstruction work and outperform existing state-of-the-art methods by a significant margin. With a watertight mesh, our GONet achieves 5.507 CD-L1, 0.8821 F-score, and 68.86% IoU, which is equal to gains of 1.377, 0.0466, and 3.59% over the previous methods using NASA3D, respectively.
1. Introduction
Surface reconstruction from point clouds is a fundamental problem in the fields of computer vision and graphics. With the development of space technology, human beings have increasingly urgent needs for the maintenance of in-orbit satellites and the inversion of geometric parameters. Reconstructing satellite target surfaces from a sparse point cloud and further providing finer geometric structure information is an important basis for satellite on-orbit service. However, the 3D data of the satellite have a large intra-class variance. The meshes of different shapes and the t-SNE [1] clustering visualization of latent codes of ShapeNet and the proposed NASA3D datasets obtained from the encoder of ConvONet are shown in Figure 1. The intra-class variance of satellites is larger than for normal objects, such as chairs, sofas, and cars, etc. However, the 3D mesh models of objects, including satellites, are hard to acquire because they cannot be acquired directly by 3D sensors. The 3D geometric information observed by sensors is usually in terms of point cloud data. Therefore, reconstructing 3D mesh from the point cloud is a popular topic of interest for researchers. Point clouds produced by 3D scanning are often sparse, and it remains challenging to reconstruct mesh from a sparse point cloud. Traditional reconstruction methods, e.g., the Poisson surface reconstruction method [2] and the improved screened Poisson surface reconstruction method [3], work well on the surface reconstruction of dense point clouds but cannot handle the mesh reconstruction task when the point cloud is sparse (e.g., 1024 points for a single model). Reconstruction methods based on deep learning alleviate this problem to some extent. These methods perform well in mesh reconstruction from the sparse point cloud through fitting complex mapping functions from the sparse point cloud to its surface. However, due to the lack of satellite datasets, all reconstruction methods [4,5,6,7,8,9,10,11,12] focus on common objects, such as tables, cars, sofas, etc. Our work hopes to break through the problem of satellite mesh reconstruction from sparse point clouds.
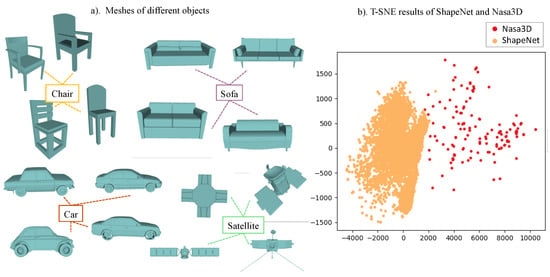
Figure 1.
Visualization of the datasets of normal objects and satellites. (a) Meshes of different objects. The intra-class distance between the geometries of satellites is larger than that of other objects. (b) T-SNE results of ShapeNet and NASA3D. The intra-class distance between the latent features of satellites is larger than that of other objects.
In order to tackle the satellite mesh reconstruction task, a powerful 3D representation is a critical component. Recently, learning-based methods, especially implicit neural representation methods, have become more and more popular in 3D object reconstruction. Compared with implicit representation methods such as point clouds, voxels, and polygonal meshes, implicit neural representation is continuous and smooth. Thus, it is more appropriate for neural networks to learn the implicit neural representation. Moreover, many studies show the effectiveness of implicit neural representation on the common object dataset. For instance, the well-known neural radiance field (NeRF) [13] and its following work [14,15] represent 3D scenes using an implicit neural representation and has demonstrated its effectiveness for view synthesis tasks; PiFu [16] uses implicit neural representation for capturing high-resolution 3D human models from a single image. Neural implicits have the benefit of representing complex geometry and topology, while not being limited to a predefined resolution.
While demonstrating promising results, most implicit approaches do not scale to satellite objects, which are more complicated than general objects, e.g., chairs, in geometry and topology. Most of the implicit methods learn the implicit representation by regressing signed distance field (SDF) or occupancy field (OF) values, which are sampled in space randomly. When there are enough sampling points, the randomly selected SDF/OF can represent the surface geometry of the object well. However, a large number of sampling points will lead to expensive computational costs for network training. Therefore, most implicit representation reconstruction methods [5,8,17,18] use less than 10,000 sampling points. Furthermore, to visualize the reconstructed surface explicitly, most implicit works conduct post-processing for isosurface extraction, where the Marching Cubes (MCs) algorithm is widely utilized. This means that the final reconstruction result is still explicit. Since the implicit neural representation methods cannot be directly derived from the explicit surface, most of the current implicit approaches cannot utilize explicit supervision on the reconstructed surface, which imposes useful constraints for training. To introduce explicit supervision, some works [19,20] adopt MCs to extract the surface from the implicit representation, which causes expensive computational costs instead.
To mitigate the above issues and tackle the satellite reconstruction task, we propose a Grid Occupancy Network (GONet), which introduces the Grid Occupancy Field (GOF), an explicit-driven implicit representation in the Convolutional Occupancy Network (ConvONet) [8]. ConvONet combines convolutional encoders and implicit decoders to infer the OF of objects and scenes and shows good performance in reconstructing geometry from noisy point clouds, whose features of input ConvONet projects onto multiple planes, and then uses 2D/3D U-Nets to aggregate local and global features on the planes. Thus, we use ConvOnet as a baseline to reconstruct satellite objects. However, there is no explicit supervision in ConvONet, either. Therefore, we introduce GOF in ConvONet, which is essentially a kind of special OF that samples at uniform 3D-grid vertices. The reason we design GOF at the uniform grid is that when surface extraction is performed with MCs, the surface position determination and interpolation are performed according to the occupancy probability values at points on the uniform 3D grid. The occupancy values at the uniform grid determine the isosurface extraction directly. Therefore, the introduction of GOF can achieve semi-explicit supervision on the reconstructed surface and improve the reconstruction quality.
Moreover, ConvONet aggregates the features on all planes by only summing them up, which is a simple but crude method to define the relationship between features of each plane and the points in 3D space. Thus, exploring how the features of planes constitute the global feature is indeed necessary for improving the accuracy of the reconstructed surface. To this end, we propose a learning-based plane feature aggregation module (PFA), which is composed of mesh-connected fully connected layers and a 3D convolution layer. Aggregating the features of planes in a learned manner enables the network to learn more robust implicit features for the decoder to infer implicit representation, thereby improving the quality of reconstructed surfaces.
To make the learning-based reconstruction method available, we collect the open-source 3D satellite models on NASA’s official website and make a dataset, named NASA3D, that contains watertight meshes, point clouds, and implicit representations based on them. To the best of our knowledge, we are the first to construct a 3D satellite dataset and utilize implicit neural representation to tackle the satellite mesh reconstruction task. We demonstrate our GONet on the NASA3D dataset, reconstructing surfaces of satellites from sparse point clouds. We outperform existing state-of-the-art methods by a significant margin. In summary, we make the following technical contributions:
- 1
- We build a dataset for tackling satellite mesh reconstruction from sparse point cloud tasks through learning-based methods. Moreover, we are the first to utilize implicit neural representation to reconstruct meshes from sparse point clouds.
- 2
- We propose a Grid Occupancy Network (GONet), introducing the Grid Occupancy Field (GOF), an explicit-driven implicit representation in ConvONet. Our GOF enables a semi-explicit supervision of 3D surfaces, and we demonstrate that the additional supervision on GOF improves the reconstruction quality of satellite meshes.
- 3
- We design a learning-based Adaptive Feature Aggregation (AFA) module to adaptively aggregate the features on multi-planes and volume, which enhances GONet on implicit feature learning. Furthermore, extensive experiments, including visual and quantitative experiments, demonstrate that our GONet can handle 3D satellite reconstruction work and outperform existing SOTAs.
2. Related Work
We review the related work on learning-based 3D reconstruction methods, which can be broadly classified according to their reconstructed output representations.
Point Clouds: As the original output of the LiDAR sensors, the point cloud plays an essential role in the 3D reconstruction field. Many researchers utilize point cloud as the output representation of 3D reconstruction. For sparse point cloud, many approaches to point cloud upsampling have been explored. Rao et al. [21] design a bidirectional reasoning strategy to learn the patterns in both local-to-global and global-to-local directions. Rozsa et al. [22] propose a new optical flow calculation method that applies optical principles (flow and expansion) to balance the spatial and temporal resolution of 3D LIDAR point cloud measurements. PF-Net [23] utilizes a feature-points-based multi-scale generating network to estimate the missing point cloud hierarchically. Dual-channel transformer and cross-attention are employed for point cloud completion [24], convening the geometric information from the local regions of incomplete point clouds for the generation of complete ones at different resolutions.
Numerous research studies have been conducted on point cloud completion for the partial point cloud. Zhang et al. [25] propose the Point Shift Network composed of a multi-resolution encoder and point cloud generator to generate gradually dense point clouds, alleviating the nonuniform density problem of the generated point cloud. Combining reinforcement learning and latent generative adversarial network (GAN), QINet [26] infers a complete surface from a partial point cloud. Cheng et al. [27] design two GAN-based modules that fit the map between global feature distributions of the partial point clouds and ground truth to tackle the point cloud completion task. However, point cloud-based methods are typically limited in terms of the number of points they can handle. Furthermore, the character of the point cloud determines that it lacks topological relations.
Voxels: Due to their unitized, regular data properties, voxels are widely used in early learning-based 3D reconstruction methods. Choy et al. [28] design a 3D recurrent neural network to map the images of objects to their 3D voxel shapes. Wu et al. [29] propose 3D-GAN to generate 3D voxel data from a probabilistic space by leveraging recent advances in 3D convolutional networks and GANs. Voxel representations are integrated by a supervised 3D convolutional neural network in Voxnet [30]. Wu et al. [31] utilize a Convolutional Deep Belief Network to represent a 3D shape as a probability distribution of binary variables on a 3D voxel grid. However, voxel-based methods are typically limited in terms of the enormous computation recourse requirement for voxel representation.
Meshes: Using the neural network to directly regress the vertices and faces of the mesh is a very intuitive idea to solve the problem of 3D reconstruction. AtlasNet [32] represents a mesh as a collection of parametric surface elements and naturally infers the mesh as the output representation. Mesh R-CNN [33] integrates object detection and 3D reconstruction into a framework. AtlasNet predicts coarse voxel representations and employs a graph convolution network to convert the voxels to meshes and refine them by operating over the vertices and edges of the meshes. DeepDT [34] reconstructs the surface from the Delaunay triangulation of the point cloud. Wang et al. [35] propose to represent a mesh in a graph-based convolutional neural network and deform a triangular mesh of ellipsoid into a certain correct geometry. An alternative differentiable formulation of Marching Cubes is proposed in DMC [20], and it is inserted as a final layer into a 3D convolutional neural network. However, to achieve the insertion of the alternative differentiable Marching Cube, the entire encoder–decoder network uses 3D convolutions such that large computational and memory resources are necessary.
Implicit Representations: Due to the continuity of the implicit representation and the success it achieves in the 3D reconstruction field, they are nowadays more often used as the output representation for learning-based 3D reconstruction. An implicit-based approach trains a neural network to fit a function that maps a 3D point to its occupancy value or distance to a surface. The explicit meshes can then be extracted from the inferred occupancy or distance field with the isosurface extraction cubes algorithm. OccNet [5] is the first approach that uses implicit representation as the output. It utilizes an input-determined encoder and an MLP-based decoder to predict the occupancy field. Moreover, the Multiresolution Isosurface Extraction (MISE) algorithm is proposed in OccNet. MISE has shown great strength [5,8,36] in extracting isosurfaces from implicit representations. Peng et al. [8] propose Convolutional Occupancy Networks (ConvONet), which implements structured reasoning in 3D space and applies it in the neural network so that ConvONet can reconstruct more details of objects. HRE-NDC [37] predicts residuals in a coarse-to-fine manner and uses tailored activation functions to increase the detail of the reconstructed meshes. SA-ConvONet [36] proposes sign-agnostic optimization on the basis of ConvONet and modifies the structure of ConvONet into 3D U-Net. To preserve and utilize the direct connection with the input points, POCO [7] uses point convolutions and computes latent features at each input point.
Although the implicit neural representation achieves notable success in reconstructing meshes from point clouds, there is still a lack of research on the reconstruction approach for satellite objects, the geometry of which is more complex than normal objects like chairs, tables, etc. Furthermore, all the methods above ignore the explicit-related information. However, the explicit mesh visualized by the isosurface extraction algorithm is the final shape viewed by a human or printed by a 3D printer. Introducing explicit-related information is of great importance for 3D reconstruction tasks. To this end, we aim to propose a novel approach to break through the problem of satellite mesh reconstruction from sparse point clouds.
Given a sparse point cloud, our goal is to reconstruct the underlying 3D geometry of a satellite in a learning manner. To this end, we first construct a dataset, as there are no relevant datasets available for the implicit representation-based reconstruction method with deep learning. Moreover, our method is based on a generalized implicit function [38], which defines a surface as a level set of a function f, e.g., . Thus, we normalize the satellite objects and utilize the same data processing pipeline as [39].
Due to the excellent performance of ConvONet [8] on the task of implicit 3D reconstruction of common objects, we use ConvONet as a baseline for our study of satellite reconstruction. However, there is no explicit supervision information in the training pipeline of ConvONet, which limits the improvement in the accuracy of the reconstructed shape. To tackle this problem, we propose a Grid Occupancy Network (GONet), introducing the Grid Occupancy Field (GOF), an explicitly driven implicit representation in ConvONet. Moreover, we design a learning-based Adaptive Feature Aggregation (AFA) module to adaptively aggregate the features on multi-planes and volume, which strengthens GONet on implicit feature learning. On benchmarks based on NASA3D, we demonstrate the superiority of GONet for reconstructing satellite shapes.
3. Methodology
3.1. Method Overview
The whole pipeline of the proposed GONet is illustrated in Figure 2, and we summarize it in Algorithm 1. It consists of an encoder, AFA, and decoder, where the structure of the encoder and decoder is the same as that of ConvONet. Due to the weak feature aggregation of ConvONet, the information loss caused by the extracted implicit features is significant. AFA is then designed and plugged into ConvONet to reduce the loss and obtain accurate global features as the implicit features used by the decoder for reconstructing 3D implicit representations. Through the gradual parameter optimization of AFA, the global implicit features obtained contain more information, thus making the 3D representation reconstructed by the decoder more accurate. But there is still a lack of explicit representation-related supervision in the network. To solve this problem, GONet proposes learning of the Grid Occupancy Field (GOF), an explicit-driven implicit representation. The introduction of GOF and AFA effectively improves the quality of reconstructed satellites.
| Algorithm 1: Surface Reconstruction using GONet |
| Input :Point cloud (P), randomly sampled points (R), and uniformly sampled points (U) Output:Reconstruction mesh
|
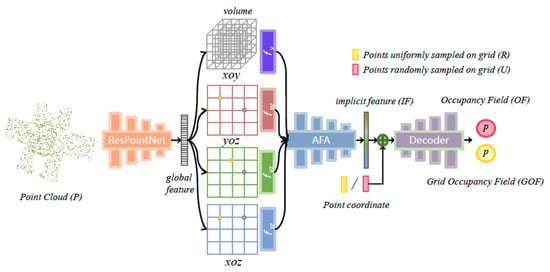
Figure 2.
The overview of the proposed GONet. GONet is composed of the encoder, which is a residual PointNet, the Adaptive Feature Aggregation Module (AFA), and the decoder.
The detailed network structure of the encoder and decoder in GONet is shown in Figure 3, the encoder is a residually connected PointNet [40] (ResFC), where the detailed structure of the ResFC block is illustrated in Figure 3c. The ResFC block is similar to the ResNet [41], which is commonly used in the field of image processing, except that the 2D convolution in the ResNet is replaced by a fully connected layer. Due to the disordered character of point cloud data, its processing is more suitable for a fully connected (FC) layer rather than 2D convolution, which convolves irrelevant positions together. The encoder processes the input point clouds with the skip-connected ResFC blocks and local pooling layers to obtain the global features. Given the global features, the planar and volume features are constructed by projecting the global features onto the , , and planes via meanly scattering the plane features from points or into a volume by average pooling. We construct both planar and volume features in GONet, which are aggregated into the implicit feature through AFA. Moreover, the detailed structure of the decoder is illustrated in Figure 3b. The goal of the decoder is to predict the occupancy value at the query points according to the implicit feature and the coordinates of the query points. To date, GONet has completed the estimation of the implicit occupancy field and the GOF of the input point cloud.
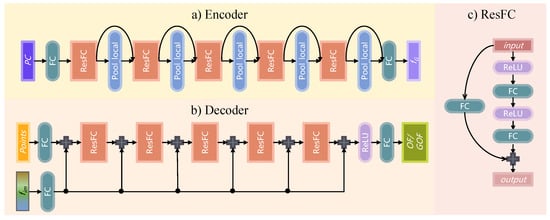
Figure 3.
The detailed network structure of (a) the encoder, (b) decoder, and (c) ResFC block. The encoder captures the global feature of the input point cloud by the skip-connected ResFC blocks and local pooling layers; the decoder uses the implicit feature and the grid point coordinates as input and predicts the occupied value or grid-occupied value by the cascaded ResFC blocks; the ResFC blocks, which are very similar in structure to the residual blocks in ResNet, are utilized in both encoder and decoder for a stronger feature extraction ability.
3.2. Grid Occupancy Field
To alleviate the effect of explicit supervised information, we propose GOF, an implicit field directly related to the isosurface extraction algorithm Marching Cubes. The isosurface extracted by Marching Cubes is the explicit representation of the satellite. Thus, how to obtain a better isosurface is of great importance for reconstructing accurate satellite surfaces. We focus on alleviating the above problem on making GONet predict the implicit field that is more conducive to isosurface extraction.
3.2.1. Marching Cubes
The Marching Cubes (MCs) algorithm extracts the isosurface, which is actually a zero-level set of the occupancy field, and it uses a set of polygons to explicitly represent the isosurface. In practical applications, the major choice of polygons is a triangle. Therefore, we analyze the MCs algorithm in the case of using triangles to represent the isosurface. The MCs algorithm determines the geometry by estimating the number and connectivity of triangles and the vertices locations of triangles in each cell of the volumetric grid. The cells are evenly divided from a volumetric grid based on a certain resolution, which is often set to 64, 32, etc., according to the limitation of computing power and the requirement of precision. As shown in Figure 4, there are kinds of combinations of vertex occupancy values, and they can be grouped into 15 equivalence categories of mesh topologies due to the rotational symmetry in each cell. Each vertex of the triangles is created in case of a sign change of occupancy values and placed on the appropriate location along the cube’s edge by linearly interpolating the occupancy values of the corners connected by that edge. Hence, the occupancy values on the vertices of the cells determine not only the mesh topologies, but also the locations of the triangles that compose the mesh.
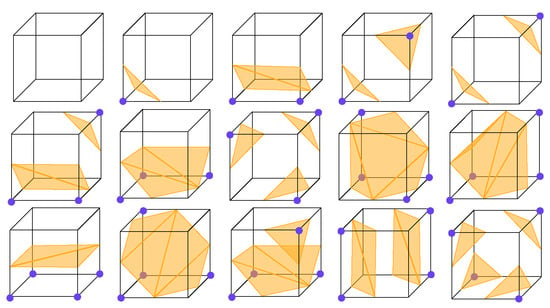
Figure 4.
The 15 possible unique mesh topologies composed of triangles in a cube during Marching Cubes.
3.2.2. GOF
Based on the analysis of MCs, given the implicit field, the MCs algorithm directly determines the quality of the satellite model explicitly. Furthermore, the MCs algorithm depends largely on the accuracy of the implicit value prediction at the vertices of the uniform grid. Therefore, we propose the definition of GOF, the occupancy field at those vertices mentioned above, as illustrated in Figure 5. Supposing the resolution of GOF is , then the vertices of all the cells in a grid can be represented as , where . Thus, GOF can be represented as a binary tensor where each element refers to a vertex. The occupancy values on the vertices are critical for more accurate isosurface extraction.
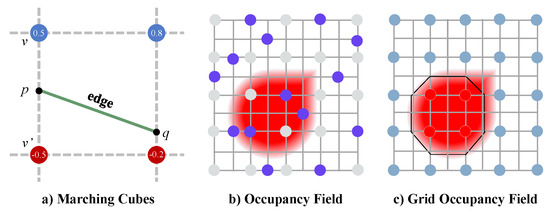
Figure 5.
Marching Cubes and Occupancy Field (OF) vs. Grid Occupancy Field (GOF)—visualized in 2D grid sampled from the same underlying shape. OF has a finer description of sharp shapes, while GOF covers the overall shape of a regular shape better than OF.
To make the occupancy value prediction of GONet at the vertices of the grid more accurate, we perform supervised learning on GOF in GONet. Specifically, GONet is designed to simultaneously learn the occupancy values GOF at and the occupancy values OF at a randomly sampled point , where K refers to the number of randomly sampled vertices in a 3D grid. This means that GONet learns two functions at the same time:
where o represents the occupancy function, and g refers to the grid occupancy function. Our key insight is that we strengthen the network’s attention to the critical points of isosurface extraction by introducing the supervised learning of GOF in the pipeline. In addition, the introduction of GOF also alleviates the problem in the shape distortion of GONet reconstruction caused by random sampling, as shown in Figure 5.
3.3. Adaptive Feature Aggregation Module
As analyzed in Section 3.1, ConvONet [8] aggregates the planar features on different planes by roughly summarizing them. This linear operation obviously cannot reasonably represent the relationship between the planar features. Moreover, the feature learning of volume and planar features in ConvONet is independent, which means that the features of different levels (2D plane and 3D space) cannot be combined. Hence, we explore a learning-based Adaptive Feature Aggregation module to obtain features in different planar and volume features.
As is illustrated in Figure 6, AFA is a module that aggregates the features of volume, plane, plane, and plane to obtain the intermediate implicit feature. Different from ConvONet, which directly adds the features of several planes, AFA obtains implicit features in a learned way through fully connected layers, 3D convolutional layer, and meshed connections of different levels of features. There are three existing levels of hidden features in the AFA module. The first level includes the volume feature and the planar features , , and , which are, respectively, fed into an fc layer and a ReLU function for the nonlinearization of feature aggregation, and the output features compose the second feature level. And, they are also concatenated together and sent to a 3D convolutional layer for fusing volume and planar features simultaneously. In addition, the 3D convolution layer can effectively extract the features of the three-dimensional space, realizing the learning-based aggregation of planar features.
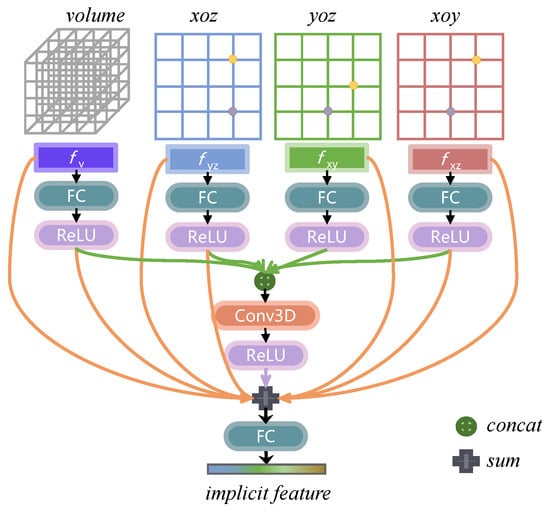
Figure 6.
Detailed network architecture of Adaptive Feature Aggregation module.
3.4. Training and Inference
At the training time, our goal is to minimize the distance between the ground-truth occupancy values of OF and GOF and their predicted occupancy values. Thus, there are both implicit and semi-explicit constraints during training to obtain a more accurate mesh. Our loss function consists of the following two parts:
where represents the parameters of GONet; and refer to the weight of the prediction losses of OF, , and GOF, , respectively.
In detail, to learn the parameters of the neural network , we sample the points in the 3D bounding volume of the object under the following considerations: for the i-th sample in a training batch, we randomly sample M points , the occupancy value of which is donated as . Similarly, we uniformly sample N points , and the . To learn both the occupancy field and the Grid Occupancy Field simultaneously, the objective function of GONet consists of the prediction errors of both. Hence, we then evaluate the mini-batch loss at those locations:
where refers to the i-th input point cloud of batch ; and denote the ground-truth of occupancy value at points and , respectively. Moreover, we use cross-entropy classification loss as to evaluate the distance of predicted occupancy values and their ground truth o:
Given the input point cloud and query point set, GONet achieves the extraction of explicit-related through supervised learning of OF and GOF.
During inference, we perform isosurface extraction on the occupancy predictions of the query point set according to GONet to obtain the explicit surface of the satellite. To efficiently extract the isosurface, we apply Multiresolution Isosurface Extraction (MISE) [5] to extract meshes with the given occupancy values, . MISE incrementally builds an octree [42,43], thus extracting high-resolution meshes without extremely expensive computing resource.
4. Experiments
4.1. NASA3D Dataset
To conduct satellite 3D reconstruction based on deep implicit methods, we construct a dataset of satellite 3D data containing watertight meshes, point clouds, and implicit occupancy values of satellites. The original open-source satellite meshes are obtained from NASA’s official website. We utilize the truncated SDF (TSDF) [39] to obtain watertight and simplified meshes from arbitrary triangular meshes of satellites. The watertight meshes are then scaled to the range of [0, 1]. The point clouds are obtained by uniformly sampling the surface of the watertight meshes of the satellite, and there are 100,000 points for each point cloud. Researchers can sample any certain number of points according to their needs as their point cloud data, and we sample 1024 points as the input point cloud in this paper. We download 70 complete satellite models from NASA’s official website and select editable models from them to use Blender, a 3D modeling software, to perform data augmentation. In detail, the augmentation strategies include changing the size of the solar wing and star body, and combining different parts, etc. We visualize the original model, simplification and augmentation data of the AcrimSat satellite in Figure 7. Through the above data augmentation, 78 augmented models are obtained, together with 70 original models, which constitute the complete NASA dataset. Then, NASA3D is randomly split into training and testing datasets, and there are 120 and 28 satellite objects in the training and testing datasets, respectively.
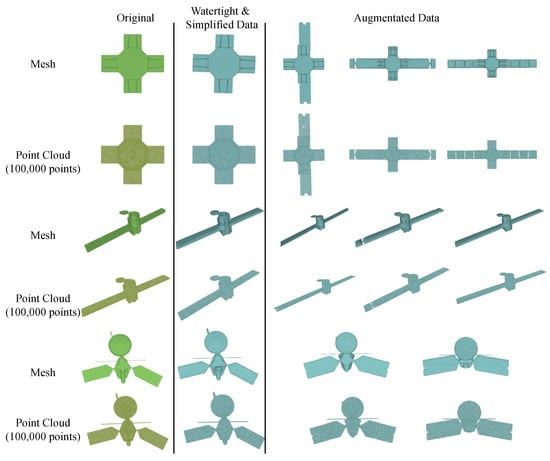
Figure 7.
Examples of mesh simplification and data augmentation.
4.2. Metrics
To evaluate the reconstruction performance, we use the following common metrics: volumetric IoU, Chamfer L1-distance, and F-Score [44] with the threshold value of , following ConvOccNet [8].
The definition of volumetric IoU is the quotient of the volume of the union of two meshes and the volume of their intersection. Following ConvOccNet [8], we select 100,000 points randomly in the unit boundary volume and determine whether these points are located inside or outside the ground truth or reconstructed mesh. Volumetric IoU reflects both the accuracy and completeness of the reconstructed mesh. For this reason, it is widely used to evaluate the quality of 3D reconstructions.
The Chamfer L1-distance between 2 point sets and is defined as:
The average L1-distance of each point and its nearest neighbour point is calculated and vice versa. We use a KD-tree to find the nearest neighbour in the point set. Chamfer L1-distance is determined by both the accuracy and coverage of the reconstructed point cloud.
4.3. Implementation Details
Our GONet is implemented in PyTorch framework and the Adam optimizer is used for training GONet. The learning rate is set as , while other coefficients, such as the exponential decay rates and for the moment estimates in Adam are set as and , respectively. We train our GONet and all the compared models on 120 satellite objects and test on the remaining 28 objects. We randomly sample 1024 points on each satellite mesh as the input point cloud. We implement PSGN [6] https://github.com/fanhqme/PointSetGeneration (accessed on 1 June 2023), DMC [20] (https://avg.is.mpg.de/research_projects/deep-marching-cubes) (accessed on 1 June 2023), OccNet [5] (https://github.com/LMescheder/Occupancy-Networks) (accessed on 1 June 2023), POCO [7] (https://github.com/valeoai/POCO) (accessed on 1 June 2023), ConvONet [8] (https://github.com/autonomousvision/convolutional_occupancy_networks) (accessed on 1 June 2023), and SAConvONet [36] (https://github.com/tangjiapeng/SA-ConvONet) (accessed on 1 June 2023) by adopting their official open source. We evaluate all the models using two NVIDIA TITAN 24 GB GPUs and a Intel i9-10900X CPU. As for the number of sampling points of GOF, we randomly sample points and uniformly sample points for OF and GOF, respectively. w, the weight for the prediction loss is, respectively, set to 0.4.
4.4. Ablation Studies
We conduct an ablation study quantifying the importance of the proposed GONet with the AFA module and GOF. We use ConvONet as the baseline and first add the proposed AFA module on it to verify the effectiveness of AFA. In order to verify the effectiveness of AFA for the adaptive aggregation of planar features and volume features, the ablation experiments are designed for Adaptive Feature Aggregation of planar features , volume features , and a combination of them (as shown in Figure 8). The experimental results reported in Table 1 show that when adding our AFA into the original ConvONet, an obvious improvement is observed in the CD-L1, F-Score, and volumetric IoU metrics compared with ConvONet; and AFA simultaneously aggregating and outperforms aggregating them alone. Furthermore, this verifies our hypothesis that the relationship between planar and volume features is not simply linear, and the adaptive aggregation performed by AFA benefits 3D reconstruction greatly. Then, on the basis of the above experiment, we introduce the proposed GOF in a supervised learning manner so that the network has explicit-related supervision, verifying whether GOF is effective for the satellite surface reconstruction task. As illustrated in Table 1, all the metrics show that the reconstruction performance is further improved with the introduction of GOF. The performance on all the evaluation metrics illustrates that the proposed AFA and GOF are effective for reconstructing satellite surfaces from the sparse point clouds. The ablation study demonstrates the effectiveness and superiority of both the AFA and GOF.
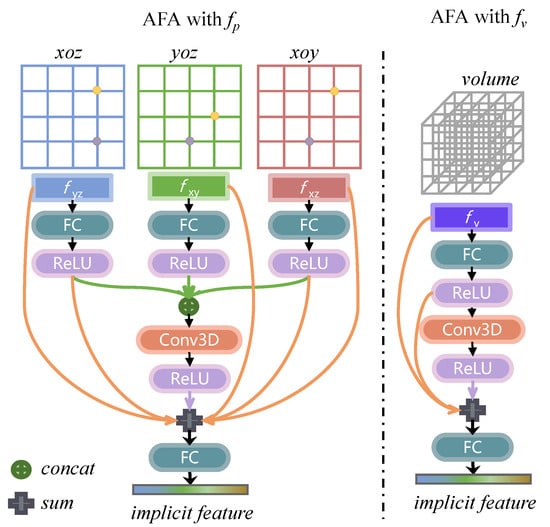
Figure 8.
Architectures of AFA when adaptively fusing the planar features and processing the volume feature . The parameter setting of the corresponding layer remains the same as when all the planar and volume features are fused.

Table 1.
Ablation study comparing satellite reconstruction performance on NASA dataset. and refer to the planar features and volume features, respectively. Results highlighted in red and blue represent the best and the second-best results, respectively. CD-L1 is multiplied by 1000.
Moreover, we conduct an ablation study on parameter w, the weight of the prediction loss to find the best weight value w. Table 2 report the reconstruction results of GONet with different w values. When setting w as 0.4, GONet achieves the best CD-L1 and F-score, and it also performs competitively in IoU. Since the best performance in CD-L1 proves the accuracy of meshes reconstructed by GONet, the slight decline in IoU is due to the reduction in w affecting the completeness of reconstructed meshes. Nevertheless, setting w to 0.4 yields the overall optimal reconstruction results for the satellite.

Table 2.
Ablation study on parameter w, the weight of . Results highlighted in red and blue represent the best and the second-best results, respectively. CD-L1 is multiplied by 1000.
4.5. Reconstruction Results
In order to verify the superiority of the proposed GONet, we quantitatively compare GONet with six state-of-the-art methods in point cloud surface reconstruction task, i.e., PSGN [6], DMC [20], OccNet [5], POCO [7], ConvONet [8], and SAConvONet [36]. For point cloud inputs, we adapt PSGN by changing the encoder to pointnet. Table 3 reports the metrics of the reconstruction results. Since the reconstruction result of PSGN is in the form of point cloud data, the F-score and volumetric IoU indicators cannot be measured. As illustrated in Table 3, the proposed GONet achieves the best performance on metrics CD-L1, F-Score, and volumetric IoU, i.e., 1.377, 4.66%, and 3.59% better than that of SAConvONet, respectively. The run time of reconstructing a satellite is also provided. For satellite 3D reconstruction from the point cloud, the superiority of GONet proves that the proposed GOF and AFA are more effective than the sign-agnostic optimization of convolutional occupancy networks [36] and point convolution of POCO [7]. The optimal performance on these metrics illustrates that the geometries of the meshes reconstructed by GONet are closer to the ground truth, and the accuracy and completeness are higher than that of the SOTAs.

Table 3.
Satellite reconstruction results from point clouds. CD-L1 is multiplied by 1000.
We further visualize the reconstructed satellite meshes to obtain qualitative results, and the results obtained are shown in Figure 9. Input point clouds for several satellites with widely different geometries, reconstruction shapes of different methods, and ground truth meshes are reported in Figure 9. The red boxes are used to highlight the shape details at the same position of the same satellite, and the yellow boxes highlight the satellites with obvious contrast in the overall shape reconstruction of the satellite by different methods. Notably, GONet reconstructs the overall shape of the no.4 satellite much better than the SOTAs, although the geometry of satellite numbered 4 is more complex than that of others and quite different from others. The best performance of GONet in satellites 4, 5, and 7 verifies that GONet mitigates the problem of excessive intra-satellite class distances. All the details and overall shape illustrate that the proposed GONet shows superior performance to other state-of-the-art methods in the reconstruction of satellite geometric details. The visualization results of satellite reconstruction, especially the satellite highlighted in the yellow box, confirm that GONet introducing explicit correlation supervision by GOF can effectively help shape reconstruction and also illustrate the importance of AFA for the effective aggregation of planar features and volume features.

Figure 9.
The satellite reconstruction results of the proposed GONet and the SOTAs. All the visualisation results of reconstructed meshes are obtained using VisPy, a high-performance interactive 2D/3D data visualization library. In order to exclude the influence of camera position, lighting conditions, etc., on the visualization effect, we adopt the same smooth shading and set the same camera parameters for all the reconstructed meshes and the ground truth meshes.
In this paper, we do not train our model with non-satellite datasets such as ShapeNet. The original 3D objects in ShapeNet might contain topological errors, such as non-manifold edges or vertices, which can hinder the conversion to a watertight mesh. Furthermore, the models might have multiple disconnected components or separate surfaces that are not part of a single watertight object. If it is forcibly converted to a watertight grid, the shape of the models will change greatly. However, as mentioned in Figure 1, the intra-class distance between the latent features of satellites is larger than that of other objects, such as chairs, cars, and sofas in ShapeNet. Both the quantitative and qualitative results on complicated satellites already show the effectiveness of our GONet.
5. Conclusions
In this paper, we propose a novel satellite mesh reconstruction network, GONet, to tackle the mesh reconstruction of satellites from point clouds in a deep learning manner. We utilize ConvONet, a powerful surface reconstruction network, as the baseline. Aiming at the defect that ConvONet’s rough linear addition operation of structured reasoning features does not match the nonlinear relationship between features in the process of obtaining implicit features, we design an Adaptive Feature Aggregation module for learning the fusion mapping of structured reasoning features, which are the different planar and volume features. Therefore, the implicit features obtained by AFA contain more geometric information, and the decoder can use them to predict more accurate occupancy values. In addition, in order to overcome the limitations that the existing methods lack information on explicit meshes, GONet introduces GOF into the supervised learning pipeline. This means that GOF, together with the OF, serves as the supervised information for GONet to learn. The proposed GOF is naturally related to the MCs isosurface extraction algorithm. Thus, it strengthens GONet’s ability to learn implicit representation on the points which are critical for the explicitization algorithm. Extensive visualization and quantitative experiments demonstrate that the proposed GONet significantly improves the accuracy and quality of reconstructed meshes. The satellite reconstruction performance of GONet outperforms the existing state-of-the-art approaches by a significant margin.
Author Contributions
X.Y., methodology, writing—original draft; M.C., software, writing—original draft; C.L., data curation, funding acquisition, visualization; H.Z., project administration, supervision, writing—review and editing; D.Y., investigation, formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 61976166; in part by the Shaanxi Outstanding Youth Science Fund Project under Grant 2023-JC-JQ-53; in part by the Fundamental Research Funds for the Central Universities under Grant QTZX23057; and in part by the Open Research Projects of Laboratory of Pinghu.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. In Proceedings of the 4th Eurographics Symposium on Geometry Processing, Cagliari, Italy, 26–28 June 2006; Volume 7. [Google Scholar]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Erler, P.; Guerrero, P.; Ohrhallinger, S.; Mitra, N.J.; Wimmer, M. Points2surf learning implicit surfaces from point clouds. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 108–124. [Google Scholar]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy networks: Learning 3d reconstruction in function space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4460–4470. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L.J. A point set generation network for 3d object reconstruction from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Boulch, A.; Marlet, R. POCO: Point Convolution for Surface Reconstruction. arXiv 2022, arXiv:2201.01831. [Google Scholar]
- Peng, S.; Niemeyer, M.; Mescheder, L.; Pollefeys, M.; Geiger, A. Convolutional occupancy networks. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 523–540. [Google Scholar]
- Tang, Y.; Qian, Y.; Zhang, Q.; Zeng, Y.; Hou, J.; Zhe, X. WarpingGAN: Warping Multiple Uniform Priors for Adversarial 3D Point Cloud Generation. In Proceedings of the of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6397–6405. [Google Scholar]
- Liu, Z.; Zhang, C.; Cai, H.; Qv, W.; Zhang, S. A Model Simplification Algorithm for 3D Reconstruction. Remote Sens. 2022, 14, 4216. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, C.; Yan, Y.; Su, N. A 3D Reconstruction Framework of Buildings Using Single Off-Nadir Satellite Image. Remote Sens. 2021, 13, 4434. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Chen, R.; Xia, W.; Yan, C. Building Floorplan Reconstruction Based on Integer Linear Programming. Remote Sens. 2022, 14, 4675. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 405–421. [Google Scholar]
- Yariv, L.; Gu, J.; Kasten, Y.; Lipman, Y. Volume rendering of neural implicit surfaces. Adv. Neural Inf. Process. Syst. 2021, 34, 4805–4815. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. 2022, 41, 102. [Google Scholar] [CrossRef]
- Saito, S.; Huang, Z.; Natsume, R.; Morishima, S.; Kanazawa, A.; Li, H. Pifu: Pixel-aligned implicit function for high-resolution clothed human digitization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2304–2314. [Google Scholar]
- Chen, Z.; Zhang, H. Learning implicit fields for generative shape modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5939–5948. [Google Scholar]
- Chen, Z.; Tagliasacchi, A.; Zhang, H. Bsp-net: Generating compact meshes via binary space partitioning. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2020; pp. 45–54. [Google Scholar]
- Remelli, E.; Lukoianov, A.; Richter, S.; Guillard, B.; Bagautdinov, T.; Baque, P.; Fua, P. Meshsdf: Differentiable iso-surface extraction. Adv. Neural Inf. Process. Syst. 2020, 33, 22468–22478. [Google Scholar]
- Liao, Y.; Donne, S.; Geiger, A. Deep marching cubes: Learning explicit surface representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2916–2925. [Google Scholar]
- Rao, Y.; Lu, J.; Zhou, J. Global-local bidirectional reasoning for unsupervised representation learning of 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 5376–5385. [Google Scholar]
- Rozsa, Z.; Sziranyi, T. Optical Flow and Expansion Based Deep Temporal Up-Sampling of LIDAR Point Clouds. Remote Sens. 2023, 15, 2487. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. Pf-net: Point fractal network for 3d point cloud completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7662–7670. [Google Scholar]
- Fei, B.; Yang, W.; Ma, L.; Chen, W.M. DcTr: Noise-robust point cloud completion by dual-channel transformer with cross-attention. Pattern Recognit. 2023, 133, 109051. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.; Zou, Y.; Liu, P.X.; Liu, J. PS-Net: Point Shift Network for 3-D Point Cloud Completion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5704313. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, W.; Li, G.; Li, T.H. QINet: Decision Surface Learning and Adversarial Enhancement for Quasi-Immune Completion of Diverse Corrupted Point Clouds. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5705314. [Google Scholar] [CrossRef]
- Cheng, M.; Li, G.; Chen, Y.; Chen, J.; Wang, C.; Li, J. Dense point cloud completion based on generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5701310. [Google Scholar] [CrossRef]
- Choy, C.B.; Xu, D.; Gwak, J.; Chen, K.; Savarese, S. 3d-r2n2: A unified approach for single and multi-view 3d object reconstruction. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 628–644. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. A papier-mâché approach to learning 3d surface generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 216–224. [Google Scholar]
- Gkioxari, G.; Malik, J.; Johnson, J. Mesh r-cnn. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 6 June 2019; pp. 9785–9795. [Google Scholar]
- Luo, Y.; Mi, Z.; Tao, W. Deepdt: Learning geometry from delaunay triangulation for surface reconstruction. In Proceedings of the AAAI Conference on Artificial Intelligence, online, 2–9 February 2021; Volume 35, pp. 2277–2285. [Google Scholar]
- Wang, N.; Zhang, Y.; Li, Z.; Fu, Y.; Liu, W.; Jiang, Y.G. Pixel2mesh: Generating 3d mesh models from single rgb images. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 52–67. [Google Scholar]
- Tang, J.; Lei, J.; Xu, D.; Ma, F.; Jia, K.; Zhang, L. Sa-convonet: Sign-agnostic optimization of convolutional occupancy networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 6504–6513. [Google Scholar]
- Liu, Q.; Xiao, J.; Liu, L.; Wang, Y.; Wang, Y. High-Resolution and Efficient Neural Dual Contouring for Surface Reconstruction from Point Clouds. Remote Sens. 2023, 15, 2267. [Google Scholar] [CrossRef]
- Sclaroff, S.; Pentland, A. Generalized implicit functions for computer graphics. ACM Siggraph Comput. Graph. 1991, 25, 247–250. [Google Scholar] [CrossRef]
- Stutz, D.; Geiger, A. Learning 3d shape completion under weak supervision. Int. J. Comput. Vis. 2020, 128, 1162–1181. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Meagher, D. Geometric modeling using octree encoding. Comput. Graph. Image Process. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Jackins, C.L.; Tanimoto, S.L. Oct-trees and their use in representing three-dimensional objects. Comput. Graph. Image Process. 1980, 14, 249–270. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Richter, S.R.; Ranftl, R.; Li, Z.; Koltun, V.; Brox, T. What do single-view 3d reconstruction networks learn? In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3405–3414. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).