Deep Learning-Based Geomagnetic Navigation Method Integrated with Dead Reckoning

Abstract

Accurate location information has significant commercial and economic value as they are widely used in intelligent manufacturing, material localization and smart homes. Magnetic sequence-based approaches show great promise mainly due to their pervasiveness and stability. However, existing geomagnetic indoor localization methods are facing the problems of location ambiguity and feature extraction deficiency, which will lead to large localization errors. To address these issues, we propose a coarse-to-fine geomagnetic indoor localization method based on deep learning. First, a multidimensional geomagnetic feature extraction method is presented which can extract magnetic features from spatial and temporal aspects. Then, a hierarchical deep neural network model is devised to extract more accurate geomagnetic information and corresponding location clues for more accurate localization. Finally, localization is achieved through a particle filter combined with IMU localization. To evaluate the performance of the proposed methods, we carried out several experiments at three trial paths with two heterogeneous devices, Vivo X30 and Huawei Mate30. Experimental results demonstrate that the proposed algorithm can achieve more accurate localization performance than the state-of-the-art methods. Meanwhile, the proposed algorithm has low cost and good pervasiveness for different devices.

1. Introduction

Location-based services (LBSs) have gradually penetrated all aspects of people’s lives and have become an indispensable application technology. Examples of their application include pedestrian navigation or object searching in airports, shopping malls, hospitals, underground parking lots, tourist route planning services, unmanned medical care, intelligent manufacturing, and intelligent meal delivery [1]. Therefore, LBSs have substantial commercial and economic value.

Reliable LBS cannot be achieved without accurate location information. Currently, the Global Navigation Satellite System (GNSS) in outdoor environments can satisfy all weather navigation requirements. Since satellite signals cannot penetrate buildings, research on indoor navigation methods has become crucial for ensuring seamless indoor and outdoor localization. However, though many indoor localization technologies seem rather similar, they are actually completely different. Indoor localization is greatly affected by the surrounding environment, and more obstacles and intricate environments, including building structures, materials, and various furniture in indoor environments, lead to complex multipath and signal attenuation effects and then cause a decrease in accuracy localization. Meanwhile, the accuracy requirement for indoor localization is much higher than that of outdoor localization.

Researchers have explored various indoor localization techniques, such as wireless-fidelity (Wi-Fi) [2,3,4,5], Bluetooth (BT) [6,7], radio frequency identification (RFID) [8,9], ultra-wideband (UWB) [10,11,12,13], ultrasound [14], and visible light [15,16] technologies. These technologies need some infrastructure facilities, and are susceptible to environmental impacts, such as multipath propagation, signal absorption and building blocking. In contrast to the abovementioned techniques, geomagnetic localization technology [17,18] and pedestrian dead reckoning (PDR) [19,20] localization technology do not need extra hardware equipment and are less susceptible to the influence of the surrounding environment. Localization methods without infrastructure facilities have been favored by a large number of researchers and consumers and have become an interesting research topic.

Ubiquitous geomagnetic signals are generated by the earth’s geomagnetic field. Ferrogeomagnetic materials such as steer bars, irons, and iron-containing alloys in indoor environments result in geomagnetic abnormalities [21]. Geomagnetic abnormalities provide obvious clues and are beneficial for indoor localization [22]. Moreover, geomagnetic sequences can be collected using smartphones and they have high stability when the indoor environment does not change. Among the geomagnetic-based approaches, the dynamic time warping (DTW) algorithm [23] is a typical method used for geomagnetic localization. Gong et al. [24] used the DTW algorithm to warp the processed geomagnetic sequence and the known base, combining it with PDR to achieve geomagnetic matching localization. Subbu et al. [25,26] used the DTW algorithm to realize localization by matching the similarity of different geomagnetic sequences to solve the influence of different walking speeds on localization. The results showed that the localization accuracy is 2–6 m. Another widespread localization approach based on geomagnetic sequences is the particle filter [27], which is a non-parametric implementation of Bayesian filtering [28,29]. Canciani et al. [30] proposed an airborne navigation system using magnetic field. A particle filter is utilized to correct the errors in an inertial navigation system. Akai et al. [31] proposed using the Gaussian model to describe the fingerprint database of the geomagnetic field, and the particle weight, which is determined by the residual between the established model parameters and the fingerprint database, to estimate the optimal location. Xie et al. [32] proposed using MaLoc to achieve localization, which is based on the proposed augmented particle filter. Experimental results showed that the MaLoc algorithm can achieve 1~2.8 m localization accuracy in a large building with a 72 m × 64 m floor plan.

Pedestrian dead reckoning (PDR) [19,20] is a representative indoor localization method. It does not require additional infrastructure and can achieve relative localization in a short time. Kang et al. [33] solved the hardware problem of using inertial measurement techniques for localization by replacing inertial sensors, which are measurement devices used in traditional PDR methods with smartphones. Poulose et al. [34] performed a comparison analysis of various sensor fusion techniques for heading estimation to identify the optimal heading direction for PDR. Yao et al. [35] proposed a robust step length and stride length detection method for smartphones to enhance localization accuracy by modifying the step length estimation model. A modified zero-velocity detection algorithm is designed for step and heading estimations in ref. [36], which can obtain a more stable localization result.

However, existing geomagnetic indoor localization methods suffer from many problems. In the DTW algorithm, location determination is achieved when the maximum similarity of the geomagnetic magnitude is matched between online geomagnetic data and the fingerprint database in the overall region. However, the geomagnetic magnitudes do not fluctuate greatly without external metal changes. Large positioning errors will occur especially in symmetric and large area environments. The DTW algorithm has significant computational complexity. On the other hand, geomagnetic magnitudes are related to geological characteristics and the external human environment, and are nonlinear and complex problems. The particle filter algorithm can be used to solve various complex problems, such as moving object tracking. However, the particle filter is also severely impacted by motion estimation errors and suffers from the particle degradation problem. Increasing particle numbers can solve these problems, but a significant computational resource is required. Thus, the practical application of particle filters with smartphones is limited. In addition, different locations in symmetric environments may have identical geomagnetic readings, which cause localization ambiguity. Therefore, it is very challenging to construct a localization system using only geomagnetic sequences [37]. PDR can achieve relative localization, which relies heavily on pre-set initial location. When long distance localization is involved, the cumulative errors and drift errors will gradually increase over time, resulting in poor localization accuracy in practical scenes. Additionally, different pedestrians have different heights, stride lengths, and walking habits, which may lead to errors in step detection and heading direction. Therefore, PDR is used more as an auxiliary optimization algorithm than other as a localization algorithm.

To address the above problems, we proposed a coarse-to-fine indoor localization algorithm based on geomagnetic and inertial data, which mitigates the effects of geomagnetic ambiguity and PDR cumulative errors. We exploited the application to collect geomagnetic sequences and inertial measurement unit (IMU) data using smartphones. A novel deep learning neural network is proposed to achieve indoor localization. The key contributions of this research are summarized as follows:

• Multidimensional geomagnetic feature extraction: To facilitate distinctive geomagnetic feature extraction, we propose a multidimensional algorithm developed from spatial and temporal information, which improves the uniqueness of the geomagnetic features.
• A novel neural network framework: To enhance the extraction of geomagnetic features and solve the problem of location ambiguity, we propose a novel neural network to realize localization with geomagnetic sequences. The hierarchical structure of this model can extract more unique features from multidimensional geomagnetic sequences and better study the correlation between geomagnetic sequences and locations. The experiments demonstrate that this network can improve localization performance.
• A coarse-to-fine localization system: To enhance localization performance, a coarse-to-fine localization system based on geomagnetic signals and IMUs is proposed. The coarse localization is realized with the geomagnetic sequence and inertial data, and the fine localization is realized through the particle filter. We conducted several experiments with heterogeneous devices at three trial paths. The experimental results indicate that the coarse-to-fine localization system can achieve superior accuracy compared to the state-of-the-art algorithms. Through this system, the localization performance can be significantly improved and it can also be utilized in various scenarios.

The rest of the paper is structured as follows: Section 2 reviews the related works. In Section 3, the methodology is introduced. Experimental results are demonstrated in Section 4. In Section 5, discussion of the experimental results is presented. Finally, conclusion of this paper is stated in Section 6.

2. Related Works

In recent years, deep learning methods have been used successfully in many academic studies. Wang et al. [38] proposed DeepML, an indoor localization system based on deep long short-term memory (LSTM), which uses geomagnetic and light sensors to achieve localization. Ashraf Imran et al. [39] used a deep neural network-based ensemble classifier to realize localization by extracting features of geomagnetic sequences. Liu et al. [40,41] proposed ST-Loc, which uses a hierarchical recurrent network to extract geomagnetic features from spatial and temporal representations for localization. Zhang et al. [42] built an LSTM network to carry out real-time indoor localization and designed a method for preprocessing geomagnetic data based on double sliding window expansion, which had satisfactory localization performance. Jin et al. [43] proposed a deep learning-based method that fuses the temporal and spatial features of geomagnetic fingerprints to obtain stable and reliable localization results. Lee et al. [44] proposed a geomagnetic indoor localization method named AMID, which used a deep neural network as a classifier to recognize geomagnetic sequence patterns for localization. Bhattarai et al. [45] utilized deep recurrent neural networks (DRNNs) to learn the spatial/temporal geomagnetic patterns and capture long-range dependencies in variable geomagnetic input lengths. Li et al. [46] aimed to achieve localization by implementing a deep residual network (ResNet) to learn the key features from a massive fingerprint image database. Ding et al. [47] designed a sliding window mechanism to expand the dimension of geomagnetic data and utilized a one-dimensional convolutional neural network and LSTM network to realize localization.

PDR is more commonly employed in combination with other localization algorithms. Zhang et al. [48] proposed a novel fusing method integrating PDR characteristics and Wi-Fi characteristics and then realized data fusion and localization through LSTM networks. Ciabattoni et al. [49] proposed a fused localization application that combines real-time model-based PDR techniques with received signal strength indicator analysis of Bluetooth Low Energy (BLE) beacons. Sun et al. [50] presented fused indoor localization, which integrated pedestrian dead reckoning and geomagnetic localization using the genetic-particle filter algorithm. Tong et al. [51] focused on integrating a PDR and a UWB-based localization algorithm, which can achieve high accuracy in harsh environments. Yan et al. [52] proposed a cost-effective and high-efficiency localization algorithm that combines inertial sensors and acoustic signals, which has higher localization accuracy than the state-of-the-art methods. In ref. [53], a novel fusion indoor localization system, CHAN-IPDR-ILS, based on acoustic signals and PDR was proposed. In this system, an improved step estimation method and a heading direction correction method were introduced to solve the problem of accumulated errors in the PDR algorithm. Qian et al. [54] proposed a new hybrid method combining PDR and Wi-Fi information, and a modified particle filter algorithm was introduced to improve the precision of the fingerprint matching phase. Tao et al. [55] introduced a smartphone PDR indoor localization method based on ambient light assistance, which implements PDR with self-correction capability using a light detection algorithm to detect the location of the light source. Sun Meng et al. [56] constructed a smartphone fusion system with geomagnetic localization and PDR based on the extended Kalman filter, which can achieve localization performance with a mean localization error and a root mean square error of 1.25 m and 1.53 m, respectively. Yu et al. [57] presented a new method for Wi-Fi/PDR localization fusion based on neural networks, which applied LSTM networks to train the historical motion states of pedestrians to reduce the cumulative error of PDR.

Inspired by the significant success of deep learning in geomagnetic indoor localization, we propose a coarse-to-fine indoor localization method using geomagnetic sequences. Our proposed method has tremendous advantages in the following aspects. First, we propose a multi-feature geomagnetic extraction method, which can extract more features from temporal and spatial information and solve the errors caused by different devices. Then, our novel deep learning neural network can achieve more accurate localization in the forward and backward directions. Finally, fine localization can be achieved via a particle filter with fusion PDR localization. In addition, the geomagnetic and IMU data can be acquired through a client application installed on the smartphone, which does not require excessive costs.

3. Methodology

The proposed coarse-to-fine localization model is elaborated in Section 3.1. In Section 3.2, we illustrate the multi-feature geomagnetic extraction method. Then, the hierarchical deep learning neural network is described in Section 3.3. Step length estimation and heading angle estimation are presented in Section 3.4 and Section 3.5, respectively.

3.1. Coarse-to-Fine Localization Model

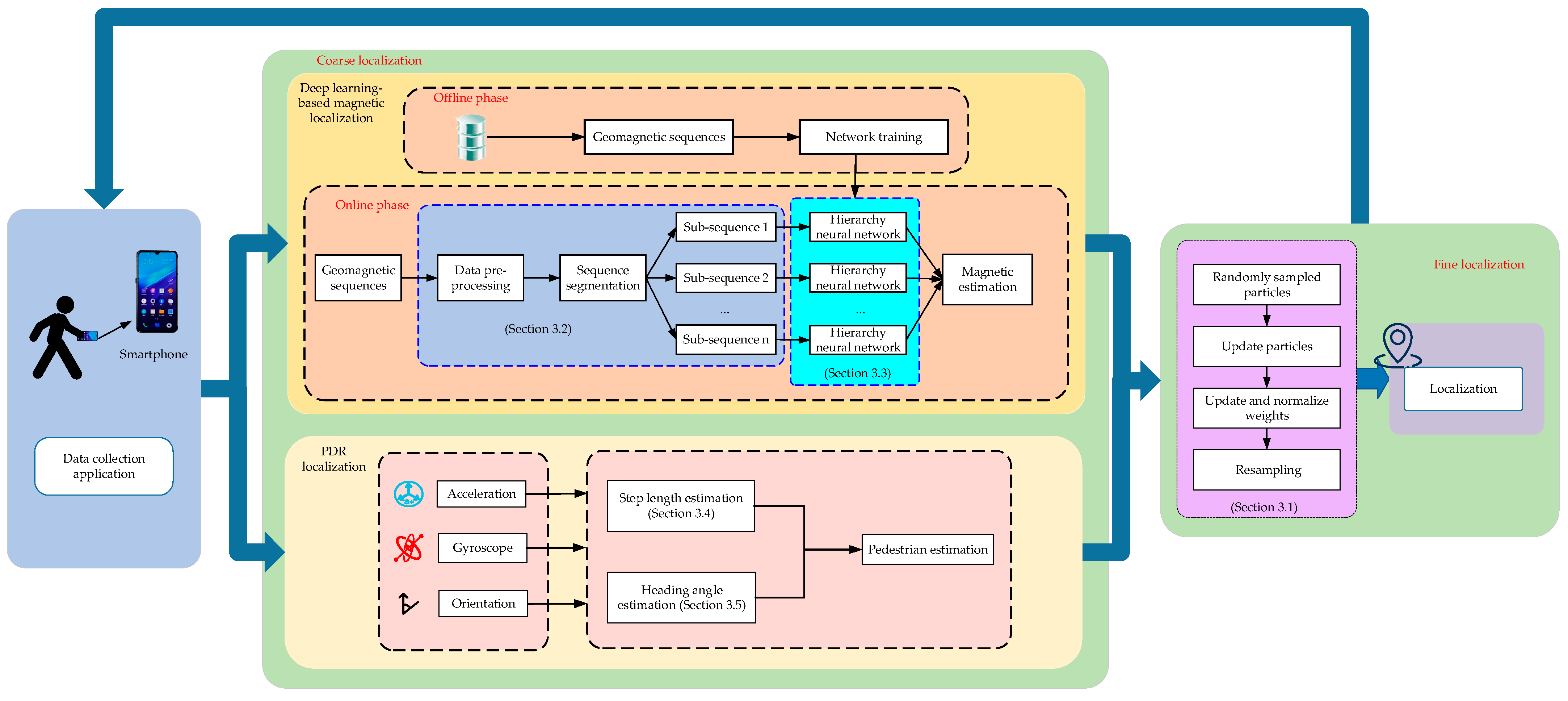
In this section, we introduce the proposed coarse-to-fine localization method, which contains data acquisition and preprocessing, coarse localization using deep learning-based geomagnetic localization and PDR localization, and fine location determination. The overall structure of the coarse-to-fine localization method is presented in Figure 1.

Figure 1. The overall structure of the coarse-to-fine localization method.

In data acquisition and preprocessing, it is necessary to plan test scenarios and data acquisition paths. The pedestrian holds a smartphone to collect the geomagnetic sequences, acceleration, gyroscope, and orientation data through a preinstalled application software. The crowdsourcing method can realize fast and low-cost data in the planned region. Afterward, these data will be sent to the server in a *.txt format and preprocessed. The cubic spline interpolation method is used to construct a geomagnetic fingerprint database.

In coarse localization, we can gain the coarse location using deep learning and PDR methods. Deep learning-based geomagnetic localization consists of an offline phase and an online phase. In the offline phase, a multidimensional geomagnetic feature extraction method is used to extract the spatial and temporal information of geomagnetic sequences. Then, a multidimensional geomagnetic fingerprint database is constructed. In the online phase, we devise a hierarchical deep neural network model to predict the target location. In PDR localization, we can obtain the target location using inertial sensor data.

In fine localization, location estimation is achieved via a particle filter. The initial location is shown using deep learning-based geomagnetic localization. Then, according to PDR localization, we construct a particle set to test the hypothesis of the target’s state as the posterior distribution. Each particle set includes 100 random particles. The state of the target contains the location and the heading angle. Finally, all particle locations are compared with the geomagnetic localization locations to generate the weights of all particles and thus achieve localization.

In this coarse-to-fine localization model, the particles state $P_t$ at time $t$ is described as shown in Equation (1):

$$P_t=[{(x}_t,y_t,{\theta }_t),{\omega }_t]$$

(1)

where $x_t,y_t,{\theta }_t$ represent the location and heading angle of the particles at time $t$. ${\omega }_t$ is the weight of particles.

Assuming the deep learning-based geomagnetic estimation $Z_t$ as the system observation, the location estimation ${Loc}_{t-1}$ at time $t-1$ is the system state. During fine localization, the state of each particle is updated in the following steps:

Step 1: $N$ particles are randomly sampled at time $t-1$, centered on the location system state ${Loc}_{t-1}$. The particles are characterized as $P_{t-1}^i,i=1,\dots ,N$ and the weight of each particle is equivalent. The particles at the next step may be updated using Equation (2):

$$\left[\begin{array}{c}{x}_t^i\\ y_t^i\end{array}\right]=\left[\begin{array}{c}{x}_{t-1}^i\\ y_{t-1}^i\end{array}\right]+\left[\begin{array}{c}sin{\theta }_t\\ cos{\theta }_t\end{array}\right]·st{p}_{len}+G_t$$

(2)

where $st{p}_{len}$ is the step length of the pedestrian at time t, ${\theta }_t$ is the heading angle at time t, and $G_t$ is the Gaussian noise with 0 mean and variance 1.

Step 2: After updating the location of all the particles, the weight of each particle needs to be re-evaluated using Equation (3):

$${\omega }_t^i=\frac{1}{{\left|V\right|}^{\frac{1}{2}}\sqrt{2\pi }}\exp \left(-\frac{1}{2}{V}^{-1}{‖<x_t^i,y_t^i>-Z_t‖}^2\right)$$

(3)

where $V$ is the observation noise covariance matrix.

Step 3: Normalize the weight of each particle using Equation (4):

$${\omega }_t^i=\frac{{\omega }_t^i}{{\sum }_{i=1}^N{\omega }_t^i}$$

(4)

Step 4: Localization at time $t$ can be achieved using Equation (5):

$${Loc}_t={\sum }_{i=1}^N{\omega }_t^i·{(x}_t^i,y_t^i)$$

(5)

The procedure of the proposed localization method is presented in Algorithm 1.

Algorithm 1: The coarse-to-fine localization procedure

Input: The geomagnetic sequence and inertial data from smartphone. Output: The localization of the target. 1: Collect data from smartphone. 2: Geomagnetic preprocessing and segmentation. 3: Multifeature geomagnetic extraction. 4: Geomagnetic localization using deep Learning. 5: Step length estimation of the pedestrian. 6: Coordinate transformation to navigation system. 7: Heading angle estimation. 8: Generate $N$ random particles based on location estimation. 9: for each step do 10: for each particle do 11:  Resample particle location $<x_t^i,y_t^i>$ by Equation (2). 12:  Re-evaluate each particle’s weight ${\omega }_t^i$ at time $t$ by Equation (3). 13: end for 14:  Normalize the particle weights ${\omega }_t^i$ by Equation (4). 15:  Resample the particles. 16:  Achieve the fine target localization ${Loc}_t$ by Equation (5). 17: end for

3.2. Multi-feature Geomagnetic Extraction

The geomagnetic field is highly affected by indoor man-made constructions, especially those involving ferrogeomagnetic materials such as steel and iron railings. Such anomalies caused by indoor infrastructure are observed to supply more clues at different locations.

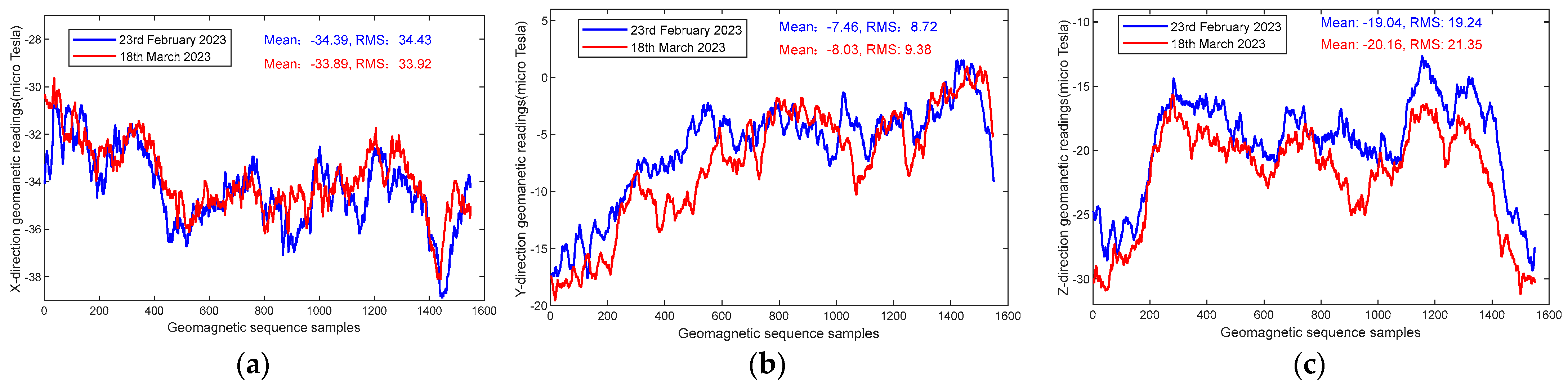
To validate the stability of the indoor geomagnetic field over time, we conducted several experiments at a corridor of 32.4 m in length in two different time periods. Figure 2 shows the three-direction geomagnetic data captured using smartphones on 23 February 2023 and 16 March 2023. Figure 2a demonstrates the geomagnetic magnitude in the x-direction; the waveform of two dates has the same tendency. Figure 2b,c show the geomagnetic magnitude in the y-direction and z-direction, respectively. It can be seen that the geomagnetic magnitude varies slightly in different time periods, but the overall trend has significant similarity.

Figure 2. Geomagnetic signal readings collected through a mobile device on 23 February 2023 and 16 March 2023: (a) geomagnetic x-direction vector; (b) geomagnetic y-direction vector; (c) geomagnetic z-direction vector.

In addition, we have compared the magnitudes and gradients of the geomagnetic data over time. Figure 3a describes the geomagnetic magnitude of the same region on 23 February 2023 and 16 March 2023, respectively. The results show that the waveform of geomagnetic magnitude maintains great similarity after a period of time. Figure 3b describes the geomagnetic gradient of the same region on 23 February 2023 and 16 March 2023, respectively. The gradient basically fluctuates around zero. Therefore, the gradient fluctuations are very small. From these two graphs, it can be seen that the geomagnetic field has good stability without external infrastructure changes.

Figure 3. Geomagnetic signal readings collected through a mobile device on 23 February 2023 and 16 March 2023: (a) geomagnetic field magnitudes; (b) geomagnetic field gradients.

Although the geomagnetic field strength and gradient have changed after a period of time, the fluctuations are less varied and basically negligible. Meanwhile, we calculate the mean and the RMS values of these geomagnetic sequence samples, as shown in Figure 2 and Figure 3. It can be seen that these values on 23 February 2023 and 16 March 2023 are very close. Therefore, the geomagnetic sequences exhibit great stability.

In summary, this stable variation feature of the indoor geomagnetic field facilitates indoor localization and endows the smartphone-based geomagnetic indoor localization system with very high potential application. Researchers have studied various works associated with geomagnetic sequence-based localization methods. However, most of them merely use a single raw sequence of geomagnetic values [58], magnitudes [26], or gradients [18] for localization estimation, leading to rough localization accuracy in a large area scene. Among the geomagnetic sequence localizations, the three-direction vector $\left(m_x,m_y,m_z\right)$ of geomagnetic sequences retains spatial information, the magnitudes of geomagnetic sequences $m_a$ retain the geomagnetic characteristics, and the gradient of geomagnetic sequences $m_g$ can effectively eliminate equipment heterogeneities. To address these issues, we propose a multidimensional geomagnetic feature extraction algorithm. Feature extraction includes data resampling, noise reduction, geomagnetic feature extraction, and normalization.

Geomagnetic data collected by different persons will lead to varying online and offline geomagnetic densities. To effectively match data, we employ the resampling method via upsampling and downsampling to satisfy different velocity targets. Based on the real-time and accuracy requirements of localization, we resample geomagnetic sequences in every step. The step length is estimated based on the work in [52], which is related to ours and can predict pedestrian states more accurately.

Then, empirical mode decomposition (EMD) [59] is adopted to reduce the noise generated during geomagnetic data acquisition and conversion. It is an adaptive signal separation method that decomposes nonstationary geomagnetic sequences $s\left(t\right)$ into a nonzero mean residue $r\left(t\right)$ and several intrinsic mode functions (Imfs), as shown in Equation (6).

$$s\left(t\right)={\sum }_{i=1}^N{Imf}_i\left(t\right)+r\left(t\right)$$

(6)

where $N$ is the number of Imfs and ${Imf}_i\left(t\right)$ is the $i$th Imf.

After preprocessing the geomagnetic data, the magnitude $m_a$ and gradient $m_g$ of the geomagnetic sequences can be obtained using Equation (7). Then, we can construct the geomagnetic vector $\left(m_x,m_y,m_z,m_a,m_g\right)$, in which $\left(m_x,m_y,m_z\right)$ represents the spatial information features and $m_a$ and $m_g$ represent the geomagnetic field temporal information.

$$\left\{\begin{array}{c}{m}_a=\sqrt{{‖m_x‖}_2+{‖m_y‖}_2+{‖m_z‖}_2}\\ m_g=\left(\frac{\partial m_x}{\partial x}\right)\stackrel{⃑}{e_x}+\left(\frac{\partial m_y}{\partial y}\right)\stackrel{⃑}{e_y}+\left(\frac{\partial m_z}{\partial z}\right)\stackrel{⃑}{e_z}\end{array}\right.$$

(7)

where $\left(\frac{\partial m_x}{\partial x}\right)\stackrel{⃑}{e_x}$, $\left(\frac{\partial m_y}{\partial y}\right)\stackrel{⃑}{e_y}$, $\left(\frac{\partial m_z}{\partial z}\right)\stackrel{⃑}{e_z}$ are the gradients of the geomagnetic field along the x-, y-, z-axis, respectively. $\stackrel{⃑}{e_x}$, $\stackrel{⃑}{e_y}$, $\stackrel{⃑}{e_z}$ are the respective unit vectors of the three axes.

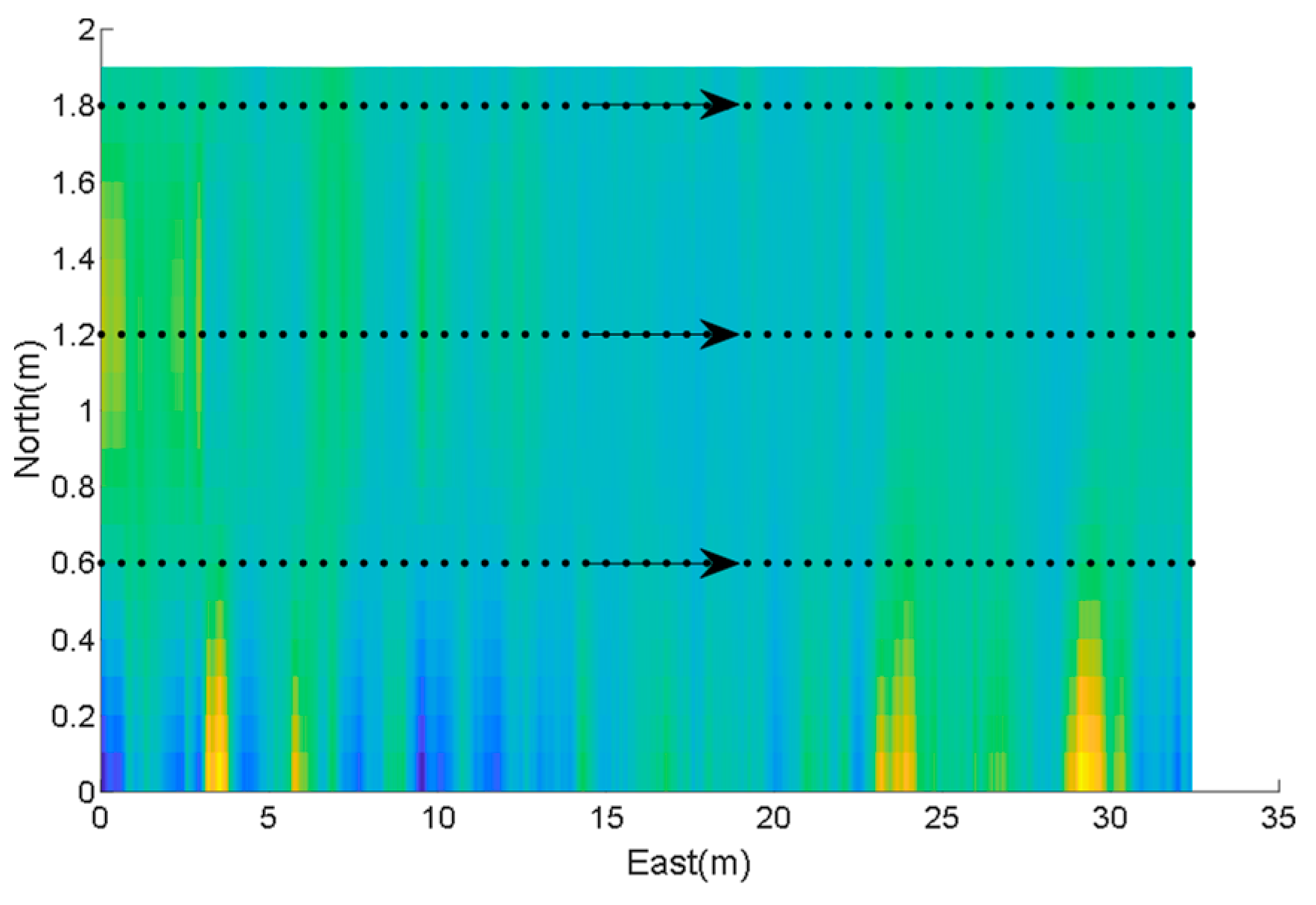
The geomagnetic sequence samples are collected in a 32.4 $\times$ 1.9 ${\mathrm{m}}^2$ area. The pedestrian walks along a 32.4 m corridor to collect data with a sampling frequency of 20 Hz. The geomagnetic magnitude of temporal representations is shown in Figure 4. The arrows represent the pedestrian walking direction, the black dots are geomagnetic samples. Each sample in the figure corresponds to a location in the graph and is also associated with the pedestrian’s walking time. Each location corresponds to a geomagnetic magnitude value. It can be seen that the geomagnetic magnitude in the corridor varies strongly in temporal terms, and the geomagnetic magnitude is clearly differentiated and can be used for indoor localization.

Figure 4. Geomagnetic magnitude of temporal representations.

To eliminate the undesirable effects caused by odd sample data, the geomagnetic data need to be normalized into the range [0, 1] with the min-max scaling approach, which is defined in Equation (8). To extract more geomagnetic features for localization, we utilize multiple geomagnetic data as input in the proposed deep learning network.

$$N(s)=\frac{s-\min \left(s\right)}{\max \left(s\right)-\min \left(s\right)}$$

(8)

where $\min \left(s\right)$ and $\max \left(s\right)$ are the minimum and maximum values of geomagnetic sequence s, respectively.

Long geomagnetic sequence data require more computational complexity during localization regardless of whether temporal correlation or fingerprint matching methods are used. Since it is very tedious and time-consuming to extract features from long input sequences, a sliding window with uniform size is adopted to fragment the geomagnetic sequences into several consecutive subsequences. The proposed localization method predicts the target location by matching the corresponding location of each frame in the subsequence.

3.3. Hierarchical Deep Learning Neural Network

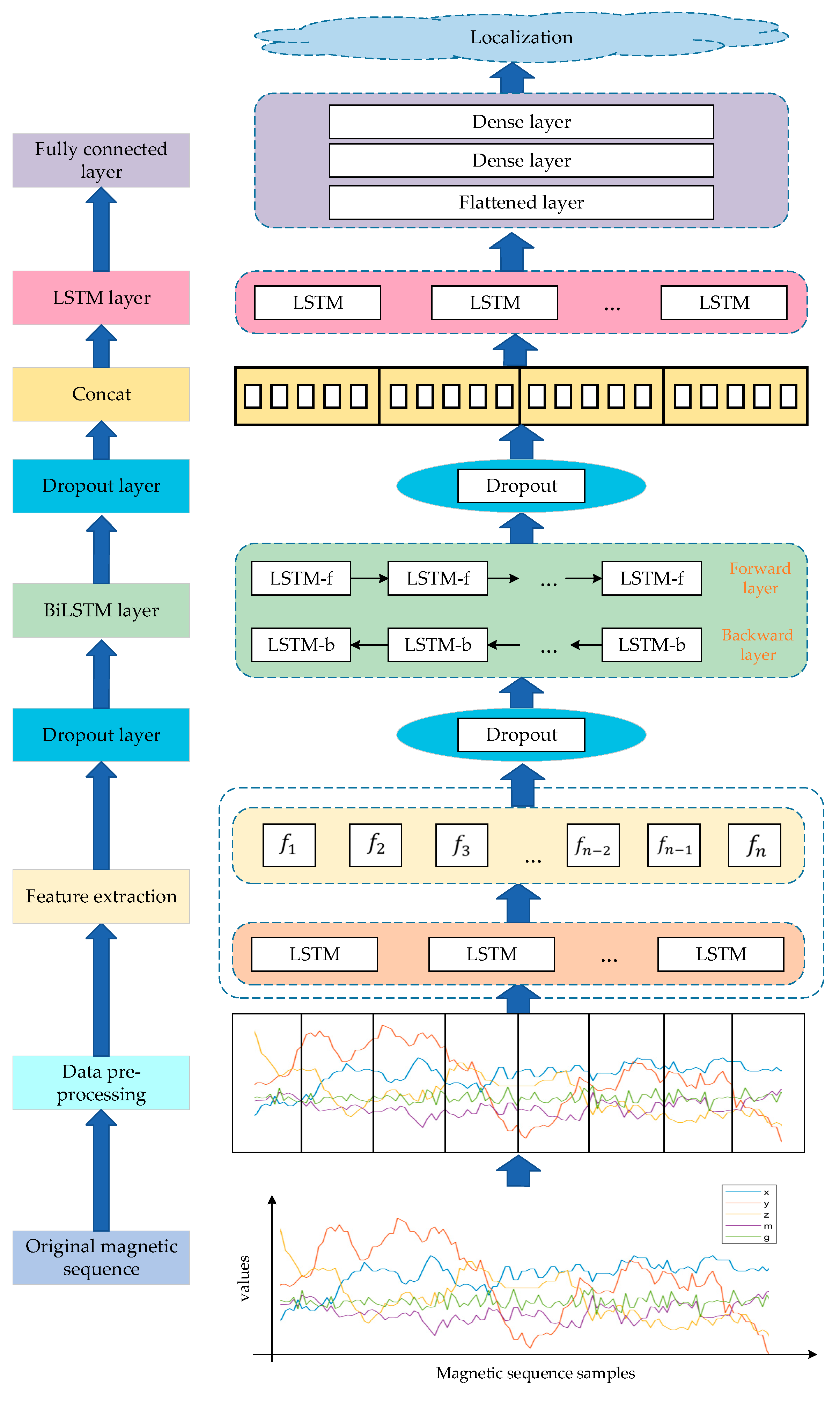
In this section, we propose a hierarchical deep learning network model for target localization that can better extract features and learn the correlation between the geomagnetic sequences and location labels. The framework of the deep learning indoor geomagnetic localization is shown in Figure 5. The proposed deep learning neural network sequentially assembles the LSTM, BiLSTM, dropout layer, and the fully connected (FC) layer.

Figure 5. Framework of the deep learning-based indoor geomagnetic localization algorithm.

In the proposed model, the LSTM layer is used to extract anomalous features from multidimensional geomagnetic sequences. To extract more context information of subsequences, the BiLSTM layer is introduced to enhance the extracted feature. Afterward, the last LSTM layer is applied to extract the enhanced features for more accurate prediction. Each layer is backed by a dropout layer with a dropout rate of 0.2, which resets certain values to zero during training and therefore avoids overfitting. Finally, the fully connected layer is applied to output the results. More specifically, the FC network contains three layers: a flattened layer and two dense layers. The first dense layer with 32 neurons is used to handle sparse output by the flattened layer. Then, the predicted value is output through the last dense layer, which has two neuron nodes activated by the sigmoid activation function. In the model training phase, the preprocessed feature data and location data are fed into the hierarchical deep learning network model for training. After completing the training stage, the target’s location can be determined.

Deep learning approaches solve the problem of localization delay and enable more accurate localization by learning more extensive abstractions and high-level features from geomagnetic sequences. Long short-term memory LSTM [60], an improved recurrent neural network (RNN) with better long-term memory, can efficiently convey and represent information in long sequences without causing useful information from long periods to be forgotten. The forget gate, input gate, output gate and cellular state are used to control the message that will be stored in the LSTM structure. The expressions of LSTM are presented below:

$$\left\{\begin{array}{c}{f}_t=\sigma \left(W_f·\left[h_{t-1},r_t\right]+b_f\right)\\ i_t=\sigma \left(W_i·\left[h_{t-1},r_t\right]+b_i\right)\\ \stackrel{\sim }{C_t}=\tanh \left(W_C·\left[h_{t-1},r_t\right]+b_C\right)\\ \hspace{1em}{C}_t=f_t\ast C_{t-1}+i_t\ast \stackrel{\sim }{C_t}\hfill \\ o_t=\sigma \left(W_o·\left[h_{t-1},r_t\right]+b_o\right)\end{array}\right.$$

(9)

where $f_t$, $i_t$, and $o_t$ are the output, input and forget gates, respectively. $C_t$ is the candidate memory cell, which is determined by combining the old cell state $C_{t-1}$ and the cell input activation vector $\stackrel{\sim }{C_t}$. $h_t$ and $h_{t-1}$ are the outputs of the current neuron and the previous layer, respectively. $r_t$ represents the input data at time t.

The loss function of the LSTM network at time t is defined as

$$l_t=a{‖p_t-y_t‖}^2$$

(10)

$$L=\sum _{t=1}^T{l}_t$$

(11)

where $p_t, y_t$ are the output and input values of LSTM at time t, respectively. $a$ is the scale factor.

The gradient ${\mathsf{\delta }}_t$ of the output layer is expressed as follows:

$${\mathsf{\delta }}_t=\frac{\partial L}{\partial p_t}=p_t-y_t$$

(12)

The update of weight value $U^{fx}$, $U^{ix},$ $U^{ax}$, and $U^{ox}$ at time t is characterized as follows:

$$\left(\begin{array}{c}\frac{\partial l_t}{{\partial U}^{fx}}\\ \frac{\partial l_t}{{\partial U}^{ix}}\\ \frac{\partial l_t}{{\partial U}^{ax}}\\ \frac{\partial l_t}{{\partial U}^{ox}}\end{array}\right)=\left(\begin{array}{c}\sum _{k=1}^t\frac{\partial l_t}{\partial U_t^{fx}}\\ \sum _{k=1}^t\frac{\partial l_t}{\partial U_t^{ix}}\\ \sum _{k=1}^t\frac{\partial l_t}{\partial U_t^{ax}}\\ \sum _{k=1}^t\frac{\partial l_t}{\partial U_t^{ox}}\end{array}\right)=\left(\begin{array}{c}\genfrac{}{}{0pt}{}{\frac{\partial l_t}{\partial U_t^{fx}}+\frac{\partial l_t}{\partial U_{t-1}^{fx}}+\dots +\frac{\partial l_t}{\partial U_1^{fx}}}{\frac{\partial l_t}{\partial U_t^{ix}}+\frac{\partial l_t}{\partial U_{t-1}^{ix}}+\dots +\frac{\partial l_t}{\partial U_1^{ix}}}\\ \frac{\partial l_t}{\partial U_t^{ax}}+\frac{\partial l_t}{\partial U_{t-1}^{ax}}+\dots +\frac{\partial l_t}{\partial U_1^{ax}}\\ \frac{\partial l_t}{\partial U_t^{ox}}+\frac{\partial l_t}{\partial U_{t-1}^{ox}}+\dots +\frac{\partial l_t}{\partial U_1^{ox}}\end{array}\right)$$

(13)

For the weight value $U^{fx}$, $\frac{\partial l_t}{{\partial U}^{fx}}$ can be obtained from the gradient of the loss function at the current and previous times. The gradient $\frac{\partial l_t}{\partial U_t^{fx}}$ at the current time is obtained as follows:

$$\frac{\partial l_t}{\partial U_t^{fx}}=\frac{\partial l_t}{\partial y_t}·\frac{\partial y_t}{\partial h_t}·\frac{\partial h_t}{\partial C_t}·\frac{\partial C_t}{\partial f_t}·\frac{\partial f_t}{\partial U_t^{fx}}$$

(14)

We can determine the gradient $\frac{\partial l_t}{\partial U_{t-1}^{fx}}$ at time t − 1 using Equation (15).

$$\begin{gathered} \frac{\partial l_t}{\partial U_{t-1}^{fx}}=\frac{\partial l_t}{\partial y_t}·\frac{\partial y_t}{\partial h_t}·\frac{\partial h_t}{\partial O_t}·\frac{\partial O_t}{\partial h_{t-1}}·\frac{\partial h_{t-1}}{\partial C_{t-1}}·\frac{\partial C_{t-1}}{\partial f_{t-1}}·\frac{\partial f_{t-1}}{\partial U_{t-1}^{fx}} \\ +\frac{\partial l_t}{\partial y_t}·\frac{\partial y_t}{\partial h_t}·\frac{\partial h_t}{\partial C_t}·\frac{\partial C_t}{\partial C_{t-1}}·\frac{\partial C_{t-1}}{\partial f_{t-1}}·\frac{\partial f_{t-1}}{\partial U_{t-1}^{fx}} \end{gathered}$$

(15)

The gradient $\frac{\partial l_t}{\partial U_{t-2}^{fx}}$ at time t − 2 is derived from Equation (16).

$$\begin{gathered} \frac{\partial l_t}{\partial U_{t-2}^{fx}}=\frac{\partial l_t}{\partial y_t}·\frac{\partial y_t}{\partial h_t}·\frac{\partial h_t}{\partial h_{t-1}}·\frac{\partial h_{t-1}}{\partial O_{t-1}}·\frac{\partial O_{t-1}}{\partial h_{t-2}}·\frac{\partial h_{t-2}}{\partial C_{t-2}}·\frac{\partial C_{t-2}}{\partial f_{t-2}}·\frac{\partial f_{t-2}}{\partial U_{t-2}^{fx}} \\ +\frac{\partial l_t}{\partial y_t}·\frac{\partial y_t}{\partial h_t}·\frac{\partial h_t}{\partial h_{t-1}}·\frac{\partial h_{t-1}}{\partial C_{t-1}}·\frac{\partial C_{t-1}}{\partial C_{t-2}}·\frac{\partial C_{t-2}}{\partial f_{t-2}}·\frac{\partial f_{t-2}}{\partial U_{t-2}^{fx}} \\ +\frac{\partial l_t}{\partial y_t}·\frac{\partial y_t}{\partial h_t}·\frac{\partial h_t}{\partial C_t}·\frac{\partial C_t}{\partial C_{t-1}}·\frac{\partial C_{t-1}}{\partial C_{t-2}}·\frac{\partial C_{t-2}}{\partial f_{t-2}}·\frac{\partial f_{t-2}}{\partial U_{t-2}^{fx}} \end{gathered}$$

(16)

For the update of weight value $U^{fx}$, all the gradients at the previous time include the gradient $\frac{\partial C_t}{\partial C_{t-1}}$ of the cell state. In the LSTM model, $\frac{\partial C_t}{\partial C_{t-1}}$ can be inferred in Equation (17). It is determined by the weight values $W_{fh}$, $W_{ih}$, and $W_{ah}$. We can adjust the parameters so that the gradient is in a controllable range.

$$\begin{gathered} \frac{\partial C_t}{\partial C_{t-1}}=C_{t-1}·sigm\left(.\right)\left(1-sigm\left(.\right)\right)·W_{fh}·O_{t-1}·\left(1-{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^2\left(C_{t-1}\right)\right)+f_t+a_t \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·sigm\left(.\right)\left(1-sigm\left(.\right)\right)·W_{ih}·O_{t-1}·\left(1-{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^2\left(C_{t-1}\right)\right)+i_t \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·\left(1-{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^2\left(C_{t-1}\right)\right)·W_{ah}·O_{t-1}·\left(1-{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^2\left(C_{t-1}\right)\right) \end{gathered}$$

(17)

Similarly, for the parameters $U_{ih}, U_{ah}, U_{oh},W_{ih}, W_{ah}, W_{fh}, W_{oh}, b_i, b_a, b_f$ and $b_o$ update of the model, we can infer the weight value $U_{fx}$. Therefore, the model can effectively mitigate gradient explosion and gradient vanishing.

The BiLSTM contains two independent hidden LSTM layers arranged in a chronological and a reverse order. The state equations for the BiLSTM are the same as those mentioned above, except that both forward $\overrightarrow{y_t}$ and backward hidden states $\overleftarrow{y_t}$ are used in each time period. The BiLSTM is defined as follows:

$$\left\{\begin{array}{c}\overrightarrow{y_t}=\overrightarrow{LSTM}\left(y_{t-1},r_t\right)\\ \overleftarrow{y_t}=\overleftarrow{LSTM}\left(y_{t+1},r_t\right)\\ h_t^b=\overrightarrow{y_t}+\overleftarrow{y_t} \end{array}\right.$$

(18)

where $h_t^b$ is the output state of BiLSTM.

BiLSTM can capture the past and future contextual temporal and spatial correlations of the input geomagnetic sequence, keeping more detailed features and reducing the loss of information. Therefore, the geomagnetic sequence features can be effectively captured and extracted.

3.4. Step Length Estimation

The peak detection algorithm estimates the pedestrian step length based on the periodic variation in acceleration during walking. We set an acceleration threshold $a_{th}$ and time difference threshold $T_{diff}$ to avoid invalid peaks. It is specified as follows:

First, assume $a_t$, $a_{t-1}$ and $a_{t+1}$ are the accelerometer values at times t, t − 1, and t + 1, respectively. When $a_t$ is the maximum value among the values $a_{t-1}, {a_t,\mathrm{a}\mathrm{n}\mathrm{d} a}_{t+1}$, then $a_t$ is labeled as the peak value. Otherwise, we will forward the time t + 1 and return this step.

Then, if the peak value $a_t$ is greater than the threshold $a_{th}$, the peak value will be retained and transferred to the next step. Otherwise, we will return to the first step.

Finally, if the time difference between the current and the previous peak value is larger than the time threshold $T_{diff}$, then the peak is a valid peak.

The methods of step length estimation include mainly the constant model [61], linear model [62], and nonlinear model [63]. The most representative nonlinear model is the Weinberg [64] algorithm. These typical models are as follows:

Constant algorithm:

$${stp}_{len}=\frac{d}{{stp}_n}$$

(19)

Linear algorithm:

$${stp}_{len}=K_1·f+K_2$$

(20)

Weinberg algorithm:

$$st{p}_{len}=K_3·\sqrt[4]{a_{max}-a_{min}}$$

(21)

where d and ${stp}_{len}$ are the walking distance and step number, respectively. $K_1$, $K_2$ and $K_3$ are model constants. $f$ is the step frequency, and $a_{max}$ and $a_{min}$ are the maximal and minimal values of the acceleration in the vertical direction at each step, respectively.

The step length cannot always be constant due to the fluctuation of the pedestrians. In addition, different pedestrians have different step frequencies at different times. Therefore, the linear model and the constant model cannot accurately describe the variation in step length and meet the application requirements. The nonlinear model uses the correlation between the step length and acceleration data to estimate the step length, which is more in line with the actual pedestrian state. An improved nonlinear step length estimation method, which is our previous work [52], can provide a more accurate pedestrian step length, as shown below:

$${stp}_{len}^i=c_1\ast {stp}_{len}^{i-1}+c_2\ast {stp}_{len}^{i-2}+c_3\ast K\ast \sqrt[4]{a_{max}^i-a_{min}^i}+\sigma$$

(22)

where ${stp}_{len}^{i-1}$ and ${stp}_{len}^{i-2}$ are the former two-step lengths. K is the model constant, $[c_1,c_2,c_3]$ is the weight, $a_{max}^i$ and $a_{min}^i$ are the maximal and minimal values of the acceleration at the i-th step, respectively, and $\sigma$ is the accelerometer compensation measured at stationary time.

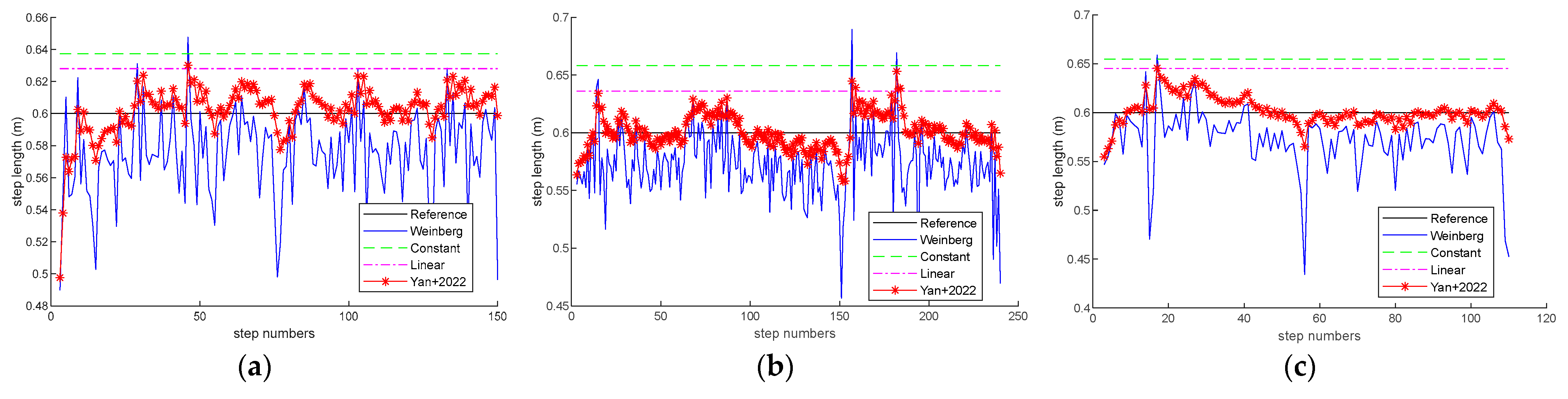
We conducted experiments with the constant, linear, Weinberg, and Yan methods at three trial paths. Trial path 1 is 92 m long with fire hydrants, iron railings, and other iron substances. Trial path 2 is 158 m long with iron, steel, and ferrous substances. Trial path 3 is 72 m long with iron frames and iron bars. Figure 6 shows the step length estimation of these methods when the pedestrian walks at a speed of 0.6 m per step. The experimental results demonstrate that our previous method can achieve more accurate step length estimation.

Figure 6. Step length estimation at different steps with the constant [61], linear [62], Weinberg [64] and Yan+2022 [52] methods: (a) trial path 1; (b) trial path 2; (c) trial path 3.

3.5. Heading Angle Estimation

During the data collection process, all sensor data are located in the built-in coordinate system of the smartphone. However, in indoor localization, a navigation coordinate system is needed. Therefore, it is necessary to transfer the coordinate system for heading direction estimation. We adopt the quaternion method, which converts the target from the phone coordinate system to the navigation coordinate system, as shown in Equation (23).

$$C_n^b=\left(\begin{array}{ccc}{q}_1^2+q_0^2-q_3^2-q_2^2& 2\left(q_1{q}_2-q_0{q}_3\right)& 2\left(q_1{q}_3+q_0{q}_2\right)\\ 2\left(q_1{q}_2+q_0{q}_3\right)& q_2^2-q_3^2+q_0^2-q_1^2& 2\left(q_2{q}_3-q_0{q}_1\right)\\ 2\left(q_1{q}_3-q_0{q}_2\right)& 2\left(q_2{q}_3+q_0{q}_1\right)& q_3^2-q_2^2-q_1^2+q_0^2\end{array}\right)$$

(23)

where $\left(q_{0, }{q}_1,q_2,q_3\right)$ denotes the normalized posture quaternion and $q_0$ is the scalar part of the quaternion.$q_1,q_2,q_3$ are the vector parts.

The heading angle is expressed in Equation (24).

$$\left\{\begin{array}{c}\phi =arctan\left(2\ast (q_3{q}_2+q_0{q}_1)/(1-2q_1^2-2q_2^2\right))\\ \theta =arcsin\left(-2\ast q_1{q}_3+2\ast q_0{q}_2\right)\\ \gamma =arctan\left(2\ast (q_2{q}_1+2q_0{q}_3\right)/\left(1-2q_2^2-2q_3^2\right)\end{array}\right.$$

(24)

where $\phi ,\theta ,\gamma$ are the yaw, pitch and roll angle, respectively.$arctan$ is the arctangent function, and $arcsin$ is the arcsine function.

4. Results

In Section 4.1, we first introduce the experimental setting. The verification and analysis are presented in Section 4.2. Finally, Section 4.3 demonstrates the localization performance.

To evaluate the performance of our proposed localization method, we conducted numerous experiments and compared the proposed method with the state-of-the-art localization approaches in two experimental scenarios. Figure 7 illustrates the floor plans of these two sites, a narrow corridor of office area in the library and a large-scale scenario of the gym, with dimensions of 34 × 17.2 × 4 ${\mathrm{m}}^3$ and 56 × 35 × 10 ${\mathrm{m}}^3$, respectively. In Figure 7, the red dashed line represents the object movement trajectory. In Figure 7a,b, the planned paths are closed rectangular; the movement trajectory follows the red solid arrow. The start and end points are depicted in Figure 7a,b. In Figure 7c, the movement trajectory of the object is along the red dashed line with different start point and end point. The object moves along the solid red arrow. Trial path 1, which is 92 m long, is in a narrow corridor in the library with several fire hydrants and iron-containing substances at fixed locations. Trial path 2, which is 158 m long, contains more iron, steel, and ferrous material in the gymnasium. There are a few iron frames, ferrous substances, and iron bars in trial path 3 which is 72 m long.

Figure 7. Floorplans of the experimental sites: (a) trial path 1; (b) trial path 2; (c) trial path 3.

4.1. Experimental Setting

The proposed coarse-to-fine localization system based on geomagnetic sequences and inertial data developed in this paper contains an application terminal and a server terminal.

The accelerometer, gyroscope, and magnetometer data are collected through smartphones wherein the application is preinstalled while the pedestrian walks along the planned path. In the three paths, the pedestrian is required to collect the data along the designed paths several times. In the experiments, this sampling frequency is 20 Hz. The crowdsourcing method is adopted to collect the geomagnetic signal strength and inertial sensor data.

A workstation acting as a server with the Windows 10 64-bit operating system is required to carry out the experiments in this paper. The CPU is an Intel Core i7-9750H with a base frequency of 3.6 GHz. The machine learning framework TensorFlow 2.9.0 with the deep learning library Keras 2.9.0 and Python 3.9.0 are utilized in the experiments.

We conducted a survey on smartphone usage in our university, which found that Vivo and Huawei are the common domestic phone models. Therefore, the Vivo X30 and Huawei Mate30 are selected in the experiments. The technical information of the mobile phones is presented in Table 1.

Table 1. Information of different mobile devices.

Device Information	Vivo X30	Huawei Mate30
Operation system	Funtouch OS 10	Android 10
CPU	Exynos 980	Snapdragon 990
RAM + ROM	8 G + 256 G	8 G + 128 G
GPU	Mali-G76	Mali-G76
Battery capacity	4350 mAh	4100 mAh
Screen	6.44 inch	6.62 inch
Image resolution	2400 $\times$ 1080	2340 $\times$ 1080
Weight	196.5 g	196 g

4.2. Verification and Analysis

4.2.1. Localization Performance with Different Geomagnetic Sequence Lengths

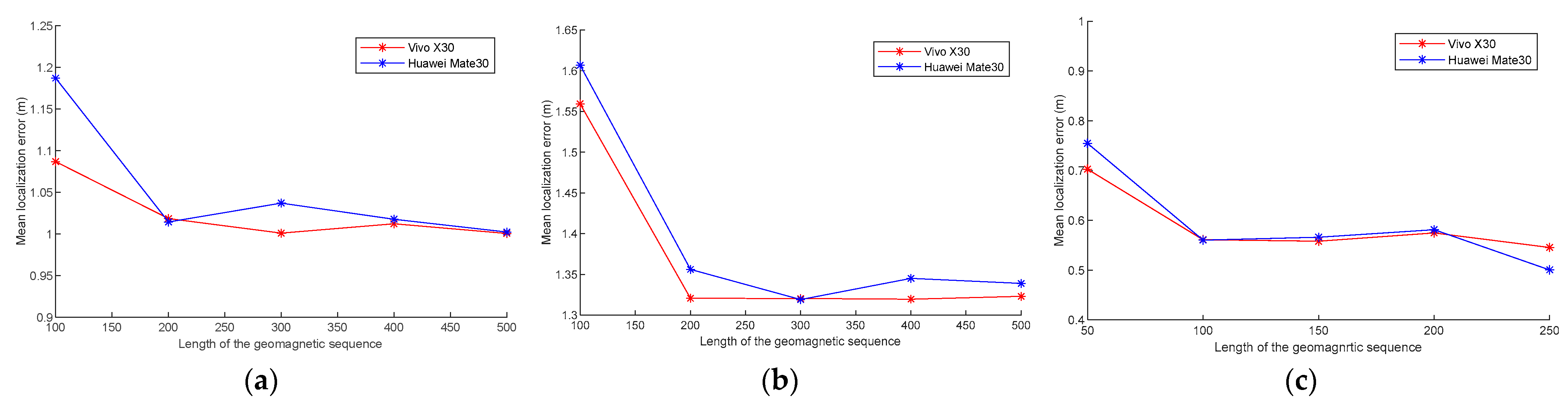
To validate the localization performance with different magnetic lengths, we invite a volunteer from the local university to collect the data along the planned path at a normal speed with both Vivo X30 and Huawei Mate30 several times. We set geomagnetic sequence samples of 100 to 500 with a step size of 100 in trial paths 1 and 2 and geomagnetic sequence samples of 50 to 250 with a step size of 50 in trial path 3 to conduct the experiments. Figure 8 shows the mean localization error with different geomagnetic sequence lengths in the three experimental paths. In Figure 8a,b, the mean localization error is minimal when the geomagnetic samples are 200. When the geomagnetic samples exceed 200, the error becomes steady. In Figure 8c, when the geomagnetic samples exceed 100, the decrease in error slows down. As can be seen in Figure 8, the localization error decreases as the geomagnetic sequence samples increases. This is because more geomagnetic samples cover longer path with more unique geomagnetic features. Therefore, the proposed hierarchical deep neural network can learn more location clues from these unique features. However, longer geomagnetic sequences will take more time to achieve localization.

Figure 8. Mean localization error with different lengths of the geomagnetic sequence: (a) Vivo X30 and Huawei Mate30 in trial path 1; (b) Vivo X30 and Huawei Mate30 in trial path 2; (c) Vivo X30 and Huawei Mate30 in trial path 3.

In addition, the time consumption of various geomagnetic sequence lengths with different devices is presented in Table 2, Table 3 and Table 4. From the tables, we can see that in the three experimental paths, the time consumption increases as the sequence length increases. Longer input geomagnetic sequences require more time to achieve localization. Shorter sequences take less time; however, the deficiency of geomagnetic abnormalities will cause high localization error.

Table 2. Time consumption with different lengths of input geomagnetic sequence using Vivo X30 and Huawei Mate30 in trial path 1(s).

Length	Vivo X30	Huawei Mate30
100	181.42	197.87
200	368.38	408.90
300	440.09	579.15
400	725.99	741.58
500	766.50	773.70

Table 3. Time consumption with different lengths of input geomagnetic sequence using Vivo X30 and Huawei Mate30 in trial path 2(s).

Length	Vivo X30	Huawei Mate30
100	323.37	339.74
200	587.18	564.14
300	782.32	818.54
400	802.44	779.54
500	999.50	859.20

Table 4. Time consumption with different lengths of input geomagnetic sequence using Vivo X30 and Huawei Mate30 in trial path 3(s).

Length	Vivo X30	Huawei Mate30
100	99.64	94.61
200	137.35	145.51
300	183.15	183.75
400	213.51	236.78
500	238.69	259.58

Considering the localization error and time overhead, the geomagnetic sequence lengths for the three trial paths are 200.

4.2.2. Localization Performance with Different Hidden Units

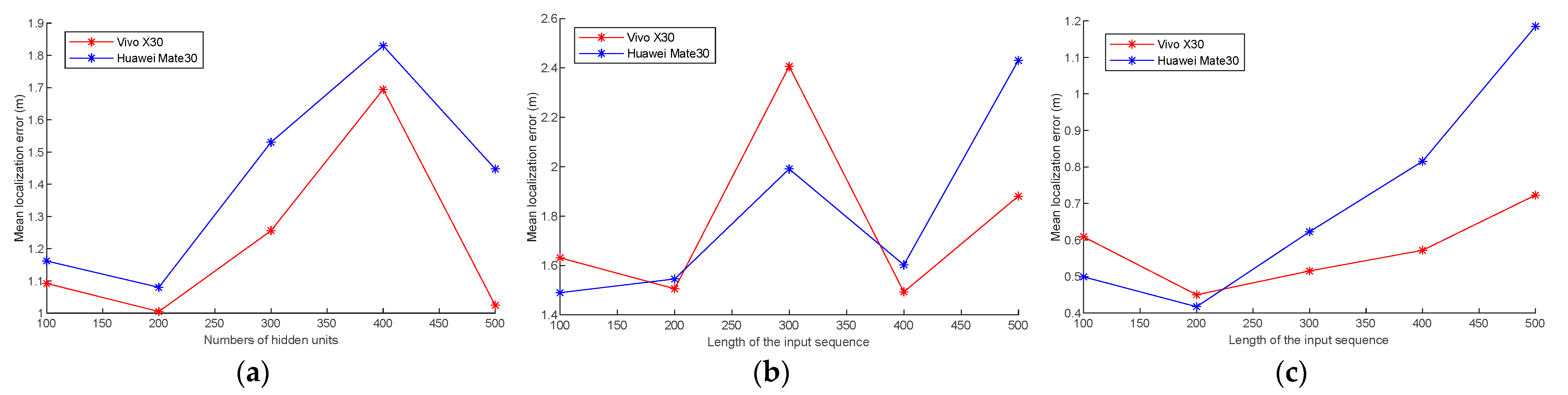
We have also evaluated the localization performance on different numbers of hidden units. Hidden units are the dimensional size of the output of a neural network layer; it is also an important factor that affects localization accuracy. In the experiment, the number of hidden units is set from 100 to 500 at a step size of 100. Figure 9 shows the mean localization error with different numbers of hidden units at three trial paths using Vivo X30 and Huawei Mate30. The experimental results show that the mean localization error fluctuates with the number of hidden units. The mean localization error is minimized when the number of hidden units in all the three experimental paths is 200. In this paper, 200 hidden units for three trial paths are selected.

Figure 9. Mean localization error with different numbers of hidden units: (a) Vivo X30 and Huawei Mate30 in trial path 1; (b) Vivo X30 and Huawei Mate30 in trial path 2; (c) Vivo X30 and Huawei Mate30 in trial path 3.

4.3. Localization Performance

In this section, the localization performances of the proposed method are evaluated with extensive experiments. We have compared the proposed method with the MaLoc method, DTW method, LSTM method, and PDR method in the three trial paths.

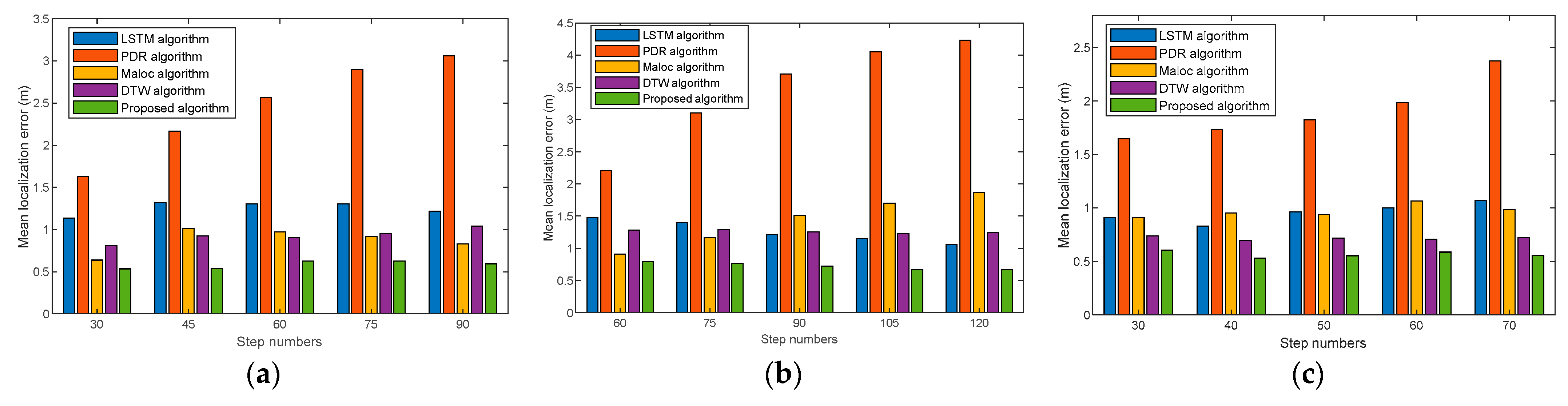
Figure 10 demonstrates the mean localization errors of LSTM, PDR, MaLoc, DTW, and the proposed algorithm for different step numbers on the three trial paths using Vivo X30. The experiments show that the proposed algorithm has a lower mean error at different step numbers compared with the state-of-the-art algorithms, and the localization has a more significant comparison, especially when the step numbers increase. This is because our method can gain more features from the temporal and spatial dimensions. In addition, the BiLSTM used in the novel neutral network matches the fingerprint from the forward and reverse order extracts more details, especially for long step numbers, and can effectively eliminate the location ambiguity of magnetic sequences and the accumulation errors of dead reckoning.

Figure 10. Mean localization error comparison of LSTM, PDR, MaLoc, DTW and the proposed algorithm at different step numbers using Vivo X30: (a) trial path 1; (b) trial path 2; (c) trial path 3.

Figure 11 shows the mean localization errors with different step numbers using Huawei Mate30. Experimental results demonstrate that our proposed algorithm can also achieve comparable localization accuracy with different devices compared with the state-of-the-art algorithms. This is because the multidimensional feature extraction method can effectively mitigate the errors caused by heterogeneous devices and solve the cumulative error problem in PDR localization.

Figure 11. Mean localization error comparison of LSTM, PDR, MaLoc, DTW and the proposed algorithm at different step numbers using Huawei Mate30: (a) trial path 1; (b) trial path 2; (c) trial path 3.

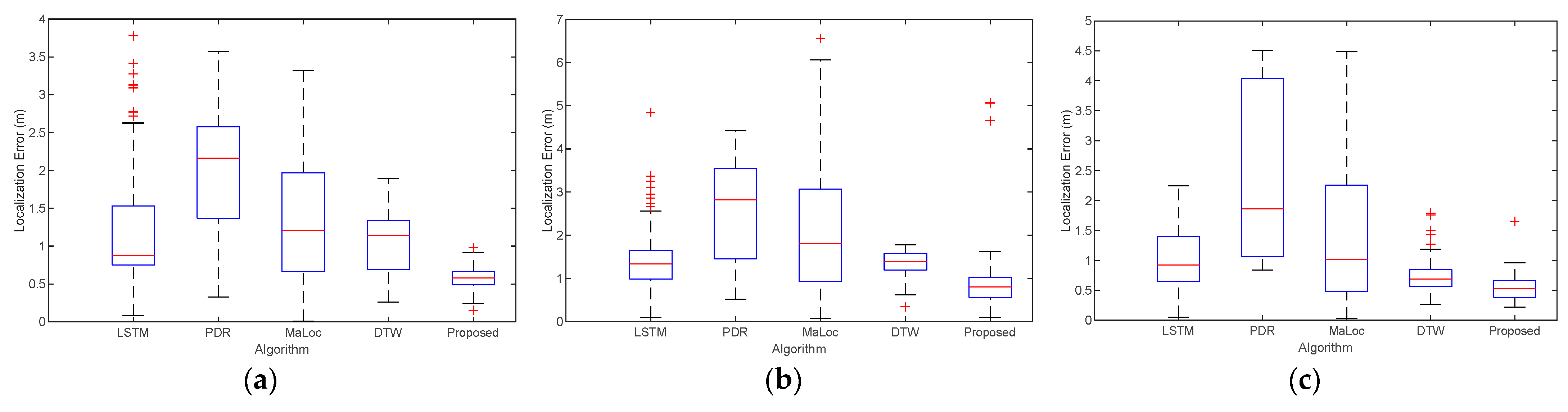
We present the localization error with Vivo X30 in the three trial paths in Figure 12. Red symbols are the location anomalies. It shows that the median and maximum values of the proposed algorithm are the smallest compared to the LSTM, PDR, MaLoc, DTW algorithms at all three different trial paths. This is mainly because our proposed algorithm can efficiently extract the geomagnetic features in both spacious and narrow spaces, and thus more accurate localization can be achieved. It can be seen that our proposed algorithm can achieve good localization performance in different scenarios, overcoming the problem of ambiguous geomagnetic localization.

Figure 12. Localization error with LSTM, PDR, MaLoc, DTW and the proposed algorithm using Vivo X30: (a) trial path 1; (b) trial path 2; (c) trial path 3.

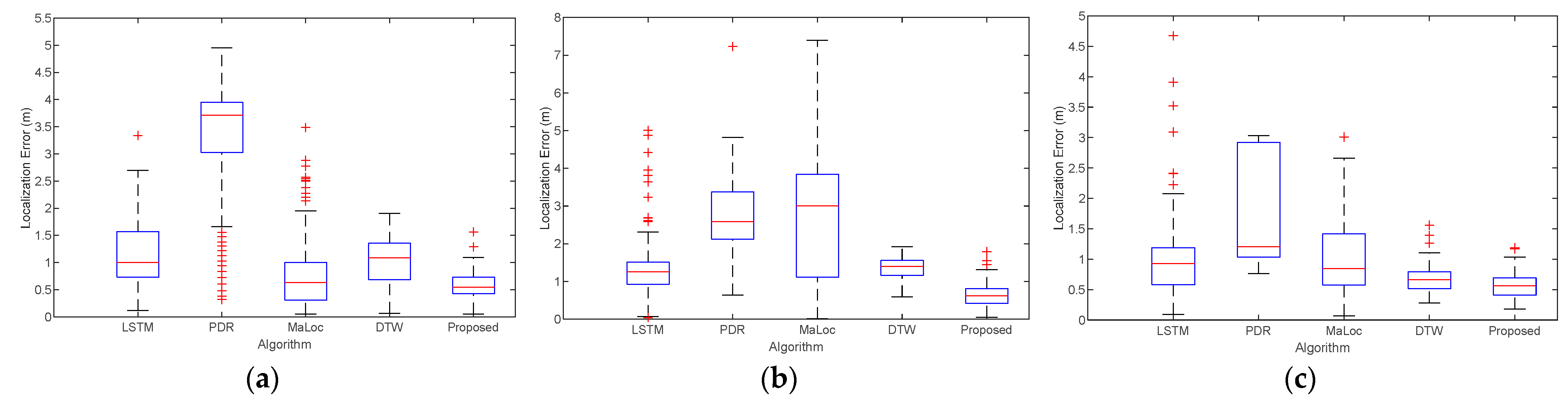
We also compare the localization error at the three trial paths using Huawei Mate30, as shown in Figure 13. The experiments illustrate that our proposed method achieves comparable localization accuracy with different devices. These results occur because our multidimensional extraction algorithm can obtain enough information to realize localization, eliminating equipment heterogeneity.

Figure 13. Localization error with LSTM, PDR, MaLoc, DTW and the proposed algorithm using Huawei Mate30: (a) trial path 1; (b) trial path 2; (c) trial path 3.

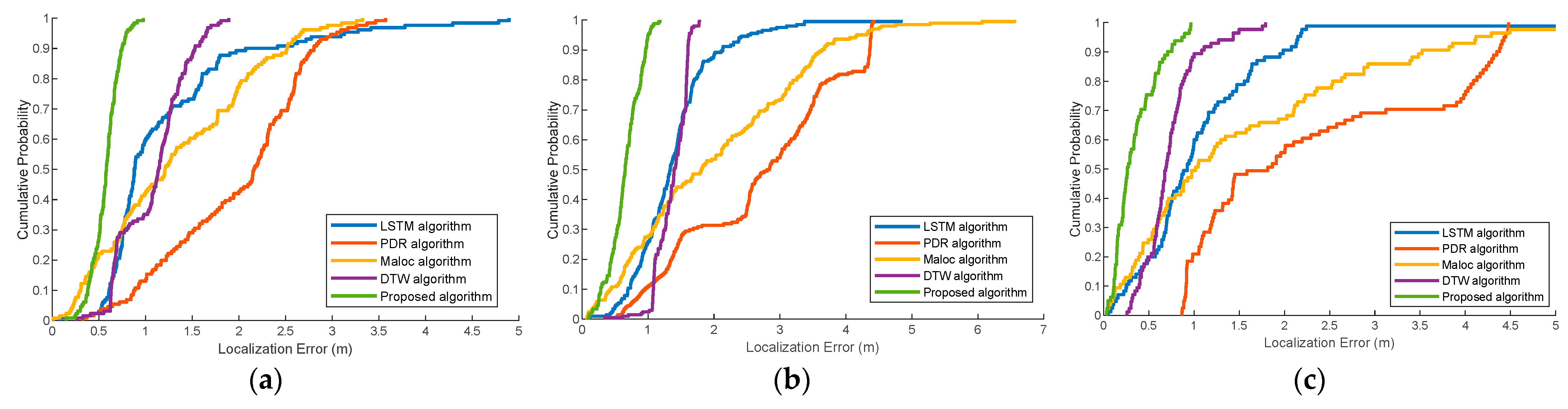
Figure 14 presents the cumulative distribution function (CDF) of the localization error with Vivo X30 at the three trial paths. These experiments demonstrate that the proposed algorithm can achieve the best localization performance compared with the typical localization methods. This is mainly due to the following reasons. First, the distinctiveness and differences of features are increased with multidimension geomagnetic sequences. Then, the hierarchical neural networks can effectively estimate the location through the fully connected layer after fine-graining all the features. Finally, the coarse-to-fine localization algorithm can solve the ambiguous location on the basis of geomagnetic estimation and dead reckoning.

Figure 14. CDF of localization errors with LSTM, PDR, MaLoc, DTW and proposed algorithms using Vivo X30: (a) trial path 1; (b) trial path 2; (c) trial path 3.

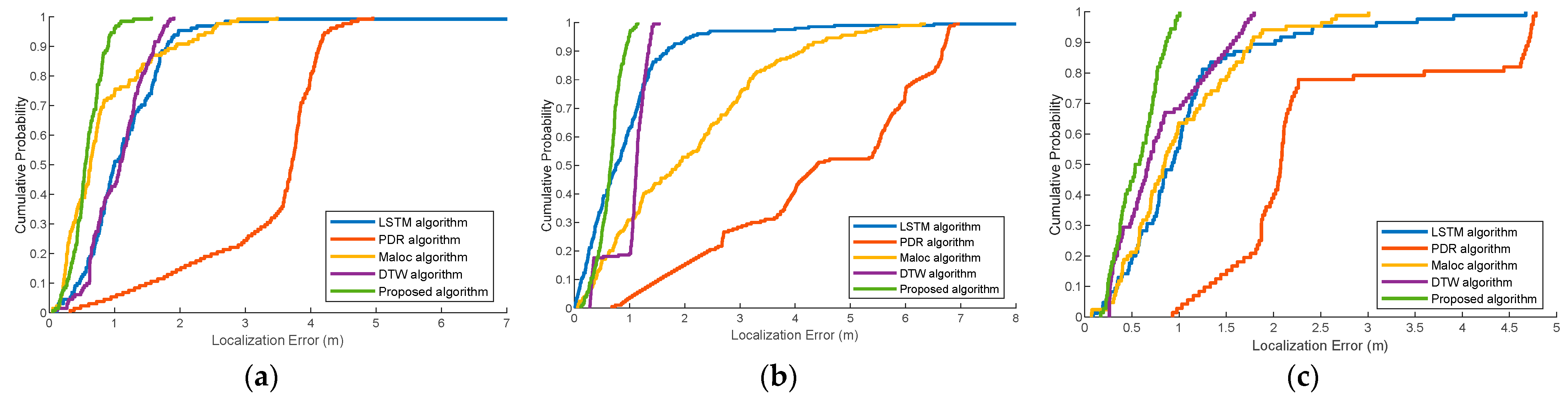
We also illustrate the CDF of localization error at the three trial paths using Huawei Mate30, as shown in Figure 15. It shows that the proposed method achieves considerable accuracy compared to the state-of-the-art methods. This is attributed to the fact that the multidimensional geomagnetic sequence contains spatial and temporal representations, avoiding the extra effort needed to calibrate different devices to a uniform standard.

Figure 15. CDF of localization errors with LSTM, PDR, MaLoc, DTW and proposed algorithms using Huawei Mate30: (a) trial path 1; (b) trial path 2; (c) trial path 3.

Table 5 shows the localization error of the 75th and 90th percentiles at the three experimental paths with both Vivo X30 and Huawei Mate30. The results demonstrate that our proposed method can achieve better accuracy than the other state-of-the-art methods. This is because our localization system can effectively extract the location information, thus eliminating the outliers caused by magnetic localization and PDR localization. Our method has great universality and feasibility in different trajectories and equipment.

Table 5. The localization error of LSTM, PDR, MaLoc, DTW and proposed algorithms with Vivo X30 and Huawei Mate30 in three experimental paths (m).

Vivo X30	Method	75th Percentile	90th Percentile
Trial path 1 (Vivo X30)	LSTM	1.5320	1.5289
	PDR	2.5758	2.8041
	MaLoc	1.9665	2.5149
	DTW	1.3371	1.5289
	Proposed	0.6649	0.7459
Trial path 1 (Huawei Mate30)	LSTM	1.5666	1.8022
	PDR	3.9488	4.1368
	MaLoc	1.0041	1.9383
	DTW	1.3554	1.6043
	Proposed	0.7340	0.9009
Trial path 2 (Vivo X30)	LSTM	1.6483	2.1335
	PDR	5.6468	6.9505
	MaLoc	3.0671	3.6445
	DTW	1.5767	1.6058
	Proposed	0.8352	0.9646
Trial path 2 (Huawei Mate30)	LSTM	1.2048	1.6760
	PDR	5.9927	6.6634
	MaLoc	2.9987	4.1362
	DTW	1.2440	1.3463
	Proposed	0.7720	0.9259
Trial path 3 (Vivo X30)	LSTM	1.4025	1.9838
	PDR	3.9867	4.3610
	MaLoc	2.2558	3.5212
	DTW	0.8428	1.0863
	Proposed	0.4879	0.7260
Trial path 3 (Huawei Mate30)	LSTM	1.1879	2.0170
	PDR	2.2519	4.7029
	MaLoc	2.6254	3.1619
	DTW	1.1743	1.5737
	Proposed	0.7461	0.8630

Table 6 displays the mean errors and root mean square error (RMSE) of different localization algorithms with Vivo X30 at the three experimental paths. The results demonstrate that the localization performance of the proposed algorithm has significantly improved in comparison with the other schemes in the trial sites. The proposed localization is an efficient way to obtain sufficient information, using multidimensional geomagnetic sequences as location clues; thus, our framework is able to extract more distinctive features for localization.

Table 6. The mean errors and RMSE of LSTM, PDR, MaLoc, DTW and proposed algorithms with Vivo X30 in three experimental paths (m).

Vivo X30	Method	Mean Error	RMSE
Trial path 1	LSTM	1.2252	1.4879
	PDR	1.9790	2.1154
	MaLoc	1.3190	1.5503
	DTW	1.0824	1.1381
	Proposed	0.5625	0.5798
Trial path 2	LSTM	1.3886	1.5216
	PDR	2.6852	2.9394
	MaLoc	1.9882	2.3735
	DTW	1.3717	1.3905
	Proposed	0.6502	0.6927
Trial path 3	LSTM	1.0751	1.4344
	PDR	2.2835	2.6560
	MaLoc	1.5126	2.0207
	DTW	0.7294	0.7887
	Proposed	0.3243	0.4045

Table 7 shows the RMSE of different localization algorithms with Huawei Mate30 at the three trial sites. The experiments show that our proposed method markedly improves the localization performance with different devices and trial paths. This is mainly because the proposed algorithm that uses a particle filter effectively eliminates the errors caused by localization. In addition, short subsequences processed using sliding windows reduce the loss of feature information that tends to occur in longer sequences. Consequently, the localization estimation route of the three trial paths fluctuates near the real reference value, and the localization performances are noticeably enhanced.

Table 7. The mean errors and RMSE of LSTM, PDR, MaLoc, DTW and proposed algorithms with Huawei Mate30 in three experimental paths (m).

Huawei Mate30	Method	Mean Error	RMSE
Trial path 1	LSTM	0.9063	1.0527
	PDR	2.8209	3.1064
	MaLoc	0.8311	1.0848
	DTW	1.0522	1.1308
	Proposed	0.5784	0.6287
Trial path 2	LSTM	0.9664	1.3970
	PDR	2.0365	2.5386
	MaLoc	2.0533	2.5115
	DTW	1.3732	1.3911
	Proposed	0.6372	0.6747
Trial path 3	LSTM	1.0583	1.3198
	PDR	2.3806	2.6330
	MaLoc	0.9995	1.1718
	DTW	0.6751	0.7165
	Proposed	0.5461	0.5891

In addition, we compare the calculation complexity between our proposed algorithm and the DTW algorithm at the three trial paths. In trial path 1, our proposed method takes 312.87 s, and the DTW algorithm takes 1452.21 s. In trial path 2, our proposed method takes 521.64 s, and the DTW algorithm takes 2695.41 s. In trial path 3, our proposed method takes 343.58 s, and the DTW algorithm takes 400.89 s. The experiments illustrate that our coarse-to-fine localization method has a relatively low computational complexity and can satisfy the real-time localization requirements. This is because our proposed method can achieve more accurate localization in a smaller area by fusing the dead reckoning instead of matching the whole area as DTW does.

5. Discussion

In this section, we analyze the experimental results presented in Section 4.2 and Section 4.3, respectively. Then, we state the future research direction.

As already demonstrated in Section 4.2, geomagnetic sequence length and hidden units of neural network are the two factors that affect localization performance. The results in Section 4.2.1 show that short geomagnetic sequences take less time to achieve localization, but localization errors may be high due to the lack of geomagnetic features. Long geomagnetic sequences may have sufficient features, but may also lead to large localization errors due to the possibility of the presence of same geomagnetic features at different locations. Additionally, long geomagnetic sequences require more time for localization. Considering localization error and time consumption, the suitable geomagnetic sequence length should be within a certain range regardless of scenarios and mobile devices. In Section 4.2.2, Figure 9 demonstrates that the localization accuracy is affected by hidden units. Large number of hidden units will lead to high computational complexity and overfitting. Therefore, it is important to choose both an adequate geomagnetic sequence length and number of hidden units.

In Section 4.3, we demonstrate the localization performance of our proposed algorithm in several aspects, including the localization error of step numbers, the boxplot and CDF of localization error, localization error of the 75th and 90th percentiles, and the mean and RMSE errors. Figure 10 and Figure 11 show the mean localization errors of different step numbers with Vivo X30 and Huawei Mate30 on the three trial paths, respectively. It can be seen that our proposed algorithm has the smallest localization error at different step numbers, even when different mobile devices on the same reference path are used. Figure 12 and Figure 13 illustrate the boxplot of localization error using Vivo X30 and Huawei Mate30, respectively. From the figures it is evident that our proposed algorithm can achieve considerable localization accuracy with both mobile devices on the same path. It implies that our multidimensional feature extraction method can alleviate the anomalies in the localization process, independent of the paths and mobile devices. Figure 14 and Figure 15 demonstrate the CDF of the localization error with Vivo X30 and Huawei Mate30, respectively. From the figures it is seen that when the accumulative probability accuracy is 80%, the localization error of our proposed algorithm with different devices in reference path 1 are 0.69 m and 0.80 m, in reference path 2 are 0.89 m and 0.80 m, in reference path 3 are 0.57 m and 0.76 m, respectively. On the other hand, the localization errors of the other state-of-the-art methods are all above 1 m. This implies that the localization accuracy of our proposed algorithm has significantly improved. Table 5 presents the localization error of the 75th and 90th percentiles at the three experimental paths with Vivo X30 and Huawei Mate30. It can be noticed that the localization errors of our proposed algorithm at the 75th and 90th percentiles are all less than 1 m, exhibiting great improvement over other algorithms. Table 6 and Table 7 show that the mean error and RMS error of our proposed algorithm are less than 0.7 m with different smartphones at all the reference paths. Moreover, we calculate the computation complexity of our proposed algorithm, which takes less time than the DTW algorithm. As can be seen from the above experimental results, our proposed algorithm can achieve better localization performance and robustness than the other state-of-the-art algorithms. The device heterogeneity problem and location ambiguity problem can be effectively solved. Moreover, our proposed algorithm can sufficiently extract geomagnetic features whether it is in a spacious area or a narrow area. Therefore, our proposed algorithm has high generality and practicality.

In future research, we will explore more complicated environments to verify the applicability of our proposed algorithm. More different mobile devices will be adopted to validate robustness. Deep learning models with higher accuracy will also be considered for exploration. Furthermore, since the PDR method still suffers from cumulative and drift errors of long-term localization, methods to improve it for precise indoor localization may be another direction for future research.

6. Conclusions

To solve the problem of location ambiguity caused by single magnetic sequence, we propose a coarse-to-fine localization method based on magnetic sequences and inertial data in this paper. Firstly, a geomagnetic multi-feature extraction algorithm is presented to extract more distinctive location features for accurate localization. Then, a novel deep learning-based model is proposed to realize indoor localization. Meanwhile, we use the PDR method based on inertial sensor data to solve location ambiguity, especially in the symmetric structure. Finally, fine localization is achieved through the particle filter using geomagnetic localization and PDR localization. Extensive experiments have been conducted at three different planned paths in two trial sites, the school library with an area of approximately 584 ${\mathrm{m}}^2$, and the school gym with an area of 1960 ${\mathrm{m}}^2$. Two different heterogeneous devices were utilized in the experiments, Vivo X30 and Huawei Mate30. The experiments demonstrate that localization performance can be affected by geomagnetic sequence length and hidden neuron network units. They also proved that our proposed method can achieve higher localization accuracy and more robustness than the state-of-the-art indoor localization methods with different mobile devices at different trial paths. In addition, the calculation complexity of our proposed algorithm is lower than that of the DTW algorithm. The localization system can effectively mitigate the accumulation errors of IMU estimation and location ambiguity caused by magnetic sequences. It has pervasiveness for different interferences, scenes and devices, which can satisfy the real-time and high accuracy localization requirements.