Fast Adaptive Beamforming for Weather Observations with Convolutional Neural Networks
Abstract
:1. Introduction
2. Method
2.1. Background on Digital Beamforming Methods
2.1.1. Deterministic Digital Beamforming
2.1.2. Adaptive Digital Beamforming
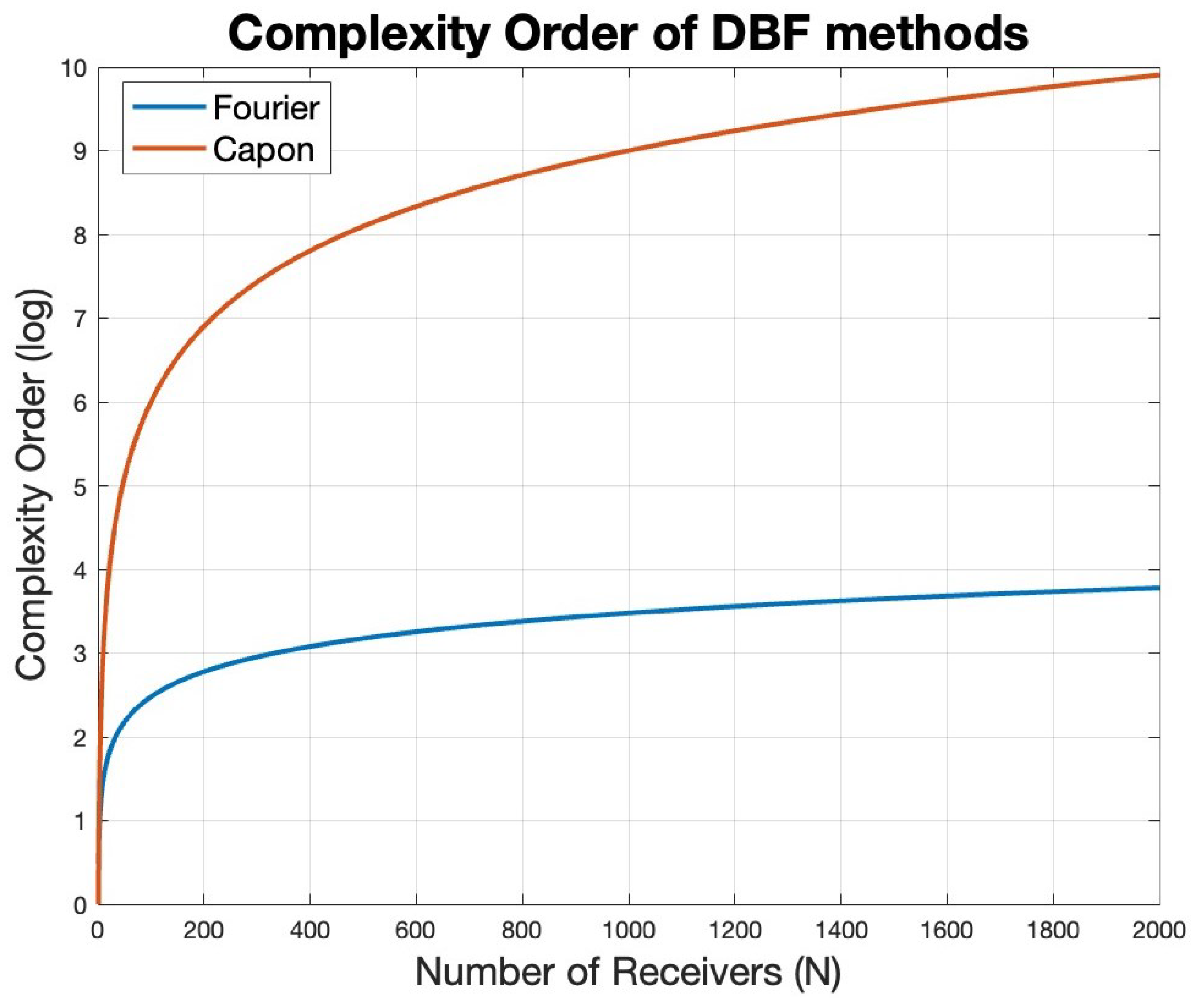
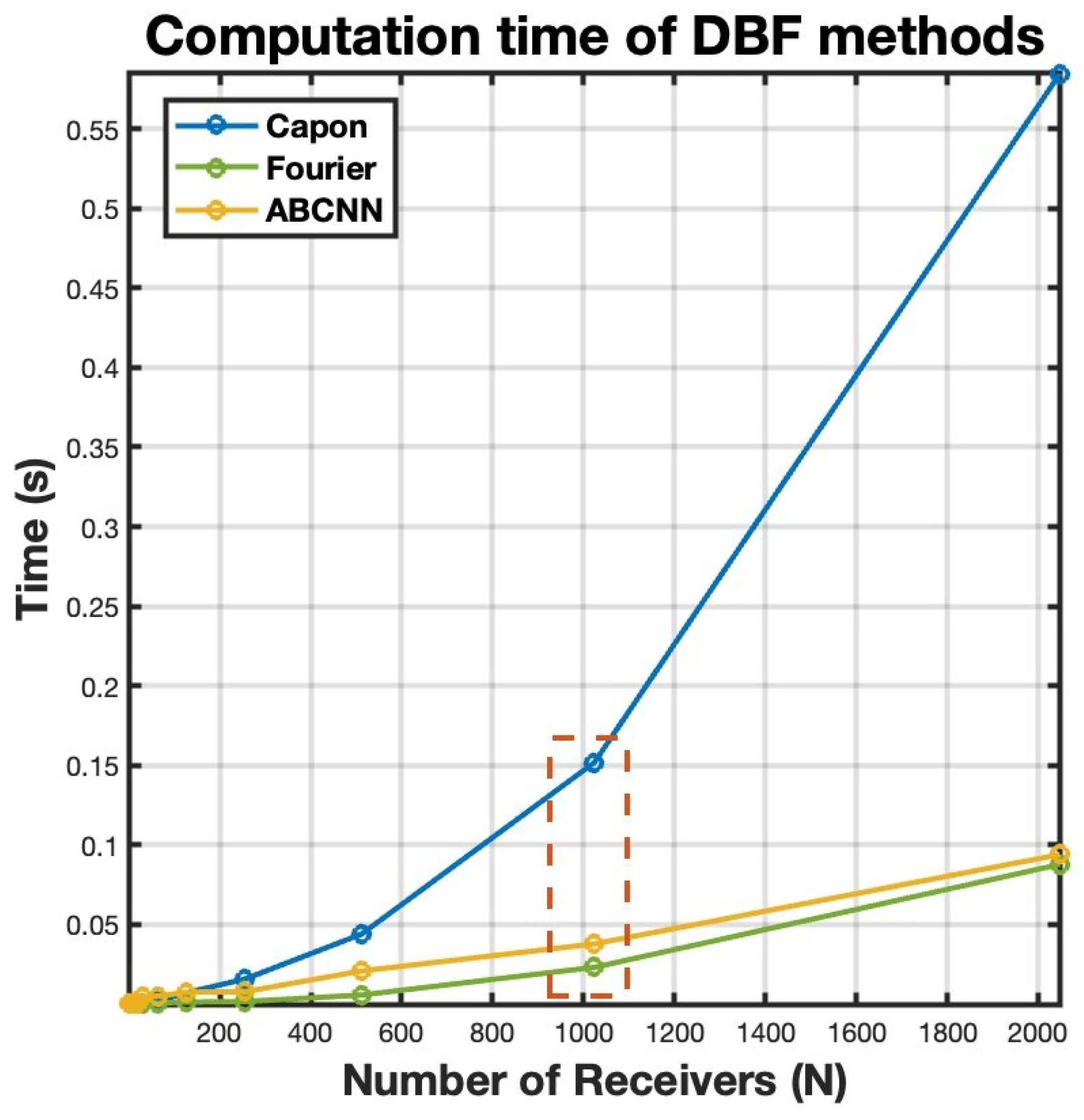
2.1.3. Computational Complexity
2.2. Simulation of Digital Array
2.3. Adaptive Beamforming with CNN
2.3.1. Architecture of the Neural Network
2.3.2. Activation Functions
2.3.3. Training Data
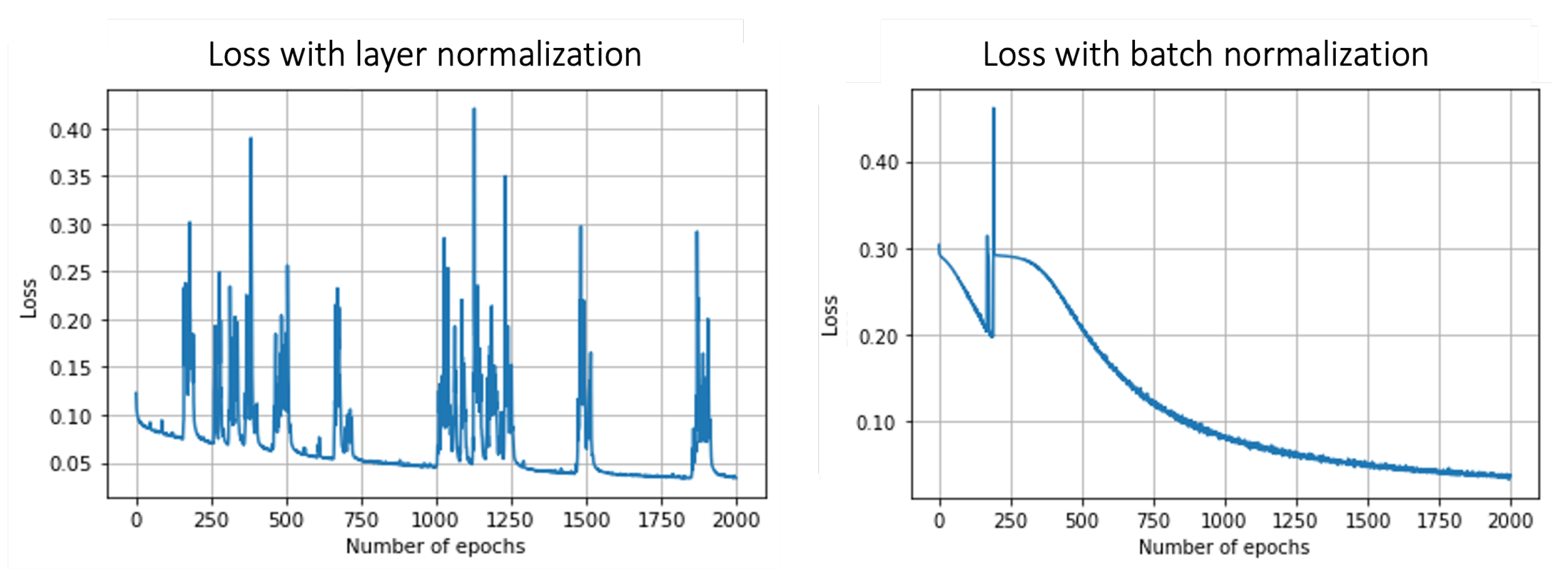
2.3.4. Training Strategy
3. Results
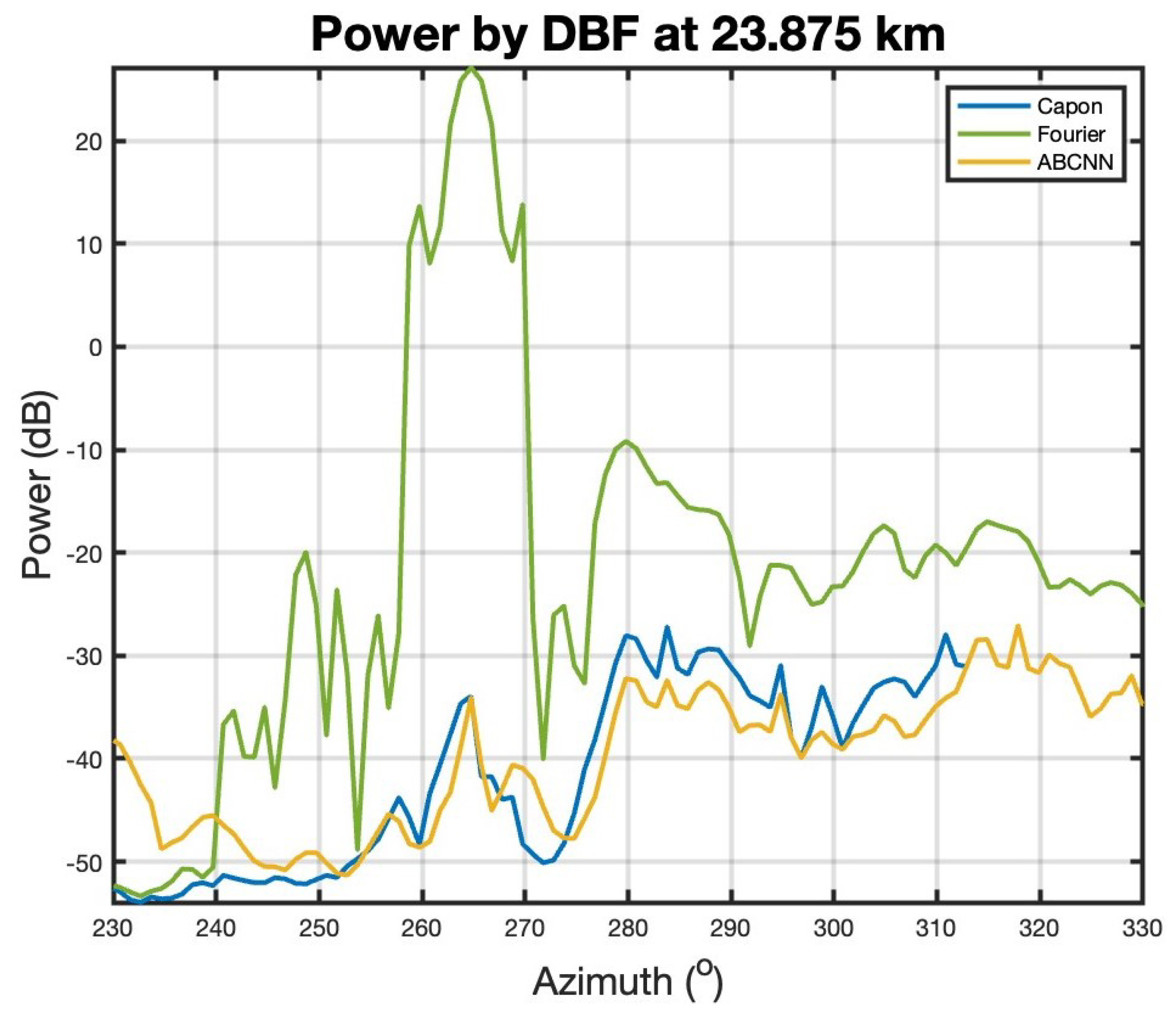
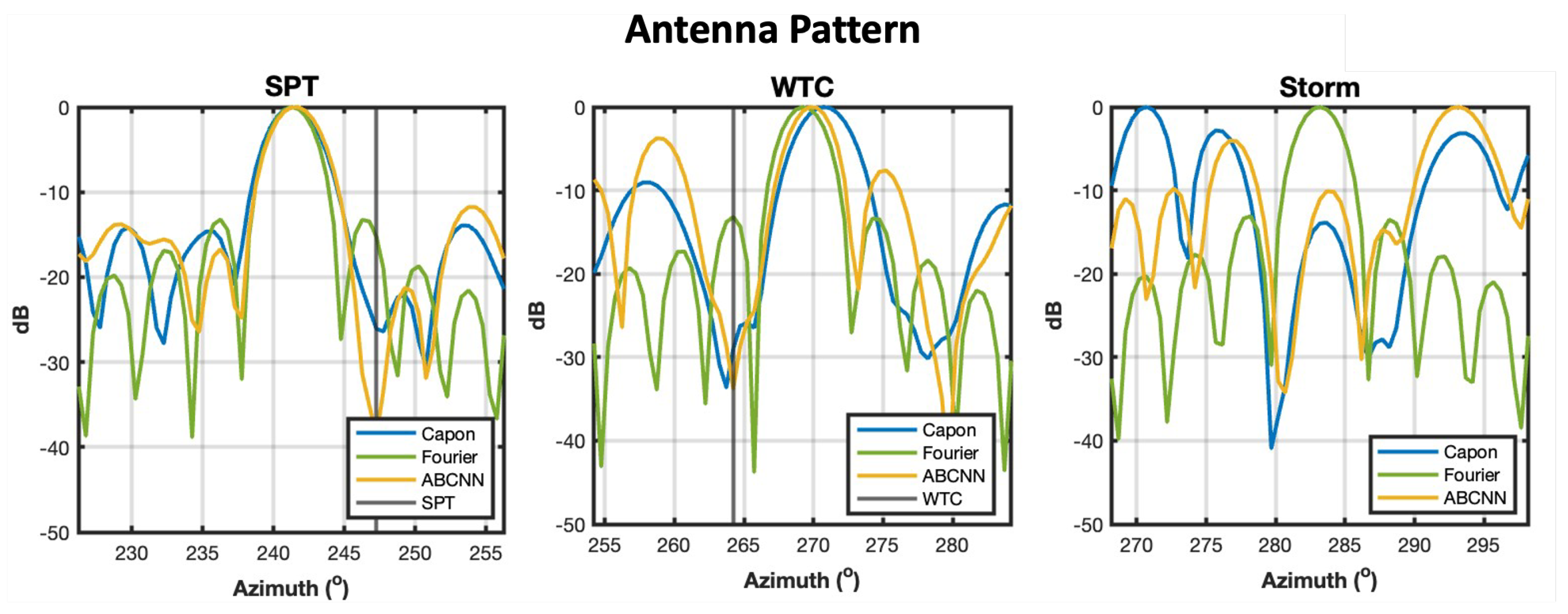
3.1. Qualitative Analysis
3.2. Quantitative Analysis
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zrnic, D.; Kimpel, J.; Forsyth, D.; Shapiro, A.; Crain, G.; Ferek, R.; Heimmer, J.; Benner, W.; McNellis, F.T.; Vogt, R. Agile-beam phased array radar for weather observations. Bull. Am. Meteorol. Soc. 2007, 88, 1753–1766. [Google Scholar] [CrossRef]
- Palmer, R.D.; Bodine, D.; Kollias, P.; Schvartzman, D.; Zrnić, D.; Kirstetter, P.; Zhang, G.; Yu, T.; Kumjian, M.; Cheong, B.; et al. A Primer on Phased Array Radar Technology for the Atmospheric Sciences. Bull. Am. Meteorol. Soc. 2022, 103, E2391–E2416. [Google Scholar] [CrossRef]
- Schvartzman, D. Signal Processing Techniques and Concept of Operations for Polarimetric Rotating Phased Array Radar. Ph.D. Thesis, The University of Oklahoma, Norman, OK, USA, 2020. [Google Scholar]
- Isom, B.; Palmer, R.; Kelley, R.; Meier, J.; Bodine, D.; Yeary, M.; Cheong, B.L.; Zhang, Y.; Yu, T.Y.; Biggerstaff, M.I. The atmospheric imaging radar: Simultaneous volumetric observations using a phased array weather radar. J. Atmos. Ocean. Technol. 2013, 30, 655–675. [Google Scholar] [CrossRef]
- Palmer, R.D.; Yeary, M.B.; Schvartzman, D.; Salazar-Cerreno, J.L.; Fulton, C.; McCord, M.; Cheong, B.; Bodine, D.; Kirstetter, P.; Sigmarsson, H.H.; et al. Horus—A Fully Digital Polarimetric Phased Array Radar for Next-Generation Weather Observations. IEEE Trans. Radar Syst. 2023, 1, 96–117. [Google Scholar] [CrossRef]
- Hondl, K.; Weber, M. NOAA’s Meteorological Phased Array Radar Research Program. In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Palmer, R.D.; Gopalam, S.; Yu, T.Y.; Fukao, S. Coherent radar imaging using Capon’s method. Radio Sci. 1998, 33, 1585–1598. [Google Scholar] [CrossRef]
- Yu, T.Y.; Palmer, R.D.; Hysell, D.L. A simulation study of coherent radar imaging. Radio Sci. 2000, 35, 1129–1141. [Google Scholar] [CrossRef]
- Mahmoud, K.R.; Eladawy, M.I.; Bansal, R.; Zainud-Deen, S.H.; Ibrahem, S.M. Analysis of uniform circular arrays for adaptive beamforming applications using particle swarm optimization algorithm. Int. J. RF Microw. Comput.-Aided Eng. 2008, 18, 42–52. [Google Scholar] [CrossRef]
- Zaman, M.A.; Abdul Matin, M. Nonuniformly spaced linear antenna array design using firefly algorithm. Int. J. Microw. Sci. Technol. 2012, 2012, 256759. [Google Scholar] [CrossRef]
- Lu, Y.; Yeo, B.K. Adaptive wide null steering for digital beamforming array with the complex coded genetic algorithm. In Proceedings of the 2000 IEEE International Conference on Phased Array Systems and Technology (Cat. No. 00TH8510), Dana Point, CA, USA, 21–25 May 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 557–560. [Google Scholar]
- McGovern, A.; Lagerquist, R.; Gagne, D.J.; Jergensen, G.E.; Elmore, K.L.; Homeyer, C.R.; Smith, T. Making the black box more transparent: Understanding the physical implications of machine learning. Bull. Am. Meteorol. Soc. 2019, 100, 2175–2199. [Google Scholar] [CrossRef]
- Carbonell, J.G.; Michalski, R.S.; Mitchell, T.M. An overview of machine learning. Mach. Learn. 1983, 1, 3–23. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Luijten, B.; Cohen, R.; de Bruijn, F.J.; Schmeitz, H.A.; Mischi, M.; Eldar, Y.C.; van Sloun, R.J. Adaptive ultrasound beamforming using deep learning. IEEE Trans. Med. Imaging 2020, 39, 3967–3978. [Google Scholar] [CrossRef] [PubMed]
- Jalal, B.; Yang, X.; Liu, Q.; Long, T.; Sarkar, T.K. Fast and robust variable-step-size LMS algorithm for adaptive beamforming. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1206–1210. [Google Scholar] [CrossRef]
- Sallam, T.; Abdel-Rahman, A.B.; Alghoniemy, M.; Kawasaki, Z.; Ushio, T. A neural-network-based beamformer for phased array weather radar. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5095–5104. [Google Scholar] [CrossRef]
- Kim, Y.S.; Schvartzman, D.; Palmer, R.D.; Yu, T.Y. Fast Adaptive Beamforming Using Deep Learning for Digital Phased Array Radars. In Proceedings of the 2022 IEEE International Symposium on Phased Array Systems & Technology (PAST), Waltham, MA, USA, 11–14 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar]
- Barrachina, J.A. NEGU93/cvnn: Complex-Valued Neural Networks. Ph.D. Thesis, Université Paris-Saclay, Paris, France, 2022. [Google Scholar]
- Gulli, A.; Pal, S. Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 20 December 2022).
- Adachi, T.; Mashiko, W. High temporal-spatial resolution observation of tornadogenesis in a shallow supercell associated with Typhoon Hagibis (2019) using phased array weather radar. Geophys. Res. Lett. 2020, 47, e2020GL089635. [Google Scholar] [CrossRef]
- Schvartzman, D.; Torres, S.M.; Yu, T.Y. Distributed Beams: Concept of Operations for Polarimetric Rotating Phased Array Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9173–9191. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Rauber, R.M.; Burgess, D.W.; Albrecht, B.; Ellis, S.M.; Richardson, Y.P.; Jorgensen, D.P.; Frasier, S.J.; Chilson, P.; Palmer, R.D.; et al. Radar in atmospheric sciences and related research: Current systems, emerging technology, and future needs. Bull. Am. Meteorol. Soc. 2014, 95, 1850–1861. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Luenberger, D.G.; Ye, Y. Linear and Nonlinear Programming; Springer: Berlin/Heidelberg, Germany, 1984; Volume 2. [Google Scholar]
- Du, D.Z.; Ko, K.I. Theory of Computational Complexity; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 58. [Google Scholar]
- Zrnic, D. Simulation of weatherlike Doppler spectra and signals. J. Appl. Meteorol. Climatol. 1975, 14, 619–620. [Google Scholar] [CrossRef]
- Schvartzman, D.; Curtis, C.D. Signal processing and radar characteristics (SPARC) simulator: A flexible dual-polarization weather-radar signal simulation framework based on preexisting radar-variable data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 135–150. [Google Scholar] [CrossRef]
- Helmus, J.J.; Collis, S.M. The Python ARM Radar Toolkit (Py-ART), a library for working with weather radar data in the Python programming language. J. Open Res. Softw. 2016, 4, e25. [Google Scholar] [CrossRef]
- Schvartzman, D.; Palmer, R.; Yu, T.Y.; Reinke, R.; Nai, F. A Pattern Synthesis Method for Polarimetric Weather Observations with the All-Digital Horus Phased Array Radar. In Proceedings of the 102nd American Meteorological Society Annual Meeting, Houston, TX, USA, 23–27 January 2022; AMS: Boston, MA, USA, 2022. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Schvartzman, D. Mitigation of Wind Turbine Clutter With Digital Phased Array Radar. IEEE Access 2023, 11, 12911–12924. [Google Scholar] [CrossRef]
- Szandała, T. Review and comparison of commonly used activation functions for deep neural networks. In Bio-Inspired Neurocomputing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 203–224. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; PMLR: Westminster, UK, 2015; pp. 448–456. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980s. [Google Scholar]
- Bock, S.; Weiß, M. A proof of local convergence for the Adam optimizer. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]



| Name of Algorithm | AI Type | Input | Output | Characteristics |
|---|---|---|---|---|
| ABLE | DL with Dense layers | Real and Imaginary parts of IQ signals | Downstream system | Learning process can be heavy, and it may result in saturation easily due to dense layers |
| Fast and Robust VSS-LMS | LSM | Received and reference signals | Array patterns | Lower complexity of the neural network |
| RBFNN | DL | Real and Imaginary parts of covariance matrix | Real and Imaginary parts of inversed covaraince matrix | Doubled length of the network due to complex value separation |
| DLAF | DL with Dense layers | Complex valued IQ signals | Complex valued beamforming weights | Easy saturation during the training and lack of flexibility of network and training due to the limited library |
| ABCNN | CNN | Phase and amplitude of IQ signals | Phase and amplitude of beamforming weights | Preserves phase information and learns the spatial relation in data |
| Parameter | Values |
|---|---|
| Operation Frequency (f) | 3 GHz (S-band) |
| Range resolution | 250 m |
| Number of antenna element (N) | 32 |
| Spacing (d) | 16.4 mm |
| Number of sample (M) | 64 |
| Range coverage | 0.125 km–35.125 km |
| Azimuth coverage | 0–360 |
| Type | Range (km) | Azimuth () |
|---|---|---|
| SPT | 20.375 | 247.25 |
| SPT | 23.625 | 248.26 |
| SPT | 25.375 | 279.74 |
| SPT | 27.375 | 277.24 |
| WTC | 21.625 | 264.23 |
| WTC | 22.125 | 263.23 |
| WTC | 22.625 | 261.76 |
| WTC | 23.125 | 260.76 |
| WTC | 23.625 | 259.26 |
| WTC | 24.375 | 259.26 |
| WTC | 25.125 | 259.26 |
| WTC | 26.125 | 259.26 |
| Clutter Type | Clutter Location () | Pointing Angle () | Capon (dB) | Fourier (dB) | ABCNN (dB) |
|---|---|---|---|---|---|
| WTC | 264.23 | 263.23 | −28.53 | −1.03 | −26.82 |
| WTC | 264.23 | 265.25 | −16.04 | −1.04 | −16.04 |
| WTC | 264.23 | 268.22 | −30.00 | −19.56 | −34.56 |
| WTC | 264.23 | 269.23 | −28.97 | −13.18 | −33.76 |
| SPT | 247.25 | 241.24 | −26.09 | −15.23 | −38.69 |
| SPT | 247.25 | 246.18 | −20.09 | −1.02 | −20.09 |
| SPT | 247.25 | 253.24 | −28.71 | −16.52 | −24.83 |
| SPT | 247.25 | 255.18 | −27.93 | −20.18 | −25.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-S.; Schvartzman, D.; Yu, T.-Y.; Palmer, R.D. Fast Adaptive Beamforming for Weather Observations with Convolutional Neural Networks. Remote Sens. 2023, 15, 4129. https://doi.org/10.3390/rs15174129
Kim Y-S, Schvartzman D, Yu T-Y, Palmer RD. Fast Adaptive Beamforming for Weather Observations with Convolutional Neural Networks. Remote Sensing. 2023; 15(17):4129. https://doi.org/10.3390/rs15174129
Chicago/Turabian StyleKim, Yoon-SL, David Schvartzman, Tian-You Yu, and Robert D. Palmer. 2023. "Fast Adaptive Beamforming for Weather Observations with Convolutional Neural Networks" Remote Sensing 15, no. 17: 4129. https://doi.org/10.3390/rs15174129
APA StyleKim, Y.-S., Schvartzman, D., Yu, T.-Y., & Palmer, R. D. (2023). Fast Adaptive Beamforming for Weather Observations with Convolutional Neural Networks. Remote Sensing, 15(17), 4129. https://doi.org/10.3390/rs15174129






