A Cascade Network for Pattern Recognition Based on Radar Signal Characteristics in Noisy Environments
Abstract
:1. Introduction
- Due to the uncertainty of scenarios, radar pulses may originate from different noise environments or different radars, and their parameter ranges are beyond the scope of “training data”, belonging to “unknown signals”. This seriously interferes with machine learning algorithms that are purely data-driven.
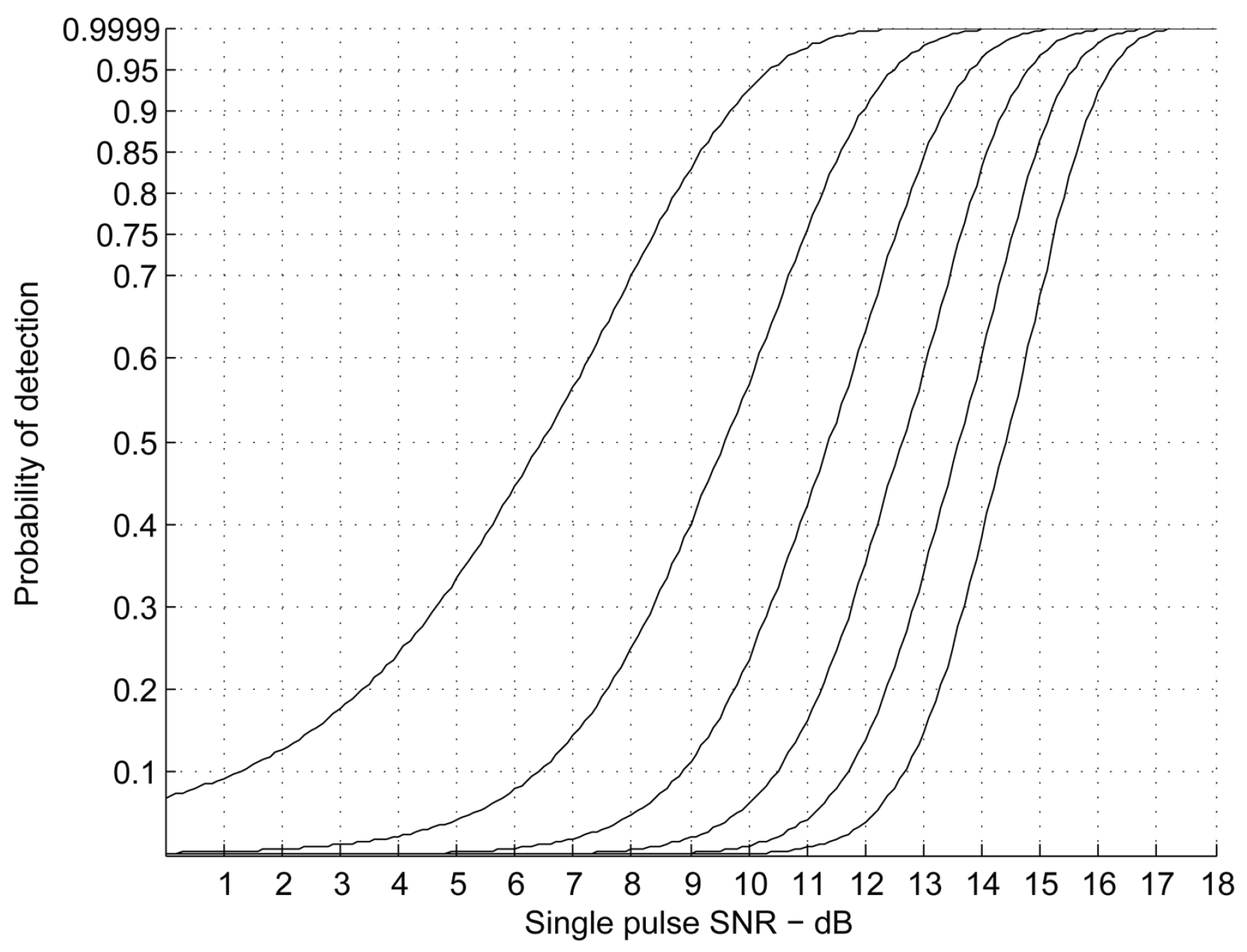
- As the signal-to-noise ratio decreases, a large amount of redundant or erroneous information will be mixed into the received radar pulses, resulting in the wrong parameters. At this point, the effective parameters cannot be determined, and originally traceable signals become chaotic.
- Defective radar signals differ from images in that the encoding and modulation styles of the signals are more diverse. The two types of inputs exhibit significant differences in terms of characteristics such as size, location, and shape. Noise has a more pronounced impact on signals, and conventional deep learning networks for computer vision are challenging to use to effectively process these differences. The comparison of a signal in an environment with significant noise is shown in Figure 2. It can be seen that the radar pulse pattern is difficult to distinguish under noise.
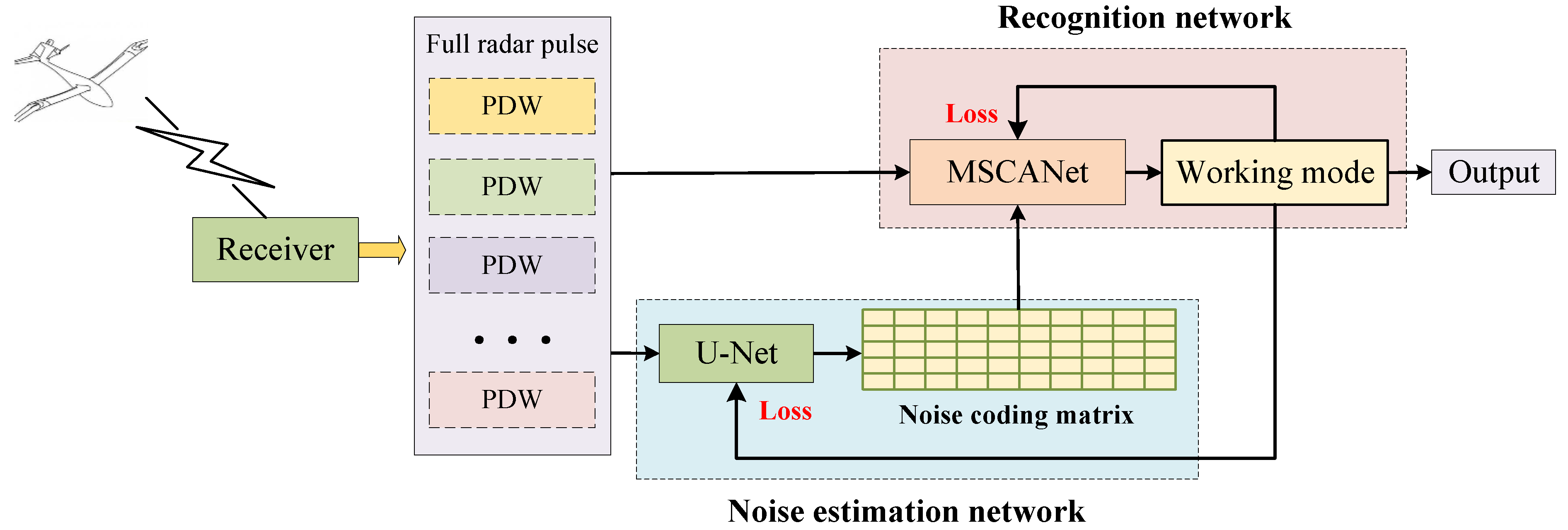
- We employ a cascade learning approach with a noise estimation network and a recognition network, enhancing the algorithm’s adaptability in environments with strong noise.
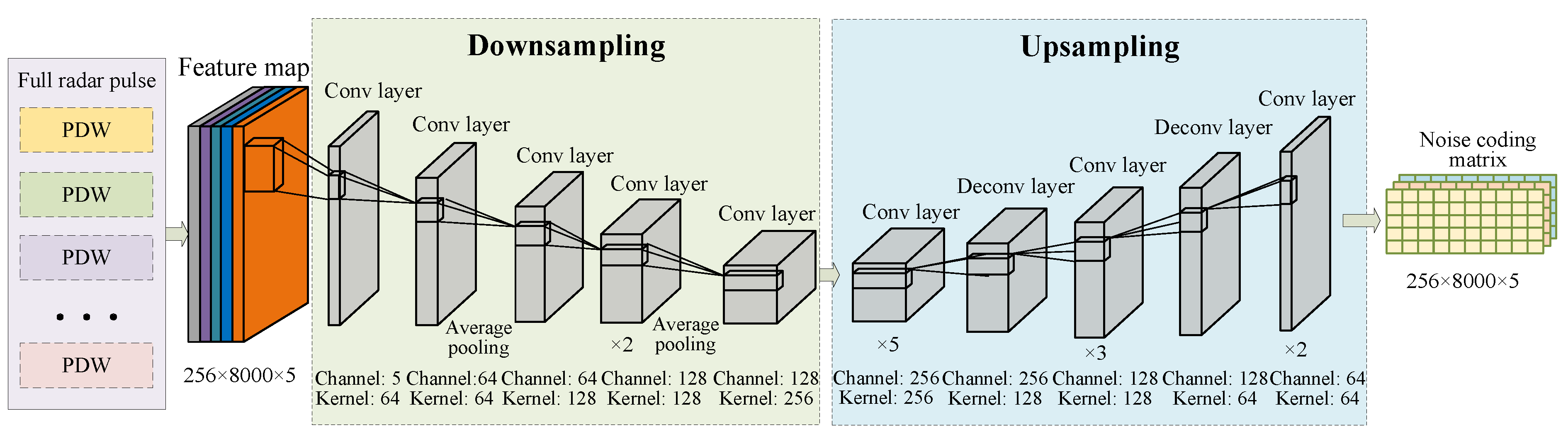
- A noise estimation network based on U-Net is designed, which utilizes a symmetrical structure of upsampling and downsampling to extract and reconstruct noise features. The network achieves adaptive noise mapping relationships in different channels and spatial areas.
- The MSCANet, which is used to address the characteristics of radar pulse signals, is presented. The network is augmented with both deep-wise group convolution, multi-scale convolution, and self-attention mechanisms, which serve to improve the network’s feature extraction capabilities and make the model more lightweight.
2. Related Work
- Recognition of unknown signals. In [12,13], the authors propose a comprehensive recognition approach based on both traditional classifiers and deep learning networks. By utilizing the classifier to assist in network training, the central vectors of known data are deduced and thus the feasibility of recognizing unknown signals through known ones is verified.
- Interpretability of recognition. This problem is a challenging research issue in various fields. From the perspective of integrating knowledge-driven and data-driven approaches, Refs. [16,17] have defined the feature representation of radar signals in deep learning networks, and have achieved embedded knowledge through prior knowledge assistance in network training.
- Low signal-to-noise ratio (SNR). It must be considered that SNR is a critical factor in the field of signal processing [18]. Reference [19] utilizes the characteristics of residual networks and adopts the naive method of deepening the network to improve recognition performance under a low SNR, with no further improvement possible after network saturation. In [20], the authors employ a fusion of CNN and the long short-term memory (LSTM) network to retain signal features and semantic relationships, but this method only focuses on short-term temporal dependencies and cannot extract global information. In [21], the authors propose a lightweight combinational neural network, which uses two networks for pre-recognition and fine recognition. The SEBlock attention module is embedded in the network to suppress noise interference. This method is suitable for multi-label classification tasks.
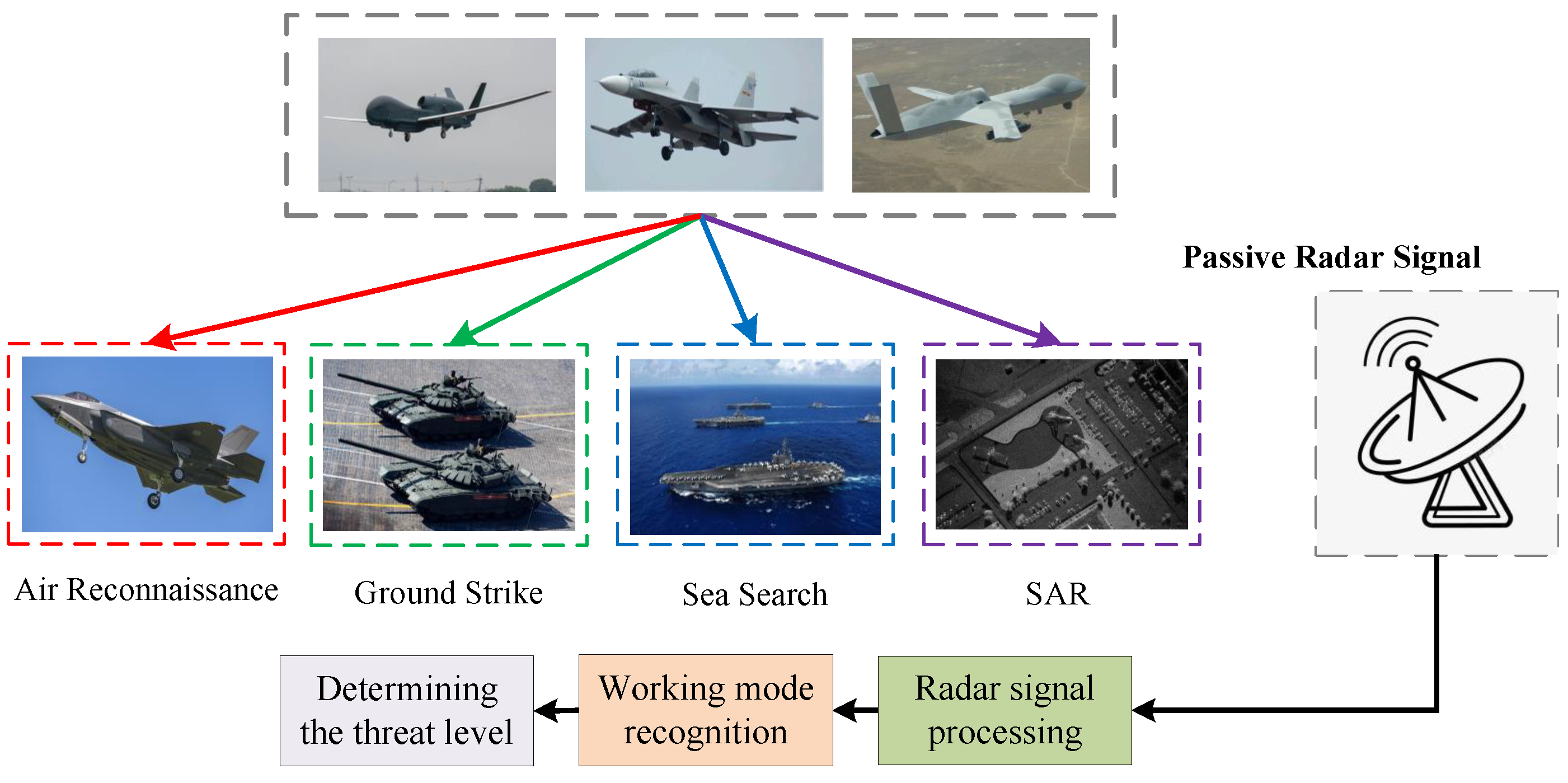
3. Radar Signal Detection in Noisy Environments
4. Algorithm Model and Implementation
4.1. Dual-Network Cascade Model
4.2. Noise Estimation Network Based on U-Net
- Each channel in the radar full pulse is affected by noise to different degrees, so it is necessary to evaluate the noise separately.
- The function describing the effect of noise on discrete radar pulses can be defined as an indicative function rather than a continuous function, so the whole sequence cannot be evaluated with a continuous mapping relationship.
- The purpose of noise evaluation is to help the classification network to recognize the working mode rather than to obtain certain information. The output noise coding sequence should match the input.
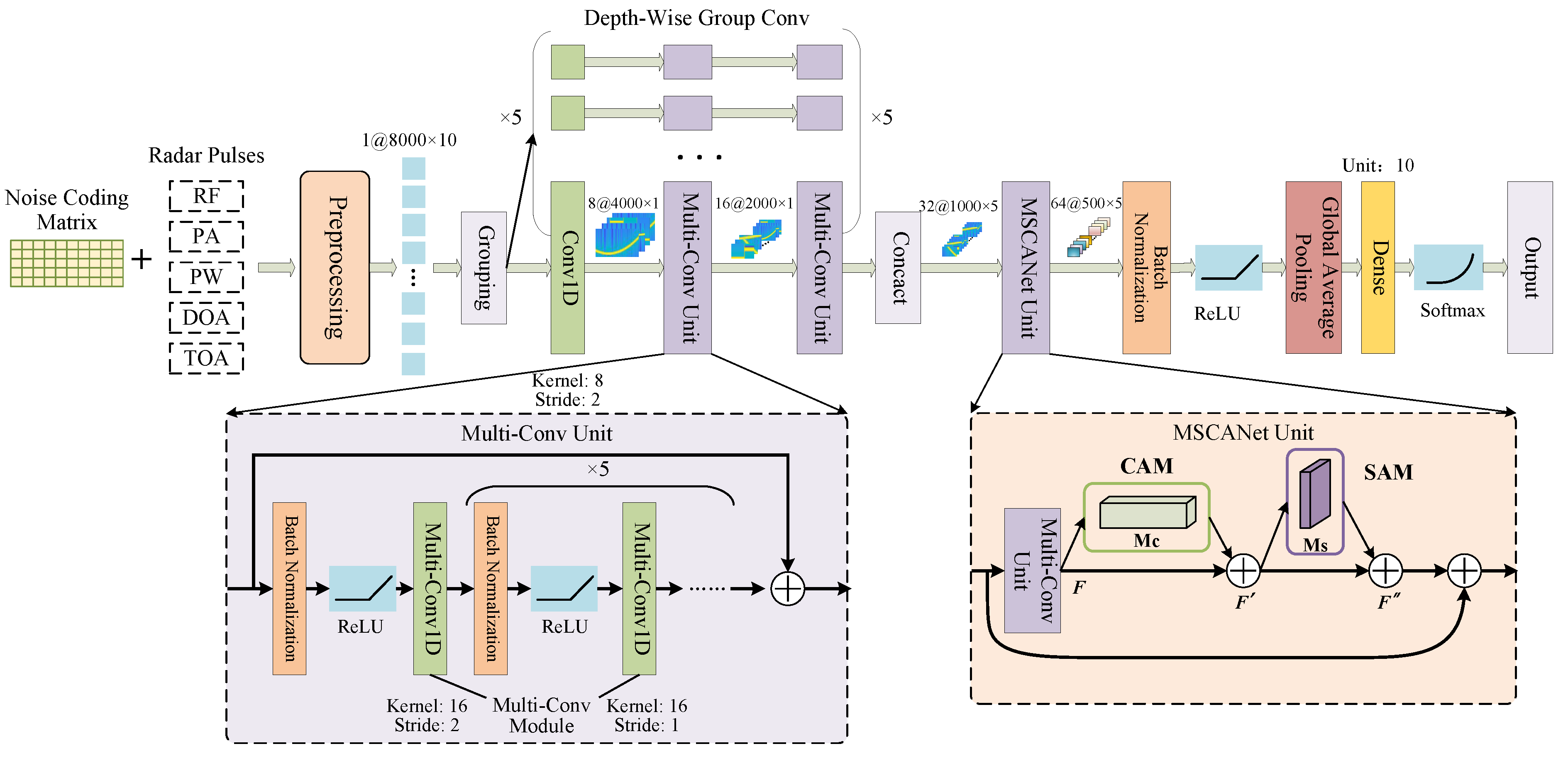
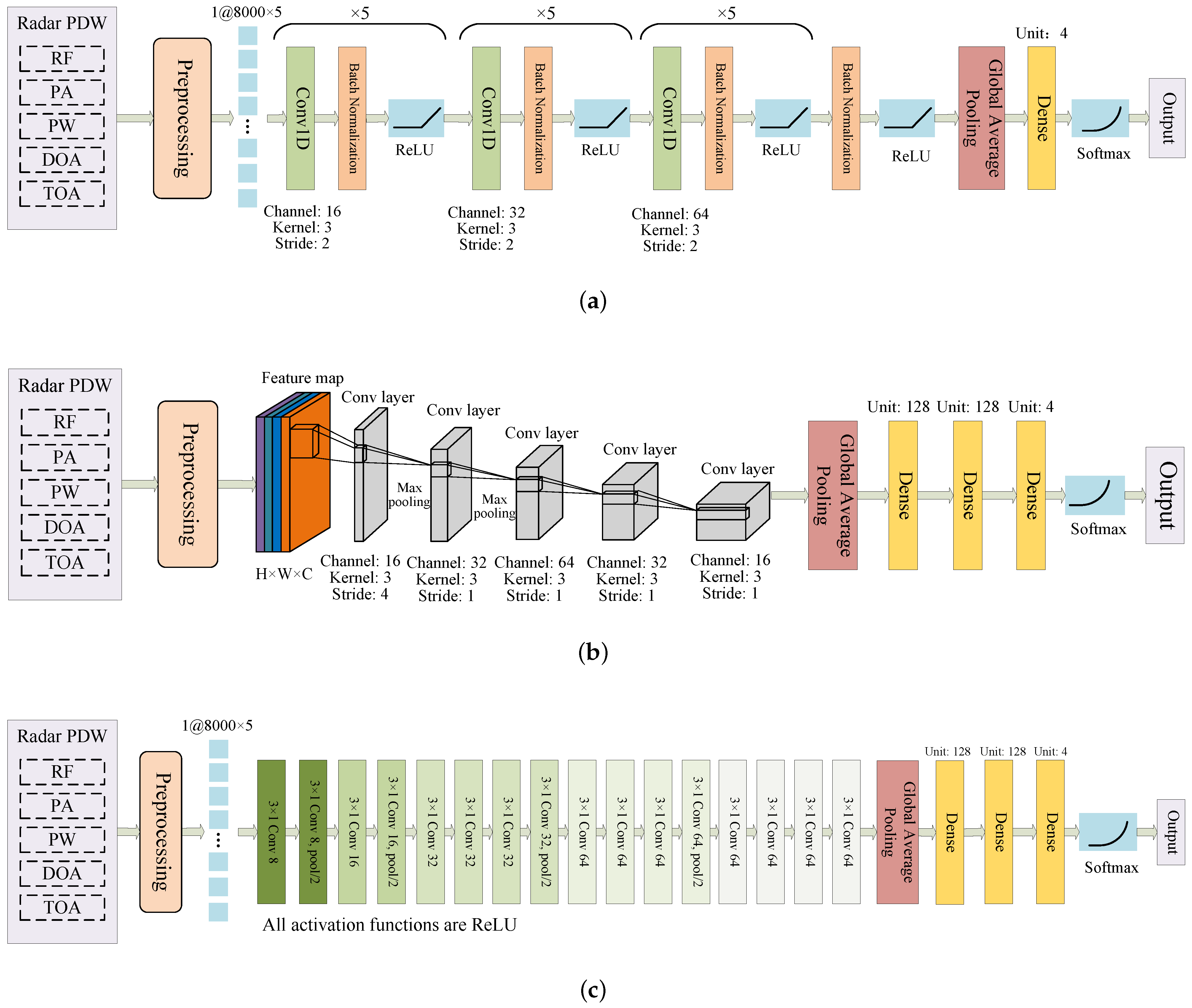
4.3. Recognition Network Based on MSCANet
4.3.1. Depth-Wise Group Convolution
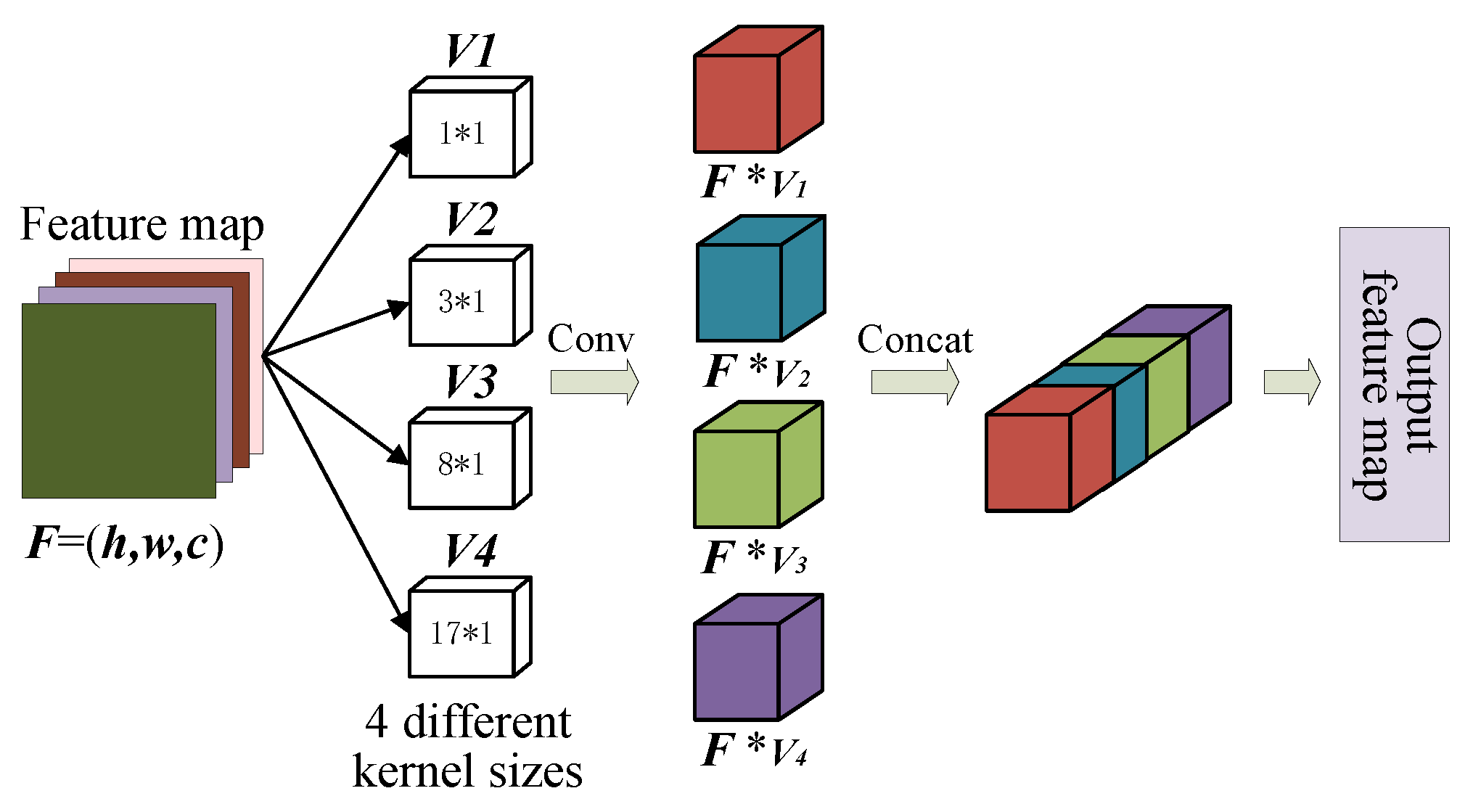
4.3.2. Multi-Scale 1D Convolution
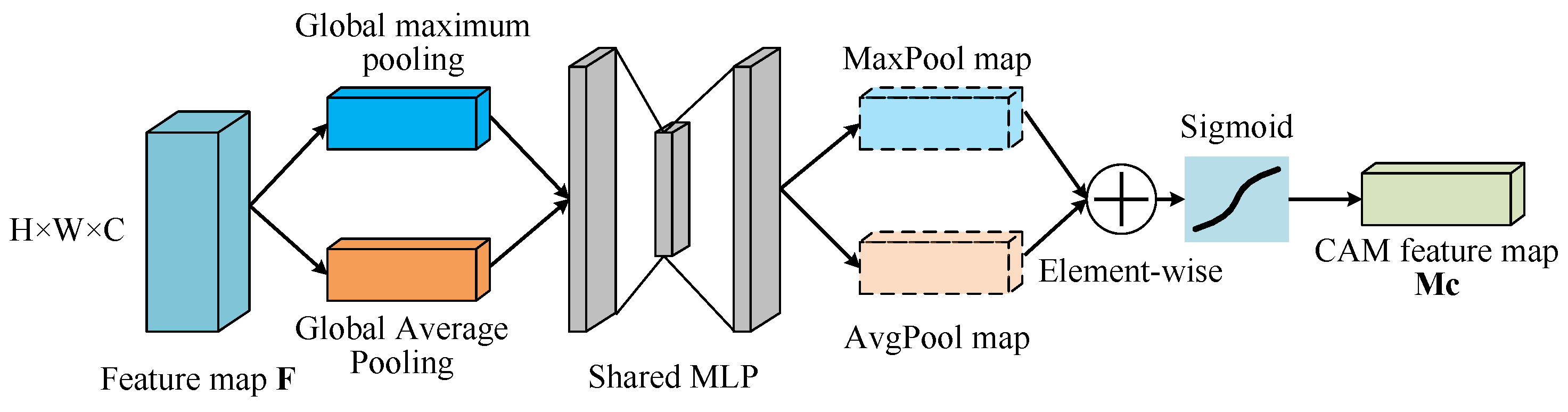
4.3.3. Self-Attention Mechanism
5. Experiments and Results
- Considering different application scenarios, 10 kinds of typical radar working modes are constructed for the demonstration of subsequent experiments.
- The performance of traditional machine learning algorithms and deep learning algorithms is tested to prove the limitations of conventional artificial intelligence algorithms in noisy environments.
- By introducing the noise estimation sub-network, the performance of the single classification model and dual-network cascade model is compared.
- The performance of the proposed MSCANet network is compared with that of the classical deep learning network, and the influence of noise on the radar working mode is analyzed.
5.1. Dataset
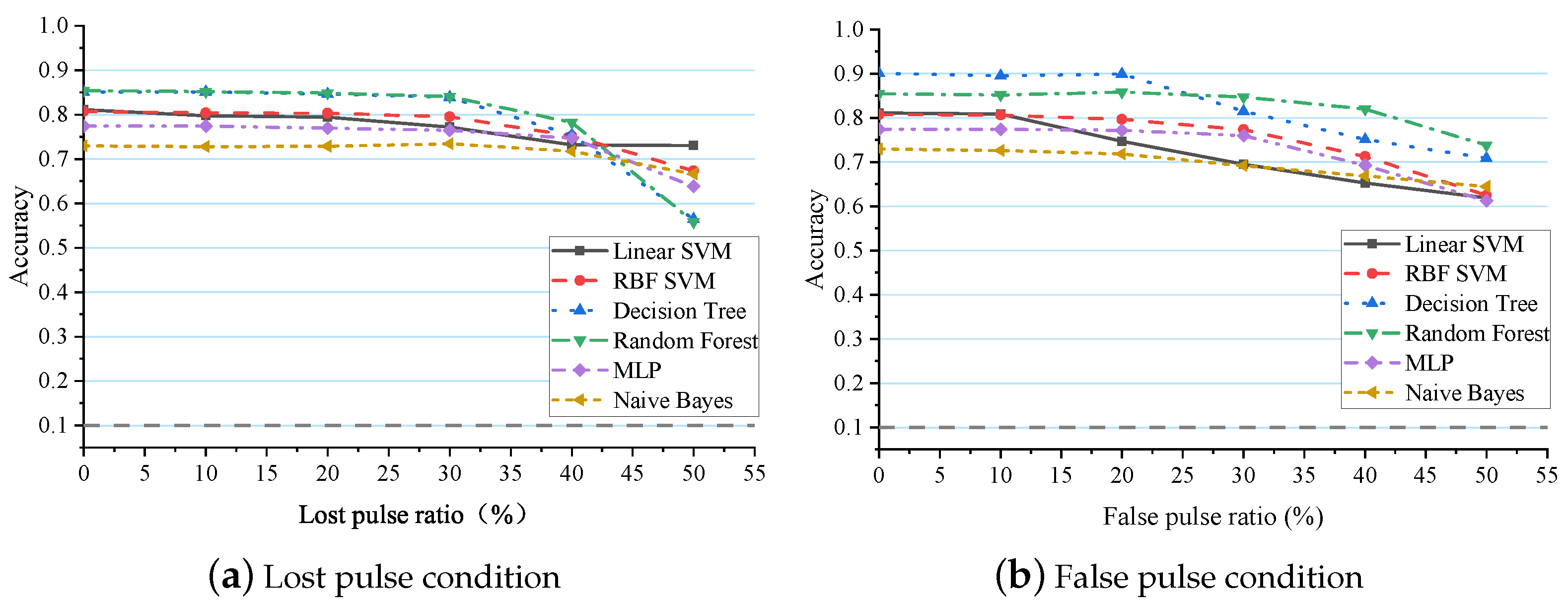
5.2. The Performance of Traditional Radar Target Recognition Algorithms
5.3. The Performance of Conventional Artificial Intelligence Algorithms
5.3.1. Traditional Machine Learning Algorithms
5.3.2. Conventional Deep Learning Algorithms
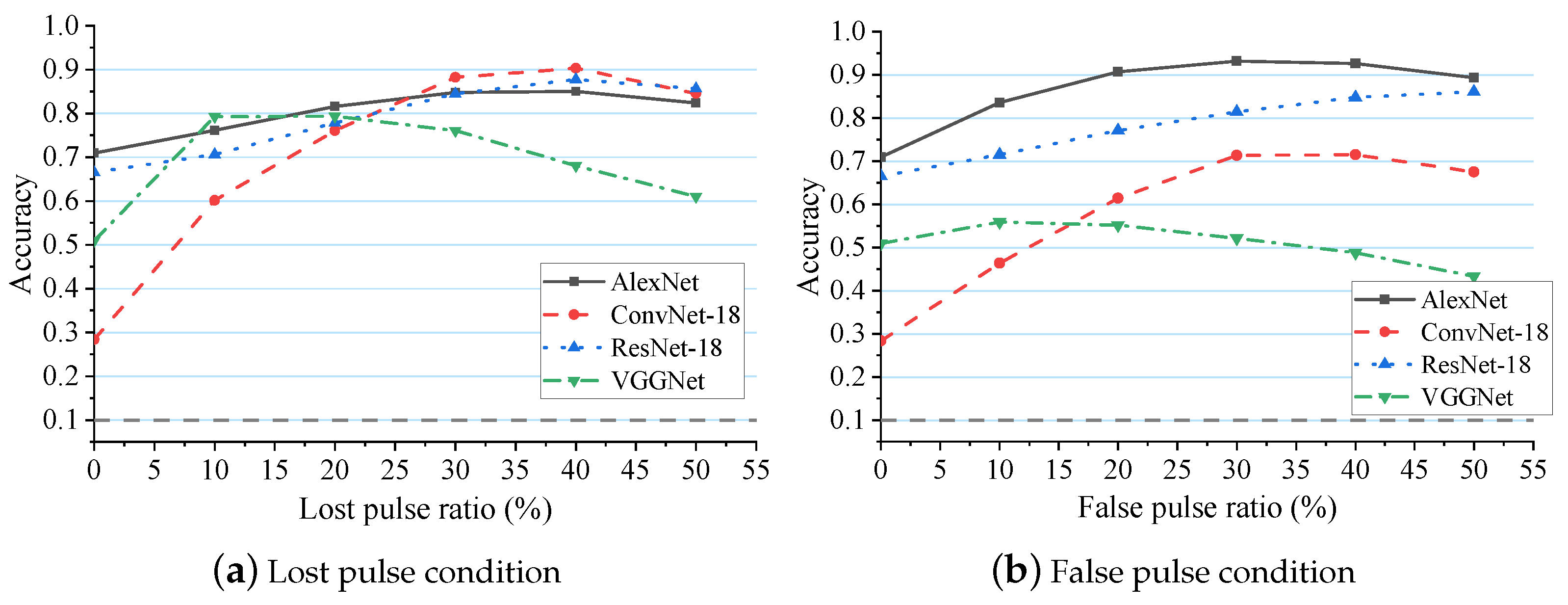
- Through experiments, we found that optimizing ResNet only resulted in an approximate 4% improvement in recognition accuracy, and the trend of accuracy change with varying lost pulses remained largely unchanged, indicating limited impact.
- Other networks using their original structures could validate that classic image recognition networks are not directly applicable to radar pattern recognition in noisy environments.
- When evaluating the performance of the noise estimation sub-network, using the optimized ResNet, as well as the original ConvNet, AlexNet, and VGGNet as baseline models, can provide more comprehensive results.
5.4. The Performance of the Proposed Noise Estimation Sub-Network
5.5. The Performance of Proposed MSCANet
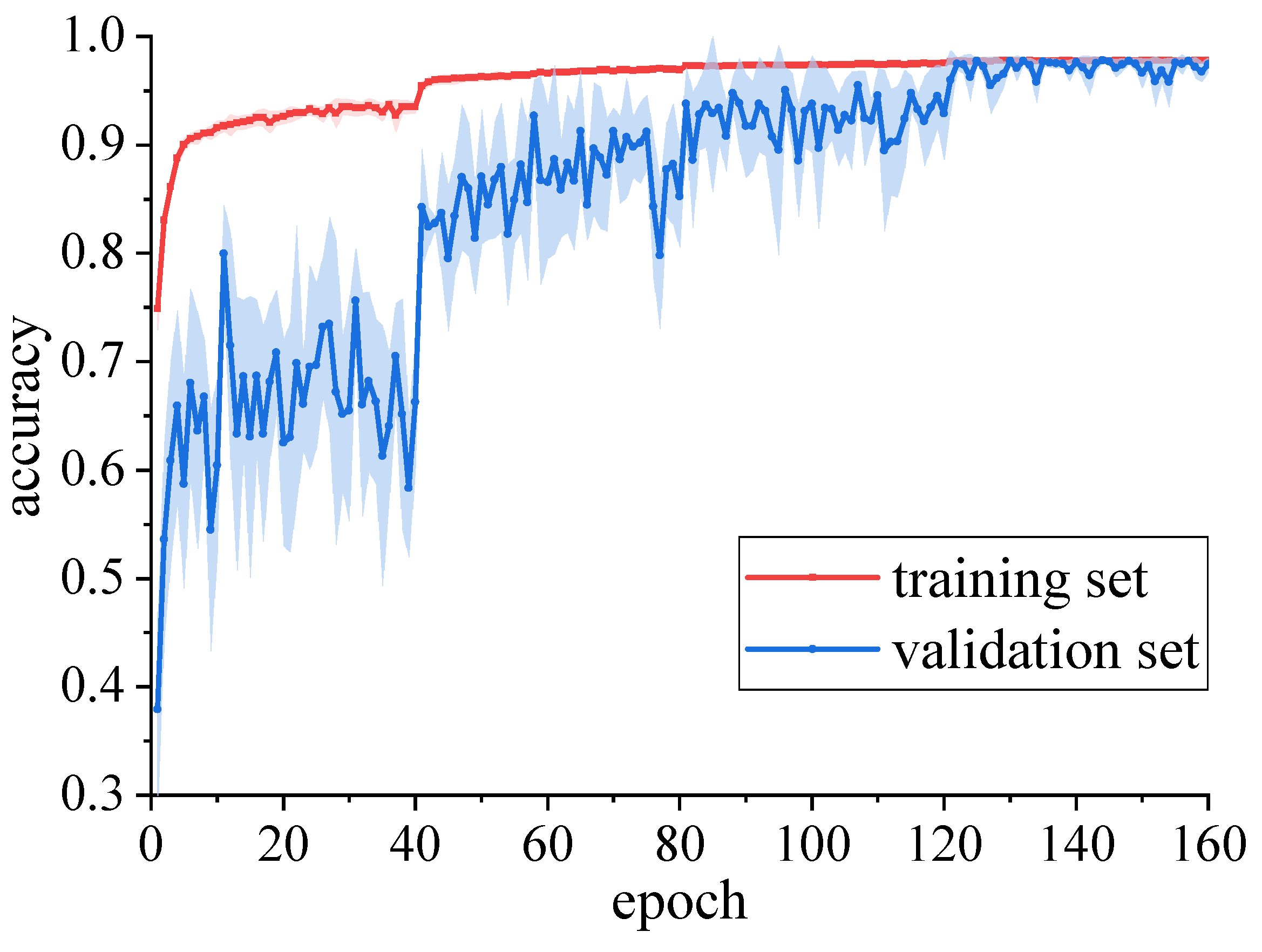
5.5.1. In-Training Views
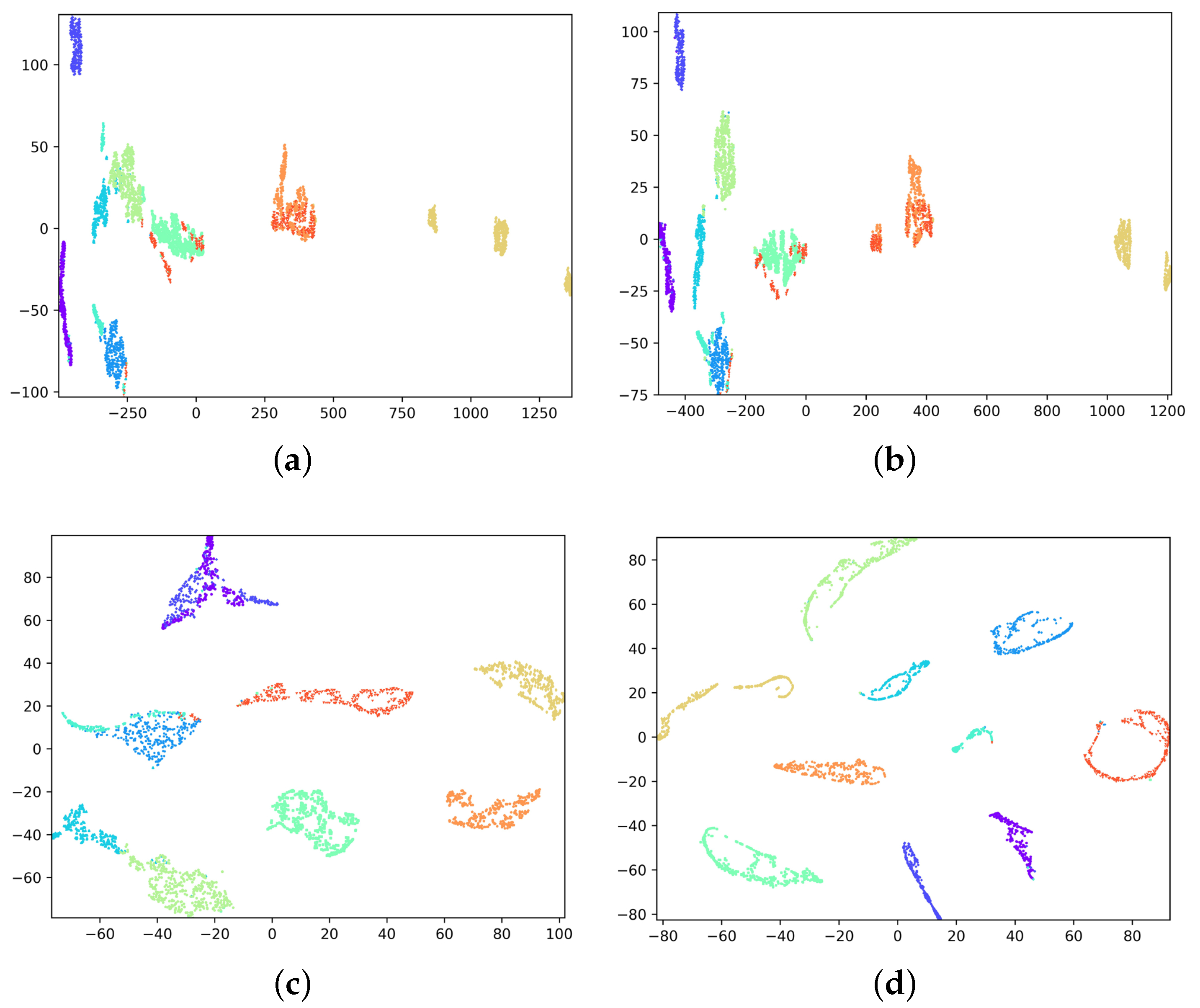
5.5.2. MSCANet Recognition Performance
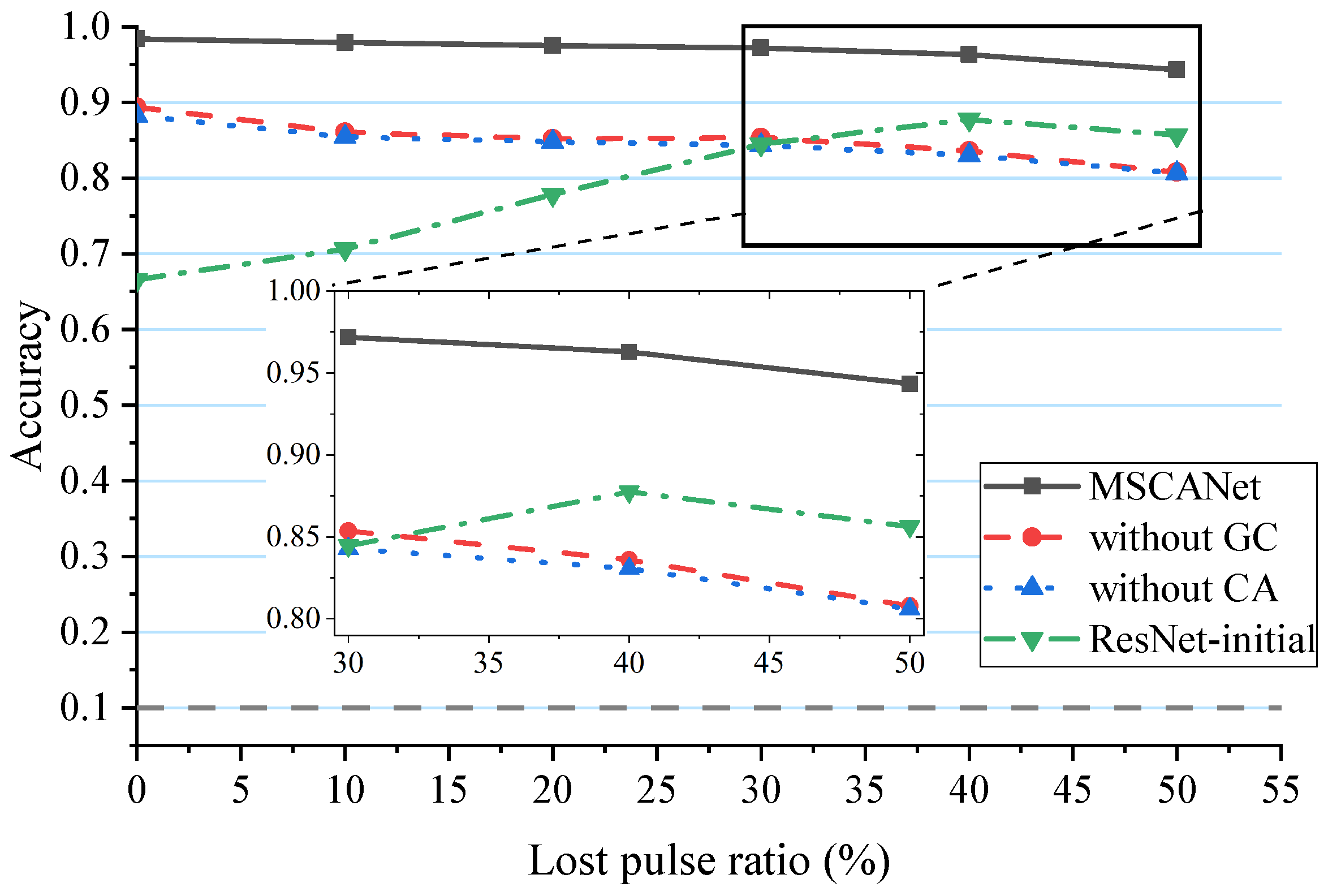
5.5.3. Ablation Study
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Martino, A. Introduction to Modern EW Systems, 2nd ed.; Electronic Warfare Library, Artech House: Boston, MA, USA, 2018; p. xi. 463p. [Google Scholar]
- Weber, M.E.; Cho, J.Y.; Thomas, H.G. Command and Control for Multifunction Phased Array Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5899–5912. [Google Scholar] [CrossRef]
- Wang, S.; Gao, C.; Zhang, Q.; Dakulagi, V.; Zeng, H.; Zheng, G.; Bai, J.; Song, Y.; Cai, J.; Zong, B. Research and Experiment of Radar Signal Support Vector Clustering Sorting Based on Feature Extraction and Feature Selection. IEEE Access 2020, 8, 93322–93334. [Google Scholar] [CrossRef]
- Weichao, X.; Huadong, L.; Jisheng, D.; Yanzhou, Z. Spectrum sensing for cognitive radio based on Kendall’s tau in the presence of non-Gaussian impulsive noise. Digit. Signal Process. 2022, 123, 103443. [Google Scholar]
- Zhiling, X.; Zhenya, Y. Radar Emitter Identification Based on Novel Time-Frequency Spectrum and Convolutional Neural Network. IEEE Commun. Lett. 2021, 25, 2634–2638. [Google Scholar]
- Chi, K.; Shen, J.; Li, Y.; Wang, L.; Wang, S. A novel segmentation approach for work mode boundary detection in MFR pulse sequence. Digit. Signal Process. 2022, 126, 103462. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, X. Multi-attribute overlapping radar working pattern recognition based on K-NN and SVM-BP. J. Supercomput. 2021, 1, 1–16. [Google Scholar]
- Qihang, Z.; Yan, L.; Zilin, Z.; Yunjie, L.; Shafei, W. Adaptive feature extraction and fine-grained modulation recognition of multi-function radar under small sample conditions. IET Radar Sonar Navig. 2022, 16, 1460–1469. [Google Scholar]
- Li, X.; Huang, Z.; Wang, F.; Wang, X.; Liu, T. Toward Convolutional Neural Networks on Pulse Repetition Interval Modulation Recognition. IEEE Commun. Lett. 2018, 22, 2286–2289. [Google Scholar] [CrossRef]
- Chen, W.; Chen, B.; Peng, X.; Liu, J.; Yang, Y.; Zhang, H.; Liu, H. Tensor RNN With Bayesian Nonparametric Mixture for Radar HRRP Modeling and Target Recognition. IEEE Trans. Signal Process. 2021, 69, 1995–2009. [Google Scholar] [CrossRef]
- Ruifeng, D.; Ziyu, C.; Haiyan, Z.; Xu, W.; Wei, M.; Guodong, S. Dual Residual Denoising Autoencoder with Channel Attention Mechanism for Modulation of Signals. Sensors 2023, 23, 1023. [Google Scholar] [CrossRef]
- Lutao, L.; Xinyu, L. Unknown radar waveform recognition system via triplet convolution network and support vector machine. Digit. Signal Process. 2022, 123, 103439. [Google Scholar]
- Xu, T.; Yuan, S.; Liu, Z.; Guo, F. Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sens. 2022, 14, 4468. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, X.; Zhou, H.; Lin, Y.; Shi, Q. SR2CNN: Zero-Shot Learning for Signal Recognition. IEEE Trans. Signal Process. 2021, 69, 2316–2329. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, D.; Zhou, M.; Lin, J.; Wang, X. Open-Set Signal Recognition Based on Transformer and Wasserstein Distance. Appl. Sci. 2023, 13, 2151. [Google Scholar] [CrossRef]
- Zheng, S.; Zhou, X.; Zhang, L.; Qi, P.; Qiu, K.; Zhu, J.; Yang, X. Towards Next-Generation Signal Intelligence: A Hybrid Knowledge and Data-Driven Deep Learning Framework for Radio Signal Classification. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 564–579. [Google Scholar] [CrossRef]
- Luo, J.; Si, W.; Deng, Z. New classes inference, few-shot learning and continual learning for radar signal recognition. IET Radar Sonar Navig. 2022, 16, 1641–1655. [Google Scholar] [CrossRef]
- Du, M.; Zhong, P.; Cai, X.; Bi, D. DNCNet: Deep Radar Signal Denoising and Recognition. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3549–3562. [Google Scholar] [CrossRef]
- Han, J.W.; Park, C.H. A Unified Method for Deinterleaving and PRI Modulation Recognition of Radar Pulses Based on Deep Neural Networks. IEEE Access 2021, 9, 89360–89375. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, D.; Sun, X.; Wang, F. Radar emitter recognition based on CNN and LSTM. In Proceedings of the 2021 International Conference on Neural Networks, Information and Communication Engineering, Qingdao, China, 27–28 August 2021; Volume 11933, p. 119331T. [Google Scholar]
- Shi, F.; Yue, C.; Han, C. A lightweight and efficient neural network for modulation recognition. Digit. Signal Process. 2022, 123, 103444. [Google Scholar] [CrossRef]
- Pan, Z.S.; Wang, S.F.; Li, Y.J. Residual Attention-Aided U-Net GAN and Multi-Instance Multilabel Classifier for Automatic Waveform Recognition of Overlapping LPI Radar Signals. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4377–4395. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Chapter 28. pp. 234–241. [Google Scholar]
- Pan, J.; Zhang, S.; Xia, L.; Tan, L.; Guo, L. Embedding Soft Thresholding Function into Deep Learning Models for Noisy Radar Emitter Signal Recognition. Electronics 2022, 11, 2142. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.N.; Girshick, R.; Dollar, P.; Tu, Z.W.; He, K.M. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 30th Ieee Conference on Computer Vision and Pattern Recognition (Cvpr 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 5987–5995. [Google Scholar]
- Yu, H.H.; Yan, X.P.; Liu, S.K.; Li, P.; Hao, X.H. Radar emitter multi-label recognition based on residual network. Def. Technol. 2022, 18, 410–417. [Google Scholar]
- Dadgarnia, A.; Sadeghi, M.T. Automatic recognition of pulse repetition interval modulation using temporal convolutional network. IET Signal Process. 2021, 15, 633–648. [Google Scholar] [CrossRef]
- Du, X.; Sun, Y.; Song, Y.; Sun, H.; Yang, L. A Comparative Study of Different CNN Models and Transfer Learning Effect for Underwater Object Classification in Side-Scan Sonar Images. Remote Sens. 2023, 15, 593. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Jie, H.; Li, S.; Samuel, A.; Gang, S.; Enhua, W. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 7132–7141. [Google Scholar]
- Feng, H.C.; Tang, B.; Wan, T. Radar pulse repetition interval modulation recognition with combined net and domain-adaptive few-shot learning. Digit. Signal Process. 2022, 127, 103562. [Google Scholar] [CrossRef]
- Hui, L.; Dong, J.W.; Dong, L.H.; Wei, C.T. Work Mode Identification of Airborne Phased Array Radar Based on the Combination of Multi-Level Modeling and Deep Learning. In Proceedings of the 35th China Command and Control Conference, Yichang, China, 20–22 May 2023; pp. 273–278. [Google Scholar]
- Skolnik, M.I. Radar Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Limin, G.; Xin, C. Low Probability of Intercept Radar Signal Recognition Based on the Improved AlexNet Model. In Proceedings of the 2nd International Conference on Digital Signal Processing, Tokyo, Japan, 25–27 February 2018. [Google Scholar]
- Goswami, A.D.; Bhavekar, G.S.; Chafle, P.V. Electrocardiogram signal classification using VGGNet: A neural network based classification model. Int. J. Inf. Technol. 2022, 15, 119–128. [Google Scholar] [CrossRef]
- Tian, T.; Zhang, Q.; Zhang, Z.; Niu, F.; Guo, X.; Zhou, F. Shipborne Multi-Function Radar Working Mode Recognition Based on DP-ATCN. Remote Sens. 2023, 15, 3415. [Google Scholar] [CrossRef]








| Working Mode | PRI (us) | PW (us) | Duty Ratio (%) | Pulse Num in CPI | Bandwidth (MHz) | Modulation |
|---|---|---|---|---|---|---|
| VS | 3.3∼10 | 1∼3 | 10∼30 | 500∼2000 | 0.3∼10 | Consatnt |
| RWS | 3.3∼10 | 1∼3 | 10∼30 | 500∼2000 | 0.3∼10 | D&S |
| VRS | 50∼165 | 1∼20 | 1∼25 | 30∼256 | 1∼10 | Constant, D&S |
| MTT | 3.3∼125 | 0.1∼20 | 0.1∼25 | 1∼64 | 1∼50 | Stagger, Sliding |
| BR | 3.3∼125 | 0.1∼20 | 0.1∼25 | 1∼64 | 1∼50 | Wobbulated |
| GMTI | 120∼500 | 2∼60 | 0.1∼25 | 20∼256 | 0.5∼15 | Stagger |
| GMTT | 62∼160 | 2∼40 | 0.1∼25 | 20∼256 | 0.5∼15 | Stagger |
| SSS | 1000∼2000 | 1∼200 | 0.1∼10 | 1∼8 | 0.2∼500 | Stagger |
| SST | 500∼1000 | 1∼200 | 0.1∼20 | 20∼256 | 0.2∼10 | Stagger |
| SAR | 100∼1000 | 3∼60 | 1∼25 | 70∼20,000 | 10∼500 | Constant |
| AlexNet | ConvNet-18 | ResNet-18 | VGGNet |
|---|---|---|---|
| 96.9% | 90.7% | 90.5% | 99.7% |
| Model | Lost Pulse Ratio (%) | False Pulse Ratio (%) | Process Time (s) | Model Capacity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | 0 | 10 | 20 | 30 | 40 | 50 | |||
| AlexNet | 70.4 | 70.3 | 76.4 | 81.5 | 88.1 | 90.2 | 70.9 | 83.6 | 90.7 | 93.2 | 95.0 | 93.6 | 2.42 | 520 K |
| ConvNet-18 | 65.2 | 73.5 | 76.6 | 82.8 | 92.1 | 88.3 | 65.2 | 66.8 | 71.3 | 77.3 | 86.9 | 86.1 | 11.46 | 954 K |
| ResNet-18 | 79.1 | 84.2 | 87.7 | 89.3 | 89.4 | 87.5 | 79.1 | 85.6 | 90.3 | 90.2 | 88.4 | 86.1 | 11.93 | 1110 K |
| VGGNet | 68.0 | 92.3 | 88.7 | 82.8 | 81.7 | 80.1 | 68.1 | 89.2 | 88.2 | 86.9 | 84.7 | 80.3 | 9.15 | 1680 K |
| MSCANet | 98.4 | 97.8 | 97.5 | 97.1 | 96.2 | 94.3 | 98.4 | 97.8 | 97.1 | 95.4 | 93.7 | 92.1 | 14.50 | 849 K |
| Model | Noise Estimation | GC | GA | Accuracy |
|---|---|---|---|---|
| 1 | √ | √ | √ | 96.9% |
| 2 | × | √ | √ | 83.3% |
| 3 | √ | × | √ | 85.0% |
| 4 | √ | √ | × | 84.4% |
| 5 | × | × | × | 78.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, J.; Pan, J.; Du, M. A Cascade Network for Pattern Recognition Based on Radar Signal Characteristics in Noisy Environments. Remote Sens. 2023, 15, 4083. https://doi.org/10.3390/rs15164083
Xiong J, Pan J, Du M. A Cascade Network for Pattern Recognition Based on Radar Signal Characteristics in Noisy Environments. Remote Sensing. 2023; 15(16):4083. https://doi.org/10.3390/rs15164083
Chicago/Turabian StyleXiong, Jingwei, Jifei Pan, and Mingyang Du. 2023. "A Cascade Network for Pattern Recognition Based on Radar Signal Characteristics in Noisy Environments" Remote Sensing 15, no. 16: 4083. https://doi.org/10.3390/rs15164083
APA StyleXiong, J., Pan, J., & Du, M. (2023). A Cascade Network for Pattern Recognition Based on Radar Signal Characteristics in Noisy Environments. Remote Sensing, 15(16), 4083. https://doi.org/10.3390/rs15164083






